A model with environmental stochasticity and alternative stable states reproduces variability in the human gut microbiome.
Abstract
The most fundamental questions in microbial ecology concern the diversity and variability of communities. Their composition varies widely across space and time, as a result of a nontrivial combination of stochastic and deterministic processes. The interplay between nonlinear community dynamics and environmental fluctuations determines the rich statistical structure of community variability. We analyze long time series of individual human gut microbiomes and compare intra- and intercommunity dissimilarity under a macroecological framework. We show that most taxa have large but stationary fluctuations over time, while a minority of taxa display rapid changes in average abundance that cluster in time, suggesting the presence of alternative stable states. We disentangle interindividual variability in a stochastic component and a deterministic one, the latter recapitulated by differences in carrying capacities. Last, by combining environmental fluctuations and alternative stable states, we introduce a model that quantitatively predicts the statistical properties of both intra- and interindividual community variability, therefore summarizing variation in a unique macroecological framework.
INTRODUCTION
Microbial communities are the prototypical complex, high-dimensional, ecosystems. Their diversity is astonishing and occurs at all scales, with many taxa coexisting in each community and many strains within each taxon. Their dynamics is driven by mechanisms operating at all temporal scales (1, 2): Gut microbiota composition changes in response to diet or other external stimuli on a daily basis (3), and with aging through the course of a lifetime (4, 5). Similarly, multiple processes determine the variation in composition across hosts, ranging from behavioral (6) to genetic factors (7).
This high-dimensional complex space of variation in community composition might conceal low-dimensional structures. For instance, it has been proposed that community compositions, when compared across hosts, cluster in a few discrete enterotypes characterized by specific taxa (8, 9) as the result of life history characteristics. These clusters are thought to correspond to different functional properties, for instance, summarized in the enrichment of different metabolic pathways (8). Their existence and biological significance are not broadly accepted. There is evidence that inter-host variation of gut community composition is continuous, with the existence of discrete types being only apparent as a result of statistical artefacts (10).
The existence of discrete clusters in community composition also concerns intra-host variability. The fluctuating composition of a host’s community might also cluster around several alternative compositions. The long autocorrelation times make it particularly challenging to formulate robust statistical methods to infer enterotypes (11).
Whether variation is discrete or continuous has important practical consequences. For instance, if cluster exists, they could provide a biomarker of health conditions and target for clinical purposes (9, 10). Beyond the health-related applications, there are important conceptual consequences. The existence of enterotypes would be an evidence that the dynamics of gut microbial communities results in alternative stable states, which appear as a consequence of the interplay between dynamics and environmental forcing.
Understanding mechanistically the properties of microbial communities is especially difficult. Realistic mechanistic models are very complex due to their high dimensionality; therefore, it is difficult to characterize the structure of their dynamic attractor in a simple way that allows to make a connection between mechanisms and observable properties of the community. This represents one of the main challenge to understand quantitatively and mechanistically the properties of microbial communities.
Macroecology, which focuses on the statistical patterns of community composition, offers a promising strategy to characterize quantitatively microbial communities. Recent works have characterized the macroecological patterns of community composition (12, 13). Under the macroecological lens, community dynamics is characterized by large and rapid fluctuations with robust and reproducible statistical properties (14–16). These regular patterns are well described by the stochastic logistic model (SLM) with environmental noise, which assumes that fast environmental fluctuations perturb abundances around a taxa-specific carrying capacity (15, 16).
Here, we study the intra-host dynamics and inter-host variability under a unique macroecological framework using the time series of 14 individuals. We show that most of the taxa display stationary dynamics over the duration of the time series (11), with rapid fluctuations around a constant carrying capacity, as predicted by the SLM. The nonstable taxa are characterized by discrete shifts of the carrying capacity, which occur coordinately in time for several taxa. This suggests that the change of community composition in time proceeds by discrete changes of the carrying capacities. Notably, differences in carrying capacity are also what explain the variability across hosts, in combination with independent stochastic fluctuations. We finally show that both the intra-host and inter-host variability can be quantitatively captured by an SLM modified to include the existence of alternative stable states.
RESULTS
Characterizing long-term community dynamics with dissimilarity
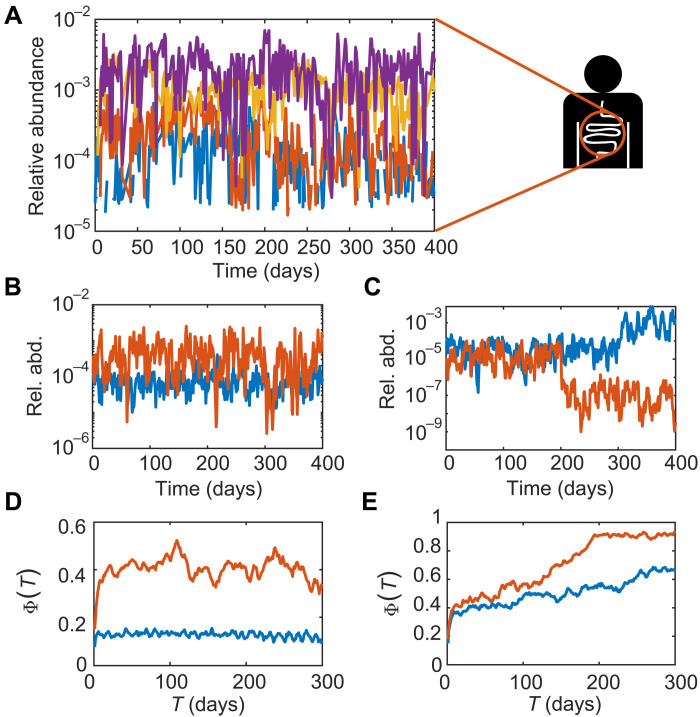
The relative abundances of operational taxonomical units (OTUs) within a community have wide fluctuations in time (see Fig. 1A). In this context, we may ask whether the difference in community composition in two snapshots of the same community at different times is only due to wide but stationary fluctuations or if, instead, the composition changes in time. In the first scenario, abundances would fluctuate around constant averages, with constant amplitudes (Fig. 1B). In the second scenario, average abundances would change in time, either continuously or discretely (Fig. 1C), possibly due to jumps between alternative stable states. We can discriminate between the two scenarios by looking at a dissimilarity measure quantifying how the abundance of each OTU changes over a given time lag T. Let us call this dissimilarity Φ(T) (see Materials and Methods). In the first scenario (Fig. 1D), Φ(T) for each OTU would show an initial increase, over the short time scale of relaxation to stationarity, and then would reach a plateau at the level of self-dissimilarity of a fluctuating random variable, which depends on the amplitude of the fluctuations. In the second scenario (Fig. 1E), instead, the dissimilarity would continue to increase over longer time scales because of the abundance getting more and more different from its past self.
Fig. 1. Characterizing long-term community dynamics with dissimilarity.
(A) Examples of relative abundance trajectories with wide short-term fluctuations. (B) Relative abundance trajectories with carrying capacity and noise intensity constant in time. (C) Relative abundance trajectories with carrying capacity changing in time and constant noise intensity. (D) Dissimilarity Φ(T) for varying lag T for the abundance trajectories in (B). (E) Dissimilarity Φ(T) for varying lag T for the abundance trajectories in (C).
Within-individual dissimilarity displays two long-term behaviors
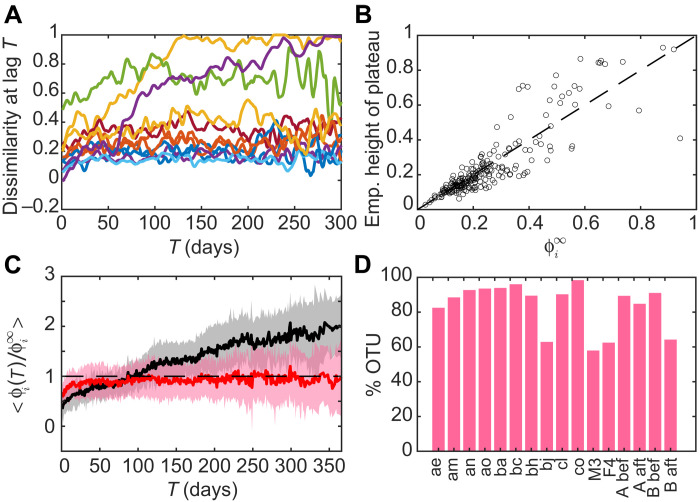
We analyzed the time series of 14 individuals’ gut microbial communities from three different datasets (see Materials and Methods). In each time series, we compute the dissimilarity Φi(T) for each OTU according to a dissimilarity measure that is not subject to the bias introduced by random sampling of the community (see Materials and Methods). Examples of curves Φi(T) obtained for some OTUs are plotted in Fig. 2A. Both the short-time and long-time behaviors appear to differ widely between OTUs. To assess the significance of these behaviors, we compare them with what is expected from a null model.
Fig. 2. Dissimilarity indicates that most OTUs have stationary dynamics, but a minority has nonstationary behavior.
(A) Examples of Φi(T) curves of individual OTUs. (B) Scatter plot of the theoretical prediction for the asymptotic value of Φi(T) for an OTU with noise intensity σ against , the empirical average value of Φi(T) for T > 10 days, for individual “bh.” The 1:1 line is plotted as reference. (C) Average of Φ(T)/Φ∞ over OTUs, where it is classified as flat (red curve) and increasing (black curve), for individual “bh.” Shaded areas represent one SD interval. (D) Percentage of OTU whose Φ(T)/Φ∞ is classified as flat in each individual.
The SLM with environmental noise (17) (see Materials and Methods) is known to describe the fluctuations of population abundance and has been recently shown to reproduce several statistical properties of abundance fluctuations of microbial species (15, 16). In particular, it predicts that the distribution of fluctuations at stationarity is a gamma distribution (17), which depends on two parameters: Ki, the carrying capacity appearing in the SLM, and σi, which can be interpreted as the amplitude of environmental noise. These two parameters depend on the identity of OTU i. The noise σi can be expressed in terms of the coefficient of variation of abundances. As a consequence, Taylor’s law on abundance fluctuation with exponent 2 (16) implies that σi and Ki are not correlated across OTUs.
Assuming that the abundance dynamics follows the SLM with parameters that remain constant in time, Φi(T) has an initial increase and then reaches a plateau. The height of this plateau can be computed analytically as the expected value of Φi(T) for large T by taking the abundances of the OTU at lag T ≫ 1 as independent gamma random variables with the same parameters (see Materials and Methods). This analytical expectation depends only on the parameter σi, which can be directly estimated from the data (see Materials and Methods). Figure 2B shows that this expected value correlates well across OTUs with the empirical height of the plateau, measured as the mean of Φi(T) over all T > 10 days.
According to the SLM, when normalized by , all the individual curves Φi(T) should have a plateau at 1. Therefore, if the empirical normalized dissimilarity curve of an OTU has a plateau at 1, it means that for that OTU, the level of dissimilarity at large time lags is consistent with stationary fluctuations of abundance. The abundance dynamics of these OTUs can be reproduced with an SLM with constant parameters over the observed time interval (ranging from 6 months to 1.5 years for the analyzed individuals). This behavior is what we observe for most OTUs in each individual.
We classified the normalized dissimilarity curves as either “flat” (if they plateau after the initial transient) or “increasing” (if they keep increasing; see Materials and Methods) and computed the average curves within the two categories (Fig. 2C). The average of the flat curves (red line) reaches a plateau of 1, indicating that the OTUs falling in this group have a stationary abundance dynamics. These stable OTUs are the majority, representing on average 84% of the total in each individual (Fig. 2D). Other OTUs do not reach a plateau, and their normalized dissimilarity grows over all the observed time interval, exceeding the expected value 1 (black line in Fig. 2C). For these OTUs, the dissimilarity grows above the value expected for stationary abundance dynamics.
These results show that a large part of the OTUs in a gut microbial community fluctuates around a stable average composition on a ∼1-year time scale, while a smaller fraction has a nonstationary behavior. We explore more carefully the properties of nonstationary OTUs in the next section.
It is important to mention two potential caveats to this analysis to correctly interpret its results. First, a flat dissimilarity for large times is consistent with stationarity but does not imply it. For instance, the average and variance of the fluctuations could change over time in a coordinated way to produce a constant dissimilarity over sufficiently large lags. While this is possible, further analyses explained below show that this is not the case. Second, and more important, the flatness of dissimilarity is always shown over a finite time interval. This means that the behavior of the corresponding OTU is consistent with the SLM with constant parameters over that interval, but it does not exclude that parameters could change over longer time scales.
Nonstationary OTUs are characterized by transitions between alternative values of the carrying capacity
If the abundance evolves according to the SLM with constant parameters, the dissimilarity Φ(T) reaches a plateau Φ∞ determined by σ. The dynamics of nonstationary OTUs, for which we observe an increasing Φ(T), could potentially still be described by the SLM with time-dependent parameters Ki(t) and σi(t), which change on the time scales of months or years.
Two paradigmatic behaviors could describe the time dependency of parameters. The first is a slow variation of the parameters, where Ki(t) and/or σi(t) change steadily over time. The second one corresponds to rapid transitions to different values of parameters spaced out by time windows where parameters are constant. These represent two extreme cases, and a mixture of the two could also describe the time dependency of parameters.
A visual inspection of the abundance time series of nonstable OTUs shows that in many cases there is a sudden jump in the relative abundance (see fig. S6, A and B) that can be interpreted as a jump in the carrying capacity K, suggesting that the second scenario might apply.
We introduced therefore a method, based on a quantity related to the Kullback-Leibler divergence, to detect jumps of K in a noisy time series (see Materials and Methods). By applying this method, we can identify, for each individual, which OTUs present jumps in their carrying capacity K. On average, 54% of OTUs with increasing slope display sudden jumps in their carrying capacity K. For 10 of 16 time series, OTUs with jumps of K are overrepresented among OTUs with increasing Φi(T) (P <0.05 according to a hypergeometric test; see fig. S6C and table S1). Cases where Φi(T) is increasing but no jump of K is detected can be due to noise in the estimate of Φi(T) or to jumps falling below the detection threshold of our method. There are also cases where a jump in K is detected but Φi(T) is flat. These are either cases where the change in K is short-lived or where the jump is small. Changes in K would affect the value of Φi(T) only if they are detectable with respect to the everyday abundance fluctuations. Examples of all these cases are shown in fig. S8.
Most OTUs displaying nonstationary dynamics are therefore associated with rapid jumps between alternative values of K. These sudden jumps are not randomly distributed over the time span of the time series. We observe that, for individuals where several OTUs have jumps in K, the times where transitions happen are localized at specific times (see fig. S9). This clustering of transitions suggests that either jumps in K are driven by external conditions that affect multiple OTUs at the same time or that the interactions between species cause multiple species to transition synchronously. A taxonomic analysis revealed no particular taxonomic enrichment among nonstationary OTU, suggesting that OTUs have a similar likelihood of jumping between states.
The dynamics of OTU abundance within an individual is therefore characterized by two main time scales: a short time scale corresponding to rapid fluctuations, which are described by the noise term appearing in the SLM, and a larger time scale that characterizes the frequency of the transition between alternative values of K.
Dissimilarity between individuals is quantitatively reproduced by a combination of stochastic fluctuations and different carrying capacities
Within an individual, we found that similarity is determined by rapid fluctuations around a constant composition and by occasional sudden jumps of the carrying capacity. It is well known that some host-specific features of microbiome composition remain stable for years (18, 19). In this context, we now investigate the dissimilarity between individuals to quantify the role of different sources of variation. In particular, we aim at disentangling the contribution of stochastic effects that are independent in the two individuals from that of reproducible differences between them. Under our framework, the stochastic aspects correspond to the rapid fluctuations of abundance, which are statistically independent between hosts. The deterministic factors correspond instead to different parameters K and σ that characterize the dynamics of each OTU in different hosts.
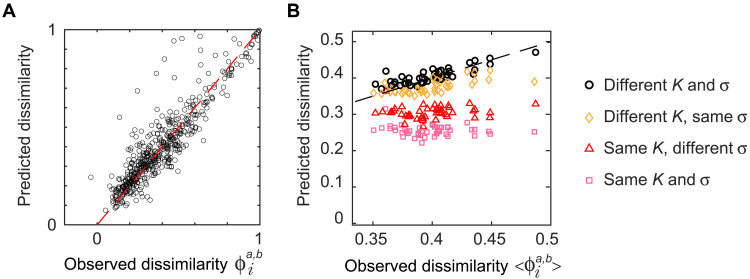
To quantify the importance of the two causes of dissimilarity, we compare the empirical dissimilarity with that predicted by the SLM under different hypotheses on the sources of variation that are present. For each OTU i, we compute the empirical dissimilarity between two individual a and b averaged over all lags T, . We then consider a first null model that includes both sources of variation: The dynamics of OTU i is described by the SLM with different parameters in the two individuals a and b, (, ) and (, ), which are estimated using the full-time series (see Materials and Methods). The difference in these parameters between the individuals aims at capturing the host-specific factors that determine community composition. The rapid fluctuations are instead determined by the stochastic term in the SLM. In Materials and Methods, we obtain an analytical prediction for the dissimilarity , which matches the empirical value with high accuracy (Fig. 3A and fig. S10). This result implies that the host-specific aspects of community composition can be effectively captured in the variability of the parameters K and σ.
Fig. 3. Dissimilarity between individuals is explained by independent stochastic fluctuations and differences in carrying capacities.
(A) Comparison of the observed dissimilarity of OTU i between the two individuals “am” and “bh,” with its theoretical expected value computed with the individual parameters estimated for each individual. Each point represents an OTU. (B) Comparison between the average over OTUs of the empirical dissimilarity between individuals a and b, , with its theoretical expected value computed using either the individual parameters estimated for each individual or the same parameters for both individuals (see legend). In the latter case, the parameters are set to the average of the individuals’ parameters. Each point corresponds to a pair of individuals from the same dataset. The 1:1 line is shown as reference.
To assess how much of the dissimilarity is due to the difference in K and σ between the two individuals and how much to the stochastic abundance fluctuations, we consider a hierarchy of four null models, which differ in whether K and/or σ vary between hosts. Figure 3B compares the predictions of these four null models with the dissimilarity averaged across OTUs.
The simplest scenario of the four is the one where the predicted dissimilarity between individuals is only due to stochastic effects, i.e., K and σ do not differ between individuals. Figure 3B shows that stochastic effects alone—as expected—do not fully explain the dissimilarity between individuals. They are nevertheless the main contributor to the variability between individuals, capturing on average 72% of it (see also fig. S11).
Consistent with what is shown in Fig. 3A for individual OTUs, Fig. 3B also shows that considering the empirical variability of both K and σ across hosts fully captures the empirical dissimilarity. On the other hand, K and σ do not contribute equally to dissimilarity. Considering only the variation of σ, while keeping K constant across hosts, performs only slightly better than the model with only stochasticity, as it explains on average 84% of the dissimilarity. On the opposite, keeping σ fixed, while K is allowed to vary across host, predicts much better the observed dissimilarity, with an average 96% accuracy.
These results imply that the difference in community composition between individuals can be explained by considering the combination of independent stochastic effects, as modeled by the SLM, and deterministic factors. The latter can be captured by differences in the carrying capacity Ki of OTUs in the two hosts.
The SLM with alternative stable states reproduces inter- and intra-host variability
The parallel between the long-time dynamics within an individual, characterized by discrete transitions of the carrying capacity K, and the difference between individuals, whose deterministic part is largely determined by differences in the carrying capacity, suggests the possibility to formulate a dynamical model capturing both.
We assume that each OTU has a characteristic, host-independent, value of the carrying capacity, . Within an individual, the actual carrying capacity of an OTU at a given time is , where ζ is a Lognormal random variable with average 1. The value of the carrying capacity is kept constant over time, until a transition happens to a new value obtained by drawing a new value of the random variable ζ. Similarly, the values of the carrying capacity in two different individuals are obtained with the same model by considering independent realizations of the random variable ζ. This model aims at capturing the statistical properties of the values of Ki, within and across hosts. The strong assumption is that the fluctuations within and across hosts can be captured under the same framework.
Important free parameters of this model are the variances of the random variable ζ, which determine how much Ki varies over time and across hosts. In the Supplementary Materials, we estimate empirically the values of the variance of ζ across hosts for each individual OTU. The results show that the variances do not differ much across OTUs and are statistically compatible (see fig. S4). We therefore choose the variance of ζ to be OTU independent, obtaining a model with no free parameter, as both the s and the variance of ζ can be estimated directly from the data.
To test whether this model can reproduce the statistical properties of the dynamics within an individual and the differences between individuals, we used it to simulate the abundance time series of each individual and compared the results with those obtained from the empirical time series.
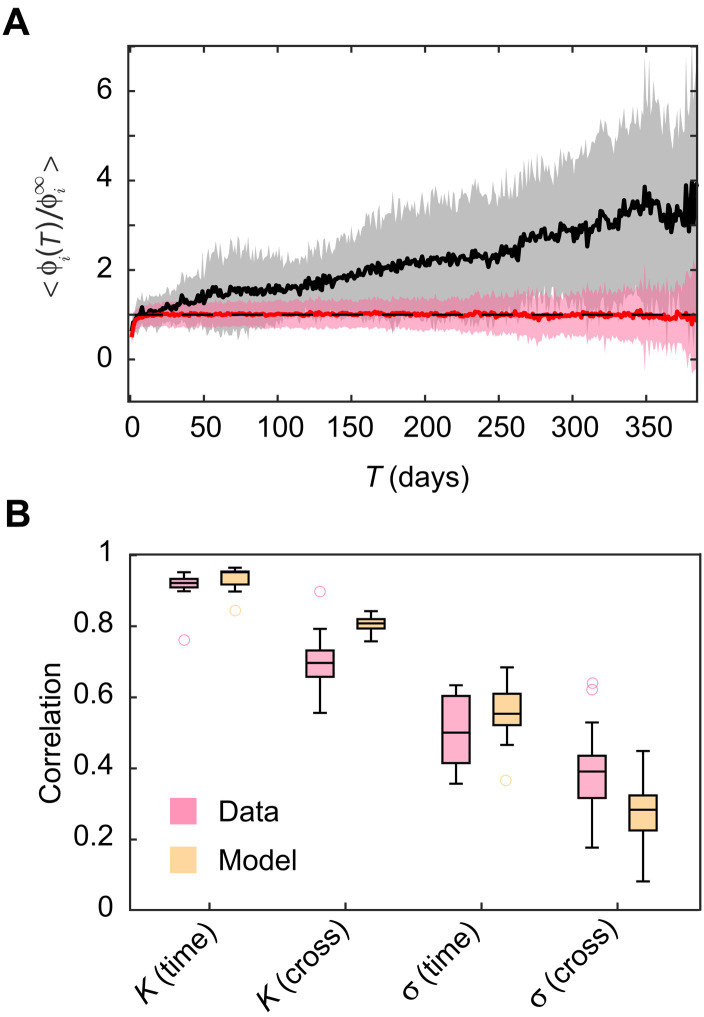
We simulated the abundance time series of each individual according to an SLM with carrying capacity that jumps according to a Poisson process and assumes new values according to the model described above (see Materials and Methods). Repeating on these simulated data the analysis performed on empirical data, we find that the intraindividual dissimilarity behaves very similarly to the empirical one (Fig. 4A). Moreover, by fixing for each individual the average number of OTUs for which a jump happens in the observation window according to the empirical observations, the percentages of OTUs with increasing dissimilarity are similar to the empirical ones (see fig. S13).
Fig. 4. A model with stochastic fluctuations and discrete jumps of the carrying capacity reproduces the statistical properties of the dynamics within one individual and the difference between individuals.
(A) Equivalent of Fig. 2C obtained from time series simulated according to an SLM model with jumps in K (see text for details). (B) Correlation of the parameters K and σ in time (between two halves of a time series) and between pairs of individuals from the same dataset, according to the data and to the simulated time series. For K, which ranges over several orders of magnitude, we compute the correlations of log(K) to avoid the correlation being dominated by a few points with large K.
The analysis of dissimilarity between hosts reveals that it can be fully captured by considering the difference in the values of K and σ. We therefore consider the correlation of these two parameters within hosts (for two separate windows of time) and across hosts as a relevant statistical feature of the dynamics that our model should reproduce. Figure 4B reports the empirical values of the correlations (see also fig. S14). In agreement with what we found previously, the carrying capacities are more correlated within host than between, indicating that their values contribute substantially to the dissimilarity between individuals. On the other hand, the values of σ are much less correlated within individuals and their correlation does not differ greatly between and within hosts, in agreement with the observation that variability in σ does not contribute much to dissimilarity across individuals. Therefore, these correlations fully summarize the results of Fig. 3B.
The model accurately predicts all the correlations, both within and between individuals. The correlation of K within a host is correctly reproduced to be higher than the correlation across hosts. This happens because of the fact that over the time scale of the empirical time series only a small fraction of the OTUs change their carrying capacity in the model. Therefore, when comparing two samples from the same host, most OTUs have the same carrying capacity, while when comparing two samples from different hosts, all of them have different carrying capacities. The model also captures the lower correlations between the noise intensities σ, even if it does not include variability of σ as an explicit ingredient, implying that differences in σ, both between individuals and within, are simply due to noise in their statistical estimates. The model is therefore able to fully capture both the variability of individuals over long periods of time as well as differences across individuals.
In light of this model, we can say that the OTUs that we were calling stationary, when observed on a time scale of ∼1 year, are actually in a transient state of this compound process (which is the stable state of an SLM with fixed carrying capacity). Given that the average time between two jumps of the carrying capacity that we estimated for each individual (see Materials and Methods) is ∼1000 days, the compound process only reaches stationarity over longer time scales (fig. S5).
DISCUSSION
We considered long time series of human gut microbiome communities from several individuals and analyzed the similarities in composition within and between individual hosts. We were able to accurately predict, under a unique quantitative modeling framework, the statistical properties of the similarities both within and between individuals.
Previous studies analyzing intra- and interindividual variation in the human gut microbiome consistently found stability in the microbiome over time at time scales of months or years and higher similarity within individuals than between individuals (11, 18–21). These studies used several similarity measures to compare communities, e.g., Jaccard index, Bray-Curtis dissimilarity, or Pearson correlation. Other studies used autocorrelation (11) or mean square displacement (14) of abundance time series to investigate the long-term behavior of single OTUs. The dissimilarity measure we use is akin to the latter approach in that it evaluates how dissimilar a single abundance time series becomes from its past values. However, our method offers two advantages. First, it corrects for sampling bias, disentangling the dissimilarity due to different community composition from that due to random sampling, an issue often overlooked. Second, we can make exact analytical predictions of its long-term behavior and value according to a well-supported model of abundance dynamics. This allows us to distinguish OTUs that are stationary from those that are not, and to dissect the different contributions of particular OTUs to interindividual dissimilarity.
Within an individual, we find that most OTUs are characterized by statistically stable dynamics, in agreement with previous findings (11). Abundances fluctuate around a value constant in time, with constant amplitude. For these OTUs, the long-term dissimilarity is due to rapid stochastic fluctuations, and its value is determined by the amplitude of such fluctuations. The SLM with constant parameters predicts correctly the time dependence and the asymptotic value of dissimilarity for these OTUs based on the noise intensity σ estimated from the time series. A consistent minority of OTUs have a dynamics characterized by processes happening on two distinct time scales. Beyond the wide daily fluctuations, they have large abrupt transitions in their abundance. Their dynamics are therefore nonstationary, and their dissimilarity increases in time beyond the value predicted for a stationary time series. These observations show that both the amplitude of the fluctuations of each OTU and the proportion of nonstationary OTUs contribute to determine the overall dissimilarity of an individual’s gut community over time, which we can think of as the average of the dissimilarities of all OTUs. The overall dissimilarity is therefore a complex quantity to interpret, while our OTU-based approach provides a more detailed understanding of the underlying dynamics.
Our findings of sudden changes in composition over long time scales at the OTU level parallel those of (22) at the strain level. Looking at the time scales of evolution in gut microbial communities, they find that strains evolve slowly over short time scales but are replaced by different, related strains on time scales of >6 months.
The large transitions observed in nonstationary OTUs can be effectively captured in changes of the typical abundance around which they are fluctuating. In the SLM framework, these transitions correspond to a change in the value of the carrying capacity. The nonstationary aspects of OTU dynamics can therefore be fully described by switches between alternative values of the carrying capacity.
Moreover, the timing of the jumps between alternative values is strongly correlated across OTUs, with windows of times where the carrying capacity of several OTUs switches and others where the dynamics is overall stationary. The natural explanation to these clustered rapid transitions is the existence of alternative stable states, which differ in the carrying capacities of a small subset of OTUs. They could be intrinsic to the dynamics, and driven by stochasticity, or could correspond to important changes in the environmental conditions (e.g., travel or change of diet) with big impact on community composition. Our approach is explicitly agnostic on the mechanism behind the alternative stable state, revealing instead their regular statistical features.
The SLM we used to describe the dynamics comprises an autoregressive and a non-autoregressive term. The importance of these two components in gut microbial dynamics is quite debated (11, 23). In the context of the SLM, the parameter σ measures the relative importance of the non-autoregressive part of the dynamics. Estimates of this parameter, corrected for the sampling bias, show that it is heterogeneous across OTUs (fig. S1) and independent of the carrying capacity (16).
The comparison between individuals revealed that most of their dissimilarity is due to the independent stochastic fluctuations of abundances. The remaining dissimilarity, due to deterministic differences between individuals, is almost completely explained by differences in the carrying capacities of OTUs. The emerging picture indicates that the gut communities of different individuals fluctuate around states with compositions that are correlated (carrying capacities have a moderate to high correlation across individuals) but different.
The observation that both the changes within an individual on the time scale of months and the differences between individuals are explained by differences in the carrying capacities motivated our model, joining the dynamics of the SLM with transitions in the carrying capacity. The model predicts quantitatively, under a unique framework, the statistical properties of within-individual dynamics and between-individual differences.
The model is a composition of SLM processes with different carrying capacities, which switch according to a Markov process. In the case of a finite state space, the process is mathematically well posed. It corresponds to a subcase of the switched Markov process studied in (24), which has a set of desirable properties: The population does not go to extinction with probability 1, and it admits a stationary distribution with finite variance. Here, we consider continuous values of carrying capacity, for which rigorous mathematical results regarding stationarity do not exist. While a sufficiently large finite state space of carrying capacity values would be indistinguishable from the continuous case from a practical point of view, showing the well posedness of the latter case represents an interesting mathematical challenge. A more in-depth discussion can be found in section S9.
Our models assume the existence of a universal dynamics of gut microbiome (25), where all individuals are characterized by the same parameters of the dynamics, σi and , and differences between individuals are uniquely determined by which dynamical alternative stable state they occupy and by random fluctuations of abundances. Such a universal dynamics necessarily creates a parallel between within-host dynamics and between-host properties, which we unveiled under our modeling framework.
On the time scale of the empirical time series that we considered (≈1 year), we are able to reproduce the difference in magnitude between intra- and interindividual variability under this assumption. This suggests that, at least over this time scale, the relevant element to capture the difference across hosts and the dynamics within a host is the jumps of carrying capacities between different values, which are distributed around a mean common to all hosts. It is important to note that on time scales much longer than the average time between two jumps of the carrying capacity, this assumption would imply that an individual eventually becomes as different from her/his past self as from another individual. This is a strong implication that is worth discussing and comparing with empirical evidence. Many previous works that found that intraindividual dissimilarity is significantly smaller than interindividual dissimilarity consider relatively short time scales, ranging from 2 to 10 months (26–28). Over these time intervals, our model agrees with these empirical observations. The average time between two jumps of the carrying capacity that we estimated in the individuals of our datasets varies between 2 years to more than 5 years. This implies that the intraindividual dissimilarity would equal the interindividual one only after several years.
To our knowledge, there are two studies that consider longer time intervals (18, 19). In (18), intervals from 2 months to 8 years are considered. The intraindividual similarity declines as the interval increases, and after 8 years, it is close to the interindividual one. This behavior qualitatively agrees with our model. Faith et al. (19), instead, obtain that after almost 6 years intraindividual similarity is still significantly larger than the interindividual one. Interpolating the decrease of similarity with time lag as a power-law, the authors conclude that the intraindividual similarity will remain larger than the interindividual one for decades. In summary, previous literature does not give a clear-cut picture of how intra- and interindividual dissimilarities compare in the very long term.
Very likely host genetics and other persisting characteristic have, even if small, detectable effects on microbiome composition in the long term, which cause persisting difference across hosts. Our model is relevant also in this scenario. We can speculate that this persisting difference corresponds to the existence of the different states between which the carrying capacity jumps that are not exactly the same for all individuals. In the model, this could be translated into the fact that the values are not exactly the same for all individuals. They must, however, be similar; otherwise, we would not observe a high correlation between the values of K across individuals. In this scenario, therefore, our assumption that all individuals are described by the same is not adequate to describe time scales much longer than the typical times between two jumps of the carrying capacity, and it should be modified to accommodate individual differences.
Irrespective to the existence of these differences, our model shows that the dynamics of gut microbiome unfolds on at least two time scales. On the time scale of hours or a few days, community composition responds to fast environmental fluctuations. These fluctuations act as perturbation to a resilient community, whose dynamics is governed by the fast population processes of birth and death (16). It is important to note that the typical time scale of these rapid fluctuations is shorter (or at most equivalent) to these population processes, of the order of a few hours. The resilient community states are, however, stable only transiently. Over months and years, these community states change, often abruptly and discontinuously.
The presence of these transient states could be explained, both mathematically and biologically, in different ways. They could be true alternative stable states, as defined in nonlinear dynamics. The nonlinearity of the community dynamics could determine the existence of multiple stable states, with their own basin of attraction, which determines different attractors depending on the initial conditions. The presence of constant perturbations (environmental but also due to demographic stochasticity or migration) could produce stochastic transitions between alternative states. The existence of alternative stable states is not rare or particularly notable. For instance, consumer-resource model with nonsubstitutable resources displays multistability (29). Alternative stable states have also been observed experimentally in simple microbial communities (30–32), where the community state can switch from one to another, e.g., due to a transient invading species (31) or due to the environmental noise.
In the presence of alternative stable states, the typical time scale associated with the transitions would depend on the relation between the magnitude of perturbations and the size of the basins of attraction. In this respect, the time scale of months or years measures the rate at which a sequence of perturbation drives the system to another basin of attraction. It is important to note that this is the product of environmental (or other) perturbations occurring at a much faster rate. Another explanation is that we are seeing a succession of quasi-stable states because of long transients in the dynamics (33). Long transients could arise because of several possible mechanisms, for example, they are likely to be present in high-dimensional complex dynamical systems, as a result of the many tangled interactions and the presence of several time scales. They might also arise in the presence of bifurcations, when tipping points are reached after a slow change of the environmental variables. In this case, the time scale of months and years would directly correspond to the existence of population and/or environmental variables (e.g., dietary changes) evolving over those time scales. Both of these scenarios (alternative stable states with stochastic switching and long transients in the dynamics) are possible. Our model sets the basis to distinguish between the two.
The next step is to understand how these transient states emerge from the dynamics. In this regard, an important factor would be to include species correlations in the modeling and understand their structure (11, 34). In the setting of this work, the correlation between OTUs is not accounted for. The dynamics accounts in an effective manner, through the value of the parameters K and σ, for the interactions between OTUs and with the environment. However, fluctuations of OTUs within the same communities are described as independent. Empirically, fluctuations can certainly be correlated because of interactions or response to the same environmental perturbations.
MATERIALS AND METHODS
Data
We analyze time series of 14 individuals coming from three different datasets: 10 individuals of the BIO-ML dataset (35) (all those for which a dense long-term time series is available), 2 individuals (M3 and F4) from the Moving Pictures dataset (20), and two individuals (A and B) from (3). The length of the time series ranges from 6 months to 1.5 years, and the sampling frequency varies (daily in the most dense series). Individuals A and B from (3) both undergo a period of strong disturbance to their gut flora due, respectively, to two diarrhea episodes during a travel abroad and a Salmonella infection. We exclude these periods from the analysis and consider for each individuals two separate time series, before and after the perturbation. Raw data for MP and D were obtained from MGnify (36), under project IDs MGYS00002184 and MGYS00001278, while for BIO-ML they were obtained from the National Center for Biotechnology Information (NCBI), under project ID PRJNA544527. More details on the data analysis can be found in the Supplementary Materials.
Measuring dissimilarity
We want to measure the dissimilarity between the composition of a community at time t and at time t + T. Let be proportional to the absolute abundance of the S OTU in the community at time t. At time t, N(t) sequences are sampled, resulting in counts . The relative OTU abundances found in the two samples at lag T differ not only due to the difference in absolute OTU abundances in the community, reflected in , but also due to random sampling. Even if we sampled twice the same community, we would find some differences in the measured relative OTU abundances, especially if the sampling depth N is small with respect to the size of the community. Therefore, any dissimilarity measure computed directly on the measured relative abundances would overestimate the dissimilarity. The overestimation, additionally, is more pronounced for rare OTUs and for samples with smaller sampling efforts. To correct for the bias introduced by random sampling, we use a dissimilarity measure, Φi(T), that is defined on the absolute abundance in the two communities, proportional to , but can be estimated from the sampled counts . The dissimilarity for OTU i between time t and t + T is defined as
| (1) |
We note that this quantity does not depend on the proportionality constant between the absolute abundances and . Φi takes values in [0,1]. It is equal to 0 when the abundances are equal and to 1 if the abundance is zero at one time and nonzero at the other. If we define di(t, T) = xi(t) − xi(t + T) and si(t, T) = xi(t) + xi(t + T), we can prove (see the Supplementary Materials) that, if N(t) = N(t + T) (which can always be obtained by down-sampling the sample with larger N)
| (2) |
where 〈 · 〉 represents the average over realizations of the sampling and is constrained to those realizations where si > 1. This average over realization cannot be computed from the data, as we have a single realization. However, its average over time t is approximated by the average over time of the single realizations (Supplementary Materials).
Therefore, we compute the dissimilarity at lag T by averaging over the time points of the time series
| (3) |
where now di(t, T) and si(t, T) are the values in a single realization of the sampling, known from the data. In this way, we obtain an estimation of the dissimilarity of real abundances λi at a lag T based on the sampled counts xi.
Estimating parameters of the dynamics from data
Previous studies (15, 16) showed that the dynamics of the abundance λ of a microbial species is best described by the SLM with environmental noise
| (4) |
where ξ(t) is Gaussian white noise. This model has three parameters: τ has the dimension of a time and determines the time scale of relaxation to stationarity, K would be the carrying capacity in the absence of noise, and σ measures the intensity of the environmental noise. The model does not include interaction among species and therefore cannot reproduce patterns of interspecies correlation but correctly reproduces several patterns of the dynamics of a single species (15, 16). If σ < 2, the stationary distribution is gamma
| (5) |
with mean and variance . Note that the coefficient of variation depends only on the parameter σ, which can thus be interpreted as the amplitude of the fluctuations.
The parameters K and σ can be computed using estimates of the mean and variance of the abundance λ derived from the time series of sampled relative abundances. As mentioned before, the variables λ are proportional to the absolute abundance. In this respect, it is convenient to choose the proportionality constant such that ∑i < λi > = 1. Under this choice, the average <λi> can be estimated from the sampled relative abundances as (16). The variance of abundance fluctuations can be estimated with the sampling-corrected formula derived in (16)
| (6) |
We note that the variance estimated with this formula may result negative if many counts are 0 or 1. The OTUs for which this happens are excluded from the analysis, as it is not possible to estimate their parameters.
Although we do not use the value of τ in our analyses, it is useful to say that it is of the order of magnitude of 1 day [estimated with the R package POMP (37), which performs statistical inference of partially observed Markov processes]. Although the interval between observations is also 1 day, it is still possible to see the effect of the relaxation time in the initial increase of Φ(T), as can be seen from the model trajectories in Fig. 1 (D and E), obtained for τ = 1. The extent of the initial increase depends on both τ and σ.
Theoretical expected values for dissimilarity
We can compute the expected value of the dissimilarity of an OTU between two snapshots of the same community at a large lag T, , by assuming that the abundances at the two times are independent and identically distributed gamma variables distributed according to (5) with the same parameters, equal to the estimated K and σ for that OTU. Note that this is the expected value of under the assumption that the dynamics is stationary. The expected value can be computed analytically, and it depends only on σ
| (7) |
Similarly, we can compute the expected value of , taking the two abundances to be Γ random variables with different parameters
| (8) |
where . See the Supplementary Materials for the expression of f.
Identifying OTUs with a plateau in intraindividual dissimilarity
To classify the curves as either flat or increasing, we performed a linear fit discarding the initial transient (T > 10) and classified as increasing those with slopes above a threshold. To establish the threshold, we accounted for the fact that, although we expect a flat dissimilarity if the abundance is stationary, a slope different from zero can be found because of the noise in the estimation of Φ, which depends on the length and density of the time series, on the sequencing depth, and from the OTU parameters. Therefore, for each individual, we computed the threshold as follows. We simulated the dynamics of each OTU according to the SLM with parameters equal to the parameters estimated for that OTU and τ = 1. From these time series of , we sampled the time series of according to the sampling depth of the corresponding samples in the data, obtaining therefore values of only for days for which the individual was sampled. We then computed and its slope for each OTU. We defined as threshold for an individual the 95% quantile of the slopes obtained for that individual, i.e., the value such that only 5% of slopes obtained from the simulation are larger. Results are robust to variations of the thresholds (Supplementary Materials).
Identifying jumps in the carrying capacity K
To identify the points of a time series where the carrying capacity K has a jump, we first estimated K in window of length w = 50 days so that for each day t we have two estimates, Kfor, estimated in the forward window (t, t + w], and Kback, estimated in the backward window (t − w, t]. The estimates of K are computed using the estimate of σ for the entire time series. Note that we accepted an estimate of K only if the corresponding window contains at least five samples. If the count is null for all samples in a window, the value of K is set to the value such that the probability to observe nonzero counts is 1/w.
The two estimates of K will differ on days around a change in K. To detect these days, we compute two quantities
| (9) |
| (10) |
| (11) |
| (12) |
D+ has a peak when Kfor does not predict well the counts observed in the backward window, while D− has a peak when Kback does not predict well the counts observed in the forward window. Therefore, we identify the jumps in K as the times where D+ or D− has a peak with height larger than a threshold (fig. S7). Results are robust to the variation of this threshold (see the Supplementary Materials).
Simulating abundance time series with K jumps
We simulate abundance time series according to an SLM with carrying capacity K that changes in time with discrete jumps. To simulate an individual, we consider the parameters K and σ of all its OTUs for which the parameters can be computed. For each individual, the values of were set to the average of the estimated Ki in all the individuals of the same dataset. Changes in K are a Poisson process, with rate such that the percentage of OTUs for which a jump is observed in the simulated time window is equal to the percentage observed empirically for that individual. The average estimated rate is 1/1117 days-1, with substantial variability across individuals: It ranges from 1/3550 days-1 for the most stable individual to 1/82 days-1 for the very unstable B post-Salmonella. The values of Ki between jumps are extracted from with a variance of ζ that is the same for all OTUs. We consider a variance of ζ equal to 2 for the main results (e.g., Fig. 4). This value is estimated by matching the observed variability of Ki in the data (see section S8 and fig. S4). We perform a sensitivity analysis in fig. S12 obtaining that different values of the variance of ζ produce similar results (see fig. S12).
The initial condition is chosen to match the expected stationary distribution of abundances: The value of Ki for each OTU is chosen from a lognormal with mean , and the initial abundance is then drawn from a gamma distribution (corresponding to the stationary distribution of an SLM with parameters Ki and σi). The obtained time series are then sampled with a sampling depth equal to the average sampling depth for that individual, and only samples corresponding to days when the individual was sampled are kept (as the time series density affects the noise in the dissimilarity). The obtained time series of counts are analyzed as the empirical ones. Correlations are computed for the OTUs for which the parameters can be estimated.
Acknowledgments
We thank M. Dal Bello and D. Amor for insightful discussions and S. de Buyl, L. Fant, and W. R. Shoemaker for useful comments on the manuscript.
Author contributions: S.Z. and J.G. designed the research, performed the analytical calculations, and wrote the manuscript. S.Z. analyzed the data and wrote the code.
Competing interests: The authors declare that they have no competing interests.
Data availability statement: This paper does not use original data. All datasets used in the paper are available from the original references. The code used in the analysis of these datasets is available at https://zenodo.org/badge/latestdoi/400120651.
Supplementary Materials
This PDF file includes:
Supplementary Information
Figs. S1 to S14
Table S1
REFERENCES AND NOTES
- 1.Uhr G. T., Dohnalová L., Thaiss C. A., The dimension of time in host-microbiome interactions. mSystems 4, e00216-18 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schlomann B. H., Parthasarathy R., Timescales of gut microbiome dynamics. Curr. Opin. Microbiol. 50, 56–63 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.David L. A., Materna A. C., Friedman J., Campos-Baptista M. I., Blackburn M. C., Perrotta A., Erdman S. E., Alm E. J., Host lifestyle affects human microbiota on daily timescales. Genome Biol. 15, R89 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Langille M. G., Meehan C. J., Koenig J. E., Dhanani A. S., Rose R. A., Howlett S. E., Beiko R. G., Microbial shifts in the aging mouse gut. Microbiome 2, 50 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nagpal R., Mainali R., Ahmadi S., Wang S., Singh R., Kavanagh K., Kitzman D. W., Kushugulova A., Marotta F., Yadav H., Gut microbiome and aging: Physiological and mechanistic insights. Nutr. Healthy Aging 4, 267–285 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Singh R. K., Chang H.-W., Yan D., Lee K. M., Ucmak D., Wong K., Abrouk M., Farahnik B., Nakamura M., Zhu T. H., Bhutani T., Liao W., Influence of diet on the gut microbiome and implications for human health. J. Transl. Med. 15, 73 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Spor A., Koren O., Ley R., Unravelling the effects of the environment and host genotype on the gut microbiome. Nat. Rev. Microbiol. 9, 279–290 (2011). [DOI] [PubMed] [Google Scholar]
- 8.Arumugam M., Raes J., Pelletier E., Paslier D. L., Yamada T., Mende D. R., Fernandes G. R., Tap J., Bruls T., Batto J.-M., Bertalan M., Borruel N., Casellas F., Fernandez L., Gautier L., Hansen T., Hattori M., Hayashi T., Kleerebezem M., Kurokawa K., Leclerc M., Levenez F., Manichanh C., Bjørn Nielsen H., Nielsen T., Pons N., Poulain J., Qin J., Sicheritz-Ponten T., Tims S., Torrents D., Ugarte E., Zoetendal E. G., Wang J., Guarner F., Pedersen O., de Vos W. M., Brunak S., Doré J.; Meta HIT Consortium (additional members), Weissenbach J., Dusko Ehrlich S., Bork P., Enterotypes of the human gut microbiome. Nature 473, 174–180 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Costea P. I., Hildebrand F., Arumugam M., Bäckhed F., Blaser M. J., Bushman F. D., de Vos W. M., Dusko Ehrlich S., Fraser C. M., Hattori M., Huttenhower C., Jeffery I. B., Knights D., Lewis J. D., Ley R. E., Ochman H., O’Toole P. W., Quince C., Relman D. A., Shanahan F., Sunagawa S., Wang J., Weinstock G. M., Wu G. D., Zeller G., Zhao L., Raes J., Knight R., Bork P., Enterotypes in the landscape of gut microbial community composition. Nat. Microbiol. 3, 8–16 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Knights D., Ward T. L., McKinlay C. E., Miller H., Gonzalez A., Donald D. M., Knight R., Rethinking “enterotypes”. Cell Host Microbe 16, 433–437 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gibbons S. M., Kearney S. M., Smillie C. S., Alm E. J., Two dynamic regimes in the human gut microbiome. PLoS Comput. Biol. 13, e1005364 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shoemaker W. R., Locey K. J., Lennon J. T., A macroecological theory of microbial biodiversity. Nat. Ecol. Evol. 1, 0107 (2017). [DOI] [PubMed] [Google Scholar]
- 13.Shade A., Dunn R. R., Blowes S. A., Keil P., Bohannan B. J. M., Herrmann M., Küsel K., Lennon J. T., Sanders N. J., Storch D., Chase J., Macroecology to unite all life, large and small. Trends Ecol. Evol. 33, 731–744 (2018). [DOI] [PubMed] [Google Scholar]
- 14.Ji B. W., Sheth R. U., Dixit P. D., Tchourine K., Vitkup D., Macroecological dynamics of gut microbiota. Nat. Microbiol. 5, 768–775 (2020). [DOI] [PubMed] [Google Scholar]
- 15.Descheemaeker L., de Buyl S., Stochastic logistic models reproduce experimental time series of microbial communities. eLife 9, e55650 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grilli J., Macroecological laws describe variation and diversity in microbial communities. Nat. Commun. 11, 4743 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dennis B., Costantino R. F., Analysis of steady-state populations with the gamma abundance model: Application to Tribolium. Ecology 69, 1200–1213 (1988). [Google Scholar]
- 18.Rajilić-Stojanović M., Heilig H. G. H. J., Tims S., Zoetendal E. G., de Vos W. M., Long-term monitoring of the human intestinal microbiota composition. Environ. Microbiol. 15, 1146–1159 (2013). [DOI] [PubMed] [Google Scholar]
- 19.Faith J. J., Guruge J. L., Charbonneau M., Subramanian S., Seedorf H., Goodman A. L., Clemente J. C., Knight R., Heath A. C., Leibel R. L., Rosenbaum M., Gordon J. I., The long-term stability of the human gut microbiota. Science 341, 1237439 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gregory Caporaso J., Lauber C. L., Costello E. K., Berg-Lyons D., Gonzalez A., Stombaugh J., Knights D., Gajer P., Ravel J., Fierer N., Gordon J. I., Knight R., Moving pictures of the human microbiome. Genome Biol. 12, R50 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.The Human Microbiome Project Consortium , Structure, function and diversity of the healthy human microbiome. Nature 486, 207–214 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Garud N. R., Good B. H., Hallatschek O., Pollard K. S., Evolutionary dynamics of bacteria in the gut microbiome within and across hosts. PLOS Biol. 17, e3000102 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shenhav L., Furman O., Briscoe L., Thompson M., Silverman J. D., Mizrahi I., Halperin E., Modeling the temporal dynamics of the gut microbial community in adults and infants. PLoS Comput. Biol. 15, e1006960 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Luo Q., Mao X., Stochastic population dynamics under regime switching. J. Math. Anal. Appl. 334, 69–84 (2007). [Google Scholar]
- 25.Bashan A., Gibson T. E., Friedman J., Carey V. J., Weiss S. T., Hohmann E. L., Liu Y.-Y., Universality of human microbial dynamics. Nature 534, 259–262 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Costello E. K., Lauber C. L., Hamady M., Fierer N., Gordon J. I., Knight R., Bacterial community variation in human body habitats across space and time. Science 326, 1694–1697 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Turnbaugh P. J., Hamady M., Yatsunenko T., Cantarel B. L., Duncan A., Ley R. E., Sogin M. L., Jones W. J., Roe B. A., Affourtit J. P., Egholm M., Henrissat B., Heath A. C., Knight R., Gordon J. I., A core gut microbiome in obese and lean twins. Nature 457, 480–484 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lloyd-Price J., Mahurkar A., Rahnavard G., Crabtree J., Orvis J., Brantley Hall A., Brady A., Creasy H. H., Cracken C. M., Giglio M. G., Donald D. M., Franzosa E. A., Knight R., White O., Huttenhower C., Strains, functions and dynamics in the expanded Human Microbiome Project. Nature 550, 61–66 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dubinkina V., Fridman Y., Pandey P. P., Maslov S., Multistability and regime shifts in microbial communities explained by competition for essential nutrients. eLife 8, e49720 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Abreu C. I., Andersen Woltz V. L., Friedman J., Gore J., Microbial communities display alternative stable states in a fluctuating environment. PLOS Comput. Biol. 16, e1007934 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Amor D. R., Ratzke C., Gore J., Transient invaders can induce shifts between alternative stable states of microbial communities. Sci. Adv. 6, eaay8676 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.S. Estrela, J. C. C. Vila, N. Lu, D. Bajic, M. Rebolleda-Gomez, C.-Y. Chang, A. Sanchez, Metabolic rules of microbial community assembly. bioRxiv 2020.03.09.984278 [Preprint]. 11 March 2020. 10.1101/2020.03.09.984278. [DOI]
- 33.Hastings A., Abbott K. C., Cuddington K., Francis T., Gellner G., Lai Y.-C., Morozov A., Petrovskii S., Scranton K., Zeeman M. L., Transient phenomena in ecology. Science 361, eaat6412 (2018). [DOI] [PubMed] [Google Scholar]
- 34.Bucci V., Tzen B., Li N., Simmons M., Tanoue T., Bogart E., Deng L., Yeliseyev V., Delaney M. L., Liu Q., Olle B., Stein R. R., Honda K., Bry L., Gerber G. K., MDSINE: Microbial Dynamical Systems INference Engine for microbiome time-series analyses. Genome Biol. 17, 121 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Poyet M., Groussin M., Gibbons S. M., Avila-Pacheco J., Jiang X., Kearney S. M., Perrotta A. R., Berdy B., Zhao S., Lieberman T. D., Swanson P. K., Smith M., Roesemann S., Alexander J. E., Rich S. A., Livny J., Vlamakis H., Clish C., Bullock K., Deik A., Scott J., Pierce K. A., Xavier R. J., Alm E. J., A library of human gut bacterial isolates paired with longitudinal multiomics data enables mechanistic microbiome research. Nat. Med. 25, 1442–1452 (2019). [DOI] [PubMed] [Google Scholar]
- 36.Mitchell A. L., Almeida A., Beracochea M., Boland M., Burgin J., Cochrane G., Crusoe M. R., Kale V., Potter S. C., Richardson L. J., Sakharova E., Scheremetjew M., Korobeynikov A., Shlemov A., Kunyavskaya O., Lapidus A., Finn R. D., Mgnify: The microbiome analysis resource in 2020. Nucleic Acids Res. 48, D570–D578 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.King A. A., Nguyen D., Ionides E. L., Statistical inference for partially observed markov processes via the r package pomp. J. Stat. Softw 69, 1–43 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information
Figs. S1 to S14
Table S1