Geometric deep learning enables 3D kinematic profiling across species and environments

Abstract

Comprehensive descriptions of animal behavior require precise measurements of 3D whole-body movements. Although 2D approaches can track visible landmarks in restrictive environments, performance drops in freely moving animals, due to occlusions and appearance changes. Therefore, we designed DANNCE to robustly track anatomical landmarks in 3D across species and behaviors. DANNCE uses projective geometry to construct inputs to a convolutional neural network that leverages learned 3D geometric reasoning. We trained and benchmarked DANNCE using a 7-million frame dataset that relates color videos and rodent 3D poses. In rats and mice, DANNCE robustly tracked dozens of landmarks on the head, trunk, and limbs of freely moving animals in naturalistic settings. We extend DANNCE to datasets from rat pups, marmosets, and chickadees, and demonstrate quantitative profiling of behavioral lineage during development.

Introduction

The study of animal behavior is central to ethology, neuroscience, psychology, and ecology. As animal behavior is primarily conveyed by movement, a general method to track movement kinematics — the 3D position of an animal’s head, trunk, and limbs — would have broad impact. Ideally, the method would be universally accessible, markerless, reproducible across laboratories, and robust across naturalistic environments with occluding features. It would also be compatible with recording external (e.g., environmental) and internal (e.g., neural activity) variables and capable of precisely phenotyping normal and pathological behaviors across species.

Existing animal tracking methods have yet to achieve these goals. While depth cameras enable coarse measurements of an animal’s head and trunk, they cannot track the full pose^1,2 (particularly limbs) and struggle in naturalistic environments due to reflections³. 2D convolutional neural networks (CNNs) have been used for 2D tracking of anatomical landmarks in confined behavioral tasks^4-6. While their 2D predictions can be triangulated to 3D using multiple independent views, it has been difficult to use them for 3D tracking in freely moving animals, because 2D CNNs lack knowledge about the animal’s pose in 3D and do not have the ability to combine image information across views. As a result, they are not well suited to deal with occlusions and cannot readily generalize across diverse animal poses and camera perspectives^4-8. Approaches using skeletal constraints and filtering have begun to address these limitations^7,9. These methods, however, have not yet demonstrated robust 3D tracking in freely moving animals, except when trained with large numbers of frames¹⁰. Thus, while existing methods can be powerful in constrained tasks, their 2D nature makes them less capable of quantifying natural behaviors in 3D.

Recent advances in object detection^11,12, hand tracking^13,14, and human 3D pose tracking^15,16 use networks that incorporate volumetric representations, allowing these networks to explicitly represent a subject’s 3D pose and learn to combine information across views. However, the few available 3D human training datasets have a limited diversity of poses, making it difficult for networks to generalize to new imaging conditions¹⁷ and species. Further, because work in 3D human pose tracking has focused on algorithmic advances, most methods use ground truth motion capture information when making final predictions^15,16,18, making them impractical for most use cases. Thus, robust pose tracking for laboratory animals requires a network tailored to laboratory applications that incorporates advances in 3D machine vision and geometric deep learning^11,19, and a comprehensive ground truth dataset to train it.

Here, we developed DANNCE (3-Dimensional Aligned Neural Network for Computational Ethology, Supplementary Video 1), a system for markerless video-based 3D landmark tracking in freely behaving animals. DANNCE uses projective geometry to construct a metric 3D feature space robust to changes in perspective, allowing a 3D CNN to infer landmark locations using shared features across cameras and learned spatial statistics of the animal’s pose. To train and benchmark DANNCE, we collected Rat 7M, a 7-million frame ground truth dataset of rodent 3D landmarks and synchronized color video. After training, DANNCE generalized to markerless rats, where it outperformed the state-of-the-art 3D animal pose triangulation approach by more than 10-fold in error and 30-fold in pose-reconstruction efficacy. With a small set of additional hand-labeled training data, DANNCE also learned to track mice, marmosets, and chickadees. DANNCE could also quantitatively assess the complexity and lineage structure of the behavior of developing rats.

Results

Markerless pose detection using geometric deep learning

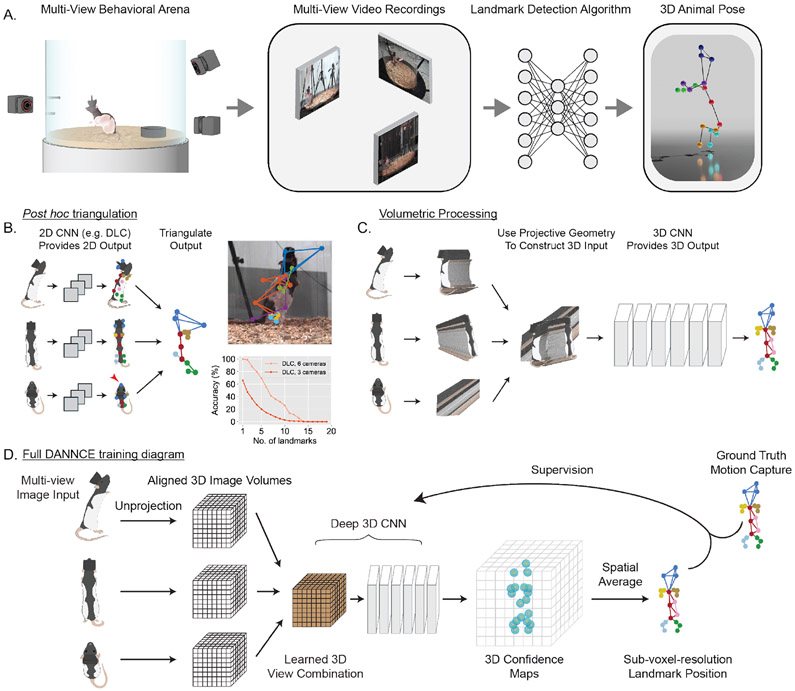
The most widely adopted state-of-the-art method for movement tracking in laboratory animals is DeepLabCut⁴ (DLC). Although DLC was originally developed for 2D applications, it can be extended to 3D via post hoc triangulation of 2D predictions made at different angles⁸ (Fig. 1). While successful for tracking restricted behaviors⁸, DLC has difficulties in tracking 3D landmarks in freely behaving rats (Fig. 1B; Supplementary Fig. 1A-B; Supplementary Video 2). DLC landmark predictions showed 60.7 ± 85.2 mm error (mean ± s.d.) with 3 cameras and 24.8 ± 24.2 mm with 6. Using a common pose tracking accuracy metric that quantifies how many landmark positions are predicted with error less than the length of a reference body segment (the distal forelimb, 18 mm), we found that DLC with 3 cameras could not accurately track more than 12 (out of 20) landmarks (Fig. 1B).

Figure 1 ∣. Fully 3D deep learning versus 2D-to-3D triangulation for naturalistic 3D pose detection.

A. Schematic of the methodological approach.

B. Left, schematic of a post hoc triangulation approach, in which a 2D pose detection network makes independent predictions of 2D landmark positions in each view and then triangulates detected landmarks. Red arrowhead: error in 2D landmark positioning. Right top, projection of a DLC 3D prediction into a frame from a single view (Supplementary Fig. 1). Right bottom, DLC accuracy as the fraction of timepoints in which at least N of 20 landmarks are successfully tracked in 3D (N = 3 animals, N = 894 landmarks, 75 timepoints).

C. The DANNCE approach, in which a 3D volume is constructed from the image in each view, and then these volumes are processed by a 3D CNN to directly predict 3D landmark positions.

D. Full schematic of DANNCE.

The weakness of post hoc triangulation arises from the independent processing of each camera view. While the method works well when landmarks are visible in all views (Supplementary Fig. 2A), its performance degrades if a landmark is occluded (Supplementary Fig. 2B), a scenario ubiquitous for freely moving animals in naturalistic environments. Further, although a landmark can, in principle, be triangulated if visible from any two cameras, image features cannot be combined across views to resolve ambiguities (e.g. between the left and right sides) or to constrain landmark predictions using features available from other perspectives. Finally, because post hoc triangulation does not incorporate 3D information when training, it cannot use learned 3D statistics of the animal’s pose.

To overcome these limitations, our approach exploits mathematical relationships between camera positions to build a 3D feature space with which a CNN can reason about landmark positions. First, we compute the location of a 3D cubic grid large enough to contain the animal and discretize it into isometric voxels (Supplementary Fig. 3). We then use camera position and orientation to “unproject” the 2D images into 3D space, with each voxel in the grid populated with the set of light rays that intersect it in 3D¹¹. This is similar to contemporaneous work in human 3D pose tracking, and preliminary work in animals, which use unprojected features derived from a 2D CNN, although at the cost of longer run times^16,20,21. Finally, we train a 3D CNN using ground-truth 3D labels to fuse features across cameras and estimate a confidence map over voxels for each landmark¹³, which is processed to provide continuous readouts of landmark position with higher resolution than individual voxels²².

Thus, the network learns to infer landmark positions from ray intersections in a 3D feature space formed from combined image content across multiple views. This feature space is metric, i.e. in units of physical coordinates rather than camera pixels, allowing the network to leverage learned spatial statistics of the body to resolve feature ambiguities and make landmark inferences even in the presence of occlusions (Supplementary Fig. 2C, D).

Rat 7M: a training and benchmark dataset for animal pose detection

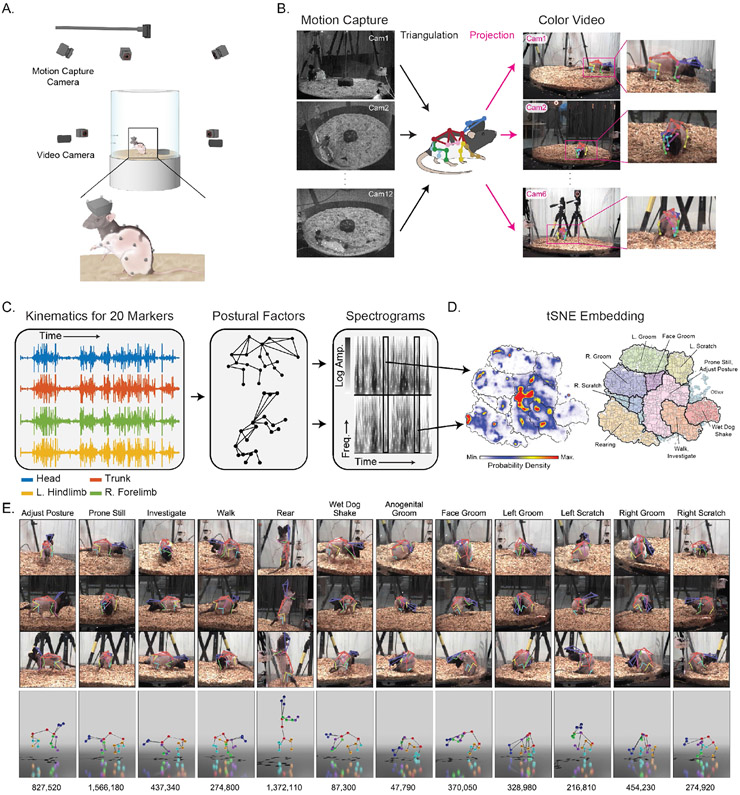
To train and benchmark DANNCE, we collected ground truth rat poses and synchronized color video using motion capture, the gold standard for recording human movement. To adapt motion capture to rats, we recently developed an approach to attach markers to 20 sites on a rat’s head, trunk, and limbs (Fig. 2A) using body piercings²³. We recorded the 3D positions of the markers using 12 motion capture and 6 color video cameras at 30 Hz in a shared coordinate system (Fig. 2B).

Figure 2 ∣. Rat 7M, a training and benchmark dataset for 3D pose detection.

A. Schematic of the Rat 7M collection setup.

B. Markers detected by motion capture cameras are triangulated across views to reconstruct the animal’s 3D pose and projected into camera images as labels to train 2D pose detection networks.

C. Illustration of process by which tracked landmarks are used to identify individual behaviors. The temporal dynamics of individual markers are projected onto principal axes of pose (eigenpostures) and transformed into wavelet spectrograms that represent the temporal dynamics at multiple scales²³.

D. tSNE representations of eigenposture and wavelet traces, as well as behavioral density maps and isolated clusters obtained via watershed transform over a density representation of the tSNE space.

E. Individual examples from each of the high-level clusters outlined in bold in (D). Reprojection of the same 3D pose onto 3 different views (Top) and 3D rendering of the 3D pose in each example (Bottom). The numbers are the total number of example images for each behavioral category. 728,028 frames with motion capture data where animal speed was below the behavioral categorization threshold are excluded.

To encourage trained algorithms to generalize to new environments and behaviors, we collected data encompassing a total of 10.8 hours across 6 different rats and 30 camera views (Supplementary Fig. 4). This Rat 7M dataset contains 6,986,058 frames and a wide diversity of rat behaviors. We subdivided these recordings into 12 high-level categories using a behavioral embedding and clustering approach based on kinematic marker features^23,24 (Fig. 2C-E). This allows training examples to be balanced over poses and establishes standardized categories for benchmarking.

DANNCE outperforms DeepLabCut in rats and mice

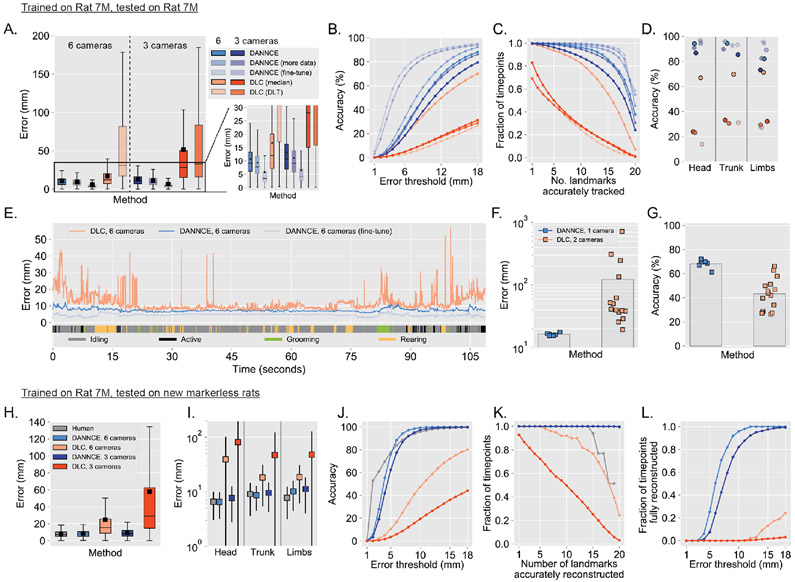
To compare the 3D DANNCE approach with post hoc triangulation used by DLC, we trained both methods on the same set of video frames and poses (180,456 unique frames, 3,609,120 markers) and tested them on new camera views in a subject withheld from training (Supplementary Fig. 4). Qualitative visualizations showed that DANNCE generalized immediately, while DLC struggled to track the same landmarks (Supplementary Video 3). To quantify this, we computed the error and accuracy of landmark predictions relative to ground truth motion capture. The published DLC triangulation protocol⁸ was sensitive to 2D tracking outliers. In both 3- and 6-camera comparisons, DANNCE showed over 30-fold lower error and over 3-fold greater accuracy (Fig. 3A-C). While DLC predictions improved when we used a modified triangulation protocol that discounted outliers (used for all our subsequent DLC analyses), DANNCE continued to outperform it. Using 3 cameras, DANNCE had nearly 4-fold lower error, over 10-fold lower uncertainty, and over 2-fold greater accuracy (DANNCE 13.1 ± 9.0 mm, 10.7 mm median error, 79.5% accuracy; DLC 51.6 ± 100.8 mm, 28.1 mm, 31.3%; Fig. 3A-C, Supplementary Video 2). Indeed, DANNCE with only 3 cameras outperformed DLC with 6. Comparing the fraction of frames with a fully reconstructed pose, DANNCE also outperformed DLC by 26- and 5-fold for 3 and 6 cameras, respectively (Fig. 3C). DANNCE tracked all marker types better than DLC (Fig. 3D) and showed higher accuracy and lower error across all behaviors (Supplementary Fig. 5A-B). DANNCE’s error was also more stable over time, providing the temporal consistency required for extracting higher-order kinematic quantities (Fig. 3E). Some, but not all, periods of correlated DANNCE and DLC error increases occurred during contorted grooming behaviors (Supplementary Fig. 5A-B).

Figure 3 ∣. DANNCE outperforms DLC on rats with and without markers.

A. Box plots of Euclidean error for the indicated methods in a recording using a validation animal not used for training. “More data” is from a model trained with 5 animals rather than 4. “Fine-tune” is after fine-tuning the “more data” model with an additional 225 3D poses from this validation animal for each recording session (Supplementary Fig. 4). In DLC (DLT), the direct linear transformation method was used to triangulate across all cameras⁸. DLC (median) takes the median of triangulations for all camera pairs. DANNCE 6-camera landmark positions are computed as the median of all 3-camera predictions (Supplementary Fig. 5C). N = 62,680 markers for all 6 camera methods, N = 1,253, 0 markers for all 3 camera methods. Inset colors follow the same legend as to the left and (A-D) use the same color legend. The box plots in (A) and (H) show median with inter-quartile range (IQR) and whiskers extending to 1.5x the IQR. The arithmetic mean is shown as a black square.

B. Landmark prediction accuracy as a function of error threshold, for the same data and methods as in (A).

C. Fraction of timepoints with the indicated number of markers accurately tracked at a threshold of 18 mm, for the same data and methods as in (A).

D. Landmark prediction accuracy at a threshold of 18 mm, broken down by landmark types, for the same data and methods as in (A).

E. Examples showing the Euclidean error over time for a section of recording in the validation animal. Thick colored lines as the bottom denote the type of behavior engaged in over time: grooming (all grooming and scratching), active (walking, investigation, and wet dog shake), rearing, and idling (prone still and adjust posture).

F-G. Mean Euclidean error (F) and accuracy (G) on the validation subject for DANNCE when using a single camera for prediction, vs. DLC when using two cameras. Squares show the mean error for individual camera sets (6 different single camera possibilities for DANNCE, 15 different pairs for DLC; N = 9·10⁶, 2.25·10⁷ markers for DANNCE and DLC, respectively).

H. Box plots of overall Euclidean error in markerless rats relative to triangulated 3D human labels, for each of the indicated methods. N = 3 animals, N = 721 landmarks.

I. Plots showing the mean Euclidean error for the same data and methods as in (H), broken down by landmark type. Each square is the mean and error bars are standard deviation.

J. Landmark reconstruction accuracy as a function of error threshold for the same animals and frames as in (H), but with all landmarks pooled across labelers for Human (N = 1,868), and all 20 predictions per frame for DANNCE and DLC (N = 1,980 and 39,600 landmarks for each 6 camera and 3 camera condition, respectively).

K. Fraction of all frames with the indicated number of landmarks accurately reconstructed at a threshold of 18 mm, for the same data as in (J). The “Human” line is truncated at 19 landmarks because labelers were unable to see the full set of landmarks in at least 2 views.

L. Fraction of all frames fully reconstructed (all 20 landmarks with error below threshold) as a function of the error threshold for the same data as in (J). (I)-(L) use the same colors as in (H).

The lower performance of DLC was not due to technical issues with the training procedure. A control evaluation of DLC on animals in the training set, i.e. after we had trained DLC with 180,456 frames from the tracked animals, showed better performance than on animals for which training data was withheld. This indicates that DLC does not develop a generalizable 3D geometric understanding applicable to unknown subjects or situations (Supplementary Fig. 5C-E).

As a further test of DANNCE’s ability to reason geometrically, we evaluated its performance on input volumes constructed from a single camera view. Here, 3D marker positions must be estimated from learned spatial priors and nuanced patterns of ray convergence. Our single-camera DANNCE version outperformed DLC with 2 cameras (DANNCE 15.6 mm error; DLC 123.2 mm; Fig. 3F-G, Supplementary Video 4), because DANNCE uses learned 3D representations to interpolate when critical information is missing. DANNCE can also correct small errors in camera calibration (Supplementary Fig. 6) and withstand decreases in image resolution (Supplementary Fig. 7).

DANNCE performance improves with additional training data and generalizes to unseen behaviors

To estimate the performance on rats in other labs, where a small sample of hand-labeled data could be used to tailor the network to new subjects, we tested DANNCE after training with additional data. First, we expanded the training set to include a fifth animal and observed that DANNCE performance increased slightly on the held-out validation subject (median error 7.8 mm, 92.3% accuracy). We then fine-tuned this expanded DANNCE using a small set of within-subject ground truth data. DANNCE error dropped substantially (median error 3.5 mm, 95.1% accuracy; Fig. 3A-E; Supplementary Fig. 8), below even a 3D voxel side length (3.75 mm). DANNCE also generalized to new behaviors not in the training set, a condition likely to be encountered in future experimental manipulations (Supplementary Fig. 9).

DANNCE outperforms DeepLabCut on markerless rodents

DANNCE’s substantial performance improvements in generalization were not restricted to rats bearing markers. We applied trained DANNCE and DLC networks to markerless rats and mice, the latter after fine-tuning DANNCE and DLC with 50 timepoints of hand-labeled data. Qualitatively, DANNCE generalized, whereas DLC struggled to track most landmarks, often making large errors on individual landmarks and collapsing the left and right sides of the body into a single plane (Supplementary Fig. 10; Supplementary Fig. 11; Supplementary Video 5).

In rats, the error of the 6-camera DANNCE predictions relative to hand-labeled points (8.4 ± 4.6 mm) was close to the error between the human labelers themselves (8.0 ± 4.8 mm), whereas the 6-camera DLC error (24.8 ± 37.2 mm) was higher and more variable (Fig. 3H). This performance gap was exacerbated when using just 3 cameras (DANNCE 9.4 ± 5.9 mm; DLC 58.0 ± 92.3 mm) and was especially prominent for the head (DANNCE mean error: 6.5 mm, 7.7; DLC: 39.3, 81.9 for 6-camera and 3-camera, respectively; Fig. 3I). DANNCE reconstruction accuracy was also better than DLC’s reconstruction accuracy, especially at small error thresholds (Fig. 3J); and DANNCE showed 33- and 4-fold increases over DLC in the fraction of timepoints with the full pose accurately reconstructed for 3 and 6 cameras, respectively (Fig. 3K-L). In addition, whereas DANNCE could infer the locations of a full set of landmarks with high reconstruction accuracy, human labeler accuracy dropped when labeling more than about 15 landmarks (Fig. 3K). In validation mouse datasets, DANNCE showed approximately 5-fold lower error and 2-fold higher accuracy than DLC (DANNCE error: 3.9 ± 6.2 mm, DLC 17.6 ± 23.0 mm; DANNCE accuracy 94.2%, DLC 38.5%; Supplementary Fig. 11A-B). DANNCE performance improved further, surpassing that of humans, when using additional cameras (5-camera DANNCE 97.2% accuracy, inter-human 94.8%; Supplementary Fig. 11C-E).

DANNCE enables precise behavioral and kinematic profiling in rodents

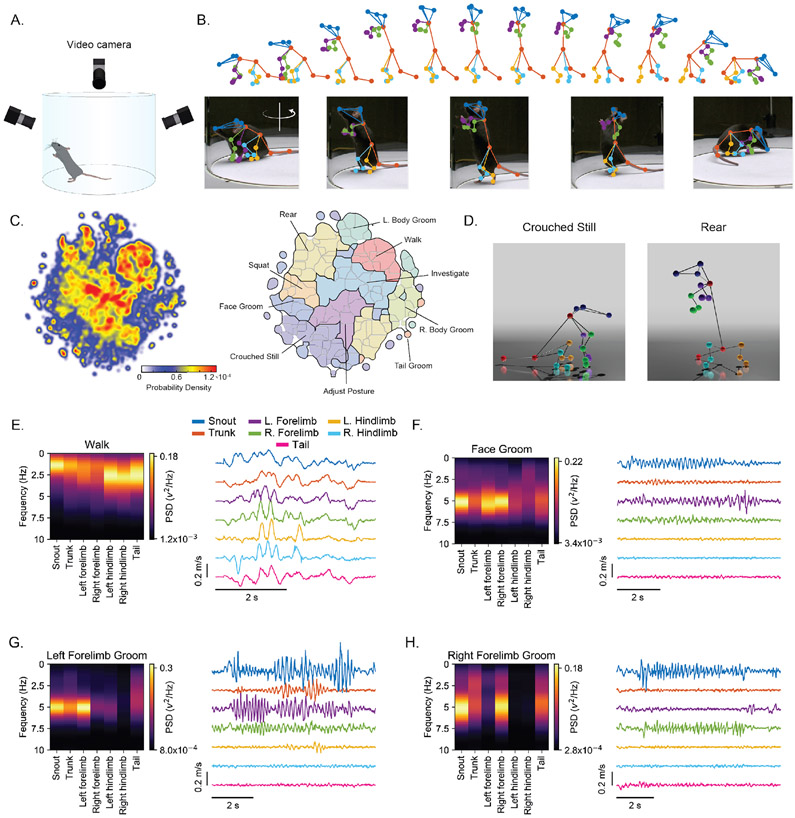
Rodents are model systems for investigating the neural basis of behavior. However, precise measurements of 3D kinematics and behavioral type have thus far been limited to constrained environments and a limited subset of behaviors^25,26. To test whether DANNCE could provide detailed 3D kinematics across a wide range of behaviors, we first created unsupervised behavioral maps (Fig. 2C-D) from DANNCE recordings. In rats, maps were qualitatively similar to those obtained from animals with markers, with human annotators confirming that all coarse Rat 7M behavioral categories were recovered (Supplementary Fig. 10D-E). In mice, behavioral maps isolated common behaviors, such as rearing and walking, and rarer behaviors that have been difficult to differentiate in the past, such as face, body, and tail grooming¹ (Fig. 4A-D, Supplementary Video 6, 7). The set of identified behaviors was larger than what has been mapped using 2D pose tracking techniques⁵.

Figure 4 ∣. Kinematic profiling of the mouse behavioral repertoire.

A. Schematic of the high-resolution mouse recording arena.

B. Example 3D DANNCE predictions (top), and video reprojections of every third frame (bottom), of a rearing sequence in a mouse not bearing markers.

C. Density map (Left), and corresponding low- and high-level clusters (light and dark outlines, respectively, Right) of mouse behavioral space isolated from 3 hours of recording in 3 mice.

D. 3D renderings of examples from the indicated behavioral categories in (C).

E-H. Left, power spectral density (PSD) for individual landmarks at the indicated anatomical positions in a single walking (E), face grooming (F), and left (G) and right (H) forelimb grooming cluster (N = 44, 41, 333, 33 repetitions, respectively). Right, example kinematic traces (x-velocity only) during a single instance of each behavior for the same markers as to the left. All examples in (E-H) are derived from a single mouse.

We then assessed DANNCE’s ability to report the 3D kinematics of unconstrained behaviors and reveal previously inaccessible characteristics of 3D body coordination. As a validation, we characterized the kinematics of walking behaviors. In agreement with past studies in constrained settings (treadmill), we found that walking comprised ~3 Hz oscillations in the limbs and tail (Fig. 4E) that were strongest in horizontal (x and y) velocity components (Supplementary Fig. 12)²⁶. This frequency peak was absent in the head and trunk, suggesting that mice, like humans, stabilize their posture and gaze during locomotion²⁷. We next characterized grooming behaviors, whose kinematic properties remain unknown, hence limiting phenotyping precision²⁸. Facial grooming was characterized by 5 Hz oscillations of the forelimbs and head and, to a lesser extent, the trunk (Fig. 4F). Similarly, left and right forelimb grooming disproportionally engaged their respective side-specific forelimbs at 5 Hz, suggesting reuse of a common pattern generator across these behaviors (Fig. 4G-H).

Lineage structure of behavioral ontogeny

To achieve an integrative understanding of behavior, it is necessary to address Tinbergen’s ‘four questions’²⁹ about function, mechanism, evolution, and ontogeny. DANNCE can shed light on the latter two, where quantification has been challenging.

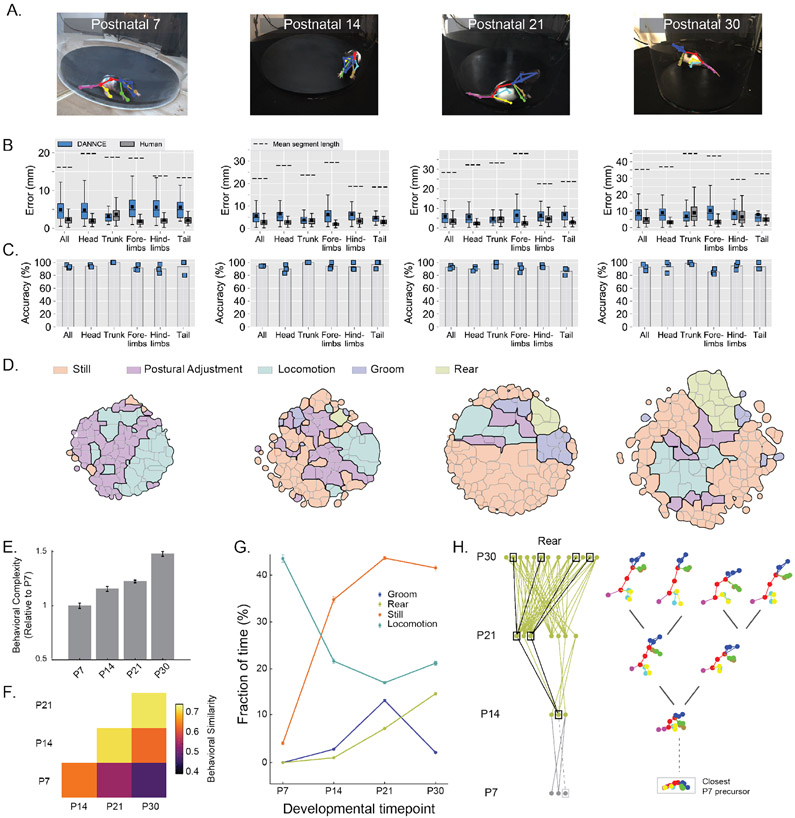
To demonstrate the utility of DANNCE for profiling behavioral development, we tracked Long-Evans rats³⁰ at postnatal days 7, 14, 21, and 30 (Fig. 5A; Supplementary Video 8). DANNCE tracked poses in developing rats with precision close to that of human labelers and with high landmark accuracy (Fig. 5B-C; Supplementary Fig. 13A). While new behaviors are known to emerge over the first month of development, it is less clear whether they emerge fully formed, are progressively expanded, or show large-scale attrition^31,32. To address this, we compared behavioral repertoires across developmental timepoints and revealed, in an unbiased manner, that the rat behavioral repertoire grows and becomes more dissimilar over time (Fig. 5D-F). Human-validated annotations showed behavioral usages consistent with past reports³³ and revealed that animals add body grooming behavioral categories over time (Fig. 5G; Supplementary Fig. 13B-C). DANNCE also revealed how rearing movement develop, showing an increase in the number of rear subtypes over time (Fig. 5D,H). These results are consistent with the mammalian motor repertoire progressively expanding. Tracking behavior over development, facilitated by DANNCE, could help inform how behavioral changes are shaped by the concurrent development of the nervous system.

Figure 5 ∣. DANNCE can report the ontogeny of behavioral complexity in rats.

A. Examples of DANNCE landmark predictions projected into a single camera view, for four different developmental stages.

B-C. Box plots of landmark Euclidean error (B) and bar plots of DANNCE mean landmark prediction accuracy (C) in validation subjects for both hand-labeled frames and DANNCE predictions, broken down by landmark type. The box plots show median with IQR and whiskers extending to 1.5x the IQR. The arithmetic mean is also shown as a black square. The mean segment length between landmarks of each type is presented for scale in (B). In (C), Blue squares show the landmark prediction accuracy for individual validation subjects. For each developmental timepoint, N = 3 animals and N = 396 – 417 landmarks.

D. Clustered and annotated maps of pup behavior for each developmental timepoint. We scaled the size of the behavioral maps to reflect the diversity of behaviors observed.

E. Bar plots of behavioral complexity, defined as the range of pairwise distances between behaviors observed in the dataset, normalized to P7 and shown across different developmental timepoints. Error bars reflect the standard deviation of the complexity across 50 bootstrapped samples.

F. Grid quantification of behavioral similarity across developmental stages. For each stage we clustered the behavioral map, identified pairs of clusters across stage pairs with highest similarity, and reported the average highest similarity per cluster.

G. Fractions of time spent in four major behavioral categories. Mean values (circles) were adjusted to reflect the fraction observed by humans in Supplementary Fig. 13. Error bars reflect the expected standard deviation in observations based on Poisson statistics (N = 484-65,008 per category, when present).

H. Ontogeny of rearing behaviors. In the graphs, individual nodes refer to unique behavioral clusters at each stage. Edges connect nodes whose similarity is greater than a set threshold. Wireframe examples show the diversification of rearing behaviors from one initial cluster at P14. This cluster was linked to a P7 behavioral precursor with similarity below threshold (dotted lines). Gray dots and lines for P7 denote that these clusters were not identifiable as rearing movements.

Extension of DANNCE across taxa and environments

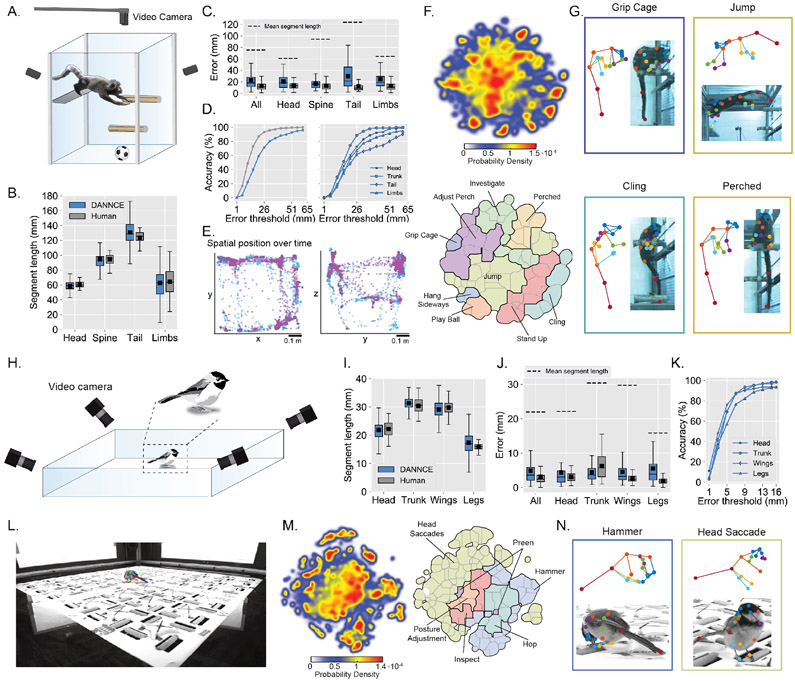
To trace evolutionary relationships and, more generally, to extend 3D tracking to other species and taxa, would require DANNCE, trained on rats, to extend to animals with different body shapes and behavioral repertoires. Such extensibility would meaningfully expand the range of applications for DANNCE. To test this, we first applied DANNCE to the marmoset³⁴. We used three cameras to record freely moving marmoset behavior in an enriched homecage containing multiple occlusions and distractors, such as perches and balls (Fig. 6A). We fine-tuned DANNCE using 96 hand-labeled timepoints and accurately tracked marmoset behavior despite the presence of substantial occlusions (Supplementary Video 9). DANNCE estimated skeletal segment lengths and landmark position with accuracy near that of human labelers, with errors well below a body segment length (Fig. 6B-D). Behavioral maps revealed 9 high-level behavioral categories, including jumping, perching, clinging, cage gripping, and object interaction (Fig. 6E-G).

Figure 6 ∣. 3D tracking across the behavioral repertoire of marmosets and chickadees.

A. Schematic of the naturalistic marmoset behavioral enclosure and video recording configuration (Supplementary Video 9).

B. Box plots of marmoset segment length distances for hand-labeled frames (“Human”; head N = 72 segments; spine N = 52; tail N = 48; limbs N = 93) and DANNCE predictions (head N = 11,689 segments; spine N = 10,462; tail N = 10,472; limbs N = 88,236). Box plots in (B-C, I-J) show median with IQR and whiskers extending to 1.5x IQR. Black squares in the box plots are arithmetic means.

C. Box plots of marmoset landmark Euclidean error in validation frames for hand-labeled frames and DANNCE predictions, broken down by landmark type. The mean segment length between landmarks of each type, in the human-annotated data, is presented for scale. N = 560 landmarks for each method. Head N = 105, spine N = 105, tail N = 70, limbs N = 280. Colors use the same key as in (B).

D. Left, landmark prediction accuracy as a function of error threshold for the same data as in (C). Color code is the same as in (C). Right, landmark prediction accuracy as a function of error threshold for DANNCE only, broken down by landmark type.

E. Plots of 3D animal position over time for a 10-minute recording session, projected onto the x-y (left) and y-z (right) planes of the arena. The color map encodes time from the start of the recording, from blue to purple.

F. Top, heat map of tSNE behavioral embeddings from 23 minutes of video (40,020 frames) in a single animal. Bottom, annotated behavioral map.

G. Individual examples extracted from clusters in (F). Colors of box outlines correspond to cluster colors.

H. Schematic of the chickadee behavioral arena and video recording configuration. Only four of the six cameras are shown (Supplementary Video 10).

I. Box plots of chickadee segment length distances for hand-labeled frames (head N = 70 segments; trunk N = 70; wings N = 140; legs N = 280) and DANNCE predictions (head N = 396,000 segments; trunk N = 396,000; wings N = 792,000; legs N = 1,584,000).

J. Box plots of chickadee landmark Euclidean error in validation frames for both hand-labeled frames and DANNCE predictions, broken down by landmark type. The mean segment length between landmarks of each type, in the human-annotated data, is presented for scale. N = 310 landmarks for each method. Head N = 62, trunk N = 62, wings N = 62, legs N = 124. Colors use the same key as in (I).

K. Landmark prediction accuracy as a function of error threshold for DANNCE only, broken down by landmark type, for the same data as in (J).

L. Example DANNCE landmark predictions on the chickadee in the arena.

M. Left, heat map of tSNE behavioral embeddings from 2 hours of video in a single animal. Right, annotated behavioral map.

N. Individual examples extracted from clusters in (M). Colors of box outlines correspond to cluster colors.

To demonstrate extensibility beyond mammals, we used DANNCE to track black-capped chickadees engaged in a foraging and caching task in a complex environment (Fig. 6H). Despite the substantial differences between rats and chickadees in body shape and behavioral repertoire, DANNCE was able to provide accurate predictions across all landmarks with precision commensurate with human labelers and errors well below body segment lengths (Fig. 6I-K; Supplementary Video 10). Analyzing the data revealed diverse locomotor, preening, gaze, and pecking behaviors (Fig. 6L-N), providing clues to how a complex foraging behavior is built from behavioral modules.

Discussion

We present DANNCE, a video-based 3D tracking technology for animal behavior that is extensible to new environments and species. DANNCE is provided to the community as an open-source python package, together with a graphical user interface for labeling 3D data (Supplementary Note).

In addition, we provide Rat 7M as a rich dataset of ground-truth rat poses with accompanying color video to the pose detection community. Such datasets are foundational both for benchmarking and training pose estimation algorithms in humans^35-38. Rat 7M, and similar datasets from a variety of species, contexts, and behaviors, should improve benchmarking and generalization of pose tracking algorithms across laboratories and behaviors.

The modular architecture of DANNCE, which separates feature space generation from landmark inference, is well suited to incorporate rapidly developing advances in computer vision. Future increases in GPU memory capacity should enable finer discretization of 3D space in our voxel grid. A present alternative is to use a recursive partitioning of space that populates successively finer grids around coarse estimates of individual landmark positions³⁹. Additionally, Rat 7M provides continuous tracking that can be used to incorporate temporal information via causal convolutions⁴⁰, recurrent neural networks⁴¹, or attention-based models⁴², features that have improved estimation of human pose⁴³. We also expect that probabilistic skeletal models of limb lengths and joint angles^7,39 will enable further refinement of predictions, especially in noisy regimes where occlusions are numerous or hand-labeled data are scarce, similar to the post hoc refinement of 3D landmarks demonstrated in Drosophila⁷. Finally, we note that by centering individual volumes on additional animals in the same arena, DANNCE could be extended to 3D tracking of social behaviors.

DANNCE opens the door to studies of animal behavior that are precise, rigorous, and comprehensive. In addition to quantitative studies of development, which should permit a precise delineation of the phases of motor development and their neural basis, we see a vast space of potential applications for DANNCE in neurobiology, biomechanics, developmental and evolutionary biology⁴⁴, ecology⁴⁵, and drug discovery⁴⁶. Armed with precise 3D kinematics of bodies and limbs in a diverse set of model systems, researchers will be able to refine their understanding of how a rich variety of movements, behaviors, and behavioral states are represented in, and generated by, different brain areas^47-50. This includes studies of motor system function in health and disease, which have typically been relegated to coarse behavioral indicators, such as position, heading direction, and running speed⁵¹. An expanded set of 3D kinematic variables could also influence our understanding of coding in sensory brain areas traditionally considered independent of movement⁵². Finally, in contrast to techniques that model behavior directly from images or depth maps^1,24,53, DANNCE tracks identified anatomical elements, allowing for precise kinematic phenotyping useful for studying motor disorders and identifying behavioral homology.

Overall, we believe DANNCE represents an important step forward for the neuroscience of movement and behavior, where the technology for measuring the brain’s activity has outpaced our ability to measure its principal output.

Methods

Animals and Husbandry

The care and experimental manipulation of all animals were reviewed and approved by Harvard University Faculty of Arts and Sciences', the Duke University School of Medicine's, the Rockefeller University's, and Columbia University’s Institutional Animal Care and Use Committees. We used 8 female Long-Evans rats (Charles-Rivers, strain 006), aged 3-12 months. For mouse quantification experiments described in Supplementary Fig. 11, we used 4 male black C57/BL6 mice (Charles-Rivers, strain 027), 8-12 weeks old. For mouse experiments described in Fig. 4, we used 3 female C57/BL6 mice (strain 000664, Jackson Labs), age 61 days, and 2 adult female C57/BL6 mice (strain 000664, Jackson Labs) for training. For rat development experiments, we used 23 male and female pups, age P7-P30, born from untimed pregnant Long-Evans rats (Charles-Rivers). For marmoset experiments, we used a 43-week-old female marmoset born in captivity and still living with its family group. Bird subjects were 5 adult black capped chickadees (Poecile atricapillus) of unknown sex, collected from multiple sites in New York State using Federal and State permits. Rats and mice kept at Harvard and Duke were kept on a normal 12/12 light/dark cycle at a temperature of 22°C ± 1 and humidity of 30-70% and were housed in ventilated cages with ad libitum water and food.

Motion Capture Recordings

We used a commercial 12-camera motion capture array to record the position of 20 retroreflective markers that were attached to each rat’s head, trunk, and limbs. We attached the three markers on the head to a custom acrylic headcap. We attached the remainder of the markers using body piercings: five to the animal’s trunk, three to each forelimb, and three to each hindlimb. Retroreflective markers consisted of high index-of-refraction (n=2.0) ball lenses (H-ZLAF, Worldhawk Optoelectronics) that we half-silvered (A1204D, Angel Gilding) and epoxied to a monel clamp (INS1005-5, Kent Scientific) or 6 mm cup earstud (H20-1585FN, Fire Mountain Gems) using high-strength epoxy (Loctite EA0151). We performed surgeries for attaching body piercings under 1–2% isoflurane anesthesia. Prior to surgery, we sterilized all tools and body piercings and shaved the animal’s head, trunk, and limbs using an electric razor. We made a longitudinal incision over the animal’s scalp, retracted the skin, placed three skull screws over the cerebellum and temporal lobes, and covered the skull with C&B Metabond (Parkell). We affixed the headcap using cyanoacrylate glue and dental cement (A-M Systems, 525000). Sites for the placement of body piercings on the skin were marked using a skin pen and then sterilized using alternating washes of betadine and 70% ethanol. To attach markers to the spine, trunk and hips, we made two small incisions, spaced by 1 cm, at each site and inserted body piercings through the ends of the incision. We secured piercings in place using pliers. For markers on the shoulders, forelimbs and hindlimbs, we similarly inserted a sterile, 18-gauge hollow needle through two points on the skin, inserted the end of the piercing through the hollow end of the needle, and retraced the needle from the skin. To then secure limb piercings, we attached earnuts (H20-A5314FN, Fire Mountain Gems) and soldered them in place. We applied antibiotic cream to marker sites and administered buprenorphine (0.05 mg/kg) and carprofen (5 mg/kg) subcutaneously following surgery. Motion capture recordings were made using Cortex (Motion Analysis). In some cases, to increase the amount of movement in the arena, animals were administered caffeine (Sigma C0750), injected at 1 ml/kg with a dosage of 10 mg/kg in Phosphate Buffered Saline (PBS).

DANNCE Software and Hardware

DANNCE is implemented in python 3.7.9 using standard free packages for scientific computing and deep learning: numpy 1.18, scipy 1.6.1, scikit-image 0.18.1, imageio 2.8.0, matplotlib 3.3.3, opencv-python 4.5.1.48, tensorflow 2.3.1 (with cuda 10.1 and cudnn 7.6), pytorch 1.7.0. The DANNCE code was tested on Windows 10, Ubuntu (Linux) 16.04, and Ubuntu (Linux) 18.04 operating systems. The DANNCE GitHub repository (https://github.com/spoonsso/dannce/) also contains code and instructions for camera synchronization, video compression, and camera calibration. We combined the synchronization and compression code into a separate github repository that is linked as submodule to DANNCE. DANNCE is designed to work with any video feeds that can be synchronized, and we have explicitly tested DANNCE on 3 different camera models: Point Grey Flea3, FLIR Blackfly BFS-U3-162M/C-CS, and Basler Aca1920-150uc. DANNCE works best with a GPU with at least 8 GB of onboard memory and has been tested on the NVIDIA Titan X Pascal, NVIDIA Titan V, NVIDIA Titan RTX, NVIDIA Tesla V100, and NVIDIA GeForce RTX 2080 Ti. We provide trained DANNCE weights for the network and note that the package was built so that new network architectures can be swapped at any time, with network classes and weights easily shared within the community. For more details, please consult the Supplementary Note and DANNCE GitHub documentation.

In addition to DANNCE, we also provide Label3D, a Matlab-based graphical user interface specifically designed for generating 3D hand-labeled poses that can be used to fine-tune DANNCE on new species or contexts. Label3D presents images from all camera views simultaneously and uses the calibrated geometry of the camera — their relative translations, rotations, and lens properties — to triangulate landmarks in 3D if they are labeled in at least two views. Label3D then projects triangulated landmarks into the image plane of cameras without labels to “fill in” estimated landmark positions. Because points only need to be labeled in two views, this fill in increases labeling throughput, for instance by at least 3-fold when using a 6-camera system. This feature also allows for points to be labeled in frames even in the presence of occlusions, as long as they are unconcluded in at least two views. To promote accurate labeling, Label3D provides closed-loop feedback between changes in landmark positions and concomitant changes in the 3D pose and image projections.

Camera Calibration

Each investigator in our team used slightly different approaches for camera calibration. For computing camera calibrations in rats, mice, marmosets, and rat pups, we used custom calibration scripts written in Matlab, drawing from camera calibration functions in the Computer Vision Toolbox (e.g. detectCheckerboardPoints, estimateWorldCameraPose, estimateCameraParameters, cameraPoseToExtrinsics). We computed camera intrinsics using a black and white checkerboard (10-20 mm side length). We computed camera extrinsics by manually labeling points on objects placed in the recording environment of known dimensions: 4 points on a motion capture ‘L-Frame’ (rats, pups, mouse – 5 camera), 5 points on a custom 3D-printed object (mouse – 6 camera), or 8 landmarks in the recording cage (marmoset).

For computing camera calibrations in chickadee experiments, we moved a laser pointer’s spot through the arena with other illumination sources turned off and collected ~200 synchronized frames in all cameras. We thresholded each image frame and computed the centroid of the illumination spot. We then calibrated cameras using sparse bundle adjustment with custom code in Python (adapted from https://scipy-cookbook.readthedocs.io/items/bundle_adjustment.html). To determine the absolute scale and orientation of cameras, we rotated and scaled calibrations post hoc using arena landmarks. All approaches generally yielded sub-pixel reprojection error.

Datasets — Rat

We collected 1,164,343 timepoints of 1320×1048 color video data at 30 Hz from 6 synchronized cameras (Flea3 FL3-U3-13S2C, Point Grey) at 30 viewpoints overall. This yielded a total of 6,986,058 images, together with motion capture data (12 cameras) for 20 landmarks, from 6 different rats with affixed retroflective markers. Animals were lightly shaved and equipped with a headcap to accommodate neural recordings for separate work. Of these ~1.2 million timepoints, we separated the first 30 minutes of recordings from 4 different rats (216,000 timepoints) into a possible training pool. From this training pool, we drew 200 samples equally from each of 40 k-means pose clusters for each animal, using only samples with a complete set of ground truth labels. We manually removed clusters with erroneous motion capture predictions. We sampled with replacement from the clusters after we drew all unique examples. In this way, we used a total of 30,076 unique timepoints (180,456 images; 3,609,120 markers) across all 4 training animals. This approach balanced the set of poses over which we trained DANNCE, although in the future it may be better to sample equally from our defined behavioral clusters, across high and low levels of granularity.

All data after the first 30 minutes in these 4 animals composed the in-sample validation dataset that was used for in-sample error metrics (Supplementary Fig. 5C-E). For the 2 animals not in the training set, we used one to create the “more data” condition in Fig. 3A and the other for out-of-sample validation metrics. This animal was recorded in two sessions (one using view 4, one using view 5, Supplementary Fig. 4F). We used error metrics from both recording sessions as the best illustration of DANNCE and DLC generalization to new animals and setups. In the “fine-tune” condition, for each session we randomly selected 225 samples used them to re-train the “more data” DANNCE, separately for each session. “Fine-tune” error metrics were calculated in the remaining samples.

To test generalization to markerless animals, we also collected 308,000 samples at the same resolution and framerate from 3 rats without markers. To evaluate predictions in markerless rats, 2 humans labeled landmarks in 3 views over 100 total timepoints from these animals. We triangulated these labels to 3D by taking the median vector of triangulations between camera pairs and use these 3D points for comparison. We used predictions from all 3 rats to create behavioral maps.

Datasets — Mouse

We used 3 different datasets for analyzing DANNCE and DLC performance on markerless mice. First, for testing DLC and DANNCE accuracy head-to-head (Supplementary Fig. 11), we collected ~68 minutes total of 1320×1048 color video data at 30 Hz from 3 synchronized cameras of 3 C57/BL6 mice behaving in an open arena without bedding. To form the training set for DANNCE and DLC, we triangulated one set of human-labeled 2D annotations of 16 landmarks over 50 randomly sampled timepoints (25 timepoints in each of 2 animals). To form the validation set, 2 human labelers annotated an additional 50 timepoints (i.e. 150 images) in these training animals, and 50 timepoints in a third animal used completely for validation.

Second, for quantifying the improvement of accuracy with a higher number of cameras, we collected 20 minutes of 1320×1048 color video data at 30 Hz (36,000 samples) from 5 synchronized cameras, also of a C57 mouse behaving in an open arena without bedding. To form the training set, we triangulated one set of human-labeled 2D annotations of 16 landmarks over 50 randomly sampled timepoints. To form the test set, 2 human labelers annotated an additional 50 timepoints.

Third, for kinematic, behavioral, and power spectral density analyses, we collected 3 hours of recordings at 100 Hz (1,080,000 total frames) from six synchronized 1152×1024 color video cameras (Aca1920-150uc, Basler) in 3 C57/BL6 mice (1 hour for each mouse). Mice explored an area enclosed by a 7.5-inch diameter glass cylinder. These 3 mice were used for the analyses in Fig. 4 after fine-tuning DANNCE. To fine-tune DANNCE, we collected data from an additional two mice and labeled an expanded set of 22 landmarks, including three points on the tail, in a total of 172 samples (1032 images). This expanded landmark set provided a more complete picture of the animal’s pose.

Datasets — Rat Development

We collected data from two litters of 10 and 13 pups each, which we weaned at P21. We recorded on each day between P7 and P22, and at P25 and P30. On each day we randomly selected six pups from the litter without regard to sex and placed them into a 12-inch open field arena sterilized with ethanol. Upon placement we immediately recorded behavior using 3 synchronized, calibrated video cameras (Flea3 FL3-U3-13S2C, FLIR Point Grey; 1320×1048 color video data at 30 Hz) for 12 minutes from P7, and 20 minutes from P14–P30. After video recording, we took gross anatomical measurements of the rat body size. These measurements informed our input for the size of the volume imposed around the rat’s center of mass in the DANNCE network.

We fine-tuned DANNCE separately for each developmental timepoint (P7, P14, P21, P30). Because rats on P20 and P22 showed similar morphology and behavior as P21, we combined them, so that all results from P21 include recordings from P20 and P22. To form the training sets, we triangulated one set of human-labeled 2D annotations of 16 landmarks in samples selected randomly from the recordings. We hand labeled 180 samples for P7, 150 for P14, 575 for P21 and 210 for P30. We found that including labeled training data from adjacent timepoints improved prediction accuracy. We did not exhaustively search all combinations of training data for each day, but additionally labeled 10 samples from P13, 30 samples from P15, 60 samples from both P20 and P22, and 105 samples from P40. For fine-tuning networks for P14 predictions, we used hand-labeled data from P13-P15 and P20-21. For P21 fine-tuning, we used data from P14 and P20-P22. For P30 fine-tuning, we used data from P30 and P40. To further improve generalization, videos on P14 and P22 were color-corrected to match the statistics of the color histogram on P21. For quantification of behavioral repertoire and behavioral ontogeny, we used predictions over all available video in all pups.

Datasets — Marmoset

We acquired 23 minutes of 1920×1200 color video data at 29 Hz using 3 synchronized cameras (Blackfly BFLY-U3-23S6C-C, FLIR Point Grey) of one marmoset as it explored in half its typical homecage enclosure (850×850×700 mm). The enclosure contained 5 wooden perches and 3 metal shelves to encourage the animal to engage in naturalistic behaviors. Of the 23 minutes, 10 minutes was collected in the enclosure without any enrichment devices. An additional 10 minutes included one food-filled ball device on the floor. Another 3 minutes included two food-filled ball devices on the floor. To form the training set, we selected 100 timepoints at random from each camera (300 frames) from the recording without ball devices and used one human labeler to annotate 16 landmarks in each 2D view. These annotations were then triangulated to 3D to provide ground truth training targets. We used 96 of these labeled timepoints for training and 4 for monitoring validation loss during training. For behavioral mapping analysis, we used predictions over the full 23 minutes of video. For validation error metrics, 2 human labelers annotated 35 timepoints of video (105 frames) not used for training in the recording without ball devices.

Datasets — Chickadee

We acquired video data from 12 sessions of 5 wild-caught Black Capped Chickadees (Poecile atricapillus) as they foraged for, cached, and retrieved food items in a custom-built, 30-in × 30-in arena. The birds’ flight feathers were clipped to prevent flight, but behavior was otherwise unconstrained. The arena contained a central feeder that could be open or closed, revealing hulled sunflower seeds, and a 12 × 12 grid of wooden perches each matched with a cache site where food could be deposited and/or withdrawn. Sessions lasted for 2 hours, during which we continually recorded video data at 60 Hz using 6 cameras (Blackfly S USB-3, FLIR equipped with a Sony IMX428-mono sensor and a Tamron 8mm C-Mount lens). Frames were acquired with 800 μs exposure and synchronized by a hardware trigger shared between all cameras. Side-views from 4 cameras were recorded at 2816×1408 pixels, and top-views from 2 cameras were recorded at 2816×1696 pixels.

From each session, we selected 25-30 frames spaced pseudo-randomly throughout the session for annotation, and we annotated the position of 18 landmarks in each 2D view along with triangulated 3D positions. This data formed our dataset for training and validation. To obtain test data, we separately selected 35 non-overlapping frames from a single session, after clustering postures obtained with a trained DANNCE network into 7 clusters and drawing 5 frames randomly from each cluster in order to sample a range of postural variability. Frames were clustered using k-means on the vector of standardized pairwise 3D distances between all 18 landmarks. This test data was independently annotated by two human labelers.

Error Metrics

As is standard in the 3D human pose estimation field⁴³, we report error (in mm units) up to a Procrustes transformation (translation and rotation, but no scaling). This error is also consistent with the way we analyze kinematics: landmark positions are first centered and rotated to align each prediction to an internal reference. For landmark accuracy metrics, we also use the standard PCK (Percent Correct Keypoints) from the human pose estimation field⁵⁴. To calculate PCK (or accuracy) for rat, we set a threshold on the error metrics approximately equal to the average distance between two forelimb markers (18 mm), and we designated all predictions above this error threshold incorrect. Accuracy is then computed as the fraction of correct labels after applying this threshold. For accuracy over number of landmarks, we plot the fraction of timepoints having at least k correct landmarks, for k = 1 to k = K, with K equal to the number of landmarks tracked in each timepoint (20 for rat, 16 for mouse error summaries). The accuracy threshold for mouse was reduced to 9 mm, reflecting the different length of the forelimb in this species. In rat pups, we used a different threshold for each developmental age, again reflecting the length of the forearm, as measured by the average distance between human annotated forelimb landmarks, in each dataset: 11.24 mm for P7, 12.08 mm for P14, 13.12 mm for P21, 17.67 mm for P30. In marmoset, we show accuracy as a function of error threshold up to the forelimb length of the animal. In birds, we show accuracy as a function of error threshold up to the length of the animal’s legs.

For markerless rats, we also calculated a reconstruction error and accuracy that indicate how well predictions on these animals are described by the top ground truth eigenpostures in our dataset. The reconstruction errors are simply the residuals of the following multivariate linear regression applied to each sample:

$$y=\beta x,$$

where y is a 60-dimensional vector of the x-y-z coordinates of each of the 20 predicted landmarks, β is a 1×20-dimensional vector of fit coefficients, and x is a 20×60 matrix of the top 20 principal components over all data from all 4 motion capture training animals. After solving the regression, $\widehat{y}=\widehat{\beta }x$, with $\widehat{\beta }$ the best-fit coefficients and $\widehat{y}$ the predicted pose. Reconstruction error is then the magnitude of the residuals, $y-\widehat{y}$ after reshaping to a 20×3 matrix representing the residual for each x-, y-, and z- coordinate for each of the 20 markers. Using these errors, reconstruction accuracy is calculated the same way as standard accuracy, above.

Building the Volumetric Representation

Our method is a 3D analog of a 2D CNN for landmark detection. Given a full 3D rendering of a subject and its environment, a 3D CNN could be used to find the positions of specific 3D landmarks, similar to how 2D CNNs can find 2D landmarks within 2D images. However, we are given only 2D images from multiple angles. To exploit the power of the 3D CNN in this context, we construct a 3D volume from the data in the individual images using projective geometry, such that each position in the volume is characterized by the RGB values of all 2D pixel values whose traced rays pass through that position. This unprojection provides a set of geometrically aligned 3D spatial features that can be processed by a 3D convolutional neural network. A visualization of this methodology is shown in Supplementary Figure 3 and is detailed below.

To arrive at this volumetric representation, we use classic results from projective geometry⁵⁵. We first begin with a block matrix representation of the extrinsic geometry of each camera, $C^i=[R_{3\times 3}^i\mid t_{3\times 1}^i]$, where Rⁱ and tⁱ are the global 3D rotation matrix and translation vector of the ith camera, respectively, relative to an anchor coordinate system. The intrinsic geometry of each camera is

$$K^i=\left[\begin{array}{ccc}\hfill f_x^i\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill s^i\hfill & \hfill f_y^i\hfill & \hfill 0\hfill \\ \hfill c_x^i\hfill & \hfill c_y^i\hfill & \hfill 1\hfill \end{array}\right],$$

where $f_x^i$ and $f_y^i$ are the ith camera’s focal length normalized by the number of pixels along the width and height of the sensor, respectively, $c_x^i$ and $c_y^i$ are the coordinates of the camera’s principal point, and sⁱ is the sensor’s skew. We then use 3D-to-2D projected, continuous coordinates to sample from the discrete 2D image with interpolation, transferring the RGB pixel values to voxel positions in a 3D volume. For a single 3D voxel coordinate $[\tilde{x},\tilde{y},\tilde{z}{]}^{\mathsf{T}}$, its projected 2D coordinates in the original pixel space of camera i are $[x^{\prime },y^{\prime }{]}^{\mathsf{T}}={\left[\frac{u}{z},\frac{v}{z}\right]}^{\mathsf{T}}$, with

$$[u,v,z{]}^{\mathsf{T}}=K^i{C}^i[\tilde{x},\tilde{y},\tilde{z},1{]}^{\mathsf{T}},$$

which represents the projective transformation of a 3D world homogeneous coordinate into a point in the camera.

We also model the lens distortion specific to each camera. From an original 2D point on the image of the i^th camera, [x′, y′]^⊺, we normalize to obtain $\widehat{p}=[\widehat{x},\widehat{y}{]}^{\mathsf{T}}=g\left([x^{\prime },y^{\prime }{]}^{\mathsf{T}},K^i\right)$, representing a normalized point relative to the center of the camera. g(·, Kⁱ) is a function normalizing points with respect to the camera's intrinsic parameters. The corrected x- and y-coordinates are then given by

$$p=[x,y{]}^{\mathsf{T}}=g^{-1}\left([t_x,t_y{]}^{\mathsf{T}}+[r_x,r_y{]}^{\mathsf{T}},K^i\right),\text{and}$$

$$[r_x,r_y{]}^{\mathsf{T}}=[\widehat{x},\widehat{y}{]}^{\mathsf{T}}([k_1^i,k_2^i,k_3^i]\cdot [{\widehat{p}}^{\mathsf{T}}\widehat{p},({\widehat{p}}^{\mathsf{T}}\widehat{p}{)}^2,({\widehat{p}}^{\mathsf{T}}\widehat{p}{)}^3{]}^{\mathsf{T}}+1),\text{with}$$

$$[t_x,t_y{]}^{\mathsf{T}}=\left[\begin{array}{cc}\hfill 2\widehat{x}\widehat{y}\hfill & \hfill 2\widehat{x}+{\widehat{p}}^{\mathsf{T}}\widehat{p}\hfill \\ \hfill 2\widehat{y}+{\widehat{p}}^{\mathsf{T}}\widehat{p}\hfill & \hfill 2\widehat{x}\widehat{y}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill {\widehat{k}}_1^i\hfill \\ \hfill {\widehat{k}}_2^i\hfill \end{array}\right],$$

where $\{k_1^i,k_2^i,k_3^i\}$ and $\{{\widehat{k}}_1^i,{\widehat{k}}_2^i\}$ are the ith camera's radial and tangential distortion coefficients, respectively. These parameters are fit by a calibration procedure done prior to data collection.

Finally, the 3D volume for view i of an image I at location $(\tilde{x},\tilde{y},\tilde{z})$ is

$$V_{\tilde{x},\tilde{y},\tilde{z}}^i=f\left(I^i,P([\tilde{x},\tilde{y},\tilde{z}{]}^{\mathsf{T}},C^i,K^i)\right),$$

where P(·) is the complete 3D-to-2D projective transformation with distortion and f(Iⁱ, [x, y]^⊺) is a function sampling the discrete image Iⁱ at continuous image coordinates (x, y). Note that this implies that $V_{\tilde{x},\tilde{y},\tilde{z}}^i=f(I^i,[x,y{]}^{\mathsf{T}})$, which reveals that for a ray in the 3D space that projects to the same point in the camera's pixel space, all values are equivalent. In this way, image features are aligned along epipolar lines through 3D space such that the 3D position of any given point is at the intersection of matched features within this volume.

Most volumetric ray tracing techniques focus on single objects centered within a small 3D space. In such cases, a 3D volume small enough for computation is large enough to encompass an entire field of view. Rather than cover our large naturalistic arena with a grid, we anchor the 3D volume on an estimate of the animal’s 3D center of mass (COM) in each frame, determined by triangulating the animal’s 2D position, which is estimated using a separate 2D CNN (see Training Details below), of the animal across all camera pairs. In this way, we have sufficient resolution to describe the animal while remaining geometrically consistent when sampling from the input images. Triangulation is implemented classically using singular value decomposition to find the least squares solution to a system of equations relating the 3D coordinates of a point to the 2D projected coordinates of the point in images from two different cameras whose intrinsic an extrinsic parameters are known⁵⁵.

Processing the Volumetric Representation

To learn feature representations within the 3D structure of the input volumes, we use a 3D U-net⁵⁶, which is designed to harness both local and global image content via skip connections. Thus, decisions about landmark location can include both local features like color and shape and also higher-level information about the relationships between landmarks across the entire body of the animal. These considerations have led to similar networks for 2D landmark detection in humans⁵⁷.

The network learns to fuse information across views using aligned local image structure, including depth cues in the form of ray tracing convergence patterns. We achieve this by concatenating the input volumes along the color axis, such that $V_n=[V_n^1,\dots ,V_n^j]$ for j total views, and feeding it as input into the CNN. To promote view invariance and to remove any dependence on camera order, we shuffled the camera order in each training example, although for applications with more static camera arrangements, this constraint can be lifted to better leverage view idiosyncrasies.

To ensure that tracked landmarks can be discovered anywhere in an image as long as they present with similar features across multiple scales, we treated the problem as pixel-wise semantic segmentation, rather than coordinate regression. This also reduces the amount of required training data¹⁵. Such supervision could be applied directly to 3D voxels for our task, but doing so would pin our resolution to a coarse grid. Instead, our network outputs an intermediate probability distribution map over 3D space for each marker, G_m, and applies a spatial softmax such that ∑_x,y,z G_m = 1. We then produce sub-voxel resolution coordinates for the mth landmark by taking the spatial expected value,

$$[x_m,y_m,z_m]={\sum }_{x,y,z}[x\cdot G_m(x,y,z),y\cdot G_m(x,y,z),z\cdot G_m(x,y,z)],$$

and we supervise with a standard L2 loss. This version of the network is called “AVG,” for the spatial average applied to produce the output. For some animals and conditions (mice, marmosets), we found that supervising the 3D output distributions directly using 3D spherical Gaussians converged to a lower error on the training set. This version of the network is called “MAX,” as landmark positions are assigned to the voxels containing the maximum value of the 3D output distributions (Supplementary Note).

Training Details — Rat

We implemented DANNCE in Tensorflow and Keras and trained using the Adam optimizer (learning rate = 0.001, β₁ = 0.9, β₂ = 0.999) for 30 epochs with a batch size of 4. We followed a standard U-Net approach, with 3×3×3 'same' padding convolutional kernels in all layers, except the last leading to the 3D probability maps, which used a 1×1×1 kernel. We used “layer normalization” layers between all convolutional layers. All activation functions were ReLU, except for the last layer, which used a linear readout. For the max pooling layers, we used 2×2×2 kernels. For the 3D Transpose layers, we used 2×2×2 kernels with 2x2x2 stride. We used the following number of features in each layer: [64, 64, 128, 128, 256, 256, 512, 512, 256, 256, 128, 128, 64, 64, N (the number of landmarks)]. We used a Glorot uniform⁵⁸ initialization for all weights. We performed no exhaustive hyperparameter search over this architecture, although we did train shallower networks that did not achieve the same level of performance, and we found that batch normalization performed significantly worse than layer normalization.

We used a 64×64×64 volumetric grid with 3.75 mm isometric voxel resolution. To reduce computational complexity, we sampled from input images using nearest neighbor interpolation. For anchor 3D COM coordinates in rat training animals, we triangulated and averaged the predictions from DLC, which were accurate within training subjects. In validation animals, where DLC performed poorly, we trained a 2D U-Net trained from motion capture projections (in training subjects) to predict the 2D COM (Supplementary Note). For the rat validation subjects and for markerless animals, we fine-tuned this network in a bootstrapping procedure, using confident DANNCE labels (projected to 2D) as training targets (no validation subject ground truth data were used other than for validation error metrics). For validation metrics on animals with markers we used only frames where all 20 markers were tracked by the motion capture system without imputation. For the validation metrics on markerless animals, we used all labeled frames.

For 3-camera rat DANNCE, we trained a version of the network that accepted only 3 volumes (from 3 views) as input. For every training example, we took a random subset of 3 cameras as input when it was called into the minibatch. In this way, we trained a network to work with 3 cameras, having seen a diversity of view combinations over the course of training, which we expected would help generalization to new views. When evaluating 3 camera predictions after training, we took a random subset of timepoints that had a corresponding complete set of ground truth motion capture for comparison. We then averaged the error across all possible 3 camera configurations in these samples. For 1-camera rat DANNCE, we trained a version that accepted only 1 volume (from 1 view) as input. During training, each minibatch comprised all 6 1-camera examples from a given timepoint. When validating 1-camera DANNCE, we centered 1-camera volumes on the 3D COM detected and triangulated from all views. Future work should explore methods to extract the animal’s global 3D position without multiple cameras.

For testing performance dependence on camera calibration accuracy (Supplementary Fig. 6), we used random perturbations of camera extrinsic rotation matrices and described the magnitude of the perturbations in terms of the angular difference between the perturbed and original matrices and in terms of their effect on reprojection error. Perturbations were applied by randomly sampling yaw, pitch, and roll angles and applying these rotations to the original matrix. To calculate the angular distance between rotations, we used a formulation based on axis-angle representations. Specifically, for original extrinsic rotation matrix R₀ and for the perturbed extrinsic rotation matrix R_p, we calculated the rotation from R₀ to R_p as $R=R_0{R}_p^{\mathsf{T}}$ and used the angular component, θ, of the axis-angle representation of R as the angular difference, with $\theta ={\cos }^{-1}\frac{\text{tr}(R)-1}{2}$. To calculate reprojection error, we triangulated and reprojected the original 2D projected motion capture points using the perturbed rotation matrices.

For testing how DANNCE and DLC performance was affected by image resolution (Supplementary Fig. 7), we simulated lower resolution input by first downsampling the images with a local mean and then resizing the images back to their original sizes using bilinear interpolation. These images were used as input to previously trained DANNCE and DLC systems (no new fine-tuning was performed at lower resolution). To assess whether DANNCE generalized to new behaviors (Supplementary Fig. 9), we used the coarse behavioral labels to remove all instances of left grooming from the Rat 7M training dataset and then trained DANNCE as before.

Training Details — Mouse

We fine-tuned DANNCE for 1200 epochs with a batch size of 4 using the Adam optimizer with the same parameters as in rat and locked weights in the first convolutional layer. We found that a version of DANNCE without the final spatial average layer converged to lower error on the training set. We instead supervised the 3D output distributions directly using 3D spherical Gaussians with σ = 10 mm, centered on the target landmark positions (“MAX” version of DANNCE). We used a 64x64x64 volumetric grid with r = 1.875 mm isometric voxel resolution. For mice used in performance quantification (Supplementary Fig. 11), the final convolutional layer was changed to output 16 landmark 3D distributions, rather than the original 20 used for rat. The 16 landmarks were: face, left ear, right ear, anterior spine, medial spine, posterior spine, middle of tail, end of the tail, left and right hand, left and right arm, left and right foot, left and right leg. For the mice used for behavioral mapping and kinematic analysis, we changed the output to 22 landmarks for a more detailed description of behavior: snout, left ear, right ear, anterior spine, medial spine, posterior spine, middle of tail, end of the tail, left and right hand, left and right elbow, left and right shoulder, left and right hip, left and right knee, and left and right foot. In Supplementary Video 6, we present predictions from an “AVG” version of the DANNCE network (Supplementary Note), which produced temporally smoother predictions than “MAX.”

Training Details — Rat Development

We fine-tuned DANNCE using the same optimizer parameters as in rats. Also, as in mouse and marmoset, the final convolutional layer was changed to output 16 landmark 3D distributions, rather than the original 20 used for rat. The predicted position of each landmark was taken as the spatial position of the expected value in each 3D output map (the “AVG” version of DANNCE).

We trained separate networks for each developmental timepoint (P7, P14, P21, P30) using the hand-labeled training dataset (c.f. Datasets — Rat Development). Each network was trained for 500 epochs with a batch size of 4. We used a 64×64×64 volumetric grid, and the spatial extent of the 3D grid was adjusted for each age so that animals maximally filled the 3D volume. For P7, the side length of the 3D volume was 160 mm (r = 1.875 mm isometric voxel resolution), 240 mm for P14 and P21 (r = 2.5 mm), and 400 mm for P30 (r = 3.125 mm).

We used the same training set as used for DANNCE to train four separate networks (one for each developmental timepoint) to find the animal COM necessary for anchoring the 3D grids. When training and predicting with DANNCE, we de-noised the COM predictions by taking a 30-frame median of the triangulated x-, y-, and z-coordinates of the 3D COM. This removed punctuated anomalies in the 3D COM positions while remaining precise enough to locate the animal and fit it into the resulting 3D grid passed to DANNCE. As DANNCE predicts absolute 3D coordinates for each landmark, it does not depend on the true position of the animal’s 3D COM. To apply DANNCE to adjacent timepoints (P21, and P22), we fine-tuned the COM network with an additional 100-200 samples of video in which only overall animal position was labeled.

Training Details — Marmoset

As with mice, we fine-tuned a version of DANNCE lacking a final soft-argmax output, locked the weights in the first convolutional layer, and used the same optimizer parameters as in rat. We tracked 16 landmarks: face, left ear, right ear, anterior spine, medial spine, posterior spine, middle of tail, end of the tail, left and right hand, left and right arm, left and right foot, left and right leg. We used 96 of the 100 labeled training samples for training and 4 for monitoring loss during training. We fine-tuned DANNCE for 1600 epochs with a batch size of 4 and chose weights from the epoch with the lowest validation loss (epoch 1368) for making subsequent predictions. We used a 64×64×64 volumetric grid with side length 600 mm (r = 9.375 mm isometric voxel resolution), and a 3D spherical Gaussian with σ = 20 mm as training targets.

For training the marmoset COM finding network, we used the 100 training samples (300 images) together with 300 additional images labeled only for the animal’s position in the frame. Before making DANNCE predictions, 3D COM traces were filtered with a 10-frame median filter to remove transient outliers. We also found that in frames with substantial occlusion, DANNCE predictions were improved when refining the output with a pictorial structures model that constrains probability mass in the output 3D maps according to a simple skeleton model³⁹, and these refined predictions were used for making behavioral maps. Plots of segment length and landmark error were made from predictions prior to the pictorial structures model. In addition, when analyzing the distributions of segment lengths (Fig. 6B), we used the maximum value of the output 3D probability maps for each landmark to select for the top 75% most confident DANNCE predictions. In Supplementary Video 9, we show predictions prior to the pictorial structures model after linearly interpolating landmarks whose segments were in the top 10^th percentile of length, and smoothing all predictions with a 10-frame median filter.

Training Details — Chickadee

We fine-tuned a version of DANNCE which was trained on the full rat dataset after converting color videos to grayscale. We locked weights in the first two convolutional layers, and the final convolutional layer was changed to output 18 landmark locations relevant to this new body plan. We predicted 8 ‘central’ landmarks: the top and bottom of the beak, top and back of head, chest center, back center, junction of trunk with tail, and tail tip. We also predicted 5 pairs of landmarks for the right and left sides: eye, tip of bib, shoulder, ankle, and foot. We selected 3 random samples from each of the 12 sessions for loss validation during training, and the remaining 22-27 samples from each session were used for training. We fine-tuned DANNCE for 2000 epochs with a batch size of 4. We used a 64×64×64 volumetric grid with side length 84 mm, corresponding to an isometric voxel resolution of 1.31 mm.

For training the chickadee COM network, we used the same training data described above, after downsampling images by a factor of 4, and averaging all shoulder, chest, and back landmarks to obtain a ‘body’ position coordinate. We also obtained a ‘head’ position coordinate by averaging left and right eye. Unlike for other species, the COM network used in this study was a stacked DenseNet (n=2, growth rate=48) implemented in DeepPoseKit⁶. The COM network was trained to predict head, body, and tail tip positions, from any camera view. A random 15% of data was used to monitor validation loss during training with the Adam optimizer (learning rate = 0.001). The learning rate was decreased by a factor of 0.2 after 20 epochs with no improvement in validation loss, training was terminated after 43 epochs with no improvement, and the weights from the epoch with best validation loss were selected for subsequent prediction. Predictions from this COM net were then handled as for other datasets, with the ‘body’ landmark used to anchor the volumetric grid fed to DANNCE.

Because not all bird landmarks were located at joints, some ground truth segment lengths were less stable than others. Thus, for analyzing bird segment lengths and landmark prediction performance, we used landmarks belonging to the most stable segments in each anatomical area. This improved the interpretability of our performance metrics, which use segment lengths to provide a sense of body scale. For the head we used the segment connecting the top of the head to the back of the head, for the trunk the segment from the center of the chest to the center of the back, for the wings the segment connecting the left and right shoulders, and for the legs the segments on both the left and right sides that connected the foot to the ankle.

Training Details — DeepLabCut

We initialized DeeperCut (the algorithm used in DeepLabCut) using ResNet 101 and fine-tuned using default training configurations^4,54. Landmark predictions were made without pairwise terms. In rats, we trained a single network on the same 180,456 unique images as for DANNCE training, using projected 2D motion capture coordinates as targets. During inference, we triangulated 2D predictions across multiple views by taking the median vector across all individual pairwise triangulations, which was far superior to multi-view direct linear transformation (DLT)^8,55. We also present the results from the DLT triangulation in Figure 3. For 3-camera predictions, we repeated these triangulation procedures for all possible sets of 3 views and report average statistics. For 2-camera predictions, we used all possible sets of 2 cameras. All triangulations used the more accurate median procedure unless stated otherwise. Note that 3- and 2-camera predictions were made using a network trained using the full dataset (i.e. all 6 views). For 5-camera and 3-camera mouse experiments, we fine-tuned the DLC network trained on rat data using the datasets described in Datasets — Mouse, using the same training configuration as with rat.

Behavioral Mapping

To create behavioral embeddings for each organism, we generated feature vectors describing the whole-body pose and kinematics in a local time window (~500 ms) on each frame for each subject. To create feature vectors for markerless rats, mice, humans, rat pups, marmosets, and chickadees, we first defined a linkage tree between tracked markers defining the major joints of each organism’s body on the head, trunk, and appendages. We computed the top 10 principal components of the linkage vectors in Euclidean space, the linkage lengths, and joint angles, yielding a set of eigenpostures for each feature category⁵⁹. We then computed the Morlet wavelet transform of each of these descriptors of animal’s pose at 25 scales, spaced dyadically from 1 to 25 Hz, yielding a 250-dimensional time-frequency representation of each feature’s kinematics. We computed the top 10 principal components of each 250-dimensional vector, and combined the postural and kinematic features, yielding a 60-dimensional feature space describing the pose and kinematics of animals on each frame. We used a common set of principal component vectors for each organism that we applied to each replicate studied. For adult rats and mice these were computed from all data from a single subject, for rat pups and marmosets these were computed from all the data from each analyzed condition. For quantifying behavioral ontogeny, we used a common set of principal components derived from postnatal day 21.

To create feature vectors for rats bearing markers in the Rat 7M dataset (Fig. 2), we computed a 140-dimensional feature vector describing the pose and kinematics of the animal on each frame. This expanded feature set consisted of a 60-dimensional feature vector described above, as well as an 80-dimensional feature vector that consisted of the eigenpostures and wavelet transforms of the position, segment lengths, and joint angles of the head, trunk, and hips, as well as summary statistics describing the velocity of the animal’s spine, head, and center of mass. We used this expanded feature set to integrate these recordings with a more extended study that created a tSNE embedding from 925 hours of rat behavior measured using motion capture²³. We reembeded points into this tSNE embedding using a nearest neighbors’ algorithm. For all analyses using rats bearing markers we did not embed frames in which animals were resting to reduce compaction of the tSNE space.

After computing the feature vector for each frame in all recordings, we concatenated feature vectors across relevant timepoints and conditions. We sampled this feature vector at 29 Hz for marmosets and 6 Hz for all other organisms and embedded them in 2D using the Barnes-Hut approximation of tSNE with θ=0.5 and perplexity of 30. We smoothed the embedding space with a density kernel that segregated the density map into distinct clusters using a watershed transform²⁴. We chose density kernels so that neighboring clusters were approximately human distinguishable. Following clustering, two humans observed 24 distinct instances of each behavior sampled and assigned it a behavioral label. Behavior labels for adult rats and mice were chosen to reference past literature, when possible. To assess the accuracy of these semi-automated behavioral labels in rat pups, we randomly drew 25 instances of each behavioral category for each developmental timepoint and had a human assign them a behavioral label (Supplementary Fig. 13).

Mouse power spectral density analysis

To demonstrate DANNCE’s ability to isolate and describe body movement, we used DANNCE predictions from 1 hour of video recording in a single subject from the 100 Hz, 6-camera acquisition dataset, and we filtered these predictions using a third order, 15-frame Savitzky-Golay filter, which reduced high frequency noise while maintaining qualitatively accurate tracking of anatomical landmarks. From these traces, we then isolated all behavioral examples for this animal in 4 different clusters extracted automatically from our behavioral mapping analysis. For the grooming examples, we excised 1000-frame (10 s) traces centered on behavioral timestamps. For the walking examples, we excised 300-frame (3 s) traces centered on behavioral timestamps, as walking behaviors were typically shorter in duration than grooming episodes.

Thus, for a given cluster and landmark, we obtained a collection of traces describing the x-, y-, and z-position of the landmark. To calculate the PSD for this landmark, we convert these traces to individual x-, y-, and z-velocity components and z-score each component (i.e. zero mean, unit variance), except for left and right forelimb grooming PSDs, in which all limb velocity traces were normalized to the standard deviation of the left and right forelimb traces, respectively. We concatenated the Euclidean components and calculated the PSD using Welch’s method and a Hann window with 50 timepoint overlap between segments (i.e. sampling rate / 2). We report PSDs in linear units.

Behavioral Comparisons across Developmental Stages

To facilitate quantitative comparisons of behavioral repertoires across developmental stages, we computed 60 dimensional postural and kinematic feature spaces as described above. Instead of using a unique set of principal components to each timepoint studied, we used a common set of principal components derived from the P21 timepoint. To make quantitative comparisons of behavioral complexity (Fig. 5E), we computed the pairwise Euclidean distance between all timepoints in this common 60 dimensional feature space for each timepoint, and computed the distance between the 95^th and 5^th percentile values of these pairwise distances, which yielded an estimate of the overall diameter of the feature space sampled on each day. We scaled the area of density maps (Fig. 5D) by the relative diameter of the feature spaces across timepoints. A similar increase in behavioral complexity was observed when z-scoring the feature space within each timepoint, to potentially account for any effects of changing body size.

To compute the similarity of behavioral repertoires across stages, we computed k-means clustering in the common feature space for each timepoint. We took k=40 clusters for the P14 timepoint, and linearly scaled the number of clusters taken at other timepoints by their feature space diameter described above. Taking different numbers of clusters, or using a shared number of clusters across timepoints, did not substantially affect the results. To compare the similarity of behavioral repertoires across pairs of timepoints (Fig. 5F), we computed the correlation coefficient across all possible pairs of cluster means. For each cluster in each timepoint, we selected the maximum correlation coefficient. The similarity across timepoints was taken as the average of these maximum correlation coefficients for all clusters.

To compute ontogeny graph of rearing (Fig. 5H), we first computed the Pearson correlation coefficient of mean behavioral feature vectors between all pairs of clusters on neighboring developmental timepoints. We then selected a subset of rearing clusters in the P30 timepoint and identified the clusters with highest correlation values to these at P21, and similarly for P14 and P7. We then displayed these selected clusters in the ontogeny graph, representing different behavioral clusters as nodes.

Statistics

All values reported as mean ± s.d. unless otherwise stated. In bar graphs, error bars correspond to standard deviation unless otherwise stated. In box-and-whisker plots, boxes show median with inter-quartile range, with whiskers extending to 1.5 times the inter-quartile range, and with the arithmetic mean shown as a black square. Videos, plot, and analyses were performed in either Matlab 2018a, Matlab 2019a, or Python 3.6.7 (with the aid of numpy 1.15.1, scipy 1.1.0, jupyter 1.0.0, and matplotlib 2.2.2).

Data Availability

The Rat 7M video and motion capture datasets are available at https://doi.org/10.6084/m9.figshare.c.5295370.v3. Mouse training labels, video, and DANNCE predictions are available at https://github.com/spoonsso/dannce/. Statistical source data for Figures 1, 5 and 6 are included with the manuscript. Source data for Fig. 3 are available at https://doi.org/10.6084/m9.figshare.13884038. Marmoset data are subject to additional veterinary restrictions and can be made available upon request.

Code Availability

The code for DANNCE is available at https://github.com/spoonsso/dannce/ and https://doi.org/10.5281/zenodo.4567514⁶⁰. Code for analyzing and plotting data is available at https://doi.org/10.5281/zenodo.4571521⁶¹. The code for labeling points in 3D is available at https://github.com/diegoaldarondo/Label3D/. The core functions used for the behavioral embedding²³ are available at https://github.com/jessedmarshall/CAPTURE_demo.