SUMMARY
Tissue-clearing methods allow every cell in the mouse brain to be imaged without physical sectioning. However, the computational tools currently available for cell quantification in cleared tissue images have been limited to counting sparse cell populations in stereotypical mice. Here, we introduce NuMorph, a group of analysis tools to quantify all nuclei and nuclear markers within the mouse cortex after clearing and imaging by light-sheet microscopy. We apply NuMorph to investigate two distinct mouse models: a Topoisomerase 1 (Top1) model with severe neurodegenerative deficits and a Neurofibromin 1 (Nf1) model with a more subtle brain overgrowth phenotype. In each case, we identify differential effects of gene deletion on individual cell-type counts and distribution across cortical regions that manifest as alterations of gross brain morphology. These results underline the value of whole-brain imaging approaches, and the tools are widely applicable for studying brain structure phenotypes at cellular resolution.
Graphical abstract
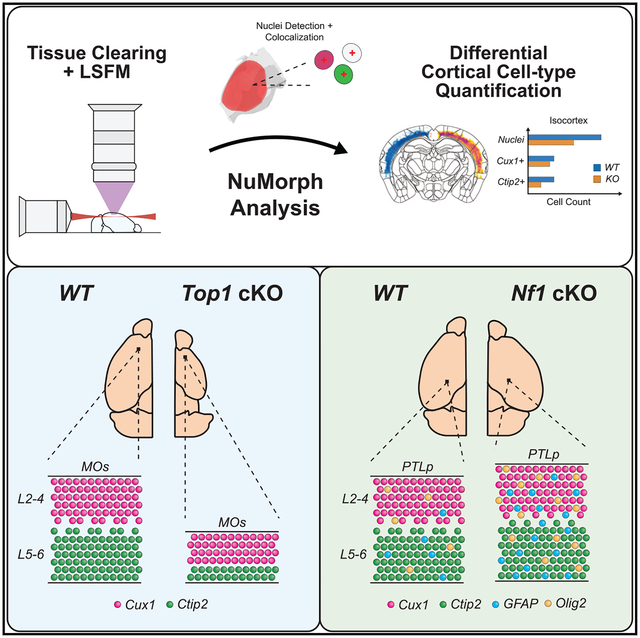
In brief
Krupa et al. develop an image analysis toolbox called NuMorph that accurately quantifies all nuclei within the mouse cortex after tissue clearing and light-sheet imaging. They implement NuMorph to characterize region- and cell-type-specific deficits present in two distinct mouse models, demonstrating the advantages of a whole-brain imaging approach.
INTRODUCTION
Tissue-clearing methods render biological specimens transparent while preserving their three-dimensional (3D) structure. Upon fluorescent labeling of protein and molecular markers, the entire cellular organization of cleared tissues can be rapidly imaged using light-sheet microscopy at acquisition rates 2–3 orders of magnitude faster than point scanning systems (Richardson and Lichtman, 2015; Ueda et al., 2020). Great strides have been made in the development of clearing protocols that are compatible with immunolabeling and the design of complementary sophisticated imaging systems (Murray et al., 2015; Park et al., 2019; Matsumoto et al., 2019; Susaki et al., 2020). Yet challenges remain in expanding the accessibility of these technologies to research labs for quantitative analysis at cellular resolution.
For example, many of the current imaging protocols for whole-brain profiling require custom light-sheet systems to image tissues at cellular resolution (Tomer et al., 2014; Pende et al., 2018; Fei et al., 2019; Matsumoto et al., 2019; Voigt et al., 2019). These systems are therefore inaccessible to those lacking the expertise or resources required to assemble the necessary microscope components. Expanding tissues during the clearing process is a potential workaround that can increase the effective spatial resolution, allowing interrogation of subcellular structures without the need for custom imaging solutions (Chen et al., 2015; Ku et al., 2016; Murakami et al., 2018; Gao et al., 2019). However, expanded tissues can fall outside of the working distance of conventional microscope objectives and require prolonged imaging times and significantly larger data storage resources. Therefore, computational tools designed for conventional light-sheet microscope users are needed to compare cell counts in a wild-type (WT)/knockout (KO) design.
With more than 100 million cells in the mouse brain and data sizes of whole-brain images approaching the terabyte scale, advanced image analysis tools are needed to achieve accurate cell quantification. Current segmentation methods for tissue-cleared brain images apply a threshold for nuclear staining intensity and filter objects with a predefined shape, size, and/or density (Renier et al., 2016; Matsumoto et al., 2019; Fürth et al., 2018). However, variations in cell size, image contrast, and labeling intensity can all lead to inaccurate counts. In addition, whole-brain images are typically registered to a standard reference, such as the Allen Reference Atlas (ARA), to assign cell locations to their corresponding structural annotations. Thus far, image registration has been performed mostly on stereotypical mice and has not been designed for mouse models with significant changes in gross morphology. With these limitations, the computational tools currently available have not been fully adopted for studying cellular organization in mouse models.
To address these issues, we developed a group of image analysis tools called NuMorph (Nuclear-Based Morphometry; available at https://bitbucket.org/steinlabunc/numorph/) for end-to-end processing to perform cell-type quantification within the mouse cortex after tissue clearing and imaging by a conventional light-sheet microscope. To demonstrate the effectiveness of the tool, we first applied and evaluated NuMorph to quantify structural changes in a mouse model with large differences in cortical structure, a topoisomerase I (Top1) conditional KO (Top1 cKO) mouse model that exhibits clear reductions in both cortical size and specific cell types (Fragola et al., 2020). We then apply NuMorph to investigate a neurofibromin I (Nf1) cKO (Nf1 cKO) model, a gene harboring mutations in individuals with neurofibromatosis type I (NF1). This disorder often results in cognitive impairment, attention-deficit/hyperactivity disorder (ADHD), and autism spectrum disorder (ASD) (Gutmann et al., 2017). Our results reveal unique genetically influenced cell-type and structural changes in each mouse model, demonstrate the broad applicability of our analysis tools for studying both severe and subtle brain structure phenotypes in combination with tissue-clearing methods, and present an alternative to two-dimensional (2D) stereology for cellular quantification that does not rely on representative sampling.
RESULTS
iDISCO+ reveals neuronal cell-type deficits in the Top1 cKO cortex
A previous study demonstrated that deletion of Top1 in postmitotic excitatory neurons within the cortex and hippocampus results in massive neurodegeneration in these structures by post-natal day 15 (P15) (Fragola et al., 2020). Interestingly, although all cortical layers were affected by Top1 deletion, the lower cortical layers (layers 5 and 6) showed a noticeably greater reduction in thickness and cell count compared with the upper cortical layers (layers 2–4) (Fragola et al., 2020). However, these previous observations were limited to 2D sections within the somatosensory cortex, which itself is a large structure that can be further decomposed into multiple functional regions. To evaluate the effects of Top1 deletion on excitatory neuron cell types throughout all cortical structures, we performed iDISCO+ (Renier et al., 2016) to clear and image the Top1 cKO (Neurod6Cre/+::Top1fl/fl) mouse. We chose to use iDISCO+ among other tissue-clearing techniques because of its demonstrated compatibility with antibody labeling, minimal tissue expansion or shrinkage, and simplified protocol (Renier et al., 2016). To go beyond qualitative evaluation, we proceeded to develop cell detection and image registration tools that could accurately quantify the number of upper layer and lower layer neurons in each cortical region in Top1 cKO mice (Figure 1A).
Figure 1. Cellular resolution analysis of brain structure phenotypes for tissue-cleared 3D brain images.
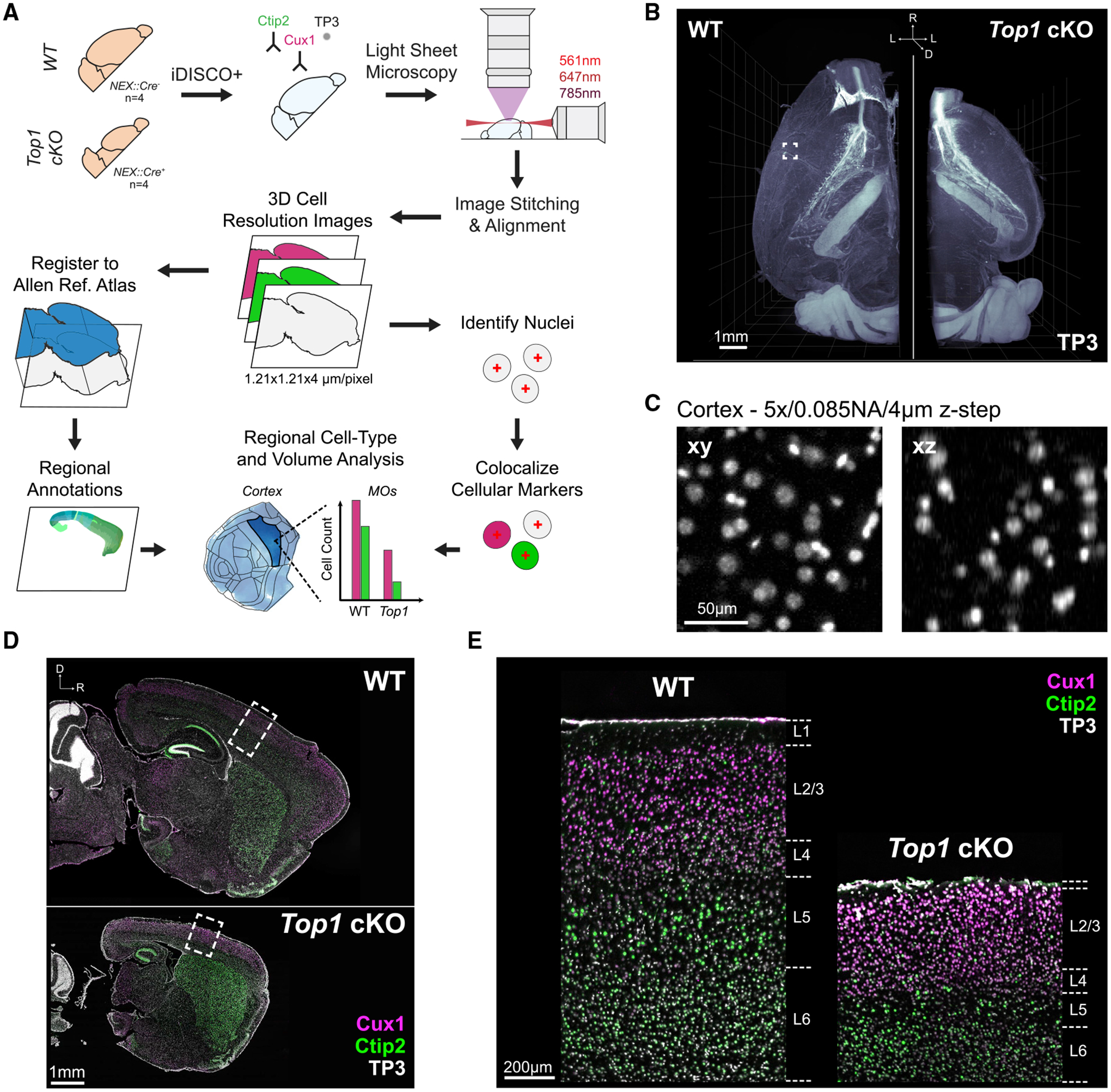
(A) Overview of tissue processing, imaging, and image analysis procedures.
(B) Three-dimensional rendering of nuclei in WT and Top1 cKO samples. Scale bar, 1mm.
(C) Example of TO-PRO-3 (TP3) labeled nuclei within a WT cortex captured at sufficient lateral (xy) and axial (xz) resolution for cell quantification. Scale bar, 50 μm.
(D) Optical sagittal sections of TO-PRO-3 nuclear staining and immunolabeling for cell-type-specific markers Ctip2 (lower layer neuron) and Cux1 (upper layer neuron) in WT and Top1 cKO samples. Scale bar, 1 mm.
(E) Zoomed-in images of boxed cortical areas in (D) demonstrating channel alignment and showing the expected localization of upper and lower layer markers. Scale bar, 200 μm.
We processed one brain hemisphere from four WT and four Top1 cKO mice at P15, when the Top1 cKO had displayed large, bilateral deficits in brain structure (Fragola et al., 2020). We labeled layer-specific cell types using antibodies for Cux1 (upper layer neuron marker) and Ctip2 (lower layer neuron marker) in addition to staining all cell nuclei with TO-PRO-3 (TP3) during iDISCO+ processing. After clearing, samples were imaged using the Ultramicroscope II, one of the most widely used commercial light-sheet microscopes for imaging cleared tissues (Ertürk et al., 2012; Tainaka et al., 2014; Susaki et al., 2015; Liebmann et al., 2016; Pan et al., 2016; Renier et al., 2016; Ye et al., 2016; Cai et al., 2019; Kirst et al., 2020). The Top1 cKO hemispheres displayed a noticeable reduction in overall cortical volume (Figure 1B). During light-sheet imaging, there is a well known trade off between optical resolution, particularly in the axial (z) dimension, and imaging speed. Although the Ultramicroscope II features axial sweeping to maintain relatively even z resolution throughout the field of view (Dean et al., 2015), the additional mechanical movement of the light-sheet significantly reduces the imaging rate. After testing various imaging schemes, we imaged at 1.21 × 1.21 × 4 μm/voxel resolution with a light-sheet thickness of 9 μm. The resulting images provided sufficient resolution to visually delineate cell nuclei in the cortex (Figure 1C) while limiting imaging time to 10–15 h for all three channels in one WT hemisphere (~9 h for Top1 cKO).
Prolonged imaging of cleared tissue samples can induce several artifacts over the course of image acquisition. In particular, drift in the sample or aberrant microscope stage movement can cause misalignment between image tile positions within and between channels. These issues become more pronounced at higher optical resolution, at which slight variations can prevent colocalization of cell nuclei with their respective immunolabeled markers. To ensure correct alignment between channels, we applied a series of rigid and non-rigid registration steps using the Elastix toolbox (Klein et al., 2010) to map the Cux1 and Ctip2 channels onto the TP3 channel without inducing non-specific local background warping (Figure S1). We also found that many of the commonly used programs for performing 3D image stitching (Bria and Iannello, 2012; Hörl et al., 2019) did not accurately align adjacent tile stacks, because of spurious stage movement, which has been noted by other groups (Kirst et al., 2020). To ensure accurate image reconstruction, we applied a simplified iterative 2D stitching procedure that uses scale-invariant feature transforms (Lowe, 2004) to produce continuous images without cell duplication along tile edges (Figure S2). Finally, differences in fluorescence intensity caused by light attenuation and photo bleaching during the course of imaging can result in uneven brightness between image tile positions. To ensure uniform signal across tiles, we measured the differences in image contrast in overlapping tile regions to estimate and correct for variations in signal intensity among tile stacks (Figure S1D).
Completion of the preprocessing steps described above resulted in aligned, fully stitched three-channel images and datasets < 1 TB per sample (~400 GB for WT and ~180 GB for Top1 cKO). The Top1 cKO hemispheres displayed clear reductions in thickness throughout the cortex (Figure 1D). Although all cortical layers showed some amount of degeneration, layer 5 and layer 6 neurons seemed to be more severely depleted (Figure 1E), and we hypothesized that certain cortical areas may be differentially affected as well.
Point correspondence improves image registration for structures with large morphological differences
Because of the significant differences in gross morphology within the Top1 cKO brain, image registration was not accurate using only intensity-based mutual information metrics (Figure 2A). To improve registration accuracy of the Top1 cKO brain, we manually selected up to 200 points at distinguishable structure landmarks in the Nissl-stained ARA and their corresponding locations in the TP3 nuclei channel for each sample. Point locations were positioned primarily around the cortex, as this was our region of interest (Figure S3A). Using Euclidean point distances as an additional metric during the registration process significantly improved cortical annotation compared with a manually delineated mask (Figure 2A). Increasing the number of points resulted in higher DICE similarity coefficient scores in Top1 cKO samples (Top1 cKO Mattes mutual information [MMI], mean = 0.526, SD = 0.189; Top1 cKO MMI + 200 Pts, mean = 0.890, SD = 0.013) indicating improvements in registration accuracy (Figures S3A–S3D). These results show that point correspondence can be used to better register mouse models with large structural variation.
Figure 2. NuMorph integrates point correspondence to register difficult structures and 3D-Unet for accurate detection of cortical nuclei.
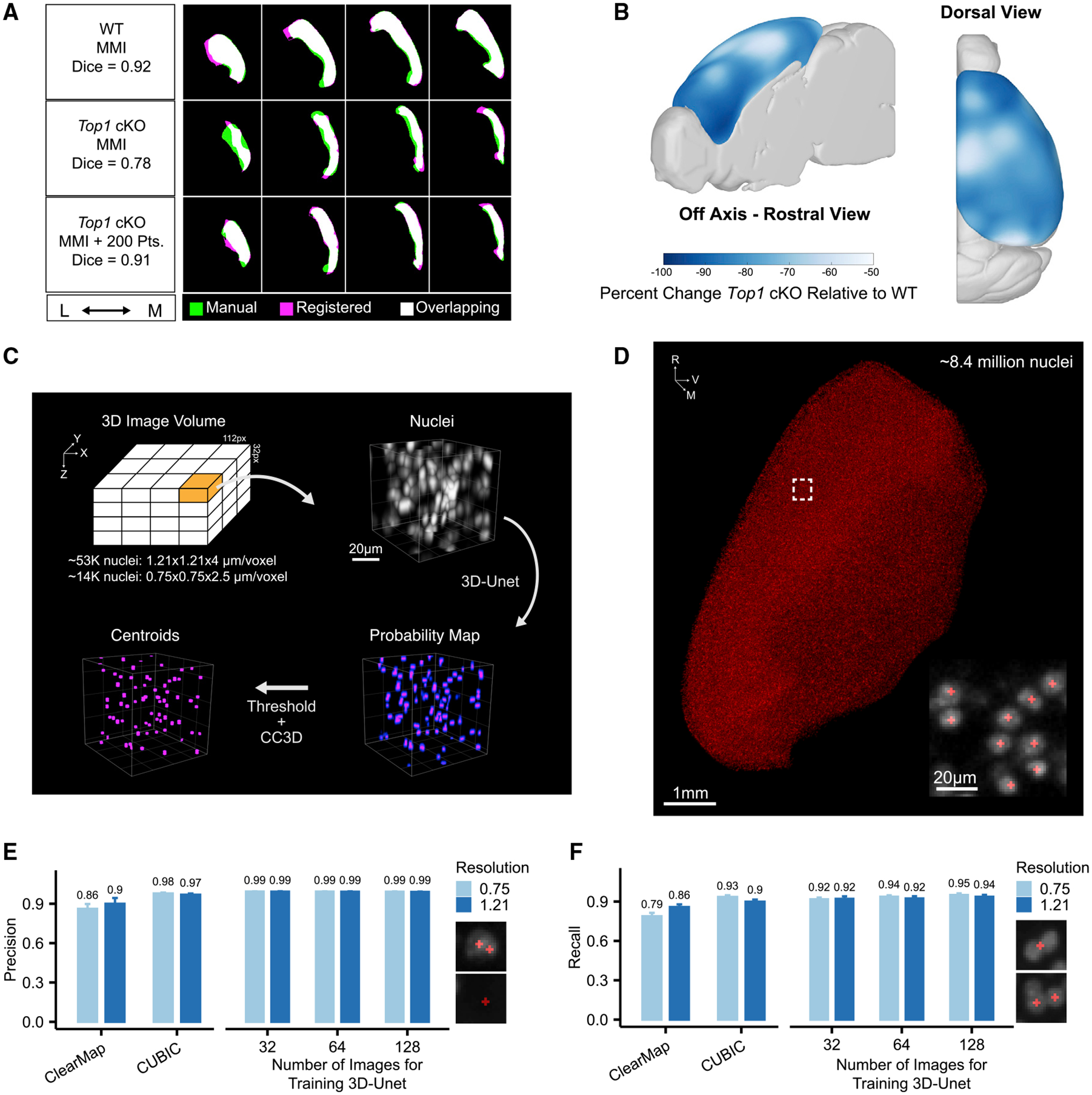
(A) Cortical masks from registered WT and Top1 cKO brain images (magenta) compared with manual labeled traces (green). Mattes mutual information (MMI) was used as the primary registration metric with additional point correspondence to guide registration in the Top1 cKO case.
(B) Voxel-wise differences in cortical volumes between Top1 cKO and WT samples.
(C) Description of 3D-Unet approach for detecting nuclei centroids (CC3D, 3D connected component analysis).
(D) Centroids of WT cortical nuclei predicted by 3D-Unet. Scale bar, 1 mm (inset, 20 μm).
(E and F) Comparison of cell detection precision (E) or recall (F) at the indicated xy resolutions (μm/pixel). Examples of misclassification instances contributing to false positive errors (E) or false negative errors (F) are shown. Data are represented as mean ± SD.
Using the spatial deformation fields generated after image registration, we analyzed which areas in the Top1 cKO cortex exhibited the largest changes in volume relative to WT. Although the cortex as a whole showed a large reduction in volume (mean = 80%, SD = 3.7%, p < 0.001), we observed slightly greater decreases in frontal regions, such as the orbitofrontal (ORB) and infralimbic (ILA) areas, as well as certain lateral regions near the temporal association area (TEa) (Figures 2B and S3E). This suggests that the neuronal cell types within these structures may be more susceptible to degeneration upon Top1 deletion.
3D-Unet accurately quantifies cell nuclei in the cortex
Three-dimensional cell segmentation of tissue-cleared images can be difficult because of the density of cells in the brain, limits of imaging resolution, and overall data complexity. Here we implemented a deep learning model, based on a 3D version of the popular U-Net framework (3D-Unet) (Çiçek et al., 2016; Isensee et al., 2018), to accurately quantify the total number of cell nuclei marked by TP3 staining within the cortex. We generated two sets of manually labeled nuclei. First, for training, ~67,000 cortical nuclei were manually delineated from 256 training image patches (112 × 112 × 32 voxels/patch) of cortical nuclei at either high (0.75 × 0.75 × 2.5 μm/voxel) or low (1.21 × 1.21 × 4 μm/voxel) spatial resolutions. To increase manual delineation efficiency, we focused only on cell detection by delineating a 2D binary mask at the middle Z position to be used as a marker for each cell nucleus. Second, for evaluation, an independent set of ~3,500 manually delineated nuclei were used in which the full 3D extent of the nucleus was labeled in order to determine accuracy of predicted centroid placement. Cell marker predictions within each 3D patch were then thresholded and analyzed for connected components to calculate final cell centroid positions (Figure 2C).
To evaluate cell detection accuracy, we compared precision and recall rates for detecting nuclei in the evaluation dataset using 3D-Unet and two previously published analysis tools for tissue-cleared images with cell counting components: ClearMap and CUBIC Informatics (CUBIC). In our tests, 3D-Unet achieved the highest precision and recall rates in both high- and low-resolution images when the full training datasets were used (Figures 2E and 2F). At low resolution, 3D-Unet achieved significantly lower error rates compared with the next best performing method (CUBIC) at higher resolution (p = 0.043, CUBIC 0.75/3D-Unet 1.21; p < 0.001, CUBIC 1.21/3D-Unet 1.21; p < 0.001, ClearMap 1.21/3D-Unet 1.21; McNemar’s test). We also tested cell detection accuracy in several regions outside of the cortex and found comparably high accuracy in moderately dense regions with a higher error rate in more dense regions such as the dentate gyrus (Figure S4D). Using the trained 3D-Unet model, we counted 8.43 (±0.05) × 106 cells in the P15 WT cortex hemisphere (Figure 2D), which was similar to previously published results in adult mice (Murakami et al., 2018). This indicates that with sufficient training, deep neural networks can compensate for a lack of imaging resolution and achieve accurate cell quantification.
Lower layer neurons in the frontal cortex are preferentially targeted by Top1 deletion
To quantify neuronal cell types in WT and Top1 cKO cortexes, we developed a supervised support vector machine (SVM) model to classify cell types on the basis of local intensity, shape, and annotation features. We found that a supervised approach, after training on 1,000 nuclei in each brain sample, achieved more accurate classification compared with an unsupervised mixture model approach (Figure S5C; Video S2). After removing outliers and summing across cortical structures, we counted 1.74 (±0.07) × 106 Ctip2+ and 1.94 (±0.05) × 106 Cux1+ in WT compared with 0.30 (±0.08) × 106 Ctip2+ and 0.73 (±0.11) × 106 Cux1+ in the Top1 cKO (Figures 3A and 3B; Video S1). Overall, this constitutes an ~83% decrease in Ctip2+ cells and ~62% decrease in Cux1+ cells. Compared with previous results in 2D sections from somatosensory cortex (Fragola et al., 2020), we saw a similar bias toward lower layer neuron degeneration (percentage decrease Ctip2/Cux1 = 1.97 in 3D SSp; 2.33 in 2D), but with a larger reduction in total neuron counts (70% decrease in Ctip2+ cells and 30% decrease in Cux1+ cells from 2D analysis). Although this can be partially attributed to differences in cell quantification methods, the increase in sampling depth from volumetric analyses can also uncover larger effects in total cell count compared with serial 2D analysis.
Figure 3. Top1 deletion induces broad degeneration of neuronal cell types, particularly in frontal regions.
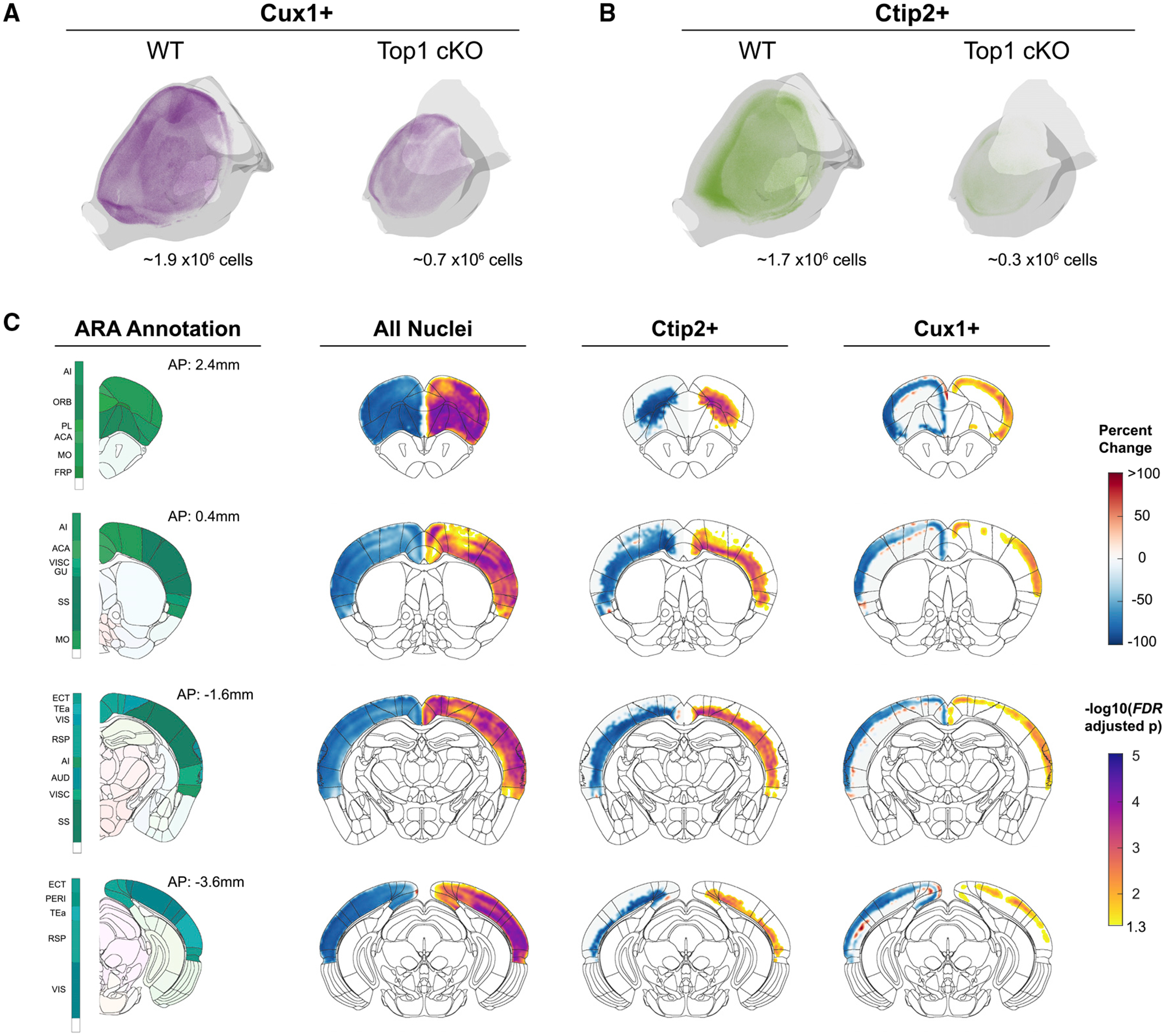
(A and B) Point cloud display of Cux1+ (A) and Ctip2+ (B) cells within WT and Top1 cKO cortexes.
(C) Coronal slice visualizations displaying voxel-wise percentage change in cell count (left hemisphere) and FDR-adjusted p values (right hemisphere).
Next, we compared differences in cell counts and density across the isocortex to determine which regions were most affected by Top1 deletion. As genetic manipulation may lead to alterations in areal identity, precise regional boundaries can be poorly defined after registering the ARA to a nuclear labeled mouse brain image. Therefore, we focused primarily on voxel-wise comparisons and, to add interpretability, supplement voxel-wise data with measured differences in 43 cortical areas in the ARA and the complete isocortex. We observed significant and broad decreases in nuclei number throughout the cortex (false discovery rate [FDR] < 0.05; Figure 3), and when using registered atlas labeled regions, all but 1 of the 43 structures showed a significant decrease in total nuclei count, indicating broad degeneration across all cortical areas in the Top1 cKO model (FDR < 0.05; Figures S6E). As expected, Ctip2+ cells mainly showed significant differences in lower layers of the cortex, whereas Cux1+ cells mainly showed significant differences in upper layers of the cortex (Figure 3). We identified 25 and 41 cortical areas with significant decreases in Cux1+ and Ctip2+ cell counts, respectively (Figure S6E). Although many structures, including several areas in somatosensory cortex (SSp-n, SS-m, SSp-bfd), shared significant losses in both Cux1+ and Ctip2+ excitatory neurons, the most significant decreases were seen in Ctip2+ cells localized in frontal areas, such as the prelimbic (PL) area and secondary motor area (MOs) not measured in previous work (Fragola et al., 2020). We then calculated cell density by normalizing counts to registered structure volumes. Interestingly, the majority of structures show significant increases in nuclei density in Top1 cKO brains (Figure S6E), suggesting that, in addition to cell loss, degeneration of neuronal processes is also contributing to differences in cortical structure. Structures with the most significant increases in density were again localized in frontal regions, such as the PL, ILA, and ORB areas, as well as medial regions, such as the anterior cingulate areas (ACAs). Decreases in nuclei number were more strongly correlated with reductions in cortical surface area compared with cortical thickness (Figures S6B–S6D). Taken together, these results show that even in cases in which genetic perturbation induces strong phenotypic effects such as in the Top1 cKO model, NuMorph can reveal more localized differences in cell-type number within specific brain regions.
Neurodegeneration is spatially correlated with genes differentially expressed in Top1 cKO
Previous evidence suggests that lower layer neurons, particularly those in L5, are most susceptible to degeneration as a result of reduced expression of long, neuronal genes in the Top1 cKO model (Fragola et al., 2020). Although the severe structural deficits in Top1 cKO precluded us from accurately quantifying neurons within L5 in individual cortical regions, we found that regions with larger L5 volumes in the ARA saw the greatest reductions in total structure volume in Top1 cKO (Figure 4A). Furthermore, these regions also saw the largest increases in cell density (Figure 4B), suggesting local degeneration of neuronal processes. We then performed spatial correlations between regional cell count differences and gene expression using in situ hybridization (ISH) data from Allen Mouse Brain Atlas (AMBA) (Lein et al., 2007). We tested whether the degree of Top1 cKO induced structural change among cortical regions was related to the expression of long genes (i.e., genes > 100 kb) within those regions, as Top1 is known to be a transcriptional regulator of long genes (King et al., 2013; Mabb et al., 2016). We found that regions with larger reductions in cell numbers in Top1 cKO were correlated with increased long gene expression (Figure 4C), providing further support that neuronal degeneration mediated by Top1 loss preferentially targets cell types with high long gene expression. Gene Ontology analysis using random null ensembles to overcome gene-enrichment bias (Fulcher et al., 2021), identified 113 functional annotations associated with greater neuronal loss, including several processes involved in axon guidance and extension (Figure S6F). We then searched for spatial correlations with individual genes differentially expressed in the P7 Top1 cKO cortex as measured by single-cell RNA sequencing (scRNA-seq) (Fragola et al., 2020). Among the 125 differentially expressed genes in Top1 cKO that also contained ISH signatures in the AMBA, 5 were significantly correlated with relative difference in excitatory neuron count (Figure 4D). The most significant gene, S100a10 (also known as p11), is predominantly expressed by L5a corticospinal motor neurons in the cortex (Arlotta et al., 2005; Milosevic et al., 2017). Large reductions in Ctip2+ neurons in the Top1 cKO MOs and other frontal areas where S100a10 is highly expressed suggest that changes in S100a10 expression may increase susceptibility for L5 degeneration in these regions (Figures 4E and 4F). These results demonstrate how existing spatial gene expression resources can be leveraged with cleared tissue analysis to identify the specific genes, cell types, and biological processes contributing to gene-structure associations.
Figure 4. Effects of Top1 deletion are associated with spatial patterns of gene expression.
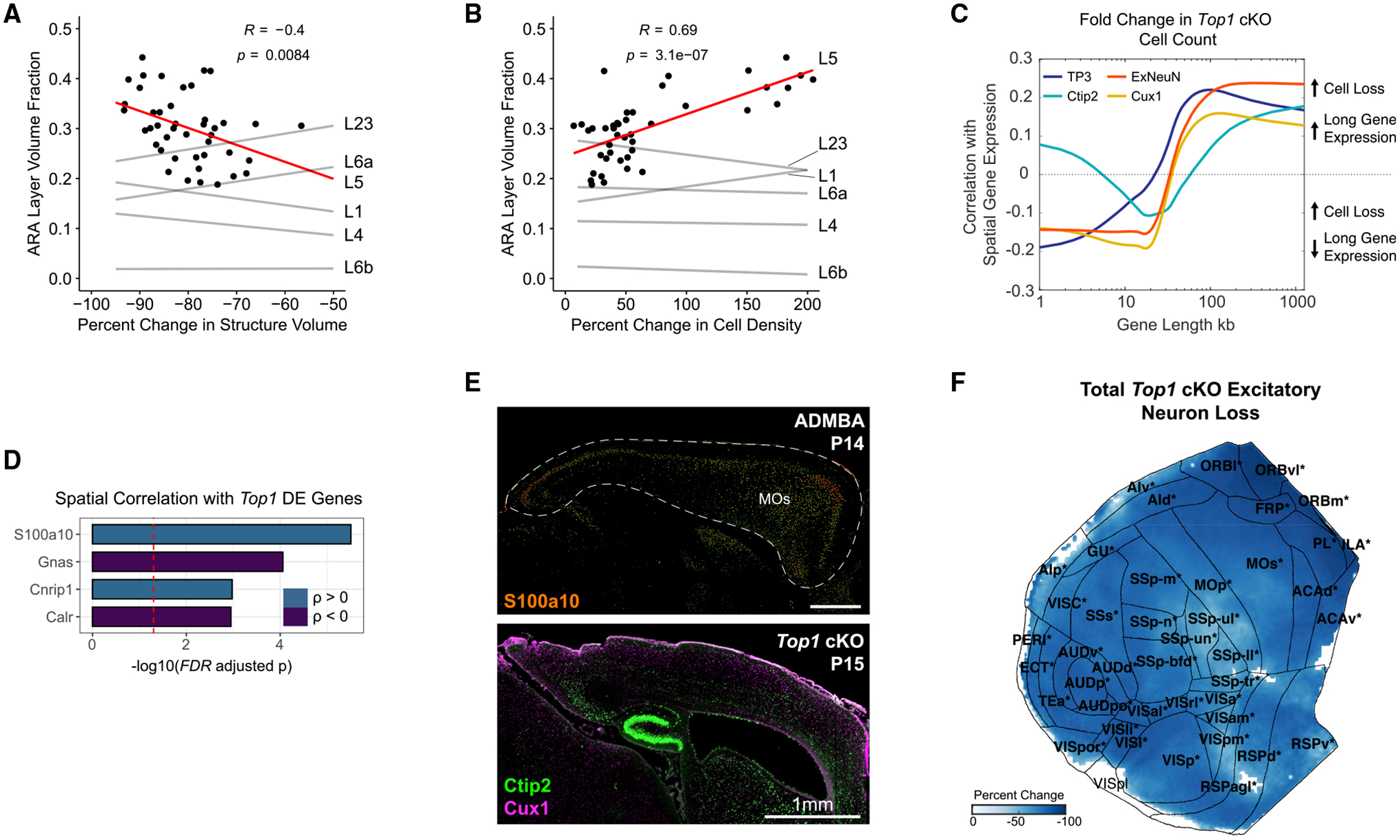
(A and B) Association between structure volume (A) and cell density (B) differences in Top1 cKO with L5 volume as a fraction of total volume in the ARA. Data points shown for L5 associations (R, Pearson correlation coefficient).
(C) Association between spatial gene expression and cell loss in Top1 cKO. Genes were ordered according to length and grouped into bins of 200 genes. Spearman correlation coefficients were calculated between binned gene expression and cell loss across cortical regions. TP3+ indicates all cells, and ExNeun indicates excitatory neurons (i.e., Ctip2+ or Cux1+). Displaying mean ± SEM.
(D) Genes differentially expressed in Top1 cKO excitatory neurons significantly correlated with relative change in excitatory neuron count across cortical regions (Spearman correlation; FDR < 0.05).
(E) ISH expression of S100a10 at P14 in the Allen Developing Mouse Brain Atlas (ADMBA) with the cortex outlined and a corresponding sagittal section of Top1 cKO (MOs, secondary motor area). Scale bar, 1 mm.
(F) Flattened isocortex displaying percentage change in excitatory neuron counts (i.e., Ctip2+ or Cux1+) in Top1 cKO relative to WT. Only significant pixels are colored, and significant regions are bolded and starred (FDR < 0.05). Structure name abbreviations are provided in Table S1.
Conditional Nf1 deletion induces a brain overgrowth phenotype that shares similarities with human MRI results
Although the Top1 cKO model served as a suitable test case for applying NuMorph to study severe brain structure deficits, germ-line loss-of-function mutations in Top1 are highly deleterious and are extremely rare in humans (Karczewski et al., 2020). To further validate the utility of NuMorph for analyzing more subtle structural phenotypes in a disease-relevant animal model, we applied NuMorph to investigate Nf1 KO models. We generated two Nf1 cKO mouse models with one (Nf1fl/+;Emx1-Cre) or both (Nf1fl/fl;Emx1-Cre) copies of the Nf1 gene conditionally deleted in dorsal telencephalic progenitor cells by Emx1 promoter-driven Cre recombination (Gorski et al., 2002). We chose Emx1:Cre mouse line because Cre recombinase activity can be detected as early as embryonic day 10.5 (E10.5), 1 and 2 days earlier than Nestin:Cre (Tronche et al., 1999) and hGFAP:Cre lines (Zhuo et al., 2001), respectively. In addition, the expression of Cre recombinase in Emx1:Cre mice is highly restricted to the dorsal telencephalic progenitor cells that allows us to investigate effects of Nf1 deletion in the cortex. We found that biallelic Nf1 inactivation resulted in increased brain weight and decreased body weight compared with control and mono-allelic inactivation (Figures S7A–S7C). The increase in brain weight is evident as early as P0, suggesting a possible alteration in cortical development at the embryonic stage, a time window that is critical for both cortical neurogenesis and gliogenesis. We sought to systematically characterize this brain overgrowth phenotype using NuMorph.
We performed tissue clearing and whole-brain imaging of six control, six heterozygous KO (Nf1fl/+;Emx1-Cre), and six homozygous KO (Nf1fl/fl;Emx1-Cre) brain hemispheres in littermate groups using the same Ctip2/Cux1 antibody panel as in the Top1 study. Nf1fl/fl;Emx1-Cre showed typical localization of Ctip2+ lower layer neurons and Cux1+ upper layer neurons but an increase in isocortical volume (17% increase, p = 0.02) (Figures 5A and 5B; Video S3). Using NuMorph we also measured voxel-wise cortical thickness and the average thickness of 43 cortical regions. We detected significantly increased thickness in posterior regions such as the posterior parietal association areas (PTLp) with cortical thinning in ORB areas in the Nf1fl/fl;Emx1-Cre model (Figure 5C). These differences along with the overall differences bear a strikingly similar pattern to human MRI findings, in which individuals with NF1 were shown to have thicker occipital and thinner frontal cortices (Barkovich et al., 2018). Much of the increase in overall cortical thickness was driven by expansion of cortical layers 5 and 6 (Figure S7D). To identify which cell types were leading to increased cortical thickness in these regions, we quantified the total number of cortical nuclei and found a noticeable increase in overall cell count in Nf1fl/fl;Emx1-Cre (25% increase, p = 0.011) that was largely attributed to greater numbers of Ctip2−/Cux1− non-excitatory neuron cell types (50% increase, p = 0.001) (Figure 5D). No significant differences in global cortical cell count were observed in the heterozygous Nf1fl/+;Emx1-Cre model.
Figure 5. Nf1 deletion induces cortical thickening driven by increased numbers of non-excitatory neuronal cell types.
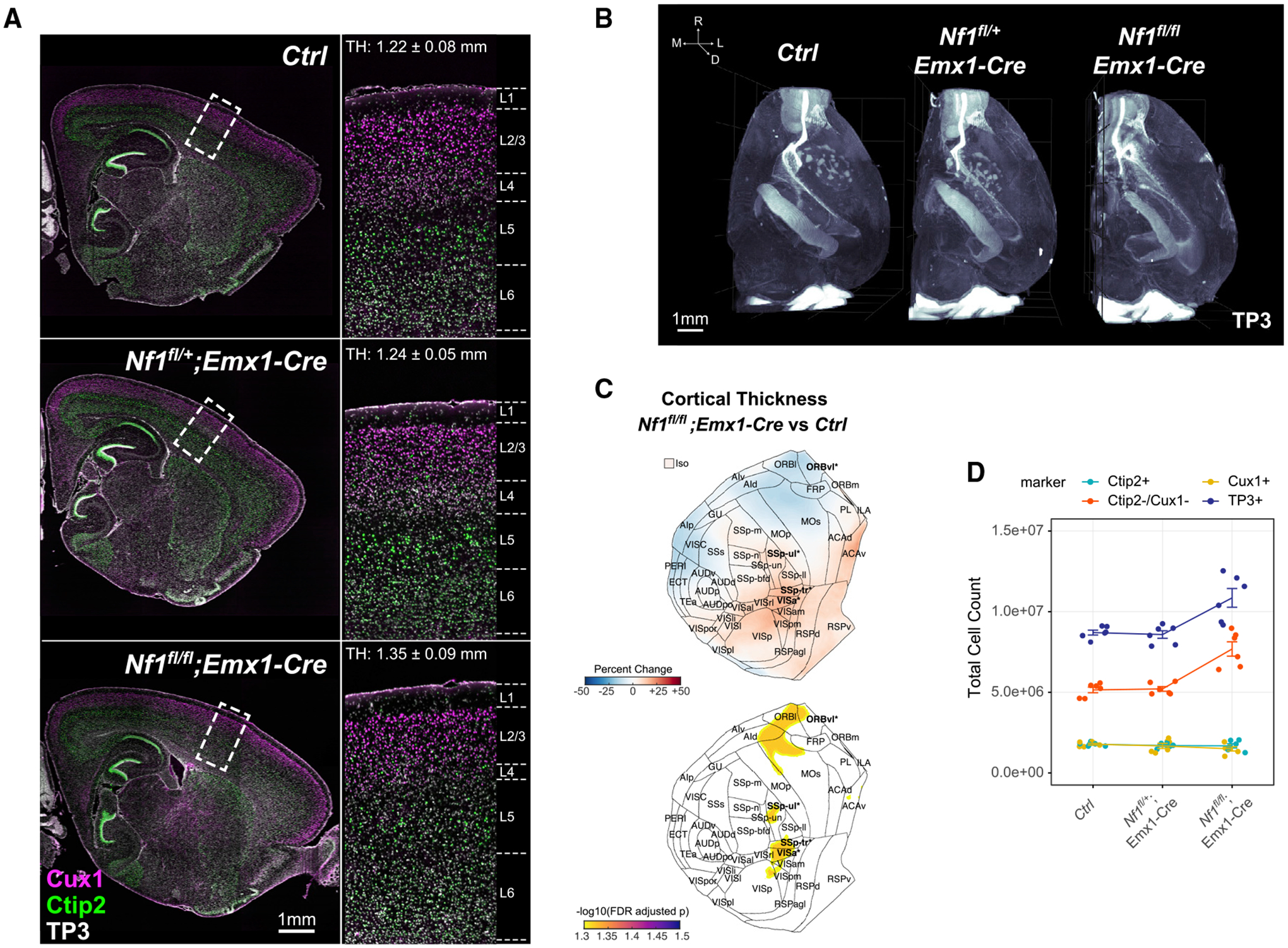
(A) Optical sagittal sections of immunolabeled lower layer (Ctip2+) and upper layer (Cux1+) neurons in P14 Ctrl, Nf1fl/+;Emx1-Cre, and Nf1fl/fl;Emx1-Cre brain hemispheres. Zoomed-in regions of boxed cortical areas near the somatosensory cortex showing expected localization of upper and lower layer neurons. Average cortical thickness (TH) measurements indicated for full 3D somatosensory volumes.
(B) Three-dimensional rendering of cell nuclei in Ctrl, Nf1fl/+;Emx1-Cre, and Nf1fl/fl;Emx1-Cre brain hemispheres.
(C) Flattened isocortex displaying percentage change and FDR-adjusted p values for cortical thickness in Nf1fl/fl;Emx1-Cre across 43 cortical regions and the full isocortex (Iso) compared with Ctrl. Significant regions are bolded (FDR < 0.05) and starred.
(D) Total isocortex counts of each cell-type class measured across all Nf1+/+, Nf1fl/+;Emx1-Cre, and Nf1fl/fl;Emx1-Cre samples (n = 6, mean ± SEM).
Astrocytes and oligodendrocytes drive increased cortical thickness in the Nf1fl/fl;Emx1-Cre model
We further investigated which specific cell types constituted the Ctip2−/Cux1− class of cells that was driving cortical expansion in the Nf1fl/fl;Emx1-Cre model and how these effects varied across cortical regions. We found broad increases in the proportion of Ctip2−/Cux1− cells throughout the cortex (in voxel-wise maps and in 40 of 44 cortical areas, FDR < 0.05) with the greatest increases seen in posterior and medial areas such as the retrosplenial (RSP), auditory (AUD), and visual (VIS) cortices (Figure 6A). As expected, regions with higher Ctip2−/Cux1− cell numbers showed a significant positive correlation with cortical thickness (Figure S7E). To identify the specific cell types within the Ctip2−/Cux1− class, we focused on non-neuronal cell types differentiated from the Emx1-Cre expressing lineage: astrocytes and oligodendrocytes. On the basis of previously estimated cell-type proportions within the adult mouse brain (Erö et al., 2018), regions with larger increases in Ctip2−/Cux1− cell numbers in the Nf1fl/fl;Emx1-Cre model typically have a higher fraction of glial cell types in the WT cortex (Figure 6B), suggesting that the non-excitatory neuronal cells were glia. Furthermore, previous studies have shown that inactivation of Nf1 results in aberrant proliferation of both astrocytes and oligodendrocytes (Gutmann et al., 1999; Bajenaru et al., 2001; Hegedus et al., 2007; Wang et al., 2012). To confirm an expansion in glial cell numbers was present, we performed immunolabeling of P14 sections taken from the somatosensory cortex for Olig2 and GFAP, markers of oligodendrocytes and astrocytes, respectively, where we detected increased numbers of both Olig2+ and GFAP+ cells in this region (Figures 6C–6F). Combined with our measurements of cortical thickness, these results suggest that increased production of glial cell types may explain the cellular mechanism that leads to increased thickness of posterior cortical regions observed in individuals with NF1.
Figure 6. Nf1 deletion increases production of astrocytes and oligodendrocytes broadly throughout the cortex.
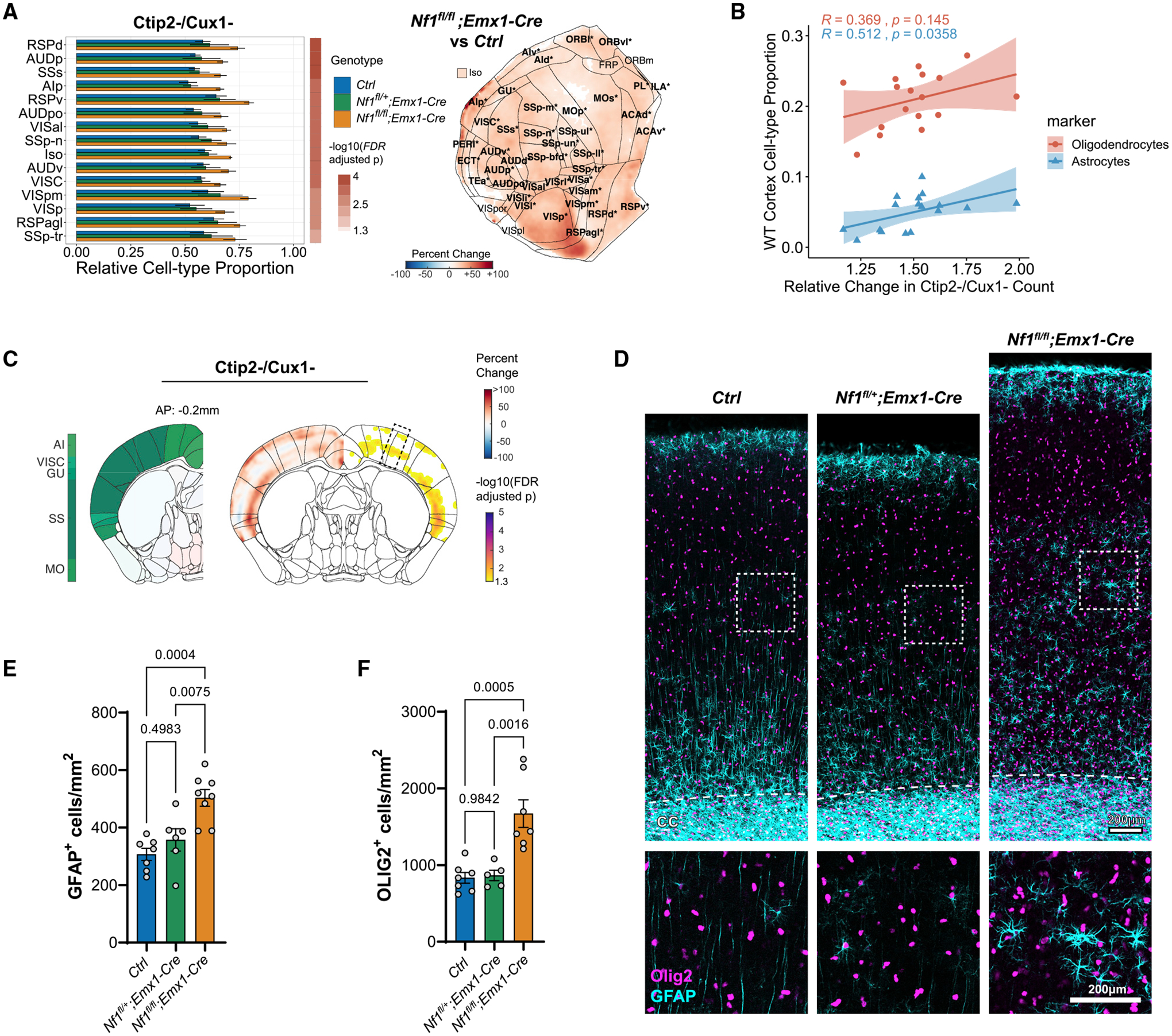
(A) Differences in relative proportion of non-excitatory neuronal cell types (i.e., [Ctip2− and Cux1−)/TO-PRO-3+) across 43 cortical regions and the full isocortex (Iso) after Nf1 deletion. The top 15 regions sorted by binned p value and fold change are shown (Nf1fl/fl;Emx1-Cre versus Ctrl, mean ± SD, FDR < 0.05). Flattened isocortex displaying percentage change in Nf1fl/fl;Emx1-Cre are shown on the right. Only significant pixels are colored, and significant regions are bolded and starred (FDR < 0.05).
(B) Association between estimated astrocyte and oligodendrocyte proportion across regions in the wild-type cortex (Erö et al., 2018) and relative change in non-excitatory neuronal cell types measured in Nf1fl/fl;Emx1-Cre (R, Pearson correlation coefficient).
(C) Coronal slice visualization displaying percentage change in cell count (left hemisphere) and FDR-adjusted p values (right hemisphere) near somatosensory cortex (SS) as measured by 3D analysis.
(D) Representative 2D sections of 1 mm cortical columns from the somatosensory region outlined in (C) showing immunolabeling for GFAP (astrocytes) and Olig2 (oligodendrocytes). Scale bars, 200 μm.
(E and F) Quantification of GFAP+ (E) and Olig2+ (F) cells within 1 mm cortical columns in (D) (n = 5–7 animals, mean ± SEM).
Nf1 deletion results in a regionally specific imbalance of upper layer and lower layer neurons
Finally, we tested whether the proportion of Ctip2+ and/or Cux1+ excitatory neurons was altered across the cortex following Nf1 deletion. Although only a small number of regions were significant for changes in raw cell count for either Ctip2 or Cux1 in Nf1fl/fl;Emx1-Cre compared with control, we detected stronger voxel-wise and regional effects when normalizing individual counts by total cell number or by volume (Figures 7A and 7B; Figure S7G). In other words, alterations in cell-type distribution become more apparent when accounting for the increased rate of gliogenesis in the Nf1fl/fl;Emx1-Cre model. Across the entire cortex, we observed a significant reduction in the relative number of excitatory neurons following biallelic Nf1 deletion, with a slightly greater reduction in the fractional proportion of Cux1+ neurons (35% decrease, p = 0.002, 19 of 44 structures, FDR < 0.05) compared with Ctip2+ neurons (24% decrease, p = 0.007), though the effect on Ctip2+ neurons was more broadly distributed (30 of 44 structures, FDR < 0.05). The organization of upper layer barrel fields was also disrupted in the Nf1fl/fl;Emx1-Cre model (Figure S7H), similar to previous work (Lush et al., 2008). In addition, we observed a strong inverse relationship in the change in Ctip2/Cux1 ratio whereby regions with a greater reductions in Cux1+ neuron proportions saw lower reductions or increases in the number of Ctip2+ neuron proportions and vice versa. This negative correlation persists when normalizing to either total cell counts or regional volume (cell density) (Figure 7C; Figure S7G). These opposing findings across the cortex show the utility of a whole-brain imaging approach, because slices within specific regions may not be representative of the effects across regions. To further investigate whether upper layer neurogenesis is disrupted in the Nf1fl/fl;Emx1-Cre model, we performed EdU pulse labeling of E16.5 mice and quantified their differentiated progeny within P14 brain sections of somatosensory cortex (Figure 7D). We saw a significant reduction of Satb2+ upper layer neurons co-labeled with EdU, indicating decreased upper layer neurogenesis at E16.5. Considering the increase in gliogenesis seen in the Nf1fl/fl; Emx1-Cre mouse, these data suggest that Nf1 deletion may accelerate the brain’s developmental trajectory, which can result in widely disparate effects on neuronal cell-type composition across cortical regions in the adult brain.
Figure 7. Nf1 deletion alters neuronal cell-type proportions in a region-specific manner.
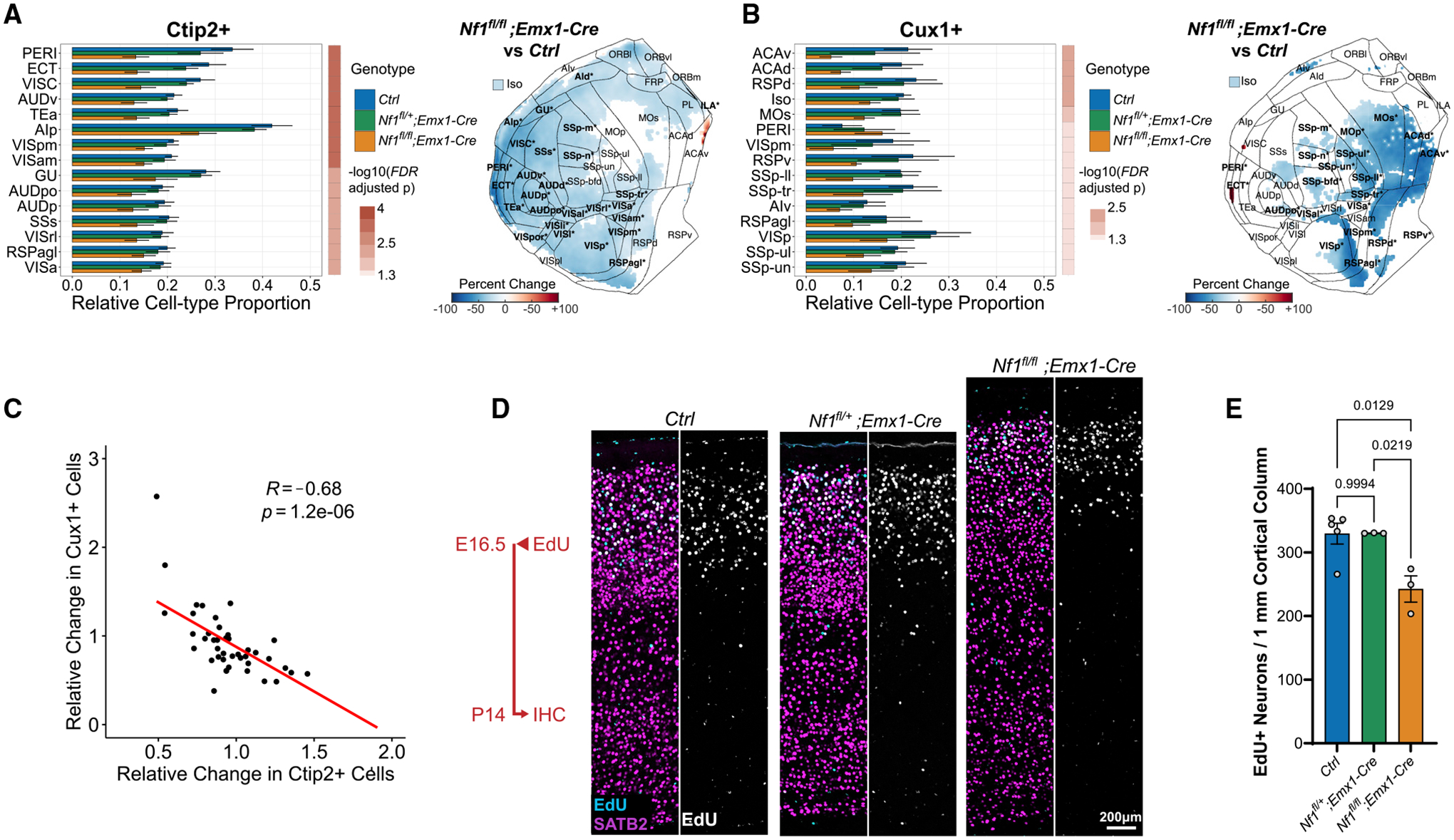
(A and B) Differences in relative proportion of Ctip2+ (A) and Cux1+ (B) cells across 43 cortical regions and the full isocortex after Nf1 deletion. The top 15 structures sorted by binned p value and fold change are shown (Nf1fl/fl;Emx1-Cre versus Ctrl, mean ± SD, FDR < 0.05). Flattened isocortex displaying percentage change in Nf1fl/fl;Emx1-Cre versus Ctrl are shown on the right. Only significant pixels are colored, and significant regions are bolded and starred (FDR < 0.05).
(C) Association between relative change in Ctip2+ and Cux1+ cell numbers across cortical regions in the Nf1fl/fl;Emx1-Cre.
(D) Representative 2D sections of 1 mm cortical columns from P14 somatosensory cortex after EdU injection at E16.5 showing colocalization with SATB2 (callosal projection neurons) immunolabeling in upper layers. Scale bar, 200 μm.
(E) Quantification of EdU+/SATB2+ cells within 1 mm cortical columns in (D) (n = 3–5 animals, mean ± SEM).
DISCUSSION
Tissue-clearing methods provide a unique opportunity to explore the cellular organization of the entire 3D brain structure. However, the current computational tools for analyzing cell types in tissue-cleared images have either been applied to sparse cell populations in which segmentation is less difficult (Renier et al., 2016; Yun et al., 2019) or taken advantage of tissue expansion and custom-built light-sheet systems to increase spatial resolution (Murakami et al., 2018; Matsumoto et al., 2019). Here, we present NuMorph, a computational pipeline for processing and quantifying nuclei within structures of the adult mouse cortex acquired by conventional light-sheet fluorescence microscopy.
In the course of developing NuMorph and an appropriate imaging protocol, a large emphasis was placed on outlining a reasonable compromise between cell detection accuracy, imaging time, and computational resources. With the imaging parameters used to resolve cortical nuclei in this study, WT brain hemispheres required 3–6 h of imaging per channel, while end-to-end processing and analysis using NuMorph required ~1 day with a graphics processing unit (GPU)-equipped workstation. By training a 3D-Unet model on a diverse set of manually labeled nuclei from multiple imaging experiments, we were able to achieve effectively equivalent error rates at this resolution compared with 1.6 times higher resolution (p = 0.91, 3D-Unet 0.75/3D-Unet 1.21; McNemar’s test) that would have otherwise required significantly longer imaging times and expanded data size by ~4 times for a whole hemisphere acquisition. We show that cell detection accuracy using the training dataset generated here remains high for analyzing other brain regions with similar cell density, while supplementation with additional training data may be needed for denser structures such as the hippocampus (Figure S4D). Furthermore, NuMorph provides additional features and flexibility, such as (1) targeting analyses to specific structures after registration to avoid unnecessary computation time, (2) detecting cells directly by nuclear protein marker expression without DNA staining, and (3) classifying cell types by cellular markers using either supervised or unsupervised methods.
Top1 is critical for maintaining genomic stability and regulating the expression of long genes important for neuronal function (McKinnon, 2016). Recent evidence suggests that many of these same long genes contribute to neuronal diversity and have the greatest expression in the forebrain (Sugino et al., 2019). In the developing cortex, scRNA-seq studies revealed that L5 neurons had higher long gene expression compared with neurons from other cortical layers (Loo et al., 2019). In this study, we found that Top1 deletion preferentially targeted many frontal areas with high L5 thickness, larger numbers of Ctip2+ lower layer neurons, and greater long gene expression. These effects likely occur much earlier than the time point studied here, as previous behavioral assays showed that severe motor deficits are present as early as P7 (Fragola et al., 2020). Interestingly, inhibition of S100a10, the gene most correlated with neuron loss, was recently shown to have a neuroprotective effect, delaying motor neuron loss in a mouse model amyotrophic lateral sclerosis (ALS) (García-Morales et al., 2019). Because Top1 deletion results in multiple stress factors that negatively affect cell health, additional studies will be needed to disambiguate which mechanisms ultimately lead to biased degeneration of certain neuronal sub-types across brain regions.
Human MRI studies have detected gross cortical structural differences in individuals with neuropsychiatric disorders compared with neurotypical controls (van Erp et al., 2018). The cellular basis underlying these differences cannot be assessed with standard in vivo MRI, because of the low resolution and lack of cellular labels. Overall increases in brain size and regional variabilities in cortical thickness were previously detected in individuals with NF1 (Payne et al., 2010; Barkovich et al., 2018). To explain the cellular basis underlying those findings, we used an approach complementary to MRI in humans, 3D cellular resolution imaging in a mouse model. Tissue shrinkage or expansion during the clearing process may alter volumetric measurements; nevertheless, the genetic effects on structure were still large enough to be detected and were consistent with MRI findings. Specifically, our Nf1 KO model exhibited a broad expansion in glial cell numbers that drove cortical thickness increases, particularly in posterior regions, which reproduced findings from human MRI measurements. Numerous studies have reported increased glial cell proliferation following Nf1 inactivation in both animal models and human induced pluripotent stem cell (iPSC) lines (Zhu et al., 2001; Hegedus et al., 2007; Wang et al., 2012; Gutmann et al., 2017). However, it was previously unknown if Nf1 inactivation leads to areal differences in the brain and what cell types lead to these structural differences. We also found striking areal differences in upper and lower layer neuron proportions upon Nf1 biallelic deletion in cortical neural progenitor cells early in development. This highlights the key advantages of 3D whole-brain imaging over 2D sectioning, which may lead to more variable results based on the anatomical location from which the tissue is sampled. A limitation in both 2D and 3D analysis is the lack of areal-specific markers that can be used for delineating precise cortical boundaries. Therefore, we generally displayed voxel-wise representations of differences that were not dependent on areal boundary position. Additionally, potential sex-specific effects were not analyzed in this study but could also affect structural phenotypes and NF1 etiology (Diggs-Andrews et al., 2014). Further coupling of immediate-early gene immunolabeling with cleared tissue analysis could reveal how specific structure-function relationships are altered at a cellular level in the Nf1 and similar models (Renier et al., 2016, 2017; Ye et al., 2016).
Although NuMorph has proved to be effective in analyzing moderately dense tissues such as the adult mouse cortex, the development of additional computational tools may be required to pursue more challenging experimental designs. For example, to achieve accurate cell quantification within highly dense structures such as the cerebellum, olfactory bulb, and dentate gyrus, increased spatial resolution and further 3D-Unet model training are essential to improve nuclei detection accuracy. In addition, structures in the embryonic brain are typically of much higher cell density and vary in gross morphology across developmental time, making both cell quantification and image registration more difficult. Technological improvements in the next generation of light-sheet systems can ultimately allow quantitative interrogation of subcellular structures at high throughput (Migliori et al., 2018; Voleti et al., 2019). However, computational tools using deep neural networks have also proved to be effective in executing diverse segmentation tasks (Schubert et al., 2019; Friedmann et al., 2020; Kirst et al., 2020; Stringer et al., 2021) or even enhancing image quality (Weigert et al., 2018). Nevertheless, community-based efforts may be needed to generate sufficient annotation data for training deep learning models to accurately perform these tasks (Roskams and Popović, 2016; Borland et al., 2021). Together we hope these imaging and computational tools will lead to greater adoption of tissue-clearing methods for quantitative analyses, rather than qualitative visualizations, of how the entire brain structure is changed by genetic or environmental risk factors for neuropsychiatric disorders.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Jason Stein (jason_stein@med.unc.edu).
Materials availability
This study did not generate new materials.
Data and code availability
Manually labeled annotations for 3D-Unet training and raw light-sheet images are available at https://braini.renci.org/ through the “Download Image” service.
NuMorph source code is available at https://bitbucket.org/steinlabunc/numorph/ and deposited at Zenodo. The DOI is listed in the Key Resource Table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Rabbit anti-Cux1 (Clone M-222) | Santa Cruz Biotechnology | Cat#: sc-13024; RRID: AB_2261231 |
| Rat anti-Ctip2 (Clone 25B6) | Abcam | Cat#: ab18465; RRID: AB_2064130 |
| Rabbit anti-SATB2 | Abcam | Cat#: ab51502; RRID: AB_2184455 |
| Rabbit anti-Olig2 | Millipore | Cat#: AB9610; RRID: AB_570666 |
| Goat anti-GFAP | Abcam | Cat#: ab53554; RRID: 880202 |
| Chemicals, peptides, and recombinant proteins | ||
| 5-ethynyl-2′-deoxyuridine (EdU) | Cayman Chem | Cat#: 20518; CAS: 61135-33-9 |
| TO-PRO-3 Iodide | Thermo Fisher | Cat#: T3065; CAS: 157199-63-8 |
| Deposited data | ||
| Raw and analyzed imaging data | This study | https://braini.renci.org/ |
| Experimental models: Organisms/strains | ||
| Mouse: Top1fl/fl | Mabb et al., 2016 | N/A |
| Mouse: Nf1fl/fl | Jackson Laboratory | JAX: 017640 |
| Mouse: Neurod6-Cre | Gift from Dr. Klaus-Armin Nave; Goebbels et al., 2006 | RRID:IMSR_CARD:2562 |
| Mouse: Emx1-Cre | Jackson Laboratory | JAX: 005628 |
| Software and algorithms | ||
| NuMorph | This study; https://zenodo.org/record/5346838 | https://bitbucket.org/steinlabunc/numorph/ |
| MATLAB vR2020a | Mathworks | RRID:SCR_001622 |
| Python v3.6 | Python Software Foundation | RRID:SCR_008394 |
| Elastix v4.9 | Klein et al., 2010 | RRID:SCR_009619 |
| 3DUnetCNN | (Ellis and Aizenberg, 2021) | https://github.com/ellisdg/3DUnetCNN |
| VLFeat | A. Vedaldi and B. Fulkerson | https://www.vlfeat.org/ |
| SHARP-Track | Shamash et al., 2018 | https://github.com/cortex-lab/allenCCF |
| Allen SDK | Allen Institute | RRID:SCR_018183 |
| ClearMap | Renier et al., 2016 | https://github.com/ChristophKirst/ClearMap |
| CUBIC-Informatics | Matsumoto et al., 2019 | https://github.com/lsb-riken/CUBIC-informatics |
| Bitplane Imaris v9.4 | Oxford Instruments | RRID:SCR_007370 |
| FIJI | NIH | RRID:SCR_002285 |
| Prism 9 | GraphPad | RRID:SCR_002798 |
| Gene Category Enrichment Analysis | Fulcher et al., 2021 | https://github.com/benfulcher/GeneCategoryEnrichmentAnalysis |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Top1 conditional knockout mice (Top1fl/fl;Neurod6-Cre, Top1 cKO) were bred by crossing Top1fl/fl mice (Mabb et al., 2016) with the Neurod6-Cre mouse line (Goebbels et al., 2006) as described previously (Fragola et al., 2020). Cre-negative mice (Top1fl/fl) were used as controls (WT). Nf1 conditional knockout mice (Nf1fl/fl) were purchased from (Jackson Laboratory, Stock No: 017639) (Zhu et al., 2001). Emx1-Cre mice were originally generated by Gorski et al. (Gorski et al., 2002) and previously validated and maintained in the lab (Xing et al., 2016). Homozygous Nf1 cKO mice (Nf1fl/fl;Emx1-Cre) and heterozygous Nf1 cKO mice (Nf1fl/+;Emx1-Cre) were generated by breeding Nf1fl/+;Emx1-Cre mice with Nf1fl/fl or Nf1fl/+ mice. Cre-negative (Nf1fl/fl, Nf1fl/+, Nf1+/+) and Nf1+/+;Emx1-Cre mice were used as littermate controls. All animal procedures were approved by the University of North Carolina at Chapel Hill Institutional Animal Care and Use Committee. Mice were maintained on a 12-hr dark/light cycle and housed at temperatures of 18–23°C, 40%–60% humidity, and ad libitum food and water. Genomic DNA extracted from tail or ear samples was utilized for genotyping by PCR. Primers for gene amplification are as follows (listed 5′-3′): Top1-F: GAGTTTCAGGACAGCCAGGA, Top1-R: GGACCGGGAAAAGTCTAAGC; Cre-F (Neurod6-Cre): GATGGACATGTTCAGGGATCGCC, Cre-R (Neurod6-Cre): CTCCCATCAGTACGTGAGAT, Nf1-F: ACATGGAGGAGTCAGGATAGT, Nf1-R: GTTAAGAGCATCTGCTGCTCT, Cre-F (Emx1-Cre): GAACGCACTGATTTCGACCA and Cre-R (Emx1-Cre): GATCATCAGCTACACCAGAG. Male P15 Top1 cKO and WT littermate controls were used for tissue clearing in the Top1 study. Male P14 Nf1fl/fl;Emx1-Cre, Nf1fl/+;Emx1-Cre and Ctrl littermates were used for tissue clearing in the Nf1 study.
METHOD DETAILS
Tissue clearing & immunolabeling
Tissue clearing was performed on 4 WT and 4 Top1 cKO for the Top1 study and 6 Ctrl, 6 Nf1fl/+;Emx1-Cre, and 6 Nf1fl/fl;Emx1-Cre for the NF1 study according to the iDISCO+ protocol (Renier et al., 2016). Genotyped samples were processed concurrently in littermate pairs/triplicates. Briefly, mice were fixed via transcardial perfusion using 4% paraformaldehyde and whole-brain samples were dissected and cut along the midline. As the effects of Top1 deletion on gross structure were bilateral upon visual inspection, only the left hemisphere was used in clearing experiments and analysis. Similarly, effects of Nf1 deletion were found to be bilateral based on 2D stereological analysis and therefore only the right hemisphere was used in the Nf1 study. Investigators were blinded to geno-type for the Nf1 study during tissue clearing and subsequent imaging and analysis. Large differences in overall brain size between Top1 cKO and WT prevented blinding in this model. Samples were then washed in phosphate-buffered-saline (PBS), dehydrated in a graded series of methanol (Fisher, A412SK), pretreated with 66% dichloromethane (Sigma- Aldrich, 270997)/methanol and 5% H2O2 (Sigma-Aldrich, H1009)/methanol, followed by rehydration, permeabilization (20% dimethyl-sulfoxide, Fisher, BP2311; 1.6% Triton X-100, Sigma-Aldrich, T8787; 23mg/mL Glycine, Sigma-Aldrich G7126), and blocking with 6% goat serum (Abcam, ab7481). Samples were then incubated with antibodies for Cux1 (Santa Cruz, sc-13024-Rb, 1:200) and Ctip2 (Abcam, ab18465-Rt, 1:500) for 5 days at 37°C in PTwH buffer (PBS; 0.5% Tween-20, Fisher, BP337; 10mg/L Heparin, Sigma-Aldrich, H3393). After 2 days of washing with PTwH, samples were then incubated with TO-PRO-3 (Thermo Fisher, T3605, 1:300), goat anti-rat Alexa Fluor 568 (Thermo Fisher, A11077, 1:200), and goat anti-rabbit Alexa Fluor 790 (Thermo Fisher, A11369, 1:50) for an additional 5 days at 37°C. Samples were then washed for 2 days with PTwH, dehydrated again using a graded methanol series, incubated in 66% dichloromethane/methanol for 3 hours, followed by a 30 minute incubation in 100% dichloromethane before storing in a dibenzyl ether solution (RI = 1.56, Sigma-Aldrich, 108014) at RT. Tissue clearing and antibody labeling required 21 days to complete.
Light-sheet imaging
Imaging of cleared brain samples was performed using the Ultramicroscope II (LaVision Biotec) equipped with MVPLAPO 2X/0.5 NA objective (Olympus), sCMOS camera (Andor), and ImSpector control software. The zoom body was set to 2.5x magnification (yielding 1.21 μm/pixel) and a single light sheet was used with NA = ~0.08 (9 μm thickness/ 4 μm z-step) as this allowed for better resolution of cell nuclei compared to using multiple light sheets. Dynamic horizontal focusing using the contrast enhanced setting in ImSpector was used to ensure axial resolution was maintained along the width of the image using the recommended number of steps depending on the laser wavelength. Samples were positioned sagittally with the cortex surface facing the single illuminating light-sheet (Figure S1D). This prevented excessive light scattering and shadowing from affecting the image quality in the cortical regions. Individual channels were acquired for tiled positions in a row-major order using 561nm (Ctip2), 647nm (TO-PRO-3), or 785nm (Cux1) laser lines. The 785nm channel was imaged first for the entire hemisphere. After refocusing the objective, the 561nm/647nm channels were then captured sequentially for each stack at a given tile position. Using these settings, mouse hemispheres were acquired using 3×3, 4×4, or 4×4 tiling schemes depending on hemisphere size with 5%–15% overlap. Typical imaging times ranged from 10 to 15 hours for all 3 imaged channels. In the Nf1 study, tissue autofluorescence was additionally imaged within a single tile using a 488nm laser at 0.8x magnification (3.86 × 3.86 × 4 μm/voxel; 0.015 light sheet NA, no horizontal focusing) for all samples.
Computing resources
All data processing was performed locally on a Linux workstation running CentOS 7. The workstation was equipped with an Intel Xeon E5–2690 V4 2.6GHz 14-core processor, 8 × 64GB DDR4 2400 LRDIMM memory, 4 × EVGA GeForce GTX 1080 Ti 11GB GPU, and 2 × 4TB Samsung EVO 860 external SSDs. Hot swap bays were used to transfer data from the imaging computer to the analysis workstation.
Intensity adjustments
Two types of image intensity adjustments were performed on raw images prior to image stitching to increase accuracy of subsequent processing. First, uneven illumination along the y dimension (perpendicular to the light path) of each 2D image caused by the Gaussian shape of the light sheet was corrected using a MATLAB implementation of BaSiC, a tool for retrospective shading correction (Peng et al., 2017). We used 10% of all images, excluding tile positions around the cerebellum, to estimate a flatfield image for each channel. Each image was then divided by the flatfield prior to alignment and stitching to correct for uneven illumination. Second, differences in intensity distributions between image tile stacks, primarily as a result of photo-bleaching and light attenuation, were measured in the horizontal and vertical overlapping regions of adjacent tiles. To ensure bright features were of equal intensity between each stack, we measured the relative difference (tadj) in the 95th percentile of pixel intensities in overlapping regions from 5% of all images. The measured image intensity Imeas at tile location x; y was then adjusted according to:
where Dis the darkfield intensity (set as a constant value based on the 5th percentile of pixel intensities in all measured regions).
Image channel alignment
As image channels are acquired one at a time, subtle drift in stage and sample positions during imaging may result in spatial misalignment between the reference nuclei channel and the remaining immunolabeled markers in a multichannel image. We tested two image registration approaches to ensure robust alignment across image channels. The first approach estimates 2D slice translations to align the immunolabeled channel images to the nuclear channel image. The axial (z) correspondence between the nuclei channel and every other channel within an image stack of an individual tile is first estimated using phase correlation at 20 evenly spaced positions within the stack. The correspondence along the axial direction with the highest image similarity (based on intensity correlation) determines the relative tile z displacement between channels (up to 50 μm in some cases). xy translations are then determined after multimodal image registration for each slice in the tile stack using MATLAB’s Image Processing toolbox. Outlier translations, defined as x or y translations greater than 3 scaled median absolute deviations within a local 10 image window in the stack, were corrected by linearly interpolating translations for adjacent images in the stack. In our data, outlier translations often occur in image slices without any sample present where the lack of image contents limits registration accuracy.
While a rigid 2D registration approach is sufficient for channel alignment when samples are securely mounted, sporadic movement of some samples during long imaging sessions can result in not only shifting translation but also rotational drift. In these cases, performing registration relying solely on translation will result in only part of the target image aligning correctly to the nuclei reference at a given z position with the remaining misaligned target features appearing in z positions immediately above and/or below (Figure S1B). To correct for these displacements, we applied a nonlinear 3D registration approach using the Elastix toolbox (Klein et al., 2010) between channels for each individual tile. Full image stacks were loaded and downsampled by a factor of 3 for the x/y dimensions to make the volume roughly isotropic and reduce computation time. Intensity histogram matching was then performed and a mask was identified for the nuclei reference channel using an intensity threshold that limits sampling positions in the background. Next, an initial 3D translational registration is performed on the entire image stack between the reference and the remaining channels. The stack is then subdivided into smaller chunks of 300 images and rigid registration is performed on each chunk to account for 3D rotation and achieve a more accurate initial alignment within local regions of the full stack. Finally, a nonlinear B-spline registration is performed on each chunk using an advanced Mattes mutual information metric to account for xy drift along the z axis and ensure precise alignment of image features. B-spline transformation grid points were set to be sparser along xy compared to z (800×800×8 voxels) as this setting well balances accurate alignment with computational cost while also preventing local warping of background intensities.
During image processing, the 2D rigid alignment approach was initially used to align each sample. Each tile was then visually inspected to ensure accurate alignment of all channels along the stack. For tiles where rigid alignment was inaccurate, the non-rigid alignment method was used to correct for misalignment.
Iterative image stitching
A custom 2D iterative stitching procedure was used to assemble whole-brain images at high resolution. First, an optimal pairwise z correspondence along the axial direction was determined for adjacent tile stacks by exhaustive image matching for the horizontally and vertically overlapped candidate regions. Specifically, a sample of 10 evenly spaced images were taken within a stack and registered to every z position within a 20 image window in the adjacent stack using phase correlation. The displacement in z with the highest count of peak correlations among the 10 images was presumed to represent the best z correspondence. The difference in correlation between the best and the 2nd best z displacement was used as a weight for the strength of the correspondence, with a larger difference representing a stronger correspondence. This resulted in 4 matrices: pairwise horizontal and vertical z displacements and their corresponding weights. To determine the final z displacement for each tile, we implemented a minimum spanning tree (Kruskal, 1956) using displacements and their weights as vertices and edges, as previously implemented (Chalfoun et al., 2017).
An intensity threshold to measure the amount of non-background signal was determined by uniformly sampling 5% of all images and calculating the median intensity. The starting point for iterative stitching going up/down the stack was selected at a position near the middle of stack with sufficient non-background signal (set to 1 standard deviation above the darkfield intensity) present in all tiles. Translations in xy were calculated using phase correlation and further refined using the Scale Invariant Feature Transform (SIFT) algorithm (Lowe, 2004). The top left tile was set as the starting point for tile placement for each stitching iteration. This ensures stitched images would not be shifted relative to each other along the z axis. Tiles were blended using sigmoidal function to maintain high image contrast in overlapping regions. Spurious translations, defined as translations greater than 5 pixels in x or y from the previous iteration, in images that lacked image content were replaced by translation results from the previous iteration.
Image registration to ARA using point correspondence
Volumetric image registration was performed using Elastix to measure the correspondence between the stitched TO-PRO-3 channel in the tissue-cleared samples and the Nissl-stained Allen Reference Atlas (ARA) (Lein et al., 2007; Dong, 2008). The atlas and corresponding volume annotations from Common Coordinate Framework v3 were downloaded using the Allen Software Development Kit (SDK) (https://allensdk.readthedocs.io/en/latest/) at 10 μm/voxel resolution. In each registration procedure, the ARA was downsampled to 25 μm/voxel resolution to perform registration and the resulting transformation parameters were rescaled and applied to the annotation volume at the native 10 μm/voxel resolution.
For registration without point guidance, an affine followed by B-spline transformation sequence was applied along 3 resolution levels to each sample using advanced mattes mutual information (MMI) as the sole metric to estimate spatial correspondence (as done previously in (Renier et al., 2016). This registration procedure allowed for direct mapping of ARA annotations to each registered sample and was applied to all WT hemispheres in the Top1 study. Adding point guidance to WT samples resulted in similar registration accuracy but slightly higher variation in structure volumes between samples (Figure S3).
A modified version of the standard registration procedure without points was also used for mapping control and Nf1 cKO hemispheres in the Nf1 study as this knockout model exhibited a lower degree of morphological variation compared to the Top1 cKO model. However, to further improve registration accuracy, we incorporated additional spectra from tissue autofluorescence that was mapped to the ARA average MRI template, in addition to the TO-PRO-3/Nissl mapping. The downsampled autofluorescence channel in each sample was initially pre-aligned to the TO-PRO-3 reference using rigid registration and the standard B-spline registration with the ARA Nissl/MRI templates proceeded while maximizing the joint mutual information correspondence between the channel pairs.
For points-guided registration in the Top1 cKO model, we first manually placed 200 landmarks within both the ARA and our to-be-registered nuclei reference image, using the BigWarp plugin in Fiji (Bogovic et al., 2016). The majority of points were located within or around the cortex, as this was our region of interest and contained the largest deformations in the Top1 cKO samples (Figure S4). The same set of reference point coordinates in the ARA were selected for each sample and used as input points in Elastix for affine and B-spline registration along 3 resolution levels. Estimates of spatial correspondence for points-guided registration was driven by a hybrid metric based on (1) minimizing the point distances between two images and (2) maximizing the voxel-wise image similarity between two images which is measured by mattes mutual information (MMI). For affine registration, voxel-wise similarity (based on MMI) was ignored and only points distance was used to estimate global translation, rotation, and scaling transformations. For B-spline registration, we gradually increased the influence of voxel-wise similarity in the hybrid metric during the registration sequence from coarse to fine resolution (1:0.2, 1:0.4, 1:0.6; MMI:Point Distance weight). The inverse of the final transformation parameters was then calculated using a displacement magnitude penalty cost function (Metz et al., 2011) and applied to the Allen Mouse Brain Common Coordinate Framework v3 annotation volume to assign anatomical labels for each voxel in the native sample space. While a more direct approach would be to register the ARA to the sample, we found that registering the sample to the ARA and calculating the inverse achieved slightly higher accuracy in Top1 cKO brains (data not shown).
To evaluate registration accuracy, 3D masks of the entire isocortex were manually labeled for each sample in Imaris (Bitplane) using the 3 acquired channels as markers to delineate cortex boundaries. Some cortical subplate structures, such as the claustrum, were included in the final mask as these were difficult to distinguish from the isocortex. The DICE similarity score was then calculated between each mask and all cortical structures in the registered annotation volume (Figure S3B) as a metric of registration accuracy.
Cortical volume, surface area, and thickness measurements
Quantitative measurements for the volume, surface area, and thickness of the isocortex and 43 cortical areas defined in (Harris et al., 2019). Additionally, voxel-wise mapping of cortical structure was also performed. Volume, surface area, and thickness measurements were normalized to the average measurement for the full isocortex in each sample.
For region-based analysis, the voxel sums (at 10 um3/voxel) represent the total volume of each structure. To calculate volumetric displacement for each sample relative to the ARA, the spatial Jacobian was measured for each set of transformation parameters, which ranges from −1 to 1, and represents voxel-wise local compression or expansion. Surface area for the isocortex was calculated based on MATLAB’s implementation of Crofton’s formula (Lehmann and Legland, 2012). The fraction of layer 1 boundary voxels over all boundary voxels was used to determine the area of only the outer cortical surface. This measurement was then further partitioned by the number of layer 1 boundary voxels for each individual structure. To calculate thickness, the center of mass for layer 1 and layer 6b were first calculated for each structure. Thickness was then measured based on the euclidean distance between 2 points within layer 1 and layer 6b that were nearest to the centers of mass. Average thickness of the full isocortex was weighted by the volume contribution of each structure.
For voxel-wise analysis, the volumetric compression and expansion was calculated for each voxel in the ARA space. Surface area was also calculated based on the compression and expansion of layer 1 boundary voxels. Thickness was then calculated for each layer 1 voxel by measuring the euclidean distance to the nearest layer 6b boundary voxel.
Nuclei detection
Imaging data for training the 3D-Unet model was acquired from 3 separate imaging experiments of TO-PRO-3 labeled nuclei across 5 different regions from the cortex of 2 WT brains. Images were captured at 0.75×0.75×2.5 μm/voxel for training a high resolution model or 1.21×1.21×4 μm/voxel for training a low resolution model. A binary approximation of the nucleus volume was initially pre-traced using the cell detection component of the CUBIC-informatics pipeline (Matsumoto et al., 2019). Specifically, the thresholded Hessian determinant after Difference-of-Gassian filtering was used to create an initial 3D mask of all nuclei in the image. Full images were then divided into patches of 224×224×64 voxels and preprocessed using min/max normalization. The corresponding 3D mask for each nucleus was reduced to its 2D component at the middle z position. Each patch was then manually inspected and corrected for segmentation error or incorrect shapes using BrainSuite v17a (Shattuck and Leahy, 2002) by 1 rater (OK) to reduce person-to-person variability. The corrected 2D nuclei masks were then eroded by removing 40% of the outer edge pixels. Each patch was then subdivided into 4 smaller patches of 112×112×32 voxels, with 1 out of the 4 patches being withheld for the validation set. The full dataset (training + validation) contained 16 patches at 224×224×64 voxels for both the high (14,554 nuclei) and low resolution (53,993 nuclei) models. Nuclei at the edge of an image stack were also included in the training. Manually labeled data are available at https://braini.renci.org/ using the Download Image service.
A modified 3D-Unet architecture (Çiçek et al., 2016; Isensee et al., 2018) was used to identify the positions of cell nuclei in whole cortex images. We built upon and modified a previous Keras implementation of 3D-Unet for volumetric segmentation in MRI (https://github.com/ellisdg/3DUnetCNN) to detect binary masks of cell nuclei positions. As originally described (Isensee et al., 2018), the 3D-Unet architecture contains a series of context modules during the contracting path that encodes abstract representations of the input image, followed by a series of localization modules on the upscaling path to localize the features of interest (Figure S4A). We similarly used a model with 5 context modules, residual weights, and deep supervision in the localization modules. The network was trained using 32 base filters on image patches of size 112×112×32 voxels with a batch size of 2. Training presumed over ~300 epochs using an Adam optimizer with a dropout rate of 0.4 and an initial learning rate 0.002 that was reduced by a factor of 2 for every 10 epochs without the loss improving. Additional image augmentations were implemented during the training to make the model more generalizable. These include random image permutations, image blurring and sharpening, the addition of random noise, and intensity variations along x,y,z dimensions in the image patch. Random scaling was removed as we found that this decreased model performance.
Nuclei detection accuracy was evaluated using an independent set of 5 images patches of TO-PRO-3− labeled nuclei where the full 3D volume of each nucleus was fully manually drawn with a unique index at 0.75×0.75×2.5 μm/voxel resolution (~3,500 nuclei total). Each patch was sampled from a unique region within 1 WT cortex. Evaluation patches were initially delineated by 4 raters and further refined by 1 rater to reduce between-rater variability. We compared our 3D-Unet detection method with those used in 2 previously published pipelines for tissue-cleared image analysis: ClearMap and CUBIC-informatics (Renier et al., 2016; Matsumoto et al., 2019). For ClearMap, we used voxel size and intensity thresholds after watersheding, as described in the published implementation. Parameters for cell size and intensity were scaled accordingly to achieve the most accurate average cell counting results possible for all the patches tested. Similarly, intensity normalization and Difference-of-Gaussian scaling parameters used in CUBIC-informatics were adjusted according to image resolution. Filtering by intensity and structureness was also performed as described in the previous work (Matsumoto et al., 2019).
In our evaluation of nuclei detection, precision is the proportion of nuclei correctly predicted out of all nuclei predictions in an image patch. Precision is therefore calculated by counting the number of cells with multiple predicted centroids in 1 manually labeled nucleus volume as well as false positives cells called in the image background divided by the total number of nuclei detected and subtracting this number from 1. Recall is the proportion of all nuclei instances that were predicted. Recall was therefore calculated by counting the number of manually labeled cell volumes that lacked any predicted cell centroids divided by the total number of cells. The majority of false negative cases were due to touching nuclei. Nuclei whose centroid were within 3 voxels of the image border were excluded from the evaluation.
Whole-brain TO-PRO-3 images were divided into chunks of 112×112×32 voxels to be fed into the trained 3D-Unet model for prediction of cell centroids. An overlap of 16×16×8 voxels was used between adjacent chunks to minimize errors from nuclei at chunk edges. Centroid positions falling in a region less than half the overlap range (i.e., < 8 pixels from xy border or < 4 pixels from z border) were assumed to be counted in the adjacent overlapping chunk and were removed. Additionally, a nearest neighbor search using kd-trees (Bentley, 1975) was performed to remove duplicate centroids within 1.5 voxels of each other, ensuring centroids in overlapping regions were not counted multiple times. Increasing overlap did not significantly affect the final cell counting results (data not shown). Total computation time for detecting all cortical nuclei in 1 WT brain hemisphere was ~2.5 hours using a single GPU.
Cell-type classification
To classify cell-types, we took a supervised approach by training a linear Support Vector Machine (SVM) classifier using MATLAB’s Statistics and Machine Learning Toolbox on a set of intensity, shape, and annotation features within a 2D patch surrounding each centroid. First, channel intensities were measured at centroid positions for each channel. Cells with intensities below the median for both Ctip2 and Cux1 were presumed negative for both markers and removed from model training and classification (~25% of cells). In the remaining cells, we took a uniform, random sample of 1,000 cells from each brain image dataset and retained 2D patches (13×13 pixels) around centroid positions. Manual classification required > 1 hour per dataset using a custom NuMorph function that allows fast navigation between cell patches. For each patch, we recorded several intensity measurements (max, mean, standard deviation, middle pixel, middle pixel/edge pixel) and applied Otsu thresholding to capture shape measurements (total filled area, inner filled area) in each channel. These were also combined with categorical annotations for cortical layer (L1, L23, L4, L5, L6a, L6b) and cortical area (Prefrontal, Lateral, Somatomotor, Visual, Medial, Auditory). Cells were then manually classified into 4 classes: (1) Ctip2−/Cux1−, (2) Ctip2+/Cux1−, (3) Ctip2−/Cux1+, (4) Outlier. The outlier class was annotated according to 4 additional subdivisions due to differences in intensity features: (1) Ctip2+/Cux1+, (2) Pial surface cell, (3) TO-PRO-3−/Ctip2−/Cux1− (4) Striatal cell (only present in Top1 cKO from residual registration error near white matter boundary). The SVM model was then trained using all intensity, shape, and annotation features. Model accuracy was evaluated using 5-fold cross-validation and applied to the remaining cells for classification. Due to differences in labeling intensity between samples, we trained a new model for each sample instead of aggregating annotation data.
We compared supervised cell classification with an unsupervised approach based on modeling fluorescence intensities at centroids positions as Gaussian mixtures (GM) for Ctip2 and Cux1. After Z normalization, high intensity cells (Z > 5 and Z < −5) winsorized and outliers expressing both markers near the sample edge were removed. GM model fitting was then performed separately on normalized Ctip2 and Cux1 intensities using 2 or 3 components (whichever had higher accuracy by visual inspection) for 20 replicates using parameters initialized by k-means++ (David Arthur, 2007). Due to spatial variation in gene expression, we stratified GM model fitting to 6 general areas defined in (Harris et al., 2019) according to each cell’s structural annotation to further improve accuracy. We then calculated posterior probabilities of each cell being positive for either marker. Cells with a posterior probability greater than 0.5 of not being background were classified as positive. As the vast majority of neurons do not co-express Ctip2 and Cux1 (Molyneaux et al., 2007), we filtered Ctip2+/Cux1+ cells according to their layer annotation. Cells in L1-L4 with P(Cux1) > P(Ctip2) were classified as Cux1+ and cells in L5-L6b with P(Ctip2) > P(Cux1) were classified as Ctip2+. The remaining Ctip2+/Cux1+ cells were classified as outliers.
3D quantification and visualization
For region-based analysis, final cell-type counts were summed for each annotation in the cortex according to its structure tree hierarchy. In our analysis, we chose to compare 43 cortical areas defined in (Harris et al., 2019) or a lower level set of 17 cortical areas (ARA structure depth = 6; Figure 6B). Structure volumes were also used to calculate cell density statistics.
For voxel-wise analysis, cell counts were binned to 100 μm3/voxel volumes that were mapped to the ARA space. We filtered out voxels with less than 10 nuclei on average among WT samples. Similarly, a minimum cell threshold of 3 and a minimum cell proportion of 0.03 was used for filtering voxels with few Ctip2+ or Cux1+ cell counts. To project 3D voxel-wise data onto an isocortical flatmap, we used a previously calculated set of paths to map cell counts within voxel bins to a specific position along the cortical surface (Allen Institute for Brain Science, 2017). This mapping associates each voxel to a streamlined path between the pial surface and the white matter boundary according to Laplace’s equation. Cell counts were then summed for each voxel along the streamline path and statistical comparisons were performed for each pixel in the 2D flatmap projection.
2D slice visualizations were created using a custom MATLAB program based on the allenAtlasBrowser in the SHARP-Track tool (Shamash et al., 2018). Structure annotations were downsampled along the anterior-posterior axis to reduce memory overhead for smoother performance and colored by volume, cell count, or cell density statistics. Additional visualizations for point clouds, surface volumes, and flattened isocortex plots were created using custom MATLAB scripts and are available in the NuMorph package. Additional animations were generated in Imaris (Bitplane) after importing cell centroid positions.
Spatial gene expression correlation
Fold change in cell counts between WT and Top1 cKO were correlated with spatial gene expression based on in situ hybridization measurements from the Allen Mouse Brain Atlas (Lein et al., 2007). Expression grid data from sagittal and coronal sections were downloaded using the Allen SDK. Expression energy for each gene was first Z-scored across all brain structures and cortical regions were retained for analysis. Duplicate sections for the same gene were combined by taking the mean Z score for each structure across sections. We filtered out any gene that did not have expression data in all cortical structures and removed genes with Z scores less than 1 in all structures as these represent genes with consistently low cortical expression or with low congruence between duplicate sections. For the remaining genes, we applied a robust sigmoidal transformation as described in (Fulcher and Fornito, 2016) to account for the presence of outliers in ISH expression data. As certain cortical regions also have greater cell density and therefore greater total ISH energy, we conducted an additional Z score normalization across cortical regions to have the same average total gene expression.
To reduce known false positive associations from gene-gene coexpression (Fulcher et al., 2021), we ran comparisons to ensemble-based random null models generated using the Gene Category Enrichment Analysis toolbox (https://github.com/benfulcher/GeneCategoryEnrichmentAnalysis). Null distributions were generated for GO categories containing between 10 and 200 genes by 10,000 random samples to create a Gaussian distribution estimate of each GO null distribution. In total, we used null models for 4,186 GO categories based on expression of 10,945 genes across 38 cortical structures. Correlations between spatial gene expression and relative cell count differences were tested and corrected for multiple-hypothesis testing using a false discovery rate of 0.05. Additional annotations for gene length comparisons were downloaded from Ensembl (Cunningham et al., 2019). The Spearman correlation between each gene’s expression and cell count or density differences across cortical regions was measured and grouped into 200 gene bins according to gene length of the longest isoform. Binned gene correlations were then smoothed using a loess curve. A list of differentially expressed genes in Top1 cKO cortex as measured by scRNA-seq was acquired from (Fragola et al., 2020) for additional comparisons.
Brain section preparation and immunofluorescence staining
For histological studies, mice were anesthetized and perfused transcardially with 4% paraformaldehyde (PFA). Brains were dissected and postfixed in 4% PFA for 16 hours. Brains were embedded in 4% low-melting point agarose and sectioned using a Leica VT1200 vibratome. Sections were stored in 1x PBS at 4°C.
For immunohistology studies, sections were rinsed in PBS and incubated in blocking solution (5% normal serum, 0.3% Triton X-100, 2% DMDO, 0.02% Sodium Azide, PBS) at room temperature. Primary antibodies were diluted in blocking solution and incubated overnight at room temperature. The following antibodies were utilized for immunofluorescence: rabbit anti-Cux1 (Santa Cruz, sc-13024; 1:500), rat anti-Ctip2 (Abcam, ab18465; 1:1000), rabbit anti-Satb2 (Abcam, ab51502; 1:1000), goat anti-GFAP (Abcam, ab53554; 1:1000) and rabbit anti-Olig2 (Millipore, AB9610; 1:2000). Brain sections were rinsed in 0.1% Triton X-100 in PBS (PBS/T) three times and incubated with secondary antibodies in blocking solution for 3 hours at room temperature. Secondary antibodies utilized include donkey anti-rabbit IgG Alexa Fluor 568 (Thermo Fisher, A10042; 1:1000), goat anti-rat IgG Alexa Fluor 488 (Thermo Fisher, A11006; 1:1000) and donkey anti-goat IgG Alexa 488 (Thermo Fisher, A11055; 1:1000). Sections were then stained with DAPI (1:1000 in PBS/T) and rinsed with PBS/T three times for 20 minutes each. Sections were mounted onto Fisherbrand Superfrost/Plus slides with an anti-fading Polyvinyl alcohol mounting medium with DABCO (Sigma-Aldrich, 10981). Images were collected with a Zeiss LSM 780 laser scanning confocal microscope.
EdU labeling and detection
To permanently label newly generated cortical neurons, pregnant dams at E16.5 were single-dosed with 5–ethynyl–2′–deoxyuridine (EdU, Cayman Chem) in 1X PBS at 30mg/kg body weight via intraperitoneal injection. Pups were perfused at P14 and sectioned as described above. EdU detection was conducted upon the completion of immunofluorescence labeling. After washing in PBS for 10 minutes, brains sections were incubated with Alexa 647-conjugated Azide (Biotium) at 1.6μM, in solution containing 0.1M Tris-HCl (pH 8.8), 0.43 X PBS, 4 mM CuSO4, and 0.1M Ascorbate, for 20 minutes. Brains sections were washed with PBS/T three times at 20 minutes each, stained with DAPI and mounted for confocal imaging.
2D confocal image analysis and quantification
Confocal images of barrel fields from 2D slices were collected for cortical thickness and cell number analysis. Images were acquired from anatomically matched coronal sections along the rostro-caudal axis. The distribution of the cortical upper layer (layer 2–4) marker, Cux1, was utilized to determine the boundaries separating layer 1, upper layers and lower layers (layer 5–6). The thickness of an individual layer was measured along the middle segment of selected regions of interests (ROIs). For cell number assessment, images were processed using ImageJ (https://imagej.net/software/imagej). Briefly, images were auto-thresholded at default setting with manual adjustment to eliminate unfocused signals and binary images were watershedded. Numbers of Cux1, Ctip2 and Olig2 expressing cells were automatically determined using the Analyze Particles function with a cut off size at 17.5μm2. To determine EdU-labeled cortical neurons, EdU and Satb2 co-labeled cells were extracted and cell numbers were automatically determined using the Analyze Particles function with a cut off size at 35.0μm2. GFAP expressing cells in the cortical plate were counted manually in Photoshop after thresholding using ImageJ. Representative images were cropped and adjusted for brightness and contrast in Photoshop for presentation. Mice from a minimum of three litters were analyzed for each experiment. 2 to 3 ROIs were analyzed and results were averaged from each animal. For all experiments, n represents the number of animals.
QUANTIFICATION AND STATISTICAL ANALYSIS
For 3D voxel-wise and region-based analyses, statistics, including mean counts, standard deviation, fold change, raw p values, and false discovery rate (FDR) adjusted p values (Benjamini-Hochberg; FDR < 0.05), were calculated in MATLAB and exported for plotting using custom R scripts and slice visualization. p values were calculated using Student’s t test and a Welch correction was applied in cases where variances between 2 groups were statistically different. Unless stated otherwise, descriptive statistics in the main text and error bars in figure plots represent mean ± standard deviation.
For 2D confocal image analysis, one-way ANOVA analyses with post hoc Tukey’s tests were performed in GraphPad Prism 9.
Supplementary Material
Highlights.
NuMorph accurately quantifies all cortical nuclei and cell-type-specific markers
Top1 deletion results in increased neuronal degeneration in frontal areas
Nf1 deletion leads to structural changes that recapitulate human MRI findings
Structural changes are driven by increased gliogenesis in the Nf1 knockout model
ACKNOWLEDGMENTS
This work was supported by the National Science Foundation (NSF) (ACI-16449916 to J.L.S., G.W., and A.K.), the NIH (R01MH121433, R01MH118349, and R01MH120125 to J.L.S.; R01NS110791 to G.W.; and R56AG058663 and R35ES028366 to M.J.Z.), the U.S. Department of Defense (DOD) (W81XWH-19-1-0402 to L.X.), the Children’s Tumor Foundation (CTFYIA 2015-01-013 to L.X.), and the Foundation of Hope (to G.W.). We thank Pablo Ariel of the Microscopy Services Laboratory and Michelle Itano of the Neuroscience Microscopy Core for assisting in sample imaging. The Microscopy Services Laboratory, Department of Pathology and Laboratory Medicine, is supported in part by Cancer Center Core Support Grant P30 CA016086 to the University of North Carolina (UNC) Lineberger Comprehensive Cancer Center. The Neuroscience Microscopy Core is supported by grant P30 NS045892. Research reported in this publication was also supported in part by North Carolina Biotech Center Institutional Support Grant 2016-IDG-1016.
Footnotes
DECLARATION OF INTERESTS
O.K. is currently employed at Scribe Therapeutics.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2021.109802.
REFERENCES
- Allen Institute for Brain Science (2017). Technical white paper: Allen Mouse Common Coordinate Framework and Reference Atlas (Allen Institute for Brain Science). http://help.brain-map.org/download/attachments/2818171/Mouse_Common_Coordinate_Framework.pdf?version=4&modificationDate=1508448259091&api=v2.
- Arlotta P, Molyneaux BJ, Chen J, Inoue J, Kominami R, and Macklis JD (2005). Neuronal subtype-specific genes that control corticospinal motor neuron development in vivo. Neuron 45, 207–221. [DOI] [PubMed] [Google Scholar]
- Bajenaru ML, Donahoe J, Corral T, Reilly KM, Brophy S, Pellicer A, and Gutmann DH (2001). Neurofibromatosis 1 (NF1) heterozygosity results in a cell-autonomous growth advantage for astrocytes. Glia 33, 314–323. [DOI] [PubMed] [Google Scholar]
- Barkovich MJ, Tan CH, Nillo RM, Li Y, Xu D, Glastonbury CM, Glenn OA, Dillon WP, Hess CP, Mueller S, et al. (2018). Abnormal morphology of select cortical and subcortical regions in neurofibromatosis type 1. Radiology 289, 499–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bentley JL (1975). Multidimensional binary search trees used for associative searching. Commun. ACM 18, 509–517. [Google Scholar]
- Bogovic JA, Hanslovsky P, Wong A, and Saalfeld S (2016). Robust registration of calcium images by learned contrast synthesis. In 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), pp. 1123–1126. [Google Scholar]
- Borland D, McCormick CM, Patel NK, Krupa O, Mory JT, Beltran AA, Farah TM, Escobar-Tomlienovich CF, Olson SS, Kim M, et al. (2021). Segmentor: a tool for manual refinement of 3D microscopy annotations. BMC Bioinformatics 22, 260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bria A, and Iannello G (2012). TeraStitcher—a tool for fast automatic 3D-stitching of teravoxel-sized microscopy images. BMC Bioinformatics 13, 316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai R, Pan C, Ghasemigharagoz A, Todorov MI, Förstera B, Zhao S, Bhatia HS, Parra-Damas A, Mrowka L, Theodorou D, et al. (2019). Panoptic imaging of transparent mice reveals whole-body neuronal projections and skull-meninges connections. Nat. Neurosci 22, 317–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalfoun J, Majurski M, Blattner T, Bhadriraju K, Keyrouz W, Bajcsy P, and Brady M (2017). MIST: accurate and scalable microscopy image stitching tool with stage modeling and error minimization. Sci. Rep 7, 4988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F, Tillberg PW, and Boyden ES (2015). Optical imaging. Expansion microscopy. Science 347, 543–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ç içek Ö, Abdulkadir A, Lienkamp SS, Brox T, and Ronneberger O (2016). 3D U-Net: learning dense volumetric segmentation from sparse annotation. arXiv, arXiv:1606.06650v1. https://arxiv.org/abs/1606.06650. [Google Scholar]
- Cunningham F, Achuthan P, Akanni W, Allen J, Amode MR, Armean IM, Bennett R, Bhai J, Billis K, Boddu S, et al. (2019). Ensembl 2019. Nucleic Acids Res 47 (D1), D745–D751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David Arthur SV (2007). K-means++: the advantages of careful seeding. In Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.360.7427. [Google Scholar]
- Dean KM, Roudot P, Welf ES, Danuser G, and Fiolka R (2015). Deconvolution-free subcellular imaging with axially swept light sheet microscopy. Biophys. J 108, 2807–2815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diggs-Andrews KA, Brown JA, Gianino SM, Rubin JB, Wozniak DF, and Gutmann DH (2014). Sex Is a major determinant of neuronal dysfunction in neurofibromatosis type 1. Ann. Neurol 75, 309–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong HW (2008). The Allen Reference Atlas: A Digital Color Brain Atlas of the C57BL/6J Male Mouse (Hoboken, NJ: John Wiley; ). [Google Scholar]
- Ellis D,G, and Aizenberg M,R. (2021). Structural brain imaging predicts individual-level task activation maps using deep learning. bioRxiv. 10.1101/2020.10.05.306951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erö C, Gewaltig MO, Keller D, and Markram H (2018). A cell atlas for the mouse brain. Front. Neuroinform 12, 84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ertürk A, Becker K, Jährling N, Mauch CP, Hojer CD, Egen JG, Hellal F, Bradke F, Sheng M, and Dodt HU (2012). Three-dimensional imaging of solvent-cleared organs using 3DISCO. Nat. Protoc 7, 1983–1995. [DOI] [PubMed] [Google Scholar]
- Fei P, Nie J, Lee J, Ding Y, Li S, Zhang H, Hagiwara M, Yu T, Segura T, Ho C-M, et al. (2019). Subvoxel light-sheet microscopy for high-resolution high-throughput volumetric imaging of large biomedical specimens. Advanced Photonics 1, 016002. [Google Scholar]
- Fragola G, Mabb AM, Taylor-Blake B, Niehaus JK, Chronister WD, Mao H, Simon JM, Yuan H, Li Z, McConnell MJ, and Zylka MJ (2020). Deletion of topoisomerase 1 in excitatory neurons causes genomic instability and early onset neurodegeneration. Nat. Commun 11, 1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedmann D, Pun A, Adams EL, Lui JH, Kebschull JM, Grutzner SM, Castagnola C, Tessier-Lavigne M, and Luo L (2020). Mapping mesoscale axonal projections in the mouse brain using a 3D convolutional network. Proc. Natl. Acad. Sci. U S A 117, 11068–11075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fulcher BD, and Fornito A (2016). A transcriptional signature of hub connectivity in the mouse connectome. Proc. Natl. Acad. Sci. U S A 113, 1435–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fulcher BD, Arnatkeviciute A, and Fornito A (2021). Overcoming false-positive gene-category enrichment in the analysis of spatially resolved transcriptomic brain atlas data. Nat. Commun 12, 2669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fürth D, Vaissière T, Tzortzi O, Xuan Y, Märtin A, Lazaridis I, Spigolon G, Fisone G, Tomer R, Deisseroth K, et al. (2018). An interactive framework for whole-brain maps at cellular resolution. Nat. Neurosci 21 (1), 139–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao R, Asano SM, Upadhyayula S, Pisarev I, Milkie DE, Liu TL, Singh V, Graves A, Huynh GH, Zhao Y, et al. (2019). Cortical column and whole-brain imaging with molecular contrast and nanoscale resolution. Science 363, eaau8302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Morales V, Rodríguez-Bey G, Gómez-Pérez L, Domínguez-Vías G, González-Forero D, Portillo F, Campos-Caro A, Gento-Caro Á, Issaoui N, Soler RM, et al. (2019). Sp1-regulated expression of p11 contributes to motor neuron degeneration by membrane insertion of TASK1. Nat. Commun 10, 3784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goebbels S, Bormuth I, Bode U, Hermanson O, Schwab MH, and Nave KA (2006). Genetic targeting of principal neurons in neocortex and hippocampus of NEX-Cre mice. Genesis 44, 611–621. [DOI] [PubMed] [Google Scholar]
- Gorski JA, Talley T, Qiu M, Puelles L, Rubenstein JL, and Jones KR (2002). Cortical excitatory neurons and glia, but not GABAergic neurons, are produced in the Emx1-expressing lineage. J. Neurosci 22, 6309–6314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutmann DH, Loehr A, Zhang Y, Kim J, Henkemeyer M, and Cashen A (1999). Haploinsufficiency for the neurofibromatosis 1 (NF1) tumor suppressor results in increased astrocyte proliferation. Oncogene 18, 4450–4459. [DOI] [PubMed] [Google Scholar]
- Gutmann DH, Ferner RE, Listernick RH, Korf BR, Wolters PL, and Johnson KJ (2017). Neurofibromatosis type 1. Nat. Rev. Dis. Primers 3, 17004. [DOI] [PubMed] [Google Scholar]
- Harris JA, Mihalas S, Hirokawa KE, Whitesell JD, Choi H, Bernard A, Bohn P, Caldejon S, Casal L, Cho A, et al. (2019). Hierarchical organization of cortical and thalamic connectivity. Nature 575, 195–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegedus B, Dasgupta B, Shin JE, Emnett RJ, Hart-Mahon EK, Elghazi L, Bernal-Mizrachi E, and Gutmann DH (2007). Neurofibromatosis-1 regulates neuronal and glial cell differentiation from neuroglial progenitors in vivo by both cAMP- and Ras-dependent mechanisms. Cell Stem Cell 1, 443–457. [DOI] [PubMed] [Google Scholar]
- Hörl D, Rojas Rusak F, Preusser F, Tillberg P, Randel N, Chhetri RK, Cardona A, Keller PJ, Harz H, Leonhardt H, et al. (2019). BigStitcher: reconstructing high-resolution image datasets of cleared and expanded samples. Nat. Methods 16, 870–874. [DOI] [PubMed] [Google Scholar]
- Isensee F, Kickingereder P, Wick W, Bendszus M, and Maier-Hein KH (2018). Brain tumor segmentation and radiomics survival prediction: contribution to the BRATS 2017 challenge. arXiv, arXiv:1802.10508. https://arxiv.org/abs/1802.10508. [Google Scholar]
- Karczewski KJ, Francioli LC, Tiao G, Cummings BB, Alföldi J, Wang Q, Collins RL, Laricchia KM, Ganna A, Birnbaum DP, et al. ; Genome Aggregation Database Consortium (2020). The mutational constraint spectrum quantified from variation in 141,456 humans. Nature 581, 434–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King IF, Yandava CN, Mabb AM, Hsiao JS, Huang HS, Pearson BL, Calabrese JM, Starmer J, Parker JS, Magnuson T, et al. (2013). Topoisomerases facilitate transcription of long genes linked to autism. Nature 501, 58–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirst C, Skriabine S, Vieites-Prado A, Topilko T, Bertin P, Gerschenfeld G, Verny F, Topilko P, Michalski N, Tessier-Lavigne M, and Renier N (2020). Mapping the fine-scale organization and plasticity of the brain vasculature. Cell 180, 780–795.e25. [DOI] [PubMed] [Google Scholar]
- Klein S, Staring M, Murphy K, Viergever MA, and Pluim JP (2010). elastix: a toolbox for intensity-based medical image registration. IEEE Trans. Med. Imaging 29, 196–205. [DOI] [PubMed] [Google Scholar]
- Kruskal JB (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc 7, 48–50. [Google Scholar]
- Ku T, Swaney J, Park JY, Albanese A, Murray E, Cho JH, Park YG, Mangena V, Chen J, and Chung K (2016). Multiplexed and scalable super-resolution imaging of three-dimensional protein localization in size-adjustable tissues. Nat. Biotechnol 34, 973–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann G, and Legland D (2012). Efficient n-dimensional surface estimation using Crofton formula and run-length encoding https://hal.inrae.fr/hal-02811118/document.
- Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, Boe AF, Boguski MS, Brockway KS, Byrnes EJ, et al. (2007). Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176. [DOI] [PubMed] [Google Scholar]
- Liebmann T, Renier N, Bettayeb K, Greengard P, Tessier-Lavigne M, and Flajolet M (2016). Three-dimensional study of Alzheimer’s disease hallmarks using the iDISCO clearing method. Cell Rep 16, 1138–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loo L, Simon JM, Xing L, McCoy ES, Niehaus JK, Guo J, Anton ES, and Zylka MJ (2019). Single-cell transcriptomic analysis of mouse neocortical development. Nat. Commun 10, 134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe DG (2004). Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis 60, 91–110. [Google Scholar]
- Lush ME, Li Y, Kwon CH, Chen J, and Parada LF (2008). Neurofibromin is required for barrel formation in the mouse somatosensory cortex. J. Neurosci 28, 1580–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mabb AM, Simon JM, King IF, Lee HM, An LK, Philpot BD, and Zylka MJ (2016). Topoisomerase 1 Regulates gene expression in neurons through cleavage complex-dependent and -independent mechanisms. PLoS ONE 11, e0156439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto K, Mitani TT, Horiguchi SA, Kaneshiro J, Murakami TC, Mano T, Fujishima H, Konno A, Watanabe TM, Hirai H, and Ueda HR (2019). Advanced CUBIC tissue clearing for whole-organ cell profiling. Nat. Protoc 14, 3506–3537. [DOI] [PubMed] [Google Scholar]
- McKinnon PJ (2016). Topoisomerases and the regulation of neural function. Nat. Rev. Neurosci 17, 673–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metz CT, Klein S, Schaap M, van Walsum T, and Niessen WJ (2011). Nonrigid registration of dynamic medical imaging data using nD + t B-splines and a groupwise optimization approach. Med. Image Anal 15, 238–249. [DOI] [PubMed] [Google Scholar]
- Migliori B, Datta MS, Dupre C, Apak MC, Asano S, Gao R, Boyden ES, Hermanson O, Yuste R, and Tomer R (2018). Light sheet theta microscopy for rapid high-resolution imaging of large biological samples. BMC Biol 16, 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milosevic A, Liebmann T, Knudsen M, Schintu N, Svenningsson P, and Greengard P (2017). Cell- and region-specific expression of depression-related protein p11 (S100a10) in the brain. J. Comp. Neurol 525, 955–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molyneaux BJ, Arlotta P, Menezes JR, and Macklis JD (2007). Neuronal subtype specification in the cerebral cortex. Nat. Rev. Neurosci 8, 427–437. [DOI] [PubMed] [Google Scholar]
- Murakami TC, Mano T, Saikawa S, Horiguchi SA, Shigeta D, Baba K, Sekiya H, Shimizu Y, Tanaka KF, Kiyonari H, et al. (2018). A three-dimensional single-cell-resolution whole-brain atlas using CUBIC-X expansion microscopy and tissue clearing. Nat. Neurosci 21, 625–637. [DOI] [PubMed] [Google Scholar]
- Murray E, Cho JH, Goodwin D, Ku T, Swaney J, Kim SY, Choi H, Park YG, Park JY, Hubbert A, et al. (2015). Simple, scalable proteomic imaging for high-dimensional profiling of intact systems. Cell 163, 1500–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan C, Cai R, Quacquarelli FP, Ghasemigharagoz A, Lourbopoulos A, Matryba P, Plesnila N, Dichgans M, Hellal F, and Ertürk A (2016). Shrinkage-mediated imaging of entire organs and organisms using uDISCO. Nat. Methods 13, 859–867. [DOI] [PubMed] [Google Scholar]
- Park Y-G, Sohn CH, Chen R, McCue M, Yun DH, Drummond GT, Ku T, Evans NB, Oak HC, Trieu W, et al. (2019). Protection of tissue physicochemical properties using polyfunctional crosslinkers. Nat. Biotechnol 37, 73–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne JM, Moharir MD, Webster R, and North KN (2010). Brain structure and function in neurofibromatosis type 1: current concepts and future directions. J. Neurol. Neurosurg. Psychiatry 81, 304–309. [DOI] [PubMed] [Google Scholar]
- Pende M, Becker K, Wanis M, Saghafi S, Kaur R, Hahn C, Pende N, Foroughipour M, Hummel T, and Dodt HU (2018). High-resolution ultramicroscopy of the developing and adult nervous system in optically cleared Drosophila melanogaster. Nat. Commun 9, 4731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng T, Thorn K, Schroeder T, Wang L, Theis FJ, Marr C, and Navab N (2017). A BaSiC tool for background and shading correction of optical microscopy images. Nat. Commun 8, 14836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renier N, Adams EL, Kirst C, Wu Z, Azevedo R, Kohl J, Autry AE, Kadiri L, Umadevi Venkataraju K, Zhou Y, et al. (2016). Mapping of brain activity by automated volume analysis of immediate early genes. Cell 165, 1789–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renier N, Dominici C, Erzurumlu RS, Kratochwil CF, Rijli FM, Gaspar P, and Chédotal A (2017). A mutant with bilateral whisker to barrel inputs unveils somatosensory mapping rules in the cerebral cortex. eLife 6, e23494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson DS, and Lichtman JW (2015). Clarifying tissue clearing. Cell 162, 246–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roskams J, and Popović Z (2016). Power to the people: addressing big data challenges in neuroscience by creating a new cadre of citizen neuroscientists. Neuron 92, 658–664. [DOI] [PubMed] [Google Scholar]
- Schubert PJ, Dorkenwald S, Januszewski M, Jain V, and Kornfeld J (2019). Learning cellular morphology with neural networks. Nat. Commun 10, 2736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shamash P, Carandini M, Harris K, and Steinmetz N (2018). A tool for analyzing electrode tracks from slice histology. bioRxiv. 10.1101/447995. [DOI] [Google Scholar]
- Shattuck DW, and Leahy RM (2002). BrainSuite: an automated cortical surface identification tool. Med. Image Anal 6, 129–142. [DOI] [PubMed] [Google Scholar]
- Stringer C, Wang T, Michaelos M, and Pachitariu M (2021). Cellpose: a generalist algorithm for cellular segmentation. Nat. Methods 18, 100–106. [DOI] [PubMed] [Google Scholar]
- Sugino K, Clark E, Schulmann A, Shima Y, Wang L, Hunt DL, Hooks BM, Tränkner D, Chandrashekar J, Picard S, et al. (2019). Mapping the transcriptional diversity of genetically and anatomically defined cell populations in the mouse brain. eLife 8, e38619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Susaki EA, Tainaka K, Perrin D, Yukinaga H, Kuno A, and Ueda HR (2015). Advanced CUBIC protocols for whole-brain and whole-body clearing and imaging. Nat. Protoc 10, 1709–1727. [DOI] [PubMed] [Google Scholar]
- Susaki EA, Shimizu C, Kuno A, Tainaka K, Li X, Nishi K, Morishima K, Ono H, Ode KL, Saeki Y, et al. (2020). Versatile whole-organ/body staining and imaging based on electrolyte-gel properties of biological tissues. Nat. Commun 11, 1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tainaka K, Kubota SI, Suyama TQ, Susaki EA, Perrin D, Ukai-Tadenuma M, Ukai H, and Ueda HR (2014). Whole-body imaging with single-cell resolution by tissue decolorization. Cell 159, 911–924. [DOI] [PubMed] [Google Scholar]
- Tomer R, Ye L, Hsueh B, and Deisseroth K (2014). Advanced CLARITY for rapid and high-resolution imaging of intact tissues. Nat. Protoc 9, 1682–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tronche F, Kellendonk C, Kretz O, Gass P, Anlag K, Orban PC, Bock R, Klein R, and Schütz G (1999). Disruption of the glucocorticoid receptor gene in the nervous system results in reduced anxiety. Nat. Genet 23, 99–103. [DOI] [PubMed] [Google Scholar]
- Ueda HR, Ertürk A, Chung K, Gradinaru V, Chédotal A, Tomancak P, and Keller PJ (2020). Tissue clearing and its applications in neuroscience. Nat. Rev. Neurosci 21, 61–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Erp TGM, Walton E, Hibar DP, Schmaal L, Jiang W, Glahn DC, Pearlson GD, Yao N, Fukunaga M, Hashimoto R, et al. ; Karolinska Schizophrenia Project (2018). Cortical brain abnormalities in 4474 individuals with schizophrenia and 5098 control subjects via the Enhancing Neuro Imaging Genetics Through Meta Analysis (ENIGMA) Consortium. Biol. Psychiatry 84, 644–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voigt FF, Kirschenbaum D, Platonova E, Pagès S, Campbell RAA, Kastli R, Schaettin M, Egolf L, van der Bourg A, Bethge P, et al. (2019). The mesoSPIM initiative: open-source light-sheet microscopes for imaging cleared tissue. Nat. Methods 16, 1105–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voleti V, Patel KB, Li W, Perez Campos C, Bharadwaj S, Yu H, Ford C, Casper MJ, Yan RW, Liang W, et al. (2019). Real-time volumetric microscopy of in vivo dynamics and large-scale samples with SCAPE 2.0. Nat. Methods 16, 1054–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Kim E, Wang X, Novitch BG, Yoshikawa K, Chang LS, and Zhu Y (2012). ERK inhibition rescues defects in fate specification of Nf1-deficient neural progenitors and brain abnormalities. Cell 150, 816–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigert M, Schmidt U, Boothe T, Müller A, Dibrov A, Jain A, Wilhelm B, Schmidt D, Broaddus C, Culley S, et al. (2018). Content-aware image restoration: pushing the limits of fluorescence microscopy. Nat. Methods 15, 1090–1097. [DOI] [PubMed] [Google Scholar]
- Xing L, Larsen RS, Bjorklund GR, Li X, Wu Y, Philpot BD, Snider WD, and Newbern JM (2016). Layer specific and general requirements for ERK/MAPK signaling in the developing neocortex. eLife 5, e11123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye L, Allen WE, Thompson KR, Tian Q, Hsueh B, Ramakrishnan C, Wang AC, Jennings JH, Adhikari A, Halpern CH, et al. (2016). Wiring and molecular features of prefrontal ensembles representing distinct experiences. Cell 165, 1776–1788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yun DH, Park Y-G, Cho JH, Kamentsky L, Evans NB, Albanese A, Xie K, Swaney J, Sohn CH, Tian Y, et al. (2019). Ultrafast immunostaining of organ-scale tissues for scalable proteomic phenotyping. bioRxiv. 10.1101/660373. [DOI] [Google Scholar]
- Zhu Y, Romero MI, Ghosh P, Ye Z, Charnay P, Rushing EJ, Marth JD, and Parada LF (2001). Ablation of NF1 function in neurons induces abnormal development of cerebral cortex and reactive gliosis in the brain. Genes Dev 15, 859–876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuo L, Theis M, Alvarez-Maya I, Brenner M, Willecke K, and Messing A (2001). hGFAP-cre transgenic mice for manipulation of glial and neuronal function in vivo. Genesis 31, 85–94. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Manually labeled annotations for 3D-Unet training and raw light-sheet images are available at https://braini.renci.org/ through the “Download Image” service.
NuMorph source code is available at https://bitbucket.org/steinlabunc/numorph/ and deposited at Zenodo. The DOI is listed in the Key Resource Table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Rabbit anti-Cux1 (Clone M-222) | Santa Cruz Biotechnology | Cat#: sc-13024; RRID: AB_2261231 |
| Rat anti-Ctip2 (Clone 25B6) | Abcam | Cat#: ab18465; RRID: AB_2064130 |
| Rabbit anti-SATB2 | Abcam | Cat#: ab51502; RRID: AB_2184455 |
| Rabbit anti-Olig2 | Millipore | Cat#: AB9610; RRID: AB_570666 |
| Goat anti-GFAP | Abcam | Cat#: ab53554; RRID: 880202 |
| Chemicals, peptides, and recombinant proteins | ||
| 5-ethynyl-2′-deoxyuridine (EdU) | Cayman Chem | Cat#: 20518; CAS: 61135-33-9 |
| TO-PRO-3 Iodide | Thermo Fisher | Cat#: T3065; CAS: 157199-63-8 |
| Deposited data | ||
| Raw and analyzed imaging data | This study | https://braini.renci.org/ |
| Experimental models: Organisms/strains | ||
| Mouse: Top1fl/fl | Mabb et al., 2016 | N/A |
| Mouse: Nf1fl/fl | Jackson Laboratory | JAX: 017640 |
| Mouse: Neurod6-Cre | Gift from Dr. Klaus-Armin Nave; Goebbels et al., 2006 | RRID:IMSR_CARD:2562 |
| Mouse: Emx1-Cre | Jackson Laboratory | JAX: 005628 |
| Software and algorithms | ||
| NuMorph | This study; https://zenodo.org/record/5346838 | https://bitbucket.org/steinlabunc/numorph/ |
| MATLAB vR2020a | Mathworks | RRID:SCR_001622 |
| Python v3.6 | Python Software Foundation | RRID:SCR_008394 |
| Elastix v4.9 | Klein et al., 2010 | RRID:SCR_009619 |
| 3DUnetCNN | (Ellis and Aizenberg, 2021) | https://github.com/ellisdg/3DUnetCNN |
| VLFeat | A. Vedaldi and B. Fulkerson | https://www.vlfeat.org/ |
| SHARP-Track | Shamash et al., 2018 | https://github.com/cortex-lab/allenCCF |
| Allen SDK | Allen Institute | RRID:SCR_018183 |
| ClearMap | Renier et al., 2016 | https://github.com/ChristophKirst/ClearMap |
| CUBIC-Informatics | Matsumoto et al., 2019 | https://github.com/lsb-riken/CUBIC-informatics |
| Bitplane Imaris v9.4 | Oxford Instruments | RRID:SCR_007370 |
| FIJI | NIH | RRID:SCR_002285 |
| Prism 9 | GraphPad | RRID:SCR_002798 |
| Gene Category Enrichment Analysis | Fulcher et al., 2021 | https://github.com/benfulcher/GeneCategoryEnrichmentAnalysis |


