Low-Dose High-Resolution TOF-PET Using Ionization-activated Multi-State Low-Z Detector Media

Abstract

We propose PET scanners using low atomic number media that undergo a persistent local change of state along the paths of the Compton recoil electrons. Measurement of the individual scattering locations and angles, deposited energies, and recoil electron directions allows using the kinematical constraints of the 2-body Compton scattering process to perform a statistical time-ordering of the scatterings, with a high probability of precisely identifying where the gamma first interacted in the detector. In these cases the Line-of-Response is measured with high resolution, determined by the underlying physics processes and not the detector segmentation. There are multiple such media that act through different mechanisms. As an example in which the change of state is quantum-mechanical through a change in molecular configuration, rather than thermodynamic, as in a bubble chamber, we present simulations of a two-state photoswitchable organic dye, a ‘Switchillator’, that is activated to a fluorescent-capable state by the ionization of the recoil electrons. The activated state is persistent, and can be optically excited multiple times to image individual activated molecules. Energy resolution is provided by counting the activated molecules. Location along the LOR is implemented by large-area time-of-flight MCP-PMT photodetectors with single photon time resolution in the tens of ps and sub-mm spatial resolution. Simulations indicate a large reduction of dose.

1. Introduction

As an outcome of developing large area MCP-PMT-based pico-second time-of-flight systems [1–3] for identification of charged particles in high-energy colliders [4, 5] and imaging of low-energy electrons in neutrino physics [6–8], we have explored PET scanners based on large-area MCP-PMT photodetectors viewing low atomic number scintillating media [9]. The goal is to resolve the location, recoil direction, and energy of the chain of successive Compton-scattered electrons in the detector medium. Simulations show that reconstructing the recoil electron tracks enables a time-ordering of the Compton scatterings in the detector, with a high probability of precisely identifying the site of the first interaction of each gamma in the detector. Connecting the locations of the first interaction for both gammas provides a precise determination of the line-of-response (LOR).

Positron-Emission Tomography (PET) uses the selective uptake of biologically active molecules labelled with one or more radioactive positron-emitting tracers to image sites of biological activity [10–12]. The emitted positron multiple-scatters and then annihilates with an electron, emitting approximately back-to-back gamma rays, each with approximately the energy of the electron mass. Time-of-flight PET (TOF-PET) uses the difference of arrival times of the two gamma rays to constrain the annihilation site along the Line-of-Response (LOR), the line connecting the measured gamma ray interaction points in the detector [12]. Here we describe an optical system based on large-area MCP-PMT-based photodetectors to provide cm-scale TOF resolution along the LOR.

The field is undergoing rapid development. Highly sophisticated whole-body scanners with large solid angle acceptance have recently been developed [13, 14]. TOF-PET with sub-nanosecond coincidence is being developed [15], and a challenge is currently in place to develop sub-10 ps TOF resolution [16]. A particularly attractive method exploiting ultra-fast timing using MCP-PMT photodetectors and Cherenkov light in pre-radiators [17–19] is being developed by Cherry et al. for higher spatial resolutions and lower doses [20].

Commercial PET scanners currently employ crystals containing high atomic number elements to localize the gamma ray interaction [21, 22]. The resolutions in time and space are typically limited by the physical dimensions of the high-Z crystals and their associated electronics [23].

We had previously proposed whole-body scanners based on large-area ‘picosecond’ (ps) MCP-PMT photodetectors viewing high-Z scintillator [24, 25] and low-Z liquid scintillator [9]. A pioneering proposal by Moskal et al. emphasized the lower cost of low-Z scintillator-based PET [26].

Moving from high-Z-inorganic to low-Z-organic media may allow optical interrogation of the interactions in the detector at significantly higher resolution in both space and time, with the goal of approaching the fundamental limits set by the underlying physical processes. These processes include positron emission, positron-electron annihilation, Compton scattering of gamma rays and electrons, ionization energy loss, the generation of scintillation light, Cherenkov emission, and the diffusion of molecules.

There are candidate low-Z media that act through different mechanisms, including those with a change in molecular states, and others in which the change is thermodynamic, as in a bubble chamber [27]. For a specific example, we discuss the potential for development of appropriate two-state photoswitchable organic dyes, ‘Switchillators’, that are activated to a fluorescent-capable state by the ionization of the recoil electrons, and which offer additional prospects for synthetic fine-tuning at the molecular level to optimize the efficiency and kinetics of photoswitching and the spectroscopic properties of the active state [28–30].

A high-resolution spatial image of the Compton interactions also enables a more precise resolution in Time-of-Flight (TOF), as the transit times of the scintillation photons are predicted by the precise location of the initial gamma interaction point. The development of large-area multi-channel optical detectors with time resolutions measured in pico-seconds [1–3, 31] allows the recording of multiple photons at high resolution in both time and space. The ability to measure the transit time of photons as well as their arrival location on the detector face allows 3D spatial reconstruction (the ‘Optical Time Projection Chamber’, OTPC [4, 6, 32]). In the case of the identification of charged particles, exploiting Cherenkov light in a radiator on the face of the MCP-PMT produces time resolutions below 5 ps [5, 17–19].

The organization of the paper is as follows; Section 2 describes analyzing the chain of successive Compton scatterings in a low-Z scintillating medium in a generic TOF-PET detector to determine the site of the first interaction of each gamma and the extraction of the LOR at high resolution. Section 3 presents results from simulations of an example implementation using two-state photoswitchable organic dyes activated to a fluorescent-capable state by the ionization of the recoil electrons. Section 4 summarizes the proposal and suggests possibilities for future implementation and impact.

2. Using Low-Z Materials to Measure the Line of Response

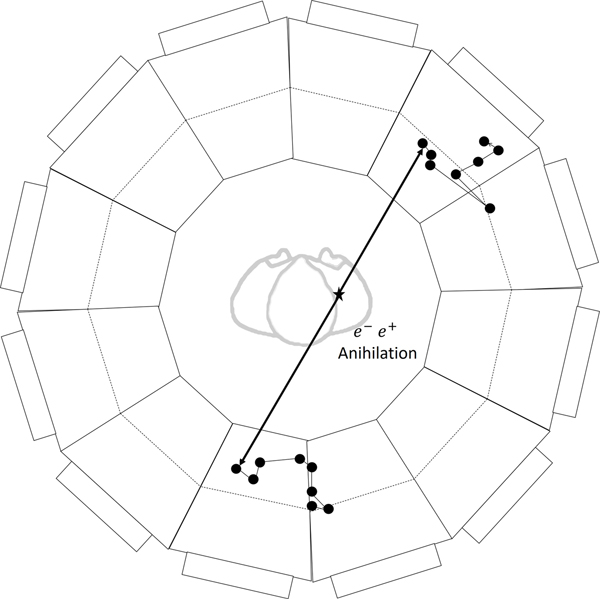
In low-Z gamma-ray detection the Compton cross-section dominates the PhotoElectric (PE) effect, resulting in a chain of successive Compton scatterings in the detector, each with monotonically decreasing energy of the scattering gamma. In the majority of events the energy-angle constraints of the 2-body Compton kinematics can be used to identify the initial interaction site of the gamma in the detector. The precision on the gamma trajectory is further improved by using the ionization along the electron track to identify which end of the track is the site of the Compton scattering [33]. Figure 1 shows an end view of the conceptual cylindrical whole-body PET scanner used in the simulation studies.

Figure 1:

An axial view of an example modular TOF-PET whole-body scanner based on low-Z organic media. The patient is located on the axis of cylindrical rings of imaging modules covering the field-of-view. Each of the two gamma-rays of a gamma-ray pair enters an imaging module and interacts via multiple Compton scatterings, producing recoil electrons that deposit energy along the recoil tracks. An event simulated using the Kamland-Zen LAB-based scintillator [34] as the medium is superposed to scale.

There are many detector media that change thermodynamic phase [27] or quantum state or chemical state locally where ionization energy is deposited. In the example detector discussed in Section 3, the recoil electron tracks are recorded by switching between two states of the molecules of a photoswitchable fluorescent dye, a ‘Switchillator’ [35–38]. The locations and number of activated molecules in the chain of successive Compton scatterings are optically recorded by repeated exposures of the activated Switchillator to excitation light that create fluorescent emission until the Switchillator eventually reverts to its inactive molecular conformation or is externally reset.

The identification of the first Compton electron track is based on: the relative fluorescence (‘brightness’) of the depositions (‘clusters’) and the distances and angles between successive clusters. The kinematic constraints of Compton-scattering [39] among clusters on the reconstructed gamma ray trajectory are used to trace the trajectory of the gamma as it scatters. The starting point of the first-scattered electron track corresponds to the interaction point of the primary gamma from the annihilation, and hence one end of the LOR. The location of the interaction can be determined from the evolution of ionization and scattering along the electron track [33].

2.1. The Gamma Trajectory: Successive Compton Scatterings

The annihilation of a positron with an atomic electron produces two approximately back-to-back gamma rays, each with an energy approximately that of the electron mass, 511 keV [40]. They may scatter within the patient, changing direction and losing energy. They subsequently interact with the active detector medium via two processes, Compton scattering [39], and the photoelectric effect (PE). The two process have distinctly different behavior with atomic number (Z) of the target material; when a 511 keV gamma ray first enters a typical low-Z organic scintillator [34] the ratio of the Compton to PE cross-sections is on the order of 10⁴ [41].

We have used Geant4 [42, 43] to simulate the successive interactions of 511 keV gamma rays entering a volume containing a typical low-Z organic liquid scintillator, in this case the LAB-based scintillator developed by the Kamland-Zen collaboration [34]. The pattern of ionization produced by the gamma is determined by the kinematics of successive Compton-scatterings, with each scatter producing a gamma of lower energy and a recoil electron in a two-body process fully constrained by conservation of energy and momentum [39, 44, 45]. For each interaction, the location, energy, and trajectory of the (ionizing) electron were recorded. In the simulation no details of the detector have been applied; a proposal for one such implementation that could in principle approach 100% detection efficiency is described in Section 3.

Figure 2 shows the simulated trajectory of a 511 keV gamma ray after entering a volume of LAB-based liquid scintillator [34]. The right-hand panel corresponds to a high-resolution camera image projected in 1-cm voxels. The inset shows the energy depositions from the most energetic Compton scattered electron projected in 10-micron voxels.

Figure 2:

An image projected in 1 cm voxels of the time-ordered energy depositions of a simulated 511 keV gamma interacting in the Kamland-Zen scintillator [34]. The gamma is shown entering the module from below. The inset on the left shows a map of the energy deposition from the most energetic Compton scattered electron in 10 micron voxels. The incident gamma energy for each of the enumerated Compton scatterings is tabulated below the image.

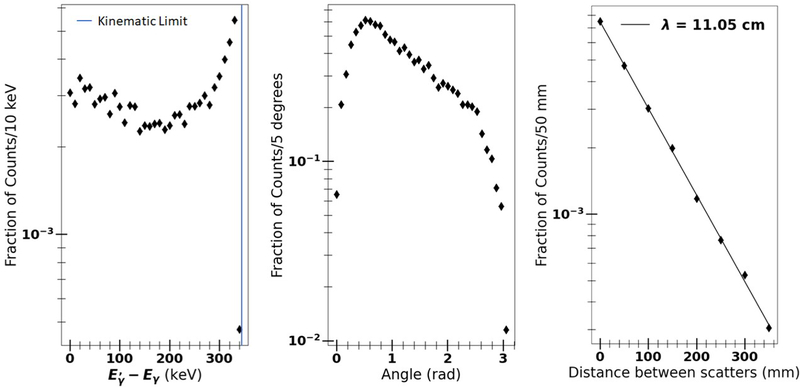
The distribution in separation between the first and second scatterings is shown in the right-hand panel of Figure 3. The separation is large compared to the resolution of an optical system, allowing in most cases the identification of individual clusters of energy corresponding to the early scatterings in the chain. The distribution in the energy of the scattering, i.e. the difference between the incoming and outgoing gamma energies, is shown in the left-hand panel. The angle of scattering in the first scatter is shown in the central panel.

Figure 3:

A Geant4 simulation of the kinematics of the first scatter of a 511 keV gamma ray in the Kamland-Zen scintillator [34]. Left: the distribution in the difference between the energies of the incident and scattered gamma; Center: the distribution in scattering angle; Right: the distribution in separation between the first and second scatterings. The line represents a fit of the separation to the form s = s₀e^−s/λ.

If there is no in-patient scattering, the first Compton scatter of the gamma ray in the detector is at the full energy of 511 keV. Successive scatterings are at successively lower incident gamma energies. The deposited energy from the first collision consequently has the highest probability of being the largest (‘brightest’) in the chain. The simulation finds that largest ionization deposition occurs in the first, second, and third scattering in 55%, 25%, and 11% of gamma interactions, respectively.

The efficiency of identifying the first interaction point can be improved beyond 55% by using the kinematic constraints inherent in Compton scattering. The energy and direction of a scattered Compton electron are fully constrained for a given incoming gamma ray energy and scattering angle. One can consequently fit the observed array of locations and energies for the time-ordering and the incoming gamma energy and direction. For example, we find that a χ² fit to the energies and angles of the six permutations of the three brightest clusters finds the correct time-ordering 86% of the time¹.

The processes of energy loss by the scattered electron allow a statistical determination of which end of the observed electron track is the point of the γe scattering, determining the recoil direction [33]. A constrained fit to the Compton kinematics of the γe scattering angles and γ energy loss of the chain of scatterings depends on this direction. We find that 96% of the electron tracks in the largest energy deposition have the correct end identified as the electron origin.

2.2. Forming the Line of Response and Rejection of In-patient Scattering

As shown in Figure 1, the two gamma ray trajectories define the LOR, on which the annihilation point will lie in the case of no intervening scattering in the patient or inert detector material. Ideally, using the Compton scattering equations to predict which energy deposition was the first will correctly define the line of response. Using only the first two detected Compton scatterings in the detector, the simulation reconstructs the LOR correctly ≈60% of the time. The transverse resolution for each LOR is consequently on the order of the uncertainty of the transverse position of the scattering sites on each end. Including more scatterings and more information (φ-dependence, distance between sites) in the kinematic fit, and using more sophisticated techniques such as machine learning [46] will improve the efficiency of correctly identifying the LOR end-points.

The LOR represents the central axis of a prior probability density (dubbed a ‘needle’ due to its elongated shape) for the true location of the e⁺e⁻ annihilation. For image reconstruction, this density distribution is modelled as Gaussian in both the transverse and longitudinal directions. In the case of no in-patient scattering and correct identification of the needle end-points, the transverse resolution, σ_T, is set by the spatial resolution on the end-points of the LOR of the optical system as described above, and for the Switchillator implementation described in Section 3 would be on the order of 40 microns. The longitudinal resolution, σ_L, is set by the resolution of the TOF system, and for the Switchillator implementation would be on the order of 1.2 cm.

In applications such as whole-body PET, in-patient scattering significantly decreases the fraction of high-resolution events [10, 12, 47]. The primary rejection of gammas that have scattered prior to the first scattering in the detector is a precision measurement of the incoming gamma energy and angle from the fit to the Compton chain of scatterings. The rejection will depend on the energy resolution; an example using switchable organic fluorophores to achieve a resolution of 1–2% (rms) is discussed in Section 3.2.

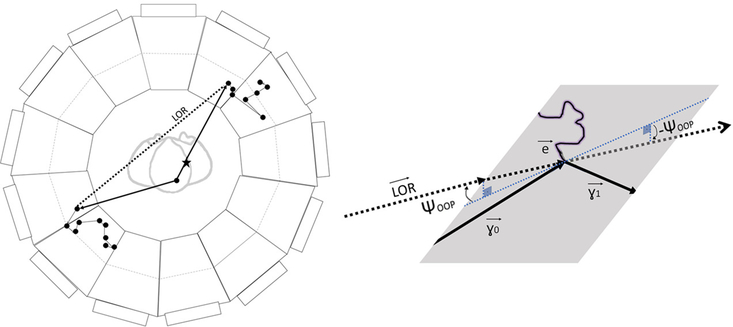
Figure 4 illustrates an additional method of rejection of mis-measured LORs in a low-Z medium. Since Compton scattering is 2-body, in the first scattering in the detector there should be no measurable component of the LOR out of the scattering plane defined by the recoil electron and the scattered gamma, i.e. the triple product $\left(\overrightarrow{e}\times {\overrightarrow{\gamma }}_1\right)\cdot L\overrightarrow{O}R$ should be consistent with zero.

Figure 4:

The LOR in the case of in-patient gamma-ray scattering. The positron annihilation point is marked by a star. The true gamma trajectories are represented by solid lines, and the reconstructed LOR connecting the two measured gamma interaction points by a dashed line. The scattered gamma (lower left-hand quadrant) will have a decreased energy and a longer flight path (larger TOF). The inset shows that a gamma-ray scattering in the patient produces a non-zero component of the LOR out of the plane defined in the detector module by the scattered electron and gamma, i.e. $\left(\overrightarrow{e}\times \overrightarrow{{\gamma }_1}\right)\cdot L\overrightarrow{O}R\ne 0$. Alternatively, the out-of-plane angle (OOP) is not zero. In addition, the polarizations of the gammas are correlated through their initial state entanglement.

Furthermore, the two gammas are quantum entangled and predominantly arise from the singlet state of positronium. The Compton scattering cross-section depends on polarization with a cos(φ) dependence. A full analysis of the cluster ordering can include this as a prior in the construction of a weight for the event.

While events with a single in-patient scattering will have transverse resolution significantly worse than σ_T, in some applications they may still carry signal beyond noise using advanced analysis techniques, although a discussion is beyond the scope of this paper [9].

To calculate the rate of triggers in which two events occur in the coincidence window (‘accidentals’), we assume the increased resolution allows the whole-body dose to be reduced by a factor of at least ten², from 200 MBq to 20 MBq. A 2-ns coincidence window produces an overall accidental rate of 4%, which can be further reduced to 1% by requiring each module to be in coincidence with 5 opposing modules in φ in 3 rings in z. This can be then further reduced using the full spatial and temporal information in the two coincident modules.

Pile-up, in which multiple events persist in the detector medium, is a more serious constraint, as the readout time is typically appreciably longer than the coincidence window. For example, a persistence time of 1 μs gives an average of 20 events simultaneously recorded in the detector at a whole-body dose of 20 MBq. Properly identifying the clusters from a given Compton chain will depend on the ability of the TOF system to measure the time of the brightest clusters in each module.

2.2.1. Positron Multiple Scattering and Acoplanarity of the Gamma Pair

The positron is emitted with a beta-decay spectrum, which for ¹⁸F has an end-point at 634 keV and a mean of 250 keV [48]. Multiple scattering and ionization loss sculpt the positron range distribution into a ‘cusp’-like distribution, with a typical FWHM for ¹⁸F of ≈50 microns [49–51]. We have included the effect of positron range by convolving the annihilation point with the distribution of Fig. 3 of Blanco et al. [49].

The initial positron momentum from nuclear beta-decay is not negligible compared to the 511 keV energy of the gamma rays, and as a consequence the motion of the center-of-mass of the electron-positron system distorts the back-to-back distribution in the frame of the annihilation [40, 52, 53]. Two effects mitigate the effect on the resolution of the annihilation point: 1) the positron typically annihilates at a lower energy due to ionization, and 2) the two-gamma emission axis and the positron momentum direction are uncorrelated. In the cases where the two directions are approximately collinear and the momentum transfer is small, the transverse momentum component to the LOR will be small, although the change in gamma energies will be large [54, 55]. A definitive treatment of the effect remains to be done [56].

2.3. Implementing a Stable Sub-nsec TOF Coincidence Window

The TOF system provides the event trigger, which initiates scanning and data acquisition for the switchable recording medium. The real-time trigger window can be refined off-line, and hence is not critical, being chosen for high efficiency, stability, and ease of implementation in a physically-extended many-channel system in which a stable tight window (e.g. below 1 nsec) would be difficult to maintain.

To tighten the coincidence window well below 1 nsec requires a system-wide precise time reference such as the IEEE1558 White Rabbit standard [57], which we have measured to be precise at the 5 ps level over 10’s of meters in a commercial off-the-shelf implementation [58].

Higher level triggers, operating off-line on the fully-reconstructed data after calibrations have been applied, can then tighten the coincidence window. For the coincidence, the times and positions of scintillation photons at the MCP-PMT face are digitized and recorded. For example, the PSEC4 waveform sampling system samples at 10–15 GS/s at a precision of 10.5 bits [2, 59–61]. The optical system records multiple scintillation photons with a resolution on each below 40 ps [2]. A fit to the leading edge of the recorded waveform determines the time, dominated by the signal-to-noise ratio and the number of samples on the leading edge [3].

3. A Concept for a Whole-Body TOF-PET Detector Based on Photoswitchable Organic Dyes

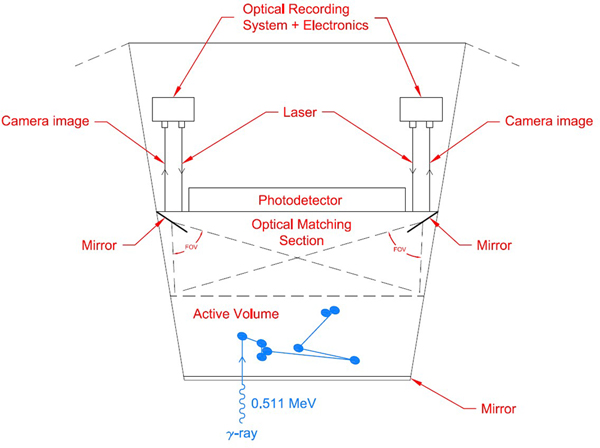
One possible phase-switchable recording medium that could be readily incorporated into a low-Z detection medium is a photoswitchable dye. Some of the energy deposited by each ionization event would be transferred by the medium to dyes in their inactive state, providing the necessary energy to chemically switch these dyes into a fluorescent, or active, molecular conformation. Combined with simple fluorescence excitation and detection optics, a Switchillator-based detector for low-Z TOF-PET could be implemented as sketched in Figure 5. Each detection module includes an active volume containing organic photoswitching fluorophores, a fast scintillator, and possibly other active elements such as a triplet sensitizer. Gamma rays from annihilations in the sample enter the active volume through the module surface facing the sample.

Figure 5:

An example module of a TOF-PET whole-body scanner based on Switchillator. One gamma of the pair from the annihilation enters through a front-side mirror. A large-area fast timing photodetector such as an LAPPD™ is optically coupled through the back surface of the module. An optical system controls the scanning and focus of twin lasers to repeatedly excite Switchillator fluorophore molecules activated by ionization from Compton electron tracks in the Switchillator volume. Similarly, the optical system allows a wide-angle stereo view of the active Switchillator volume through the backside surface. A passive optical transition volume optically matched to the active volume allows the laser and camera systems to reach any point in the active volume.

An optical subsystem to excite the activated Switchillator molecules is mounted on the back surface of the module. In the example shown in Fig. 5 the excitation system is implemented using twin diode lasers steered and focused by an optical system of controllable mirrors and lenses to provide wide-angle stereo coverage of the entire Switchillator volume. A similar optical subsystem images the fluorescence light from each excitation of the Switchillator molecules by the laser system. To facilitate full coverage with wide-angle stereo, each module has an optical transition region containing transparent liquid with a matching index of refraction between the active Switchillator volume and the module back face that supports the optical systems.

TOF measurements using the initial scintillation light are provided by a large-area MCP-PMT such as an LAPPD™ mounted on the back module surface. In the simulation the internal surface of the module front face has been made reflective to roughly locate energy depositions and to improve the time resolution by measuring the difference in scintillation light transit times to the front and back module surfaces. Electronics subsystems to support control, data acquisition, calibration, and local data analysis, including a complete imaging of the gamma ray trajectory in the module, are mounted on the back module surface.

3.1. Scintillator and Switchillator Properties

The medium in the active volume consists of a fast scintillator, a Switchillator fluorophore, and possibly other components to facilitate energy transfer to the Switchillator molecules or to enable deactivation after many excitation cycles. The required characteristics, and an estimate of typical values, for the scintillator and Switchillator are given in Table 2.

Table 2:

The signal-to-noise ratios and the value of the FWHM determined from the fit to the image of the Derenzo phantom shown in Figure 8. The six rows correspond to the six angular regions of identical rods. The difference between the fitted FWHM and the true rod diameter is comparable to or less than the 1 mm pixel size of the image.

Rod Diameter (mm)	Number of Rods	S/N Ratio	FWHM (mm)
19.1	6	4.4	18.0
12.7	10	4.0	12.5
11.1	10	3.6	10.9
9.5	15	3.5	9.6
7.5	21	3.5	7.2
6.4	26	3.2	6.0

3.2. Energy Resolution: Counting Scintillator Molecules as a Proxy for Deposited Ionization Energy

The Switchillator concept [62] incorporates ionization-activated photoswitchable organic fluorophores [35–38, 63, 64] directly into the low-Z liquid scintillation medium. When an ionizing particle, in this case a Compton electron scattered from a 511 keV gamma ray, deposits ionizing energy in the solvent of a liquid scintillation material, excited states are produced in the solvent molecules. These excited states in turn transfer their excitations to the fluorophore solute molecules, converting them from an inactive state that neither strongly absorbs visible light nor fluoresces, to an active state that absorbs visible light and fluoresces with high efficiency. Once activated, the fluorophores can be excited by a light source and the resulting fluorescence can be recorded to produce an image. The activated fluorophores can be repeatedly excited by the excitation light source before either reverting to their inactive state by a mechanism inherent in the material or excitation process, or being externally reset.

The ionizing tracks produced by electrons scattered along the trajectory of the gamma ray are recorded by the location and number of the activated fluorophore molecules. In typical solvents these molecules remain within about 10 microns of the path of the energy transfer for many milliseconds, enabling high resolution imaging of the successive individual gamma ray interactions along its trajectory in the scintillation material. The number of activated molecules is proportional to the deposited ionization energy, with a conversion factor that can be more than 10⁴ molecules per MeV [62].

By way of illustration, in toluene there are initially 1.35×10⁴ singlet excitations per MeV from 10 MeV electrons [65]. To achieve a 1% energy resolution at 511 keV requires 20,000 activated Switchillator fluorophore molecules per MeV. A process using only singlet excitations of the solvent with an efficiency of 0.4 would provide an energy resolution of ≈ 1.5%. There are 2.8 × 10⁴ triplet excitations per MeV; a process able to use both triplet and singlet excitations at an efficiency of 0.4 would achieve an energy resolution of 0.8% at 511 keV.

3.3. Cluster Finding

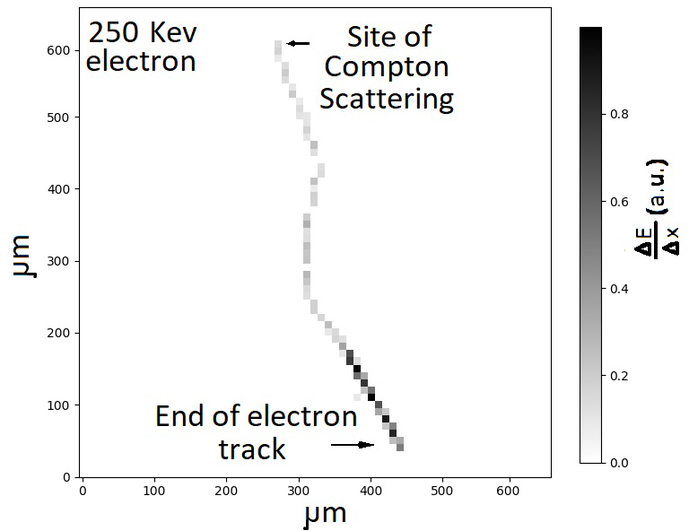
Each interaction will produce a pattern of pixels containing activated molecules at a density above background. We have used a simple seed-shoulder algorithm [66] to form ‘clusters’ of contiguous pixels based on deposited ionization energy. Figure 6 displays the output of the algorithm for the brightest cluster in Figure 2.

Figure 6:

The output of a seed-shoulder cluster algorithm [66] applied to a GEANT4 simulation of a 250 keV electron imaged in pixels of 10 microns. The electron deposits energy in the medium along its path. The most energy per voxel is deposited as the electron ranges out. This can be used to identify the position of the Compton scattering and the initial direction of the electron at the start of the track.

3.4. Time-of-Flight System and Resolution

The concept module shown in Figure 5 uses a method of event reconstruction from the precise measurements of time-of-arrival and position of Cherenkov light [4, 32]. In analogy to the TPC technique of using drift trajectories of electrons in a uniform electric field to make time-sliced 3-dimensional images of ionization [67], we have dubbed imaging by time-slicing the drifting of photons as the ‘Optical Time Projection Chamber’. In the conceptual design of Figure 5, each module supports a TOF system consisting of a large-area MCP-PMT such as an LAPPD™ and a mirror on the inside of the entrance window. In the simulation results quoted below the module sides were also reflective.

The design of the multi-level coincidence system of Section 2.3 removes the need to narrow the real-time coincidence window below that needed for deadtimeless operation of the DAQ system [66].

Off-line fits to the multi-photon photodetector pad or strip waveforms are expected to provide time resolutions on the order of 40 ps or below [2, 68], dependent on the speed and light output of the scintillator and the details of the optical/MCP system.

A simulation of the geometry of Figure 5 and an infinitely fast scintillator with the light output of the Kamland-Zen scintillator returns a 40 ps resolution (rms), corresponding to a longitudinal resolution σ_L = 1.2 cm. Consequently a short coincidence window of a nsec or less, with the width set by the difference in travel times needed to cover the region-of-interest, can be used in the real-time trigger.

The TOF measurements can be further sharpened post-data acquisition by using the locations and time-ordering of the clusters. The performance will depend on the speed, light-yield, and spectrum of the combined scintillating and switching medium. In the simulation we use an estimate of 40 ps (sigma) for the TOF resolution.

3.5. Constructing an Image from the Lines of Response

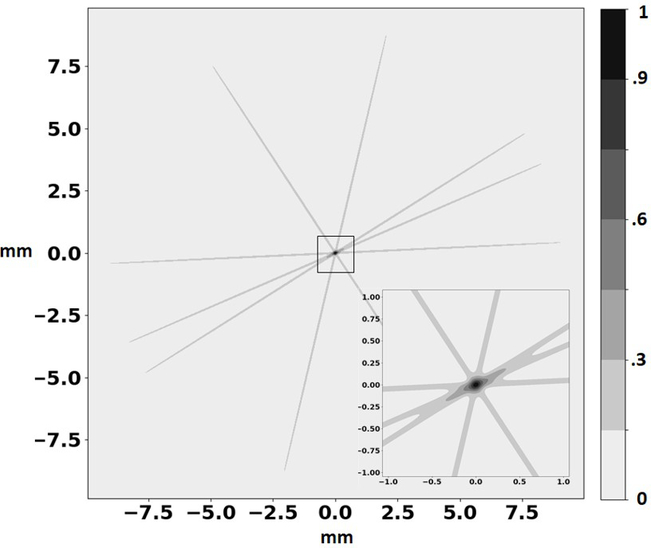
Figure 7 shows a 1-sigma surface of the probable location of the positron-electron annihilation for a small number of events. The transverse resolution is set by the resolution on the entry points of each gamma ray, ≈40 microns when the first cluster (efficiency ϵ = 85%) and gamma-electron scattering location in the cluster (efficiency ϵ = 95%) are identified from the kinematics. The overall efficiency for correct identification of both gamma interaction points is ≈ 65%. The resolution along the LOR axis is larger than the transverse resolution by a factor of ≈ 12000/40 = 300. The shape for one event is like that of a narrow needle with Gaussian projections.

Figure 7:

An illustration of image reconstruction from a small number of LORs. Each ‘needle’ is characterized by Gaussian distributions in the transverse and longitudinal directions, with σ_T ≈ 40 microns and σ_L ≈ 1.2 cm, with a volume of ≈ 0.02 mm³. The intersection of many such volumes is dominated entirely by σ_T.

For images with many bright features close to each other, the ‘needle stacking’ produces a low-frequency background due to pile-up of needle crossings in high density areas in the image. There are a number of sophisticated algorithms in both image space and the corresponding Fourier space for filtering and performing likelihood fits to PET scanner images [69]. In the case that the detector resolution is smaller than the voxel size, a series of ortho-normal functions can be used to subtract low-frequency pile-up directly from the image.

The left-hand panel of Figure 8 shows an image of simulated annihilation locations for a 10 minute exposure of the Derenzo phantom [70] loaded with the low dose of ¹⁸F at 30 Bq/cc in the source (rod) regions and at 10 Bq/cc in the surrounding background volume [71]. For each annihilation the positron range is selected from the distribution of Blanco et. al.[49]. The detector simulation accepts all annihilations regardless of angle, and no corrections for detector inefficiencies or in-patient absorption/scattering are applied. The positron range was drawn from the distribution in Blanco et. al. To model the raw image on the left, for each of the simulated annihilations we generate a random gamma emission direction to determine a LOR, and then randomly shift the LOR according to the detector resolution (see Figure 7). The LORs are then added together, and a 1 mm slice is taken across the phantom to generate the image.

Figure 8:

Imaging the Derenzo phantom [70] with the unfiltered back-projection of the needle stack. Left: an 1 mm-thick slice through the input source distribution density of annihilations with a 10-minute exposure using the reduced dose of 30 Bq/cc of ¹⁸F in the rods and 10 Bq/cc in the surrounding volume [71]. The white dots represent voxels with annihilations. Middle: the reconstructed projected image from summing the weights of needles crossing each voxel. Right: the reconstructed projected image after subtracting a least-mean-squares fit to the 136 terms of an expansion in Zernike functions up to order 15. The detector accepts all annihilations regardless of angle and no efficiencies or in-patient absorption or scattering corrections have been applied.

The image reconstructed from the density of needles in each voxel is shown before and after subtracting a fit to the 136 terms of the Zernike functions up to order 15 [72] in the middle and right-hand panels. No detector efficiencies or in-patient absorption/scattering corrections have been applied. More details and a table of signal-to-noise ratios are given in Appendix A.

The TOF information from the initial scintillation light contains the positions and times of the individual photons, with intrinsic sub-mm resolution in the detector plane. Including the TOF information in the determination of the initial gamma direction from the list of cluster locations is sufficiently complex to provide an opportunity for advanced likelihood techniques such as machine learning [46].

4. Summary and Conclusions

We propose the development of PET scanners that use ionization-activated multi-state low-Z detector media to achieve spatial resolutions limited by the underlying physics rather than by detector segmentation. A gamma from the positron annihilation produces a chain of successive Compton scatterings in the detector medium, activating the medium along the mm-scale paths of the Compton recoil electrons. Measurement of the individual scattering locations, deposited energies, and recoil electron directions allows using the kinematical constraints of Compton scattering to perform a statistical time-ordering of the scatterings. The locations of the first interactions of both gammas determine the Line-of-Response with a transverse rms determined by the precision of locating the start of the corresponding recoil electron track. A simple least-mean squares fit to simulated events in an organic scintillator identifies the initial scattering location of a gamma >85% of the time. Mistaken identifications typically have rms transverse resolutions orders-of-magnitude larger, and contribute to the image as a low-frequency low-contrast background, removable by filtering.

A time-of-flight system based on large-area MCP-PMTs provides a stable real-time coincidence event trigger with a coincidence window on the order of several nanoseconds. With the single-photon resolution below 40 ps of MCP-PMTs, the window can be substantially reduced using the combined data of real-time photon times and positions and the off-line analysis of the locations and directions of the Compton-chain electrons, with a time-base provided by a commercial multi-channel system with sub-10 ps resolution over the system [58].

As an example of a persistent low-Z medium capable of high spatial and energy resolution, we have simulated an ideal two-state photoswitchable organic dye [62], activated to a fluorescent-capable state by the ionization of the recoil electrons. The activated state can be optically excited multiple times to image individual activated molecules. Energy resolution is provided by counting the activated molecules. Location along the LOR is implemented by large-area time-of-flight MCP-PMT photodetectors [31] with single photon time resolution in the tens of ps and deep sub-mm spatial resolution.

Simulations of the Derenzo PET imaging phantom indicate a substantial reduction in dose would be possible. The 30/10 Bq/cc dose that produces signal-to-noise figures greater than 3 in the simulation is lower than a typical 30/10 KBq/cc [71] by a factor of 1000. However no detector efficiencies or corrections for in-patient absorption/scattering have been applied; these will lower the dose reduction factor, but depend on the application and details of the low-Z medium and detector. The concept seems promising, but a quantitative estimate of dose reduction is not yet possible.

The concepts described here will require development efforts on ionization-activated multi-state low-Z media such as photoswitchable organic fluorophores (‘Switchillator;) [62], large-scale production of low-cost robust ‘commodity’ large-area ps MCP-PMTs [1], and economical 10 GS/sec or higher wave-form sampling electronics systems such as the PSEC4 system [4, 60]. However achieving doses a factor of 100 lower or more with spatial resolutions set by the intrinsic limitations due to the underlying physics would have an impact on public health world-wide.

Appendix A: Signal-to-Noise Ratios

The low-frequency background of the image from the 30/10 Bq/cc simulation of the Derenzo phantom [70] shown in Figure 8 was fitted using the first 15 orders of Zernike polynomials, comprising 136 terms. After removing the fitted background from the image, the average signal-to-noise (S/N) ratio and FWHM of the rods were determined as follows.

The Derenzo phantom comprises six angular slices, each containing identical rods ranging from 6.4 mm to 19.1 mm in diameter. The rods in each slice were fit to a model rod in a 4-parameter fit over the 1-mm² image pixels. Each of the rod sizes was modelled as a cylindrical trapezoid using 4 parameters: 1) the diameter of a disk of constant value around the rod center; 2) the average background in the angular slice excluding the rods; 3) the average value in the center disk, and 4) the slope of a cone extending from the edge of the center disk down to the background value.

The signal (S) in each slice was calculated as the difference between the value of the central disk and the background. The noise (N) was measured as the standard deviation of the background pixels. The FWHM was calculated using the trapezoidal shape with the height defined by the value of the center disk, and the sloped sides extending down to the background value. The signal-to-noise ratios S/N and FWHM values are presented in Table 1.

Table 1:

Physical properties and estimated associated desired values for a diarylethene-based scintillator-switchillator detector medium containing both a fast scintillator and the photoswitchable Switchillator molecules [35–38]. Switchillator properties of particular concern and that are targeted for development include the Dye Ratio (selectivity), On-state lifetime (resetting), and Absorption Length (optical depth) [62].

	Parameter	Symbol	Value	Comment
Scintillator Properties
1	Scintillation Yield	Yscint	> 2 × 103	# of scintillation photons per MeV
2	Scintillation Rise Time	τr	TBD	1/e rise time of scintillation light
3	Scintillation Decay Time	τd	TBD	1/e decay time of scintillation light
Switchillator Properties
1	Activation Yield	Yact	> 5 × 103	# of ON fluorophores per MeV deposited
2	Activation Wavelength	λact	< 400 nm	Peak inactive to active wavelength
3	Excitation Wavelength	λex	350–650 nm	At max separation
4	Dye Ratio	Zdye	< 10−12	Ratio of rates of background activation to fluorescence at λex
5	On-State Lifetime	λON	3×10−7–10−1 s	1/e Lifetime of ON fluorophores
6	Fluorescence brightness	ε · Φfl	> 103/(M cm)	Rate of emission from active dye
7	Mean Absorption Length	χ(λex)	> 6 m	1/e absorption length at λex
8	Emission Wavelength	λfl	400–700 nm	Wavelength of fluorescence light
9	# of photons per activated fluorophore	Nfl	> 500	Mean # of fluorescent photons extracted per fluorophore before deactivation