Bayesian metamodeling of complex biological systems across varying representations

Significance

Cells are the basic units of life, yet their architecture and function remain to be fully characterized. This work describes Bayesian metamodeling, a modeling approach that divides and conquers a large problem of modeling numerous aspects of the cell into computing a number of smaller models of different types, followed by assembling these models into a complete map of the cell. Metamodeling enables a facile collaboration of multiple research groups and communities, thus maximizing the sharing of expertise, resources, data, and models. A proof of principle is provided by a model of glucose-stimulated insulin secretion produced by the Pancreatic β-Cell Consortium.

Abstract

Comprehensive modeling of a whole cell requires an integration of vast amounts of information on various aspects of the cell and its parts. To divide and conquer this task, we introduce Bayesian metamodeling, a general approach to modeling complex systems by integrating a collection of heterogeneous input models. Each input model can in principle be based on any type of data and can describe a different aspect of the modeled system using any mathematical representation, scale, and level of granularity. These input models are 1) converted to a standardized statistical representation relying on probabilistic graphical models, 2) coupled by modeling their mutual relations with the physical world, and 3) finally harmonized with respect to each other. To illustrate Bayesian metamodeling, we provide a proof-of-principle metamodel of glucose-stimulated insulin secretion by human pancreatic β-cells. The input models include a coarse-grained spatiotemporal simulation of insulin vesicle trafficking, docking, and exocytosis; a molecular network model of glucose-stimulated insulin secretion signaling; a network model of insulin metabolism; a structural model of glucagon-like peptide-1 receptor activation; a linear model of a pancreatic cell population; and ordinary differential equations for systemic postprandial insulin response. Metamodeling benefits from decentralized computing, while often producing a more accurate, precise, and complete model that contextualizes input models as well as resolves conflicting information. We anticipate Bayesian metamodeling will facilitate collaborative science by providing a framework for sharing expertise, resources, data, and models, as exemplified by the Pancreatic β-Cell Consortium.

Cells are the basic structural and functional units of life (1). Different aspects of the cell have been studied extensively, including experimentally, computationally, and theoretically. As is the case for any model, a cell model is expected to provide more information about the cell than any of the input information used for its construction. In particular, the model should rationalize known facts and make testable predictions. We consider a desired cell model and its construction by discussing a progression from an impractical atomic model, an impractical integrative model, actual current models, and finally culminating in the modeling approach proposed here.

Modeling of the Cell

Impractical Physical Modeling of the Cell.

Hypothetically, a most precise model of the physical cell structure specifies trajectories for each of its atoms over its life span. Such a model could in principle be obtained from molecular dynamics simulations (2, 3). In practice, however, computing accurate trajectories for ∼10¹⁴ atoms over days or longer is limited by inaccurate molecular mechanics force fields and slow computers with insufficient memory, as well as lack of sufficient knowledge about the starting state and environment. Moreover, even if such a model could be computed, it still would not abstract all cellular properties of interest, such as molecular signaling networks.

Recalcitrant Integrative Modeling of the Cell.

To attempt to address these challenges, we could adopt an integrative approach. Integrative modeling is defined as modeling that uses multiple types of information about the modeled system, be it from different experiments or prior models (4, 5). It is motivated by the resulting increase in accuracy, precision, and completeness of a model. Integrative modeling is particularly effective for modeling complex biological systems, for which no single experimental or theoretical approach can provide all needed information. For example, structures of large macromolecular assemblies recalcitrant to traditional structural biology methods have been determined by integrative structure determination (6). Integrative modeling of the cell could rely on a multiscale representation and multimodal experimental data, in addition to the first principle of physics (4). In practice, however, even integrative modeling of all aspects of the entire cell is not feasible at this time, due to insufficient data and computing power as well as limitations of existing integrative modeling methods.

Current Models of Aspects of the Cell.

Although an accurate, precise, and complete model of the cell cannot yet be computed, it is possible to model some aspects of the cell or its parts with useful accuracy and precision (5). Most of these models rely on a single type of representation of the cell, such as spatiotemporal (7), ordinary differential equation (ODE) (8), and flux balance analysis representations (9). In addition to whole-cell models, there are a myriad of models of different parts of the cell, too numerous to review here. These models may provide a useful starting point for whole-cell modeling due to their encoding of expertise, data, and computing used to produce them. However, no general approach yet exists for combining different kinds of models, although steps in this direction have been made (Discussion) (10–14).

Bayesian Metamodeling of the Cell.

Here we propose a divide-and-conquer modeling approach that integrates input models of varied representations into a metamodel. Metamodeling can be seen as a special case of integrative modeling in which the focus is on integrating prior models instead of data (4). The large problem of computing an integrative model of the cell is broken into a number of smaller modeling problems corresponding to computing models of some aspects of some parts of the cell. Each such input model may be informed by different subsets of available data, relying on its distinct model representation at any scale and level of granularity. Metamodeling then proceeds by assembling and harmonizing the input models into a complete map of the cell. Here the input models are harmonized through a Bayesian statistical model of their relations with each other and/or the physical world. This Bayesian approach enables us to update our beliefs in the distribution of model variables (including best single-value estimates and their uncertainties), given information provided by all input models. By shifting the focus from data integration to model integration, Bayesian metamodeling facilitates the sharing of data, computational resources, expertise in diverse fields, and already existing models of the cell and its parts.

Proof of Principle: Prototype Metamodel of Glucose-Stimulated Insulin Secretion.

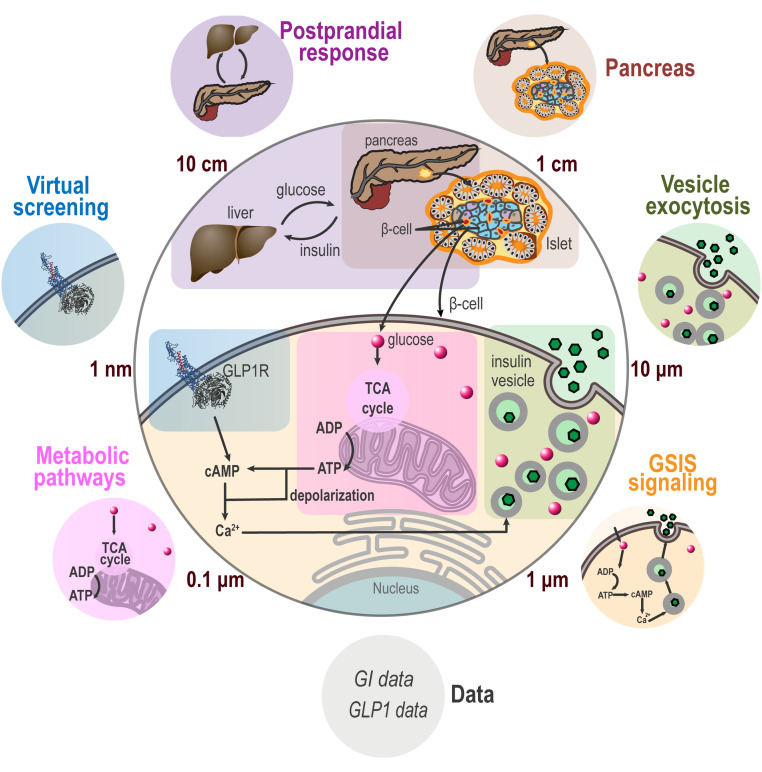
The Pancreatic β-Cell Consortium (https://pbcconsortium.org/) brought together research groups in biology, chemistry, physics, mathematics, computer science, and the digital arts (15). The consortium provides a nurturing environment for developing methods for whole-cell modeling. For developing the method of metamodeling, we narrowed our focus on glucose-stimulated insulin secretion (GSIS) (16), one of the key functions of the β-cell (Fig. 1). Insulin secretion encompasses many of the complexities of the whole cell, including aspects that are best described using different types of models at different scales, thus providing a useful testing ground for Bayesian metamodeling of the cell.

Fig. 1.

Metamodeling of GSIS. Eight input models, including two data models, describe different aspects of GSIS (Table 1). They are represented by small circles with different background colors. These input models are integrated into a single metamodel of GSIS, indicated by a large gray circle in the center.

Results

Definitions.

We are using a number of common terms that may have different definitions in different fields. Thus, we begin by defining our usage here. We are working in the Bayesian framework that estimates a model based on data and prior information (17). Thus, a model is the joint posterior probability density function (PDF) over the model variables. We distinguish among three kinds of model variables. First, free parameters (i.e., degrees of freedom) are quantities that are fit to input information (e.g., the coefficients of a polynomial model and atomic coordinates of a protein structure model). Second, independent variables (i.e., regressors, features, or inputs) are quantities whose values are supplied when evaluating a model (e.g., the abscissa of a polynomial model). Third, dependent variables (i.e., response variables, regressands, outcomes, labels, predictions, or outputs) are quantities whose values are computed when evaluating a model (e.g., the ordinate of a polynomial model). As an aside, fixed parameters (i.e., constants or hyperparameters) are quantities whose values are defined and fixed (e.g., stereochemistry parameters in protein structure modeling). Systematic error of a model (variable) is the mean difference between the model (variable) and the ground truth. Random error of a model (variable) is the spread (e.g., SD, SEM, and entropy) of the model (variable). While the ground truth is never known, systematic error can still be approximated by the difference between the model and an independent reference that represents the ground truth as closely as possible (a gold standard). Accuracy and precision (uncertainty) are equivalent to systematic error and random error, respectively, except they increase as their counterparts decrease. Ideally, accuracy is approximated by precision. Metamodeling couples and harmonizes all input models by updating the PDFs of their free parameters.

The Input Models.

Information for GSIS metamodeling is provided by eight input models (Fig. 1, Table 1, and SI Appendix, Supplementary Text 1). The models have been selected to cover a diverse range of representations, spatiotemporal scales, and data. They include a coarse-grained spatiotemporal simulation of insulin vesicle exocytosis, a molecular network model of GSIS signaling, a network model of insulin metabolism, an atomic structural model of glucagon-like peptide-1 receptor (GLP1R) activation, a linear model of the pancreatic cell population, ODEs for systemic postprandial insulin response, synthetic data on glucose intake (glucose intake data model), and synthetic data on GLP1 and GLP1 analog levels (GLP1 data model).

Table 1.

The input models for GSIS metamodeling

Model (abbreviation)	Representation	Description	Scale (spatial, temporal)	Granularity (spatial, temporal)	Experimental data and prior information	Ref. and sections
Postprandial response (PR)	ODEs	Model of systemic postprandial change in plasma insulin and glucose levels after a meal	Body, 103 s	Organ, 101 s*	Insulin, glucose measurements	(22) 1.1†
Pancreas (Pa)	Linear equations	Model of insulin secretion by the entire population of β-cells in the pancreas	Organ, N/A	Cell, N/A	Microscopic examination and morphometric measurements for quantifying islets in a pancreas (87); electrical tomography and morphometric analysis for quantifying β-cells in an islet (88)	1.2†
Vesicle exocytosis (VE)	Spatiotemporal	Coarse-grained Brownian dynamics simulation of insulin granule trafficking, docking, and exocytosis	Cell, 10−1 s	Molecule/granule, 10−8 s	Soft X-ray tomography (21)	1.3†
GSIS signaling (Sg)	Network /linear ODEs	Model of signaling pathway of GSIS	Cell, 102 s	Molecule, N/A	KEGG pathways (89); fluorescence imaging and Förster-resonance energy transfer microscopy (FRET) (90–93)	1.4†
Insulin metabolism (Mb)	Network	Model of cellular metabolic pathways up-regulation or down-regulation under different treatment conditions	Cell, 102 s	Molecular concentration, N/A	Proteomic/metabolomic screens, KEGG pathways (89)	1.5†
Virtual screening of GLP1R (VS)	Spatial	List of GLP1R ligands ranked by their estimated activation of GLP1R, based on structure-based virtual screening of a library of GLP1 analogs	Macromolecule, N/A	Atom, N/A	Virtual screening assay (94) based on structure-based modeling and X-ray crystallography	1.6†
Glucose intake data (GI)	Time series	Rate of glucose intake after a meal	Body, 103 s	Organ, 101 s	Synthetic data derived from the glucose rate of appearance from the postprandial response model	1.7†
GLP1 data (GL)	Synthetic data	GLP1R activation at different agonist levels	Macromolecule, <s	Atom, N/A	Synthetic data	1.8†

^*The model is continuous but trained over data obtained at 1-min resolution, with the precision on the order of seconds.

^†The model was computed here, based on prior publications, as described in SI Appendix, Supplementary Text 1, sections as marked. Ref., reference.

Bayesian Metamodeling Workflow.

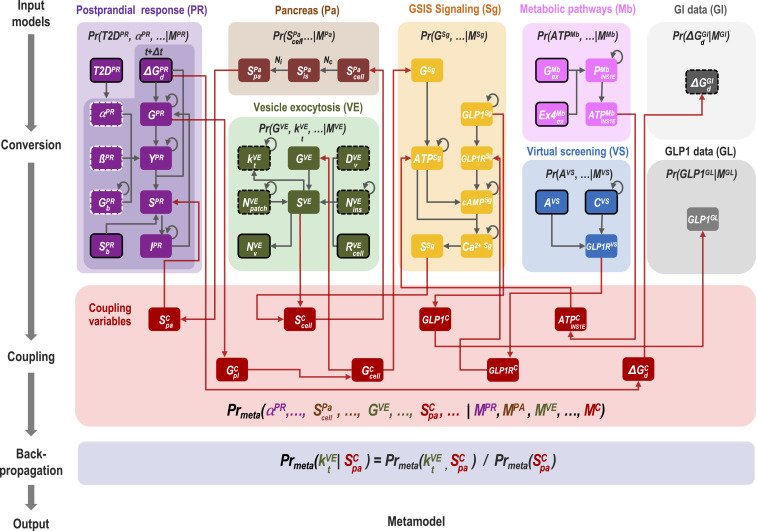
Given the input models, Bayesian metamodeling proceeds through three steps (Fig. 2): 1) conversion of the input models into surrogate probabilistic models, 2) coupling of these surrogate models through subsets of statistically related variables, and 3) backpropagation to update the original input models by computing the PDFs of free parameters for each input model in the context of all other input models. Thus, the output from metamodeling includes the joint PDF over all surrogate and reference variables (step 2) as well as the updated input models (step 3). We now describe each step in turn, both in general terms and by one or more examples.

Fig. 2.

From input models to coupled surrogate models in a metamodel of GSIS. Nodes indicate variables, and directed edges indicate probabilistic relations between a parent and child variable in a BN; a child variable is conditionally independent of any of its nondescendants, given the values of its parent variables (19). Each model and its variables are indicated by a specific color. Reference variables are in red, data variables are in gray, fixed parameters in the input models are encircled in white dashed lines, free parameters are encircled in black dashed lines, independent variables are encircled in continuous line, and dependent variables are not encircled. Gray edges are defined by the input models, whereas red edges are defined by the couplers. Self-loops indicate dependency on the value of the same variable in a previous time slice. Annotated variables and edges indicate examples discussed in the text.

Step 1: Conversion of Input Models into Surrogate Probabilistic Models.

A surrogate model is an approximation of a more complex input model whose primary purpose is to facilitate relating variables across multiple input models (18). In the first step of metamodeling, we create a surrogate model for each input model by converting it into a corresponding probabilistic model. Formally, a surrogate model specifies a PDF over some input model variables and any additional variables deemed necessary. This PDF encodes model uncertainty and statistical dependencies among its variables. Model uncertainty arises from insufficient information, imperfect modeling, and/or stochasticity of the system. Statistical dependencies are exemplified by the dependency between the values of independent and dependent variables, the effect of free parameter values on such dependency, and spurious correlations due to confounding factors or coincidence.

In principle, a surrogate model could be obtained by any approach for modeling statistical distributions, such as probabilistic graphical models (PGMs) (19) and various deep generative models (20). For the current proof of concept, we used Bayesian networks (BNs), which are a well-studied class of PGMs (19). BNs are often used for representing PDFs over many variables using a directed graph (network), with nodes and edges representing variables and conditional statistical dependencies, respectively. They are supported by efficient methods for Bayesian inference, parameter fitting, and learning of network topology from data. Finally, BNs include dynamic Bayesian networks (DBNs) that generalize both hidden Markov models and Kalman filters, allowing us to model dynamic processes (19), such as vesicle exocytosis. In a nutshell, for a given input model, we tabulate dependent variables as a function of free parameters and independent variables, followed by manually constructing and parametrizing a surrogate PGM that approximates this table.

Examples.

We constructed a surrogate model for the vesicle exocytosis model (Figs. 1 and 2, green). Insulin vesicle exocytosis is described by spatiotemporal trajectories of insulin granules undergoing trafficking, docking, and exocytosis within a pancreatic β-cell over 200 ms, following glucose stimulation (SI Appendix, Supplementary Text 1.3 and Movie S1) (21). A simplified cell representation incorporates the cell membrane, nucleus, hundreds of insulin vesicles, and thousands of glucose molecules. The trajectories of these components are computed using Brownian dynamics simulations restrained by various experimental data, including soft X-ray tomograms of the cell. The free parameters include parameters of the data-driven potential function and diffusion constants. The independent variables are the coordinates of the starting configuration. The dependent variables are millions of cell frames in a trajectory, each specifying coordinates of thousands of components. For practical reasons, the proof-of-principle surrogate model abstracts the billions of variables describing a trajectory by sampling it at a fraction of frames and including only a subset of variables for each sampled frame. Uncertainty in the values of the surrogate model variables reflects uncertainty in the corresponding input model.

As a second example, we constructed a surrogate model for the postprandial response model (22) (Figs. 1 and 2, purple, and SI Appendix, Supplementary Text 1.1). Insulin and glucose fluxes through different body systems in the hours following a meal are described by ODEs. The variables of the postprandial response surrogate model include free parameters of the model ODEs (i.e., coefficients in ODEs) in either healthy or type 2 diabetic subjects; independent variables corresponding to the change in plasma glucose levels due to digestion; and dependent variables indicating predicted glucose and insulin plasma levels over time (G and I), glucose-dependent insulin secretion (Y), and total insulin secretion (S). While the ODEs are deterministic, their free parameter values are uncertain: they were obtained by fitting noisy and sparse measurements of insulin and glucose levels (22), and they do not account for variability in insulin response as a function of hidden (unseen) variables, such as an individual, time of day, and meal composition other than glucose. To reflect the uncertainty in the free parameters, we specified a prior distribution over each parameter value. In addition, we used a DBN to describe the change in insulin and glucose levels over time, given these parameters and glucose intake during a meal. Last, we introduce a Boolean variable T2D, indicating a diabetic or healthy subject. Thus, the surrogate model now accounts for both the large uncertainty in the model parameters and the statistical dependencies among the model variables over time (Fig. 2).

Step 2: Coupling Surrogate Models.

Surrogate models enable us to couple multiple input models through subsets of statistically related variables. Their coupling requires some shared reference variables (i.e., coupling variables). Suitable coupling variables can often be found with the aid of a high-resolution representation of the physical world (e.g., atomic coordinates in space and time) or some function of these variables (e.g., coarse-grained coordinates over particles or time). These latent (hidden) variables serve only to formally relate variables from different surrogate models; their values do not need to be known. To couple variables from two or more surrogate models, we describe their relations with the coupling variables, as follows. First, we identify subsets of potentially related variables from multiple surrogate models, as currently determined by an expert based on prior knowledge. Second, for each such subset of surrogate variables, we define corresponding coupling variables. Finally, we devise conditional PDFs (couplers) on each subset of surrogate and coupling variables. We aim to couple as many surrogate models with each other as possible, culminating in a joint PDF over all surrogate models. Importantly, there is generally not one correct choice for the coupling step. Instead, coupling is an external modeling choice and a model in and of itself, just like the input and surrogate models (M_C in Fig. 2). Automated methods for performing this step are conceivable (Discussion). In addition to priors corresponding to input models, we also use data likelihoods when convenient to define couplers (e.g., GI data model; Fig. 2).

Example.

Four of the eight surrogate models in the metamodel include variables referring to rates of insulin secretion, although in different contexts and spatiotemporal scales. The postprandial response (PR) and pancreas (Pa) surrogate models include a variable referring to the total secretion rate from pancreas to plasma ($S_P^R$ and $S_{pa}^{Pa}$, respectively; Fig. 2). The pancreas (Pa), vesicle exocytosis (VE), and GSIS signaling (Sg) models include a variable referring to the secretion rate from a single β-cell ($S_{cell}^{Pa}$, $S_V^E$, and $S_S^g$, respectively). To relate these variables, we introduce two coupling variables: the true insulin secretion rate from pancreas to the portal vein averaged over population and time ($S_{pa}^C$) and the true (but unknown) secretion rate from a primary pancreatic β-cell to the extracellular matrix averaged over population of cells ($S_{cell}^C$). Finally, we impose conditional PDFs on subsets of these surrogate and coupling variables, relying on the pancreas model as a straightforward bridge between different scales. At the plasma level, S^PR in the pancreas response model is conditionally dependent on the coupling variable $S_{pa}^C$, which is in turn conditionally dependent on $S_{pa}^{Pa}$ in the pancreas model. At the cell level, $S_{cell}^{Pa}$ is conditionally dependent on $S_{cell}^C$, which is in turn conditionally dependent on $S^{VE}$ and $S^{Sg}$. Thus, four surrogate models, each describing different scales and aspects of insulin secretion, are coupled. This example provides a blueprint for how more complex models of variation among cells and individuals can also be included. For example, reference variables may describe secretion rates for different individual cells within a single islet or different cell lines.

Step 3: Harmonize Input Models by Backpropagation of Updated Variable PDFs.

In the last step, information in the coupled surrogate models is propagated back to the original input models. This update is achieved by first updating surrogate models (Fig. 2). A surrogate model PDF can be updated by either marginalizing out or conditioning on each variable in all other surrogate models. In fact, a PDF spanned by any combination of variables from any surrogate models can be computed by marginalizing out and/or conditioning on the other surrogate variables. Finally, we update each input model by relying on a mapping between the surrogate and input model variables. Alternative backpropagation schemes can be performed in parallel (e.g., conditioning on different values of some variable). Other backpropagation schemes may be explored in the future (Discussion).

Examples.

The postprandial response model includes an input parameter for basal plasma glucose level, $G_b^{PR}$ (Fig. 2) (22). Its surrogate model includes a corresponding variable that is distributed normally (mean value of 5.1 ± 1 and 9.2 ± 1 mM for healthy and diabetic individuals, respectively), thus describing its prior uncertainty. Following the coupling step, we obtain a joint PDF spanned by variables in all surrogate models, including $G_b^{PR}$. To update a $G_b^{PR}$ estimate for the postprandial response surrogate model, we compute its marginal PDF from this joint PDF, conditioned on the variable indicating a healthy or diabetic individual. The $G_b$ parameter in the original postprandial response model is then replaced with the mean estimate of $G_b^{PR}$ in the surrogate model. This process is repeated for other free parameters of the postprandial response model individually or jointly. Either way, as a result, the updated postprandial response model reflects information from all other input models, via the coupling of insulin secretion rates in different surrogate models performed in step 2.

Another example is provided by the vesicle exocytosis model, which specifies positions of thousands of cellular components over millions of Brownian dynamics trajectory frames (step 1). As discussed above, the surrogate model has significantly fewer variables. Nonetheless, the PDF of the surrogate model itself encodes the statistical relations among key free parameters and other variables of the input model (example in step 1). Thus, useful information can be extracted directly from the PDF of the harmonized surrogate model. For example, an updated estimate of vesicle trafficking rate in the vesicle exocytosis model $k_t^{VE}$ as a function of insulin secretion rate over time in the postprandial response model $S^{PR}$ can be computed directly from the marginal PDF of $k_t^{VE}$, conditioned on $S^{PR}$ (Fig. 2, backpropagation step). In addition, estimates of the corresponding free parameter $k_t$ and other free parameters of the original input model are updated by backpropagation from the harmonized surrogate model, followed by recomputing spatiotemporal trajectories of vesicle exocytosis using these parameters, now harmonized based on all other input models.

A Proof-of-Concept Bayesian Metamodel of GSIS.

By applying conversion, coupling, and backpropagation (Fig. 2), we divided and conquered the task of modeling GSIS, thus decentralizing required computing and expertise. We now discuss how Bayesian metamodeling produces a more complete description of GSIS than the original input models, contextualizes them, increases their accuracy and precision, and resolves conflicting information in the input models. Several simplifying assumptions in the input, surrogate, and coupling models are deemed acceptable at the present time because the current purpose is to illustrate metamodeling rather than advance knowledge about GSIS.

Completeness and Contextualization.

Completeness of a model is the degree to which the model describes all relevant aspects of the modeled system, given the questions asked. By construction, Bayesian metamodeling provides a more complete description of GSIS than any of the input models on their own. It also contextualizes the different input models by relating previously uncoupled variables (from different input models) to each other. As a consequence, Bayesian metamodeling can be used to assess the effect of different models on one another and augment each model with information in other models to which it was oblivious prior to metamodeling.

Examples.

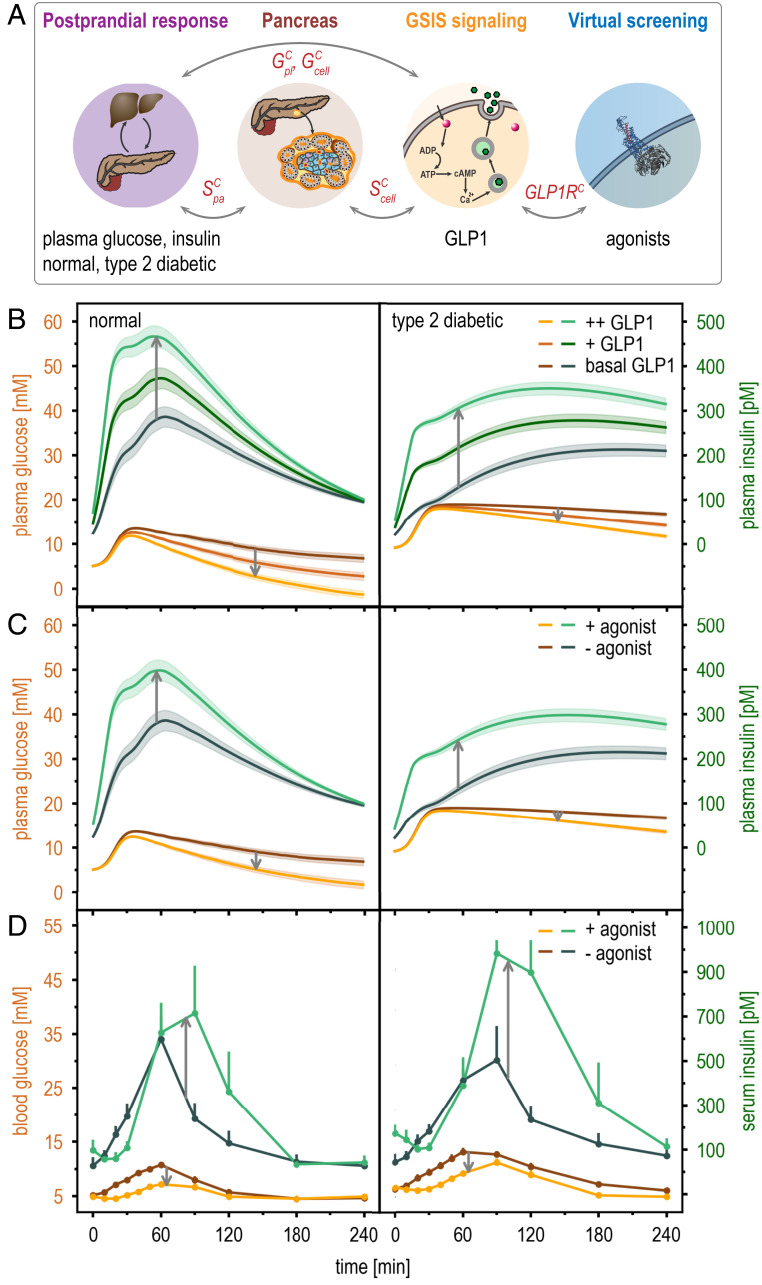
Incretins, such as the GLP1 peptide (23), are hormones secreted from the endocrine pancreas that regulate plasma glucose levels (24). In the presence of glucose stimulus, GLP1 increases insulin secretion by activating GLP1R, the cognate receptor of GLP1 on pancreatic β-cells. Indeed, GLP1R agonists are commonly used to treat type 2 diabetes (23), although clinical significance of this activation in β-cells versus other tissues is yet to be determined (25). The postprandial model (22) does not include any information on GLP1, GLP1R, nor their effect on systemic insulin response after a meal (Fig. 2 and SI Appendix, Supplementary Text 1.1). In contrast, this information is included in the GSIS signaling model, which describes how GLP1 activates GLP1R, insulin biosynthesis, and secretion pathways downstream of GLP1R, within a single β-cell (Fig. 2 and SI Appendix, Supplementary Text 1.4). In the metamodel, variables from both models are coupled (Fig. 2). This coupling enables us to reestimate the free parameters of the postprandial model for different choices of extracellular concentrations of GLP1 (Fig. 3B). Consequently, the updated postprandial model successfully recapitulates the incretin effect (i.e., the empirically observed effect of elevated GLP1 concentrations on postprandial insulin and glucose levels) (23); in other words, the postprandial model was contextualized by the model of GSIS signaling.

Fig. 3.

Contextualization of input models by metamodeling is illustrated by the effect of GLP1 and incretins on GLP1R. (A) Coupling among four input models is indicated schematically. Gray arrows indicate the flow of information between the models, via the coupling variables in red. Time courses of postprandial glucose (orange shades) and insulin (green shades) plasma levels are shown for normal (Left) and type 2 diabetic subjects (Right). (B) Metamodeled time courses are shown for three glucagon-like peptide 1 (GLP1) concentrations in the GLP1 data model: basal, medium (+), and high (++). The shaded areas indicate SD in the posterior PDFs. (C) Metamodeled time courses are shown for postprandial response with and without a GLP1R agonist in the virtual screening model, using analog M2 in the virtual screening library (94). (D) Experimental time courses are shown for postprandial response with and without a GLP1R agonist, exenatide (synthetic Exendin-4) (25).

A second example is provided by the GLP1R model, which is an atomic spatial model of GLP1R activation by GLP1 analogs (Table 1). In the GSIS metamodel, this input model augments both the postprandial and the GSIS signaling network models with binding affinities of various GLP1 analogs for GLP1R, as predicted by virtual ligand screening (Fig. 3A and Table 1). The GLP1R model thus facilitates predicting the effect of GLP1 analogs on insulin secretion at the systemic and cellular levels (Fig. 3C). These predictions recapitulate the clinical observations of the effect of GLP1 analogs on postprandial insulin and glucose levels (Fig. 3D). This example also illustrates the modularity of metamodeling: additional input models can be incorporated into an existing metamodel, iteratively increasing its completeness.

Effect of Metamodeling on Accuracy and Precision.

A useful model needs to be sufficiently accurate and precise, given the questions asked. Metamodeling aims to increase the accuracy (decrease the systematic error) of variable estimates as much as possible, given the accuracy and precision of the input models.

Accuracy and precision of metamodeling can be benchmarked in two ways, as is the case for any modeling method. First, a metamodel can be validated retrospectively by comparison against an independently determined reference (e.g., the validation of the GSIS metamodel by experiment in Fig. 3D). Second, the accuracy of metamodeling can be assessed with a synthetic benchmark. In such a benchmark, true values of free parameters for the various input models are defined, followed by enumerating the input models and the corresponding output metamodels for combinations of input free parameter values. We can then systematically assess the impact of metamodeling on the accuracy and precision simply by comparing the output joint PDFs in the corresponding metamodels with the true values of the free parameters. Consistently with the broad definition above, systematic error of a variable is defined specifically as the difference between the mean of its output PDF and the true value, indicated by $\overline{err}$, and precision (random error) is defined as the SD of its output PDF, indicated by $\sigma$.

Example.

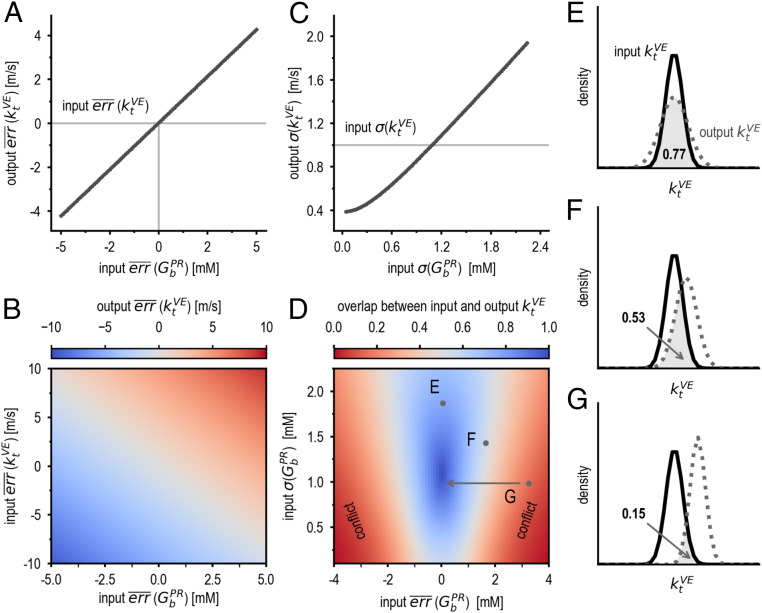
In a synthetic benchmark, we assess the impact of metamodeling on the systematic and random errors of free parameters $G_b^{PR}$ in the postprandial model and $k_t^{VE}$ in the vesicle exocytosis model. $G_b^{PR}$ corresponds to the basal glucose level in plasma, and $k_t^{VE}$ corresponds to the effective rate of vesicle trafficking toward the cellular periphery. Prior uncertainties in their values (e.g., due to variation among individuals and over time) are reflected in their input PDFs; for example, the PDF for $G_b^{PR}$ of healthy individuals is a Gaussian distribution with the mean of 5.1 mM and the SD of 1.0 mM (SI Appendix, Table S1). In the metamodel of GSIS, $G_b^{PR}$ and $k_t^{VE}$ are coupled indirectly via reference variables (Fig. 2). As a result of metamodeling, the systematic and random errors of both variables may in principle either increase, decrease, or remain constant, depending on the magnitude and directionality of the errors in the prior estimates of $G_b^{PR}$ and $k_t^{VE}$ (Fig. 4 and SI Appendix, Fig. S14). To illustrate this general point, we compute actual changes in the systematic and random errors of $G_b^{PR}$ and $k_t^{VE}$ produced by GSIS metamodeling (output accuracy and precision), as a function of the accuracy and precision of $G_b^{PR}$ and $k_t^{VE}$ in the input models (input accuracy and precision).

Fig. 4.

Effect of metamodeling on model accuracy (systematic error) and precision (random error). (A) Statistical dependency of the output systematic error ($\overline{err}$) of the variable $k_t^{VE}$ in the vesicle exocytosis model on the input systematic error of the variable $G_b^{PR}$ in the postprandial response model. The coupling coefficient corresponds to the slope of the line. (B) The output systematic error of $k_t^{VE}$ given different input systematic errors of $k_t^{VE}$ and $G_b^{PR}$. (C) Statistical dependency of the output random error ($\sigma$) of $k_t^{VE}$on the input random error of $G_b^{PR}$. (D) The overlap between input and output $k_t^{VE}$, as a function of input systematic error (x axis) and random error (y axis) of $G_b^{PR}$. Conflicting models correspond to the red areas. (E–G) The input and output PDFs of $k_t^{VE}$corresponding to points E, F, and G in D, respectively. Arrow in D indicates the direction of resolving conflict by improving the accuracy in input $G_b^{PR}$. All output values are at t = 100 min.

We first discuss the output accuracy (systematic error) as a function of the input accuracy. A coupling coefficient of a variable with respect to another variable is defined as the sensitivity of systematic error in its output PDF to systematic error in the input PDF of the other variable (slope in Fig. 4A and SI Appendix, Fig. S14A). As expected, the magnitude of the coupling coefficients of $k_t^{VE}$ with respect to $G_b^{PR}$ and $G_b^{PR}$ with respect to $k_t^{VE}$ is relatively high (0.84 m/s per mM and 0.25 mM per 1.00 m/s, respectively). Indeed, slower trafficking of insulin granules may lower insulin secretion rate in dysfunctional β-cells (26), potentially explaining elevated basal glucose levels in the plasma of diabetic individuals. Thus, metamodeling correctly couples two variables that were not coupled before metamodeling (because they occurred in separate input models). The coupling coefficient of $k_t^{VE}$ with respect to $G_b^{PR}$ is positive because these two variables are positively correlated in the metamodel. Thus, when $G_b^{PR}$ is overestimated and $k_t^{VE}$ is underestimated in their input models, or vice versa, these two estimation errors are likely to diminish each other in metamodeling (Fig. 4C, gray diagonal). Conversely, when both are either underestimated or overestimated, metamodeling likely decreases their accuracy (Fig. 4B, red and blue regions). Nonetheless, in analogy with the law of large numbers (27), we expect that the larger the number of input models, the more likely the random errors in the input models cancel out, in turn leading to more accurate estimates in the metamodel. We assume that for a sufficiently large set of at least partially independent models, systematic errors will not be correlated and will thus average out.

Next, we discuss the output precision as a function of input precision. When the random error of $G_b^{PR}$ in the input model (input $\sigma$) increases, the random error of $k_t^{VE}$ in the output metamodel (output $\sigma$) also increases (Fig. 4C). Thus, input models with lower random error contribute to lower random error of variables from other models. In other words, metamodeling correctly weighs the uncertainties of the different input models and updates output precisions accordingly. In contrast, when the input random error of $k_t^{VE}$ increases, the output random error of $G_b^{PR}$ still increases but significantly more slowly (SI Appendix, Fig. S14). An explanation is that $G_b^{PR}$ is stabilized through its coupling to variables from multiple models (e.g., the GSIS signaling model and pancreas model) and is thus less sensitive to random errors in coupled variables from a single input model. This observation illustrates one potential benefit of weighing information from multiple models via metamodeling.

Conflicting Models.

Changes in variable estimates after metamodeling can be used to identify conflicts between a variable in one input model and other input models. After metamodeling, a variable PDF may change significantly relative to its precision (Fig. 4 D–G). Thus, conflict between the variable and other input models is quantified by the overlap between variable PDFs before and after metamodeling (Fig. 4D) (28). When the systematic error of $G_b^{PR}$ in the input postprandial model is low (point E in Fig. 4D), it is consistent with the value of $k_t^{VE}$ in the input vesicle exocytosis model; consequently, the overlap between its input and output PDFs is high (Fig. 4E). Even when the input systematic error of $G_b^{PR}$ is high, but its input random error ($\sigma$) is also high (point F in Fig. 4D), the overlap between the input and output PDFs for $k_t^{VE}$ remains relatively large, indicating conflicting information that is tolerable given the high prior uncertainty in $G_b^{PR}$ (Fig. 4F). In contrast, when the input systematic error of $k_t^{VE}$ is high and its input random error is low (point G in Fig. 4D), the overlap between the input and output PDFs for $G_b^{PR}$ becomes smaller, indicating conflicting information that is not tolerable given prior uncertainty in $G_b^{PR}$ (Fig. 4G). Thus, tolerability of conflicting information in different input models is identified by comparing the overlap among PDFs before and after metamodeling. Moreover, variables leading to untolerable conflicts can be prioritized for experimental follow-up to refine the input models and thus resolve the conflicts. For instance, given a conflict between $G_b^{PR}$ and $k_t^{VE}$, an improved measurement of $G_b^{PR}$ could result in a refined postprandial model with higher accuracy and precision, removing the conflict (arrow from point G in Fig. 4D). Last, as with accuracy, introduction of additional models to the metamodel can also resolve such conflicts by providing an additional source of information about conflicting variables.

Discussion

Summary.

Here we developed Bayesian metamodeling, a divide-and-conquer approach to modeling complex systems, such as the cell. Metamodeling is not meant to replace other modeling methods, including cell modeling methods. Instead, it is meant to integrate, refine, and harmonize all other relevant models. Next, we discuss 1) combining different models, 2) the relationship of metamodeling with other whole-cell modeling approaches and integrative modeling, 3) the advantages of metamodeling, 4) major limitations of metamodeling and how they might be addressed, and 5) the application of metamodeling to cell modeling by the Pancreatic β-Cell Consortium.

Combining Multiple Models.

Combining multiple models using the same representation (i.e., same type of model and same modeled system) is performed relatively often with the goal of increasing the accuracy, precision, and/or completeness of the combined model. For example, different protein structure models can be averaged into a hopefully more accurate and precise average model (29), multiple types of classification models can be combined to obtain a more accurate classification model (30), multiple cellular networks increase the coverage of the cell (9), and docking of multiple subunit structures results into a model of the complex (31). Likewise, multiple models of different types can also be combined to get a model that describes a larger system more comprehensively. For example, the 2013 Nobel prize in chemistry was awarded to M. Karplus, M. Levitt, and A. Warshel for harmonizing quantum mechanics and molecular mechanics, thus providing an early example of coupling and multiscaling at atomic resolution (2, 3), and different types of models are combined for weather prediction (32). In an early example of multiscale modeling of GSIS, first crystallographic structures of insulin and glucagon gave rise to more holistic, functional depictions of signaling and storage in insulin granules (33). Cell mapping in particular has also been addressed by combining models of different representations. A groundbreaking method propagates a complete cell model from an initial time point by using output from some models as input for other models at the next time point on the trajectory, with different models being coupled via metabolites (10, 12). In a second example, stochastic reaction diffusion master equation models of chemical reaction networks, describing the formation of splicing machinery, were combined with a spatial model of the HeLa cell to study the influence of spatial organization on splicing, based on data from cryoelectron tomography, mass spectrometry, fluorescence microscopy/live-cell imaging, and -omics (11). However, to the best of our knowledge, a general approach to combining heterogeneous input models of any type or scale into a unified model does not yet exist.

Here we formalized the model integration problem in general terms and described one practical approximate solution, termed Bayesian metamodeling. The solution depends on the universality of representing the statistical uncertainties and dependencies among the variables spanning any model or dataset. As a result, any model or dataset can in principle be input for metamodeling.

Relationship to Other Cell Modeling Approaches.

Most generally, any modeling can be seen as sampling of instances of a model of a certain type, using some sampling scheme guided by some scoring function informed by input experimental data and/or prior models. For example, in addition to the above-mentioned approaches, a variety of methods have been used to model various aspects of the cell, based on a variety of data (34–36). Deep-learning approaches were applied to learn cell phenotypes from their genotypes, using a network that mirrors the structural and functional hierarchy of a cell (37), based on genomics and proteomics data (38). Manual curation was used to construct a repository of genome-scale metabolic models (9), based on various genomics, proteomics, and metabolomics data. A stochastic simulation algorithm was combined with flux balance analysis to model stochastic dynamics of metabolism in Mycoplasma pneumoniae, based on metabolic and proteomic data (39). More generally, several modeling platforms were developed for spatiotemporal simulations of reactions, mass transport, and other processes in the entire cell (40–44). Packing algorithms were used to assemble macromolecules in a complete HIV-1 virus particle and Mycoplasma mycoides cell at 10 to 100 nm resolution (45), based on data from structural biology and systems biology. Atomistic molecular dynamics and coarse-grained Brownian dynamics simulations were used to model crowded cytoplasmic environments, resulting in trajectories of millions of particles over microseconds for sections of Mycoplasma genitalium (46) and Escherichia coli (7). Satisfaction of spatial restraints resulted in architectures of genomes in various types of cells, based on genome-wide mapping of chromatin interactions (47). Similarly, spatial restraints were satisfied to create a snapshot of a synaptic bouton at atomic resolution based on data from quantitative immunoblotting, mass spectrometry, electron microscopy, and superresolution fluorescence imaging (48). A number of methods rely on image processing or machine learning from images. For example, three-dimensional (3D) reconstruction and segmentation were used to create a model of mouse pancreatic β-cell ultrastructures using data from serial section electron tomography (49); convolutional neural networks were applied to compute fluorescent 3D cellular maps from 3D label-free transmitted-light live-cell images or 2D electron microscopy images (50); image processing and machine learning techniques were used to compute subcellular sarcomeric organization states in cardiomyocytes based on data from single-cell RNA sequencing and quantitative imaging of gene expression, transcript localization, and cellular organization (51); and finally, a pipeline for multiplexing different imaging modalities was used to map protein–ultrastructure relationships from cryogenic superresolution fluorescence microscopy and focused ion beam–milling scanning electron microscopy (52). Thus, most cell mapping approaches are limited in the types of cell representation and reliance on limited types of data and/or prior models. In contrast, metamodeling can in principle use any set of representations that can be informed by any available data and prior models.

Relationship to Integrative Modeling.

As mentioned in Bayesian Metamodeling of the Cell, metamodeling is a special case of integrative modeling. In addition to integrative structure modeling (4), other variants of integrative modeling include integrative pathway mapping (53); modeling of spatial organization of genomes (54); integration of imaging and -omics data (55); studying of splicing codes based on multiple sources of data (56); integration of single cell transcriptomic, epigenetic data, and protein counts (57); integration of multimodal neuroimaging data (58); and general machine learning techniques for dealing with multimodal data (20). Bayesian metamodeling is in fact a decentralized form of integrative modeling in which the focus is shifted from integrating data to integrating prior models. In addition to using data to compute input models, data can also be used as an input model itself, as exemplified by the GI data and GLP1 data models (Fig. 2, Table 1, and SI Appendix, Supplementary Text 1.7 and 1.8); in other words, data can be incorporated directly via data likelihoods in the joint PDF during the coupling stage. Thus, an integrative modeling problem can also be formulated as a metamodeling problem, benefitting from the advantages of its divide-and-conquer strategy.

Advantages of Metamodeling.

We outline here a number of advantages of metamodeling over more centralized approaches to data integration: First, metamodeling is highly modular and benefits from heterogeneity of representations. Different aspects of the cell and its functions are modeled by different methods, informed by different data, and represented with different variables at varying levels of granularity (Figs. 1 and 2). Second, metamodeling facilitates multiscaling. This advantage arises from modularity that also allows combining models at different scales. Third, metamodeling is computationally efficient. The large task of computing a model of the cell is distributed among smaller parallel computations required to compute individual input models. Fourth, metamodeling is collaborative. It allows autonomous contributions by different research groups with expertise spanning diverse scientific disciplines, thus maximizing flexibility, scalability, and efficiency among collaborating experimentalists and modelers. Fifth, metamodeling is statistically objective. This objectivity derives from the use of Bayesian formalism for modeling the relations among different system parts. Sixth, metamodeling increases model completeness. A metamodel provides a maximally complete view of all cellular aspects, given the available input models (Figs. 3 and 4). Seventh, metamodeling can couple previously independently modeled cellular aspects. This advantage results from harmonizing different input models with respect to each other, thus providing more context for each input model (Fig. 3). Eighth, metamodeling often improves accuracy and precision. This improvement is achieved by updating model variables and their uncertainties by considering information from multiple input models, thus often improving the final estimates (Fig. 4 A–C). Finally, metamodeling helps with resolving conflicts among input models. If different input models contain contradictory information, metamodeling highlights these inconsistencies and thus helps identify new experiments that may resolve them (Fig. 4D). Next, we discuss a few of these advantages in more detail.

Modularity.

Bayesian metamodeling can in principle use any type of an input model, including deterministic or stochastic, static or dynamic, and spatial or nonspatial. The only requirement is that an input model is specified quantitatively. Importantly, metamodeling does not require the data used to construct each model. Therefore, input for metamodeling can be obtained relatively easily from independent research groups that do not necessarily collaborate or share expertise. Moreover, a metamodel can be updated iteratively with additional models, utilizing new datasets, technologies, and modeling techniques as they emerge. Thus, metamodeling enables a plug-and-play approach to building complex models from simpler models.

To illustrate the benefits of this modularity, we now discuss practical examples of upgrading the current GSIS model to better account for variation across 1) multiple cells of the same type and 2) different types of the cell. Each one of these variations can be modeled either by improving an existing input model or by adding a new input model, without changing other input models, as follows. First, variation across multiple cells of the same type could be modeled by replacing the current linear pancreas model with a more elaborate model that accounts for electrical synchronization in networks of β-cells (59) and data on the role of leader β-cells in these networks (60); such a model could be coupled to insulin vesicle exocytosis and/or GSIS signaling models, each parametrized to reflect cell variation. Thus, metamodeling may provide an effective path to investigate the source of cell heterogeneity in glucose responsiveness, an open question of great biological interest (61). Second, variation across cell types could be accounted for by including a separate input model for each type of the cell [e.g., primary β-cells and insulin-secreting model cell lines, such as INS-1 and INS-1E tumor cells (62, 63)]. During the coupling stage, the weight of variables from each input model should reflect the confidence in it. For instance, data from model cell lines are often considered significantly less informative about primary cells than the data from the primary cells themselves (64). Indeed, variables from the insulin metabolism model, which was informed by experiments in INS-1E cells, are only weakly coupled to variables from other models (SI Appendix, Tables S10 and S11). Other variations, such as those among different individuals, can in principle also be addressed similarly.

Multiscaling.

Metamodeling can couple different input models despite significant differences in their scales. In fact, even the current GSIS metamodel covers the scales from atomic and femtoseconds of molecular dynamics simulations to the whole body and hours of the postprandial response model (Table 1). Thus, multiscaling is another advantage of modularity. This coupling is achieved by imposing statistical correlations among variables on different scales. Thus, metamodeling may bypass the need to compute the propagation of signals across scales explicitly, which typically necessitates specialized model representations and algorithms (65). For example, the pancreas model provides a simple description of the expected statistical relation between secretion of insulin at the cell and systemic levels, thus helping to couple the postprandial response and GSIS signaling models. Likewise, the GLP1R model at atomic scale is coupled to all other models via the GSIS signaling model at cellular scale by imposing expected statistical correlation between receptor activation by a small molecule agonist and activation of GSIS signaling in the cell. This coupling allows us to use the GSIS metamodel to correctly predict the effect of incretins and other small molecule ligands on systemic insulin response (Fig. 3).

Facilitating Community Collaboration.

Due to its modularity, metamodeling is expected to provide a community tool for contributing to whole-cell modeling, as exemplified by its use within the Pancreatic β-Cell Consortium (15). We developed tutorials serving as onboarding material to allow others to contribute their input models (SI Appendix, Supplementary Text). In the future, we will also create a website to serve as a graphical user interface and develop methods for automated conversion of input models into surrogate models. This functionality will provide nonexperts in computational modeling with an opportunity to contribute and improve their individual models. At its core, metamodeling is rooted in collaboration and appreciation for the details of disparate data, methods, and models, which cannot be achieved by any individual scientist, research group, or institution. To further support the collaboration, the Pancreatic β-Cell Consortium is creating cyberinfrastructure for archiving and disseminating experimental data and models that will be integrated with metamodeling. Thus, each time an input model, surrogate model, and/or a coupler is provided or upgraded, the metamodel and input models can be updated automatically.

Many of the most important questions in biology are centered around issues of data integration and at the intersection of multiple fields. Thus, the development of methods and tools that build bridges between siloed research is essential. An existing example is the Protein Data Bank (PDB) of known protein structures, which in many ways nucleated the structural biology community (66). Indeed, the latest effort of the PDB to support integrative structures based on varied data from multiple methods (67) is narrowing the gap between the PDB and the whole-cell mapping. Other key community resources provide for standardization, archival, and dissemination of models, thus facilitating explicit and implicit collaboration among a diverse set of researchers (9, 13, 68–70).

Limitations of Metamodeling.

While Bayesian metamodeling can in principle be used to couple any set of input models, it is not always clear that they can be coupled usefully. Next, we identify a number of limitations of the current implementation of metamodeling and outline how they might be addressed.

First, to incorporate complex input models more accurately, alternative approaches for converting these models into a unified surrogate probabilistic representation should be explored (step 1). While nonlinear models can be approximated by DBNs (Fig. 3), other methods for learning complex PDFs spanned by a large number of interdependent variables include a nonlinear implementation of PGMs (http://github.com/tanmoy7989/bayesian_metamodeling_tutorial). In addition, deep-learning approaches, such as variational autoencoders, generative adversarial networks, and temporal variants, might also be useful, although they generally require a large amount of training data, and they are not always easily interpretable (20). Nonetheless, deep neural networks have already been shown to provide practical solutions for representing low-dimensional surrogate models for complex physical systems (71). Finally, nonprobabilistic approaches, such as integer programming (72), might also be explored.

Second, only a limited set of coupling schemes have been used so far, based on imposing statistical dependencies via PGMs (step 2). While PGMs and other probabilistic approaches (e.g., generative deep learning models) provide a relatively general solution for coupling models of any type, some types of models may be coupled more efficiently and/or accurately by other types of couplers. For example, the coupling of ligand and receptor structural models in molecular docking can be achieved naturally, accurately, and efficiently via minimizing the free energy of the complex (73). Thus, future work should explore additional types of couplers for common types of models. As a special case, couplers for input models at different spatiotemporal scales should be improved. Multiscale integration is currently performed ad hoc, based on prior knowledge about expected correlations across scales. Standardized schemes and automated methods for integrating models across scales should be developed, including more efficient representations for multiscale PDFs. As discussed above, at the very least, metamodeling facilitates a formal integration by imposition of statistical correlations across scales in cases where explicit physically inspired coupling is not yet possible.

Third, to maximize modeling accuracy and precision, metamodeling should be guided by formal optimality criteria (loss or fitness functions) for 1) ranking surrogate models, 2) reference variables used to couple the surrogate models, 3) the couplers themselves, and 4) the backpropagation scheme. For example, good surrogate models should recapitulate statistical dependencies in the input models, and good couplers may be required to recapitulate experimental data on statistical dependencies among input models.

Fourth, the metamodeling process should be entirely automated, in part benefiting from the optimality criteria above. Such automation will require sampling in the space of alternative metamodels to choose an optimal metamodel, for example, by sampling the free parameters and topologies of surrogate models and couplers (19). Automation will also be facilitated by developing tools that streamline interactions with nonexperts in modeling (Facilitating Community Collaboration).

Fifth, we should develop methods to validate a metamodel. Although the uncertainty of a metamodel is already quantified by its PDF, additional assessment may be useful. A relatively general approach to model assessment has been developed for integrative structure modeling, quantifying the degree of sampling exhaustiveness, the match between the model and the data used to construct the model, the match between the model and the data not used to construct the model, and model uncertainty (74). In metamodeling, additional opportunities for assessment include identifying conflicts between input models and assessing error propagation (Fig. 4). For example, while our results indicate that random or uncorrelated systematic errors in different models are likely to be averaged out through their coupling, such coupling may also lead to amplification of error in one input model as it propagates across models. Methods for detecting and minimizing such errors should be developed, possibly by borrowing from methods for stabilization of dynamic systems (75).

Finally, our primary purpose here was to illustrate metamodeling rather than advance our understanding of GSIS biology. Thus, our current metamodeling relies on a small set of relatively simple input models and numerous simplifying assumptions, some of which are summarized in SI Appendix. While even this simplified metamodel has been validated by data not used in its construction (Fig. 4), we have not yet obtained any new insights into GSIS. Future implementations of metamodeling should be tested using a larger number of input models of higher complexity.

Future Application to Whole-Cell Modeling.

Together with the entire Pancreatic β-Cell Consortium (15), we are working to enrich the current GSIS metamodel with additional input models based on diverse types of data to create a more accurate, precise, and complete model of the pancreatic β-cell. These additional input models cover key aspects of GSIS biology in health and disease, including glucose sensing (76, 77); insulin vesicle biosynthesis, trafficking, docking, and exocytosis (78); recycling of misfolded proteins by proteasomes and autophages (79); membrane phospholipid biosynthesis at mitochondria-associated endoplasmic reticulum membranes (80); regulation of intracellular calcium flux from ER to mitochondria (81); global spatiotemporal dynamics of islet insulin secretion (82); pulsatile insulin secretion (83); interaction with hepatocytes (84); phosphoproteome map (85); and spatial genome organization (86). The upgraded metamodel is expected to be useful for designing more effective future experiments, discovering biological mechanisms, and generating hypotheses, which will in turn enhance the model itself. We also anticipate metamodeling of β-cells by the Pancreatic β-Cell Consortium will serve as a template for modeling other types of cells and, indeed, other complex systems.

Methods

The software, input files, and example output files for the present work are available at http://github.com/salilab/metamodeling. The metamodel was implemented using the BNET package in MATLAB by Kevin Murphy, http://github.com/bayesnet/bnt (commit 21dfdfa) with minor modifications of the DBN module (https://github.com/salilab/metamodeling/tree/master/bnt_master); the PGMs in the tutorial (http://github.com/tanmoy7989/bayesian_metamodeling_tutorial) were implemented in the Python package PyMC3 (version 3.8) (http://github.com/pymc-devs/pymc3/releases/tag/v3.8). For an outline of the approach, see Results; for details, see SI Appendix.

Data Availability

Computer files and data have been deposited in GitHub (http://github.com/salilab/metamodeling).