Abstract
In this article, we examine study designs for extending (generalizing or transporting) causal inferences from a randomized trial to a target population. Specifically, we consider nested trial designs, where randomized individuals are nested within a sample from the target population, and nonnested trial designs, including composite data-set designs, where observations from a randomized trial are combined with those from a separately obtained sample of nonrandomized individuals from the target population. We show that the counterfactual quantities that can be identified in each study design depend on what is known about the probability of sampling nonrandomized individuals. For each study design, we examine identification of counterfactual outcome means via the g-formula and inverse probability weighting. Last, we explore the implications of the sampling properties underlying the designs for the identification and estimation of the probability of trial participation.
Keywords: causal inference, generalizability, randomized trials, transportability
Methods for addressing selective study participation (1) can be used to extend (i.e., generalize or transport (2, 3)) causal inferences from a randomized trial to a target population (4–10). The methods require baseline covariate, treatment, and outcome data from persons participating in the trial and baseline covariate data from nonrandomized individuals. Estimation of counterfactual outcome means in the target population may be based on models for the probability of trial participation (4), the expectation of the outcome under each treatment among trial participants (8), or both (6, 10). Prior work on these methods has largely focused on identifiability conditions and estimation approaches rather than study design principles; yet, different study designs determine which counterfactual quantities (i.e., causal estimands) can be identified and have implications for identifying and estimating the conditional probability of trial participation.
Two types of study designs that combine data from randomized individuals with data from a sample of nonrandomized individuals have been used for the explicit goal of estimating counterfactual outcome means and treatment effects in a target population of substantive interest: 1) nested trial designs, in which the randomized trial is embedded in a sample from the target population (6), and 2) nonnested trial designs, in which observations from randomized individuals are combined with a separately obtained sample of nonrandomized persons from the target population. The sampling probability of nonrandomized individuals is known in nested trial designs (5) but unknown in nonnested trial designs (7, 9, 10). In both types of study designs, baseline covariate data are collected from all randomized individuals and from sampled nonrandomized individuals; treatment and outcome data need only be collected from randomized individuals. Though treatment and outcome data from nonrandomized individuals can be used to evaluate assumptions or improve efficiency, they are not necessary for identification and estimation under the assumptions used in this paper or in the bulk of the related literature (e.g., as reviewed by Lesko et al. (8)).
In this paper, we show how knowledge about the sampling of nonrandomized individuals determines which counterfactual quantities can be identified in each study design. For each design, we examine identification of counterfactual outcome means under time-fixed treatments via the g-formula and inverse probability weighting, and we explore the implications of the design’s sampling properties for modeling the probability of trial participation.
SAMPLING PROPERTIES AND THE OBSERVED DATA
Investigators can specify a set of eligibility criteria that define an actual population of individuals to whom research findings would be applicable, in the sense that in principle we can identify the finite (“real-world”) population of persons who meet the eligibility criteria. For instance, when designing a randomized trial, the trial eligibility criteria define an actual population of all trial-eligible individuals who could be recruited into the trial. Here, as is often done in statistical work, we view the actual population as a simple random sample from an (infinite) superpopulation of individuals (11); we refer to this superpopulation as the target population. We are interested in counterfactual quantities that pertain to the target population or to its subsets (e.g., defined by trial participation status).
To introduce some notation, let  denote a vector of p baseline covariates; A the (time-fixed) treatment assignment indicator; Y the observed outcome; and S the trial participation indicator, with S = 1 for randomized individuals and S = 0 for nonrandomized individuals (persons who either are not invited to participate in the trial or are invited but decline). To capture the notion that some nonrandomized individuals in the actual population (S = 0) may not be sampled, let D be an indicator for whether a person in the actual population is sampled and contributes data to the analyses, with D = 1 for sampled individuals and D = 0 for nonsampled individuals.
denote a vector of p baseline covariates; A the (time-fixed) treatment assignment indicator; Y the observed outcome; and S the trial participation indicator, with S = 1 for randomized individuals and S = 0 for nonrandomized individuals (persons who either are not invited to participate in the trial or are invited but decline). To capture the notion that some nonrandomized individuals in the actual population (S = 0) may not be sampled, let D be an indicator for whether a person in the actual population is sampled and contributes data to the analyses, with D = 1 for sampled individuals and D = 0 for nonsampled individuals.
We can now discuss the sampling properties that underlie nested and nonnested study designs. These properties describe how the observed study sample relates to the actual population; the underlying actual population and (hypothetical) target population are the same across designs. Figure 1 illustrates the conceptual relationships between designs, their sampling properties, and the observeddata.
Figure 1.
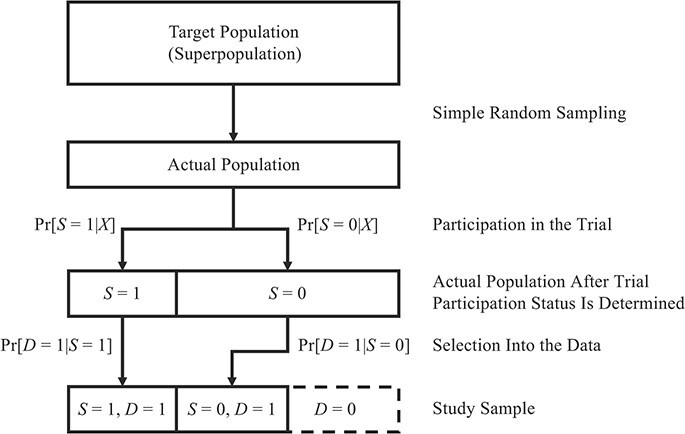
Sampling designs for studies extending inferences from a randomized trial to a target population. For detailed descriptions of notation, see the main text. Briefly, X denotes baseline covariates, S the trial participation indicator, and D the indicator for sampling into the study sample. The dashed box around D = 0 denotes the fact that covariate data may not be available from this subset and that in nonnested trial designs the size of the subset may be unknown.
In the main text of this paper, we consider simple random samples, with known or unknown sampling probabilities, from the actual population or from the nonrandomized subset of the actual population. As we discuss below, our main results, with minor modifications, hold when the sampling probability is a known function of auxiliary baseline covariates rather than a known constant (i.e., when we have random sampling, not simple random sampling). Allowing the sampling probabilities to depend on auxiliary covariates, however, does not lead to additional insights regarding study design (12); for this reason, in the main text, we assume that the sampling probability does not depend on covariates.
Nested trial designs
We consider 2 variants of the nested trial design, for situations where 1) a census of the actual population is taken and 2) the nonrandomized individuals are subsampled.
Census of the actual population.
In the first variant of the nested trial design, the persons contributing data to the analysis are assumed to be a census of the actual population—that is,
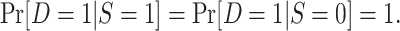 |
Thus, nested trial designs can be viewed as simple random samples from the superpopulation. In this design, it is common to define the target population implicitly, based on the actual population in which the trial is nested. For example, in comprehensive cohort studies (13), investigators nest a trial within a cohort of all persons who met the trial’s eligibility criteria and were invited to participate in the trial. They then define the target population as the population from which cohort members (i.e., the actual population of trial-eligible individuals invited to participate in the trials) could have been a simple random sample. Thus, in this design, investigators need to ensure that the cohort represents the target population they are interested in; that is, the trial eligibility criteria need to be broad enough to address the research question and the individuals invited to participate in the trial (who form the cohort in which the trial is nested) need to represent the target population of interest.
Subsampling of nonrandomized individuals.
In the second variant of the design, we collect data from all randomized individuals in the actual population but only collect baseline covariate data from a subsample of the nonrandomized individuals in the actual population, with sampling probability that is a known constant. The sampling properties can be summarized as
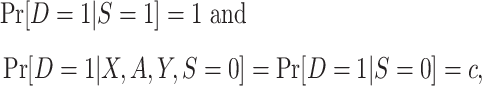 |
where c is a known constant, with 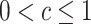 . Note that the nested trial design with a census of the actual population can be viewed as a special case of the subsampling design, with c = 1. Using c < 1 is statistically less efficient than using c = 1, but it may improve research economy—for example, if the collection of covariate data among all nonrandomized individuals is expensive or otherwise infeasible (12). Furthermore, as noted, a variant of the nested trial design with subsampling allows the selection of nonrandomized individuals to depend on auxiliary baseline covariates; we give the sampling properties of this design variant in Web Appendix 1 (available online at https://doi.org/10.1093/aje/kwaa270).
. Note that the nested trial design with a census of the actual population can be viewed as a special case of the subsampling design, with c = 1. Using c < 1 is statistically less efficient than using c = 1, but it may improve research economy—for example, if the collection of covariate data among all nonrandomized individuals is expensive or otherwise infeasible (12). Furthermore, as noted, a variant of the nested trial design with subsampling allows the selection of nonrandomized individuals to depend on auxiliary baseline covariates; we give the sampling properties of this design variant in Web Appendix 1 (available online at https://doi.org/10.1093/aje/kwaa270).
Nonnested trial designs
In nonnested trial designs, data from randomized and nonrandomized individuals are obtained separately. Investigators assume that data from all randomized individuals can be combined with data from a simple random sample of nonrandomized individuals from the actual population, with a sampling probability that is an unknown constant (e.g., see Westreich et al. (7)). The sampling properties can be summarized as
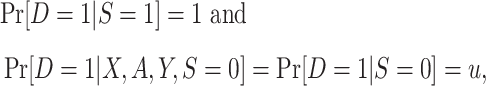 |
where u is an unknown constant, with 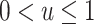 . An example of a nonnested trial design is the composite data-set design (7, 10). Here, investigators append the data from a randomized trial to data from a convenience sample of nonrandomized individuals, often obtained from routinely collected data sources (e.g., claims or electronic medical records databases) or prospective cohort studies. The assumption is that the sample of nonrandomized individuals is a simple random sample from the population of nonrandomized individuals (or a subset thereof) to whom the investigators wish to extend the trial results. This assumption, often unstated, appears to be implicit in all applied analyses using nonnested designs that we are awareof.
. An example of a nonnested trial design is the composite data-set design (7, 10). Here, investigators append the data from a randomized trial to data from a convenience sample of nonrandomized individuals, often obtained from routinely collected data sources (e.g., claims or electronic medical records databases) or prospective cohort studies. The assumption is that the sample of nonrandomized individuals is a simple random sample from the population of nonrandomized individuals (or a subset thereof) to whom the investigators wish to extend the trial results. This assumption, often unstated, appears to be implicit in all applied analyses using nonnested designs that we are awareof.
In many applications it is not possible to establish that a simple random sample of nonrandomized individuals in the actual population has been taken, and in some cases there may even exist nonidentifiable overlap between the trial and the sample of ostensibly nonrandomized individuals from the actual population. Such overlap would complicate statistical analyses (14), but in most practical situations the impact is likely to be negligible because the trial and the sample of the target population are only a small part of the actual population. In effect, when the sample of nonrandomized individuals has not been obtained by formal simple random sampling of the nonrandomized subset of the actual population, most investigators appear to be comfortable proceeding as if the sample had been obtained by such sampling.
A related difficulty in nonnested designs arises when the nonrandomized individuals are not selected from the entire nonrandomized subset of the actual population but from a narrower group. For example, suppose that a randomized trial takes place in the United States and that the sample of nonrandomized individuals is obtained by identifying members of a private health insurance plan who, during trial enrollment, met the trial eligibility criteria. Clearly, these nonrandomized individuals do not exhaust the nonrandomized members of the actual population (because of the existence of other nonoverlapping insurance plans with trial-eligible members). Such situations can be handled by the results presented in our paper by redefining S = 0 to mean “nonparticipant who is a member of the particular plan” and defining D = 1 for trial participants and eligible nonparticipants who are members of the particular plan and contribute data. These changes, however, narrow the scope of the inferences that can be drawn from the data and may make the identifiability conditions discussed below less plausible.
The observed data
In both nested and nonnested designs, we collect data on baseline covariates, treatment, and outcome from randomized individuals; in contrast, as we shall show, only baseline covariate data are needed from nonrandomized individuals.
More specifically, for nested designs the observed data consist of realizations of (X, A, Y, S = 1, D = 1) for trial participants; (X, S = 0, D = 1) for sampled nonrandomized individuals; and (S = 0, D = 0) for nonsampled nonrandomized individuals. Because all randomized individuals are sampled, 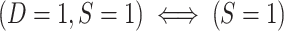 . No covariate, treatment, or outcome data are available for nonsampled nonrandomized individuals
. No covariate, treatment, or outcome data are available for nonsampled nonrandomized individuals 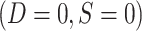 . Note also that in nested trial designs with a census of the actual population, the
. Note also that in nested trial designs with a census of the actual population, the 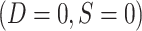 subset does not exist.
subset does not exist.
In nonnested trial designs, we typically do not know the number of nonsampled nonrandomized individuals; thus, the observed data consist of realizations only of (X, A, Y, S = 1, D = 1) for trial participants and (X, S = 0, D = 1) for sampled nonrandomized individuals.
COUNTERFACTUAL QUANTITIES AND IDENTIFIABILITY CONDITIONS
Counterfactual quantities of interest
In order to define the counterfactual quantities (causal estimands) of interest, let 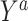 be the counterfactual (potential) outcome under intervention to set treatment to a (15, 16). We are interested in the mean of each of these counterfactual outcomes in the target population
be the counterfactual (potential) outcome under intervention to set treatment to a (15, 16). We are interested in the mean of each of these counterfactual outcomes in the target population 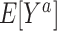 or in the nonrandomized subset of the target population
or in the nonrandomized subset of the target population 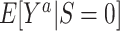 . For example,
. For example, 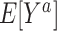 is the expected outcome under the strategy of treating all persons in the target population with treatment a. It is often scientifically and methodologically interesting to compare
is the expected outcome under the strategy of treating all persons in the target population with treatment a. It is often scientifically and methodologically interesting to compare 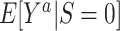 with
with 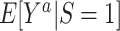 , to examine whether the counterfactual outcome mean under treatment a differs among trial participants and nonparticipants in the target population (6).
, to examine whether the counterfactual outcome mean under treatment a differs among trial participants and nonparticipants in the target population (6).
Identifiability conditions
For all study designs, the following identifiability conditions are sufficient to extend inferences from a trial to a target population (6, 10):
Consistency of counterfactual outcomes: Interventions are well-defined, so that if
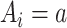 , then
, then 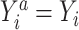 for every individual i. Implicit in this notation is that the offer to participate in the trial and trial participation itself do not have an effect on the outcome except through treatment assignment (e.g., there are no Hawthorne effects (17)) (3, 18).
for every individual i. Implicit in this notation is that the offer to participate in the trial and trial participation itself do not have an effect on the outcome except through treatment assignment (e.g., there are no Hawthorne effects (17)) (3, 18).Conditional mean exchangeability among trial participants:
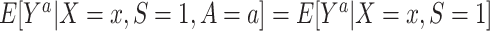 for every a and for every x with positive density
for every a and for every x with positive density  . This condition is expected to hold because of randomization (marginal or conditional on X).
. This condition is expected to hold because of randomization (marginal or conditional on X).Positivity of treatment assignment in the trial:
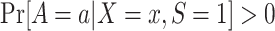 for each a and each x with positive density
for each a and each x with positive density  . This condition is also expected to hold because of randomization.
. This condition is also expected to hold because of randomization.Conditional mean exchangeability over S:
 for every a and for every x with positive density in the target population
for every a and for every x with positive density in the target population 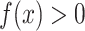 . For binary S, this condition implies the mean transportability condition
. For binary S, this condition implies the mean transportability condition 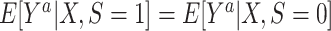 , provided both conditional expectations are well-defined.
, provided both conditional expectations are well-defined.Positivity of trial participation:
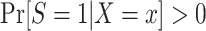 for each x with positive density in the target population
for each x with positive density in the target population  .
.
In these conditions, we have used X generically to denote baseline covariates. It is possible, however, that strict subsets of X are adequate to satisfy different exchangeability conditions. For example, in a marginally randomized trial, the mean exchangeability among trial participants holds unconditionally. Furthermore, to focus on issues related to selective trial participation, we will assume that there is full adherence to the assigned treatment and no loss to follow-up.
The identifiability conditions involving counterfactual variables above (and the identification results in equations 1 and 2, presented below) may be obtained using graphical causal models (e.g., directed acyclic graphs with selection nodes (19, 20) or single world intervention graphs (21) treating trial participation as an intervention (18, 22)). In this paper, we treat the identifiability conditions as primitive (i.e., not derived) in order to focus on issues related to study design, sampling of participants, and statistical modeling. Such issues have not been adequately addressed in the generalizability and transportability literature. For example, a recent review of study design issues for generalizability and transportability did not identify any work explicitly discussing the interplay between study design and identifiability or model specification/estimation (23).
Trial eligibility criteria and choice of target population
Now that we have specified the counterfactual quantities of interest and listed identifiability conditions, we can consider the choice of target population in more detail. As noted above, the target population should be determined by the scientific question investigators plan to address. In many cases, when using the methods described in this paper, it is sensible to limit the target population to the population of persons meeting the trial eligibility criteria or to a subset of that population. To the extent that the variables used to define the trial eligibility criteria are needed for conditional mean exchangeability over S to hold, restriction of the target population to trial-eligible individuals is needed to satisfy the ``positivity of trial participation'' condition—persons not meeting the criteria are not allowed to enter the trial. In some cases, however, investigators may be able to argue that only a subset of the variables used to determine trial eligibility are necessary for conditional mean exchangeability over S to hold. In such cases, the target population can be broader than the population of trial-eligible individuals. The essential requirement is that the distributions of covariates needed for conditional mean exchangeability should have common support between the randomized and nonrandomized subsets.
IDENTIFICATION VIA THE G-FORMULA
We begin by considering identification by the g-formula (24). Using the identifiability conditions listed above, it is straightforward to show that the counterfactual outcome mean in the target population (6) can be reexpressed as
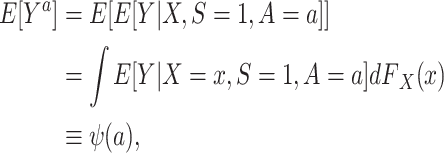 |
(1) |
where  denotes the distribution of X in the target population.
denotes the distribution of X in the target population.
The counterfactual outcome mean among nonrandomized individuals in the target population (10) can be reexpressed as
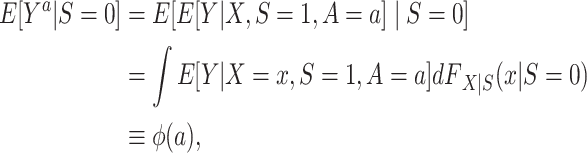 |
(2) |
where 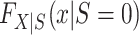 denotes the distribution of X among nonrandomized individuals in the target population (i.e., the subset with S = 0).
denotes the distribution of X among nonrandomized individuals in the target population (i.e., the subset with S = 0).
First, we note that both results involve the conditional expectation of the outcome Y among trial participants assigned to treatment a, 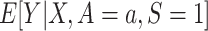 . Because both nested and nonnested designs assume that all randomized individuals are sampled, this expectation is identifiable in both designs.
. Because both nested and nonnested designs assume that all randomized individuals are sampled, this expectation is identifiable in both designs.
Next, we turn our attention to the identification of 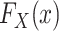 and
and 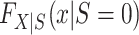 , which are necessary for
, which are necessary for 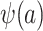 and
and 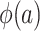 , respectively. There are interesting differences between the designs when it comes to identifying these distributions, and we consider each design individually below.
, respectively. There are interesting differences between the designs when it comes to identifying these distributions, and we consider each design individually below.
Nested trial designs
Census of the actual population.
Identification is most straightforward in this design, because data are available from all members of the actual population (both randomized and nonrandomized) and the actual population is a simple random sample from the target population. Thus, 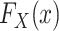 is identifiable. Furthermore, in this design, every subset of the actual population defined on the basis of baseline covariates or trial participation is a simple random sample from the corresponding subset in the target population. Thus, the distribution of covariates among nonrandomized individuals
is identifiable. Furthermore, in this design, every subset of the actual population defined on the basis of baseline covariates or trial participation is a simple random sample from the corresponding subset in the target population. Thus, the distribution of covariates among nonrandomized individuals 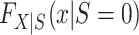 can also be identified. It follows that all of the components on the right-hand sides of equations 1 and 2 are identifiable, establishing that all components of
can also be identified. It follows that all of the components on the right-hand sides of equations 1 and 2 are identifiable, establishing that all components of 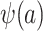 and
and 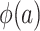 are identifiable.
are identifiable.
Subsampling of nonrandomized individuals.
For this design, identification of the marginal distribution of X is slightly more involved because the nonrandomized individuals contributing data to the analysis are a subsample from the nonrandomized individuals in the actual population.
By the law of total probability, for binary S,
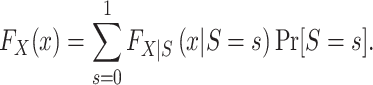 |
Clearly, 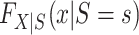 , for s = 0, 1 is identifiable because the randomized and nonrandomized sampled individuals are simple random samples of the target population subsets with S = 1 and S = 0, respectively. Thus,
, for s = 0, 1 is identifiable because the randomized and nonrandomized sampled individuals are simple random samples of the target population subsets with S = 1 and S = 0, respectively. Thus, 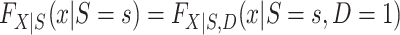 , for s = 0, 1. The only difficulty, then, is identification of the marginal probability of trial participation,
, for s = 0, 1. The only difficulty, then, is identification of the marginal probability of trial participation, 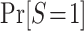 , because
, because 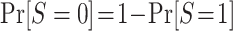 . As we show in Web Appendix 2, under the sampling properties of the nested trial design with subsampling of nonrandomized individuals,
. As we show in Web Appendix 2, under the sampling properties of the nested trial design with subsampling of nonrandomized individuals,
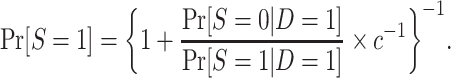 |
(3) |
The odds of nonparticipation in the trial among sampled individuals, 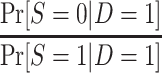 , are identifiable; and, as defined above, c is a known constant. It follows that
, are identifiable; and, as defined above, c is a known constant. It follows that  is identifiable and, consequently,
is identifiable and, consequently,  is identifiable because all of the components of the integral on the right-hand side of equation 1 are identifiable.
is identifiable because all of the components of the integral on the right-hand side of equation 1 are identifiable.
Turning our attention to  , we note that it is identifiable because the sampled nonrandomized individuals are a simple random sample from the nonrandomized individuals in the actual population,
, we note that it is identifiable because the sampled nonrandomized individuals are a simple random sample from the nonrandomized individuals in the actual population, 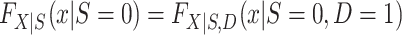 . It follows that
. It follows that 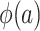 is identifiable because all of the components of the integral on the right-hand side of equation 2 are identifiable. In Web Appendix 3, we extend these results to the case of covariate-dependent sampling of nonrandomized individuals.
is identifiable because all of the components of the integral on the right-hand side of equation 2 are identifiable. In Web Appendix 3, we extend these results to the case of covariate-dependent sampling of nonrandomized individuals.
Nonnested trial designs
Using an argument parallel to that for nested trial designs with subsampling, when the probability of sampling a nonrandomized individual is unknown, the probability of trial participation, 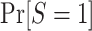 , can be expressed in the form of equation 3, substituting the u for c:
, can be expressed in the form of equation 3, substituting the u for c:
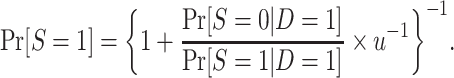 |
Because, as defined above, u is an unknown constant, 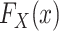 is not identifiable, and consequently
is not identifiable, and consequently 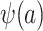 is also not identifiable.
is also not identifiable.
Turning our attention to 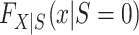 , we note that it is identifiable because the nonrandomized individuals contributing data to the analysis are a simple random sample from the nonrandomized individuals in the actual population (even though the sampling probability is unknown),
, we note that it is identifiable because the nonrandomized individuals contributing data to the analysis are a simple random sample from the nonrandomized individuals in the actual population (even though the sampling probability is unknown), 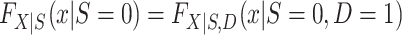 . It follows that
. It follows that 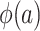 is identifiable in nonnested trial designs because all of the components of the integral in equation 2 are identifiable.
is identifiable in nonnested trial designs because all of the components of the integral in equation 2 are identifiable.
IDENTIFICATION VIA WEIGHTING
There has been considerable recent interest (4–7, 10) in using weighting methods to identify the counterfactual outcome means in equations 1 and 2, presumably because the specification of models for the probability of trial participation is often considered a somewhat easier task than the specification of models for the expectation of the outcome among trial participants.
First, consider 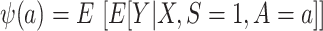 , which we argued is identifiable in nested trials. As is shown in a previous paper (6), we can reexpress the right-hand side of equation 1 to use weighting—that is,
, which we argued is identifiable in nested trials. As is shown in a previous paper (6), we can reexpress the right-hand side of equation 1 to use weighting—that is,
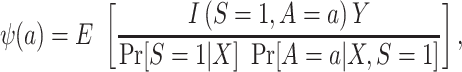 |
(4) |
where 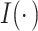 denotes the indicator function.
denotes the indicator function.
Now consider 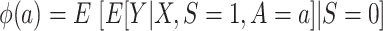 , which we argued is identifiable by the g-formula in both nested and nonnested trials. As is shown in Dahabreh et al. (10), we can reexpress the right-hand side of equation 2 to use weighting—that is,
, which we argued is identifiable by the g-formula in both nested and nonnested trials. As is shown in Dahabreh et al. (10), we can reexpress the right-hand side of equation 2 to use weighting—that is,
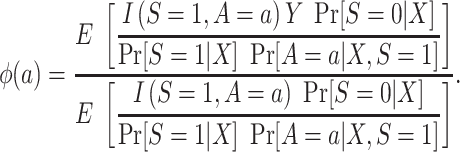 |
(5) |
The probability of treatment among trial participants, 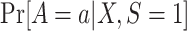 , is under the control of the investigators and does not pose any difficulties for identification of either functional. Now, for each design, we focus our attention on the conditional probability or the conditional odds of trial participation, which appear in equations 4 and 5, respectively.
, is under the control of the investigators and does not pose any difficulties for identification of either functional. Now, for each design, we focus our attention on the conditional probability or the conditional odds of trial participation, which appear in equations 4 and 5, respectively.
Nested trial designs
Census of the actual population.
Identification of 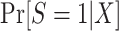 in this design is an obvious consequence of the fact that persons contributing data to the analysis are a simple random sample from the target population. In other words, because we have sampled all individuals in the actual population, which is a simple random sample of the target population,
in this design is an obvious consequence of the fact that persons contributing data to the analysis are a simple random sample from the target population. In other words, because we have sampled all individuals in the actual population, which is a simple random sample of the target population, 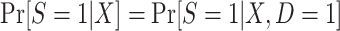 .
.
Subsampling of nonrandomized individuals.
For this design, it helps to note that
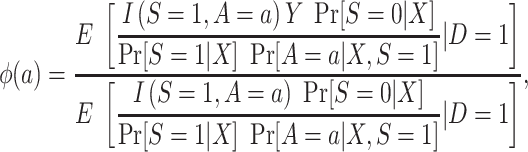 |
(6) |
which can be verified by multiplying the numerator and denominator of the right-hand side of the equation by  and noticing that, by design,
and noticing that, by design, 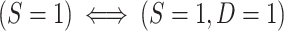 . Thus, in this design, as when there is no subsampling of nonrandomized individuals, we only need to worry about the identification of
. Thus, in this design, as when there is no subsampling of nonrandomized individuals, we only need to worry about the identification of 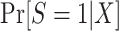 . As we show in Web Appendix 3, under the sampling properties of this design,
. As we show in Web Appendix 3, under the sampling properties of this design,
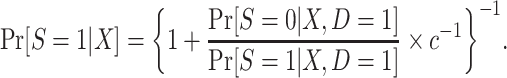 |
(7) |
In this design, the conditional odds of trial participation among sampled individuals, 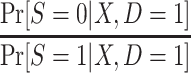 , are identifiable, and c is a known constant; thus,
, are identifiable, and c is a known constant; thus, 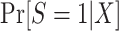 is also identifiable. Furthermore, the population odds of trial participation can be written as
is also identifiable. Furthermore, the population odds of trial participation can be written as
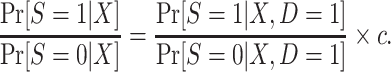 |
(8) |
In sum, and as expected based on our results about identification using the g-formula, the weighting reexpressions of the functionals of interest are identifiable in nested trial designs. Furthermore, the probability of trial participation conditional on covariates, which is useful for studying determinants of trial participation, is also identifiable both when we have a census of the actual population and when we subsample the nonrandomized individuals.
Nonnested trial designs
Equation 6 also applies to nonnested trial designs; thus, we only need to consider the identifiability of 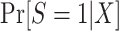 . We can use an argument parallel to that for nested trial designs with subsampling to establish that when the sampling probability for nonrandomized individuals is unknown, the probability of trial participation,
. We can use an argument parallel to that for nested trial designs with subsampling to establish that when the sampling probability for nonrandomized individuals is unknown, the probability of trial participation, 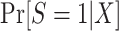 , can be expressedas
, can be expressedas
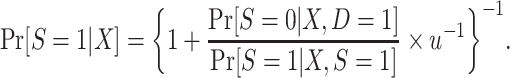 |
(9) |
Because, as defined above, u is unknown, the conditional probability of trial participation, which appears on the right-hand side of equation 4, is not identifiable; this confirms our earlier result that 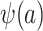 cannot be identified in nonnested trials.
cannot be identified in nonnested trials.
Furthermore, the conditional odds of trial participation are also not identifiable because they depend on u. In fact, using equation 8, substituting u for c, we see that the odds of trial participation in the target population are, up to an unknown multiplicative constant, equal to the odds of trial participation among sampled individuals,
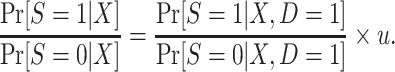 |
(10) |
We have come to an apparent conflict: The right-hand sides of equations 5 and 6 involve the conditional odds of trial participation, a quantity that is not identifiable in nonnested designs. Yet, we argued in the previous section that 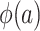 , which appears on the left-hand sides of equations 5 and 6, is identifiable. The conflict can be easily resolved by noting that, because both the numerator and the denominator in equation 5 are multiplied by the unknown constant u, which cancels out, identification via weighting by the inverse of the odds of trial participation is possible (see Dahabreh et al. (10) for technical details).
, which appears on the left-hand sides of equations 5 and 6, is identifiable. The conflict can be easily resolved by noting that, because both the numerator and the denominator in equation 5 are multiplied by the unknown constant u, which cancels out, identification via weighting by the inverse of the odds of trial participation is possible (see Dahabreh et al. (10) for technical details).
Table 1 summarizes the sampling properties and identification results for each study design.
Table 1.
Sampling Properties and Identification Results for Several Study Designs for Extending Causal Inferences From a Randomized Trial to a Target Populationa
| Study Design | Sampling Probabilities | Marginal Probability of Trial Participation b | Conditional Probability of Trial Participation b | Identifiable Counterfactual Outcome Means (When the Identifiability Conditions Hold) |
|---|---|---|---|---|
| Nested trial | ||||
| Census of actual population |
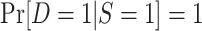 and
and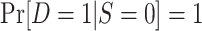
|
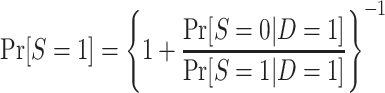
|
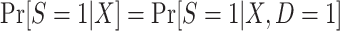
|
 and
and 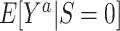
|
| Subsampling of nonrandomized individuals |
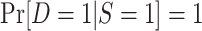 and
and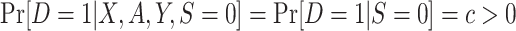 ; c is a known constant ; c is a known constant |
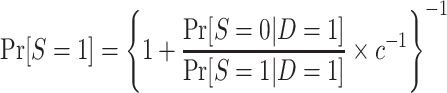
|
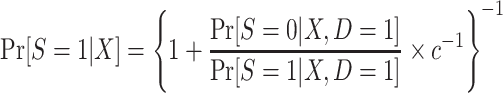
|
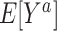 and
and 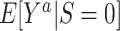
|
| Nonnested trial |
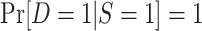 and
and ; u is an unknown constant ; u is an unknown constant |
Not identifiable | Not identifiable |
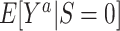
|
Abbreviation: Pr, probability.
a For detailed descriptions of notation, see the main text. Briefly, X denotes baseline covariates, S the trial participation indicator, A the assigned treatment, Y the outcome, and D the indicator for sampling into the study sample.  is the counterfactual outcome under intervention to set treatment to a; c and u are positive constants.
is the counterfactual outcome under intervention to set treatment to a; c and u are positive constants.
b Formulae for the marginal and conditional probabilities of trial participation in nested-trial designs with a census of the actual population can be obtained from the formulae for the nested trial design with known sampling probabilities by setting c = 1.
ESTIMATING THE PROBABILITY OF TRIAL PARTICIPATION
In realistic analyses, the dimension of X will be fairly large, necessitating some modeling assumptions about 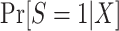 or
or 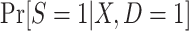 (25). Below we discuss the relationship between study design and model specification and estimation approaches.
(25). Below we discuss the relationship between study design and model specification and estimation approaches.
Nested trial designs
Census of the actual population.
In this type of nested trial design, it is straightforward to estimate the probability of trial participation, 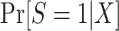 , in the sense that we can use the model we believe is most likely to be correctly specified for the target population.
, in the sense that we can use the model we believe is most likely to be correctly specified for the target population.
For concreteness, suppose that we are willing to assume a parametric model, 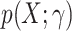 , for the probability of trial participation in the target population,
, for the probability of trial participation in the target population, 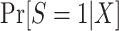 , with γ a finite dimensional parameter. In the nested-trial designs with a census of nonrandomized individuals, we typically estimate the parameters by maximizing the likelihood function
, with γ a finite dimensional parameter. In the nested-trial designs with a census of nonrandomized individuals, we typically estimate the parameters by maximizing the likelihood function
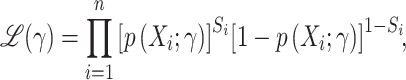 |
where 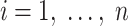 and n is the number of persons in the study (i.e., the actual population). Under reasonable technical conditions (26), the usual maximum likelihood methods use a sample-size normalized objective function that converges uniformly in probability to
and n is the number of persons in the study (i.e., the actual population). Under reasonable technical conditions (26), the usual maximum likelihood methods use a sample-size normalized objective function that converges uniformly in probability to
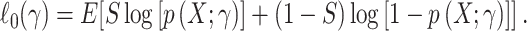 |
(11) |
For example, when 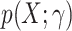 is a logistic model,
is a logistic model, 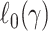 is the large-sample limit of the sample-size normalized log-likelihood function for logistic regression.
is the large-sample limit of the sample-size normalized log-likelihood function for logistic regression.
Subsampling of nonrandomized individuals.
When we subsample the nonrandomized individuals in the actual population, it is not possible to maximize the likelihood function above, because data are not available from all nonrandomized individuals in the actual population. A natural idea is to use equation 7, which provides an explicit formula for identifying the conditional probability of trial participation, 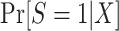 , using the probability of trial participation among sampled individuals,
, using the probability of trial participation among sampled individuals, 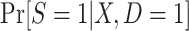 , and the sampling probability for nonrandomized individuals,
, and the sampling probability for nonrandomized individuals, 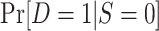 .
.
When modeling the probability of trial participation among sampled individuals, however, the following difficulty arises: In general, when sampling depends on trial participation status, the correctly specified model for trial participation does not necessarily have the same form as the correctly specified model in the target population. In other words, when sampling depends on trial participation status, as it does in the nested trial design with subsampling, the “true” model for 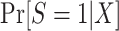 does not have the same form as the “true” model for participation conditional on being sampled,
does not have the same form as the “true” model for participation conditional on being sampled, 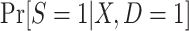 . This means that naive estimation of the parameters of the model for trial participation among sampled individuals (“naive” in the sense that it does not account for subsampling nonrandomized individuals) will typically be inconsistent for the population model.
. This means that naive estimation of the parameters of the model for trial participation among sampled individuals (“naive” in the sense that it does not account for subsampling nonrandomized individuals) will typically be inconsistent for the population model.
Nevertheless, because the sampling probability of nonrandomized individuals is known, we can use the following weighted pseudolikelihood function, which uses only data from sampled individuals (27, 28):
 |
with 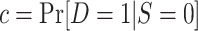 . Weighted maximum likelihood methods use a sample-size normalized objective function that converges uniformly in probability to
. Weighted maximum likelihood methods use a sample-size normalized objective function that converges uniformly in probability to
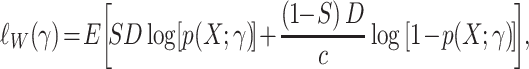 |
(12) |
which is restricted to sampled individuals (D = 1).
As we show in Web Appendix 4, under the sampling properties for this design, the large-sample limits of the objective functions in equations 11 and 12 are equal, 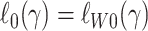 . It follows that, under reasonable technical conditions (26), weighted likelihood estimation of γ in the nested trial design with subsampling of nonrandomized individuals converges in probability to the same parameter as unweighted regression in the actual population.
. It follows that, under reasonable technical conditions (26), weighted likelihood estimation of γ in the nested trial design with subsampling of nonrandomized individuals converges in probability to the same parameter as unweighted regression in the actual population.
In practical terms, as long as a reasonable parametric model for the probability of participation can be specified for the target population, the model parameters can be estimated using weighted maximum likelihood methods (27) on data from sampled individuals, with individual-level weights equal to 1 for randomized individuals, 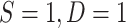 ;
; 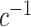 for sampled nonrandomized individuals,
for sampled nonrandomized individuals, 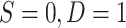 ; and 0 for unsampled individuals, D = 0. In Web Appendix 5, we extend these results to the case of covariate-dependent sampling of nonrandomized individuals.
; and 0 for unsampled individuals, D = 0. In Web Appendix 5, we extend these results to the case of covariate-dependent sampling of nonrandomized individuals.
Nonnested trial designs
In nonnested trial designs, the weighting approach described above is not applicable because the sampling probability of nonrandomized individuals is unknown. Provided, however, that the sampling probability does not depend on X (i.e., the assumed sampling property), we can show that, if a logistic model for trial participation is correctly specified in the target population, then a logistic model with the same functional form is correctly specified in the nonnested trial design. In fact, the 2 models have the same coefficients but different intercepts. To see this, suppose that we are willing to assume a logistic regression model in the population, such that
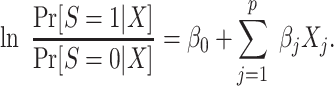 |
Using the result in equation 9 and taking logarithms, we have that
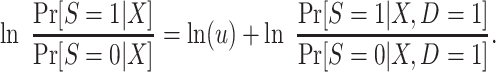 |
Equating the right-hand sides of the last 2 equations, we obtain
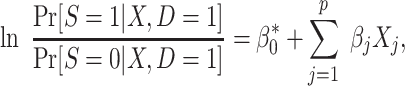 |
(13) |
where 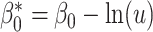 , a well-known result in the context of case-referent studies (29). Thus, if a logistic model is correctly specified in the target population, then a model of the same functional form is correctly specified in the nonnested trial design. In fact, the coefficients in the two models are equal, and only the intercept differs. Because
, a well-known result in the context of case-referent studies (29). Thus, if a logistic model is correctly specified in the target population, then a model of the same functional form is correctly specified in the nonnested trial design. In fact, the coefficients in the two models are equal, and only the intercept differs. Because 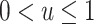 ,
, 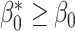 : The subsampling of nonrandomized patients simply results in an intercept that is “shifted” upwards. As we showed in the section on weighting, the resulting shift in the odds of participation does not affect identification of the counterfactual outcome mean in the nonrandomized individuals,
: The subsampling of nonrandomized patients simply results in an intercept that is “shifted” upwards. As we showed in the section on weighting, the resulting shift in the odds of participation does not affect identification of the counterfactual outcome mean in the nonrandomized individuals, 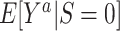 , which is the parameter of interest in nonnested trial designs with unknown sampling probability of nonrandomized individuals.
, which is the parameter of interest in nonnested trial designs with unknown sampling probability of nonrandomized individuals.
The above result is also important for estimation of the model parameters: Combined with the results in the papers by Prentice and Pyke (30) and Breslow et al. (31), it implies that the unconstrained and unweighted maximum likelihood estimator for the logistic model in equation 13, fitted among sampled individuals, is the efficient estimator for 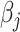 ,
, 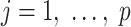 .
.
Of course, there is no reason to expect that the population participation model for 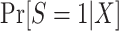 follows a logistic form—in fact, substantive knowledge about that model will often be insufficient to specify any parametric functional form. Therefore, in high-dimensional settings with large samples, it will often be a good idea to use more flexible modeling strategies (e.g., data-adaptive machine learning methods) to estimate
follows a logistic form—in fact, substantive knowledge about that model will often be insufficient to specify any parametric functional form. Therefore, in high-dimensional settings with large samples, it will often be a good idea to use more flexible modeling strategies (e.g., data-adaptive machine learning methods) to estimate 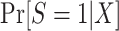 or
or 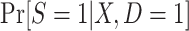 .
.
DISCUSSION
In this paper, we have presented a unified description of study designs for extending inferences from randomized trials to a target population and have shown that commonly invoked identifiability conditions need to be combined with the sampling properties of each study design in order to determine which counterfactual quantities can be identified. Our approach uses a superpopulation framework, which is a natural choice for extending trial findings beyond the sample of randomized individuals (32).
In nonnested trial designs, where the sampling probability for nonrandomized individuals is unknown, the marginal counterfactual outcome means in the entire target population are not identifiable, but the counterfactual outcome means in the subset of nonrandomized individuals are identifiable. This restriction may be less severe than it appears: For most trials, we want to estimate the effect of applying the interventions to a new population, which can be represented by a well-chosen sample of nonrandomized individuals (10). In any case, when available, knowledge of the sampling probability of nonrandomized individuals can be used to mitigate these limitations, without requiring the collection of covariate information from all nonrandomized individuals in the actual population. Thus, in general, nested trial designs will often be the preferred approach for generalizing trial findings when it is possible to define and sample the actual population when a randomized trial is planned. Such nested trial designs will typically have broad (pragmatic (33)) eligibility criteria and define the target population as the population of persons meeting the trial eligibility criteria. When that is not possible, as is the case with already completed randomized trials, nonnested trial designs might be a reasonable alternative. For example, in nonnested trial designs, the comparison of estimates for the counterfactual outcome means among randomized (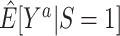 ) and nonrandomized (
) and nonrandomized (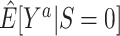 ) individuals is of practical interest: Provided the identifiability conditions hold, if
) individuals is of practical interest: Provided the identifiability conditions hold, if  , we may conclude that the trial results are likely to apply to the population underlying the sample of nonrandomized individuals (up to sampling variability); in contrast, if the estimates are different, trial results may not apply to that population.
, we may conclude that the trial results are likely to apply to the population underlying the sample of nonrandomized individuals (up to sampling variability); in contrast, if the estimates are different, trial results may not apply to that population.
We also showed that the different study designs have implications for identifying and estimating the conditional probability of trial participation. This probability may be of inherent interest because it captures aspects of decision-making related to trial participation (34, 35). We showed that the probability is identifiable in nested trial designs but not in nonnested trial designs (e.g., composite data set designs). Indeed, any reasonable model for the probability of participation in the population can be identified in nested trial designs. In nested trial designs with subsampling of nonrandomized individuals, estimation of model parameters can be facilitated by the use of weighted estimation, in which randomized patients are given weight 1 and nonrandomized patients are given a weight equal to the inverse of the probability of being sampled among nonrandomized persons in the actual population. In nonnested trial designs, model specification is complicated by the fact that, when sampling depends on trial participation status, the model for the probability of trial participation among sampled individuals is not of the same form as the model in the population (the logistic regression model being a notable exception (27)).
The probability of trial participation in the target population is also important for identification and estimation using weighting methods. Our argument that the odds of participation after selection of nonrandomized individuals are equal to the odds of participation in the target population up to an unknown multiplicative constant clarifies how the validity of estimators when using composite data-set designs (10) depends critically on the assumed sampling properties (an issue that had not been fully addressed in earlier work, such as the paper by Westreich et al. (7)).
Astute readers will have noticed the many connections between our results and the theory of case-referent (``case-control'') studies (27–29, 36, 37). Indeed, our approach can be placed in the case-base paradigm, viewing randomized individuals as “cases” in a cumulative incidence case-referent study (36) nested in the “cohort” of the actual population. An interesting parallel with case-referent studies: The difficulties in specifying the population of nonrandomized individuals that should be sampled in nonnested trial designs (e.g., composite data-set designs) are similar in nature to the validity issues of case-referent studies with a secondary base (38–40).
In this paper, for simplicity, we focused on counterfactual quantities that are most meaningful for point treatments with complete adherence and no loss to follow-up. Our results can be extended to address time-varying treatments using well-known extensions of the identifiability conditions for randomized trials (24, 32, 41), without any changes to the sampling properties or the modeling assumptions about the probability of trial participation (18). Perhaps, then, the most consequential causal assumption we required was that the invitation to participate in the trial and trial participation itself do not have an effect on the outcome except through treatment assignment (3, 18). Unless investigators are willing to contemplate more complex study designs involving multistage data collection about (and possibly randomization of) the invitation to participate, trial participation itself, and treatment assignment (42), our results are best viewed as applying to trials where the not-through-treatment effects of the invitation to participate in the trial and of trial participation are negligible compared with the effects of treatment. For example, they are applicable to pragmatic randomized trials embedded in large health-care systems or registries, where trial procedures other than treatment assignment can be assumed to be similar to usual medical practice (33, 43, 44).
In conclusion, we have presented a unified description of different study designs for extending causal inferences from a randomized trial to a target population and have examined the implications of each design’s sampling properties for identifying causal quantities and modeling the probability of trial participation. We hope that our approach will be useful to investigators conducting generalizability and transportability analyses using the designs we described or closely related variants.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Center for Evidence Synthesis in Health and Department of Health Services, Policy, and Practice, School of Public Health, Brown University, Providence, Rhode Island, United States (Issa J. Dahabreh, Sarah E. Robertson); Department of Epidemiology, School of Public Health, Brown University, Providence, Rhode Island, United States (Issa J. Dahabreh); Department of Epidemiology, Harvard T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts, United States (Issa J. Dahabreh, James M. Robins, Miguel A. Hernán); Department of Biostatistics, Harvard T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts, United States (Sebastien J.-P. A. Haneuse, James M. Robins, Miguel A. Hernán); Department of Pharmacy Practice, College of Pharmacy, University of Rhode Island, Rhode Island, United States (Ashley L. Buchanan); Departments of Mental Health, Biostatistics, and Health Policy and Management, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland, United States (Elizabeth A. Stuart); and Harvard-MIT Division of Health Sciences and Technology, Boston, Massachusetts, United States (Miguel A. Hernán).
This work was supported in part by awards ME-1306-03758 and ME-1502-27794 (I.J.D.) from the Patient-Centered Outcomes Research Institute; grant R37 AI102634 (M.A.H.) from the National Institutes of Health; and National Research Service Award T32AGHS00001 (S.E.R.) from the Agency for Healthcare Research and Quality.
We thank Drs. Angela Bengtson and Nina Joyce of Brown University (Providence, Rhode Island) for helpful comments on earlier versions of this paper.
The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the Patient-Centered Outcomes Research Institute (PCORI), the PCORI Board of Governors, the PCORI Methodology Committee, the National Institutes of Health, or the Agency for Healthcare Research and Quality.
Conflict of interest: none declared.
REFERENCES
- 1. Keiding N, Louis TA. Perils and potentials of self-selected entry to epidemiological studies and surveys. J R Stat Soc Ser A Stat Soc. 2016;179(2):319–376. [Google Scholar]
- 2. Hernán MA. Discussion of “perils and potentials of self-selected entry to epidemiological studies and surveys”. J R Stat Soc Ser A Stat Soc. 2016;179(2):346–347. [Google Scholar]
- 3. Dahabreh IJ, Hernán MA. Extending inferences from a randomized trial to a target population. Eur J Epidemiol. 2019;34(8):719–722. [DOI] [PubMed] [Google Scholar]
- 4. Cole SR, Stuart EA. Generalizing evidence from randomized clinical trials to target populations: the ACTG 320 trial. Am J Epidemiol. 2010;172(1):107–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Buchanan AL, Hudgens MG, Cole SR, et al. Generalizing evidence from randomized trials using inverse probability of sampling weights. J R Stat Soc Ser A Stat Soc. 2018;181(4):1193–1209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Dahabreh IJ, Robertson SE, Tchetgen Tchetgen EJ, et al. Generalizing causal inferences from individuals in randomized trials to all trial-eligible individuals. Biometrics. 2019;75(2):685–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Westreich D, Edwards JK, Lesko CR, et al. Transportability of trial results using inverse odds of sampling weights. Am J Epidemiol. 2017;186(8):1010–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Lesko CR, Buchanan AL, Westreich D, et al. Generalizing study results: a potential outcomes perspective. Epidemiology. 2017;28(4):553–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Rudolph KE, van der Laan MJ. Robust estimation of encouragement design intervention effects transported across sites. J R Stat Soc Series B Stat Methodol. 2017;79(5):1509–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Dahabreh IJ, Robertson SE, Steingrimsson JA, et al. Extending inferences from a randomized trial to a new target population. Stat Med. 2020;39(14):1999–2014. [DOI] [PubMed] [Google Scholar]
- 11. Robins JM. Confidence intervals for causal parameters. Stat Med. 1988;7(7):773–785. [DOI] [PubMed] [Google Scholar]
- 12. Dahabreh IJ, Hernán MA, Robertson SE, et al. Generalizing trial findings in nested trial designs with sub-sampling of non-randomized individuals [preprint]. arXiv. 2019. (doi: arXiv:1902.06080v2s). Accessed November 3, 2020. [Google Scholar]
- 13. Olschewski M, Scheurlen H. Comprehensive cohort study: an alternative to randomized consent design in a breast preservation trial. Methods Inf Med. 1985;24(3):131–134. [PubMed] [Google Scholar]
- 14. Saegusa T. Large sample theory for merged data from multiple sources. Ann Stat. 2019;47(3):1585–1615. [Google Scholar]
- 15. Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol. 1974;66(5):688–701. [Google Scholar]
- 16. Robins JM, Greenland S. Causal inference without counterfactuals: comment. J Am Stat Assoc. 2000;95(450):431–435. [Google Scholar]
- 17. Landsberger HA. Hawthorne Revisited: Management and the Worker, Its Critics, and Developments in Human Relations in Industry. (Cornell Studies in Industrial and Labor Relations). Ithaca, NY: Cornell University; 1958. [Google Scholar]
- 18. Dahabreh IJ, Robins JM, Haneuse SJ-P, et al. Generalizing causal inferences from randomized trials: counterfactual and graphical identification [preprint]. arXiv. 2019. (doi: arXiv:1906.10792). Accessed November 3, 2020. [Google Scholar]
- 19. Pearl J, Bareinboim E. External validity: from do-calculus to transportability across populations. Stat Sci. 2014;29(4):579–595. [Google Scholar]
- 20. Bareinboim E, Pearl J. Causal inference and the data-fusion problem. Proc Natl Acad Sci. 2016;113(27):7345–7352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Richardson TS, Robins JM. Single world intervention graphs (SWIGs): a unification of the counterfactual and graphical approaches to causality. (CSSS Working Paper no. 128). Seattle, WA: Center for Statistics and the Social Sciences, University of Washington; 2013. https://www.csss.washington.edu/research/working-papers/single-world-intervention-graphs-swigs-unification-counterfactual-and. Accessed November 3, 2020. [Google Scholar]
- 22. Dahabreh IJ, Robins JM, Hernán MA. Benchmarking observational methods by comparing randomized trials and their emulations. Epidemiology. 2020;31(5):614–619. [DOI] [PubMed] [Google Scholar]
- 23. Stuart EA, Ackerman B, Westreich D. Generalizability of randomized trial results to target populations: design and analysis possibilities. Res Soc Work Pract. 2018;28(5):532–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Robins JM. A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Math Model. 1986;7(9):1393–1512. [Google Scholar]
- 25. Robins JM, Ritov Y. Toward a curse of dimensionality appropriate (CODA) asymptotic theory for semi-parametric models. Stat Med. 1997;16(1–3):285–319. [DOI] [PubMed] [Google Scholar]
- 26. Newey WK, McFadden D. Large sample estimation and hypothesis testing. In: Engle RF, McFadden DL, eds. Handbook of Econometrics. Vol. Vol. 4. Amsterdam, the Netherlands: Elsevier BV; 1994:2111–2245. [Google Scholar]
- 27. Manski CF, Lerman SR. The estimation of choice probabilities from choice based samples. Econometrica. 1977;45(8):1977–1988. [Google Scholar]
- 28. Cosslett SR. Maximum likelihood estimator for choice-based samples. Econometrica. 1981;49(5):1289–1316. [Google Scholar]
- 29. Mantel N. Synthetic retrospective studies and related topics. Biometrics. 1973;29(3):479–486. [PubMed] [Google Scholar]
- 30. Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66(3):403–411. [Google Scholar]
- 31. Breslow NE, Robins JM, Wellner JA, et al. On the semi-parametric efficiency of logistic regression under case-control sampling. Bernoulli. 2000;6(3):447–455. [Google Scholar]
- 32. Hernán MA, Robins JM. Causal Inference: What If. Boca Raton, FL: Chapman & Hall/CRC Press; 2021. [Google Scholar]
- 33. Ford I, Norrie J. Pragmatic trials. N Engl J Med. 2016;375(5):454–463. [DOI] [PubMed] [Google Scholar]
- 34. McFadden D. Conditional logit analysis of qualitative choice behavior. In: Zarembka P, ed. Frontiers in Econometrics. Berkeley, CA: Institute of Urban and Regional Development, University of California, Berkeley; 1973:105–142. [Google Scholar]
- 35. Stuart EA, Cole SR, Bradshaw CP, et al. The use of propensity scores to assess the generalizability of results from randomized trials. J R Stat Soc Ser A Stat Soc. 2001;174(2):369–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Miettinen OS. Estimability and estimation in case-referent studies. Am J Epidemiol. 1976;103(2):226–235. [DOI] [PubMed] [Google Scholar]
- 37. Scott AJ, Wild C. Fitting logistic models under case-control or choice based sampling. J R Stat Soc B Methodol. 1986;48(2):170–182. [Google Scholar]
- 38. Miettinen OS. The “case-control” study: valid selection of subjects. J Chronic Dis. 1985;38(7):543–548. [DOI] [PubMed] [Google Scholar]
- 39. Miettinen OS. Response: the concept of secondary base. J Clin Epidemiol. 1990;43(9):1017–1020. [Google Scholar]
- 40. Wacholder S, McLaughlin JK, Silverman DT, et al. Selection of controls in case-control studies: I. principles. Am J Epidemiol. 1992;135(9):1019–1028. [DOI] [PubMed] [Google Scholar]
- 41. Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Halloran ME, Berry D, eds. Statistical Models in Epidemiology, the Environment, and Clinical Trials. New York, NY: Springer-Verlag New York; 2000:95–133. [Google Scholar]
- 42. Heckman JJ. Randomization and social policy evaluation revisited. (Technical Working Paper 107). Cambridge, MA: National Bureau of Economic Research; 1991. https://www.nber.org/papers/t0107. Accessed November 3, 2020. [Google Scholar]
- 43. van Staa T-P, Dyson L, McCann G, et al. The opportunities and challenges of pragmatic point-of-care randomised trials using routinely collected electronic records: evaluations of two exemplar trials. Health Technol Assess. 2014;18(43):1–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Choudhry NK. Randomized, controlled trials in health insurance systems. N Engl J Med. 2017;377(10):957–964. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


