Abstract
Motivation
Structure-conditioned information statistics have proven useful to predict and visualize tRNA Class-Informative Features (CIFs) and their evolutionary divergences. Although permutation P-values can quantify the significance of CIF divergences between two taxa, their naive Monte Carlo approximation is slow and inaccurate. The Peaks-over-Threshold approach of Knijnenburg et al. (2009) promises improvements to both speed and accuracy of permutation P-values, but has no publicly available API.
Results
We present tRNA Structure–Function Mapper (tSFM) v1.0, an open-source, multi-threaded application that efficiently computes, visualizes and assesses significance of single- and paired-site CIFs and their evolutionary divergences for any RNA, protein, gene or genomic element sequence family. Multiple estimators of permutation P-values for CIF evolutionary divergences are provided along with confidence intervals. tSFM is implemented in Python 3 with compiled C extensions and is freely available through GitHub (https://github.com/tlawrence3/tSFM) and PyPI.
Availability and implementation
The data underlying this article are available on GitHub at https://github.com/tlawrence3/tSFM.
Supplementary information
Supplementary data are available at Bioinformatics online.
In bioinformatics, a structure–function map predicts functional properties of biological macromolecules from their structural features. A transfer RNA (tRNA) structure–function map predicts tRNA identity elements that promote functional interactions with specific (cognate) tRNA-binding proteins or that diminish non-cognate interactions (Collins-Hed and Ardell, 2019; Giegé et al., 2012). Earlier, we developed bioinformatic predictors of tRNA identity elements called Class-Informative Features (CIFs), measured in bits of structure-conditioned functional information and visualized in stacked bar-graphs called Function Logos (Freyhult et al., 2006). Structure-conditioned functional information reverses the conditioning inherent in Sequence Logos (Gorodkin et al., 1997; Schneider and Stephens, 1990). Later, we introduced Information Difference (ID) and Kullback-Leibler Divergence (KLD) logos to quantify and visualize evolutionary divergences between two taxa in the total information of tRNA CIFs and their functional associations respectively (Freyhult et al., 2007). These statistics quantify complementary and concurrent modes of evolution of CIFs: ID quantifies gains and losses of functional information by features while KLD quantifies changes in their functional associations.
In Kelly et al. (2020), we introduced version 0.9 of the tRNA Structure–Function Mapper (tSFM), a tool to compute CIF statistics in any RNA, protein or gene/genetic element family, with several improvements over previously published methods, including prediction and visualization of structurally paired-site CIFs in non-coding RNA families, improved small-sample bias-correction and accuracy with the Nemenman-Shafee-Bialek (NSB) Bayesian entropy estimator (Nemenman et al., 2002), quantification of the significance of CIFs with a Monte Carlo permutation P-value-based approach (Hollander et al., 2013), and methods to correct for multiple testing by control of the Family-wise Error Rate (FWER) or False Discovery Rate (FDR) (Benjamini and Hochberg, 1995; Strimmer, 2008). However, tSFM v0.9 did not provide a means to compute the statistical significance of ID and KLD evolutionary divergence metrics for CIFs. In initial work, we found that Monte Carlo approximations to permutation P-values for CIF divergences were slow and inaccurate for large divergence values, which permutation replicates never exceed, resulting in a constant P-value upper bound estimates that depend only on the Monte Carlo sample size. Although the permutation P-value ‘Peaks-over-Threshhold’ (PoT) tail-approximation approach described in Knijnenburg et al. (2009) is a promising remedy for this problem, we could not find an accessible and free implementation. Furthermore, their algorithm does not provide confidence intervals for P-values. We re-implemented their algorithm with modifications in tSFM v.1.0 resulting in improvements to both speed and accuracy of permutation-based P-value calculations as detailed below and in the Supplementary Materials.
tSFM v1.0 is written in Python 3 with compiled C extensions and released under GNU Lesser General Public License v3.0. Its input is any number of structurally co-aligned non-coding RNA, gene/DNA element or protein sequences, partitioned into separate FASTA or ClustalW files by taxon and functional class. An additional optional input file specifies a consensus secondary structure annotation for input RNA gene alignments in one of several standard formats. The output of tSFM includes one or more function logos in EPS format and one or more tables of statistics about CIFs, as detailed in the documentation. tSFM implements the exact entropy bias calculation of Schneider et al. (1986) in a C extension with Cython and the NSB estimator using mpmath. For KLD and ID contrasts of features between any pair of taxa, tSFM implements Algorithm Approximate in Supplementary Material, a modified version of the algorithm of Knijnenburg et al. (2009). Maximum Likelihood estimates of the shape and scale parameters of the Generalized Pareto Distribution (GPD) function are computed by the genpareto.fit routine of SciPy v1.5.4 using keyword option floc = 0. The Anderson-Darling Test is computed with a modified version of scikit-gof v0.1.3 migrated into the tSFM installation. We computed P-values from the distribution function, falling back on other P-value estimators in rare cases if the distribution function returned 0. We found that transforming data and permutation replicates to the fifth power increased the number of features with non-zero estimates, confirming the recommendations and findings of Knijnenburg et al. (2009). We abandoned testing convergence of as described in Knijnenburg et al. (2009, 2011), opting instead to calculate confidence intervals to quantify uncertainty by the ‘boundary method’ described in Glotzer et al. (2017); Campbell et al. (2016) and in Supplementary Material (Algorithm Boundary).
tSFM provides options to estimate P-values exclusively by the naive Monte Carlo method using pseudo-counts (), by the Monte Carlo method terminating after S = 10 exceedances () or by algorithm Approximate, with T = 500 ‘target’ (minimum number of) permutations, and a maximum number of permutations per feature of R = 10 000 (). Table 1 shows that for this data, terminating after 10 exceedances reduced run time by 37% for KLD and by 80% for ID. The full algorithm including the GPD-based tail approximation reduced run time for both statistics more than ten-fold. As shown in Figure 1, P-value estimates by the three algorithms show marked stability for smaller divergence signals, while the full algorithm vastly improves the obtainable range of P-value estimates for larger signals. A small fraction of features with small-to-medium sample sizes and larger divergences showed instability in estimates, and appear with atypically large or small surprisals and larger confidence intervals in Supplementary Figures S1 and S2.
Table 1.
Run times (without confidence interval calculations) under three methods of P-value calculation for the contrast from Kelly et al. (2020) between human tRNAs (431 genes) and the L. enriettii clade (2 genomes; 160 genes) computed on a Linux compute node with 20 cores at 2301 MHz and 120 GB of RAM.
| Statistic | Estimator | Run time (h) |
|---|---|---|
| KLD | 7.72 | |
| 4.86 | ||
| 0.68 | ||
| ID | 48.96 | |
| 9.57 | ||
| 3.19 |
Fig. 1.
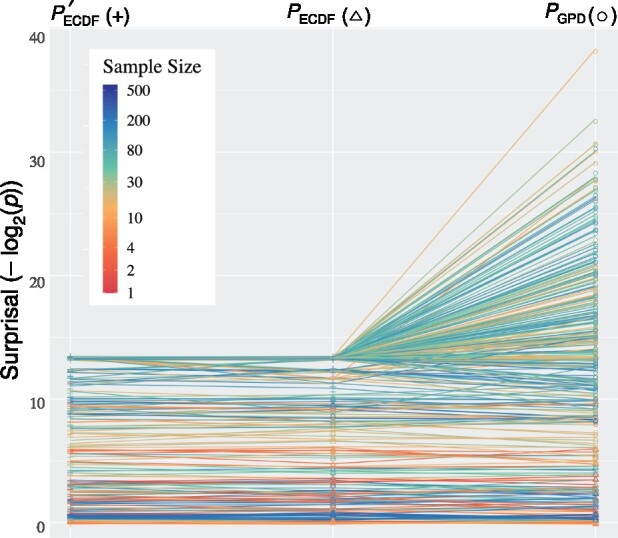
Slopegraph of three different P-value estimate algorithms for KLD CIF divergences of L.enriettii clade tRNA genes (n = 160 genes) against human tRNA genes (n = 431 genes). is the naive Monte Carlo method with 10 000 permutations per feature, using pseudo-counts when there are fewer than S exceedances (by default, 10). terminates after S exceedances () or a maximum of 10 000 permutations, using pseudo-counts unless there are S exceedances. uses algorithm Approximate with T = 500 target permutations and a maximum of 10 000 permutations. Colors show the harmonic mean of the number of sequences containing a given CIF in the two taxa. Points but not lines are jittered against overplotting. See online for color version.
Funding
D.H.A. and T.J.L. were financially supported by the National Science Foundation (INSPIRE-1344279). D.H.A. was financially supported by National Institutes of Health/National Institute of Allergy and Infectious Diseases 1R21AI127582-0 and a Julius Kuhn Professorship at Martin Luther University Halle-Wittenberg. Computational research was performed on the MERCED HPC cluster supported by the National Science Foundation (ACI-1429783). Oak Ridge National Laboratory is managed by UT-Battelle, LLC, for the U.S. Department of Energy under contract DE-AC05-00OR22725.
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Travis J Lawrence, Quantitative and Systems Biology Program, University of California, Merced, CA 95343, USA; Biosciences Division, Oak Ridge National Lab, Oak Ridge, TN 37830, USA.
Fatemeh Hadi-Nezhad, Quantitative and Systems Biology Program, University of California, Merced, CA 95343, USA.
Ivo Grosse, Institute of Computer Science, Martin Luther University Halle–Wittenberg, Halle 06099, Germany; German Centre for Integrative Biodiversity Research (iDiv) Halle-Jena-Leipzig, Leipzig 04103, Germany.
David H Ardell, Quantitative and Systems Biology Program, University of California, Merced, CA 95343, USA; Department of Molecular and Cell Biology, University of California, Merced, CA 95343, USA.
References
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat Soc. Ser. B, 57, 289–300. [Google Scholar]
- Campbell B. et al. (2016) Application of the envelope peaks over threshold (EPOT) method for probabilistic assessment of dynamic stability. Ocean Eng., 120, 298–304. [Google Scholar]
- Collins-Hed A.I., Ardell D.H. (2019) Match fitness landscapes for macromolecular interaction networks: selection for translational accuracy and rate can displace tRNA-binding interfaces of non-cognate aminoacyl-tRNA synthetases. Theor. Popul. Biol., 129, 68–80. [DOI] [PubMed] [Google Scholar]
- Freyhult E. et al. (2006) Visualizing bacterial tRNA identity determinants and antideterminants using function logos and inverse function logos. Nucleic Acids Res., 34, 905–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freyhult E. et al. (2007) New computational methods reveal tRNA identity element divergence between Proteobacteria and Cyanobacteria. Biochimie, 89, 1276–1288. [DOI] [PubMed] [Google Scholar]
- Giegé R. et al. (2012) Structure of transfer RNAs: similarity and variability. WIRES RNA, 3, 37–61. [DOI] [PubMed] [Google Scholar]
- Glotzer D. et al. (2017) Confidence intervals for exceedance probabilities with application to extreme ship motions. REVSTAT Stat. J., 15, 537–563. [Google Scholar]
- Gorodkin J. et al. (1997) Displaying the information contents of structural RNA alignments: the structure logos. Bioinformatics, 13, 583–586. [DOI] [PubMed] [Google Scholar]
- Hollander M. et al. (2013) Nonparametric Statistical Methods. John Wiley & Sons, Inc., Somerset, USA. [Google Scholar]
- Kelly P. et al. (2020) Targeting tRNA-synthetase interactions towards novel therapeutic discovery against eukaryotic pathogens. PLOS Neglect. Trop. D, 14, 1–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knijnenburg T.A. et al. (2009) Fewer permutations, more accurate P-values. Bioinformatics, 25, i161–i168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knijnenburg T.A. et al. (2011) EPEPT: a web service for enhanced P-value estimation in permutation tests. BMC Bioinformatics, 12, 411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nemenman I. et al. (2002) Entropy and inference, revisited. Adv. Neur., 14, 471–478. [Google Scholar]
- Schneider T.D., Stephens R.M. (1990) Sequence logos: a new way to display consensus sequences. Nucleic Acids Res., 18, 6097–6100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider T.D. et al. (1986) Information content of binding sites on nucleotide sequences. J. Mol. Biol., 188, 415–431. [DOI] [PubMed] [Google Scholar]
- Strimmer K. (2008) A unified approach to false discovery rate estimation. BMC Bioinformatics, 9, 303. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


