Unsupervised Classification During Time-Series Model Building

Abstract

Researchers who collect multivariate time-series data across individuals must decide whether to model the dynamic processes at the individual level or at the group level. A recent innovation, group iterative multiple model estimation (GIMME), offers one solution to this dichotomy by identifying group-level time-series models in a data-driven manner while also reliably recovering individual-level patterns of dynamic effects. GIMME is unique in that it does not assume homogeneity in processes across individuals in terms of the patterns or weights of temporal effects. However, it can be difficult to make inferences from the nuances in varied individual-level patterns. The present article introduces an algorithm that arrives at subgroups of individuals that have similar dynamic models. Importantly, the researcher does not need to decide the number of subgroups. The final models contain reliable group-, subgroup-, and individual-level patterns that enable generalizable inferences, subgroups of individuals with shared model features, and individual-level patterns and estimates. We show that integrating community detection into the GIMME algorithm improves upon current standards in two important ways: (1) providing reliable classification and (2) increasing the reliability in the recovery of individual-level effects. We demonstrate this method on functional MRI from a sample of former American football players.

Introduction

Researchers across varied domains of psychology widely acknowledge that individuals are heterogeneous in terms of their dynamic processes (e.g., Molenaar, 2004; Molenaar & Nesselroade, 2012). Functional MRI (fMRI) literature in particular highlights heterogeneity in brain processes as a major analytic hurdle that has yet to be reconciled (Ramsey et al., 2010; Seigher & Price, 2016; Smith, 2012). Heterogeneity in brain processes surfaces even within specific diagnostic categories, such as major depressive (e.g., Price et al., 2016), autism spectrum (e.g., Volkmar, Lord, Bailey, Schultz, & Klin, 2004), and attention-deficit (e.g., Fair et al., 2012; Gates, Molenaar, Iyer, Nigg, & Fair, 2014) disorders. Normative samples have also evidenced heterogeneity in fMRI research (e.g., Beltz, Beekman, Molenaar, & Buss, 2013; Finn et al., 2015; Laumann et al., 2015; Nichols, Gates, Molenaar, & Wilson, 2013). Analytically, ignoring heterogeneity can give rise to models that fail to explain any one individual in the sample (Molenaar, 2004), which severely hampers the utility of results for any research paradigm. Taken together, emerging research highlights the necessity of individual-level modeling with a specific need for approaches that can reliably model directed (i.e., not correlational) relations among brain regions. At present, the most promising class of approaches for arriving at directed temporal relations among brain regions of interest are Bayes net techniques that utilize some information from the sample (Mumford & Ramsey, 2014; Ramsey, Hanson, & Glymour, 2011; Ramsey, Sanchez-Romero, & Glymour, 2014), including the group iterative multiple model estimation (GIMME) algorithm (Gates & Molenaar, 2012). The present article improves upon the GIMME approach by clustering individuals into relatively homogeneous subsets based entirely on features of their temporal models. Most importantly, we show that this step further improves the already exceptional rate of reliable model building with GIMME. The final results enable generalizable inferences in addition to the identification of subgroups of individuals with shared model features and person-specific paths and parameter estimates.

The original GIMME has been shown to obtain highly reliable directed temporal patterns of effects at the individual level at rates superior to many methods (Gates & Molenaar, 2012; Mumford & Ramsey, 2014; see Smith et al., 2011). It is generally accepted that for any time-series analysis, model misspecification may occur when researchers attempt to arrive at one dynamic model to describe all participants by concatenating individuals (Gonzales & Ferrer, 2014; Molenaar, 2004, 2007). When the analysis erroneously assumes homogeneity across individuals in this manner, the group-level model may fail to describe any of the individuals comprising the sample (Molenaar & Campbell, 2009). GIMME circumvents this issue by detecting signal from noise across individuals and conducting analysis for each individual separately to arrive at a group-level model. In this way, GIMME arrives at group-level paths that truly are valid for the majority of individuals without concatenating individuals or otherwise assuming homogeneity in their dynamic processes. This group-level pattern of effects is then used as a prior for building the individual-level models. Starting with the shared information obtained by looking across the sample (i.e., the group-level model) has been shown to greatly improve recovery of individual-level paths (Gates & Molenaar, 2012). It follows that using shared information within subgroups of individuals who have similar temporal patterns can further increase the reliability of individual-level results. The present article describes an extension to the GIMME algorithm that clusters individuals during model building by using information available after the group-level search and before the individual-level searches.

Using parameters obtained from time series models represents one common approach in the clustering of time-series data of any type (Liao, 2005). Functional MRI researchers currently cluster individuals on the basis of parameters from final time-series models to arrive at relatively homogeneous subsets of individuals in terms of their brain processes (e.g., Gates et al., 2014; Yang et al., 2014). These inquiries offered support for previously argued notions that varied biological markers can give rise to the same behaviors and symptoms (Gottesman & Gould, 2003). Thus, the current standard of placing individuals with the same diagnostic category into subgroups according to the assumption of within-category homogeneity may be ill advised. These lines of questions that seek to uncover subsets of individuals with similar dynamic processes further motivate the aim of arriving at reliable subgroups within GIMME. Directly following from the features scientists typically use to examine differences between a priori subgroups (e.g., Yang, Gates, Molenaar, & Li, 2015), we seek to organize individuals according to the presence and the sign (i.e., negative or positive) of relations estimated from time-series analysis. That is, individual-level nuances in the pattern of effects (as indicated with significance testing) as well as the sign of the effect will be utilized. We will investigate three candidate approaches for feature selection, which as explained in the following, utilize parameter estimates obtained during different stages of the model-building process. Finally, we apply a reliable clustering algorithm called Walktrap (Pons & Latapy, 2006) to classify individuals according to these features.

One might argue that individuals would be best described along a multidimensional continuum rather than in discrete classes. However, clustering individuals on the basis of time-series parameters aids in arriving at parsimonious models (Ravishanker, Hosking, & Mukhopadhyay, 2010) and thus might be easier to interpret and immediately translate into practice. For example, Yang and colleagues (2014) clustered individuals according to patterns of brain connectivity and found subgroups of individuals diagnosed with early-onset schizophrenia. A specific pattern of effects that emerged in one subgroup related to negative symptoms. In this way, identifying discrete subgroups of individuals with similar temporal patterns may assist in a better understanding of the underlying biological markers relating to specific sets of symptoms or behaviors. Data-driven classification based on dynamic processes will thus help guide hypothesis formation, as well as the development of intervention, diagnostic, and treatment protocols, by revealing underlying patterns of effects for clusters of individuals that would not be revealed by using predefined subgroups (e.g., diagnostic category).

We present here a new approach that (a) arrives at subgroups of individuals (should they exist) entirely on the basis of their dynamic processes and (b) obtains reliable group-, subgroup-, and individual-level dynamic process patterns even in the presence of heterogeneity. All estimates are obtained separately for individuals with no assumptions regarding their distributions. The algorithm presented here, subgrouping within group iterative multiple model estimation (referred to as “S-GIMME”), works from within an SEM framework much like the existing GIMME algorithm (Gates & Molenaar, 2012). The present article is organized as follows. First, we provide information on an example of fMRI data obtained from a sample known to be heterogeneous in their functional neural processes: former collegiate American football and National Football League (NFL) athletes. This example will be used to illustrate aspects of the algorithm. Second, we offer a brief introduction of the original GIMME algorithm, followed by a technical description of the development of S-GIMME that enables classification of individuals according to temporal patterns. Third, Monte Carlo simulations are presented to evaluate S-GIMME and to examine conditions leading to optimal and suboptimal performance. Finally, we discuss the implications, current drawbacks, and future directions.

Empirical data example

American football players are at high risk for head injuries, including concussion. The biomechanics of concussion are known to vary across individuals (Guskiewicz & Mihalik, 2011). For this reason, individuals who have played American football are highly likely to be heterogeneous in their functional neural patterns and thus provide an ideal example with which to demonstrate empirical results obtained with S-GIMME. The data come from a larger study investigating the extent to which the degree of exposure to risk of concussion (i.e., years playing football) related to changes in brain processing. As such, participants in this study were recruited according to the level of exposure to risk of concussion from playing. The final sample contained 31 former professional NFL players who played a minimum of two seasons of professional football (high-exposure sample) and 32 former college football players from Division 1 schools on east-coast United States (low exposure). The football players were matched on demographics, number of concussions sustained, and position played (age in years: M = 58.46, SD = 0.47; all male). Data used in the present project were gathered while participants engaged in a 1-back task, a task often used to assess working memory (Kirchner, 1958). The total number of timepoints for each individuals was 158. Eleven brain regions of interest from the frontal parietal network were used in the present analyses. The frontal parietal network is implicated in adaptive task-level control (Dosenbach, Fair, Cohen, Schlaggar, & Petersen, 2008; Silk et al., 2005). Individuals in other samples experiencing head trauma have been found to be heterogeneous in terms of their brain processes across these regions as assessed with fMRI (Hillary et al., 2011). Full details regarding data acquisition and task can be found in the Supplemental Material. These data will be used throughout the explanation of the S-GIMME algorithm as an illustrative example.

Original GIMME

The original GIMME algorithm (Gates & Molenaar, 2012) provides the basis of the current extension. GIMME obtains reliable group- and individual-level patterns of temporal effects with all effects being estimated uniquely for each individual. GIMME works from within a unified SEM (uSEM; Gates, Molenaar, Hillary, Ram, & Rovine 2010; Kim, Zhu, Chang, Bentler, & Ernst, 2007) framework. Broadly, uSEM is a technique for conducting time-series analysis with SEM. It has been used across various fields in the social sciences, including neuroimaging (e.g., Karunanayaka et al., 2014; Nichols et al., 2013), economics (e.g., Dungey & Pagan, 2000), and social behaviors (e.g., Beltz, Beekman, Molenaar, & Buss, 2013). Two types of effects of interest are simultaneously estimated. First, uSEMs can contain effects representing the influence that the available variables have on each given variable at the next timepoint, much like traditional multivariate or vector autoregression (VAR). Second, uSEMs arrive at the directed (i.e., not correlational) contemporaneous effects of how one variable statistically predicts another variable at the same time, controlling for any lagged or contemporaneous effects.

Three immediate benefits arise from simultaneously arriving at the lagged and contemporaneous effects (Gates et al., 2010). First, including lagged effects prevents spurious effects that often occur if only contemporaneous relations are modeled in the presence of unmodeled lagged relations in the generative model. Second, including the autoregressive (AR) effects enables inference into which of two given variables statistically predicts the other from within a Granger causality framework. In this framework, a variable η₁ is said to Granger-cause a different variable η₂ if η₁ explains variance in η₂ beyond the variance explained in η₂ by its AR term. Granger causality can be tested in this way for lagged or contemporaneous (or “instantaneous”) relations (Granger, 1969). Third, including the contemporaneous effects in the model prevents these effects from erroneously being captured as correlations among errors or as inflated lagged effects. As described by Granger (1969), when data are under-sampled such that observations are collected at a rate slower than the construct under examination, the relations among variables may best be modeled contemporaneously. In fMRI, data are collected on the order of seconds whereas the neural activity they seek to capture occurs on the order of milliseconds. As such, contemporaneous relations generally contain the information regarding underlying neural processes (Smith et al., 2011). It is important to note that nothing is lost when allowing for the possibility of both lagged and contemporaneous effects when using a reliable search procedure.

The uSEM is formally defined as follows:

$${\eta }_t=A{\eta }_t+\Phi {\eta }_{t-1}+{\zeta }_t,$$ (1)

where A is the p × p matrix of contemporaneous effects for p variables and contains a zero diagonal; Φ is the matrix of lagged effects with AR effects along the diagonal; η is the manifest time series (either for a group or individual in this general formula); and ζ is the residual for each point in time t. Please note that while observed variables are used throughout the present implementation, extension to latent variables is feasible. The subscript t-1 indicates the values at the prior timepoint. Henceforth, “effects” will be used as a general term to indicate these lagged and contemporaneous effects (also termed “paths,” “edges,” or “connections” in other literature). Figure 1 presents a graphical depiction of uSEMs using a traditional SEM path diagram and introduces a conceptually equivalent yet simpler depiction that will be used for the remainder of the article. Note that the total number of variables is twice the number of original variables, representing the p original variables and the p variables at a lag of one.

Figure 1.

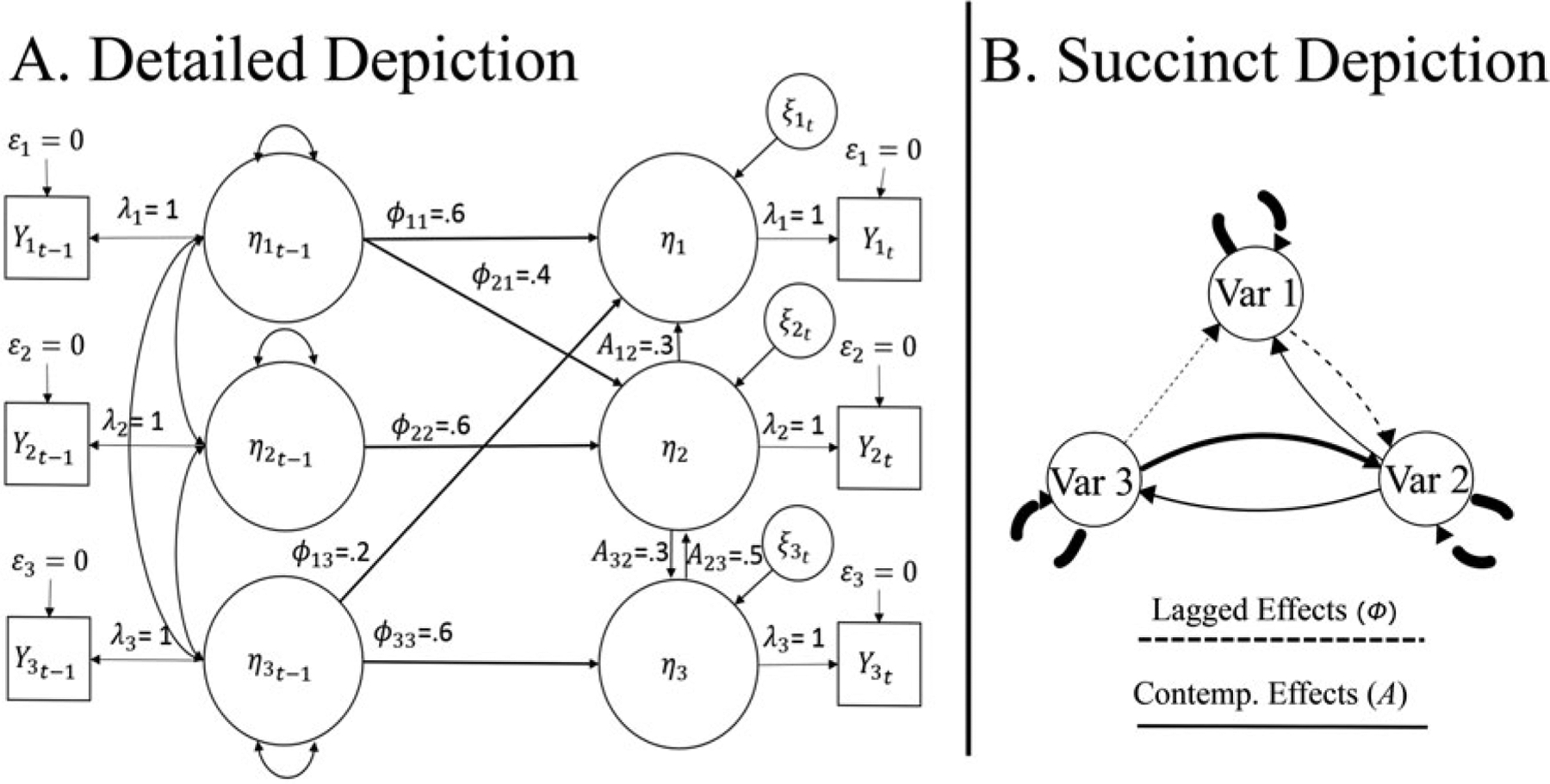
Depiction of unified SEM model. (A) Detailed and (B) succinct depictions of identical uSEM models. In (A), ε indicates measurement errors, λ the factor loadings, η the variables to be modeled in the structural equation, and ζ the regression errors. Values next to the parameters ϕ and A indicate the weights for the respective lagged and contemporaneous effects included in the model. In (B), the path width reflects weights, the measurement model is omitted, “Var”replaces η to reflect “Variable,”and lagged effects are dashed lines rather than including the lagged variables explicitly.

As written in Equation (1), the uSEM can be applied at the individuals’ level or at the group level by vertically concatenating individuals person-centered multivariate time series. Since it is highly implausible to expect individuals to have identical models, concatenating across individuals to arrive at one group model is not a recommended approach (Molenaar, 2004). For this reason, the GIMME algorithm estimates all models at the individual level throughout a model search procedure that culminates in individual-level models and estimates. However, an important first step utilizes information for all individuals in the sample to find effects that replicate across individuals. Prior work has demonstrated that using effects that exist consistently across individuals helps to detect signal from noise and that using group-level effects as a prior greatly improves the recovery of the directionality of effects at the individual level. As described briefly in the following, GIMME arrives at a group-level structure, or pattern of effects, that describes the majority of individuals in the sample; this process is done in a manner that is not subject to outliers as seen in other aggregating approaches. Full details can be found in Gates and Molenaar (2012); we also provide additional information regarding estimation of uSEMs in the Supplemental Material of the present article.

The group-level search is guided by the use of modification indices (MIs), related to Lagrange multipliers (Engle, 1984), which are scores that indicate the extent to which the addition of a potential effect will improve the overall model fit (Sörbom, 1989). As MIs are asymptotically chi-square distributed, significance can be directly tested for each MI. It has previously been suggested that models built using MIs need to be replicated to demonstrate consistency of effects (MacCallum, 1986). As such, GIMME only includes effects at the group level that exist across individuals. The GIMME algorithm begins by counting, for each effect, the number of individuals whose models would significantly improve should that effect be freely estimated. This results in a count matrix, and the element from the constrained set that has the highest count is selected. Due to the testing of MIs across all individuals, the criterion for significance uses a strict Bonferroni correction of .05/N, where N = the number of individuals. This starkly contrasts methods that identify effects to include in the group model by looking at the average of effects, as the GIMME approach cannot be influenced by outlier cases and is impervious to sign differences (such as large absolute values for all individuals that are negative for some individuals and positive for others). In fact, information regarding the sign of the weight is not used in the group-level search—here, only the absolute magnitude is considered (although the sign is used in the following for subgrouping). Should there be a tie in the count of significant MIs then the algorithm selects the element with the highest sum of MIs taken across all individuals.

This brings us to another important point that differentiates model searches conducted from within the uSEM framework from other search procedures that have been previously conducted using MIs. The MIs for candidate paths in the A matrix will be equivalent across the diagonal if no other effects have been estimated. As an example, it is well understood that the simple regression η₁ = Bη₂ + ζ will have the same standardized B weight as η₂ = Bη₁ + ζ. This equivalence will be seen in the MI matrix with the MIs relating to the prediction of η₁ from η₂ having the same value as the MI for the matrix element corresponding to η₂ being predicted by η₁ if there are no other predictors of either variable. However, when the AR effects are freed for estimation in the Φ matrix prior to conducting the model search, the equivalences across the diagonal of the A matrix disappear and thus do not encumber the model search procedure. Controlling for these AR effects, the estimate of any element in the A matrix will now be unique. An additional benefit is that Granger causality testing, described in the preceding, can immediately proceed by including the AR effects. By starting the model search with the AR effects freed for estimation (which is often appropriate in many lines of research), one can capitalize on the fact that MIs take into account the relations that already explain variance in a given variable when arriving at the expected change in the model fit should a given effect be freed (see Gates et al., 2010 for further details).

The algorithm iteratively continues until there are no effects that would significantly improve the majority of individuals’ models. What constitutes the majority in a meaningful sense can vary from researcher to researcher. While 51% would technically be the majority, here we use a stricter cutoff of 75%. This stricter cutoff serves two purposes. First, prior work has shown that this percentage provides an optimal trade-off for arriving at group-level models that truly describe the majority of individuals in the presence of noise (Gates & Molenaar, 2012; Smith et al., 2011), and this percentage is a common threshold used when attempting to identify an effect that exists for the “majority” from individual-level results in fMRI studies (e.g., van den Heuvel & Sporns, 2011). Second, for the present goal of classification, having a strict denotation of what constitutes the majority will provide a greater number of candidate individual-level effects upon which to cluster individuals. Specifically, a meaningful subgroup could be a large portion of the sample (e.g., 50%) and could erroneously drive the group-level search if we employed a looser criterion for group-level selection of effects. One could also argue in favor of obtaining a set of parameter values that are valid for 100% of the subjects (e.g., Meinshausen & Bühlmann, 2015). As described in the preceding, there might not be one model that is valid for all individuals. Still, one might argue in favor of using this strict criterion during this stage of the model building, knowing that individual-level paths will be added later. This likely would not be useful since the ability to detect effects in the presence of the expected noise in fMRI studies has been shown to be less than 100% even for the best methods (Smith et al., 2011). Hence, a criterion of 100% seems too strict and would likely result in numerous missed effects at the group level, thus reducing the potential benefits from this approach.

The bold black lines in Figure 2 depict the group-level results obtained on our empirical example. There were 12 group-level paths in addition to the AR effects. All of the paths were contemporaneous, which is expected given the low temporal resolution of the fMRI signal (Granger, 1969) and is consistent with previous findings from data simulated to emulate fMRI data (Smith et al., 2011). These group-level paths indicate a temporal pattern of relations that describe this sample and thus may be generalizable to the greater population of former U.S. football players.

Figure 2.

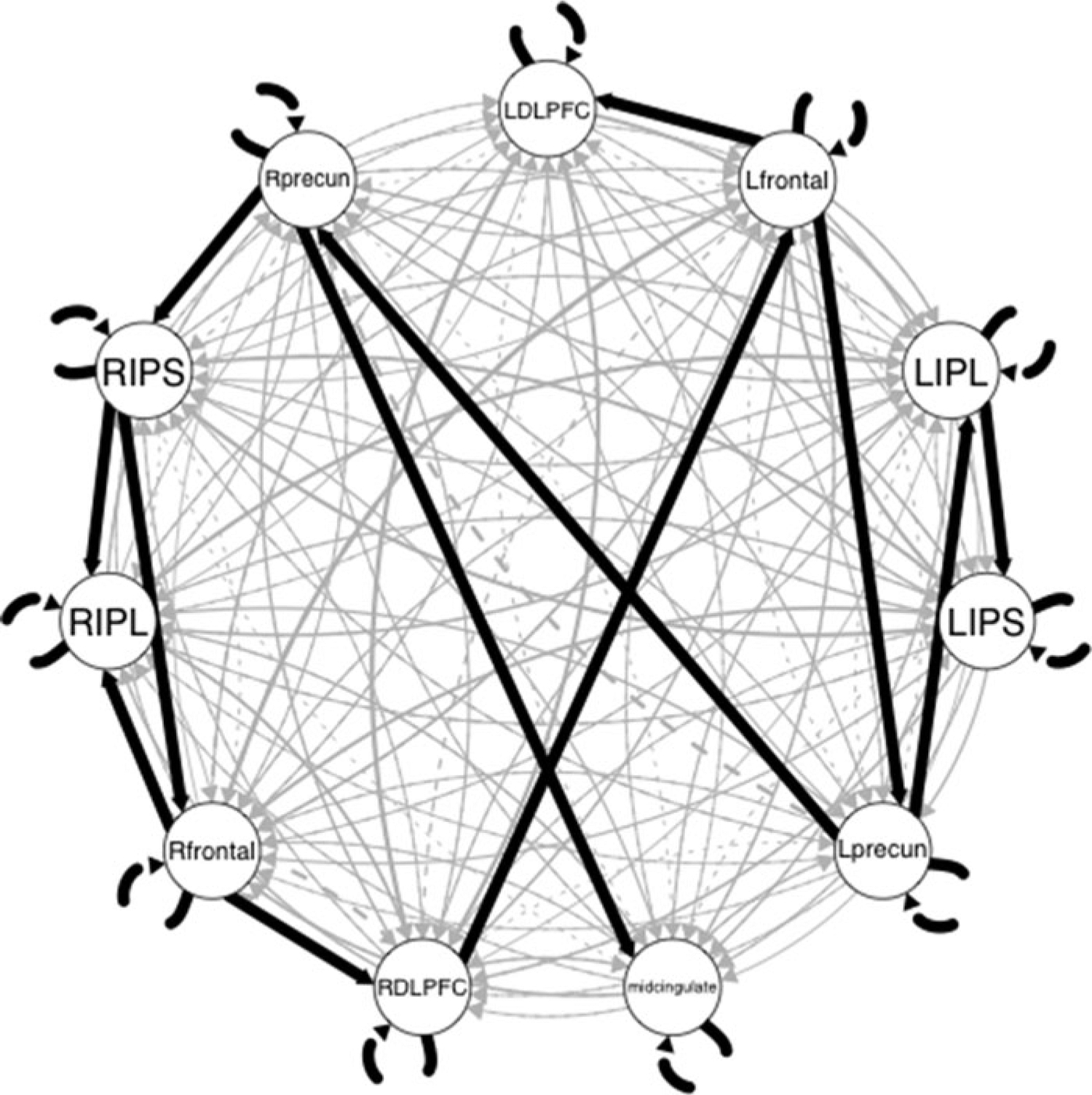
Original GIMME results obtained from the empirical example. Black lines indicate group-level effects; gray lines indicate individual-level effects. Line width corresponds to proportion of individuals having the effect. Dashed lines are lagged; solid lines are contemporaneous relations.

Using the group-level paths as a prior, the original GIMME then conducts individual-level searches. The individual-level searches are also guided by MIs with effects being iteratively selected until an excellent-fitting model is obtained as indicated by commonly used fit indices: RMSEA, SRMR, NNFI, and CFI. Two of the four must be excellent to meet the criteria to stop searching for additional paths, with “excellent” being ≤ .05 for the RMSEA and SRMR and ≥ .95 for the NNFI and CFI (Brown, 2006). It should be noted that these fit indices assume independence of observations, an assumption that is violated here since each row is sequentially dependent on the previous timepoint. Violation of this assumption does not render these fit indices useless for these data. Prior work has demonstrated that these fit indices are able to consistently identify excellent uSEM model fits when the models are in fact the generative model (Gates & Molenaar, 2012; Gates et al., 2010). Stopping the search according to fit indices rather than continuing even if MIs are still significant produces more parsimonious models. More important, it prevents the modification search from capitalizing on chance, a risk that increases the longer the search continues (MacCallum, Roznowski, & Necowitz, 1992).

The grey lines in Figure 2 depict the individual-level paths obtained from using the original GIMME algorithm on the data example from the former U.S. football players. Despite the presence of a number of group-level paths, additional paths were needed at the individual level in order to explain variability in brain regions using other brain regions for each person. This highlights the high degree of heterogeneity and need for person-specific models that allow for unique effects in addition to the individual-level weight estimates of group-level effects.

Subgroups within GIMME

As mentioned in the preceding, starting with some known priors (in this case, the group-level paths) greatly decreases errors in detection of true effects at the individual level of analysis. It follows that if group-level information can help guide individual-level searches, then subgroup-level information can further refine the search for individuals’ effects. We thus extend the approach of the data-driven group-level pattern selection to subgroups prior to arriving at individual-level models. First, we must identify the subgroups of individuals that have similarities in their temporal patterns. This requires using (a) the features that are useful and meaningful as well as (b) an optimal approach for classification.

Feature selection

Feature selection represents a critical decision point for any cluster analysis approach. As such, much work has been done to investigate optimal features for clustering of time-series analysis (Liao, 2005). Since we aim to cluster individuals on the basis of dynamic processes, we must identify the most relevant and useful features with which to do so. A few pieces of work point us in the direction of features that may satisfy this. First, the temporal features used would have to be reliable and accurately reflect the process under study. For fMRI research, it has been shown that relations among brain regions are best captured with contemporaneous effects, with lag-0 correlation estimates reliably recovering true effects (Smith et al., 2011). The first approach uses these lag-0 correlation matrices as features with which to identify the degree of similarity among individuals. Since lagged information has been shown to also exist in fMRI literature (Gates et al., 2010; Goebel, Roebroeck, Kim, & Formisano, 2003), our second feature-selection approach utilizes a combined lag-1 and lag-0 correlation matrix. A final and highly reliable set of features that describe individuals’ temporal processes is obtained from GIMME during model selection. We hypothesize that using features available within the search procedure could provide more reliable subgroups than using features available prior to subgrouping.

We explore here three methods for arriving on model features with which to subgroup individuals: lag-0 cross-correlation matrices; block-Toeplitz (lag-1 and lag-0) correlation matrices; and clustering using information during the GIMME model search procedure (S-GIMME). As noted in the introduction, two groups have previously clustered individuals using features obtained from analysis of fMRI data (Gates et al., 2014; Yang et al., 2014). The features used for these approaches are not appropriate here. Gates and colleagues used the results from GIMME and conducted a community-detection algorithm on a dichotomized matrix depicting similarity in temporal patterns among individuals. That article introduced a novel approach for arriving at the optimal threshold with which to dichotomize the relations. The present approach will take advantage of developments in community detection that improve upon the reliability of results for weighted matrices. Thus we do not include Gates and colleagues’ (2014) approach here since the use of unweighted graphs is already vastly improved upon with the use of weighted algorithms. Yang and colleagues (2014) clustered individuals according to the lag-0 component scores found in ICA. Since there is no analogue between this and the GIMME approach, we do not include ICA for feature selection.

Feature selection approaches tested for comparison

The lag-0 approach is commonly referred to as “functional connectivity” in fMRI literatures (Friston, 2011). The cross-correlation matrix r_within at a lag of zero represents the contemporaneous relations among the variables (brain regions) for a given person, with each element in r_within indicating the correlation estimate for two given variables. These lag-zero r_within matrices are a predominant method used in fMRI research, with graph theory measures that describe brain processes often derived from these types of matrices (Rubinov & Sporns, 2010). While a lag-0 correlation matrix presents an appropriate comparison as it is the current standard, we also wished to test a cross-correlation matrix that includes information regarding a lag of one (i.e., a lag-1 approach). In addition to including information known to exist in an fMRI signal, this approach better aligns with the information used in S-GIMME, which is both lagged and contemporaneous. Here, the r_within matrix described in the preceding contains not only the contemporaneous lag-0 correlations, but also the lag-1 correlations. This is in a block-Toeplitz framework, which is a block-diagonal matrix with contemporaneous effects on the diagonal and lagged effects on the off-diagonal.

For these correlation-based approaches, we first generate N correlation matrices of the variables (r_within,i) for each i from i = 1…N individuals. These are then used to generate a similarity matrix (r_between) with each element indicating how similar each individual is to each other individual. To arrive at this r_between, each individual’s correlation matrix is vectorized and only the unique m = [(p − 1)(p)]/2 elements are retained (i.e., those in the strictly lower triangle matrix for the lag-0 matrices and the unique lag-1 and lag-0 correlations of the block-Toeplitz matrices). These vectors are then Fisher transformed and used to arrive at correlation coefficients for how each individual’s transformed cross-correlations relate to every other individual’s transformed cross-correlations. This results in the N × N similarity matrix r_between separately for both of the cross-correlation feature selection approaches described here. While an intuitive approach, using cross-correlation matrices may not provide a satisfactory signal-to-noise ratio since it does not take into account indirect effects or third-variable arguments (Marrelec et al., 2006; Zalesky, Fornito, & Bullmore, 2012). Hence, it is expected that the S-GIMME approach will outperform these commonly used methods for quantifying dynamic processes.

Feature selection used in S-GIMME

We introduce an approach for feature selection, referred to as the S-GIMME approach here, that is based on information available following the initial group-level search. This leads to an algorithm where the classification is integrated within the data-driven model selection procedures at the group and individual levels, thereby controlling for indirect effects that have surfaced as well as individual-level effects that may arise. Here, the features that are of the greatest utility in describing individuals’ processes drive subgroup identification. Specifically, as noted in the preceding, both the patterns of effects and the sign of effects have been shown to vary meaningfully across individuals. Hence, we utilize estimates at the individual level of the expected parameter change (EPC) associated with each modification index and the B weights obtained for each individual’s group-level paths. The value of the EPC indicates the expected weight for a given parameter should it be estimated in the current model, and it has been promoted as a useful measure for model modification (Kaplan, 1991). EPC and B estimates for effects have two characteristics that make them particularly useful for classifying individuals on the basis of their temporal processes. One, the EPC and B weights are normally distributed and are provided along with standard error estimates, enabling straightforward identification of significance. Two, while MIs are always positive, EPC and B values take negative and positive values. Thus, we can utilize this information to take into account differences in sign between two given individuals in addition to the significance of effects.

To arrive at the similarity matrix using EPC and B estimates, we first identify which effects are significant for each individual according to both the corresponding EPC for each candidate effect (i.e., possible effect after the group-level model) and B weight for each group-level path in the uSEM. The level of significance for the EPC elements is Bonferroni corrected using a strict criterion of .05 divided by the number of unique lagged and contemporaneous elements in the block-Toeplitz correlation matrix. The rationale behind the strict criteria for EPC elements is that the resulting similarity matrix is simultaneously utilizing information across all candidate paths, and some of these paths will be significant for that individual simply by chance. Next, the signs of the significant EPCs and B are noted. The similarity matrix is generated by counting, for each pair of individuals, the number of candidate effects (EPCs) and estimated effects (Bs) that are both significant and in the same direction (i.e., positive or negative). This results in an N × N similarity matrix (s) where s_{i j} indicates a count of the number of candidate and estimated paths that are significant and in the same direction for each unique pair of individuals i and j. The lowest number in this matrix is then subtracted from all elements to induce sparsity.

Classification approach

Hierarchical cluster analysis has long been used in the social sciences to cluster individuals into subgroups according to similarities. The difficulty with cluster analysis is that oftentimes an arbitrary decision must be made regarding the optimal cut-point, or place on the dendrogram to stop splitting clusters (or combining, when using agglomerative approaches that iteratively combine smaller subgroups into larger ones). Without a stopping point, all individuals might be placed into a cluster by themselves (or everyone in one group). This would result in the same number of clusters as individuals, which is not the intended goal.

A stopping mechanism called “modularity” has been introduced within graph theoretic literatures (Newman, 2004). Modularity is a score that indicates the degree to which similarity with others within a cluster is high relative to the degree of similarity between clusters. The optimal cut-point in hierarchical clustering is the one with the maximum modularity. Using a quantitative approach for arriving at a cut-point obviates the need for the researcher to decide how many clusters to allow. Community detection, a class of algorithms for clustering, often uses modularity, and a proliferation of algorithms has emerged in the years since modularity was first introduced (see Fortunato, 2010 and Porter, Onnela, & Mucha, 2009 for extensive reviews). From the numerous community-detection options available, we must identify which algorithm to utilize on the two correlation similarity matrices described in the preceding for feature selection (i.e., cross-correlation matrices obtained prior to model search) and the sparse count similarity matrix from the third method (i.e., during the model selection procedure). Walktrap has emerged as a community detection approach that uniquely performs optimally for both correlation and count matrices (Gates, Henry, Steinley, & Fair, in press; Orman & Labatut, 2009). Additional details regarding Walktrap can be found in the Supplemental Material.

Model building within S-GIMME

While we test two other approaches for clustering of time-series data (i.e., the cross-correlation matrices obtained prior to model building), the final S-GIMME algorithm utilizes the third feature-selection approach described. Having arrived at subgroups following the group-level search, S-GIMME searches for subgroup-level effects in a similar manner to the group-level search (see Figure 3). While the significance and sign of the group-level estimates are used to inform subgroup classification, these paths are always considered to be group-level paths (i.e., they do not become subgroup-level paths on the basis of sign). Beginning with the group-level effects as a prior, S-GIMME identifies the effect that, if estimated for everyone in the subgroup, would improve the greatest number of individuals’ models. It must also improve the majority of individuals’ models. This effect is then estimated for everyone in the subgroup, with each effect estimated uniquely for each individual and not influenced by others in the group or subgroup. As with the group-level search, the procedure stops adding effects to the models once there are none that will improve the model for the majority of individuals in that subgroup, which is 51% here since the subgroups might be small. Finally, using the group-and subgroup-level paths as priors, S-GIMME searches for any additional paths that are needed to best explain each individual’s temporal process. Formally, S-GIMME identifies the relations among the p observed variables of length T (with t = 1, 2, … T ranging across the ordered sequence of observations):

$${\eta }_{i,t}=\left(A_i+A_{i,k}^s+A_i^g\right){\eta }_{i,t}+\left({\Phi }_i+{\Phi }_{i,k}^s+{\Phi }_i^g\right){\eta }_{i,t-1}+{\zeta }_{i,t},$$ (2)

where, as before, A is the p × p matrix of contemporaneous effects among the p variables (with a zero diagonal), Φ is the p × p matrix of lagged effects where AR effects are found on the diagonal, and ζ is the p-variate matrix of errors for the prediction of each variable’s activity across time. The superscripts s and g for the parameters indicate that the matrix has the structure of effects consistent across the kth subgroup and entire group, respectively. Note that subgroup identification k does not change across time but does differ across individuals, with the possibility of all individuals being in the same subgroup (i.e., there are no subgroups). Subscript i indicates individual, which in the case of the parameters indicates individual-level estimates. All parameters are estimated for each individual separately.

Figure 3.

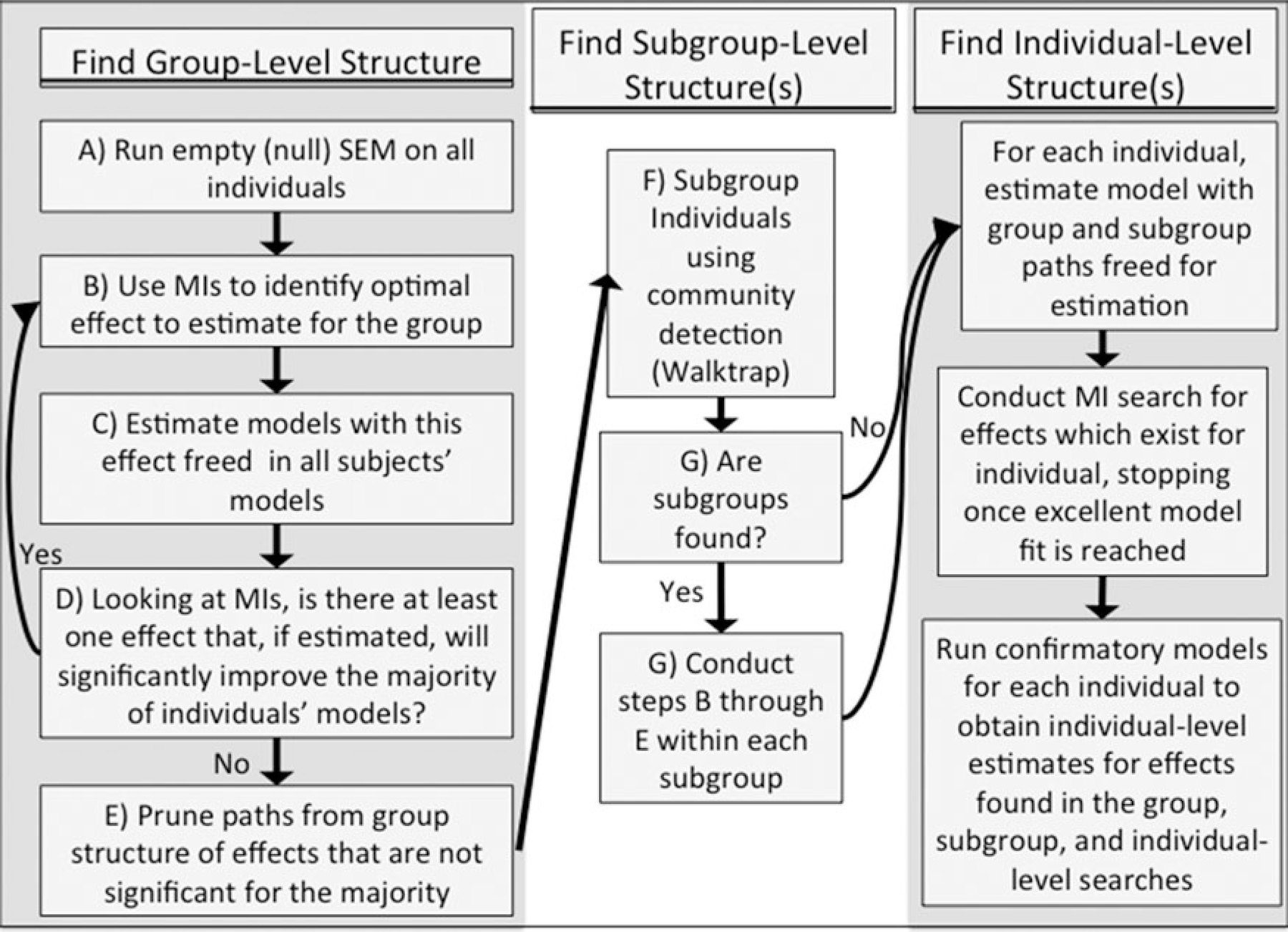
Schema for subgrouping within GIMME (S-GIMME).

Figure 4 visually conceptualizes the modeling approach used on fMRI data. In Figure 4, part (c), the black lines indicate group-level effects that are identified in S-GIMME and are estimated for all individuals. Please note that paths can emerge during the subgroup level that exist for all subgroups. Since everyone in the sample has the path estimated, it is considered a group-level path. Next, the subgroups are obtained using the EPC and B estimates to arrive at an N × N similarity matrix (Figure 4, part (d)) that is then subjected to the community-detection algorithm Walktrap. Two subgroups were found in this empirical example, with one containing 36 individuals and the other having 25. The models for two individuals in the entire sample did not achieve convergence and are removed from this count. Following subgroup identification, subgroup-level paths are obtained uniquely for each subgroup (Figure 4, part (e)). One subgroup found seven subgroup-specific paths whereas the other obtained three. Using the group-and subgroup-level paths as priors, a semiconfirmatory search is then conducted to arrive at individual-level paths that are needed to improve that individual’s model fit (Figure 4, part (f)). As can be seen by the grey lines depicting individual-level paths, there was a high amount of heterogeneity. Finally, confirmatory models are run separately for each individual to arrive at individual-level estimates for the group-, subgroup-, and individual-level effects.

Figure 4.

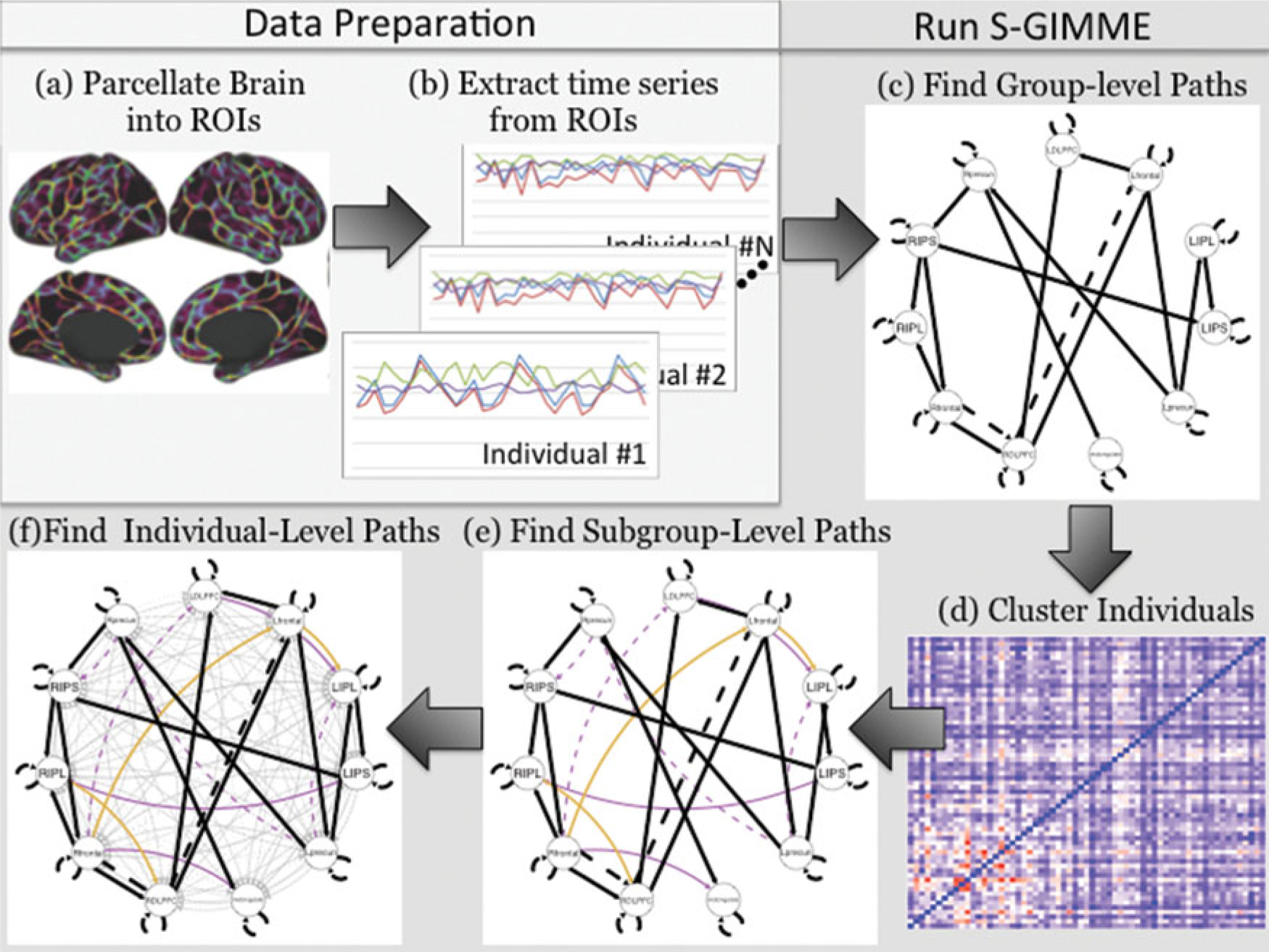
Steps for obtaining S-GIMME models with empirical fMRI data. (A) and (B) depict the data processing steps to extract time series for each brain region of interest. Steps (C) through (F) automatically occur within the S-GIMME algorithm: (C) illustrates identification of group-level effects; (D) presents the similarity matrix that was applied to Walktrap for clustering individuals into subgroups; (E) presents the subgroup-level effects; and (F) depicts the final models containing group-, subgroup-, and individual-level effects.

Monte Carlo simulation and evaluation criteria

We conduct a series of simulations to evaluate the ability of the approaches to recover the subgroups and the data-generating model. First, we provide a description of the data simulations and conditions. Next, we describe the analyses and criteria that will be used to test performance.

Data simulations

Data simulations align with parameters seen in empirical fMRI data. As such, the S-GIMME algorithm is evaluated here along three criteria commonly of interest in fMRI studies: (a) sample sizes of 25, 75, and 150 in terms of number of individuals (N); (b) number of subgroups (K) ranging from 2 to 4; and (c) inequality of the subgroup sizes (h). While the former two conditions may seem rather intuitive, the third one, inequality of cluster size, is motivated by the inability of some unsupervised classification algorithms to identify the appropriate number of subgroups when the subgroup sizes differ (Lancichinetti & Fortunato, 2011; Milligan, Soon, & Sokol, 1983). Here, h is defined as the percentage of the total sample that is composed of the largest group minus the percentage of the sample that is the smallest group. We used two levels: equally sized groups (h = 0) and one group comprising 50% of the sample (not applicable for K = 2; h = .25 for K = 3, and h = .34 for K = 4).

The pattern of group- and subgroup-level effects across the three levels of K are depicted in Figure 5. In line with our empirical example, the number of variables (or brain regions) here is 10 across all simulations. This number also aligns with simulations of fMRI data generated by Smith and colleagues (2011). Prior work that placed participants into subgroups a priori has found that the average number of individual-level paths ranged from one to five across four subgroups (Nichols et al., 2013). This same study, which used seven brain regions, found that some subgroups had up to four subgroup-level paths in addition to those found in the group level. The present empirical example used herein found three subgroup-level paths for one subgroup and seven for the other (see Figure 4, part (e)). Individuals here had, on average, six paths in addition to paths found for the group and their subgroup (SD = 1.5). This is a higher level of heterogeneity than sometimes observed in fMRI studies but is expected given the heterogeneity seen in symptoms and biomechanics underlying brain processes for those repeatedly exposed to risk for concussion (Guskiewicz & Mihalik, 2011). Following from this information, we generated data to have 10 group-level paths, six subgroup-level paths, and four individual-level paths (see Figure 5).

Figure 5.

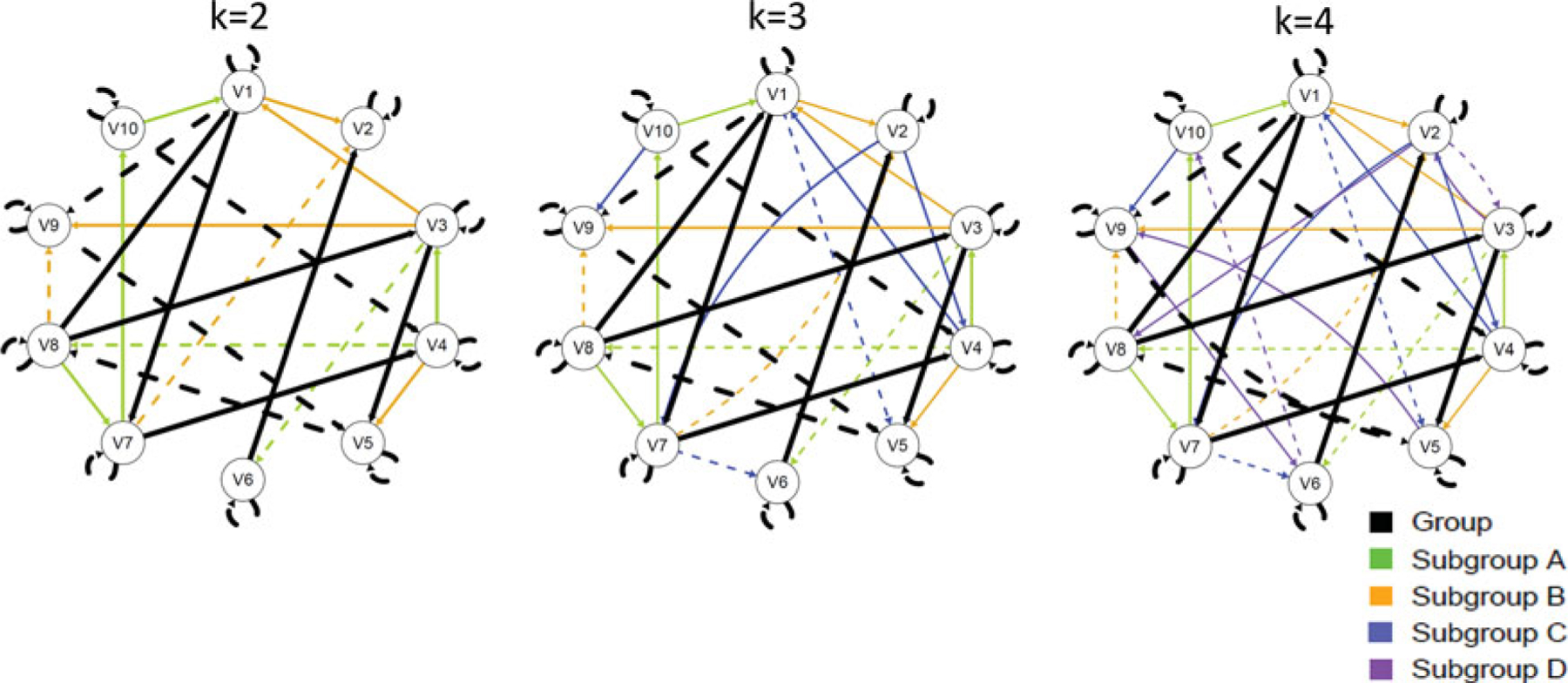
Temporal patterns of effects for Monte Carlo simulations. K above each graph indicates the number of subgroups in the data simulation. Line width corresponds with proportion of individuals in that condition who have a given path.

Algebraic manipulation of Equation (2) provides the data-generative model:

$${\eta }_{i,t,k}={\left(I_p-\left(A_i+A_{i,k}^s+A_i^g\right)\right)}^{-1}\left({\Phi }_i+{\Phi }_{i,k}^s+{\Phi }_i^g\right){\eta }_{i,t-1}+{\left(I_p-\left(A_i+A_{i,k}^s+A_i^g\right)\right)}^{-1}{\zeta }_{i,t}.$$ (3)

Using results seen in fMRI literature (e.g., Hillary et al., 2011) and values used in prior fMRI simulations (e.g., Gates et al., 2014), the values for the AR effects (i.e., the diagonal of the Φ^g matrices) were set to be .6 for all individuals. Path weights for off-diagonal elements in Φ the matrix were −.5, with the contemporaneous values being .5. While variability in estimates would be expected in a sample of individuals, prior work has demonstrated that GIMME is robust to fluctuations in simulation parameters that have a standard deviation as large as .3 in the parameters (Gates & Molenaar, 2012). Since we utilize only significant values here to cluster and arrive at final models, these fluctuations are presently not a point of interest. In addition to the group and subgroup paths, four paths were randomly added to the Φ and A matrices for each individual that followed this pattern of weights. This offers a high level of individual-level paths. The random paths were selected from the remaining paths that were not used in the group or subgroup-level paths. Model errors were generated to be white noise (N(0, 1)). A total of 250 observations were simulated for each individual, of which the first 50 were discarded to remove deviations due to initialization. This number of observations is at the lower end of the range of observations expected in fMRI studies (typically from 150 to 600 observations per person).

The data and results can be found here: https://gateslab.web.unc.edu/simulated-data/heterogeneous-time-series/.

Omitted variable analysis

The present article focuses on uSEM conducted with observed variables and does not allow for correlations or bidirectional relations among variables. This inherently presupposes that all variables needed to appropriately model the data are contained in the data provided. In many cases, this assumption may not be met. The topic of omitted causal variables is widely discussed in fMRI-related texts (e.g., Pourahmadi & Noorbaloochi, 2016) as well as literature on other causal graph search approaches (Spirtes, Glymour, & Scheines, 2000) and Granger causality (Eichler, 2005, 2010; Lütkepohl, 1982), which, as noted in the preceding, is the approach used here to evaluate temporal effects.

One option to circumvent the possibility of omitted causal variables would be to allow for latent variables that reflect underlying constructs (in the case of brain data, neural networks) or common causes. Complicating this option, it is well known that individuals likely differ in their dynamic processes as described using latent factors for many temporal processes (Molenaar & Nesselroade, 2012) including the functional organization of brain regions into networks (Wang et al., 2015). The idiographic filter introduced by Nesselroade and colleagues (Nesselroade, Gerstorf, Hardy, & Ram, 2007) circumvents this by allowing for individuals to have different estimates relating observed variables to latent constructs. Unfortunately, it is recommended that researchers hold the temporal effects among the latent variables constant (Molenaar & Nesselroade, 2012), which undermines the focus of the present algorithm, which seeks to arrive at individual-level directed temporal patterns and estimates among (latent or observed) variables.

Ancestral graphs (Richardson & Spirtes, 2002) also circumvent the spurious relations that can surface due to unmodeled common causes without the use of latent variables. This is done by marginalizing and conditioning on the original causal model. It is important to note that in this transformed model the absence of a relation between two variables indicates independence. Path diagrams that (a) only allow for one directed or bidirected (correlational) relation for a given pair of variables and (b) do not allow for “backward” directions (i.e., no feedback loops) could be considered ancestral graphs. While a promising approach to circumvent spurious results due to omitted variables, these properties prevent further exploration of ancestral graphs in the present modeling approach because the current GIMME search would always favor correlation over directed arrows since more variance is explained. In addition, feedback loops are expected in brain imaging data (even among the contemporaneous relations), and thus ancestral graphs may not always depict the underlying biophysiological process being examined.

Given the importance of the topic of omitted variables, we conducted auxiliary analyses to identify the extent to which variable omission may have a deleterious effect on the recovery of paths. One might expect an increase of false positives since the lack of a common cause variable for two given variables may induce a spurious directed connection that is not in the generative model. Given space constraints, we selected one optimal condition for these analyses: the condition with 150 individuals, 2 subgroups, and equal subgroup sizes. The rationale for choosing the condition for which methods will likely perform optimally is to be able to immediately identify the effect of omitted variables on S-GIMME without other confounds. Of course, any decrease in recovery in this optimal setting would perpetuate down to the other conditions. For this analysis, we iteratively removed one variable at a time and ran S-GIMME across the 100 repetitions in this condition. Since each variable has differing degrees of relations with other variables in the system, running the analysis with each variable removed allows for examination of the average expected decrease in performance taken across all possible omissions of one variable.

Hubert-Arabie adjusted Rand index to evaluate reliability in subgroup detection

The Hubert-Arabie adjusted Rand index (ARI_HA; Hubert & Arabie, 1985) has been presented as an optimal metric with which to evaluate the accuracy of the subgroup detection. In particular, a Monte Carlo simulation study demonstrated that the ARI_HA is fairly consistent across conditions that varied in terms of the density of similarity among individuals, the number of individuals, and the number of clusters (Steinley, 2004). The ARI_HA provides a strict assessment of correct placement of individuals into their subgroup by accounting for chance placement of individuals. Formally,

$$AR{I}_{HA}=\frac{\left(\begin{array}{c}N\\ 2\end{array}\right)(a+d)-[(a+b)(a+c)+(c+d)(b+d)]}{{\left(\begin{array}{c}N\\ 2\end{array}\right)}^2-[(a+b)(a+c)+(c+d)(b+d)]},$$ (4)

where each pair of individuals contributes to the count for either a, b, c, or d. The value a indicates the number of pairs correctly placed in the same community when they were in the same community for the “true” generative algorithm. Both b and c indicate pairs placed in the wrong communities, with the former indicating individuals that are truly in the same subgroup but were placed in different ones and the latter a count of the number of pairs placed in the same community but truly belonging in different ones. Finally, d indicates the count of pairs that were correctly placed in different communities. ARI_HA has an upper limit of 1, which indicates perfect recovery of the true subgroup structure. Values at or greater than 0.90 can be considered an indication of excellent recovery, with values at or over 0.80 being good recovery, values equal to or over 0.65 being moderate, and under 0.65 indicating poor recovery (Steinley, 2004).

Ramsey indices to evaluate recovery of temporal patterns of effects

The Ramsey indices are outcome measures used to evaluate accurate path recovery. They rely on counts of the number of (a) paths and (b) directions of paths in the true and fitted models. The four indices are termed here, “Path Recall,” “Path Precision,” “Direction Recall,” and “Direction Precision” (Ramsey et al., 2011). “Recall” indicates the proportion of paths or directions recovered in the fitted model that exist in the true model. This measure assesses the algorithm’s ability to find relations that do exist, but does not take into account the presence of false positives, or phantom paths that were recovered but do not exist in the true generative model. For this reason we also use “precision,” which indicates the ratio of true paths (directions) recovered in the results to the total number of paths (directions) that exist in the recovered model. With these indices, we assess the recovery rates of true and false relations.

Effect sizes

Cohen’s d is used to quantify the effect sizes for comparisons between the methods and the conditions, which is preferred over significance testing due to the multiple tests as well as the high power. Conventional interpretations of effect sizes are followed, with values of 0.20, 0.50, and 0.80 indicating small, medium, and large effect sizes, respectively (Cohen, 1988).

Monte Carlo results

Subgroup recovery

Across all conditions, classifying individuals during model selection (i.e., S-GIMME) arrived at the true subgroup classification at higher rates (94%) than classification prior to model selection with either the lag-0 (66%) or lag-1 (65%), with effect sizes for the difference aggregated across conditions being large when compared against the lag-0 (d = 1.30) and lag-1 approach (d = 1.32). All approaches did share some similar features. Specifically, the recovery rates decreased as sample size decreased, as the number of subgroups increased, and as the subgroup allocation became unequal. However, throughout all conditions, the S-GIMME algorithm outperformed the cross-correlation feature selection approaches.

Looking across sample size for equally sized groups (top panel of Figure 6), the S-GIMME method for feature selection nearly perfectly recovered the true subgroup pattern across all sample sizes and number of subgroups tested. As N decreased, S-GIMME markedly outperformed the correlation-based methods, with d = 1.42 for the aggregate difference between the cross-correlation and S-GIMME approaches for N = 25 with equally sized subgroups. In fact, the S-GIMME method performed excellently at each level of N when equal subgroup sizes were present, with ARI_HA averaging 0.94 across the conditions (see Supplemental materials for average ARI_HA and standard deviations for each condition).

Figure 6.

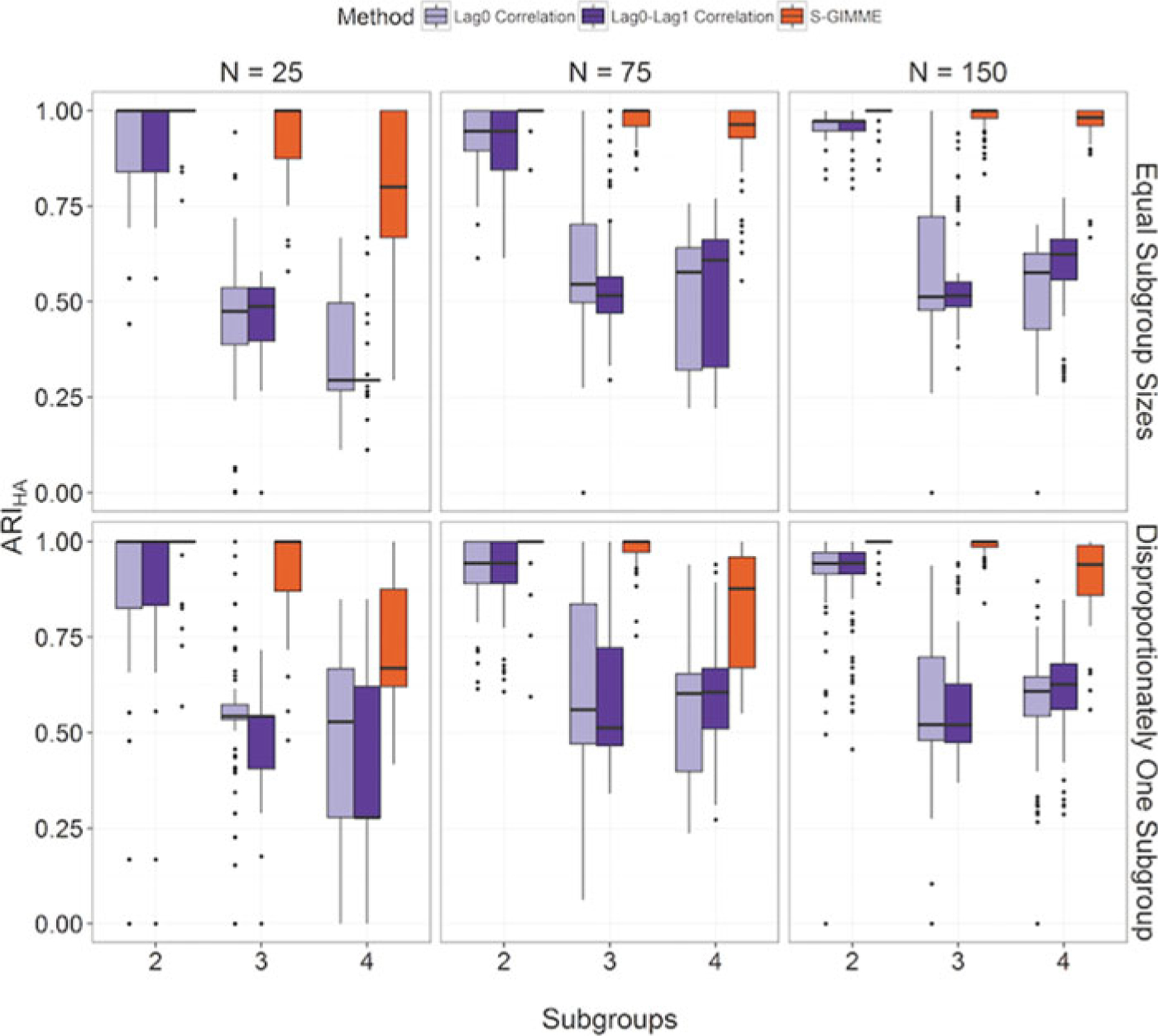
Accuracy in classification. Depiction of accuracy in correct subgroup designations across the conditions as assessed by the Hubert-Arabi adjusted Rand index (ARI_HA). N indicates total number of individuals simulated in condition; “Lag0 Correlation” and “Lag0-Lag1 Correlation”refer to classification prior to GIMME cross-correlation matrices at lag-0 and lag-1, respectively; “S-GIMME”refers to classification occurring during GIMME model search procedure (S-GIMME) using expected parameter change and B estimates. S-GIMME outperformed classifying prior to model search using cross-correlation matrices.

The largest difference in performance for the correlation-based versus S-GIMME methods occurred for equal subgroup sizes in the N = 25 and k = 4 condition, which had a very low average ARI_HA of .36 for lag-0 and .33 for the lag-1 correlation-based methods. This highlights a problem of much interest in the community-detection literature: techniques for unsupervised classification often fail to recover small subgroups (Lancichinetti & Fortunato, 2011). Walktrap, however, has been found to be uniquely able to recover small subgroups (Gates et al., in press) and was used for all clustering in the present article. Here, the S-GIMME method had an average ARI_HA of 0.80, which is considered good by standard cutoff values (Steinley, 2004). There was a large effect size of d = 2.28 for the difference between the approaches for this specific condition. This suggests that a combination of appropriate feature detection and clustering method must be used to appropriately recover subgroup assignments.

S-GIMME also performed excellently across most of the unequal subgroup size conditions (i.e., one subgroup comprises 50% of individuals) with an average ARI_HA of .93. The correlation-based methods performed notably worse as the subgroup sizes became unequal (average ARI_HA = .67). This further highlights the difficulty in arriving at the true subgroup structures in nuanced data that contain smaller subgroup sizes using the features available prior to model selection. Neither of the cross-correlation feature-selection methods could recover four disproportionately sized subgroups even with a moderate sample size of N = 150 (average ARI_HA = .56 and .61 for lag-0 and lag-1, respectively). By contrast, the S-GIMME method recovered the true subgroup structure at a far higher rate (average ARI_HA = .90), with a large effect size of d = 2.61 for the difference in the two approaches for this condition.

The S-GIMME method did evidence decreased recovery rates with smaller sample sizes and greater number of subgroups in the unequal subgroup condition. For example, with N = 75 and N = 25 with subgroups of four, average ARI_HA decreased to .83 and .73, respectively. While still acceptable, these rates do not match the rate seen in N = 150. When there were two subgroups at these sample sizes, S-GIMME performed excellently (average ARI_HA of .99 and .89, respectively). In summary, our results demonstrate that the S-GIMME method that detects subgroups during GIMME’s data-driven model discovery is a better option for researchers than classifying individuals by using the raw correlation matrices depicting temporal processes.

Modularity as an indication of accurate subgroup recovery

The results indicate that utilizing the Walktrap approach can return subgroup classifications consistent with the generation of the simulated data. As described in the preceding, modularity can be used to indicate how well the individuals (“nodes” or “vertices”) in our similarity matrices were partitioned (Porter et al., 2009). While useful for detecting the best partition within a set obtained for the same sample, using modularity on its own to evaluate the appropriateness of a solution when looking across studies may not be appropriate (Karrer, Levina, & Newman, 2008). The present results further suggest that caution must be used when relying on modularity as a measure of accurate subgroup recovery. Recall from the preceding that modularity has an upper limit of one. Despite near-perfect classification across all conditions, the S-GIMME method averaged a rather low modularity of .15 (SD = .08). Furthermore, the relation between modularity and ARI_HA returned a small effect with a Pearson’s correlation coefficient of .105. Thus, while modularity appears to work well as a stopping mechanism for arriving at final solutions in some community-detection algorithms by rank ordering partitions according to this score, fluctuations in modularity did not indicate better or worse recovery of subgroups in these data when looking across data sets. Thus, modularity may not be an appropriate mechanism for assessing absolute (as opposed to relative) quality of subgroup partitions.

Path recovery

GIMME recovered the true underlying paths, including the direction of paths, in the models at an exceptionally high rate with or without using the classification procedures. As expected, using S-GIMME improved upon the recall of the recovery of both the presence and directions of paths when looking across all of the conditions (see Figure 7 and Supplemental Tables 2 and 3). GIMME and S-GIMME both performed nearly perfectly in terms of recovering the group-level paths (Table 1). However, the accuracy in path recall for the subgroup- and individual-level paths differed between the two approaches with S-GIMME performing better on these (d = 4.78). Both of these methods performed slightly worse in the presence of disproportionate subgroup sizes. Otherwise, the approaches consistently returned reliable results despite the number of subgroups or the number of individuals.

Figure 7.

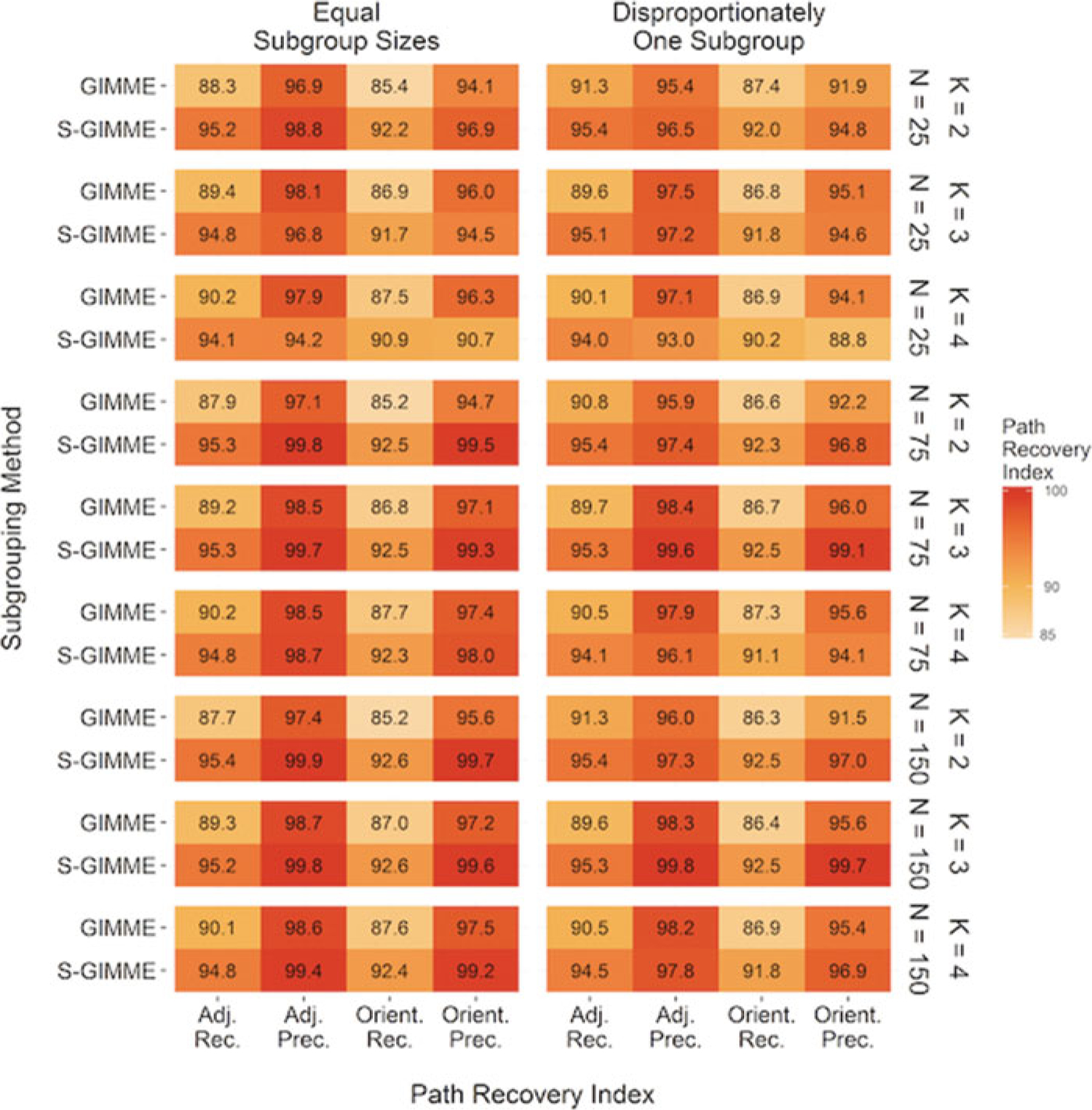
Heat map depicting the accuracy in recovery of presence and directions of paths. N indicates total number of individuals simulated in condition; K indicates the number of subgroups in the data simulation; Path Rec. = path recall (proportion of true paths recovered); Path Prec. = path precision (proportion of paths recovered that are true); Direct. Rec. = direction recall (proportion of true path directions recovered); Direct. Prec. = direction precision (proportion of path directions recovered that are true). Classification with EPC (expected parameter change [EPC-Based] during GIMME model selection; S-GIMME) recovered the true presence and direction of paths at the highest rates at high precision.

Table 1.

Average Ramsey indices for group-level and other paths separately.

Path type	Index	Original GIMME	S-GIMME
Group-level	Path Recall	98.38 (1.89)	100.00 (0.07)
	Path Precision	100.00 (0.00)	100.00 (0.00)
	Dir. Recall	97.92 (2.11)	99.55 (0.40)
	Dir. Precision	99.59 (1.14)	99.70 (0.75)
Other	Path Recall	67.63 (3.04)	80.26 (2.28)
	Path Precision	87.56 (7.60)	93.06 (8.01)
	Dir. Recall	63.85 (3.069)	76.77 (3.12)
	Dir. Precision	84.41 (8.12)	91.23 (9.96)

Note. “Other” refers to both subgroup- and individual-level paths; Dir. = direction.

Overall, false positives are not a problem for any of the GIMME approaches tested, with averages for path precision being well above 80% for both the original GIMME and S-GIMME approaches. Across all conditions the precision was higher than recall for each approach, indicating that the GIMME algorithms did not recover all the true paths in some conditions because the search procedure stopped too early rather than running the risk of adding paths that do not truly exist. This appears to be the cost for ensuring that false paths are not selected, and this favoring of parsimony is common in these types of model searches (e.g., Ramsey et al., 2010). Still, a smaller but still noteworthy difference was seen in the precision of the recall of paths in favor of S-GIMME (d = 0.70), but both approaches performed exceptionally well in terms of precision even when only considering the subgroup- and individual-level paths. Thus, the improvements in recovery rates for S-GIMME did not come at the expense of increased false positive rates.

Omitted variable analysis

Overall, subgroup recovery was not greatly influenced by an omitted variable with an average ARI_HA = .98 (SD = .03), which is comparable to results on S-GIMME (ARI_HA = 1.00, SD = .02) run on the full set of variables with a small to moderate Cohen’s d of .39 for the difference. Path recall was similarly somewhat robust to the presence of an omitted variable. Recall of paths actually increased when a variable was omitted, which is likely due to there being fewer paths to recover. As anticipated, precision was slightly lower but still in the acceptable range with the average across all variable omissions being 94%. This suggests that a greater number of false positives were obtained when compared to the original, which had very few false positives as revealed by an average path precision of 100%. Thus while favoring parsimony generally assists in the prevention of false negatives, the omission of even one variable will likely increase the likelihood of false positives even in the most optimal conditions. This is particularly true if the data-generative model for omitted variable has a higher number of paths relating it to other variables. Additional details on these results are found in the Supplemental Materials and in Supplemental Table 4.

Discussion

The present article introduces an approach, subgrouping within GIMME (S-GIMME), for unsupervised classification of individuals according to their dynamic processes. Specifically, S-GIMME conducts the community-detection algorithm Walktrap (Pons & Latapy, 2006) on temporal features available during GIMME model building. After arriving at the group-level effects (i.e., dynamic relations that can be considered nomothetic or present for the majority), S-GIMME identifies effects that may be specific to each subgroup. Finally, as with the original GIMME algorithm, S-GIMME conducts individual-level searches. All weights are estimated at the individual level—even for those temporal relations found to exist at the group or subgroup levels. S-GIMME is freely available within an R package (Lane, Gates, & Molenaar, 2016). By providing these three patterns of effects, researchers are able to make generalizable inferences, identify effects that are specific to subgroups of individuals, and control for and discover individual-level effects.

We demonstrated that classifying individuals in this manner provides two benefits. First, individuals are placed in subgroups with other individuals who share some of their patterns of dynamic effects. The success rate for recovering the true subgroup structure by utilizing S-GIMME, which classifies individuals during model selection, was higher than classifying individuals according to features available prior to the beginning of the model-selection process (i.e., cross-correlation matrices). S-GIMME demonstrated robustness for sample sizes as small as 25. Results were robust at this sample size even when subgroups were small and when the subgroup sizes were unequal. These last two issues are commonly discussed in the field of community detection since they are difficult to circumvent (Lancichinetti & Fortunato, 2011). While there still is room for improvement in these conditions, using Walktrap in addition to our refined feature-selection approach appears to accommodate this issue. In the end, S-GIMME provides reliable subgroup assignments based on temporal patterns of effects.

As a second benefit, S-GIMME slightly improves recovery of the presence and direction of effects when compared to the original GIMME. It has been established previously that GIMME is one of the few data-driven approaches that can robustly detect both the presence and direction of effects in individuals that exhibit heterogeneous processes across time (Gates & Molenaar, 2012; Mumford & Ramsey, 2014; see Smith et al., 2011 for competing approaches). One reason GIMME performs so well is that it begins the individual-level searches with prior information obtained by detecting signal from noise across the entire sample. It has been demonstrated previously that using these priors (which are considered the “group-level” patterns of effects) vastly improves the correct detection of model recovery as compared to conducting individual-level model searches with no prior information (Gates & Molenaar, 2012). S-GIMME builds from this knowledge by conducting a subgroup-level search to further improve upon the precision and recall of effects at the individual level. By adding additional prior information to the individual-level search informed by other individuals with similar patterns of effects, S-GIMME is even better able to arrive at reliable results.

In the end, the present set of simulations found that (a) S-GIMME appropriately clusters individuals into subgroups according to their temporal models and (b) reliable group-, subgroup-, and individual-level patterns of dynamic effects were returned. This was tested across various conditions typical in fMRI research: varying number of individuals (with the number being smaller than typical in other psychology research); varying number of subgroups; varying subgroup sizes; and omission of a variable. Decreased performance was seen for small sample size and numerous subgroups, but indices reflecting the quality of results were still in acceptable ranges and outperformed the correlational approaches. While performing robustly in the optimal setting when one variable was omitted, S-GIMME could likely be improved upon by enabling the inclusion of latent variables to capture omitted common causes. From a statistical standpoint, S-GIMME can immediately be extended to include latent factors from within a dynamic factor analytic framework (Molenaar, 1985). However, heterogeneity in the latent structures across individuals poses a hurdle that requires more testing. In particular, more work needs to be done to examine the robustness of S-GIMME in the presence of latent variables and the conditions in which commonalities across individuals must be retained.

While development of statistical methods for individual-level analysis of humans has long been under way (e.g., Cattell, Cattell, & Rhymer, 1947; Molenaar, 1985), widespread application is in its early stages. The work presented here marks one of many intermediate points. Daily diary or momentary assessments will likely present a number of obstacles not considered here or seen in neuroscience applications. One potential problem for the proposed technique would be low variability for some individuals on some variables, which may occur when an individual reports the same response across all timepoints. Two, it is highly likely that the time series will be shorter than what is presented here or anticipated in fMRI research, thus reducing the power with which to detect effects and the number of variables than can be included. A third issue is that some processes may best be captured solely with contemporaneous effects, which likely poses problems for an algorithm that only includes the directionality of effects (MacCallum, Wegener, Uchino, & Fabrigar, 1993). Allowing for bidirectional or correlational effects is done in other directed search procedures (as discussed in Spirtes et al., 2000) and could inform this development in S-GIMME. In terms of correctly identifying the direction of an effect, including even weak autoregressive effects may still enable the algorithm’s ability to recover directionality from within a Granger causality framework. As another option, Beltz and Molenaar (2016) introduced an algorithm for arriving at multiple solutions for GIMME to circumvent this issue. More work is needed to integrate these developments into S-GIMME to enable robust recovery of contemporaneous effects.

A fourth issue is that, at the other end of the spectrum, perhaps other forms of data require lags greater than one. As the S-GIMME operates from within a block-Toeplitz framework, the addition of additional lags greatly increases the number of variable but may be necessary in some cases (see Beltz & Molenaar, 2015). This might cause problems for estimation if the number of variables becomes large relative to the number of observations (Bollen, 1989). It might also introduce issues with the use of fit indices in this context. Future work could arrive at fit indices by adapting the approach used in the DyFA program for arriving at model likelihood. Here, only the unique correlation matrices (i.e., contemporaneous and lagged in the uSEM case) would be used to arrive at the residual sum of squares (Browne & Zhang, 2005). A fifth noteworthy property of ecological momentary assessments that is not seen in psychophysiological observations is that of unequal intervals. While this poses a problem for the current approach, models of continuous time (e.g., Boker & Bisconti, 2006; Chow, Ram, Boker, Fujita, & Clore, 2005; Deboeck, 2013) can overcome this issue. In this case, perhaps S-GIMME could be used to identify the model on data that have been interpolated to provide equally distant timepoints. Following arrival at the structure of effects, continuous time-series models can be fit using R packages such as dynr (Ou, Hunter, & Chow, 2016) or ctsem (Voelkle, Oud, & Driver, 2016). Finally, the procedure used here is an unsupervised classification approach. Some researchers may wish to have static features, such as diagnostic category, help drive the subgroup search or allow for continuous class assignments. These issues and more can help guide development of S-GIMME and other methods used for the study of individual-level processes.

The developments presented here are timely and could be helpful across varied domains of inquiry within psychological sciences given the high degree of heterogeneity seen in humans’ temporal patterns. The field of neuroscience has already embraced this reality, with individual-level temporal processes highlighted as a golden standard that researchers should aim for (Finn et al., 2015; Laumann et al., 2015) and much work being done to identify statistical methods for doing so. Using functional MRI data, researchers have been able to identify clusters of individuals within a clinical sample who have shared brain features (Gates et al., 2014; Yang et al., 2014), indicating the utility of such approaches in refining the field’s diagnostic process. Psychophysiological data have long provided ample timepoints for individuals, making time-series analysis historically more applicable to neuroscientists than other researchers. However, with the increasing use of wearable data technologies, ecological momentary assessments, and encoding of observed behavioral data, researchers across varied domains of the social sciences are primed to conduct time-series analysis. Indeed, one application has utilized cluster analysis to find meaningful subgroups of individuals on behavioral time series (Babbin, Velicer, Aloia, & Kushida, 2015), suggesting the utility of this type of approach on behavioral data in addition to neuroscience applications. S-GIMME provides one solution for researchers with multivariate time series. By identifying clusters of individuals with shared temporal features, S-GIMME may help guide prevention, intervention, diagnostic criteria, and treatment protocols as well as inform basic science regarding human processes.