MRI Super-Resolution Through Generative Degradation Learning

Abstract

Spatial resolution plays a critically important role in MRI for the precise delineation of the imaged tissues. Unfortunately, acquisitions with high spatial resolution require increased imaging time, which increases the potential of subject motion, and suffers from reduced signal-to-noise ratio (SNR). Super-resolution reconstruction (SRR) has recently emerged as a technique that allows for a trade-off between high spatial resolution, high SNR, and short scan duration. Deconvolution-based SRR has recently received significant interest due to the convenience of using the image space. The most critical factor to succeed in deconvolution is the accuracy of the estimated blur kernels that characterize how the image was degraded in the acquisition process. Current methods use handcrafted filters, such as Gaussian filters, to approximate the blur kernels, and have achieved promising SRR results. As the image degradation is complex and varies with different sequences and scanners, handcrafted filters, unfortunately, do not necessarily ensure the success of the deconvolution. We sought to develop a technique that enables accurately estimating blur kernels from the image data itself. We designed a deep architecture that utilizes an adversarial scheme with a generative neural network against its degradation counterparts. This design allows for the SRR tailored to an individual subject, as the training requires the scan-specific data only, i.e., it does not require auxiliary datasets of high-quality images, which are practically challenging to obtain. With this technique, we achieved high-quality brain MRI at an isotropic resolution of 0.125 cubic mm with six minutes of imaging time. Extensive experiments on both simulated low-resolution data and clinical data acquired from ten pediatric patients demonstrated that our approach achieved superior SRR results as compared to state-of-the-art deconvolution-based methods, while in parallel, at substantially reduced imaging time in comparison to direct high-resolution acquisitions.

1. Introduction

MRI is critically important in clinical and scientific research studies. High spatial resolution in MRI allows for the precise delineation of the imaged tissues. However, the high spatial resolution requires a long scan time, and in turn unfortunately increases the potential of subject motion [1, 22] and reduces the signal-to-noise ratio [2, 16]. Super-resolution reconstruction (SRR) has recently emerged as a technique of post-acquisition processing, which allows for obtaining MRI images at a high spatial resolution, high SNR, and short scan time [7–9, 19, 26]. Among these SRR techniques, deconvolution-based methods [16, 20, 21, 23, 24] have recently received significant interest due to the convenience of using the image space only. However, the deconvolution requires an accurate estimate in the blur kernel that characterizes the degradation process of the acquired images, which are usually difficult to obtain. Current methods take handcrafted filters as an approximation of the blur kernel, such as Gaussian filters [7, 20]. As the image degradation is complex and varies with different sequences and scanners, however, handcrafted approximations do not necessarily ensure the success of the deconvolution, and even possibly lead to unusable reconstructions.

Blur kernel estimation is often used in natural image deblurring, also known as blind deconvolution [3], in particular equipped with deep neural networks [6]. Unfortunately, no techniques focus on blur kernel estimation for deconvolution-based SRR in MRI. Although deep learning-based techniques have been widely used in natural image super-resolution, the majority of deep SRR methods for MRI are performed with 2D slices [4, 28, 30] as the large-scale, auxiliary datasets of high-quality volumetric MRI images are practically challenging to obtain at a high resolution and suitable SNR. It has been shown that the deep SRR model learned on volumetric data achieved better results than on 2D slice data [15].

We sought to develop a methodology that allows for accurately estimating blur kernels from the image data itself. We designed a deep architecture that utilizes an adversarial scheme with a generative neural network against its degradation counterparts. Our design enables the SRR tailored to an individual subject, as the training of our deep SRR model requires the scan-specific image data only. We achieved high-quality brain MRI images through our SRR method at an isotropic resolution of 0.125 cubic mm with six minutes of imaging time. We assessed our method on simulated low-resolution (LR) image data and applied it to ten pediatric patients. Experimental results show that our approach achieved superior SRR as compared to state-of-the-art deconvolution-based methods, while in parallel, at substantially reduced imaging time in comparison to direct high-resolution (HR) acquisitions.

2. Methods

2.1. Theory

It is difficult for SRR to enhance 2D in-plane or true 3D MRI resolution due to the frequency encoding scheme [14, 18], but effective to improve through-plane resolution for 2D slice stacks [10]. Therefore, we focus on reducing the slice thickness of LR scans¹ with large matrix size and thick slices. The thick slices lead to reduced scan time and increased SNR. Thus, we can acquire a set of LR images with different orientations to facilitate the SRR to capture the HR signals distributed in different directions, while keeping the total scan time short.

Forward Model.

Let x denote the HR reconstruction and ${\left\{{\text{y}}_j\right\}}_{j=1}^n$ denote the n acquired LR images. The forward model that describes the acquisition process is formulated as

$${\text{y}}_j={\text{D}}_j{\text{B}}_j{\text{T}}_j\text{x+}\nu \text{,\hspace{1em}\hspace{0.17em}}j=1,2,\dots ,n.$$ (1)

The transform T_j compensates for subject motion and is obtained by aligning the n LR images together. B_j describes the image degradation defined by a blur kernel. D_j is the downsampling operator that discards a certain amount of data from the HR signal. The noise ν is additive and Gaussian when SNR > 3 [11].

Generative Degradation Learning.

Our SRR targets a joint estimate in both the HR reconstruction and blur kernel. We use a generative neural network to generate an HR estimate by x = f_θ (z_x ), and n generative networks to generate n blur kernels by B_j = g_{ω j}(z_bj). These generations are constrained by the image degradation process as described in the forward model. Therefore, the generative degradation learning is found by

$$\begin{array}{l}\underset{\text{x},\theta ,{\text{B}}_j,{\omega }_j}{\min }\mathcal{\ell }\left(\text{x}-f_{\theta }\left({\text{z}}_x\right)\right)+{\displaystyle \sum _{j=1}^n{\mathcal{\ell }}_{b_j}\left({\text{B}}_j-g_{{\omega }_j}\left({\text{z}}_{b_j}\right)\right)},\\ s.t.{\text{y}}_j={\text{D}}_j{\text{B}}_j{\text{T}}_j\text{x}+\nu ,j=1,2,\dots ,n.\end{array}$$ (2)

where f_θ and g_{ω j} are nonlinear functions that generate data, parameterized by θ and ω_j, respectively, ℓ and ℓ_bj are the loss functions in the optimization, and z_x and z_bj are the initial guesses for x and B_j, respectively. The function f_θ here is also known as the deep image prior [25]. When the loss functions are ℓ₂ loss, we can substitute x and B_j with the generative functions, and the optimization is then re-formulated as

$$\underset{\theta ,{\omega }_j}{\min }{\displaystyle \sum _{j=1}^n{‖{\text{y}}_j-{\text{D}}_j{g}_{{\omega }_j}\left({\text{z}}_{b_j}\right){\text{T}}_j{f}_{\theta }\left({\text{z}}_x\right)‖}_2^2+\lambda {\mathcal{R}}_{TV}\left(f_{\theta }\left({\text{z}}_x\right)\right)},$$ (3)

with a total variation (TV) [17] term imposed to regularize the HR reconstruction for edge sharpness, and a weight parameter λ > 0.

We implement these generative functions by deep neural networks. f_θ is realized by a 3D UNet-like encoder-decoder network [31]. g_{ω j} is implemented by a fully connected network containing four hidden linear layers and one Tanh layers. Each layer is followed by a dropout regularization and a ReLU activation. The architecture of our generative degradation networks (GDN) is shown in Fig. 1. A degradation network comprises a generative function for the blur kernel in combination with the constraint delivered by the forward model. We solve the optimization by an Adam algorithm [12]. The training for the GDN is an optimization problem. It is thus carried out on the scan-specific LR images y_j themselves only, and in turn, allows for the SRR tailored to an individual subject.

Fig. 1.

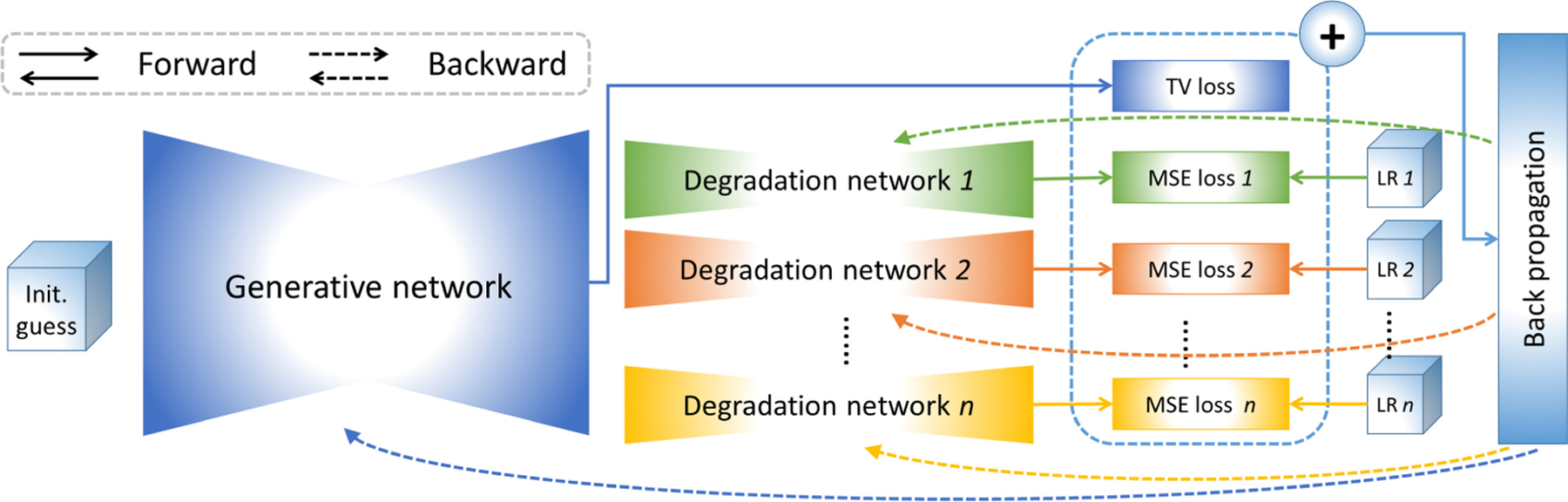
Architecture of our proposed approach to generative degradation learning.

The HR reconstruction is obtained directly from x = f_θ (z_x ) once the GDN model has been trained. Also, to ensure the appropriate scale of the voxel intensity, a standard TV-based SRR with the learned blur kernels B_j can be optionally applied to obtain the HR reconstruction.

2.2. GDN-Based SRR

Since we focus on enhancing the through-plane resolution, the degradation process is assumed to be associated with the blurs from the slice excitation and downsampling. The downsampling is carried out by truncating the high frequency in the Fourier domain, and it is thus determined by a sinc low-pass filter. The slice excitation is characterized by the slice profile that is generated by the radio frequency (RF) pulse during scans. Therefore, the blur kernel we estimate is the convolution between the slice profile and the sinc filter.

The motion compensation is implemented by a rigid body image registration as we focus on brain MRI in this work. We interpolate the LR images to those with the resolution and size the same as the HR reconstruction, and align them together. The obtained transformations are used as T_j in the forward model.

We initialize the blur kernels as a sinc filter convolved with a Gaussian low-pass filter whose full width at half maximum (FWHM) is equal to the slice thickness of the LR image over that of the HR reconstruction. We compute an initial guess of the HR reconstruction by a standard TV-based SRR [16] with the above initialized blur kernels. We set λ = 0.01 in Eq. (3) according to our empirical results. We run 4k iterations with a learning rate of 0.01 to minimize Eq. (3). It took about 2.5 h to reconstruct an HR image of size 384 × 384 × 384 voxels from three LR scans on an NVIDIA Titan RTX GPU with PyTorch [13].

2.3. Materials

We simulated an LR dataset based on the Human Connectome Project (HCP) database [5]. We randomly selected forty subjects from the HCP database, including five T1w and five T2w HR images with an isotropic resolution of 0.7 mm as the ground truths. We generated four blur kernels, as shown in Figs. 2(b) and 2(c), based on a Dirac pulse, a Gaussian, a sinc, and a boxcar functions depicted in Fig. 2. We simulated four groups of LR images according to the four types of blur kernels. We downsampled each ground truth image to three LR images in the complementary planes with a slice thickness of 2 mm after convolving it with the blur kernel in its group. Gaussian noise was added in each LR image with a standard deviation of 5% of maximum voxel intensity.

Fig. 2.

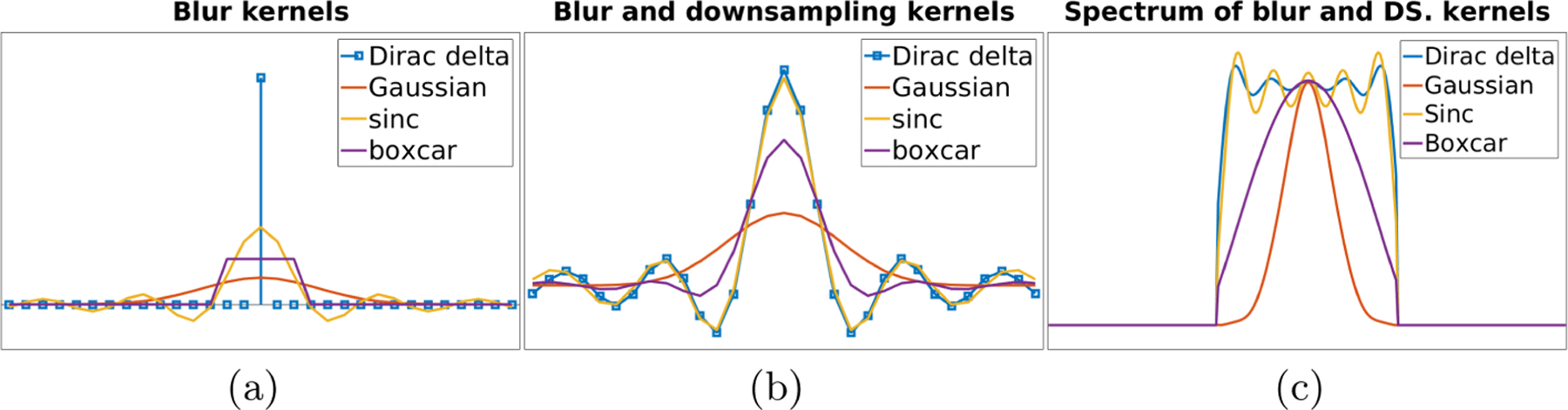
Illustrations of the mock slice profiles (a), generated blur kernels (b), and spectrum magnitudes of these kernels (c).

We acquired thirty LR T2-FSE scans from ten pediatric patients - three images in complementary planes per patient - on a 3T scanner. The field of view (FOV) was 192 mm × 192 mm, matrix size was 384 × 384, slice thickness was 2 mm, TE/TR = 93/12890 ms with an echo train length of 16 and a flip angle of 160^◦. It took about two minutes in acquiring an LR image.

2.4. Experimental Design

As our SRR is an unsupervised deconvolution-based approach, we compared our approach to state-of-the-art methods in the same category, including a TV-based method [16], a gradient guidance regularized (GGR) method [20], and a TV-based method with joint blur kernel learning (TV-BKL) implemented by ourselves. The parameters of the baselines were set according to their best PSNR.

Experiment 1: Assessments on Simulated Data.

The goal of this experiment is two-fold: to assess the accuracy of the blur kernel estimates and to demonstrate that the estimated blur kernels lead to superior HR reconstructions. We reconstructed each HR image at an isotropic resolution of 0.7 mm from three LR images on the HCP dataset. We investigated the estimation error defined by the ℓ₂ norm of the difference between the estimated kernel and ground truth over the ℓ₂ norm of ground truth ‖k_est − k_gt‖₂ /‖k_gt‖₂. To evaluate the reconstruction quality, we investigated the PSNR and SSIM [27] of the HR reconstructions.

Experiment 2: Assessments on Clinical Data.

This experiment aimed at assessing the applicability of our SRR for clinical use. We reconstructed each HR image at an isotropic resolution of 0.5 mm on the clinical dataset. We evaluated the sharpness of these reconstructions by average edge strength [29]. We checked the estimated blur kernels and qualitatively assessed these reconstructions.

Experiment 3: Impact on Deconvolution-Based Algorithms.

This experiment aimed at evaluating the impact of our generative degradation learning on deconvolution-based algorithms. We expected our estimated blur kernels can improve the TV and GGR algorithms in their SRR quality on the HCP dataset.

3. Results

Experiment 1: Assessments on Simulated Data.

Figure 3 shows the estimation errors in the blur kernels obtained from our method and TV-BKL. Our method, SR-GDN, considerably outperformed TV-BKL on the HCP dataset. The average errors of SR-GND and TV-BKL were respectively 10.1% ± 4.6% and 25.8% ± 12.0%. Two-sample t-test showed that SR-GND offered significantly lower errors on the simulated data than TV-BKL at the 5% significance level (p = 2.16e⁻¹¹⁸).

Fig. 3.

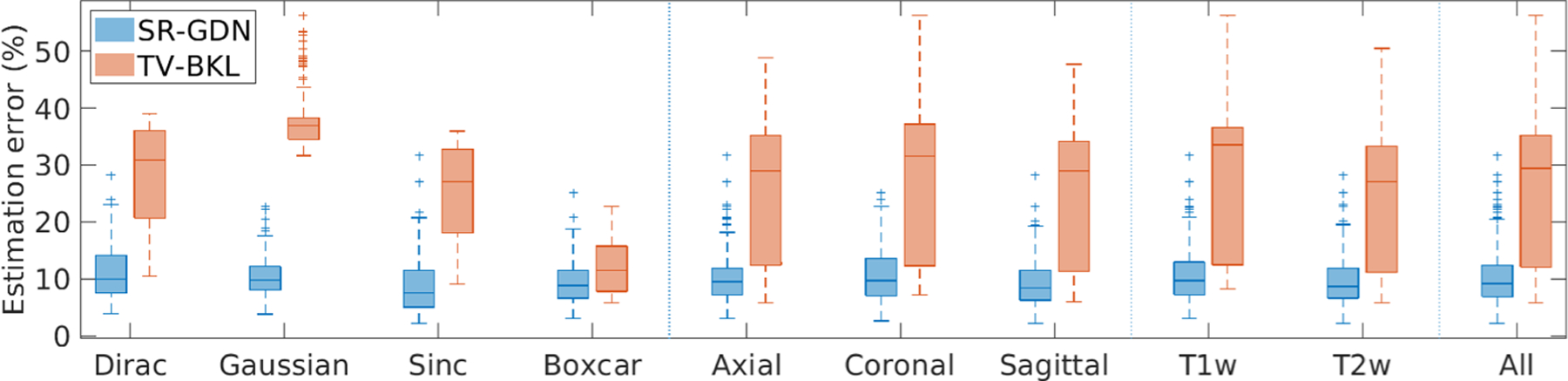
Estimation errors in the blur kernels obtained from the two methods. Our methods, SR-GDN, considerably outperformed TV-BKL on the HCP dataset.

Figure 4 shows the spectrum of true and estimated blur kernels from SR-GDN and TV-BKL on four representative simulations. Our estimates (SR-GDN) closely followed the true kernels and offered higher accuracy than TV-BKL with all types of kernels on the HCP dataset.

Fig. 4.

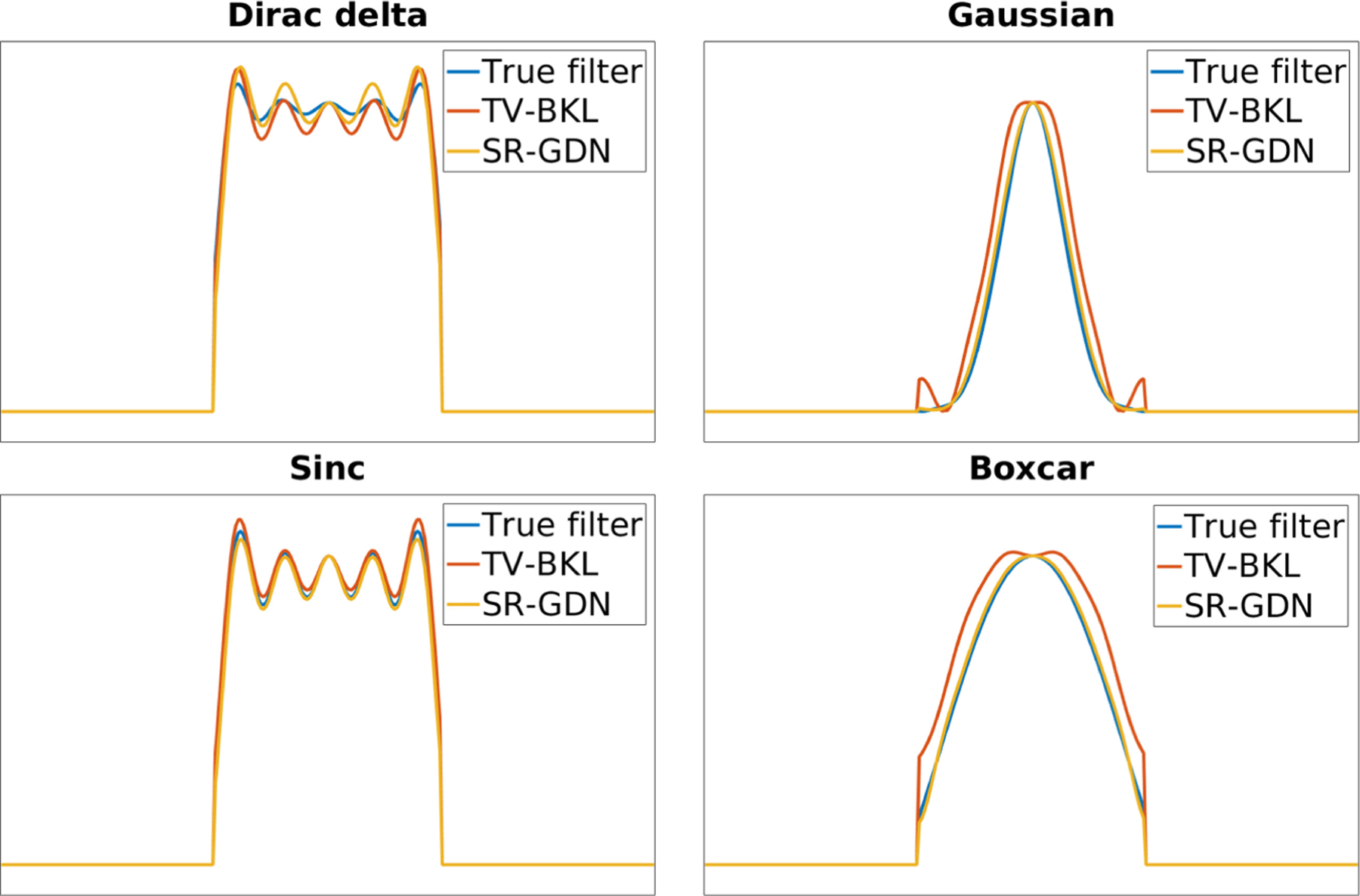
Spectrum of true and estimated blur kernels from SR-GDN and TV-BKL on four representation simulations. Our estimates (SR-GDN) closely followed the true kernels and offered higher accuracy than TV-BKL with all types of kernels.

Figure 5 shows the quantitative assessment of our approach (SR-GDN) and the three baselines on the HCP dataset in terms of PSNR and SSIM. Our method achieved an average PSNR at 41.2 dB ± 3.74 dB and SSIM at 0.98 ± 0.01, which were considerably higher than obtained from the three base-lines. Two-sample t-tests showed that SR-GDN significantly outperformed the three baselines in terms of SSIM at the 5% significance level with p = 2.36e⁻¹⁸ against TV, 4.37e⁻¹⁸ against GGR, and 1.81e⁻⁷ against TV-BKL.

Fig. 5.

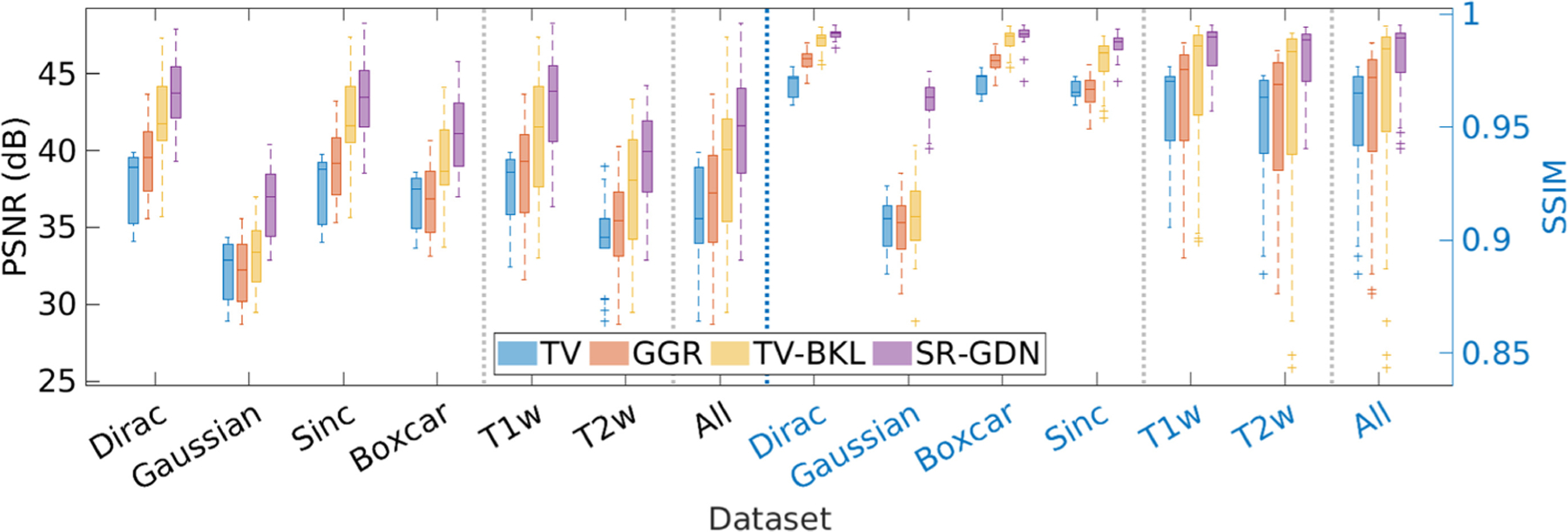
Quantitative assessment of the four SRR methods in terms of PSNR and SSIM.

Experiment 2: Assessments on Clinical Data.

Figures 6(a) and 6(b) show the mean and standard deviation of the blur kernels estimated by TV-BKL and SR-GDN from ten sets of clinical scans acquired on a 3T scanner. The results show that both methods led to small standard deviations of estimations. Figure 6(c) shows the spectrum magnitudes of the handcraft Gaussian filter and the mean blur kernels estimated by TV-BKL and SR-GND. In comparison to the simulation results shown in Fig. 4, the results show that our approach (SR-GND) estimated the slice profile as a close approximation to a boxcar function.

Fig. 6.

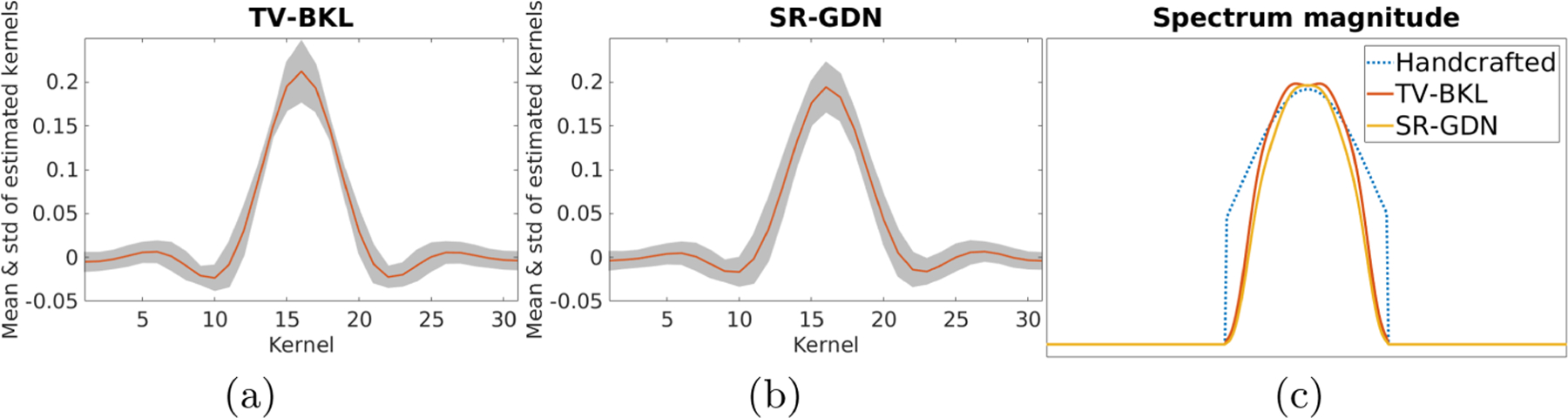
Mean and standard deviation of the blur kernels estimated by (a) TV-BKL and (b) SR-GDN from ten sets of clinical scans. (c) Spectrum magnitudes of the handcraft Gaussian filter and the mean blur kernels estimated by TV-BKL and SR-GDN.

We evaluated the average edge strength (AES) of the HR reconstructions obtained from our approach and the three baselines on the ten sets of clinical scans. The results, as shown in Table 1, suggests that our approach, SR-GDN achieved the highest AES. TV-BKL yielded the lowest AES as the noise in the reconstructions led to blurry edges.

Table 1.

Average edge strength obtained from our approach and the three baselines on the ten sets of clinical scans.

TV	GGR	TV-BKL	SR-GDN
2.73 ± 0.72	3.12 ± 0.90	1.78 ± 0.50	3.49 ± 0.97

Figure 7 shows the qualitative assessment of our approach and the three baselines in the slices of representative clinical data. The results show that SR-GDN offered high-quality brain MRI with the clinical LR data. GGR smoothed the images excessively so missed some anatomical details, while TV and TV-BKL generated noisy images and caused artifacts as shown in the coronal image.

Fig. 7.

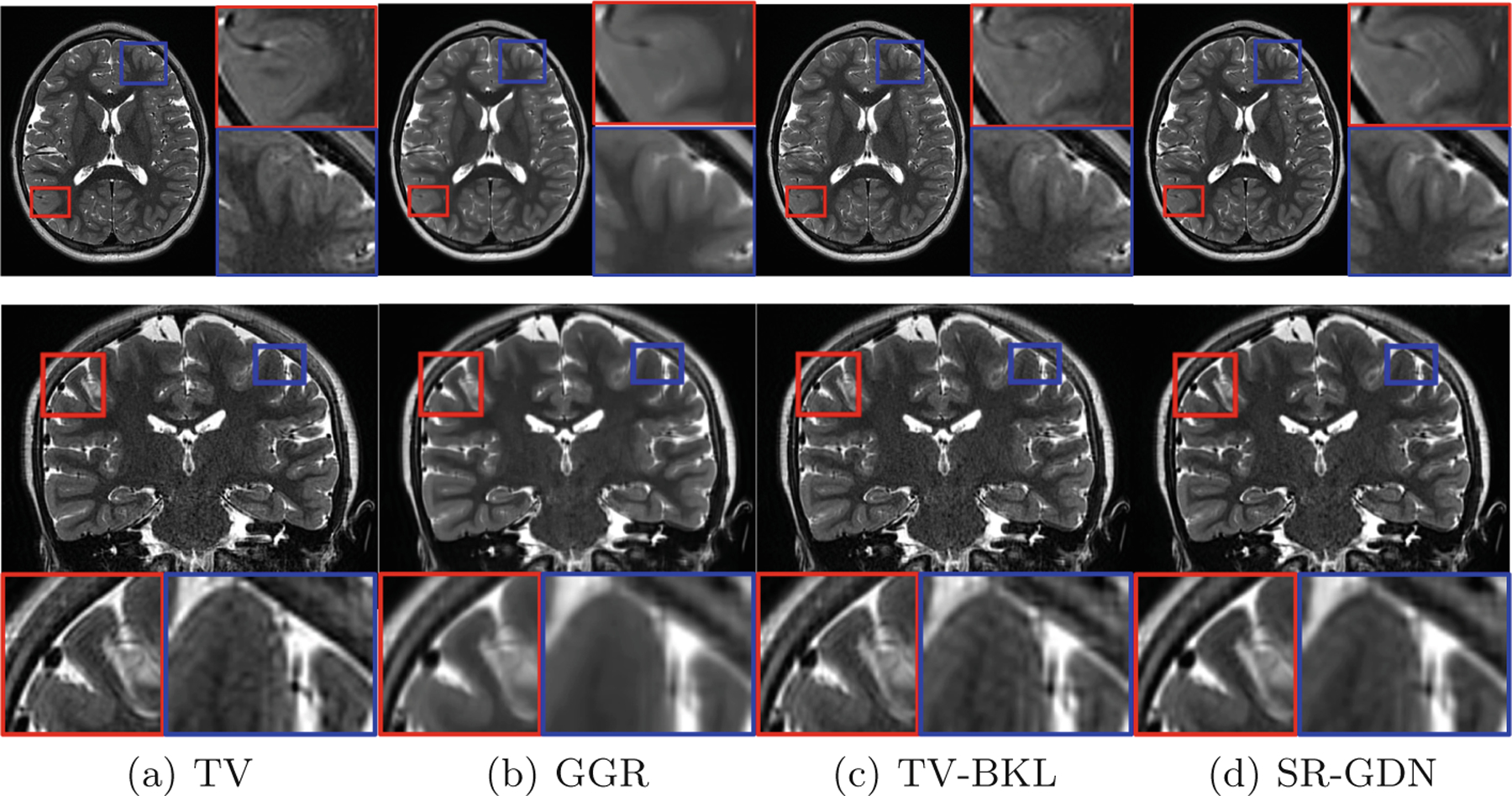
Qualitative assessment of our approach (SR-GDN) and the three baselines in the slices of representative clinical data.

Experiment 3: Impact on Deconvolution-Based Algorithms.

We replaced the handcrafted Gaussian filter used in TV and GRR with our estimated blur kernels and ran the two methods on the HCP dataset. The increased PSNR/SSIM were respectively: TV = 13.90%/3.15% and GGR = 3.35%/2.44%. The results show that our estimated blur kernels led to improved deconvolution-based algorithms.

4. Discussion

We have developed a deconvolutional technique that enabled accurately estimating blur kernels from the image data itself. We have designed a deep architecture that utilizes an adversarial scheme with a generative neural network against its degradation counterparts. This design has been demonstrated to allow for the SRR tailored to an individual subject. We have thoroughly assessed the accuracy of our approach on a simulated dataset. We have successfully applied our approach to ten pediatric patients, and have achieved high-quality brain MRI at an isotropic resolution of 0.125 cubic mm with six minutes of imaging time. Experimental results have shown that our approach achieved superior SRR results as compared to state-of-the-art deconvolution-based methods, while in parallel, at substantially reduced imaging time in comparison to direct HR acquisitions.