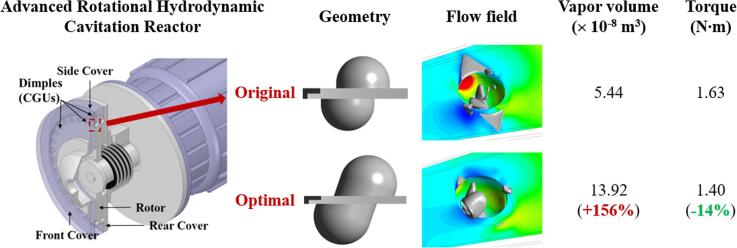
Graphical abstract
Keywords: Hydrodynamic cavitation reactor, Multi-objective optimization, CGU structure, Genetic algorithm, Process intensification, Computational fluid dynamics
Abstract
Hydrodynamic cavitation (HC) has been widely considered a promising technique for industrial-scale process intensifications. The effectiveness of HC is determined by the performance of hydrodynamic cavitation reactors (HCRs). The advanced rotational HCRs (ARHCRs) proposed recently have shown superior performance in various applications, while the research on the structural optimization is still absent. The present study, for the first time, identifies optimal structures of the cavitation generation units of a representative ARHCR by combining genetic algorithm (GA) and computational fluid dynamics, with the objectives of maximizing the total vapor volume, , and minimizing the total torque of the rotor wall, . Four important geometrical factors, namely, diameter (D), interaction distance (s), height (h), and inclination angle (θ), were specified as the design variables. Two high-performance fitness functions for and were established from a central composite design with 25 cases. After performing 10,001 simulations of GA, a Pareto front with 1630 non-dominated points was obtained. The results reveal that the values of s and θ of the Pareto front concentrated on their lower (i.e., 1.5 mm) and upper limits (i.e., 18.75°), respectively, while the values of D and h were scattered in their variation regions. In comparison to the original model, a representative global optimal point increased the by 156% and decreased the by 14%. The corresponding improved mechanism was revealed by analyzing the flow field. The findings of this work can strongly support the fundamental understanding, design, and application of ARHCRs for process intensifications.
1. Introduction
In accordance with the data from United Nations in 2019, the world population may exceed nine billion in 2050 [1]. With the rapid growth of human population and the consequent development of chemical industry, how to meet the requirement in energy savings, CO2 emission reduction, and improved cost competitiveness throughout the process industry has been a significant global problem worldwide [2], [3]. Currently, process intensification is considered to be one of the most promising progress paths for the development of a more sustainable process industry [4], [5]. To enhance effectiveness, eliminate the need for costly raw materials, and reduce reaction condition requirements, several alternative energy sources, including plasma, microwave, solar energy, and sonochemistry, have been widely applied in various process intensifications [6], [7]. Among them, hydrodynamic cavitation (HC) technology, which can effectively induce sonochemical effect, has great potential for industrial-scale applications mainly because of its good scalability, low cost, and high synergy effect with other physical and chemical methods, e.g., ultrasound [8], catalysts [9], electrochemistry [10], ultraviolet [11], plasma [12], and chemicals (oxidants [13] and acids [14]).
Hydrodynamic cavitation reactors (HCRs) mechanically generate the HC phenomenon, and the effectiveness of HC technology is therefore directly dependent on the performance of HCRs [15]. In accordance with the mechanical structure, HCRs can be categorized into non-rotational and rotational [16]. Since Pandit and Joshi [17] firstly utilized a cavitating valve for hydrolysis of fatty oils in 1993, non-rotational HCRs, such as Venturis and orifices, have been widely applied and studied [18]. More recently, advanced rotational HCRs (ARHCRs) containing a rotor-stator assembly have demonstrated superior performance in disinfection [19], biodiesel production [20], food treatment [21], disintegration of waste activated sludge (WAS) [22], degradation of organics [23], fibrillation [24], delignification [25], and heat generation [26] etc., from effective and economical points of view. For instance, the conventional HCRs obtain low disintegration degrees (DDs) of WAS ranging from 7.7–40% [27], [28], [29], while a well-designed pilot-scale ARHCR can solely achieve a DD at 57% for 196 L in only 20 passes, as reported in Petkovšek, et al. [30]’s work. For the conventional HCRs, such high DDs can be only achieved in synergy with alkalis (e.g., NaOH) [31], [32], [33].
In general, the performance of various HCRs relies on their geometrical structures [34]. Even though ARHCRs have been studied, developed, and commercialized for the last ten years [35], [36], only few studies focused on the experimental flow visualization [19], [24], [26], [30], [37], [38], [39], [40], [41], external characteristics [26], [37], [38], [40], and computational fluid dynamics (CFD) [42], [43] of various ARHCRs. Moreover, the effect of structure on their performance is rarely focused on, let alone structural optimization. Recently, for the first time, we investigated the effect of the cavitation generation unit (CGU) structure (i.e., five key factors including shape, diameter, interaction distance, height, and inclination angle) of a representative ARHCR on its cavitation generation and required shaft power [44]. The results indicate that the CGU structure determines the performance, and the variation trend of the cavitation generation and power for one single factor was contradictious. Therefore, to further improve the performance and develop the design criterion of ARHCRs, a multi-objective optimization on the ARHCR structure, which has been not conducted in the past to the best of our knowledge, is necessary.
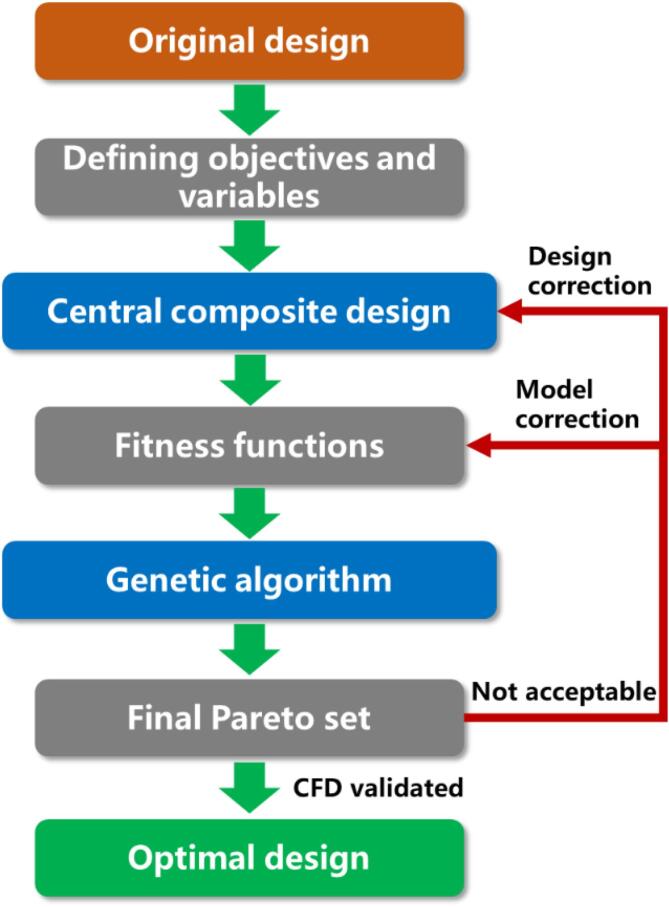
To this, we herein provide a multi-objective optimization on the CGU structure of the representative ARHCR [38], [15], [45], [46] by combining genetic algorithm (GA) and CFD for the first time. The chosen objectives were to minimize the shaft power (standing for energy consumption) and to maximize the cavitation generation. Four important geometrical factors of the CGU, namely, diameter, interaction distance, height, and inclination angle, as confirmed in our previous study [44], were selected as the design variables. The central composite design (CCD) was performed to establish the response surface models for the two objectives as the fitness functions utilized in the GA. A total of 100 generations with a population of 100 was simulated by Non-Dominated Sorting Genetic Algorithm II (NSGA-II). The optimization process was analyzed in terms of the parallel coordinate, individual and point number distributions, and correlation table. Finally, the performance and flow field of the original and optimal models were compared with physical explanations. The flow chart of the whole optimization process can be found in Fig. 1.
Fig. 1.
Illustration of the flow chart for the optimization process.
2. Methods
2.1. Numerical simulation
To obtain the responses (i.e., the objectives) for various design variables, the commercial CFD code ANSYS Fluent 18.2 was applied to predict the ARHCR performance by combining the shear stress transport k-omega model (i.e., the turbulence model) and Schnerr-Sauer model (i.e., the cavitation model) [47]. Because the flow field periodically changes, the full flow path of the ARHCR can be simplified to 1/32 of the interaction region as the computational domain, which was well validated in our previous works. In the ARHCR, the periodic interaction between the rotor and stator forms low-pressure regions inside the CGUs and on the downstream side of the CGUs. As a result, vortex cavitation and sheet cavitation regions are induced. The detailed description on the computational domain, solver setup, boundary conditions, mesh, validation, and flow mechanism can be found in the studies by Sun, et al. [43] and Sun, et al. [44], and is not repeated here.
2.2. Multi-objective optimization
2.2.1. Design variables and objectives
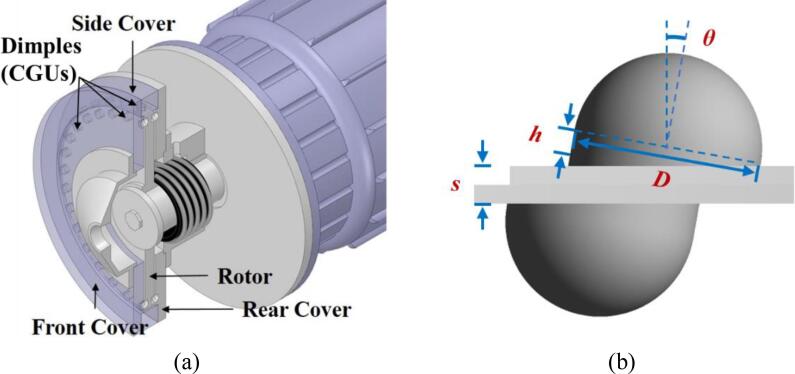
In the present study, the hemisphere-shaped CGU in interaction mode was selected as the reference model, due to its superior performance compared with other common designs, e.g., cone-cylinder, cone, or cylinder shapes [44]. Four geometrical factors with important influences, i.e., diameter (D), interaction distance (s), height (h), and inclination angle (θ), were selected as the design variables, as presented in Fig. 2. Based on the experience derived from our previous experimental and numerical studies [26], [38], [43], [44], [15], [45], [46], [40], the basic values and suitable ranges utilized in the CCD for the four design variables were shown in Table 1.
Fig. 2.
Schematic diagram of the ARHCR (a) and the design variables of the CGU (b). D: diameter, s: interaction distance, h: height, θ: inclination angle.
Table 1.
The design variables utilized in the CCD and GA (CCD: central composite design, GA: genetic algorithm).
| Design variable | Basic design | Lower limit | Upper limit | ||
|---|---|---|---|---|---|
| CCD | GA | CCD | GA | ||
| x1: diameter, D (mm) | 10 | 8 | 9 | 12 | 11 |
| x2: interaction distance, s (mm) | 2 | 1 | 1.5 | 3 | 2.5 |
| x3: height, h (mm) | 1 | 1 | 1.5 | 3 | 2.5 |
| x4: inclination angle, θ (°) | 0 | 0 | 6.25 | 25 | 18.75 |
To evaluate the ARHCR performance, the total vapor volume, , and the total torque of the rotor wall, , were utilized. can be a reasonable parameter representing the cavitation intensity generated by the ARHCR, which is defined as follows:
| (1) |
where is the total number of cells in the computational domain, is the vapor volume fraction of each cell, and is the volume of each cell. , which can stand for the required shaft power of the motor, is calculated by summing the cross products of the pressure and the viscous force vectors for each face with the moment vector:
| (2) |
where is the vector from the moment center to the force origin, is the pressure force vector, and is the viscous force vector. Since the two objectives periodically change during the interaction process, they were collected at the last time step before the coinciding stage for all cases [44].
2.2.2. Central composite design
The CCD, proposed by Box and Wilson in 1951, is one of the most widely utilized designs in the response surface methodology. In general, a full uniformly rotatable CCD includes several cube, star (or axial), and center points, which can be written as:
| (3) |
where , , and are the numbers of the design points, design variables, and replicate center points, respectively. In addition, the distance of each star point from the center point in the design domain, , can be determined as [48]:
| (4) |
Generally, the accuracy of GA optimization relies on the performance of fitness functions. The fitness function with poor quality may cause inaccurate solutions or divergence of the genetic process. The present work utilized the second-order response surface model as a fitness function for the objectives, :
| (5) |
where , , , and are the regression coefficients for the intercept, linear, quadratic, and interaction terms, respectively, and can be obtained by implementing the CCD experiment [26].
2.2.3. Genetic algorithm
In the present study, the NSGA-II, which is a typical, widely used global multi-objective optimization method with fast non-dominated sorting and congestion mechanism, was utilized to conduct the GA optimization in the platform of Isight 2016, based on our previous experience [49].
The number of generations was specified as 100 with a population of 100. The crossover probability, crossover distribution index, and mutation distribution index were 0.9, 10, and 20, respectively. The upper and lower limits of the design variables were set as shown in Table 1. The optimization direction was to achieve the maximum value for and the minimum value for . Because the GA needs to constantly call computing resources to guide the evolution of the individuals in each generation, it is unrealistic for CFD simulation to provide calculation results for each step. As a result, the approximate model has to be applied in the optimization process. In the current research, the fitness models obtained from CCD were adopted in place of the CFD as the criteria of calculation and evaluation, which can significantly save computing resources with totally acceptable errors. As to the dual-objective problem, the ideal solution for both of the objectives cannot be achieved simultaneously, and certain levels of the equilibrium have to be established between the two directions, thereby, the diversity of the solutions will be created.
3. Results and discussion
3.1. Central composite design
In the present study with four design variables (i.e., ), 25 cases with 16 cube points, eight star points, and one center points () were conducted for the full uniformly rotatable CCD. In addition, all variables were studied in five levels (−2, −1, 0, 1, and 2) where the distance was determined as . The CCD results are presented in Supplementary Table S1. To determine the influence of the variables on the objectives, the analysis of variance (ANOVA) for the linear, square, and two-way interaction terms of the two fitness models was conducted, as shown in Supplementary Tables S2 and S3. To improve the quality of the models, several terms with considerably high P-values were deleted, the final form of the fitness models is as follows:
| (6) |
| (7) |
The , Adjuseted , and Predicted of the revised fitness models are 96.77, 94.32, 82.56% and 96.83, 94.06, 81.76%, respectively. This indicates the reasonable goodness-of-fit of the models which can provide accurate prediction for new observations in the GA optimization.
To visualize the effects of the design variables on the objectives, 2D contour and 3D response surface plots for all possible pairs of variables were generated, as shown in Figs. S1 and S2 where the other variables were held at their center values. It can be found that higher D and lower s, h, and θ are beneficial to the cavitation generation, while energy consumption can be saved by decreasing D, s, h, θ and increasing s. No interaction effect on between h and θ was observed, as evident from the straight iso-lines in Fig. S1 (g), while the remaining three variables have strong interaction effects on the two objectives. The more detailed explanation on the ANOVA and response surface can be found in our previous works [26], [48].
3.2. Multi-objective optimization by genetic algorithm
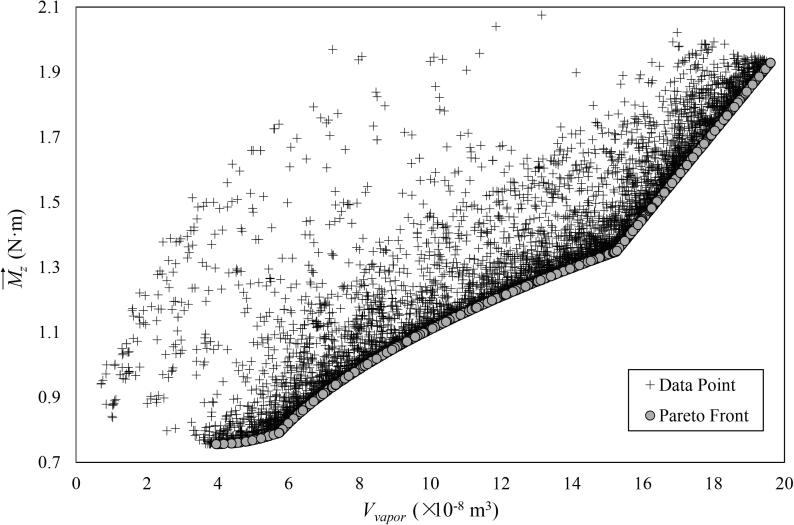
The multi-objective optimization process was started from the basic design values shown in Table 1, and the GA process with 10,001 simulations were conducted utilizing the two fitness functions obtained by the CCD. A Pareto front of 1630 non-dominated optimum design points (i.e., individuals), marked as the grey circle, was acquired, as demonstrated in Fig. 3. The other individuals were marked as the scattered cross. It can be found that enhancing along the Pareto curve (a positive feature) invariably corresponds to a continuous increase in (a negative feature). Therefore, such obvious trade-off relationships between and indicate that the appropriate CGU structure can be only determined by reasonable compromises.
Fig. 3.
Solutions of the multi-objective GA optimization.
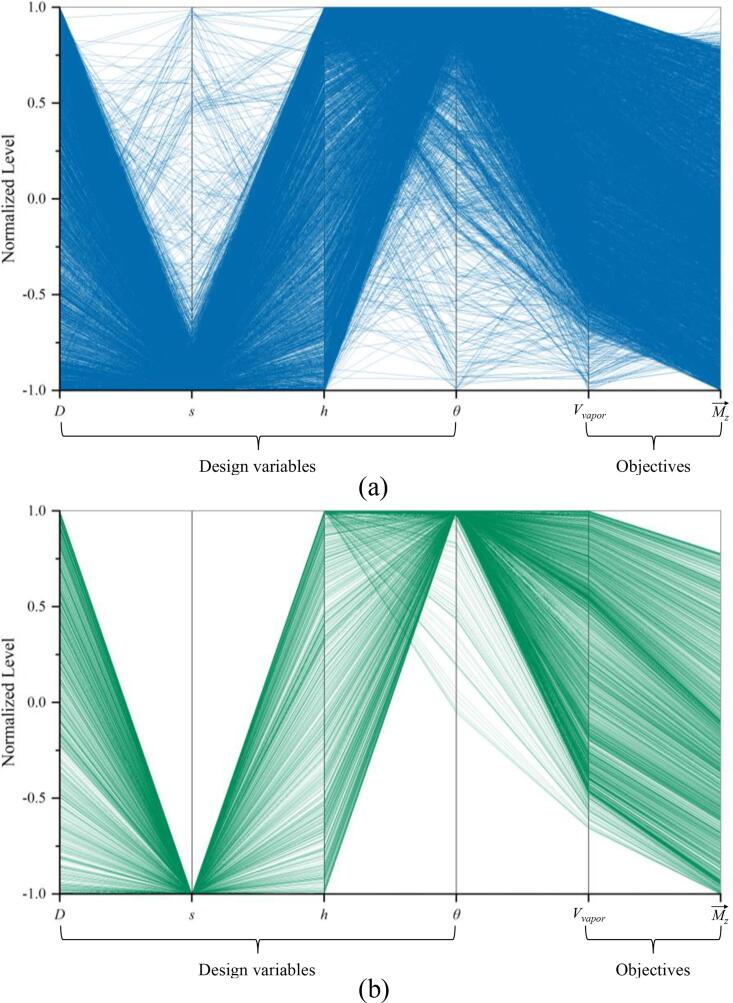
To simplify high-dimensional data to 2D, the results of all 10,001 simulations in the form of parallel coordinates are presented in Fig. 4, demonstrating the relationship between the design variables and objectives during the GA optimization. The horizontal axis represents the design variables (left) and the objectives (right), and the vertical axis is the normalized level of each parameter. For all points (Fig. 4 (a)), the whole variation ranges of the four variables were almost fully covered in the GA optimization. While in the case of the Pareto front (Fig. 4 (b)), the values of s and θ were concentrated on their lower (i.e., 1.5 mm) and upper limits (i.e., 18.75°), respectively, while D and h were scattered in their variation regions. Therefore, compared with adjusting s and θ towards the optimization direction, determining the appropriate values of D and h in the GA optimization is more vital due to the wider adjustment ranges and more possible combinations.
Fig. 4.
Parallel coordinates showing the relationship between the design variables and the objectives for (a) all points and (b) Pareto front.
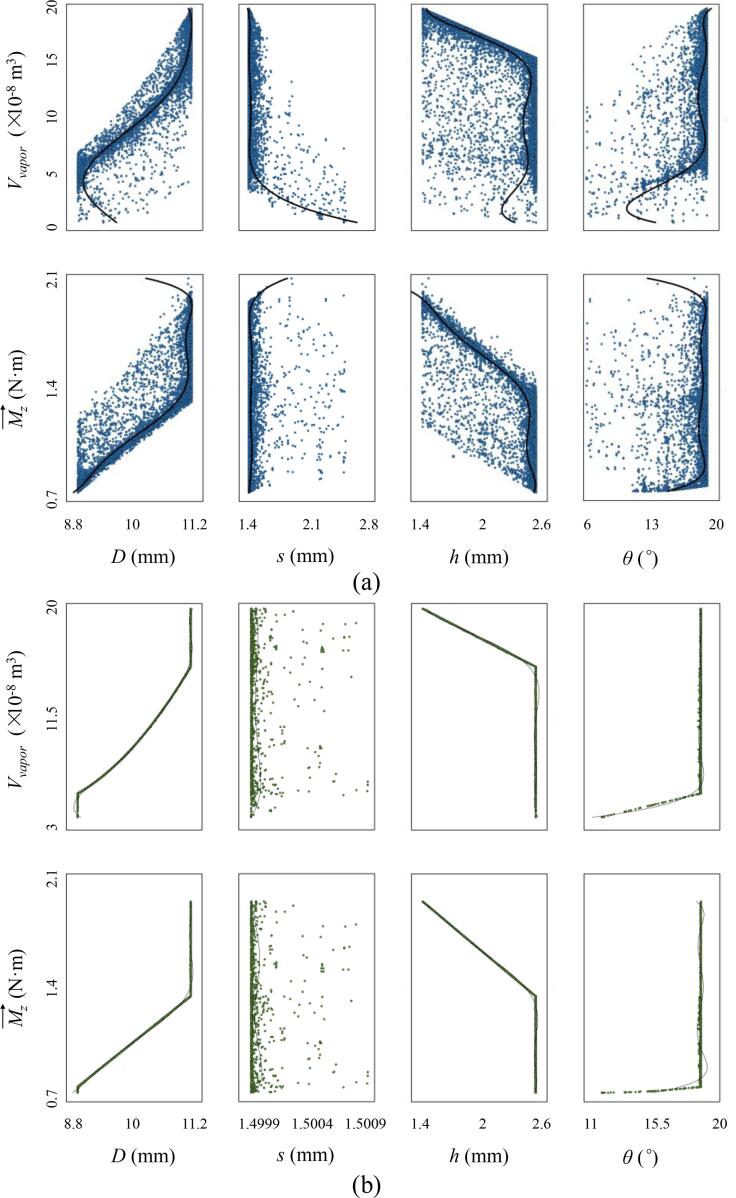
To visualize high-dimensional data in a more efficient manner, Fig. S3 shows the correlation table of the design variables and objectives for all points and Pareto front. Similar to the results of the parallel coordinates, D and h emerge notably positive (the correlation values > 0.89) and negative (the correlation values < -0.76) linear correlations in Pareto front (Fig. S3 (b)), respectively. This means the effects of these two design variables on the objectives are progressive, adjustable, controllable, and predictable. In contrast, the correlation effects of s and θ are considerably weaker, especially for s whose correlation value is close to zero. Similar conclusions can be also obtained in the individual distributions of all variables for all the points (Fig. 5 (a)) and the Pareto front (Fig. 5 (b)), where the best linear fit is represented by the black curve on each plot. For the Pareto front, the D and h curves have obvious finite slopes for both of the objectives, which means the magnitude of parameter variation is consistent with the strength of the effect. While the distribution slopes of the s and θ curves are close to infinity, indicating that a minor variation in the design variables will have a significant impact on the objectives. This is the reason why the individuals of s and θ were restricted on one side, as shown in Fig. 4 (b). Overall, D and h have much stronger linear relationships with the objectives in wider adjustment ranges, as the effects of both D and h on the two objectives are conflicting, unlike s and θ. Therefore, the compromise between D and h is the key to the success of the GA optimization. From another perspective, the effects of s and θ within the ranges were under secondary consideration, and their values were mainly used to fit D and h.
Fig. 5.
Individual distributions of the design variables and objectives for (a) all points and (b) Pareto front.
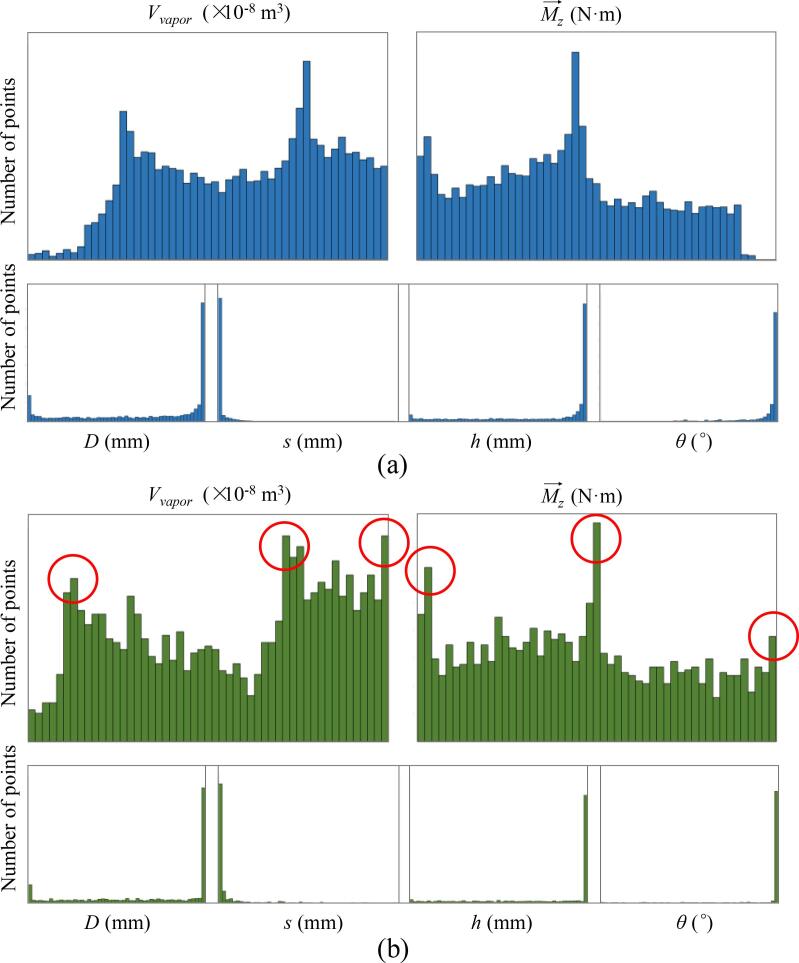
To show the potential directions in which the objectives may advance, the solution point number distributions for all points and Pareto front in the optimization process are illustrated in Figs. 6 (a) and (b), respectively. The upper two histograms in each figure represent the number distributions in terms of the objectives, while the lower four histograms stand for the number distributions according to the design variables. In addition, in each histogram, the horizontal axis represents the value of the design variables or the objectives ranging from the lower limit (left) to upper limit (right). The vertical axis represents the number of solution points. The purpose of the GA optimization is to select the optimal individuals in accordance with the law of survival of the fittest: The greater the number of survivors, the stronger the adaptation to the objective function. It can be found that the values of either or gathered around the three regions (marked with red circles). These distributions were generated from the same individuals, so the gathered regions were matched with each other, representing three elite subgroups. During the evolution process, the genes of these subgroups achieved comparative advantages, and more offspring individuals were produced and preserved compared with the other groups, which has a great influence on the direction of evolution and the distribution of the Pareto front. These subgroups are the basis for selecting the final results.
Fig. 6.
Point number distributions of the design variables and objectives for (a) all points and (b) Pareto Front.
Based on the above analysis, three global optimal points (i.e., A, B, and C) were finally selected from the Pareto front, as illustrated in Fig S4, with the corresponding design parameters shown in Table 2. They are the representatives of the diversiform optimized directions: The main targets of points A and C are to reduce the energy consumption (A) and enhance the cavitation generation (C), respectively. For point B, two objectives are properly compromised with the minimum distance to the Utopia point, revealing both the performance and economics were maximized. In addition, Table 2 also presents a comparison between the objectives of points A, B, and C obtained from the CFD and GA. The small errors between the results (less than 10%) demonstrate that the reasonable performance of the fitness functions and the high reliability of the GA optimization.
Table 2.
Selected optimal points of the GA optimization.
| Point | D (mm) | s (mm) | h (mm) | θ (°) | (× 10-8 m3) | (N∙m) | ||
|---|---|---|---|---|---|---|---|---|
| GA | CFD | GA | CFD | |||||
| Original | 10.00 | 2.00 | 1.00 | 0 | - | 5.44 | - | 1.63 |
| A | 9.00 | 1.50 | 2.50 | 18.70 | 5.73 | 6.23 | 0.76 | 0.82 |
| B | 11.00 | 1.50 | 2.49 | 18.75 | 15.27 | 13.92 | 1.35 | 1.40 |
| C | 11.00 | 1.50 | 1.50 | 18.75 | 19.61 | 20.82 | 1.93 | 1.94 |
3.3. Comparison between the original and optimal designs
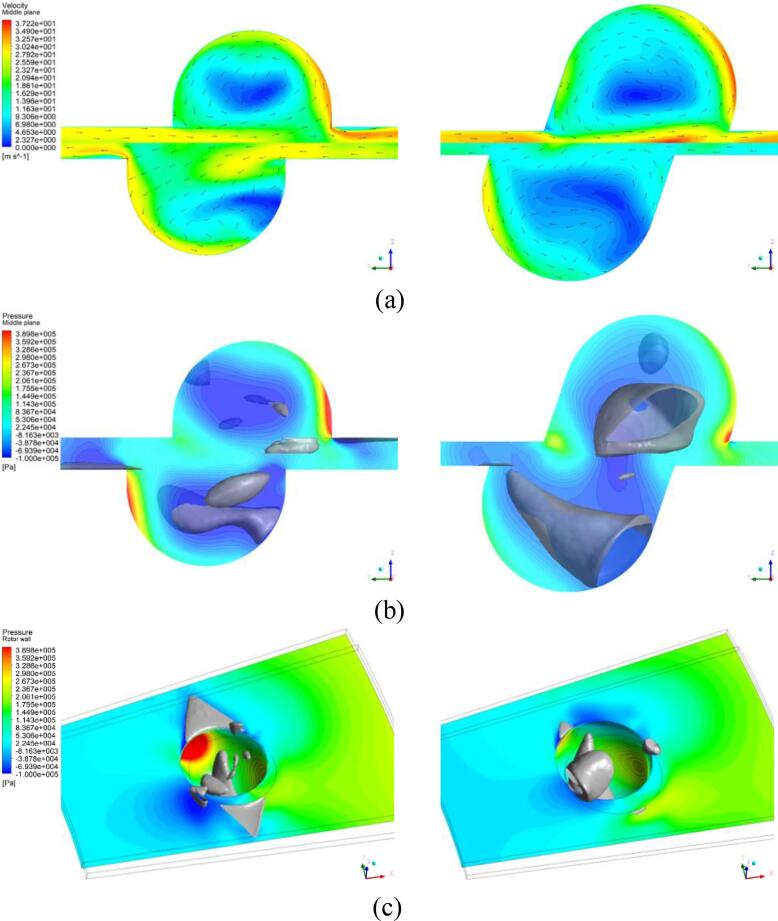
To examine why such significant improvements were achieved by the GA optimization, Fig. 7 presents a comparison of the velocity and pressure distributions and cavitation region in the original and selected optimal models (taking point B as an example). In the ARHCR, cavitation phenomenon is generated by the interaction between the static CGU (located on the stator) and moving CGU (located on the rotor): The fluid, which was driven by the rotor with a high rotational speed at 3600 rpm, formed a vortex inside each CGU, and the impacting flow induced a separation region on its downstream side (Fig. 7 (a)). When the static pressures in the vortexes and separation regions drop below the local saturated vapor pressure, vortex cavitation (VC) and sheet cavitation (SC) can be induced (Figs. 7 (b) and (c)). The detailed description on the flow field analysis and cavitation generation mechanism can be found in our previous studies [43], [44].
Fig. 7.
Comparison between the original (left) and selected optimal model B (right). The iso-surfaces in grey color in the middle and right represent cavitation patterns with the volume fraction of gas phase at 0.3. Velocity and vector distributions in relative reference frame on the middle plane (a), static pressure distribution and cavitation regions on the middle plane (b), and bird’s-eye view with the static pressure distribution of the rotor surface (c). The rotational direction of the rotor (lower part) in (c) is clockwise.
During the GA optimization, in comparison to the original CGU, the of the optimal CGU was increased by 155.9% (from 5.44 to 13.92 × 10-8 m3). This can be attributed to the following reasons: First, the inclination angle of the optimal CGU is 18.75°, while the direction of the original CGU is vertical to the rotor wall. Due to the identical open direction of the two CGUs, the induced interaction effect became considerably intense. The two well-developed vortexes were formed inside both the static and moving CGUs, which are significantly greater than those in the original model (Fig. 7 (a)). As a result, considerably larger VC regions were generated (Figs. 7 (b) and (c) Right). Second, the smaller interaction distance (reduced from 2 to 1.5 mm) also promoted the vortex intensity. This is because the narrow interaction distance can enhance the compressing effect between the two vortexes, which can be confirmed by the higher flow velocity in the clearance and inside the CGUs (Fig. 7 (a) Right).
On the contrary, SC regions generated in the optimal model were considerably suppressed compared with the original model, as demonstrated in Figs. 7 (b) and (c). The development of the separation regions was largely limited due to the smaller distance. More importantly, because of the inclined wall of the optimal CGU, the direction of the impact flow was almost parallel to the rotor and stator walls (Fig. 7 (a) Right), resulting in considerably smaller separation and cavitation regions. At the same time, this phenomenon significantly reduced the area of the high-pressure regions on the wall of the two CGUs, leading to a lower torque (decreased from 1.63 (original model) to 1.40 N∙m (optimal model)).
In summary, the CCD and GA processes utilized in the present work are highly effective: Compared with the original model, 1.56 times more cavitation generation was acquired by the optimal model while saving 14% of energy consumption. In the present GA optimization, s in all Pareto front was concentrated to 1.5 mm (i.e., the lower limit), because narrow distance can improve both cavitation generation and economical efficiency. The benefit of narrow distances was confirmed by Petkovšek, et al. [30], who found that when the distance of an ARHCR was reduced from 3.5 to 0.8 mm, the pressure amplitudes were increased from 0.7 to 1.7 bar on average. However, such benefits may be only achieved in interaction-type ARHCRs. Because the physical mechanism of the effect of D, h, s, and θ was explained in detail in our previous work [44], and is not discussed here. Nevertheless, they are needed to be further investigated by experimental methods since there is still no corresponding research so far.
4. Conclusions
In the present study, the multi-objective optimization of the CGU structure of a representative ARHCR was conducted by GA and CFD for the first time, with the objectives of maximizing the cavitation generation (i.e., ) and minimizing the energy consumption (i.e., ). The design variables included all important geometrical parameters of the CGU: D (9–11 mm), s (1.5–2.5 mm), h (1.5–2.5 mm), and θ (6.25°–18.75°). To identify the optimal structure, the global optimization algorithm NSGA-II was utilized after achieving the two fitness functions from the CCD. By analyzing 100 generations with a population of 100, 1630 non-dominated optimum design points with trade-off relationships were obtained. The results suggest that smaller s and greater θ in proper ranges always benefit the performance, while the values of D and h are needed to be appropriately selected with a compromise consideration. A selected global optimal point can improve the cavitation generation by 1.56 times while saving 14% of energy consumption, compared with the original model, indicating high effectiveness and reliability of the GA optimization. Nevertheless, it should be noticed that the cavitation intensity of an ARHCR in certain applications cannot characterized by the which was used in this study, therefore, the effects of the four variables obtained by CFD are needed to be further investigated by experiments.
CRediT authorship contribution statement
Xun Sun: Conceptualization, Investigation, Methodology, Writing – original draft, Writing – review & editing. Ze Yang: Methodology. Xuesong Wei: Writing – original draft, Methodology, Conceptualization. Yang Tao: Writing – review & editing. Grzegorz Boczkaj: Writing – review & editing. Joon Yong Yoon: Writing – review & editing. Xiaoxu Xuan: Conceptualization, Supervision. Songying Chen: Supervision, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (grant nos. 51906125, 51906126, U2006221); China Postdoctoral Science Foundation (grant nos. 2020T130364, 2019M650162, 2020M672058); Post-doctoral innovation project of Shandong Province (grant no. 202002006); Shandong Provincial Natural Science Foundation (grant nos. ZR2020KB004) and Youth Interdisciplinary Science and Innovative Research Groups of Shandong University (grant no. 2020QNQT014).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ultsonch.2021.105771.
Contributor Information
Xun Sun, Email: xunsun@sdu.edu.cn.
Ze Yang, Email: 201800162003@mail.sdu.edu.cn.
Xuesong Wei, Email: weixuesong@sdu.edu.cn.
Yang Tao, Email: yang.tao@njau.edu.cn.
Grzegorz Boczkaj, Email: grzegorz.boczkaj@pg.edu.pl.
Joon Yong Yoon, Email: joyoon@hanyang.ac.kr.
Xiaoxu Xuan, Email: xiaoxuxuan@sdu.edu.cn.
Songying Chen, Email: chensy66@sdu.edu.cn.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.United Nations, World Population Prospects 2019. https://population.un.org/wpp/., 2019.
- 2.A. Górak, A. Stankiewicz, Research Agenda for Process Intensification Towards a Sustainable World of 2050, 2011.
- 3.Chen Z., Xu X., Ding Z., Wang K., Sun X., Lu T., Konarova M., Eguchi M., Shapter J.G., Pan L., Yamauchi Y. Ti3C2 MXenes-derived NaTi2(PO4)3/MXene nanohybrid for fast and efficient hybrid capacitive deionization performance. Chem. Eng. J. 2021;407:127148. doi: 10.1016/j.cej.2020.127148. [DOI] [Google Scholar]
- 4.Cremaschi S. In: Computer Aided Chemical Engineering. Eden M.R., Siirola J.D., Towler G.P., editors. Elsevier; 2014. A perspective on process synthesis: Challenges and prospects; pp. 35–44. [Google Scholar]
- 5.Tao Y., Li D., Siong Chai W., Show P.L., Yang X., Manickam S., Xie G., Han Y. Comparison between airborne ultrasound and contact ultrasound to intensify air drying of blackberry: Heat and mass transfer simulation, energy consumption and quality evaluation. Ultrason. Sonochem. 2021;72:105410. doi: 10.1016/j.ultsonch.2020.105410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stankiewicz A.I., Moulijn J.A. Process intensification: transforming chemical engineering. Chem. Eng. Prog. 2000;96:22–34. [Google Scholar]
- 7.Tao Y., Wu Y., Han Y., Chemat F., Li D., Show P.L. Insight into mass transfer during ultrasound-enhanced adsorption/desorption of blueberry anthocyanins on macroporous resins by numerical simulation considering ultrasonic influence on resin properties. Chem. Eng. J. 2020;380:122530. doi: 10.1016/j.cej.2019.122530. [DOI] [Google Scholar]
- 8.Yi C., Lu Q., Wang Y., Wang Y., Yang B. Degradation of organic wastewater by hydrodynamic cavitation combined with acoustic cavitation. Ultrason. Sonochem. 2018;43:156–165. doi: 10.1016/j.ultsonch.2018.01.013. [DOI] [PubMed] [Google Scholar]
- 9.Jawale R.H., Gogate P.R. Novel approaches based on hydrodynamic cavitation for treatment of wastewater containing potassium thiocyanate. Ultrason. Sonochem. 2019;52:214–223. doi: 10.1016/j.ultsonch.2018.11.019. [DOI] [PubMed] [Google Scholar]
- 10.Jung K.-W., Park D.-S., Hwang M.-J., Ahn K.-H. Decolorization of Acid Orange 7 by an electric field-assisted modified orifice plate hydrodynamic cavitation system: Optimization of operational parameters. Ultrason. Sonochem. 2015;26:22–29. doi: 10.1016/j.ultsonch.2015.02.010. [DOI] [PubMed] [Google Scholar]
- 11.Rajoriya S., Bargole S., George S., Saharan V.K., Gogate P.R., Pandit A.B. Synthesis and characterization of samarium and nitrogen doped TiO2 photocatalysts for photo-degradation of 4-acetamidophenol in combination with hydrodynamic and acoustic cavitation. Sep. Purif. Technol. 2019;209:254–269. doi: 10.1016/j.seppur.2018.07.036. [DOI] [Google Scholar]
- 12.Abramov V.O., Abramova A.V., Cravotto G., Nikonov R.V., Fedulov I.S., Ivanov V.K. Flow-mode water treatment under simultaneous hydrodynamic cavitation and plasma. Ultrason. Sonochem. 2021;70:105323. doi: 10.1016/j.ultsonch.2020.105323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fedorov K., Sun X., Boczkaj G. Combination of hydrodynamic cavitation and SR-AOPs for simultaneous degradation of BTEX in water. Chem. Eng. J. 2021;417:128081. doi: 10.1016/j.cej.2020.128081. [DOI] [Google Scholar]
- 14.Gągol M., Cako E., Fedorov K., Soltani R.D.C., Przyjazny A., Boczkaj G. Hydrodynamic cavitation based advanced oxidation processes: Studies on specific effects of inorganic acids on the degradation effectiveness of organic pollutants. J. Mol. Liq. 2020;307:113002. doi: 10.1016/j.molliq.2020.113002. [DOI] [Google Scholar]
- 15.Sun X., Wang Z., Xuan X., Ji L.i., Li X., Tao Y., Boczkaj G., Zhao S., Yoon J.Y., Chen S. Disinfection characteristics of an advanced rotational hydrodynamic cavitation reactor in pilot scale. Ultrason. Sonochem. 2021;73:105543. doi: 10.1016/j.ultsonch.2021.105543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sun X., Chen S., Liu J., Zhao S., Yoon J.Y. Hydrodynamic cavitation: A promising technology for industrial-scale synthesis of nanomaterials. Front. Chem. 2020;8:259. doi: 10.3389/fchem.2020.00259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pandit A.B., Joshi J.B. Hydrolysis of fatty oils: effect of cavitation. Chem. Eng. Sci. 1993;48(19):3440–3442. doi: 10.1016/0009-2509(93)80164-L. [DOI] [Google Scholar]
- 18.Wang B., Su H., Zhang B.o. Hydrodynamic cavitation as a promising route for wastewater treatment – A review. Chem. Eng. J. 2021;412:128685. doi: 10.1016/j.cej.2021.128685. [DOI] [Google Scholar]
- 19.Gostiša J., Širok B., Repinc S.K., Levstek M., Stražar M., Bizjan B., Zupanc M. Performance evaluation of a novel pilot-scale pinned disc rotating generator of hydrodynamic cavitation. Ultrason. Sonochem. 2021;72:105431. doi: 10.1016/j.ultsonch.2020.105431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Y.M. Oo, G. Prateepchaikul, K. Somnuk, Continuous acid-catalyzed esterification using a 3D printed rotor–stator hydrodynamic cavitation reactor reduces free fatty acid content in mixed crude palm oil, Ultrason. Sonochem., 72 (2021) 105419, https://doi.org/10.1016/j.ultsonch.2020.105419. [DOI] [PMC free article] [PubMed]
- 21.Sim J.Y., Beckman S.L., Anand S., Martínez-Monteagudo S.I. Hydrodynamic cavitation coupled with thermal treatment for reducing counts of B. coagulans in skim milk concentrate. J. Food Eng. 2021;293:110382. doi: 10.1016/j.jfoodeng.2020.110382. [DOI] [Google Scholar]
- 22.J. Vilarroig, R. Martínez, E. Zuriaga-Agustí, S. Torró, M. Galián, S. Chiva, Design and optimization of a semi-industrial cavitation device for a pretreatment of an anaerobic digestion treatment of excess sludge and pig slurry, 92 (2020) 2060-2071, https://doi.org/10.1002/wer.1366. [DOI] [PubMed]
- 23.Maršálek B., Zezulka Š., Maršálková E., Pochylý F., Rudolf P. Synergistic effects of trace concentrations of hydrogen peroxide used in a novel hydrodynamic cavitation device allows for selective removal of cyanobacteria. Chem. Eng. J. 2020;382:122383. doi: 10.1016/j.cej.2019.122383. [DOI] [Google Scholar]
- 24.Kosel J., Šinkovec A., Dular M. A novel rotation generator of hydrodynamic cavitation for the fibrillation of long conifer fibers in paper production. Ultrason. Sonochem. 2019;59:104721. doi: 10.1016/j.ultsonch.2019.104721. [DOI] [PubMed] [Google Scholar]
- 25.Badve M.P., Gogate P.R., Pandit A.B., Csoka L. Hydrodynamic cavitation as a novel approach for delignification of wheat straw for paper manufacturing. Ultrason. Sonochem. 2014;21(1):162–168. doi: 10.1016/j.ultsonch.2013.07.006. [DOI] [PubMed] [Google Scholar]
- 26.Sun X., Kang C.H., Park J.J., Kim H.S., Om A.S., Yoon J.Y. An experimental study on the thermal performance of a novel hydrodynamic cavitation reactor. Exp. Therm. Fluid Sci. 2018;99:200–210. doi: 10.1016/j.expthermflusci.2018.02.034. [DOI] [Google Scholar]
- 27.Mancuso G., Langone M., Andreottola G. A swirling jet-induced cavitation to increase activated sludge solubilisation and aerobic sludge biodegradability. Ultrason. Sonochem. 2017;35:489–501. doi: 10.1016/j.ultsonch.2016.11.006. [DOI] [PubMed] [Google Scholar]
- 28.Suenaga T., Nishimura M., Yoshino H., Kato H., Nonokuchi M., Fujii T., Satoh H., Terada A., Hosomi M. High-pressure jet device for activated sludge reduction: Feasibility of sludge solubilization. Biochem. Eng. J. 2015;100:1–8. doi: 10.1016/j.bej.2015.03.022. [DOI] [Google Scholar]
- 29.Zhang S., Zhang P., Zhang G., Fan J., Zhang Y. Enhancement of anaerobic sludge digestion by high-pressure homogenization. Bioresour. Technol. 2012;118:496–501. doi: 10.1016/j.biortech.2012.05.089. [DOI] [PubMed] [Google Scholar]
- 30.Petkovšek M., Mlakar M., Levstek M., Stražar M., Širok B., Dular M. A novel rotation generator of hydrodynamic cavitation for waste-activated sludge disintegration. Ultrason. Sonochem. 2015;26:408–414. doi: 10.1016/j.ultsonch.2015.01.006. [DOI] [PubMed] [Google Scholar]
- 31.Lee G., Lee I., Han J.-I. A combined method of hydrodynamic cavitation and alkaline treatment for waste-activated sludge solubilization; N/P recovery from anaerobic granular sludge. J. Environ. Chem. Eng. 2019;7(5):103329. doi: 10.1016/j.jece:2019.103329. [DOI] [Google Scholar]
- 32.Fang W., Zhang P., Zhang G., Jin S., Li D., Zhang M., Xu X. Effect of alkaline addition on anaerobic sludge digestion with combined pretreatment of alkaline and high pressure homogenization. Bioresour. Technol. 2014;168:167–172. doi: 10.1016/j.biortech.2014.03.050. [DOI] [PubMed] [Google Scholar]
- 33.Zhang Y., Zhang P., Zhang G., Ma W., Wu H., Ma B. Sewage sludge disintegration by combined treatment of alkaline+high pressure homogenization. Bioresour. Technol. 2012;123:514–519. doi: 10.1016/j.biortech.2012.07.078. [DOI] [PubMed] [Google Scholar]
- 34.Abbasi E., Saadat S., Karimi Jashni A., Shafaei M.H. A novel method for optimization of slit Venturi dimensions through CFD simulation and RSM design. Ultrason. Sonochem. 2020;67:105088. doi: 10.1016/j.ultsonch.2020.105088. [DOI] [PubMed] [Google Scholar]
- 35.Sun X., Liu J., Ji L.i., Wang G., Zhao S., Yoon J.Y., Chen S. A review on hydrodynamic cavitation disinfection: The current state of knowledge. Sci. Total Environ. 2020;737:139606. doi: 10.1016/j.scitotenv.2020.139606. [DOI] [PubMed] [Google Scholar]
- 36.Milly P.J., Toledo R.T., Harrison M.A., Armstead D. Inactivation of food spoilage microorganisms by hydrodynamic cavitation to achieve pasteurization and sterilization of fluid foods. J. Food Sci. 2007;72(9):M414–M422. doi: 10.1111/j.1750-3841.2007.00543.x. [DOI] [PubMed] [Google Scholar]
- 37.Kwon W.C., Yoon J.Y. Experimental study of a cavitation heat generator. Proc. Inst. Mech. Eng, Part E. 2013;227(1):67–73. doi: 10.1177/0954408912451535. [DOI] [Google Scholar]
- 38.Sun X., Park J.J., Kim H.S., Lee S.H., Seong S.J., Om A.S., Yoon J.Y. Experimental investigation of the thermal and disinfection performances of a novel hydrodynamic cavitation reactor. Ultrason. Sonochem. 2018;49:13–23. doi: 10.1016/j.ultsonch.2018.02.039. [DOI] [PubMed] [Google Scholar]
- 39.Šarc A., Kosel J., Stopar D., Oder M., Dular M. Removal of bacteria Legionella pneumophila, Escherichia coli, and Bacillus subtilis by (super)cavitation. Ultrason. Sonochem. 2018;42:228–236. doi: 10.1016/j.ultsonch.2017.11.004. [DOI] [PubMed] [Google Scholar]
- 40.Sun X., Jia X., Liu J., Wang G., Zhao S., Ji L.i., Yong Yoon J., Chen S. Investigation on the Characteristics of an Advanced Rotational Hydrodynamic Cavitation Reactor for Water Treatment. Sep. Purif. Technol. 2020;251:117252. doi: 10.1016/j.seppur.2020.117252. [DOI] [Google Scholar]
- 41.Kosel J., Šuštaršič M., Petkovšek M., Zupanc M., Sežun M., Dular M. Application of (super)cavitation for the recycling of process waters in paper producing industry. Ultrason. Sonochem. 2020;64:105002. doi: 10.1016/j.ultsonch.2020.105002. [DOI] [PubMed] [Google Scholar]
- 42.Badve M.P., Alpar T., Pandit A.B., Gogate P.R., Csoka L. Modeling the shear rate and pressure drop in a hydrodynamic cavitation reactor with experimental validation based on KI decomposition studies. Ultrason. Sonochem. 2015;22:272–277. doi: 10.1016/j.ultsonch.2014.05.017. [DOI] [PubMed] [Google Scholar]
- 43.Sun X., Xuan X., Song Y., Jia X., Ji L.i., Zhao S., Yong Yoon J., Chen S., Liu J., Wang G. Experimental and numerical studies on the cavitation in an advanced rotational hydrodynamic cavitation reactor for water treatment. Ultrason. Sonochem. 2021;70:105311. doi: 10.1016/j.ultsonch.2020.105311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sun X., You W., Xuan X., Ji L.i., Xu X., Wang G., Zhao S., Boczkaj G., Yoon J.Y., Chen S. Effect of the cavitation generation unit structure on the performance of an advanced hydrodynamic cavitation reactor for process intensifications. Chem. Eng. J. 2021;412:128600. doi: 10.1016/j.cej.2021.128600. [DOI] [Google Scholar]
- 45.Sun X., Xuan X., Ji L.i., Chen S., Liu J., Zhao S., Park S., Yoon J.Y., Om A.S. A novel continuous hydrodynamic cavitation technology for the inactivation of pathogens in milk. Ultrason. Sonochem. 2021;71:105382. doi: 10.1016/j.ultsonch.2020.105382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kim H., Koo B., Sun X., Yoon J.Y. Investigation of sludge disintegration using rotor-stator type hydrodynamic cavitation reactor. Sep. Purif. Technol. 2020;240:116636. doi: 10.1016/j.seppur.2020.116636. [DOI] [Google Scholar]
- 47.LinminLi, ZhengdongWang, XiaojunLi, ZuchaoZhu, Multiscale modeling of tip-leakage cavitating flows by a combined volume of fluid and discrete bubble model, 33 (2021) 062104, 10.1063/5.0054795.
- 48.Sun X., Kim S., Yang S.D., Kim H.S., Yoon J.Y. Multi-objective optimization of a Stairmand cyclone separator using response surface methodology and computational fluid dynamics. Powder Technol. 2017;320:51–65. doi: 10.1016/j.powtec.2017.06.065. [DOI] [Google Scholar]
- 49.Wei X., Wang X., Chen S. Research on parameterization and optimization procedure of low-Reynolds-number airfoils based on genetic algorithm and Bezier curve. Adv. Eng. Software. 2020;149:102864. doi: 10.1016/j.advengsoft.2020.102864. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.