Abstract
Background:
Recent work showed that the temporal growth of the novel coronavirus disease (COVID-19) follows a sub-exponential power-law scaling whenever effective control interventions are in place. Taking this into consideration, we present a new phenomenological logistic model that is well-suited for such power-law epidemic growth.
Methods:
We empirically develop the logistic growth model using simple scaling arguments, known boundary conditions and a comparison with available data from four countries, Belgium, China, Denmark and Germany, where (arguably) effective containment measures were put in place during the first wave of the pandemic. A non-linear least-squares minimization algorithm is used to map the parameter space and make optimal predictions.
Results:
Unlike other logistic growth models, our presented model is shown to consistently make accurate predictions of peak heights, peak locations and cumulative saturation values for incomplete epidemic growth curves. We further show that the power-law growth model also works reasonably well when containment and lock down strategies are not as stringent as they were during the first wave of infections in 2020. On the basis of this agreement, the model was used to forecast COVID-19 fatalities for the third wave in South Africa, which was in progress during the time of this work.
Conclusion:
We anticipate that our presented model will be useful for a similar forecasting of COVID-19 induced infections/deaths in other regions as well as other cases of infectious disease outbreaks, particularly when power-law scaling is observed.
Keywords: COVID-19, Subexponential power-law growth, Logistic growth, Non-linear least squares
1. Introduction
The COVID-19 pandemic has reinvigorated efforts at an unprecedented scale to better understand the dynamics and mechanism of infectious disease spread. Presently, there is significant interest worldwide to model region-specific infection and mortality curves, while also working on effective intervention and containment strategies. It is hoped that such a collective endeavor would contribute towards preventing an uncontrolled proliferation of the disease, while simultaneously countering near irreparable socio-economic damage from multiple waves of infections. This has resulted in a deluge of scientific literature related to the pandemic, that have proved to be a challenge to keep up with (Brainard, 2020). A large subset of research papers investigated the spatio-temporal evolution of the disease (Chinazzi et al., 2020, Gatto et al., 2020, Gross et al., 2020), mostly using variants of the compartmental SIR (Susceptible-Infected-Removed) epidemiological model (Maier and Brockmann, 2020, Brandenburg, 2020, Barman et al., 2020, Wu et al., 2020b, Bustamante-Castañeda et al., 2021, Li et al., 2020, Roques et al., 2020) to analyze the number of infections (or deaths) in specific regions. Other methods involved the use of phenomenological models (Majumder and Mandl, 2020, Roosa et al., 2020), time-varying and non-linear Markov processes (Wang et al., 2020a, Gourieroux and Jasiak, 2020), superpositions of epidemic waves (Koltsova et al., 2020), hybrid nonparametric models (Wang et al., 2020b) and other data-driven approaches (Salas, 2021, Schneble et al., 2021, Altmejd et al., 2020), including those based on artificial intelligence (Chen et al., 2020), etc. Along these lines, we recently performed a random walk Monte Carlo study to make temporal growth exponent predictions for COVID-19-like disease spread (Triambak and Mahapatra, 2021), particularly for a spatially constrained, yet stochastically interacting population. In that work, similar to other simulational approaches (Mollison, 1977, Filipe and Gibson, 1998), the spread of the disease was modeled on the basis of ‘contact’ interactions. We identified certain similarities between our simulation results and those obtained from other differential-equation-based extended SIR models (Maier and Brockmann, 2020, Brandenburg, 2020). Our results further showed that spatial mobility plays a key role in determining the eventual growth in the total number of infections/deaths as a function of time. While this conclusion should not be surprising (Hallatschek and Fisher, 2014), it was corroborated by a recent data-driven analysis of the ‘mobility-network’ in Germany, using cellular phone data (Schlosser et al., 2020). These investigations established a connection between the three approaches (data-driven, simulation, and compartmental model) used to better understand infectious disease spread.
In terms of phenomenological modeling, logistic growth models (LGMs) (Roosa et al., 2020, Masjedi et al., 2020, Wu et al., 2020a, Singer, 2020, Batista, 2020, Vattay, 2020, Morais, 2020, Shen, 2020, Yang et al., 2021, Jia et al., 2020, Dattoli et al., 2020, Sonnino and Nardone, 2020, Molina-Cuevas, 2020) were extensively used for making COVID-19 related predictions. This is not completely unexpected, as LGMs were successfully used in the past for predicting growth curves in epidemics such as Ebola, SARS, H1N1, dengue, etc. (Pell et al., 2018, Chowell et al., 2019, Wang et al., 2012). Along these lines, our previous work (Triambak and Mahapatra, 2021) showed that although the most commonly used generalized LGM (Richards, 1959) works well for exponential growth, it fails to satisfactorily fit data that have power-law scaling. As a continuation of our engagement with this problem, in this work we present a logistic growth model that describes such data more accurately.
2. Logistic growth models
In the context of the COVID-19 pandemic, the simplest LGM used by some research groups (Singer, 2020, Batista, 2020, Vattay, 2020, Morais, 2020, Shen, 2020) is described by the well-known Verhulst differential equation
| (1) |
where is the intrinsic growth constant and (also called the carrying capacity) is the asymptotic (saturation) limit for , as . The general solution of Eq. (1) is of the form
| (2) |
where the point of inflection is at . The above is a special case of the Richards LGM (Richards, 1959)
| (3) |
which solves the differential equation
| (4) |
Here, the parameter decides both the shape of the growth curve as well as its inflection point. For example, as , Eq. (4) becomes the Gompertz growth curve (Gompertz, 1825, Laird, 1964). The special case of describes classical logistic growth, shown in Eqs. (1), (2). To be consistent with other recent literature and given the fact that we are only interested in the family of curves with , we rewrite Eq. (4) as
| (5) |
where and .
Recently, it was shown (Chowell et al., 2016) that in order to allow for sub-exponential growth, one can further generalize the Richards equation by replacing with in Eq. (5), where is a ‘deceleration’ parameter (Viboud et al., 2016). Such sub-exponential growth was observed with initial COVID-19 data from China, where an analysis (Maier and Brockmann, 2020) of the number of reported cases from several provinces in the country showed a type power-law growth in . This was attributed to effective containment and mitigation measures, as well as behavioral changes of the population (Maier and Brockmann, 2020). Such control interventions prevent a homogeneous mixing (Fofana and Hurford, 2017) of the population, which if unchecked would lead to exponential growth, provided there is no appreciable depletion of the susceptible population (Bailey, 1975). Our previous simulations (Triambak and Mahapatra, 2021) showed that the minimum growth obtained under the most stringent mobility restrictions is quadratic in nature . More realistically one would expect growth exponents that are slightly higher than 2, even under effective containment (Maier and Brockmann, 2020, Triambak and Mahapatra, 2021) and strict lockdown measures. It is reasonable to expect that during the first wave of the pandemic (in 2020) most countries followed similarly stringent containment strategies (at various levels) to counter the spread of COVID-19 within their population. Therefore their cumulative infection (and fatality) curves are expected to have power-law growth exponents in the range of 2 to 3 (Triambak and Mahapatra, 2021). Below we develop a new LGM that can adequately describe such data, and make reasonably accurate and consistent predictions.
3. Methods
3.1. Development of the power-law LGM
To develop the model, we start similarly as in Eq. (1), with the ansatz that the daily infection rate is proportional to , the number of individuals who are already infected by the disease. Furthermore, it is apparent that for bounded (logistic) growth, one requires the daily rate to also be proportional to a term similar to the ones described in the parentheses of Eqs. (1), (5). Therefore, for power-law growth, with , we write a general form of daily infection rate, analogous to Eq. (5) as
| (6) |
It is important to note that here has an explicit dependence on time, unlike Eqs. (1), (5). The parameter is in units of time, so that in the asymptotic limit as (well past the peak of the epidemic curve, for large values of ), . The , and parameters are dimensionless, while has units of .
In the next step we empirically tested and developed this model, by fitting the above function to available data from four countries, Belgium, China, Denmark and Germany, during the first wave of infections in 2020. These countries were chosen because the data show a reasonably successful containment of the spread of COVID-19 within their population (World Health Organisation, 2021), during the first wave. Similar to our previous work (Triambak and Mahapatra, 2021), we performed a time-series analyses for the number of reported daily deaths,2 instead of infections. This was due to several reasons. Firstly, the death toll is far more important to quantify than the infection rate in a given population, although they are related. Secondly, when performing a global comparison of data from different countries, we assume that COVID-19-related deaths are more accurately and uniformly recorded in general. And finally, given the strong correlation between the number of infected cases and number of deaths, the time-series trends in both death and infection rates are expected to be similar to one another.3
3.2. Analysis
The fits were performed using a non-linear least squares (NLS) algorithm that minimized the sum of squared residuals (SSR), defined by
| (7) |
with respect to the daily reported deaths , where
| (8) |
and is the cumulative number of deaths in the model. This initial NLS fitting procedure showed that the five parameter fit in Eq. (6) was not optimal for such analysis. The parameters were found to be highly correlated, with correlation coefficients in the range of . Successive fits to the same data, for different initial values for the parameters resulted in arbitrary and widely-varying converged fit parameters, particularly , and . Despite this, the fits yielded very similar values for the minimum SSR and nearly indistinguishable results. The above showed that the model in Eq. (6) was not feasible, particularly for an ‘out-of-sample’ forecasting using partial epidemic curves. Consequently, we modified Eq. (6) to
| (9) |
as a means to bypass the problem. For this part of the analysis, the parameter was kept fixed at a large value ( days). This prescription reduced the problem to four parameters, while placing significant restrictions on the allowed parameter space. Furthermore, the fits showed a negligible dependence on (as long as it is large and fixed), with the parameters consistently converging to very similar values.
4. Results and discussion
4.1. Results for first wave data from 2020
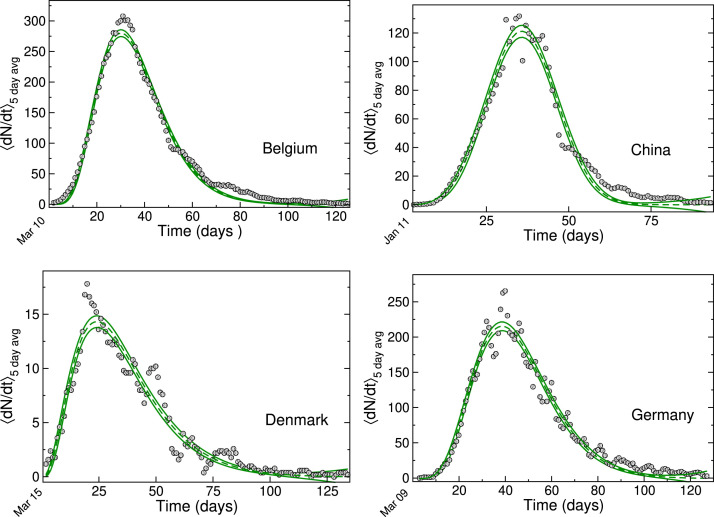
On fitting the data using our modified power-law logistic function, we obtain good agreement with the daily mortality curves for the four countries considered earlier. This is shown in Fig. 1. As expected, the product of and mainly contribute to the rising part of the curve. The other two parameters and contribute to truncating the rise. Together, these parameters describe the features of individual epidemic curves. The tailing in each curve mainly depends on country-specific mitigation and containment measures. It is found to be more prominent in the cases of Belgium, Denmark, and Germany.
Fig. 1.
Power-law growth model fits to reported deaths for Belgium, China, Denmark and Germany, shown with 95% confidence interval (CI) bands (shown in green). The data points (filled circles) are generated from a 5 day moving average of number of daily deaths reported by the World Health Organisation (2021), for the first wave of infections in 2020. In each case, the date of the first reported death (day 1) is indicated at on the time axis. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article).
While this part of the analysis was necessary to show the more than satisfactory agreement of our power-law growth model with data, particularly from countries where the pandemic peak had long passed, this is not a robust test of the forecasting ability of the model. We next performed an out-of-sample forecasting test, this time only using data points from the rising part of the curve. To avoid fit convergences to ‘fake’ minima that do not correspond to realistic values, we used a comparison with available data to empirically develop the procedure described below. First the parameter space was mapped to arrive in the vicinity of the correct SSR minimum. This was done by performing a first round of non-linear SSR minimization with the constraints4 , , and . After this initial step, the restrictions on , and were removed and the iterative grid-search NLS algorithm was used evaluate the values that yielded the minimum SSR in that region of parameter space.
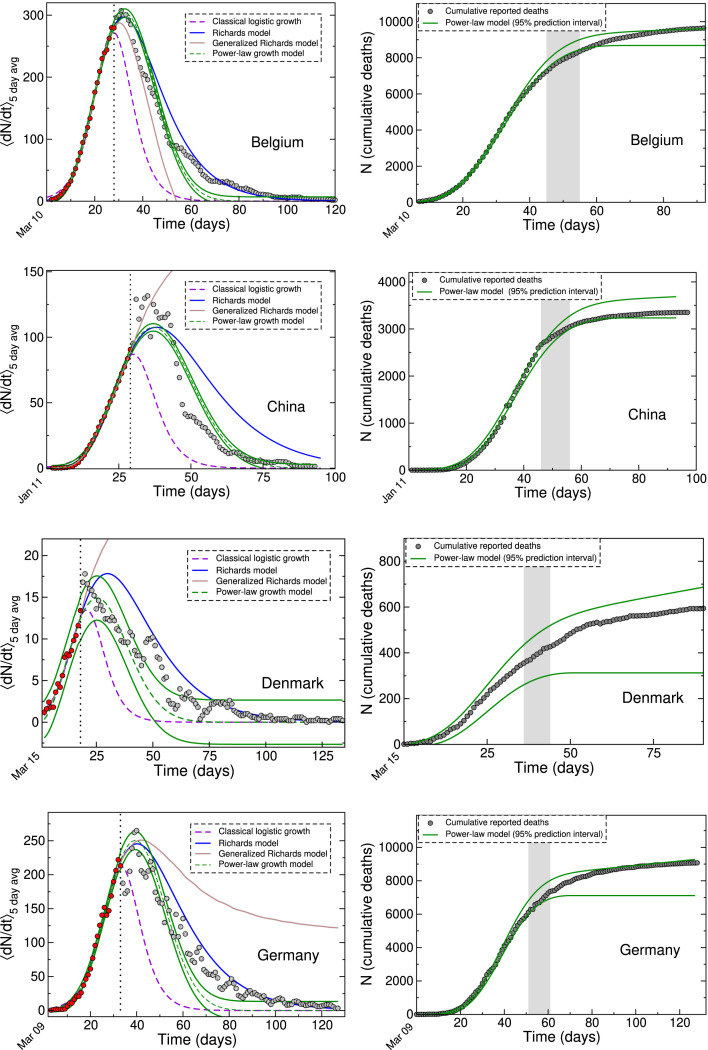
Our analyses showed that the procedure described above yielded reasonable agreement with the full data from different countries consistently. This agreement is illustrated in Fig. 2, that also compares our fit results to those obtained from the classical LGM and both versions of the Richards LGM. The forecasting performance of the four models are further compared in Table 1, which lists three performance metrics. These include the root mean squared (RMS) error,
| (10) |
where is the total number of data points in the curve, the mean absolute percentage error (MAPE),
| (11) |
and the coverage of the 95% prediction interval, which quantifies the proportion of observations that fell within that range. As evident in Fig. 2 and Table 1, the predictions of the classical LGM and the generalized Richards model yield least agreement with the full data, while the Richards model agrees with some of the data. The power-law growth model is found to be the most consistent in its forecasting performance, showing reasonable agreement with the data in all cases. Fig. 2 also shows cumulative fatality data for each of the four countries, together with predictions of the power-law model. Here as well one observes excellent agreement with the data.
Fig. 2.
Left panel: Various LGM fits to the daily death data from Belgium, China, Denmark and Germany, shown together with 95% prediction intervals for the power-law model. The data points are the same as shown in Fig. 1 and correspond to the first waves in 2020. The red filled circles represent the ‘in-sample’ calibration points used to test the forecasting ability of each LGM. Right panel: Cumulative data shown together with 95% prediction intervals from power-law growth model fits. The gray band shows the approximate date range when the curves begin to flatten out. In each case, the date of the first reported death (day 1) is indicated at on the time axis. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article).
Table 1.
Out-of-sample forecasting performance metrics for the four countries, using different LGM models described in this work.
| Country | Growth | Root mean | Mean absolute | Percentage coverage of |
|---|---|---|---|---|
| model | squared error | percentage error | 95% prediction interval | |
| Logistic | 51.7 | 76.4 | 17 | |
| Belgium | Richards | 17.4 | 25.8 | 76 |
| Gen. Richards | 31.8 | 64.1 | 21 | |
| Power-law | 18.8 | 56.9 | 60 | |
| Logistic | 28.8 | 112.7 | 40 | |
| China | Richards | 22.7 | 175.2 | 32 |
| Gen. Richards | 109.3 | 1679.5 | 31 | |
| Power-law | 11.4 | 40.8 | 58 | |
| Logistic | 3.9 | 78.0 | 61 | |
| Denmark | Richards | 2.6 | 53.6 | 73 |
| Gen. Richards | 24.2 | 3434.0 | 15 | |
| Power-law | 2.0 | 64.7 | 88 | |
| Logistic | 57.1 | 85.7 | 26 | |
| Germany | Richards | 22.6 | 28.0 | 59 |
| Gen. Richards | 90.1 | 465.1 | 25 | |
| Power-law | 25.1 | 56.8 | 47 | |
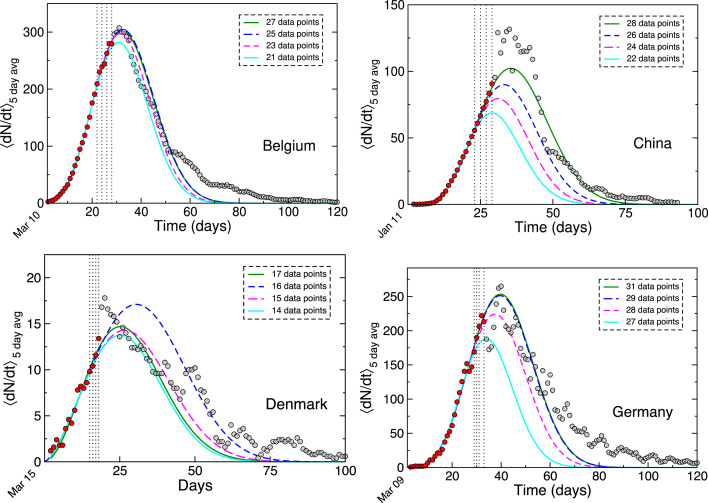
Another check of the robustness of our analysis was performed by systematically reducing the number of in-sample calibration points (marked in red in Fig. 2) in the NLS fitting procedure. This effectively tested the stability of our model predictions. The results of this systematic check are shown in Fig. 3 and Table 2. The latter lists the number of in-sample data points used for the fits in each case, and the corresponding RMSE values as a forecasting metric. It is evident that as long as a reasonable number of in-sample data points are used, the power-law model makes reliable predictions.
Fig. 3.
Power-law logistic growth model predictions using different ranges of data in the rising part of the curve. The dotted lines mark the final in-sample calibration points from the data in Fig. 2. Similar to the other plots, the date of the first reported death (day 1) is indicated at on the time axis. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article).
Table 2.
Stability tests for power-law LGM forecasts, performed by a systematic removal of in-sample data points.
| Country | Number of | Color in | RMSE |
|---|---|---|---|
| data points | Fig. 3 | (full data) | |
| 27 | Green | 18.4 | |
| Belgium | 25 | Blue | 19.1 |
| 23 | Magenta | 19.5 | |
| 21 | Cyan | 22.2 | |
| 28 | Green | 10.0 | |
| China | 26 | Blue | 16.6 |
| 24 | Magenta | 24.5 | |
| 22 | Cyan | 31.7 | |
| 17 | Green | 2.1 | |
| Denmark | 16 | Blue | 2.7 |
| 15 | Magenta | 1.8 | |
| 14 | Cyan | 2.2 | |
| 31 | Green | 24.8 | |
| Germany | 29 | Blue | 24.7 |
| 28 | Magenta | 30.5 | |
| 27 | Cyan | 50.1 | |
4.2. Results for second and third wave data from South Africa (2020/ 2021)
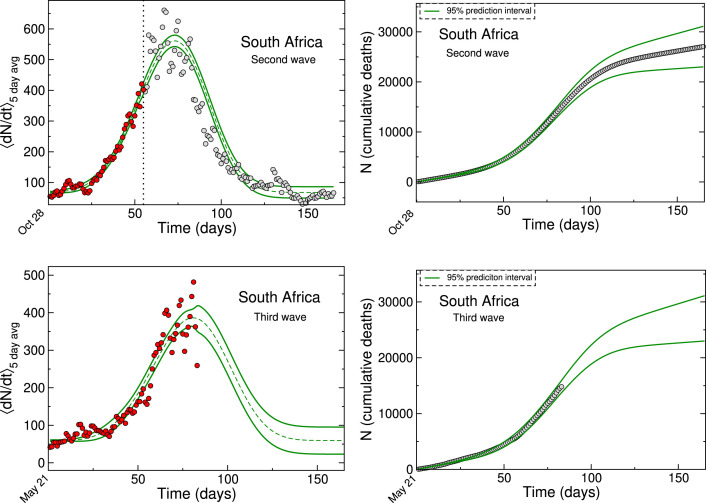
Once assured that our data analysis procedure was on a secure footing, we performed a similar analysis for the second and third waves in South Africa. It may be noted that strict lock down and containment policies were not imposed in these scenarios (compared to the first wave) and that only partial data were available for the third wave at the time of this work. Furthermore, the vaccinated status of part of the population and the different variants of the SARS-CoV-2 virus add additional complications that allow a rigorous test of the power-law growth model.
Fig. 4 shows power-law growth model fits to the second and third wave fatality data from South Africa. The in-sample red data points were fit similarly as before, with two minor differences. Since the growth exponent is expected to be higher due to comparatively relaxed lockdown scenarios (Triambak and Mahapatra, 2021), the ranges on and were increased to 2–6 in the initial restricted fit. An additional ‘background’ parameter was required to be added to Eq. (9). This parameter took into account the roughly constant number of deaths/infections that occur between the waves. For the second wave, we observe excellent agreement between the data and the model predictions, which further validates the power-law LGM. The model also showed good agreement with cumulative fatality data, obtained from the reported number of deaths during this time. Based on this validation, we used the power-law fit to make forecasts on the partial third wave epidemic curve for South Africa. The fit indicated that during the time of our data analysis, South Africa was approaching the peak of its third wave for Covid-19 induced fatalities. Similarly, the corresponding cumulative data showed that the flattening of it growth curve was imminent .
Fig. 4.
Left panel: Power law LGM fits to second and third wave fatality data from South Africa. The data are obtained from World Health Organisation (2021) and are represented by filled circles. The start dates on the -axis are for the years 2020 and 2021, for the second and third waves respectively. The red points show the in-sample calibration points used for the forecasting. The green curves show prediction intervals. In each case, the date that marks the beginning of the data-analysis region for the epidemic wave is indicated at on the time axis. Right panel: Cumulative deaths obtained from the World Health Organization, shown together with our model forecasts at the 95% prediction interval.(For interpretation of the references to color in this figure, the reader is referred to the web version of this article).
5. Summary
In summary, we used an empirical analysis to develop a new logistic power-law growth model (LGM) that was applied to COVID-19 fatality data. This is relevant, as sub-exponential power-law growth is not adequately described by earlier variants of LGMs. Our model is found to be rather robust in accurately predicting peak and saturation values in epidemic growth curves from Belgium, China, Denmark and Germany. Following this validation, the power-law LGM is used to predict the COVID-19 induced-fatalities in the second and third waves for South Africa, after validating the model predictions for the former. We anticipate that our presented growth model will be useful for forecasting COVID-19 induced infections/deaths in other regions and for studies of epidemic spread in general.
CRediT authorship contribution statement
S. Triambak: Conceptualization, Data analysis, Writing – original draft, Editing. D.P. Mahapatra: Conceptualization, Data analysis, Writing – original draft, Editing. N. Mallick: Data analysis, Software. R. Sahoo: Data analysis, Software.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We are thankful to Prof. Niranjan Barik for useful discussions related to this work. ST acknowledges support from the NRF (National Research Foundation), South Africa , under Grant. No. 85100.
Footnotes
All data described in this work are 5-day rolling averaged.
We caution that one must be careful in making this assumption, which may fail when live-saving treatment options are put in place (or inaccessible) midway, thereby affecting daily mortality rates. Such real-time interventions affect all phenomenological models.
In some computer programs care should be taken that the fitted values for the parameters do not converge to their upper or lower bounds.
References
- Altmejd Adam, Rocklöv Joacim, Wallin Jonas. 2020. Nowcasting Covid-19 statistics reported withdelay: a case-study of Sweden. arXiv preprint arXiv:2006.06840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey Norman T.J. Charles Griffin and Company Limited; 1975. The Mathematical Theory of Infectious Diseases and its Applications. [Google Scholar]
- Barman Madhab, Nayak Snigdhashree, Yadav Manoj K., Raha Soumyendu, Mishra Nachiketa. 2020. Modeling control, lockdown & exit strategies for COVID-19 pandemic in India. arXiv preprint arXiv:2007.07988. [Google Scholar]
- Batista Milan. Estimation of the final size of the COVID-19 epidemic. MedRxiv. 2020 doi: 10.1101/2020.02.16.20023606. [DOI] [Google Scholar]
- Brainard Jeffrey. New tools aim to tame pandemic paper tsunami. Science. 2020;368(6494):924–925. doi: 10.1126/science.368.6494.924. [DOI] [PubMed] [Google Scholar]
- Brandenburg Axel. Piecewise quadratic growth during the 2019 novel coronavirus epidemic. Infect. Dis. Model. 2020;5:681–690. doi: 10.1016/j.idm.2020.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante-Castañeda F., Caputo J.-G., Cruz-Pacheco G., Knippel A., Mouatamide F. Epidemic model on a network: Analysis and applications to COVID-19. Physica A. 2021;564 doi: 10.1016/j.physa.2020.125520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Jianguo, Li Kenli, Zhang Zhaolei, Li Keqin, Yu Philip S. 2020. A survey on applications of artificial intelligence in fighting against COVID-19. arXiv preprint arXiv:2007.02202. [Google Scholar]
- Chinazzi Matteo, Davis Jessica T., Ajelli Marco, Gioannini Corrado, Litvinova Maria, Merler Stefano, y Piontti Ana Pastore, Mu Kunpeng, Rossi Luca, Sun Kaiyuan, Viboud Cécile, Xiong Xinyue, Yu Hongjie, Halloran M. Elizabeth, Longini Jr. Ira M., Vespignani Alessandro. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368(6489):395–400. doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell Gerardo, Hincapie-Palacio Doracelly, Ospina Juan, Pell Bruce, Tariq Amna, Dahal Sushma, Moghadas Seyed, Smirnova Alexandra, Simonsen Lone, Viboud Cécile. Using phenomenological models to characterize transmissibility and forecast patterns and final burden of zika epidemics. PLoS Curr. 2016;8 doi: 10.1371/currents.outbreaks.f14b2217c902f453d9320a43a35b9583. URL https://pubmed.ncbi.nlm.nih.gov/27366586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell Gerardo, Tariq Amna, Hyman James M. A novel sub-epidemic modeling framework for short-term forecasting epidemic waves. BMC Med. 2019;17(1):164. doi: 10.1186/s12916-019-1406-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dattoli Giuseppe, Palma Emanuele Di, Licciardi Silvia, Sabia Elio. 2020. A note on the evolution of Covid-19 in Italy. arXiv preprint arXiv:2003.08684. [Google Scholar]
- Filipe J.A.N., Gibson G.J. Studying and approximating spatio-temporal models for epidemic spread and control. Philos. Trans.: Biol. Sci. 1998;353(1378):2153–2162. doi: 10.1098/rstb.1998.0354. [DOI] [Google Scholar]
- Fofana Abdou Moutalab, Hurford Amy. Mechanistic movement models to understand epidemic spread. Philos. Trans. R. Soc. B. 2017;372(1719) doi: 10.1098/rstb.2016.0086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatto Marino, Bertuzzo Enrico, Mari Lorenzo, Miccoli Stefano, Carraro Luca, Casagrandi Renato, Rinaldo Andrea. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. 2020;117(19):10484–10491. doi: 10.1073/pnas.2004978117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompertz Benjamin. XXIV. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1825;115:513–583. doi: 10.1098/rstl.1825.0026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gourieroux C., Jasiak J. Time varying Markov process with partially observed aggregate data: An application to coronavirus. J. Econometrics. 2020 doi: 10.1016/j.jeconom.2020.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross Bnaya, Zheng Zhiguo, Liu Shiyan, Chen Xiaoqi, Sela Alon, Li Jianxin, Li Daqing, Havlin Shlomo. Spatio-temporal propagation of COVID-19 pandemics. EPL (Europhys. Lett.) 2020;131(5):58003. doi: 10.1209/0295-5075/131/58003. [DOI] [Google Scholar]
- Hallatschek Oskar, Fisher Daniel S. Acceleration of evolutionary spread by long-range dispersal. Proc. Natl. Acad. Sci. 2014;111(46):E4911–E4919. doi: 10.1073/pnas.1404663111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia Lin, Li Kewen, Jiang Yu, Guo Xin, zhao Ting. 2020. Prediction and analysis of coronavirus disease 2019. arXiv preprint arXiv:2003.05447. [Google Scholar]
- Koltsova E.M., Kurkina E.S., Vasetsky A.M. 2020. Superposition of waves for modeling COVID-19 epidemic in the world and in the countries with the maximum number of infected people in the first half of 2020. arXiv preprint arXiv:2007.02283. [Google Scholar]
- Laird Anna Kane. Dynamics of tumor growth. Br. J. Cancer. 1964;13(3):490–502. doi: 10.1038/bjc.1964.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Zhijian, Zheng Yunling, Xin Jack, Zhou Guofa. 2020. A recurrent neural network and differential equation based spatiotemporal infectious disease model with application to COVID-19. arXiv preprint arXiv:2007.10929. [Google Scholar]
- Maier Benjamin F., Brockmann Dirk. Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science. 2020;368(6492):742–746. doi: 10.1126/science.abb4557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majumder Maimuna S., Mandl Kenneth D. 2020. Early transmissibility assessment of a novel coronavirus in Wuhan, China. [DOI] [Google Scholar]
- Masjedi Hamidreza, Rabajante Jomar F., Bahranizadd Fatemeh, Zare Mohammad Hosein. Nowcasting and forecasting the spread of COVID-19 in Iran. MedRxiv. 2020 doi: 10.1101/2020.04.22.20076281. [DOI] [Google Scholar]
- Molina-Cuevas Emiro A. 2020. Choosing a growth curve to model the Covid-19 outbreak. arXiv preprint arXiv:2007.03779. [Google Scholar]
- Mollison Denis. Spatial contact models for ecological and epidemic spread. J. R. Stat. Soc. Ser. B Stat. Methodol. 1977;39(3):283–326. URL https://www.jstor.org/stable/2985089. [Google Scholar]
- Morais Apiano F. 2020. Logistic approximations used to describe new outbreaks in the 2020 COVID-19 pandemic. arXiv preprint arXiv:2003.11149. [Google Scholar]
- Pell Bruce, Kuang Yang, Viboud Cecile, Chowell Gerardo. Using phenomenological models for forecasting the 2015 Ebola challenge. Epidemics. 2018;22:62–70. doi: 10.1016/j.epidem.2016.11.002. [DOI] [PubMed] [Google Scholar]
- Richards F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959;10(2):290–301. doi: 10.1093/jxb/10.2.290. [DOI] [Google Scholar]
- Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M., Yan P., Chowell G. Real-time forecasts of the COVID-19 epidemic in China from february 5th to february 24th, 2020. Infect. Dis. Model. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roques L., Bonnefon O., Baudrot V., Soubeyrand S., Berestycki H. A parsimonious approach for spatial transmission and heterogeneity in the COVID-19 propagation. R. Soc. Open Sci. 2020;7(12) doi: 10.1098/rsos.201382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salas Joaquin. Improving the estimation of the COVID-19 effective reproduction number using nowcasting. Stat. Methods Med. Res. 2021;30:275–284. doi: 10.1177/09622802211008939. [DOI] [PubMed] [Google Scholar]
- Schlosser Frank, Maier Benjamin F., Jack Olivia, Hinrichs David, Zachariae Adrian, Brockmann Dirk. COVID-19 lockdown induces disease-mitigating structural changes in mobility networks. Proc. Natl. Acad. Sci. 2020;117(52):32883–32890. doi: 10.1073/pnas.2012326117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneble Marc, Nicola Giacomo De, Kauermann Göran, Berger Ursula. Nowcasting fatal COVID-19 infections on a regional level in Germany. Biom. J. 2021;63(3):471–489. doi: 10.1002/bimj.202000143. [DOI] [PubMed] [Google Scholar]
- Shen Christopher Y. Logistic growth modelling of COVID-19 proliferation in China and its international implications. Int. J. Infect. Dis. 2020;96:582–589. doi: 10.1016/j.ijid.2020.04.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer H M. The COVID-19 pandemic: growth patterns, power law scaling, and saturation. Phys. Biol. 2020;17(5) doi: 10.1088/1478-3975/ab9bf5. [DOI] [PubMed] [Google Scholar]
- Sonnino Giorgio, Nardone Pasquale. 2020. Dynamics of the COVID-19 – comparison between the theoretical predictions and the real data, and predictions about returning to normal life. arXiv preprint arXiv:2003.13540. [Google Scholar]
- Triambak S., Mahapatra D.P. A random walk Monte Carlo simulation study of COVID-19-like infection spread. Physica A. 2021;574 doi: 10.1016/j.physa.2021.126014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vattay Gábor. 2020. Predicting the ultimate outcome of the COVID-19 outbreak in Italy. arXiv preprint arXiv:2003.07912. [Google Scholar]
- Viboud Cécile, Simonsen Lone, Chowell Gerardo. A generalized-growth model to characterize the early ascending phase of infectious disease outbreaks. Epidemics. 2016;15:27–37. doi: 10.1016/j.epidem.2016.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Ziqi, Broccardo Marco, Mignan Arnaud, Sornette Didier. The dynamics of entropy in the COVID-19 outbreaks. Nonlinear Dynam. 2020;101(3) doi: 10.1007/s11071-020-05871-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Li, Wang Guannan, Gao Lei, Li Xinyi, Yu Shan, Kim Myungjin, Wang Yueying, Gu Zhiling. 2020. Spatiotemporal dynamics, nowcasting and forecasting of COVID-19 in the United States. arXiv preprint arXiv:2004.14103. [Google Scholar]
- Wang Xiang-Sheng, Wu Jianhong, Yang Yong. Richards model revisited: Validation by and application to infection dynamics. J. Theoret. Biol. 2012;313:12–19. doi: 10.1016/j.jtbi.2012.07.024. [DOI] [PubMed] [Google Scholar]
- World Health Organisation, 2021. https://covid19.who.int/WHO-COVID-19-global-data.csv.
- Wu Ke, Darcet Didier, Wang Qian, Sornette Didier. Generalized logistic growth modeling of the COVID-19 outbreak: comparing the dynamics in the 29 provinces in China and in the rest of the world. Nonlinear Dynam. 2020;101(3):1561–1581. doi: 10.1007/s11071-020-05862-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Joseph T., Leung Kathy, Leung Gabriel M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in wuhan, China: a modelling study. Lancet (London, England) 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Wuyue, Zhang Dongyan, Peng Liangrong, Zhuge Changjing, Hong Liu. Rational evaluation of various epidemic models based on the COVID-19 data of China. Epidemics. 2021;37:100501. doi: 10.1016/j.epidem.2021.100501. [DOI] [PMC free article] [PubMed] [Google Scholar]