swCRTdesign: An R Package for Stepped Wedge Trial Design and Analysis

Abstract

Background and objective:

Stepped wedge trials (SWTs) are a type of cluster-randomized trial that are commonly used to evaluate health care interventions. Most SWT-related software packages have restrictive assumptions about the study design and correlation structure of the data. The objective of this paper is to present a package and corresponding web-based graphical user interface (GUI) that provide researchers with another, more flexible option for SWT design and analysis.

Methods:

We developed an R package swCRTdesign (‘stepped wedge Cluster Randomized Trial design’), which uses a random effects model to account for correlation in the data induced by a SWT design. Possible sources of correlation include clusters, time within clusters, and treatment within clusters.

Results:

swCRTdesign allows a user to calculate power, simulate SWT data to streamline simulation studies (e.g. to estimate power), and create descriptive summaries and plots. Additionally, a GUI, developed using shiny, is available to calculate power and create power curves and design plots.

Conclusions:

The swCRTdesign package accommodates a wide variety of SWT designs, and makes it easy to account for some sources of correlation which are not found in other packages. The user-friendly web-based GUI makes some swCRTdesign features accessible to researchers not familiar with R. These two resources will make appropriately complex SWT calculations more accessible to scientists from a wide variety of backgrounds.

1. Introduction

1.1. Basics of stepped wedge trials

Scientists in medicine, public health, and many other fields rely on randomized controlled trials as the gold standard method to evaluate interventions. Typically, individuals are randomized to intervention or control. However, sometimes clusters of individuals (e.g., families, clinics, or communities) are randomized, in which case individual-level observations are correlated; this is called a cluster randomized trial (CRT). The motivation for choosing a CRT instead of a traditional randomized trial may be due to the nature of the intervention (e.g., policy changes at a hospital) or for practical or logistical reasons. To date, most CRTs have mirrored the design of individually randomized trials and used a parallel or matched parallel two group design. One exception is the stepped wedge trial (SWT) design. The SWT is a more recently developed type of CRT that has been growing in popularity [1]. The most common design for a SWT dictates that all clusters begin in the control state at baseline, and at every subsequent time point (also called periods) some of the clusters cross over until all clusters have received treatment. Cross-over times are pre-specified for each cluster and usually evenly spaced after baseline. A group of clusters that cross over to treatment at the same time is called a sequence or wave. See Hughes, Granston, and Heagerty [2] for a more thorough introduction to stepped wedge designs. SWTs may have logistical or ethical advantages compared to other CRT designs, since the researcher only needs to implement the intervention in a few clusters at a time and every cluster eventually receives the intervention [1]. However, because of the complex design and correlated observations, specialized statistical methods and software are needed for designing SWTs.

The R [3] package swCRTdesign [4] is a tool to aid in the design and analysis of SWTs, including calculating power, simulating SWT data, and generating descriptive summaries. Additionally, a web-based graphical user interface (GUI) for calculating power is available, with the hope of making some swCRTdesign features more accessible to researchers not familiar with R.

1.2. Motivating example

As a motivating example, we consider the stepped wedge trial on expedited partner therapy (EPT) in Washington state summarized by Golden et al [5]. With EPT, when an individual tests positive for a sexually transmitted infection, their sex partners are then offered treatment without medical evaluation. In this study, the clusters were local health jurisdictions (LHJs), which typically corresponded to counties. Although the authors analyzed several primary and secondary outcomes, here we focus on the effect of EPT on the percent of chlamydia tests that were positive among women between 14 and 25 years old at sentinel clinics within each LHJ. Researchers planned on randomizing 24 LHJs into four sequences of 6 LHJs each, stratified by region and LHJ size. Every sequence was observed in the control state at baseline, and at each subsequent time one sequence crossed over, resulting in a total of five time points. Figure 1 depicts the study design for this motivating example. Note that although the x-axis is labeled "Time 1", "Time 2", etc., the distance between observed times was between six and eight months, so these times could alternatively be labeled "Month 1", "Month 7", etc.

Figure 1:

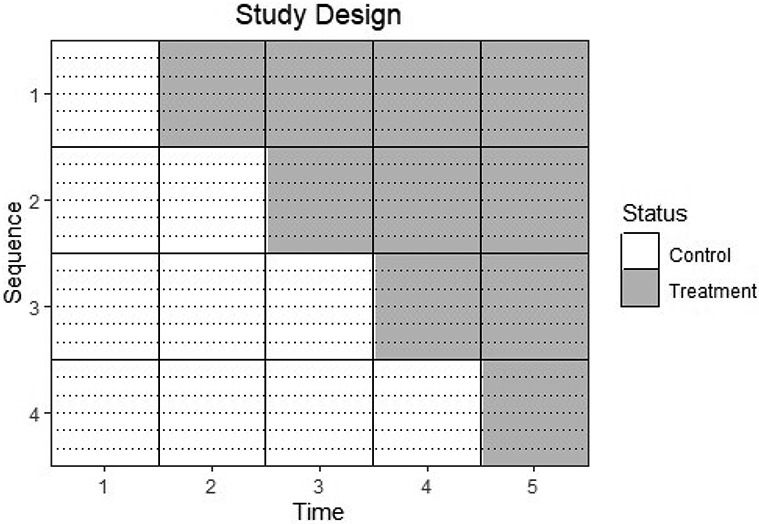
The design of the EPT trial with 4 sequences in which all sequences start in the control group. In each sequence, there are 6 independent clusters, separated by dotted lines.

1.3. Summary of methods and software

There are a wide variety of methods for designing and analyzing SWTs [1]. For calculating power, the two most common methods are based on (i) application of normal-theory models via weighted least squares (WLS), with approximations for binary and count outcomes [6] and (ii) simulation [7]. A ‘design effect’ or ‘sample size correction factor’ is sometimes also used [8]. Baio et al [7] also provide an overview of these three techniques and their use for SWTs. swCRTdesign uses method (i). Very briefly, this method uses a mixed model structure to compute the variance of the WLS estimate of the treatment effect; power is based on a Wald statistic and relies on asymptotic Normality. For details, see [6] and [2] (especially Appendix A).

There are two other R packages that can be used for designing and analyzing SWTs. SamplingDataCRT [9] allows the user to simulate data and calculate power, but only for Gaussian outcomes and limited covariance structures. Power calculations are based on Hussey and Hughes [6] for cross-sectional data. SWSamp allows the user to simulate data and calculate power based on Hussey and Hughes, a design effect, or simulations, but most functionality is only supported for a limited number of covariance structures [10]. A web-based GUI developed by Hemming et al [11] allows the user to calculate power based on a design effect for Gaussian, binary, or count outcomes and several possible covariance structures. swCRTdesign provides support for more complex SWT designs (e.g., a sample size that varies over time and cluster) and alternative ways of specifying correlation structures.

1.4. Overview

The remainder of this manuscript is organized as follows. Section 2 describes the underlying analytic model used to compute power for a SWT design and simulate SWT data. Section 3 contains an overview of the swCRTdesign package, followed by examples with R code in section 4. Section 5 describes the web-based GUI tool. We conclude with a discussion in section 6. We hope that making both swCRTdesign and the GUI freely available will help support the needs of investigators designing or analyzing a SWT.

2. The model

2.1. Primary parameterization

To account for the correlation within clusters, we use a random effects model [2]. This model is used for both the power calculations, and simulating SWT data. Let Y_ijk denote the response recorded for individual k from cluster i at time j. In the swCRTdesign package, Y_ijk may follow a Gaussian, Bernoulli, or (for simulations only) Poisson distribution. Also, let X_ij have a value of one if cluster i is assigned to treatment at time j, and zero otherwise. In this paper and package, time is modeled as an unordered categorical factor. Then the mean response for cluster i at time j is:

$${\mu }_{ij}=\mu +{\beta }_j+\theta \ast X_{ij}+u_i+w_{ij}+v_i\ast X_{ij}.$$ (1)

Here, μ is the baseline average (i.e., the average response among those assigned to control at the first time point), θ represents the treatment effect, and β_j represents the mean difference between time j and time 1, with β₁ = 0. The random effects are represented by u_i, w_ij, and v_i; each follows a Gaussian distribution with mean zero. The random intercepts, u_i, represent each cluster’s unique baseline and have a standard deviation of τ. The random time effects, w_ij, represent cluster- and time- specific deviations and have a standard deviation of γ. The random treatment effects, v_i, represent the cluster-specific variations in the impact of treatment, and have a standard deviation of η. We assume that the correlation between u_i and v_i is ρ, and the correlation between w_ij and both u_i and v_i is zero. In addition, we assume the correlation between w_ij and w_ij′ with j ≠ j′ is zero. So in cluster i with times j=1,…,J, the covariance of the vector of random effects is:

$$\mathsf{COV}\left[\begin{array}{c}\hfill u_i\hfill \\ \hfill v_i\hfill \\ \hfill w_{i1}\hfill \\ \hfill ⋮\hfill \\ \hfill w_{iJ}\hfill \end{array}\right]=\left[\begin{array}{ccccc}\hfill {\tau }^2\hfill & \hfill \rho \tau \eta \hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill \rho \tau \eta \hfill & \hfill {\eta }^2\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\gamma }^2\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill {\gamma }^2\hfill \end{array}\right].$$ (2)

When the response Y_ijk is assumed to be Gaussian, Y_ijk = μ_ij + ϵ_ijk where ϵ_ijk is Gaussian with mean zero and standard deviation σ; that is, the mean of Y_ijk is μ_ij and the standard deviation is sd(Y_ijk∣u_i, w_ij, v_i) = σ. The ϵ_ijk are mutually independent, and independent of all random effects. When Y_ijk is assumed to be Bernoulli, the mean is μ_ij and the standard deviation is defined by the function $\text{sd}(Y_{ijk}\mid u_i,w_{ij},v_i)=\sqrt{{\mu }_{ij}(1-{\mu }_{ij})}$. Similarly, when Y_ijk is assumed to be Poisson, the mean is μ_ij and the standard deviation is defined by the function $\text{sd}(Y_{ijk}\mid u_i,w_{ij},v_i)=\sqrt{{\mu }_{ij}}$.

Note that these calculations assume that each subject in the data set is only observed once, at a single time point. If the same subjects are observed at multiple time points, we refer to this as a ‘cohort’ design; this requires additional random effects [12]. Currently, swCRTdesign does not support power calculations or simulations for cohort data. The application developed by Hemming et al [11] allows the user to calculate power for some cohort designs. SamplingDataCRT also provides some support for cohort data, but only for Gaussian outcomes and cluster random effects [9].

2.2. Alternative parameterization

Instead of using the variance components above to quantify correlation (which we will refer to as the standard deviation or SD parameterization), some researchers prefer to use measures such as the within-period intra-cluster correlation (ICC) and cluster auto-correlation (CAC) [12]. When there are no random treatment effects (η=0), the two parametrizations are equivalent. However, the SD parameterization allows for random treatment effects (through η) and a correlation between the random treatment effects and the random intercepts (ρ), while a single ICC and CAC do not [13]. The ICC/CAC parameterization is less flexible than the SD parameterization since it requires the assumption that there are no random treatment effects (that is, η = 0 and ρ = 0). Despite this limitation, ICC and CAC are widely used in the literature both to summarize SWT data and perform power calculations [1].

The ICC is the correlation between individuals sampled from the same cluster at the same time, or the ratio of between-cluster variance to total variance [12]. In terms of the random effects parameters defined above,

$$\text{ICC}=\frac{{\tau }^2+{\gamma }^2}{{\tau }^2+{\gamma }^2+{\sigma }^2}.$$ (3)

When the outcome is assumed to be Gaussian, σ is well defined. When the outcome is assumed to be Bernoulli, we substitute $\sigma =\sqrt{\overline{\mu }(1-\overline{\mu })}$, where $\overline{\mu }$ is the average of the mean outcomes for the baseline control and baseline treatment groups, (μ₀ + μ₁)/2. The CAC is the ratio of the between-period ICC to the within-period ICC, or the ratio of the correlation between individuals from the same cluster at different times to the correlation between individuals from the same cluster within the same period [12]. In this scenario,

$$\text{CAC}=\frac{{\tau }^2}{{\tau }^2+{\gamma }^2}.$$ (4)

In this package, ICC and CAC input is translated to random effect standard deviations. If the ICC is zero, both τ and γ are zero and the CAC is not well-defined. If the ICC is one, either σ is zero or either τ or γ is extremely large. Since solving for the random effects parameters is not possible in this case, it is best to use the SD parameterization directly when the ICC is close to one.

The formulas below can be used to manually convert from ICC, CAC, and σ to the SD parameterization:

For CAC=1, γ = 0 and $\tau =\sigma \ast \sqrt{\text{ICC}∕(1-\text{ICC})}$.

For CAC<1, $\gamma =\sigma \ast \sqrt{\text{ICC}\ast (1-\text{CAC})∕(1-\text{ICC})}$ and $\tau =\gamma \ast \sqrt{\text{CAC}∕(1-\text{CAC})}$.

2.3. Fractional treatment effect

In the case described above, we assume that the clusters receive the full treatment effect θ as soon as they cross over to treatment (i.e., X_ij changes from 0 to 1). However, the effect of an intervention is not always immediate, and usually depends on the scientific setting, mechanism of the intervention, and the planned timing of assessments in a trial. For example, perhaps when a cluster first crosses over to treatment the effect size is $\frac{\theta }{2}$, then θ at every subsequent time point. Fractional treatment effects may extend over as many time points as desired by specifying a series of X_ij between 0 and 1. Depending on the planned trial duration, some clusters may not be followed long enough for researchers to observe the full treatment effect. For more detail, see Hughes, Granston, and Heagerty [2].

3. swCRTdesign overview

The swCRTdesign package contains five main functions: swDsn for defining a SWT design, swPwr for calculating power, swSim for simulating data, and swPlot and swSummary for plotting and summarizing a SWT data set. The full documentation can be found at https://cran.r-project.org/web/packages/swCRTdesign/swCRTdesign.pdf.

The functions swPwr and swSim both depend on defining a SWT design through swDsn. To define a design, a vector (clusters) specifies the number of sequences (the length of the vector) and number of clusters per sequence. Designs can either begin with all sequences in the control setting (default), or begin with the first sequence on treatment. Extra time periods can be added while all sequences are on control, or after all sequences have switched to treatment. Designs may also have extra time points throughout the study during which no sequences cross over, or have transition periods (see Examples and supplemental file).

swPwr calculates power for either a Bernoulli or Gaussian outcome. The number of observations per cluster may vary by cluster and over time. When simulating data with swSim, the outcome may be Gaussian, log-Gaussian, Poisson (identity or log link), or Bernoulli (identity, log, or logit link). Both swPwr and swSim allow either ICC/CAC or the SD parameterization in some cases. See supplemental files for an example of how to use swSim to estimate power.

swSummary summarizes stepped wedge data over time with respect to sequences, or with respect to individual clusters. The summaries can be by mean, sum, or number of observations. swPlot can plot trends by sequence or by cluster, either in a single plot or with one plot for each sequence. Default colors, symbols, and line types differentiate between different clusters or sequences, and indicate when each sequence or cluster was under treatment or control. If desired, these can be customized or eliminated.

More details can be found in the supplemental file on the syntax and flexibility of the swCRTdesign package. The examples below are meant to illustrate the capabilities of the package, but not provide a thorough tutorial of the package’s use.

4. Examples

4.1. Gaussian example

To illustrate the use of the swCRTdesign package, suppose we are interested in a traditional SWT with 5 sequences and 6 clusters per sequence. We start by creating a design, and printing the design matrix (swDsn.unique.clusters). Rows and columns correspond to clusters and time points, respectively. Control and treatment status are represented by 0’s and 1’s.

R> library("swCRTdesign")
R> design <- swDsn(clusters = c(6, 6, 6, 6, 6))
R> design$swDsn.unique.clusters
     [,1] [,2] [,3] [,4] [,5] [,6]
     [1,] 0 1 1 1 1 1
     [2,] 0 0 1 1 1 1
     [3,] 0 0 0 1 1 1
     [4,] 0 0 0 0 1 1
     [5,] 0 0 0 0 0 1

Next, using our planned design and external information about the assumed variability in the data, we can calculate power. Here, we have Gaussian data with 50 individuals in every cluster at every time point. Argument names mirror the symbols in the model described above.

R> swPwr(design = design, distn = "gaussian", n = 50, mu0 = 0, mu1 = 0.003,
+    sigma = .03, tau = .01, eta = 0, rho = 0, gamma = 0.001, silent = TRUE)
[1] 0.7399873

Alternatively, transforming from the SD parameterization to the ICC/CAC parameterization, we can obtain the same power estimate using ICC and CAC. Note that this is possible only because we assumed there are no random treatment effects (η = 0) in this scenario.

R> icc.ex <- (.01 ^ 2 + .001 ^ 2) / (.01 ^ 2 + .001 ^ 2 + .03 ^ 2)
R> icc.ex

[1] 0.1008991

R> cac.ex <- .01 ^ 2 / (.01 ^ 2 + .001 ^ 2)
R> cac.ex

[1] 0.990099

R> swPwr(design = design, distn = "gaussian", n = 50, mu0 = 0, mu1 = 0.003,
+    sigma = .03, icc = icc.ex, cac = cac.ex, silent = TRUE)

[1] 0.7399873

Additionally, we can simulate SWT data based on the assumed design and parameters. Note that we added a positive time trend (with time.effect); this corresponds to the vector of β₁ … β₆ in the model above. The default output contains the outcome (response.var), treatment indicator (tx.var), and the time and cluster IDs (time.var,cluster.var).

R> set.seed(4)
R> example.data <- swSim(design = design, family = "gaussian", n = 50,
+    mu0 = 0, mu1 = 0.003, time.effect = (0 : 5) * .002, sigma = .03,
+    tau = .01, eta = 0, rho = 0, gamma = 0.001)
R> head(example.data)
  response.var tx.var time.var cluster.var
1 −0.004442856      0        1           1
2 −0.004531357      0        1           1
3 −0.005274664      0        1           1
4  0.064369213      0        1           1
5  0.049816709      0        1           1
6 −0.028956710      0        1           1

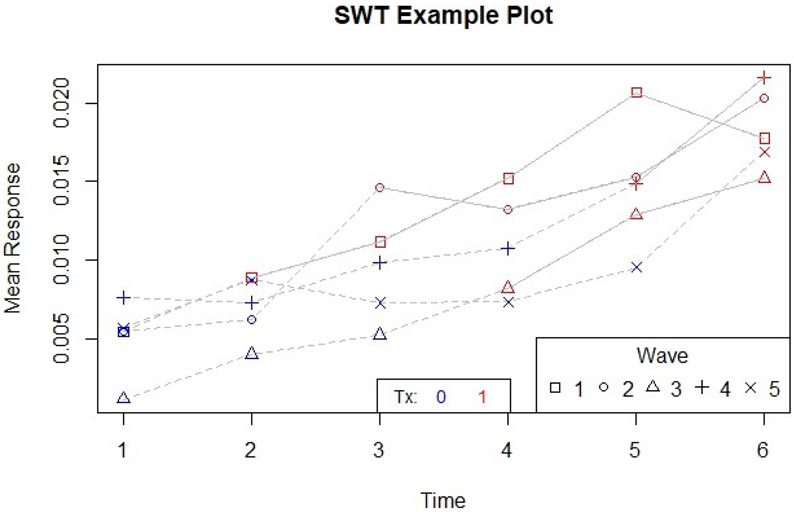
Using swSummary, we can examine the mean response for each sequence over time, and plot that using swPlot (Figure 2). The additional arguments in swPlot customize the location and width of the legends and provide a title; see package documentation for details.

Figure 2:

Plot created using swPlot for the Gaussian example.

R> example.summary <- swSummary(response.var = response.var, tx.var = tx.var,
+    time.var = time.var, cluster.var = cluster.var, data = example.data,
+    type = "mean")
R> #To view the matrix of means by sequence and time, we could run:
R> #example.summary$response.wave

R> swPlot(response.var = response.var, tx.var = tx.var, time.var = time.var,
+    cluster.var = cluster.var, data = example.data, choose.ncol = 5,
+    choose.tx.pos = "bottom", choose.legend.pos = "bottomright",
+    choose.main = "SWT Example Plot")

4.2. Bernoulli example (EPT trial)

Recall the motivating example from the introduction, in which Golden et al [5] examined the effect of EPT on the percent of chlamydia tests that were positive. Each cluster is a LHJ, and each individual observation is a chlamydia test result (positive or negative), which follows a Bernoulli distribution. When planning the study, researchers identified 24 eligible LHJs, and planned on randomizing them into four sequences. Below, we construct this design and check the design matrix (note that this design is identical to the one in Figure 1).

R> design.bernoulli <- swDsn(clusters = c(6, 6, 6, 6))

To estimate power for this SWT design, researchers assumed that there would be 162 tests per LHJ at each observed time, and that 5% of the tests would be positive in the control setting. They also estimated that τ = 0.0165, and assumed that there would be no other random effects. The trial was powered to detect a multiplicative change of 0.7; that is, 3.5% positive in the treatment group. With a significance level of 0.05, the calculation below aligns with the researchers’ desired power of at least 80%.

R> swPwr(design = design.bernoulli, distn = "binomial", n = 162,
+    mu0 = 0.05, mu1 = 0.035,
+    tau = 0.0165, eta = 0, rho = 0, gamma = 0, silent = TRUE)

[1] 0.8468701

The researchers stated that they wished to use a log link in their model for the relationship between EPT and chlamydia positivity. We can simulate data that accounts for this. Because we are using a log link, mu0 and mu1 are on the log scale, so we enter the log of the prevalences. Similarly, tau, eta, rho, and gamma correspond to random effects that are linear on the log scale, so we use the predicted coefficient of variation between LHJs for tau. Note that this data does not exactly correspond with the mixed effects model used by Golden et al [5], since they also included random effects for individual clinics within the LHJs and a fixed time trend. The WLS technique used by swPwr for estimating power cannot easily account for a nonlinear link, but the data can be simulated; this is one scenario where simulation-based power calculations may be useful (see supplemental files).

R> example.data.bernoulli <- swSim(design = design.bernoulli,
+    family = binomial(link = "log"), n = 162,
+    mu0 = log(0.05), mu1 = log(0.035), time.effect = 0,
+    tau = .33, eta = 0, rho = 0, gamma = 0)
R> #To view the simulated data, we could run:
R> #head(example.data.bernoulli)

Unfortunately, while the researchers planned on 24 LHJs and 162 tests per LHJ at each time point, when the study was conducted they only had 22 LHJs and about 107 tests per LHJ at each time point. Researchers assigned six LHJs to each of the first three waves, and only four LHJs to the last wave, resulting in the design below.

R> design.bernoulli.post <- swDsn(clusters = c(6, 6, 6, 4))

For the purpose of this example, suppose we know the exact number of observations in each LHJ at each time point. A plausible matrix of sample sizes is simulated below. Each row represents a LHJ, and each column represents a time point. LHJs are ordered by sequence, from first to cross over to last to cross over, so the sample sizes printed below correspond to the six LHJs in the first sequence to cross over. Within a sequence, the order of clusters is arbitrary.

R> n.bernoulli.post <- matrix(data = rpois(n = 110, lambda = 107),
+    nrow = 22, ncol = 5)
R> head(n.bernoulli.post)
    [,1] [,2] [,3] [,4] [,5]
[1,]  99   95  118  108  110
[2,] 105  139  104   93  121
[3,] 100   95  118  105  111
[4,]  95  113   85  124   96
[5,] 112  101  107  102  120
[6,] 116  117  113   97  128

Now we can see how these changes impact the power of the study.

R> swPwr(design = design.bernoulli.post, distn = "binomial",
+    n = n.bernoulli.post, mu0 = 0.05, mu1 = 0.035,
+    tau = 0.0165, eta = 0, rho = 0, gamma = 0, silent = TRUE)

[1] 0.6432843

5. Web-based power calculator

The web-based GUI power calculator provides investigators with an alternative tool (that does not require knowledge of R) to compute power for SWTs and explore the impact on power of candidate SWT designs. This was developed using the shiny package [14]. The app can be accessed online here or downloaded and run in R from here. The language and inputs are very similar to the swCRTdesign package, described above, and a manual is provided in the ‘Help and References’ tab.

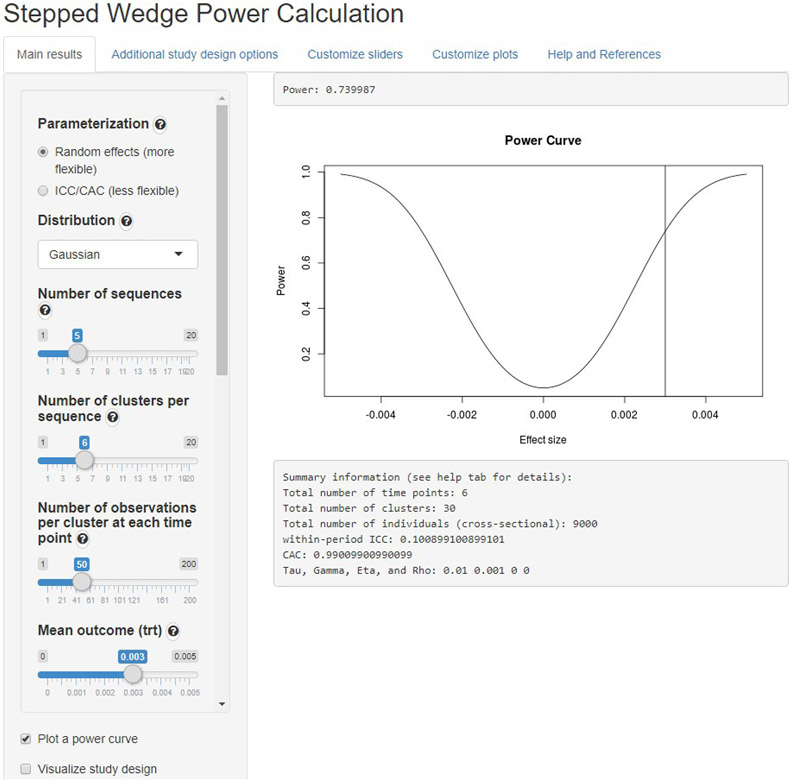
In addition to calculating the power for a specific design, the app can also plot a power curve, visualize and summarize the study design, and help translate between the ICC/CAC and SD parameterization. Some plots use the package ggplot2 [15]. Figure 3 shows the power calculations from the Gaussian example above. Not pictured is the plot of the study design which the GUI also generates, in the same style as Figure 1.

Figure 3:

Power calculations for the Gaussian example, done in the web-based GUI. Inputs for all the arguments were entered using the sliders in the left-hand column. The range and appearance of the plot were changed in the "Customize plots" tab.

6. Discussion

The R package swCRTdesign provides useful tools for the design and analysis of SWTs. These functions make it easy to calculate power, simulate data, and plot and summarize SWT data. The online power calculator app makes power calculations accessible without knowledge of R, and facilitates exploration of different designs. We believe these will be useful tools for applied researchers from a variety of backgrounds, as the use of SWTs continues to grow.

A limitation of swCRTdesign is that, currently, power cannot be calculated for cohort designs. Calculating power for SWTs with more complex correlation structures is an important extension that may be added in a future version of the package. Other potential additions include allowing more flexible specification of the design matrix and random effects covariance matrix, and adding power calculations for logit and log link models.