Minipatch Learning as Implicit Ridge-Like Regularization

Abstract

Ridge-like regularization often leads to improved generalization performance of machine learning models by mitigating overfitting. While ridge-regularized machine learning methods are widely used in many important applications, direct training via optimization could become challenging in huge data scenarios with millions of examples and features. We tackle such challenges by proposing a general approach that achieves ridge-like regularization through implicit techniques named Minipatch Ridge (MPRidge). Our approach is based on taking an ensemble of coefficients of unregularized learners trained on many tiny, random subsamples of both the examples and features of the training data, which we call minipatches. We empirically demonstrate that MPRidge induces an implicit ridge-like regularizing effect and performs nearly the same as explicit ridge regularization for a general class of predictors including logistic regression, SVM, and robust regression. Embarrassingly parallelizable, MPRidge provides a computationally appealing alternative to inducing ridge-like regularization for improving generalization performance in challenging big-data settings.

I. Introduction

Ridge-like regularization often leads to improved generalization error by mitigating overfitting, and it is used explicitly in a wide variety of learning frameworks including support vector machines (SVM), kernel learning, and deep learning. However, directly training explicitly ridge-regularized learners could become challenging in various data scenarios, for instance: i) optimizing the ridge-regularized objective function can become computationally intractable with millions of examples and features; ii) the full training data are stored in distributed databases with each node having access to only a subset of examples and/or features; and iii) the training data suffer from a large degree of missingness.

Recently, the topic of implicit regularization has attracted much attention, and researchers have shown that it is possible to obtain models of lower complexity without explicitly applying regularization during training in certain scenarios [1, 2, 3]. In particular, [4] showed that a large ensemble of independent ordinary least squares (OLS) predictors that are trained using random submatrices of the training data can achieve the optimal ridge regression risk under mild assumptions. In addition, another line of work reveals that the dropout technique combined with stochastic gradient descent in deep learning can induce ridge-like regularization in the context of generalized linear models (GLMs) [5].

In this work, we tackle the aforementioned challenges of applying ridge-regularized machine learning methods in big-data settings by proposing a general approach named Minipatch Ridge (MPRidge). Inspired by [4], MPRidge is an ensemble of the parameter coefficients of unregularized learners trained on many tiny, random subsamples of both the examples and features of the training data (Sec. II). We empirically show that MPRidge elicits an implicit ridge-like regularizing effect (Sec. III). In particular, while no explicit regularization is applied during training, we empirically demonstrate that the resulting predictor of the MPRidge ensemble performs nearly the same as the explicitly ridge-regularized predictor fit using the entire training data in terms of in-sample and out-of-sample risk for a general class of predictors including the logistic regressor, SVM classifier, and robust regressor. Additionally, we empirically show that MPRidge can largely recover the entire regularization path of parameter coefficients for the explicitly ridge-regularized counterpart. Because training unregularized learners on many tiny subsets of data in parallel has major computational advantages, MPRidge provides a computationally efficient alternative to inducing ridge-like regularization in big-data scenarios where direct training of explicitly ridge-regularized learners via optimization could be challenging.

II. Method

A. Minipatch Ridge (MPRidge)

Our proposed approach is based on taking many tiny, random subsamples of both the examples and features of the training data simultaneously. We call these random subsamples “minipatches”, as illustrated in Fig. 1. This term is reminiscent of patches in imaging processing and minibatches commonly used in machine learning. While random sampling of the training data has been extensively used in ensemble learning techniques (e.g., Random Forest (RF) [6], Bagging [7, 8], Boosting [9], Random Patch [10]), we are following up on [4] to specifically investigate the implicit ridge-like regularization properties elicited by aggregating learners trained on many random minipatches for a general class of learners.

Fig. 1.

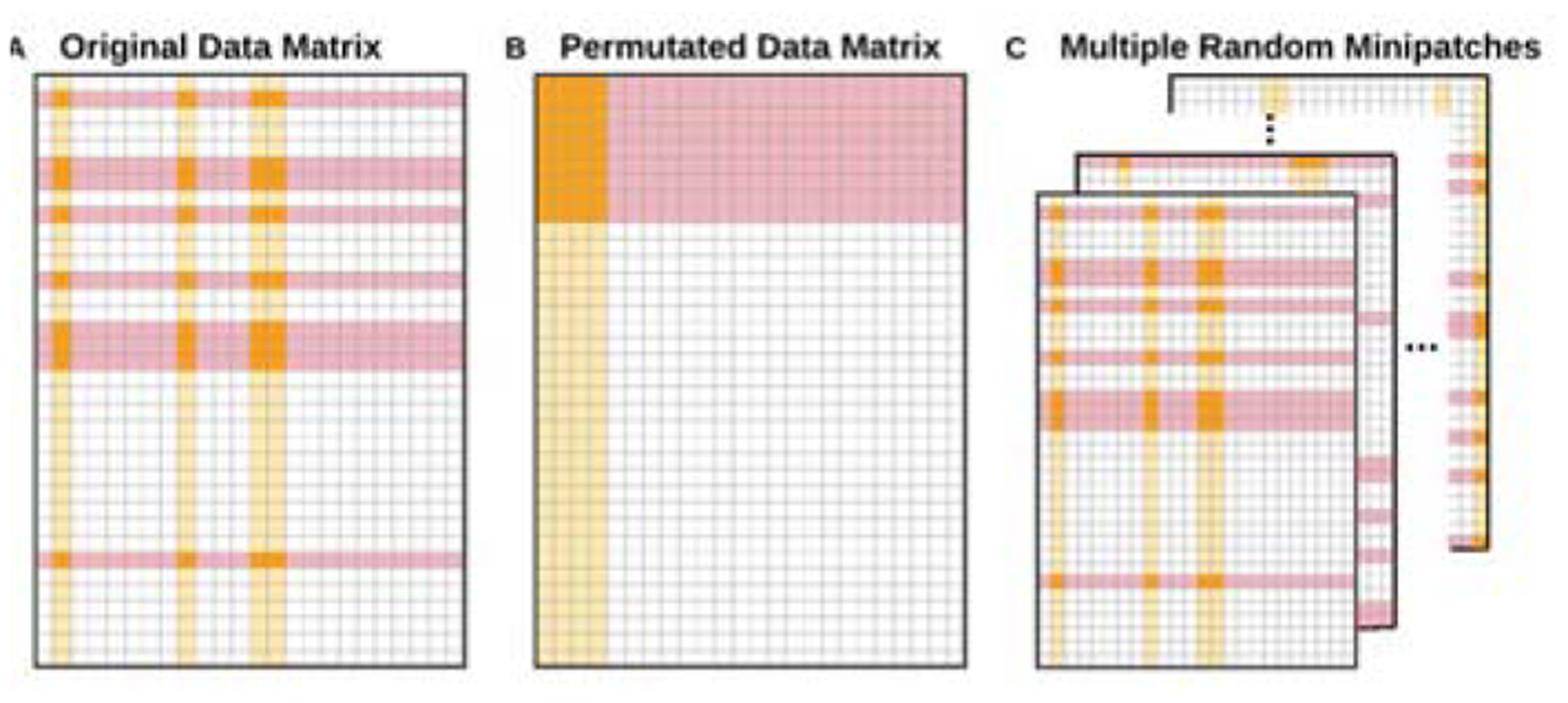
A. Simultaneous random subsampling of examples (rows in red) and features (columns in yellow) without replacement from the original data matrix yields a “minipatch” (orange). B. The same minipatch in A is a random submatrix of the data matrix after a permutation. C. Minipatch learning is an ensemble of learners trained on many random minipatches.

Leveraging the idea of minipatches, we propose and develop the Minipatch Ridge (MPRidge) method—a general meta-algorithm that can be employed with a wide range of learners. MPRidge is summarized in Algorithm 1. Here, $\mathcal{L}(·;\beta )$ denotes an unregularized loss function with parameter coefficient vector β whose specific form depends on the learning task at hand. For instance, $\mathcal{L}$ could be the logistic loss or hinge loss (i.e., SVM) for classification tasks. In essence, MPRidge trains K unregularized learners independently on K random minipatches in parallel and subsequently produces an ensemble estimator ${\widehat{\mathit{\beta }}}_{\text{ens}}$ for the learner parameter coefficients by aggregating unregularized estimates over these minipatches.

B. Practical Considerations

Our MPRidge method mainly has two tuning hyperparameters: the example subsampling ratio η ∈ (0, 1) and the feature subsampling ratio α ∈ (0, 1). Our empirical studies in Sec. III suggest that the feature subsampling ratio α controls the amount of implicit ridge-like regularization induced by MPRidge. In fact, there appears to be an one-to-one correspondence between α and the tuning hyperparameter for the corresponding explicitly regularized counterpart. Therefore, α can be chosen in data-driven manners such as cross-validation. Similar to findings in [4], the performance of MPRidge doesn’t seem to depend on the amount of example subsampling η provided that η well exceeds the sample complexity of the unregularized learner $\mathcal{L}$, so we focus our attention on the effect of α. Last but not least, our empirical results reveal that setting K = 1000 is sufficient for most problems.

C. Advantages & Possible Extensions

Embarrassingly parallelizable, MPRidge has major computational advantages, especially in big-data settings where direct training of the corresponding explicitly ridge-regularized learner via optimization could be challenging. In addition to computational advantages, MPRidge provides statistical benefits as it implicitly induces ridge-like regularizing effects to help achieve better generalization performance. We look to further investigate the statistical benefits of MPRidge theoretically in future work.

Furthermore, unavailability of the full training data poses another set of challenges to applying machine learning methods in some big-data scenarios. Such situations can arise when, for instance, i) only a subset of the training data can fit in the computer memory at a time; ii) the training data is stored in distributed databases with each node having access to only a subset of both the examples and features; and iii) the training data itself has a large amount of missingness. Because the training of MPRidge only relies on subsets of the training data, MPRidge is well-suited to eliciting ridge-like regularization implicitly in these settings. We save the investigation of such extensions for future work.

III. Empirical Studies

In this section, we empirically demonstrate that our proposed MPRidge method induces an implicit ridge-like regularizing effect and it performs nearly the same as the explicitly ridge-regularized counterpart fit using the entire training data in terms of both in-sample and out-of-sample risks for a variety of learners including the robust regressor and SVM classifier. Moreover, we empirically show that MPRidge can largely recover the entire regularization path of parameter coefficients.

A. Synthetic Data

1). Data Generation:

For the following empirical studies, we consider the autoregressive Toeplitz design for the data matrix $X\in {ℝ}^{N\times M}$: the M-dimensional feature vector follows a $\mathcal{N}(0,\Sigma )$ distribution, where Σ_ij = ρ^|i−j| with ρ = 0.6. Such design represents a range of realistic data scenarios commonly found in machine learning applications. The M-dimensional parameter coefficient vector β is generated from $\mathcal{N}\left(0,\frac{1}{M}{I}_M\right)$. Here, I_M denotes the M × M identity matrix. To simulate various learning tasks, we consider the following outcome vectors $y\in {ℝ}^N$:

• Linear regression: generate y = Xβ + ϵ where the noise vector (ϵ₁, …, ϵ_N) is IID $\mathcal{N}(0,1)$.

• Regression with outliers: randomly pick N/2 examples to be outliers. For the i^th outlier example, generate $y_i=x_i^T\beta +{ϵ}_i$ with ${ϵ}_i~\mathcal{N}(0,100)$. For the i^th inlier example, generate $y_i=x_i^T\beta +{ϵ}_i$ with ${ϵ}_i~\mathcal{N}(0,1)$.

• Classification: for the i^th example, generate $y_i~\text{Bernoulli}\left(\frac{\text{exp\hspace{0.17em}}\left(x_i^T\beta \right)}{1+\text{exp\hspace{0.17em}}\left(x_i^T\beta \right)}\right),\forall i=1,\dots ,N$.

For each of the learning tasks above, we consider two scenarios: Scenario I with N = 2000 examples and M = 100 features; and Scenario II with N = 10000 examples and M = 500 features. For both scenarios, we split the data set into 60% training data and 40% test data via stratified sampling, if applicable.

2). Results:

We train our MPRidge meta-algorithm with various unregularized loss functions $\mathcal{L}(·;\beta )$ for the different learning tasks described above (see Table I). In particular, we compare our MPRidge employed with unregularized loss $\mathcal{L}$ with its explicitly ridge-regularized counterpart in terms of prediction risks and regularization path of coefficient estimates. For instance, for the linear regression task, the explicitly ridge-regularized counterpart is the ridge regressor, so on and so forth. Software implementations from Scikit-learn [11] are used for all explicitly ridge-regularized methods.

TABLE I.

Summary of loss functions $\mathcal{L}(·;\beta )$ employed with MPRidge.

Task	Loss Function	$\mathcal{L}\left(\left(y_i,x_i\right);\mathit{\beta }\right)$
Linear regression	Least-square loss	${\left(y_i-x_i^T\mathit{\beta }\right)}^2$
Regression with outliers	Huber loss	$\{\begin{array}{l}{\left(y_i-x_i^T\mathit{\beta }\right)}^2,\text{\hspace{0.17em}if\hspace{0.17em}}\left|y_i-x_i^T\mathit{\beta }\right|<\delta \hfill \\ 2\delta \left|y_i-x_i^T\mathit{\beta }\right|-{\delta }^2,\text{O}.\text{W}.\hfill \end{array}$
Classification	Logistic loss	$-y_i{x}_i^T\mathit{\beta }+\text{\hspace{0.17em}log\hspace{0.17em}}\left(1+\text{exp\hspace{0.17em}}\left(x_i^T\mathit{\beta }\right)\right)$
Classification	Hinge loss	$\text{max}\left\{0,1-y_i{x}_i^T\mathit{\beta }\right\}$

Our qualitative results for both linear regression and regression with outliers tasks from Scenario I are shown in Fig. 2. In the top row (A1, B1), we compare the in-sample risk R_{ens, in}(α) (out-of-sample risk R_{ens, out}(α)) of our MPRidge method for a sequence of feature subsampling ratio α ∈ (0, 1) against the in-sample risk R_{ridge, in}(λ) (out-of-sample risk R_{ridge, out}(λ)) of the explicitly ridge-regularized counterpart for a sequence of its tuning hyperparameter $\lambda \in {ℝ}_{+}$. Larger values of λ indicate larger amounts of explicit ridge regularization. The optimal tuning hyperparameters that result in the lowest out-of-sample risk are denoted with a vertical dashed line at (α*, λ*). In the bottom row (A2, B2), we display a subset of the regularization path, or coefficient estimates over the sequence of tuning hyperparameters, for our MPRidge method and its explicitly ridge-regularized counterpart. For both learning tasks, we clearly see that our MPRidge method achieves nearly the same prediction risk (both in-sample and out-of-sample) as the explicitly ridge-regularized counterpart and largely recovers the corresponding regularization path. These observations suggest that our MPRidge method implicitly elicits ridge-like regularization even though no regularization is explicitly applied to the loss functions during training. Additionally, there appears to be an one-to-one correspondence between the feature subsampling ratio α and the tuning hyperparameter λ for the explicitly ridge-regularized method. Specifically, a smaller α corresponds to a larger λ, signifying a larger amount of implicit ridge-like regularizing effect for MPRidge. The results for logistic loss and hinge loss are similar and are not included due to the page limit.

Fig. 2.

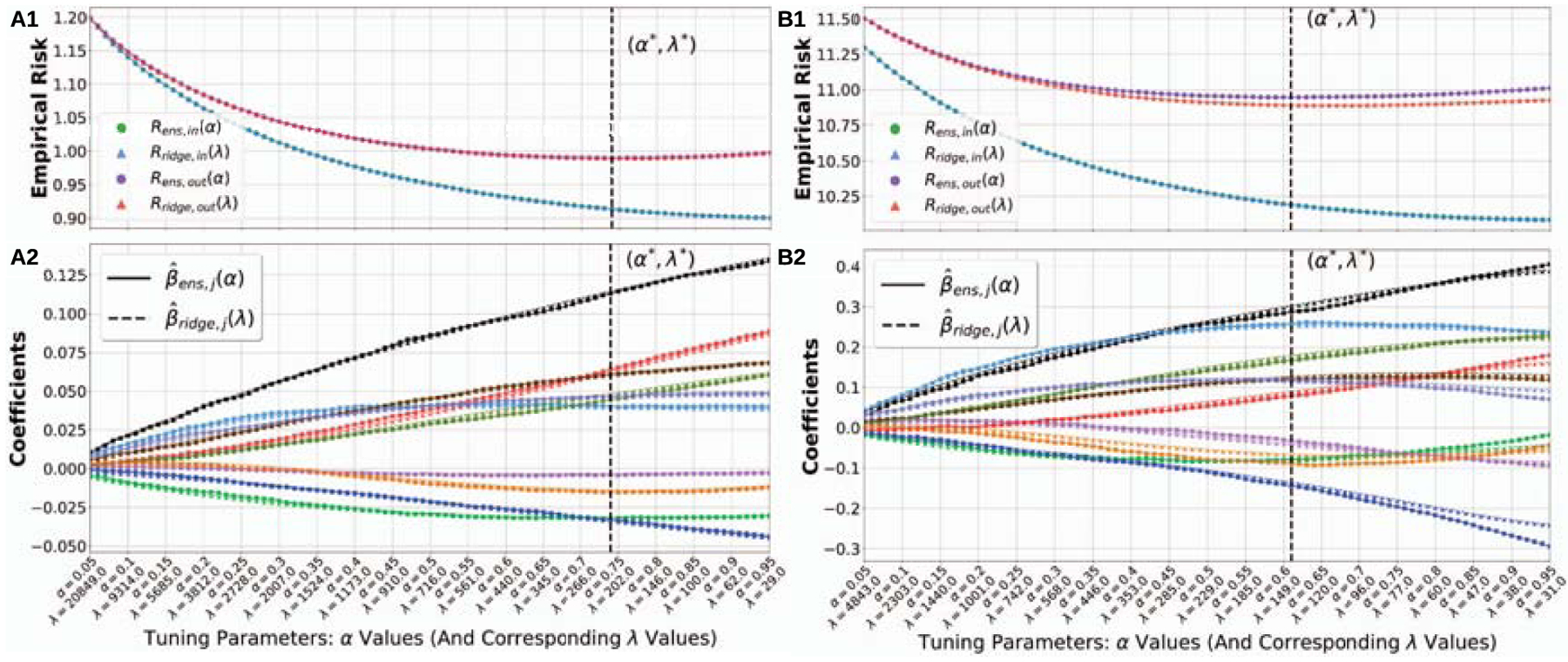
For both linear regression (A1, A2) and regression with outliers (B1, B2) from Scenario I, MPRidge attains nearly the same out-of-sample risk as the explicitly ridge-regularized counterpart: in A1 and B1, the α- and λ-axes are aligned based on in-sample risk, so that R_ens, in (green dot) aligns perfectly with R_{ridge, in} (blue triangle). This results in the out-of-sample risk R_ens, out (purple dot) also aligning approximately with R_{ridge, out} (red triangle). Additionally, MPRidge largely recovers the corresponding regularization path, as shown in A2 and B2. This suggests that our MPRidge method elicits ridge-like regularizing effects implicitly.

Quantitative results of various learning tasks for both Scenario I and II are summarized in Table II. Here, we report the largest absolute difference for in-sample risk, out-of-sample risk, and coefficient estimates between MPRidge and the explicitly ridge-regularized counterpart at their respective optimal tuning hyperparameters. Note that the optimal α* and optimal λ* are independently determined for the respective method. Clearly, we see that our MPRidge method performs nearly the same as its explicitly ridge-regularized counterpart across both scenarios for a range of commonly used learners including the logistic regressor, SVM classifier, and robust regressor. These results suggest that our MPRidge can achieve approximately the same optimal prediction risks (both in-sample and out-of-sample) and coefficient estimates as its explicitly ridge-regularized counterpart by eliciting implicit ridge-like regularization.

TABLE II.

Results of various learning tasks for Scenario I & II.

	Loss Function	|Rens,in(α*) − Rridge,in(λ*)|	|Rens,out(α*) − Rridge,out(λ*)|	$\Vert {\widehat{\mathit{\beta }}}_{\text{ens}}\left(\alpha *\right)-{\widehat{\mathit{\beta }}}_{\text{ridge}}\left(\lambda *\right){\Vert }_{\infty }$
Scenario I	Least-square	0.00152	0.00006	0.00546
	Huber	0.00001	0.05360	0.04732
	Logistic	0.00025	0.00046	0.00865
	Hinge	0.09410	0.04726	0.13034
Scenario II	Least-square	0.00339	0.00006	0.00258
	Huber	0.02615	0.05867	0.02284
	Logistic	0.00117	0.00047	0.00820
	Hinge	0.09697	0.05072	0.08414

B. Real Data Examples

We further demonstrate the performance of MPRidge using data from the ROSMAP study [12], which is a clinical-pathological study of Alzheimer’s disease (AD). Specifically, we consider a regression task with the numeric cognition score as the outcome and a classification task with the clinician’s diagnosis as the outcome; a subset of the gene expression via RNASeq data are used as features in both cases. Even though no distributional assumptions are made on the real data, MPRidge still exhibits ridge-like behavior, as shown in Fig. 3.

Fig. 3.

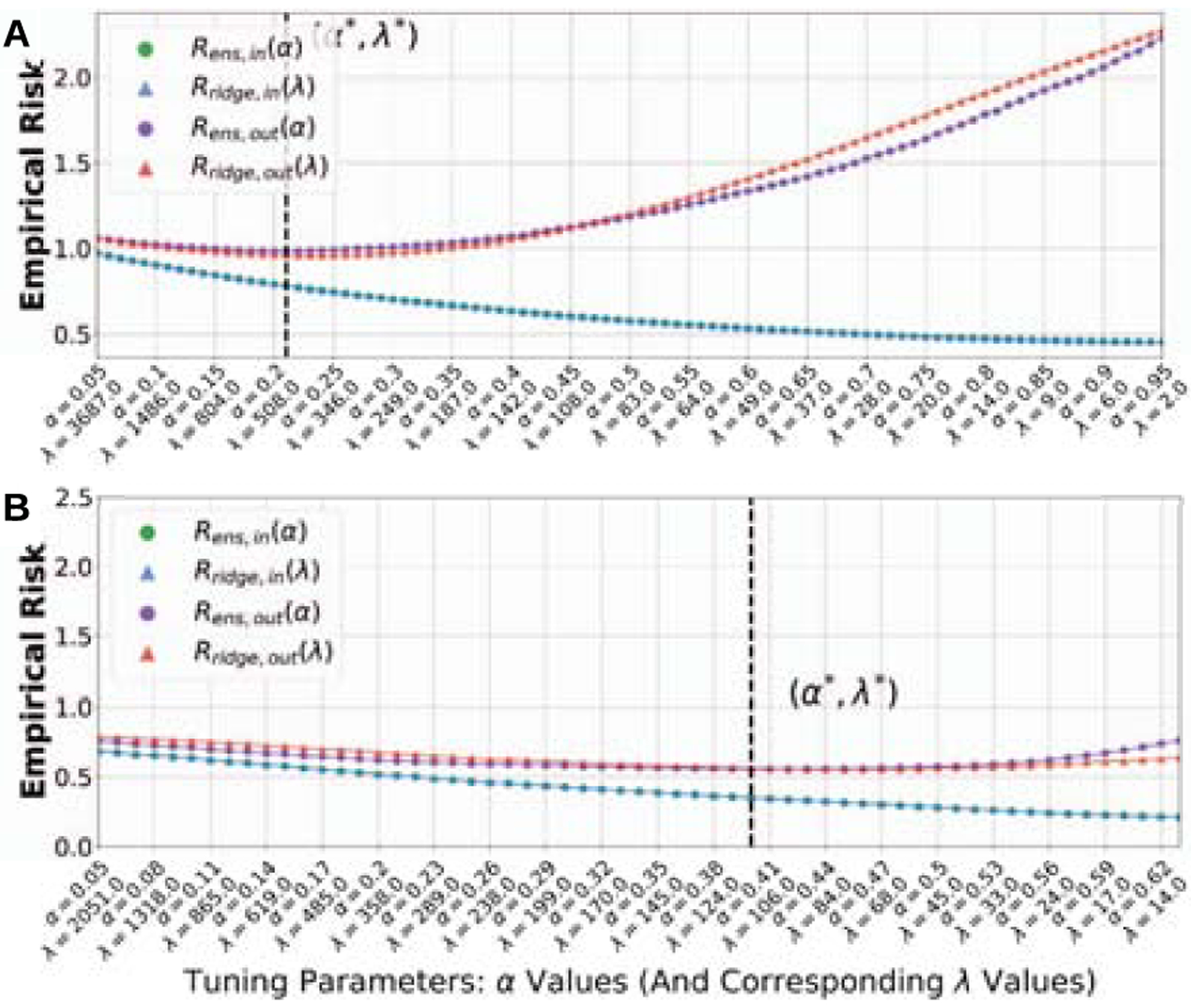
Real gene expression via RNASeq data are used as features. A. Regression with the cognition score as the outcome; MPRidge employs the least-square loss as the unregularized base learner. B. Binary classification with the clinician’s diagnosis (AD versus non-AD) as the outcome; MPRidge uses the hinge loss as the unregularized base learner. Both real data examples show a near-match in out-of-sample risks, especially at (α*, λ*) which denotes the matched parameter pair minimizing out-of-sample risk.

IV. Conclusions

We have developed MPRidge, which is a general meta-algorithm that can be employed to implicitly yield ridge-like regularization for a general class of machine learning methods including the SVM classifier and robust regressor. Parallelizable and flexible, MPRidge provides an appealing alternative to direct training of explicitly ridge-regularized methods in challenging big-data scenarios. In future works, we look to investigate the theoretical properties of MPRidge so as to better understand the underlying mechanisms that impart such implicit ridge-like behavior.