Elastic turbulence generates anomalous flow resistance in porous media

Microscopy reveals that polymers cause chaotic flow fluctuations in a porous medium, increasing macroscopic flow resistance.

Abstract

Many energy, environmental, industrial, and microfluidic processes rely on the flow of polymer solutions through porous media. Unexpectedly, the macroscopic flow resistance often increases above a threshold flow rate in a porous medium, but not in bulk solution. The reason why has been a puzzle for over half a century. Here, by directly visualizing flow in a transparent 3D porous medium, we demonstrate that this anomalous increase is due to the onset of an elastic instability in which the flow exhibits strong spatiotemporal fluctuations reminiscent of inertial turbulence, despite the small Reynolds number. Our measurements enable us to quantitatively establish that the energy dissipated by pore-scale fluctuations generates the anomalous increase in the overall flow resistance. Because the macroscopic resistance is one of the most fundamental descriptors of fluid flow, our results both help deepen understanding of complex fluid flows and provide guidelines to inform a broad range of applications.

INTRODUCTION

Diverse applications, ranging from groundwater remediation (1) and oil recovery (2, 3) to filtration (4) and chromatography (5), rely on the viscous-dominated flow of polymer solutions through disordered three-dimensional (3D) porous media. One of the most fundamental descriptors of such flows is the “apparent viscosity” η_app, which quantifies the macroscopic resistance to flow through the tortuous pore space. At low flow rates, the apparent viscosity matches the dynamic shear viscosity of the bulk solution, η. Above a threshold flow rate, however, η_app abruptly increases for many polymer solution—even though the shear viscosity η of the bulk solution decreases with increasing shear rate (3, 6–9). The reason for this anomalous increase has remained a puzzle ever since it was first reported over half a century ago (10).

This anomalous increase in flow resistance is often thought to reflect the accumulated extension of individual polymer molecules as they are transported through constrictions of the pore space (11–15), although direct validation of this idea remains lacking. Some recent simulations (16) and experiments in ordered 2D geometries (7, 17–20) have instead suggested that this anomalous increase in flow resistance is linked to the onset of an elastic instability, arising from the buildup of polymer-induced elastic stresses during transport. These instabilities are well studied in a range of simplified geometries (21–32) and can generate chaotic flow fields reminiscent of those observed in inertial turbulence (20, 28, 33)—often termed “elastic turbulence.” However, whether this phenomenon arises in disordered 3D porous media, and, if so, how exactly it influences macroscopic transport, is still debated; typical 3D media are opaque, precluding direct characterization of the flow in situ. Indeed, while magnetic resonance measurements of the diffusivity of a secondary fluid phase have hinted that elastic turbulence can arise in disordered 3D porous rocks (34), direct verification remains lacking. Furthermore, recent experiments in model 2D media indicate that geometric disorder, inherent in most naturally occurring media, can instead suppress the onset of elastic turbulence (35), casting doubt on this mechanism entirely; however, other experiments have shown that this suppression is sensitive to the specific choice of 2D geometry (36), and thus, disorder may not generally suppress elastic turbulence. In addition, while studies in 2D provide a straightforward way to visualize the flow and thereby yield powerful insights, such models differ in their connectivity, porosity, and complexity from 3D pore spaces. Therefore, it is unclear how results obtained in 2D can be extrapolated to 3D media. As a result, despite its fundamental importance and strong impact in applications, why the macroscopic flow resistance of polymer solutions anomalously increases in porous media is still unknown.

Here, by directly visualizing the flow of a polymer solution in a transparent 3D porous medium, we demonstrate that this anomalous increase is indeed dominated by the added dissipation arising from elastic turbulence. We find that the transition to unstable flow in each pore is continuous, arising because of the increased temporal persistence of discrete bursts of instability above an onset flow rate; however, this onset value varies from pore to pore. Hence, unstable flow is spatially heterogeneous across the different pores of the medium, with unstable and laminar regions coexisting. Guided by these findings, we quantitatively establish that the energy dissipated by unstable pore-scale fluctuations generates the anomalous increase in flow resistance through the entire medium. Our results thus help resolve this long-standing puzzle. Moreover, by linking the onset of unstable flow at the pore scale to flow resistance at the macroscale, our work yields generally applicable guidelines for predicting and controlling polymer solution flows.

RESULTS

Anomalous increase in macroscopic flow resistance coincides with the pore-scale onset of elastic turbulence

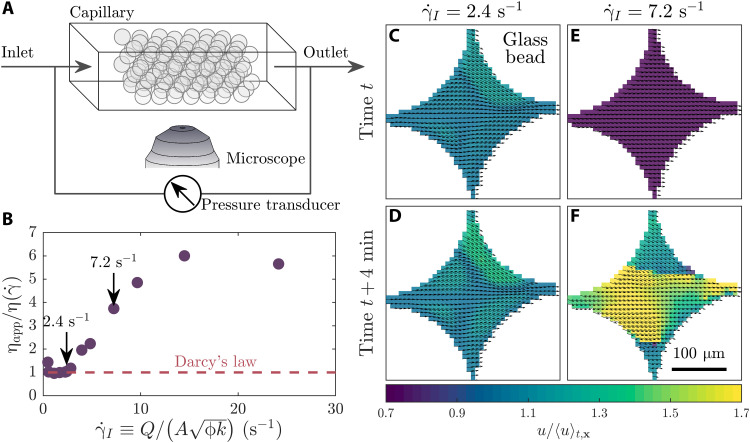
Bead packings are established models of disordered 3D porous media, with demonstrated reproducibility in pore size statistics and flow properties that can often be generalized to other more complex media (37). Therefore, as a model porous medium, we use a consolidated random packing of borosilicate glass beads (Fig. 1A) of porosity ϕ ≈ 0.41. The polymeric fluid used is a dilute solution of 18-MDa partially hydrolyzed polyacrylamide (HPAM) in a viscous aqueous solvent, formulated to precisely match its refractive index to that of the glass beads, thus rendering the medium transparent when saturated. Additionally dispersing a dilute fraction of 200-nm-diameter fluorescent latex microparticles, which act as flow tracers, therefore enables measurement of the 2D fluid velocities u in the pore space via particle image velocimetry using confocal microscopy (Materials and Methods). We characterize the macroscopic flow behavior by injecting the polymer solution into the medium at a constant volumetric flow rate Q and measuring the corresponding steady-state pressure drop 〈ΔP〉_t across the medium; the angled brackets indicate an average over time t. For a Newtonian fluid, the relationship between these quantities is given by Darcy’s law: 〈ΔP〉_t/ΔL = η(Q/A)/k, where η is the fluid dynamic shear viscosity measured using shear rheology (figs. S1 to S3) and ΔL, A, and k are the length, cross-sectional area, and absolute permeability of the medium, respectively. For a polymer solution, for which the viscosity can change depending on flow conditions, this relationship is still used in practice, but with η replaced by the apparent viscosity ${\mathrm{\eta }}_{\text{app}}\equiv \frac{{\langle \mathrm{\Delta }P\rangle }_t/\mathrm{\Delta }L}{(Q/A)/k}$ that represents the macroscopic flow resistance. To facilitate comparison to the bulk shear viscosity, we therefore represent the pressure drop measurements by plotting the reduced apparent viscosity ${\mathrm{\eta }}_{\text{app}}/\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$ as a function of the interstitial shear rate ${\stackrel{·}{\mathrm{\gamma }}}_I\equiv \frac{Q/(\mathrm{\varphi }A)}{\sqrt{k/\mathrm{\varphi }}}$ defined using the characteristic pore flow speed Q/(ϕA) and length scale $\sqrt{k/\mathrm{\varphi }}$ (38, 39); because all the other parameters are independently known, this relationship provides a direct mapping from the measured pressure drop to the apparent viscosity. As expected, at low flow rates, ${\mathrm{\eta }}_{\text{app}}=\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$. However, above a critical flow rate corresponding to ${\stackrel{·}{\mathrm{\gamma }}}_I\approx 4$ s⁻¹, η_app increasingly exceeds $\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$, eventually peaking at $\approx 6\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$, as shown in Fig. 1B; the corresponding pressure drop data reflect the same behavior, as shown in fig. S4. This anomalous increase and eventual peak in the macroscopic flow resistance parallels previous reports (3, 6–10).

Fig. 1. Pore-scale visualization reveals that the anomalous increase in flow resistance coincides with the onset of elastic turbulence.

(A) Our porous medium is a lightly sintered random packing of borosilicate glass beads confined in a quartz capillary with a square cross section. We inject the polymer solution containing fluorescent tracers into the medium using a syringe pump and simultaneously image the flow in situ using a confocal microscope while measuring the pressure drop across the medium using differential pressure transducers. (B) Above a threshold flow rate, parameterized by the characteristic shear rate ${\stackrel{·}{\mathrm{\gamma }}}_I$, the macroscopic pressure drop, represented by the reduced apparent viscosity ${\mathrm{\eta }}_{\text{app}}/\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$, anomalously increases and deviates from the prediction of Darcy’s law given by the shear viscosity of the bulk solution. (C to F) Flow visualization in an example pore; applied flow is left to right. Arrows indicate the vector field, and colors indicate the velocity magnitude u = ∣u∣ normalized by its value averaged spatially over the pore and temporally over the entire duration of the experiment, 〈u〉_{t, x} = 〈∣u∣〉_{t, x}. (C and D) At a low flow rate, the flow does not change over time. (E and F) At a higher flow rate, the flow exhibits strong spatiotemporal fluctuations characteristic of elastic turbulence.

Simultaneous visualization of the pore-scale flow provides a clue to the underlying reason for this anomalous increase. Figure 1 (C to F) shows the velocity field within an example pore measured at two different times. At low flow rates, for which ${\mathrm{\eta }}_{\text{app}}=\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$, the flow is laminar and steady over time (Fig. 1, C and D, and movie S1). Notably, concomitant with the anomalous increase in flow resistance, we observe strong spatial and temporal fluctuations in the flow at high flow rates (Fig. 1, E and F), despite the negligible influence of inertia in the flow, as indicated by the Reynolds number Re ≲ 10⁻⁴ ≪ 1. As shown in movie S2, the fluid pathlines continually cross and vary over time, indicating the emergence of an elastic instability. These flow fluctuations are chaotic, with spatial and temporal power spectra that decay as power laws (figs. S5 and S6)—a defining feature of elastic turbulence (33,40). Our visualization thus reveals that elastic turbulence does arise in 3D porous media, contrary to previous suggestions based on studies in 2D media that the disordered structure of the medium suppresses elastic turbulence (35).

The pore-scale transition to fully unstable flow is continuous, with an onset that varies from pore to pore

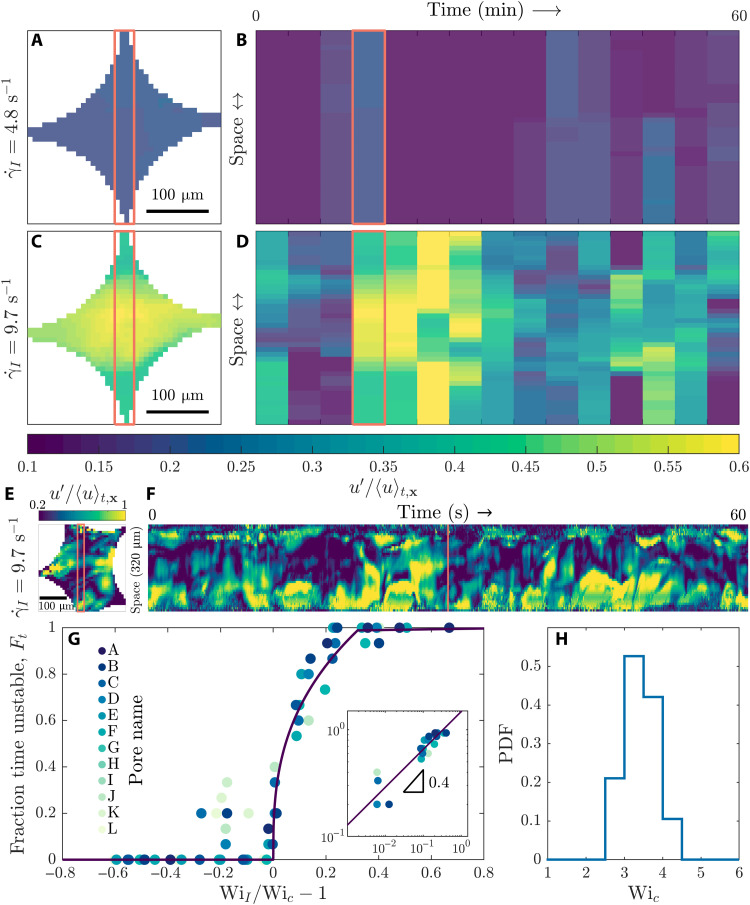
To further characterize the conditions under which elastic turbulence arises in this pore, we subtract the temporal mean from each velocity vector, point by point, to focus on the fluctuations u′ = u − 〈u〉_t. Near the onset of the anomalous increase in flow resistance, flow fluctuations (blue in Fig. 2, A and B) manifest as intermittent, abrupt bursts that coexist with the base laminar flow (purple in Fig. 2B), but quickly decay (movie S3). Well above this onset, however, these fluctuations (blue-green-yellow in Fig. 2C) still coexist with the laminar flow but persist over time (Fig. 2D and movies S4 and S5); moreover, their normalized magnitudes are considerably larger (fig. S7). Further examples corroborating this finding with higher-speed imaging are shown in Fig. 2 (E and F) and fig. S5. Similar behavior is observed in the intermittent transition to inertial turbulence: For sufficiently large Re, discrete bursts of unstable flow appear and decay, persisting for longer durations as Re increases (41). Thus, the transition to inertial turbulence is, in many cases, thought to be a non-equilibrium transition characterized by a continuously growing turbulent fraction (42, 43). Our results suggest the tantalizing possibility that the pore-scale transition to fully unstable flow—in this case, driven by an elastic instability—may similarly be a continuous non-equilibrium transition, as suggested recently in simulations (44).

Fig. 2. The pore-scale transition to elastic turbulence is a continuous non-equilibrium transition between distinct flow states.

(A and B) Near the onset of elastic turbulence, flow fluctuations are intermittent and short lived; (A) shows the normalized magnitude of flow fluctuations in a given pore at a given time, while (B) shows how the fluctuations in the red box vary over time. (C and D) Well above the onset of elastic turbulence, flow fluctuations are stronger and persist over time. (E and F) Continuous higher-speed imaging in another pore, also above the onset of elastic turbulence, again shows that flow fluctuations persist over time, even at short time scales. (G) The fraction of time F_t a pore spends in an unstable state (u′/〈u〉_t,x > 0.2) continually grows above a threshold flow rate, parameterized by the threshold Weissenberg number Wi_c. Different pores are characterized by different values of Wi_c, as shown by the probability density function (PDF) in (H); however, they all exhibit a similar transition to elastic turbulence, as shown by the collapse of the measurements of F_t in (G) when the imposed Wi_I is rescaled by Wi_c for each pore. The inset shows the power-law scaling F_t ∼ (Wi_I/Wi_c − 1)^0.4; the exponent is obtained from the best fit to the data, with an uncertainty of ±0.1 determined by varying the instability threshold by ±10%.

We test this hypothesis by measuring the fraction of time F_t a pore spends in the unstable state, as is often done to characterize the transition to inertial turbulence (43), for 12 different pores over a broad range of flow rates. This quantity characterizes flow intermittency; in particular, as F_t increases, unstable bursts become more persistent over time, lasting for longer durations. Eventually, F_t = 1 corresponds to the turbulent state in which the flow is always unstable. Because the unstable flow is driven by polymer elasticity rather than fluid inertia, we describe the pore-scale transition to elastic turbulence using the characteristic Weissenberg number defined using the macroscopic imposed flow conditions, ${\text{Wi}}_I\equiv N_1({\stackrel{·}{\mathrm{\gamma }}}_I)/2\mathrm{\sigma }({\stackrel{·}{\mathrm{\gamma }}}_I)$; this parameter compares elastic stresses quantified by the first normal stress difference N₁ to viscous stresses quantified by the shear stress σ and represents the upper limit of the spatially varying local Weissenberg number (fig. S8). It can also be related to the largest destabilizing term in a linear stability analysis of the creeping flow limit of the Cauchy momentum equation for a viscoelastic fluid (23). For each pore, at low Wi_I, the flow is laminar and unchanging in time, with F_t = 0. Above a critical value Wi_c, however, the pore is unstable for a nonzero fraction of time, and F_t smoothly increases above zero. It eventually saturates at unity for Wi_I ≫ Wi_c, indicating that the elastic turbulence has fully developed. Notably, this transition is general: While the critical value Wi_c varies from pore to pore (Fig. 2G), presumably because of the disordered structure of the pore space, F_t grows similarly with the rescaled Wi_I/Wi_c for all 12 pores, as shown by the different colors in Fig. 2G, indicating a continuous transition. We observe some scatter in the data, possibly due to the influence of polydispersity in polymer properties and local correlations in the flow between neighbors; investigating these effects will be a useful direction for future work. However, in all cases, the data for Wi_I near Wi_c appear to follow the power-law scaling F_t ∼ (Wi_I/Wi_c − 1)^0.4 (Fig. 2G, inset). Thus, the pore-scale transition to elastic turbulence is a continuous transition reminiscent of the intermittent transition to inertial turbulence (41, 44).

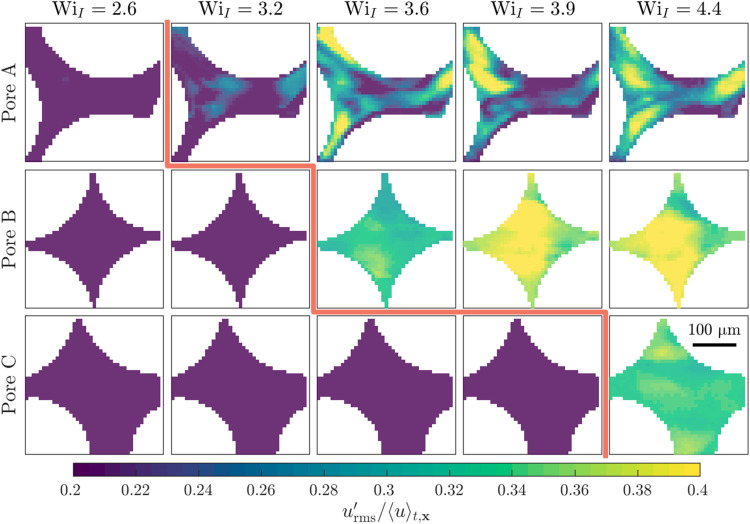
An unexpected consequence of the pore-to-pore variability in Wi_c, which ranges from Wi_c,min ≈ 2.6 to Wi_c,max ≈ 4.4 (Fig. 2H), is that the occurrence of elastic turbulence is spatially heterogeneous throughout the medium. In particular, because some pores become unstable at different values of Wi_I than others, unstable pores coexist amid stable, laminar pores for Wi_I in this range. An example is shown in Fig. 3, which displays the normalized root mean square of the flow fluctuations u′ over time, $u_{\text{rms}}^{\prime }/{\langle u\rangle }_{t,\mathbf{x}}$, for three different pores. At low flow rates and therefore Wi_I, all three pores are stable, as shown in the first column. As flow rate and Wi_I is increased, pore A (2.6 < Wi_c ≤ 3.2) becomes unstable first, while pores B and C remain stable, as shown in the second column. At a higher Wi_I, pore B (3.2 < Wi_c ≤ 3.6) next becomes unstable, as shown in the third column. Last, at an even higher Wi_I, pore C (3.9 < Wi_c ≤ 4.4) also becomes unstable, as shown in the last column. Hence, as Wi_I increases from ≈2.6 to 4.4, an increasing fraction of pores become unstable. This observation that single pores exposed to the same macroscopic flow rate become unstable in different ways provides a fascinating pore-scale analog of “molecular individualism” (45), in which single polymers exposed to the same extensional flow elongate in different ways; we therefore term it “porous individualism.” Monitoring a larger field of view spanning multiple pores on a side confirms that the flow states in neighboring pores are not appreciably correlated (fig. S9).

Fig. 3. The occurrence of elastic turbulence is spatially heterogeneous throughout a porous medium, reflecting porous individualism.

Images show the normalized magnitude of root mean square flow fluctuations over 60 min in different pores and at different flow rates, parameterized by Wi_I. Applied flow is left to right. Pore A becomes unstable at the lowest flow rate, as shown by the red line in the first row. Pore B becomes unstable at the next highest flow rate, shown by the red line in the second row. Pore C becomes unstable only at even higher flow rates.

Simplified power balance enables pore-scale flow fluctuations to be linked to macroscopic transport

How does this variability in the occurrence of elastic turbulence affect the macroscopic flow resistance? Motivated by the similarities between elastic and inertial turbulence revealed by our pore-scale imaging, as well as by previous studies in a range of simplified geometries (20, 28, 33), we hypothesize that the flow fluctuations that arise in elastic turbulence impart additional viscous dissipation to the flow—akin to fluctuations in inertial turbulence. We quantify this hypothesis using the power density balance for viscous-dominated flow (46)

$$-\nabla ·P\mathbf{u}=\mathbf{\tau }:\nabla \mathbf{u}$$ (1)

where the left-hand side represents the rate of work done by the fluid pressure and the right-hand side represents the rate of viscous energy dissipation per unit volume; here, τ and ∇u are the stress and velocity gradient tensors, respectively. Averaging Eq. 1 over time and the entire volume V of the medium then provides a relation for the time-averaged pressure drop 〈ΔP〉_t across the medium

$$\frac{{\mathrm{\Delta }P}_t}{\mathrm{\Delta }L}=\frac{{\langle {\langle \mathbf{\tau }:(\mathbf{s}+\mathbf{\omega })\rangle }_t\rangle }_V}{Q/A}$$ (2)

where s = (∇u + ∇u^T)/2 and ω = (∇u − ∇u^T)/2 are the strain rate and vorticity tensors, respectively. In principle, Eq. 2 provides a direct link between the measured pore-scale flow field, quantified on the right-hand side, and macroscopic pressure drop, given on the left-hand side, as explored in recent simulations (16). However, in practice, evaluating the right-hand side of Eq. 2 requires knowledge of the full dependence of stress τ on polymer strain history in 3D (47), which is currently inaccessible in our experiments.

Nevertheless, two features of the flow, further detailed in Materials and Methods, motivate the development of a simplified version of Eq. 2 that permits us to examine the influence of unstable pore-scale flow fluctuations on macroscopic transport. First, while the flow fluctuates strongly over a broad range of time scales, the majority of the measured spectral power is contained in fluctuations occurring over a duration longer than the characteristic polymer relaxation time λ (fig. S6). Hence, we approximate the measured time-dependent flow as being quasi-steady over the polymer relaxation time, enabling us to adopt a generalized Newtonian fluid approach (47) in which the stress is parameterized by the shear viscosity η_s, which is a function of the local strain rate, and the extensional viscosity η_e, which is a function of accumulated strain in the quasi-steady flow field. Second, analysis of the measured flow field indicates that the Hencky strain accumulated by fluid elements over the polymer relaxation time is much smaller than 1 (fig. S10), whereas the polymer contribution to extensional viscosity is known to become appreciable only when Hencky strain exceeds ≈2 to 3 (48). Thus, while local polymer extension drives the onset of the unstable flow, accumulated extension is likely not a strong contributor to the global viscous dissipation as is often suggested (11–15); we therefore neglect any polymer contributions to the extensional viscosity and take the Newtonian limit of the Trouton ratio Tr ≡ η_e/η₀ = 3.

These assumptions then allow us to decompose the strain rate tensor into the sum of a base laminar component s₀ and an additional component due to velocity fluctuations s′ and the vorticity tensor similarly into two components ω₀ and ω′, ultimately yielding an expanded form of Eq. 2 (46)

$$\frac{{\mathrm{\langle }\mathrm{\Delta }P\mathrm{\rangle }}_t}{\mathrm{\Delta }L}\equiv \frac{{\mathrm{\eta }}_{\text{app}}(Q/A)}{k}\approx \underset{\text{Darcy}’\mathrm{s}\text{law}}{\underbrace{\frac{\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)(Q/A)}{k}}}+\underset{\text{Fluctuations}}{\underbrace{\frac{\mathrm{\langle }\mathrm{\chi }{\mathrm{\rangle }}_{t,V}}{(Q/A)}}}+\left\{\begin{array}{c}\text{Strain}\\ \text{history}\\ \text{effects}\end{array}\right\}$$ (3)

The first term on the right-hand side of Eq. 3, which arises from homogenization over the entire porous medium, represents Darcy’s law for a laminar, steady flow. The second term represents the additional contribution to the macroscopic pressure drop from viscous dissipation by the solvent induced by the unstable flow fluctuations, much like the dissipation arising from chaotic fluctuations in inertial turbulence (49); 〈χ〉_t ≈ η〈s′:s′〉_t quantifies the rate of added viscous dissipation per unit volume due to pore-scale flow fluctuations, where η is the time-averaged shear viscosity of the polymer solution (46). The final term represents additional contributions arising from the full dependence of stress τ on polymer strain history in 3D that are not considered in our generalized Newtonian fluid approach. We provide an estimate for the magnitude of this term in fig. S12; exploring the influence of these additional complexities will be a valuable extension of our work.

Viscous dissipation due to flow fluctuations generates the anomalous increase in flow resistance

Equation 3 provides a way to quantitatively link the pore-scale flow fluctuations arising in elastic turbulence and the anomalous increase in macroscopic flow resistance. In particular, as a first step toward this goal, we will neglect the third term on the right-hand side of the Equation in what follows and examine the influence of the first two terms. All the components of these first two terms are controlled or can be directly determined in our experiments (Materials and Methods).

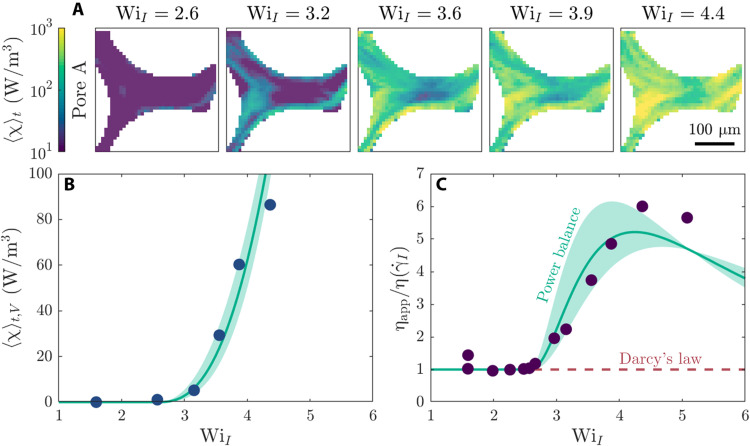
We directly measure the rate of added dissipation 〈χ〉_t using flow visualization in each pore; an example is shown in Fig. 4A. Consistent with our expectation, the rate of local viscous dissipation sharply increases by nearly three orders of magnitude at the onset of elastic turbulence and continues to increase as Wi_I increases above Wi_c (Fig. 4A, green/yellow regions). These measurements, performed for each pore, thereby enable us to directly test the validity of our simplified form of Eq. 3, assuming spatially isotropic, but not homogeneous, fluctuations within each pore (46). In particular, we directly compute 〈χ〉_t,V by averaging 〈χ〉_t over the imaged area of each pore and then averaging over all the imaged pores. As anticipated, the overall rate of added dissipation increases as a greater fraction of pores becomes unstable (Fig. 4B, symbols), consistent with the power-law scaling shown by the green curve. Incorporating this empirical relationship for 〈χ〉_t,V in our simplified form of Eq. 3 then yields a final prediction for the dependence of the apparent viscosity η_app on the imposed Wi_I (Fig. 4C, green curve) that is derived directly from our pore-scale imaging of the unstable flow fluctuations. Our prediction shows excellent agreement with the macroscopic pressure drop measurements (Fig. 4C, symbols) without using any fitting parameters. This agreement confirms that the anomalous increase in the macroscopic flow resistance is primarily due to the added dissipation arising from the flow fluctuations generated by pore-scale elastic turbulence.

Fig. 4. Anomalous increase in macroscopic flow resistance is determined by the added viscous dissipation due to unstable flow fluctuations.

(A) The rate of added viscous dissipation 〈χ〉_t directly measured from flow visualization for the example of pore A sharply increases above the onset of elastic turbulence. (B) Averaging the spatially averaged 〈χ〉_t over all pores imaged yields the overall added viscous dissipation, which increases as a power law ∼(Wi_I/Wi_c − 1)^2.6 above the macroscopic threshold Wi_c ≈ 2.6, as shown by the green curve. (C) The measured power-law fit to 〈χ〉_t,V enables prediction of the macroscopic apparent viscosity η_app via the power balance Eq. 3, as shown by the green curve and detailed in the Supplementary Materials; the uncertainty associated with the fit to 〈χ〉_t,V [shaded region in (B)] yields an uncertainty in this prediction, as shown by the shaded region. Points indicate the independent measurements of η_app from the macroscopic pressure drop.

A simple picture for the sigmoidal variation of η_app with flow rate, observed in our experiments (Fig. 1B) and in numerous previous studies (3, 6–10), thereby emerges. At low flow rates, corresponding to Wi_I < Wi_c,min, all of the pores in the medium are laminar and steady over time; thus, ${\mathrm{\eta }}_{\text{app}}=\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$. As flow rate is increased, Wi_I eventually exceeds Wi_c,min ≈ 2.6 in our experiments, causing an increasing fraction of pores to become unstable. The added viscous dissipation due to the flow fluctuations in these pores then causes η_app to increasingly exceed $\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$ (Fig. 4C, 8th to 12th points). Eventually, as Wi_I exceeds Wi_c,max ≈ 4.4 in our experiments, all of the pores are unstable. Further increases in Wi_I do not appreciably generate additional flow fluctuations, and η_app saturates (Fig. 4C, last point). The steepness of the increase of η_app with flow rate therefore reflects the distribution of the different Wi_c; while these values depend on the complex 3D geometry of each pore and are challenging to predict a priori (23), reducing the polydispersity of the medium likely sharpens the distribution of Wi_c and thus steepens the increase in η_app, consistent with the results of studies in 2D obstacle arrays (50). As the flow rate is further increased, we expect that η_app eventually converges back to $\mathrm{\eta }({\stackrel{·}{\mathrm{\gamma }}}_I)$, reflecting the increased relative influence of viscous dissipation from the base laminar flow—although strain history effects, inertia, and chain scission will likely also play a role in this regime, imparting new complexities to the flow.

DISCUSSION

Although it is well documented (3, 6–10), the anomalous flow resistance exhibited by polymer solutions in porous media has evaded explanation for over half a century. Many have speculated that this phenomenon is due to the onset of elastic turbulence, given that elastic instabilities have been reported to generate increased flow resistance in a range of simplified geometries (7, 17–21, 33). However, a quantitative link between the associated flow fluctuations in a porous medium—if they exist—and the macroscopic flow resistance has remained elusive. Indeed, whether elastic turbulence even arises in disordered 3D porous media has been recently called into question (35). Our experiments help to resolve this uncertainty by providing the first visualization of elastic turbulence in disordered 3D porous media. Furthermore, by quantitatively linking the pore-scale features of elastic turbulence to macroscopic transport, our work establishes that the energy dissipated by unstable pore-scale fluctuations generates the anomalous increase in flow resistance. More broadly, our findings that the pore-scale transition to elastic turbulence is a continuous non-equilibrium transition akin to the intermittent transition to inertial turbulence, and that the resulting dissipation similarly controls macroscopic transport behavior, highlight the connections between these distinct forms of turbulence.

For simplicity, our analysis does not consider the full polymer strain history in 3D. Instead, motivated by the observations that the flow is quasi-steady and does not appreciably accumulate strain over a polymer relaxation time, we use a generalized Newtonian fluid model that successfully captures ≈90% of the measured peak in the flow resistance, as well as the overall sigmoidal shape of ${\mathrm{\eta }}_{\text{app}}({\stackrel{·}{\mathrm{\gamma }}}_I)$. This close agreement suggests that while local polymer extension generates unstable flow fluctuations, the resulting viscous dissipation of the fluid itself is the primary contributor to the overall flow resistance—not the polymer extensional viscosity, as is often thought to be the case (11–15). Similar behavior has been considered in analyses of elasto-inertial turbulence, where polymer stretching is thought to be highly transient and localized (51). However, we do observe slight discrepancies between our model prediction and the pressure drop measurements, particularly at the largest flow rates tested (last two points in Fig. 4C); we anticipate that strain history effects play a non-negligible role in this regime, as suggested by a calculation of the added contribution due to the steady-state extensional viscosity (fig. S12). Incorporating these effects into our analysis will be an important next step.

We expect our results to particularly affect geological applications involving polymer solution flows in porous media, given that polymers with relaxation times λ as long as ∼10 s (7) are regularly used to aid the removal of trapped nonaqueous liquids from subsurface formations during groundwater remediation (1) and oil recovery (2, 3). Our results suggest that elastic turbulence may arise in these settings: We find that the transition to unstable flow occurs for $\text{Wi}\gtrsim {\text{Wi}}_c\approx \mathrm{\lambda }{\stackrel{·}{\mathrm{\gamma }}}_I~1$, corresponding to interstitial shear rates ${\stackrel{·}{\mathrm{\gamma }}}_I$ and flow speeds Q/A exceeding ∼0.1 s⁻¹ and ∼0.1 m s⁻¹, respectively (32)—well within the range encountered in the field. Thus, by deepening fundamental understanding of how macroscopic transport behavior depends on imposed flow conditions and solution properties, our analysis yields guidelines for predicting and controlling polymer solution flows in such settings. Moreover, because such flows also play key roles in determining separation performance in filtration (4) and chromatography (5), improving heat and mass transfer in microfluidic devices (17, 52, 53), and enabling extrusion-based manufacturing (54), we expect these results to inform a broader range of applications.

MATERIALS AND METHODS

Porous medium fabrication and physical characteristics

Our porous medium is a granular packing of borosilicate glass beads with diameters D_p ranging from 300 to 355 m (Mo-Sci). We pack these grains into a quartz capillary with a square cross section of area A = 3.2 mm by 3.2 mm (VitroCom), tap them for a minute to densify, and then lightly sinter the medium in a furnace at 1000°C for 3 min. In addition, we shave down the ends of the packing to provide flat inlets and outlets. This protocol forms a rigid, consolidated, disordered granular packing with a porosity ϕ ≈ 0.41, pore throat diameter d_t ≈ 0.16D_p ≈ 52 m, and tortuosity ≈2, as we previously measured using confocal microscopy (55, 56). The length of the medium along the imposed flow direction is ΔL = 8.1 cm. To control and characterize flow in the pore space, we glue inlet and outlet tubing into the inlet and outlet of the medium, respectively, with valves for pressure taps. We determine the medium permeability k = 79 μm² using Darcy’s law, using the values of the pressure drop measured at the lowest (laminar) flow rates; this permeability is in good agreement with our previous measurements of similar porous media (56) and with the prediction of the established Kozeny-Carman relation (57).

Polymer solution preparation and characterization

Our polymer solution is made by dissolving 18-MDa HPAM (30% carboxylated monomers; Polysciences) and NaCl (Sigma-Aldrich) in ultrapure Millipore water and then diluting with glycerol (Sigma-Aldrich) and dimethyl sulfoxide (DMSO; Sigma-Aldrich) to obtain a solution whose refractive index is precisely matched to that of the glass beads. The final solution of 300–parts per million (ppm) HPAM, 82.6 weight % (wt %) glycerol, 10.4 wt % DMSO, 6 wt % water, and 1 wt % NaCl has a measured refractive index of 1.479. All solutions are used within 1 month of preparation.

We characterize all flow properties using shear rheology measurements of a 1-ml sample of the polymer solution. We use a cone-plate geometry in an Anton-Paar MCR301 rheometer, using a 1° 5-cm-diameter cone set at a 50-μm gap. We measure the shear stress σ and first normal stress difference N₁ over a range of shear rates $\stackrel{·}{\mathrm{\gamma }}=0.1$ to 50.1 s⁻¹, which spans the range of characteristic interstitial shear rates encountered during the flow experiments in porous media, calculated as ${\stackrel{·}{\mathrm{\gamma }}}_I\equiv Q/(A\sqrt{\mathrm{\varphi }k})$, where Q is the volumetric flow rate of polymer solution, A is the capillary cross-sectional area, ϕ is the medium porosity, and k is the absolute permeability of the medium. To assess reproducibility, we collect data from four different samples and find identical results for all four samples. Both the shear stress and first normal stress difference vary with shear rate according to power laws $\mathrm{\sigma }(\stackrel{·}{\mathrm{\gamma }})\approx A_s{(\stackrel{·}{\mathrm{\gamma }})}^{{\mathrm{\alpha }}_s}$ and $N_1(\stackrel{·}{\mathrm{\gamma }})\approx A_n{(\stackrel{·}{\mathrm{\gamma }})}^{{\mathrm{\alpha }}_n}$, where σ and N₁ have units of Pa, $\stackrel{·}{\mathrm{\gamma }}$ has units of s⁻¹, A_s = 0.369 Pa · s^α_s, α_s = 0.934 ± 0.001, A_n = 1.46 Pa · s^α_n, and α_n = 1.23 ± 0.04 (fig. S1). The shear stress varies approximately linearly with shear rate, indicating that shear thinning effects are small because of the high viscosity of the background solvent, which is approximately β = 0.2 times the measured solution viscosity. However, for accuracy, we use the rate-dependent shear viscosity $\mathrm{\eta }(\stackrel{·}{\mathrm{\gamma }})\equiv \mathrm{\sigma }(\stackrel{·}{\mathrm{\gamma }})/\stackrel{·}{\mathrm{\gamma }}$ in all calculations. We define the zero shear viscosity using the lowest tested interstitial shear rate, ${\mathrm{\eta }}_0\equiv {[\mathrm{\sigma }(\stackrel{·}{\mathrm{\gamma }})/\stackrel{·}{\mathrm{\gamma }}]}_{{\stackrel{·}{\mathrm{\gamma }}}_I=0.14 {\mathrm{s}}^{-1}}=0.419 \text{Pa}·\mathrm{s}$.

We use shear rheology of the diluted polymer solution to characterize molecular properties. In particular, shear rheology measurements of a dilution series at different polymer concentrations c (fig. S3) yield the pure solvent viscosity η_s = 0.226 ± 0.009 Pa · s and the intrinsic viscosity [η] = (3 ± 1) × 10⁻⁴ ppm⁻¹. This quantity directly yields an estimate of the polymer overlap concentration c^* as established previously (58), c^* ≈ 0.77/[η] = 600 ± 300 ppm, and therefore, our experiments use a dilute polymer solution at ≈0.5 times the overlap concentration. We also use this quantity to estimate the mean polymer radius of gyration R_g using the relation c^* ≈ (M_w/V)/N_A, where M_w is the polymer molecular weight, $V=4\mathrm{\pi }{R}_g^3/3$ is the volume occupied by a single polymer molecule, and N_A is Avogadro’s number (59), yielding R_g ≈ 220 nm. We independently verify this estimate using dynamic light scattering of a dilute 10-ppm HPAM solution in the same index-matched solvent used in the flow experiments; we measure a mean hydrodynamic radius R_h ranging from 40 to 320 nm, which corresponds to R_g ≈ 160 to 210 nm using the shape factor ρ ≡ R_g/R_h ≈ 1.3 to 1.7 established previously (60).

We define the Reynolds number comparing inertial to viscous stresses as $\text{Re}\equiv \mathrm{\rho }(Q/\mathrm{\varphi }A)d_t/\mathrm{\eta }(\stackrel{·}{\mathrm{\gamma }})$, where ρ is the density of the solvent. In our porous media experiments, Re ranges from 2.5 × 10⁻⁶ to 1.6 × 10⁻⁴, indicating that viscous stresses dominate over inertial stresses.

We describe the influence of elasticity using the Weissenberg number, which compares elastic stresses to viscous stresses. As is conventionally done, we define this parameter as $\text{Wi}\equiv N_1(\stackrel{·}{\mathrm{\gamma }})/2\mathrm{\sigma }(\stackrel{·}{\mathrm{\gamma }})$. In our porous media experiments, Wi is greater than one, ranging from 1.6 to 5.1, indicating that elastic stresses dominate. Moreover, the corresponding values of the elasticity number El ≡ Wi/Re, which compares elastic stresses to inertial stresses, range from 3.3 × 10⁴ to 6.7 × 10⁵, much greater than one. Our experiments thus probe the elasticity-dominated flow regime. Using the shear rheology measurements, we also calculate the rheological relaxation time $\mathrm{\lambda }(\stackrel{·}{\mathrm{\gamma }})=\frac{\mathit{Wi}}{\stackrel{·}{\mathrm{\gamma }}}=\frac{N_1(\stackrel{·}{\mathrm{\gamma }})}{2\mathrm{\sigma }(\stackrel{·}{\mathrm{\gamma }})\stackrel{·}{\mathrm{\gamma }}}$, whose value ranges from 0.2 to 3 s, in good agreement with previous experiments (40).

To assess possible degradation of polymers due to unstable flow in the porous media (61), we also characterize the rheology of the same polymer solution before and after performing flow experiments at the highest flow rate tested, Q = 5 ml/hour. We do not find observable variation in the shear rheology, indicating that polymer degradation due to the unstable flow is minimal (fig. S2).

Characterization of flow in the porous medium

Before each experiment, we remove air bubbles under vacuum and then fill the medium with water. We then displace the water with the miscible polymer solution, injected into the medium at a constant flow rate Q using a Harvard Apparatus PHD 2000 syringe pump, for at least 3 hours to equilibrate the solution in the medium before flow characterization. After each subsequent change in flow rate, the flow is given 1 hour to equilibrate before characterization.

We measure the pressure drop across the medium ΔP using an Omega PX26 differential pressure transducer, averaging measurements obtained over 60 min; the temporal fluctuations in these measurements are minimal, and as a result, the corresponding error bars in Fig. 1B are smaller than the symbol size.

To visualize the pore-scale flow in situ, we seed the polymer solution with 5 ppm of fluorescent carboxylated polystyrene tracer particles (Invitrogen), D_t = 200 nm in diameter; the particles have excitation between 480 and 510 nm with an excitation peak at 505 nm, and emission between 505 and 540 nm with an emission peak at 515 nm. Particles are tracked using a 488-nm excitation laser and detected with a 500- to 550-nm sensor. To visualize the pore space, we also dye the solution with 0.5 ppm of rhodamine red dye, which has an excitation wavelength between 480 and 600 nm with an excitation peak at 560 nm, and emission between 550 and 700 nm with an emission peak at 580 nm. The dyed pore space is imaged using a 561-nm excitation laser and detected with a 570- to 620-nm sensor. Choice of these fluorescent markers allows us to image both the pore space and the dynamic flow within it at high resolution, with no observable cross-talk or bleed through on the laser channels. The particles can be considered faithful tracers of the streamlines because their advection dominates over diffusion, as described by the particle-scale Péclet number Pe ≡ (Q/A)D_p/𝒟 > 10⁵ ≫ 1, where 𝒟 = k_BT/3πη₀D_t = 6 × 10⁻³ m²/s is the Stokes-Einstein particle diffusivity.

We monitor the flow in individual pores using a Nikon A1R+ laser scanning confocal fluorescence microscope. We use a 10× objective interrogating a 318 μm by 318 μm field of view with the confocal resonant scanner at a temporal resolution of 30 frames per second and a spatial resolution of 0.62 m from an optical slice of 8 μm thickness at a depth of ∼200 μm within the medium. To monitor the slow changes in the flow field over time, we record the flow in 2-s intervals every 4 min for 60 min. We repeat this measurement for 9 pores randomly chosen near the inlet of the medium and 10 pores randomly chosen near the outlet; we do not observe noticeable differences in the results obtained depending on position along the medium. We then measure the 2D velocity field within each pore, with spatial discretization Δx = 7.74 m, using particle image velocimetry for each frame (62). Gradients are computed using a finite central difference scheme, adjusted as needed at the boundaries (46). We observe minimal fluctuations over the course of each 2-s interval, so we average the velocity field obtained in each such interval to give a quasi-steady snapshot of the velocity field at each time point separated by 4 min, u(x, t) ≡ (u(x, t), v(x, t)), where the position vector x ≡ (x, y). Of the 19 pores imaged, 12 exhibit a well-defined critical Wi_c below which the pore-scale flow is stable and laminar, above which the pore-scale flow is unstable. For the other seven pores (≈37%), we cannot determine a clear Wi_c within the range of Wi explored in our experiments; thus, the analysis in Fig. 2 (E and F) omits these pores. The analysis in Fig. 4, however, does not.

Power spectral density of unstable flow fluctuations

To characterize the spatial and temporal scales associated with unstable flow fluctuations, we monitor the fluctuations in two pore above the instability onset (Wi_I = 3.9 and 4.4) for 60 s (movie S5 and fig. S5). We use the measured time-dependent velocity field to directly compute the frequency- and wave number–dependent power spectral density of flow fluctuations, as shown in fig. S6. Both show power-law decays with exponents ∼1.1 to 1.4 and ∼0.8 to 1.1, respectively. While these differ from some other previous reported exponents for elastic turbulence, they are consistent with the range of values observed for elastic turbulence in various other studies exploring different geometries and polymer solutions, which report exponents ∼1 to 4.6 (33, 35, 36, 40, 44, 63–66) and ∼1 to 3 (33, 40), respectively. Investigating how these exponents vary across different geometries and solutions will be a useful direction for future work. The complementary cumulative density function of the power spectral density (shown in fig. S6) indicates that the majority of the measured spectral power is contained in fluctuations occurring over a duration longer than the characteristic polymer relaxation time λ, motivating the assumption of quasi-static polymer stress fields over the time scale of polymer relaxation.

Measurement of Hencky strain

We assess the role of extensional viscosity by directly computing the strain history of sample fluid elements along Lagrangian paths in the flow field measured in three representative pores. For a selected fluid element voxel, we use the measured time-dependent 2D velocity field to compute its propagation; specifically, using the pixel-by-pixel local velocity dx/dt = u(x, t), we compute the time to move to the next voxel as Δt ≈ Δx/u(x, t), where Δx is the pixel size and u(x, t) is the local velocity magnitude. For this computed pathline, we then compute the accumulated Hencky strain over one polymer relaxation time $\mathrm{\lambda }=\text{Wi}/{\stackrel{·}{\mathrm{\gamma }}}_I=0.3 \text{to} 1$ s as $\mathrm{\epsilon }={\int }_0^{\mathrm{\lambda }}\stackrel{·}{\mathrm{\epsilon }}(\mathbf{x},t)\mathrm{d}t$. We perform this measurement for five different starting locations throughout a pore for each of the 15 quasi-steady flow field snapshots, and repeat this set of 75 measurements for three different pores, to obtain a representative distribution of Hencky strains. The resulting distributions for each flow rate show that Hencky strains are much smaller than 1 (fig. S10), suggesting that extensional viscosity effects can be neglected, which typically arise when ε ≳ 2 to 3 (48).

Supplementary Materials

This PDF file includes:

Supplementary text

Legends for movies S1 to S5

Figs. S1 to S12

Table S1

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S5