Mediation analysis for survival data with high-dimensional mediators

Abstract

Motivation

Mediation analysis has become a prevalent method to identify causal pathway(s) between an independent variable and a dependent variable through intermediate variable(s). However, little work has been done when the intermediate variables (mediators) are high-dimensional and the outcome is a survival endpoint. In this paper, we introduce a novel method to identify potential mediators in a causal framework of high-dimensional Cox regression.

Results

We first reduce the data dimension through a mediation-based sure independence screening method. A de-biased Lasso inference procedure is used for Cox’s regression parameters. We adopt a multiple-testing procedure to accurately control the false discovery rate when testing high-dimensional mediation hypotheses. Simulation studies are conducted to demonstrate the performance of our method. We apply this approach to explore the mediation mechanisms of 379 330 DNA methylation markers between smoking and overall survival among lung cancer patients in The Cancer Genome Atlas lung cancer cohort. Two methylation sites (cg08108679 and cg26478297) are identified as potential mediating epigenetic markers.

Availability and implementation

Our proposed method is available with the R package HIMA at https://cran.r-project.org/web/packages/HIMA/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Mediation analysis was first proposed in the field of social science (Baron and Kenny, 1986). It has been widely applied in different areas, including neuroscience (Chén et al., 2017; Zhao et al., 2020), genomics and epigenomics (Fang et al., 2021; Valeri et al., 2017), microbiome studies (Sohn and Li, 2019; Zhang et al., 2018), etc. With the advancement of data collection techniques, it is now interesting and desirable to make inference on high-dimensional mediators. In recent years, substantial research efforts have been devoted to developing methodology for high-dimensional mediation analysis. For example, Zhang et al. (2016) and Gao et al. (2019) proposed innovative methods on testing mediation effects in high-dimensional epigenetic studies. Derkach et al. (2019) considered a model for high-dimensional mediation analysis with latent variables. Zhang (2019) introduced two procedures for mediator selection with high-dimensional exposures and high-dimensional mediators. Djordjilović et al. (2019) considered the testing for groups of potential mediators in high-dimensional mediation models. Zhang et al. (2019, 2021a, b) and Wang et al. (2020) considered the statistical inference for mediation effects with high-dimensional and compositional microbiome data. Liu et al. (2020) developed a powerful Divide-Aggregate Composite-null Test for large-scale mediation hypotheses. Loh et al. (2020) proposed a nonlinear framework for mediation analysis with high-dimensional mediators. Zhou et al. (2020) presented new inference procedures for the indirect effect in high-dimensional linear mediation models. Shi and Li (2020) developed a hypothesis testing procedure for high-dimensional mediators using the logic of Boolean matrices. Dai et al. (2021) developed a multiple-testing procedure that accurately controls the false discovery rate (FDR) when testing high-dimensional mediation hypotheses.

The above-mentioned results are mainly focused on noncensored outcomes. In low-dimensional case, some authors have studied the mediation analysis with survival data. For example, Lange and Hansen (2011), VanderWeele (2011), Tchetgen (2011) and Fulcher et al. (2017) proposed several causal mediation analysis frameworks with a single mediator and a survival outcome. Gelfand et al. (2016) presented a comparison of semiparametric proportional hazards and fully parametric accelerated failure time approaches to causal mediation analysis. Wang and Albert (2016) considered causal mediation analysis for the Cox model with a smooth baseline hazard estimator. Liu et al. (2018), Didelez (2019) and Zheng and Liu (2021) considered the mediation analysis for longitudinal and survival data. Fasanelli et al. (2019) proposed a method to estimate the marginal time-dependent causal effects in mediation analysis with survival data. Huang and Yang (2017) and Yu et al. (2019) studied mediation analysis of survival outcomes with multiple mediators. Cho and Huang (2019) investigated mediation analysis with causally ordered mediators using the Cox model.

However, there is a dearth of suitable models for high-dimensional mediation analysis on the survival outcome. To the best of our knowledge, Luo et al. (2020) was the first work toward high-dimensional mediator selection for the survival endpoint. In this paper, we propose a novel mediator identification procedure for the high-dimensional Cox model. Compared with Luo et al. (2020), our method has the following advantages. First, we use a series of marginal mediation effect ($\alpha \beta$) pathways (exposure → mediator → outcome), which roughly describe the mediation effect of each individual mediator, to screen out potentially significant mediators. On the other hand, Luo et al. (2020) only considered the effect β (mediator → outcome) as the term of screening criterion. Therefore, our mediation-based screening could be more accurate than Luo et al. (2020)’s screening method. Second, we adopt the de-biased Lasso (Fang et al., 2016) to estimate the effect β (mediator → outcome), where the estimate and its standard error are available. Therefore, our method can give inference results for all the de-biased Lasso estimators. In comparison, Luo et al. (2020) used the minimax concave penalty (MCP; Zhang, 2010) technique to estimate the effect β, which only provides statistical inference on nonzero MCP-based estimators. Third, we employ Dai et al. (2021)’s joint significance test with an mixture null distribution, which can more accurately control the FDR for large-scale multiple testing. However, Luo et al. (2020) used a naive joint significance rule with a uniform null distribution for the maximum P-value. Their procedure results in a valid but overly conservative test with low power (Dai et al., 2021; Huang, 2018).

The remainder of this paper is organized as follows. In Section 2, we present the regression model for mediation analysis with a survival outcome. We propose a three-step testing procedure for mediation effects in the high-dimensional Cox model. In Section 3, we evaluate the performance of our method via numerical simulations. In Section 4, an application to The Cancer Genome Atlas (TCGA) lung cancer cohort is provided. Some concluding remarks are given in Section 5.

2 Statistical methods

We use the counterfactual framework as VanderWeele and Vansteelandt (2014) and Huang and Yang (2017) to formally define the mediation effects and list assumptions for the identification of such effects. We denote the exposure for the ith individual as X_i and the baseline adjusted covariates (e.g. age and gender) as ${\mathit{Z}}_i=(Z_{i1},\dots ,Z_{iq})\prime$. Under stable unit treatment value assumption (Imbens and Rubin, 2015), let $\mathbf{m}=(m_1,\dots ,m_p)\prime$, we use $T_i(x,\mathbf{m})$ to denote the potential survival time, respectively, for individual i when the exposure is set to x, and the mediators are set to m. We use $M_{ik}(x)$ to denote the potential value of the kth mediator for individual i when the exposure is set to x. Here, we assume that the mediators are not causally related to each other. Formally, let ${\mathbf{m}}_{-k}=(m_1,\dots ,m_{k-1},m_{k+1},\dots ,m_p)\prime$ and use $M_{ik}(x,{\mathbf{m}}_{-k})$ to denote the potential value of the kth mediator for individual i when the exposure is set to x and all mediators except the kth mediator are set to ${\mathbf{m}}_{-k}$, then we assume $M_{ik}(x,{\mathbf{m}}_{-k})=M_{ik}(x)$ for all $k=1,\dots ,K$ and all possible $(x,{\mathbf{m}}_{-k})$. We would like to point out that this assumption does not require all mediators to be independent given the exposure X and the baseline adjusted covariates Z, and it allows for potential unmeasured common causes (either induced by the exposure or not) between mediators. In our example, where all the mediators are measured at the same time and a direct causal relationship between them is less likely, this assumption is reasonable. Under the consistency assumption (Imbens and Rubin, 2015), we have the observed mediators ${\mathbf{M}}_i=(M_{i1},\dots ,M_{ip})\prime =\left(M_{i1}\right(X_i),\dots ,M_{ip}(X_i\left)\right)\prime$ and the survival time $T_i=T_i(X_i,M_{i1}(X_i),\dots ,M_{ip}(X_i\left)\right)$.

As discussed in VanderWeele and Vansteelandt (2014) and VanderWeele et al. (2014), the following assumptions regarding potential confoundings, in addition to the positivity assumption (Imbens and Rubin, 2015), will allow us to nonparametrically identify the joint causal mediation effect as well as path-specific causal effects in the framework above:

(C.1) $X\perp T(x,\mathbf{m})|\mathbf{Z},\hspace{0.17em}\forall x,\mathbf{m}$, i.e. no unmeasured confounders between the exposure and the survival outcome;

(C.2) $\mathbf{M}(x)\perp T(x,\mathbf{m})|X,\mathbf{Z},\hspace{0.17em}\forall x,\mathbf{m}$, i.e. no unmeasured confounders between the mediators and the survival outcome;

(C.3) $X\perp \mathbf{M}(x)|\mathbf{Z},\hspace{0.17em}\forall x$, i.e. no unmeasured confounders between the exposure and the mediators;

(C.4) $\mathbf{M}(x^{*})\perp T(x,\mathbf{m})|\mathbf{Z},\hspace{0.17em}\forall x,x^{*},\mathbf{m}$, i.e. no exposure-induced confounding between the mediators and the survival outcome.

To separate the effect of each mediator, we consider the following Cox model for the hazard of the potential survival time $T_i(x,\mathbf{m})$ and multivariate linear model for the distribution of potential mediators ${\mathbf{M}}_i(x)$:

$${\lambda }^{x\mathbf{m}}(t|\mathbf{Z})={\lambda }_0(t)\hspace{0.17em}\text{exp}(\gamma x+\mathit{\beta }\prime \mathbf{m}+\mathit{\eta }\prime \mathbf{Z}),$$ (1)

 

$$M_k\left(x\right)={\alpha }_{k}x+{\zeta }_k\prime Z+e_k,\hspace{0.17em}\text{for}\hspace{0.17em}k=1,\dots ,p,$$ (2)

where ${\lambda }_0(t)$ is an unspecified baseline hazard function, γ is the direct effect of the exposure on the survival outcome; $\mathit{\beta }=({\beta }_1,\dots ,{\beta }_p)\prime$ is the regression parameter vector relating the mediators to the survival outcome adjusting for the effect of the exposure; $\mathit{\alpha }=({\alpha }_1,\dots ,{\alpha }_p)\prime$ is the parameter relating the exposure to mediators; $\mathit{\eta }$ and ${\mathit{\zeta }}_k$ are regression coefficients for the covariates; $\mathbf{e}=(e_1,\dots ,e_p)\prime$ is a vector of error terms with $\mathit{Cov}(\mathbf{e})={\Sigma }_e$, which quantifies the correlation between mediators due to unmeasured common causes.

Let C be the censoring time. The observed failure time is $\tilde{T}=\min (T,C)$, and the censoring indicator is $\delta =I(T\le C)$. Under assumptions (C.1), (C.2) and (C.3), the potential outcome model above can derive the following high-dimensional mediation-based Cox model (Luo et al., 2020), for the survival outcome T  

$$\lambda (t|X,\mathbf{M},\mathbf{Z})={\lambda }_0(t)\hspace{0.17em}\text{exp}(\gamma X+\mathit{\beta }\prime \mathbf{M}+\mathit{\eta }\prime \mathbf{Z}),$$ (3)

 

$$M_k={\alpha }_{k}X+{\mathbf{\zeta }}_k^{\prime }\mathbf{Z}+e_k,\hspace{0.17em}\text{for}\hspace{0.17em}k=1,\dots ,p.$$ (4)

Assuming the censoring time C is noninformative, we can identify the parameters in these models.

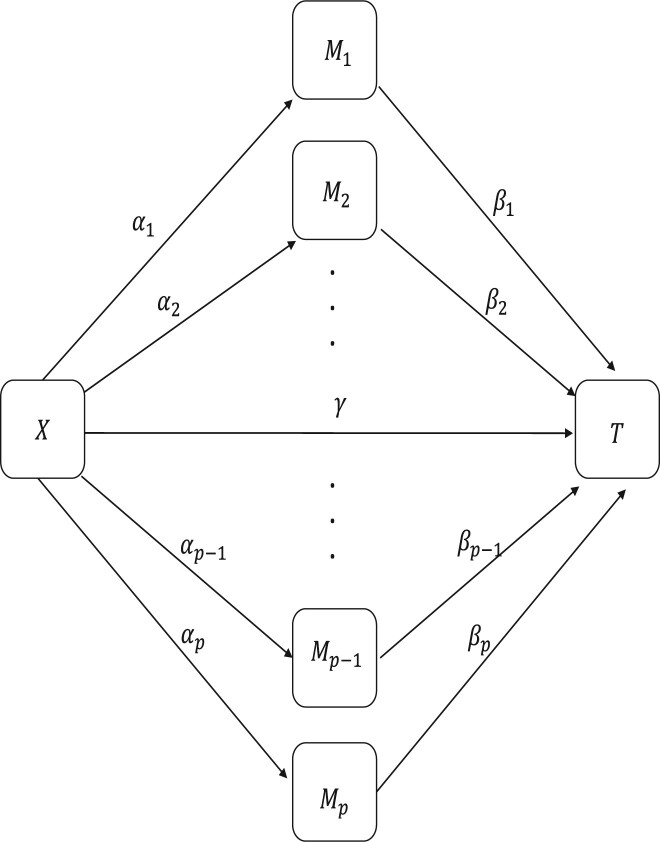
Here, we point out that Luo et al. (2020)’s method adapts Zhang et al. (2016)’s framework to the survival endpoint. In Figure 1, we illustrate a scenario of high-dimensional mediation-based Cox model with omitted confounding variables, where the p mediators could be correlated with each other. Of note, the situation with causally ordered mediators described in Cho and Huang (2019) will not be captured by our suggested procedure.

Fig. 1.

A scenario of high-dimensional mediation-based Cox model (confounding variables are omitted)

We define the causal effect at the difference in log-hazard scale following the idea of Huang and Yang (2017) and its extension to high-dimensional mediators with the Cox model (Luo et al., 2020). Let ${\tilde{\lambda }}^{x,x^{*}}(t|Z)$ denote the hazard function of $T(x,M_1(x^{*}),\dots ,M_p(x^{*}\left)\right)$, the population natural direct effect and natural indirect effect can be defined as

$$\begin{array}{c}NDE(x,x^{*})=E[\text{log}\hspace{0.17em}{\tilde{\lambda }}^{x^{*}x}(t|\mathbf{Z})-\text{log}\hspace{0.17em}{\tilde{\lambda }}^{xx}(t|\mathbf{Z})]\\ \approx (x^{*}-x)\gamma ,\\ NIE(x,x^{*})=E[\text{log}\hspace{0.17em}{\tilde{\lambda }}^{x^{*}{x}^{*}}(t|\mathbf{Z})-\text{log}\hspace{0.17em}{\tilde{\lambda }}^{x^{*}x}(t|\mathbf{Z})]\\ \approx (x^{*}-x)({\alpha }_1{\beta }_1+\cdots +{\alpha }_p{\beta }_p),\end{array}$$

where the approximation holds under the rare event assumption given

$$\begin{array}{c}{\tilde{\lambda }}^{x,x^{*}}(t|Z)=E[{\lambda }^{x\mathbf{M}(x^{*})}(t|Z)|T\ge t,Z]\\ \approx E[{\lambda }^{x\mathbf{M}(x^{*})}(t|Z)|Z]\\ ={\lambda }_0(t)\hspace{0.17em}\text{exp}\hspace{0.17em}\{\gamma x+\sum _{k=1}^p{\beta }_k({\alpha }_k{x}^{*}+{\mathit{\zeta }}_k^{\prime }\mathbf{Z})+\mathit{\eta }\prime \mathbf{Z}+\frac{1}{2}\mathit{\beta }\prime {\Sigma }_e\mathit{\beta }\},\end{array}$$

where the last equation holds by the normality assumption of $\mathbf{M}(x)$ and assumptions (C.1)–(C.4). The total effect defined as below can be decomposed to the NDE and NIE

$$\begin{array}{c}TE(x,x^{*})=E[\text{log}\hspace{0.17em}{\tilde{\lambda }}^{x^{*}{x}^{*}}(t|\mathbf{Z})-\text{log}\hspace{0.17em}{\tilde{\lambda }}^{xx}(t|\mathbf{Z})]\\ =\mathit{NIE}(x,x^{*})+\mathit{NDE}(x,x^{*})\\ \approx (x^{*}-x)(\gamma +{\alpha }_1{\beta }_1+\cdots +{\alpha }_p{\beta }_p).\end{array}$$

Similarly, the path-specific causal effect on the log-hazard difference scale for the mediator M_k ($X\to M_k\to T$) can be defined as a comparison of log hazard for $T(x,M_1(x),\dots ,M_{k-1}(x),M_k(x^{*}),\hspace{0.17em}{M}_{k+1}(x),\dots ,M_p(x\left)\right)$ and $T(x,M_1(x),\dots ,M_p(x\left)\right)$, which can be approximated as ${\alpha }_k{\beta }_k(x^{*}-x)$. We would like to point out that even when the rare event approximation does not hold, testing the null hypothesis ${\alpha }_k{\beta }_k=0$ is still valid for testing the existence of such path-specific causal effect through M_k.

Our aim is to estimate and test the path-specific mediation effects ${\alpha }_k{\beta }_k$ of the kth mediator M_k, for $k=1,\dots ,p$. Denote by ${\mathcal{S}}_0=\{k:{\alpha }_k{\beta }_k\ne 0\}$ the index set of those significant mediators. Assume that we have n i.i.d. samples $\left\{\right(X_i,{\mathbf{M}}_i,{\mathbf{Z}}_i,{\tilde{T}}_i,{\delta }_i),\hspace{0.33em}i=1,\dots ,n\}$. For practical analysis, we first conduct a standardization of the mediator variables with mean zero and variance one. The proposed approach is as follows:

Step 1: (Mediators screening). Motivated by the sure independence screening (SIS) (Fan and Lv, 2008; Fan et al., 2010), we consider a series of marginal models:

$$\begin{array}{c}\lambda \left(t\right|X,M_k,\mathbf{Z})={\lambda }_0(t)\hspace{0.17em}\text{exp}(\gamma X+{\beta }_k{M}_k+\mathit{\eta }\prime `\mathbf{Z}),\\ Mk={\alpha }_{k}X+\mathit{\zeta }\mathit{k}\prime `\mathbf{Z}+{\mathit{e}}_{\mathit{k}}.\end{array}$$

Select a subset $\mathcal{D}=\{k:M_k\text{is among the top}d=[n/\log \left(n\right)]\text{large}$  $\text{effect}\left|{\widehat{\alpha }}_k{\widetilde{ \beta }}_k\right|,\text{for}k=1,\dots ,p\}$, where ${\widehat{\alpha }}_k$ and ${\tilde{\beta }}_k$ are the ordinary least square (OLS) and maximum partial likelihood estimators based on the above marginal models, respectively.

Step 2: (De-biased Lasso estimates). Conditional on the selected set $\mathcal{D}$, we focus on the following submodel:

$$\lambda (t|X,{\mathbf{M}}_{\mathcal{D}},\mathbf{Z})={\lambda }_0(t)\hspace{0.17em}\text{exp}(\gamma X+{\mathit{\beta }}_{\mathcal{D}}^{\prime }{\mathbf{M}}_{\mathcal{D}}+\mathit{\eta }\prime \mathbf{Z}),$$

where ${\mathit{\beta }}_{\mathcal{D}}$ denotes a subvector of $\mathit{\beta }$ with index belonging to $\mathcal{D}$, and ${\mathbf{M}}_{\mathcal{D}}$ has a similar interpretation. To estimate the parameter of interest ${\mathit{\beta }}_{\mathcal{D}}$, we employ the de-biased Lasso method in Fang et al. (2016). For any $k\in \mathcal{D}$, the de-biased Lasso estimator ${\widehat{\beta }}_k$ and its standard error ${\widehat{\sigma }}_{{\beta }_k}$ can be obtained by (3.8) and (4.3) of Fang et al. (2016), respectively. For $k\in \mathcal{D}$, the corresponding P-values are given as

$$P_{{\beta }_k}=2\{1-\Phi (\left|{\widehat{\beta }}_k\right|/{\widehat{\sigma }}_{{\beta }_k})\},$$ (5)

where $\Phi (·)$ is the cumulative distribution function of N(0, 1). As one reviewer pointed out, $P_{{\beta }_k}$ in (5) could only be regarded as a valid P-value conditional on the selected set $\mathcal{D}$ in Step 1. In view of Fan and Lv (2008) and Fan et al. (2010), the selected set $\mathcal{D}$ includes the true mediators with probability tending to one, i.e. $P({\mathcal{S}}_0\subset \mathcal{D})\to 1$ as $n\to \infty$.

Step 3: (Multiple-testing procedure). Conditional on the selected set $\mathcal{D}$, we focus on the multiple-testing problem:

$${\mathrm{H}}_{0k}:\hspace{0.17em}{\alpha }_k{\beta }_k=0\hspace{0.17em}\hspace{0.17em}\text{vs}.\hspace{0.17em}\hspace{0.17em}{\mathrm{H}}_{1k}:\hspace{0.17em}{\alpha }_k{\beta }_k\ne 0,\hspace{0.17em}k\in \mathcal{D},$$ (6)

which can be equivalently expressed as the union of the following three disjoint component null hypotheses:

$$\begin{array}{c}{\mathrm{H}}_{00,k}:\hspace{0.17em}{\alpha }_k=0\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\beta }_k=0,\\ {\mathrm{H}}_{01,k}:\hspace{0.17em}{\alpha }_k=0\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\beta }_k\ne 0,\\ {\mathrm{H}}_{10,k}:\hspace{0.17em}{\alpha }_k\ne 0\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\beta }_k=0.\end{array}$$

Toward (6), one commonly used approach is the joint significant test (Luo et al., 2020; Zhang et al., 2016), which is referred to as the ‘JS-uniform’. Specifically, the P-value for (6) is defined as

$$P_{\mathit{max},k}=\max (P_{{\alpha }_k},P_{{\beta }_k}),$$ (7)

where $P_{{\beta }_k}$ is given in (5), $P_{{\alpha }_k}=2\{1-\Phi (\left|{\widehat{\alpha }}_k\right|/{\widehat{\sigma }}_{{\alpha }_k})\},\hspace{0.17em}{\widehat{\alpha }}_k$ and ${\widehat{\sigma }}_{{\alpha }_k}$ are based on the OLS estimators. Note that the significance rule using the uniform null distribution for $P_{\mathit{max},k}$ results in a valid but overly conservative test (Huang, 2018). In fact, the null distribution of $P_{\mathit{max},k}$ is a three-component mixture distribution (Dai et al., 2021). To correct the conservativeness of the ‘JS-uniform’ procedure, Dai et al. (2021) proposed a novel multiple-testing procedure that accurately controls the FDR (referred to as ‘JS-mixture’ procedure). For $t\in [0,1]$, we define the following empirical processes: $V_{00}(t)=\#\{P_{\mathit{max},k}\le t|H_{00}\},\hspace{0.17em}{V}_{01}(t)=\#\{P_{\mathit{max},k}\le t\left|H_{01}\right\},\hspace{0.17em}{V}_{10}(t)=\#\{P_{\mathit{max},k}\le t|H_{10}\},\hspace{0.17em}{V}_{11}(t)=\#\{P_{\mathit{max},k}\le t\left|H_{11}\right\}$ and $R(t)=V_{00}(t)+V_{01}(t)+V_{10}(t)+V_{11}(t)$. According to Dai et al. (2021), an estimated FDR for testing mediation is

$$\widehat{\text{FDR}}(t)=\frac{{\widehat{\pi }}_{01}t+{\widehat{\pi }}_{10}t+{\widehat{\pi }}_{00}{t}^2}{\max \{1,R(t)\}/d},$$

where ${\widehat{\pi }}_{01},\hspace{0.17em}{\widehat{\pi }}_{10}$ and ${\widehat{\pi }}_{00}$ are the estimates of the proportions of $H_{01,j},\hspace{0.17em}{H}_{10,j}$ and $H_{00,j}$, respectively. For more theoretical details on ${\widehat{\pi }}_{01},\hspace{0.17em}{\widehat{\pi }}_{10}$ and ${\widehat{\pi }}_{00}$, we refer to the lines of Storey (2002) and Storey et al. (2004). For application, the three terms are available by the R package HDMT. To control the FDR at level b, we define the significance threshold for $P_{\mathit{max},k}$ as

$${\widehat{t}}_b=\sup \{t:\widehat{\text{FDR}}(t)\le b\},$$ (8)

which is available from the R package HDMT in practical applications. Of note, a finite sample adjustment was provided by Dai et al. (2021) to improve the performance of the proposed procedure. With probability tending to one, an estimated index set of significant mediators is given as $\widehat{\mathcal{S}}=\{k:P_{\mathit{max},k}\le {\widehat{t}}_b,k\in \mathcal{D}\}$, where $P_{\mathit{max},k}$ and ${\widehat{t}}_b$ are defined in (7) and (8), respectively.

Of note, we have made statistical inference in Steps 2 and 3 of our proposed method conditional on the selected set $\mathcal{D}$ (Step 1). As mentioned before, $P({\mathcal{S}}_0\subset \mathcal{D})=1$ as $n\to \infty$. Asymptotically, we assume that $\mathcal{D}={\mathcal{S}}_0\cup {\mathcal{S}}_0^{\perp }$, where ${\mathcal{S}}_0^{\perp }\subset \{1,\dots ,p\}$ and ${\mathcal{S}}_0\cap {\mathcal{S}}_0^{\perp }=\varnothing$. Basically, the randomness of $\mathcal{D}$ is actually due to ${\mathcal{S}}_0^{\perp }$. Because the key idea of de-biased Lasso is to project the scores of interested parameters (e.g. ${\mathit{\beta }}_{{\mathcal{S}}_0}$) onto the linear span of the score functions of nuisance parameters (e.g. ${\mathit{\beta }}_{{\mathcal{S}}_0^{\perp }}$), the corresponding estimation function of ${\mathit{\beta }}_{{\mathcal{S}}_0}$ is uncorrelated with the score function of ${\mathit{\beta }}_{{\mathcal{S}}_0^{\perp }}$ (Fang et al., 2016). Hence, the randomness of ${\mathcal{S}}_0^{\perp }$ has very limited impact on the de-biased Lasso estimator of ${\mathit{\beta }}_{{\mathcal{S}}_0}$ asymptotically.

3 Simulation studies

In this section, we conduct two simulation studies to assess the performance of our proposed method. First, we generate failure times $T_1,\dots ,T_n$ from Cox Model (3) with ${\lambda }_0(t)=1$. The exposure X_i follows from N(0, 2), and $\gamma =0.5$; the covariates ${\mathbf{Z}}_i=(Z_{i1},Z_{i2})\prime$, where $Z_{i1}$ and $Z_{i2}$ are independently generated from N(0, 2), $\mathit{\eta }=(0.5,0.5)\prime$; ${\beta }_1=0.6,\hspace{0.17em}{\beta }_2=-0.5,\hspace{0.17em}{\beta }_3=0.4,\hspace{0.17em}{\beta }_4=-0.3,\hspace{0.17em}{\beta }_5=0.25,\hspace{0.17em}{\beta }_6=0.15,\hspace{0.17em}{\beta }_7=0.5,\hspace{0.17em}{\beta }_8=0.35,\hspace{0.17em}{\beta }_9=0.15,\hspace{0.17em}{\beta }_{10}=0.12,\hspace{0.17em}{\beta }_{11}=0.5$ , and ${\beta }_k=0$ otherwise; the mediators are generated from Model (2), where ${\alpha }_1=0.6,\hspace{0.17em}{\alpha }_2=-0.5,\hspace{0.17em}{\alpha }_3=0.4,\hspace{0.17em}{\alpha }_4=-0.3,\hspace{0.17em}{\alpha }_5=0.25,\hspace{0.17em}{\alpha }_6=0.15,\hspace{0.17em}{\alpha }_7=0.5,\hspace{0.17em}{\alpha }_8=0.35,\hspace{0.17em}{\alpha }_9=0.45,\hspace{0.17em}{\alpha }_{10}=0.5,\hspace{0.17em}{\alpha }_{12}=0.5$, and ${\alpha }_k=0$ otherwise; i.e. the ${\left\{M_k\right\}}_{k=1}^{10}$ are active mediators. ${\mathit{\zeta }}_k=(0.3,0.3)\prime$, and the error terms ${\mathbf{e}}_i=(e_{i1},\dots ,e_{ip})\prime$ are generated from $N(0,{\Sigma }_e)$. To simulate the dependency structure of mediators close to the real data, we use the first step of our method (mediators screening) to pick up the top p DNA methylation markers from the real data in Section 4. Σ_e is set to the correlation matrix of those p DNA methylation markers. In Supplementary Figure S1, we present the histogram for the lower triangular of the correlation matrix Σ_e, which indicates that some of the mediators are highly correlated. For illustration, in Supplementary Figure S2, we show the 10 × 10 upper submatrix of Σ_e for the active mediators ${\left\{M_k\right\}}_{k=1}^{10}$. Moreover, the censoring times C_i are generated from a uniform distribution over $(0,c_0)$, where $c_0=150$ (censoring rate is about 20%) and 5 (censoring rate is about 40%), respectively. All the simulations are based on 200 replications, where p = 10 000, n = 300 and 500, respectively.

For fair comparison, we consider Luo et al. (2020)’s method (denoted as ‘Luo et al.’), where the number of survived variables in their first step is the same as our method with $d=[n/\hspace{0.17em}\text{log}(n)]$. In Table 1, we present the probabilities to be screened in for those active mediators (Step 1) over 200 replications. The results indicate that Luo et al. (2020)’s screening method has a poor performance, while our mediation-based screening has a higher probability to include those active mediators ${\left\{M_k\right\}}_{k=1}^{10}$.

Table 1.

The frequency of those active mediators being kept after the screening step over 200 repetitions^a

		CR = 20%		CR = 40%
		Proposed	Luo et al.	Proposed	Luo et al.
n = 300	M 1	200	50	200	43
	M 2	158	0	152	0
	M 3	200	131	200	115
	M 4	98	0	116	0
	M 5	196	8	190	1
	M 6	90	0	81	0
	M 7	200	141	200	125
	M 8	200	24	199	18
	M 9	200	11	199	18
	M 10	177	1	179	0
n = 500	M 1	200	60	200	63
	M 2	179	0	179	0
	M 3	200	167	200	159
	M 4	101	0	126	0
	M 5	200	6	200	9
	M 6	132	0	128	0
	M 7	200	190	200	171
	M 8	200	35	200	31
	M 9	200	19	199	26
	M 10	195	0	182	0

^a‘Proposed’ denotes our method; ‘Luo et al.’ denotes Luo et al. (2020)’s method; ‘CR’ denotes the censoring rate of failure times.

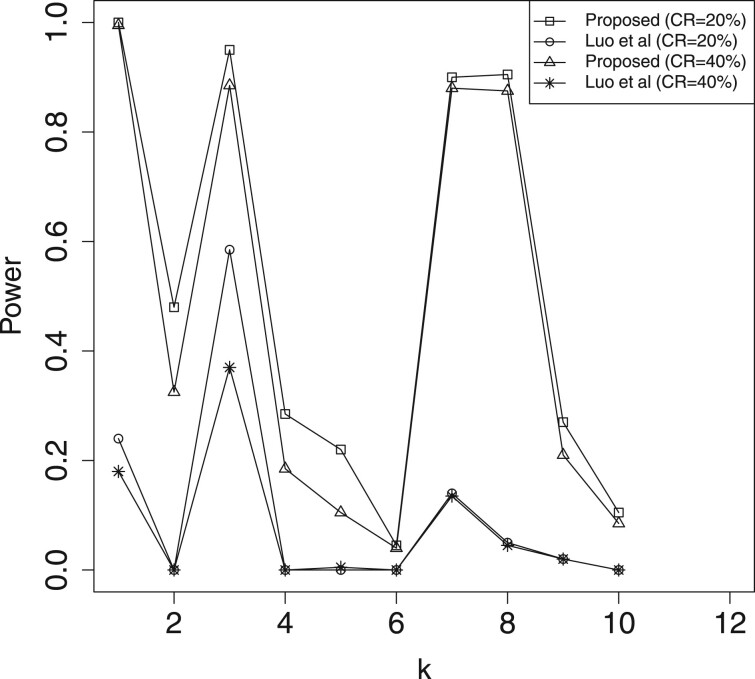
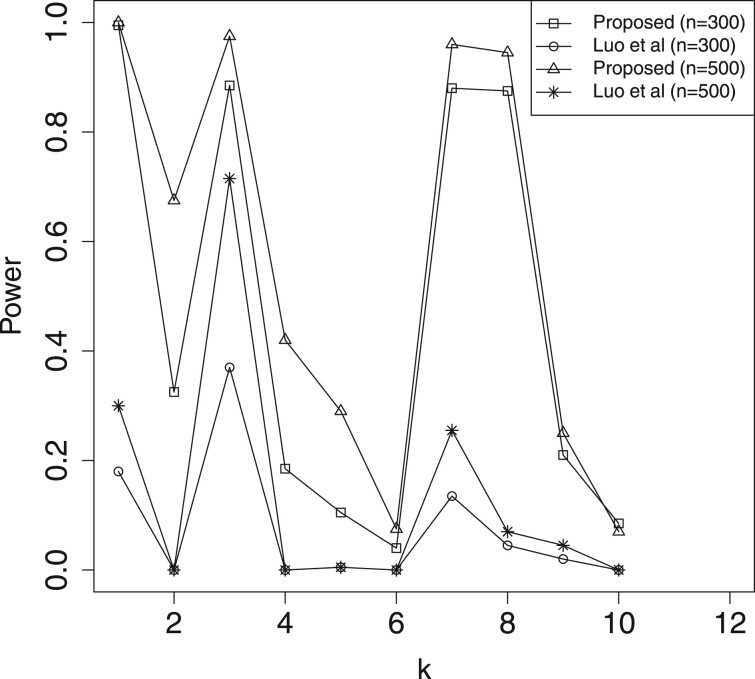
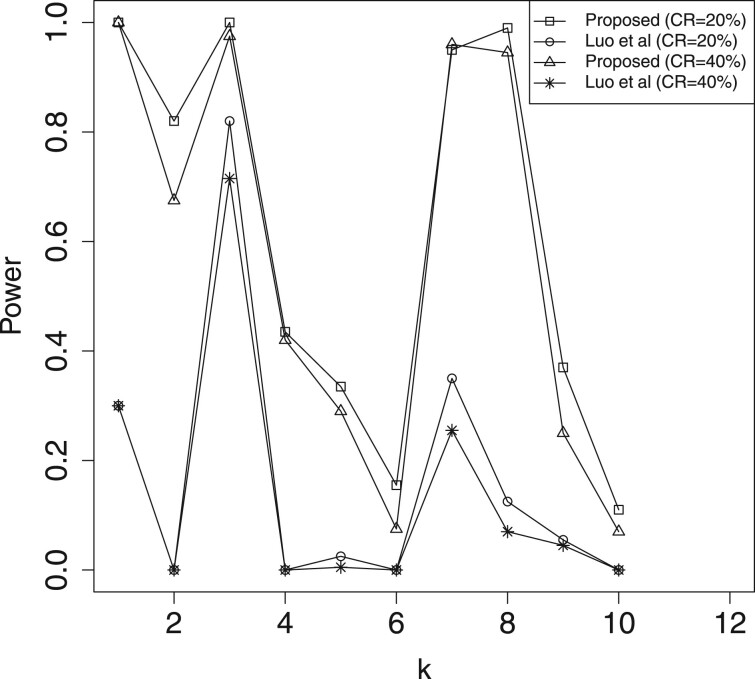
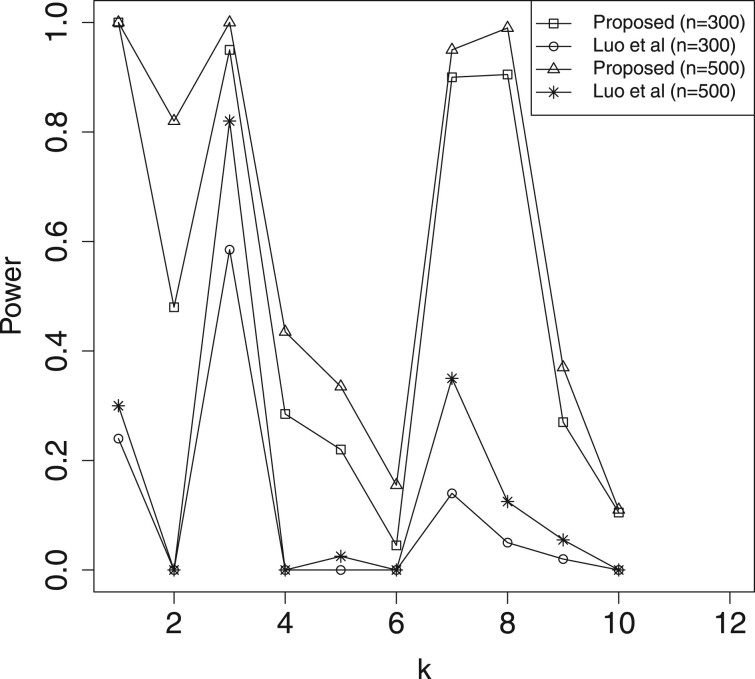
In Table 2 and Supplementary Table S1, we report the estimation results for mediation effects ${\left\{{\alpha }_k{\beta }_k\right\}}_{k=1}^{13}$, which include the estimated biases (Bias) given by the sample mean of the estimates minus the true value, and the mean squared errors (MSE) of the estimates. Here, we omit the results for ${\left\{{\alpha }_k{\beta }_k\right\}}_{k=14}^p$, because their performances are similar to that of ${\alpha }_{13}{\beta }_{13}$. For significant mediators, the Bias and MSE of our method (denoted as ‘Proposed’) are much smaller than those of ‘Luo et al.’. Hence, the proposed approach is more efficient than Luo et al. (2020)’s method toward the estimation of active mediation effects. In Table 3, we present the estimated FDR of mediation effects, where the FDR threshold level is 0.05. The results indicate that both methods can control the FDR under the threshold level. In Figures 2–5, we illustrate the empirical power for each of the active mediators separately. The figures indicate that our procedure is much more powerful than Luo et al. (2020)’s method in selecting significant mediators. All the above reported results become much better when the sample size n is increasing. However, it seems that the increasing of censoring rate has a negative affect on both methods, which is common in survival analysis.

Table 2.

Bias and MSE (in the parentheses) of estimation for mediation effects in simulation study 1 (n = 500)^a

	CR = 20%		CR = 40%
${\alpha }_k{\beta }_k$	Proposed	Luo et al.	Proposed	Luo et al.
${\alpha }_1{\beta }_1$	–0.0197	–0.2650	–0.0271	–0.2649
	(0.0029)	(0.0921)	(0.0037)	(0.0921)
${\alpha }_2{\beta }_2$	–0.1036	–0.2500	–0.1157	–0.2500
	(0.0162)	(0.0625)	(0.0190)	(0.0625)
${\alpha }_3{\beta }_3$	–0.0135	$-0.0517$	–0.0173	$-0.0597$
	(0.0011)	(0.0059)	(0.0014)	(0.0080)
${\alpha }_4{\beta }_4$	–0.0515	–0.0900	$-0.0466$	$-0.0900$
	(0.0044)	(0.0081)	(0.0037)	(0.0081)
${\alpha }_5{\beta }_5$	–0.0231	$-0.0609$	–0.0235	–0.0619
	(0.0009)	(0.0038)	(0.0011)	(0.0039)
${\alpha }_6{\beta }_6$	–0.0107	–0.0225	–0.0118	–0.0225
	(0.0003)	(0.0005)	(0.0003)	(0.0005)
${\alpha }_7{\beta }_7$	–0.0395	$-0.1767$	–0.0404	$-0.1919$
	(0.0038)	(0.0420)	(0.0036)	(0.0462)
${\alpha }_8{\beta }_8$	0.0218	–0.1089	0.0222	$-0.1131$
	(0.0015)	(0.0132)	(0.0022)	(0.0139)
${\alpha }_9{\beta }_9$	–0.0035	–0.0609	–0.0007	–0.0621
	(0.0009)	(0.0044)	(0.0010)	(0.0046)
${\alpha }_{10}{\beta }_{10}$	–0.0168	–0.0600	–0.0151	–0.0600
	(0.0016)	(0.0036)	(0.0016)	(0.0036)
${\alpha }_{11}{\beta }_{11}$	0.0002	0.0001	$-0.0005$	$-6\times {10}^{-5}$
	($1.7\times {10}^{-5}$)	($3.3\times {10}^{-6}$)	($2\times {10}^{-5}$)	($3\times {10}^{-6}$)
${\alpha }_{12}{\beta }_{12}$	0.0013	0	0.0082	0
	(0.0007)	(0)	(0.0007)	(0)
${\alpha }_{13}{\beta }_{13}$	$-1.7\times {10}^{-5}$	0	$3.5\times {10}^{-6}$	0
	($5.6\times {10}^{-8}$)	(0)	($4\times {10}^{-7}$)	(0)

^a‘Proposed’ denotes our method; ‘Luo et al.’ denotes Luo et al. (2020)’s method; ‘CR’ denotes the censoring rate of failure times.

Table 3.

The FDR of mediation effect testing in simulation study 1^a

	CR = 20%		CR = 40%
Methods	n = 300	n = 500	n = 300	n = 500
Proposed	0.0097	0.0047	0.0092	0.0039
Luo et al.	0.0125	0.0063	0.0325	0.0117

^a‘Proposed’ denotes our method; ‘Luo et al.’ denotes Luo et al. (2020)’s method; ‘CR’ denotes the censoring rate of failure times.

Fig. 2.

A comparison of empirical power for all the active mediators ${\left\{M_k\right\}}_{k=1}^{10}$ with n = 300

Fig. 5.

A comparison of empirical power for all the active mediators ${\left\{M_k\right\}}_{k=1}^{10}$ with $CR=40\%$

Fig. 3.

A comparison of empirical power for all the active mediators ${\left\{M_k\right\}}_{k=1}^{10}$ with n = 500

Fig. 4.

A comparison of empirical power for all the active mediators ${\left\{M_k\right\}}_{k=1}^{10}$ with $CR=20\%$

As suggested by one reviewer, we conduct the second simulation to study the performance of our method when there are no indirect effects for any mediators. The settings are identical with the first simulation, except that ${\beta }_1=0.5,\hspace{0.17em}{\beta }_k=0$ for other k; and ${\alpha }_2=0.5,\hspace{0.17em}{\alpha }_k=0$ for other k. The estimation results for ${\left\{{\alpha }_k{\beta }_k\right\}}_{k=4}^p$ are similar to those of ${\alpha }_3{\beta }_3$. Hence, we only report the Bias and MSE for ${\alpha }_1{\beta }_1,\hspace{0.17em}{\alpha }_2{\beta }_2$ and ${\alpha }_3{\beta }_3$ in Table 4 (other cases are similar and omitted). From the results, we can see that both methods are unbiased on the estimation of mediation effects. In Table 5, we give the FDR of multiple-testing in the case when there are no mediation effects. It seems that both method can well control the FDR.

Table 4.

Bias and MSE (in the parentheses) of estimation for mediation effects in simulation study 2^a

		CR = 20%		CR = 40%
	${\alpha }_k{\beta }_k$	Proposed	Luo et al.	Proposed	Luo et al.
n = 300	${\alpha }_1{\beta }_1$	–0.0003	$-9\times {10}^{-5}$	0.0009	0.0008
		(0.0001)	(0.0001)	(0.0001)	(0.0001)
	${\alpha }_2{\beta }_2$	0.0572	0	0.0608	0
		(0.0053)	(0)	(0.0059)	(0)
	${\alpha }_3{\beta }_3$	0	$-3\times {10}^{-5}$	0	0
		(0)	($1.4\times {10}^{-7}$)	(0)	(0)
n = 500	${\alpha }_1{\beta }_1$	0.0004	0.0006	0.0002	$8.3\times {10}^{-5}$
		($9\times {10}^{-5}$)	(0.0001)	($7\times {10}^{-5}$)	($8.1\times {10}^{-5}$)
	${\alpha }_2{\beta }_2$	0.0446	0	0.0488	0
		($3\times {10}^{-3}$)	(0)	(0.0004)	(0)
	${\alpha }_3{\beta }_3$	0	0	0	0
		(0)	(0)	(0)	(0)

^a‘Proposed’ denotes our method; ‘Luo et al.’ denotes Luo et al. (2020)’s method; ‘CR’ denotes the censoring rate of failure times.

Table 5.

The FDR of mediation effect testing in simulation study 2^a

	CR = 20%		CR = 40%
Methods	n = 300	n = 500	n = 300	n = 500
Proposed	0.040	0.030	0.050	0.045
Luo et al.	0.050	0.060	0.030	0.025

^a‘Proposed’ denotes our method; ‘Luo et al.’ denotes Luo et al. (2020)’s method; ‘CR’ denotes the censoring rate of failure times.

4 An application to lung cancer data

We apply our proposed method to the TCGA lung cancer cohort study including lung squamous cell carcinoma and lung adenocarcinoma, where the data are freely available at https://xenabrowser.net/datapages/. Our interest is to identify potential epigenetic markers linking smoking and survival of lung cancer patients. In the analysis, we focus on 593 patients with nonmissing clinical and epigenetic information, whose ages ranged from 33 to 90 years. The survival endpoint is defined as the number of days from initial diagnosis to death, which could be censored. The median survival time is 678 days. Two hundred and forty-three patients died during the follow-up, with a censoring rate of 59%. A total of 379 330 DNA methylation markers (M) profiled by Infinium HumanMethylation450 BeadChip array are potential mediators. The exposure X is the number of packs smoked per years, and the survival time is the outcome variable. Other covariates (Z) include age at initial diagnosis, gender (male = 1; female = 0), tumor stage (Stage I = 1; Stage II = 2; Stage III = 3; Stage IV = 4) and radiotherapy (yes = 1; no = 0).

In Table 6, we report the summary results on the two selected mediators by our method, where the FDR threshold level is 0.05. For cg08108679 (in gene PRKCZ, chromosome 1, position: 2 003 274), the estimated pathway effect (α) on $X\to M$ is –0.0092 (0.0024), where the number in parenthesis is the corresponding standard error (SE); the estimated pathway effect $(\beta )$ on $M\to T$ is –3.4997 (1.0248). For cg26478297 (in gene PRKCG, chromosome 19, position: 54 387 436), the estimated pathway effects on $X\to M$ and $M\to T$ are –0.0256 (0.0068) and –1.3362 (0.4011), respectively. Hence, the two selected CpGs have positive log-hazard indirect effect (smoking increases the mortality). The two CpGs are located in different chromosomes but belonging to the same gene family of protein kinase C (PKC). PKC family members are known to be involved in diverse cellular signaling pathways and have been studied extensively as a group of proteins that involve in cancer development (Dowling et al., 2017). Previous studies (Guo et al., 2008; Wyatt et al., 1999) have found that PKC is activated in human epithelial cells when exposed to cigarette smoke extract, which may in turn influence the invasion and metastasis of lung cancer (Gopalakrishna et al., 1994).

Table 6.

Summary of selected CpGs with significant mediation effects (${\widehat{\alpha }}_k{\widehat{\beta }}_k>0$)^a

CpGs	Chromosome	Gene	${\widehat{\alpha }}_k$	${\widehat{\beta }}_k$	$P_{\mathit{max},k}$
			(SE)	(SE)
cg08108679	Chr1:2003274	PRCKZ	–0.0092	–3.4997	0.0006
			(0.0024)	(1.0248)
cg26478297	Chr19:54387436	PRCKG	–0.0256	–1.3362	0.0009
			(0.0068)	(0.4011)

^a‘SE’ denotes standard error; ‘$P_{\mathit{max},k}$’ is given in (7).

For comparison, we also use Luo et al. (2020)’s method to analyze this dataset. However, their approach fails to identify any significant mediators. In summary, our proposed method works well for mediation testing with survival outcomes in practical applications.

5 Concluding remarks

We have proposed a multiple-testing procedure for high-dimensional mediation effects with the survival outcome. To address the ultra high-dimensional DNA methylation markers, we used a screening technique to reduce the dimension of potential mediators. Moreover, we adopted the de-biased Lasso method and ‘JS-mixture’ procedure to identify significant mediators. Simulation results indicated that our method has a satisfactory performance. An application to TCGA lung cancer cohort was provided to illustrate the utility of our proposed approach.

There are several topics to be studied in the future. First, we have adopted marginal screening in Step 1 of our method. As pointed out already in the original SIS paper by Fan and Lv (2008), correlations among the mediators may cause problems. Fan and Lv (2008) alleviated this by introducing the iterative SIS. Although our approach works well in the simulated examples, it is interesting to further study the iterative SIS in our method from both the theory and application aspects. Second, group testing for mediation effects is an attractive direction (Derkach et al., 2020; Djordjilović et al., 2019; Krull and MacKinnon, 2001), it is interesting to consider the group mediators in high-dimensional survival data. Third, we have imposed some traditional assumptions related to no unmeasured confounding in our method. However, in the high-dimensional mediator situation, additional complications occur. Specifically, the interrelationship among the (potential) mediators plays a crucial role. As suggested by one reviewer, it is interesting to consider the situation with causally ordered mediators described in Cho and Huang (2019). Fourth, we have used $P_{{\beta }_k}$ in (5) as valid p-values conditional on the selected set $\mathcal{D}$ in Step 1. As one reviewer suggested, it is desirable to consider the randomness of $\mathcal{D}$ for our method in the nonasymptotic situation. There are two possible ways to guarantee valid p-values theoretically: (i) apply the proposed Steps 2 and 3 directly without using the mediator screening step. However, the computational burden for de-biased Lasso is extremely heavy for ultra high-dimensional mediators, e.g. there are a total of 379 330 DNA methylation markers in the real application; (ii) split the samples into two equal parts, one part for Step 1 and the other part for Steps 2 and 3. However, this sample-splitting technique suffers from loss of efficiency, because only half of the whole samples are used in the screening (Step 1) and inference (Steps 2 and 3), respectively.