Reviewing and assessing existing meta-analysis models and tools

Abstract

Over the past few years, meta-analysis has become popular among biomedical researchers for detecting biomarkers across multiple cohort studies with increased predictive power. Combining datasets from different sources increases sample size, thus overcoming the issue related to limited sample size from each individual study and boosting the predictive power. This leads to an increased likelihood of more accurately predicting differentially expressed genes/proteins or significant biomarkers underlying the biological condition of interest. Currently, several meta-analysis methods and tools exist, each having its own strengths and limitations. In this paper, we survey existing meta-analysis methods, and assess the performance of different methods based on results from different datasets as well as assessment from prior knowledge of each method. This provides a reference summary of meta-analysis models and tools, which helps to guide end-users on the choice of appropriate models or tools for given types of datasets and enables developers to consider current advances when planning the development of new meta-analysis models and more practical integrative tools.

Introduction

Recent advances in high-throughput technologies and computational scanning approaches have led to the availability of enormous amounts of publicly available clinical and biological datasets [1–4]. These datasets, however, are often produced by different research projects or sites, and in most cases, often have some limitations when trying to combine them, including increased heterogeneity, as samples type collected are generally not standardized across sites; limited sample size in each site, which may lead to insufficient power for inferences; unbalanced sample sizes between cases and controls, which may yield high biases in the outcome and often inconclusive results; and also batch effects and noise introduced into datasets from the technical origin that do not reflect biological variation [5, 6]. Combining these datasets is advantageous to researchers in increasing statistical power to detect biological phenomena from studies where logistical considerations restrict sample size or in studies that require the sequential hybridization of arrays [5].

Through funder or journal requirements, many of the large datasets which have accumulated from different studies are available in public data repositories and databases including Gene Expression Omnibus (GEO) @ http://www.ncbi.nlm.nih.gov/geo/, The Cancer Genome Atlas (TCGA) @ http://cancergenome.nih.gov, Array Express @ http://www.ebi.ac.uk/arrayexpress/ and Sequence Read Archive (SRA) @ http://www.ncbi.nlm.nih.gov/sra/. There is potential value in combining related datasets for further analysis, but the challenges mentioned earlier limit this potential. To address this, effective statistical analyses have been widely suggested in biomedical research [7], one of which is meta-analysis. Meta-analysis is described as a statistical analysis of a large collection of analysis results from individuals to integrate the findings to increase statistical power and obtain more precise effect size estimates [8, 9]. In meta-analysis, two types of information integration are often considered: horizontal meta-analysis and vertical integrative analysis [10].

Horizontal meta-analysis, also known as multi-study data integration combines multiple genomic studies (e.g. multiple microarray, methylation or GWAS studies) to increase statistical power, accuracy and validation [10], while vertical integrative analysis combines multi-omics data (e.g. gene expression, CNV, genotyping, methylation, somatic mutation, miRNA and clinical variables) to investigate disease subtypes, disease associated or driving genes and related regulatory networks [11]. Over the years, there has been exponential growth in the application of meta-analysis to different types of datasets, most especially Genome Wide Association studies (GWAS) and microarray gene expression datasets (see Figure 1), which have generated promising results.

Figure 1.

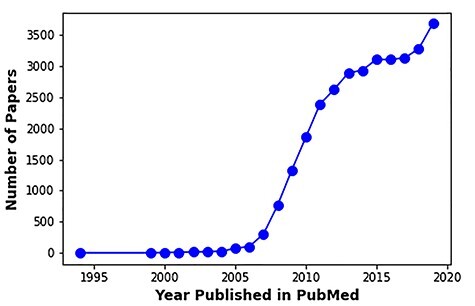
Number of publications on the application of meta-analysis to GWAS or gene expression datasets over the years. Search query used in PubMed search: [(meta-analysis[Title/Abstract]) AND (gene expression[Title/Abstract]) OR (genome wide association[Title/Abstract])].

Several statistical methods have been proposed for performing meta-analysis [6, 7, 11–21]. This article comparatively reviews three different categories of these meta-analysis techniques: Combining P-values, Combining Effect Sizes and Combining Ranks. We applied these methods to datasets retrieved, assessed their pros and cons, and discussed each performance based on our result as well as assessment results from previous research. Finally, we briefly discuss available meta-analysis software such as METASOFT [22], MANTRA [11], GWAMA [23], METAL [24], rmeta [25], MetABEL [26], catmap [27], Metafor [28] and MetaOmics [29]. This provides information to help orient the implementation of new models and practical integrative tools, as well as enables researchers to choose appropriate models or tools for given types of datasets.

Meta-analysis methods

Meta-analysis techniques have been widely developed and applied in genomic applications, especially for combining multiple transcriptomic studies. The most commonly used meta-analysis methods in the analysis of clinical and transcriptomic datasets mainly aim to identify genes associated with an outcome in the case where the expected outcome is continuous, multi-class or survival censored, or to identify differentially expressed genes in the case where the expected outcome is binary [6, 29]. These meta-analysis methods used for combining such data are grouped into three categories, namely, combining P-values, combining effect sizes and combining ranks. Figure 2 shows a graphical representation of the most commonly used meta-analysis methods, indicating the time each method was developed, while Table 1 provides a summary of existing meta-analysis methods and their features. We discuss each category in detail below.

Figure 2.

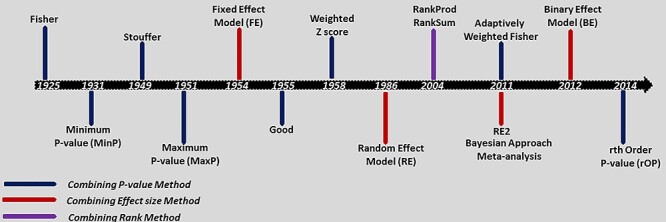
Timeline of existing meta-analysis methods showing the evolution of the meta-analysis model development. (Fisher [8], MinP [19] Stouffer [18], MaxP [21], FE [37], Good [13], weighted z-score [33], RE [10, 20], RankProd/Ranksum [15, 41], adaptive weighted Fisher [16], RE2 [22], BE [10] and roP [17]).

Table 1.

Summary of existing meta-analysis methods—Yes means feature is present and No implies absence of feature in each model

Model	AWF	Baye	BE	FE	Fisher	MaxP	MinP	RankProd/RankSum	RE	roP	SR/PR	Stouffer	WZscore
Effect size	no	yes	yes	yes	no	no	no	no	yes	no	yes	no	no
Fold change	no	no	no	no	no	no	no	yes	no	no	no	no	no
Heterogeneity estimate	no	no	no	no	no	no	no	no	yes	no	no	no	no
HSA	no	no	no	no	no	yes	no	no	yes	no	yes	no	no
HSB	yes	no	no	no	yes	no	yes	yes	no	yes	no	yes	no
HSr	no	no	no	no	no	no	no	no	yes	yes	no	no	no
M-value	no	no	yes	no	no	no	no	no	no	no	no	no	no
MCMC	no	yes	no	no	no	no	no	no	no	no	no	no	no
P-value	yes	no	no	no	yes	yes	yes	no	no	yes	yes	yes	yes
Sample size	no	no	no	no	no	no	no	no	no	no	no	no	yes
Standard error	no	no	no	yes	no	no	no	no	yes	no	no	no	no
Weight	yes	no	yes	yes	no	no	no	no	yes	no	no	no	yes
Z-score	no	no	yes	yes	no	no	no	no	yes	no	no	no	yes

Combining P-values methods

Combining P-values is a popular approach used in meta-analysis. It provides simplicity and flexibility to different outcome variables including survival, multi-class and continuous outcomes. There are several methods of P-value combinations from independent statistical tests with each having different statistical properties [6, 29, 30]. Next, we provide a summary of some methods used in combining P-values across several studies.

Fisher’s method: Fisher developed this method in 1925 [8]. It is the most straightforward statistical approach used in combining P-values across studies to estimate the accuracy of a unified P-value [7]. It combines log-transformed P-values from independent datasets/studies. The Fisher’s statistical formula is given by

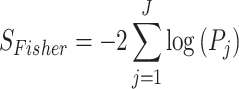where 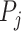is the P-value for the 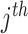study, and 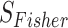follows a chi-squared distribution under the null hypothesis (assuming null P-values are uniformly distributed), with 2 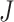degrees of freedom, where 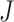is the total number of studies [8]. One major constraint this method has is that all studies are weighted uniformly, and this is likely inappropriate when combining GWAS studies with different sample sizes [6]. Also, it is impossible to estimate the average magnitude of differential expression when working with P-values [31]. An implementation of this method is found in metap an R package for meta-analysis of significance values [32].

Stouffer method (Z-transform test): Stouffer introduced this method in 1949 [18]. Unlike the Fisher method, Stouffer’s method adopted a different approach by using a simple transformation to transform the P-values 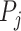from an individual study into a new variable say:

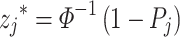where 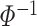is the inverse cumulative distribution function of the standard normal distribution which follows a standard normal N(0,1) under the null hypothesis [18]. Stouffer’s statistical formula is given by

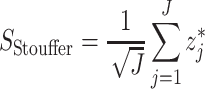which also follows a normal distribution to obtain its combined P-value. Advantages of this method include: (i) It is more robust and has little loss of efficiency compared to combining effect sizes methods where estimated effect sizes and standard error are considered as input; (ii) It is useful in cases where effect size estimates cannot be retrieved [18].

Weighted Z-score method: This method is a major improvement over the Stouffer method and was introduced by Liptak in 1958 [33]. In this case, P-values are transformed to Z-scores in a one-to-one transformation and also incorporate weight. Unlike the Stouffer method, the weighted Z-score is more efficient and powerful by allowing different weights for different studies [7]. Its statistical formula is given by

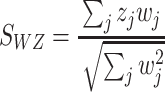where

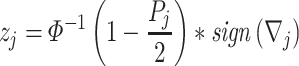with 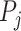the P-value for the 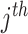study, 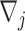, the direction of the effect for study 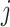and weight 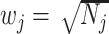with 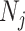being the sample size of the 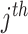study [34]. In the case where a study has unequal numbers of cases and controls, Willer et al. [24] recommended that the effective sample size should be calculated as

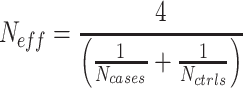Also 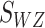follows a normal distribution to obtain its combined P-value. An implementation of this method is the METAL software which provides a fast and efficient meta-analysis of genome wide association scans.

Adaptively Weighted (AW) Fisher’s method: This method is an extension of the Fisher method and was developed by Li and Tseng in 2011 [16]. The method includes adaptive weights for individual studies in order to characterize effective studies contributing to the meta-analysis for an improved biological interpretation and statistical power of the results. It searches for all possible weights that will be identified as the best adaptive weight of an individual study with the smallest derived P-value. The adaptive weighted statistic given by

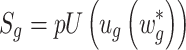is the P-value of the minimum P-value among all possible weights, where the observed weighted statistics

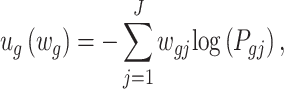and

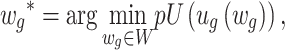is the optimal weight that gives an indication of which studies contribute to the statistical significance or differentially expressed evidence of the meta-analysis. The corresponding P-value of the AW-statistics 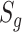is calculated as

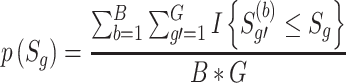(See Supplementary File for details). One disadvantage of this method is its inadequacy for traditional meta-analysis in evidence-based medicine research or epidemiology, and it also introduces bias toward studies with consistent significant effects [16].

Minimum P-value method (minP): Tippet in 1931 developed the minP method to detect differentially expressed genes whenever a small P-value exists in any one of the 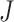studies [19]. Its statistical formula is written as

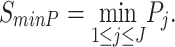It uses the minimum P-value among the 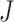studies which follows a Beta(α,β) distribution with degrees of freedom α = 1 and β = 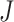as the test statistic under the null hypothesis [19].

Maximum P-value method (maxP): The maxP method was developed by Wilkinson [21] in 1951 to target differentially expressed genes that have small P-values in all studies. Its statistical formula is written as

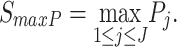It takes the maximum P-value which follows a Beta(α, β) distribution with degrees of freedom α = 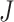and β = 1 as the test statistic under the null hypothesis [21].

rth ordered P-value method (rOP): Song and Tseng [17] developed the rOP method in 2014. This method uses the r-th ordered P-values from J combined studies. This method is considered a strong form of maxP (where 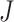/2 ≤ r ≤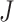) to identify candidate markers differentially expressed in most studies. The minP and maxP methods are special cases of rOP [17]. It also follows a Beta(α, β) distribution with degrees of freedom α = r and β = 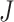− r + 1 as the test statistic under the null hypothesis [17].

The implementation of all these methods mentioned above can be found in MetaDE [35] an R package for microarray meta-analysis for differentially expressed gene detection. A significant advantage of using the combining P-value approaches is the allowance for standardization of the associations from genomic studies to a common scale. Compared to combining effect sizes, its simplicity and extensibility to different kinds of outcome variables is also a major advantage. Also, where the effect size may not be well defined, the association P-values can still be calculated when the outcome variable is not binary [6]. Disadvantages of combining P-value include failure to provide an overall estimate of effect sizes, inaccessibility of between-study heterogeneity and it may be erroneous when there is inconsistency in the direction of effects of the combined studies [34]. The combining P-value methods are primarily applied to gene expression datasets [16, 31].

Combining effect sizes methods

The effect size combination method uses a two-group comparison to derive standardized effect sizes and its associated standard error across combined studies. Choi et al. [36] was among the first to apply the two most popular approaches namely fixed effects model (FE) and random effects model (RE) to microarray meta-analysis. In any given study of measuring differentially expressed genes, effect sizes are calculated using a standardized mean difference, that is,

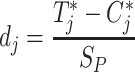where 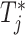and 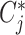are the treatment and control group of the 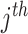study, respectively, and 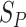is the estimated standard deviation [31, 36]. Other effect size measures can be of log odds ratios or regression coefficients of the J independent studies [22]. We briefly illustrate the models used in combining effect sizes from multiple studies (See details in Supplementary File).

Fixed effect model (FE): Cochran in 1954, in his paper the combination of estimates from different experiments developed the fixed effect model (FE) [37], which assumes that all the studies under consideration share a common/fixed true effect size [10, 20]. Let 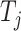be the effect size estimate of each study which follows a normal distribution with mean μ and variance 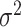. Also, let the weight assigned to each study 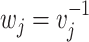be the inverse of the variance, where 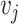is the within-study variance for study 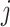in a meta-analysis of 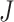studies. The test statistic for the FE model is given by

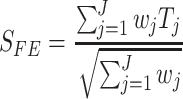which follows N(0,1) under the null hypothesis that there is no association. If we assume a one-tailed test, the P-value of the association is given by

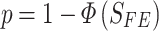while for a two-tailed test,

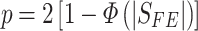where 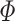is the standard normal cumulative distribution function [10, 20]. According to Evangelou et al. [34], FE is the best approach for prioritizing and identifying phenotype associated SNPs when combining GWAS data [34]. A major advantage FE has over the random effect model (RE) is its ability to maximize discovery power [34, 38]. This model is mostly applied to GWAS datasets [10, 20].

Random effect model (RE): Unlike the FE model, the RE model assumes that the effect sizes for each study in the meta-analysis are different and are drawn from a normal distribution with mean μ and variance 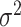[10, 20]. The RE analysis approach is to decompose the observed variance into its two component parts, i.e. the within-study variance 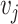and between-study variance 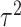. DerSimonian and Laird [11] in 1986 proposed a method of moments estimator for 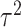using Cochran’s Q test statistics (See Supplementary File for details). The test statistics for RE model is given by

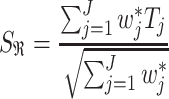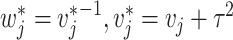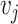where with and 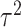the within-study and between-study variance values, respectively. Similarly, the P-value is

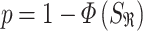for one-tailed test, and

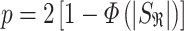for a two-tailed test, where 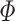is the standard normal cumulative distribution function. In comparison to FE, RE has limited power in discovery effort. However, RE is better off when considering the generalized observed association, uncertainty across different studies and estimating average effect size of the associated variant [34, 38, 39]. This model is mostly applied to GWAS datasets [10, 20]. Furthermore, Han and Eskin [22] made improvements on the RE (see ref [22] for details). They developed RE2 by assuming no heterogeneity under the null hypothesis, which contradicts the former RE. This was done in order to improve discovery power in the presence of between-study heterogeneity in the effect sizes [22, 34]. This model is mostly applied to GWAS datasets [10, 20].

Binary effect model (BE): BE is a new type of random effect model of meta-analysis developed by Han and Eskin in 2012 [10]. This model captures studies with or without an effect together. This model is the weighted sum of z-scores method where the m-values, that is, the posterior probability that an effect exists in each study of a meta-analysis, are incorporated into the weights. It assigns more weight to studies predicted to have an effect and lesser weight to the studies predicted not to have an effect. Let 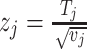be the z-score of the jth study. The binary effect model statistic is given as

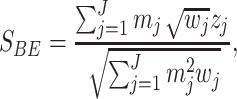where the weight 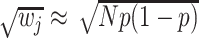with 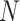the sample size and 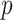the effect size (minor allele) frequency while 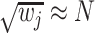when the effect size is the same between studies. 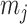is the corresponding m-value of study 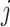(see Appendix for details). This model is mostly applied to GWAS datasets [10].

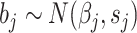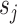Bayesian meta-analysis: A Bayesian approach to meta-analysis was developed in 2011 by Morris [40] to specifically perform trans-ethnic meta-analysis [11]. It assumes that a given population cluster with the same ethnic group may share the same effect size, but there is a difference in effect sizes among different population clusters. It assume the observed effect size of the jth study where is the corresponding standard error and 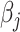is the population-specific effect for the jth population cluster. Then let 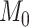be the null hypothesis of no association and 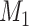the alternative hypothesis in a Bayesian framework. The evidence of association can be assessed by means of Baye’s factor

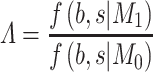where

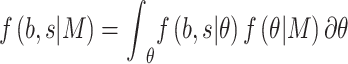is the marginal likelihood of the observed effect size under the model 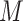with 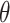denoting the unknown model parameter which includes the population-specific effect 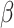and hyper-parameters relating to prior distribution (see Supplementary File for details). This approach performs better compared to fixed-effects and random effect meta-analysis, especially in terms of power to detect association and localization of the causal variant over a range of models of heterogeneity between ethnic groups and also has increased power and mapping resolution when the similarity in allelic effects between populations is well captured by their relatedness [36]. A minor limitation might be that its implementation can be computationally intensive [34]. This model is also mostly applied to GWAS datasets [11].

Even though combining effect size methods are well known, they are powerful and also have a strong Gaussian assumption on effect size. They often fail in transcriptomic data due to their restriction to only two group comparisons [29].

Combining ranks methods

Combining rank statistics methods are used to avoid results which can be influenced by outliers, which methods such as combining effect sizes and P-values may overlook. What the rank-based method does is to calculate the ranks of differentially expressed evidence for each gene in each study instead of calculating their effect size or P-value. Methods used in combining ranks are discussed below.

RankProd (RP) & RankSum (RS) methods: Breitling et al. [41] introduced the rank product (RP) method, which aims to detect differentially expressed genes [15]. Suppose we have a total of 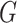genes in differential expression data across 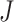replicated experiments. Let 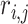be the position of the 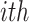gene in the 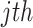replicate experiment in a list ordered according to fold changes. The rank product (RP) statistics for the 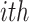gene is defined as the geometric mean of all the rank of genes obtained in each replicate. That is,

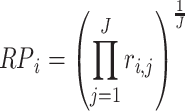Also, the rank sum (RS) statistics is defined as the arithmetic mean of all the ranks. That is,

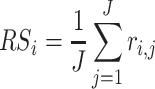In the case where the datasets to be analyzed are unpaired datasets, the RP/RS is performed using the algorithm explained in Supplementary File [15, 41]. This method has advantages over linear models, including fewer assumptions and better robustness, and a biologically intuitive fold change (FC), thereby increasing power in low sample size and/or large noise settings [41].

Sum of ranks (SR): This method applies a naive sum of the differentially expressed evidence ranks across studies. The test statistic of SR is obtained as follows:

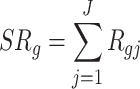where 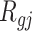is the rank of P-value of gene 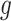among all genes in the 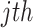study [42, 43].

Product of ranks (PR): Similarly, this method applies a naive product of the differentially expressed evidence ranks across studies. The test statistic of PR is obtained as follows:

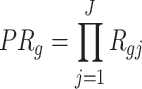where 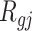is the rank of P-value of gene 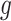among all genes in the 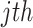study [42, 43].

The P-values of these test statistics can be calculated analytically or obtained from a permutation analysis as shown in Supplementary File. Note that genes with the smallest RP or RS values are the most likely to be upregulated or downregulated based on your choice of order when ranking the fold changes. One major disadvantage is that combining ranks methods only consider gene ranks rather than absolute expression values, which often leads to its robustness against heterogeneity across different studies. The implementation of this method can be found in a Bioconductor package (RankProd) [15] and it is mostly applied to differentially expressed datasets.

Hypothesis setting

Considering a meta-analysis of 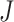combined transcriptomic studies, with each study 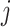containing 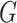genes, it is essential in meta-analysis to choose an appropriate method suitable for any type of research based on the objectives of the studies. This is due to the influence that the correctly identified method has on the final result of the differential expression analysis. Thus, depending on the aim of identifying different types of targeted markers based on the biological question or objectives under consideration, researchers have developed three main hypothesis settings as a guide in identifying targeted differentially expressed markers using the right meta-analysis method [16, 17, 44]. Given the null hypothesis for each gene :

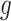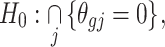where 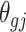is the effect size of gene g and study j with 1 ≤ g ≤ G, 1 ≤ j ≤ J and following Birnbaum [45], Li & Tseng [16] and Song & Tseng’s [17] convention, the complementary hypotheses settings are:

(1) 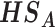for detecting targeted biomarkers that are differentially expressed in all studies or cohorts

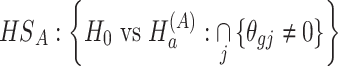Under the alternative hypothesis 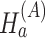, gene 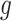is identified only when it is differentially expressed in all studies. It also implies that for gene 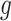, the effect sizes of all 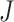combined studies are nonzero. The suitable meta-analysis methods for 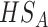are maxP [16, 17, 44], sum of ranks [29], product of ranks [29] and RE model [16, 17].

(2) 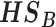for detecting targeted biomarkers that are differentially expressed in one or more studies

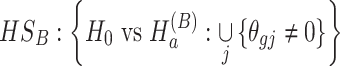Under the alternative hypothesis 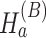, gene 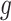is identified only if it is differentially expressed in one or more studies. It also implies that for gene g, the effect sizes of at least one of the J combined studies are nonzero. This is with the hope that an extremely small P-value in one study is usually enough to influence the meta-analysis and bring about statistical significance. Suitable meta-analysis methods for are Fisher [16, 17, 29, 44], Stouffer [16, 17, 29, 44], AW-Fisher [16, 17, 29, 44], minP [16, 17, 29, 44], rankprod and the FE model [29].

(3) for detecting targeted biomarkers that are differentially expressed in most of the studies

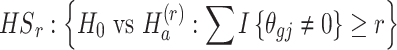where r is pre-specified with 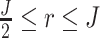and I{·} is an indicator function. Under the alternative hypothesis 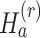, gene g is identified only if it is differentially expressed in the majority of studies. It also implies that for gene g, the effect sizes of at least r with 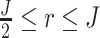of the 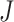combined studies are nonzero. The suitable meta-analysis methods for 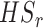are rOP [17, 29, 44] and the RE model [29].

In meta-analysis applications, it is more appealing to detect differentially expressed markers in all studies, that is 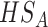, however, in the case where we have large 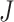combined studies, it is difficult to detect those markers in all the studies. This is because there is always additional noise/bias present in experimental data. Thus, most researchers prefer the hypothesis 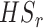which detects differentially expressed markers in the majority of studies, i.e. >70% of the studies. 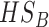is useful when considering statistically significant biomarkers in at least one study and when heterogeneity is expected [17].

Meta-analysis software

There are several existing tools that are used to carry out meta-analysis. Table 2 provides some existing meta-analysis software and their respective attributes with a brief explanation as follows.

Table 2.

Existing meta-analysis software and their attributes

Software	Graphical tool	Heterogeneity metric	Meta-analysis models	Preprocess software	Reference
catmap	NA	Q, I2	FE, RE	NA	[27]
GWAMA	Manhattan, QQ plots	Q, I2	FE, RE	SNPTEST, PLINK	[23]
MANTRA	NA	NA	Bayesian analysis	NA	[11]
MetABEL	Forest plot	Q, I2	FE	ABEL	[26]
Metafor	Forest plot Funnel plot	Q, I2	FE, RE, Mixed effect model	NA	[28]
METAL	NA	Q, I2	Weighted Z-score	NA	[24]
MetaOmics	HeatMap	Q, I2	MetaDE (Fisher, Stouffer, AWF, MinP, MaxP, roP, FE, RE, RankProd, RankSum, SR, PR)	MetaQC	[29]
METASOFT	Forest-PMPlot	Q, I2	FE, RE, RE2, BE	NA	[22]
rmeta	Funnel plot	Q, I2	FE, RE	NA	[25]

METAL was initially released in 2008 and then later published in 2010 (http://www.sph.umich.edu/csg/abecasis/metal/) [24]. It is a fast and efficient computational tool for meta-analysis of large datasets such as genome wide association scans, and is the most widely used meta-analysis software package [7] which was designed to improve complex traits gene mapping studies. METAL was written in C++ and applies two main approaches in combining evidence for association from individual studies using appropriate weight. These approaches are (1) the weighted Z score approach as discussed above which is based on the sample size, P-value and direction of effect in each study, and (2) the effect-size based method weighted by the study-specific standard error. It requires effect size estimates and their standard errors to be in consistent units across studies.

Genome-Wide Association Meta-Analysis (GWAMA) (2010) [23] is an open-source software (http://www.well.ox.ac.uk/GWAMA) designed for performing meta-analysis of summary statistics generated from genome-wide association studies of dichotomous phenotypes or quantitative traits. The software incorporates existing tools such as SNPTEST and PLINK to preprocess genome-wide association analysis files, aligns studies to the same reference strand irrespective of the genome-wide association genotyping product, and performs fixed effect meta-analysis, and in the presence of heterogeneity can perform random-effects meta-analysis. It calculates two heterogeneity measures (Cochran’s Q statistic, I²) of allelic effects between studies and provides graphical visualization of meta-analysis results using separate scripts for Manhattan and quantile–quantile (QQ) plots, and also accounts for automated genomic control for population structure.

METASOFT (http://genetics.cs.ucla.edu/meta/) is also an open-source software designed for performing a range of basic and advanced meta-analytic methods in an efficient manner. The methods incorporated in METASOFT include Fixed Effects model (FE) which is based on inverse-variance-weighted effect size as previously discussed, Random Effects model (RE) also based on inverse-variance-weighted effect size, Han and Eskin’s Random Effects model (RE2) optimized to detect associations under heterogeneity and Binary Effects model (BE) optimized to detect associations when some studies do or do not have an effect. Similar to GWAMA, the heterogeneity measures used are Cochran’s Q statistic and 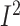. It uses ForestPMPlot, a visualization tool to display results such as the P-value, study name, log odds ratio and its standard error and summary statistics for each study. It produces a computed m-value, that is, the posterior probability that the effect exists in each study and the PM-Plot visualizes the m-value of each study along with its P-value [22]. The MANTRA (Meta-ANalysis of Transethnic Association studies) software has been developed to implement two independent runs of the MCMC algorithm used in the Bayesian approach meta-analysis and also estimate the Baye’s factor for each variant resulting in a summary output of the MCMC algorithm. This software is only available on request from the author [11].

MetaOmics is an analysis pipeline and browser-based software suite for transcriptomic meta-analysis. It is freely available at https://github.com/metaOmics/metaOmics. There are several R software packages and modules incorporated in MetaOmics. They include the MetaPreprocess module which allows users to input and preprocess multiple transcriptomic datasets for storage and later meta-analysis implementation of other analytical modules, such as MetaQC, a microarray meta-analysis in quality control that provides a quantitative and objective tool to assist with study inclusion/exclusion criteria for meta-analysis, and MetaDE, a microarray meta-analysis which implements 12 major meta-analysis methods for differential expression (DE) analysis to identify candidate markers associated with disease outcome. Output results include differentially expressed gene lists with corresponding raw P-values, q-values and various visualization tools. Another module incorporated in this software is MetaPath, a microarray meta-analysis in pathway enrichment detection tool which is used to identify the pathways associated with disease outcome. Others are MetaNetwork used for detecting differential co-expression networks (DCN), MetaPredict for prediction analysis, MetaClust for disease subtype discovery and MetaPCA for dimension reduction and exploratory visualization [29, 35].

Some R software packages for meta-analysis include rmeta software which incorporates methods such as fixed and random effects meta-analysis models for two-sample comparisons and cumulative meta-analyses. It produces outputs which include standard summary plots, funnel plots and computes summaries and tests for association and heterogeneity [25]. MetABEL is an R software for meta-analysis of genome-wide association scans between quantitative or binary traits and SNPs [26] and catmap (Case–Control and TDT Meta-Analysis Package) is an R software package which performs meta-analyses on genetic case–control data by combining case–control and family-based (TDT) studies. It conducts fixed-effects (with inverse variance weighting) and random-effects meta-analyses on combined genetic data by specifically implementing a fixed-effects model and a random-effects model for combined studies [27]. Likewise, Metafor (meta-analysis package for R) an R package is made up of comprehensive functions used in meta-analysis. It includes functions to estimate effect sizes or outcome measures and fit fixed, random and mixed effect models to data, as well as performing meta-regression analyses. It outputs meta-analytic plots including forest and funnel plots [28].

Results

We used the GEO2R tool [46] to download four gene expression datasets each for malaria and breast cancer case studies from the Gene Expression Omnibus (GEO) repository. The GEO2R tool using the GEOquery and limma R packages from the Bioconductor project was also employed to analyze each of the dataset to produce P-values for individual differentially expressed genes. For the two case studies, results from individual analysis of the four datasets were combined using different combining P-value meta-analysis methods. Furthermore, the performance of each individual and meta-analysis results were assessed using evaluation metrics from a confusion matrix, that is, true positive rate (TPR), precision, accuracy and F1-score as shown in Table 3 and Table 4 for malaria and breast cancer case studies, respectively. Table 3 and Table 4 also include the total number of differentially expressed genes identified in both individual and meta-analysis by setting a threshold P-value of 0.05.

Table 3.

Results from assessing combining P-value meta-analysis methods using malaria study

Analysis	#Significant Genes	ACCURACY	F1SCORE	PRECISION	TPR
Individual-analysis
GSE33811	562	0.4762	0.0571	0.3333	0.0313
GSE1124	3465	0.5333	0.3636	0.5263	0.2778
GSE7586	4739	0.5263	0.3077	0.5714	0.2105
GSE5418	6741	0.6000	0.4828	0.5833	0.4118
Meta-analysis
AWFisher	4290	0.5500	0.4906	0.5652	0.4333
Fisher	2319	0.6000*	0.4783	0.6875	0.3667
MaxP	939	0.5167	0.1714	0.6000	0.1000
MinP	2319	0.6000*	0.4286	0.7500*	0.3000
rOP	1268	0.5333	0.2632	0.6250	0.1667
Stouffer	1903	0.5167	0.3256	0.5385	0.2333
Weighted Z-score	6648*	0.5833	0.6154*	0.5714	0.6667*

Table 4.

Results from assessing combining P-value meta-analysis methods using breast cancer study

Analysis	# Significant Genes	ACCURACY	F1SCORE	TPR
Individual-analysis
GSE37139	5142	0.5294	0.4783	0.4231
GSE7904	16 253	0.4648	0.4722	0.4474
GSE36295	6448	0.5800	0.5116	0.4231
GSE3744	10 240	0.5323	0.4314	0.3438
Meta-analysis
AWFisher	10 087	0.4783	0.5862	0.7391
Fisher	7182	0.4783	0.5556	0.6522
MaxP	2995	0.5870	0.5128	0.4348
MinP	6926	0.4348	0.5000	0.5652
rOP	4288	0.6087*	0.5714	0.5217
Stouffer	6101	0.5000	0.5660	0.6522
Weighted Z-score	12 815*	0.5000	0.6462*	0.9130*

Assessing the methods using the malaria case study, we deduced that the well-known Fisher and MinP methods perform better in the combining P-value category with an accuracy of 60% as shown in Table 3. However, the story was not the same while assessing the methods using the breast cancer case study. As we can see in Table 4, the rOP method has the highest prediction accuracy of 60.87%, classifying it as the best method. However, we noticed that the weighted z-score method happens to perform well by having the highest total number of significance genes in both case studies. Not only that, but it also had the highest F1-score of 61.54 and 64.62% for both malaria and breast cancer studies, respectively. F1 score seems to be a good criterion to choose the best method when aiming for a positive interpretation of biological result. Therefore, we recommend the use of the weighted z-score method, followed by Fisher and so on when considering meta-analysis of gene expression datasets in combining P-value categories. However, it is evident that there might be changes in this recommendation with dataset complexity [8], for example, the maxP model performance varies across different datasets. This is in agreement with ‘no free lunch’ theorems for optimization, which highlight the danger of comparing models by their performance on a single dataset [47], suggesting that no single model can produce the best performance across all datasets.

Assessment of combining effect size methods is based on prior knowledge from the literature. Han and Eskin [22], in their paper, did a comparison of fixed effect model (FE), random effect model (RE) and Han and Eskin’s Random Effect model (RE2). Several analyses were done to justify the performance of these methods (see ref [22] for details) and they concluded that the FE model performs best by constantly achieving the highest statistical significance at low heterogeneity, while the RE2 model performs best when high heterogeneity exists between studies. Also, it was clearly stated that the RE model does not produce a more significant P-value than FE as expected when there is heterogeneity between studies thereby forfeiting its main goal [22]. Based on this, we highly recommend the use of the FE model for meta-analysis of GWAS when there is little or no heterogeneity between studies and RE2 when high heterogeneity between studies is observed. Furthermore, Han and Eskin (2012) [14] also recommend the binary effect model (BE), a type of RE approach that considers whether an effect is present or not between studies, to produce increased numbers of identified associations showing heterogeneity [10]. However, Morris (2011) [40] have strongly recommended the use of Bayesian meta-analysis when considering meta-analysis of transethnic GWAS [11]. Combining rank methods are best used on differentially expressed datasets [15, 31, 41]. Hong et al. [31] suggest that preference be given to the RankProd/RankSum method when dealing with small sample size or large between-study variation. Based on these recommendations, Figure 3 provides a decision tree that guides users on the choice of methods with respect to specific dataset.

Figure 3.

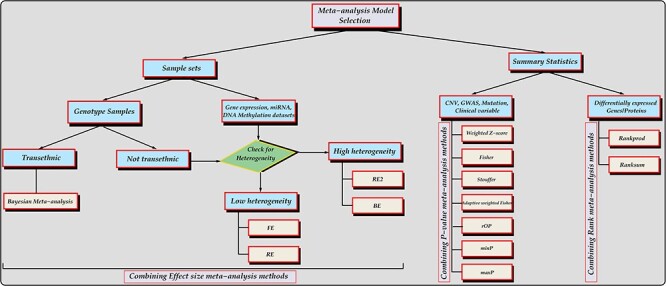
Decision tree of meta-analysis methods with respect to specific datasets. Method abbreviations: FE - Fixed effect, RE - Random effect, RE2 - Han and Eskin’s random effect, BE - Binary effect, rOP - rth ordered P-value, minP - Minimum P-value, maxP - Maximum P-value.

Discussion

We evaluated and compared the combining P-value meta-analysis methods, that is, Fisher, Stouffer, weighted z-score, adaptive weighted Fisher, roP, minP and maxP methods, using two case studies. These case studies consist of eight publicly available gene expression datasets, including four Malaria and four breast cancer datasets. The reason why we chose two different case studies was to show how flexible these meta-analysis methods are, and how well their performance can be controlled under different levels of difficulty when combining multiple datasets from different platforms. The performance of these methods was assessed using evaluation metrics from a confusion matrix.

The four publicly available datasets on malaria used to evaluate meta-analysis methods include the Krupka et al. [48] dataset (GSE33811), which uses the Affymetrix Human Gene 1.0 ST Array platform with 10 samples of five Malawian patients with severe and mild malaria; samples from the Affymetrix Human Genome U133A Array platform of the Boldt et al. [49] dataset (GSE1124), with 25 samples of African children of which there are five asymptomatic Plasmodium falciparum infection (A); five uncomplicated malaria (U); five severe malarial anemia (A); five cerebral malaria (Ce) and five that are healthy. The Ockenhouse et al. [50] dataset (GSE5418), which also utilizes the Affymetrix Human Genome U133A Array platform with 71 samples from patients with naturally acquired malaria infection compared to those from volunteers in a challenge model vaccine trial; and the Muehlenbachs et al. [51] dataset (GSE7586), which uses the Affymetrix Human Genome U133 Plus 2.0 Array platform with 20 samples of women with 10 active and 10 negative placental malaria (PM) status.

Likewise, four publicly available datasets were used for breast cancer meta-analysis study. These datasets include the Ingles et al. [52] dataset (GSE37139), which uses the Affymetrix Human Gene 1.0 ST Array platform with 12 samples of MCF7 breast cancer cells; the Richardson et al. [53] datasets comprising 62 samples designed to compare expression of tumor to normal breast tissue on the Affymetrix Human Genome U133 Plus 2.0 Array, with 43 tumor and 19 normal breast samples (GSE7904) and another 47 samples of human breast tumor cases (GSE3744); the Merdad et al. [54] dataset (GSE36295), which utilizes the Affymetrix Human Gene 1.0 ST Array platform with 50 samples corresponding to 45 samples of breast cancer tissues and five samples of healthy breast tissues. Visualization of different datasets is represented using box plots (Figures in Supplementary File). Although the use cases stated above focus on human, mainly due to data availability, these meta-analysis methods can be applied to any organism, including plants [55].

Meta-analysis techniques have been widely used in several applications, especially in clinical and biomedical contexts, such as in experimental study, e.g. randomized controlled clinical trials (RCTs) [56, 57], as well as in observational studies for group comparisons (e.g. cohort and case–control studies) [58, 59]. As indicated previously, meta-analysis provides a systematic integrative and quantitative framework combining independent study outputs for the same biological question to draw more effective and accurate inferences, thus playing an essential role in evidence-based medicine [57]. In the context of RCTs, meta-analysis technique produces more precise estimate of medical treatment effect and effective health intervention strategies [56]. The two common meta-analysis biomedical use cases are the post-GWAS [60] and expression level pattern [61] analyses of multiple cohorts with the same or different phenotypes to identify contextual biological markers related to conditions under consideration with an increased statistical power [60, 61].

Though existing meta-analysis methods [10, 15, 22, 31, 41, 62–64] have been deployed in different applications, as highlighted above, there is still a limited ability to assess and compare the performance of these different methods. Currently, a trial-and-error approach is applied to produce better, more significant results by fine-tuning features of the existing meta-analysis methods. So, there is a need to implement a meta-analysis integrative simulation framework, which assesses all existing methods to enable end users to select effective models for their applications. Furthermore, looking at the performance of different methods (see Tables 3 and 4), no meta-analysis method achieves a performance score higher than 75%, except for the weighted z-score method achieving approximately 91% true positive rate for the breast cancer dataset, likely at the cost of high false positives, considering the high number of significant genes predicted. Thus, there is a need for improvement on existing meta-analysis methods and tools by developing new models which account for the limitations of the existing models.

Conclusion

This article comparatively reviews several existing meta-analysis methods under three categories: Combining P-values, Combining Effect Sizes and Combining Ranks methods. We provide recommendations based on our results and findings while assessing the performance of different methods in our analysis and also from prior knowledge obtained from literature. We therefore recommend Combining P-values methods to researchers interested in carrying out meta-analysis of gene expression datasets. However, when performing GWAS meta-analysis, methods that fall under combining effect size category are best to use, while methods for combining rank category best suite meta-analysis of differentially expressed datasets.

Key Points

• Comprehensive summary and consistent classification of existing meta-analysis models and tools.

• There are three categories meta-analysis methods: Combining P-values, Combining Effect sizes and Combining Ranks.

• Assessing existing meta-analysis models and discussing the performance of different models.

• Revealing that effect size combination best fit sample sets, P-value combination best fit for sample data summary statistics and combining rank best suit differentially expressed genes.

• Guiding meta-analysis model and tool end-users based on data type driven performance evaluation.

Funmilayo L. Makinde, PhD candidate in the Computational Biology Division at University of Cape Town in collaboration with the African Institute for Mathematical Sciences (AIMS) South Africa.

Milaine SS. Tchamga, Postdoctoral fellow in the Division of Human Genetics at University of Cape in collaboration with the African Institute for Mathematical Sciences (AIMS) South Africa.

James Jafali, Researcher at Pathogen Biology Research Group, Malawi-Liverpool-Wellcome Trust Clinical Research Programme, Malawi.

Segun Fatumo, Assistant Professor at London School of Hygiene and Tropical Medicine, University of London, UK.

Emile R. Chimusa, Associate Professor at the Division of Human Genetics, Department of Pathology, University of Cape Town, South Africa.

Nicola Mulder, Professor and Head of the Computational Biology Division at University of Cape Town, South Africa.

Gaston K. Mazandu, Senior Lecturer position at the Division of Human Genetics, Department of Pathology at University of Cape Town, and Associate Researcher at the African Institute for Mathematical Sciences (AIMS), South Africa.

Data availability statement

Datasets used in different illustrations in this review are freely available in public repositories.

Funding

Some of the authors are supported partially by The German Academic Exchange Service (DAAD). This study is supported by the National Institutes of Health (NIH), USA, Common Fund under H3ABioNet (U24HG006941) and SADaCC (U24HL135600). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funders.