Bayesian Optimization of High‐Entropy Alloy Compositions for Electrocatalytic Oxygen Reduction

Abstract

Active, selective and stable catalysts are imperative for sustainable energy conversion, and engineering materials with such properties are highly desired. High‐entropy alloys (HEAs) offer a vast compositional space for tuning such properties. Too vast, however, to traverse without the proper tools. Here, we report the use of Bayesian optimization on a model based on density functional theory (DFT) to predict the most active compositions for the electrochemical oxygen reduction reaction (ORR) with the least possible number of sampled compositions for the two HEAs Ag‐Ir‐Pd‐Pt‐Ru and Ir‐Pd‐Pt‐Rh‐Ru. The discovered optima are then scrutinized with DFT and subjected to experimental validation where optimal catalytic activities are verified for Ag–Pd, Ir–Pt, and Pd–Ru binary alloys. This study offers insight into the number of experiments needed for optimizing the vast compositional space of multimetallic alloys which has been determined to be on the order of 50 for ORR on these HEAs.

This study combines kinetic modeling and density functional theory calculations with Bayesian optimization to find optimal alloy compositions for the oxygen reduction reaction while sampling a minimum number of compositions. Starting from the Ag‐Ir‐Pd‐Pt‐Ru and Ir‐Pd‐Pt‐Rh‐Ru alloy systems, the discovered optimal Ag–Pd, Ir–Pt, and Pd–Ru alloys are subsequently validated experimentally.

Introduction

High‐entropy alloys (HEAs; in the form of single‐phase compositionally complex solid solutions) offer a vast composition space for optimization of catalytic properties.[ ¹ , ² , ³ , ⁴ , ⁵ ] The many multi‐element atomic surface sites found on such complex surfaces contribute to a near‐continuum of the reaction intermediate adsorption energies that are descriptive of catalytic activity. Tailoring the HEA composition can improve the distribution of these adsorption energies to yield better catalysts. ^[1] This is advantageous since new catalysts are especially needed to facilitate chemical reactions for sustainable energy conversion in order to meet the increasing global energy demand and to combat climate change. ^[6] One example of a key reaction in the hydrogen cycle is the oxygen reduction reaction (ORR), where current catalysts are still far from ideal and cannot meet the demands for commercially viable industrial implementation on a global scale. Thus, further innovations are highly sought after, to get to that ultimate goal.[ ⁷ , ⁸ ]

Combinatorial exploration of vast alloy composition spaces has been actively used as a tool in experimental catalyst discovery for a variety of reactions and constituent elements,[ ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ] and efficient sampling of catalyst materials has also progressed. ^[17] However, as the number of constituent elements increases, the number of possible compositions grows combinatorially large and individual point testing cannot be accomplished within realistic time scales (see Supporting Information (SI), Figure S2). This calls for the need to sample the composition space more efficiently, such as by guiding the search with the aid of a surrogate function. Bayesian optimization of a Gaussian process (GP) is a feasible choice for intelligent sampling problems, ^[18] and Bayesian optimization has also been employed to optimize the catalytic activity for methanol oxidation of a ternary alloy. ^[19] However, knowing beforehand how many experiments would be needed in such a compositional search is crucial for determining if such a search is tractable in the first place.

Modeling the catalytic activity of highly diverse and complex surfaces is still in its infancy with only a few studies conducted,[ ¹ , ³ , ⁴ , ²⁰ , ²¹ ] and modeling of other aspects relevant for catalysis, such as surface stability under reaction conditions, is also being investigated.[ ²² , ²³ ] We propose a way to estimate the number of experiments needed using a model that has been found to correctly predict experimental trends for electrocatalytic ORR across hundreds of different alloy compositions within the Ag‐Ir‐Pd‐Pt‐Ru system. ^[4] Because of that, we expect the model to reproduce the complexity of an equivalent experimental search, and therefore be likely suitable as a proxy for substituting most of the necessary experiments by simulations. By sampling alloy compositions from the model, the number of experiments needed for future composition optimizations can thus be estimated.

Using the Ag‐Ir‐Pd‐Pt‐Ru and Ir‐Pd‐Pt‐Rh‐Ru HEAs as exemplary systems for a composition optimization, we use the kinetic model combined with Bayesian optimization to suggest alloy compositions for which high catalytic activities for the ORR are predicted. Doing this affords sampling of as few compositions as possible and yields the estimate of the minimum number of experiments needed to discover activity optima. The predicted optima subsequently undergo experimental validation. Moreover, by sampling the whole space of alloy compositions with the model in, for example, 5 atomic percent (at. %) intervals, it is possible to assure with reasonable certainty that all local and global optimal compositions have indeed been identified by the Bayesian optimization.

Results and Discussion

We apply our previously published model ^[4] for predicting current densities at 0.82 V vs. the reversible hydrogen electrode (RHE) on the face‐centered cubic (fcc) (111) surfaces of the disordered quinary alloy systems of Ir‐Pd‐Pt‐Rh‐Ru and Ag‐Ir‐Pd‐Pt‐Ru. This kinetic model is based on the *OH and O* adsorption energies and their success at describing the catalytic activity for the ORR through the associative mechanism.[ ²⁴ , ²⁵ ] The dissociative mechanism, where O₂ dissociates on the catalyst surface, will not contribute to the current density when the potential exceeds 0.8 V vs. RHE. ^[26] For construction of the model, thousands of *OH and O* adsorption energies were calculated with DFT in order to enable *OH and O* adsorption energy predictions on any surface site of the alloy at any composition (for details see SI). Due to the linear scaling between *OH and *OOH adsorption energies, focusing on the *OH and O* intermediates is sufficient to predict the catalytic activity. ^[27] The model effectively maps an alloy composition to a relative measure of a current density at a given potential using Equations 1–3. By doing so it takes as input net adsorption energies of on‐top *OH and hollow site O* obtained by considering an intersite neighbor blocking effect that ensures that no neighboring on‐top and hollow sites can adsorb intermediates at the same time (for details see SI).

$${\displaystyle j=\frac{1}{N}\sum _i^{N_{ads}}{j}_i}$$ (1)

$${\displaystyle \frac{1}{j_i}=\frac{1}{j_D}+\frac{1}{j_{k,i}}}$$ (2)

$${\displaystyle j_{k,i}=-exp\left(\frac{-\Delta G_i-\Delta G_{opt}\vee -0.86eV+eU}{k_{B}T}\right)}$$ (3)

Here j is the per site current density (in arbitrary units only used for comparing catalytic activity between compositions), N is the number of surface atoms in the simulated surface, N _ads is the number of sites at which adsorption has happened (after considering the intersite neighbor blocking), j_i is the current at surface site i modeled using the Koutecký–Levich equation, j _D is the diffusion‐limited current (set to −1) ensuring that the current at each site only increases sigmoidally at high overpotentials, j _k,i is the kinetically limiting current for site i modeled using an Arrhenius‐like expression assuming a Sabatier volcano relationship with the adsorption energies, ΔG_i is the *OH or O* adsorption free energy, ΔG _opt is the optimal *OH or O* adsorption free energy (set to 0.1 eV ^[24] and 0.2 eV ^[25] larger than for Pt(111) for *OH and O* respectively as suggested by theory and experiment), e is the elementary charge, U _RHE is the applied potential vs. RHE, k _B is the Boltzmann constant, and T is the absolute temperature (set to 300 K).

The posterior mean of a GP was used to construct a surrogate function mapping alloy composition to current density. For estimating the uncertainty at any composition, the posterior variance of the GP was used. The GP prior mean was set to zero everywhere, and the squared exponential kernel in Equation 4 was used as the covariance function. This prior mean and kernel are convenient standard choices that have applicability for many problems and therefore form a natural starting point for an unbiased analysis (see SI for details).

$${\displaystyle k\left(x_i,x_j\right)=C^{2}exp\left(\frac{-{\left(x_j-x_i\right)}^T\left(x_j-x_i\right)}{2l^2}\right)}$$ (4)

In Equation (4), x _i and x _j are molar fraction vectors, specified as the molar concentrations of each of the constituent elements in the alloy. For example, the alloy Ag₂₀Ir₃₀Pd₁₀Pt₄₀ corresponds to the molar fraction vector x =(0.2, 0.3, 0.1, 0.4, 0.0) ^T . C and $l$ are the constant value and length scale hyperparameters, respectively, of the kernel, which were optimized with every update of the sampled data. The superscript T denotes taking the transpose of the vector.

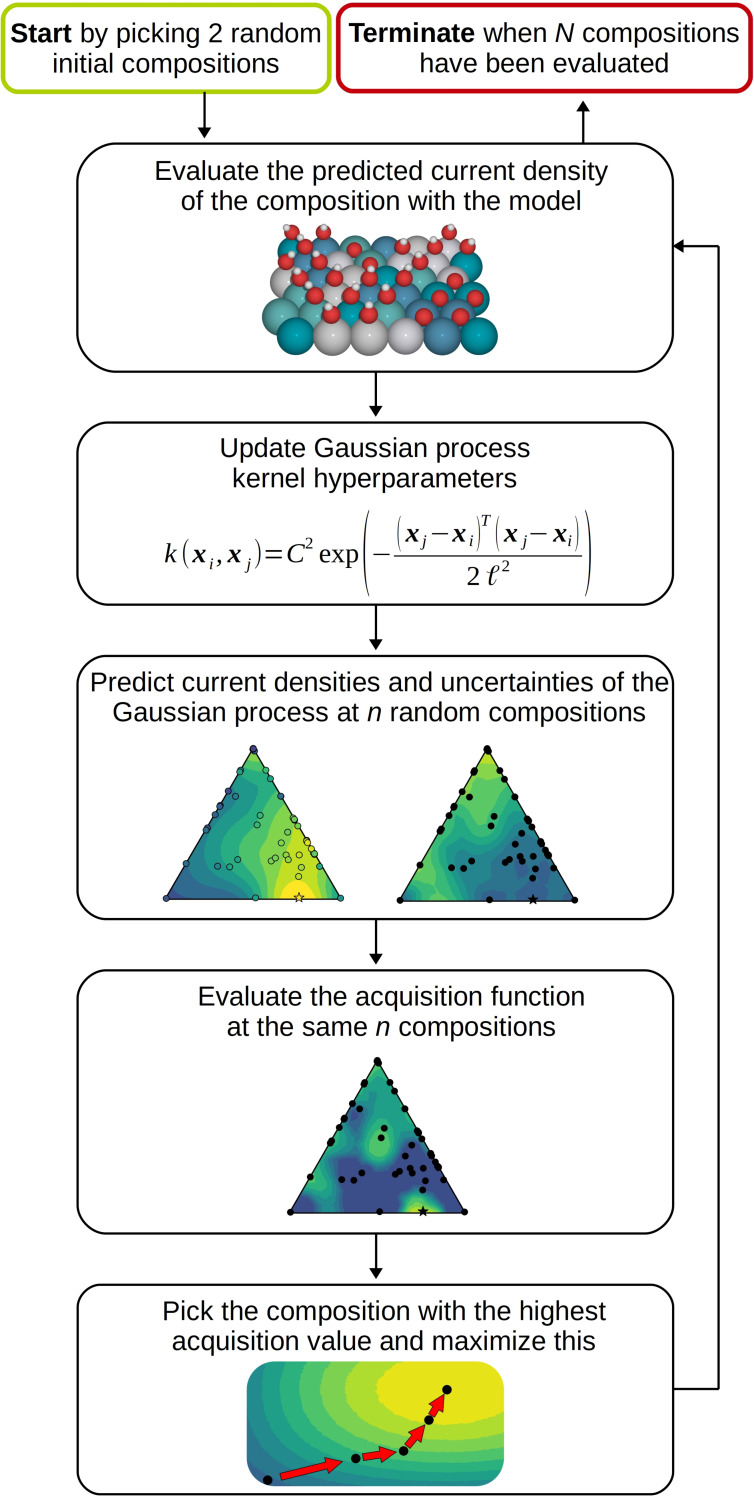
Figure 1 shows the workflow of the Bayesian optimization algorithm. Two random compositions were initially chosen to initiate the surrogate function. The expected improvement acquisition function was then used to suggest the next composition to investigate. The expected improvement takes into consideration the current densities predicted by the surrogate function as well as the readily obtained uncertainties of the predictions. ^[28] It is a standard choice and a widely used acquisition function, ^[29] making it a natural starting point for the current study (see the SI for details on the implementation). The kinetic model was then used to compute the catalytic activity of the selected composition via Equations (1)–(3), and the GP posterior was updated with this new sample using Bayesian inference as implemented in scikit‐learn. ^[30] By repeating this process we let the updated acquisition function choose the next composition of interest, and allowing the optimization to run for 150 iterations was enough to discover the most active locally optimal compositions in most cases.

Figure 1.

Workflow of the Bayesian optimization algorithm. The algorithm was terminated after N=150 samples to ensure enough evaluations for gauging the deviation in the number of samples needed for discovery of the optimal compositions. For evaluation of the acquisition function n=1000 random compositions were sampled.

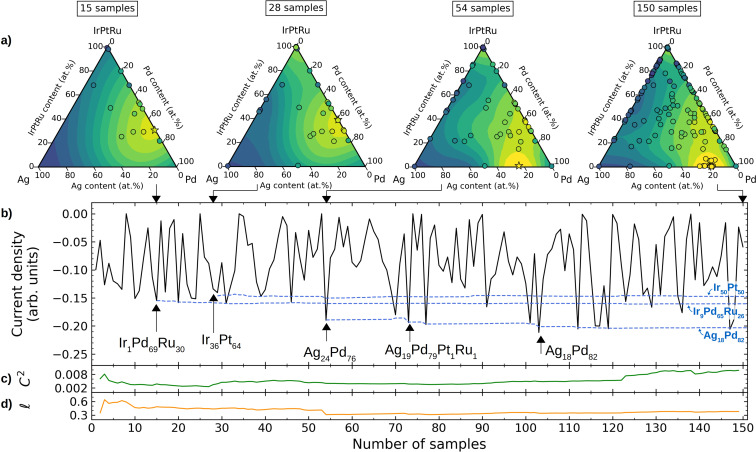
The quinary alloy composition space is equivalent to the set of all points in a 4‐simplex (the 4‐dimensional version of a regular tetrahedron), so plotting the resulting surrogate functions directly is hindered by the dimensionality of the plot. Instead, the local optima obtained from the resulting surrogate functions for each of the quinary alloys are listed in Table 1 in order of descending catalytic activity with the most active catalyst at the top. For illustration, a projection of the surrogate function for the Ag‐Ir‐Pd‐Pt‐Ru HEA at various stages of the optimization is given in Figure 2 a. Figure 2 b shows the modeled current densities that are sampled during a run of the optimization with some noticeable minima (i.e. compositions with high absolute values of modeled current densities) shown explicitly as well as the emergence of the local minima of the surrogate function. Figure 2 c,d shows the evolution of the constant value and length scale kernel hyperparameters in Equation (4) as more compositions are sampled. Important to notice is the length scale of the kernel which, although not directly transferable to the compositions, does give an indication of the frequency with which the current density is expected to change with composition. To be specific, the found length scale of about 0.4 is rather large compared to the molar fractions with values between 0 and 1, indicating that the current density is expected to vary with rather low frequencies. This is also indicated by the contours of the surrogate function in Figure 2 a which is seen to vary slowly with changes in the molar fractions. This also means that only a few local optima are expected for this hypersurface which will likely decrease the number of samples needed for their discovery.

Table 1.

Locally optimal compositions and the number of compositions needed to identify them for the two quinary HEAs.

HEA	Local optimum[a]	Predicted current density (arb. units)[b]	Idenfication success rate [%][c]	Number of samples for identification of local optimum[b,d]
Ag‐Ir‐Pd‐Pt‐Ru	Ag18Pd82	−0.203(2)	100	50(21)
	Ir9Pd64Ru27	−0.160(2)	100	28(28)
	Ir48Pt52	−0.147(2)	100	25(10)
	Ag78Ru22	−0.063(3)	69	93(27)
	Ir46Ru54	−0.003(0)	2	73(20)
	Ir10Ru90	−0.002(1)	14	110(27)
	Ru	−0.001(1)	14	48(33)
Ir‐Pd‐Pt‐Rh‐Ru	Ir42Pt58	−0.165(2)	100	23(8)
	Ir12Pd56Rh4Ru28	−0.164(1)	100	19(10)
	Rh	−0.001(2)	27	48(42)

[a] Determined as the local optima of the resulting surrogate function after sampling of 150 compositions for 64 random realizations of the two initial compositions (one such realization is shown in Figure 2). The spread in these compositions is on the order of 1 at. %. [b] Given as the mean followed by the sample standard deviation on the last digit(s) in parentheses. [c] Determined as the proportion of the resulting surrogate functions after sampling of 150 compositions for 64 random initializations that identify the optimum as a local maximum. [d] Determined as the number of samples needed for those of 64 surrogate functions with random initializations that successfully identified the optimum. The optimum has been considered identified when the molar fraction is within a 10 at. % difference of the optimum, for example, Ag₂₃Pd₇₇ would be regarded as a successful discovery of the Ag₁₈Pd₈₂ optimum.

Figure 2.

Example of a Bayesian ORR composition optimization for the quinary Ag‐Ir‐Pd‐Pt‐Ru system. a) Pseudo‐ternary plots (with Ir, Pt, and Ru collected into a single concentration) of the surrogate function after sampling of 15, 28, 54, and 150 compositions. Yellow colors signify regions with high absolute values of modeled current density, and blue colors signify regions with correspondingly low values. Previously sampled compositions are shown as black circles, and the best composition found so far is marked with a star. When projecting current densities from the quinary to the pseudo‐ternary composition space, more compositions will inevitably occupy the same points in the diagram. In the shown plots the maximal absolute value of the current density for overlapping compositions has therefore been depicted. b) Current densities sampled during the Bayesian optimization (black solid line) and the emergence of the three most active locally optimal compositions (blue dashed lines). c,d) Variation of the GP squared exponential kernels’ [Eq. (4)] constant term (c) and length scale (d) hyper‐parameters.

Indeed, the most active discovered optimal compositions in Table 1 form three groups of alloys, namely the binaries Ag₁₈Pd₈₂, Ir_≈50Pt_≈50, and the ternary Ir_≈10Pd_≈60Ru_≈30, with the latter two compositions discovered independently from both the Ag‐Ir‐Pd‐Pt‐Ru and the Ir‐Pd‐Pt‐Rh‐Ru quinary alloy models, supporting the robustness of the presented methodology.

For proof of concept and to verify that all local optima had indeed been discovered by the Bayesian optimization, we simulated all compositions in 5 at. % for both HEA systems, corresponding to 10 626 simulations for each. This is a much more demanding task compared to Bayesian optimization. Without a high degree of automation it is also an impractical objective for an actual experimental realization, not to mention the cost associated with the precursor materials and the automated instrumentation.

The discovered locally optimal compositions using this 5 at. % grid search of the quinary composition space are shown in Table 2. It indeed appears that the most important compositions for catalysis were found by the Bayesian optimization. Most noticeably, the locally optimal compositions Ag₂₀Pd₈₀ and Ir_≈50Pt_≈50 with high absolute values of predicted current densities are confirmed. Simplifying the list of optimum compositions by grouping similar compositions makes it possible to match the other optima found by Bayesian optimization in Table 1 with corresponding counterparts in the 5 at. % grid search analysis in Table 2. For example, the closely related Ir₉Pd₆₄Ru₂₇ optimum for the Ag‐Ir‐Pd‐Pt‐Ru HEA and the Ir₁₂Pd₅₆Rh₄Ru₂₈ optimum for the Ir‐Pd‐Pt‐Rh‐Ru HEA with a modeled current density of about −0.16 (arb. units) in Table 1 correspond to the Ag_≈0Ir_≈10Pd_≈60Pt_≈0Ru_≈30 and Ir_≈10Pd_≈60Pt_≈0Rh_≈0Ru_≈30 groups of compositions with similar current density highlighted in boldface in Table 2. In fact, the optima found with Bayesian optimization may constructively be thought of as the locally optimal compositions that the 5 at. % grid search would converge to if the step resolution was increased. We note that the trace amounts of other elements in the group of Pd‐Ru‐rich optima appear not to be very influential on the modeled current density, because the quinary composition space forms a rather flat plateau around Pd₆₅Ru₃₅ as shown in Figure S4. We therefore simplify our analysis of this optimum in the following, and treat it as a binary Pd–Ru alloy.

Table 2.

Locally optimal compositions found using a 5 at. % grid search over the two quinary composition spaces.

HEA	Local optimum[a]	Modeled current density (arb. units)
Ag‐Ir‐Pd‐Pt‐Ru	Ag20Pd80	−0.21
	Ag5Ir10Pd60Pt5Ru20	−0.16
	Ag5Ir5Pd65Ru25	−0.16
	Ir20Pd60Ru20	−0.16
	Pd65Pt5Ru30	−0.16
	Pd55Pt20Ru25	−0.15
	Ir55Pt45	−0.15
	Ir45Pt55	−0.15
	Ag5Ir10Pd20Pt65	−0.09
	Ag85Ru15	−0.06
Ir‐Pd‐Pt‐Rh‐Ru	Ir10Pd55Rh5Ru30	−0.17
	Ir50Pt50	−0.17
	Ir40Pt60	−0.17
	Ir15Pd60Pt5Ru20	−0.16
	Ir15Pd20Pt55Ru10	−0.08
	Pt65Rh35	−0.07

[a] Defined as compositions for which a ±5 at. % change in any molar fraction would result in a less active catalyst. Compositions in boldface refer to the group of Ir_≈10Pd_≈60Ru_≈30 compositions with similar predicted current densities.

Similarly, the less optimal Ag₇₈Ru₂₂, can be assigned a counterpart (Ag₈₅Ru₁₅) in Table 2. However, it also appears that local optima with relatively low absolute current densities are not matched as well between the Bayesian optimization and the grid search. For instance, the similar compositions Ag₅Ir₁₀Pd₂₀Pt₆₅ (from Ag‐Ir‐Pd‐Pt‐Ru) and Ir₁₅Pd₂₀Pt₅₅Ru₁₀ (from Ir‐Pd‐Pt‐Rh‐Ru) from the grid search in Table 2 do not have counterparts from the Bayesian optimization in Table 1. The reason for this is either that these compositions are not actually local optima and therefore not identified as such by the Bayesian optimization, or that they are weak local optima but were not sampled by the acquisition function due to small predicted absolute current densities. In either case this highlights the advantage of efficient sampling, where compositions that are not expected to be active are left untested.

We note that the Bayesian optimization algorithm in the current study could have been implemented in a number of other ways. For instance, the constraint that the molar fractions add to unity could be accounted for using constrained GPs. ^[31] In the current study this constraint was only included in the sense that evaluations only were done for valid molar fractions. This, however, appears to have been sufficient, which is evident from the fact that the 5 at. % grid search gave identical optima to the Bayesian optimization. Moreover, for a practical experimental composition optimization, a proper termination criterion is needed to know when to stop the search with confidence that the global optimum has been found. This criterion could for instance be based on the value of the acquisition function. ^[29]

Since the model uses calculated adsorption energies of the quinary alloys, it is essentially extrapolating to the edges of the composition space when predicting the current density of the discovered near‐binary optimal compositions. This is because only the most central composition space is likely to be sampled when generating random configurations of five elements for the simulated surfaces. To confirm the current density optima and the model's predictive ability for the binary alloys, DFT adsorption energies computed solely on the Ag–Pd, Ir–Pt and Pd–Ru binary alloys were used as input for the model.

Additionally, several regression algorithms were tested with two schemes for choosing the features of the simulated adsorption sites in order to predict the adsorption energies accurately on the binary alloys (see Tables S6, S7 and Figure S6). This confirmed that a combination of a per‐unique‐site based linear regression model and the most influential neighboring atoms[ ³² , ³³ ] maintains a low model complexity while still providing high adsorption energy prediction accuracy. However, for the binary alloys it was possible to achieve exceptionally low prediction error by using a non‐linear regression algorithm (a gradient‐boosted decision tree) and an extensive description of the adsorption site motif. This is true even though the simulated 2×2 atom‐sized surfaces limit the variations of the nearest neighbors due to the periodic boundary conditions (see SI for details).

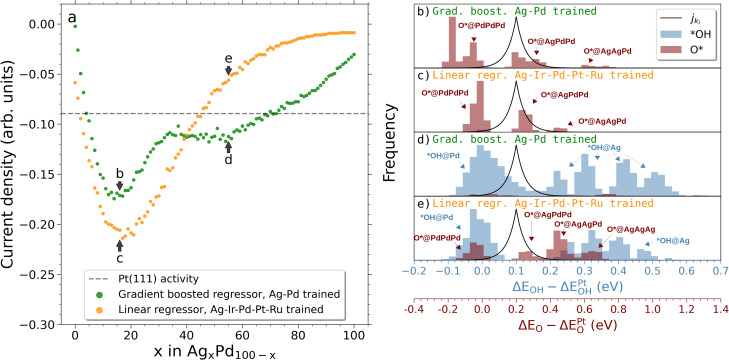
Plotting the predicted current density of the binary alloy gradient‐boosted model against the same results from the linear model trained on the quinary alloys, it is seen for the Ag–Pd system in Figure 3 that at high Pd content both models predict an activity maximum around Ag₁₅Pd₈₅. This activity stems almost exclusively from O* bound in fcc hollow sites composed of two Pd atoms and one Ag atom with some contribution from three‐fold Pd sites as shown in Figure 3 b,c. However, due to the discrepancy of the models’ prediction of *OH bound at on‐top Pd sites (Figure 3 d,e), the binary‐trained model retains high catalytic activity for a wider span of compositions compared to the quinary‐trained model which drops below the activity of Pt(111) at around 45 at. % Ag content as shown in Figure 3 a. We would thus still expect appreciable catalytic activity for Ag–Pd at the equimolar composition using the binary alloy model.

Figure 3.

a) Simulated current densities of the Ag–Pd system in a composition range from pure Pd to pure Ag with 1 at. % increments. A linear regression model trained on DFT‐calculated samples of the Ag‐Ir‐Pd‐Pt‐Ru alloy is used alongside a gradient‐boosted model trained on DFT‐calculated samples of Ag–Pd to predict the adsorption energies of the simulated surface. These predictions serve as input for Equations (1)–(3) which yield the resulting current densities. b–e) *OH and O* net adsorption energy distributions (after intersite blocking) for selected compositions corresponding to the annotations in (a). A scaled visualization of the modeled current density in Equation (3) is shown (black solid line).

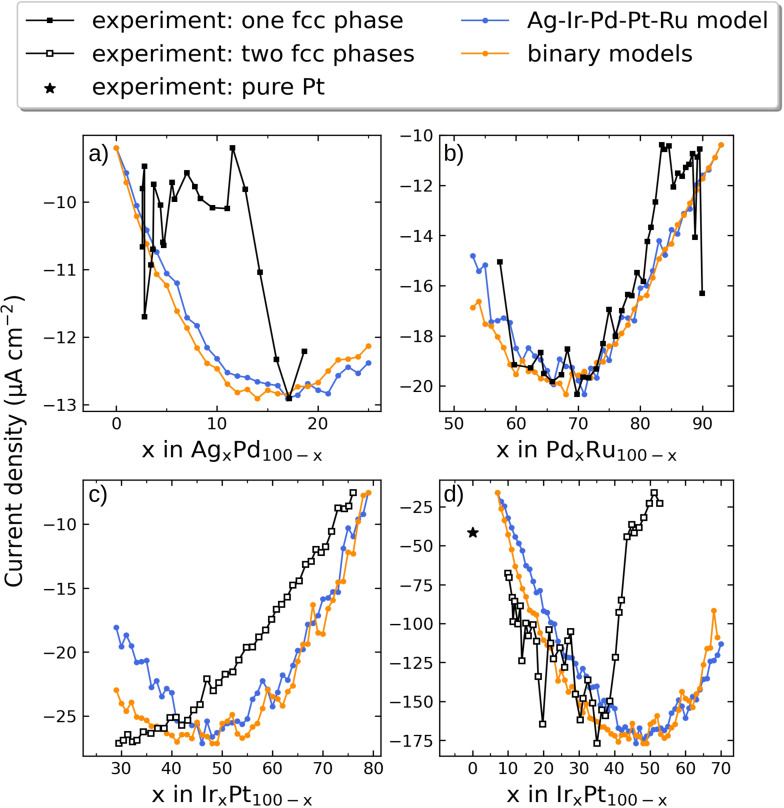
Ir–Pt and Pt–Ru were similarly scanned as shown in Figure 4 and more detailed in Figures S7 and S8 and display overall good agreement with the quinary alloy model. Both models predict optimum compositions around Ir₄₅Pt₆₅ and Pd₆₅Ru₃₅, and equivalent trends in the predicted current densities for the entire composition spans are observed.

Figure 4.

Comparison of simulated and experimental catalytic activities (black curves) for a) Ag–Pd, b) Pd–Ru, and c,d) Ir–Pt (for different composition ranges in (c) and (d)) at 800 mV vs. RHE. The simulated current densities were normalized to the experimental current densities by ensuring that the minimum and maximum current densities match up. For Pd–Ru in (b) three outliers that gave rise to very high current densities were left out (see Figure S9b).

The high catalytic activity of the Ag–Pd, Ir–Pt, and Pd–Ru alloys is not surprising since alloying the active elements Pd and Pt is a general way to enhance the activity for ORR. ^[34] Moreover, these alloys have indeed been tested experimentally with optimal compositions determined for the respective reaction conditions to be around Ag₁₀Pd₉₀, ^[35] Ir₁₅Pt₈₅, ^[36] and Pd₅₀Ru₅₀. ^[37]

To validate and compare the proposed catalytic trends of the discovered binary compositions, thin‐film composition spreads of the predicted Ag–Pd, Ir–Pt, and Pd–Ru binary alloys were synthesized and then analyzed by the use of a scanning droplet cell (SDC) in 0.1 m HClO₄. This high‐throughput electrochemical technique allows localized characterization of selected compositions along the compositional gradient. Precise positioning above the investigated sample is enabled by assembling the SDC head with robotic arms and a force sensor. An electrochemical cell is formed by pressing the Teflon tip to the surface of the sample, defining the surface of the working electrode in every measurement area (MA).

We used an automated setup to exclude any human error and provide the same measuring conditions for each measurement. Together with the high reliability and accuracy of the data this allows credible comparison of the activity between different MAs and samples. Figure 4 shows measured current density values vs. the composition of the Ag–Pd, Pd–Ru, and Ir–Pt systems. All linear sweep voltammograms (LSVs) are available in Figure S9. We note that catalytic trends on the quinary alloys obtained with the same experimental setup have been reported previously. ^[4] Therefore the scope of the current study is on the verification of the discovered optimal compositions. For the Pd–Ru composition spread we observed a broad minimum in ORR current densities for compositions ranging from ca. Pd₆₈Ru₃₂ to Pd₅₉Ru₄₁, covering the predicted optimal composition of Pd₆₅Ru₃₅. In the case of the Ag–Pd composition spread, only the lower Ag content compositions could be measured without visible corrosion (see Figure S9a). Here, a current density optimum was found at the composition Ag₁₄Pd₈₆, corresponding very well to the predicted optimum of Ag₁₅Pd₈₅.

In contrast, the Ir–Pt composition spread shows a clear increase of the activity toward ORR with decreasing content of Ir, that is, here we do not observe an agreement with the predicted optimal composition. In order to examine if the plateau at low Ir content observed in Figure 4 c is the expected optimum, a sample covering higher Pt contents was prepared and tested as shown in Figure 4 d.

To ensure the enhanced activity can indeed be fully assigned to the composition effect and the impact of changes in surface roughness can be ruled out, atomic force microscopy (AFM) measurements of surface roughness at different spots of the binary thin‐film composition spreads were made. For all of the considered samples the changes in surface roughness between different areas of the sample are negligible. Correlation of measured current densities with composition of the samples and their surface roughness are presented in Figure S10.

In order to determine the crystal structure and fully understand the measured correlation between current densities and binary compositions, X‐ray diffraction (XRD) was conducted. The crystal structures of as‐deposited Ag–Pd, Pd–Ru, and Ir–Pt thin films for various compositions were determined from XRD diffractograms shown in Figure S11. Five XRD peaks were observed in all three binary systems, which are characteristic for Bragg reflections from fcc structures. The diffraction patterns exhibit the highest intensity reflection along the (111) plane and four weak reflections along the (200), (220), (311), and (222) planes. For Ag–Pd and Pd–Ru, the diffraction peaks continuously shift to lower 2θ values with increasing Ag or Pd amount. The lattice parameters for these two systems are determined from Bragg's law, and the calculated results show that the variation of lattice parameters with chemical composition agrees well with a linear dependence based on Vegard's law. This reveals that as‐deposited Ag–Pd and Pd–Ru binary systems with different compositions form continuous solid solutions with an fcc structure. In the case of the Ir–Pt system, the (111) peak splits into two peaks. This is due to the coexistence of two phases and implies that Ir and Pt are not completely mixed, which is consistent with the large miscibility gap of the Ir–Pt phase diagram.

Conclusion

To summarize, we have combined a kinetic model with Bayesian optimization to predict compositions of highest current density for ORR starting from the quinary HEAs Ag‐Ir‐Pd‐Pt‐Ru and Ir‐Pd‐Pt‐Rh‐Ru. The most important locally optimal compositions come out at around Ag₁₅Pd₈₅, Ir₅₀Pt₅₀, and Ir₁₀Pd₆₀Ru₃₀. The model, trained on DFT‐calculated *OH and O* adsorption energies on Ag‐Ir‐Pd‐Pt‐Ru and Ir‐Pd‐Pt‐Rh‐Ru HEAs, was successful in extrapolating catalytic activity trends to the discovered optimal binary alloys Ag–Pd, Ir–Pt, and Pd–Ru as confirmed by training new models with new data specific for these. The model was also shown to reasonably reproduce the catalytic activity trend from synthesized thin‐film composition spreads of the Ag–Pd, Ir–Pt, and Pd–Ru systems for which optimal compositions of around Ag₁₄Pd₈₆, Ir₃₅Pt₆₅, and Pd₆₅Ru₃₅ were determined. A direct comparison between the model and the experiment, however, should be done with caution since many reaction condition parameters are not accounted for in the model. While suggesting optimal alloy catalysts, the model is at the same time able to estimate the number of experiments needed for the discovery of optimal compositions in the vast compositional space of quinary alloy systems. With the Bayesian optimization of the kinetic model employed herein, the number of experiments comes out at about 50 for discovery of the most important optima for the two investigated quinary HEAs. This number gives hope that composition optimizations of vast multi‐metallic composition spaces are indeed experimentally realizable in the laboratory.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Löffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig, J. Rossmeisl, Angew. Chem. Int. Ed. 2021, 60, 24144.

Data Availability Statement

All data and commented code necessary to reproduce the presented results have been made freely available at https://nano.ku.dk/english/research/theoretical‐electrocatalysis/katladb/bayesian‐optimization‐of‐hea/.