Prediction of shiftworker alertness, sleep, and circadian phase using a model of arousal dynamics constrained by shift schedules and light exposure

Abstract

Study Objectives

The study aimed to, for the first time, (1) compare sleep, circadian phase, and alertness of intensive care unit (ICU) nurses working rotating shifts with those predicted by a model of arousal dynamics; and (2) investigate how different environmental constraints affect predictions and agreement with data.

Methods

The model was used to simulate individual sleep-wake cycles, urinary 6-sulphatoxymelatonin (aMT6s) profiles, subjective sleepiness on the Karolinska Sleepiness Scale (KSS), and performance on a Psychomotor Vigilance Task (PVT) of 21 ICU nurses working day, evening, and night shifts. Combinations of individual shift schedules, forced wake time before/after work and lighting, were used as inputs to the model. Predictions were compared to empirical data. Simulations with self-reported sleep as an input were performed for comparison.

Results

All input constraints produced similar prediction for KSS, with 56%–60% of KSS scores predicted within ±1 on a day and 48%–52% on a night shift. Accurate prediction of an individual’s circadian phase required individualized light input. Combinations including light information predicted aMT6s acrophase within ±1 h of the study data for 65% and 35%–47% of nurses on diurnal and nocturnal schedules. Minute-by-minute sleep-wake state overlap between the model and the data was between 81 ± 6% and 87 ± 5% depending on choice of input constraint.

Conclusions

The use of individualized environmental constraints in the model of arousal dynamics allowed for accurate prediction of alertness, circadian phase, and sleep for more than half of the nurses. Individual differences in physiological parameters will need to be accounted for in the future to further improve predictions.

Statement of Significance.

The current work examines how well a physiologically based model of arousal dynamics can predict sleep, circadian phase, and alertness of nurses working rotating shifts in intensive care unit (ICU). We show that the mean error in prediction of alertness during shifts is similar in the model using individual shift schedules to constrain sleep dynamics and that using self-reported sleep as an input. This is an important finding for making prospective predictions of alertness during shiftwork and optimization of shift schedules. Further work is needed to test the model against larger datasets and to incorporate inter-individual variability in physiological parameters to make more accurate individual predictions.

Introduction

Modern lifestyles combined with 24/7 operations, transmeridian travel and man-made lighting disrupt circadian rhythms and sleep, leading to reduced alertness and increased risk of disease [1–5]. Approximately 20% of the workforce engage in shiftwork, which is associated with adverse effects on health, safety and performance, leading to a 60% higher risk of workplace accidents compared to daytime workers [1]. There is large inter-individual variability in the response to sleep loss associated with shiftwork, [6–9] with the most vulnerable individuals likely being at higher risk of errors and accidents. Prediction of an individual’s alertness during shiftwork is therefore critical for the design of alertness-safe work schedules, development of interventions, and personalized management of shiftwork.

Mathematical models have been developed to capture the dynamics of the key physiological processes underlying the human sleep-wake cycle and subsequent effects on alertness [10–29]. Models of alertness provide a predictive framework to guide shift design and interventions to potentially alleviate the negative impacts of shiftwork. The challenge of applying these models is in producing accurate predictions under real-world shiftwork conditions, which incorporate the interplay of physiology, environment, exposure to stimulants, behavioral choices, and inter-individual differences.

Accurate prospective predictions of alertness require prospective predictions of circadian timing and sleep [23] (note that here and in the following we refer to alertness as a generic cognitive property—not a specific measure or test). Several existing two-step alertness models predict sleep based on the work-rest schedules of individual shiftworkers and then predict alertness using these sleep times [15, 24, 30–37]. Conversely, one-step models use reported sleep as a model input to predict alertness, which is retrospective by design [38, 39]. So far, published models have not considered simultaneous prediction of both sleep and circadian timing and their effects on alertness in shiftworkers. Similarly, inclusion of individual-specific light exposure has not yet been studied.

There are two key groups of factors that affect an individual’s alertness during real-world shiftwork and lead to inter-individual variability. One group consists of the environmental and behavioral influences, such as, shift schedules, lighting, commuting, task on shift, use of stimulants, stress, and social and behavioral choices [1, 5, 30, 31, 37]. The other group consists of an individual’s endogenous physiological parameters, manifesting in their chronotype, response to sleep deprivation, habitual sleep times, sensitivity to light and sleep disorders, to name a few [7, 8, 40–42]. The physiological differences are best highlighted in controlled laboratory experiments, for example during a “constant routine,” where the environmental and behavioral influences are kept the same for all participants [43]. In real-world shiftwork the effects of the environmental and physiological differences are mixed, making individual predictions a challenging task [17, 44, 45].

The aim of this study was to test our model of arousal dynamics for real-world shiftwork applications by comparing its predictions for sleep, circadian phase and alertness with data collected from a cohort of intensive care unit (ICU) nurses engaged in rotating shiftwork. In the terminology of alertness models, our model of arousal dynamics is a three-step model as it predicts sleepiness and performance from model-predicted sleep and circadian phase. In this work, we use the model with default parameter settings, representing group average or a “typical” individual [12, 46, 47], assuming no knowledge about participants’ physiology. We focus on the impact of the different environmental constraints in which the model is evaluated. Specifically, we include shift schedules, times that individuals need to be awake before/after work including both the commute and preparation for work/rest (labeled “commute”), and individual-specific light exposure. We also investigate how predictions of alertness and circadian phase are affected by using individual reported sleep times.

Methods

Experimental protocol and data collection

Data were collected for 2–3 weeks from nursing staff working rotating shifts in the ICU at Austin Health, Australia [48–52]. The study was conducted during usual hospital operation with no manipulation of shift or sleep-wake times. Shift patterns were comprised of day (07:00–15:30), evening (13:00–21:30), and night (21:00–07:30) shifts, and days off. Typically, participants were studied when they had a diurnal schedule (series of day and evening shifts and days off) followed by a nocturnal schedule (≥3 consecutive night shifts). Other shift combinations were also included, such as schedules with day and evening shifts only, and schedules with blocks of night shifts separated by days off. The details of the protocol and data collection have been published previously [48–52].

Participants recorded their sleep and shift schedules in daily logs and wore wrist-actigraphs measuring activity and light (photopic illuminance) at 1-min resolution (Actiwatch Spectrum, Respironics, Bend, OR, USA). Self-reported sleep times were checked against actigraphy to verify that reported sleep coincided with low activity levels. Circadian phase was assessed from the acrophase (peak) of urinary 6-sulphatoxymelatonin (aMT6s) rhythms during both the diurnal schedule and night shifts. An alertness and performance test battery was administered on a day shift during a diurnal schedule and the first and the last night shifts during a nocturnal schedule. Relevant to this analysis, the tests included subjective sleepiness ratings on the Karolinska Sleepiness Scale (KSS, 1 = “very alert” to 9 = “very sleepy”) and 5-min visual Psychomotor Vigilance Task (PVT) measuring sustained attention [29]. The tests were performed 2–3 times during the shifts, at the start, middle and end of shift. Nurses missing data for either shift and sleep logs, aMT6s acrophase, actigraph light or KSS and PVT, as well as nurses who experienced daylight saving time (DST) transition during the shiftwork protocol, were excluded from the modelling study. The final set of participants included 21 nurses (16 female), aged 33.14 ± 9.34 years.

Assessment of model predictions

Model structure

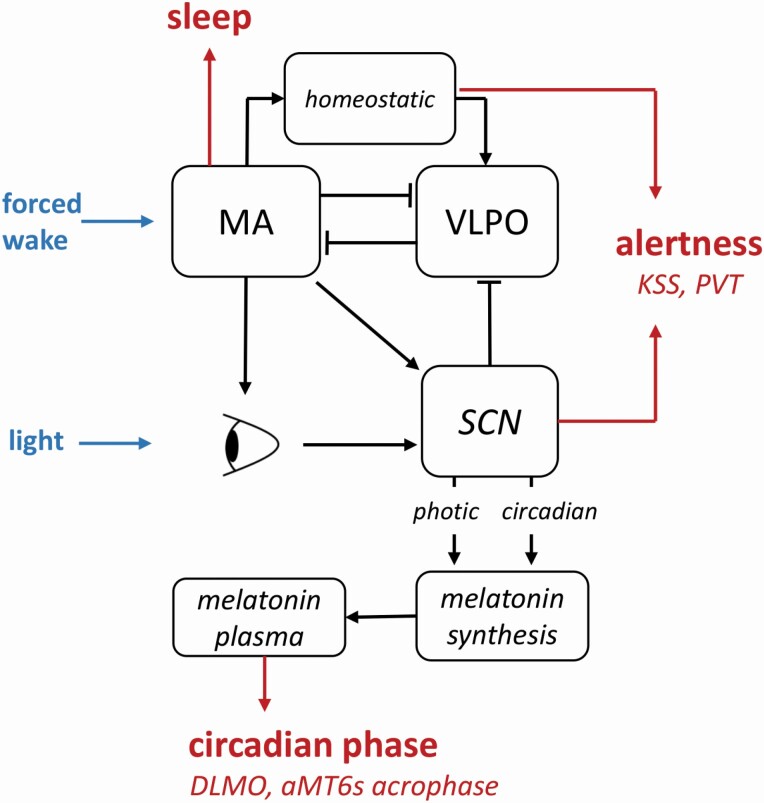
Our model of arousal dynamics [12, 46] was used to predict sleep, circadian phase, subjective sleepiness (KSS) and objective performance (PVT) under a range of individual environmental and behavioral constraints. The schematic in Fig. 1 shows the key model structures relevant to this analysis. Inputs provided to the model act either to keep the sleep-wake switch in a wake state (forced wake) or provide light input (light) to the central circadian clock. Sleep is predicted to occur when the modelled homeostatic and circadian drives combine to cause the electrical activity of the wake-active monoaminergic nuclei (MA) to fall below a critical threshold. Circadian phase is calculated based on predicted daily profiles of urinary aMT6s, the major metabolite of pineal melatonin, considered a reliable marker of the central circadian pacemaker. Sleepiness and performance measures in the model, including KSS and PVT, depend on the combined action of the homeostatic drive due to time awake and the circadian drive controlled by the suprachiasmatic nucleus (SCN) of the hypothalamus. Model equations and parameters have been published previously [12, 46].

Figure 1.

Key components of the model of arousal dynamics. Light activates photoreceptors in the eye, which transmit activation to the central circadian clock in the suprachiasmatic nucleus (SCN). The circadian drive from the SCN suppresses the sleep-active neurons in the ventrolateral preoptic nucleus (VLPO), thereby reducing inhibition of the wake-active monoaminergic neurons in the hypothalamus and brainstem (MA). MA has mutually inhibitory connections with the VLPO, so only one population is active at a time. Activation of the MA leads to increase of the homeostatic sleep drive, which together with the circadian drive from the SCN produce a total sleep drive controlling the switch between sleep and wake. The homeostatic and circadian drives together determine alertness levels. When MA is inactive, sleep state is predicted by the model and the eyelids are closed so the light input is reduced to zero. SCN controls synthesis of melatonin, which is released to blood circulation, diffused to saliva and metabolized into 6-sulphatoxymelatonin (aMT6s) which is excreted in the urine. Circadian phase markers, including aMT6s acrophase and dim light melatonin onset (DLMO) are calculated from the hormone profiles. Shifts and commute are simulated by keeping MA awake.

Default model dynamics

In the absence of specified forced-wake episodes and light input, the model’s default parameter configuration produces a 24-h sleep–wake cycle with ~8.5 h sleep starting at ~23:30. The default 24-h light cycle is set to 250 lux from 08:00 to 20:00 and 40 lux at other times if awake, while during sleep light is set to 0 lux [12, 46, 47]. Default entrained initial conditions for model variables were used for all constraints without light input (i.e. those labeled Shift, Shift+Commute, and Sleep, as described in the following section). To set the model’s initial conditions for evaluation under specific lighting conditions (identical for all participants), sleep-wake cycles were simulated for 1 week prior to the start of shift schedules using an average light-profile derived from all participants during day-shifts.

Protocol simulations and input combinations

The dynamics of each participant were simulated for the entire duration of their monitored shift schedule and compared to their experimental data for sleep, circadian phase, and alertness. To assess what input information produces the most accurate predictions, four shift-based combinations of input constraints were tested:

• (i) Shift: Each individual’s shift schedule was the only input to the model, which was implemented by imposing forced wakefulness during shifts.

• (ii) Shift+Commute: Each individual’s shift schedule and estimated commute times were provided as inputs to define times of forced wakefulness. For this study, commute times were defined as the times the participants had to be awake before/after shifts and include both commute and getting ready for work/rest. These were estimated for each participant by taking the median time between wake and start of day shift (07:00) for duration of commute to work and the median time between end of night shift (07:30) and start of sleep for commute from work. Commute times of >2.5 h were considered outliers and were excluded from the calculation.

• (iii) Shift + Light: Each individual’s light exposure from the actigraph was provided as an input along with their shift schedule. Any gaps in the light data (median of 11% of protocol data across individuals), were filled with average light profiles across all nurses for the relevant shift or shift transition type.

• (iv) Shift + Commute + Light: Combination of the three constraints above. This imposed forced wakefulness during both shift and commute to/from work times and added an individual’s light exposure.

To investigate how individual self-reported sleep affects model predictions, we tested two additional input constraints:

• (v) Sleep: Each individual’s self-reported sleep times, including naps, were provided as the only model input. This enforced wakefulness at all times except for the sleep opportunity starting 15 min before the self-reported sleep. Self-reported sleep rather than actigraphy-based rest-activity times were used because actigraphy fails to distinguish between sleep and immobility during quiet wakeful rest.

• (vi) Sleep + Light: Each individual’s light exposure from actigraphy was added as an input together with their self-reported sleep.

For each participant we ran six simulations, one for each of these constraints, and compared predictions to experimental data. For each input combination, mean prediction errors were calculated by averaging errors across all participants.

Sleep overlap

To quantify the quality of sleep predictions with each of the six input constraints we evaluated how well the model’s predictions overlap with the participant-reported sleep during the entire study. Minute-by-minute sleep-wake state in the model and in the study data were compared to obtain two different percentages: state percentage overlap, which considers any time when both model and participants report the same state and converts that to a percentage of total duration; and sleep percentage overlap, which only considers times when both model and participants report sleep and converts that to percentage of the total sleep time, where total sleep time is taken to be whichever is maximum between the model and study data—this definition being necessary to avoid a model that predicts continuous sleep being identified as having 100% overlap with the study-data.

The percentage values, however, are susceptible to biases that can produce misleading interpretations. For example, the state percentage overlap on a day with 8 h sleep in both model and data cannot fall below ~33%. These measures would also report false misalignment in cases of missing data. For this reason, we also included surrogate normalized values for the overlap between participant-reported and model-predicted sleep. These provide improved discrimination while avoiding the potential misinterpretations.

The steps to calculate the surrogate normalized values were to (1) generate large numbers of surrogate datasets by resampling original self-reported sleep data. The re-sampling preserved the distributions of the total sleep times between shifts across all data while randomizing over individuals, their past schedule, and specific timing of sleep episodes. The resulting datasets thus include all the original sleep durations between pairs of shift types but distributed randomly across individuals. (2) Compute sleep overlap between 4,096 surrogate datasets and the original study data, resulting in a distribution of sleep overlap percentages. The large number of datasets is needed to accurately determine mean overlap values. (3) Rescale the percentage sleep-overlap obtained for the model using the mean percentage sleep-overlap from 4,096 surrogate datasets. With this approach, the surrogate normalized sleep overlap can take values less than or equal to 1. A value of zero means the model prediction has equivalent predictive power to the surrogate (i.e. to re-sampled original data), negative values indicate the model has less predictive power than the surrogate, while positive values indicate the model has greater predictive power than the surrogate—a value of one means perfect prediction by the model.

Day partitioning for sleep distributions

For calculation of sleep distributions, the simulated and the experimental data for all participants were partitioned by uniquely assigning each calendar day to one of four day types based on the shift that starts that day: day shift (D); night shift (N); evening shift (E); or day off (O). Day-type (and thus transition) definitions were based on what shift, if any, started on a given calendar day (00:00 to 23:59). If no shift started during that 24-h episode, then that day was counted as a day-off. To consistently assign boundaries to shift transitions, and enable consistent counting of sleep episodes, days off were given an effective “shift” boundary at 12:00. The resulting sequence was used to group sleep episodes by the shift transition type they occur within. Only the transitions that appeared three or more times across the study data set were included, resulting in 12 out of a possible 16 shift-to-shift combinations.

Circadian phase

The model predicts melatonin and aMT6s dynamics as well as circadian phase markers derived from them. For aMT6s acrophase prediction, the predicted urine quantity of aMT6s for each individual was sampled by averaging over two-hour blocks—equivalent to taking urine samples every two hours [46]. A nonlinear least-squares fit of a cosine function to the two-hour averages was then performed to obtain predictions of circadian acrophase on each day for comparison to the experimental data. In the experiment urinary aMT6s acrophase was measured across 1–2 days during the diurnal schedule including day/evening shifts and days off, and also across 1–2 days at the end of the nocturnal schedule (night shifts only), typically on a third or fourth night shift. The same measurements were performed in the model. Phase change was calculated as the difference between aMT6s acrophase on the diurnal and nocturnal schedules.

Alertness

The model produces predictions of sleepiness and performance measures (collectively we call it alertness throughout the paper), including KSS scores and PVT reaction times (PVT RT) on a 10-min test as described in detail in a previous publication [12]. To compare with the study data, prediction values were taken at the same times on the protocol as the experimental measurements. The non-integer KSS values in the model were rounded to the closest integer value. For calculation of average KSS profiles the data were binned into 3-h bins resulting in four bins for day shifts and five bins for night shifts. Direct quantitative comparison to study data was only possible for KSS. In the experiment PVT was measured in a 5-min test (as opposed to 10-min in the model), so only qualitative comparison was included for PVT.

Results

Model predictions of sleep, circadian phase, and alertness were compared against data collected from ICU nurses engaged in shiftwork. Six different input constraints were tested to investigate how well individual-specific constraints can explain shiftwork dynamics using a typical individual model that was previously calibrated on group average data. Statistics for all six input constraints are presented in the Tables, while figures show results for representative constraints of Shift, Shift + Commute + Light, and Sleep.

Sleep

On average, model performance predicting self-reported sleep is similar for all Shift-based constraints, demonstrating only minor differences in sleep overlap values (Table 1). Importantly, even minimal information (i.e., Shift constraint) was sufficient for the model to outperform the surrogate datasets as shown by the positive surrogate normalized values of $0.53\pm 0.15$ ($73\pm 12\mathrm{\%}$ and 87$\pm 5\mathrm{\%}$ for sleep overlap and state overlap, respectively). This value was similar when light was added as a model input (Shift + Light) but decreased when commute information was used (Shift + Commute and Shift + Commute + Light). The results for the sleep-based constraints (Sleep and Sleep + Light) are reported for completeness. As expected, restricting sleep opportunity time in the model based on the sleep diary data for each individual resulted in near perfect prediction of sleep times with mean surrogate normalized values of $0.90\pm 0.06$. They are not identical, however, because the model predicts sleep only when the sleep drive is sufficiently high during the defined sleep opportunity window.

Table 1.

Sleep-wake overlap between the model and the study data. Surrogate normalized and percentage overlap between model and study data (mean $\pm$SD). The first column indicates the context used for the model’s evaluation; the next column presents surrogate normalized values for the sleep-only percentage overlap. The remaining two columns are direct percentage overlap values, the first for sleep only state and the second for sleep–wake states

Evaluation constraint	Sleep [surrogate normalized]	Sleep (%)	Sleep–wake state (%)
Shift	0.53 ± 0.15	73 ± 12	87 ± 5
Shift + Light	0.53 ± 0.17	73 ± 12	87 ± 5
Shift + Commute	0.39 ± 0.19	66 ± 14	81 ± 6
Shift + Commute + Light	0.49 ± 0.18	71 ± 13	85 ± 5
Sleep	0.90 ± 0.06	94 ± 3	98 ± 1
Sleep + Light	0.90 ± 0.06	95 ± 3	98 ± 1

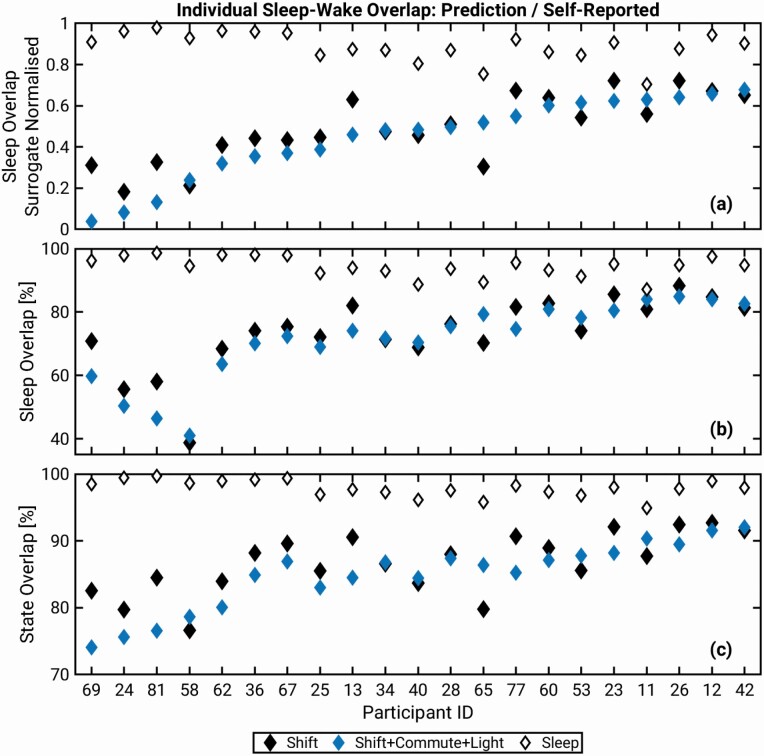
Individual sleep overlap. The degree of overlap for the shift-based constraints between model and data was different across individuals, as shown in Figure 2. For example, when using the Shift + Commute + Light constraint the surrogate normalized values vary from 0.04 for participant 69 to 0.68 for participant 42. The overall trend is similar for the overlap values for Shift and Shift + Commute + Light constraints in Figure 2, a–c but there are differences. Normalized sleep overlap values are >0.1 higher for participants 69, 81, 13, and 77 when using Shift vs. Shift + Commute + Light constraint, while the opposite is true for participant 65. The Sleep constraint results in high individual overlap values, which are also varied across individuals. The three different overlap measures show similar dynamics, but their ordering of overlap values from lowest to highest is not identical.

Figure 2.

Overlap between the model-predicted and self-reported individual sleep. Comparisons for three evaluation constraints are shown: Shift, Shift+Commute+Light and Sleep. (a) Surrogate normalized overlap for participants, (b) sleep overlap, and (c) sleep-wake state overlap. The participants on the X-axes in all panels are ordered from low to high of the surrogate normalized overlap values for Shift + Commute + Light condition.

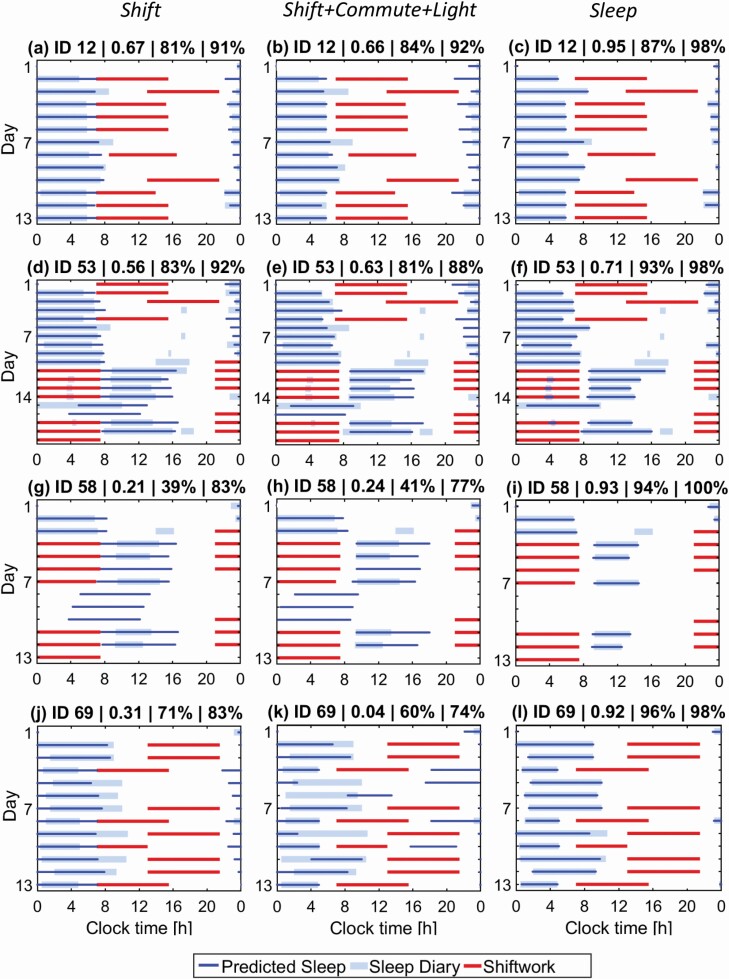
To illustrate the source of differences in the overlap values under different constraint conditions, the raster plots in Figure 3 show predicted and self-reported sleep for four representative participants with high (ID 12), medium (ID 53), and low (IDs 69 and 58) overlap values under the Shift, Shift + Commute + Light, and Sleep constraints. A weakness of the Shift constraint for all participants is that it does not capture the awake time straight before day and after night shifts (Figure 3, left panels). This is corrected with the Shift + Commute + Light constraint in, but also leads to earlier sleep onset on diurnal schedules (Figure 3, middle panels). Using the Sleep constraint leads to near identical sleep between the model and the data for all participants. Daytime naps in participants 53 and 58 are not reproduced by any of the model constraints used here, because accumulated sleep debt is predicted to remain below the sleep threshold. Conversely, naps during night shifts for participant 53, Figure 3, d–f, are reproduced with the Sleep constraint, but not with the Shift-based constraints, because these impose forced wakefulness during shifts. Participant 58 in Figure 3, g–i did not report sleep on days 8–10 and reported short sleep duration on the other days. As a result, the overlap between the model and the data is low for all Shift-based constraints where sleep prediction is free outside of shifts, but the overlap is high for the Sleep constraint. For participant 69, Shift constraint in Figure 3, j produces reasonable prediction with the surrogate normalized overlap of 0.31, but the predicted sleep starts and ends earlier than the self-reported times. Addition of commute and light information in Figure 3, k further advances sleep onset time, resulting in a large discrepancy with the data for this participant (normalized overlap of 0.04).

Figure 3.

Example raster plots comparing predicted and self-reported sleep during shiftwork schedules. Three evaluation constraints are illustrated: Shift in the left column, Shift + Commute + Light in the middle, and Sleep in the right. (a–c) Raster plots for participant 12 for Shift, Shift + Commute + Light, and Sleep constraints; (d–f) raster plots for participant 53; (g–i) raster plots for participant 58; and (j–l) raster plots for participant 69. Panel titles show participant ID, surrogate normalized sleep overlap (0–1), percentage sleep overlap, and percentage state overlap.

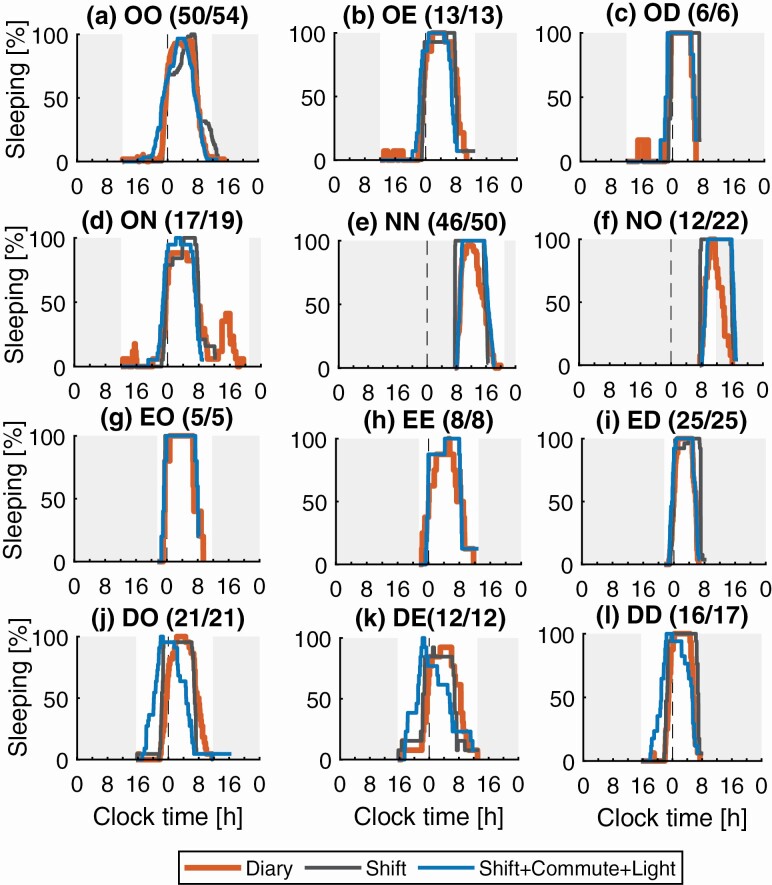
Sleep distributions. Sleep distributions in Figure 4 allow us to assess how well the model predicts sleep-wake patterns across all participants and shift transitions. For nine of the 12 shift transitions, Figure 4, a–i, all Shift-based constraints predicted a main peak in sleep distributions at the same time as that observed in the study data. The addition of Commute information allowed for better alignment of the model-predicted sleep onset time with the study data during NN and NO transitions, with predicted distributions rising through 50% sleeping within 15 min of the study-data, while without Commute there is more than 1 h difference, (Figure 4, e, f, and i). Similarly, it allowed for a better alignment of the predicted wake onset with the study data during transitions to day shift, again improving from more than 1 hour difference at the 50% sleeping mark to only 15 min difference when including Commute (OD, ED, and DD in Figure 4, c, i, and l). For the day shift to day off, evening and day shifts (DO, DE, and DD in Figure 4, j–l), the addition of commute and light led to worse agreement between the model and the data, compared to use of the shift schedules alone, due to the advance of sleep onset and wake times. This resulted in a longer sleep duration in the model compared to the study data on these shift transitions. Overall, sleep duration was well predicted by the model as seen from the distribution overlaps (see Supplementary Table S1 for quantitative data).

Figure 4.

Comparison of predicted and reported sleep distributions for common shift to shift transitions. Model predictions are shown for Shift and Shift+Commute+Light inputs. Shifts notation is: D $\Rightarrow$ day shift; E $\Rightarrow$ evening shift; N $\Rightarrow$ night shift; and O $\Rightarrow$ day off. (a) Sleep distribution for the day off to day off transition, OO; (b) day off to evening shift, OE; (c) day off to day shift, OD; (d) day off to night shift, ON; (e) night shift to night shift, NN; (f) night shift to day off, NO; (g) evening shift to day off, EO; (h) evening shift to evening shift, EE; (i) evening shift to day shift, ED; (j) day shift to day off, DO; (k) day shift to evening shift, DE; (l) day shift to day shift, DD. The Y-axis shows percentage of participants sleeping at any time between shifts of a given type. The white background indicates the time between a shift end and the subsequent shift start. The title for each panel contains: transition-type; and number of transitions with reported sleep/total number of transitions. Sleep-based inputs produce predicted distributions that are almost identical to the study data—therefore, those results are omitted from the figure.

The transition from day off to night shifts (ON in Figure 4, d) features a second smaller peak of 38% in the distribution, appearing at around 16:00. This indicates a second sleep episode, a nap, which appears between the end of the main night-time sleep and start of the night shift. This nap is also seen in the raster plots for the participants 53 and 58 in Figure 3. The modelpredicted distribution does not have this second peak, indicating that the nap is not reproduced for any of the participants.

Circadian phase

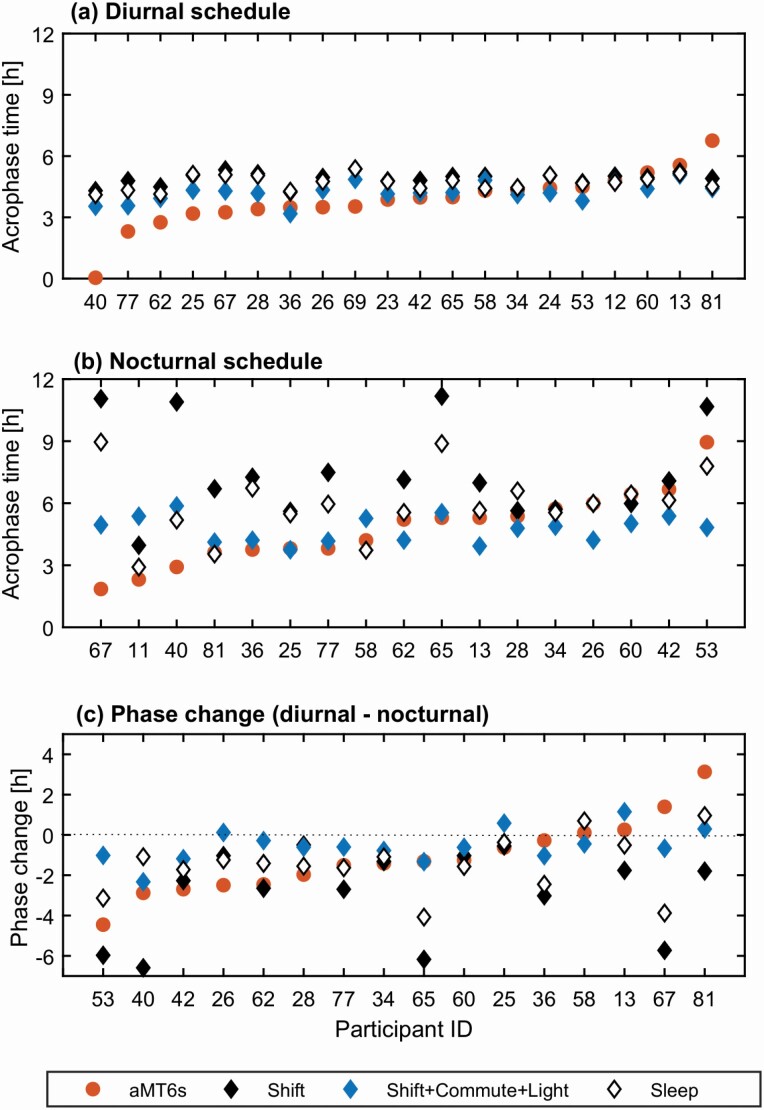
Of the 21 nurses, 16 were monitored during both diurnal (day/evening shifts and days off) and nocturnal (night shifts) schedules and have acrophase reported for both schedules. Two nurses were on both diurnal and nocturnal schedules but missing acrophase measurement on one of them, and three were on diurnal schedules only (Table 2 and Figure 5). For most evaluation constraints, during both diurnal and nocturnal schedules, the model predicts average aMT6s acrophase at a later time than that observed in the data (Table 2). The largest mean absolute error is obtained using the Shift constraint, with the values of 1.26$\pm$1.02 h and 3.01$\pm$ 2.98 h for the diurnal and nocturnal schedules, respectively. The errors are reduced once individual light information is added to the model. The lowest mean absolute error on the diurnal schedule is obtained for the Shift + Commute + Light constraint (0.87$\pm 0$.83 h), closely followed by Sleep + Light (0.90$\pm$0.88 h) and Shift + Light (0.96$\pm$0.84 h). For the nocturnal schedule the lowest absolute error is for Sleep + Light constraint (1.41$\pm$1.19 h), followed by Shift + Commute + Light (1.42$\pm$1.19 h) and Sleep (1.45$\pm$1.82 h). Shift + Light produces the lowest absolute prediction error (1.31$\pm$1.13 h) for the phase change followed by Sleep, Shift + Commute + Light, and Sleep + Light, while the Shift condition results in the highest absolute error and standard deviation of the error (3.05$\pm 4$.22 h).

Table 2.

Comparison of study data and model predictions for the urinary aMT6s acrophase. aMT6s was measured during the diurnal (day and evening shifts) and nocturnal (night shifts) schedules. The rows include mean and standard deviation (std) of error and absolute error and the percentage of individual predictions that fall within plus minus one hour of the study data

		Diurnal (N = 20)	Nocturnal (N = 17)	Phase change (N = 16)
Study data	Mean acrophase ± SD (h)	3.86 ± 1.35	4.78 ± 1.77	−1.15 ± 1.83
Shift	Mean acrophase ± SD (h) Mean error ± SD /9h) Mean absolute error ± SD (h) Percent within ± 1 h	4.88 ± 0.32 −1.02 ± 1.27 1.26 ± 1.02 50 %	7.73 ± 2.45 −2.95 ± 3.04 3.01 ± 2.98 29 %	−1.63 ± 5.38 −0.48 ± 5.24 3.05 ± 4.22 31%
Shift + Light	Mean acrophase ± SD (h) Mean error ± SD (h) Mean absolute error ± SD (h) Percent within ± 1 h	4.37 ± 0.39 −0.51 ± 1.16 0.90 ± 0.88 65 %	5.29 ± 0.51 −0.51 ± 1.89 1.55 ± 1.13 35 %	−0.95 ± 0.80 0.20 ± 1.75 1.31 ± 1.13 50%
Shift + Commute	Mean acrophase ± SD (h) Mean error ± SD (h) Mean absolute error ± SD (h) Percent within ± 1 h	4.51 ± 0.66 −0.65 ± 1.27 1.10 ± 0.89 50 %	6.04 ± 2.49 −1.26 ± 2.85 2.21 ± 2.14 35 %	−1.82 ± 2.30 −0.67 ± 2.55 1.91 ± 1.76 44%
Shift + Commute + Light	Mean acrophase ± SD (h) Mean error ± SD (h) Mean absolute error ± SD (h) Percent within ± 1 h	4.22 ± 0.46 −0.36 ± 1.16 0.87 ± 0.83 65 %	4.74 ±0.63 0.04 ± 1.89 1.42 ± 1.19 47 %	−0.55 ± 0.82 0.61 ± 1.61 1.38 ± 0.97 50%
Sleep	Mean acrophase ± SD (h) Mean error ± SD (h) Mean absolute error ± SD (h) Percent within ± 1 h	4.70 ± 0.36 −0.85 ± 1.28 1.15 ± 1.00 55 %	5.95 ± 1.65 −1.17 ± 2.02 1.45 ± 1.82 53 %	−1.50 ± 1.40 −0.35 ± 1.88 1.35 ± 1.31 50%
Sleep + Light	Mean acrophase ± SD (h) Mean error ± SD (h) Mean absolute error ± SD (h) Percent within ± 1 h	4.39 ± 0.42 −0.53 ± 1.17 0.96 ± 0.84 65 %	4.78 ± 1.77 0.01 ± 1.88 1.41 ± 1.19 53 %	−0.46 ± 0.86 0.69 ± 1.64 1.41 ± 1.05 44%

Figure 5.

Comparison of study data and representative model predictions for aMT6s acrophase. Model predictions for three evaluation constraints are shown: Shift, Shift + Commute + Light and Sleep as indicated in the legend. (a) aMT6s acrophase data and predictions for participants during diurnal schedule. (b) aMT6s acrophase data and predictions for participants during night shifts, i.e. nocturnal schedule. (c) Acrophase difference between the diurnal and nocturnal schedules. Negative values correspond to phase delay and positive to phase advance. Only 16 of the 21 participants have both diurnal and nocturnal acrophase data. Participant 11 did not have acrophase measured on the diurnal schedule, 12, 24, and 69 did not have night shifts, and 23 had night shifts but acrophase was only measured for the diurnal schedule.

Individual phase predictions. The later prediction of mean acrophase on the diurnal schedule compared to the study data comes from approximately half of the participants, IDs 40–69 in Figure 5a, while there is better overlap for the other participants (IDs 23-13). One participant’s (81) acrophase is predicted ~2.2 h earlier than the data. Inclusion of individual light reduces the discrepancy between the model and the study data for 14 out of 20 participants, with the percentage of individual acrophases predicted within $\pm$1 h of the data increasing from 50% for Shift and Shift + Commute, and 55% for Sleep to 65% for Shift + Commute + Light, Shift + Light, and Sleep + Light. On the nocturnal schedule in Figure 5b, both Shift and Sleep conditions result in a wider range of discrepancy between the model and the data (e.g. see ID 67, 40, 65) compared to the Shift + Commute + Light case. The percentage of participants’ acrophase predicted within $\pm$1 h was lowest for Shift at 29$\mathrm{\%}$ and highest (53%) for both Sleep and Sleep + Light, followed closely by Shift + Commute + Light (47%). For the phase change in Figure 5c, of the 16 participants who were studied under a diurnal and then a nocturnal shift schedule, 11 delayed, three did not change (phase shift less than 15 min), and two advanced. All evaluation constraints reproduce the direction of change for a majority of participants (12–13 out of 16 depending on the constraint used).

Alertness

The model predicts sleepiness and performance using a linear weighted sum of the homeostatic and circadian drives (Postnova et al., 2018), so that both sleep and circadian phase predictions feed into the prediction of subjective sleepiness on the Karolinska Sleepiness Scale (KSS) and sustained attention measured with the Psychomotor Vigilance Task (PVT).

Subjective sleepiness, KSS. The absolute prediction error for KSS and its standard deviation were similar across all six evaluation constraints for both day and night shifts (Table 3). On the day shift the mean absolute prediction error varied from 1.45$\pm$0.99 for Shift + Commute + Light to 1.55$\pm$0.96 for Sleep. On the night shift the lowest absolute errors of 1.50$\pm$1.11 and 1.51$\pm$1.04 were obtained with the Shift + Light and Shift + Commute + Light constraints, while the highest errors of 1.64$\pm$1.30 and 1.66$\pm$1.28 were obtained with Sleep and Sleep + Light constraints respectively. Overall, there is no one inputs constraint combination that is decidedly better than others—all produce similar prediction errors. The differences in the absolute error between constraints are small compared to the standard-deviation of absolute error for each constraint. The mean (not absolute) error is less than 1 KSS score for all input constraints, but the standard deviation ranged from 1.75 to 2.09. The percentage of participants’ KSS scores predicted within $\pm$1 varied between 56$\mathrm{\%}$ and 60$\mathrm{\%}$ on the day shifts and 48$\mathrm{\%}$ and 52$\mathrm{\%}$ on the night shifts.

Table 3.

Comparison of study data and model predictions for KSS during day and night shifts. The rows for model predictions include mean and standard deviation (SD) of error and of absolute error relative to the study data and the percentage of individual predictions that fall within plus minus one KSS score of the study data

		Day shift (N = 20)	Night shifts (N = 17)
Shift	Mean error ± SD	0.30 ± 1.94	0.58 ± 1.77
	Mean absolute error ± SD	1.53 ± 1.11	1.54 ± 1.05
	Percent within ± 1	58 %	52 %
Shift + Light	Mean error ± SD	0.53 ± 1.90	0.26 ± 1.83
	Mean absolute error ± SD	1.52 ± 1.25	1.50 ± 1.07
	Percent within ± 1	60%	51%
Shift + Commute	Mean error ± SD	−0.34 ± 1.75	0.50 ± 1.84
	Mean absolute error ± SD	1.49 ± 0.96	1.55 ± 1.11
	Percent within ± 1	58 %	52 %
Shift + Commute + Light	Mean error ± SD	−0.08 ± 1.76	0.25 ± 1.82
	Mean absolute error ± SD	1.45 ± 0.99	1.51 ± 1.04
	Percent within ± 1	56 %	50 %
Sleep	Mean error ± SD	−0.40 ± 1.79	−0.19 ± 2.09
	Mean absolute error ± SD	1.55 ± 0.96	1.64 ± 1.30
	Percent within ± 1	56 %	48 %
Sleep + Light	Mean error ± SD	−0.36 ± 1.79	−0.38 ± 2.07
	Mean absolute error ± SD	1.53 ± 0.97	1.66 ± 1.28
	Percent within ± 1	56 %	49 %

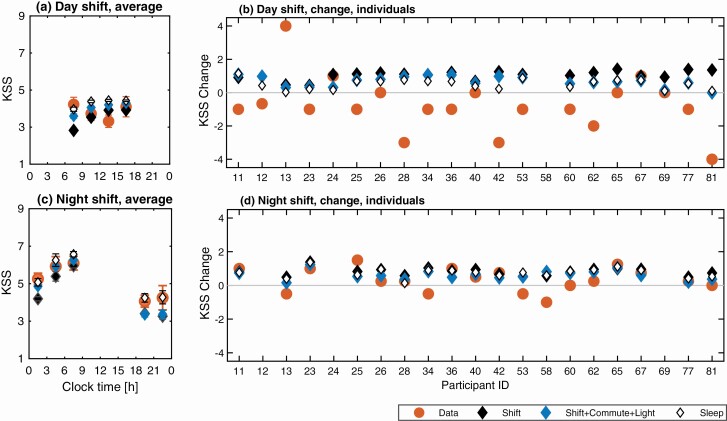
The averaged KSS profiles in Figure 6, a, c show nearly flat KSS across the day shift and rising KSS values during the night shift for both the model and the data. The biggest discrepancy in the predicted and experimental average profiles was observed during the first 3 h of the day shift where higher KSS is reported in the study data compared to the model.

Figure 6.

Comparison of study data and model predictions for subjective sleepiness on the KSS. Model predictions for three evaluation constraints are shown: Shift, Shift + Commute + Light, and Sleep. (a) Group average KSS profile across all participants and data points on the day shift against clock time. (b) Individual predictions and study data for KSS change between the start and end of day shift ($KS{S}_{end}-KS{S}_{start}$). (c) Group average KSS profile across all participants and data points on the night shift. (d) Predictions and study data for KSS change between the start and end of the night shift for each participant. In (a, c), the KSS values are binned in 3-h blocks and are plotted in the middle of each bin. Glyphs show mean values within each bin with bars indicating plus and minus the standard error in the mean. Blank spaces indicate missing data, typically due to the shift type being absent in a nurse’s schedule.

On the day shift in Figure 6, b, three out of 20 participants reported increased sleepiness (IDs 24, 67, 13) towards the end of the shift, four reported no change (IDs 26, 40, 65, 69) and the remaining 13 participants reported a decrease of subjective sleepiness. The model predicts a narrower range of KSS change on the day shift than that seen in the study data. All input constraints result in either no change in KSS between the start and end of the day shift or an increase of KSS towards the shift’s end as the homeostatic drive increases. The individual KSS trend on the day shift is correctly predicted for seven participants. The discrepancy is likely explained by the lack of sleep inertia component in the model. Conversely, on the night shift (Figure 6, d) the model predicts an increase of KSS towards the end of the shift for all participants, which agrees with the data for 12 of the 17 participants. The overall change of KSS is better predicted on the night shift than on the day shift, which is also reflected in the lower absolute error and standard deviation of the error on the night shift for Shift, Shift + Light, Shift + Commute + Light, and Sleep + Light constraints (Table 3).

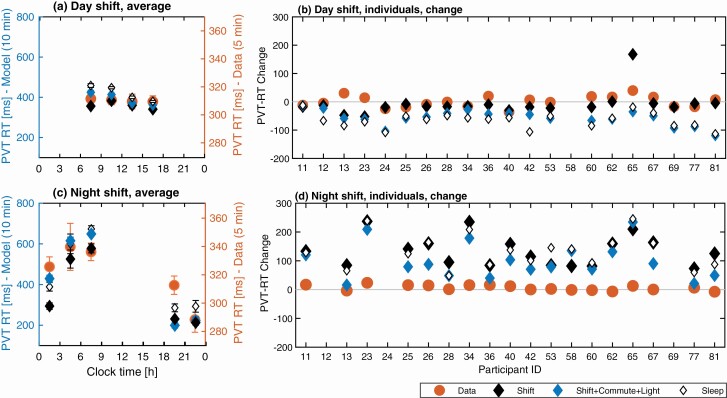
Objective performance, PVT. Direct quantitative comparison for predicted and experimentally measured PVT outputs is not feasible in this study because the model was calibrated for a 10-min test while the experimental study reported results for a 5-min test. It is useful, however, to compare qualitative trends for changes in PVT metrics during shifts, i.e. increase, decrease or no change, as these should not be strongly affected by the duration of the test.

Figure 7 shows mean PVT reaction times (RT) for the group average and change in PVT RT for individuals as predicted by the model (10-min test) and measured in the experiment (5-min) on the day and night shifts. The study data shows nearly flat group average PVT RT on the day shift (Figure 7, a), but an increasing trend on the night shift (Figure 7, c). This is reproduced by the model with a weak decrease of RT predicted on the day shift (~60 ms range) compared to stronger increase on the night shift (~500 ms range). Individual PVT RT on the day shift (Figure 7, b) decreased for 11 nurses and increased for nine. The model correctly predicted these trends for 11 of the 20 participants when using Sleep-based and Shift + Commute + Light constraints, and for 13 participants when using the other Shift-based constraints. On the night shift, Sleep-based constraints and Shift + Commute + Light predicted an increase in PVT RT on the night shift for all 18 individuals. Overall, the increase of PVT RT on night shifts is correctly predicted for 10 of the 17 participants but the range of change in the data are much smaller because of the shorter test duration.. Similar dynamics were observed for PVT lapses (Figure S1).

Figure 7.

Comparison of study data and model predictions for objective performance measured with the PVT RT. Model predictions for three evaluation constraints are shown: Shift, Shift + Commute + Light, and Sleep. (a) Group average PVT RT profile across all participants on the day shift against clock time. (b) Individual predictions and study data for PVT RT change between the start and end of day shift $(PVTR{T}_{end}-PVTR{T}_{start}$). (c) Group average PVT RT profile on the night shift. (d) Predictions and study data for PVT RT change between the start and end of the night shift for each participant. In (a, c), the PVT RT values are binned in three-hour blocks and are plotted in the middle of each bin. Glyphs show mean values within each bin with bars indicating plus and minus the standard error in the mean. The experimental data (Data) are plotted against the range on the right Y-axis, model predictions are shown against the range on the left Y-axis in (a) and (c). The y-axis scales are identical in (b) and (d).

Discussion

In occupational settings it is often necessary to predict alertness on future shift schedules to guide development of safe rosters and minimize risk of accidents and errors at work. This requires prospective prediction of alertness and thus requires prospective prediction of sleep and circadian timing [33]. The Shift-based constraints in our model allow for such prospective predictions and we used Sleep-based constraints for comparison. As expected, Sleep and Sleep + Light resulted in higher sleep overlap values (e.g. normalized overlap of 0.90 ± 0.06 for Sleep, see Table 1 for corresponding percentage values) but Shift-based constraints performed well too with normalized overlap for Shift being 0.53 ± 0.15. Likewise, the Sleep- and Shift-based constraints produce similar KSS prediction errors on both day and night shifts, and similar qualitative trends for objective performance measured with PVT. The model with Shift-based constraints predicted up to 60% of KSS scores within ±1 on the day shift and up to 52% on the night shift, while using Sleep resulted in 56% and 48% respectively. For circadian phase, light is the key input needed to reduce prediction error with both Shift- and Sleep-based constraints producing similar results when light was included. The model using Shift + Commute + Light, and Sleep + Light predicted 65% of acrophase values within ±1 h of study data on the diurnal schedule and 47% vs. 53% on the nocturnal schedule, respectively.

Several other models previously tested predictions of both sleep and alertness in shiftwork settings [15, 30–35, 53, 54]. The three-process model was calibrated to predict group average sleep [35] and applied to predict KSS scores during rapidly rotating shift schedules of paper mill workers [34]. This study used shift times as input and showed accurate predictions for KSS on night and afternoon shifts but not on the morning shifts. Similarly to our study they found that using individuals’ sleep times as an input does not improve predictions of KSS compared to using shift information only. This model was further modified and applied to predict KSS and sleep in aircrew [15]. Individual predictions, however, were not reported. Similarly, Darwent et al. [24, 32, 33] developed a probabilistic model to predict sleep distributions in pilots during transmeridian flight schedules [32], which was later adjusted and calibrated based on data from train drivers [33]. When using the train drivers’ shift times as the only input their model predicted sleep-wake percentage overlap of 85% across all participants. Predictions of alertness, however, were not presented. We found similar state overlap values for our group of ICU nurses when using Shift constraint (87 ± 5%). Addition of other constraints had marginal impact on the sleep overlap.

Circadian phase is the second physiological factor determining alertness dynamics, together with sleep. Most alertness models do not include prediction of individual circadian phase. In our study, the most accurate circadian phase predictions were obtained when light was used as one of the input constraints. Further improvement in predictions is likely with access to a longer period of light data for diurnal schedules to entrain the model’s circadian pacemaker. In this study only 3–6 days of data were typically available before the first circadian phase prediction. We had previously tested different models for their ability to predict individual circadian phase in real-world shiftworkers and healthy nocturnal sleepers [51, 52, 55]. The limit cycle oscillator model with photic and non-photic time cues (the same as the circadian component in the current analysis) showed the lowest prediction error for aMT6s acrophase during shiftwork [51]. Compared to that earlier limit cycle oscillator study, the current model predicted a later mean circadian phase compared to the study data on the diurnal schedule and demonstrated slightly larger prediction error. This comes from (1) using a slightly different set of participants to allow analysis of sleep distributions (we did not include registrars on 12 h/12 h schedules), and (2) having different initial conditions in the two models. In Stone et al.[51] we used the average diurnal mid-sleep time to fit initial conditions for each individual, while in the present study we assumed no knowledge of future dynamics at the start of simulations.

Most discrepancies between our model predictions and the study data were seen for individuals whose dynamics can be described as atypical, e.g., short habitual sleep time, earlier/later habitual sleep, or high sleepiness on diurnal schedules. There are, however, some systematic errors in the model predictions. One is the failure to predict naps before night shift when transitioning from a day off. Nearly a third of participants demonstrate this behavior, which is not replicated in the model. A similar shortcoming was observed in the three-process model [34]. A potential explanation is that this afternoon nap is choice-driven (as opposed to a physiological need) in preparation for the night shift to ensure shorter time since wake while on shift. Another discrepancy is that the model predicts lower average KSS values at the start of the day shift compared to the study data. This is likely explained by sleep inertia experienced by the participants due to early start of the shift relative to their circadian timing, which is not yet incorporated in our model.

So far, none of the existing alertness models have demonstrated individual predictions that account for differences in both the environment and the physiology. Our use of the model with default parameter values and a selection of input constraints such as shift, commute, and light, have demonstrated accurate predictions for more than half of the participants. Other external factors like caffeine, stress, and type of task on shift, also affect alertness dynamics and including those may further improve predictions [56, 57]. To incorporate the variability in physiology, model parameters need to be adjusted separately for each individual. Several modelling studies demonstrated how changes in model parameters manifest as differences in sleep-wake dynamics. For example, Skeldon et al. [58, 59] showed how variation of the circadian and homeostatic parameters allows reproduction of changing sleep patterns due to aging. Similarly, Phillips et al. [60] identified parameters that can account for different chronotypes. The difficulty in applying these findings to individuals is that different sets of parameters may produce similar dynamics under some conditions but distinct dynamics under others. Other studies used statistical modelling to fit individual parameters and predict PVT during sleep deprivation [29, 61–64] and sleep restriction [64] using prior PVT measures. These, however, do not yet account for circadian misalignment or environmental differences.

Overall, incorporating individual shift, commute and light constraints in the model, with parameters set to a typical individual, allowed for accurate predictions of alertness, circadian phase, and sleep for more than half of the participants. For the other half, accurate individual predictions require accounting for physiological differences. Thus, while the model with the default parameters is successful at predicting group average dynamics in the real world, its application to individual predictions requires additional calibration. It should be noted that our study included a relatively small number of participants (N = 21) so specific details beyond the broad general agreement between model predictions and study data should not be over-interpreted. A future study testing the model against a larger number of participants would be useful to draw stronger conclusions on the differences among predictions with various input constraints. Quantitative comparison for objective measures of performance, such as PVT RT or lapses, is also required in the future as subjective measures like KSS are inherently noisy and may not reflect objective underlying alertness.

To enable external use and testing of the model of arousal dynamics, we have incorporated it in a web-based application programming interface, Alertness API, which can be found at https://www.alertnessapi.com. This interface allows simulation of customized work and wake schedules, including shiftwork and transmeridian travel as well as chronobiological and sleep experimental protocols. Both environmental constraints presented in this study and model parameters are enabled as inputs to the Alertness API with customizable outputs including alertness measures, sleep, and circadian rhythms.

Statement of Contribution

S.A.K. developed all codes, and analysed model predictions and their comparison to experimental data, S.P. designed the study, S.P. and S.A.K. wrote the manuscript. M.M., T.L.S., J.E.S., S.G., M.D.M. collected and analysed experimental data. M.E.H., S.M.W.R, S.W.L., and T.L.S. designed the experimental protocol. All authors edited the manuscript.

Disclosure Statement

Financial disclosure: S.A.K. has no conflicts to report. M.M. served as a Project Leader in the CRC for Alertness, Safety and Productivity. J.E.S. has no conflicts to report. M.E.H. served as a Theme Leader in the CRC for Alertness, Safety and Productivity, which funded this work; and has received grants from Prevention Express, ResMed Foundation and TEVA, and equipment support for research from Optalert and Seeing Machines which are not related to the work reported in this paper. S.G. has no conflicts to report, M.D.M. has no conflicts to report. S.W.L. has had a number of commercial interests in the last 3 years (2018–2020). His interests were reviewed and managed by Brigham and Women’s Hospital and Partners HealthCare in accordance with their conflict of interest policies. He was a Program Leader for the CRC for Alertness, Safety and Productivity, Australia, which funded this work. No other interests are directly related to the research or topic reported in this paper but, in the interests of full disclosure, are outlined below. S.W.L. has received consulting fees from the BHP Billiton, EyeJust Inc., Noble Insights, Rec Room, Six Senses, Stantec and Team C Racing; and has current consulting contracts with Akili Interactive; Apex 2100 Ltd; Consumer Sleep Solutions; Headwaters Inc.; Hintsa Performance AG; KBR Wyle Service, Light Cognitive; Lighting Science Group Corporation; Look Optic; Mental Workout and View Inc. He has received honoraria and travel or accommodation expenses from Emory University, Estée Lauder, Ineos, MIT, and Roxbury Latin School, and travel or accommodation expenses (no honoraria) from IES, Mental Workout, Solemma, and Wiley; and royalties from Oxford University Press. He holds equity in iSleep pty. He has received an unrestricted equipment gift from F. Lux Software LLC, a fellowship gift from Stockgrand Ltd and holds an investigator-initiated grant from F. Lux Software LLC and a Clinical Research Support Agreement with Vanda Pharmaceuticals Inc. He is an unpaid Board Member of the Midwest Lighting Institute (non-profit). He holds a process patent (pending) for “Method and system for generating and providing notifications for a circadian shift protocol” through Mental Workout. He has served as a paid expert in legal proceedings related to light, sleep and health. S.M.W.R. served as a Program Leader for the CRC for Alertness, Safety and Productivity, Australia, which funded this work. He reports grants from Vanda Pharmaceuticals, Philips Respironics, Cephalon, Rio Tinto and Shell, and has received equipment support and consultancy fees through his institution from Optalert, Tyco Healthcare, Compumedics, Mental Health Professionals Network, and Teva Pharmaceuticals, which are not related to this paper. T.L.S. served as a Project Leader in the CRC for Alertness, Safety and Productivity which has funded this work. She has received equipment support through her institution from Philips Respironics, consultancy fees from Vanda Pharmaceuticals, and research funding from Teva Pharmaceuticals and Qantas Airways Ltd, which are not related to this paper. S.P. served as a Theme Leader and previously as a Project Leader in the CRC for Alertness, Safety and Productivity which has funded this work. She reports research grants from Qantas Airways Ltd, which are not related to this paper.

Non-financial disclosure: Authors have no non-financial conflicts to report.