Abstract
Motivation
Recent technological advances produce a wealth of high-dimensional descriptions of biological processes, yet extracting meaningful insight and mechanistic understanding from these data remains challenging. For example, in developmental biology, the dynamics of differentiation can now be mapped quantitatively using single-cell RNA sequencing, yet it is difficult to infer molecular regulators of developmental transitions. Here, we show that discovering informative features in the data is crucial for statistical analysis as well as making experimental predictions.
Results
We identify features based on their ability to discriminate between clusters of the data points. We define a class of problems in which linear separability of clusters is hidden in a low-dimensional space. We propose an unsupervised method to identify the subset of features that define a low-dimensional subspace in which clustering can be conducted. This is achieved by averaging over discriminators trained on an ensemble of proposed cluster configurations. We then apply our method to single-cell RNA-seq data from mouse gastrulation, and identify 27 key transcription factors (out of 409 total), 18 of which are known to define cell states through their expression levels. In this inferred subspace, we find clear signatures of known cell types that eluded classification prior to discovery of the correct low-dimensional subspace.
Availability and implementation
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Recent technological advances have resulted in a wealth of high-dimensional data in biology, medicine and the social sciences. In unsupervised contexts where the data are unlabeled, finding useful representations is a key step toward visualization, clustering and building mechanistic models. Finding features which capture the informative structure in the data has been hard, however, both because of unavoidably low data density in high dimensions (the ‘curse of dimensionality’; Donoho, 2000) and because of the possibility that a small but unknown fraction of the measured features define the relevant structure (e.g. cluster identity) while the remaining features are uninformative (Chang, 1983; Witten and Tibshirani, 2010).
Identifying informative features has long been of interest in the statistical literature. When the data are labeled, allowing for a supervised analysis, there are successful techniques for extracting important features using high-dimensional regressions. When there is no labeled training data, unsupervised discovery of features is difficult. Standard feature extraction methods such as PCA are effective in reducing dimensionality, yet do not necessarily capture the relevant variation (Chang, 1983; and see Supplementary Fig. S1). Other methods (Witten and Tibshirani, 2010; Xu et al., 2005) attempt to co-optimize a cost function depending on both cluster assignments and feature weights, which is computationally difficult and tied to specific clustering algorithms (see section on existing methods). Feature extraction guided by clustering has also been effective as a preprocessing step for regression tasks. In Coates and Ng (2012), classification and regression is done with data represented in the basis of centroids found with K-means. In Ngiam et al. (2011), features are constructed such that representations of data points are sparse, but no explicit discrimination is encoded between clusters beyond a sparsity constraint. We consider here an example where clusters are distinguished from each other by sparse features, but overall representations of each data point is not necessarily sparse in this new basis. We show here that optimal features are discovered by their ability to separate pairs of clusters, and we find them by averaging over proposed clustering configurations.
Using gene expression data to understand processes in developmental biology highlights this challenge. In a developing embryo, multipotent cells make a sequence of decisions between different cell fates, eventually giving rise to all the differentiated cell types of the organism. The goal is both to determine the physiological and molecular features that define the diversity of cell states, and to uncover the molecular mechanisms that govern the generation of these states. Decades of challenging experimental work in developmental biology suggests that a small fractions of genes control specific cell fate decisions (Gilbert, 2016; Graf and Enver, 2009; Takahashi and Yamanaka, 2006). Recent experimental techniques measure tens of thousands of features—gene expression levels—from individual cells obtained from an embryo over the course of development, producing high-dimensional datasets (Briggs et al., 2018; Farrell et al., 2018). Clustering these data to extract cell states and identifying the small fractions of key genes that govern the generation of cellular diversity during development has been difficult (Furchtgott et al., 2017; Kiselev et al., 2019). However, mapping cellular diversity back to specific molecular elements is a crucial step toward understanding how gene expression dynamics lead to the development of an embryo.
Here, we show that as the fraction of relevant features decreases, existing clustering and dimensionality reduction techniques fail to discover the identity of relevant features. We show that when the linear separability of clusters is restricted to a subspace, the identity of the subspace can be found without knowing the correct clusters by averaging over discriminators trained on an ensemble of proposed clustering configurations. We then apply it to previously published single-cell RNA-seq data from the early developing mouse embryo (Pijuan-Sala et al., 2019), and discover a subspace of genes in which a greater diversity of cell types can be inferred. Further, the relevant subspace of genes that we discover not only cluster the data but are known from the experimental literature to be instrumental in the generation of the different cell types that arise at this stage. This approach provides unsupervised sparse feature detection to further mechanistic understanding and can be broadly applied in unsupervised data analysis.
2 Approach
2.1 Uninformative data dimensions corrupt data analysis
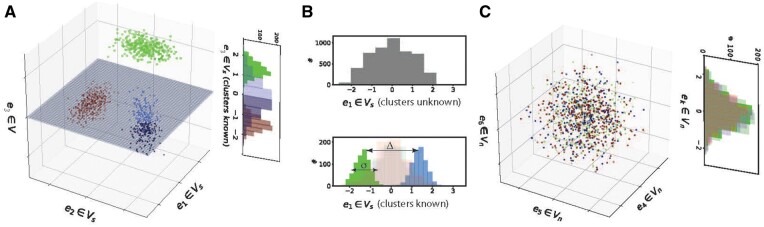
To understand how the decreasing fraction of relevant features affects data analysis, consider data from Ktrue classes in a space V with dim(V) = D features. Assume that V can be partitioned into two subspaces. First, an informative subspace Vs of dimension Ds, in which the Ktrue clusters are separable. And second, an uninformative subspace Vn with dimension in which the Ktrue clusters are not separable. An example of such a distribution is shown inFigure 1 with two clusters, Ds = 1 and Dn = 2.
Fig. 1.
Gaussian data with unit variance shown along three axes. The marginal distribution of contains signature of distinct clusters, with a bimodal marginal distribution where each mode corresponds to a cluster. Here, the clusters are linearly separable along the e1 axis. The marginal distributions of and are unimodal, and do not linearly separate groups of data points. Here, we designate as part of Vs as it contains multimodal signal, and do not. The three axes shown here represent a subspace of a D > 3-dimensional distribution
The correlation between the distances computed in the full space V with that in the relevant subspace Vs scales as (see Supplemental Text). When the fraction of relevant features is small, or equivalently , correlations between samples become dominated by noise. In this regime, without the correct identification of Vs, unsupervised analysis of the data is difficult, and typical dimensionality reduction techniques (PCA, ICA, UMAP, etc.) fail. We demonstrate this by constructing a Gaussian mixture model with 7 true clusters which are linearly separable in a subspace Vs with dimension Ds = 21, and drawn from the same distribution (thus not linearly separable) in the remaining dimensions. As the ratio increases, the separability of the clusters in various projections decreases (Supplementary Fig. S1).
In many cases, identifying the ‘true’ Vs may be challenging. However, eliminating a fraction of the uninformative features and moving to a regime of smaller could allow for more accurate analysis using classical methods. We next outline a method to weight dimensions to construct an estimate of Vs and to reduce .
2.2 Minimally informative features: the limit of pairwise informative subspaces separating clusters
To develop a framework to identify the relevant features, consider data where samples are represented in the measurement basis . Assume that the data is structured such that each data point is a member of one of Ktrue clusters, . Let be the subspace of V in which the data points belonging to the pair of clusters Cl, Cm are linearly separable. Let be unit vector normal to the max-margin hyperplane separating clusters Cl and Cm. In the space orthogonally complement to , the two clusters are not linearly separable. One can similarly define such subspaces and associated hyperplanes , one for each pair of clusters in . We define a weight for each dimension by its component on the s:
| (1) |
Knowing the cluster configuration would allow us to directly compute by finding max-margin classifiers and using Equation 1. Conversely, knowing would allow for better inference of the cluster configuration because restriction to a subspace in which would move to a regime of smaller . Existing work has focused on finding and simultaneously, through either generative models or optimizing a joint cost function. Such methods either rely on context specific forward models, or tend to have problems with convergence on real datasets [see Witten and Tibshirani (2010) and section on existing methods].
We focus here on estimating when is unknown. We consider the limit in which the dimensions of each take on the smallest possible value of 1, which maximizes the ratio for all l, m. Further, this limit resides in the regime of large where conventional methods fail. We further consider the limit where the intersection between any pair of the subspaces in is null. In this limit, the marginal distribution of all of the data in any one of the can be appear unimodal due to a dominance of data points from the clusters for which this subspace is irrelevant, despite data in the clusters Cl, Cm showing a bimodal signature in this subspace. Hence, finding the identity of the informative subspaces by distinguishing moments of the marginal distribution is not possible as grows or data density decreases, even in the case of normally distributed data (Fig. 2). In this limit, the values of gd corresponding to informative dimensions are , and 0 for uninformative dimensions. Our reason for studying this limit of pairwise separability is that an algorithm that can find the informative subspaces of V in these limits should be able to do so in instances where in the dimensions of are larger than one and intersecting.
Fig. 2.
For K clusters with multimodal subspaces with , we consider the limit as each has minimal dimension (=1) and are non-intersecting. (A) shows a Gaussian example of a collection of one-dimensional pairwise informative subspaces, which are uninformative for clusters . Here, e1 is multimodal in the blue and green clusters, but not red, e2 is multimodal in the red and blue clusters, but not green, and e3 is multimodal in the red and green clusters, but not blue. (B) Despite containing multimodal signature, non-intersecting pairwise informative subspaces can corrupt marginal distributions to hide separability (top). Same data with points colored by cluster, where separation of means is denoted by Δ, and the variance of distributions in their informative dimensions is given by σ. (bottom). (C) shows dimensions that are uninformative for all clusters
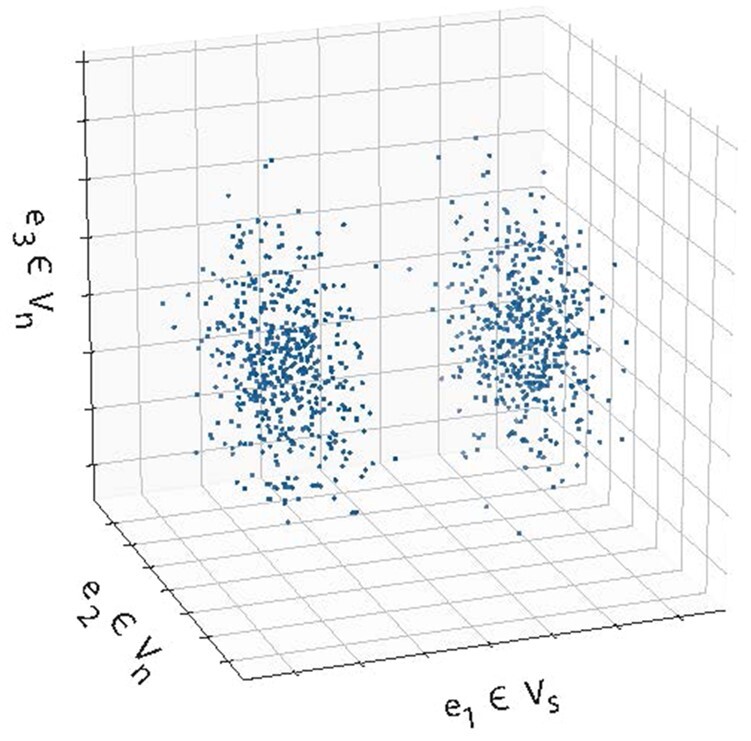
We generate data such that the mean of the marginal distributions of clusters Cl and Cm along a specific whose span defines are separated by Δ , and the sample variance of each cluster’s marginal distribution is σ. The marginal distribution of cluster Cl in all other dimensions, i.e. , is unimodal with zero mean and unit variance. Therefore, in all, there are dimensions (one dimension for each pair of clusters) in each of which a pair of clusters are linearly separable, while the other clusters are not, and dimensions where all clusters are drawn from the same unimodal distribution. Normalizing each feature to have unit variance leaves one free parameter, , which controls the pairwise separability of clusters within their informative subspace (Fig. 2B). Indeed, computing pairwise distances between data points generated from 7 clusters and does not reveal cluster identity (Fig. 3A).
Fig. 3.
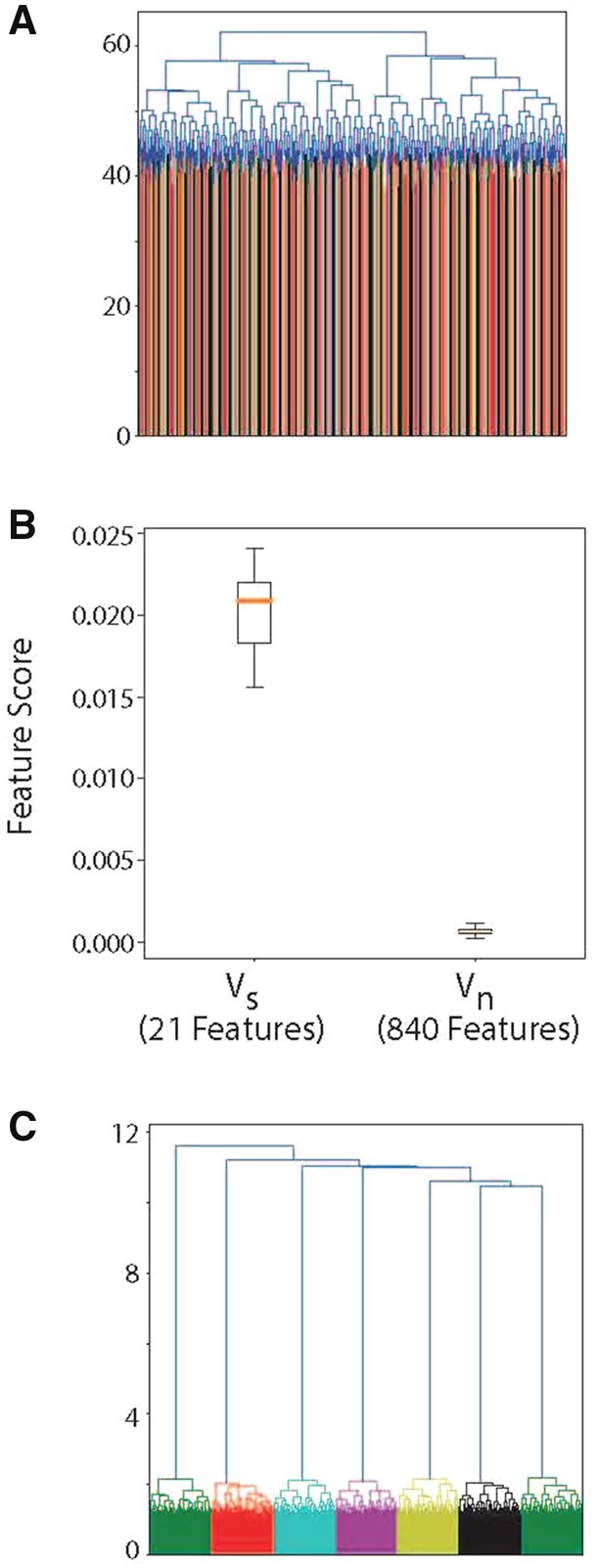
Gaussian data were generated in which 1400 data points from 7 clusters are pairwise distinguishable in only one feature, and 840 features contain no information as to cluster identity (thus ). (A) Computing pairwise distances between points and constructing a dendrogram does not resolve the existence of clusters. (B) Ensemble of 1000 proposal clusters is constructed using K-means, with , and max-margin classifiers are constructed for each pair of cluster per proposal. Each feature is scored according to how frequently it separates two proposed clusters. A histogram of the scores of each feature is shown. Features in the informative subspace (Vs), have substantially higher scores than those in the uninformative subspace (Vn). (C) A dendrogram computed in the space weighted by feature scores reveals the existence of seven clusters
3 Materials and methods
3.1 Identifying a sparse set of pairwise informative features
We develop an approach to estimate the weight vector knowing neither the identity of points belonging to each cluster nor the total number of clusters. To estimate , we propose to average estimates of over an ensemble of clustering configurations. Specifically, we sample an ensemble of possible clustering geometries, , from each of which a collection of max-margin classifiers are computed to compute using Equation 1:
| (2) |
where is the probability of a clustering configuration given the data. This sum can be approximated numerically through a sampling procedure, where cluster proposals are sampled according to
| (3) |
where Kp is the number of clusters, and is our prior over the number of proposal clusters.
Consider one such proposed clustering configuration with Kp clusters, denoted by where each indexes the data points that belong to the lth proposed cluster. For this proposed clustering configuration, we compute a set of classifiers that separate each pair of clusters. Based on the assumption that is sparse, or equivalently that the true are low dimensional, we impose an L1-regularized max-margin classifier to compute from the data X and the proposed cluster configuration as in the study by Zhu et al. (2003):
| (4) |
where indicates the positive component, and λ is a sparsity parameter. We set λ such that the expected number of non-zero components in each is 1. Specifically, we sample T cluster configurations by clustering on random subsets of the data, and average the weights of max-margin classifiers over this ensemble:
| (5) |
This procedure can be carried out explicitly as follows:
(N instances in D dimensions).
For t < T:
Pick nsubsample points from
Sample
Cluster into Kp clusters
- For :
- For d < D:
Return
For a graphical representation of this algorithm, and a plain word description (see Supplementary Material). A python implementation is available at github.com/smelton/SMD.
While computing pairwise distances in the full-space V lacks structure (Fig. 3A), this algorithm produces substantially higher weights for the informative features on simulated data (Fig. 3B). Comparisons of pairwise distances in the reduced subspace found by the algorithm reveal richer structure and the presence of seven distinct clusters (Fig. 3C). The algorithm reliably discovers the correct set of informative features while using both K-means and Hierarchical clustering to construct the proposal clusters, and for a range of the prior over Kp (Supplementary Fig. S2).
3.2 Scaling of inferred weights with dimensionality and data density
In the challenging regime of large , this algorithm can robustly identify key features in the data. In particular, as D increases, there is a scaling of the algorithms performance as a function of , as well as a dependence on the number of data points N. First, we sample a variety of proposal clusters , each with Kp clusters drawn from a prior P(K). Using counting arguments (see Supplemental Text), we can estimate the frequency of proposed aligning with informative with a bimodal signature and uninformative features without. This ratio of the average weights of informative dimensions to the average of the uninformative dimensions, , scales as . The scaling, however, also depends on data density. Specifically, consider the length scale separating two neighboring data points in the full-space V scales as . In the relevant subspace Vs, this length scale translates to a volume of which must be compared to the characteristic volumes in this subspace that reflect the multimodal structure of the data. If the identities of the true clusters in Vs are known, one can ask what the errors are in clustering in the full space V instead of in Vs by computing the entropy, S of the composition of inferred clusters based on the true cluster identities of data points. This entropy has to be a function of the ratio of the characteristic volumes in Ds to . Or equivalently, the entropy of the clusters should be a monotonically increasing function , denoting increasing errors in clustering. The form of the function F depends on the true data distribution and the clustering method. Therefore, our expectation for the ratio of counts for the informative dimensions and counts for the uninformative dimensions should scale like
| (6) |
We numerically generated Gaussian distributed data for using Ktrue = 7, Ds = 21 and ran 2000 iterations of the algorithm with and found close agreement for the range of parameters (Fig. 4A, B).
Fig. 4.
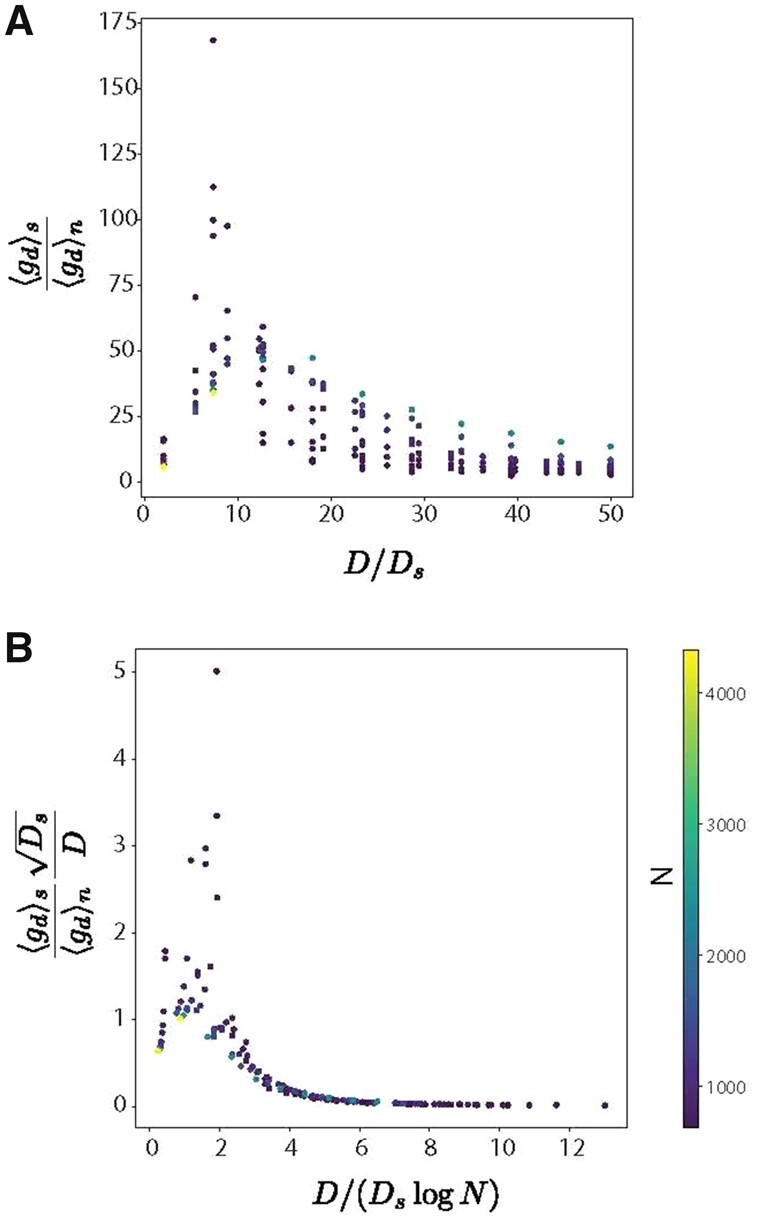
(A) We numerically generated Gaussian distributed data for using Ktrue = 7, Ds = 21, and ran 2000 iterations of the algorithm with and the proposal clusters inferred by standard K-means. (B) We find that by scaling by , we see a consistent trend across number data points and the ratio of counts on informative dimensions to uninformative dimensions matches the predicted scaling. For larger values of , the points collapse onto one trend line for various values of N
3.3 Significance and sources of error
To estimate the significance of gd frequencies produced by the algorithm, we constructed a null models to estimate gd in the absence of signal. First, each column of the data matrix is shuffled to produce a null distribution . This leaves marginal distributions of each dimension unchanged. Next, each feature can be scored based on the null distribution, , and statistics , and can be computed from these scores. We then can compute a Z-score for each dimension as . Motivated by the work of Tibshirani et al. (2001) and Candès et al. (2018), more precise estimates could be obtained by generating synthetic marginals without multimodality, which is an area for future work.
Correlations in the uninformative subspace can lead to erroneous counts in the correlated axes. This is caused by correlations in uninformative dimensions biasing the proposal clusters to be differentially localized in these axes. Despite these false positives, the false-negative rate remains low, resulting in minimal degradation of the ROC curve (see Supplementary Fig. S3A). In practice, eliminating any number of uninformative dimensions is effective in restricting analysis to a smaller regime of . Thus, even in the presence of false positives, removing uninformative dimensions before conventional analysis can increase the accuracy of clustering or dimensionality reduction techniques.
A free parameter in the synthetic data is , the ratio of mean separation to variance of distributions in the informative subspace, which controls the separability of clusters. As S decreases, we see degradation in the AUROC for our algorithm, but the identification of key dimensions is still possible even as the mean separation approaches the noise level in the distributions (see Supplementary Fig. S3B, inset).
4 Results
4.1 Application to single cell RNA-sequencing from early mouse development
A central challenge in developmental biology is the characterization of cell types that arise during the course of development, and an understanding of the genes which define and control the identity of cells as they transition between states. Starting at fertilization, embryonic cells undergo rapid proliferation and growth (Baldock, 2015; Gilbert, 2016). In a mouse, these cells form the epiblast, a cup-shaped tissue surrounded by extraembryonic cells by E6, or 6 days after fertilization. Only the cells of the epiblast will go on to give rise to all the cells of the mouse. These cells are pluripotent, meaning they have the developmental potential to become any cell type in the adult mouse body (Rossant and Tam, 2017). At E6, proximal and distal subpopulations of both the epiblast and surround extraembryonic cell types begin secreting signaling proteins (Rivera-Pérez and Hadjantonakis, 2015), which when detected by nearby cells, can increase or decrease the expression of transcription factors—proteins that modulate gene expression, and can thus change the overall expression profile of a cell. Signaling factors direct genetic programs within cells to restrict their lineage potential and undergo transcriptional as well as physical changes. Posterior—proximal epiblast cells migrate toward outside of the embryo forming a population called the primitive streak, in a process called gastrulation which takes place between E6.5 and E8. This time frame is notably marked by the emergence of three populations of specified progenitors known as the germ layers (Tam and Behringer, 1997): endoderm cells, which later differentiate into the gastrointestinal tract and connected organs, mesoderm cells, which have the potential to form internal organs such as the muscoskeletal system, the heart, and hematopoietic system, and ectoderm cells, which later form the skin and nervous system. The mesoderm can be subdivided into the intermediate mesoderm, paraxial mesoderm and lateral plate mesoderm, which each have further restricted lineage potential. Identifying the key transcription factors that define and control the genetic programs that lead to these distinct subpopulations will allow for experimental interrogation and a greater understanding of the gene regulatory networks which control development.
Recent advances in single-cell RNA-sequencing technology allow for simultaneous measurement of tens of thousands of genes (Briggs et al., 2018; Farrell et al., 2018) during multiple time points during development. These technological advances promise to provide insight into the identity and dynamics of key genes that guide the developmental process, yet even clustering cells into types of distinct developmental potential, and identifying the genes responsible for the diversity has been difficult (Grün et al., 2015; Weinreb et al., 2018). Existing methods typically find signal in correlations between large numbers of genes with large coefficients of variation to determine a cell’s states. However, experimental evidence suggests that perturbations of a small number of transcription factors are sufficient to alter a cell’s developmental state and trajectory (Gilbert, 2016; Graf and Enver, 2009; Takahashi and Yamanaka, 2006). Further, recent work suggests that a small set of four to five key transcription factors is sufficient to encode each lineage decision (Furchtgott et al., 2017; Petkova et al., 2019). We therefore believe that signature of structure in these data resides in a low-dimensional subspace. While many existing methods rely on hand-picking known transcription factors responsible for developmental transitions (Pijuan-Sala et al., 2019), we attempt to discover a low-dimensional subspace of gene expression which encodes multimodal expression patterns indicating the existence of distinct cell states.
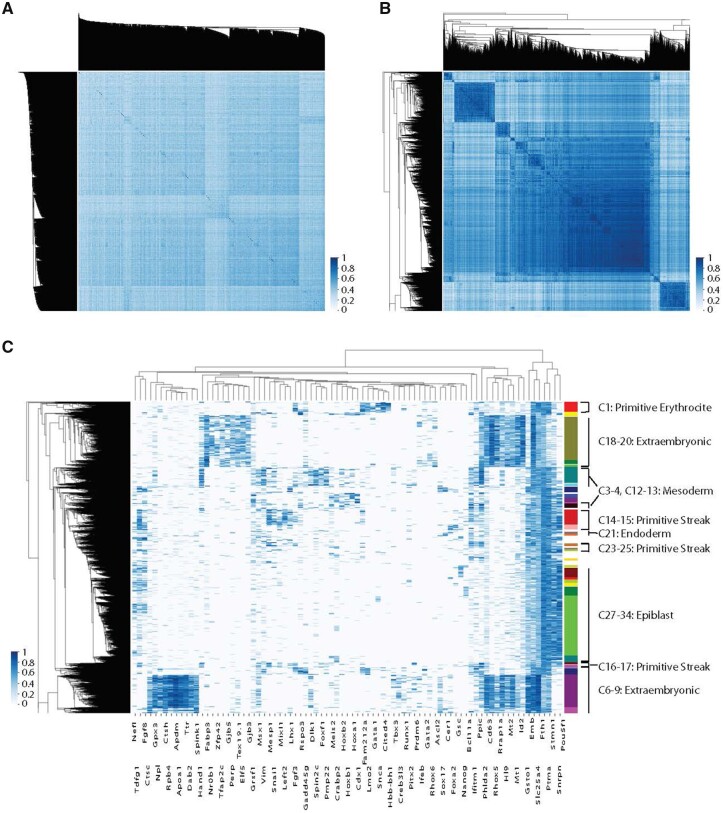
In the study by Pijuan-Sala et al. (2019), single cells are collected from a mouse embryo between E6.5 and E8.5, encompassing the entirety of gastrulation, and profiled with RNA sequencing to quantify RNA transcriptional abundance. We considered 48 692 cells from E6.5 to E7.75 which had more than 10 000 reads mapped to them. We then subsampled reads such that each cell had 10 000 reads. Individual genes were removed from analysis if they had a mean value of less than 0.05, or a standard deviation of less than 0.05 (based onGrün et al., 2015; Weinreb et al., 2018). We restricted our analysis to transcription factors because, as regulators of other genes, variation in transcription factor expression is a strong indication of biological diversity between cells, or cell types. We normalized the 409 transcription factors with expression above these thresholds to have unit variance. A cell–cell correlation analysis, followed by hierarchical clustering fails to capture the fine grained diversity of cell types that is known to exist at this time point (Fig. 5A).
Fig. 5.
(A) Single-cell RNA-seq data from the study by Pijuan-Sala et al. (2019) does not immediately segregate into cell types. Analysis for (A)–(C) was conducted on all 48 692 cells from E6.5 to E7.75 with at least 10 000 mapped reads, however, only 4000 randomly selected cells are shown for visualization purposes. Here, we show the cell–cell correlation matrix where each row/column corresponds to a single cell, organized by hierarchical clustering, and the correlation in computed in the 409-dimensional space of expressed transcription factors. (B) Inference of 27 transcription factors with pairwise multimodal signature provides a subspace in which to recompute cell–cell correlations, revealing population structure in comparison to (A). (C) Inferred transcription factors include known regulators of development and lineage transitions, allowing identification of previously hidden cell types and subpopulations. Here, we show normalized expression of inferred transcriptions and correlated genes (columns) versus single cells (rows) which were clustered hierarchically in this subspace. Differential expression of small numbers of genes distinguishes cell types, such as differential expression of Nanog in C27–C34
We attempted to discover a low-dimensional subspace in which signatures of cell-type diversity could be inferred using the algorithm outlined in the previous section. We sampled 3000 clustering configurations based on hierarchical (ward) clustering of 5000 subsampled cells, with , chosen to cover a range around the 37 clusters found by Pijuan-Sala et al. (2019). We find 27 transcription factors with a z-score , 18 of which have known have previously identified essential functions in the regulation of differentiation during gastrulation (Table 1).
Table 1.
Transcription factors with Z-score greater than 1 based on 3000 cluster proposals
| Gene name | zg | Associated cell type | Citation |
|---|---|---|---|
| Creb3l3 | 34.20 | ||
| Tfeb | 13.37 | ||
| Rhox6 | 10.15 | ||
| Elf5 | 9.45 | Extraembryonic ectoderm | Latos et al. (2015) |
| Gata1 | 8.77 | Primitive erythrocyte | Baron (2013) |
| Pou5f1 | 8.38 | Epiblast, primitive streak | Mulas et al. (2018) |
| Sox17 | 5.61 | Endoderm | Viotti et al. (2014) |
| Nr0b1 | 5.58 | ||
| Hoxb1 | 4.54 | Mesoderm | Carapuço et al. (2005) |
| Foxf1 | 3.36 | Lateral plate mesoderm | Mahlapuu et al. (2001) |
| Gata2 | 3.27 | Extraembryonic mesoderm | Silver and Palis (1997) |
| Prdm6 | 3.12 | ||
| Bcl11a | 2.99 | ||
| Foxa2 | 2.70 | Anterior visceral endoderm, anterior primitive streak | Perea-Gomez et al. (2001) and Arnold et al. (2008) |
| Gsc | 2.67 | Anterior primitive streak | Lewis et al. (2007) |
| Hand1 | 2.57 | Posterior mesoderm, lateral plate mesoderm | Riley et al. (1998) |
| Ascl2 | 2.52 | Ectoplacental cone | Simmons and Cross (2005) |
| Mesp1 | 2.46 | Posterior primitive streak | Arnold and Robertson (2009) |
| Hoxa1 | 2.44 | Mesoderm | Carapuço et al. (2005) |
| Nanog | 2.24 | Epiblast | Mulas et al. (2018) |
| Zfp42 | 2.14 | Extraembryonic ectoderm | Pelton et al. (2002) |
| Cdx1 | 2.12 | Paraxial mesoderm | van den Akker et al. (2002) |
| Runx1 | 1.82 | ||
| Hoxb2 | 1.73 | Mesoderm | Carapuço et al. (2005) |
| Id2 | 1.51 | Extraembryonic ectoderm | Jen et al. (1997) |
| Tbx3 | 1.31 | ||
| Pitx2 | 1.20 |
Note: For each transcription factor, we list the associated cell type from early mouse gastrulation.
Our hypothesis is that the variation in the 27 discovered transcription factors provides a subspace Vs in which multimodal signatures allow the identification of cell types. However, single-cell measurements of individual genes are known to be subject to a variety of sources of technical noise (Grün and van Oudenaarden, 2015). To decrease reliance on individual measurements, we take each of the 27 transcription factors with high scores, and extend the subspace to include 5 genes (potentially not transcription factors) that have the highest correlation with each of the 27 discovered transcription factors, resulting in an expanded subspace of 83 genes in which to cluster the data (full list in Supplementary Material). The cell–cell covariance matrix in this subspace (Fig. 5B), reveals distinct cell types and subtypes, and a heat map of the expression levels of these 83 genes shows differential expression between subtypes of cells.
We hierarchically clustered the cells into 35 cell types based on expression of these 83 genes. The corresponding identity of these cell types was determined using the expression pattern of all genes (Table 2, Fig. 5C), and identify extraembryonic populations (C5–9, C18–20), epiblast populations (C27–34), primitive streak populations (C14–17, C23–25), mesoderm subtypes (C2–4, C12, C13, C16, C17, C22), endoderm (C21) and primitive erythrocyte (C1). For example, we find a subpopulation of epiblast cells that have upregulated Nanog (as well as other early markers of the primitive streak), suggesting that these cells are positioned on the posterior-proximal end of the epiblast cup (Mulas et al., 2018). The large primitive streak population, which extends along the proximal side of the embryo, contains subtypes distinguished by Gsc (Lewis et al., 2007) and Mesp1 (Arnold and Robertson, 2009), which give rise to distinct fates. We find a distinct population of anterior visceral endoderm cells, marked by Otx2 and Hhex, which define the population responsible for the anterior-posterior body axis (Perea-Gomez et al., 2001). This population, which is distinguished from other Foxa2-expressing subpopulations of the visceral endoderm, is crucial for proper development.
Table 2.
Clusters (or cell types) discovered in the reduced subspace and their associated markers
| Cluster ID | Label | Markers |
|---|---|---|
| 0 | Unclustered | |
| 1 | Primitive erythrocyte progenitor (Baron, 2013) | Hba-x (Leder et al., 1992), Hbb-bh1 (Kingsley et al., 2006), Gata1 (Baron, 2013), Lmo2 (Palis, 2014) |
| 2 | Mesoderm | Car3, Spag5, Hoxb1 (Carapuço et al., 2005), Cnksr3, Smad4, Zfp280d, Vim (Saykali et al., 2019), Ifitm1 |
| 3, 4 | Lateral plate mesoderm | Foxf1 (Mahlapuu et al., 2001), Hand1 (Riley et al., 1998) |
| 5 | Anterior visceral endoderm | Sox17, Foxa2 (Perea-Gomez et al., 2001), Cer1 (Torres-Padilla et al., 2007), Frat2, Lhx1 (Costello et al., 2015), Hhex (Norris et al., 2002), Gata6, Ovol2, Otx2 (Perea-Gomez et al., 2001), Sfrp1 (Pfister et al., 2007) |
| 6,7 | Extraembryonic mesoderm | Fgf3 (Niswander and Martin, 1992), Lmo2 (Palis, 2014), Gata2 (Silver and Palis, 1997), Bmp4 (Fujiwara et al., 2001) |
| 8,9 | Visceral endoderm 1 | Rhox5 (Lin et al., 1994), Emb (Shimono and Behringer, 1999), Afp (Kwon et al., 2006) |
| 10,11 | Neuromesodermal progenitor | Sox2, T (Koch et al., 2017) |
| 12,13 | Paraxial mesoderm/presomitic mesoderm | Hoxa1, Hoxb1 (Carapuço et al., 2005), Cdx1, Cdx2 (van den Akker et al., 2002) |
| 14 | Posterior primitive streak | Mesp1 (Arnold and Robertson, 2009), Snai1 (Smith et al., 1992), Lhx1 (Costello et al., 2015; Shawlot et al., 1999), Smad1 (Tremblay et al., 2001) |
| 15 | Anterior primitive streak, organizer-like cells | Foxa2 (Arnold et al., 2008), Gsc (Lewis et al., 2007), Eomes (Arnold et al., 2008) |
| 16,17 | Posterior primitive streak derived mesoderm, lateral plate mesoderm progenitors | Msx2 (Catron et al., 1996), Snai1 (Smith et al., 1992), Foxf1 (Mahlapuu et al., 2001), Hand1 (Riley et al., 1998), Gata4 (Simon et al., 2018) |
| 18,19 | Extraembryonic ectoderm | Cdx2 (Beck et al., 1995), Rhox5 (Lin et al., 1994), Id2 (Jen et al., 1997), Gjb5 (Frankenberg et al., 2007), Tfap2c (Latos et al., 2015), Zfp42(aka Rex1) (Pelton et al., 2002), Elf5 (Latos et al., 2015), Gjb3 (Frankenberg et al., 2007), Ets2 (Donnison et al., 2015) |
| 20 | Ectoplacental cone | Plac1 (Donnison et al., 2015), Ascl2 (Simmons and Cross, 2005) |
| 21 | Definitive endoderm | Sox17 (Viotti et al., 2014), Foxa2 (Burtscher and Lickert, 2009), Apela (Hassan et al., 2010) |
| 22 | Mesendo progenitor, primitive streak | Tcf15 (Chal et al., 2018), Cer1, Hhex (Thomas et al., 1998) |
| 23 | Posterior primitive streak, cardiac mesoderm progenitors | Mesp1 (Arnold and Robertson, 2009), Gata4 (Simon et al., 2018), Lhx1 (Shawlot et al., 1999), Smad1 (Tremblay et al., 2001) |
| 24,25 | Primitive streak | T, Mixl1, Eomes, Fgf8, Wnt3 |
| 26 | Klf10, Gpbp1l1, Hmg20a, Rbm15b, Celf2 | |
| 27-28 | Posterior-proximal epiblast | Nanog (Mulas et al., 2018), Sox2 (Avilion, 2003), Pou5f1 (Mulas et al., 2018), Otx2 (Kurokawa et al., 2004) |
| 29-34 | Epiblast | Sox2 (Avilion, 2003), Pou5f1 (Mulas et al., 2018), Otx2 (Kurokawa et al., 2004) |
Most importantly, in extracting the relevant features from the data, our algorithm identifies known and validated transcription factors that are crucial to the developmental processes happening in this time frame. Further, by eliminating extraneous measurements, we are able to identify clear differential expression patterns between subtypes of cells which were indistinguishable through previous methods. In particular, identification of primitive streak subpopulations provides novel insight into a central developmental process, and we identify key genes that would allow for experimental interrogation of the spatial organization of the subtypes and their dynamics.
4.2 Comparison to existing methods
To benchmark our approach’s performance, we compared it against existing methods on two classes of distributions (Table 3). In the first class, relevant dimensions are globally separable, i.e. each relevant dimension is informative for every cluster. Such a distribution is shown in Figure 1, where e1 is globally informative and e2 and e3 are uninformative. We generated data with similar structure, with Ds = 1 relevant dimension (like e1 in Fig. 1) and Dn = 29 irrelevant dimensions (distributed like e2 and e3), resulting in a ratio . Each distribution had N = 1000 data points, and the ratio between variance and mean separation in the informative dimension . In the second class of distributions, data were generated such that clusters were pairwise separable, as described in Section 2.2, with Ktrue = 7 true clusters, N = 1400, Ds = 21. Similar to the first class, we set and .
Table 3.
AUROCs for various methods for selecting features
| Algorithm | Parameters |
Distributions |
||
|---|---|---|---|---|
| K | α | Globally separable | Pairwise separable | |
| Sparse PCA (Zou et al., 2006) | 1 | 0.38 ± 0.21 | 0.97 ± 0.03 | |
| 5.75 | 0.59 ± 0.21 | |||
| 10.5 | ||||
| 15.25 | 0.65 ± 0.08 | |||
| 20 | 0.59 ± 0.01 | |||
| K true | 1 | 0.47 ± 0.29 | ||
| 5.75 | 0.56 ± 0.21 | |||
| 10.5 | ||||
| 15.25 | 0.48 ± 0.01 | 0.78 ± 0.07 | ||
| 20 | 0.63 ± 0.02 | |||
| 1 | 0.52 ± 0.32 | |||
| 5.75 | ||||
| 10.5 | ||||
| 15.25 | 0.47 ± 0.01 | 0.80 ± 0.7 | ||
| 20 | 0.64 ± 0.01 | |||
| Sparse K-means (Witten and Tibshirani, 2010) | 1 | 0.80 ± 0.40 | ||
| 5.75 | 0.84 ± 0.32 | |||
| 10.5 | 0.87 ± 0.18 | |||
| 15.25 | 0.86 ± 0.23 | |||
| 20 | 0.80 ± 0.40 | |||
| K true | 1 | 0.96 ± 0.08 | ||
| 5.75 | 0.88 ± 0.24 | |||
| 10.5 | 0.80 ± 0.40 | |||
| 15.25 | 0.94 ± 0.12 | |||
| 20 | ||||
| 1 | 0.91 ± 0.18 | |||
| 5.75 | 0.85 ± 0.30 | |||
| 10.5 | ||||
| 15.25 | 0.84 ± 0.32 | |||
| 20 | 0.83 ± 0.34 | |||
| Sparse hierarchical clustering (Witten and Tibshirani, 2010) | N/A | 1 | 0 ± 0 | 0.54 ± 0.03 |
| 5.75 | 0.57 ± 0.04 | |||
| 10.5 | 0.59 ± 0.02 | |||
| 15.25 | 0.56 ± 0.03 | |||
| 20 | 0.59 ± 0.02 | |||
| LFSBSS (Li et al., 2008) | N/A | |||
| K true | ||||
| Spectral selection (Zhao and Liu, 2007) | N/A | N/A | ||
| SMD (hierarchical proposal clusters) | Unif | N/A | ||
| Unif | 1.0 ± 0.02 | |||
| Unif | ||||
| SMD (K-means proposal clusters) | Unif | N/A | ||
| Unif | 0.94 ± 0.05 | |||
| Unif | ||||
Note: Here, we generate two classes of distributions: globally separable, where one dimension separates two clusters, and other dimensions are uninformative, and pairwise separable, where each dimension separates only a pair of clusters, and the rest are uninformative. In both cases, the ratio of informative to uninformative dimensions is . For each class of distributions, we generated 5 instances of the class, and used the algorithm in the left column to infer weights for each dimension. Some of the algorithms have input parameters, which are given in columns K (the number of clusters, or in the case of Sparse PCA, the number of components) and α (a sparsity parameter). From these weights, we calculated the AUROC score, and report the average, and standard deviation over the five trials.
Next, we compared the method against existing feature selection methods. For each class of distribution, we asked if existing methods could discover weights that identified the informative dimensions, and measured this success by calculating the AUROC for a range of algorithmic parameters over five instances of each distribution. Traditional approaches to feature selection have relied on correlation analysis (e.g. principal component analysis, or PCA), which are not suited for discovering sparse representations. This has been addressed through Sparse PCA (Witten et al., 2009; Zou et al., 2006), which adds an L1 penalty to the typical matrix completion form of PCA. Sparse PCA has two free parameters: the number of components considered (K) and a sparsity parameter (α). We tested a range of both of these parameters, and found that Sparse PCA is sensitive to parameter choice, but can identify features of importance only when such importance is reflected in the correlation structure (as is the case with the pairwise separable features). However, Sparse PCA does not optimize for any notion of separability, so when there is no signature in the correlation structure (as is the case with the globally separable distribution class).
Another class of methods attempts to optimize different measures of feature importance with respect to a clustering configuration. Spectral feature selection (Zhao and Liu, 2007), does so by constructing a graph representation of the data, yet fails to identify the key features in either class of distributions tested (Table 3). In Li et al. (2008), features are discovered based on ability to define individual clusters, but this method cannot resolve distinct clusters in either setting in the large limit (Table 3). The identification of a small subset of informative features can also be formulated as a Bayesian inference problem, where a log likelihood function is maximized over the hidden parameters via an expectation maximization scheme (Dempster et al., 1977). Model-based clustering has been explored in depth in McLachlan and Peel (2000) and Fraley and Raftery (2002), and adapted to feature selection by the inclusion of a lasso term on the separation of the first moments in Pan and Shen (2007), Wang and Zhu (2008) and Xie et al. (2008). These methods all rely on accurate forward models of the data. Advantages and drawbacks of these are discussed in Witten and Tibshirani (2010), which provides a more general framework. We tested two methods proposed in Witten and Tibshirani (2010) (Table 3), in which a feature weight vector is introduced and learned by amending a clustering cost function with a L1 penalty on the feature weights. Each of these algorithms requires a parameter for the number of clusters (K), and a sparsity parameter (α). We tested this alteration to K-means, and hierarchical clustering, and found that while the K-means variant successfully discovered the informative features in the case of pairwise separable distributions, it failed to reliably find sparse representations for globally separable features, and was sensitive to the input parameters. The hierarchical clustering variant had limited success on these classes of distributions, and in situations with a large number of data points N, the hierarchical clustering approach requires the construction of a matrix, which is computationally difficult. Sparse K-means/Hierarchical clustering, LFSBSS, Sparse PCA or any model-based selection procedure rely on knowing the number of clusters, which is an input to each algorithm, and is difficult to infer (Sun et al., 2012). Our method sidesteps this obstacle by integrating over a prior distribution of this parameter.
Finally, we applied our proposed method (labeled SMD for Sparse Manifold Decomposition) to both classes of distributions, using both K-means and hierarchical (ward) clustering to construct the ensemble of cluster proposals, and found that the relevant features were discovered reliably using both clustering algorithms and for a range in the bounds of the prior over cluster numbers (Table 3). Our approach has a number of general advantages. First, it does not make assumptions about the number of clusters, the types of generating distributions or the relative sizes of the different clusters. Second, by integrating over an ensemble of proposal cluster configurations constructed on subsets of the data, the algorithm is computationally efficient in regimes of large N (does not suffer from the N2 scaling of sparse hierarchical clustering). Third, by building on existing clustering methods to construct proposals, our method can be generally applied over any clustering procedure to discover relevant features.
Finally, we attempted to apply a variation of the method described by Witten and Tibshirani (2010) to the single-cell data discussed in Section 4.1, using a similar alternating optimization procedure. We iterated, starting with weights gi for all i, (i) finding clusters according to hierarchical (ward) clustering with K = 50 with distances weighted by , (ii) finding weights for each feature according to 2. We iterated until convergence in 10 separate trials on the mouse data, and found poor agreement of results between trials (see Supplementary Fig. S4).
Gene expression data analysis has been an active area of research involving multiple approaches. A successful approach has been biclustering techniques (Henriques et al., 2015; Xie et al., 2019). These approaches have been demonstrated to capture modules of genes that covary over distinct biological samples (Henriques et al., 2017; Zhang et al., 2017). These approaches, however, focus on finding defining expression patterns involving correlated classes of genes, which could potentially miss more subtle diversity caused by just a small number of genes. To demonstrate this, we ran BicPAMS (Henriques et al., 2017) and QUBIC (Zhang et al., 2017) on the two aforementioned synthetic datasets in which signal is restricted to a subspace of dimension , and neither of which were able to identify the known cluster assignments (see Supplementary Material). This is likely due to the lack of global correlation structure associated with the signal, and is thus related to the failure of PCA (see Supplementary Fig. S1). A potential solution would be to impose a sparsity constraint on the discovered features, an adaptation that is conceptually discussed by Witten and Tibshirani (2010). Biclustering techniques continue to be an important resource in understanding diversity in cellular expression datasets, and are complementary to our approach.
5 Conclusion
Identifying subspaces which define classes and states from high-dimensional data is an emerging problem in scientific data analysis where an increasing number of measurements push the limits of conventional statistical methods. Techniques such as PCA and ICA provide invaluable insight in data analysis, but can miss multimodal features, particularly in high-dimensional settings. These methods which have reduced success in the regime can be supplemented by our technique by finding a lower-dimensional subspace in which further analysis can be conducted. Crucially, eliminating any informative dimensions decreases the ratio, moving to a regime in which conventional methods are more effective. By reducing the dimensionality of the data, it is possible to artificially increase data density, and mitigate associated problems that are prevalent in high-dimensional inference. Further, as our algorithm can be a wrapper over any clustering algorithm to construct the proposal clusters, it has varied applicability in settings where K-means or other specific clustering algorithms are unsuccessful.
Biological data from neural recordings, behavioral studies or gene expression are increasingly high dimensional. Identifying the underlying constituents of the system that define distinct states is crucial in each setting. In contexts such as transcriptional analysis in developmental biology, finding the key genes that define cell states is a central problem that bridges the gap between high-throughput measurements and mechanistic experimental follow ups. Identification of transcription factors with multimodal expression that define cellular states allows for the study of dynamics of state transitions and spatial patterning of the embryo. Our method rediscovers known factors in well-studied developmental processes and predicts several gene candidates for further study. Identifying defining features in high-dimensional data is a crucial step in understanding and experimentally perturbing systems in a range of biological domains.
Supplementary Material
Acknowledgements
The authors thank Deniz Aksel for extensive help with annotating the clusters. In addition, the authors thank Cengiz Pehlevan, Sam Kou, Matt Thomson, Gautam Reddy, Sean Eddy, Ariel Amir and members of the Ramanathan lab for discussions and comments on the manuscript.
Funding
This work was supported by DARPA W911NF-19-2-0018 and R01HD100036 (S.R.). S.M. was partially supported by DMS-1764269.
Conflict of Interest: none declared.
References
- Arnold S.J., Robertson E.J. (2009) Making a commitment: cell lineage allocation and axis patterning in the early mouse embryo. Nat. Rev. Mol. Cell Biol., 10, 91–103. [DOI] [PubMed] [Google Scholar]
- Arnold S.J. et al. (2008) Pivotal roles for eomesodermin during axis formation, epithelium-to-mesenchyme transition and endoderm specification in the mouse. Development, 135, 501–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avilion A.A. et al. (2003) Multipotent cell lineages in early mouse development depend on sox2 function. Genes Dev., 17, 126–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldock R. (2015) Kaufman’s Atlas of Mouse Development Supplement: Coronal Images. Academic Press, Amsterdam. [Google Scholar]
- Baron M.H. (2013) Concise review: early embryonic erythropoiesis: not so primitive after all. Stem Cells (Dayton, Ohio), 31, 849–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck F. et al. (1995) Expression of cdx-2 in the mouse embryo and placenta: possible role in patterning of the extra-embryonic membranes. Dev. Dyn., 204, 219–227. [DOI] [PubMed] [Google Scholar]
- Briggs J.A. et al. (2018) The dynamics of gene expression in vertebrate embryogenesis at single-cell resolution. Science (New York, N.Y.), 360, eaar5780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burtscher I., Lickert H. (2009) Foxa2 regulates polarity and epithelialization in the endoderm germ layer of the mouse embryo. Development, 136, 1029–1038. [DOI] [PubMed] [Google Scholar]
- Candès E. et al. (2018) Panning for gold: ‘model-x’ knockoffs for high dimensional controlled variable selection. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 80, 551–577. [Google Scholar]
- Carapuço M. et al. (2005) Hox genes specify vertebral types in the presomitic mesoderm. Genes Dev., 19, 2116–2121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catron K.M. et al. (1996) Comparison of msx-1 and msx-2 suggests a molecular basis for functional redundancy. Mech. Dev., 55, 185–199. [DOI] [PubMed] [Google Scholar]
- Chal J. et al. (2018) Recapitulating early development of mouse musculoskeletal precursors of the paraxial mesoderm in vitro. Development, 145, dev157339. [DOI] [PubMed] [Google Scholar]
- Chang W.-C. (1983) On using principal components before separating a mixture of two multivariate normal distributions. J. R. Stat. Soc. Ser. C (Appl. Stat.), 32, 267–275. [Google Scholar]
- Coates A., Ng A.Y. (2012) Learning Feature Representations with K-Means. Springer, Berlin, Heidelberg, pp. 561–580. [Google Scholar]
- Costello I. et al. (2015) Lhx1 functions together with otx2, foxa2, and ldb1 to govern anterior mesendoderm, node, and midline development. Genes Dev., 29, 2108–2122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A.P. et al. (1977) Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodological), 39, 1–38. [Google Scholar]
- Donnison M. et al. (2015) Elf5 and Ets2 maintain the mouse extraembryonic ectoderm in a dosage dependent synergistic manner. Dev. Biol., 397, 77–88. [DOI] [PubMed] [Google Scholar]
- Donoho D.L. (2000) High-dimensional data analysis: the curses and blessings of dimensionality. In: Proceedings Donoho00high-dimensionaldata. AMS Conference on Math Challenges of the 21st Century.
- Farrell J.A. et al. (2018) Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science, 360, eaar3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraley C., Raftery A.E. (2002) Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc., 97, 611–631. [Google Scholar]
- Frankenberg S. et al. (2007) Novel gene expression patterns along the proximo-distal axis of the mouse embryo before gastrulation. BMC Dev. Biol., 7, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujiwara T. et al. (2001) Bone morphogenetic protein 4 in the extraembryonic mesoderm is required for allantois development and the localization and survival of primordial germ cells in the mouse. Proc. Natl. Acad. Sci. USA, 98, 13739–13744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furchtgott L.A. et al. (2017) Discovering sparse transcription factor codes for cell states and state transitions during development. eLife, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert S. (2016) Developmental Biology. Sinauer Associates, Inc., Publishers, Sunderland, Massachusetts. [Google Scholar]
- Graf T., Enver T. (2009) Forcing cells to change lineages. Nature, 462, 587–594. [DOI] [PubMed] [Google Scholar]
- Grün D., van Oudenaarden A. (2015) Design and analysis of single-cell sequencing experiments. Cell, 163, 799–810. [DOI] [PubMed] [Google Scholar]
- Grün D. et al. (2015) Single-cell messenger RNA sequencing reveals rare intestinal cell types. Nature, 525, 251–255. [DOI] [PubMed] [Google Scholar]
- Hassan A.S. et al. (2010) Expression of two novel transcripts in the mouse definitive endoderm. Gene Expr. Patterns, 10, 127–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henriques R. et al. (2015) A structured view on pattern mining-based biclustering. Pattern Recognit., 48, 3941–3958. [Google Scholar]
- Henriques R. et al. (2017) Bicpams: software for biological data analysis with pattern-based biclustering. BMC Bioinformatics, 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jen Y. et al. (1997) Each member of the id gene family exhibits a unique expression pattern in mouse gastrulation and neurogenesis. Dev. Dyn., 208, 92–106. [DOI] [PubMed] [Google Scholar]
- Kingsley P.D. et al. (2006) “maturational” globin switching in primary primitive erythroid cells. Blood, 107, 1665–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiselev V.Y. et al. (2019) Challenges in unsupervised clustering of single-cell RNA-seq data. Nat. Rev. Genet., 20, 273–282. [DOI] [PubMed] [Google Scholar]
- Koch F. et al. (2017) Antagonistic activities of Sox2 and brachyury control the fate choice of neuro-mesodermal progenitors. Dev. Cell, 42, 514–526.e7. [DOI] [PubMed] [Google Scholar]
- Kurokawa D. et al. (2004) Regulation of Otx2 expression and its functions in mouse epiblast and anterior neuroectoderm. Development, 131, 3307–3317. [DOI] [PubMed] [Google Scholar]
- Kwon G.S. et al. (2006) Tg(Afp-Gfp) expression marks primitive and definitive endoderm lineages during mouse development. Dev. Dyn., 235, 2549–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latos P.A. et al. (2015) Elf5-centered transcription factor hub controls trophoblast stem cell self-renewal and differentiation through stoichiometry-sensitive shifts in target gene networks. Genes Dev., 29, 2435–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leder A. et al. (1992) In situ hybridization reveals co-expression of embryonic and adult alpha globin genes in the earliest murine erythrocyte progenitors. Development, 116, 1041–1049. [DOI] [PubMed] [Google Scholar]
- Lewis S.L. et al. (2007) Genetic interaction of Gsc and Dkk1 in head morphogenesis of the mouse. Mech. Dev., 124, 157–165. [DOI] [PubMed] [Google Scholar]
- Li Y. et al. (2008) Localized feature selection for clustering. Pattern Recognit. Lett., 29, 10–18. [Google Scholar]
- Lin T.-P. et al. (1994) The Pem homeobox gene is X-linked and exclusively expressed in extraembryonic tissues during early murine development. Dev. Biol., 166, 170–179. [DOI] [PubMed] [Google Scholar]
- Mahlapuu M. et al. (2001) The forkhead transcription factor foxf1 is required for differentiation of extra-embryonic and lateral plate mesoderm. Development, 128, 155–166. [DOI] [PubMed] [Google Scholar]
- McLachlan G.J., Peel D. (2000) Finite Mixture Models. Wiley Series in Probability and Statistics, New York. [Google Scholar]
- Mulas C. et al. (2018) Oct4 regulates the embryonic axis and coordinates exit from pluripotency and germ layer specification in the mouse embryo. Development (Cambridge, England), 145, dev159103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngiam J. et al. (2011) Sparse filtering. In: Shawe-Taylor J.et al. (eds.) Advances in Neural Information Processing Systems, Vol. 24. Curran Associates, Inc., pp. 1125–1133. [Google Scholar]
- Niswander L., Martin G. (1992) Fgf-4 expression during gastrulation, myogenesis, limb and tooth development in the mouse. Development, 114, 755–768. [DOI] [PubMed] [Google Scholar]
- Norris D. et al. (2002) The Foxh1-dependent autoregulatory enhancer controls the level of nodal signals in the mouse embryo. Development, 129, 3455–3468. [DOI] [PubMed] [Google Scholar]
- Palis J. (2014) Primitive and definitive erythropoiesis in mammals. Front. Physiol., 5, 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W., Shen X. (2007) Penalized model-based clustering with application to variable selection. J. Mach. Learn. Res., 8, 1145–1164. [Google Scholar]
- Pelton T.A. et al. (2002) Transient pluripotent cell populations during primitive ectoderm formation: correlation of in vivo and in vitro pluripotent cell development. J. Cell Sci., 115, 329–339. [DOI] [PubMed] [Google Scholar]
- Perea-Gomez A. et al. (2001) Otx2 is required for visceral endoderm movement and for the restriction of posterior signals in the epiblast of the mouse embryo. Development, 128, 753–765. [DOI] [PubMed] [Google Scholar]
- Petkova M.D. et al. (2019) Optimal decoding of cellular identities in a genetic network. Cell, 176, 844–855.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfister S. et al. (2007) Gene expression pattern and progression of embryogenesis in the immediate post-implantation period of mouse development. Gene Expr. Patterns, 7, 558–573. [DOI] [PubMed] [Google Scholar]
- Pijuan-Sala B. et al. (2019) A single-cell molecular map of mouse gastrulation and early organogenesis. Nature, 566, 490–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley P. et al. (1998) The Hand1 bHLH transcription factor is essential for placentation and cardiac morphogenesis. Nat. Genet., 18, 271–275. [DOI] [PubMed] [Google Scholar]
- Rivera-Pérez J.A., Hadjantonakis A.-K. (2015) The dynamics of morphogenesis in the early mouse embryo. Cold Spring Harbor Perspect. Biol., 7, a015867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossant J., Tam P.P. (2017) New insights into early human development: lessons for stem cell derivation and differentiation. Cell Stem Cell, 20, 18–28. [DOI] [PubMed] [Google Scholar]
- Saykali B. et al. (2019) Distinct mesoderm migration phenotypes in extra-embryonic and embryonic regions of the early mouse embryo. eLife, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shawlot W. et al. (1999) Lim1 is required in both primitive streak-derived tissues and visceral endoderm for head formation in the mouse. Development, 126, 4925–4932. [DOI] [PubMed] [Google Scholar]
- Shimono A., Behringer R.R. (1999) Isolation of novel cDNAs by subtractions between the anterior mesendoderm of single mouse gastrula stage embryos. Dev. Biol., 209, 369–380. [DOI] [PubMed] [Google Scholar]
- Silver L., Palis J. (1997) Initiation of murine embryonic erythropoiesis: a spatial analysis. Blood, 89, 1154–1164. [PubMed] [Google Scholar]
- Simmons D.G., Cross J.C. (2005) Determinants of trophoblast lineage and cell subtype specification in the mouse placenta. Dev. Biol., 284, 12–24. [DOI] [PubMed] [Google Scholar]
- Simon C.S. et al. (2018) A Gata4 nuclear GFP transcriptional reporter to study endoderm and cardiac development in the mouse. Biol. Open, 7, bio036517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith D. et al. (1992) Isolation of Sna, a mouse gene homologous to the drosophila genes snail and escargot: its expression pattern suggests multiple roles during postimplantation development. Development, 116, 1033–1039. [DOI] [PubMed] [Google Scholar]
- Sun W. et al. (2012) Regularized k-means clustering of high-dimensional data and its asymptotic consistency. Electr. J. Stat., 6, 148–167. [Google Scholar]
- Takahashi K., Yamanaka S. (2006) Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures by defined factors. Cell, 126, 663–676. [DOI] [PubMed] [Google Scholar]
- Tam P.P.L., Behringer R.R. (1997) Mouse gastrulation: the formation of a mammalian body plan. Mech. Dev., 68, 3–25. [DOI] [PubMed] [Google Scholar]
- Thomas P. et al. (1998) Hex: a homeobox gene revealing peri-implantation asymmetry in the mouse embryo and an early transient marker of endothelial cell precursors. Development, 125, 85–94. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. et al. (2001) Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 63, 411–423. [Google Scholar]
- Torres-Padilla M.-E. et al. (2007) The anterior visceral endoderm of the mouse embryo is established from both preimplantation precursor cells and by de novo gene expression after implantation. Dev. Biol., 309, 97–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay K. et al. (2001) Mouse embryos lacking smad1 signals display defects in extra-embryonic tissues and germ cell formation. Development, 128, 3609–3621. [DOI] [PubMed] [Google Scholar]
- van den Akker E. et al. (2002) Cdx1 and Cdx2 have overlapping functions in anteroposterior patterning and posterior axis elongation. Development, 129, 2181–2193. [DOI] [PubMed] [Google Scholar]
- Viotti M. et al. (2014) Sox17 links gut endoderm morphogenesis and germ layer segregation. Nat. Cell Biol., 16, 1146–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S., Zhu J. (2008) Variable selection for model-based high-dimensional clustering and its application to microarray data. Biometrics, 64, 440–448. [DOI] [PubMed] [Google Scholar]
- Weinreb C. et al. (2018) SPRING: a kinetic interface for visualizing high dimensional single-cell expression data. Bioinformatics, 34, 1246–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D.M., Tibshirani R. (2010) A framework for feature selection in clustering. J. Am. Stat. Assoc., 105, 713–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten D.M. et al. (2009) A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics, 10, 515–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie B. et al. (2008) Penalized model-based clustering with cluster-specific diagonal covariance matrices and grouped variables. Electr. J. Stat., 2, 168–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie J. et al. (2019) It is time to apply biclustering: a comprehensive review of biclustering applications in biological and biomedical data. Brief. Bioinf., 20, 1450–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu L. et al. (2005) Maximum margin clustering. In: Saul L.K.et al. (eds.) Advances in Neural Information Processing Systems, Vol. 17. MIT Press, pp. 1537–1544. [Google Scholar]
- Zhang Y. et al. (2017) Qubic: a bioconductor package for qualitative biclustering analysis of gene co-expression data. Bioiinformatics, 42 450–452. [DOI] [PubMed] [Google Scholar]
- Zhao Z., Liu H. (2007) Spectral feature selection for supervised and unsupervised learning. In Proceedings of the 24th International Conference on Machine Learning, ICML ’07. Association for Computing Machinery, New York, NY, USA, pp. 1151–1157.
- Zhu J. et al. (2003) 1normm support vector machines. In Proceedings of the 16th International Conference on Neural Information Processing Systems, NIPS’03. MIT Press, Cambridge, MA, USA, pp. 49–56. [Google Scholar]
- Zou H. et al. (2006) Sparse principal component analysis. J. Comput. Graph. Stat., 15, 265–286. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.