REHE: Fast Variance Components Estimation for Linear Mixed Models

Abstract

Linear mixed models are widely used in ecological and biological applications, especially in genetic studies. Reliable estimation of variance components is crucial for using linear mixed models. However, standard methods, such as the restricted maximum likelihood (REML), are computationally inefficient in large samples and may be unstable with small samples. Other commonly used methods, such as the Haseman-Elston (HE) regression, may yield negative estimates of variances. Utilizing regularized estimation strategies, we propose the restricted Haseman-Elston (REHE) regression and REHE with resampling (reREHE) estimators, along with an inference framework for REHE, as fast and robust alternatives that provide non-negative estimates with comparable accuracy to REML. The merits of REHE are illustrated using real data and benchmark simulation studies.

1. Introduction

Linear mixed model are a convenient and powerful tool for analyzing correlated data, with a wide range of applications in scientific research. It is especially useful for genetic studies of complex traits, including heritability estimation (Sofer 2017), genome-wide association studies (GWAS) (Aulchenko, De Koning, and Haley 2007), and network-based pathway enrichment analysis (NetGSA) (Shojaie and Michailidis 2009). Variance components estimation is an essential step when applying linear mixed models and the restricted maximum likelihood (REML) approach is considered to be the gold-standard for this task (Patterson and Thompson 1971). REML works by iteratively maximizing the residual likelihood with respect to the variance component parameters. During each iteration, REML computes the inverse of two $n\times n$ matrices, where $n$ is the sample size of the data set. As a result, the computation for REML quickly becomes prohibitive for large sample sizes, especially when the correlations among observations are non-sparse – such as between-subject correlations due to genetic relatedness (Kang et al. 2010). Despite efforts to improve the computational efficiency of REML, such as average information REML (Gilmour, Thompson, and Cullis 1995), Monte Carlo REML (Matilainen et al. 2013), and REML based on grid search (Jiang et al. 2019), the scalability of REML to very large data sets is often limited in many applications. On the other hand, consistency and asymptotic normality of REML estimates are large sample properties. In this paper we illustrate that REML can be numerically unstable and can also provide unreliable estimates and/or confidence intervals of variance components in some settings (Section 4, Supplementary Note 2.3 and Note 2.4). Given these shortcomings, new approaches for fast and reliable estimators of variance components for linear mixed model are needed.

When computational efficiency is a primary concern, moment estimators of variance components have frequently been used as alternatives to REML. These include analysis of variance (ANOVA), minimum norm quadratic unbiased estimation (MINQUE), and the Haseman-Elston (HE) regression estimator (Rasch and Masata 2006; Rao 1970; Haseman and Elston 1972; Sofer 2017). These methods bypass the most time-consuming step in REML — the inversion of $n\times n$ matrices. An essential component of of these alternative methods to REML is to set up estimating equations by equating the mean squared errors to its expectation, the error variance. ANOVA, originated from ideas by R. A. Fisher in 1920s, has been well established for estimating variance components. The resulting estimators are minimum variance quadratic unbiased (Graybill and Hultquist 1961), and minimum variance unbiased under normality assumptions on the random effects and the errors (Graybill 1954; Graybill and Wortham 1956). MINQUE (Rao 1970), which can be viewed as an extension of the ANOVA method, is equivalent to the first iteration of REML (Searle 1995). It relaxes the assumption of normality using estimating equations that rely on initial values for the variance components. The HE estimator, first introduced in (Haseman and Elston 1972), has been recently used for linear mixed model variance component estimation in genetic studies (Sofer 2017; Zhou 2017). Its simple implementation and fast computation make it favorable when working with large and densely correlated data sets. A key limitation of these moment estimators, however, is that they do not guarantee non-negative estimates for the variance components. This leads to difficulties in both interpretation and downstream analyses.

To address the shortcomings of existing approaches in variance component estimation, we propose a new estimation method based on restricted Haseman-Elston (REHE) regression. REHE is computationally efficient, and ensures non-negative estimates of variance components. We demonstrate that the REHE estimates are comparably accurate to the REML estimates when REML performs well, and are robust in the settings where REML does not provide good estimates. To accommodate the need for a strictly positive variance estimates in some applications, we also propose REHE with resampling (reREHE), which provides positive variance components estimates with high probability. Furthermore, to facilitate inference, we propose bootstrap confidence intervals for REHE estimates. We demonstrate that the REHE boostrap confidence intervals are more robust than their REML counterparts. Finally, we also show that REHE in combination with correlation matrix sparsification (Gogarten et al. 2019), when applicable, can result in a substantial increase in computational speed for variance component inference. REHE is both computationally efficient and flexible, and can be used across a broad range of study designs. Here we demonstrate the utility of REHE in three different contexts: heritability estimation, GWAS and NetGSA. We benchmark the proposed methods’ performance with simulation studies, and illustrate their advantages using data from the Hispanic Community Health Study/Study of Latinos (HCHS/SOL) (Sorlie et al. 2010; Conomos et al. 2016), where there is extensive non-zero genetic correlations among the 12,803 study subjects with GWAS data available, and The Cancer Genome Atlas (TCGA) breast cancer data set (TCGA 2012).

The rest of the paper is organized as follows. In Section 2, we introduce the REHE estimator, discuss its properties and propose a bootstrap inference framework. We also introduce the reREHE estimator as an alternative to the REHE estimator. We demonstrate the performance of the REHE and reREHE estimators with real data applications in Section 3. In Section 4, we benchmark their performance with extensive simulation studies. Section 5 concludes the paper with discussions on the results and potential improvements. Additional results on REHE, reREHE and matrix sparsification are provided in the Supplementary Notes.

2. Methods

Consider a generic linear mixed model for an outcome vector $Y$ of length $n$:

$$Y=X\mathbf{\beta }+\sum _{k=1}^K{\sigma }_k{\mathbf{\gamma }}_{\mathbf{k}}+{\sigma }_0\mathbf{ϵ}$$ (1)

Here, $X$ is an $n\times p$ design matrix for $p$ covariates, and $\mathbf{\beta }$ is a $p$-dimensional fixed effect coefficient vector. For k = 1, 2, …, K, γ_k is a length $n$ vector of random effects following $N_n(0,D_k)$, where each $n\times n$ matrix $D_k$ defines one source of correlation among the observations, and is assumed to be known. The noise $\mathbf{ϵ}$ is a length $n$ vector following $N_n(0,{\mathbf{I}}_n)$. The parameters ${\sigma }_k$’s $(k=0,1,\dots ,K)$ are the variance components. For k = 1, …, K, h_k = ${\sigma }_k^2/\sum _{l=0}^K{\sigma }_l^2$ estimates the proportion of variation explained by $D_k$. In the context of genetic studies, a genetic relatedness matrix (GRM) is often used for $D_1$ and $h_1$ is viewed as a measure of heritability, i.e., the proportion of the total trait variation that is due to genetic variation.

Our main objective is to estimate the variance components ${\sigma }_k^2(k=0,1,\dots ,K)$. For expositional clarity, we assume the model has no fixed effect, and the outcome vector $Y$ is centered. We also assume $K=1$ such that the correlations among the observations can be modeled by a single random effect ${\mathbf{\gamma }}_{\mathbf{1}}$. However, our methods can be easily extended to models with fixed effects (Section 2.2.2), or with more than one random effects. Denoting $D_0={\mathbf{I}}_n$ and ${\mathbf{\gamma }}_{\mathbf{0}}=\mathbf{ϵ}$, the simplified form of model [1] becomes

$$Y={\sigma }_0{\mathbf{\gamma }}_{\mathbf{0}}+{\sigma }_1{\mathbf{\gamma }}_{\mathbf{1}}.$$ (2)

2.1. The Haseman-Elston Regression

The Haseman-Elston (HE) regression approach (Haseman and Elston 1972; Sofer 2017; Zhou 2017) estimates the variance components via the method of moments. Specifically, since model [2] implies that $Var(Y)={\sigma }_0^2{D}_0+{\sigma }_1^2{D}_1,n^2$ estimating equations are constructed:

$$\text{E}\left[Y_i{Y}_j\right]={\sigma }_0^2{D}_0^{ij}+{\sigma }_1^2{D}_1^{ij},i,j=1,2,\dots n,$$

where $D_k^{ij}$ denotes the $(i,j)$ entry of matrix $D_k(k=\mathrm{0,1})$. Estimation of the variance components can thus be recast as a linear regression problem. Let $\tilde{Y}=\mathrm{v}\mathrm{e}\mathrm{c}\left(Y{Y}^{\mathrm{\top }}\right)$ denote the vectorization of the $n\times n$ matrix $Y{Y}^{\text{⊤}}$ by stacking its columns, $\tilde{X}=\left(\mathrm{v}ec\left(D_0\right),\mathrm{v}ec\left(D_1\right)\right)$ and ${\mathbf{\sigma }}^2=({\sigma }_0^2,{\sigma }_1^2{)}^{\text{⊤}}$. We then have $\mathrm{E}\left(\tilde{Y}\right)=\tilde{X}{\mathbf{\sigma }}^2$. HE solves for variance components ${\mathbf{\sigma }}^2$ by linear regression, specifically, by minimizing the residual sum of squares

$${\left(\tilde{Y}-\tilde{X}{\mathbf{\sigma }}^2\right)}^{\top }\left(\tilde{Y}-\tilde{X}{\mathbf{\sigma }}^2\right).$$ (3)

The resulting estimator has a closed form expression ${\hat{\mathbf{\sigma }}}^2=({\tilde{X}}^{\mathrm{\top }}\tilde{X}{)}^{-1}{\tilde{X}}^{\mathrm{\top }}\tilde{Y}$. A nice property of the HE estimator is unbiasedness, even if we only use a subset of the $n^2$ estimating equations to compute the estimates; see the Appendix A for details.

The computational complexity of HE is $O\left(K{n}^2\right)$ compared to $O\left(n^3\right)$ for REML. When the sample size $n$ is large and the number of variance components $K$ is small, as is typically the case in practice, HE offers substantial improvement in computation over REML. However, the ordinary least squares solution for variance components by HE is not guaranteed to be non-negative, leading to difficulties in downstream analyses and interpretation. In practice, negative estimates from HE are often truncated at zero; yet such naive truncation does not minimize the residual sum of squares in [3] within the parameter space (${\sigma }_k^2\ge 0,k=\mathrm{0,1}$). In addition, as will be illustrated in simulation studies in Section 4 and the Supplementary Note 2.3, naive truncation-based HE estimates generally have larger mean square error than estimates by both REML and our proposed REHE method, which we introduce in the next subsection.

2.2. The Restricted Haseman-Elston Regression

To prevent negative estimation of variance components by HE, while still preserving its computational efficiency, we propose a new variance components estimation method, termed the restricted Haseman-Elston (REHE) regression. Similar to HE, REHE is a moment estimator which regresses the empirical covariance of the observations on pre-specified correlation matrices that encode sample relatedness. However, instead of the ordinary least squares estimate by HE, REHE finds the non-negative minimizer of the residual sum of squares, ensuring sensible estimation of variance components (Supplementary Figure S10). Following [3], the REHE estimates of the variance components are expressed as:

$$\left({\tilde{\sigma }}_0^2,{\tilde{\sigma }}_1^2\right)=\arg \underset{\left({\sigma }_0^2\ge 0,{\sigma }_1^2\ge 0\right)}{\min }\sum _{l=1}^{n^2}{\left({\tilde{Y}}_l-{\tilde{X}}_{l1}{\sigma }_0^2-{\tilde{X}}_{l2}{\sigma }_1^2\right)}^2.$$ (4)

There is a closed form solution to [4] with only two variance components (Supplementary Note 1.1). With more than two variance components, iterative algorithms for non-negative least squares (NNLS) can easily solve [4] (Lawson and Hanson 1995; Goldfarb and Idnani 1983; Kim, Sra, and Dhillon 2006; Franc, Hlaváč, and Navara 2005). The convexity of [4] guarantees the numerical solutions of different solvers converge to the same global minimizer. Using the R package quadprog (v1.5–7, Berwin A. Turlach 2019), REHE estimation has approximately the same computational cost as HE, and is thus substantially faster than REML. In addition, the REHE estimator is consistent under mild conditions, and asymptotically normal when the correlation matrix for the random effect is sparse and block-diagonal, such as a sparse empirical kinship matrix; see the Appendix B for details.

2.2.1. REHE with resampling (reREHE)

Estimates obtained from REHE are non-negative. However, in some applications, a zero estimate for the variance component may still make the interpretation and/or subsequent analyses challenging. To address this issue, we equip REHE with a resampling procedure that provides strictly positive variance component estimates with high probability. The resampling procedure utilizes repeated subsamples, which can further improve the computational efficiency of REHE. The resulting approach is termed reREHE.

The idea of subsampling for REHE is simple: instead of estimating the variance components based on all the observations at the same time, we only use a small subsample of the data. The full-sample-based estimates and inference are usually well approximated by statistics based on subsamples (Politis, Romano, and Wolf 1999). Similar subsampling techniques are also extensively used in stochastic gradient descent methods (Metel 2017). Recently, subsampling has also been used with HE-based estimating equations (Zhou 2017). Our proposed reREHE procedure described in Algorithm [1] is unique in that it subsamples repeatedly to obtain the estimates. Although at a cost of reduced computational efficiency compared to using a single subsample, this resampling offers considerable advantages.

By averaging the estimates from repeated subsamples, the reREHE estimates have much higher accuracy compared to estimates based on a single subsample. At the same time, we obtain strictly positive estimates, unless in extremely rare cases when all subsamples yield zero estimates. Other summaries, such as median, can also be used to summarize estimates from repeated subsamples. When the sampling rate $r_s$ and the number of subsamples $B$ satisfy $r_s^{2}B<1$, reREHE achieves higher computational efficiency than REHE. On the other hand, choosing larger $r_s$ and $B$ results in more stable results. In the simulation studies and data applications, we chose $B=50$ and varied $r_s$ within $(0.05,0.1)$ to achieve a balance between accuracy and computational efficiency.

Algorithm 1.

reREHE Approach Estimation.

for $b=1$ to $B$ do

(a) Sample with replacement from $Y$ to obtain a length $\left[n{r}_s\right]$ vector $Y^{\left(b\right)}$ with sampling rate $r_s$, where $\left[x\right]$ is a function to round $x$ to the nearest integer; subset the correlation matrices accordingly as $D_k^{\left(b\right)}$, for $k=0,1.$

(b) Compute the variance component estimates $\left({\tilde{\sigma }}_{0,re}^{2\left(b\right)},{\tilde{\sigma }}_{1,re}^{2\left(b\right)}\right)$ based on $Y^{\left(b\right)}$ and $D_k^{\left(b\right)}$’s using REHE [4].

end for

Estimate the variance components as ${\tilde{\sigma }}_{k,re}^2=\frac{1}{B}\sum _{b=1}^B{\tilde{\sigma }}_{k,re}^{2\left(b\right)},k=0,1.$

2.2.2. REHE with Fixed Effects

The REHE estimation procedure can be easily modified to accommodate fixed effects. Consider the full model [1] where $X$ is the design matrix with $p$ covariates and $\mathbf{\beta }$ is the fixed effect coefficient vector. Let $P_X^{\perp }=I_n-X{\left(X^{\mathrm{\top }}X\right)}^{-1}{X}^{\mathrm{\top }}$ denote the projection matrix onto the orthogonal complement of the column space of $X$. We project the outcome $Y$ and the random effects ${\mathbf{\gamma }}_{\mathbf{k}}$’s (including the noise term ${\mathbf{\gamma }}_0$) as

$$\begin{array}{r}{Y}^{†}=P_X^{\perp }Y,{{\mathbf{\gamma }}_{\mathbf{k}}}^{†}=P_X^{\perp }{\mathbf{\gamma }}_{\mathbf{k}}.\end{array}$$

Recall that each random effect ${\mathbf{\gamma }}_{\mathbf{k}}$ follows a normal distribution with zero mean and covariance $D_k$. Writing $D_k^{†}=P_X^{\perp }{D}_k{P}_X^{\perp }$, model [1] becomes

$$Y^{†}=\sum _{k=0}^K{\sigma }_k{\mathbf{\gamma }}_{\mathbf{k}}{}^{†},{\mathbf{\gamma }}_{\mathbf{k}}{}^{†}\sim N_n\left(0,D_k^{†}\right),k=0,\dots ,K.$$ (5)

With model [5], we can directly apply the REHE approach as introduced in Section 2.2 to estimate the variance components. When the sample size $n$ is large, computing the projected correlation matrices $D_k^{†}$ is time-consuming. In genetic and genomics applications, the number of fixed effect covariates $p$ is much smaller than the sample size $n$. We also have balanced design in many of these applications. In those settings we are able to obtain good estimates of the fixed effects, and we can directly use the original correlation matrices $D_k$ instead of projected matrices $D_k^{†}$. In such cases, as in our data applications and simulation studies, we expect results based on $D_k^{†}$ to be very close to those based on $D_k$. We thus suggest using $D_k$ for computational efficiency when estimating model [5] via REHE or reREHE.

If the fixed effect coefficients $\mathbf{\beta }$ are of interest, they can be estimated using ordinary least squares as $\hat{\mathbf{\beta }}={\left(X^{\mathrm{\top }}X\right)}^{-1}{X}^{\mathrm{\top }}Y$, or weighted least squares as $\hat{\mathbf{\beta }}={\left(X^{\mathrm{\top }}{\hat{\Sigma }}^{-1}X\right)}^{-1}{X}^{\mathrm{\top }}{\hat{\Sigma }}^{-1}Y$, where $\hat{\Sigma }=\sum _{k=0}^K{\hat{\sigma }}_k^2{D}_k$ is based on previously estimated variance components ${\hat{\sigma }}_k^2$’s. While the resulting $\hat{\mathbf{\beta }}$ is consistent for $\mathbf{\beta }$, one can iteratively update ${\hat{\sigma }}_k^2$’s and $\hat{\mathbf{\beta }}$ as in (Sofer 2017).

2.2.3. Constructing Confidence Intervals with REHE

To obtain confidence intervals for variance component estimates, we use a parametric bootstrap procedure as summarized in Algorithm [2].

Algorithm 2.

Parametric Bootstrap Confidence Interval Construction for REHE.

Compute REHE estimates ${\tilde{\sigma }}_0^2,{\tilde{\sigma }}_1^2$ from [4], based on $\tilde{Y},D_0,D_1$;

for $b=1$ to $B$ do

(a) Generate outcome vector ${\tilde{Y}}^{*\left(b\right)}$ from $N_n\left(0,{\tilde{\sigma }}_0^2{D}_0+{\tilde{\sigma }}_1^2{D}_1\right)$;

(b) Compute REHE estimates ${{\tilde{\sigma }}_0}^{2\left(b\right)},{{\tilde{\sigma }}_1}^{2\left(b\right)}$ from [4], based on ${\tilde{Y}}^{*\left(b\right)},D_0,D_1$;

end for

Using the bootstrap samples of REHE estimates, ${\left({\tilde{\sigma }}_k^{2\left(b\right)}\right)}_{b=1}^B$, for $k=0,1$, we can construct Wald-type confidence intervals as

$$\left[{\tilde{\sigma }}_k^2-z_{\alpha /2}\times \mathrm{S}\mathrm{D}\left({\tilde{\sigma }}_k^{2\left(b\right)}\right),{\tilde{\sigma }}_k^2+z_{\alpha /2}\times \mathrm{S}\mathrm{D}\left({\tilde{\sigma }}_k^{2\left(b\right)}\right)\right],k=0,1,$$

where $z_{\alpha /2}$ is the $(1-\alpha /2)\times 100\text{th}$ percentile of the standard normal distribution, and $\mathrm{S}\mathrm{D}(\cdot )$ denotes the sample standard deviation over bootstrap samples. Wald-type confidence intervals are valid, provided that the estimates are normally distributed. We can also construct quantile bootstrap confidence intervals as

$$\left[{\tilde{\sigma }}_k^2-{\left({\tilde{\sigma }}_k^{2\left(b\right)}-{\tilde{\sigma }}_k^2\right)}_{1-\alpha },{\tilde{\sigma }}_k^2-{\left({\tilde{\sigma }}_k^{2\left(b\right)}-{\tilde{\sigma }}_k^2\right)}_{\alpha }\right],k=0,1,$$

where ${\left({\tilde{\sigma }}_k^{2\left(b\right)}-{\tilde{\sigma }}_k^2\right)}_{\alpha }$ is the $(1-\alpha )\times 100\text{th}$ empirical quantile of ${\left({\tilde{\sigma }}_k^{2\left(b\right)}-{\tilde{\sigma }}_k^2\right)}_{b=1}^B$.

For small sample sizes, the quantile confidence intervals are expected to be more robust than their Wald-type counterparts. When the REHE estimator is close to be normally distributed under large sample size, Wald-type confidence interval might have higher accuracy based on the same number of bootstrap samples. In simulation studies and real data applications, we chose the number of bootstrap samples $B=50$ to balance computational time and confidence interval accuracy. Confidence intervals for functions of variance components, such as heritability, can be similarly obtained by transforming the bootstrap samples accordingly.

When the correlation matrix $D_1$ is dense and the sample size $n$ is large, it can be computationally prohibitive to compute a matrix decomposition (through Cholesky or singular value decomposition) of $D_1$, which is required for the sampling step (a) in the Algorithm [2]. To speed up the inference procedure in this case, we propose using correlation matrix sparsification (Gogarten et al. 2019). The sparsification approximates the dense correlation matrix $D_1$ by a sparse block-diagonal matrix $D_1^{*}$, and largely accelerates matrix decomposition. Such a sparse block-diagonal structure is often approximately satisfied in genetic studies: for example, subjects are highly genetically correlated within the same family, and are remotely correlated across families (see Supplementary Figure S12 for an example of the kinship matrix). Note that a standard GRM calculated from genome-screen data may not be sparse. However, an empirical kinship matrix that reflects close familial relationship (and that can be sparsified) along with principal components for population structure has been proposed as an alternative to using a single GRM in linear mixed models (Gogarten et al. 2019; Hu et al. 2021). This approach has been used in various genetic studies with relatedness and population structure, including the HCHS/SOL (Conomos et al. 2016), the Population Architecture using Genomics and Epidemiology (PAGE) study (Wojcik et al. 2019), and a recent analysis for the Trans-Omics for Precision Medicine (TOPMed) program (Hu et al. 2021). (Gogarten et al. 2019) provides a detailed comparison of using a linear mixed model with a GRM, a dense kinship matrix (with PCs), and a sparse kinship matrix (with PCs). The genetic association testing results were shown to be very similar for all three approaches, but with a substantial increase in computational efficiency by using a sparse empirical kinship matrix. In the examples presented in Section 3, we use a dense empirical kinship matrix and PCs to model the correlation structure in the sample. We investigate the performance of sparsification in the additional simulation studies in Supplementary Note 2.1 and Note 2.3. Our application of matrix sparsification for inference of variance components in genetic studies is novel, and is discussed in detail in Supplementary Note 1.2.

3. Applications

3.1. GWAS and Heritability Studies with HCHS/SOL Data

To evaluate the performance of REHE and reREHE in genetics applications, we conducted a genome-wide association analysis as well as a heritability analysis using a publicly available data set from the HCHS/SOL (Sorlie et al. 2010; Conomos et al. 2016). The HCHS/SOL sample survey design consisted of a two-stage probability sample of households at four recruitment centers. For each center, census block groups were selected in defined communities, and households were sampled within census block groups (LaVange et al. 2010; Conomos et al. 2016). Among a total of 16,415 subjects enrolled in the study at baseline, 12,803 subjects were genotyped on a genome-wide single nucleotide polymorphisms (SNP) array containing 4,100,028 SNPs.

To perform a genome-wide association analysis, we tested the association between each SNP and the red blood cell count using a linear mixed model (Conomos et al. 2016). We first fit a null model, which was a linear mixed model without any genotype effect (Aulchenko, De Koning, and Haley 2007). We included fixed effects covariates age, gender, cigarette use, field center indicator, genetic subgroup indicator, the first five principal components for population stratification effect, and individual sampling weights (Conomos et al. 2016). We removed subjects that have missing values for the above covariates, and included 12,502 subjects in the analysis. Correlations among subjects was modelled by three random effects: genetic relatedness represented by estimated kinship, membership of household, and membership of community group (Conomos et al. 2016).

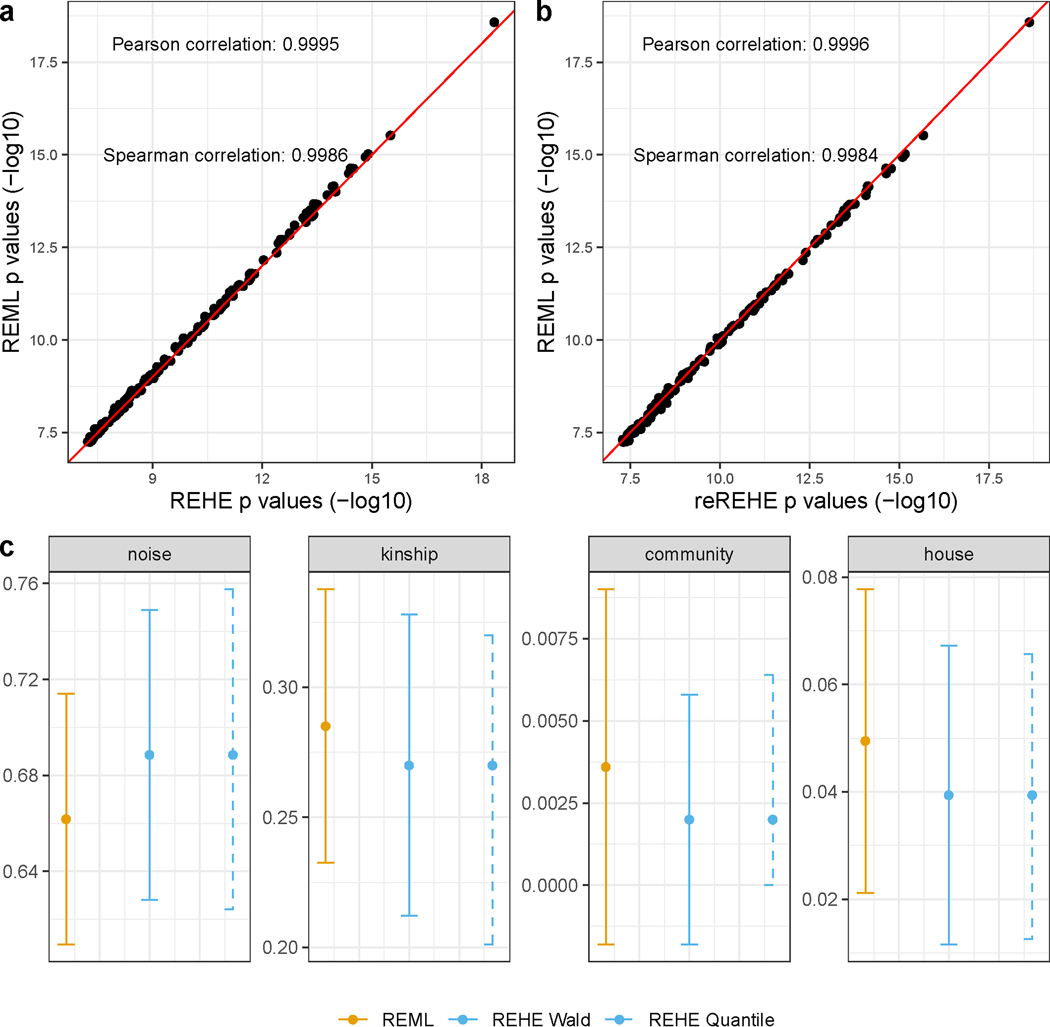
We separately applied REHE, reREHE and REML to estimate the null model with household membership matrix, community membership matrix, and estimated dense kinship matrix. For reREHE, we chose sampling rate $r_s=0.1$ and used mean summary function based on 50 repeated subsamples. With $n=\mathrm{12,502}$ subjects to be analyzed, REML took 23.9 minutes to estimate the null model, while REHE took only 2.4 minutes, a 10-fold improvement compared to REML. reREHE was similarly fast as REHE. Based on each estimated null model, we applied score tests for the association between each SNP and the red blood cell count (Conomos et al. 2016), and compared the resulting $p$-values. We focus here on the 164 SNPs with $p$-values no larger than the family-wise error rate (FWER) threshold of $5\times {10}^{-8}$ by at least one approach (Dudbridge and Gusnanto 2008), and presented $p$-values for all SNPs in the Supplementary Figure S11. As shown in Figure 1a and 1b, results based on REHE and reREHE have negligible differences from those based on REML. The correlations are all higher than 0.99 for the $p$-values on the $-{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ scale between REHE and REML, as well as between reREHE and REML. This concordance among REML, reREHE and REHE is not surprising as the estimated variance components are similar (Figure 1c).

Figure 1:

Results of genome-wide association testing analysis and heritability analysis with a HCHS/SOL data set. Association score test $p$-values ($-{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ scale) based on: a - REML against REHE estimated null models; b - REML against reREHE estimated null models. Only 164 SNPs with resulted $p$-values no larger than $5\times {10}^{-8}$ by at least one approach were presented. c - Dots represent point estimates of proportion of variance attributed to noise, kinship (heritability), community membership and household membership; bars represent corresponding confidence intervals. Results by REHE and REML are displayed. Two types of REHE-based confidence intervals are presented: Wald-type confidence intervals (REHE Wald), and quantile-type confidence intervals (REHE Quantile).

For the heritability analysis, we used the same data set and fit the same linear mixed null model as in the above genome-wide association analysis. The model was estimated based on REML and REHE separately. We obtained point estimates and confidence intervals for heritability (corresponding to the estimated dense kinship correlation matrix), proportions of variance explained by household membership, community block membership, and noise. REHE took 18.2 minutes to conduct the inference, compared to 23.9 minutes by REML. Heritability and variance proportions estimates, as well as the confidence intervals obtained by the REHE approach are all very similar compared to those obtained by REML (Figure 1c).

We used the R package GENESIS (v2.14.3, Conomos et al. 2019) for REML estimation and for conducting the genome-wide association analysis. All analyses were conducted on a computer with 2 $\times$ 6-core Intel Xeon CPU E5–2620 @ 2.00GHz 128GB RAM.

3.2. Network-based Pathway Enrichment Analysis with Breast Cancer Data

To further demonstrate that REHE and reREHE facilitate downstream analysis with fast variance component estimation, we performed a network-based pathway enrichment analysis, with a breast cancer data set from The Cancer Genome Atlas (TCGA) (TCGA 2012), preprocessed by Ma, Shojaie, and Michailidis (2019). The data set contains RNA-seq measurements for 2,598 genes from 100 genetic pathways, with 403 subjects from the ER positive subtype and 117 from the ER negative subtype.

Network-based pathway enrichment analysis tests for differential gene pathways associated with particular phenotypes under different conditions (Ma, Shojaie, and Michailidis 2016). It assumes a linear mixed model for the relationship between gene expressions and the phenotype (see Supplementary Note 1.3 and Ma, Shojaie, and Michailidis (2016) for details). Here, we compared the activities of 100 genetic pathways between the two ER groups. The ER group-specific gene networks — more specifically, the adjacency and influence matrices supplied to the linear mixed model — were estimated according to Ma, Shojaie, and Michailidis (2016). We estimated the variance components using REML, REHE and reREHE. For reREHE, we chose the sampling rate $r_s=0.1$ for sampling the subjects, and additionally sampled gene entries within each subject with sampling rate $0.5$ (see Supplementary Note 1.3 for details). The reREHE estimate was based on the mean of 50 repeated subsamples. After obtaining the variance components estimates, we tested for differences in the activity of each of the 100 genetic pathways (Shojaie and Michailidis 2009).

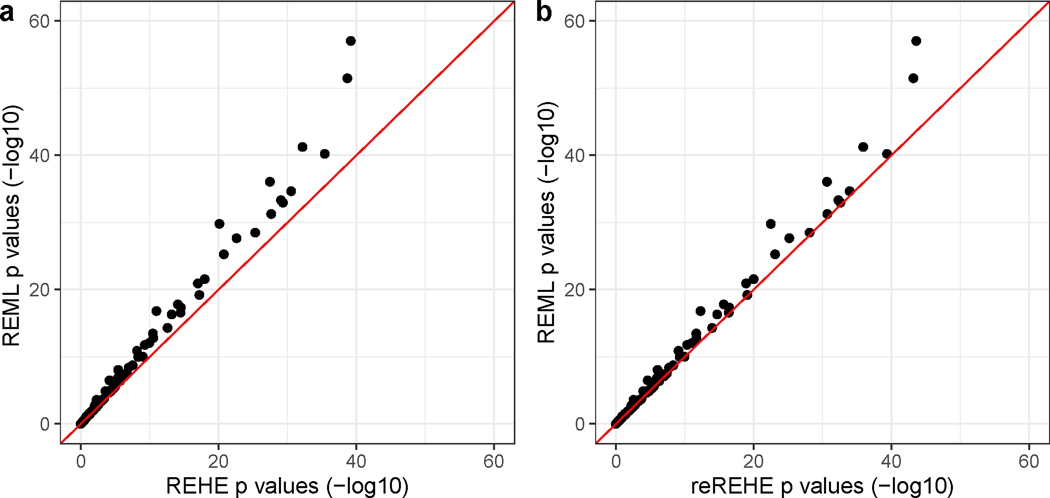
We observed substantial improvement in computational efficiency of reREHE and REHE compared to REML: reREHE- and REHE-based analyses both took less than 2 minutes, whereas analysis with REML took over 1 hour. Comparing the resulting $p$-values, REHE and reREHE produce slightly more conservative $p$-values than REML (Figure 2). Moreover, REHE yields a zero estimate for the noise variance component, the reREHE estimate is 0.0120, while the REML estimate is 0.266. The corresponding network variance estimates are also quite different: 0.273 by REML, 0.534 by reREHE and 0.610 by REHE. This may be an evidence that the variation explained by the network is much larger than the variation from noise in the true model. As illustrated in our additional simulation studies in Supplementary Note 2.4, REML may yield unreliable estimates under similar settings. We should thus take extra caution when interpreting REML-based estimates and test results in this application.

Figure 2:

Results of network-based pathway enrichment analysis based on a breast cancer data set. $p$-values ($-{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ scale) of t-tests for group difference of each gene pathway: a - compare REHE results against REML results; b - compare reREHE results against REML results. Two out-of-range data points are omitted from the plots, which correspond to: Glycosphingolipid biosynthesis - lacto and neolacto series pathway, with $p$-value $1.09\times {10}^{-307}$ by REML, $5.67\times {10}^{-276}$ by REHE, $3.74\times {10}^{-304}$ by reREHE; and Caffeine metabolism pathway with $p$-value $3.97\times {10}^{-201}$ by REML, $2.60\times {10}^{-179}$ by REHE, and $2.13\times {10}^{-198}$ by reREHE.

We conducted analyses for NetGSA using the R package netgsa (v3.1.0, Ma, Shojaie, and Michailidis 2016) on a computer with 2 $\times$ 6-core Intel Xeon X5650 @ 2.67 GHz, 96GB RAM.

4. Simulation Studies

4.1. Simulation Settings

To benchmark the improvement of REHE and reREHE over HE and REML for variance components and heritability estimation, we generated synthetic data based on the HCHS/SOL design (Sorlie et al. 2010; Conomos et al. 2016). HE and reREHE approaches were implemented only for point estimation comparison. We truncated negative HE estimates at zero. For reREHE, we used $B=50$ repeated subsamples, and chose sampling rates $r_s=0.05$ (reREHE 0.05) and $r_s=0.1$ (reREHE 0.1). Point estimates were evaluated in terms of the root mean squared error (RMSE). We constructed Wald-type (REHE-Wald) and quantile-type (REHE-quantile) confidence intervals at 95% level for REHE estimates, and compared their performances with REML-based confidence intervals in terms of coverage and interval width.

We simulated data based on the linear mixed model [2]. We used sample size $n\in$ {3,000, 6,000, 9,000, 12,000}. For each sample size, we set the true values of the variance components to $({\sigma }_0^2,{\sigma }_1^2)\in$ {$(0.1,0.1)$, $(0.04,0.1)$, $\left(\mathrm{0.1,0.04}\right)$, $(0.01,0.1)$, $(0.1,0.01)$}. These values were chosen based on previous simulation study settings (Sofer 2017) and estimates from real data applications (Fenger 2007). For each sample size $n$ selected, we generated the correlation matrix $D_1$ as a random sub-matrix of the kinship correlation matrix from the HCHS/SOL data set. For example, for $n=\mathrm{3,000}$, we subsampled 3,000 out of 12,803 subjects without replacement, and used the corresponding (subsample) kinship correlation matrix as $D_1$. Under each scenario, we ran 200 replicates. Computation was performed on a computer with 2 $\times$ 6-core Intel Xeon CPU E5–2620 @ 2.00GHz 128GB RAM.

We also conducted additional simulation studies to compare the approaches under different correlation structures; details of these experiments can be found in Supplementary Note 2.3.

4.2. Simulation Results

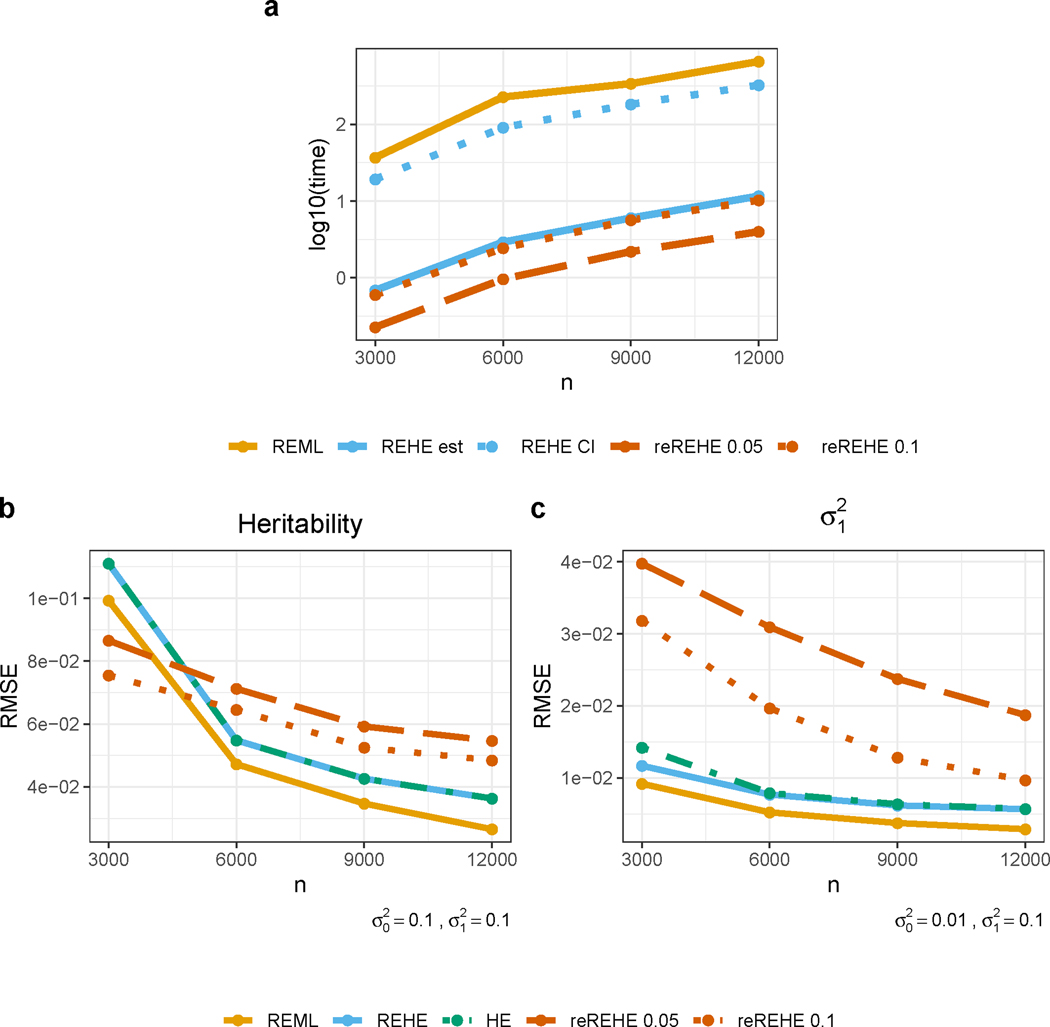
Simulation results clearly demonstrate the improvement in computational efficiency by REHE compared to REML. For point estimation, REHE was over 50 times faster than REML (Figure 3a). At the same time, REHE does not compromise estimation accuracy. Figure 3b and 3c show that REHE estimates of both the variance components and heritability are very close to those obtained by REML. Another advantage of REHE is that it corrects negative variance estimates from HE. To quantify this difference, We calculated the proportion of simulation replicates resulting in negative HE estimates (before zero-thresholding). This proportion reaches 23% with $n=\mathrm{3,000}$, $({\sigma }_0^2=0.01,{\sigma }_1^2=0.1)$, but reduces to 1.5% at $n=\mathrm{12,000}$. As pointed out before, REHE automatically corrects the issue of negative estimates without hard-thresholding. Besides, REHE has lower RMSE for point estimates when HE estimates are likely being negative (Figure 3c).

Figure 3:

Simulation results for REHE and reREHE compared to REML. a - CPU time in seconds (${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}$ scale): time is presented separately for fitting the model using REML (REML), for only computing point estimates by REHE (REHE est), for constructing confidence interval for variance components with REHE (REHE CI), for only computing point estimates by reREHE with subsampling rate $r_s=0.05$ (reREHE 0.05) and reREHE with subsampling rate $r_s=0.1$ (reREHE 0.1). b - Root mean squared error (RMSE) for heritability estimation; simulation was based on true values ${\sigma }_0^2=0.1,{\sigma }_1^2=0.1$, where ${\sigma }_0^2$ is the variance for noise, and ${\sigma }_1^2$ is the variance for the random effect. c - RMSE for ${\sigma }_1^2$ estimation; simulation was based on true values ${\sigma }_0^2=0.01,{\sigma }_1^2=0.1$.

The simulation results confirm that reREHE can provide strictly positive estimates with high probability. By providing a positive variance estimate where REHE gives a zero estimate (up to 23% of the simulation repetitions), reREHE is helpful for interpretation and downstream analysis, especially under small sample sizes. As shown in Figure 3b, reREHE based estimates have smaller RMSE than all other methods at sample size $n=\mathrm{3,000}$. With larger samples, the RMSE of reREHE is comparable to other methods under some settings (Figure 3b), but is much larger in other settings (Figure 3c, Supplementary Note 2.1 and Note 2.3). Setting a higher subsampling rate ($0.1$ compared with $0.05$) reduces RMSE (Figure 3b and 3c), but comes at the cost of reduced computational efficiency — reduction in computation time compared to REHE diminishes from 67% to 10% (Figure 3a).

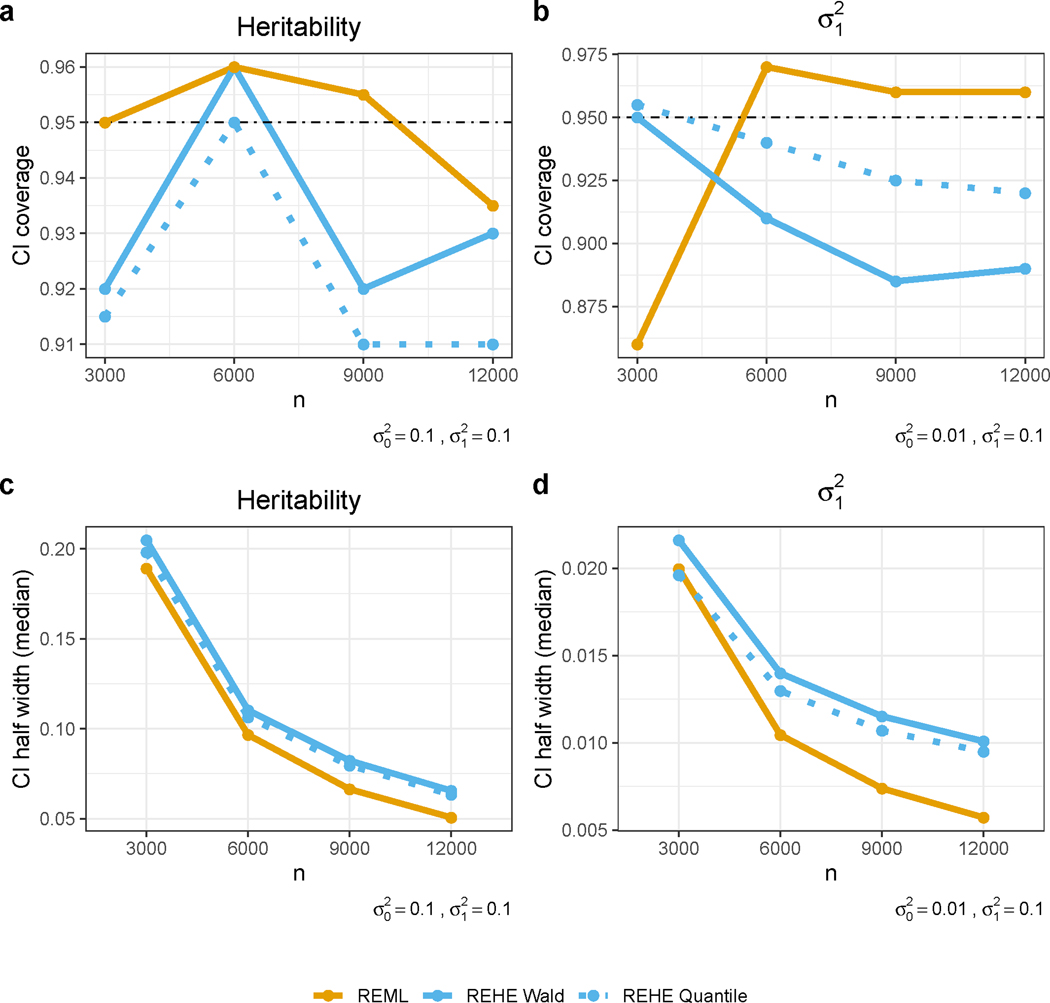
Turning to inference of variance components and heritability, both REHE based quantile-type and Wald-type confidence intervals provide reasonably good coverage with comparable interval width to REML confidence intervals (Figure 4). The empirical coverage is close to nominal level under most cases (Figure 4a and 4b), considering a Monte Carlo error of 0.03 based on 200 simulation replicates. REHE quantile-type intervals generally have better coverage than Wald-type intervals when the true variance components are very different (Figure 4b). In terms of confidence interval width, quantile-type REHE confidence intervals are generally narrower than Wald-type, and both are comparable to REML-based intervals (Figure 4c and 4d). Inference based on REHE is more time-consuming than REHE-based point estimation; however, it still achieves 50% reduction of computation time compared to REML (Figure 3a).

Figure 4:

Simulation results for confidence interval performance in terms of coverage and width. ${\sigma }_0^2$ is the variance for noise, and ${\sigma }_1^2$ is the variance for the random effect. a - Coverage for heritability confidence interval (CI); simulation was based on true values ${\sigma }_0^2=0.1,{\sigma }_1^2=0.1$. Monte Carlo error of 0.03 is expected for 200 simulation replications. b - Coverage for ${\sigma }_1^2$ CI; simulation was based on true values ${\sigma }_0^2=0.01,{\sigma }_1^2=0.1$. Monte Carlo error of 0.03 is expected for 200 simulation replicates. c - Line charts of median half width of heritability CI with increasing sample sizes; simulation was based on true values ${\sigma }_0^2=0.1,{\sigma }_1^2=0.1$. d - Line charts of median half width of ${\sigma }_1^2$ CI with increasing sample sizes; simulation was based on true values ${\sigma }_0^2=0.01,{\sigma }_1^2=0.1$.

Finally, in some simulation settings, we noticed that REML confidence intervals may suffer from under-coverage. For instance, with $n=\mathrm{3,000}$ samples, when one variance component is substantially smaller, the coverage of REML confidence intervals drop below 87% (Figure 4b). In other settings, REML confidence intervals even have coverage below 60%, and have little improvement with increasing sample size (Supplementary Note 2.3). Another concern is the numerical stability of REML, which fails to provide a confidence interval if the estimate of any variance component becomes zero during the iterative updates. We noticed frequent occurrence of this issue when the true variance components are unbalanced and the sample size is small — for $n=\mathrm{3,000}$ and $({\sigma }_0^2,{\sigma }_1^2)=\left(\mathrm{0.1,0.01}\right)$, REML is unable to provide a confidence interval in 17.5% of the replicates. This proportion increases to 30.5% in other settings (Supplementary Note 2.3). We view these two issues as a warning sign for REML-based inference in real applications, especially when the underlying variance components are very different and the sample size is small. In contrast, REHE-based inference is robust across different settings with valid confidence intervals and acceptable empirical coverage.

The above simulation results are supported by evidence from additional simulation studies in Supplementary Note 2.3.

5. Discussion

We proposed REHE for fast estimation of variance components in linear mixed models. This new approach is motivated by large-scale genetic studies, including HCHS/SOL, but is applicable more broadly to a wide range of study designs. Through simulation studies and data applications, we demonstrated its substantial gain in computational efficiency over REML, with little compromise in point estimation accuracy. We also showed in several simulation settings that REHE can be more robust than REML for estimating the variance components (Supplementary Note 2.4). Compared to HE, REHE corrects the issue of negative estimates, and offers potentially large gains in estimation accuracy. Therefore, REHE can be superior compared to HE and be a good alternative to REML for point estimation of variance components in linear mixed models.

We also proposed reREHE based on the resampling technique to produce strictly positive variance component estimates with high probability. Strictly positive estimates are more interpretable and may be more appealing for downstream analyses. Though reREHE estimates may have lower accuracy than REHE, the magnitude of the increase in RMSE was small in our experiments. We have also seen in the real data application that based on a subsampling rate of 0.1 and 50 subsamples, reREHE-based downstream analysis results are close to REML-based results. With suitably chosen subsampling rate and number of subsampling replicates, reREHE can achieve higher computational efficiency than REHE.

As mentioned previously, one can also use the median of the subsample results as the reREHE estimate. We explored this choice in the Supplementary Note 2.2 and Note 2.3. When the underlying variance components are very different, median-based reREHE estimates generally have smaller RMSE; otherwise mean-based reREHE performs better. However, median-based reREHE is more likely to yield zero estimates. A post hoc selection of the summary function can be made after observing the distribution of the subsample estimates based on reREHE.

As illustrated in the genome-wide association and pathway enrichment analysis examples in Section 3, in many applications, only variance component estimates are needed for downstream analyses. The computational burden of REML-based estimation prohibits these analyses on large data sets. Restricting the analysis to subsets of data reduces reliability and may yield contradictory conclusions. Given the fast and reliable estimates by REHE and reREHE in large data sets, we see great potential for their application in areas that only require point estimation of variance components.

When confidence intervals are also of interest, REHE remains a competitive alternative to REML for its robustness and numerical stability. As illustrated in our simulation studies, when the sample size is small and the true variance components are unbalanced, REML based inference may suffer from numerical instability and/or poor coverage. REHE consistently provides valid inference across all settings. Therefore, when the true variance components are expected to be very different and the sample size is not large, we recommend REHE over REML if inference on variance components is needed, as REML-based inference results may be unreliable.

Constructing confidence intervals for variance components when sample size is large (e.g. $n>\mathrm{10,000}$) is inherently computationally challenging. REHE only offers marginal improvements in computational efficiency over REML when it comes to inference. However, we can improve the computational efficiency for REHE confidence interval by parallelizing the bootstrap procedure. An alternative acceleration approach is to use correlation matrix sparsification (Gogarten et al. 2019, Supplementary Note 1.2). In the Supplementary Note 2.1 and Note 2.3, we explored the application of sparsification for constructing confidence intervals. Our conclusion is that sparsification improves computational efficiency in large sample settings ($n>\mathrm{12,000}$); however, it may result in less robust confidence intervals for both REHE and REML. We did not explore application of sparsification to linear mixed models with more than one random effect. We expect a much larger sample size beyond which sparsification would show improvement in computational efficiency.

We did not explore confidence interval construction for reREHE estimates in this paper. Due to the repeated subsampling procedure of reREHE, an analytical expression for the confidence intervals is not trivial. The parametric bootstrap procedure for REHE confidence interval construction is readily extendable to reREHE, which we expect to have similar performance as REHE confidence intervals. However, the computational burden will also be similar to those of REHE confidence intervals. Future research should explore fast inference procedure for REHE and reREHE estimates.

Appendix

A. HE Unbiasedness

The HE estimator is unbiased. The unbiasedness holds even if we use only a subset of the $n^2$ estimating equations, i.e., ignoring some entries of the relatedness matrices $D_k$’s.

Recall $n^2$ estimating equations are constructed:

$$\mathrm{E}\left[Y_i{Y}_j\right]={\sigma }_0^2{D}_0^{ij}+{\sigma }_1^2{D}_1^{ij},i,j=1,2,\dots n.$$

Suppose we use $S$ out of the $n^2$ estimating equations without duplicates to compute the HE estimates, $S\le n^2$. Let $(i_1,j_1),\dots ,(i_S,j_S)$ denote the selected indices. Similar to Section 2.1, we recast the problem of solving the $S$ estimating equations as the following linear regression problem. Let ${\tilde{Y}}_S=(Y_{i_1}{Y}_{j_1},\dots ,Y_{i_S}{Y}_{j_S})$ denote the linear regression outcome vector, and let ${\tilde{X}}_S$ denote the design matrix by stacking the tuples $(D_0^{i_s{j}_s},D_1^{i_s,j_s})$, $s=1,\dots ,S$. Note that we have

$$\mathrm{E}\left[{\tilde{Y}}_S\right]={\tilde{X}}_S{\mathbf{\sigma }}^2,$$

where the equality holds regardless of the higher moments of $Y$ or the positions of the $S$ indices. The closed form expression of the HE estimates in this case is ${\hat{\mathbf{\sigma }}}^2=({\tilde{X}}_S^{\mathrm{\top }}{\tilde{X}}_S{)}^{-1}{\tilde{X}}_S^{\mathrm{\top }}{\tilde{Y}}_S$. We thus have:

$$\begin{array}{rr}\mathrm{E}\left({\hat{\mathbf{\sigma }}}^2\right)& =\left({\tilde{X}}_S^{\mathrm{\top }}{\tilde{X}}_S{)}^{-1}{\tilde{X}}_S^{\mathrm{\top }}\mathrm{E}\right({\tilde{Y}}_S)=({\tilde{X}}_S^{\mathrm{\top }}{\tilde{X}}_S{)}^{-1}{\tilde{X}}_S^{\mathrm{\top }}{\tilde{X}}_S{\mathbf{\sigma }}^2={\mathbf{\sigma }}^2.\end{array}$$

Therefore, the HE estimates is unbiased, even if a subset of the $n^2$ estimating equations is used.

B. REHE Consistency and Asymptotic Normality

The REHE estimator is consistent under mild conditions, and is asymptotically normal when the random effect correlation matrix is sparse and block-diagonal.

For expositional clarity, we assume the diagonal entries of the kinship matrix $D_1$ are scaled to 1. We proceed with first establishing consistency of the HE estimator. By [3], the HE estimate is the ordinary least squares solution to a linear regression problem. We write out the model for this linear regression as

$$\tilde{Y}=\tilde{X}{\mathbf{\sigma }}^2+\widetilde{ϵ},$$

for the length $n^2$ outcome vector $\tilde{Y}=\mathrm{v}\mathrm{e}\mathrm{c}\left(Y{Y}^{\mathrm{\top }}\right)$, the $n^2\times 2$ fixed effect design matrix $\tilde{X}=\left(\mathrm{v}\mathrm{e}\mathrm{c}\right(D_0),\mathrm{v}\mathrm{e}\mathrm{c}(D_1\left)\right)$ and the length $n^2$ error vector $\widetilde{ϵ}$ with covariance matrix $R$. Note that $R^{ij}=\mathrm{C}\mathrm{o}\mathrm{v}({\tilde{Y}}_i,{\tilde{Y}}_j)$, which is related to the forth moment of $Y$. Thus $R$ is not a diagonal matrix. Under this framework, the HE estimator is a special case of the generalized estimating equations estimator, with $I_n$ as the working correlation matrix, the total number of clusters bounded (equals to $1$ in this case), and the cluster size $n^2$ going to infinity. Such as estimator has been studied in Xie and Yang (2003), see Example 2.1 and Example 5.1. The consistency of HE estimates holds under the condition ($I_{\omega }$) or ($I_{\omega }^{*}$) in Xie and Yang (2003), which in our case corresponds to

$$\left({\mathrm{I}}_{\mathrm{\omega }}\right):{\mathrm{\lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathrm{H}}_{\mathrm{n}}{\mathrm{M}}_{\mathrm{n}}^{-1}{\mathrm{H}}_{\mathrm{n}}\right)\stackrel{n\to \mathrm{\infty }}{\to }\mathrm{\infty }$$

$$\left({\mathrm{I}}_{\mathrm{\omega }}^{\mathrm{*}}\right):{\mathrm{\lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}(\mathrm{H}\_\mathrm{n})/{\mathrm{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\mathrm{R}\right)\stackrel{n\to \mathrm{\infty }}{\to }\mathrm{\infty }$$

where

$$\begin{gathered} H_n={\tilde{X}}^{\mathrm{\top }}\tilde{X} \\ {M}_n={\tilde{X}}^{\mathrm{\top }}R\tilde{X}, \end{gathered}$$

and ${\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(X\right)$ (${\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(X\right)$) denotes the smallest (largest) eigenvalue of the symmetric matrix $X$. As discussed in Xie and Yang (2003), for ($I_{\omega }$) or ($I_{\omega }^{*}$) to hold it suffices to bound the correlation of $\widetilde{ϵ}$ by $|R^{ij}/\sqrt{R^{ii}{R}^{jj}}|\le {\rho }_h$, where $h=|i-j|$ and $\{{\rho }_h{\}}_{h=1}^{\infty }$ is a sequence of values with $\underset{h\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}{\mathrm{\rho }}_h=0$. One can then verify that Assumption [1] is sufficient to guarantee that the correlations of $\widetilde{ϵ}$ are properly bounded, based on $\mathrm{C}\mathrm{o}\mathrm{v}(Y_i{Y}_j,Y_{i\text{'}}{Y}_{j\text{'}})=V_Y^{ii\text{'}}{V}_Y^{jj\text{'}}+V_Y^{ij\text{'}}{V}_Y^{ji\text{'}}$, for $V_Y=\mathrm{E}\left(Y{Y}^{\mathrm{\top }}\right)={\sigma }_0^2{D}_0+{\sigma }_1^2{D}_1$.

Assumption 1 (Weak Condition).

The covariance matrix $D_1$ satisfies $\left|D_1^{ij}\right|\le {\rho }_h^{\mathrm{*}},h=|i-j|$, for some sequence of values $\{{\rho }_h^{\mathrm{*}}{\}}_{h=1}^{\mathrm{\infty }}$ with $\underset{h\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{\mathrm{\rho }}_h^{\mathrm{*}}=0$.

Assumption [1] is natural in many genetic studies as it is expected that off-diagonal correlation entries would decrease to zero after properly rearranging the rows and columns of the correlation matrix.

The asymptotic normality of the HE estimator requires an stronger assumption on the structure of $D_1$. Note that we do not need this strong assumption to show the consistency of REHE or to construct bootstrap confidence intervals for the REHE estimator. Suppose Assumption [2] holds for a sparse and block-diagonal kinship matrix $D_1$.

Assumption 2 (Strong Condition).

$D_1$ is sparse and block-diagonal such that

$$D_1=\left(\begin{array}{cccc}{D}_1^{\left(1\right)}& 0& 0& \dots \\ 0& D_1^{\left(2\right)}& 0& \dots \\ ⋮& & \ddots & \\ 0& 0& 0& D_1^{\left(M\right)}\end{array}\right),$$

where $D_1^{\left(m\right)}(m=1,\dots ,M)$ are square blocks along the diagonal of $D_1$, and $M$ is the total number of blocks.

Such correlation structures are often approximately satisfied in genetic studies: for example, subjects are highly genetically correlated within the same family, and are remotely correlated across families. Let $s_m$ denote the number of rows/columns in $D_1^{\left(m\right)}$, and $Y^{\left(m\right)}$ denote the $s_m\times 1$ subvector of $Y$ corresponding to the $m^{th}$ block. For example, $Y^{\left(1\right)}$ is the subvector corresponding to the first $s_1$ elements of $Y$. By construction, $Y^{\left(m\right)}$’s are independent and normally distributed with zero mean and covariance ${\sigma }_0^2{I}_{s_m}+{\sigma }_1^2{D}_1^{\left(m\right)}$, for $m=1,\dots ,M$. For sparse block-diagonal $D_1$, we simplify $\tilde{Y}$ and $\tilde{X}$ in [3] by discarding elements corresponding to zero entries of $D_1$:

$$\begin{array}{rr}\tilde{Y}& =\left(\begin{array}{c}{\tilde{Y}}^{\left(1\right)}\\ {\tilde{Y}}^{\left(2\right)}\\ ⋮\\ {\tilde{Y}}^{\left(M\right)}\end{array}\right),\tilde{X}=\left(\begin{array}{c}{\tilde{X}}^{\left(1\right)}\\ {\tilde{X}}^{\left(2\right)}\\ ⋮\\ {\tilde{X}}^{\left(M\right)}\end{array}\right),\end{array}$$

where we denote ${\tilde{Y}}^{\left(m\right)}=\mathrm{v}\mathrm{e}\mathrm{c}\left(Y^{\left(m\right)}{Y}^{\left(m\right)\mathrm{\top }}\right)$ and ${\tilde{X}}^{\left(m\right)}=\left(\mathrm{v}\mathrm{e}\mathrm{c}\left(I_n^{\left(m\right)}\right),\mathrm{v}\mathrm{e}\mathrm{c}\left(D_1^{\left(m\right)}\right)\right),$ for $m=1,\dots ,M$. The independence of $Y^{\left(m\right)}$’s implies independence of ${\tilde{Y}}^{\left(m\right)}$’s. As the number of blocks $M\to \infty$, the HE estimates ${\hat{\mathbf{\sigma }}}_M^2=\left({\hat{\sigma }}_{0,M}^2,{\hat{\sigma }}_{1,M}^2\right)$ converge in probability to the true variance components ${\mathbf{\sigma }}^2=\left({\sigma }_0^2,{\sigma }_1^2\right)$ at a rate of $\sqrt{M}$ or faster (Xie and Yang 2003). Moreover, when the maximum block size $s=\underset{1\le m\le M}{\mathrm{m}\mathrm{a}\mathrm{x}}\left(s_m\right)$ does not go to infinity too fast as $M\to \infty$, the HE estimates are asymptotically normal, with a rate of $\sqrt{M}$ (Xie and Yang 2003):

$$W_M^{-1/2}{H}_M\left({\widehat{\mathit{\sigma }}}_M^2-{\mathit{\sigma }}^2\right)\stackrel{d}{\to }{N}_2(0,I_2),$$ (6)

where

$$W_M=\sum _{m=1}^M{\left({\tilde{X}}^{\left(m\right)}\right)}^{\mathrm{\top }}{R}^{\left(m\right)}{\tilde{X}}^{\left(m\right)},R^{\left(m\right)}=\mathrm{C}\mathrm{o}\mathrm{r}\left({\tilde{Y}}^{\left(m\right)}\right),H_M=\sum _{m=1}^M{\left({\tilde{X}}^{\left(m\right)}\right)}^{\mathrm{\top }}{\tilde{X}}^{\left(m\right)}.$$

In genetic studies, it is typical that subjects belong to small unrelated groups so that $s$ is bounded, and the number of groups $M$ increases with increasing sample sizes. These settings satisfy the conditions for the HE estimator’s consistency and asymptotic normality.

We are now ready to establish the asymptotic properties of the REHE estimator. As implied by [4], the REHE estimates ${\tilde{\mathbf{\sigma }}}^2$ are different from the HE estimates ${\hat{\mathbf{\sigma }}}^2$ only when HE yields negative estimates for some variance components. Let $\mathbb{P}\left({\hat{\sigma }}_0^2\ge 0,{\hat{\sigma }}_1^2\ge 0\right)$ denote the probability of the HE estimates being non-negative, which equals $\mathbb{P}\left({\tilde{\mathbf{\sigma }}}^2={\hat{\mathbf{\sigma }}}^2\right)$. Based on the consistency of the HE estimator, we have:

$$\mathbb{P}\left({\tilde{\mathbf{\sigma }}}^2={\hat{\mathbf{\sigma }}}^2\right)=\mathbb{P}\left({\hat{\sigma }}_0^2\ge 0,{\hat{\sigma }}_1^2\ge 0\right)\stackrel{n\to \infty }{\to }1,$$

indicating asymptotic equivalence of the HE and REHE estimators. This implies the consistency of the REHE estimator, which only requires Assumption [1] on $D_1$. Note that despite their asymptotic equivalence, our simulation results in Section 4 clearly show the advantages of REHE over HE in finite samples.

Next, we show that under the stronger Assumption [2], $W_M^{-1/2}{H}_M({\tilde{\mathbf{\sigma }}}^2-{\hat{\mathbf{\sigma }}}^2)$ is $o_p\left(1\right)$:

$$\mathbb{P}\left(W_M^{-1/2}{H}_M\left({\tilde{\mathbf{\sigma }}}^2-{\hat{\mathbf{\sigma }}}^2\right)=0\right)\ge \mathbb{P}\left({\tilde{\mathbf{\sigma }}}^2-{\hat{\mathbf{\sigma }}}^2=0\right)\stackrel{M\to \infty }{\to }1.$$

We then have

$$\begin{gathered} W_M^{-1/2}{H}_M({\tilde{\mathbf{\sigma }}}^2-{\mathbf{\sigma }}^2)=W_M^{-1/2}{H}_M({\tilde{\mathbf{\sigma }}}^2-{\hat{\mathbf{\sigma }}}_{}^2)+W_M^{-1/2}{H}_M({\hat{\mathbf{\sigma }}}_{}^2-{\mathbf{\sigma }}^2) \\ =o_p\left(1\right)+W_M^{-1/2}{H}_M({\hat{\mathbf{\sigma }}}_{}^2-{\mathbf{\sigma }}^2). \end{gathered}$$

Therefore, we have established that under Assumption [2], the REHE estimator ${\tilde{\mathbf{\sigma }}}^2$ satisfies:

$$W_M^{-1/2}{H}_M\left({\tilde{\mathbf{\sigma }}}^2-{\mathbf{\sigma }}^2\right)\stackrel{d}{\to }{N}_2\left(0,I_2\right).$$ (7)

Here we note that the REHE estimator is slightly biased in finite samples due to the correction of negative estimates. However, as we have observed in the simulation studies, the variance and mean squared error of the REHE estimator were smaller than those of the HE estimator, indicating the REHE a better estimator.