A Gaussian Approximation Approach for Value of Information Analysis

Abstract

Most decisions are associated with uncertainty. Value of information (VOI) analysis quantifies the opportunity loss associated with choosing a suboptimal intervention based on current imperfect information. VOI can inform the value of collecting additional information, resource allocation, research prioritization, and future research designs. However, in practice, VOI remains underused due to many conceptual and computational challenges associated with its application. Expected value of sample information (EVSI) is rooted in Bayesian statistical decision theory and measures the value of information from a finite sample. The past few years have witnessed a dramatic growth in computationally efficient methods to calculate EVSI, including metamodeling. However, little research has been done to simplify the experimental data collection step inherent to all EVSI computations, especially for correlated model parameters. This article proposes a general Gaussian approximation (GA) of the traditional Bayesian updating approach based on the original work by Raiffa and Schlaifer to compute EVSI. The proposed approach uses a single probabilistic sensitivity analysis (PSA) data set and involves 2 steps: 1) a linear metamodel step to compute the EVSI on the preposterior distributions and 2) a GA step to compute the preposterior distribution of the parameters of interest. The proposed approach is efficient and can be applied for a wide range of data collection designs involving multiple non-Gaussian parameters and unbalanced study designs. Our approach is particularly useful when the parameters of an economic evaluation are correlated or interact.

Economic evaluation is a framework to quantify the expected costs and benefits across several strategies and determine the overall optimal strategy by simplifying real-life complexity. However, recommendations from these analyses are rarely definitive due to uncertain input parameters that may translate to “suboptimal” recommendations. Choosing the optimal strategy at the time of decision making can incur a large opportunity cost because the overall optimal strategy might be suboptimal in certain realizations of the input parameter values. Value of information analysis (VOI) quantifies this opportunity cost and sets the maximum limit on how much new information is potentially worth. For example, expected value of perfect information (EVPI) measures the value of eliminating uncertainty from all model parameters while expected value of partial perfect information (EVPPI) measures the EVPI for a subset of parameters of interest. Eliminating uncertainty can only be achieved with an infinitely large sample, which is not feasible in practice. Thus, expected value of sample information (EVSI) is generally more informative than EVPPI because it measures the value of reducing uncertainty from a finite sample of size n.

EVSI is defined as the value of information from a finite sample (n) for 1 or more parameters in a decision-analytic model.¹ EVSI is rooted in Bayesian statistical decision theory and measures the value of information by generating potential new data before any actual data collection is conducted.^2–5

Thus, EVSI can be of important practical application in research prioritization, allocation of scarce resources, and informing the type and size of the study design for future data collection efforts.^1,6–8 In practice, however, EVSI remains underused due to many computational and conceptual challenges associated with its practical implementation.⁹

EVSI is currently an area of active methodological research. In the past 2 decades, several new approaches have been proposed to help researchers implement EVSI. For example, Brennan and others¹⁰ proposed a nested 2-level Monte-Carlo simulation (2MCS) to numerically compute EVSI as an approximation to the double integrals involved in the EVSI equation. Although their approach applies to many situations, in practice it is often computationally expensive. In addition, it may be challenging to implement when there exist correlations between the parameters of interest (θ_I) and the complementary set of the parameters (θ_C), where θ = {θ_I, θ_C}. Brennan and Kharroubi^5,11 have proposed a Bayesian Laplace approximation that replaces both the Bayesian updating and the inner Monte Carlo sampling to compute the posterior expectation of the parameters of interest. However, this approach may still be computationally expensive and generally assumes that the observations are independent and identically distributed (iid), where the number of study participants represents the sample size used to estimate the mean and standard error of the parameters. Ades and others¹² have developed an analytic approach to calculate EVSI that is generally computationally efficient. However, this technique is limited to models with certain structural forms and certain independence assumptions on the parameters are made.

More recent developments have used a metamodeling approach to simplify the inner expectation. For example, Jalal and others¹³ adopted the unit normal integral function (UNLI) in addition to linear regression metamodeling to calculate EVSI. Their technique assumes that the parameters of interest have a normal distribution, and it can only be used for a single parameter at a time if there are multiple strategies. Strong and others¹⁴ have proposed a generalized additive models (GAM) metamodeling approach to approximate the inner expectation by defining a summary statistic. Furthermore, Menzies¹⁵ adopts an efficient algorithm that uses importance sampling in addition to a metamodel to simplify EVSI computations. This approach requires the user to define 2 functions: a function for creating data sets from the prior and another function for computing the likelihood given the data sets. Thus, significant advances have been made in increasing the computational efficiency of EVSI.¹⁶ However, little research has been done to overcome a second challenge of EVSI, which involves Bayesian updating for study designs that involve multiple correlated parameters or when a study design is unbalanced involving several parameters informed by different sample sizes.

In this study, we propose a simplification of the data collection process via a Gaussian approximation (GA) of the traditional Bayesian updating process. This approximation generalizes Raiffa and Schlaifer’s original work^3,4,17 for a normal prior and normal data likelihood to a wide range of univariate and multivariate non-Gaussian distributions. The GA approach only requires a data set of prior values and their associated prior effective sample size n₀. In addition, the GA allows complex correlation structures among the model parameters θ. Similar to the previous approaches,^13–15 our approach uses a metamodel on a single probabilistic sensitivity analysis (PSA) data set, which is routinely obtained in economic evaluations.^18,19

Methods

EVSI

EVSI is typically expressed as^10,12

$${\text{EVSI}}_{{\text{θ}}_I}={\mathbb{E}}_X\left[\underset{d}{\max }{\mathbb{E}}_{\text{θ}}[B(d,\text{θ})\mid X]\right]-\underset{d}{\max }{\mathbb{E}}_{\text{θ}}[B(d,\text{θ})],$$ (1)

where θ are the parameters of the decision model and consist of the parameters of interest θ_I and the complementary parameters θ_C, X are new potential data, and B(d, θ) is the net benefit from strategy d. Thus, EVSI is the difference between the expected maximum benefit given new potential data X and the maximum benefit with current information. Alternatively, EVSI can be expressed as a function of the opportunity loss from choosing a suboptimal decision rather than difference between 2 benefits, such that

$${\text{EVSI}}_{{\text{θ}}_I}={\mathbb{E}}_X\underset{d}{\max }{\mathbb{E}}_{\text{θ}}[L(d,\text{θ})\mid X],$$ (2)

where L(d, θ) = B(d, θ) – B(d*, θ) is the opportunity loss from choosing the optimal decision d* among all possible decisions D, given a set of parameter values θ. (Appendix A shows the steps of deriving equation (2) from equation (1).)

The inner expectation ${\mathbb{E}}_{\text{θ}}[L(d,\text{θ})|X]$ computes the opportunity loss from choosing d instead of d* given a set of parameter values θ and a potential candidate for X . Here, we are interested in avoiding the maximum loss from any strategy d, and therefore we take the ${\max }_d{\mathbb{E}}_{\text{θ}}[L(d,\text{θ})|X]$. Since we do not know what the new data X may look like a priori, we take the expectation over all possible candidates of X and compute ${\mathbb{E}}_X{\max }_d{\mathbb{E}}_{\text{θ}}[L(d,\text{θ})|X]$. Thus, EVSI sets our upper limit on how much we should be willing to pay to avoid the expected maximum opportunity loss over all strategies.

The 2 nested expectations in equations (1) and (2) could be approximated with 2 nested Monte Carlo loops,¹⁰ which are often computationally expensive even for relatively simple models. We simplify equation (2) using 2 approximations: 1) we approximate the opportunity losses L as a linear relation of the parameters of interest (or a transformation of these parameters), and 2) we propose a Gaussian approximation approach to further simplify the Bayesian updating process to compute θ|X. Previous studies have described the first approximation.^13,14 The main contribution of this article is related to simplifying some of the computational and conceptual burdens of conducting the Bayesian updating and the data generation process using a Gaussian approximation approach.

Linear Metamodel Approximation

We propose a linear metamodeling approach to simplify the inner expectation in equation (2). The linear metamodel (LM) is a second model involving regressing the model output, such as the opportunity loss L, on the input parameters (or a transformation of these parameters).²⁰ LM has been used on PSA data sets to reveal the characteristics of a model²¹ and to simplify VOI computations.^13,14,22 The LM can range from a simple linear regression that describes a linear relation between the model inputs and outputs to spline regressions that are more flexible and can describe a linear relation between transformations of a set of basis functions of θ and L.²³

In VOI analysis, we are generally interested in the opportunity loss L(d, θ) explained by θ_I; therefore, we can define a linear metamodel as

$$\text{L}(d,\text{θ})={\text{β}}_{\text{0}}+{\text{β}}_{\text{1}}{\text{θ}}_I+e,$$ (3)

where β₀ is an intercept, β₁ is a regression coefficient for θ_I, and e is a residual term. This residual term captures the complementary parameters, θ_C, and the nonlinearity in the model. In addition, e also captures Monte Carlo noise in stochastic models, such as microsimulation models. Thus, the expected loss is estimated using the LM given θ_I by

$$\widehat{L}(d,\text{θ})|{\text{θ}}_I={\widehat{\text{β}}}_0+{\widehat{\text{β}}}_1{\text{θ}}_I,$$ (4)

where ${\widehat{\text{β}}}_0$ and ${\widehat{\text{β}}}_1$ can be estimated by regressing L on θ_I in equation (3) via ordinary least squares (OLS) using a PSA data set. Equation (4) simplifies the inner expectation in EVPPI because it computes the expected opportunity loss while averaging over θ_C. Various versions of this equation have been used as a step in the calculation of EVPPI.^13,22 This simple equation is appealing because the regression coefficients can be easily estimated in any standard statistical software such as using the function lm in R by defining lm1 <– lm (L ~ theta_I). Then, it is usually straightforward to compute the conditional loss using the predict function, such that L_hat <– predict(lm1).

In EVSI, the inner expectation measures the opportunity loss given the updated distribution of θ after observing a potential data set X⁽ⁱ⁾ from all possible candidates. This inner expectation then needs to be reevaluated for all the possible X⁽ⁱ⁾ candidates that are sampled from the outer expectation. This nested expectation structure renders EVSI computationally expensive via Monte Carlo simulation because it requires the model to be reevaluated many times inside these nested expectations to compute L(d, θ) for each sample from the posterior distribution of θ_I|X⁽ⁱ⁾ and the prior distribution of θ_C.

The LM is a linear approximation of the original simulation model. This LM defines a linear relation between L(d, θ) and θ. That is, the structure of the LM is independent on the values of θ once the LM is defined for a particular model. Thus, we can plug in the posterior mean of θ_I, ${\mathbb{E}}_{\text{θ}}\left[{\text{θ}}_I|X^{(i)}\right]$ and use the LM to compute the conditional loss given each data set X⁽ⁱ⁾. The LM simplifies the nested computation in EVSI because the inner expectation can be simplified to a linear combination of the posterior expectation of θ_I. Specifically, the inner expectation of EVSI given X⁽ⁱ⁾ in equation (2), ${\mathbb{E}}_{\text{θ}}\left[L(d,\text{θ})\mid X^{(i)}\right]$, can be estimated as a linear function of the posterior mean of θ_I, ${\mathbb{E}}_{\text{θ}}\left[{\text{θ}}_I|X^{(i)}\right]$, such that

$${\tilde{L}}_d^{\left(i\right)}={\widehat{\text{β}}}_0+{\widehat{\text{β}}}_1{\varphi }^{(i)},$$ (5)

where we denote ${\tilde{L}}_d^{(i)}=\widehat{L}(d,\text{θ})|X^{(i)}$, and ${\varphi }^{(i)}={\mathbb{E}}_{\text{θ}}\left[{\text{θ}}_I|X^{(i)}\right]$.

Notice that if θ_I and θ_C are correlated a priori, then data collection on θ_I will likely inform θ_C as well. Fortunately, ${\widehat{\beta }}_1$ captures this correlation, and it allows the opportunity loss to also reflect the impact of the new data X on θ_C.

Thus, we only need ${\widehat{\beta }}_0$, ${\widehat{\beta }}_1$, and ϕ to compute ${\tilde{L}}_d$ for each strategy. In R, we can achieve this by using the predict function again using ϕ instead, such that L_tilde <– predict (lm1, newdata = phi). Thus, we can approximate EVSI using

$${\widehat{\text{EVSI}}}_{{\text{θ}}_I}={\mathbb{E}}_X\underset{d}{\max }\left({\tilde{L}}_d\right),$$ (6)

where all the variables have been previously defined.

So far, we have assumed that we know ϕ, θ_I is a single parameter, and the relation between L and θ_I is linear. In the next section, we show how to approximate ϕ using our Gaussian approximation approach, and in the following sections, we relax the other assumptions.

Gaussian Approximation of ϕ

The posterior mean ϕ is a random variable because X is random. The distribution of ϕ is often referred to as the “preposterior” distribution because it defines the distribution of the posterior mean prior to actual data collection. In this section, we first show that if θ_I has a Gaussian distribution and the data likelihood of X|θ_I is also Gaussian, then we can estimate ϕ directly from θ_I by assuming that the prior is the only source of randomness in ϕ. Later, we apply this relation to non-Gaussian prior-likelihood pairs and compare the approximation numerically to traditional Bayesian updating for these non-Gaussian cases.

Let’s assume that our prior knowledge of θ_I is based on a study of size n₀, such that

$${\text{θ}}_I\sim N\left({\text{μ}}_{\text{0}},\frac{{\text{σ}}^{\text{2}}}{n_0}\right),$$ (7)

where μ₀ and σ² are the population mean and variance of θ_I, respectively.

We are interested in generating a “new” sample mean from n new participants given the distribution of θ_I. This new mean X also follows a Gaussian distribution such that

$$X|{\text{θ}}_I\sim N\left({\text{θ}}_I,\frac{{\text{σ}}^2}{n}\right).$$ (8)

Because the data likelihood and the prior are conjugate, we can express the posterior distribution as

$${\text{θ}}_I|X\sim N\left(\frac{n_0{\text{μ}}_0+nX}{n_{\text{0}}+n},\frac{{\text{σ}}^2}{n+n_0}\right).$$ (9)

The mean of this distribution is ϕ:

$$\text{ϕ}=\frac{n_0{\text{μ}}_0+nX}{n_0+n}.$$ (10)

Notice that ϕ is a function of the marginalized X, and as such it is also a random variable that has the same mean as θ_I, that is,

$$\begin{gathered} {\mathbb{E}}_X[\text{ϕ}]={\mathbb{E}}_X\left[{\mathbb{E}}_{{\text{θ}}_I}\left[{\text{θ}}_I\mid X\right]\right] \\ {\mathbb{E}}_X[\text{ϕ}]={\mathbb{E}}_{{\text{θ}}_I}\left[{\text{θ}}_I\right] \\ {\mathbb{E}}_X[\text{ϕ}]={\text{μ}}_0. \end{gathered}$$ (11)

It is important here to distinguish between the posterior mean, which is a random variable denoted by ϕ, from the mean of ϕ with respect to X, which is a single value equal to μ₀. The variance of ϕ can be defined from both equation (10) and the variance of the marginalized X, which is equal to the sum of the prior variance and the variance of the data likelihood,²⁴ such that Var(X) = σ²/n + σ²/n₀. Therefore, the variance of ϕ is expressed as

$$\begin{gathered} {\text{Var}}_X(\varphi )={\left(\frac{n}{n_0+n}\right)}^2\left(\frac{{\text{σ}}^2}{n}+\frac{{\text{σ}}^2}{n_0}\right) \\ {\text{Var}}_X(\varphi )=\frac{n}{n_0+n}\left(\frac{{\text{σ}}^2}{n_0}\right) \\ {\text{Var}}_X(\varphi )=v\text{Var}\left({\text{θ}}_I\right). \end{gathered}$$ (12)

The term v is defined as the variance fraction n/(n₀ + n), indicating that the variance of the preposterior distribution is always a fraction of the prior variance as it has been shown previously.^3,12 The Var_X(ϕ) tends to zero as n → 0 because with a small sample, we know that our posterior mean will be very similar to the prior mean. Conversely, Var_X(ϕ) → Var(θ_I) as n → ∞ because the prior is the source of all information; thus, as n increases, our uncertainty regarding ϕ will mimic prior uncertainty.¹² In addition, the expectation of ϕ equals μ₀ regardless of n. Figure 1 illustrates the relation between the prior and the preposterior distributions for various n in the Gaussian-Gaussian prior-likelihood case.

Figure 1.

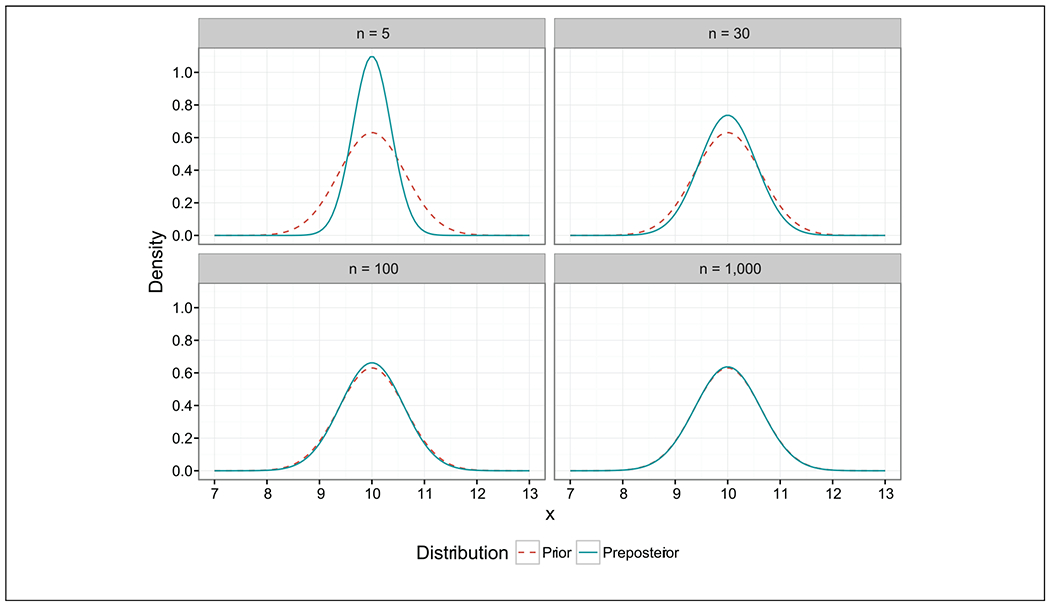
Gaussian preposterior and Gaussian prior distribution for different sample sizes n. The preposterior mean is the same for different ns. As n increases, the preposterior variance increases until it approximates that of the prior.

Equations (11) and (12) define the mean and variance of ϕ, respectively. From equation (10), we can see that ϕ is normally distributed because X is normally distributed and the rest of the terms are constants. As a result, we can express ϕ in terms of its mean, variance, and a standard normal distribution Z ~ N(0, 1), such that

$$\text{ϕ}={\text{μ}}_0+Z\frac{\sqrt{v}\text{σ}}{\sqrt{n_0}}.$$ (13)

Adding and subtracting $\sqrt{v}{\mu }_0$ results in

$$\text{ϕ}={\text{μ}}_0+Z\frac{\sqrt{v}\text{σ}}{\sqrt{n_0}}+\sqrt{v}{\text{μ}}_0-\sqrt{v}{\text{μ}}_0,$$ (14)

and rearranging the terms produces

$$\text{ϕ}=\sqrt{v}\left({\text{μ}}_0+Z\frac{\text{σ}}{\sqrt{n_0}}\right)+(1-\sqrt{v}){\text{μ}}_0.$$ (15)

Since X is not observed, and θ_I is the source of all information, we attribute all randomness in ϕ to randomness in the prior of θ_I, which allows us to replace ${\mu }_0+Z\sigma /\sqrt{n_0}$ with θ_I and obtain

$$\text{ϕ}=\sqrt{v}{\text{θ}}_I+(1-\sqrt{v}){\text{μ}}_0.$$ (16)

Again, if the proposed data collection sample relative to n₀ is small, $\sqrt{v}\to 0$ and the estimated posterior mean will be very similar to the prior mean (i.e., ϕ → μ₀). $\varphi \to {\text{μ}}_0$). But if the proposed sample size is relatively large, $\sqrt{v}\to 1$ the posterior mean converges to the prior (i.e., ϕ → θ_I).

Equation (16) can be extended to the multivariate Gaussian prior Gaussian likelihood because it can be applied to each component of the multivariate Gaussian distribution. The resulting correlation structure of these preposterior components will then be the same as the correlation structure among the prior components. This equation plays a key role in our approach to compute EVSI because it simplifies Bayesian updating by computing the posterior mean as a simple weighted average of the prior and the prior mean. This relation allows us to apply equation (16) in other non-Gaussian prior-likelihood pairs. Later, we test the performance of this approximation in a variety of non-Gaussian prior-likelihood distribution pairs where the priors and the data likelihoods are conjugate or nonconjugate and univariate or multivariate.

Using equation (16), a researcher only needs a set of K PSA simulations to compute ϕ. Thus, given an observation ${\text{θ}}_I^{(i)}$, an estimate ${\stackrel{\_}{\text{θ}}}_I$ of μ₀ and v = n/(n + n₀), we can estimate ϕ⁽ⁱ⁾ such that

$${\varphi }^{(i)}=\sqrt{v}{\text{θ}}_I^{(i)}+(1-\sqrt{v}){\stackrel{\_}{\text{θ}}}_I,$$ (17)

for all i = 1, …, K, where ${\stackrel{\_}{\text{θ}}}_I$ is the prior mean and can be estimated from the same PSA sample ${\stackrel{\_}{\text{θ}}}_I=\frac{1}{K}{\sum }_{i=1}^K{\text{θ}}_I^{(i)}$.

EVSI with Gaussian Approximation and Linear Metamodeling

After obtaining ϕ and estimating ${\widehat{\text{β}}}_0$ and ${\widehat{\text{β}}}_1$, we can compute ${\tilde{L}}_d^{\left(i\right)}$ from equation (5) and approximate EVSI by

$${\widehat{\text{EVSI}}}_{{\text{θ}}_I}=\frac{1}{K}\underset{i=1}{\overset{K}{{\sum }^{\text{}}}}\underset{d}{\max }\left({\tilde{L}}_d^{(i)}\right).$$ (18)

In the previous equation, ${\tilde{L}}_d$ is an approximation of the loss as a linear function of a single parameter. In the next couple sections, we extend the definition of ${\tilde{L}}_d$ to cases with more than one parameter and where the relation between the parameters and the loss function can be expressed with more flexible relations, such as splines.

Splines as Linear Metamodels

If the relation between L and θ_I is not linear, it is still possible to use a linear metamodel by defining a linear relation between L and a transformation of θ_I, namely, f(θ_I). A common choice for f(θ_I) is a spline function, such that f(θ_I) = α₀ + bα₁, $f\left({\text{θ}}_I\right)={\alpha }_0+b{\alpha }_1$, where b represents a set of basis functions of θ_I that form the spline, α₀ is the new intercept, and α₁ is a vector of regression coefficients of the set of basis functions, b.²³

We now can reexpress equation (3) in terms of splines as

$$L(d,\text{θ})={\alpha }_0+b{\alpha }_1+u,$$ (19)

where u is the new residual term. Similar to the lm function above, we can use the gam function in the R package mgcv to estimate the coefficients α₀ and α₁ by transforming θ_I into a set of basis functions, such that lm2 <– gam(L ~ s(theta_I)).²³ Then, we can use the fitted values using lm2$fitted to obtain the loss L conditional on θ_I. We refer to this conditional loss as $\widehat{L}$.

Using equation (19), we can also estimate the loss conditional on ϕ, referred to as $\widehat{L}$. Because equations (16) and (19) are both linear, we can apply the variance reduction to the basis functions directly by using the predict.ga function provided in the appendix to estimate $\tilde{L}$, such that L_tilde <– predict.ga(lm2, n, n0). Finally, we can use equation (18) to compute EVSI.

Notice that by letting n → ∞, ${\tilde{L}}_d^{(i)}\to {\widehat{L}}_d^{\left(i\right)}$, transforming equation (18) to the equation of EVPPI as a function of the loss conditional on the prior θ_I

$${\widehat{\text{EVPPI}}}_{{\text{θ}}_I}=\frac{1}{K}\underset{i=1}{\overset{K}{{\sum }^{\text{}}}}\underset{d}{\max }\left({\widehat{L}}_d^{(i)}\right).$$ (20)

In Box 1 and Appendix B, we provide a step-by-step summary and examples of R code to compute EVPPI and EVSI with Gaussian approximation and spline linear metamodeling.

EVSI for Multiple Parameters

Here we consider the case where ${\theta }_I=\left\{{\theta }_{I1},{\theta }_{I2}\right\}$, and the loss function can be expressed as

$$\text{L}(d,\text{θ})={\delta }_0+f_1\left({\text{θ}}_{I1}\right)+f_2\left({\text{θ}}_{I2}\right)+f_{12}\left({\text{θ}}_{I1}{\text{θ}}_{I2}\right)+\mathit{ϵ},$$ (21)

where δ₀ is the new intercept; f₁, f₂, and f₁₂ represent the spline functions for θ_I1, θ_I2, and their interaction, respectively; and ϵ is the new residual term. Equation (21) is often referred to as a GAM and can be estimated using mgcv.²³

This setup also allows one to compute EVSI for studies that collect information on multiple parameters with different n₀. In addition, this setup can be applied to unbalanced data collection study designs that propose to collect information on more than 1 parameter from a different number of participants. These data collection designs can be implemented by computing different v for various parameters of interest (e.g., θ_I1 and θ_I2). Appendix B provides further R code implementations for the Gaussian approximation when there are multiple parameters and unbalanced data collection designs where n and n₀ vary by the parameter of interest.

Estimating n ₀

The effective sample size n₀ denotes the “amount” of information in the prior.²⁵ In some instances, n₀ can be directly inferred from the prior distribution of the parameters and the data likelihood or elicited from experts’ judgments. Table 1 includes examples of direct assessment of n₀ from 3 different prior distributions. For example, n₀ for a beta prior p ~ beta(α, β) and binomial data likelihood x|p ~ binomial(p, n) can be computed as n₀ = α + β, where n₀ is simply the sum of the number of successes and failures. It is important to emphasize that the data likelihood also determines n₀. For example, in Table 1, we illustrate the case of a gamma prior and exponential data likelihood, in which n₀ = a, where a represents the shape parameter of the gamma distribution. However, if the data likelihood has a Poisson distribution to count the number of events, n₀ = 1/b, where b represents the scale parameter of the gamma distribution. We refer the reader to Morita and others²⁵ for a more detailed discussion on computing n₀.

Table 1.

Traditional Bayesian Updating Experiments for Testing the Performance of the Gaussian Approximation

	Experiment 1: Beta-Binomial	Experiment 2: Gamma-Exponential	Experiment 3: Normal-Weibull	Experiment 4: Dirichlet-Multinomial
Prior	p ~ beta(α = 1, β = 9)	λ ~ gamma(a = 10, b = 0.1)	θ ~ normal(μ = 1, σ2 = 0.04)	p ~ Dirichlet(α = [1, 5, 4])
Likelihood	x ~ binomial(n, p)	x ~ exponential(λ)	x ~ Weibull(v = 1, λ = 1/θ)	x ~ multinomial(n, p)
Posterior	p|x ~ beta (α + x, β + n – x)	λ|x ~ gamma $\left(a+n,b/\left(1+b{\sum }_{i=1}^n{x}_i\right)\right)$	Non-conjugate	p|x ~ Dirichlet(α + x)
${\widehat{n}}_0$ from the prior	${\widehat{n}}_0=\alpha +\beta =10$	${\widehat{n}}_0=a=10$	${\widehat{n}}_0\approx 25$ (using MCMC)	${\widehat{n}}_0=\sum {\alpha }_i=10$
n	n = {10, 100, 1000}	n = {10, 100, 1000}	n = {10, 100, 1000}	n = 100
Univariate v. multivariate	Univariate	Univariate	Univariate	Multivariate

Whenever n₀ is not readily available, we propose 2 alternative approaches to estimate it, both using the Gaussian approximation. The first approach involves computing a summary statistic, and the second approach involves estimating n₀ indirectly from a Bayesian data collection experiment. The second approach can be generalized to a wide variety of situations, including cases in which the prior and data likelihoods are not conjugate.

Computing n₀ using a summary statistic S.

This Gaussian approximation approach to compute n₀ requires a summary statistic S to describe the data collection step. In the Gaussian prior-Gaussian likelihood case, the marginalized X represents the summary statistic, that is, S = X. Therefore, Var(S) = σ²/n + σ²/n₀. Since, we know Var(θ_I) = σ²/n₀, we can solve for n₀

$${\widehat{n}}_0=n\left(\frac{\text{Var}(S)}{\text{Var}\left({\text{θ}}_I\right)}-1\right),$$ (22)

where Var(S) and Var(θ_I) are the variances of the summary statistic and the prior, respectively. We can use this equation to estimate n₀ in other prior-likelihood pairs. However, in these cases, we need to compute the summary statistic first because the prior and the likelihood may represent different quantities. For example, the prior in a beta-binomial is typically a probability between zero and 1, while the binomial likelihood is generally the distribution of the number of successes. Therefore, a summary statistic is needed to convert the marginalized likelihood of successes to the same scale as the prior probability. In the case of the beta-binomial, this can be easily achieved by dividing the number of successes k by the total sample n, such that S = k/n. However, calculating a summary statistic may not be always trivial. For such cases, we propose an indirect Markov chain Monte Carlo (MCMC) approach that does not require computing the summary statistic.

Computing n₀ indirectly via MCMC.

The indirect method involves computing n₀ for each parameter using an analytic method or MCMC. In most cases, n₀ can be estimated by generating new data from the prior and the likelihood function using equation (12), such that

$${\widehat{n}}_0=n\left(\frac{\text{Var}\left({\text{θ}}_I\right)}{{\text{Var}}_X(\varphi )}-1\right).$$ (23)

In Box 2, we summarize the steps involved in calculating n₀ using both the summary statistic and MCMC methods. (Appendix C provides the detailed steps for computing n₀ and its implementation in R.)

Case Study 1: Testing the Gaussian Approximation

In this section, we compare the distribution of the posterior mean estimated using the Gaussian approximation as defined in equation (16) to the posterior distribution estimated using traditional Bayesian updating through either conjugacy or MCMC. We tested the Gaussian approximation on 4 different examples: 1) beta-binomial, 2) gamma-exponential, 3) normal-Weibull, and 4) Dirichlet-multinomial prior-likelihood pairs. The distributions, their parameters, and the size of the data collection experiments are defined in Table 1.

The first experiment describes a discrete data collection exercise from a beta prior and a binomial data likelihood. The prior is conjugate to the data likelihood; therefore, the posterior is also beta distributed and can be computed analytically. The second experiment describes a gamma prior that is conjugate with the exponential data likelihood. The third experiment involves a normal prior that is not conjugate to the Weibull data likelihood. In this case, the posterior mean is computed via MCMC using JAGS.²⁶ The fourth example involves a Dirichlet prior with 3 components and a conjugate multinomial data likelihood.

In all cases, the prior sample size n₀ can be calculated directly using the parameters of the distributions through a closed-form solution except for the normal-Weibull case.²⁵ Therefore, we computed n₀ numerically using the indirect MCMC approach following the steps described in Box 2: 1) draw ${\text{θ}}_I^{(1)},\dots ,{\text{θ}}_I^{(m)}$ samples from the prior distribution of θ_I ~ Normal(μ = 1, σ² = 0.04). 2) For each value of ${\text{θ}}_I^{(i)}$, i = {1, …, m}, we took j = {1, …, n} samples from the data likelihood, such that x^(i,j) ~ Weibull(v = 1, λ = 1/θ⁽ⁱ⁾). We obtained q samples from the posterior distribution of θ|x⁽ⁱ⁾. Then, we calculated the posterior mean for each value of ${\theta }_I^{(i)}$, such that ${\varphi }^{(i)}=\frac{1}{q}{\sum }_{k=1}^q{\text{θ}}^{\left(k\right)}|x^{\left(i\right)}$. Finally, we estimated ${\widehat{n}}_0\approx 25$ using equation (23).

Case Study 2: Calculating EVSI in a Markov Model

We computed the EVSI of different parameters of an economic evaluation using a Markov model to compare the performance of the GA to the 2MCS approach. We chose a Markov model because Markov models are commonly used in economic evaluations and generally involve nonlinear relations among some of the model parameters and the net benefits.²⁷ (Details of the Markov model are described in Appendix D.) In summary, the model simulated a cohort with a hypothetical genetic disorder (syndrome X). Syndrome X is mostly asymptomatic but may cause a sudden flare-up that may necessitate hospitalization. There are 3 alternatives available for preventing progression to permanent disability: A, B, and C, where C is standard care. If treatment fails, permanent disability occurs and quality of life (QoL) decreases from 1.0 to 0.8. For ease of calculations, we assumed that patients face a constant annual mortality rate of 0.044. In addition, syndrome X is assumed to be associated with a 0.5% increase in absolute mortality. Furthermore, if disabled, mortality rate is assumed to increase by an additional 1%. Given that all transition probabilities are time invariant, we used a fundamental matrix solution²⁸ of the Markov model to speed up the computation time.

Four parameters in the model are uncertain. The parameters representing the mean number of visits for interventions A and B have a linear relation with the net monitory benefit (NMB). However, the probability of failing A and B has a nonlinear relation with their respective interventions. This is because Markov models are typically linear in state payoffs but nonlinear in the state transition probabilities.

The n₀ is 10 for all parameters, which can be easily confirmed from the distribution characteristics of these parameters and their corresponding data likelihoods. For example, we assumed that the mean number of hospital visits for intervention A is distributed as gamma(a = 10, b = 0.1). Because, the likelihood follows a Poisson distribution, this prior contains information equivalent to n₀ = 1/b = 10. In addition, the probability of failing A is distributed as beta(α = 2, β = 8) and the n₀ = α + β = 2 + 8 = 10 because the data likelihood follows a binomial distribution.

We compared the estimated EVSI and EVPPI using 2 approaches: GA with splines as the linear metamodel (GA) and Bayesian updating with 2-level Monte Carlo simulations (2MCS). Each EVSI estimation with 2MCS using the fundamental matrix solution of the Markov model took about 6 hours on 16 parallel cores.

Results

Results of Case Study 1: Testing the Performance of the Gaussian Approximation

Figure 2 compares the empirical cumulative density function (ECDF) of the preposterior distribution for the 3 univariate experiments in Table 1 computed with traditional Bayesian updating and GA using equation (16). GA asymptotically approximates the preposterior distribution obtained with classic Bayesian updating. The step function for the preposterior distribution in the beta-binomial case through Bayesian updating is explained by the discrete nature of the binomial distribution. Numerically, the Kolmogorov-Smirnov (KS) statistic was close to zero for most experiments, indicating that the preposterior distributions computed with both Bayesian updating and GA were similar. In addition, the similarity between the preposterior distributions increased as n increased because with higher n, the Gaussian assumption becomes more appropriate.

Figure 2.

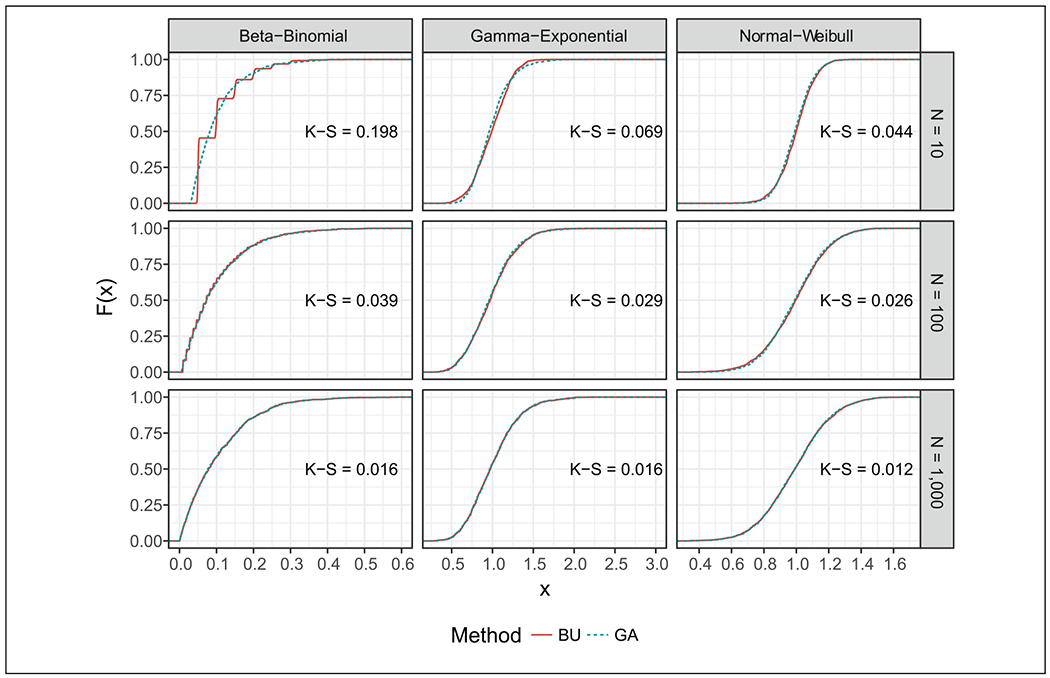
Comparison of the empirical cumulative distribution function (ECDF) of the Gaussian approximation (GA) to the traditional Bayesian updating (Bayesian updating) for 3 univariate data collection experiments: beta-binomial, gamma-exponential, and normal-Weibull prior-likelihood pairs. The posterior mean (ϕ) is shown on the x-axis and the ECDF (F (x)) at each value of ϕ is shown on the y-axis. The Kolmogorov-Smirnov (K-S) statistic quantifies a distance between the empirical distribution functions of 2 samples, where a smaller value provides stronger evidence that both samples come from the same distribution.

Figure 3 compares the GA to Bayesian updating for the Dirichlet-multinomial experiment. This figure presents both the marginal and joint preposterior distributions for pairs of components of the Dirichlet distribution. The GA provides a good approximation of these distributions compared to the Bayesian updating. In addition, the correlation coefficients for pairs of components were also very similar.

Figure 3.

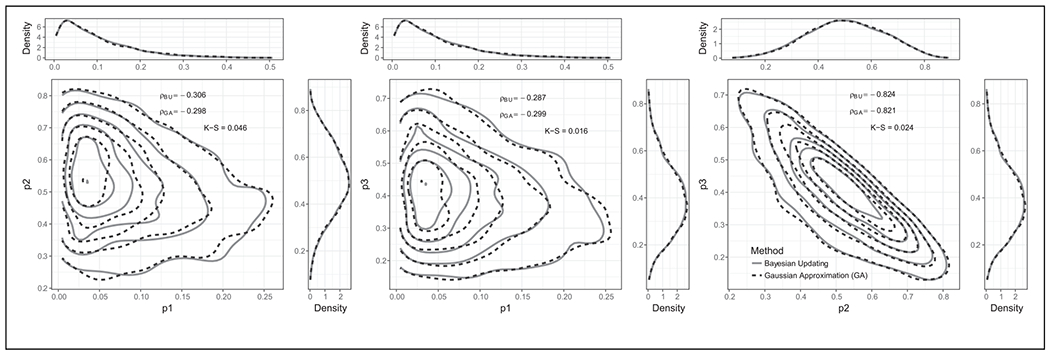
Joint preposterior distribution for pairs of parameters in the fourth experiment involving a Dirichlet-multinomial prior-likelihood computed using the Gaussian approximation (GA) and traditional Bayesian updating. The marginal preposterior distributions are shown in the upper and right-hand side margins. ρ_BU and ρ_GA are the correlation coefficients between the prior component pairs using Bayesian updating and GA, respectively. The Kolmogorov-Smirnov (K-S) statistic quantifies a distance between the empirical distribution functions of 2 samples, where a smaller value provides stronger evidence that both samples come from the same distribution.

Results of the Case Study 2: Calculating EVSI in a Markov Model

Base case analysis.

In the base case analysis, intervention B is the optimal strategy with the highest expected NMB at a willingness to pay (WTP) threshold of $50,000/quality-adjusted life year (QALY) (Appendix D). However, intervention B is optimal in less than 50% of the PSA scenarios, indicating that based on current information, the decision maker faces a 54% chance of some opportunity loss.

VOI.

The EVPI was $5480, which sets the upper limit on future research involving all the parameters in the decision model with current information. In addition, the EVPPI for the individual parameters and their corresponding standard errors (SEs) for GA and 2MCS are shown in Table 2. The SEs of the GA were calculated following a Monte Carlo approach²⁹ by evaluating equation (18) on n sets of coefficients α^d(i), where i = 1, …, n is sampled from a multivariate Normal distribution with mean ${\widehat{\alpha }}^d$ and covariance ${\widehat{\Sigma }}^d$. ${\widehat{\alpha }}^d$ and ${\widehat{\Sigma }}^d$ are the estimated parameters and their corresponding covariance matrix obtained from the mgcv package. This approach has been previously used in the context of VOI by Strong and others.¹⁴ The SEs for the 2MCS were computed following Ades and others.¹² The estimated EVPPI using the GA closely resembles that obtained with the 2MCS approach but with higher SEs, which is the result of the additional errors from the metamodel approximation.

Table 2.

Estimated Expected Value of Partial Perfect Information for Each Parameter with Spline Regression and with 2-Level Monte Carlo Simulations (2MCS)

	Spline Regression		2MCS
Parameter	Mean ($)	Standard Error ($)	Mean ($)	Standard Error ($)
Mean number of visits (intervention A)	985	70	1098	22
Mean number of visits (intervention B)	1414	44	1384	33
Probability of failing A	1952	67	1928	46
Probability of failing B	1535	49	1524	24

A single EVSI evaluation using the GA technique took 0.02 seconds on a single core while the 2MCS approach took 10 minutes on 16 parallel cores. Despite the efficiency of using the fundamental matrix solution, conjugate priors, and 16 parallel processing cores to compute EVSI using the 2MCS, it was still many folds slower compared to the GA technique.

Figure 4 compares the EVSI computed using GA and 2MCS for different sample sizes (n = {0, 5, 10, 50, 100, 1000, 10000}) and the associated CIs. When the sample size was greater than 10, the GA performed similar to the 2MCS for all parameters. Both approaches show that as the sample size increase, EVSI approaches EVPPI.

Figure 4.

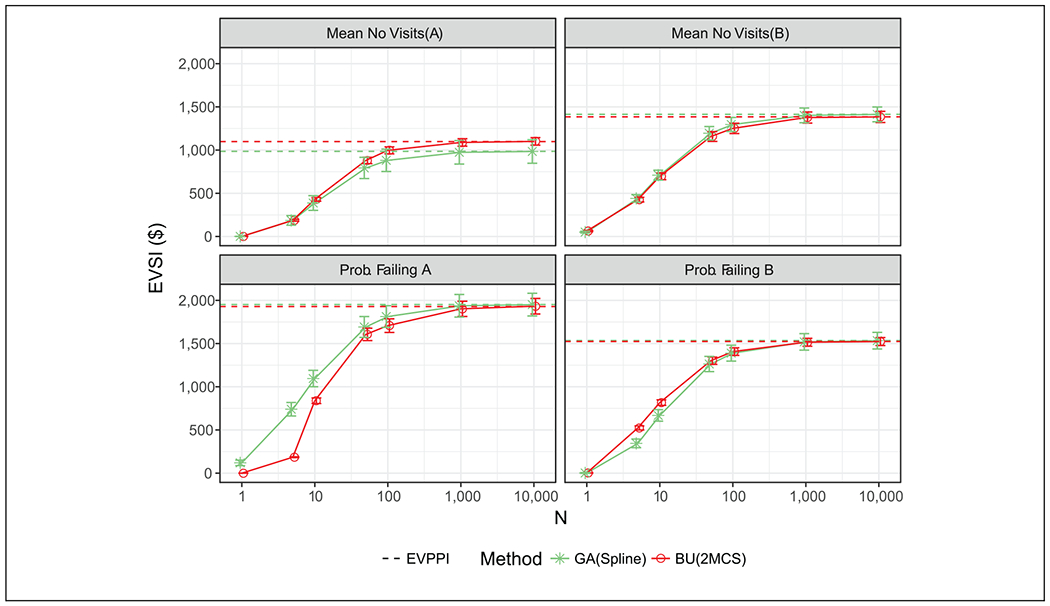
Expected value of sample information (EVSI) of each parameter for various sample sizes using Gaussian approximation (GA) with splines and traditional Bayesian updating with 2-level Monte Carlo simulations (2MCS) with their corresponding confidence intervals. The expected value of partial perfect information (EVPPI) using GA and Bayesian updating (BU) are also shown with the horizontal lines.

The GA approach generally produces smoother EVSI curves, especially for small n. This is mainly because the data likelihood used in the Bayesian updating samples integers from discrete distributions, causing larger variation in the posterior mean for smaller n.

Correlation.

In VOI, all evidence must be used to accurately define prior uncertainties. Such evidence often translates into correlated parameters. To illustrate the importance of correlation, we tested how VOI varies at different levels of correlations between different pairs of parameters of interest. The level of correlation was induced using a previously described algorithm.^30,31 Briefly, this correlation induction involves taking a large number of samples from the independent prior distributions of the parameters and then sorting them in a way that induces the desired correlation structure. Because this algorithm only involves sorting the parameters, it preserves their marginal distributions. The algorithm can be extended to multiple correlated parameters.³² In case study 1, we illustrated the performance of the GA in approximating the joint preposterior distribution in the case of a Dirichlet prior and multinomial data likelihood. Furthermore, the GA can be easily extended to models that involve multiple correlated parameters that are not jointly sampled from the same multivariate distribution.

In Figure 5, we examine the effect of correlations (ρ) on the EVSI for all possible pairs of parameters. Correlations among parameters of interest have a drastic impact on the EVSI in all cases. The maximum effect can be seen between the mean number of hospital visits for intervention A and the probability of failing intervention A. The extremes of ρ in this figure may not be realistic but illustrate the importance that correlation has on EVPPI and EVSI.

Figure 5.

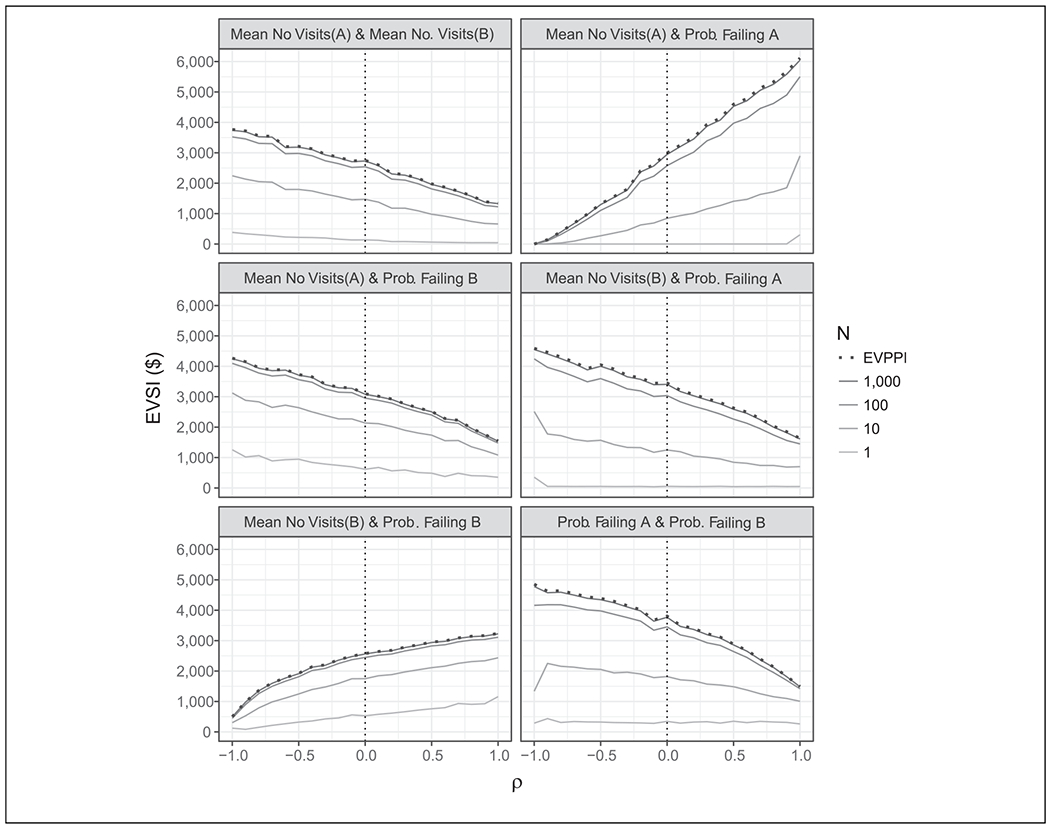
Impact of correlation on expected value of sample information (EVSI). This figure shows the change in EVSI for various sample sizes _n for each pair of parameters in case study 2 over different levels of correlation between the parameters. The dotted vertical line represents the case where the parameters are independent. EVPPI, expected value of partial perfect information.

Discussion

We propose a general approach to compute EVSI that consists of 2 components: 1) a linear metamodel between θ_I and the opportunity loss L and 2) a Gaussian approximation of the posterior mean of the data collection experiments involving a set of parameters of interest θ_I. In a first case study, we illustrated the GA performance in terms of accuracy in 4 numerical exercises involving conjugate, nonconjugate, univariate, and multivariate priors. The second case study compared the accuracy and efficiency of the GA to the traditional Bayesian updating via the 2MCS approach in estimating EVPPI and EVSI of an economic evaluation using a Markov model with nonlinear relations between the net benefits and the non-Gaussian prior parameters.

The GA extends our previous efforts¹³ to calculate EVSI to a wide range of prior and likelihood combinations, multiple correlated parameters, and multiple strategies. The GA is an alternative to the traditional Bayesian updating process that can be extended to other non-Gaussian prior-likelihood pairs because it only requires the prior distribution. The GA does not impose any distributional form on the prior or the likelihood directly, and it works by generating a preposterior distribution that is the result of shrinking the prior toward its mean similar to updating a Gaussian prior using a Gaussian data likelihood. In addition, the GA generally offers additional computational gains over previous methods. For example, for each set of parameters, the analyst can use the same metamodel for various sample sizes n unlike previous approaches that may require refitting the metamodel for different n.¹⁴

Similar to Jalal and others,¹³ Strong and others,¹⁴ and Menzies,¹⁵ this study also adopts a regression metamodeling approach to facilitate the computation in EVSI. The linear regression metamodel approach is generally fast and simple to implement because it only requires the PSA data set and there is no need to rerun the simulation model after the PSA data set has been created, similar to previous approaches.^13–15 In addition, when n → ∞, our EVSI equation translates to an EVPPI equation that is similar to Strong and others³³ and Madan and others³⁴ using splines.

The GA approach simplifies the Bayesian updating process, which, in combination with the linear regression metamodeling, allows the posterior mean of the opportunity loss to be expressed as a function of the posterior mean values of the individual parameters. The GA approach can be used with various forms of regression metamodeling (e.g, simple linear or spline metamodels). In this article, we chose splines as a linear metamodel because splines are generally more flexible metamodels than simple linear metamodels and are easily implemented with mathematical and statistical software, such as R.^14,15 The mgcv package contains algorithms to choose an appropriate number of basis functions. However, splines can fail if the number of basis functions in the spline exceeds the number of PSA samples, especially if multiple interactions of a large number of parameters are desired.¹⁴ In such cases, researchers can choose to explicitly define a simpler linear metamodel or a polynomial metamodel with fewer terms than the PSA samples. The choice of an appropriate metamodeling technique may improve the accuracy of VOI computations, but researchers must always balance increased accuracy v. overfitting and should choose a metamodel that neither oversmooths nor overfits the data. This is an important step in all methods that use metamodels to compute either EVPPI^13,33,34 or EVSI.^13–15 Fortunately, many techniques (e.g., cross-validation) can be used to reduce model overfitting if overfitting is particularly important.

Since the prior is the source of all information in VOI, the GA assumes that all the randomness in ϕ is attributable to randomness in θ_I, resulting in ϕ and θ_I to be perfectly correlated. This assumption allowed us to express ϕ as a function of θ_I and extend the GA approach to cases in which the prior parameters are correlated as we illustrated above. This approach is different from traditional Bayesian updating because in traditional Bayesian updating, we assume that X is observed. Thus, the variability in the preposterior becomes a function of the variability in the prior and the data likelihood, which are often sampled from independent random distributions.

Theoretically, n₀ and n must be sufficiently large for the GA to perform well in approximating the preposterior distributions in non-Gaussian prior-likelihood cases. We tested the performance of this approximation numerically on various conjugate, nonconjugate, univariate, and multivariate non-Gaussian distributions when n and n₀ were as small as 10. In all cases, the GA approach performed well in approximating the Bayesian updating process. In addition, Pratt and others³⁵ have shown that when the sample size is large enough and its variance is known and finite, the Bayesian updating can be approximated by a Gaussian-Gaussian Bayesian update regardless of the nature of the functional form of the likelihood due to the central limit theorem.³⁵

However, if the sample sizes are particularly small or if the priors are highly skewed, the GA approach may not perform well. In these cases, researchers may conduct a full Bayesian updating or adopt other techniques such as transforming the parameters to be less skewed. For example, a log transformation can be used for rates or a logit transformation can be used for probabilities, but care must be given in all cases to compute n₀ accordingly.

A potential speed-limiting task in our approach is computing n₀ for complex study designs that require MCMC. Fortunately, n₀ needs to be computed only once for each parameter of interest, and then it can be reused as long as the prior distributions and the data likelihoods are not altered. As we have shown above, there are closed-form solutions for n₀ for some commonly used priors and data likelihood experiments. We illustrated the case of beta-binomial, gamma-exponential, gamma-Poisson, and Dirichlet-multinomial. We also proposed 2 novel approaches to calculate the value of n₀ from the prior and data likelihood using a GA through either a summary statistic or MCMC methods. In addition, numerical techniques have been proposed to calculate n₀ via Monte Carlo simulations.²⁵

In summary, the GA technique has several advantages: 1) it requires only the prior and the prior sample size n₀, which can be estimated in various ways; 2) it can be used with different types of linear metamodels; 3) it is simple and efficient to compute compared to the traditional Bayesian updating; and 4) it can be applied when the model parameters are correlated or interact.

Conclusion

EVSI is one of the most powerful concepts in medical decision making because it can inform future research, resource allocation, and data collection study designs. We propose a general GA approach to estimate EVSI that addresses some of the challenges associated with traditional EVSI calculations, especially when complex Bayesian updating of the prior uncertainties is required and when the prior evidence suggests that these uncertainties are correlated. The GA approach relies on defining the prior sample size n₀, and it extends our prior efforts¹³ to multiple strategies and various distributional forms. We hope that this approach along with the other recent developments in computing EVSI can provide a useful set of tools for analysts to effectively conduct VOI.

Box 1.

Summary of the Steps and R Code for Computing EVSI Using Gaussian Approximation from a PSA Data Set for a Parameter of Interest θ_I from a New Sample n

1.	Conduct probabilistic sensitivity analysis (PSA) and load the PSA data set.
	library(mgcv); library(matrixStats)
	psa <– read.csv(“example_psa_dataset.csv”)
	n.sim <– nrow(psa) # number of simulations in psa
	theta_I <– psa[, 1] # parameter of interest is column 1
	nmb <– psa[, 5:7] # the strategies’ net monetary benefits are columns 5 through 7
2.	Determine the optimal strategy d*.
	d.star <– which.max(colMeans (nmb))
3.	Compute the opportunity loss L(d, θ).
	loss <– nmb – nmb[, d.star]
4.	Estimate a linear metamodel for the opportunity loss of each d strategy, Ld, by regressing them on the spline basis functions of θI.
	lmm1 <– gam(loss[, 1] ~ s(theta_I)
	lmm2 <– gam(loss[, 2] ~ s(theta_I)
	lmm3 <– gam(loss[, 3] ~ s(theta_I)
5.	Compute EVPPI using the estimated losses for each d strategy, ${\widehat{L}}_d$, and applying equation (20).
	Lhat <– cbind(lmm1$fitted, lmm2$fitted, lmm3$fitted) # estimated losses
	evppi <– mean(rowMaxs(Lhat)) # evppi equation
6.	Load the predict.ga function.
	source(GA_functions.R)
7.	Compute the predicted loss for each d strategy, ${\widehat{L}}_d$, given the prior sample size (n0) and new sample size (n).
	Ltilde1 <– predict.ga(lmm1, n = n, n0 = n0)
	Ltilde2 <– predict.ga(lmm2, n = n, n0 = n0)
	Ltilde3 <– predict.ga(lmm3, n = n, n0 = n0)
	loss.predicted <– cbind(Ltilde1, Ltilde2, Ltilde3)
8.	Compute EVSI using equation (18)
	evsi <– mean(rowMaxs(loss.predicted)) # evsi equation

Appendix B provides example R codes for implementing this approach when there are multiple parameters and unbalanced data collection study designs.

Box 2.

Summary of Steps for Computing n₀ from the Prior with Gaussian Approximation Using Summary Statistic and Markov Chain Monte Carlo (MCMC) Approaches

A.	Summary statistic
1.	Take i = 1, …, m samples from the prior distribution of θI.
2.	Take n samples from the likelihood distribution of $x|{\theta }_I^{(i)}$.
3.	Compute a summary statistic S from the n samples of $x|{\theta }_I^{(i)}$.
4.	Finally, estimate ${\widehat{n}}_0$ using equation (22).
B.	MCMC
1.	Take i = 1, …, m samples from the prior distribution of θI.
2.	Take n samples from the likelihood distribution of $x|{\theta }_I^{(i)}$.
3.	Obtain the posterior θI|x using a specialized package such as JAGS.
4.	Compute the posterior mean ϕ.
5.	Finally, estimate ${\widehat{n}}_0$ using equation (23).

Appendix C provides examples in R for implementing these approaches.