Comparing information diffusion mechanisms by matching on cascade size

Significance

Do different types of information spread differently online? In recent years, studies have sought answers to such questions by comparing statistical properties of network paths taken by different kinds of content diffusing online. Here, we demonstrate the importance of controlling for correlations between properties being compared. In particular, we show that previously reported structural differences between diffusion paths of false and true news on Twitter disappear when comparing only cascades of the same size; differences between diffusion paths of images, videos, news, and petitions persist. Paired with a theoretical analysis of diffusion processes, our results suggest that, in order to limit the spread of false news, it may be enough to focus on reducing the mean “infectiousness” of the information.

Abstract

Do some types of information spread faster, broader, or further than others? To understand how information diffusions differ, scholars compare structural properties of the paths taken by content as it spreads through a network, studying so-called cascades. Commonly studied cascade properties include the reach, depth, breadth, and speed of propagation. Drawing conclusions from statistical differences in these properties can be challenging, as many properties are dependent. In this work, we demonstrate the essentiality of controlling for cascade sizes when studying structural differences between collections of cascades. We first revisit two datasets from notable recent studies of online diffusion that reported content-specific differences in cascade topology: an exhaustive corpus of Twitter cascades for verified true- or false-news content by Vosoughi et al. [S. Vosoughi, D. Roy, S. Aral. Science 359, 1146–1151 (2018)] and a comparison of Twitter cascades of videos, pictures, news, and petitions by Goel et al. [S. Goel, A. Anderson, J. Hofman, D. J. Watts. Manage. Sci. 62, 180–196 (2016)]. Using methods that control for joint cascade statistics, we find that for false- and true-news cascades, the reported structural differences can almost entirely be explained by false-news cascades being larger. For videos, images, news, and petitions, structural differences persist when controlling for size. Studying classical models of diffusion, we then give conditions under which differences in structural properties under different models do or do not reduce to differences in size. Our findings are consistent with the mechanisms underlying true- and false-news diffusion being quite similar, differing primarily in the basic infectiousness of their spreading process.

From the diffusion of ideas, content, and innovations in social networks to the propagation of epidemics, computer viruses, and bank defaults, understanding spreading processes in interconnected systems is of utmost importance in many diverse settings. The recent dramatic increase in the scale at which behavioral data can be gathered and analyzed has provided unique opportunities to compare how different kinds of content spread among users of social media platforms. By studying the propagation patterns of online content, scholars hope to understand the basic principles underlying their spread. Do some types of content spread faster than others? Does visual content reach a larger audience than written content? If so, how come? And how can we design platforms to control or attenuate the spread of potentially unwanted content?

The quantitative study of diffusion has a long history (1–3), while the large-scale analysis of the structure of diffusion has its modern origins in the study of the spread of blog links (4–6), word-of-mouth product recommendations (7), and the propagation of online chain letters (8, 9). Since these pioneering studies, the scale of data has increased tremendously, and the spreading dynamics of a wide range of content types have been analyzed. These include differences in how videos, images, news, and petitions spread on the social media platform Twitter (10), verified true and false news spreading on Twitter (11, 12), invitations to join the networking platform LinkedIn (13), photos on Facebook (14), cross-platform comparisons of cascades (15), and more (16–19).

In this fast-growing field of diffusion research, the analysis of the diffusion structure begins by mapping the branching paths that the content takes through the underlying network as it spreads. The resulting rooted, directed, time-stamped tree that records the spread of a single diffusion event is commonly referred to as a “cascade.” Usually, a large collection of individual cascades are collected into a single dataset, labeled as associated with different kinds of content. By quantifying statistical properties of these cascade populations—for example, their maximum depth and breadth—one hopes to discover clues as to how different contents diffuse differently. For example, if news cascades typically have high breadth and low depth, while petition cascades have low breadth and high depth, this could indicate how the mechanisms underlying the spreading dynamics of news and petitions differ.

In the present work, we examine how conclusions stemming from this style of analysis can be complicated by tight dependencies between structural features of cascades. Informally, these dependencies can be thought of as correlations or collinearities, though we emphasize that these relationships are rarely linear. Most significantly, almost all features of cascades are known to vary with the size of the cascade, both in data (6, 14, 20) and in models of such data (21). To better understand the role of size in the analysis of various cascade properties, we present a matching procedure that constructs paired corpuses of cascades while controlling for size.

We apply this matching methodology to reanalyze the data from two recent landmark studies: an analysis of the spread of true and false news on Twitter by Vosoughi et al. (11) and a comparison of the spread of videos, images, news, and petitions on Twitter by Goel et al. (10). In their analysis, Goel et al. found that cascades of different content types had several structural differences, while Vosoughi et al. found that false news spreads “farther, faster, deeper, and more broadly than the truth.” Using our matching approach, we show that when controlling for cascade size, differences in depth and structural virality of images, videos, news, and petitions largely persist, whereas differences in the depth, breadth, structural virality, and speed of false- and true-news cascades disappear. This observation leads us to the conclusion that, although false-news and true-news cascades are structurally distinguishable online, the observed structural differences can be explained almost entirely by a significant, but one-dimensional, difference in size. In combination with theoretical results and simulations, we argue that this latter finding suggests that the deeper, broader, and faster propagation of false news can be addressed by targeting a single thing: the higher person-to-person infectiousness of the information. We similarly find that reported differences in the spread of political news and news on other topics also collapse when controlling for size.

If the observed structural differences between real-world cascades of false and true news can be explained by size differences, does this explanation mean that false and true news spread according to the same underlying statistical rules? This type of question is extremely difficult to answer well without a complex, randomized experiment that would control for the timing, topic, and network origination of a cascade, randomizing the truth of the story being shared. A more approachable question is whether spreading according to the same underlying statistical rules is sufficient to cause the observed size-induced differences in cascade statistics. To investigate this question, we turn to modeling.

Many models of cascade growth have size as an explicit/exogenous parameter, e.g., the preferential attachment (22, 23), copy (24), fitness (25), and random recursive tree (26, 27) models. For such models, controlling for size means choosing the size. For other models, notably, the widely studied Susceptible–Infectious–Recovered (28) (SIR) and Independent Cascade (29, 30) (IC) models of diffusion, cascade size is an implicit/endogenous feature. For these latter two model families, we rigorously characterize a theoretical analog to our empirical observation. We show how, controlling for size, differences in all other cascade statistics collapse when one compares collections of cascades generated by the SIR or IC model. More specifically, we find that the distribution over labeled trees induced by different instances from the same model family (e.g., two SIR models with different parameter settings) are identical when controlling for size. As a result, any summary statistics of the two collections are also identical when controlling for size. The observed collapse is, however, far from generic and does not occur if comparing cascade collections from different model families (e.g., SIR vs. IC).

Online Information Diffusion Data

True and False News

In recent years, much focus has been given to the influence of online misinformation, disinformation, and “fake news” (11, 12, 31, 32), particularly in political elections and international conflicts (33–35). Already in 2013, massive digital misinformation was listed as a global risk by the World Economic Forum, which stated that it was “conceivable that a false rumor spreading virally through social networks could have a devastating impact before being effectively corrected” (36). Understanding the spread of false news is clearly central to understanding how such risks can be mitigated.

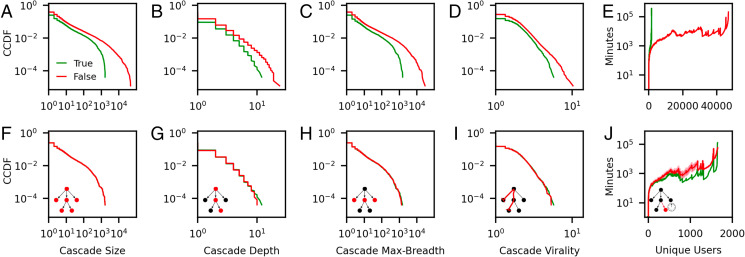
The work of Vosoughi et al. (11) constitutes a landmark study in the analysis of false- and true-news cascades. To recapitulate their analysis, the authors collected and analyzed retweet cascades of all fact-checked true or false content that spread on Twitter in its history from 2006 to 2017, as verified by six independent fact-checking organizations. They then analyzed structural and temporal properties of the 24,409 verified-true-news cascades and 82,605 verified-false-news cascades and compared them to each other. In Fig. 1 A–E, we reproduce four statistical quantities that were compared in that important work: the cascade size (number of retweets), cascade depth (maximal distance of a node from the root), cascade maximal breadth (maximal number of nodes located the same distance from the root), cascade “virality” [a normalized version of what is also known as the Wiener index (10), the average pairwise distance of nodes in the cascade, when converting all directed edges into undirected edges], and the geometric mean of the time it takes a cascade to be retweeted by a number of unique users. The first four plots compare the complementary cumulative distribution function (CCDF) of these statistical quantities for the two datasets. Based on these plots, the authors concluded that cascades of fact-checked false news are bigger, broader, more viral, and spread faster than the cascades of fact-checked true news.

Fig. 1.

(A–E) Structural and temporal statistics of false-news and true-news cascades diffusing on Twitter, as presented in ref. 11. Cascades in the two datasets have different size distributions (A). (F–J) The same analyses as the plots directly above, carried out for two subsampled datasets with matched size distributions. Controlling for size collapses statistical differences in these properties. Insets depict each statistic on a simple cascade.

Images, Videos, News, and Petitions

A broader line of research has studied the diffusion patterns of different content types and on different media platforms. Notable in this broader literature is the analysis of Goel et al. (10), which investigated the extent to which online diffusion was mostly driven by a few large “broadcast” events or a more decentralized “viral-like” process. The authors analyzed a large dataset consisting of all tweets posted on Twitter between July 2011 and July 2012 that contained URLs pointing to one of a selected set of domains. Based on the URL, each tweet was taken to belong to a content category: images, videos, news, or petitions. The total dataset included 1.2 billion posts of ∼622 million unique pieces of content.

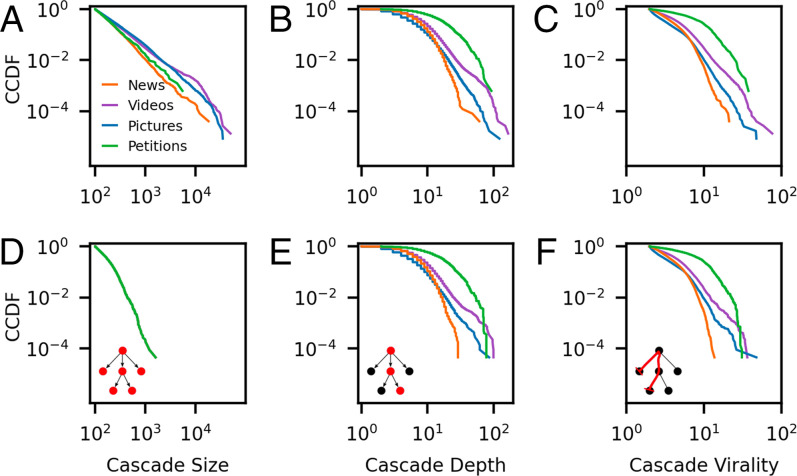
In Fig. 2 A–C, we reproduce the main empirical analysis of Goel et al., showing the cascade size, depth, and structural virality for the content types (only size and structural virality were plotted in the original paper), again in the form of CCDFs, for the different content types. From these plots, the authors concluded that cascades of popular petitions are “substantially more structurally viral than any other type of content, followed by videos, images, and news stories.”

Fig. 2.

(A–C) Structural statistics of videos, images, news, and petitions on Twitter, as presented by ref. 10. Note that only cascades containing at least 100 posts are included in the analysis. Cascades in the four categories of content have different size distributions (A). (D–F) The same analyses as the plots directly above, carried out for subsampled datasets with matched size distributions. Controlling for size does not collapse statistical differences in these properties. Insets depict each statistic on a simple cascade.

Size-Controlled Cascade Comparisons

Cascade size, depth, and max breadth are not necessarily independent from each other: If a cascade doubles in size, one would expect it to increase in depth and maximum breadth. In the same way, one would imagine that speed of propagation is not independent of cascade size either: The very largest cascades will probably reach 1,000 adoptions faster than cascades of more moderate size. As a result, size differences visible in Figs. 1A and 2A are expected to influence the distributions of other properties in Figs. 1 B–E and 2 B and C.

Investigating the extent to which the observed statistical differences between cascade properties in Figs. 1 and 2 are not merely a result of differences in cascade sizes requires controlling for cascade size in our analysis. Because cascade properties such as size, depth, and breadth are intertwined in subtle ways, we adopt a matching framework (37) that makes minimal assumptions about the relationship between properties (as opposed to, say, regression controls in a linear model). Without loss of generality, we focus our description on comparing false-news and true-news cascades. To create a size-matched corpus of cascades, we consider each true-news cascade and randomly sample a matching cascade of false news, uniformly at random with replacement, from the set of false-news cascades of the same size. If no false-news cascade of the same size exists (an occurrence affecting only a relatively small fraction of cascades in both datasets, but not necessarily in a more general setting), the true cascade is not included in the subsampled cascade corpus. We refer to this process as matching false cascades to true cascades. The result is two subsampled cascade corpuses with the exact same distribution of sizes; the included cascade sizes are a subset of the cascade sizes in the original datasets.

This procedure is only one of several possible approaches that could be taken to size-match two cascade populations. One could equally well match the true cascades to the false cascades (where sampling with replacement would play a greater role) or match both populations to a third distribution of sizes (e.g., the overall size distribution of news cascades, regardless of true/false labels). Our choice of procedure amounts to a choice of target population, the natural distribution of true-news cascade sizes.

In Fig. 1 F–J, we show the analyses of Vosoughi et al. (11) repeated on the matched datasets, where each panel corresponds to the unmatched analysis directly above. We see that all the observed structural differences do not persist when controlling for size. Examining Fig. 1 E and J closely, one might even argue that true news diffuses slightly faster than false news when cascade sizes are comparable. SI Appendix, Figs. S2 and S3 provide a supplementary visualization of the pairwise joint distribution of these cascade statistics. Further exploring the statistics jointly, in SI Appendix, section S-I, we train a logistic regression model to predict veracity of cascades from their depth, size, virality, and max breadth. When using a size-matched balanced dataset, the accuracy of the resulting model is consistent with random guessing ($\approx 50\%$). Because we draw random false-news cascades to include in the subsampled dataset, our matched false-news corpus is only one instance out of a large number of possible subsampled false-news datasets. In SI Appendix, Table S1, we repeat the subsampling a large number of times and provide details on the distribution of test statistics obtained across 10⁴ realizations.

Beyond their headline comparison of true and false news, Vosoughi et al. (11) also found that that political false news spread deeper, more broadly, more virally, and reached more people than false news about other topics diffusing on Twitter. When we compare the spread of false political news and false news on other topics using our subsampling procedure to control for size, matching on the nonpolitical news sizes, we find no significant difference in the statistical properties of the size-matched cascade datasets (SI Appendix, section S-I).

Turning to the analysis by Goel et al. (10) of content types, we are faced with four categories of diffusion cascades: images, videos, news, and petitions. In order to make all four cascade datasets comparable at once, we match all four datasets to the same set of cascade sizes. We choose to match all four categories to a target distribution defined by the intersection of sizes present in all four datasets. Fig. 2 D–F show the analysis of Goel et al. repeated on the matched datasets, where each panel corresponds to an unmatched analysis in the panel directly above. In these data, the differences in cascade structure persist after size matching. In SI Appendix, section S-I, a logistic regression model is again used to predict the cascade category from depth, size, virality, and max breadth. When using a size-matched balanced dataset, the accuracy of the resulting model is $\approx 43\%$, significantly exceeding random guessing (25%). We again present test statistics obtained across 10⁴ matching realizations in SI Appendix, section S-I. As a supplementary analysis, in SI Appendix, section S-I, we also perform our size-matching analysis on all pairwise combinations of types (six in total), where similar differences in structure again persist.

Size Collapse in Models of Diffusion

Having seen that controlling for size can make otherwise-clear structural differences in structural features disappear, as in the case of true- and false-news cascades above, it is natural to ask what such an observation can tell us about the possible underlying diffusion dynamics. In models of diffusion, when can the structural differences between resulting cascades be reduced to differences in size?

The two most widely studied models of spreading processes on networks, the SIR and IC models, are both parameterized principally by a single contact-level infectiousness parameter. In the IC model, an infectious node i gets to infect each of its susceptible neighbors j with independent probability p_ij (30). Defining $p_{ij}=p$ for all node pairs makes p a single adjustable parameter governing infectiousness. In the SIR model, an infectious node infects each of its susceptible neighbors with rate r_I and recovers with rate r_R. A recovered node cannot infect or get infected. The ratio $R_0=r_I/r_R$ is the basic reproduction number and is a single adjustable parameter for the infectiousness of an SIR process.

To examine the joint evolution of size and structural features, we start with simulations of the IC and SIR models. We perform simulations on different underlying network topologies, ranging from empirical social networks to the stylized setting of an infinite clique. We focus on results for the infinite clique here, as these dialogue directly with later theoretical results; simulations on other network topologies are shown in SI Appendix, section S-III. All simulations start with a single infectious node (chosen uniformly at random), and we run the simulation until new infections no longer occur. We keep track of who infects whom in the simulation and save the resulting directed, rooted tree. For each parameter setting, we collect 30,000 cascades.

As discussed in SI Appendix, section S-II, the SIR and IC models on the infinite clique are both instances of Galton–Watson processes (38): They can be realized as probabilistic processes where the number of children are independent and identically distributed, natural-numbered, random variables. When performing IC simulations on an infinite clique, we take advantage of the fact that the cascade out-degree distribution approaches a Poisson distribution with mean value $R_0=Np$ for large network size N and small edge probability p. Consequently, this setting is equivalent to simulating a Galton–Watson branching process with a Poissonian offspring distribution. Likewise, the SIR model on an infinite clique is equivalent to simulating a Galton–Watson branching process with a geometric offspring distribution. In both cases, R₀ is the mean of the distributions governing the number of children of infectious nodes.

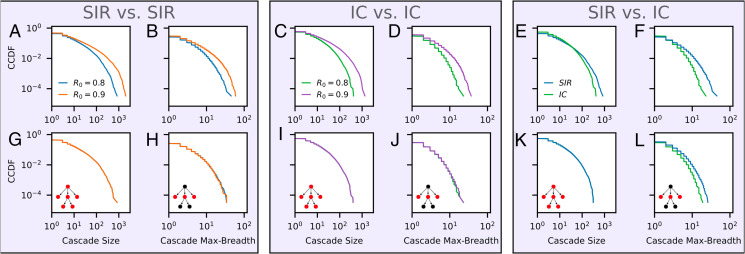
Fig. 3 A and B show the sizes and breadth obtained by simulations of the SIR model on an infinite clique. Comparing datasets created with different values of R₀, we see that a higher R₀ generally results in larger and broader cascades. To control for the effect of size, we perform our size-matching procedure on the simulated datasets, shown in Fig. 3 G and H. Here, we see the statistical differences in structural properties disappear after controlling for size. The same collapse happens for other cascade features, such as depth and virality, both on infinite cliques and for cascades grown on real-world network topologies (SI Appendix, section S-III). The fact that we observe the same distributional collapse on real-world networks as on infinite cliques suggests that the specific structure of the network may not be crucial to the observed phenomenon (39).

Fig. 3.

(A–F) Structural statistics of datasets of cascades simulated using the SIR and IC models. (A and B) Size and maximum breadth of SIR cascades with two different values of the infectivity parameter R₀. (C and D) Size and maximum breadth of IC cascades with two different values of R₀. (E and F) Size and maximum breadth of SIR vs. IC cascades with the same choice of $R_0=0.8$. (G–L) The same analyses as the plots directly above, carried out for two subsampled datasets with matched size distributions. Controlling for size collapses statistical differences in structural properties when simulations come from the same underlying model (IC or SIR), even for different choices of infectivity R₀. The collapse does not happen if the underlying models are different. Insets again depict each statistic on a simple cascade. Only size and breadth are shown here due to space constraints; the collapses of the remaining statistical quantities are shown in SI Appendix, Figs. S14, S18, and S22.

Fig. 3 C and D show the sizes and breadth obtained by simulations of the IC model on an infinite clique. Again comparing datasets created with different values of R ₀, we see that typical sizes and breadths increase with R₀. Fig. 3 I and J show that the observed differences disappear when controlling for size using our subsampling procedure. Again, a similar collapse happens for other cascade features, such as depth and virality, both on infinite cliques and for cascades grown on empirical network topologies (SI Appendix, section S-III).

The fact that all distributions of the examined structural statistics seem to be exactly the same for datasets created under the same model and different values of R₀ raises a very interesting question about the generality of this phenomenon. The following theorem, proven in SI Appendix, section S-II, clarifies that the distribution of cascades of a given size s created under an SIR or IC model on an infinite clique is independent of the value of R₀. In other words, no matter what structural feature we compare, the conditional distributions, conditional on size s, will come out identical if the datasets were created using the same model, even if the parameter settings were different. The proof of this theorem follows from a more general result we establish for Galton–Watson processes, of which the SIR and IC model on an infinite clique are both special cases.

Theorem 1

(SIR and IC Model). Let $P_{\text{SIR}}(T|s,R_0)$ and $P_{\text{IC}}(T|s,R_0)$ denote the probability of obtaining the tree T when growing a self-terminated cascade of size s on the infinite clique using the SIR model with parameter $R_0=r_I/r_R$ or the IC model with parameter R₀, respectively. Then, both $P_{\text{SIR}}(T|s,R_0)$ and $P_{\text{IC}}(T|s,R_0)$ are independent of R₀.

Moving beyond Theorem 1, what happens when the diffusion models behind two datasets are not the same? Can size collapse be used to distinguish sets of cascades created under different diffusion rules? In Fig. 3E and F, we compare sizes and breadths obtained by simulations of the IC and SIR models on an infinite clique and identical choices of R₀. We see that the size distributions differ, even though their means are the same, and we see that SIR cascades have a higher max breadth. Fig. 3 K and L show the corresponding plots when controlling for size. Interestingly, no collapse of the breadth distributions takes place: SIR cascades still have higher max breadth. The distributions of depth and structural virality also do not collapse (SI Appendix, Figs. S22 and S23). Unlike comparisons within a single model family (IC or SIR), here, the different diffusion rules manifest themselves in how often a cascade with a given topology is created. That the cascade distributions are different under the models can be proven rigorously (SI Appendix, section S-II, Theorem 2). Differences in the shape of the offspring distributions of Galton–Watson processes, Poisson for the IC model and geometric for the SIR model, create differences in cascade structure that go beyond cascade size.

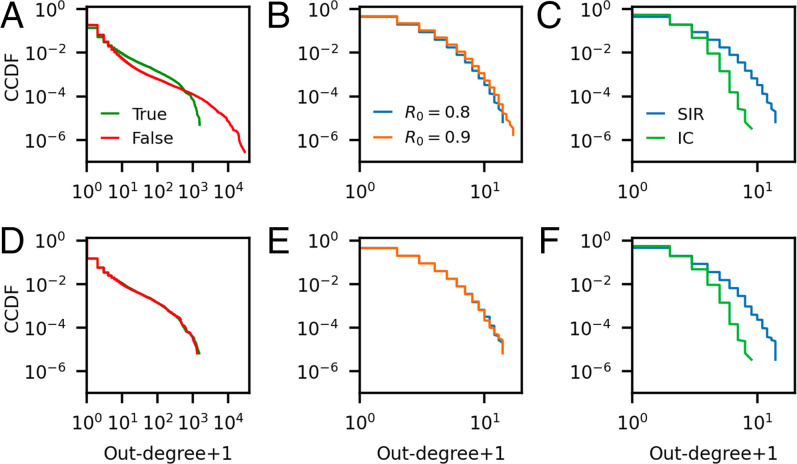
In order to understand whether two size-matched datasets are likely to create similar cascade topologies, Theorems 1 and 2 suggest that it is natural to investigate the offspring distribution of the cascades, also known as the out-degree distribution. For two cascade datasets from Galton–Watson processes matched on size, the shape of the offspring distributions determines everything about the other structural statistics. Returning to the Vosoughi et al. dataset of true and false news (11), Fig. 4A shows the out-degree distributions of the true-news and false-news cascades, while Fig. 4D shows the out-degree distributions for two subsampled datasets with matched size distributions. The out-degree distributions of the matched datasets are indistinguishable. Meanwhile, Fig. 4 B and C show the offspring distributions of cascades generated by SIR and IC models: Poisson and geometric, respectively. When the cascades from these models are matched on size, Fig. 4 E and F show the offspring distributions of the matched cascades. Extending the observations in Fig. 3, we see that the offspring distributions collapse for model instances within the SIR family, but do not collapse when matching between SIR and IC instances.

Fig. 4.

(A) CCDF of out-degree distributions in the Vosoughi et al. dataset (11) of false-news and true-news cascades on Twitter. (B) CCDF of out-degree distributions in SIR cascades with two different values of the infectivity parameter R₀. (C) CCDF of out-degree distributions in SIR cascades and IC cascades with the same choice of $R_0=0.8$. (D–F) The same analyses as the plots directly above, carried out for two subsampled datasets with matched size distributions. Controlling for size collapses statistical differences in structural properties for the datasets of true and false news and the simulated data created under the same model with different parameter settings. The collapse does not happen if the underlying models differ. We show KS-test statistics for 1,000 instances of size-matched datasets in SI Appendix, section S-I.

Discussion

In recent years, significant attention has been paid to the structure of online diffusion cascades. Studies have compared the structure of cascades for different types of content, but it has been difficult to discern whether diffusion mechanisms of the different content types differ or not. Here, we have shown that juxtaposing size-matched datasets of cascades provides one way to reject, or not, differences in diffusion mechanisms.

We find that previously reported structural and temporal differences between true- and false-news cascades can be explained almost entirely by differences in cascade size, whereas the observed differences persist when comparing size-matched cascades of videos, images, news, and petitions. The observation that differences were absent in size-matched true-news and false-news cascades can explain why recent efforts to use machine-learning techniques to resolve differences between false- and true-news cascades based on structural properties alone have had limited success (40). To accurately classify the veracity of Twitter cascades, these studies use additional metadata about network nodes, highlighting the importance of graph-representation learning (41) methods capable of ingesting rich data types in such endeavors.

We emphasize that that the cascades of Vosoughi et al. (11) are limited to true- and false-news cascades that have been fact-checked. The structure of fact-checked true-news cascades is likely not reflective of true-news cascades in general, and fact-checked true-news cascades are plausibly much more similar (than generic true-news cascades) to fact-checked false-news cascades. But comparing these two populations of fact-checked cascades, false fact-checked cascades are larger. Yet, we find that the differences in diffusion can be explained by differences in infectiousness alone. The focus on fact-checked cascades may be viewed as a limitation, but by focusing on fact-checked content, our analysis (and the analysis of Vosoughi et al.) focuses on the boundary of veracity, where it is most important to understand the effect on diffusion as stemming from the truth or falsity of the content. Further, recent work has shown that directing attention to accuracy of news on Twitter helps limit the spread of misinformation (42). Through the lens of our analysis, that recent work has the greatest effect at the boundary of veracity and can be seen as an intervention that specifically targets the further transmission of false information (the infectiousness), which should then also organically limit the breadth and depth of the diffusion.

Through our theoretical analysis of Galton–Watson processes, we find that when two such processes have offspring distributions from the same family, differing only in their infectiousness (correspondingly, their mean size), controlling for size eliminates all structural differences between cascades generated by those processes at different infectiousness. Meanwhile, when the offspring distributions are from different families, controlling for cascade size no longer necessarily collapses the distributions of other structural properties. In the context of true and false news, this result tells us that observing two cascade datasets that differ only in size is consistent with similar underlying diffusion processes. For videos, images, news, and petitions, our results suggest that the diffusion mechanics for these more diverse content types are more deeply different, though we note that the persistent structural differences could also be explained by, e.g., differences in the types of seed nodes, differences in the network location of the seeds, or differences in when the cascades are seeded.

Having seen that some content types show indistinguishable cascade characteristics upon size matching, whereas the differences persist for others, we wonder: Can content types be divided into “classes,” for which the collapse of structural property distributions takes place upon size matching? How may this collapse differ across platforms (e.g., Twitter vs. Facebook)? Do measures exist that can reveal whether size-matching will lead to a collapse of structural property distributions, even before carrying out the size-matching? These are all natural directions of future research.

As a limitation, our theoretical results apply only to infinite cliques and only to diffusion processes that can be characterized as Galton–Watson processes. But even in this limited setting, we find the theoretical analysis instructive. We have not proven a general result about how different diffusion rules may or may not give rise to distributional collapses when matching for size, and this question and further analytical results for more general network topologies are important directions for further research.

We have shown that the joint distributions of statistical properties of diffusion cascades, long known to be important in the theory of random trees (43), can greatly impact the conclusions of comparative data analyses. In the fast-moving field of diffusion research, we hope that a careful consideration of joint statistical distributions, particularly the joint distribution with size, can diffuse quickly through the literature.

Materials and Methods

The main text describes our size-matching procedure and all details necessary to replicate the work presented in this manuscript. SI Appendix provides details of our theoretical results. It also includes supplementary data analysis of both empirical datasets, Kolmogorov–Smirnov (KS) test statistics for Figs. 1–4, and a demonstration of our size-matching procedure for SIR and IC processes simulated on empirical networks.

Data Availability

Previously published data (10, 11) were used for this work.