Real-time handheld probe tracking and image formation using digital frequency-domain diffuse optical spectroscopy

Abstract

Objective:

Frequency-domain diffuse optical spectroscopic imaging (FD-DOS) is a non-invasive method for measuring absolute concentrations of tissue chromophores such as oxy- and deoxy-hemoglobin in vivo. The utility of FD-DOS for clinical applications such as monitoring chemotherapy response in breast cancer has previously been demonstrated, but challenges for further clinical translation, such as slow acquisition speed and lack of user feedback, remain. Here, we propose a new high speed FD-DOS instrument that allows users to freely acquire measurements over the tissue surface, and is capable of rapidly imaging large volumes of tissue.

Methods:

We utilize 3D monocular probe tracking combined with custom digital FD-DOS hardware and a high-speed data processing pipeline for the instrument. Results are displayed during scanning over the surface of the sample using a probabilistic Monte Carlo light propagation model.

Results:

We show this instrument can measure absorption and scattering coefficients with an error of 7% and 1% respectively, with 0.7 mm positional accuracy. We demonstrate the equivalence of our visualization methodology with a standard interpolation approach, and demonstrate two proof-of-concept in vivo results showing superficial vasculature in the human forearm and surface contrast in a healthy human breast.

Conclusion:

Our new FD-DOS system is able to compute chromophore concentrations in real-time (1.5 Hz) in vivo.

Significance:

This method has the potential to improve the quality of FD-DOS image scans while reducing measurement times for a variety of clinical applications.

I. Introduction

FREQUENCY-DOMAIN diffuse optical spectroscopy (FD-DOS) is a non-invasive method capable of measuring absolute concentrations of tissue chromophores such as oxy- and deoxy-hemoglobin centimeters below the surface of biological tissue [1], [2]. This method utilizes light that is intensity modulated at radio frequencies (typically 50-500 MHz) to produce photon density waves that traverse through tissue. By comparing the effect of the tissue on the amplitude and phase of these waves, it is possible to disentangle the effects of absorption and scattering. Knowledge of the absorption coefficient (μ_a) at several wavelengths enables the calculation of chromophore concentrations. Over the past several decades, FD-DOS has been extensively studied for a wide variety of application areas including neuro-imaging [3]-[5], exercise physiology [6], [7], and monitoring cyanide poisoning [8]. One of the most promising areas of research has been the investigation of FD-DOS to monitor the response of breast tumors to neoadjuvant chemotherapy [9]-[12]. While the advances discussed in the manuscript are potentially relevant to a variety of clinical applications, we motivate the work through a discussion of the prior limitations of FD-DOS for neoadjuvant chemotherapy monitoring in breast cancer.

Breast cancer is one of the most common types of cancer diagnosed in women, with over 250,000 diagnoses per year leading to over 40,000 deaths annually in the United States [13]. Patients who are diagnosed with locally advanced breast cancer increasingly undergo 3-6 months of chemotherapy prior to surgery (neoadjuvant chemotherapy). However, only about 30% of patients receiving neoadjuvant chemotherapy are considered pathologic complete responders [14]. Standard-of-care imaging technologies such as Magnetic Resonance Imaging (MRI) can be used to monitor tumors during this period [15], but are typically only employed in the research setting due to high cost and limited availability. Prior work, including our own, has shown that FD-DOS can be used to predict response to chemotherapy as soon as one day after treatment [9], [16]. A recent large, multi-center clinical study investigating the utility of a variant of FD-DOS for chemotherapy treatment monitoring found no statistically significant differences in the longitudinal changes in tumor chromophore concentrations between responders and non-responders when analyzing the patient population as a single, large, cohort [12]. It is of note that FD-DOS was effective at discriminating responders and non-responders in a non-hypoxic subset of the measured subjects. The authors of this study (D.R. was a co-author) identified several potential problems that reduced the sample size of this study, and may have contributed to the observed results. Out of 60 patients who were enrolled, 22 of them (37%) were excluded from the final analysis due to incomplete or low-quality data. The reasons for these exclusions were identified as being mainly due to operator error leading to poor data quality, as well as clinical time-pressure leading to incomplete data [12]. The time pressure observed in this study was due partially to the specific measurement protocol, which involved point-by-point scanning on a pre-defined grid and could take up to an hour per patient. Additionally, there was limited feedback provided by the instrument during the measurement procedure due to the relatively slow speed of data processing. This bottleneck left operators with limited information as to whether they had collected clinically relevant and high quality data during the measurement, while strictly defined treatment timetables made it challenging to retake measurements.

In this work, we describe a real-time FD-DOS system that aims to address the slow acquisition and limited feedback of prior handheld FD-DOS devices. Our proposed system is, to our knowledge, the first demonstrated FD-DOS system capable of collecting, processing, and displaying 2D FD-DOS images live in real-time (1.5 Hz) without requiring that the measurements be taken on a grid. It uses a single overhead camera to track the location of the FD-DOS probe during measurements, eliminating the need for grid-based scanning. This work builds on prior work that used a similar probe tracking technique for FD-DOS [17]. However, in that work, the tracking, processing, and display were performed after the data had been collected. In the real-time system described here, FD-DOS data were collected with a custom-built digital FD-DOS system that processes FD-DOS data at high speed using a lookup-table approach that is capable of estimating optical properties from calibrated amplitude and phase data in real-time. The location and orientation of the probe, combined with a Monte Carlo model of light propagation in tissue, was then used to generate a live, probabilistic image of the calculated absorption coefficient, scattering coefficient, and tissue chromophore concentrations.

In the following sections, we first describe the custom high-speed (HS) FD-DOS system capable of data collection rates up to 15 kHz. We then discuss our approach to real-time processing and display. Next, we describe the characterization of the FD-DOS system along with our quantification of tracking accuracy and visualization methodology. Finally, we demonstrate two in vivo measurements in the human forearm and healthy breast.

II. Methods

We have developed an integrated FD-DOS data collection and visualization instrument that enables the real-time generation of chromophore concentration images in biological tissue. This system (Fig. 1) consists of a custom FD-DOS instrument for collection of optical property data, an overhead camera to monitor measurement location, a specially designed probe that allows its orientation to be precisely calculated, and a microcontroller that is used to synchronize the components of the instrument. The operator can view live images of the measurement in real-time using a laptop computer.

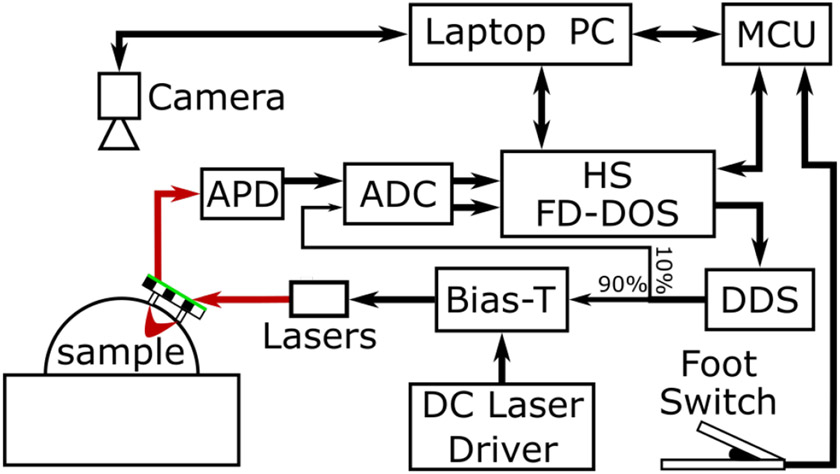
Fig. 1.

Block diagram of the real-time FD-DOS system. A probe consisting of a source optical fiber and a detector optical fiber along with a green outlined checkerboard target was moved freely over the surface of a sample. During measurements, this target was imaged by an overhead camera (FLIR Blackfly, 1.3 MP). These images were used to calculate the location of the source and detector fibers on the surface of the sample. FD-DOS measurements were performed by the HS FD-DOS system. This system was used to control 5 Direct digital synthesis (DDS) chips which generated radio frequency modulation signals. These signals were combined with a constant drive current using Bias-Ts and used to modulate the laser diodes. Optical signal was detected by an avalanche photodiode (APD) and the resulting electrical signal was digitized by a 250 MHz analog to digital converter (ADC). Measurements were triggered using a foot switch so the operator could have both hands free for collecting measurements. A microcontroller (MCU) was used to monitor the state of the foot switch as well as synchronize FD-DOS measurement and probe location calculations.

A. High-speed FD-DOS

The HS FD-DOS system used for these studies was a significantly improved version of our previous digital FD-DOS technology that has been described in detail previously [18]. Briefly, that system used 6 direct digital synthesis (DDS) chips to generate sinusoidally modulated signals at frequencies between 50 and 500 MHz. The modulation signal was combined with a constant DC current to drive 6 laser diodes at wavelengths of 690, 730, 785, 808, 830, and 850 nm. Each laser was coupled to a 400 μm core diameter optical fiber (Fiberoptic Systems, Inc., Simi Valley, CA). These fibers were combined into a single bundle that was placed in contact with the sample. A 2.3 mm detector fiber was used to collect light at a fixed distance from the source. The detector fiber was coupled to a 3 mm diameter avalanche photodiode (APD) (S11519-30, Hammamatsu Photonics) which converted the optical signal to an analog voltage. A two channel 250 MHz analog to digital converter (ADC) digitized the signal for processing. The system used a Zynq system on a chip (SOC) that integrates a field-programmable gate array (FPGA) with a single board computer. Time varying signals from the ADC were stored in a block of shared memory where they could be transferred to an external PC, or processed using the single board computer. The previous system was limited in that it provided no on-board data processing, and required that the full time-varying signal for each measurement (typically 16 kB in size) be transferred from the system to an external computer. We deveoped custom firmware to perform on-board processing of the time-varying signal allowing for an increased measurement speed and reduction in data load of about two orders of magnitude. We have previously demonstrated the ability of this system to display live traces of chromophore concentrations in vivo [19].

The system used in this work was extended in several important ways from our prior works through co-developed hardware, firmware, and software. We updated the ADC from 14-bits to 16-bits and added two independent programmable gain amplifiers to pre-amplify the collected signals prior to digitization, helping to ensure they occupied the full-scale range of the ADC. The most important change to the new system is the enhanced utilization of the programmable logic (PL) component of the SOC, which dramatically improved data processing speeds. A block diagram of the data flow through the system is shown in Fig. 2. We utilized the PL to process the incoming time varying signal from the ADC and directly calculate the amplitude and phase values from each channel at each modulation frequency. The transformation between the time varying signal from the ADC and the frequency-domain data at discrete modulation frequencies was performed by a bank of 12 Goertzel filters implemented in the PL [20]. A Goertzel filter is second order infinite impulse response digital filter that, when appropriate coefficients are selected, can be used to calculate a single bin of a discrete Fourier transform [21]. The results are complex-valued and can be readily converted to amplitude and phase using the Euler equation. Goertzel filters require fewer operations than the more traditional Fast Fourier Transform when the number of frequencies is fewer than log₂(N), where N is the length of the time varying signal [22]. In this FD-DOS system, data from the ADC were first saved into a block of random access memory (RAM) before being fanned out to each filter. Frequency selection in these filters was accomplished by choosing from an array of pre-computed filter coefficients. The output of each Goertzel filter was placed in a memory location where it could be accessed by the CPU of the SOC. Final data were transferred to a host laptop using a 1 Gbit Ethernet cable. Saving and processing operations were performed sequentially. The available block RAM in the PL limited the time varying signal to 65,536 values which were acquired at a clock rate of 250 MHz for a total acquisition time of approximately 260 μs. Processing through the Goertzel filters was done in parallel at a slower clock rate of 50 MHz. This implementation of the Goertzel algorithm required 4 clock cycles per sample leading to a maximum processing time of 5.2 ms for each modulation frequency used in the measurement.

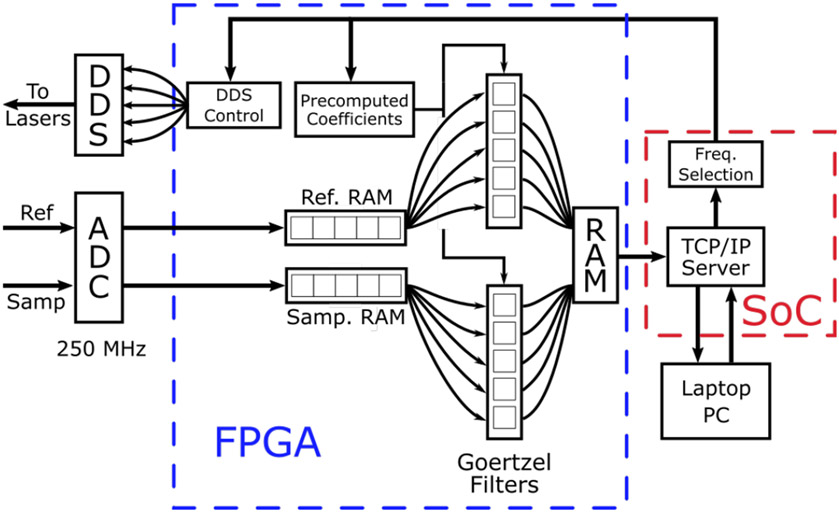
Fig. 2.

Block diagram of data flow through the programmable logic (PL) of the field programmable gate array (FPGA). Data from the reference and sample arms of the HS FD-DOS system were digitized by a high-speed analog to digital converter (ADC) and saved to separate blocks of random access memory (RAM). These data were read sequentially and distributed to 12 Goertzel filters which were used to calculate the Discrete Fourier Transform (DFT) at 6 different frequencies. The results were saved in a separate block of RAM where they could be read by the single board computer (SOC). The SOC was programmed to run a TCP/IP server that was used to communicate with a laptop computer via an Ethernet cable. The laptop was used to set acquisition parameters such as the number of modulation frequencies to be used as well as the number of ADC samples to save for each frequency. This information was passed to the FPGA which was used to tune the Goertzel filters and control the direct digital synthesis (DDS) chips. These improvements increase the acquisition speed by about 3x compared to our prior digital FD-DOS system.

A laptop computer with an i5-5300U processor was used to interface with the SOC over an Ethernet connection. We used a custom Python-based graphical user interface (GUI) to select desired scan parameters such as the number of wavelengths, the number of ADC samples saved, as well as the desired modulation frequencies. A TCP/IP server running on the SOC parsed data coming from the laptop and returned the amplitude and phase data at the conclusion of each measurement.

The improvements to the previous version of this system resulted in the ability to acquire significantly longer acquisitions (65,536 samples vs. 8,192) without the need to transfer additional data to the host computer. Longer signals resulted in an estimated 20 dB increased signal to noise ratio due to process gain [23]. The use of the PL also enabled processed data to be pushed to the host PC as it was generated, allowing the system to run continuously without data storage issues.

B. Probe pose estimation

To generate a 2D FD-DOS optical property map, it is necessary to know the probe location whenever a measurement is taken. Previous work has required that the probe operator collect measurements on a pre-determined grid [12]. However, unrestricted movement of the probe would allow for faster measurements and result in less of a burden for both the subject and the operator. To accomplish this at high-speed, we used a two-phase monocular pose estimation approach.

Monocular pose estimation involves the use of a single image to determine the 6 degrees-of-freedom pose (location and orientation) of an object in 3D space [24]. The use of a single camera reduces the cost and hardware complexity compared to other 3D imaging systems. Since only a single point-of-view is used, a priori knowledge about the target object must be incorporated into the estimation model. We printed a checkerboard pattern with a number of salient points with known spatial interrelationship onto the probe surface. From this information, a theoretical point distribution of the known points can be generated for any location and orientation using perspective transforms [17]. In each image, the apparent position of each of those points is recorded and the pose determined by finding the location and orientation of the object that minimizes the error between the theoretical location of the points and the location of the points in the image. We investigated both an iterative approach (Levenberg-Marquardt) to minimizing this error as well as a single-shot approach [25] and found no meaningful difference in accuracy or speed between the two.

We attached a checkerboard pattern (Fig. 3C) with a square size of 4.75 mm to the top of our probe (Fig. 3B) which measured 4.2 by 4.0 by 1.4 cm, to use as the target object. We used the open computer vision library (OpenCV) in Python to calculate the probe pose for a series of images. A primary bottleneck of the tracking was searching for candidate checkerboards within the entire frame. To speed up the measurement, we outlined the checkerboard pattern with a green border to allow rapid segmentation of the probe from the background. Prior to object detection, a color threshold was used to identify regions of the image that matched the green color of the border. The largest of these regions was assumed to be the probe and was used to crop the image around the target. Identification and pose estimation was then performed on the cropped image which increased the speed of object detection. The details of pose estimation from a checkerboard pattern have been previously described [17]. Briefly, the intersections of the checkerboard were identified and refined to the subpixel level in the cropped image using OpenCV. The pose estimation was performed as described above to determine the orientation and position of the checkerboard relative to the camera sensor. This calculation required knowledge of the camera’s intrinsic matrix which was determined through calibration. The goal of estimating the pose of the probe was to accurately measure the probe’s location on tissue. The probe pose provided the location and orientation of the checkerboard target expressed as 3D translation and rotation vectors relative to the camera sensor. The location of the source and detector fibers in the image could then be calculated by measuring their relative distance from the checkerboard origin, and applying the rotation and translation measured during the pose estimation procedure. Once calculated, we were able to use the position of the source and detector fibers to generate a 2D estimate of optical properties using a model-based visualization strategy.

Fig. 3.

A. 2D sensitivity map constructed from a Monte Carlo simulation with a 20 mm source-detector separation used as the weighting matrix for real-time visualization of FD-DOS data with a logarithmic color scale. The simulation volume had an absorption coefficient of 0.1 mm⁻¹ and a reduced scattering coefficient of 1 mm⁻¹. The area immediately surrounding the source, located at (20,30), and the detector, at (40,30), are the regions of highest sensitivity. The number of detected photons passing through each pixel rapidly decays as the distance from the line connecting the source and detector increases. B. Photo of the underside of the probe with source and detector fiber ends indicated by arrows. C. Photo of the top of the probe illustrating the checkerboard pattern used for pose estimation.

C. Visualization

A method was developed to enable live visualization of optical property and chromophore data based on Monte Carlo simulations of light propagation in tissue. Our method attempted to correct for several issues that occur with free scanning. For example, the pose estimation method previously described allows the user to scan freely over the surface of tissue, which can lead to irregular spatial sampling potentially missing of important features of the tissue. A second issue arises because each point measurement samples a relatively large volume of tissue, necessitating a way of accounting for multiple overlapping measurements taken in close proximity. To account for these issues, we developed a visualization method that weighted each measurement based on a spatial sensitivity estimate theoretically derived from photon transport using a Monte Carlo simulation. Using this technique, locations that are sparsely sampled will lead to visualizations that contain “holes” without data, indicating to the user that additional measurements are needed. If multiple measurements are collected near one another, the weighted average of these measurements is visualized.

We computed a weighting function that takes into account the probability of photon interactions with the tissue by simulating photon transport in a representative tissue using Monte Carlo eXtreme (MCX) [26]. 10⁹ photon packets were launched in a medium with an absorption coefficient of 0.01 mm⁻¹, a scattering coefficient of 10 mm⁻¹, a Henyey-Greenstein scattering phase function (g) of 0.9, and an index of refraction (n) of 1.4. A point source and detector matching the radius and geometry of the experimental source and detector fiber were simulated. MCX’s “replay” mode was used to run a second simulation consisting only of detected photons. The total flux through each voxel in this second simulation was used to estimate the spatial sensitivity of the measurement. The 3D sensitivity matrix was projected onto the surface of the sample by taking the sum of each voxel along the Z-axis. An adjustable cutoff value was used to set the sensitivity matrix to zero at locations more than 15 mm from the measurement center location. Finally, the weight matrix was normalized by dividing each pixel by the maximum value. An example weight matrix is shown in Fig. 3A.

The sensitivity matrix was scaled such that pixels in the matrix were the same size as pixels in the camera image. Similarly, the known rotation of the probe allowed the sensitivity matrix to be similarly rotated such that the simulated source and detector fibers matched with the apparent location of the source and detector fibers at each measurement. The final value at each image pixel was defined as the weighted average of all the measurements in the scan where the values in the average were the measured μ_a and ${\mu }_s^{\prime }$, and the weights were determined from the sensitivity matrix.

D. Lookup table optical property estimation

A new inverse model was developed to map amplitude and phase information to optical properties (μ_a and ${\mu }_s^{\prime }$) in real-time. In much prior work using handheld FD-DOS systems, a diffusion theory-based iterative technique was used in which an initial optical property guess was used to generate simulated values of amplitude and phase. The simulated data were compared with the experimental data, and the optical property guess updated until the difference between simulated and experimental data was minimized. Using this method for a single wavelength on a modern desktop PC (Intel i9-9900), about 30 optical property calculations can be performed per second. For a 6 wavelength system, roughly 5 chromophore concentrations (calculated using Beer’s law [27] from the μ_α values at 6 wavelengths) can be calculated per second.

We recently developed a lookup-table approach to increase the speed of optical property extraction. The details of this method have been described in detail elsewhere [28]. Briefly, the P1 approximation to the radiative transport equation in a semi-infinite geometry was used to pre-compute the complex frequency response for a grid of 500 x 500 optical property pairs with μ_α values falling between 0.0001 and 0.05 mm⁻¹ and ${\mu }_s^{\prime }$ values between 0.1 and 3 mm⁻¹. The Euclidean distance between the measured data and at each frequency and every point on the pre-computed lookup table were calculated, and the sum of these distances was used as an error metric. The optical property pair where the error was minimized was assumed to be the solution. For a single modulation frequency, this method is capable of performing over 1300 estimations per second. In this study, we used 35 modulation frequencies which could be processed at a rate of approximately 50 optical property extractions per second. This nearly two-times increase in processing speed over the iterative method described above allowed faster processing of measurements.

E. Synchronization

The combined HS FD-DOS and real-time visualization technique required synchronization of FD measurements, FD data processing, and probe pose tracking. This was accomplished using a microcontroller (MCU) (Arduino, Uno) and a laptop PC. A custom Python script continuously monitored whether new data were available from the HS FD-DOS system. If new data were available, a trigger signal was sent to acquire a new camera image, and the location and orientation of the probe were determined as well as the pixel scaling factor for the sensitivity matrix. The absorption coefficients, scattering coefficients, and chromophore concentrations were also calculated and used to update the live visualization display. If no new FD-DOS data were available, a new camera image was still acquired, and prior measurement results were overlaid onto the live camera image to allow the operator to monitor the scan results in real-time.

A foot switch was used to trigger new FD-DOS measurements which allowed the operator to lift and reposition the FD-DOS probe during a measurement. The trigger signal was sensed by the MCU and read by the laptop. If the foot switch was pressed, and all the calculations from the previous measurement were complete, the MCU was used to send a trigger signal to the HS FD-DOS system to collect the next measurement. This synchronization guaranteed that the location data and the measurement data were appropriately linked.

Taken together, this system allowed the operator to freely scan the probe over the surface of the sample while collecting data. During measurements, the position and location of the probe was constantly calculated and displayed and, when new FD-DOS data were acquired, the visualization of the results was updated. A second foot switch was used to stop the measurement and save the data.

III. Results

A. System validation

We characterized the new FD-DOS system by measuring its accuracy against a previously validated FD-DOS system [18]. Accuracy was assessed by measuring 5 tissue simulating optical phantoms 20 times with 5 wavelengths using both the digital FD-DOS system and a gold standard, network analyzer based system, yielding a total of 500 measurements per system. At the wavelengths used, the μ_a values ranged from 0.002 to 0.04 mm⁻¹ and the ${\mu }_s^{\prime }$ values fell between 0.4 and 0.9 mm⁻¹. This range of values encompassed many types of tissue including skin, muscle, and brain [29]. Network analyzer based systems have a long history of use in clinical studies and have been shown to be capable of accurately measuring optical properties over a wide range [30]-[32].

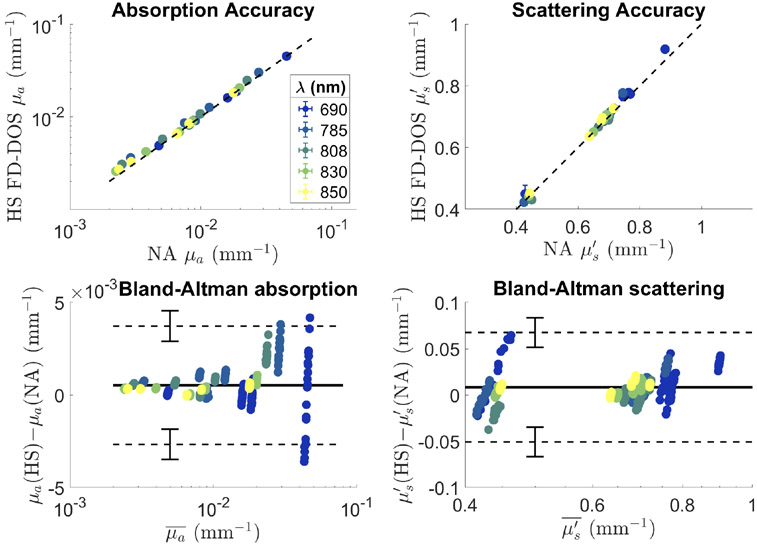
The error between the two systems was −7 ± 7% in μ_a and −1 ± 2% in ${\mu }_s^{\prime }$. We performed a Bland-Altman analysis on these measurements to characterize the agreement between the proposed and previously validated system. We found minimal bias in both absorption and scattering of 5 × 10⁻⁴ and 8 × 10⁻³ mm⁻¹ respectively. The Bland-Altman analysis also allowed for the calculation of limits of agreement between the two instruments. For absorption, the limits of agreement were found to be between 3.7 ± 0.8 × 10⁻³ mm⁻¹and −2.7 ± 0.8 × 10⁻³ mm⁻¹. A change in μ_α of 4 × 10⁻³ mm⁻¹ at all wavelengths represents a change of about 0.02 μM of hemoglobin. For scattering, the limits of agreement were 0.07 ± 0.2 and −0.05 ± 0.2 mm⁻¹. The Bland-Altman plot for absorption shows a clear increase in the variability of the measurements as absorption coefficient increases which should be considered when highly absorbing tissues are measured. Large errors observed with the 690 nm laser in Fig. 4 are due to the fact that the absorption coefficient at 690 nm tends to be higher than the other wavelengths tested as well as a smaller modulation depth for that laser compared with the other wavelengths.

Fig. 4.

Top: Accuracy of absorption (left) and reduced scattering coefficient (right) for the high-speed FD-DOS (HS FD-DOS) system and the network analyzer (NA) based system. Points represent the average values for 20 repeated measurements. Error bars indicating ± one standard deviation are mostly smaller than the points used to indicate the mean values. Bottom: Bland-Altman plots for absorption (left) and reduced scattering coefficient (right). Solid horizontal lines show the average difference between measurements while the dashed lines show the limits of agreement between the two systems. Error bars on the dashed lines show the 95% confidence interval for the location of the limits of agreement. HS stands for the high-speed FD-DOS system while NA stands for the network analyzer based system. μ_a values are shown on a logarithmic scale.

B. Probe pose estimation

The accuracy of the pose estimation algorithm was assessed by measuring the position and orientation of the probe when securely fastened to a 1 axis translation stage. The stage was fixed to an optical table with two mounting bolts and placed such that the probe was initially located along the bottom of the camera image (the camera was mounted above the optical table pointing down). The probe was programmatically moved horizontally 150 mm in 5 mm increments with a measurement collected at each increment. The stage was then displaced and remounted 25.4 mm away on the optical table such that the stage and probe moved vertically toward the top of the camera image. The stage was again scanned horizontally 150 mm with a measurement taken every 5 mm. This procedure was repeated seven times and resulted in a set of 217 measurements spanning the entire camera image where the true position and orientation of the probe were known.

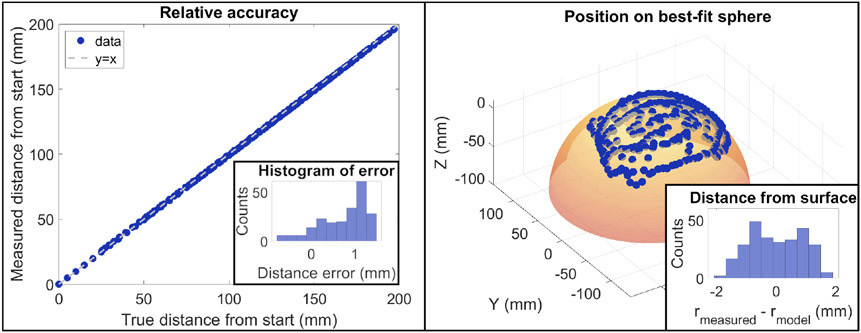
The accuracy of the pose estimation was assessed in two ways. The first was to assess the relative error of the method by calculating the distance of each point to the first measured location. Using this approach, we found the average difference in distance was 0.7 ± 0.5 mm (Fig. 5 left). We also assessed point-by-point accuracy using the known programmed probe path. With this method, the distance of each point from its known location was 1.3 ± 0.5 mm. Given the low-resolution nature of FD-DOS imaging, a position error around 1 mm was deemed acceptable.

Fig. 5.

Left: Relative tracking accuracy. A linear stage was used to move the probe to 217 known locations. The true distance of each point from the first location is plotted on the X-axis and the measured distance from the first location is plotted on the Y axis. Inset into this plot is a histogram of the difference between the known and measured locations. The average error was 0.7 ± 0.5 mm. Right: The probe was randomly scanned over the surface of a sphere and the recorded coordinates are displayed as points. A best-fit sphere was constructed based on those locations to ensure the points followed a spherical shape. Inset into this plot is a histogram of the measured distance from the sphere center at each point minus the radius of the best-fit sphere. The deviation from the model was 0.0 ± 0.9 mm.

Finally, we scanned the probe over the surface of a spherical object with a 118.5 mm radius to assess the accuracy of the probe tracking method over a curved surface (Fig. 5 right). The probe was moved randomly over the surface of the object and the position of the surface in 3D space was calculated using the pose estimation approach described above. A best-fit sphere was constructed based on the results to examine how well the estimated probe locations mapped onto the spherical surface. The radius of the best-fit sphere was 112.2 mm which is very close to the measured value. We attribute the 6.3 mm difference between the two methods primarily to the difficulty of accurately measuring a sphere of this size due to surface imperfections. Visual examination of the sphere and the measured probe location show good agreement (Fig. 5). We quantified this by comparing the distance of each measured point to the modeled sphere center. Ideally, every point would be the same distance away from the center and the difference between the modeled radius and each point would be zero. The average difference in distance from the sphere center was 0.0 mm as expected for a best-fit sphere. The standard deviation of radii was 0.9 mm. This result indicates that the tracking algorithm is able to accurately track the surface of an object over large changes in the angle of the probe.

C. Optical property map visualization

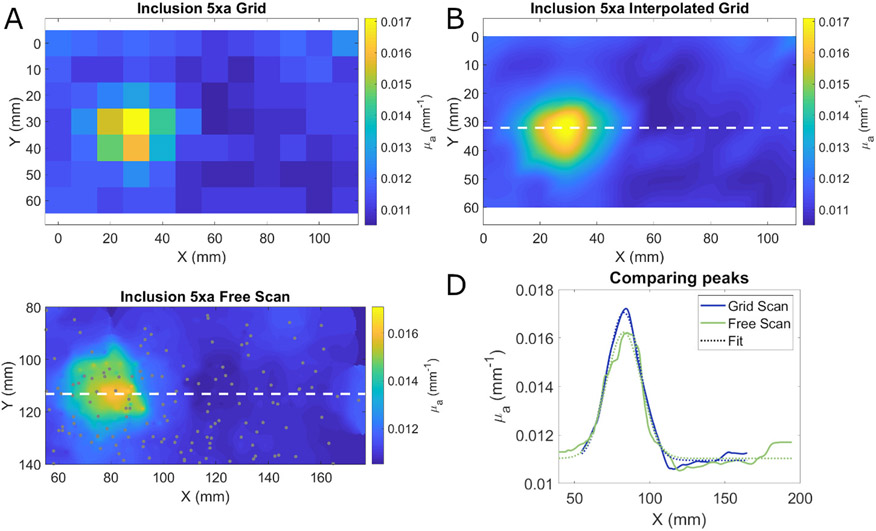
The visualization method was tested by imaging a tissue simulating optical phantom with a 40 mm diameter hemispherical absorbing inclusion located 5 mm below the surface of the phantom. This phantom was imaged two times. In one measurement, a grid of 126 points with 1 cm by 1 cm spacing was drawn onto a transparency using a surgical marker to mimic a previously used clinical imaging protocol [12]. The grid pattern was transferred onto the sample by placing the transparency on top of the sample and applying firm pressure. FD-DOS measurements were collected at each grid point except points less than 10 mm from the edge of the phantom which were excluded. The absorption coefficient at 850 nm was calculated at each point and interpolated using a bicubic scheme. The size of the resulting inhomogeneity was assessed by fitting a Gaussian function to a single line of the interpolated image that passed through the center of the object. In the second measurement, the same phantom was measured while freely moving the probe over the surface. The density of measurements was driven by real-time visual feedback so measurement points were clustered around the absorbing object. The visualizations were generated as described in Section II-C. The size and shape of the absorbing structure was assessed in the same way as the grid based measurement.

The results of these measurements are shown in Fig. 6. As expected, the grid-based scanning without interpolation led to a relatively low-resolution image. Upon interpolation, the resulting image has a smoother appearance that accurately captures the underlying geometry of the inhomogeneity. Fig. 6C shows the results of freely scanning the probe including the location of each measurement point indicated by gray circles. The measurement points occur at higher density near the inhomogeneity as the operator focused their measurements in that location using the real-time feedback provided by the system. The shape of the inhomogeneity was very similar using the two visualization methods as seen in Fig. 6D. When a Gaussian function was fit to the interpolated grid-based scan profile, the full width at half maximum (FWHM) of the inclusion was found to be 37.3 mm. For the free scanning method, the FWHM of the Gaussian fit to the profile was 36.1 mm.

Fig. 6.

A. Absorption coefficients at 850 nm from a phantom with an absorbing inhomogeneity where data were collected on a 1 cm x 1 cm grid. B. Bicubic interpolation of the grid based measurement. The dashed white line indicates the location of the profile graphed in panel D. C. Estimation of absorption coefficient from a free scanning measurement using weighted average based visualization. The dashed white line indicates the location of the profile graphed in panel D. Gray circles indicate the location of each measurement. D. Profiles through the center of the inclusion using the grid-based measurement (blue) and free scanning measurement (green) method. Dotted lines show the Gaussian fit to each profile. Profiles were shifted to align the peaks. The FWHM of the Gaussian fits were 36.1 and 37.3 mm for the interpolation and weighted average visualization methods respectively.

Despite their apparent similarities, the number of measurements and the measurement time for these methods were quite different. The grid-based measurement consisted of 84 points that were collected over a period of 242 seconds (0.35 measurements/s). In addition to the measurement time, the grid first needed to be drawn on the transparency and transferred to the phantom which took approximately 4 minutes to complete. In contrast, the free scan consisted of 153 measurements that were collected over a period of just 85 seconds (1.8 measurements/s) and required no set up time. Without considering the time needed to construct and transfer the grid, the free scanning method was over five times faster than the grid-based approach. When the time needed to transfer the grid is taken into account, the free scanning method was ten times faster than the grid-based method.

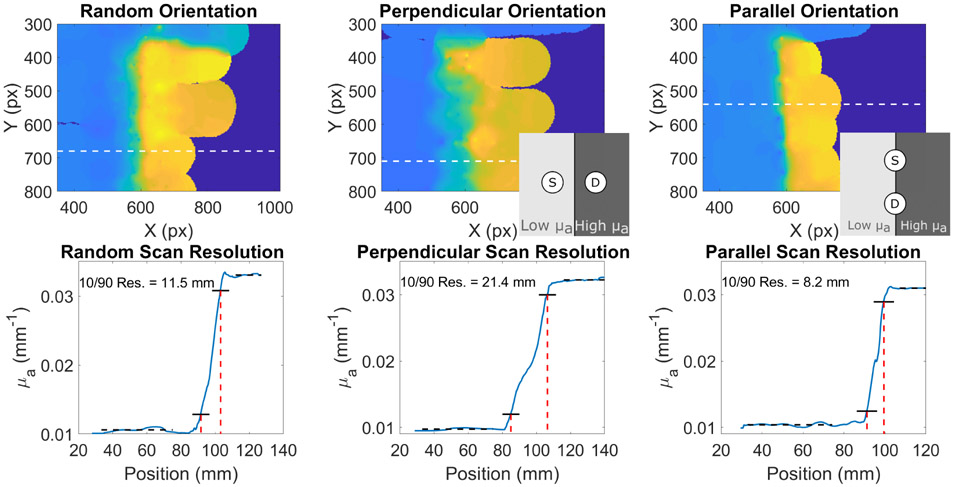
We next investigated the effects of probe orientation on subsurface optical property reconstruction. The probe was scanned over a tissue simulating optical phantom that contained a step discontinuity. On one side the absorption coefficient was low (~ 0.01 mm⁻¹ at 850 nm) and on the other side, μ_a was higher (~0.03 mm⁻¹at 850 nm). The weighting function in Fig. 3 is not rotationally symmetric, so we hypothesized that the reconstructed spatial resolution would depend on the orientation of the optical fibers. We measured the step phantom while keeping the fibers parallel to the discontinuity, while keeping the fibers perpendicular to the discontinuity, and while attempting to measure the discontinuity with a variety of different probe angles (Fig. 7). A line profile plotted perpendicular to the line of discontinuity was used to determine the resolution which we defined as the distance between the location where the absorption coefficient was 10% of the difference between the two μ_a regions and the location where the absorption coefficient was 90% of the difference. We found that the resolution when the fibers were kept perpendicular to the discontinuity was significantly worse (21.4 mm) than when the fibers were held strictly parallel to the edge (8.2 mm). With random fiber orientation the resolution was between the two at 11.5 mm. These results indicate that, when measuring structures with unknown shape, it is important to vary the orientation of the fibers to ensure the highest possible resolution. With conventional grid-based scanning, the resolution is limited to the chosen grid spacing. The free-scanning method employed here allows for the determination of spatial resolution that is based on the visualization method described in Section II-C and the fiber orientation.

Fig. 7.

HS FD-DOS images of a phantom with a step discontinuity. The top row shows images of the phantom with the optical fibers of the probe oriented at random (left) perpendicular to the discontinuity (center), and parallel to the discontinuity (right). Insets in the middle and right images show a schematic of the position of the fibers relative to the discontinuity. The bottom row shows profiles of the locations indicated by dashed white lines. Black dotted lines show the constant region before and after the discontinuity. Solid black lines show the level of 10% of the change and 90% of the change. Dashed red lines show the positions of the 10% and 90% levels. The distance between the 10% and 90% absorption coefficients are notated in each image.

D. In vivo measurements

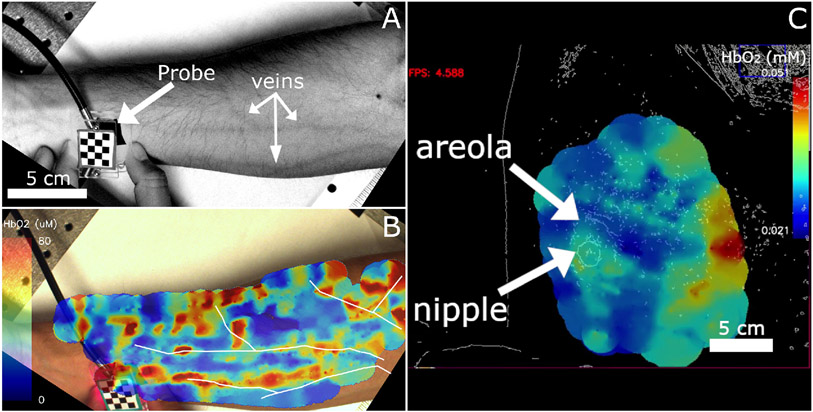
Two in vivo measurements were taken with the HS FD DOS system. All procedures were approved by the Boston University Institutional Review Board (protocol number: 3367, approved: 9/28/20) or were determined exempt by the IRB, and we received informed consent from all subjects. The first measurement was performed on the ventral forearm as shown in Fig. 8A and 8B. This dataset consisted of 668 measurements collected in 404 seconds with a source-detector separation of 5 mm. Fig. 8A is a white light image of the forearm with superficial vasculature clearly visible. Fig. 8B shows the total hemoglobin concentration measured on the arm. Vasculature visible in panel A was hand traced and then overlaid onto the image in panel B to show that regions of high oxy-hemoglobin correspond to visible blood vessels. This image is a single frame taken from a video produced after all of the images were collected. The full video is available in Visualization 1 which shows the hemoglobin concentration as the measurement progresses. This video was adapted from the live data to tune the color scale to better show the vessel-like structures. Probe tracking allows the point of contact between the probe and surface of the tissue to be localized independent of the curvature of the tissue, however, the Monte Carlo simulation used for live visualization assumes the tissue surface is parallel to the camera. This mismatch results in chromophore data appearing past the edge of the tissue in Fig. 8A.

Fig. 8.

A. Grayscale camera image with enhanced contrast showing superficial blood vessels. The probe is also indicated in the image B. Still image from a video showing oxyhemoglobin measurements made with a source-detector separation of 5 mm overlaid on an image of the forearm seen in panel A. White outlines indicate the paths of superficial blood vessels visible in panel A which were then overlaid on panel B such that they overlapped with regions of high oxy-hemoglobin concentrations. This image was produced after the measurements occurred and the color scale adjusted to highlight vessel-like structures. C. Still image from a screen capture of a measurement on a healthy breast displaying calculated oxy-hemoglobin concentration. Breast images from healthy volunteers were passed through an edge-detection filter prior to being displayed to preserve patient privacy. The nipple and areola region of the right breast are indicted by arrows show higher oxyhemoglobin concentration than the surrounding breast tissue. Higher concentrations on the right side of the image (medial) are likely due to the effect of underlying muscle or bone.

We also performed a breast imaging case study. For this measurement, the subject was asked to lie flat on her back with her right arm over her head. This pose is standard for breast self-exams and has the effect of flattening the breast tissue. Once the subject was in position, the operator scanned the probe over the surface of the right breast while collecting measurements. Fig. 8C shows a still frame from a screen capture of the breast measurement. It shows a live view of the instrument with the color bar is scaled automatically based on the range of hemoglobin concentrations found in the image. To protect the subject’s privacy, the video images were passed through an edge-detection filter prior to being saved or displayed on-screen. The areola and nipple are indicated in the figure and the measurement area encompassed the entire breast. This image was constructed from 258 measurements collected over 198 seconds. The measurements showed an increase in oxy-hemoglobin localized around the areola which is consistent with previous work [12]. Higher concentrations of hemoglobin are also located on the right side of the image where the breast tissue was thinner possibly leading to the sampling of muscle or bone in the chest wall. The region surrounding the nipple had a lower oxy-hemoglobin concentration than the areola which is typical of healthy breast tissue [12]. Visualization 2 shows the screen capture of the entire measurement and demonstrates the type of feedback available to the operator of the system.

IV. Discussion

We described here a new high-speed FD-DOS system coupled to a real-time tracking and visualization interface. The live tracking allowed for fast, grid-free scanning over the surface of the measured tissue. A fast LUT method allowed the calculation of tissue optical properties and chromophores to be computed at high speed, while a new weighted average approach to visualization allowed data to be presented live at 1.5Hz. It is, to our knowledge, the first demonstration of an FD-DOS system capable of visualizing processed spatial maps in real-time.

Compared to the point-by-point scanning paradigm of previous FD-DOS instruments, the current method did not require a predefined measurement grid and the visualization method provided a model-based imaging scheme as opposed to the simpler interpolated methods previously implemented [31], [33]. Compared to diffuse optical tomographic (DOT) imaging, our visualization method could be implemented in real-time as it does not attempt to rigorously solve the ill-posed and underdetermined inverse problem associated with localizing contrast in three dimensions [34]. The use of only a single source and detector fiber, unlike the dozens typically used with DOT [35], potentially allows the system to be used to image almost any anatomical location while remaining both low-profile and low-cost. The lack of tomographic reconstruction also represents a limitation of this method. Going forward it may be possible to implement additional source and detector geometries in the handled probe to recover 3D information. Recent developments in sources and detectors for FD-DOS may help to enable more complex and compact robe geometries in the future [36], [37].

The new system described here helps to solve some of the major bottlenecks that have limited the clinical impact of FD-DOS. Rapid imaging can reduce the amount of time needed to scan each patient which can reduce the burden of this technology on both the patient and the operator. Similarly, by providing real-time feedback, the operator of the probe can be sure that they are collecting high-quality data. The free-scanning paradigm also allows operators to focus their scans in particular regions of interest, such as a tumor, which enables the collection of more clinically relevant data in a shorter amount of time. This feature is especially important for small tumors. Using grid-based scanning, contrast from small tumors would be washed out due to insufficient sampling. With grid-free scanning, so long as a priori information about the tumor location is known, the operator can focus collection around the tumor location to improve contrast. Importantly, this system is not restricted to monitoring breast cancer. The small form-factor probe can easily be applied to most anatomical locations. Other potential applications include monitoring major muscle groups for use in sports medicine and performance testing [38], investigations of other types of cancer such as sarcoma [39], monitoring blood flow in the brain during recovery following a stroke [40], and measurements of cardiovascular function [41].

There are several limitations of this technique that should be noted. Despite the high-speed of each individual process, the overall measurement speed was approximately 1.5 Hz. The major bottlenecks included the time needed to process the data using the LUT as well as time needed to identify and calculate the pose of the probe. The current LUT inversion utilized 35 modulation frequencies for each measurement. Our recent work has demonstrated that single modulation frequency FD-DOS measurements have similar accuracy to FD-DOS modulation frequency sweeps (work under review). By switching to a single frequency LUT, the speed of the inversion could be increased significantly. Additionally, the system is currently implemented on a laptop computer which has limited computational and graphical power. The use of a computer with a dedicated GPU may also significantly improve the speed of image processing and increase the achievable frame rate.

A second limitation is the need for the operator to avoid obscuring the camera’s view of the top of the probe. In a fast-paced clinical setting this could prove to be an inconvenience for the operator. Incorporating complementary sensor information such as an inertial measurement unit (IMU) may allow the probe to measure its own orientation and position. We still anticipate that the camera will be needed to provide an initial absolute location, but an IMU would allow the device to continue to function even if the probe were briefly obscured.

Third, this system is susceptible to patient motion. If the patient or the tissue moves during the scan, the apparent location of a tumor or other structure of interest may differ from its actual location. In this work we attempted to limit motion for the breast measurement by asking the subject to lie flat with her arm above her head. This posture stretches the skin over the surface of the breast and can limit motion during scanning. In the future we hope to add fiducial marks to the surface of the tissue, or make use of endogenous tissue features, that will enable the camera to identify landmarks. As those landmarks shift and move during imaging, the visualization can be updated to reflect the subject’s new position.

In future work, we hope to demonstrate the generalizability of the technique by imaging additional healthy volunteers to ensure that the device is suitable for women with different breast sizes and skin tones. We also hope to extend the visualization methodology to generate 3D images of chromophore distributions and better account for tissue curvature.

V. Conclusion

We presented here a high-speed, free scanning FD-DOS device capable of measuring human tissue at a rate of about 1.5 Hz, with real-time data processing and visualization. Scanning of large volumes of tissue was accomplished rapidly as there was no need to prepare the surface prior to scanning. We demonstrated this system’s ability to measure μ_a and ${\mu }_s^{\prime }$ across a wide range, and validated probe tracking accuracy. We used a Monte Carlo simulation to spatially weight the results of each measurement and demonstrate the equivalency of this method with more traditional interpolation approaches. Going forward, this technique may be advantageous for clinical measurements as scans are faster, areas of interest can be identified and scanned more thoroughly, and the user has the ability to rescan areas of interest if necessary.