Semiparametric regression analysis of length-biased interval-censored data

Abstract

In prevalent cohort design, subjects who have experienced an initial event but not the failure event are preferentially enrolled and the observed failure times are often length-biased. Moreover, the prospective follow-up may not be continuously monitored and failure times are subject to interval censoring. We study the nonparametric maximum likelihood estimation for the proportional hazards model with length-biased interval-censored data. Direct maximization of likelihood function is intractable, thus we develop a computationally simple and stable expectation-maximization algorithm through introducing two layers of data augmentation. We establish the strong consistency, asymptotic normality and efficiency of the proposed estimator and provide an inferential procedure through profile likelihood. We assess the performance of the proposed methods through extensive simulations and apply the proposed methods to the Massachusetts Health Care Panel Study.

1 |. INTRODUCTION

Interval-censored data arise when a failure time is not recorded precisely but is rather known to lie within a time interval. Such data are encountered in prospective follow-up studies, where the ascertainment of the event of interest is made over a series of examination times. Regression analysis of unbiased interval-censored survival data has been extensively studied. In particular, nonparametric maximum likelihood estimation for the proportional hazards and transformation models have been studied by Huang (1996) and Zeng et al. (2016), respectively. Due to intractable likelihood, sieve estimation is also proposed for the proportional hazards model by Huang and Rossini (1997) and Cai and Betensky (2003), among others. A comprehensive review is given in Sun (2007).

Although sampling incident cases in a follow-up study is common, it may require a long follow-up period to observe enough failure events for meaningful analysis. Alternatively, a prevalent cohort design samples individuals who have experienced an initial event but not the failure event at enrollment, and is often considered as a more focused and economical design (Brookmeyer and Gail, 1987). However, subjects with a longer survival time are preferentially sampled in a prevalent cohort. When the incidence of the initial event is stationary over time, a prevalent cohort collects length-biased data (Wang, 1991; Shen et al., 2009), where the probability of observing the failure time is proportional to its value.

Prospective follow-up of a prevalent cohort can be subject to interval censoring. An example is the Massachusetts Health Care Panel Study (Chappell, 1991), where the time to loss of active life for elderly individuals were assessed approximately 1.25, 6, and 10 years after study recruitment. Since only functionally independent individuals were enrolled, subjects with a longer time to loss of active life were more likely to be sampled. Although a prevalent cohort is a biased sample that requires special methods for analysis, it may provide information that is otherwise unavailable in an incident cohort. For example, in an incident sampling design, the right tail of survival distribution may not be identified because of limited study duration. Using prevalent sampling design, the identifiable region for the survival distribution and marked variables that are observed only at the event occurrence could be enlarged (Chan and Wang, 2010). In the Massachusetts Health Care Panel Study data, even though the last monitoring time is 10 years after study recruitment, we can identify a survival distribution that ranges over 30 years (see Section 3.2), because individuals are event-free for a period before enrollment. An added advantage for interval-censored data is that, even when the monitoring time has a discrete distribution, we can identify the continuous survival distribution of the failure event because the event-free period before enrollment is typically continuous. For incident sampling with discrete monitoring time, in contrast, we can only identify a discrete survival distribution.

Statistical methodology for regression modeling of length-biased data are mostly proposed for uncensored and right-censored data. Wang (1996) and Chen (2010) considered uncensored data. For right-censored data, Qin and Shen (2010) proposed inverse weighted estimating equation and Huang and Qin (2012) proposed a composite likelihood approach for the proportional hazards model. Qin et al. (2011) considered the nonparametric maximum likelihood estimator and derived an expectation-maximization (EM) algorithm for computation, and showed that the estimator is efficient.

Even though there has been limited literature on length-biased interval-censored data, several methods were proposed for left-truncated interval-censored data without the length-biased assumption for the truncation time. In particular, Pan and Chappell (1998) considered the proportional hazards model and applied a gradient projection-based method for non-parametric maximum likelihood estimation, where the baseline survival function may be underestimated. Pan and Chappell (2002) considered the same model and suggested a marginal likelihood approach that avoids estimating the baseline hazards function and a monotone maximum likelihood approach assuming that the baseline distribution has a nondecreasing hazard function. Kim (2003) studied the special case of left-truncated current status data, where there is only one examination time, and established the asymptotic properties of the nonparametric maximum likelihood estimators. Recently, Wang et al. (2015) studied the additive hazard model with left-truncated interval-censored data and proposed a sieve estimation method.

In this paper, we study the nonparametric maximum likelihood estimation for the proportional hazards model with length-biased interval-censored data. Through introducing pseudo-truncated data and latent Poisson random variables, we develop a simple and computational stable EM algorithm. We establish the strong consistency and asymptotic normality of the proposed estimators and provide inference through a profile likelihood approach. We assess the performance of the proposed estimator and inferential procedures through extensive simulations and apply the proposed methods to the Massachusetts Health Care Panel Study data.

2 |. THE PROPOSED METHODOLOGY

2.1 |. Model and data

For individuals in the target population, let $\tilde{T}$ be the time to a failure event and $\tilde{\mathit{Z}}$ be a p-vector of covariates. We assume that $\tilde{T}$ follows a proportional hazards model with a cumulative hazard function

$$\text{Λ}(t\mid \tilde{\mathit{Z}})=\text{Λ}(t)\exp \left({\beta }^{\text{T}}\tilde{\mathit{Z}}\right),$$

where β is a p-vector of unknown regression parameters, and Λ(·) is an arbitrary increasing function with Λ(0) = 0.

For length-biased sampling, it is common to assume that the incidence rate of the initial event is constant over calendar time and $\tilde{A}$, the truncation time, is uniformly distributed in [0, τ], where τ is the maximum support of $\tilde{T}$ (Wang, 1991; Qin et al., 2011). In a prevalent cohort study, a subject is included only if the failure time does not occur before the truncation time, that is, $\tilde{T}\ge \tilde{A}$. We let T, A, and Z be the failure time, truncation time and covariates, respectively, in the prevalent cohort. Then, (T, A, Z) has the same joint distribution as $(\tilde{T},\tilde{A},\tilde{\mathit{Z}})$ conditional on $\tilde{T}\ge \tilde{A}$. Suppose that the occurrence of the failure is not exactly observed but only determined at a sequence of examination times, denoted as $A<U_1\cdots <U_M\le \tau$. The failure time is then known to lie in the interval (L, R), where $L=\max \left\{U_m:U_m<T,m=0,\dots ,M\right\}$, $R=\min \{U_m:U_m\ge T$, m = 1, …, M + 1}, U₀ = A, and $U_{M+1}=\infty$. In particular, if the failure occurs before the first examination time, then (L, R) = (A, U₁); if the failure has not occurred at the last examination time, then $(L,R)=\left(U_M,\infty \right)$. Let $V_m=U_m-A$ for m = 0, …, M, so that V₀ = 0.

We assume the following non-informative sampling time condition, that M and $\left\{V_m:m=1,\dots ,M\right\}$ are independent of (T, A) conditional on Z. For a length-biased sample of n subjects, the observed data are $\left\{{\mathcal{O}}_i:i=1,\dots ,n\right\}$, where ${\mathcal{O}}_i=\left\{L_i,R_i,A_i,{\mathit{Z}}_i\right\}$. The observed-data likelihood is then given by

$$L_n(\mathit{\beta },\text{Λ})=\prod _{i=1}^n\frac{\left[\exp \left\{-\text{Λ}\left(L_i\right)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}-I\left(R_i<\infty \right)\exp \left\{-\text{Λ}\left(R_i\right)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}\right]}{{\int }_0^{\tau }\exp \left\{-\text{Λ}(a)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}da/\tau }.$$ (1)

The likelihood function $L_n(\mathit{\beta },\text{Λ})$ involves τ, which is a constant related to study design but not a parameter of interest. In the E-step of the proposed EM algorithm, however, it is required to redistribute mass on [0, τ], and an approximation of τ is required. Let $0=t_0<t_1<\cdots <t_k<\infty$ be the ordered sequence of all L_i and $R_{i}I\left(R_i<\infty \right)$. Following Qin et al. (2011), we approximate τ by t_k, which converges to τ at a rate faster than n^1/2, and therefore does not alter subsequent results.

2.2 |. Nonparametric maximum likelihood estimation

We adopt the nonparametric maximum likelihood estimation approach, where the estimator for Λ is a step function with nonnegative finite jumps at the ends of the intervals that bracket the failure times. Specifically, we let λ₀, λ1,…, λ_k be the respective jump sizes at t₀, t₁,…,t_k, where λ₀ = 0. Write $\lambda =\left({\lambda }_1,\dots ,{\lambda }_k\right)$. We maximize the objective function

$$\begin{gathered} l_n(\mathit{\beta },\lambda )\equiv \sum _{i=1}^n(\text{log}[\exp \left\{-\sum _{t_j\le L_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\} \\ -I\left(R_i<\infty \right)\exp \left\{-\sum _{t_j\le R_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}] \\ -\log {\int }_0^{\tau }\frac{1}{\tau }\exp \left\{-\sum _{t_j\le a}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}da). \end{gathered}$$

Direct maximization of $l_n(\mathit{\beta },\lambda )$ is difficult due to a lack of analytical expressions. We introduce two layers of data augmentation and propose an EM algorithm to facilitate computation. First, to handle left truncation, we introduce pseudo-truncated data, which is also referred to as “ghost data” (Turnbull, 1976). In particular, let ${\mathcal{O}}_i^{\ast }\equiv \{\left(T_{im}^{\ast },A_{im}^{\ast },{\mathit{Z}}_i\right):T_{im}^{\ast }<A_{im}^{\ast },m=1,\dots ,n_i\}$ denote the pseudo-truncated samples corresponding to subject i, where $\left(T_{i1}^{\ast },A_{i1}^{\ast }\right),\dots ,\left(T_{i,n_i}^{\ast },A_{i,n_i}^{\ast }\right)$ are independent and identically distributed given Z_i. Since the estimator for Λ only takes jump at $t_j(j=1,\dots ,n)$, the failure time $T_{im}^{\ast }$ can only take values from $\left\{t_1,\dots ,t_k\right\}$. The number of truncated samples n_i follows a negative binomial distribution with parameter

$$\begin{gathered} {\pi }_i=P\left(T_{im}^{\ast }<A_{im}^{\ast }\mid {\mathit{Z}}_i\right)=\sum _{j=0}^{k}P\left(T_{im}^{\ast }=t_j,A_{im}^{\ast }>t_j\mid {\mathit{Z}}_i\right) \\ =\sum _{j=1}^k\left(1-t_j/\tau \right){\lambda }_j\exp \left({\beta }^{\text{T}}{\mathit{Z}}_i\right)\exp \left\{-\sum _{l=1}^j{\lambda }_l\exp \left({\beta }^{\text{T}}{\mathit{Z}}_i\right)\right\}, \end{gathered}$$

such that $E\left(n_i\mid {\mathcal{O}}_i\right)={\pi }_i/\left(1-{\pi }_i\right)$. Let $n_{ij}={\sum }_{m=1}^{n_i}I(T_{im}^{\ast }=t_j)$. Given the total number $n_i,\left(n_{i1},\dots ,n_{ik}\right)$ follows a multinomial distribution with probabilities $\left(p_{i1},\dots ,p_{ik}\right)$, where

$$\begin{gathered} p_{ij}=P\left(T_{im}^{\ast }=t_j\mid T_{im}^{\ast }<A_{im}^{\ast },{\mathit{Z}}_i\right) \\ =\frac{\left(1-t_j/\tau \right){\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\exp \left\{-{\sum }_{l=1}^j{\lambda }_l\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}{{\pi }_i}. \end{gathered}$$ (2)

By the missing information principle (Lai and Ying, 1994), the maximization of $l_n(\mathit{\beta },\lambda )$ is equivalent to maximizing the conditional expectation of the log-likelihood function of the “complete-data” $\left\{\left({\mathcal{O}}_i,{\mathcal{O}}_i^{\ast }\right):i=1,\dots ,n\right\}$ given the observed data. The “complete-data” log-likelihood function is given by

$$\begin{gathered} {\tilde{l}}_n^C(\mathit{\beta },\lambda )\equiv \sum _{i=1}^n(\text{log}[\exp \left\{-\sum _{t_j\le L_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\} \\ -I\left(R_i<\infty \right)\exp \left\{-\sum _{t_j\le R_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}] \\ +\sum _{j=1}^k{n}_{ij}\log [{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right) \\ \times \exp \left\{-\sum _{l=1}^j{\lambda }_l\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}]). \end{gathered}$$

While we may propose an EM algorithm based on ${\tilde{l}}_n^C(\mathit{\beta },\lambda )$, its maximization step is still difficult to obtain, since β and λ cannot be separated in the complete-data log-likelihood function due to the interval censoring structure.

Therefore, we further introduce data augmentation based on independent Poisson random variables $W_{ij}(i=1,\dots ,n;j=1,\dots ,k,t_j\le R_i^{\ast })$ with means ${\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)$, where $R_i^{\ast }=L_{i}I\left(R_i=\infty \right)+R_{i}I\left(R_i<\infty \right)$. The joint density function for $W_{ij}\left(j=1,\dots ,k,t_j\le R_i^{\ast }\right)$ is given by

$$\prod _{j=1,t_j\le R_i^{\ast }}^k\frac{{\left\{{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}^{W_{ij}}}{W_{ij}!}\exp \left\{-{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}.$$

Let $N_{i1}={\sum }_{t_j\le L_i}{W}_{ij}$ and $N_{i2}=I\left(R_i<\infty \right){\sum }_{L_i<t_j\le R_i}{W}_{ij}$. Suppose that we observe N_i1 = 0 and N_i2 > 0. The observed-data likelihood for ${\tilde{\mathcal{O}}}_i\equiv \left\{N_{i1}=0,N_{i2}>0\right\}$ is equal to

$$\begin{gathered} \mathrm{Pr}\left(N_{i1}=0,N_{i2}>0\right) \\ =\mathrm{Pr}(\sum _{t_j\le L_i}{W}_{ij}=0)\left\{1-I\left(R_i<\infty \right)\mathrm{Pr}\left(\sum _{L_i<t_j\le R_i}{W}_{ij}=0\right)\right\} \\ =\exp \left\{-\sum _{t_j\le L_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\} \\ -I\left(R_i<\infty \right)\exp \left\{-\sum _{t_j\le R_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}. \end{gathered}$$

Therefore, ${\tilde{l}}_n^C(\mathit{\beta },\lambda )$ can be viewed as the observed log-likelihood function for $\tilde{\mathcal{O}}\equiv \left\{\left({\tilde{\mathcal{O}}}_i,{\mathcal{O}}_i^{\ast }\right);i=1,\dots ,n\right\}$ with $W_{ij}\left(i=1,\dots ,n;j=1,\dots ,k,j\le R_i^{\ast }\right)$ and $n_{ij}(i=1,\dots ,n;j=1,\dots ,k)$ as latent variables. In particular, the complete-data log-likelihood function based on $\left(W_{ij},n_{ij}\right)$ is given by

$$\begin{gathered} \sum _{i=1}^n\sum _{j=1}^{k}I\left(t_j\le R_i^{\ast }\right)\{-\log \left(W_{ij}!\right) \\ +W_{ij}\left(\log {\lambda }_j+{\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)-{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\} \\ +\sum _{i=1}^n\sum _{j=1}^k{n}_{ij}\{\log \left(1-t_j/\tau \right) \\ +\log {\lambda }_j+{\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i-\sum _{l=1}^j{\lambda }_l\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\}. \end{gathered}$$

Based on this formulation, we propose the following EM algorithm. In the E-step, we evaluate the conditional expectations of W_ij and n_ij given the observed data. In particular, we have

$$\begin{gathered} \widehat{E}\left(W_{ij}\right)=I\left(L_i<t_j\le R_i,R_i<\infty \right) \\ \times \frac{{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)}{1-\exp \left\{-{\sum }_{L_i<t_l\le R_i}{\lambda }_l\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}, \end{gathered}$$

and

$$\widehat{E}\left(n_{ij}\right)=\frac{\left(1-t_j/\tau \right){\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\exp \left\{-{\sum }_{l=1}^j{\lambda }_l\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}{1-{\pi }_i},$$

where $\widehat{E}(\cdot )$ denote the conditional expectation with respect to the observed data $\tilde{\mathcal{O}}$. In the M-step, we maximize the expected complete-data log-likelihood function. We update λ_j by

$${\lambda }_j=\frac{{\sum }_{i=1}^n\left\{I\left(t_j\le R_i^{\ast }\right)\widehat{E}\left(W_{ij}\right)+\widehat{E}\left(n_{ij}\right)\right\}}{{\sum }_{i=1}^n\left\{I\left(t_j\le R_i^{\ast }\right)+{\sum }_{l=j}^k\widehat{E}\left(n_{il}\right)\right\}\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)}$$

and update β by solving

$$\begin{gathered} {\sum }_{i=1}^n{\sum }_{j=1}^k\left\{I\left(t_j\le R_i^{\ast }\right)\widehat{E}\left(W_{ij}\right)+\widehat{E}\left(n_{ij}\right)\right\} \\ \times \left[{\mathit{Z}}_i-\frac{{\sum }_{i^{\prime }=1}^n\left\{I\left(t_j\le R_{i^{\prime }}^{\ast }\right)+{\sum }_{l=j}^k\widehat{E}\left(n_{i^{\prime },l}\right)\right\}\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_{i^{\prime }}\right){\mathit{Z}}_{i^{\prime }}}{{\sum }_{i^{\prime }=1}^n\left\{I\left(t_j\le R_{i^{\prime }}^{\ast }\right)+{\sum }_{l=j}^k\widehat{E}\left(n_{i^{\prime },l}\right)\right\}\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_{i^{\prime }}\right)}\right]=\mathbf{0}. \end{gathered}$$

We iterate between the E-step and M-step until convergence. We denote the final estimators for β and λ as $\widehat{\mathit{\beta }}$ and $\widehat{\mathit{\lambda }}$.

In summary, through introducing two layers of latent random variables, we proposed a stable computing algorithm to obtain the estimators that maximize the nonparametric likelihood function. The latent truncated “ghost data” were introduced to deal with the complications that arise from left truncation and the latent Poisson random variables were introduced to deal with the incomplete data caused by interval-censoring.

2.3 |. Asymptotic properties

In this section, we establish the strong consistency and asymptotic normality of the proposed estimators. We assume the following regularity conditions.

Condition 1. The true value of β, denoted by β₀, belongs to the interior of a known compact set $\mathcal{B}\subset {\text{ℝ}}^p$.

Condition 2. The true value Λ₀(·) of Λ(·) is strictly increasing and continuously differentiable in [0, τ] with Λ₀(0) = 0.

Condition 3. The covariate Z has bounded support and is not concentrated on any proper subspace of ${\text{ℝ}}^p$.

Condition 4. The examination times have finite support $\mathcal{V}$ with the least upper bound τ. The number of potential examination times M is positive with E(M) < ∞. There exists a positive constant η such that $\mathrm{Pr}\left(U_{m+1}-U_m\ge \eta \mid M,Z\right)=1$. In addition, there exists a probability measure μ in $\mathcal{V}$ such that the bivariate distribution function of (U_m, U_m+1) conditional on (M, Z) is dominated by μ × μ and its Radon-Nikodym derivative, denoted by ${\tilde{f}}_m(u,v;M,\mathit{Z})$, can be expanded to a positive and twice-continuously differentiable function in the set $\{(u,v):0\le u\le \tau ,0\le v\le \tau ,v-u\ge \eta \}$.

Conditions 1, 2, and 3 are standard conditions for failure time regression. Condition 4 pertains to the joint distribution of examination times. It requires that two adjacent examination times are separated by at least η; otherwise, the data may contain exact observations, which require a different theoretical treatment. The dominating measure μ is chosen as the Lebesgue measure if the examination times are continuous random variables and as the counting measure if the examinations occur only at a finite number of time points. The number of potential examination times M can be fixed or random, is possibly different among study subjects, and is allowed to depend on covariates.

We state the strong consistency of $(\widehat{\mathit{\beta }},\widehat{\mathit{\lambda }})$ and the weak convergence of $\widehat{\mathit{\beta }}$ in two theorems.

Theorem 1.

Under Conditions 1–4, $\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert {\to }_{\mathit{\text{a.s.}}}0$, and ${\Vert \widehat{\text{Λ}}-{\text{Λ}}_0\Vert }_{l^{\infty }(\mathcal{V})}{\to }_{\mathit{\text{a.s.}}}0$, where $\parallel \cdot {\parallel }_{l\infty (\mathcal{V})}$ denotes the supremum norm on $\mathcal{V}$, and $\widehat{\text{Λ}}(t)={\sum }_{t_j\le t}{\widehat{\lambda }}_j$.

Theorem 2.

Under Conditions 1–4, $n^{1/2}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$ converges weakly to a p-dimensional zero-mean normal random vector with a covariance matrix that attains the semiparametric efficiency bound.

The proofs of both theorems are provided in Appendix A.

2.4 |. Variance estimation

We estimate the covariance matrix of $\widehat{\mathit{\beta }}$ by a profile likelihood approach. Let ${\widehat{\text{Λ}}}_{\mathit{\beta }}=\arg \max {\log }_{\text{Λ}\in \mathcal{C}}{L}_n(\mathit{\beta },\text{Λ})$, where $\mathcal{C}$ is the set of bounded step functions with non-negative jumps at t_l (l = 1,…, m). The maximizer ${\widehat{\text{Λ}}}_{\mathit{\beta }}$ can be obtained using the EM algorithm of Section 2.2 if we fix β and only update λ in the M-step. The profile log-likelihood function is defined as

$$p{l}_n(\mathit{\beta })=\underset{\text{Λ}\in \mathcal{C}}{\max }\log L_n(\mathit{\beta },\text{Λ})=\log L_n\left(\mathit{\beta },{\widehat{\text{Λ}}}_{\mathit{\beta }}\right).$$

Let $\tilde{p}{l}_i(\mathit{\beta })$ be the ith subject’s contribution to $p{l}_n(\mathit{\beta })$. We estimate the covariance matrix of $\widehat{\mathit{\beta }}$ by the inverse of

$$\sum _{i=1}^n{\left(\begin{array}{c}\underset{\_}{\tilde{p}{l}_i\left(\widehat{\mathit{\beta }}+h_n{e}_1\right)-\tilde{p}{l}_i(\widehat{\mathit{\beta }})}\\ h_n\\ ⋮\\ \frac{\tilde{p}{l}_i\left(\widehat{\mathit{\beta }}+h_n{e}_p\right)-\tilde{p}{l}_i(\widehat{\mathit{\beta }})}{h_n}\end{array}\right)}^{\otimes 2},$$

where e_j is the jth canonical vector in ${\text{ℝ}}^p,{\mathit{a}}^{\otimes 2}=\mathit{a}{\mathit{a}}^{\text{T}}$, and h_n is a constant of order n^−1/2. In the numerical studies, we used h_n = 5n^−1/2 as suggested by Zeng et al. (2016).

The above profile likelihood approach is different from that of Murphy and Vaart (2000). They estimate the covariance matrix of $\widehat{\mathit{\beta }}$ by the negative inverse of the Hessian matrix of pl_n(β) at $\widehat{\mathit{\beta }}$, which is obtained by second order numerical differences. The estimated matrix may not be positive semidefinite, especially in small samples. Here, we estimate the covariance matrix by the inverse of the empirical covariance matrix of the gradient of $\tilde{p}{l}_i(\mathit{\beta })$ using the first-order numerical differences, similar to Zeng et al. (2017). The calculation is quicker than the approach requiring second-order numerical differences, and the estimated covariance matrix is guaranteed to be positive semidefinite.

3 |. NUMERICAL STUDIES

3.1 |. Simulation

We conducted simulation studies to evaluate the performance of the proposed methods. We considered two covariates Z₁ ∼ Bernoulli(0.5) and z₂ ∼ Uniform(−0.5, 0.5). We set β = (0.5, 1)^T, Λ(t) = 0.3t, and τ = 15. We generated the truncation time $\tilde{A}$ from Uniform(0, τ) and generated the sequence of potential examination times U_m ∼ U_m−1 + 0.1 + Uniform(0, 2) with U₀ = $\tilde{A}$. We set n = 100, 200, or 400 and examined 10000 replicates for each sample size. We compared the proposed nonparametric maximum likelihood method with the maximum conditional likelihood method of Pan and Chappell (1998), which is applicable to left-truncated interval-censored data. For coherent comparisons, we compute both estimators by EM algorithms, where the algorithm for the conditional likelihood estimator is an adaption of the proposed algorithm and is given in Appendix B. We set the initial value of β to 0 and the initial value of λ_l to 1/k.

Table 1 summarizes the simulation results on the estimation of β using the proposed and conditional likelihood approaches. The biases for the proposed estimators are small and decrease as sample size increases. The biases for the conditional likelihood estimators are larger than those for the proposed estimators for all sample sizes, but decrease as sample size increases. The variance estimators for $\widehat{\mathit{\beta }}$ using both approaches are accurate and the confidence intervals have proper coverage probabilities. As expected, the proposed estimator shows substantial efficiency gain compared to the conditional likelihood estimator. Web Figure S1 in the Supplementary Materials gives the estimated baseline survival functions. The nonparametric maximum likelihood estimation gives unbiased estimates, while the condition likelihood estimators tend to underestimate the true values, as indicated in Pan and Chappell (1998).

TABLE 1.

Summary statistics for the simulation studies with length-biased assumption

		NPMLE					CLE
		Bias	SE	SEE	RMSE	CP	Bias	SE	SEE	RMSE	CP
n=100	β 1	0.008	0.169	0.171	0.169	0.956	0.049	0.253	0.235	0.258	0.928
	β 2	0.015	0.295	0.317	0.295	0.965	0.089	0.444	0.436	0.453	0.942
n=200	β 1	0.004	0.117	0.116	0.117	0.950	0.025	0.170	0.159	0.172	0.933
	β 2	0.005	0.206	0.212	0.206	0.957	0.044	0.296	0.290	0.299	0.943
n=400	β 1	0.002	0.082	0.081	0.082	0.944	0.014	0.115	0.111	0.116	0.937
	β 2	0.002	0.144	0.146	0.144	0.951	0.024	0.200	0.199	0.202	0.949

Note: NPMLE and CLE are the nonparametric maximum likelihood and conditional likelihood estimators. SE, SEE, RMSE, and CP are the empirical standard error, mean standard error estimator, root mean squared error, and empirical coverage probability of the 95% confidence interval, respectively.

We further assess the robustness of the nonparametric maximum likelihood estimator when the uniform assumption for the truncation time does not hold. In particular, we considered the same simulation setting but generated the truncation time $\tilde{A}$ from Exp(0.1) such that the stationary incidence assumption is violated. Table 2 shows the simulation results. The nonparametric maximum likelihood estimators are slightly biased, while the coverages of the 95% confidence intervals are acceptable. Even though the bias of the proposed estimator is larger than the conditional likelihood estimator when sample size is large (n = 400) and length-biased sampling is violated, the mean squared error of the proposed estimator is still smaller.

TABLE 2.

Summary statistics for the simulation studies without length-biased assumption

		NPMLE					CLE
		Bias	SE	SEE	RMSE	CP	Bias	SE	SEE	RMSE	CP
n=100	β 1	−0.039	0.160	0.167	0.165	0.953	0.045	0.244	0.231	0.248	0.933
	β 2	−0.077	0.285	0.307	0.295	0.951	0.083	0.442	0.428	0.450	0.941
n=200	β 1	−0.044	0.111	0.113	0.119	0.933	0.023	0.164	0.157	0.165	0.935
	β 2	−0.088	0.198	0.205	0.217	0.930	0.045	0.293	0.285	0.296	0.943
n=400	β 1	−0.047	0.078	0.078	0.091	0.899	0.012	0.113	0.109	0.113	0.938
	β 2	−0.095	0.137	0.140	0.167	0.894	0.021	0.198	0.196	0.199	0.947

Note: NPMLE and CLE are the nonparametric maximum likelihood and conditional likelihood estimators. SE, SEE, RMSE, and CP are the empirical standard error, mean standard error estimator, root mean squared error, and empirical coverage probability of the 95% confidence interval, respectively.

3.2 |. Massachusetts health care panel study

We apply the proposed methods to the Massachusetts Health Care Panel Study, which has been described and analyzed previously (Chappell, 1991; Pan and Chappell, 1998; Hudgens, 2005). The study aimed at assessing the risk at which elderly individuals lose active life, which is defined as a continued ability to perform various activities of daily living such as dressing and bathing. The study was first conducted in 1975 taking a baseline survey of Massachusetts residents over the age of 65. Since only subjects who were active at baseline were included, the time to loss of active life was subject to left truncation. Three follow-up waves were then taken at 1.25, 6, and 10 years after baseline to determine if subjects are still living actively, so the time to loss of active life was also interval-censored.

The data set includes 1286 subjects with enrollment age ranges from 65 to 97.3. Since the study population were defined to be over age 65, we consider the failure time as age at loss of active life minus 65. Since the subjects are active at the enrollment, the truncation time is the age at enrollment minus 65. We applied the proposed methods to study the association between loss of active life and gender.

Table 3 shows the estimation results for the regression parameter in the Massachusetts Health Care Panel Study. The point estimates from the proposed approach and the conditional likelihood approach are both positive, indicating that male subjects are associated with a higher risk of losing active life than females. The standard error estimate of the proposed nonparametric maximum likelihood estimator is smaller than that of the conditional likelihood estimator, so that at a 5% significance level, the null hypothesis of no association between gender and loss of active life is only rejected by the nonparametric maximum likelihood approach.

TABLE 3.

Estimation results for the regression parameter in the Massachusetts Health Care Panel Study

	NPMLE			CLE
Covariate	Estimate	Std Err	p-value	Estimate	Std Err	p-value
Male	0.144	0.059	0.014	0.133	0.076	0.081

Note: NPMLE and CLE are the nonparametric maximum likelihood and conditional likelihood estimators.

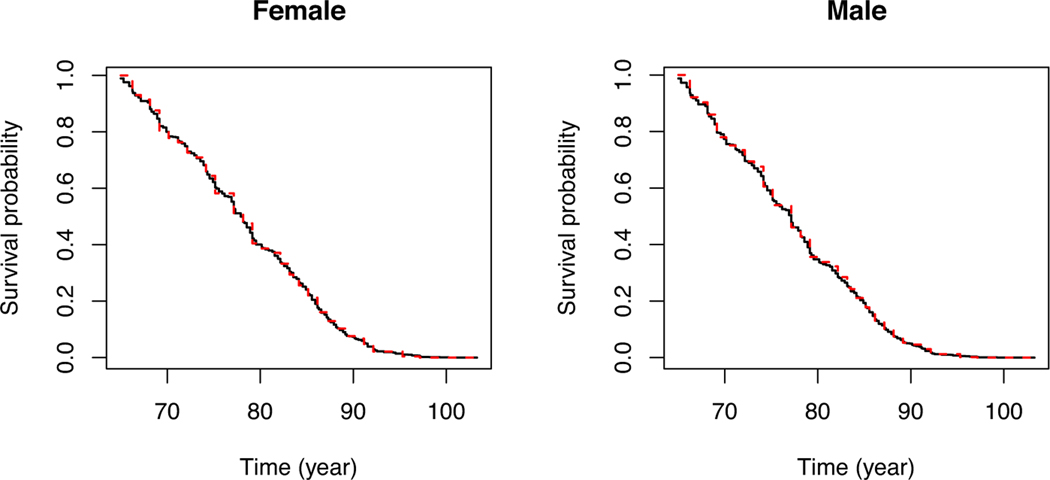
Figure 1 shows the estimated survival probabilities for male and female subjects using the two approaches. Even though they give similar estimates for the survival probabilities, the nonparametric maximum likelihood approach gives an estimate with finer jumps, resulting from the additional assumption on the truncation time. Using both approaches, the female subjects have a higher survival probability than the male subjects.

FIGURE 1.

Estimated survival probabilities for subgroups of subjects in the Massachusetts Health Care Panel Study. The solid and dashed curves pertain to the nonparametric maximum likelihood and conditional likelihood estimation approaches, respectively.

If the length-biased sampling assumption does not hold, the regression coefficients of the two methods would converge to different values. Therefore, we estimated the difference of the estimators and construct a 95% confidence interval by bootstrapping with 1000 replications, to see if the stationary assumption for the truncation time holds. The differences of the two estimators was 0.011 with a 95% confidence interval (−0.092, 0.107), indicating that the length-biased assumption is possibly valid.

4. | DISCUSSION

In this paper, we adopt the nonparametric maximum likelihood estimation where the estimator for Λ is a step function that is right-continuous which is usually considered in the literature. As mentioned by a reviewer, if Λ is only restricted to be nondecreasing, then the true maximizer of the likelihood should involve a left-continuous Λ, that is, Λ(t) = Λ(t_j+1) on (t_j, t_j+1] for j = 0, …, m − 1. The two versions are asymptotically equivalent since any two adjacent step points get closer as sample size increases. In Web Appendix A of the Supplementary Materials, we implemented the version with left-continuous Λ and demonstrated that the numerical difference between the two versions is ignorable.

The iterative convex minorant (ICM) algorithm (Pan, 1999) is an alternative algorithm for the EM algorithm adopted in the paper to obtain the nonparametric maximum likelihood estimators for interval-censored data. Even though it is generally faster than the EM algorithm considered in the paper, it may become unstable for large datasets because it attempts to update a large number of parameters simultaneously using a quasi-Newton method (Zeng et al., 2016). Wang et al. (2016) also advocated the use of an EM algorithm by comparing it with the R package intcox (Henschel and Mansmann, 2013) that adopts the algorithm of Pan (1999). They found that ICM algorithm often exhibits larger biases, indicating that it may not converge to the true maximizer of the likelihood function.

In this paper, we studied the nonparametric maximum likelihood estimation of the proportional hazards model for length-biased interval-censored data. Although length-biasedness requires a stationary incidence distribution for the initial event, the proposed methods can be extended to situations when the incidence distribution follows a parametric model (Huang et al., 2015). In that case, the denominator of the individual components in L_n(β, Λ) need to be modified corresponding to the distribution of the truncation time, and the proposed EM algorithm can be adjusted accordingly.

The efficiency gain of the proposed nonparametric maximum likelihood estimators over the conditional likelihood estimators mainly comes from the information of the (uniform) distributional assumption on the truncation time. Relatively, the conditional likelihood estimators are more robust against the assumption. In practice, one need to carefully ascertain the assumption to apply the proposed approach. For the right-censored left-truncated data, graphical methods (Wang, 1991; Asgharian et al., 2006) and a goodness-of-fit test (Mandel and Betensky, 2007) have been proposed to test the length-biasedness assumption. In the numerical examples, we used a bootstrapped method to the difference of the nonparametric maximum likelihood and conditional likelihood approaches as an indirect test of length-biasedness. The diagnostic methods for right-censored data cannot be directly extended to the interval-censoring case, since the estimator for the survival function converges in a different, n^1/3, rate. Formal tests for the length-biased assumption with interval-censored data will be developed in the future.

The individuals in the MHCPS data may also be subject to the risk of a competing cause, for example, death, such that the subjects who died before loss of active life were right-censored. In addition, there may be selection effect such that only alive subjects were included in the study. Therefore, the assumptions of conditional independent censoring and truncation times may be questionable. However, the information on the cause of right censoring is not available in MHCPS data, so we are not able to access the validity of the assumptions. The regression analysis of competing risks interval-censored data has been studied (Mao et al., 2017), however, no existing methods considered the scenario when the competing risks interval-censored data are also subject to left truncation. Methods incorporating such complications are important future research.

Appendix A

Proof of asymptotic results

We use ${\text{ℙ}}_n$ to denote the empirical measure from n independent subjects and $\text{ℙ}$ to denote the true probability measure. Write ${\mathbb{G}}_n=n^{1/2}\left({\text{ℙ}}_n-\text{ℙ}\right)$. Let L(β, Λ) be the observed-data likelihood for a single subject

$$L(\mathit{\beta },\text{Λ})=\frac{{\sum }_{m=0}^M{\text{Δ}}_m\left[\exp \left\{-\text{Λ}\left(U_m\right)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}-\exp \left\{-\text{Λ}\left(U_{m+1}\right)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}\right]}{{\int }_0^{\tau }\exp \left\{-\text{Λ}(a)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}da/\tau },$$

where ${\text{Δ}}_m=I\left(U_m<T\le U_{m+1}\right)$.

Write $l(\mathit{\beta },\text{Λ})=\log L(\mathit{\beta },\text{Λ})$. Let $\widetilde{\text{Λ}}$ be a step function that takes jumps only at t₁, …, t_k with $\widetilde{\text{Λ}}\left(t_j\right)={\text{Λ}}_0\left(t_j\right)$ for j = 1,…, k. Let

$$m(\mathit{\beta },\text{Λ})=\log \left\{\frac{L(\mathit{\beta },\text{Λ})+L\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right)}{2}\right\}$$

and

$$\mathcal{M}=\left\{m(\mathit{\beta },\text{Λ}):\mathit{\beta }\in \mathcal{B},\text{Λ}\in D_M\right\},$$

where D_M = {Λ : Λ is increasing with Λ(0) = 0, Λ(τ) ≤ M}, and M < ∞. The proofs make use of two lemmas, whose proofs are given in Web Appendix B.

Lemma 1.

Under Conditions 1–4, the classes of functions $\mathcal{M}$ is ℙ-Donsker.

Lemma 2.

Under Conditions 1–4,

$$E\left[\sum _{m=0}^M{\left\{\widehat{\text{Λ}}\left(U_m\right)-{\text{Λ}}_0\left(U_m\right)\right\}}^2\right]=O_P\left(n^{-2/3}\right)+O\left({\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert }^2\right).$$

Proof of Theorem 1

The jump points {t₁,..., t_k} depend on sample size n and for any ϵ > 0, ⋃_jB_ϵ(t_j) covers the support $\mathcal{V}$ as n → ∞, where B_r(t) is the open ball around t_j with radius r. By the continuity of Λ₀, $\widetilde{\text{Λ}}(t)$ converges uniformly to Λ₀(t). It follows from Lemma 1 that the class $\mathcal{M}$ is Donsker. By the concavity of the log function,

$$\begin{gathered} {\text{ℙ}}_{n}m(\widehat{\mathit{\beta }},\widehat{\text{Λ}})\ge \frac{1}{2}\left\{{\text{ℙ}}_{n}l(\widehat{\mathit{\beta }},\widehat{\text{Λ}})+{\text{ℙ}}_{n}l\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right)\right\} \\ \ge {\text{ℙ}}_{n}l\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right)={\text{ℙ}}_{n}m\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right). \end{gathered}$$

Since $\mathcal{B}$ is bounded, for any subsequence of $\widehat{\mathit{\beta }}$, we can find a further subsequence converging to ${\mathit{\beta }}_{\ast }\in \mathcal{B}.$. In addition, by Helly’s selection lemma, for any subsequence of $\widehat{\text{Λ}}$, there exists a further subsequence that converges to some increasing function Λ_*. We choose the converging subsequences of $\widehat{\mathit{\beta }}$ and $\widehat{\text{Λ}}$ such that we can obtain without loss of generality that $\widehat{\mathit{\beta }}\to {\mathit{\beta }}_{\ast }$ and $\widehat{\text{Λ}}\to {\text{Λ}}_{\ast }$ pointwise on any interior set of $\mathcal{V}$. Therefore,

$$\begin{gathered} 0\le {\text{ℙ}}_{n}m(\widehat{\mathit{\beta }},\widehat{\text{Λ}})-{\text{ℙ}}_{n}m\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right) \\ =\text{ℙ}\log \frac{L(\widehat{\mathit{\beta }},\widehat{\text{Λ}})+L\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right)}{2L\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right)}+o_P(1) \\ =\text{ℙ}\log \left\{\frac{1}{2}+\frac{L\left({\mathit{\beta }}_{\ast },{\text{Λ}}_{\ast }\right)}{2L\left({\mathit{\beta }}_0,\widetilde{\text{Λ}}\right)}\right\}+o_P(1), \end{gathered}$$

such that the negative Kullback-Leibler information is positive. Therefore,

$$\begin{gathered} \frac{{\sum }_{m=0}^M{\text{Δ}}_m\left[\exp \left\{-{\text{Λ}}_{\ast }\left(U_m\right)\exp \left({\mathit{\beta }}_{\ast }^{\text{T}}\mathit{Z}\right)\right\}-I(R<\infty )\exp \left\{-{\text{Λ}}_{\ast }\left(U_{m+1}\right)\exp \left({\mathit{\beta }}_{\ast }^{\text{T}}\mathit{Z}\right)\right\}\right]}{{\int }_0^{\tau }\exp \left\{-{\text{Λ}}_{\ast }(a)\exp \left({\mathit{\beta }}_{\ast }^{\text{T}}\mathit{Z}\right)\right\}da} \\ =\frac{{\sum }_{m=0}^M{\text{Δ}}_m\left[\exp \left\{-{\text{Λ}}_0\left(U_m\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}-I(R<\infty )\exp \left\{-{\text{Λ}}_0\left(U_{m+1}\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}\right]}{{\int }_0^{\tau }\exp \left\{-{\text{Λ}}_0(a)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}da} \end{gathered}$$

with probability 1. For any m ∈ {0,..., M}, we set Δ_m′ = 1 in the above equation m′ = m,..., M and take the sum of the resulting equations to obtain

$$\begin{gathered} \frac{\exp \left\{-{\text{Λ}}_{\ast }\left(U_m\right)\exp \left({\mathit{\beta }}_{\ast }^{\text{T}}\mathit{Z}\right)\right\}}{{\int }_0^{\tau }\exp \left\{-{\text{Λ}}_{\ast }(a)\exp \left({\mathit{\beta }}_{\ast }^{\text{T}}\mathit{Z}\right)\right\}da}= \\ \frac{\exp \left\{-{\text{Λ}}_0\left(U_m\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}}{{\int }_0^{\tau }\exp \left\{-{\text{Λ}}_0(a)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}da}. \end{gathered}$$

Because m is arbitrary, we can replace U_m in the above equation by any t ∈ $\mathcal{V}$. We take the logarithm and differentiate both sides with respect to t to find

$${\text{Λ}}_{\ast }^{\prime }(t)\exp \left({\mathit{\beta }}_{\ast }^{\text{T}}\mathit{Z}\right)={\text{Λ}}_0^{\prime }(t)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right),$$

such that β_* = β₀ and ${\text{Λ}}_{\ast }^{\prime }(t)={\text{Λ}}_0^{\prime }(t)$ for t ∈ $\mathcal{V}$. Hence, Λ_*(t) = Λ₀(t) for t ∈ $\mathcal{V}$. We conclude that $\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert \to 0$ and $\left|\widehat{\text{Λ}}(t)-{\text{Λ}}_0(t)\right|\to 0$ for any t ∈ $\mathcal{V}$. Because Λ₀ is continuous, $\widehat{\text{Λ}}$ converges uniformly to Λ₀ on $\mathcal{V}$.

Proof of Theorem 2.

Let

$$Q_1(t,u,v;\mathit{\beta },\text{Λ})=\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\frac{I(t\le v)\exp \left\{-\text{Λ}(v)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}-I(t\le u)\exp \left\{-\text{Λ}(u)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}}{\exp \left\{-\text{Λ}(u)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}-\exp \left\{-\text{Λ}(v)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}},$$

$$\begin{gathered} Q_2(t;\mathit{\beta },\text{Λ})=\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right) \\ \times \frac{{\int }_0^{\tau }I(t\le a)\exp \left\{-\text{Λ}(a)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}da}{{\int }_0^{\tau }\exp \left\{-\text{Λ}(a)\exp \left({\mathit{\beta }}^{\text{T}}\mathit{Z}\right)\right\}da}, \end{gathered}$$

and $Q(t;\mathit{\beta },\text{Λ})={\sum }_{m=0}^M{\text{Δ}}_m{Q}_1\left(t,U_m,U_{m+1};\mathit{\beta },\text{Λ}\right)+Q_2(t;\mathit{\beta },\text{Λ})$. The score equations for β is given by

$${\mathit{l}}_{\mathit{\beta }}(\mathit{\beta },\text{Λ})=Z\int Q(t;\mathit{\beta },\text{Λ})d\text{Λ}(t).$$

The score operator for Λ along the submodel dΛ_ϵ,h = (1 + ϵh)dΛ for h ∈ L₂(μ) is given by

$$l_{\text{Λ}}(\mathit{\beta },\text{Λ})(h)=\int Q(t;\mathit{\beta },\text{Λ})h(t)d\text{Λ}(t).$$

Clearly,

$${\mathbb{G}}_n\left\{{\mathit{l}}_{\mathit{\beta }}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})\right\}=-\sqrt{n}\text{ℙ}\left\{{\mathit{l}}_{\mathit{\beta }}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})-{\mathit{l}}_{\mathit{\beta }}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)\right\},$$

and

$${\mathbb{G}}_n\left\{l_{\text{Λ}}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})(h)\right\}=-\sqrt{n}\text{ℙ}\left\{l_{\text{Λ}}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})(h)-l_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)(h)\right\}.$$

We apply the Taylor series expansions at (β₀, Λ₀) to the right sides of the above two equations. In light of Lemma 2, the second-order terms are bounded by $O_P\left(n^{-1/6}+\sqrt{\parallel }\widehat{\mathit{\beta }}-{\mathit{\beta }}_0{\parallel }^2\right)$. Therefore,

$$\begin{gathered} {\mathbb{G}}_n\left\{{\mathit{l}}_{\mathit{\beta }}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})\right\}=-\sqrt{n}\text{ℙ}\left\{{\mathit{l}}_{\mathit{\beta }\mathit{\beta }}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)+{\mathit{l}}_{\mathit{\beta }\text{Λ}}\left(\widehat{\text{Λ}}-{\text{Λ}}_0\right)\right\} \\ +O_P\left(n^{-1/6}+\sqrt{\parallel }\widehat{\mathit{\beta }}-{\mathit{\beta }}_0{\parallel }^2\right), \end{gathered}$$

and

$$\begin{gathered} {\mathbb{G}}_n\left\{l_{\text{Λ}}(\widehat{\beta },\widehat{\text{Λ}})(h)\right\}=-\sqrt{n}\text{ℙ}\left\{l_{\text{Λ}\beta }(h)\left(\widehat{\beta }-{\beta }_0\right)+l_{\text{ΛΛ}}\left(h,\widehat{\text{Λ}}-{\text{Λ}}_0\right)\right\} \\ +O_P\left(n^{-1/6}+\sqrt{\parallel }\widehat{\beta }-{\beta }_0{\parallel }^2\right), \end{gathered}$$

dΛ_ϵ,h, l_Λβ(h) is the derivative of l_Λ(h) with respect to β, and l_ΛΛ(h, $\widehat{\text{Λ}}$ − Λ₀) is the derivative of l_Λ(h) along the submodel dΛ₀ + ϵd($\widehat{\text{Λ}}$ − Λ₀). All derivatives are evaluated at (β₀, Λ₀).

If the least favorable direction exists, we denote it as h* ∈ L₂(μ)^p. We first show the existence of h*, which is the solution of $l_{\text{Λ}}^{\ast }{l}_{\text{Λ}}\left({\mathit{h}}^{\ast }\right)=l_{\text{Λ}}^{\ast }{\mathit{l}}_{\mathit{\beta }},$ where $l_{\text{Λ}}^{\ast }$ is the adjoint operator of l_Λ. We equip L₂(μ) with an inner product defined as

$$<h^{(1)},h^{(2)}>=\int h^{(1)}(t)h^{(2)}(t)d\mu (t).$$

On the same space, we define

$$\begin{gathered} \parallel h\parallel =\text{ℙ}{\left\{l_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right){(h)}^2\right\}}^{1/2} \\ =\text{ℙ}{\left[{\left\{\int Q\left(t;{\mathit{\beta }}_0,{\text{Λ}}_0\right)h(t)d\text{Λ}(t)\right\}}^2\right]}^{1/2}. \end{gathered}$$

It is easy to show that ∥·∥ is a seminorm on L₂(μ). Furthermore, if ∥h∥ = 0, then $\text{ℙ}\left\{l_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right){(h)}^2\right\}=0$. Thus, with probability 1, $l_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)(h)=0$. By the arguments in the Lemma 2, h(t) = 0 for t ∈ $\mathcal{V}$. Clearly, ∥h∥ ≤ c < h, h >^1/2 for some constant c by the Cauchy-Schwarz inequality. According to the bounded inverse theorem in Banach spaces, we have ${\langle h,h\rangle }^{1/2}\le \tilde{c}\parallel h\parallel$ for another constant $\tilde{c}$. By the Lax-Milgram theorem (Zeidler, 1995), there exists ${\mathit{h}}^{\ast }\in L_2{(\mu )}^p$ that satisfies

$$\begin{gathered} {\int }_0^{\tau }\text{ℙ}\left\{Q\left(t;{\mathit{\beta }}_0,{\text{Λ}}_0\right)Q\left(s;{\mathit{\beta }}_0,{\text{Λ}}_0\right)\right\}{\mathit{h}}^{\ast }(s)d{\text{Λ}}_0(s)= \\ {\int }_0^{\tau }\text{ℙ}\left\{\mathit{Z}Q\left(t;{\mathit{\beta }}_0,{\text{Λ}}_0\right)Q\left(s;{\mathit{\beta }}_0,{\text{Λ}}_0\right)\right\}d{\text{Λ}}_0(s) \end{gathered}$$

for t ∈ $\mathcal{V}$. Differentiation of the integral equations with respect to t yields

$$q_1(t){\mathit{h}}^{\ast }(t)+{\int }_t^{\tau }{q}_2(s,t){\mathit{h}}^{\ast }(s)ds+{\int }_0^t{q}_3(s,t){\mathit{h}}^{\ast }(s)ds={\mathit{q}}_4(t),$$

where q₁(t) > 0, and q_j (j = 1, 2, 3) and q₄ are continuously differentiable functions. Thus, h* can be expanded to be a continuously differentiable function in $\mathcal{V}$ with bounded total variations. It follows that

$$\begin{gathered} {\mathbb{G}}_n\left\{{\mathit{l}}_{\mathit{\beta }}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})\right\}-{\mathbb{G}}_n\left\{l_{\text{Λ}}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})\left(h^{\ast }\right)\right\} \\ =-\sqrt{n}\text{ℙ}\left\{{\mathit{l}}_{\mathit{\beta }\mathit{\beta }}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)+{\mathit{l}}_{\mathit{\beta }\text{Λ}}\left(\widehat{\text{Λ}}-{\text{Λ}}_0\right)\right\} \\ +\sqrt{n}\text{ℙ}\left\{l_{\text{Λ}\mathit{\beta }}\left({\mathit{h}}^{\ast }\right)\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)+l_{\text{ΛΛ}}\left({\mathit{h}}^{\ast },\widehat{\text{Λ}}-{\text{Λ}}_0\right)\right\} \\ +O_P\left(n^{-1/6}+\sqrt{n}\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0{\Vert }^2\right) \\ =\sqrt{n}\text{ℙ}\left[{\left\{l_{\mathit{\beta }}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)-{\mathit{l}}_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)\left({\mathit{h}}^{\ast }\right)\right\}}^{\otimes 2}\right]\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right) \\ +O_P\left(n^{-1/6}+\sqrt{n}\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0{\Vert }^2\right). \end{gathered}$$

Using the arguments in the proof of Lemma 1, we can show that ${\mathit{l}}_{\mathit{\beta }}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)-l_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)\left({\mathit{h}}^{\ast }\right)$ belongs to a Donsker class. Next, we show that $\text{ℙ}\left[{\left\{{\mathit{l}}_{\beta }-l_{\text{Λ}}\left({\mathit{h}}^{\ast }\right)\right\}}^{\otimes 2}\right]$ is invertible. If the matrix is singular, then there exists an vector $\mathit{v}\in {\text{ℝ}}^p$ such that ${\mathit{v}}^{\text{T}}\text{ℙ}\left[{\left\{{\mathit{l}}_{\mathit{\beta }}-l_{\text{Λ}}\left({\mathit{h}}^{\ast }\right)\right\}}^{\otimes 2}\right]\mathit{v}=0$. It follows that, with probability 1, the score function along the submodel $\{{\mathit{\beta }}_0+ϵ\mathit{v},{\text{Λ}}_{ϵ,-{\mathit{v}}^{\text{T}}{\mathit{h}}^{\ast }}\}$ is zero. That is,

$$\begin{gathered} \sum _{m=0}^M{\text{Δ}}_m\int \frac{I\left(t\le U_{m+1}\right)\exp \left\{-{\text{Λ}}_0\left(U_{m+1}\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}-I\left(t\le U_m\right)\exp \left\{-{\text{Λ}}_0\left(U_m\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}}{\exp \left\{-{\text{Λ}}_0\left(U_m\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}-\exp \left\{-{\text{Λ}}_0\left(U_{m+1}\right)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}} \\ \times {\mathit{v}}^{\text{T}}\left\{\mathit{Z}-{\mathit{h}}^{\ast }(t)\right\}d{\text{Λ}}_0(t)+\int \frac{{\int }_0^{\tau }I(t\le a)\exp \left\{-{\text{Λ}}_0(a)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}da}{{\int }_0^{\tau }\exp \left\{-{\text{Λ}}_0(a)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}da}{\mathit{v}}^{\text{T}}\left\{\mathit{Z}-{\mathit{h}}^{\ast }(t)\right\}d{\text{Λ}}_0(t)=0. \end{gathered}$$

For any m ∈ {0,…, M}, we sum over all possible Δ_m′ with m′ = m,…, M to obtain

$$\begin{gathered} -{\int }_0^{U_m}{\mathit{v}}^{\text{T}}\left\{\mathit{Z}-{\mathit{h}}^{\ast }(t)\right\}d{\text{Λ}}_0(t) \\ +\int \frac{{\int }_0^a\exp \left\{-{\text{Λ}}_0(a)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}da}{{\int }_0^{\tau }\exp \left\{-{\text{Λ}}_0(a)\exp \left({\mathit{\beta }}_0^{\text{T}}\mathit{Z}\right)\right\}da}{\mathit{v}}^{\text{T}} \\ \times \left\{\mathit{Z}-{\mathit{h}}^{\ast }(t)\right\}d{\text{Λ}}_0(t)=0. \end{gathered}$$

Because m is arbitrary, we can replace U_m in the above equation by t ∈ $\mathcal{V}$. We differentiate both sides with respect to t to obtain

$${\mathit{v}}^{\text{T}}\left\{\mathit{Z}-{\mathit{h}}^{\ast }(t)\right\}{\text{Λ}}_0^{\prime }(t)=0$$

for any t ∈ $\mathcal{V}$. It then follows that υ = 0. Hence, the matrix $\text{ℙ}\left[{\left\{{\mathit{l}}_{\beta }-l_{\text{Λ}}\left({\mathit{h}}^{\ast }\right)\right\}}^{\otimes 2}\right]$ is invertible.

Then, $\widehat{\mathit{\beta }}-{\mathit{\beta }}_0=O_P\left(n^{-1/2}\right)$, and

$$\begin{gathered} \sqrt{n}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)={\left(\text{ℙ}\left[{\left\{l_{\mathit{\beta }}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)-l_{\text{Λ}}\left({\mathit{\beta }}_0,{\text{Λ}}_0\right)\left(h^{\ast }\right)\right\}}^{\otimes 2}\right]\right)}^{-1} \\ \times {\mathbb{G}}_n\left\{l_{\mathit{\beta }}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})-l_{\text{Λ}}(\widehat{\mathit{\beta }},\widehat{\text{Λ}})\left(h^{\ast }\right)\right\}+o_P(1). \end{gathered}$$

The influence function for $\widehat{\mathit{\beta }}$ is the efficient influence function, such that $\sqrt{n}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$ converges weakly to a zero-mean normal random vector whose covariance matrix attains the semiparametric efficiency bound.

Appendix B

An EM algorithm for maximum conditional likelihood estimation

A nonparametric maximum conditional likelihood estimator is considered in Pan and Chappell (1998) for the proportional hazards model with left-truncated interval-censored data. A slight variation of the proposed EM algorithm can be used to compute their estimator, and is used in the numerical comparisons.

The observed-data conditional likelihood given the truncation time is given by

$$\prod _{i=1}^n\frac{\exp \left\{-\text{Λ}\left(L_i\right)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}-I\left(R_i<\infty \right)\exp \left\{-\text{Λ}\left(R_i\right)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}{\exp \left\{-\text{Λ}\left(A_i\right)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}.$$

We estimate Λ nonparametrically such that the estimator for Λ is a step function that jumps only at t₁,…, t_k, which are the ordered sequence of all L_i, R_i, and A_i. We maximize the objective function

$$\begin{gathered} \sum _{i=1}^n(\text{log}[\exp \left\{-\sum _{A_i\le t_j\le L_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\} \\ -I\left(R_i<\infty \right)\exp \left\{-\sum _{A_i\le t_j\le R_i}{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}]). \end{gathered}$$

We introduce a sequence of independent Poisson random variables $W_{ij}\left(i=1,\dots ,n;j=1,\dots ,k,A_i\le t_j\le R_i^{\ast }\right)$ with means ${\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)$. Let $N_{i1}={\sum }_{A_i\le t_j\le L_i}{W}_{ij}$, and $N_{i2}=I\left(R_i<\infty \right){\sum }_{L_i<t_j\le R_i}{W}_{ij}$. The objective function can be viewed as the observed-data log-likelihood for {N_i1 = 0, N_i2 > 0 : i = 1,…, n} with $W_{ij}(j=1,\dots ,k,A_i\le t_j\le R_i^{\ast })$ as latent variables. We propose an EM algorithm. In the E-step, we evaluate

$$\begin{gathered} \widehat{E}\left(W_{ij}\right)=I\left(L_i<t_j\le R_i,R_i<\infty \right) \\ \times \frac{{\lambda }_j\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)}{1-\exp \left\{-{\sum }_{L_i<t_l\le R_i}{\lambda }_l\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)\right\}}. \end{gathered}$$

In the M step, we update λ_j by

$${\lambda }_j=\frac{{\sum }_{i=1}^{n}I\left(A_i\le t_j\le R_i^{\ast }\right)\widehat{E}\left(W_{ij}\right)}{{\sum }_{i=1}^{n}I\left(A_i\le t_j\le R_i^{\ast }\right)\exp \left({\mathit{\beta }}^{\text{T}}{\mathit{Z}}_i\right)}$$

and update β by solving

$$\begin{gathered} \sum _{i=1}^n\sum _{j=1}^{k}I\left(A_i\le t_j\le R_i^{\ast }\right)\widehat{E}\left(W_{ij}\right) \\ \times \left\{Z_i-\frac{\sum _{i^{\prime }=1}^{n}I\left(A_{i^{\prime }}\le t_j\le R_{i^{\prime }}^{\ast }\right)\exp \left({\mathit{\beta }}^{\text{T}}{Z}_{i^{\prime }}\right)Z_{i^{\prime }}}{\sum _{i^{\prime }=1}^{n}I\left(A_{i^{\prime }}\le t_j\le R_{i^{\prime }}^{\ast }\right)\exp \left({\mathit{\beta }}^{\text{T}}{Z}_{i^{\prime }}\right)}\right\}=\mathbf{0}. \end{gathered}$$

We iterate between the E-step and M-step until convergence.