Network-based forecasting of climate phenomena

Abstract

Network theory, as emerging from complex systems science, can provide critical predictive power for mitigating the global warming crisis and other societal challenges. Here we discuss the main differences of this approach to classical numerical modeling and highlight several cases where the network approach substantially improved the prediction of high-impact phenomena: 1) El Niño events, 2) droughts in the central Amazon, 3) extreme rainfall in the eastern Central Andes, 4) the Indian summer monsoon, and 5) extreme stratospheric polar vortex states that influence the occurrence of wintertime cold spells in northern Eurasia. In this perspective, we argue that network-based approaches can gainfully complement numerical modeling.

If societies are able to anticipate disruptive events, they can take measures to save thousands of lives and to avoid billions of economic costs (1–5). A most evident, globally disruptive event is certainly the current COVID-19 pandemic. Even though it seems impossible to accurately predict the emergence of such a virus itself, the pandemic bears several characteristics that are also shared by other disruptions: The general risk of something like this happening was known before, but economic and societal preparations to limit harmful impacts are strongly dependent on a credible, science-based warning, preferably with significant time before the event or at least before its full unfolding (the spreading, in the case of a virus) and with specifications of foreseeable impacts. Such a warning is not always possible, but there are promising new avenues. Here, we describe our perspective on this research challenge from the point of view of network theory and its usefulness for better understanding and for forecasting specific climate phenomena.

Relevant climate phenomena that have the potential to produce major disruptions in societies are, for instance, the El Niño phenomenon, the Indian summer monsoon, and extreme weather patterns like persistent heat waves, cold spells, or rainstorms as associated with stalling planetary Rossby waves (6). For instance, a popular saying in India—that the “true finance minister” is the monsoon—is based on the fact that water resources are vital for India, where the rural economy accounts for about 45% of GDP (7). El Niño occurrences are well known for their global impacts on weather patterns and therefore societies. Floods and heatwaves, especially concurring with droughts, directly affect humans and nature, and can wreak havoc in agriculture. Beyond the climate system, highly challenging events of a disruptive nature are large-magnitude earthquakes, outbreaks of epidemics, and, on the individual level, physiological disasters like heart attacks. These phenomena often emerge with little precursory signal or no warning time at all, making effective adaptation challenging, if not impossible. The pertinent lack of predictive power, however, is not surprising, since most of those high-impact events are generated by complex systems composed of many nonlinearly interacting entities.

In the case of weather and climate, forecasting relies predominantly on numerical models (8). Starting with Richardson (9) in the 1920s, it has been a long way to the first successful prediction (10) in 1950 and, eventually, to the highly sophisticated general circulation and Earth system models of today (11). These simulators rely on initial conditions (especially for weather forecasts, i.e., the prediction of atmospheric dynamics for up to 2 wk) and boundary conditions (which are more relevant for seasonal and longer-ranging forecasts, involving slower climate components like the oceans) and deliver very good forecasts for a broad range of physical quantities. However, their predictive power for certain climate phenomena beyond the weather timescale can be rather limited: The dependence on precise initial and boundary conditions and the necessity to simplify, inherent to any modeling approach, as well as the chaotic nature of the system under study will hit hard limits to further improvement (12, 13).

Despite multiple efforts toward seamless prediction, a gap remains in prediction skill between the subseasonal weather forecast and seasonal and longer climate predictions. Near-term climate prediction is one of the Grand Challenges of the World Climate Research Program (14). There have also been other significant efforts in this domain, for instance, with the subseasonal to seasonal (S2S) prediction project (15, 16). But, in many cases, numerical modeling still does, and also might continue to, leave vulnerable societies with insufficient warning time ahead of climate phenomena, within as well as outside of the above mentioned gap: There are types of climate phenomena that still notoriously elude reliable long-term forecasting through numerical modeling. For five specific climate phenomena examples discussed below, network theory has led to (in some cases) considerably earlier forecasts compared to state-of-the-art operational forecasts (SI Appendix, Table S1).

Here we argue that the predictability limitations of existing operational forecasts are partly due to the basic intention of numerical models: the goal of faithfully mirroring the local nature of direct interactions in the physical world. However, the models are not perfect mimicries of nature. Processes, for example, turbulence, are not resolved at all or only at a possibly insufficient resolution, and tuned parametrizations have to be employed (17). In particular, teleconnections present in observational data may be not well represented or even absent within numerical models. Thus, identifying and then analyzing the evolution of teleconnections with time can provide an additional avenue to predicting large-scale climate phenomena. The beginnings of this promising avenue can be traced back to Sir Gilbert Walker (18) in the early 20th century, when he first noticed teleconnections, and has now gained a new and much broader perspective through the advent of complex network analyses.

Here we suggest that the evolving interactions (manifesting, e.g., via correlations) between different and often rather distant locations can provide new insights and serve as predictors for a large variety of climate phenomena. The philosophy behind this approach is that, even in a simple system, composed, for instance, of two coupled nonlinear oscillators, one will observe aleatoric behavior providing very limited information when measuring the motion of each oscillator individually. However, when evaluating the coupling between them, for example, via synchronization [as already detected in the 17th century by Christiaan Huygens (19)], one will obtain new and valuable information about the system (20). Analogously, while one might not necessarily extract useful information from measurements of single locations on the globe, the links, for example, the interactions between the sites and their evolution in time, can provide, as in the examples below, critical novel information for forecasting.

Network Analysis Opens a Second Avenue

Consequently, we propose to complement the established state of the art for predicting climate phenomena through explicit numerical modeling by the maturing approach of network theory (21–23). The idea is to obtain additional information about the climate system by capturing the connectivity of different locations (including long-distance ones), through measuring the similarity in the evolution of their physical quantities. This similarity between different locations (nodes) can be quantified by different linear and nonlinear measures like Pearson correlation, event synchronization, mutual information, transfer entropy, partial correlations, or Granger causality. For an overview of the different methods, see refs. 24 and 25.

The similarity is then translated into links connecting the nodes in the network and measuring cooperativity, that is, the property of not acting independently of each other. Commonly, cutoff thresholds are applied on these similarity measures to select only the statistically significant links. These thresholds can be obtained by analyzing surrogate data, for example, shuffled versions of the original time series or synthetic time series that match the relevant statistical properties of the original time series. For more details on surrogate methods, see refs. 24 and 25. For an illustration of a network framework, see Fig. 1.

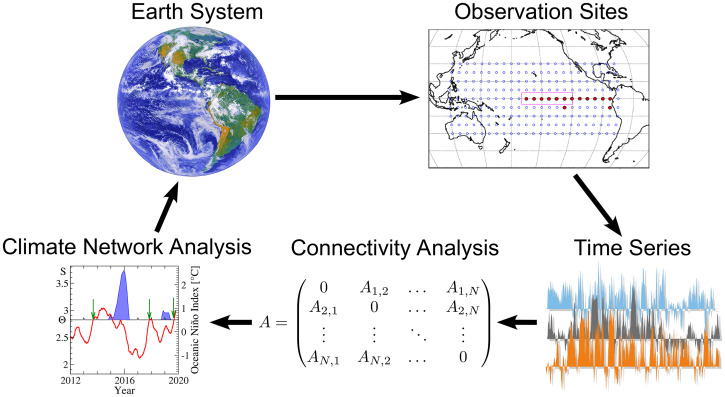
Fig. 1.

The climate network framework as a tool for prediction. Observational data of physical quantities, for example, temperatures, are available at different geographical locations. These data can be used directly or via a reanalysis (numerical weather model) which assimilates and maps them onto a regular grid. Thus, for each node (observational site or reanalysis grid point) of the climate network, a time series of the regarded physical quantity is available. Cooperativity between nodes can be detected from the similarity in the evolution of these time series and translated into links connecting the corresponding nodes. The links or their strengths may change with time. These nodes and their links constitute the evolving climate network, which can be represented by the adjacency (connectivity) matrix A. The analysis of this network can enable early predictions of climate phenomena and provide insights into the physical processes of the Earth system. For example, for forecasting El Niño, the nodes are in the Pacific, and the links are between the El Niño basin (full red circles) and the rest of the tropical Pacific (open blue circles). The rising of the network’s mean link strength S (red curve) above a certain threshold Θ serves as a precursor (green arrows) for the start of an El Niño event (blue areas) in the subsequent calendar year (32). Observation sites and Climate network analysis images are reprinted with permission from ref. 32.

The final network can be represented by an adjacency (connectivity) matrix A, which encodes the links between the nodes or their absence and is defined as

$${\mathbf{A}}_{ij}=\{\begin{array}{c}\mathrm{non}-\mathrm{zero,if there is a link from node j} \text{to} \text{node} i\\ 0,\text{otherwise}\end{array}.$$

The value of the element ${\mathbf{A}}_{ij}$ represents the weight of the link. Links connecting nodes to themselves are not included; that is, ${\mathbf{A}}_{ii}=0$. If the links are not directed, then the adjacency matrix is symmetric, ${\mathbf{A}}_{ij}={\mathbf{A}}_{ji}$. However, links can also be defined as directed links, with a starting node j and a target node i. For instance, in the case of correlation-based links, a direction can be defined via the sign of the time lag of the cross-correlation function. When links are directed, A is generally nonsymmetric, ${\mathbf{A}}_{ij}\ne {\mathbf{A}}_{ji}$.

The thus obtained adjacency matrix allows the calculation of network quantities like in- and out-degrees, clustering coefficients or betweenness coefficients of nodes. For a detailed description of these and other network quantities, see refs. 21 and 22. Many of these quantities, which represent topological features of the network, have a physical interpretation. For example, it was found, by analyzing advection–diffusion dynamics on model background flows, that a high absolute flow velocity coincides with a high node degree, that is, a high number of links attached to a node (26).

While teleconnections can be emerging properties in dynamical models, which mainly concentrate on data at specific grid cells and their immediate neighbors, the basis of the network approach is the direct analysis of the links between grid points of a large variety of distances and their temporal evolution. This approach avoids the necessity of mimicking the entire climate system, enabling the forecasters, instead, to pursue specific questions about particular nonlocal phenomena. Since network-based prediction schemes often rely only on assessing the current state of the regarded system, measurement errors play a much smaller role for them than for numerical models, where small errors in the initial conditions can lead to exponentially increasing errors in the prediction, as can be the case for weather forecasting (8, 27).

In contrast to, for example, online social networks, where the existence of the structure is already known and subject to direct analysis, the existence and structure of networks in the climate context is often not obvious—they can be purely functional. In this respect, climate networks are comparable to networks in neuroscience, where the structural networks of synapses can be different from the functional network derived from the connectivity of time series, for example, EEG measurements (28).

In the following, we focus on forecasting, and highlight several cases where the climate network (24, 29–31) approach substantially improved the prediction of high-impact climate phenomena: 1) El Niño events (32–38), 2) droughts in the central Amazon (39), 3) extreme rainfall in the eastern Central Andes (40, 41), 4) the Indian summer monsoon (42–44), and 5) extreme stratospheric polar vortex (SPV) states (45, 46).

For most of these climate network-based analyses, the initial motivation was to better understand and describe the regarded climate phenomena and not primarily the discovery of a new forecasting method, which often happens serendipitously. Generally, there is currently no recipe to follow to surely obtain a network-based prediction algorithm for a specific climate phenomenon or to rule out that a network approach can address the phenomenon. However, complex networks provide ideal tools for data exploration to uncover spatial and temporal patterns in the data that can later potentially be explained with domain knowledge about the phenomenon, leading to new physical insights. When this is the case, as for some of our examples below, then the discovered relationships may enable the development of new forecasting methods, which, at this point, could be entirely detached from the original climate network-based analyses that led to their discovery. However, network-based quantities can potentially also serve as direct predictors in a forecasting algorithm if the underlying processes are not yet identified, as is the case in our first example.

El Niño

El Niño events (47–49) are part of the El Niño–Southern Oscillation (ENSO), the most important driver of interannual global climate variability. ENSO can be perceived as a self-organized dynamical see-saw pattern in the tropical Pacific Ocean–atmosphere system, featuring rather irregular warm (“El Niño”) and cold (“La Niña”) excursions from the long-term mean state.

The existing operational El Niño predictions have been especially limited by the so-called spring barrier, obscuring the anomaly’s onset until about 6 mo before its beginning (49, 50). In contrast, the climate network-based prediction method can cross this barrier and roughly double the prewarning time to about 1 y ahead (32). For example, in September 2013, the method forecasted the onset of an El Niño event in 2014 with 75% probability, and, based on this, a warning was issued (33). The forecast turned out to be correct, as an extreme El Niño event started in 2014 (51) and ended in 2016. For comparison, in December 2013, that is, 3 mo after the network-based forecast, the most far-reaching plume-based forecast of the International Research Institute for Climate and Society/Climate Prediction Center predicted a neutral event with 46% probability, an El Niño with 44%, and a La Niña with 10% for August–September–October 2014 (52).

This successful prediction was based on a detailed analysis of the meteorological connectivity of locations inside the so-called El Niño basin with locations distributed across the rest of the Pacific (32). This analysis area was chosen since the evolution of the ENSO takes place across the Pacific. Previous studies (30, 53) had found that the connectivity usually drops strongly during an El Niño event. Accordingly, the cooperativity has to increase before an event, and this feature serves as the basis for the early prediction.

To obtain a measure for the cooperativity, the approach builds on daily surface atmospheric temperatures at grid points (“nodes”) in the tropical Pacific (see the map in Fig. 1), obtained from a reanalysis (54). The time evolution of the links between the temperature nodes inside the “El Niño basin” (14 nodes) and the nodes outside the basin (193 nodes) is analyzed. The strengths of these 2,702 links are derived from the magnitudes of the lagged cross-correlation functions between the temperature time series at the corresponding sites. For further details, see the original publications (32, 33). The rising of the network’s mean link strength S above a certain threshold Θ serves as a precursor for the start of an El Niño event in the subsequent calendar year. This empirical threshold was optimized using a learning phase (1950–1980), and the approach’s skill was tested in a hindcasting phase (1981–2011); see Fig. 2 A and B. Fig. 2C compares the prediction accuracy of the network approach via a receiver operating characteristic (ROC) analysis with the 6- and 12-mo forecasts based on dynamical climate models (55, 56). Based on this analysis, the network approach considerably outperforms conventional 6-mo and 1-y forecasts through dynamical modeling. The method was tested and validated, for example, by discarding 80% of the nodes outside the El Niño basin randomly, leading to about the same prediction performance, and by randomly (block) shuffling the data to obtain statistical error estimates for the observed performance of the method (32).

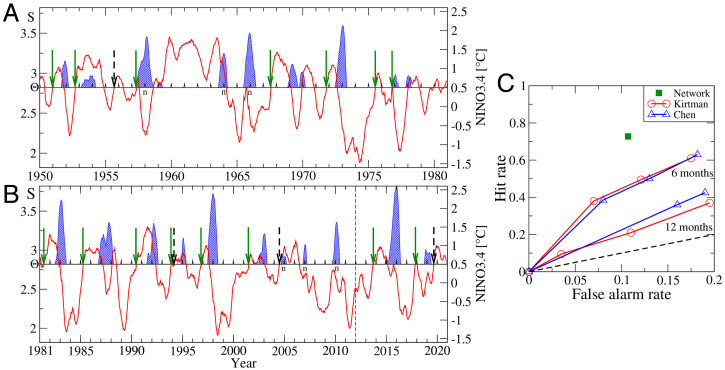
Fig. 2.

The El Niño forecasting algorithm; updated figures from the original publication (32). (A and B) The mean link strength S(t) (red curve) of the climate network (Fig. 1) is compared to a decision threshold Θ (horizontal line, here $\mathrm{\Theta }=2.82$) (left scale) with the Oceanic Niño Index (ONI) (right scale). The ONI is defined as the 3-mo running mean of the SST anomalies in the Niño3.4 area in the Pacific (pink rectangle in Fig. 1). When the link strength crosses the threshold from below outside of an El Niño episode, an alarm is given, and the start of an El Niño in the following calendar year is predicted. El Niño episodes (when the ONI is above 0.5 ^∘C for at least 5 mo) are shown by blue areas. A shows the learning phase 1950–1980, where the decision threshold was optimized. In B, the threshold obtained in A is used to hindcast and forecast El Niño episodes. The hindcasting and forecasting phases are separated by a dashed vertical line. Correct predictions are marked by green arrows, and false alarms are marked by dashed arrows. The index n marks unpredicted El Niño episodes. The lead time between a correct alarm and the beginning of the El Niño episodes is 1.01 ± 0.28 y, while the lead time to the maximal Niño3.4 value is 1.35 ± 0.47 y (32). (C) The prediction accuracy (ROC-type analysis). In a ROC analysis, the hit rate (the number of correctly predicted events divided by the total number of events) is plotted against the false alarm rate (the number of false alarms divided by the number of nonevents). The figure compares the performance of the network-based method (forecasting and hindcasting phase, 1981–2020; see B) with the 6- and 12-mo forecasts based on climate models (55, 56). In contrast to ensemble methods, the network-based “ROC-curve” is a single point, since, by construction, the method does not allow arbitrarily increasing of the hit rate at the expense of increasing the false alarm rate. The black dashed line shows the diagonal corresponding to random predictions. Adapted figures with permission from ref. 32.

The network approach has proven its operational skill not merely in hindcasting but also in forecasting since it was introduced in 2012: Between 1981 and 2020, that is, after the learning phase, the El Niño onset predictions are correct to 73%, and the no-show predictions are correct even to 89%; see Fig. 2. Based on random guessing with the climatological average El Niño occurrence probability, the corresponding P value is $5.8·{10}^{-5}$ and, for the forecasting phase alone, p = 0.029 (eight out of nine forecasts were correct).

The question of which physical processes generate the cooperative mode and how they are related to the El Niño buildup is still open and offers interesting new research opportunities. Possible answers lie in an understanding of the Walker circulation as a synergetic phenomenon, of slow oceanic Rossby waves, or of oceanic turbulence structures. The relationship between the cooperative mode and the El Niño buildup should also be present in dynamical models, which makes this relationship a useful test criterion for a model’s ability to accurately reflect the underlying mechanisms.

Climate network-derived quantities have also shown predictive skill for El Niño/ENSO in other studies (34–38, 57) and show that an upcoming El Niño provides early warning signals, which can be picked up by suitable climate networks.

Predicting Droughts in the Central Amazon

Droughts have severe impacts on ecosystems all around the globe. They increase tree mortality and the risk of wildfires, which threaten forests in addition to ongoing large-scale deforestation. The Amazon rainforest has experienced several extreme droughts in the last decades, during which the rainforest temporarily turned from a carbon sink to a carbon source (58). More persistent and more frequent droughts in the Amazon increase the risk of a large-scale transition from rainforest to savanna (59). A dieback of the rainforest would shift this ecosystem from a carbon sink into a carbon source (60).

Although the tropical Atlantic Ocean is the main source of moisture inflow into South America (61), it has long been thought that droughts in the Amazon basin are dominantly caused by El Niño events and associated longitudinal displacements of the atmospheric Walker circulation. Only more recently, it has been suggested that sea surface temperature (SST) anomalies in the tropical Atlantic Ocean could provoke hydrological extremes in the Amazon as well (62).

Based on this hypothesis, a complex network was applied to identify oceanic regions with a strong impact on Amazon rainfall. By introducing a bivariate network approach (39), it was possible to reveal the two regions in the tropical Atlantic Ocean where SST anomalies have the strongest impact on seasonal-scale rainfall anomalies in the central Amazon (Fig. 3 A and B). The spatial pattern revealed with this network-based data analysis is then explained in terms of the relevant atmospheric and oceanic processes. It was shown, in ref. 39, that the development of an SST dipole between these regions in the northern and southern tropical Atlantic and associated latitudinal shifts of the Intertropical Convergence Zone lead to large-scale droughts in the central Amazon.

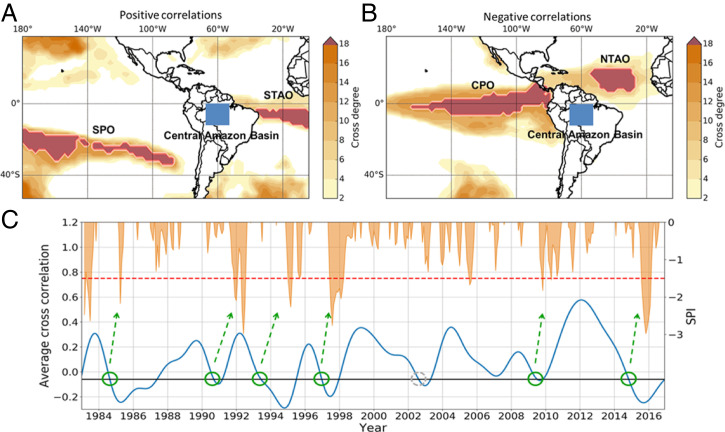
Fig. 3.

Drought prediction analysis based on correlation structure of SST anomalies in the northern and southern tropical Atlantic Ocean. (A and B) Cross degree between SSTs and continental rainfall anomalies. For each SST grid cell of the Atlantic and Pacific Ocean, the cross degree toward rainfall in the Central Amazon Basin (blue box) is shown, for (A) positive and (B) negative correlations. Darker shading indicates a larger cross degree, implying a larger number of links, and thus significant correlations with rainfall at more grid points in the Central Amazon Basin. Red areas outline coherent oceanic regions with the 20% highest cross degrees. Strong positive correlations are present between Central Amazon rainfall and the southern Pacific ocean (SPO) SSTs as well as southern tropical Atlantic ocean (STAO) SSTs. Strong negative correlations can be inferred, in contrast, for the central Pacific ocean (CPO) and the northern tropical Atlantic ocean (NTAO). (C) Early warning signal for droughts in the Central Amazon Basin. The time evolution of the average cross-correlation of the northern and southern tropical Atlantic Ocean (blue) is compared with the standardized precipitation index (SPI, orange) of the Central Amazon Basin. Negative SPI anomalies with SPI ¡ –1.5 (red dashed line) indicate severely dry periods. A drought event is predicted within the following one and a half years whenever the average cross-correlation between the SST anomalies falls below an empirically found threshold of -0.06. Green circles indicate a matching prediction, with one false alarm in 2002 indicated by a gray circle, where the threshold is crossed but no drought took place in the direct aftermath. The temporal evolution of the average cross-correlation shown here is smoothed using a Chebyshev type-I low-pass filter and cutoff at 24 mo. Reproduced with permission from ref. 39.

The analysis of the correlation structure between SST anomalies in the two identified tropical Atlantic regions reveals clear early warning signals for droughts in the Amazon (Fig. 3C). A drought warning is issued once the correlation turns significantly negative, indicating the beginning of the development of the tropical Atlantic SST dipole. Based on this scheme, six out of the seven most severe droughts in the central Amazon that occurred during the last four decades were successfully hindcasted at lead times between 12 and 18 mo.

Extreme Rainfall in the Eastern Central Andes

During the core season of the South American monsoon from December through February, the eastern slopes of the Central Andes are frequently affected by extreme rainfall events. These events can lead to floods and landslides with devastating socioeconomic impacts, but, until the development of the network approach (40, 41), no early-warning scheme had been proposed.

Complex networks were again used as a data exploration method to reveal patterns that might be useful for prediction when combined with mechanistic insights. The spatiotemporal structure of those extreme rainfall events (above the 99% percentile), as inferred from high-resolution satellite data, can be mapped onto a directed and weighted network: The link weights between two grid points are a measure for how often two grid points show a time-delayed, significantly similar precipitation event pattern, and the direction is determined by the temporal sequence of the events. The resulting network allows for identifying the source and the sink regions of extreme precipitation across the South American continent. SI Appendix, Fig. S1 shows that the Intertropical Convergence Zone and the northern Amazon are a source of extreme events, while the central parts of South America are sink regions of extremes.

Surprisingly, the network approach reveals that the exit region of the low-level monsoonal wind flow in southeastern South America turns out to be a source area of extreme rainfall events. The directed network structure allows the inference that events occurring there tend to be followed by further events along a narrow band extending northwestward to the Bolivian Central Andes, and thus in the opposite direction of the low-level monsoon circulation. Combining the results of this data exploration with process knowledge reveals the mechanisms underlying these extreme events and opens the door for prediction. A detailed analysis of the atmospheric conditions exhibits that not the rainfall systems themselves, but rather the atmospheric conditions that favor the development of large convective systems and thus lead to extreme rainfall, propagate against the direction of the monsoon circulation (41). These atmospheric conditions are determined by westward-moving Rossby wave trains that originate from the southern Pacific Ocean and turn northward after crossing the southern tip of the continent. The interaction of the pressure anomalies embedded on these Rossby wave trains with the warm, moist monsoon flow from the tropics leads to the propagation of extreme rainfall from southeastern South America northwestward to the Central Andes.

The thus gained knowledge establishes a forecasting rule for extreme rainfall in the eastern Central Andes based on two preconditions, namely, 1) strong rainfall in southeastern South America and 2) an anomalously deep low-pressure system over northwestern Argentina. With a lead time of 2 d, this forecast rule correctly predicts 60% (and 90% during El Niño conditions) of the extreme rainfall events in the eastern Central Andes (41). Note that these 60% true positives correspond to a Heidke Skill Score of 0.47 and thus clearly outperform a random forecast, for which this score would yield a value of zero. The better prediction skill during El Niño conditions can be explained by the fact that the atmospheric pattern described above, based on which the forecast rule has been established, occurs more often, and more concisely, during these episodes.

Teleconnections for extreme rainfall not only operate at regional to continental but also at global scales (63). In particular, atmospheric Rossby waves can be identified as dominant transcontinental processes. The forecasting potential of continental and global synchronization patterns for extreme rainfall has, so far, only been systematically assessed in a few cases and should be exploited for other regions. Moreover, extreme-rainfall teleconnection patterns determined from observational data can, in principle, yield a methodological framework to benchmark and constrain atmospheric general circulation models with respect to their capability to reproduce these patterns.

Indian Summer Monsoon

The Indian summer monsoon is an intense rainy season lasting from June to October. The monsoon delivers more than 70% of the country’s annual rainfall, which is the primary source of freshwater for India. Although the rainy season happens every year, the monsoon onset and withdrawal dates vary within a month from year to year. Such variability greatly affects the life and property of more than a billion people in India, especially those living in rural areas and working in the agricultural sector, which employs 70% of the entire population. Only Kerala in South India receives an official monsoon forecast (64) 2 wk in advance, while the other 28 states rely on the operational weather forecast of about 5 d (64). The demand for an earlier monsoon forecast is highest in central India, which is most exposed and vulnerable to droughts before the monsoon onset. Moreover, while, under climate change, severe storms and floods during the monsoon withdrawal are becoming more frequent, there is, currently, no official forecast for the withdrawal date.

Exploratory network-based analyses of extreme rainfall across the Indian subcontinent (42, 43) enabled the identification of geographical domains displaying far-reaching links, influencing distant grid points. Especially north Pakistan and the Eastern Ghats turn out to be crucial for the transport of precipitation across the subcontinent (43).

The combination of the network-based analysis and nonlinear dynamics in the tipping elements approach (44) allowed uncovering of the critical nature of the spatiotemporal transition to the monsoon. It was found that the temporal evolution of the daily mean air temperature and relative humidity exhibit critical thresholds on the eve and at the end of the monsoon. The spatial analysis of the critical growth of the fluctuations (65) in the weekly mean values of the same variables revealed the same two geographical areas with maximum fluctuations (Fig. 4 A–C): the Eastern Ghats and north Pakistan. A highly developed instability occurring in these regions creates the conditions necessary for the spatially organized and temporally sustained monsoon rainfall. Thus, the two critical regions appear to play the role of the tipping elements of the monsoon system. The most interesting feature is how the tipping elements are connected: On the eve of the onset and the withdrawal of the monsoon in the central part of India, the temperature and relative humidity in two tipping elements equalize (Fig. 4D). This insight creates the foundation for predictions of the monsoon timing.

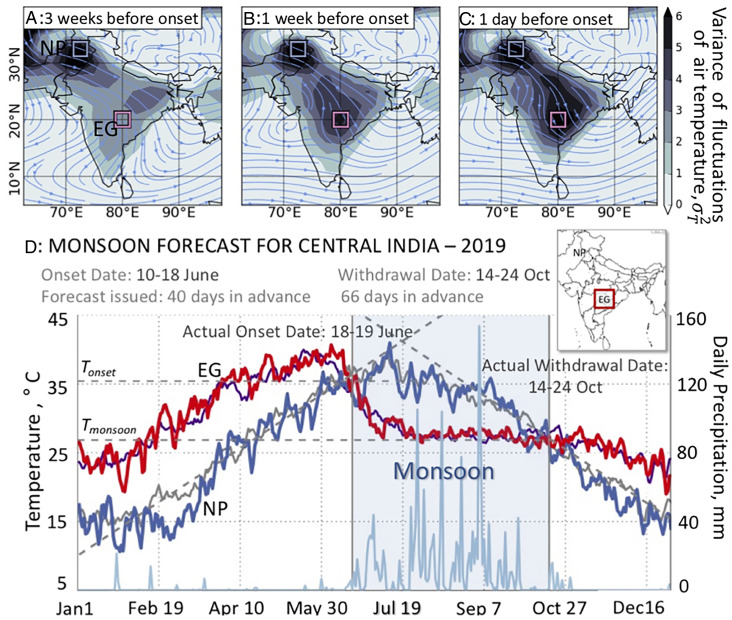
Fig. 4.

Tipping elements of the Indian summer monsoon: forecast of onset and withdrawal dates for 2019 (based on the methodology in ref. 44). The tipping elements of the Indian summer monsoon are geographical regions in north Pakistan (NP) and the Eastern Ghats (EG), which are revealed by the premonsoon growth of the variance ${\sigma }_T^2$ of fluctuations of the weekly mean values of the near-surface air temperature T, (A) 21 d, (B) 7 d, and (C) 1 d before the monsoon onset in the EG. Two boxes, where ${\sigma }_T^2$ is maximal, show the location of the tipping elements. The composites of ${\sigma }_T^2$ and the 700-hPa winds (indicated by the blue lines) for the period 1958–2001 from the ERA40 reanalysis dataset (87) are shown in A–C. (D) Forecasting scheme of the onset and withdrawal dates for central India in the EG region for 2019 based on daily mean near-surface (1,000 hPa) air temperatures (National Centers for Environmental Prediction/National Center for Atmospheric Research) (54, 88) in 2019 in the EG (red) and NP (blue), and the previous 5-y average temperature in the EG (purple) and NP (gray). Vertical gray lines represent the forecasted monsoon onset and withdrawal dates, which we call the tipping points of the monsoon. The tipping points occur when the temperatures in the EG and NP (the tipping elements of the monsoon) become equal, which happens twice during a year. At the end of May, the temperature in the EG decreases from its maximum value; then, it reaches a critical threshold ($T_{\text{onset}}$), and an abrupt transition occurs—the temperature inevitably falls, and the rainy season begins in the EG region. At the same time, the temperature in NP increases, and the two time series intersect at $T_{\text{onset}}$ at the onset date of the monsoon in the EG. In October, when the temperature in NP falls below $T_{\text{monsoon}}$ at the second intersection of the two time series, the monsoon withdraws from the EG. This feature allows estimation of the dates when the two critical temperatures ($T_{\text{onset}}$ and $T_{\text{monsoon}}$) are reached and forecasting of the onset and withdrawal dates of the monsoon. (See details in ref. 44.) The daily precipitation in the EG region obtained from National Oceanic and Atmospheric Administration (89) is shown superimposed in light blue. The sudden increase and decrease in precipitation coincide with the monsoon period defined by the light blue band. The results of forecasts for the period 2016–2020 are presented in ref. 66. The Inset in D illustrates the locations of NP and the EG. Portions of figure reprinted with permission from ref. 44, John Wiley and Sons, copyright American Geophysical Union.

Based on this knowledge, a scheme was developed for forecasting the upcoming monsoon onset and withdrawal dates in the central part of India 40 and 70 d in advance, respectively, thus considerably improving the time horizon of conventional forecasts (44). The new scheme has proven its skill (73% of onset and 84% of withdrawal predictions correct) not only in retrospective predictions (for the years 1951–2015); it has proven to be successful in the prediction of future monsoons already 5 y in a row since its introduction in 2016 (66). The methodology appears to be robust under climate change and has proven its skill also under the extreme conditions of 2016, 2018, and 2019.

The approach creates new monsoon forecasting possibilities around the globe, for instance, for the African, Asian, and American monsoon systems. In particular, it also offers the possibility for regional monsoon forecasting schemes, like the above one for the central part of India.

Stratospheric Polar Vortex

The Northern Hemisphere extratropical stratosphere in boreal winter is characterized by a westerly circumpolar flow, the SPV (67). The strength of the SPV can influence the tropospheric midlatitude circulation, and a weak SPV increases the chances of cold air outbreaks there. Thus, extremely weak SPV states can lead to cold spells in parts of North America and Eurasia. Given the rather persistent surface impacts, the SPV is an important source of S2S predictability for winter weather (68). To predict extremely weak and strong SPV states, a climate network was constructed via the Peter Clark Momentary Conditional Independence (PCMCI) algorithm (45, 69) and has been successfully applied to identify the precursor processes of these states.

While, in the previous climate network examples, nodes were single grid points on the globe, in this approach, each node of the network stands for an individual subprocess, and the links, derived, for instance, from partial correlations, have a causal interpretation (45, 46, 69, 70). A quantitative representation of a subprocess (node) might be, for instance, the mean value of a physical quantity over a particular spatial area (e.g., sea-level pressure anomalies over the Ural Mountains region).

Then the aim is to estimate a directed network representation of the regarded system’s subprocesses, that is, to identify which subprocesses causally influence which other subprocesses (for details, see ref. 69). This goal is addressed by discriminating between the direct causal connections between the subprocesses and spurious, noncausal correlations (69, 70). The latter can arise due to common causes of two regarded subprocesses, intermediate mediating processes or autocorrelations in the subprocesses. The PCMCI algorithm identifies those spurious correlations and removes them from the network.

At the start of the SPV analysis, potential relevant variables affecting vortex variability were expected in variables such as SSTs, sea-level pressure, and lower stratospheric poleward eddy heat flux. From these fields, regional precursors indices were first formed by cross-correlating the fields against the SPV time series and then averaging over the significantly correlated regions. In the next step, these precursors indices were then evaluated using the PCMCI algorithm for their causal interactions. Thus, while domain knowledge was crucial to choose the input variables, selecting the exact precursor regions as well as identifying and quantifying the involved causal processes was done using the algorithm described in refs. 46 and 70, which yields statistically more reliable estimates than relying on Granger causality (69).

The algorithm enabled the prediction of SPV behavior with predictive skill up to 45 d for extreme 15-d-mean events (46). For instance, the scheme hindcasts 58% of the extremely weak polar vortex states with a lead time of 1 d to 15 d and a false alarm rate of only about 5%. Dynamical forecast methods can provide predictability up to 30 d for daily events, so-called sudden stratospheric warmings, but the prediction lead time varies strongly for individual events and is usually much shorter (71).

This approach of reconstructing causal interactions is a powerful tool in Earth system sciences (70): It can be applied to test specific hypotheses about interaction mechanisms or to weigh the importance of components as gateways for spreading perturbations in the network. But it also offers a novel approach to prediction: For prediction targets as different as the amount of Indian summer monsoon rainfall (72) and seasonal Atlantic hurricane activity (73), precursors with lead times of several months could be identified. Additionally, the algorithm also allows more process-based model evaluations (74) beyond simple correlation analyses to understand potential biases in representing teleconnection pathways. This might, in particular, be useful in the form of hybrid forecasts (75) which combine numerical models with statistical methods.

The PCMCI algorithm is particularly useful if the main goal is understanding the underlying mechanisms of different processes by reconstructing causal relationships hidden in correlations of observed data. The algorithm requires sufficient domain expertise to optimally preselect the variables and processes of the phenomena one is interested in and can be sensitive to different parameter settings. Although causal discovery algorithms have been successfully applied to high-dimensional settings as well (including the here discussed SPV case; see also refs. 69 and 76), a low-dimensional, parsimonious set of variables representing the considered mechanisms is often beneficial to reduce the number of statistical independence tests in order to assure interpretability of results. In contrast, complex correlation networks provide a more explorative approach, helping to detect patterns in large high-dimensional data, which can give rise to new hypotheses, which could, in turn, be tested with the PCMCI approach.

Climate Networks and Artificial Neural Networks

Extending the avenues for climate phenomena forecasting beyond numerical modeling is not limited to climate network theory. Artificial neural networks (ANNs), and especially their currently most popular application, deep learning (77, 78), are inspired by the functioning of the brain and are also composed of nodes (“neurons”), which are connected (linked) to other nodes. However, the similarity to climate networks is primarily structural: In climate networks, the individual nodes represent grid locations or physical processes, thereby creating an alternative description of the physical world. By contrast, the nodes in ANNs and their links (the ANN’s architecture) have, generally, no physical meaning, and the link (and bias) weights, trained on the data, create an internal representation of useful aspects of the physical world. If enough training data have been presented to a suitable ANN, it is able to capture characteristics of the underlying system and make predictions. For instance, deep learning has been recently proposed to forecast the ENSO (79) and the amount of Indian summer monsoon rainfall (80). Furthermore, ANNs and other machine learning techniques have been successfully applied to a wide range of weather and climate questions and can be powerful tools for tackling climate change; see ref. 81 for a detailed review. However, an issue at the forefront of research remains the black box character of ANNs (82), although promising advances toward explainable or interpretable artificial intelligence have recently been made (83).

We believe that climate network analyses and ANNs can gainfully combine (37, 84). The ANNs’ strength of being able to learn complex nonlinear relationships in the presented data and the climate networks’ ability to identify and compress/merge spatially dispersed information about cooperativity and their potential to provide a physical interpretation makes them well-fitting complements for climate phenomena forecasting.

Outlook

The above (incomplete) list of successful applications of network theory to climate phenomena demonstrates the potential of this approach. We argue that it complements established concepts and schemes with a new possibility to reveal precursor processes or even entire causal chains of climate phenomena. Network theory applied to climate science is still in its infancy and the subject of ongoing research. The analyses of complex climate phenomena such as the ones discussed above require individual case-by-case approaches, and there are no simple general recipes yet. Climate networks are versatile tools for exploratory analysis to uncover spatial and temporal patterns in the data, which may potentially lead, with domain expertise, to new forecasting methods.

The examples highlighted in this perspective can, however, serve as useful analogies/templates for a network-based forecasting of climate phenomena that are similar to them. For instance, the example of El Niño can serve as a template to forecast other large-scale cooperative phenomena like the Indian Ocean Dipole or the Atlantic El Niño. As in the case of the Amazon droughts, the quantification of the impacts of SST patterns on rainfall anomalies over adjacent continents should be possible also for other tropical regions where land–ocean temperature gradients drive moisture flow and hence rainfall anomalies. The approach developed for the extreme rainfall prediction in the Central Andes should be applicable also to other regions where interactions between subtropical and extratropical weather phenomena are relevant, such as in North America or eastern Asia. Developed for forecasting the Indian summer monsoon, the tipping elements approach is applicable to other climate and weather phenomena that exhibit a critical transition. In particular, it could be applied to other monsoon systems in West and East Africa, and also North and South America. Finally, the PCMCI algorithm is particularly useful if the primary goal of an analysis is an understanding of the underlying mechanisms of a regarded phenomenon.

Network theory applied to climate science is rapidly developing, but there are still open challenges in the realm of application, as well as challenges of a methodological nature.

Since climate networks are constructed from observational data via similarity measures, for example, correlations, their underlying physical processes may not be immediately apparent. Uncovering the physical processes can lead to a better understanding of the regarded system, which could translate into better predictions within the network framework or improved numerical models. Causally interpretable networks and machine learning techniques could be instrumental in uncovering the underlying processes. As recently argued regarding the role of theory in modeling-dominated climate science (85), a delicate balance between, and a skillful combination of, observations, theory, and application-driven simulations (be it through numerical modeling or network methods, or, rather, both) may provide the best path forward.

Then, there are some challenges related to the data itself: First, as an entirely data-dependent approach, network analysis may be subject to the underlying uncertainty in the data. Based on experience, the network-based schemes appear to be robust (see, e.g., ref. 32), and, in practice, data uncertainty might not be a significant issue. However, this remains to be studied systematically.

Another concern is how to incorporate multivariate datasets. Most current approaches construct climate networks by relying on a single physical quantity, for example, temperature or precipitation data. For instance, reanalysis datasets offer a wide range of physical quantities at each grid point. Exploiting multivariate networks, also called multilayer networks, can enable new ways for both understanding the underlying phenomena and finding improved prediction schemes.

New reanalysis data, for example, European Centre for Medium-Range Weather Forecasts Re-Analysis 5 (ERA5) (86), which create ensembles of plausible trajectories instead of only a single one, as previous products mostly did, may improve predictions, for example, when uncertain input data can be identified and possibly omitted or down-weighted. Also, robustness tests for the prediction methods to intraensemble uncertainties are now becoming feasible. Climate networks are often constructed only based on one assimilation product, often due to the lack of viable alternatives, and, in the future, systematic interdataset comparisons would be desirable.

Apart from these “data uncertainty problems,” there is also the case where there is not enough data available: For instance, how can the often short observational records be dealt with? This is especially relevant for extreme events, which are, by definition, rare, and only a few extreme events might be on record to validate more complex prediction models based on network characteristics. Possible solutions could be applying the prediction methods from network theory to the output of general circulation model (GCM) runs or validating on corresponding phenomena at different geographical locations. Additionally, long paleoclimatological records, for instance, tree-ring or coral-based reconstructions, could provide opportunities to validate complex prediction models. Finally, when looking into the future of the method itself, does climate change impact a forecasting scheme, and does it need to be extended accordingly, for example, by evolving networks? Statistical prediction methods, in general, entail stationarity assumptions, which may or may not be fulfilled in a changing climate, where unprecedented configurations could appear. Applying the prediction schemes to GCM future scenario outputs or an understanding of a method’s underlying processes could reveal whether and how schemes should be modified.

Most importantly, and despite all these standing challenges, network analysis can serve both as a toolbox to develop early-warning schemes as well as concrete leads or as a scientific inspiration for identifying physical mechanisms that relate spatially and/or temporally distant observations, where no connection was suspected before.

These first successes encourage us to invite the research community to intensively investigate the applicability of the network approach to climate dynamics, but also to other data-rich problems of a nonlocal nature. We are confident that, based on network approaches, critical advances are possible in the understanding and prediction of emerging phenomena, with topics ranging from jet stream dynamics, sea ice melting, and earthquakes to epidemics containment and physiological systems collapse.

Data Availability

There are no data underlying this work.