BLaDE: A Basic Lambda Dynamics Engine for GPU Accelerated Molecular Dynamics Free Energy Calculations

Abstract

There is accelerating interest in practical applications of alchemical free energy methods to problems in protein design, constant pH simulations, and especially computer-aided drug design. In the present paper we describe a Basic Lambda Dynamics Engine (BLaDE) that enables alchemical free energy simulations, including multisite λ dynamics (MSλD) simulations, on GPUs. We find that BLaDE is five to eight times faster than the current GPU implementation of MSλD-based free energy calculations in CHARMM. We also demonstrate that BLaDE running standard molecular dynamics attains efficiency approaching the highly optimized OpenMM GPU code. BLaDE is available as a standalone program and through an API in CHARMM.

1. Introduction

There is growing interest in the practical applications of alchemical free energy calculations for protein design,^1–6 constant pH simulations,^7–10 and especially computer-aided drug design.^11–14 Alchemical methods utilize molecular dynamics simulations to evaluate the relative free energy change of some physical process, such as ligand binding, upon a chemical perturbation to the system; this free energy can then be used to guide design by enhancing the binding affinity of a drug candidate. As alchemical methods have matured, and their applications become increasingly relevant, it is critical to have efficient software implementations to explore larger swaths of drug candidate chemical space or protein design sequence space. Ideally, such software solutions should take full advantage of recent hardware advances, including the advent of graphical processor units (GPUs).

Many alchemical free energy methods exist, including free energy perturbation (FEP),¹⁵ thermodynamic integration (TI),¹⁶ nonequilibrium methods,^17,18 enveloping distribution sampling,¹⁹ and multisite λ dynamics (MSλD).^20,21 MSλD is a uniquely efficient and scalable alchemical method, requiring fewer simulations per perturbation and scaling more readily to larger chemical spaces than traditional FEP or TI calculations. Due to the shorter history of MSλD, it has primarily been implemented in the CHARMM molecular dynamics software package,^22,23 though it can be implemented inefficiently in OpenMM through the application of custom potentials.²⁴ The most efficient implementation of MSλD within CHARMM is the GPU-enabled DOMDEC (domain decomposition) module.²⁵ DOMDEC was optimized to spatially parallelize large systems, with much larger atom counts than are typically encountered in MSλD simulations, into domains handled by many different CPUs. DOMDEC can offload the most expensive portions of the calculation, especially nonbonded interactions, to the GPU for additional performance gains, but is fundamentally a CPU-based code, requiring slow communication between the CPU and GPU every time step. While DOMDEC is well optimized to run large systems on CPU clusters, it does not scale efficiently to multiple GPUs for typical MSλD simulations and is rate limited by the SHAKE and update portions of the calculation that have not been offloaded to the GPU. Although significant work has gone into making the DOMDEC module efficient for alchemical free energy calculations, especially using MSλD, and MSλD has been demonstrated to provide significant gains over conventional free energy approaches,^{14,21,26–28} the overall performance of DOMDEC in alchemical simulations remains limiting, especially for large alchemical spaces that require extensive sampling.

To address this shortcoming, we have developed a Basic Lambda Dynamics Engine (BLaDE) to run MSλD simulations more efficiently on GPUs. Benchmarking runs demonstrate that BLaDE runs MSλD simulations five to eight times faster than the DOMDEC GPU module of CHARMM, depending on computational hardware and the molecular system. While BLaDE efficiency is unmatched for MSλD simulations, it also executes standard molecular dynamics around three times faster than DOMDEC with efficiency approaching that of the widely used molecular dynamics package OpenMM. We anticipate this improved efficiency will transform the scope of problems that can be addressed with alchemical free energy methods.

2. Implementation

Alchemical free energy methods utilize non-physical or alchemical transformations within molecular simulations to compute relative free energies. To evaluate the relative binding free energy of two candidate drug molecules, one can either take the difference of two physical processes (the binding of each molecule) or the difference of two alchemical processes (transforming from one molecule to the other in in both the bound and unbound physical ensembles).^29,30 For processes like binding that are slow on the time scale of typical molecular simulations, computing the physical free energy differences is impractical, while for reasonable perturbations up to at least a dozen heavy atoms, computing the alchemical free energy differences converges fairly rapidly.

Most alchemical free energy methods introduce an alchemical coupling parameter λ into the potential energy function U to accomplish the alchemical transformation, but vary widely in how this coupling parameter is used to compute free energy differences. More conventional methods like FEP run many simulations at fixed λ values, which simplifies implementing them in standard molecular dynamics packages. Others, like MSλD or nonequilibrium methods, require additional code to change λ during the simulation and evaluate alchemical forces on λ.

While most alchemical methods only consider pairwise transformations along a single dimensional λ variable, MSλD can achieve greater scalability by generalizing to a multidimensional alchemical λ space

$$U=U_0+\sum _{s=1}^M\sum _{i=1}^{N_s}{\lambda }_{si}{U}_{si}+\sum _{s=1}^M\sum _{t=s+1}^M\sum _{i=1}^{N_s}\sum _{j=1}^{N_t}{\lambda }_{si}{\lambda }_{tj}{U}_{si,tj}$$ (1)

where N_s different substituents at a site s each have their interactions U_si scaled by their respective λ_si values, and interactions U_si,tj between M different sites are scaled by the product of their λ_si and λ_tj values.²¹ The ability to make perturbations at multiple sites allows chemical spaces of hundreds^5,14,27 or thousands⁶ of molecules to be explored with a single pair of simulations.

BLaDE was designed to run MSλD efficiently on GPUs. In order to overcome the limitations inherent in the implementation of DOMDEC in CHARMM, the entire calculation is performed on the GPU both to minimize slow CPU computation and costly data transfer between the CPU and GPU, mirroring the approach of OpenMM²⁴ and Amber thermodynamic integration.^31,32 Details of the implementation are described below.

2.1. BLaDE Interface

BLaDE has been implemented as a CUDA and C++ program that can be called from CHARMM through an API and also as a standalone executable. Running the implementation of BLaDE in CHARMM only requires a command to turn BLaDE on after using CHARMM functionality to set up the molecular system and establish potential energy partitioning for free energy calculations. Running standalone BLaDE requires an interface to set up the simulations. One of the strengths of CHARMM is its scripting language that allows complex calculations, therefore a limited scripting language allowing script control flow, variable definitions, mathematical calculations, and atom selections was designed for standalone BLaDE. Functions for setting up structures and topologies were not implemented in BLaDE, instead BLaDE reads the topology from a PSF file generated by CHARMM and the coordinates from a PDB or CRD file. Force field parameters are read from standard CHARMM PRM files.

2.2. Architecture

In BLaDE, force calculations are broken up into four different streams to allow concurrency: bonded interactions, reciprocal nonbonded interactions that account for the Fourier space portion of particle mesh Ewald (PME) electrostatics,^10,33,34 MSλD specific biases, and direct (spatial) nonbonded interactions. In the CUDA paradigm, kernels may be thought of as functions that execute serially within a stream. Placing independent kernels in different streams allows them to execute concurrently to enable more efficient use of the GPU. Figure 1 illustrates the tasks performed by these four streams, along with the update stream, which are described in more detail in subsequent sections.

Figure 1:

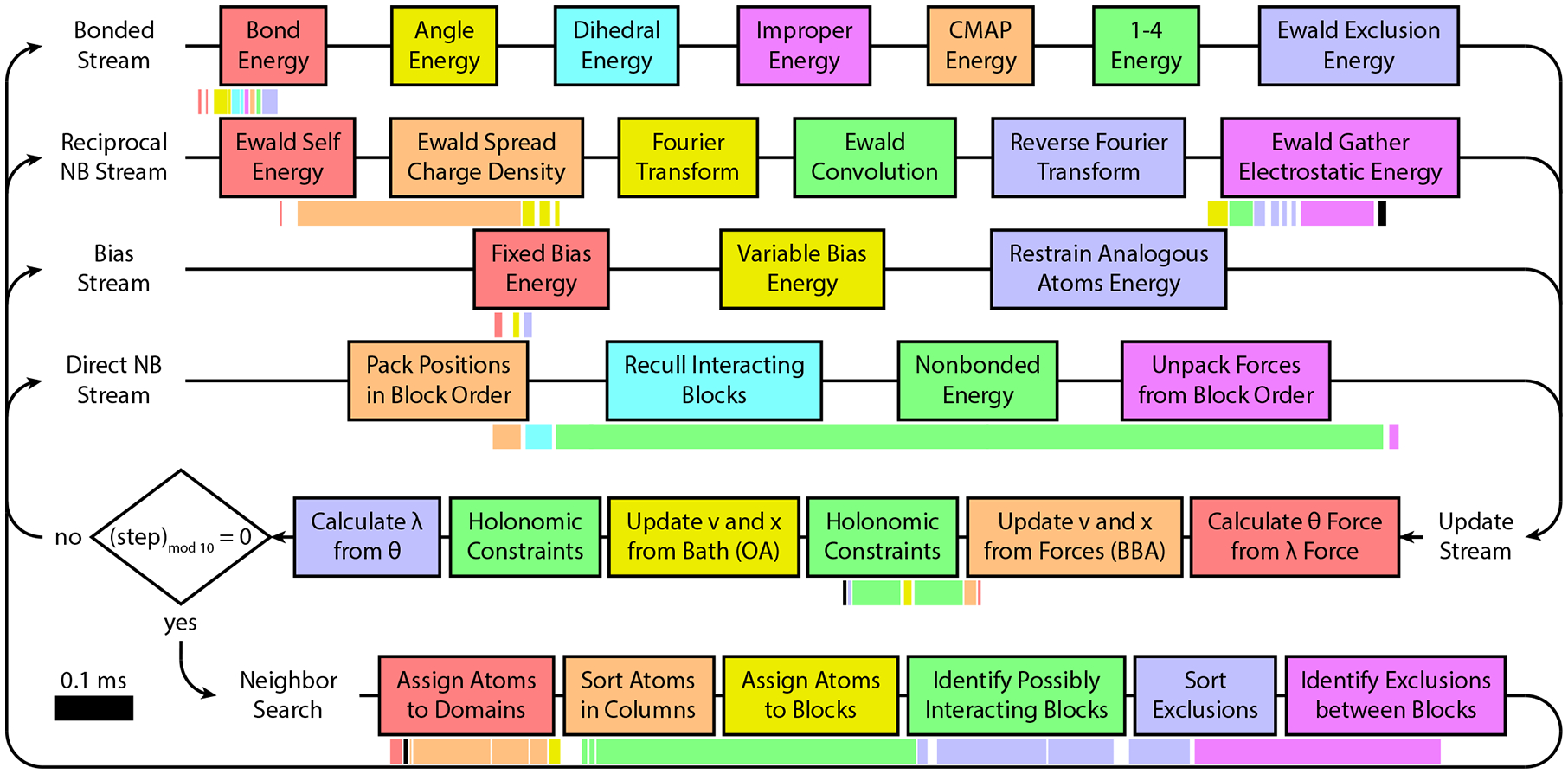
BLaDE flowchart. The force calculation is broken into four independent streams as shown, followed by update and occasionally by neighbor search. Individual tasks are shown in boxes, and may involve one or several kernels. Below each stream, the execution time for individual kernels is shown to scale for the RNase H test system on a GTX 1080 Ti GPU. Kernels are color coded to match the task in the stream above them, black kernels are unmentioned minor tasks such as rounding from double to single precision, and the kernels of the four force calculation streams are aligned so that kernels directly above and below each other executed concurrently. OA and BBA in the update stream refer to specific portions of the g-BAOAB update.³⁵

BLaDE can run on a single GPU, or can run on multiple GPUs on the same node using OpenMP parallelization to coordinate GPU work. BLaDE was optimized for GeForce GPUs due to their low cost, but is expected to perform comparably on data center GPUs, except with faster communication between GPUs on the same node. During molecular dynamics calculations, at least some forces and updated positions must be communicated between GPUs on every time step. On current GPUs the system sizes typically encountered in alchemical calculations are not large enough to cover the costs of MPI communication between GPUs on different nodes. Because of the small number of GPUs on a single node, a relatively simple domain decomposition is sufficient. Update of all coordinates is performed on the head GPU, all positions are passed to the other GPUs, and all forces are passed back to the head GPU. Direct nonbonded forces constitute the largest portion of the computational expense (Figure 1), and are split between GPUs by one dimensional domain decomposition. For two GPUs, the head and second GPU each take a slab, and the second GPU also takes all bonded calculations. For calculations utilizing more GPUs, the head GPU does not take a slab. All other force components are handled by the head GPU. Thus, BLaDE can be thought of as a single GPU program that can offload some work to other GPUs for modest performance gains rather than a fully parallel code. A more sophisticated parallelization scheme may provide further performance gains, but the high cost of communication between GPUs means these gains are likely to be modest; on two RTX 2080 Ti GPUs, 24% of time is spent on communication for the RNase H test system described below.

2.3. Bonded Stream

Other GPU implementations have placed all bonded interactions within a single kernel to reduce kernel launch latency,³⁶ however in the present case we opt for simpler code, and hide most of this latency behind concurrency, allowing other streams of the force calculation to do their work. In addition to the standard bonded kernels for bonds, angles, dihedrals, improper dihedrals, and cross torsion CMAP terms,^37,38 kernels for breaking these bonded terms with soft bonds^39,40 were also implemented, along with nonbonded 1–4 interactions and PME exclusions.^10,33,34 These kernels include additional parameters and complexity for the calculation of alchemical forces, which would render packing them together unwieldy.

2.4. Reciprocal Nonbonded Stream

PME electrostatics are used to treat long range electrostatic forces accurately, and do so by splitting the long range electrostatic potential into a short range piece that can be computed with neighbor lists and cutoffs, and a smoothly varying piece that can be calculated in Fourier or reciprocal space.^33,34 The reciprocal space component involves a spread function to interpolate charges onto a charge density grid, a convolution using Fourier transforms, and a gather function to interpolate the potential and electric field at a point from the grid. Using PME with MSλD is nontrivial, and we follow the approach of Shen and coworkers by scaling the charge of each particle by its λ value.^5,10 Due to the artifacts caused by truncating the dispersion potential, there is a growing push to treat van der Waals interactions with Ewald summation, and the kernels described below should be easily adapted to this purpose in the future.^34,41–43

PME interpolation orders of 4, 6, and 8 are supported in BLaDE. The self energy term must be computed during every step because charges are scaled by λ; fortunately the kernel is simple and fast. NVIDIA GPUs group work into blocks of communicating threads. At the hardware level, groups of 32 threads, called warps, execute instructions simultaneously. The PME spread and gather kernels each use 8 threads per atom, allowing 4 atoms per warp. Each thread communicates with its neighbors using shuffle operations to determine the B-spline coefficients in each of the three dimensions, with extra threads remaining idle if the interpolation order is less than 8. Shuffle operations allow a thread to read the memory register of another thread in the warp with lower latency than most other memory reads. The 8 spread threads then work together to add the charge of this atom to the PME grid affected by an atom in 2 × 2 × 2 chunks using shuffle to read the B-spline coefficients from the relevant threads. The 8 gather threads read in the potential grid as a texture in 2×2×2 chunks and then reduce using shuffle operations. An alternative approach assigning each atom a number of threads equal to the interpolation order was also implemented, and performed comparably on the spread kernel, but was substantially slower for the gather kernel. Fourier transforms utilized the standard cuFFT library, and the convolution kernel is straightforward with each thread managing one complex grid point.

2.5. Bias Stream

Several MSλD specific biases and methods are implemented as GPU kernels within their own stream, including the linear fixed biases on λ,^26,44 variable biases,^5,44 and scaling of restrained analogous atoms.⁴⁰ These biases are simple and not rate limiting.

2.6. Direct Nonbonded Stream and Neighbor Search

The direct bonded interactions include both van der Waals terms, which utilize force switching equation 10 from reference 45, as well as the short range portion of the PME coulomb interaction, both optionally modified by a soft core potential⁴⁴ to prevent simulation instabilities and free energy estimator errors when λ is close to zero. These interactions are conventionally treated with a neighbor list because interactions beyond a certain cutoff distance are negligible. Because fetches and writes to and from global memory are slow on a GPU, atoms are grouped into blocks of 32 atoms, and for a pair of interacting blocks, all 32 × 32 interactions can be computed by a warp of 32 threads, each of which only needs to fetch coordinates and write forces for one atom of the block. The direct nonbonded calculations thus require kernels to group atoms into blocks and identify interacting blocks during neighbor searches, and kernels to compute interactions between blocks during force calculation.

In order to avoid neighbor searching every step, a buffer region beyond the cutoff is set for twice the distance a hydrogen atom with 30kT of kinetic energy can travel ballistically in 10 time steps, which prevents atoms from getting close enough to interact with atoms not on their neighbor lists before the next neighbor search. Neighbor searching is implemented entirely on the GPU to avoid slow transfers between CPU and GPU memory. The box is divided into domains that are slabs in the z direction for each GPU, and the head GPU translates diffusing atoms back into the unit cell, identifies which slab each atom is in, and then sends the domain assignments to each GPU. Atoms are then grouped into discrete columns within a domain. The width of each column in the x and y dimensions is chosen to match the size of a cube containing 32 atoms at the average number density of the box, rounded down to evenly divide the domain. Atoms are then sorted using a tree sort kernel by the x and y index of the column, and then by the z coordinate, and blocks are read off from consecutive groups of atoms, starting a new block when a column ends. Hydrogens can end up in different slabs or different blocks than their heavy atom if geometry dictates. Positions and nonbonded properties are then packed into this new atom order to enable more efficient coalesced reads from kernels acting on the block.

Potentially interacting blocks are identified and stored in a neighbor list. In order to facilitate rapidly checking distances between whole blocks rather than individually checking all their particles, tight bounding boxes are defined by the maximum and minimum x, y, and z coordinates of any atom in the block, and two blocks are stored in the neighbor list if the closest two points between tight bounding boxes are within a distance of the cutoff plus the buffer. Eight warps of 32 threads each search for partners for 8 blocks together. If a particular domain or its periodic image is too far away from the box bounding all eight blocks, that domain is not searched for partners, which resulted in a factor of three improvement in the kernel execution time in one test. Within a domain, the 32 threads per block screen potential partner blocks in groups of 32, and record any hits in a candidate list. Nonbonded exclusions are renumbered to match the sorted order of the atoms, and then exclusions are tree sorted with a kernel for easy lookup. A kernel then notes any exclusions between each candidate pair of blocks.

During force calculation, the positions of the particles must be packed into the order of the blocks, and then a fast kernel re-culls the candidate list of interacting blocks to only include blocks within the cutoff, rather than the cutoff plus the buffer, which saves substantial time during the nonbonded kernel. The nonbonded kernel computes interactions between a particular block i and all partner blocks j. Each thread loops through j atoms and computes interactions of its own i atom with the same j atom simultaneously. If the j atom is too far from the box bounding block i, it is skipped. Because each thread treats the same j atom simultaneously, spatial and alchemical forces are reduced with shuffle operations. Previous studies have used different kernels for blocks with few j atoms, where the extra effort to reduce forces is worthwhile, and blocks with a nearly full complement of 32 atoms where the reduce operation can be avoided by staggering.⁴⁶ We tried several more sophisticated kernels, but found the simple reduction approach was best, suggesting the efficiency of reduction operations has improved (see Supporting Information for details). After direct nonbonded forces are computed, they are reordered from block order back into the original order of atoms, then transferred back to the head GPU and reduced.

2.7. Update

The update step consists of utilizing the spatial and alchemical forces to update atom positions and alchemical coordinates. Within CHARMM this requires enforcement of holonomic bond length constraints,^47–51 and for constant volume simulations can use a Langevin or Nose-Hoover thermostat^52–54 to maintain temperature, or in constant pressure simulations uses a Nose-Hoover thermostat and Langevin Piston barostat.⁵⁵ Within BLaDE, the thermostat and barostat were chosen to optimize the efficiency of the update step while maintaining thermodynamic rigor.

Simulations utilize a Langevin thermostat. Integration followed the g-BAOAB procedure (where B is a kick due to the force, A is linear drift, and O thermalizes the momentum) utilized by OpenMM, which has been shown to capture spatial configuration properties well.³⁵ In this case holonomic bond length constraints were maintained with SHAKE,^47–49 and we utilized fast SHAKE,⁵¹ which reduces the number of SHAKE iterations by updating connected holonomic constraints together. Different kernels were written for heavy atoms bonded to one, two, or three hydrogen atoms. For rigid three site water models such as TIP3P, all three atoms are connected in a rigid body by three bonds, and a kernel implementing the analytical, non-iterative SETTLE algorithm was written.⁵⁰ These four kernels were packed into a single kernel to hide kernel launch latency and GPU underutilization due to serial execution. The positions are updated in double precision and then rounded to single precision for force calculations because rounding errors in single precision positions led to drift in the velocity when positions were used to calculate the SHAKE Lagrange multipliers for velocity update (λ_RR in equation A4 of reference 49 or λ in the appendix of reference 35). We also note that zeroing the component of the velocity perpendicular to the constraints is superfluous, because either way SHAKE will correct the positions to the same values, which will backcorrect the velocities to the same values. Therefore, for efficiency, velocities are only corrected to be perpendicular to the constraints when the kinetic energy is evaluated.

The Langevin piston barostat utilized by CHARMM was undesirable for two reasons. First, solving the equations of motion with holonomic constraints requires calling SHAKE three times per time step to ensure the volume, virial, and bond constraints are all consistent. Second, the barostat requires extra work in most kernels to compute the virial, including the slow direct nonbonded kernel. Instead, we utilize the Monte-Carlo barostat,^56,57 the same solution utilized by OpenMM. The Monte-Carlo barostat does not require computation of the virial, and instead relies on an additional energy evaluation for a trial volume change. The frequency of the trial volume change can be reduced to the point that it introduces negligible computational effort. BLaDE uses a different procedure than OpenMM to scale positions during the volume change. In OpenMM, only the centers of mass of each molecule are scaled, while the absolute size of each molecule is unscaled. The N in the Monte Carlo acceptance criteria is then the number of molecules. In contrast, in BLaDE, all spatial coordinates are scaled with the volume, and then the holonomic constraints are rectified by moving the hydrogens closer or further from the fixed heavy atom. In this context, N is the number of heavy atoms; each atom or holonomically restrained cluster acts as a separate molecular entity. Numerical experiments revealed that this approach had the same system volume distribution as the CHARMM Langevin piston.

3. Results

It is necessary to test the accuracy of BLaDE, to ensure results are reliable, as well as its computational efficiency, to determine the speedups that may be obtained. Accuracy and efficiency are each described in turn.

3.1. Accuracy

The most basic test of accuracy requires that energies and forces in BLaDE are consistent with each other and match the implementation of DOMDEC in CHARMM for the same configuration. After ensuring this condition was met, the accuracy of the implementation was assessed using two other metrics. First, energy conservation and numerical stability of the g-BAOAB integrator were evaluated and compared with published results. Second, free energies were computed with BLaDE and with DOMDEC and checked for consistency.

Energy conservation in the NVE ensemble can reveal errors in the implementation. Two systems, a cubic, periodic box of 216 TIP3P water molecules,⁵⁸ and the standard DHFR benchmark system were checked for energy conservation. After an initial NVT equilibration, the NVE ensemble was simulated by turning off pressure coupling and setting the Langevin friction coefficient to 0. See Supporting Information for simulation conditions. With SHAKE and a 2 fs time step, energy drift in the water box averaged −4.3 × 10⁻⁴ kT/ns/dof (dof is degree of freedom) with a standard deviation of 9.8 × 10⁻⁴ kT/ns/dof over ten 1 ns trials. Energy drift in DHFR was 1.9 × 10⁻⁵ kT/ns/dof with a standard deviation of 5.8 × 10⁻⁵ kT/ns/dof. These levels of drift compare favorably with other reports from the literature; for DHFR, GROMACS reported an absolute energy drift of 0.005 kT/ns/dof for a 2.5 fs time step,⁵⁹ and for a different protein system, OpenMM reported an absolute energy drift between 0.06 and 0.006 kT/ns/dof for a 1 fs time step, depending on the SHAKE tolerance.³⁶

Previous studies have revealed the high stability of the g-BAOAB integrator, which is stable to a time step of 10 fs for the water box, and to a time step of 4 fs for a solvated peptide system.³⁵ Furthermore, the average potential energy of the g-BAOAB integrator at constant temperature has the desirable property of being constant with respect to time step, which affords another check for correctness. Indeed, BLaDE is numerically stable out to the expected time steps of 10 fs for the water box and 4 fs for DHFR, and the average potential energy is nearly constant with respect to time step (Figure 2).

Figure 2:

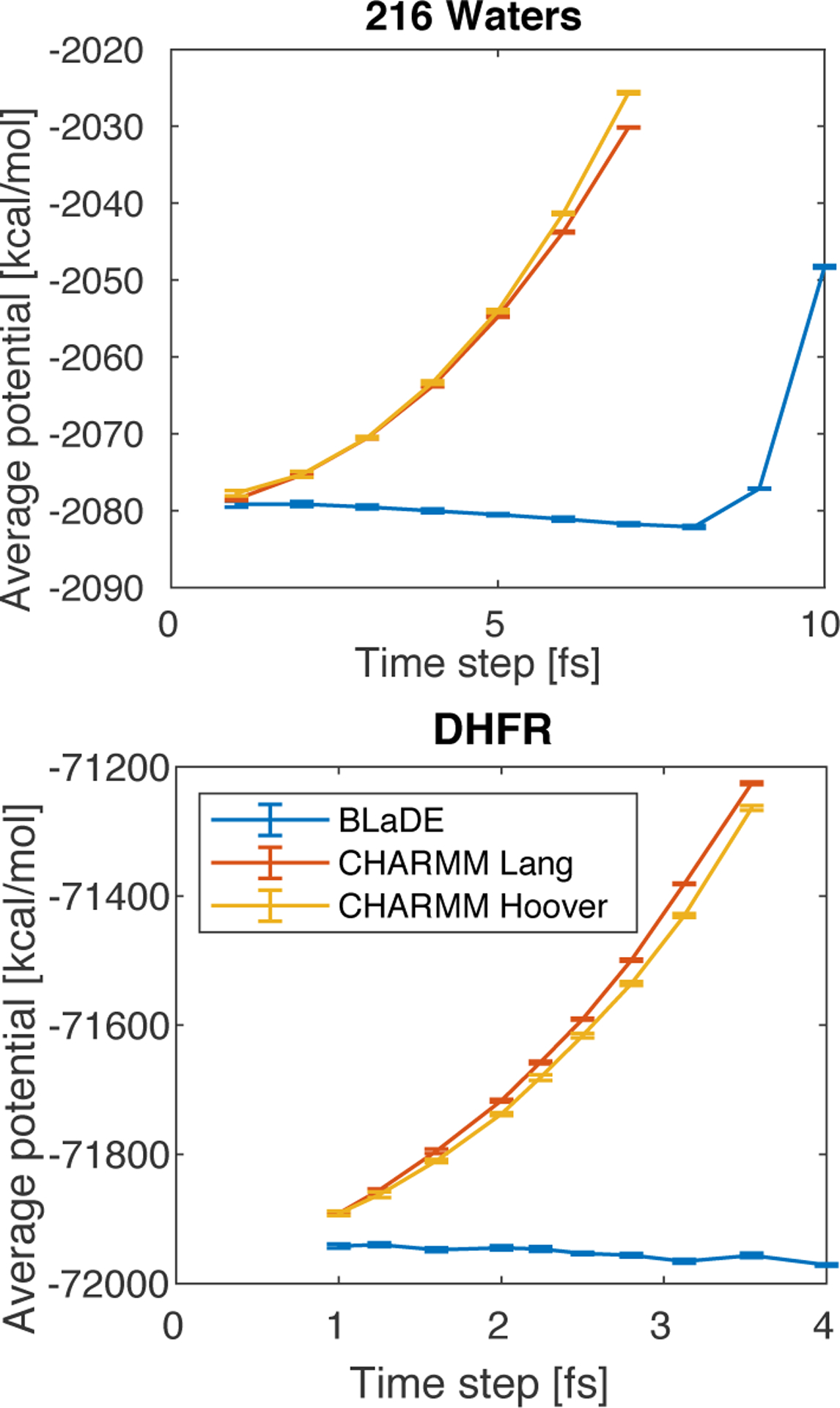
The g-BAOAB integrator implemented in BLaDE is stable to a time step of 10 fs in pure water and a time step of 4 fs in protein systems, and the average potential energy in nearly independent of time step, as expected from previous studies.³⁵

Free energies were evaluated for three systems with BLaDE and DOMDEC in CHARMM to ensure the programs give consistent free energies to within statistical noise. Systems spanning the gamut of MSλD applications were chosen, including both simple and challenging protein mutations as well as ligand perturbations. The L99, M106, V149, and F153 side chain mutation sites previously studied with MSλD in T4 lysozyme (T4L) were again examined with 5 independent trials of 40 ns at each of the 4 sites.⁵ These sites explored 6, 6, 3, and 6 sequences, respectively, for a total of 18 unique sequences (each site included the native sequence). As a more challenging protein perturbation system, a previously studied set of 2¹⁵ = 32768 combinatorial ribonuclease H (RNase H) sequences were examined in 12 trials of 400 ns each, comparing only the free energies from the folded ensemble.⁶ Finally, the HSP90–1 system of 30 ligands binding to heat shock protein 90 (HSP90) was taken from reference 14 as an example of ligand perturbation, and studied in 5 trials of 30 ns each.

Results in Table 1 reveal that BLaDE gives consistent free energies with DOMDEC in CHARMM. A DOMDEC run was used as a reference, and DOMDEC and BLaDE runs were compared to it using the centered root mean square (RMS) difference (〈Δx²〉 − 〈Δx〉²)^1/2. The difference between a second DOMDEC run and the reference reveals the expected level of statistical deviation. Standalone BLaDE and the implementation of BLaDE in CHARMM are expected and observed to give statistically identical results to each other. The slightly larger differences between BLaDE and DOMDEC observed in HSP90 may occur because the different integrator, thermostat, and barostat affect how the system relaxes to equilibrium. Table S1 in the Supporting Information reveals comparable agreement with experiment for all systems. While the correctness of BLaDE is determined by its ability to reproduce the correct result for the force field, and not necessarily the experimental value, closer agreement with experiment suggests lower sampling errors, because sampling errors and forcefield errors are typically independent. Thus BLaDE gives comparable results to the implementation of DOMDEC in CHARMM.

Table 1:

RMS Differences of MSλD Free Energies from a Reference Simulation^a (kcal/mol)

	T4L	RNase H	HSP90
	Protein MSλD	Protein MSλD	Ligand MSλD
Standalone BLaDE	0.20	0.33	0.42
BLaDE in CHARMM	0.22	0.38	0.34
DOMDEC in CHARMM	0.16	0.36	0.25

^aCompared to a reference simulation in DOMDEC in CHARMM

3.2. Efficiency

To assess the computational efficiency of BLaDE, benchmark simulations were run on DHFR to test its efficiency for standard molecular dynamics simulations, and on the three alchemical systems used to compare free energy results with DOMDEC in CHARMM, specifically the folded side of the T4L L99 mutations, the folded side of RNase H, and the complex side of the HSP90 ligand perturbations. These systems were run with varying numbers of GPUs in standalone BLaDE and the implementation of BLaDE in CHARMM, and compared to the implementation of DOMDEC in CHARMM. Because DOMDEC in CHARMM is CPU limited, it is sensitive to the number of OpenMP threads employed. Four OpenMP threads per GPU were used for DOMDEC in CHARMM because this provides near optimal throughput on our computational resources; all other methods used one OpenMP thread per GPU. Comparison with the implementation of OpenMM in CHARMM was also performed for the DHFR system where possible. Three different hardware configurations were tested: GTX 980 Ti GPUs on Intel Xeon E5–2650 v3 CPUs, GTX 1080 Ti GPUs on the same CPUs, and RTX 2080 Ti GPUs on Intel Xeon Gold 6242 CPUs.

The speeds for various hardware, software, and molecular system choices for simulations run with a time step of 2 fs are shown in Table 2. BLaDE is 5–8 times faster than DOMDEC in CHARMM for alchemical systems on the GTX 1080 Ti and RTX 2080 Ti GPUs. For the non-alchemical system DHFR, BLaDE is only marginally slower than OpenMM, which has been extensively optimized for GPUs, but has less of a performance advantage over DOMDEC. This is in part because alchemical benchmarks used pressure coupling and DHFR did not. The use of the Langevin piston barostat slows DOMDEC by a factor of 1.4, but has a negligible effect on BLaDE and OpenMM because they use a Monte Carlo barostat. The shorter cutoffs and lower interpolation order used in DHFR also reduce the performance gain observed with BLaDE.

Table 2:

Computational Efficiency Benchmarking Results (ns/day)

	DHFR	T4L	RNase H	HSP90
	MD	Protein MSλD	Protein MSλD	Ligand MSλD
Atoms	23558	37723	43002	26685
λ dimensions	0	6	30	11
Standalone BLaDE (1 GTX 980 Ti)	96.1	43.1	38.0	57.7
Standalone BLaDE (2 GTX 980 Ti)	139.3	62.7	55.7	80.1
Standalone BLaDE (4 GTX 980 Ti)	164.2	93.1	81.6	120.1
BLaDE in CHARMM (1 GTX 980 Ti)	94.0	41.5	36.7	53.6
BLaDE in CHARMM (2 GTX 980 Ti)	134.1	59.3	52.1	77.9
DOMDEC in CHARMM (1 GTX 980 Ti)	50.2	16.4	13.9	22.4
OpenMM in CHARMM (1 GTX 980 Ti)	116.7	-	-	-
Standalone BLaDE (1 GTX 1080 Ti)	210.3	102.2	89.2	133.8
Standalone BLaDE (2 GTX 1080 Ti)	285.9	142.9	128.6	177.8
Standalone BLaDE (4 GTX 1080 Ti)	276.6	168.4	153.0	206.8
BLaDE in CHARMM (1 GTX 1080 Ti)	199.9	93.2	84.1	116.0
BLaDE in CHARMM (2 GTX 1080 Ti)	275.8	128.7	116.6	156.8
DOMDEC in CHARMM (1 GTX 1080 Ti)	62.4	19.4	15.0	25.7
OpenMM in CHARMM (1 GTX 1080 Ti)	216.8	-	-	-
Standalone BLaDE (1 RTX 2080 Ti)	250.6	150.0	136.7	187.7
Standalone BLaDE (2 RTX 2080 Ti)	271.5	186.1	170.8	234.9
Standalone BLaDE (4 RTX 2080 Ti)	228.7	177.3	157.4	210.8
BLaDE in CHARMM (1 RTX 2080 Ti)	240.5	135.5	124.4	167.8
BLaDE in CHARMM (2 RTX 2080 Ti)	265.7	168.5	157.5	198.3
DOMDEC in CHARMM (1 RTX 2080 Ti)	89.7	26.9	21.0	35.0
OpenMM in CHARMM (1 RTX 2080 Ti)	335.6	-	-	-

Across all four benchmark systems, the primary factors controlling relative performance of the various software implementations are the relative speed of the GPU and CPU and the cost of communication. The ratio of GPU speed to CPU speed is greatest on the GTX 1080 Ti GPUs, and least on the GTX 980 Ti GPUs, because the faster RTX 2080 Ti GPUs also have faster CPUs. Because BLaDE and OpenMM are GPU limited and DOMDEC in CHARMM is CPU limited, BLaDE exhibits the largest performance gains relative to DOMDEC on GTX 1080 Ti GPUs. Communication is relatively least expensive on the GTX 980 Ti GPUs because calculations are slower, and most expensive on the RTX 2080 Ti GPUs because calculations are faster and because the NVIDIA disabled direct peer to peer GPU communication without an NVLink cable on the RTX 2080 Ti GPUs. Consequently, BLaDE benefits substantially from parallelization on GTX 980 Ti GPUs and negligibly on RTX 2080 Ti GPUs.

4. Discussion and Conclusions

The nearly order of magnitude increase in MSλD efficiency that BLaDE enables transforms what is possible with MSλD. Not only can more systems be studied on limited resources, but more ambitious studies on larger alchemical spaces or more slowly relaxing systems that require longer sampling periods become feasible.

Several new applications open up in the field of protein mutations. A recent MSλD study of RNase H explored simultaneous mutations at 15 sites for protein design.⁶ A few 100 ns simulations were insufficient to characterize this large space of 32768 sequences, and many 400 ns simulations were required to obtain robust results. The runtimes for these simulations were about a month on a GTX 1080 Ti, but with BLaDE they could be completed in less than four days on two GTX 1080 Ti GPUs, or less than three days on one RTX 2080 Ti. The increased efficiency of BLaDE makes such applications routine, and opens the way for even larger sequence spaces to be investigated. In the case of point mutations, several sites have been examined in T4 lysozyme,⁵ but the substantial increase in efficiency brings studies of every possible point mutant in a protein within reach.⁶⁰

In the context of using MSλD to predict ligand affinity for computer-aided drug design, there is clear evidence that alchemical methods provide value in drug discovery, and that the computational efficiency to screen thousands of compounds is necessary.^12,61,62 Computing the affinity of the 30 HSP90 ligands required about 210 GPU hours with DOMDEC in CHARMM on GTX 1080 Ti GPUs, but could be accomplished in about 40 GPU hours with BLaDE on the same hardware. Likewise, recent large scale MSλD studies could be completed with substantially less computational effort.¹⁴

Finally, the availability of BLaDE within the CHARMM molecular dynamics package should make it more immediately accessible to users. This accessibility together with the substantially improved computational efficiency of BLaDE should open up new applications of MSλD.