Optical tweezers in single-molecule biophysics

Abstract

Optical tweezers have become the method of choice in single-molecule manipulation studies. In this Primer, we first review the physical principles of optical tweezers and the characteristics that make them a powerful tool to investigate single molecules. We then introduce the modifications of the method to extend the measurement of forces and displacements to torques and angles, and to develop optical tweezers with single-molecule fluorescence detection capabilities. We discuss force and torque calibration of these instruments, their various modes of operation and most common experimental geometries. We describe the type of data obtained in each experimental design and their analyses. This description is followed by a survey of applications of these methods to the studies of protein–nucleic acid interactions, protein/RNA folding and molecular motors. We also discuss data reproducibility, the factors that lead to the data variability among different laboratories and the need to develop field standards. We cover the current limitations of the methods and possible ways to optimize instrument operation, data extraction and analysis, before suggesting likely areas of future growth.

Single-molecule methods were born out of the desire to follow the dynamics of molecular processes in real time and the impossibility of synchronizing the behaviour of molecules in an ensemble. Most biomolecular processes are thermally activated and subjected to the stochastic nature of molecular collisions from the thermal bath. As a result, attempts to follow the time course of a molecular process necessarily contain the asynchronous contributions of all molecules in the ensemble, which yield at best an unphysical ‘average’ of their behaviour. By contrast, monitoring the time evolution of single molecules as they undergo chemical or biochemical reactions makes it possible to characterize their ‘molecular trajectories’, at the price of obtaining data often dominated by noise from which the signals must be extracted. Once this is done, however, it is frequently possible to gain a greater degree of mechanistic insight into the underlying molecular process than from the average molecular behaviour derived from bulk or ensemble measurements.

Optical tweezers are a method to exert forces or torques on individual molecules and/or to directly measure the forces or torques generated in the course of their biochemical reactions. In 1970, Arthur Ashkin exploited the fact that photons carry momentum to entrain and transport micron-sized latex spheres suspended in water using laser beams¹. In 1986, Ashkin et al. demonstrated for the first time the single-beam ‘optical trap’ or ‘optical tweezers’ when they showed that light focused tightly can be used to hold and maintain microscopic particles stably in all three dimensions². One year later, Ashkin et al. showed that it was possible to use optical tweezers to trap and manipulate bacteria and red blood cells, as well as organelles inside cells³. Optical tweezers also yield the changes in displacement that accompany the application (or generation) of forces and torques. Accordingly, these experiments permit direct access to the work done on (or by) the system of interest. Other methods have been used to accomplish these same tasks, such as atomic force microscopy and magnetic tweezers⁴. Atomic force microscopy affords higher forces (>100 pN), whereas magnetic tweezers are better suited for low-force applications (sub-piconewtons). However, in some single-molecule applications, atomic force microscopy can be limited by its force resolution; magnetic tweezers, although affording the simultaneous manipulation of many molecules on a surface, have lower spatial and temporal resolution when compared with optical tweezers⁴. Therefore, because of their force (or torque), spatial and temporal resolution, and versatility and dynamic range, optical tweezers are the method of choice in many biophysical applications.

Photons carry energy, as well as linear and angular momentum. When an object encounters a beam of light, there are two forces exerted by the light on the object: the gradient force and the scattering force. We first define the gradient force F_grad. For objects much smaller than the wavelength of light, the object behaves as a Rayleigh scatterer whose response to an electric field is characterized by a polarizability α (assumed here to be real). The electric field of light at position $\stackrel{\rightharpoonup }{r}$ where the object is located, and at time t, $\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)=\text{Re}\left[{\stackrel{\rightharpoonup }{E}}_0(\stackrel{\rightharpoonup }{r}){\text{e}}^{i\omega t}\right]$ (where ${\stackrel{\rightharpoonup }{E}}_0(\stackrel{\rightharpoonup }{r})$ is the amplitude of the electric field) induces an electric dipole moment $\stackrel{\rightharpoonup }{\mu }(\stackrel{\rightharpoonup }{r},t)=\alpha \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)$ in the object. The energy (U) of the induced dipole in the electric field is then: $U=-\stackrel{\rightharpoonup }{\mu }(\stackrel{\rightharpoonup }{r},t)\cdot \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)=-\alpha \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)\cdot \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)$. The intensity of a laser beam is proportional to the square of the amplitude of its electric field. Accordingly, the energy of the dipole attains a minimum at the place where the intensity of the beam is a maximum. Therefore, if the field is not homogeneous, as is the case with a Gaussian laser beam, the dipole will experience a force attracting it towards the higher intensities of the beam; this force is proportional to the gradient of the light intensity (I) and tends to minimize the induced dipole’s energy⁵:

$$\begin{gathered} {\stackrel{\rightharpoonup }{F}}_{\text{grad}}=-\langle (-\alpha \stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)\cdot \nabla )\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r},t)\rangle \\ =\frac{\alpha }{2}\nabla \langle E^2(\stackrel{\rightharpoonup }{r},t)\rangle \\ =\frac{\alpha }{4}\nabla \left|E_0^2\right| \\ =\left(\alpha /2c{n}_{\text{m}}{\epsilon }_0\right)\nabla I \end{gathered}$$ (1)

where 〈〉 denotes the time average, c the speed of light in vacuum, n_m the index of refraction of the particle and ε₀ the permittivity of vacuum. Here, we have used the fact that $\langle E^2(\stackrel{\rightharpoonup }{r},t)\rangle =(1/2)\left|E_0^2\right|$ to write the intensity of the beam as $I=(1/2)c{n}_{\text{m}}{\epsilon }_0\left|E_0^2\right|$. This is the ‘gradient force’. For particles with positive polarizability (for example, when the polarizability of the particle is greater than that of the surrounding medium), this force attracts the particle towards the higher intensities of the light.

We now define the scattering force F_scat. Particles will also experience a force due to the absorption, and the scattering (refraction or reflection) of light. The scattering force for a Rayleigh particle can be written as:

$${\stackrel{\rightharpoonup }{F}}_{\text{scat}}=\frac{n_{\text{m}}{\sigma }_{\text{ext}}}{c}\langle {\stackrel{\rightharpoonup }{S}}_i\rangle =\frac{n_{\text{m}}\left({\sigma }_{\text{abs}}+{\sigma }_{\text{scat}}\right)}{c}\langle {\stackrel{\rightharpoonup }{S}}_i\rangle$$ (2)

where σ_ext is the extinction cross-section of the particle with an absorption (σ_abs) and a scattering (σ_scat) contribution, and $\langle {\stackrel{\rightharpoonup }{S}}_i\rangle$ is the time-averaged Poynting vector of the beam, which points in the direction of the propagation of the light and has units of energy per unit area, per unit time. As shown in FIG. 1a, for a Rayleigh particle present in a focused laser beam, the gradient force tends to attract the particle towards the axis of the beam and towards the focus, thus counteracting the effect of the scattering force that tends to push the particle in the direction of the incident light.

Fig. 1 |. Principles of optical tweezers.

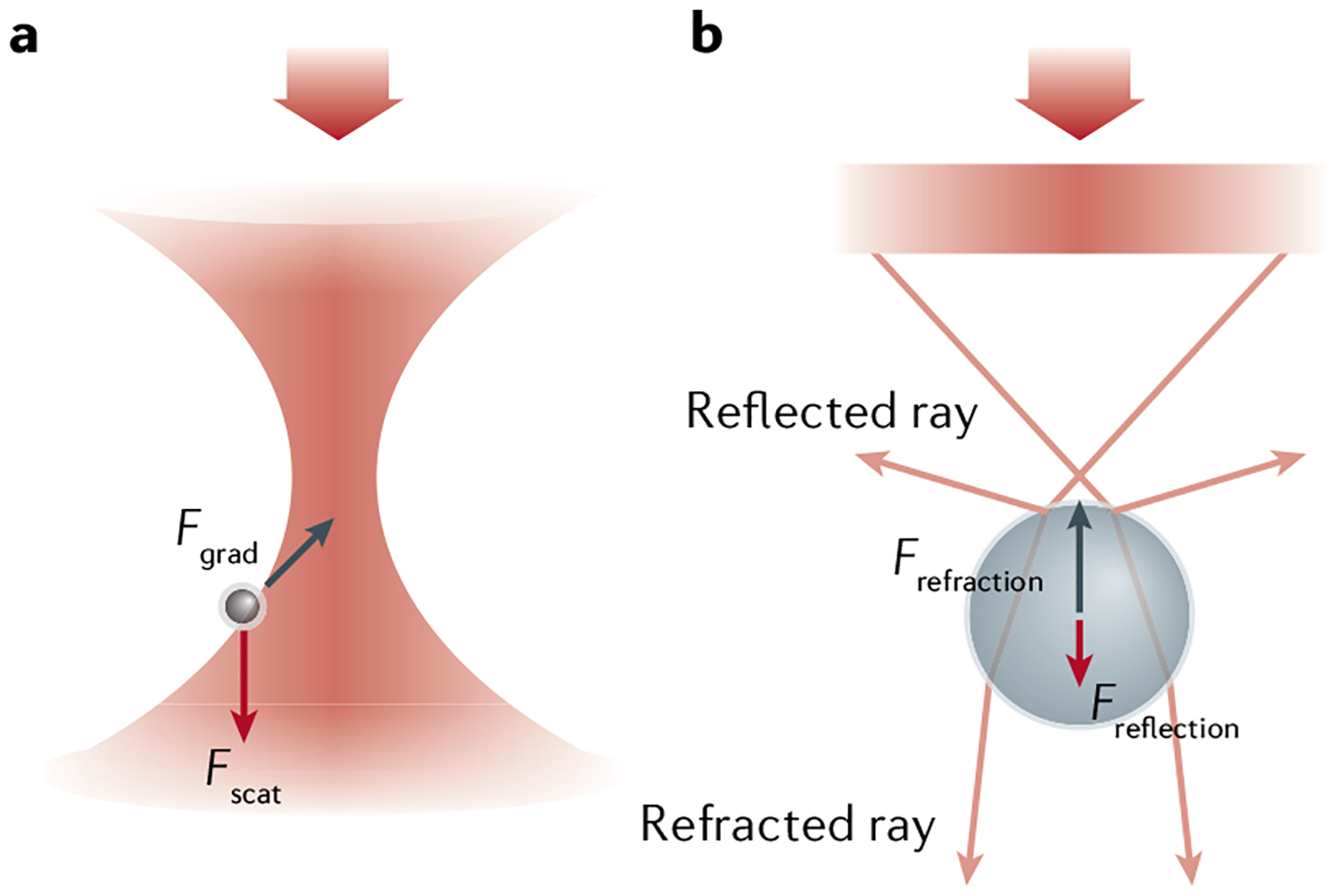
Forces acting on a dielectric sphere interacting with light, with the incident light beam focused by a high-numerical aperture (NA) lens. a | A Rayleigh particle smaller than the wavelength of light experiences a scattering force (F_scat, red arrow) that pushes the particle along the direction of propagation of the light and a gradient force (F_grad, black arrow) that attracts it towards the focus. b | A dielectric sphere larger than the wavelength of light either reflects or refracts light (pink arrows) focused by a high-NA lens. The change in direction of each ray corresponds to a change in momentum of the light and an equal and opposite change in bead momentum. Reflected rays of light lose forward momentum that is gained by the bead, leading to a net force (F_reflection, red arrow) pushing the bead along the direction of propagation of the light. Refracted rays are deflected forward because of the high incidence angle of the light, which generates momentum change and reactive force (F_refraction, black arrow) that pulls the bead towards the focus.

For particles larger than the wavelength of light, such as the beads used in most optical tweezers experiments, the particle acts as a refractive object. Here, the beam of light impinging on the object can be treated as a collection of rays and the force acting on the particle can be described using geometric or ray optics. Newton’s second law defines force as the rate of change of momentum $(\stackrel{\rightharpoonup }{F}=\frac{\text{d}\stackrel{\rightharpoonup }{p}}{\text{d}t})$, where $\stackrel{\rightharpoonup }{p}$ is the momentum of the object. Because the momentum of light changes either by being absorbed, reflected or scattered by the particle, conservation of linear momentum dictates that the rate of change of momentum of the light must be accompanied by an identical rate of change of momentum of the object (or force) of opposite sign acting on that object. FIGURE 1b illustrates this limit for a bead in a focused beam. In FIG. 1b, the incident light gains forward momentum by being refracted by the particle (forward pink arrows), which generates a recoil force F_refraction that pulls the bead towards the focus (black arrow). Similarly, the light reflected by the beam (backward pink arrows) loses forward momentum, thus pushing the bead forward with a force F_reflection (red arrow). Stable trapping is obtained when these two forces balance each other. A similar argument can be used to show that the bead will be pulled towards the beam axis if the beam intensity is higher there than in the periphery.

In practice, optical tweezers use a beam of laser light, focused through a microscope objective lens, to trap, move and apply calibrated forces to microscopic refractive objects. The most important component of an optical trap is the objective lens, which focuses the trapping beam into the sample chamber. In most optical tweezers experiments, the sample of interest (a protein, RNA molecule and so on) is too small to interact significantly with the trapping light. Instead, the system must be tethered to a micron-sized bead (typically made of polystyrene or silica 0.2–5 μm in diameter⁶). In order to tether the molecule of interest to the beads, linker molecules are often used; the most common linkers are double-stranded DNA (dsDNA) fragments, referred to as ‘molecular handles’⁷. If such a molecule attached to a surface is also tethered via a DNA handle to a bead held in an optical trap, then by moving the trap relative to the surface, the trapped bead will follow the beam and a force will be exerted on the molecule through the DNA handle. This force acting on the molecule is equal and opposite to the force sensed by the bead in the trap. Because this force represents a rate of change of momentum of the bead, by conservation of linear momentum, the beam in the optical trap must also experience a rate of change of momentum (or force) of the opposite sign, which can be measured directly from the deflection of the trapping beam using a position-sensitive photo-detector. Thus, optical tweezers not only make it possible to exert forces on molecules but also to measure the forces being exerted.

Single-molecule optical tweezers assays also require a measurable change in a spatial coordinate of the system (for example, conformational change, displacement of the centre of mass, force-induced unfolding of a protein) whose magnitude is well within the spatial resolution of the instrument. In some cases, the change in the spatial coordinate is not large or discrete enough to be directly detected. In such cases, combined optical tweezers and single-molecule fluorescence detection may provide a way to monitor these changes while retaining the ability to act mechanically on the system via the tweezers. In general, in most optical tweezers experiments, the system must be studied one molecule at a time. Therefore, systems that can be repeatedly manipulated (as in protein or RNA mechanical unfolding/refolding studies) or whose operation is cyclical, as in the case of enzyme reactions or molecular motors, make it possible to obtain good statistics on the system. We emphasize that optical tweezers-based single-molecule experiments should not be attempted if a robust bulk biochemistry assay of the system does not already exist, typically arrived at from bulk approaches.

This Primer is not an exhaustive or comprehensive review of all of the main applications of optical tweezers in biophysics; we have limited this review to single-molecule studies. As such, we have not covered the use of optical tweezers to manipulate cells or organelles. Here, we concentrate on the physical foundations of the method and on the best approaches to interpret the data. We describe the instrumentation and experimental designs used in most single-molecule optical tweezers assays (Experimentation), present representative examples of optical tweezers data, data correction and data analysis (Results), and describe the type of information that can be derived from the use of this method to study systems of great biophysical interest, including DNA elasticity, protein and RNA folding, and the dynamics of molecular motors (Applications). We also discuss data reproducibility given the inherent stochastic behaviour of individual molecules, suggest community practices to standardize the results from different laboratories (Reproducibility and data deposition), discuss the current limitations in both instrument performance and the data analysis, and suggest ways to overcome these limitations (Limitations and optimizations). Finally, we explore areas of likely future growth and development of the method and its applications (Outlook). Several reviews are now available that can provide further details on some of the topics addressed here^8–13.

Experimentation

In this section, we provide the basic information needed to set up an optical trap experiment. We describe the components of the instrument and its layout, how the instrument is calibrated, the various experimental geometries used and modes of operation, and how samples are prepared. Although commercial systems are becoming increasingly popular, to date a majority of optical tweezers continue to be custom-built instruments and, therefore, designs and operation procedures can vary widely. For the sake of brevity, we do not describe here the variety of instrument layouts in exhaustive detail but, rather, focus on key design features and highlight important differences between set-ups. This section is organized around three main categories of instruments: standard optical tweezers (FIG. 2a) used to measure and exert forces and displacements, optical tweezers supplemented with fluorescence detection and imaging (‘fleezers’) (FIG. 2b) and angular optical tweezers (AOT) (FIG. 2c) that permit one to measure and exert torques and rotations.

Fig. 2 |. Basic designs of optical traps.

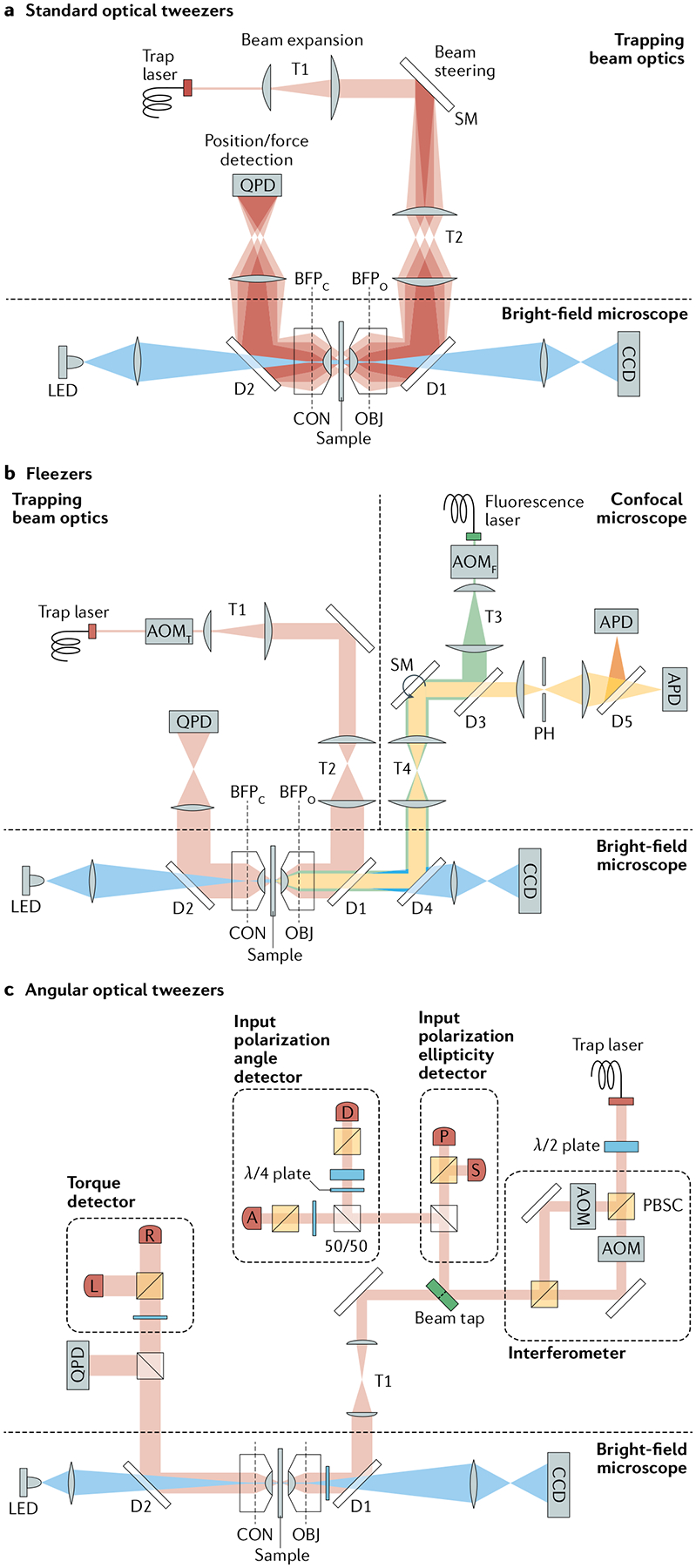
a | Optical layout of a standard single-beam optical trap. A high-power laser generates the trapping beam (pink), which is expanded by telescope T1. Beam-steering optics (here, a steerable mirror (SM)) control the tilt in the beam axis. A high-numerical aperture objective (OBJ) focuses the trapping beam into the sample. T2 images the steering plane (at SM) onto the objective back focal plane (BFP_O), so that tilting the beam displaces the trap in the sample plane. A condenser (CON) collects the light scattered by the trapped particle. A lens images the light at the condenser back focal plane (BFP_C) onto a position-sensitive quadrant photodetector (QPD) for position/force detection. Two dichroic mirrors (D1 and D2) reflect the trapping beam and transmit visible light (blue) for bright-field illumination (light-emitting diode (LED)) and imaging (charge-coupled device (CCD)) of the sample plane. b | Optical layout for a representative fleezers set-up (dual traps with a confocal microscope)⁴³. A fluorescence excitation beam (green) is expanded (T3) and directed (D3, SM, T4, D4) into the trapping OBJ. The OBJ focuses the beam to a diffraction-limited spot on the sample plane and collects light emitted within the spot. The excitation spot is displaced in the sample plane by a SM. The emitted light (yellow) travels back along the emission path, passing through a dichroic mirror (D3) and into a pinhole aperture (PH) to reject out-of-focus light. Emission light is detected by an avalanche photodiode (APD) (or by two APDs for Förster resonance energy transfer measurements). The trapping and fluorescence excitation beams are interlaced by two out-of-phase acousto-optic modulators (AOM_T and AOM_F, respectively). The trap layout is similar to that shown in part a, with dual traps generated by time-sharing using AOM_T. c | Representative optical layout of angular optical tweezers¹⁰¹. The trapping laser is linearly polarized and split equally into two orthogonally polarized beams at a polarization beam splitter cube (PBSC). Each beam then passes through an AOM, and the two beams are recombined at another PBSC. Prior to the objective, the ellipticity of the laser is measured by the ‘input polarization ellipticity detector’ via photodetectors P and S, while the polarization angle is measured by the ‘input polarization angle detector’ via photodetectors A and D. After the laser interacts with a trapped cylinder in the sample plane, the transmitted laser becomes elliptically polarized, and the optical torque is measured by the ‘torque detector’ via photodetectors R and L. The force on the cylinder is measured by a QPD.

Standard optical tweezers

A standard layout of optical tweezers is shown in FIG. 2a. A high-power laser generates the beam of light used to create the trap. The beam is expanded by a telescope and then passed into a high numerical aperture objective lens (which can be water or oil immersion) that focuses it into a diffraction-limited spot — the optical trap — inside a sample chamber. A condenser lens collects the transmitted light, which is then imaged onto a position-sensitive detector used to measure the displacements of the trapped particle and the force exerted on it. In many designs, the angle of the beam entering the objective is actively steered (for example, with a motorized mirror or with an acousto-optic or electro-optic deflector) to control the trap position inside the sample chamber. In addition, the sample chamber is often mounted on an actuated stage to control its position in all three directions. A camera and bright-field illumination are used to image the sample chamber and traps. Although the set-up is often integrated into a commercial microscope body, this is not essential and many designs are built entirely from individual parts.

The trapping laser is one critical component of the instrument. As the maximum attainable force and the trap stiffness are both proportional to the laser power, a high-power (>1 W) laser is desirable, with high stability to maintain a constant stiffness. As a general rule, a maximum force of ~10–20 pN and a trap stiffness of 0.1–0.3 pN/nm can be achieved per 100 mW of trap power at the specimen plane for a micron-sized bead^6,14,15, although the specifics of the instrument design and the material, size and shape of the trapped particle will affect these numbers. The emission wavelength of the laser is another important parameter. In standard designs, near-infrared (750–1,200 nm) lasers are used owing to the availability of high-power (>1 W) lasers emitting in this wavelength range⁶ and owing to several advantages of this spectral window with respect to biological samples: the relative transparency of aqueous buffers¹⁴ and the mitigation of optical damage¹⁶.

The most important component of the instrument is the objective lens as it forms the trap. A strongly converging objective with a high numerical aperture (typically 1.2–1.4) is needed to generate the large gradients in light intensity for trapping⁶. In most designs, stable trapping also requires expanding the trapping beam to ‘overfill’ the back aperture of the objective (FIG. 2a). The reason for this is because the marginal light rays of the beam that are farthest from the optical axis contribute most to the gradient forces when focused by the objective, in contrast to the central rays that contribute mainly to scattering forces. In alternative designs, the trap is formed by two oppositely travelling beams focused at the same point by two objectives to cancel the scattering forces¹⁷, removing the need to overfill the objectives.

For detection, most optical tweezers use a technique called back focal plane interferometry^18–21. This technique can be implemented using the same light that forms the trap, or using a separate, low-power laser source solely for detecting the particle position (a ‘detection beam’)⁶. The condenser lens collects this light, and a lens images it onto a position-sensitive photodetector (FIG. 2a). This interferometric method for detecting trapped particle displacements provides a wide linear range of ~100 nm (REF.²²) combined with extremely high position sensitivity and temporal resolution. It is possible to detect 1-Å displacements of the trapped particle over a 0.1-ms measurement time, limited only by the detector background noise²³, and measurement bandwidths can reach into hundreds of kilohertz. The sensitivity of back focal plane interferometry is a major factor in the high spatial and temporal resolution of optical tweezers.

Calibration.

When reading the position of a trapped particle, the photodetectors output raw signals measured in volts. For quantitative measurements to be possible, these raw signals must be converted into physical displacements (in nanometres). Moreover, to obtain the force exerted on the particle (in piconewtons), the trap stiffness (in piconewtons per nanometre) must be determined. Although some instruments are designed to measure optical forces directly from the change in linear momentum of the light¹⁷, most designs require calibration procedures to determine these parameters.

The most common calibration method uses the Brownian motion of the trapped particle as a reference signal^6,24. A particle held in an optical trap will undergo Brownian motion owing to thermal forces from the surrounding bath, and its position relative to the trap centre will fluctuate over time. For a harmonic trap, where the force on the particle is proportional to its displacement x from the trap centre (that is, F_x = κ_xx, where κ_x is the trap stiffness in the x direction), these fluctuations can be modelled precisely. Specifically, one can derive the following expression for the power spectrum S_xx(f) of the particle position x, which measures the distribution of noise power over frequency f:

$$S_{xx}(f)=\frac{k_{\text{B}}T}{{\pi }^2\gamma \left(f^2+f_{\text{c}}^2\right)}$$ (3)

where k_B is the Boltzmann constant. T is the temperature and γ the hydrodynamic drag coefficient of the trapped particle, both usually known parameters (for a spherical bead, the drag coefficient is γ = 3πηd, where η is the viscosity of the fluid and d the bead diameter). f_c is the characteristic frequency of the trapped particle, given by:

$$f_{\text{c}}=\frac{{\kappa }_x}{2\pi \gamma }$$ (4)

and represents the fact that drag on the particle sets a limit to how fast it can move in the surrounding fluid.

The power spectrum S_xx(f) is determined experimentally by recording the position of a trapped particle x in the trap over time t and taking the Fourier transform of |x(t)|². Fitting these data to the predicted power spectrum S_xx(f) in Eqs 3 and 4, one extracts both the volts-to-nanometres conversion factor and the trap stiffness κ_x along the x direction. This approach can easily be extended to the other dimensions y and z. Although this calibration method is standard, there exist many variations and alternatives, and the interested reader is encouraged to refer to the rich literature on this subject^6,24,25.

Trapping geometries.

In a single-molecule optical tweezers measurement, trapped micron-sized polystyrene or silica beads (of diameter range 0.2–5 μm) are used to exert forces on the system of interest. Various approaches can be used to this end. For example, in measurements of cytoskeletal motors such as kinesin or dynein, forces are applied by attaching the motor directly to a trapped bead^26,27. In other studies, the track on which a motor moves (for example, actin with myosin) is attached to beads^18,28. In applications on nucleic acid-binding proteins and nucleic acid-processing motors, a DNA molecule is tethered to trapped beads^29–31. Owing to its well-characterized mechanical properties, dsDNA is often used as ‘handles’ to link beads to nucleic acid structures and proteins in mechanical unfolding studies. The choice of tethering approach is as much dictated by the system of study and the desired measurement as by the creativity of the researcher. However, it must be understood that all tethering molecules have mechanical properties and will thus be affected by applied force, which has consequences on the signals measured and on the measurement resolution.

The geometry of the measurement also depends on whether a single-trap or dual-trap instrument is used. In single-trap measurements, one end of the system of interest is attached to the trapped bead and the other is bound to the sample chamber surface²⁹ (FIG. 3a) or to a second bead held by suction on the end of a micropipette^10,32–34 (FIG. 3b). In dual-trap systems, the molecule is instead tethered between two optically trapped beads (FIG. 3c). Although the choice of single-trap versus dual-trap design is often dictated by the system of study, it has an impact on trap performance. Surface-based applications are subject to unwanted motion of the sample stage or ‘drift’, which can be significant (~0.1 nm/s) and can limit measurement resolution^9,35. Drift in the laser focus, particularly along the axial (z) direction, can arise from heating of the objective by the trapping laser³⁶. Feedback control over the stage position^9,37 and temperature control³⁶ of the objective can be implemented to mitigate this drift. In contrast to the above instrument designs, in dual-trap set-ups the traps are decoupled from the surface and its drift. Furthermore, dual traps are usually formed from the same laser, either by splitting the laser into two orthogonally polarized beams^38–40 or by ‘time-sharing’, scanning the laser rapidly between two positions using rapid-switching and rapid-steering optics such as acousto-optic and electro-optic modulators and deflectors^28,41–43. As a result, they are less sensitive to pointing drift of the laser as both traps are produced from the same source. Dual-trap set-ups generally provide superior stability, with drift in the separation between the traps maintained below 5 nm/h (REF.³⁸), a performance approaching fundamental noise limits set by Brownian motion⁴⁰.

Fig. 3 |. Measurement geometries of standard optical traps, fleezers and angular optical traps.

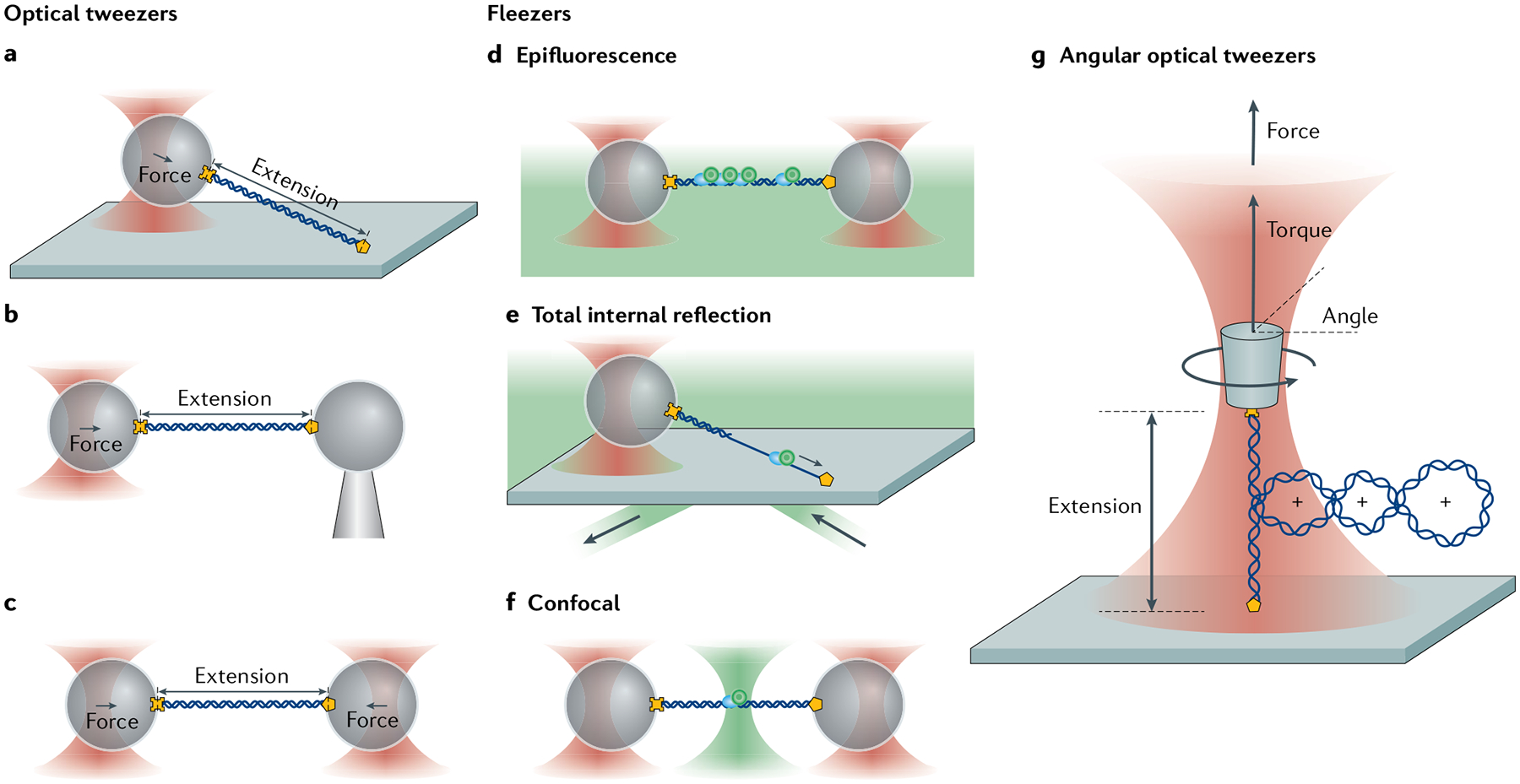
a–c | Common optical trapping geometries¹¹ Single-trap, surface-based geometry where a molecule (here, DNA) functionalized at both ends (yellow cross and pentagon) is tethered between a trapped bead and the sample chamber surface (part a). Single-trap, micropipette-based geometry where the molecule is attached to a trapped bead and a second bead held by suction on the end of a micropipette (part b). Dual-trap geometry where the molecule is tethered between two trapped beads (part c). d–f | Example fleezers configurations¹¹ Dual traps with wide-field, epifluorescence microscopy, where excitation light bathes the specimen plane and fluorescence is collected from dyes (green circles) emitting in the focal plane (part d). Single trap with total internal reflection fluorescence microscopy, where excitation occurs at the chamber surface, in an exponentially decaying evanescent field (typically ~100–200 nm in depth) (part e). Dual traps with confocal fluorescence microscopy, where the excitation light is focused into a diffraction-limited spot inside the sample chamber, and only light emitted from within the spot is collected (part f). g | Basic operational geometry of angular optical tweezers (AOT)^91,171. In AOT, a nanofabricated quartz cylinder is trapped. Shown is an example where the AOT are used to investigate the torsional properties of a DNA molecule by twisting the DNA. During this measurement, the AOT exert and measure torque, control rotation and supercoiling, and measure the displacement and force of the trapped cylinder, all at the same time.

Sample preparation.

To carry out an optical trap measurement, the biological system of interest, the beads used to exert forces on the system and the sample chamber in which the measurements are made must all be prepared in advance. As described above, some component of the system must be tethered to trapped beads and/or to the sample chamber surface. Commonly used linkages are streptavidin–biotin and antibody–antigen pairs owing to their strength under force and commercial availability. DNA molecules to be tethered are usually functionalized with biotin and/or digoxigenin — a small-molecule tag that binds to an antibody — via incorporation of modified bases or modified DNA primers, all commercially available. Various approaches have been developed to tether proteins. Protein samples can be attached to beads through a specific antibody or via an affinity peptide tag (for example, 6× histidine). Biotinylation is also possible in recombinant proteins containing the Avi peptide tag using the BirA biotin ligase^38,44. Micron-sized beads coated with streptavidin or protein G (to which an antibody can be bound), available from several manufacturers, are then used to bind the molecule of interest. In many protein folding studies, the protein of interest is attached covalently to molecular handles — usually, dsDNA — which separates the protein from the beads and eliminates unwanted interactions. A common strategy is a disulfide bond linkage between a free cysteine in the protein and maleimide-functionalized DNA^45–48. Enzyme-based coupling methods have also been used for covalent protein–DNA linkages. In these approaches, a fusion protein (for example, HaloTag) or peptide tag (for example, YbbR tag) engineered into the protein of interest undergoes an enzymatic reaction with a substrate cross-linked to DNA^44,49,50.

Beyond their function in applying force to the tethered molecule, the beads play an important but underappreciated role in trap performance, affecting the trap stiffness¹⁵ and the maximum force that can be exerted^6,14, and the spatial and temporal resolution^34,40,51. The beads can also affect the degree to which the traps cause photodamage to the sample; polystyrene beads can act as sensitizers for trap-mediated generation of reactive oxygen species that cause oxidative damage. This effect, however, can be mitigated by adding enzyme-based oxygen scavenging systems to the experimental buffers to remove molecular oxygen or by using beads of a different material such as silica^47,52. In sum, bead selection is important in the experimental design.

Optical trap measurements are carried out inside microscope sample chambers, typically consisting of two microscope coverslips bonded together by double-sided tape or melted parafilm, into which buffers and samples are flowed via attached tubing. Measurements are usually carried out at room temperature (or slightly higher, as there can be some residual heating of the sample due to absorption of the laser light by the aqueous buffer⁵³). Temperature control of the sample is possible by heating/cooling the sample chamber with a Peltier device⁵⁴ or the objective with a water circulation system⁵⁵, or by laser-based heating⁵⁶. In surface-based applications (for example, with single-trap instruments; FIG. 3a) where a tether is formed to the chamber surface, streptavidin or antibody is pre-adsorbed to the chamber surface to coat it. Trapping of beads is done in situ and one at a time. Beads are flowed into the sample chamber and the user manually captures one by moving the sample stage or trap position to overlap the bead with the trap focus. Formation of tethers is similarly user-intensive. The tethering molecule is usually coated onto the chamber surface or bead by pre-incubation. Then, the surface and bead (FIG. 3a) or the two beads (FIG. 3b,c) are brought into contact. The presence of a tether is confirmed by retracting the two and observing the appearance of a force on the bead(s). To mitigate the formation of multiple attachments to the same bead, it is advisable to work under conditions where the probability of tether formation per bead is low (<20%).

Operation modes.

Optical tweezers can be operated in various measurement modes depending on the system of interest and the parameters to be extracted from that system. In the simplest measurement mode, the trap or stage position remains fixed (that is, ‘passive’) during instrument operation. Mechanical signals from the tethered molecule — for example, extension changes from folding/unfolding transitions in a molecule or the translocation of a molecular motor — displace the beads out of the centres of the traps, leading to a measured change in the force. As the tether is elastic, it will stretch or relax in response to the increase or decrease in force. Although this mode of operation is simple to implement, it requires knowing the force-dependent compliance of the tether to interpret the force change signal. This problem is overcome by applying a constant force. A ‘force clamp’ can be achieved with passive trap operation in dual-trap systems with unequal traps²²: one trap is operated at high power and used to measure force, and the other at low power and used to exert constant force. The low-power trap is configured to hold a bead at the edge of its trapping potential (where the bead is at the cusp of falling out) and where the trap stiffness is effectively zero, leading to a constant force generated as the bead is displaced. This configuration requires a detection beam to monitor the displacements of the bead in the weaker trap. A constant-force operation mode is often used to track the position of a molecular motor over time or to follow transitions between conformational states of a system of interest in real time.

In contrast to passive operation, active control over the trap and/or stage positions allows the application of precisely defined forces over time. Several active modes are commonly used to apply constant forces, force ramps or force jumps to systems of interest during a measurement. To implement a force clamp actively, the tension applied to the tethered molecule is chosen at a preset value and the trap/stage position is adjusted via a negative feedback loop to maintain that tension over time⁵⁷. In contrast to passive implementations of a force clamp, distance changes in the tethered molecule are obtained from the changes in trap/stage position that maintain the constant tension. There are merits and drawbacks to passive versus active force clamps, with the choice of approach dependent on the application. In the force-ramp operation mode, the traps are moved monotonically (typically at tens of or a few hundred nanometres per second), stretching (or relaxing) the tethered molecule. During stretching, the end-to-end extension of the tethered molecule increases, which in turn leads to a continuous increase of the force acting on it. This operation mode is commonly used to obtain force–extension curves of a molecule and determine its elastic properties, or to obtain the rupture forces at which conformational transitions in the molecule occur. In the force-jump operation mode, the trap/stage position is changed suddenly to attain a preset force⁵⁸. Usually, the tethered molecule will undergo a conformational transition in response to the force jump. For example, this measurement mode is used in mechanical unfolding applications where the force range at which the folded and the unfolded states coexist is too narrow to permit constant force or passive mode experiments¹³.

Fleezers

Hybrid instruments combining fluorescence with optical tweezers (fleezers) have become increasingly popular as they enable measurements of mechanical signals and forces simultaneously with fluorescence imaging or Förster resonance energy transfer (FRET) of the same system. A wide variety of fluorescence-trap instrument designs have been implemented integrating both single-trap and dual-trap configurations with wide-field epifluorescence^59–61, total internal reflection (TIRF)^62–65, and confocal^43,66–68 and stimulated emission depletion⁶⁹ microscopy (discussed below and reviewed in REFS^10,11,70,71). In fluorescence microscopy, light at one wavelength is used to excite fluorescent molecules (such as organic dyes or fluorescent proteins) optically, which then emit at a longer wavelength as they relax to the ground state. Thus, only molecules of interest that are fluorescently tagged are imaged, allowing their number, position and dynamics to be tracked in real time. With FRET, an excited ‘donor’ dye transfers its energy to a second ‘acceptor’ dye that emits at a longer wavelength than the first. This energy transfer is extremely sensitive to small (sub-nanometre) changes in dye separation, making it a useful probe for intramolecular and intermolecular dynamics. These fluorescence techniques combined with optical tweezers have been used for single-colour⁵⁹ and multicolour imaging⁶⁰, single-molecule fluorescence counting^65,72 and tracking^65,69,73,74, to monitor chemical processes and displacements simultaneously⁷³, and to measure molecular dynamics by FRET^{64,66,72,75–77}.

Instrument layouts.

Hybrid instruments integrate standard optical trap layouts with fluorescence excitation lasers and detection optics (see, for example, FIG. 2b). Specific excitation lasers are selected to match the absorption wavelengths of the fluorescent dyes to be used. In most cases, the same objective that forms the trap(s) is used both to transmit the fluorescence excitation light into the sample chamber and to collect fluorescence emission. Dichroic mirrors and optical filters, which selectively transmit certain wavelengths and reflect or absorb others, are used to combine the trapping and excitation laser beams into the objective and to separate the trapping and emission light for their respective detection stages. In this way, trapping and fluorescence detection can be done concurrently.

The detailed layout and required optics of the hybrid instrument depend on the type of fluorescence microscopy used. In wide-field microscopy, excitation light bathes the entire sample, which is achieved by focusing the excitation beam onto the back focal plane of the objective^59,60 (FIG. 3d). Fluorescence emission is collected from dyes at the sample focal plane. By contrast, with TIRF microscopy, only dyes within a thin layer (~100–200 nm) at the sample surface are excited and their emitted light collected^62–65 (FIG. 3e). To achieve TIRF, the excitation beam is positioned at the edge of the objective back aperture, so that it refracts onto the chamber surface at a glancing angle and generates an exponentially decaying light field into the sample. In confocal microscopy, the excitation light is instead focused by the objective to a diffraction-limited spot (~250 nm in diameter) inside the sample, and light emitted only from this spot is collected^43,66 (FIG. 3f). The fluorescence emission is focused through a pinhole aperture to reject out-of-focus light (FIG. 2b). Stimulated emission depletion microscopy, one of several super-resolution techniques, breaks the diffraction limit by selective excitation of a smaller area (~50 nm in diameter) than confocal microscopy and requires a more complex instrument set-up. The fluorescence is configured similarly to confocal microscopy, but with two pulsed, co-aligned laser systems, one generating an excitation spot and the other a doughnut-shaped deactivation spot that depletes fluorescence, leaving a small central area capable of fluorescence⁶⁹.

On the detection end, an electron-multiplying charged-coupled device (EMCCD) camera is typically used with epifluorescence and TIRF microscopy where a wide field is illuminated at once and imaged. EMCCDs have the sensitivity to detect the light from a single fluorophore at each pixel over many pixels. As confocal and stimulated emission depletion microscopy require integrating light emitted from a single spot at one time, a sensitive photodetector such as an avalanche photodiode is a more economical option than an EMCCD and can provide single-photon sensitivity (FIG. 2b).

One technical hurdle in combining fluorescence detection with optical traps is that many fluorophores photobleach rapidly (within 1–2 s) when exposed to the trapping light^78,79. The mechanism for photobleaching is a two-photon process involving absorption of a fluorescence excitation photon and an optical trap photon⁷⁸. In applications in which light from a few dye molecules is collected, rapid photobleaching is a significant limitation. The careful selection of dyes for which absorption at trapping wavelengths is minimal can mitigate this effect^64,80, but limits the dyes that can be used. A more common solution is to separate spatially the trap(s) from the dyes to be imaged. In numerous applications (see, for example, REFS^{60,62,65,66,81,82}), the imaging area is spatially separated from the traps by the use of long tethers >10 μm in length (several times the trap diameter). However, this approach comes at a cost in trap spatial resolution, because longer molecules are less stiff mechanically and spatial resolution is proportional to the stiffness of the tethered molecule^34,40,51.

An alternative solution is to separate the two light sources temporally, or to interlace them, such that a dye molecule is never exposed to both trapping and fluorescence excitation light simultaneously. In practice, the trapping laser and fluorescence excitation laser(s) are switched on and off out of phase at high rates using rapid-switching optics such as acousto-optic or electro-optic modulators⁷⁹. High switching rates (typically >10 kHz) prevent the bead from diffusing out of the trapping region in the off period, avoiding the degradation of trap performance⁷⁹. Interlacing has been implemented in instruments combining a single trap with TIRF microscopy⁷⁹ and dual traps with confocal microscopy⁴³, allowing the spatial overlap of trap and fluorescence light sources and the use of more compact tethers. A spatial resolution better than 1 nm over a 1-s measurement window with single-molecule fluorescence detection sensitivity was demonstrated with the latter design⁴³. Despite the improved trap performance, this design requires a more complex instrument control/data acquisition architecture to implement the microsecond-level timing accuracy for interlacing the light sources and to synchronize trap and fluorescence data collection within the interlacing cycle^43,83.

Apart from the exceptions with interlacing, the data collection and calibration in fleezers are identical to those in standard optical tweezers. Bead displacements from position-sensitive photodetectors are collected in parallel with fluorescence images from EMCCDs or photon counts from avalanche photodiodes. In addition, well-designed hybrid instruments allow the full range of operational modes (for example, force ramp and force clamp) in parallel with fluorescence modalities.

Sample preparation.

Special considerations must be made for sample preparation when incorporating fluorescence measurements. First, the molecule(s) of interest must be labelled fluorescently. DNA stains such as intercalating dyes can be used for imaging the entire molecule, and DNA oligonucleotides chemically modified for labelling with organic dyes are commercially available. Proteins can be labelled by fusion to fluorescent proteins, but these have low fluorescence emission and photobleach rapidly. Thus, proteins are more commonly covalently labelled with organic dyes. Labelling is typically achieved through cysteine-specific chemistry on the protein. Site-directed mutagenesis must often be used to remove native cysteines (whose labelling is undesirable as it can adversely affect protein activity) and to introduce cysteines at the desired positions on the protein. Owing to these difficulties, alternative labelling approaches using genetically encodable tags (such as an aldehyde tag⁸⁴ and SNAP-tag⁸⁵) are seeing increased use. Second, all experimental buffers for fluorescent samples must generally be supplemented with oxygen scavengers and quenchers to improve dye stability^86–88.

Measurements made near the sample chamber surface (such as TIRF-based assays) also present potential fluorescence background issues due to autofluorescence and non-specific binding of fluorescently labelled molecules to the surface. Fortunately, the single-molecule fluorescence community has largely solved these problems and developed protocols for surface preparation, cleaning and passivation^89,90. The trapped beads are another source of fluorescence background due to auto fluorescence and non-specific fluorophore binding. This issue can be significant for applications in which fluorescence must be detected close to the trapped beads, for example when using short tethers. To date, however, less work has been done in developing good practices for bead selection and passivation to reduce this background source.

Angular optical tweezers

In order to investigate and control rotational motion of biomolecules, optical tweezers need to be extended to trap a particle angularly as well as spatially. Stable angular trapping requires confinement of all three angles of the trapped particle orientation. AOT, also termed the optical torque wrench, have allowed stable confinement of all three angles by using birefringent cylinders made of quartz^91,92. AOT are capable of direct control and detection of torque and rotation of individual biomolecules, expanding the capability of optical trapping beyond force and extension measurements. There are three core features of AOT⁸: a birefringent cylinder as the trapping particle, control of the cylinder orientation and detection of the torque on the cylinder. It is worth noting that torque detection has also been demonstrated using the rotary bead assay^93,94 and magnetic tweezers^95,96.

First, instead of trapping a dielectric microsphere, AOT trap a birefringent cylinder, which is initially nanofabricated out of a quartz wafer⁹² and is not commercially available (FIG. 3g; see BOX 1 for more details). The cylinder is designed to have its extraordinary axis perpendicular to its cylindrical axis and one of its ends chemically functionalized for attachment to a biological molecule of interest⁹². Once the cylinder is trapped, its cylindrical axis orients along the direction of light propagation as a result of shape anisotropy, and the cylinder can be rotated about its axis via rotation of the laser polarization.

Box 1 |. Principles of angular optical tweezers.

In angular optical tweezers, the most commonly employed trapping particle thus far is a quartz cylinder. Crystalline quartz has an anisotropic electric susceptibility $\overleftrightarrow{\chi }:{\chi }_{\text{e}}$ along the extraordinary axis is greater than χ_o along the ordinary axes, such that the extraordinary axis of the crystal is more easily polarized than the ordinary axes. The cylinder is designed to have its extraordinary axis perpendicular to its cylindrical axis and one of its ends chemically derivatized for attachment to a biological molecule of interest⁹². Once the cylinder is trapped, its cylindrical axis orients along the direction of light propagation $\left(\widehat{z}\right)$ as a result of shape anisotropy. In the presence of a linearly polarized electric field of the trapping laser $\stackrel{\rightharpoonup }{E}$, the quartz cylinder develops a polarization $\stackrel{\rightharpoonup }{P}$, dependent on the electric susceptibility $\overleftrightarrow{\chi }$ of the cylinder:

$$\stackrel{\rightharpoonup }{P}={\chi }_{\text{e}}{E}_x\widehat{x}+{\chi }_{\text{o}}{E}_y\widehat{y}$$ (11)

where $\widehat{x}$ and $\widehat{y}$ are unit vectors along the principal axes of the crystal. If the linearly polarized electric field makes an angle θ with the extraordinary axis (FIG. 3g), then a torque is exerted on the cylinder⁹¹:

$$\stackrel{\rightharpoonup }{\tau }=\int d^3\stackrel{\rightharpoonup }{r}\stackrel{\rightharpoonup }{P}\times \stackrel{\rightharpoonup }{E}=\widehat{z}\frac{1}{2}\left({\chi }_{\text{e}}-{\chi }_{\text{o}}\right)\text{sin}(2\theta )\int d^3\stackrel{\rightharpoonup }{r}{E}_0^2(\stackrel{\rightharpoonup }{r})=\widehat{z}{\tau }_0\text{\hspace{0.17em}sin}(2\theta )$$ (12)

where $\widehat{z}$ is the unit vector along the direction of light propagation, and τ₀ is the maximum torque that can be exerted on the cylinder where the integration extends over the cylinder’s volume⁹¹. Thus, a torque will act on the cylinder until the extraordinary axis is aligned with $\stackrel{\rightharpoonup }{E}$, at which point $\stackrel{\rightharpoonup }{\tau }=0$. Eq. 12 also shows that the torque varies with θ sinusoidally, with a periodicity of π radians.

Second, rapid and flexible control of the input polarization of the trapping laser beam is essential, not only to rotate the trapped cylinder but also to calibrate its angular properties. These capabilities may be achieved via a pair of acousto-optic modulators that independently control the amplitudes and phases of the left (L) and right (R) circular polarizations⁹¹. The rotation angle of the polarization Θ is specified by the phase difference ϕ between the two acousto-optic modulators, Θ = ϕ / 2, and polarization may be rotated at an arbitrary rate up to hundreds of kilohertz by modulating this phase difference. Alternatively, an electro-optic modulator may also be used to rotate the laser polarization⁹⁷. A trapped particle may also be rotated via a circularly polarized light⁹⁸ or a Laguerre–Gaussian beam⁹⁹, although their applications to single-molecule studies have yet to be demonstrated.

Third, the optical torque that rotates the cylinder is measured directly as the change in the angular momentum of the trapping laser⁹¹ (BOX 1). When the laser exerts a torque on the cylinder, the polarization of the trapping laser will change from linear to elliptical. Thus, the trapping laser that initially carried zero net angular momentum (linearly polarized) leaves the cylinder carrying a net angular momentum (elliptically polarized). This change in angular momentum results in a difference in the power of the left and right-handed circular components (P_L and P_R) and gives rise to an optical torque⁹¹. As shown in FIG. 2c, this optical torque is measured via the torque detector:

$$\tau =\frac{P_{\text{R}}-P_{\text{L}}}{{\omega }_0}$$ (5)

where ω₀ is the angular frequency of the laser. Because the same laser is used for both torque application and detection, this torque detection method is direct and relies solely on a change in laser angular momentum.

Torque calibration.

In principle, torque may be calculated by change of angular momentum content of the laser (Eq. 5). In practice, the torque detector needs to calibrated to determine a prefactor due to photon losses in the optical system⁹¹.

The first step in the torque calibration is to relate the torque signal voltage of the torque detector V_τ, which measures P_R − P_L, to the cylinder’s angular displacement θ from the trapping laser’s linear polarization direction, using Eqs 5 and 12:

$$V_{\tau }=V_0\text{\hspace{0.17em}sin}(2\theta )$$ (6)

where V₀ is the maximum value of the torque signal. This relationship is established via rapid rotation of the polarization (for example, 500 Hz at 10-mW input to the objective). As a trapped cylinder cannot follow such a rapid rotation due to viscous drag, the polarization vector effectively scans a quasi-stationary cylinder. Once V₀ is determined, θ is then found via the torque signal V_τ according to Eq. 6.

The second step in the torque calibration is the conversion of the torque signal to physical units of torque⁹¹. This step requires the determination of the angular trap stiffness, which is obtained by measuring the Brownian angular fluctuations in θ values of the cylinder. Under a small θ value, the angular trapping potential is effectively harmonic. Using the power spectrum analysis of θ (an angular equivalence of Eq. 3), the angular trap stiffness k_θ and the rotational viscous damping coefficient ξ are determined. Both k_θ and ξ can be tuned by varying the cylinder size and the birefringent material¹⁰⁰. Thus, the torque signal (V_τ) is converted to torque (τ):

$$\tau =\frac{k_{\theta }}{2}\frac{V_{\tau }}{V_0}$$ (7)

Forces exerted on the cylinder.

In addition to torque, AOT can also exert a force on the trapped cylinder. Because the optical torque is exerted axially (Eq. 12), the optimal direction for force application is also the axial direction⁹². By contrast, conventional optical tweezers typically exert forces transverse to the direction of light propagation (FIG. 3b,c). In an AOT experiment, a molecule of interest (for example, DNA) may be torsionally constrained at one end to the surface of a coverslip, and at the other end to the bottom of a trapped quartz cylinder (FIG. 3g). Thus, the molecule may be twisted, while being stretched axially. This axial stretching may be achieved by moving the sample chamber via a piezoelectric stage to change the distance between the trapped cylinder and the sample chamber surface. For absolute extension measurements, the trap position at which the extension is zero must be established, for example, by finding the piezo position at which the trapped cylinder encounters resistance to further movement as it approaches the surface¹⁰¹.

For an oil immersion objective, the index of refraction mismatch necessitates the use of a factor called the focal shift ratio to convert piezo movement into trap height change. This shift may be determined by using the Fabry–Pérot effect that results from laser beam interference between surfaces of the cylinder and the coverslip^6,101,102. Alternatively, it may be obtained by unzipping a DNA molecule of known sequence and using the resulting unzipping signature as a calibration¹⁰². Furthermore, both the force trap stiffness and the sensitivity of the z-position detector are functions of trap height. These may also be characterized using the DNA unzipping method¹⁰². Once all linear and angular parameters are determined, the AOT are then prepared for precision mechanical studies of a biomolecule.

Results

All variants of optical tweezers, including standard optical tweezers, fleezers and AOT, share the common ability to measure forces and displacements of a trapped particle. In this section, we discuss some typical results from these three types of instrument. We illustrate the use of these instruments using representative examples of operation and discuss alternative ways of operating these instruments.

Optical tweezers

Optical tweezers experiments yield rich information on the mechanical behaviour of tethered molecules, which is manifested as real-time recordings of two measurables: force and extension. Force is calculated as the product of the trap stiffness and the displacement of the trapped bead from the trap centre. Extension is calculated as the distance between the bead centres minus the radii of the two beads. Determination of the absolute extension, however, remains a challenge owing to bead size variation and instrumental uncertainty; the former source is largely dependent on the manufacturer’s quality control, whereas the latter can be mitigated by strategies implemented in the laboratory. Force–extension curves are typically generated from force-ramp experiments. These curves can be used to analyse the elastic properties of the tethered biopolymer by fitting them to theoretical models such as the worm-like-chain model of polymer elasticity^103,104 (BOX 2). This type of analysis has been employed to describe the mechanical nature of nucleic acids^32,105, peptides^106,107, chromatin fibres^108,109 and nucleoprotein filaments¹¹⁰.

Box 2 |. Elastic properties of DNA.

The elastic energy of DNA has multiple contributions^{104,250,255–257}, with the following leading terms:

$$E=E_{\text{bend}}+E_{\text{twist}}+E_{\text{stretch}}+E_{\text{twist-stretch}}$$ (13)

where E_bend, E_twist, E_stretch and E_{twist–stretch} correspond to the bending energy, the twist energy, the stretching energy and the twist–stretch coupling energy, respectively. Theoretical models of DNA elasticity, built upon statistical mechanics principles, have been developed to characterize relationships among four thermodynamic mechanical quantities that are directly measurable: force, extension, rotation and torque^{104,250,255–257}. However, the exact relationship among these quantities is complicated, and analytical solutions are typically unavailable.

The worm-like chain (WLC) model, first formulated by Kratky and Porod²⁵⁸, describes the elastic properties of a semi-flexible polymer in a thermal bath with a single parameter: its persistence length L_p, which can be intuitively understood as the characteristic length scale of a polymer chain beyond which the initial direction of the polymer is randomized by thermal fluctuations. The force–extension relation of double-stranded DNA (dsDNA), under no torsion and in the low force regime (<5 pN), is well described by an interpolating formula of the WLC model^103,104. The approximation is given by:

$$F(x)=\frac{k_{\text{B}}T}{L_{\text{p}}}\left[\frac{1}{4{\left(1-\frac{x}{L_0}\right)}^2}-\frac{1}{4}+\frac{x}{L_0}\right]$$ (14)

where F is the applied force, x the molecular extension and L₀ the contour length (maximum end to end distance). To extend this model to the high-force regime, a modified formula (that is, extensible WLC model) takes into account contributions from the stretch modulus K₀, resulting in the following force–extension relation¹⁰⁵ (see the figure):

$$F(x)=\frac{k_{\text{B}}T}{L_{\text{p}}}\left[\frac{1}{4{\left(1-x/L_0+F/K_0\right)}^2}-\frac{1}{4}+\frac{x}{L_0}-\frac{F}{K_0}\right]$$ (15)

In comparison, elastic properties of single-stranded DNA (ssDNA) are simplified as it can twist freely and does not accumulate torsion, but are complicated by the possible formation of secondary structures. Various models, including the WLC and the alternative freely jointed chain models, have been proposed to describe the force–extension relationship of ssDNA under different conditions^{32,183,253,259}. A thorough review of the elastic properties of single-stranded nucleic acids can be found in REF.¹⁸⁴.

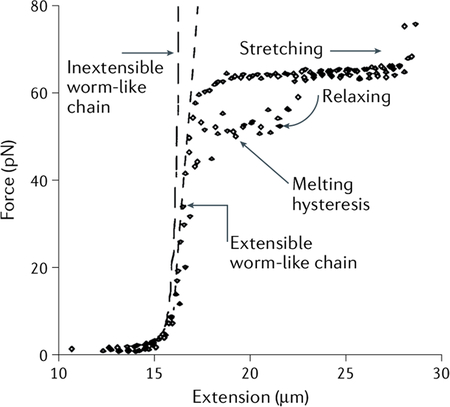
Adapted with permission from REF.³², AAAS.

When the tethered molecule is folded into higher-order structures, the force increases monotonically as the beads are separated until a sudden increase in extension (or ‘rip’), indicating the unfolding of the molecule. Conversely, when the molecule is relaxed by bringing back the beads closer together, the monotonic decrease of the force is interrupted by a sudden contraction in extension (or ‘zip’) that indicates the refolding of the molecule (FIG. 4a). Note that the zips and rips occur each time at different forces (FIG. 4b,c), reflecting the stochastic, thermally induced crossing of the energy barrier. Experiments of this type make it possible to obtain information about the energy landscape over which the molecule transits between the folded and the unfolded states. The unfolding and refolding force distributions obtained at given force-loading rates (dF/dt) can be transformed into force-dependent lifetimes of the folded and unfolded states^111,112, whose inverse yields the force-dependent rates of unfolding and refolding of the molecule, respectively. The slope of the logarithm of these rates as a function of force yields the distance to the transition state (FIG. 4d), a key parameter in the description of the energy landscape of the folding process (BOX 3). The unfolding and refolding force distributions often do not coincide, indicating that the molecule is taken out of equilibrium during the process. Accordingly, the area under the rips and zips corresponds to the irreversible work done by the tweezers to unfold the molecule and by the molecule to refold against the tweezers, respectively. Powerful fluctuation theorems^113,114 can be used to recuperate the reversible work or free energy of unfolding and refolding from experiments performed out of equilibrium^115–117 (BOX 4). This bypasses the requirement for reversible paths and allows the deduction of equilibrium free energies from an ensemble of irreversible force–extension curves. If the zip and rip forces are not too different, then it is possible to find an intermediate range of forces at which the molecule can spend a measurable fraction of time in both its folded and unfolded states. Under these preset forces (with or without active feedback), the molecule is seen to repeatedly ‘hop’ between different states, whose force-dependent lifetimes and their associated unfolding/refolding rates can be directly measured. The folding energy landscape can thus be mapped as described above.

Fig. 4 |. Example optical trapping data.

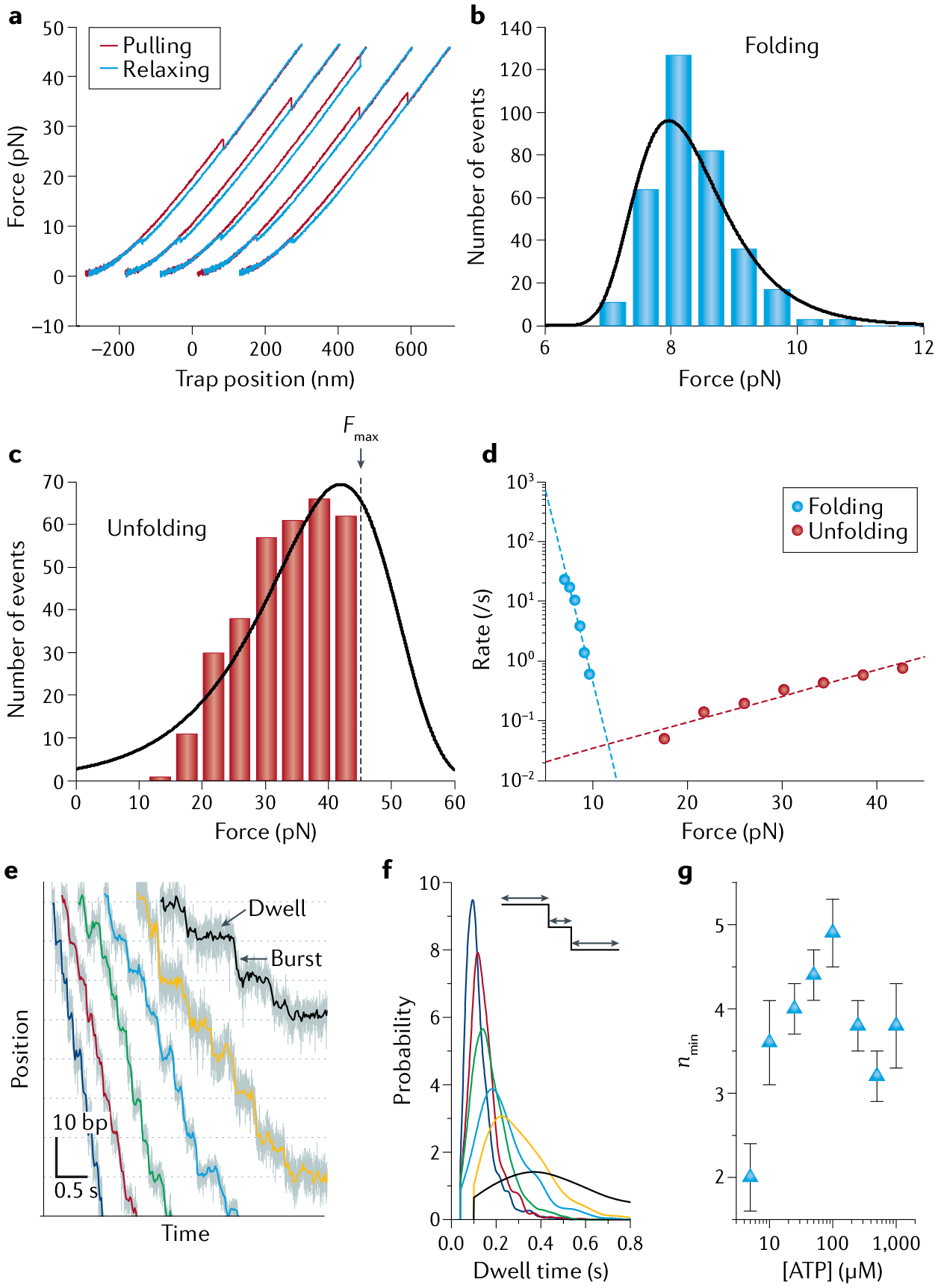
a | Force-ramp cycles of Top7, a de novo designed protein. Successive pulling (red) and relaxing (blue) cycles are offset along the x axis for clarity. b,c | Folding and unfolding force distributions, respectively, of Top7 at a pulling speed of 100 nm/s. Black lines are distributions derived from model fitting in part d. The unfolding distribution in part c is right-censored because the maximum force (F_max) was set at 45 pN during pulling experiments to avoid tether rupture. d | Force-dependent rates of unfolding (red dots) and refolding (blue dots) extracted from the corresponding force distributions in parts b and c. Dashed lines are fits to Bell’s model²⁵⁴. e | Representative trajectories showing the processive translocation of individual φ29 packaging motors on double-stranded DNA (dsDNA) under a constant force of ~8 pN and different [ATP] (250 μM, 100 μM, 50 μM, 25 μM, 10 μM and 5 μM in blue, red, green, cyan, yellow and black, respectively). Each translocation cycle is composed of a stationary dwell phase and a stepping burst phase. f | Probability distributions of the lifetimes of the dwell phase at different [ATP]. Colour scheme as in part e. g | Values of n_min, the minimum number of rate-limiting kinetic events during the dwell, derived from the dwell time distributions for different [ATP]¹⁵⁴. Parts a–d adapted with permission from REF.²⁵⁴, AAAS. Parts e–g adapted from REF.¹⁵⁴, Springer Nature Limited.

Box 3 |. Determining the energy landscape of molecular transitions.

Optical tweezers have enabled the characterization of several parameters of the energy landscape for many biomechanical reactions such as RNA/protein folding and molecular motor-driven processes^118,211. The application of force F on the molecule amounts to subtracting a term Fx from the free energy surface, where x is the reaction coordinate. The result is to tilt this surface, shifting the equilibrium towards the longer (unfolded) state of the molecule, favouring the spontaneous, thermally induced crossing of the energy barrier between the two states (see the figure).

The effect of force on the equilibrium between the folded and unfolded states is described by²¹¹:

$$\Delta G(F)=-k_{B}T\text{\hspace{0.17em}ln\hspace{0.17em}}{K}_{\text{eq}}(F)=\Delta G^0-F\Delta x+\Delta G_{\text{stretch}}(F)$$ (16)

where K_eq(F) is the force-dependent equilibrium constant, ΔG⁰ the standard Gibbs free energy (where the superscript denotes the standard state), Δx the difference in extension between the folded and unfolded states at F = 0, and ΔG_stretch = G_stretch,2 − G_stretch,1 is the difference in the free energy to stretch the folded (1) and the unfolded (2) states to their respective extensions at force F. G_stretch,i for each state i is calculated by integrating the force over the extension; that is, determining the area under the force–extension curve F_i(x) for that state:

$$G_{\text{stretch},i}(F)=\underset{0}{\overset{x_i(F)}{\int }}{F}_i\left(x^{\prime }\right)d{x}^{\prime }$$ (17)

F_i(x) would typically be given by the WLC model in Eq. 14 or 15. At the force at which the molecule spends the same amount of time in the folded state and in the unfolded state F_1/2, K_eq(F_1/2) = 1 and:

$$\Delta G^0=F_{1/2}\Delta x-\Delta G_{\text{stretch}}$$ (18)

Similarly, force increases the unfolding rate by lowering the energy barrier to unfolding. This effect can be approximated by Bell’s model^260,261, which reduces the energy to the transition state, ΔG^‡, in the standard Arrhenius equation, by the term −Fx^‡, where x^‡ is the distance to the transition state:

$$k(F)=A{k}_o{\text{e}}^{-\left(\Delta G^{‡}-F\Delta x^{‡}\right)/k_{B}T}$$ (19)

This is the simplest model to describe the dependence of the kinetic rates on force. However, it is phenomenological and does not always accurately describe the experimental data. The observation of a non-linear dependence of ln(k) on F opposite to the linear dependence predicted by Eq. 19 represents the breakdown of Bell’s model^262,263. In this case, a more rigorous treatment such as that of Dudko et al. derived using Kramer’s theory²⁶³ should be used.

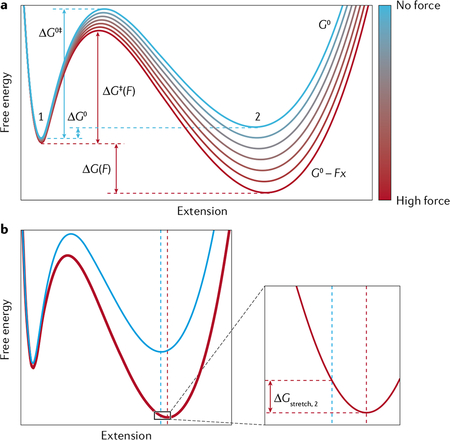
Adapted with permission from REF.¹³, Annual Reviews.

Box 4 |. Fluctuation theorems.

The second law of thermodynamics states that the mean value of the work (W) done on a system is always larger than or equal to the free energy change (ΔG) of that system depending on whether the process is carried out irreversibly (W_irrev, with dissipation W_diss) or reversibly (W_rev), respectively:

$$\langle W_{\text{irrev}}\rangle \equiv \langle W_{\text{rev}}+W_{\text{diss}}\rangle \ge \langle W_{\text{rev}}\rangle \equiv \Delta G$$ (20)

In 1997, Christopher Jarzynski showed that the Gibbs free energy change for a process (RNA unfolding, for example), could be recovered from the Boltzmann average of the W_irrev values obtained over N realizations performed out of equilibrium, in the limit of large N^113,264:

$${\langle {\text{e}}^{-W_{\text{irrev}}/k_{\text{B}}T}\rangle }_{N\to \infty }={\text{e}}^{-\Delta G/k_{B}T}$$ (21)

A second result, the Crooks fluctuation theorem (CFT)^114,265 relates the probability distribution P_F(W) of the work done on a system (W) along a forward (F, unfolding for example) trajectory, and the distribution P_R(−W) of the work done by the system (−W) along the reverse (R, refolding) trajectory, with the amount of dissipation in the process (W − ΔG):

$$\frac{P_{\text{F}}(W)}{P_{\text{R}}(-W)}={\text{e}}^{\left(\frac{W-\Delta G}{k_{B}T}\right)}$$ (22)

The amount of dissipation can be increased or decreased by pulling/relaxing the molecule faster or slower, respectively. Note that when W = ΔG, P_F(W) = P_R(−W). In other words, the value of W at which both distributions (unfolding and refolding) cross is the free energy change of the process ΔG (see the figure, depicting the test of CFT by unfolding and refolding an RNA hairpin at different loading rates).

Both the Jarzynski and Crooks relationships permit obtaining the free energy of a process from non-equilibrium realizations of that process and have found particularly useful applications in the analysis of single-molecule optical tweezers experiments^117,266. These methods work because fluctuations occur around the mean and, although more often than not non-equilibrium trajectories dissipate work, once in a while a fluctuation occurs in which the work done irreversibly is smaller than the reversible work, that is W_irrev < W_rev. This rare situation is reflected in the tails of the distributions on both sides of the value of ΔG (grey dashed line) in the figure. These irreversible work values are smaller and contribute more to the average in Eq. 21. Thus, if enough of them have been recorded (N is large), they can offset the more common, larger irreversible work values, yielding the correct value of the free energy. The larger the amount of dissipation (or hysteresis in the force–extension curves), the greater the number of iterations required for the left-hand side of Eq. 21 to converge to its right-hand side. For dissipations that are not too large (~3–4k_BT), ~50 iterations may be necessary, but this number increases fast with the amount of dissipation. In general, the Crooks formulation converges faster than its Jarzynski counterpart, and thus can be used to estimate free energy changes in systems with larger dissipations. Related theorems have been derived during the last few years. A particularly useful one is an extension of the CFT that makes it possible to extract the binding free energy from ligands bound to a macromolecule that is subjected to binding and unbinding via out of equilibrium mechanical unfolding and refolding²⁶⁷.

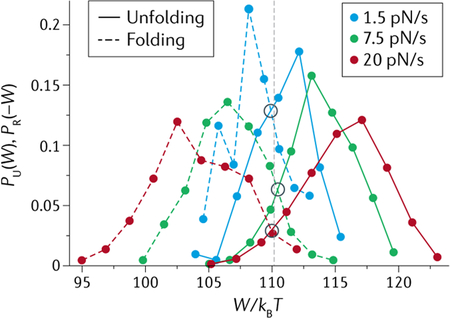
Adapted from REF.¹¹⁷, Springer Nature Limited.

Single-molecule recordings of extension as a function of time generated from constant-force experiments are often used to study dynamic biomolecular processes ranging from reversible interconversions in folding/unfolding of nucleic acids and proteins¹¹⁸ to processive movements of molecular motors¹¹⁹. Various step-finding algorithms, including those based on the residual χ², the Bayesian information criterion, hidden Markov modelling or machine learning, have been developed to idealize noisy trajectories into discrete stepwise transitions^120–124, yielding characteristic step sizes and dwell times (FIG. 4e). The step size (change in extension per transition) can also be inferred from periodogram analysis such as pairwise distance distributions and autocorrelation functions^26,125. The dwell time t (duration between steps) harbours all kinetic transitions that precede the mechanical stepping. The shape of the dwell time distribution, which informs on the underlying kinetic mechanism of the biomolecular process, can be formulated by the randomness parameter r or its inverse, n_min (REFS^126,127) (FIG. 4f,g):

$$n_{\text{min}}=r^{-1}=\langle t^2\rangle /(\langle t^2\rangle -{\langle t\rangle }^2)$$ (8)

An r value of 1 corresponds to a single-exponential decay, indicating that a single kinetic step dominates the dwell duration; values of r < 1 correspond to a peaked distribution and indicate at least n_min kinetic steps during the dwell; values of r > 1 typically correspond to a multi-exponential, long-tailed distribution and indicate the existence of parallel pathways or off-pathway states in the kinetic scheme.

Fleezers

Fleezers provide additional and complementary information about the system to that obtained with optical tweezers alone. Increasingly, applications of fleezers have exploited the full, combined power present in simultaneously acquired trap and fluorescence data to carry out correlative analysis of the two (reviewed elsewhere^10,11,34,70). A popular example is wide-field epifluorescence or TIRF imaging of DNA and DNA-binding proteins (FIG. 5). The ability to ‘see’ fluorescently labelled proteins allows their location on DNA to be determined as a function of time and applied force^59,60. Force is used in combination with microscopy to control the extension of the tethered DNA, which in turn can modulate the location and dynamics of the bound proteins that are imaged^59,60. Where fluorescently labelled molecules are sparse and can be localized individually, fluorescence imaging can be used for tracking measurements. The fluorescence intensity profile of an individual dye molecule is well described by a 2D Gaussian function. Thus, the centre-of-mass position of a labelled molecule in each frame of the fluorescence movie is determined by fitting its image to a 2D Gaussian function, and its motion is tracked as a function of force^61,63,65,69. A common analysis tool used in imaging applications is the kymograph, in which the fluorescence intensity profiles in one dimension are stacked in a time series to reveal the molecular trajectories of the labelled components. FIGURE 5a–c illustrates this analysis method, where a filament of the fluorescently labelled recombinase RAD51 on DNA is stretched with dual traps and imaged by epifluorescence microscopy⁸¹. To create the kymograph, a line scan of RAD51 fluorescence along the stretched tether is obtained for each frame of the fluorescence movie. The line scans are then stacked into a single image, with the position on the tether along one axis (FIG. 5b, y axis) and the frame number (or, equivalently, time) along the other axis (FIG. 5b, x axis). The kymograph thus shows both the location of the bound proteins along the tether and their bound lifetime. In this particular example, the trap is operated in a passive mode, and an increase in force (measured by optical trap) coincides with the DNA contraction triggered by RAD51 dissociation (measured by fluorescence; FIG. 5c).

Fig. 5 |. Example fluorescence-trap data.

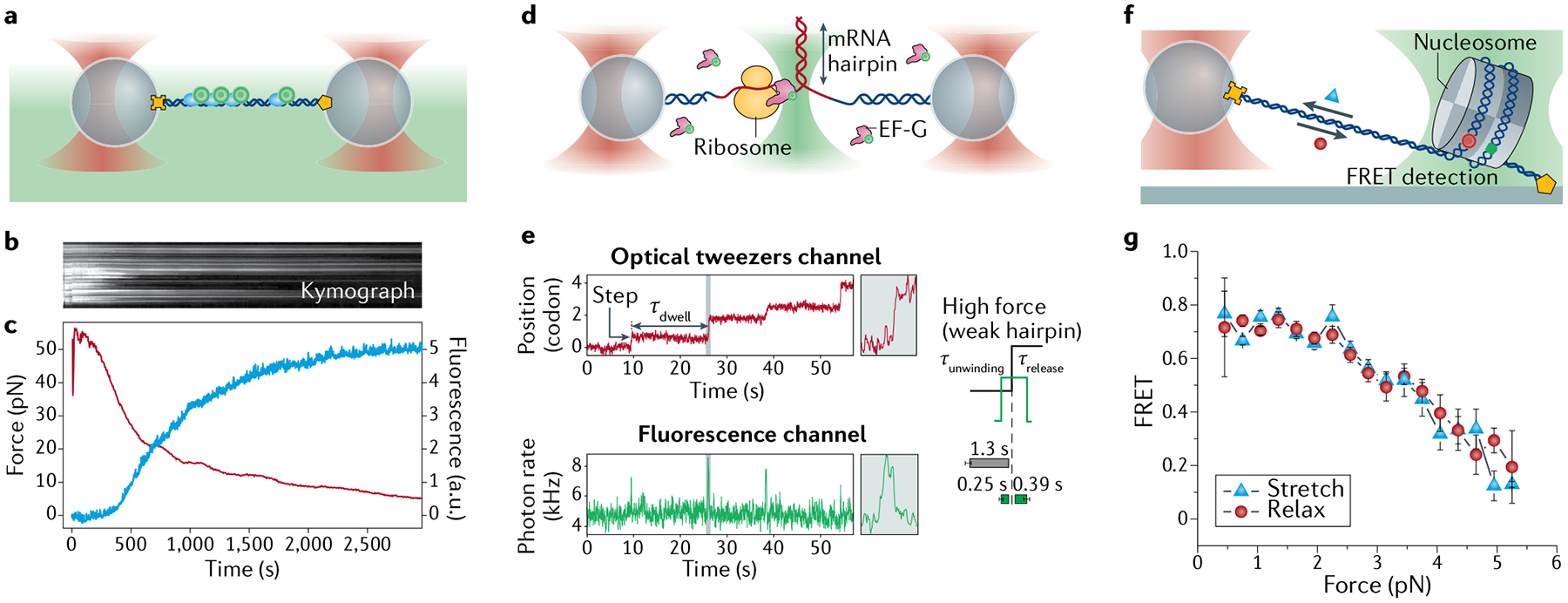
a | Dual-trap plus epifluorescence configuration, showing labelled RAD51 bound to DNA (DNA functionalized at both ends (yellow cross and pentagon) and fluorescence collected from dye (green circles)). b | Kymograph of a RAD51–double-stranded DNA (dsDNA) complex, held at fixed length, triggered to disassemble. c | Fluorescence intensity (red) decreases as tension (blue) increases owing to disassembly-induced DNA contraction⁸¹. d | Dual-trap plus confocal configuration, showing a ribosome opening a messenger RNA (mRNA) hairpin and labelled elongation factor G (EF-G) binding. e | Time trace of ribosome translocation in one-codon steps separated by dwells of duration τ_dwell (red) with simultaneous fluorescence intensity (green) indicating binding and dissociation of EF-G⁷³. Average EF-G residence times before mRNA unwinding (τ_unwinding) and after unwinding (τ_release) are displayed for a weak hairpin at high force. f | Surface-based, single-trap plus confocal configuration, showing a single nucleosome bound to Förster resonance energy transfer (FRET)-labelled DNA under force. g | Resulting FRET decrease versus force as the nucleosome is unravelled mechanically⁷⁶. Parts b and c adapted from REF.⁸¹, Springer Nature Limited. Parts d and e adapted with permission from REF.⁷³, Elsevier. Parts f and g adapted with permission from REF.⁷⁶, Elsevier.

The time course of the fluorescence intensity is another result that can be combined with optical trap data. The onset and disappearance of fluorescence signals can determine the bound lifetime of a labelled molecule on a tethered molecule under force^62,128. Co-temporal analysis of fluorescence and mechanical signals can further uncover causal relationships between molecular processes, revealing, for example, how molecular motor dynamics correlate with binding of fluorescently labelled substrates or molecular partners^62,73. FIGURE 5d,e shows an illustrative example of co-temporal analysis, where ribosome translocation on RNA is monitored with optical traps while binding of fluorescently labelled elongation factor G (EF-G) is detected simultaneously with confocal microscopy⁷³. Analysing the time traces in both channels reveals when EF-G binds and unbinds in relation to the ribosome’s translocation by one codon (three nucleotides) (FIG. 5e). Fluorescence intensity can also be used to count labelled molecules. Over time, fluorescent dyes photobleach, undergoing an irreversible transition into a dark state. This behaviour can be exploited to count the number of labelled molecules at one position, by counting the number of stepwise drops in fluorescence intensity as each dye expires¹²⁹. Thus, the stoichiometry of a molecular complex may be determined by fluorescence and correlated to its dynamic behaviour as measured by optical trapping. An example of this approach determined how the monomeric versus dimeric forms (counted by fluorescence) of a helicase impact its DNA unwinding activity (measured by an optical trap)^65,72. Intensity-based counting approaches are useful in situations where it is impossible to rely on spatial localization to distinguish multiple proteins.

Finally, spectroscopic data obtained from single-molecule FRET⁸⁶ can be used to probe conformational dynamics in a molecule or complex labelled with a donor–acceptor dye pair. As FRET measures the distance separating the dye pair, it can be combined with optical trapping to monitor, as a function of force, distance changes due to conformational interconversions of nucleic acid structures and nucleoprotein complexes^{66,75–77,130}. An illustrative example of this approach is shown in FIG. 5f,g, in which a single nucleosome is unravelled by force⁷⁶. Here, the DNA on the histone is labelled with a donor–acceptor dye pair at positions selected such that the two dyes are close when DNA is wrapped (leading to high FRET and acceptor emission) and are far apart when the DNA is unwrapped (leading to low FRET and donor emission). As a force ramp is applied with the optical trap to stretch and relax the tethered DNA, the donor and acceptor dye emission intensities are measured. FIGURE 5g shows how the FRET efficiency — determined from the relation E = I_A/(I_D + I_A), where I_A and I_D are the acceptor and donor intensities, respectively — decreases as force increases and the nucleosome is unravelled. This approach can be extended to study protein diffusion on DNA by placing one dye of the FRET pair on the protein and the other on the DNA⁷⁵. As FRET provides measurements of inter-dye distances independent of those obtained from the optical traps, it can be used to track reaction coordinates to which the traps are insensitive. The access to ‘orthogonal’ reaction coordinates enables mapping of multidimensional energy landscapes^66,77. As with fluorescence intensity, co-temporal analysis of FRET and mechanical signals can reveal correlations between the conformational states and dynamics of molecular motors⁷².

Angular optical tweezers

AOT can simultaneously measure multiple physical parameters — torque, angle, force and displacement — and may be operated in different modes depending on the needs of a specific application. The most commonly employed mode is the ‘rotation’ mode, where a trapped cylinder attached to the molecule of interest is twisted via rotation of the laser polarization, as the cylinder closely tracks this polarization^92,131,132. This mode is well suited for torsional studies of chromatin fibres and is illustrated with an example in FIG. 6a¹⁷¹. Here, one end of a chromatin fibre was torsionally constrained to the surface of a microscope coverslip and its other end was torsionally constrained to the bottom of a quartz cylinder. The cylinder was first stretched axially and held under a constant force. To introduce turns into DNA, the cylinder was rotated at a constant rate, and the torques exerted on the DNA and the DNA extension were recorded from the change in the polarization of the light and the displacement of the cylinder from the trap centre, respectively (FIG. 6b,c). The measured torque provides information about the torsional modulus of the nucleosomal DNA (FIG. 6c). To date, torques as small as 1 pN·nm have been detected using AOT¹³³.

Fig. 6 |. Example angular optical tweezers data.

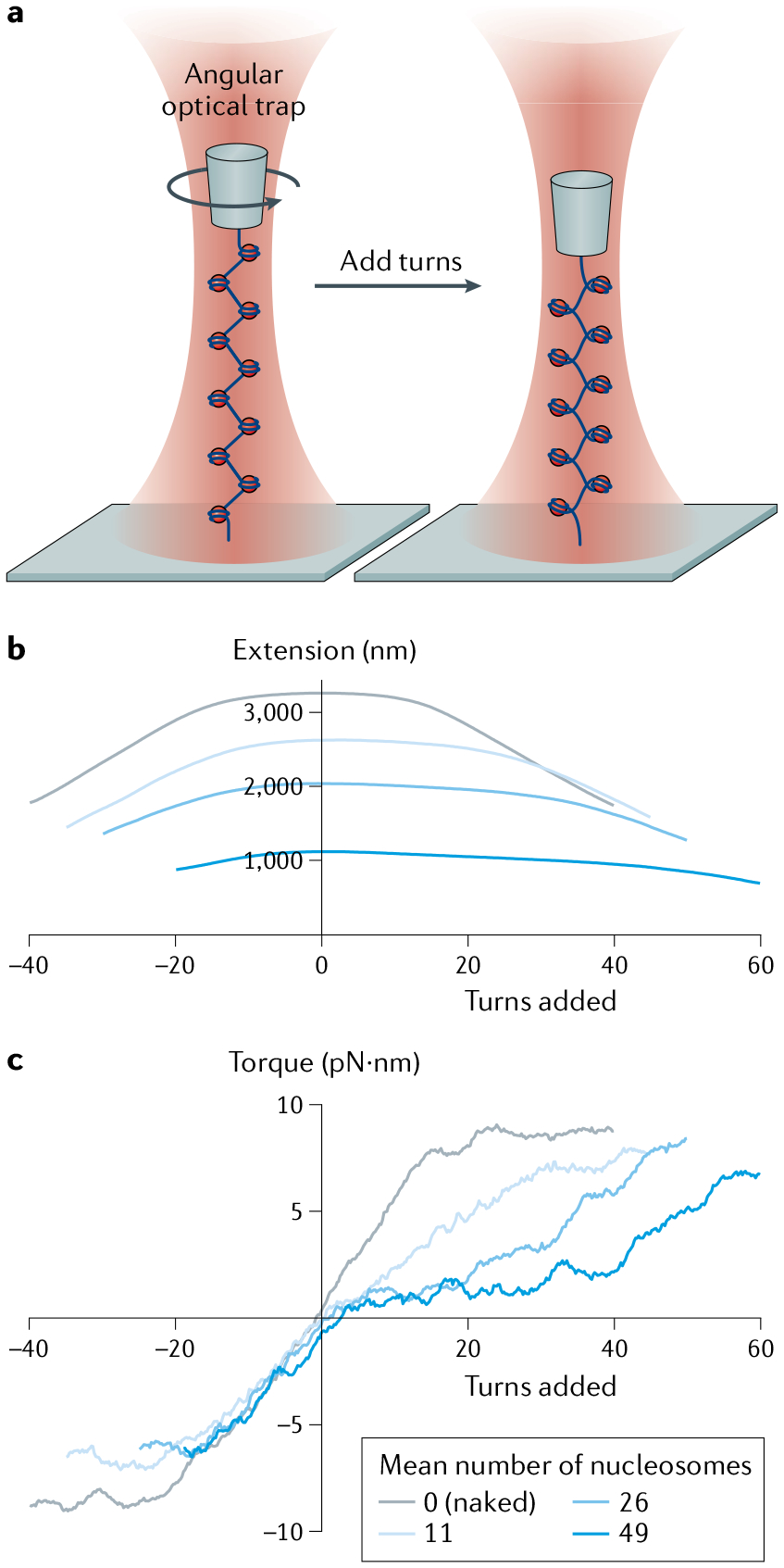
a | Experimental configuration for torsional measurements of a chromatin fibre. Angular optical tweezers are used to twist a chromatin fibre at 4 turns/s, while holding the chromatin fibre under a constant force of 0.5 pN. b | Resulting extension. c | Resulting torque. Measurements are conducted on chromatin fibres containing different numbers of nucleosomes. Extension and torque signals are smoothed by sliding windows of 1 turn and 4 turns, respectively. Torsional properties of each type of substrate may be determined from the torque–turn relation. Adapted with permission from REF.¹⁷¹, Elsevier.

In addition to the rotation mode, AOT can also operate in an active torque wrench mode where a constant torque is maintained on a trapped particle via active feedback on the input polarization angle⁹¹. This mode is best suited for applications where the measured torque is much greater than the torque noise. For applications requiring zero or extremely low constant torque, the passive torque wrench mode may be employed¹³⁴. In this latter mode, a constant optical torque is achieved by a rapid rotation of the laser polarization at a rate much greater than the rotational corner frequency of the cylinder, such that the trapped particle is not able to follow the rotation. This method bears some resemblance to that used during the torque detector calibration. This leads to a constant torque exerted on the particle, with the torque tunable by the polarization rotation rate. In both the active and passive torque wrench modes, torque is directly measured.

Applications

In this section, we discuss several key areas of research where optical tweezers have made revolutionary advances. Although the initial applications of optical tweezers were centred on cytoskeletal motors, the use of optical tweezers rapidly expanded into problems centred around nucleic acids, nucleic-acid based processes and protein folding. In this section, we hope to give the reader a sense of the types of problem that can be uniquely addressed with optical tweezers. Instead of providing an exhaustive list of the applications, below we highlight applications related to nucleic acids, protein–nucleic acid interactions, RNA and protein folding and unfolding, and mechanochemistry of nucleic acid-based motor enzymes.

Protein–nucleic acid interaction studies

DNA is an essential component of protein–DNA interactions, and thus its elastic properties play a direct role in regulating these interactions. In addition, DNA is often used as a molecular handle to study other processes, such as protein folding, and a thorough characterization of the DNA handles is required to subtract their contribution to the overall extension and twist.

Conventional optical tweezers and AOT are excellent tools for the measurement of DNA elastic parameters (BOX 2) such as the persistence lengths of dsDNA and single-stranded DNA (ssDNA)^32,105, the stretch moduli of dsDNA and ssDNA^32,105, the twist modulus of dsDNA^93,131,135 and the twist–stretch coupling modulus of dsDNA^136,137 (TABLE 1). The elastic parameters of single-stranded nucleic acids are known to be sequence-dependent^138,139, and thus only representative examples are shown in TABLE 1. These studies also showed that when subjected to high forces, dsDNA undergoes an overstretch phase transition^32,140–143, and, when subjected to twist, dsDNA transitions to different phases^{92,131,132,135,137}. These behaviours are concisely described in a force–torque diagram^8,93,135.

Table 1 |.

Intrinsic elastic parameters of nucleic acids

Parameter	Value
dsDNA persistence lengtha	53 nm (REFS103,249)
	43 nm (REF.105)
dsDNA stretch modulus	1200 pN (REF.105)
dsDNA twist persistence lengtha	100 or 107 nm (REF.93)
	102 nm (REFS131,250)
dsDNA twist-stretch coupling modulus	22 (REF.136)
	21 (REF.137)
ssDNA persistence lengtha	0.75 nm (REF.32)
	0.71 nm (REF.163)
ssDNA stretch modulus	800 pN (REF.32)
	420 pN (REF.163)
dsRNA persistence lengtha	60 nm (REF.251)
ssRNA persistence lengtha	1.3 nm (REF.183)
ssRNA stretch modulus	150 pN (REF.183)

Measurements were conducted under various physiological buffers. For simplicity, only representative average values are provided. Note that the values of these parameters depend on the ionic composition of the medium^183,252,253.

dsDNA, double-stranded DNA; dsRNA, double-stranded RNA; ssDNA, single-stranded DNA; ssRNA, single-stranded RNA.

^aMultiply by k_BT (where k_B is the Boltzmann constant, T is the temperature) to obtain the corresponding modulus.

Once the elastic properties of DNA have been well characterized, optical tweezers can then be used in various experimental configurations to investigate DNA processing enzymes and other protein–DNA interactions. Below, we highlight three primary configurations — stretching, unzipping and twisting — each tailored to a specific type of application.

The DNA stretching configuration is the most widely employed configuration and can operate under two primary modes: disruption mode or tracking mode (FIG. 7a). In the disruption mode, a DNA molecule is stretched to disrupt a bound protein, providing information on the disruption force and the length of DNA released from the disruption^144–147, which characterize the protein–DNA interactions in terms of the strength of the interaction and the amount of DNA associated with the interaction, respectively. In the tracking mode, a motor protein moving along DNA is anchored to a surface or trapped bead, whereas the upstream or downstream end of the DNA is anchored to another trapped bead or surface. The position of the motor protein on DNA is indirectly inferred from changes in the end-to-end distance between the motor protein and the end of the DNA^{29,31,148–153}. This approach is useful when studying processive motors such as RNA polymerase. For distributive motor proteins, that is, those displaying small processivity such as DNA polymerases, motor movement may also be tracked via the difference in elastic response between ssDNA and dsDNA³⁰. Advanced optical tweezers are capable of detecting motor movement at base pair-scale resolution^{39,40,124,154–156}.

Fig. 7 |. Example applications of optical tweezers to study protein–DNA interactions.

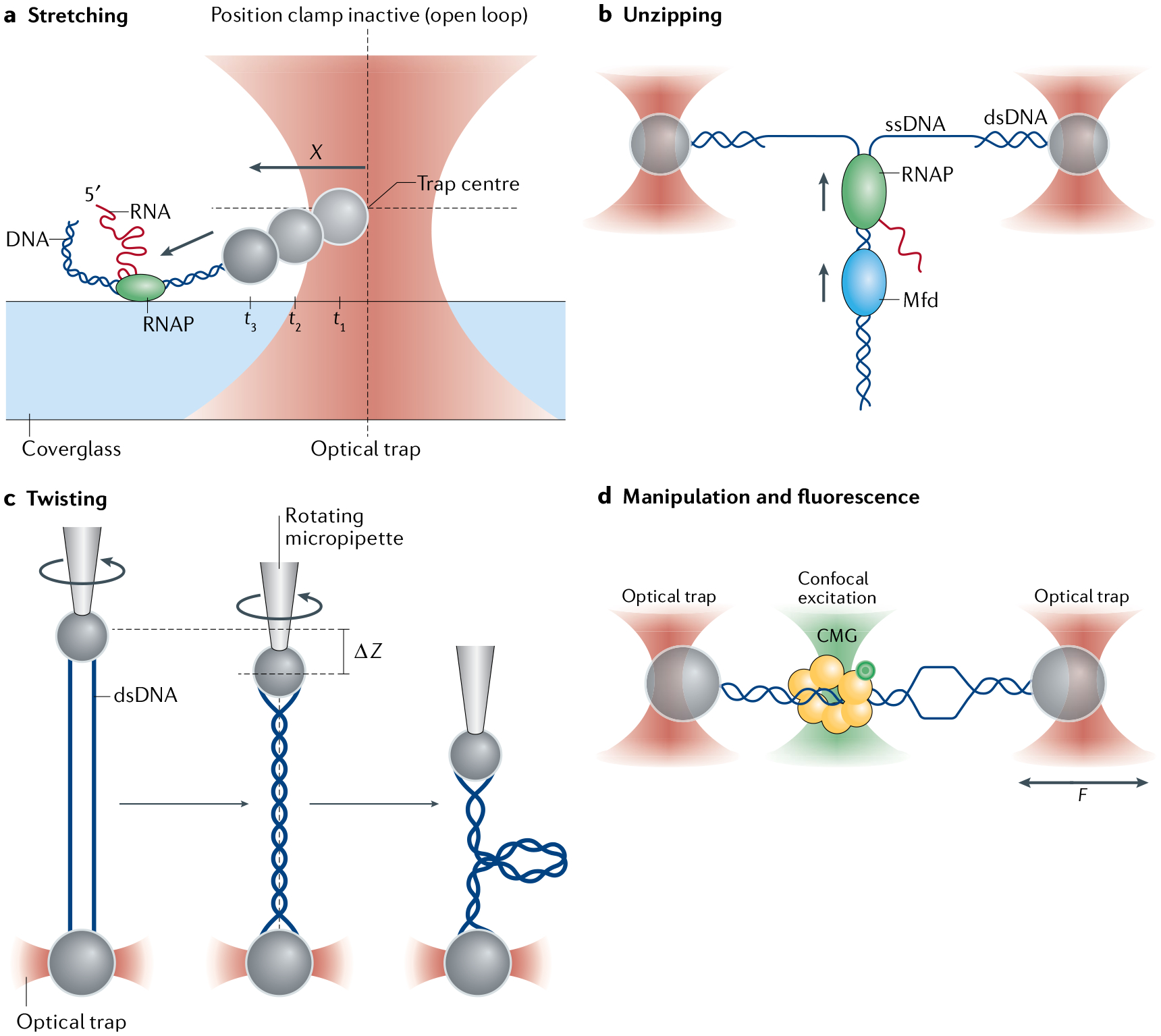
a | By stretching a double-stranded DNA (dsDNA) molecule, RNA polymerase (RNAP) is tracked in real time and stalled under an applied load¹⁴⁸. t₁, t₂ and t₃ represent three successive time points as the bead is pulled from the trap centre. b | By unzipping a dsDNA molecule, RNAP, which is trailed by another motor, Mfd, is tracked in real time¹⁶⁹. c | By twisting two dsDNA molecules via a combination of optical tweezers and a micropipette, a DNA braid is formed and used to study topoisomerase relaxation¹⁷⁴. d | By combining fluorescence detection and force manipulation, the replicative helicase CMG is observed to dynamically transition between single-stranded DNA (ssDNA) and dsDNA¹⁷⁸.

The DNA unzipping configuration can employ versatile and flexible modes of operation to probe protein–DNA interactions (FIG. 7b). In the ‘unzipping mapper’ mode, dsDNA is mechanically separated into two single DNA strands to disrupt bound proteins. This approach has been used to characterize the strength of the dsDNA base pairing as a function of sequence¹⁵⁷ or to generate a high-resolution map of both the locations and strengths of these protein–DNA interactions^158–162. Recent improvements in this technique enable detection of the absolute location at sub-base pair accuracy and precision¹⁶³. The ‘unzipping tracker’ mode allows detection of motor protein translocation without the need to tag the motor. Unlike the ‘unzipping mapper’ that disrupts a bound protein, this mode is typically operated under a constant force that is high enough to keep the DNA unzipped but low enough not to displace the motor protein off the DNA. The fork position indicates the location of a motor protein interacting with the fork junction via binding to either the ssDNA (as with helicases and DNA polymerases)^164–168 or the dsDNA (as with dsDNA translocases)¹⁶⁹. If the motor moves towards the fork, the DNA is re-zipped, whereas if the motor moves away from the fork, the DNA is unzipped. A variation of the ‘unzipping tracker’ mode is the ‘unzipping staller’ mode that uses the DNA fork as a barrier to stall a DNA translocase moving towards the fork¹⁶⁹.

Finally, the DNA twisting configuration using the AOT (FIG. 7c) allows studies of biological processes under both torsion and force. Some examples include disrupting protein–DNA interactions under torsion¹⁷⁰, measuring the torsional stiffness of a substrate (for example, single and braided chromatin fibre)¹⁷¹ and measuring torque generated by motor proteins^172,173. In addition, optical tweezers can be combined with other manipulation tools such as a rotary micropipette and a rotor bead, providing alternative means of investigating torque and rotation of DNA-based processes^{93,136,153,174}.

Fluorescence allows visualization of the locations of molecules, such as proteins and regions of dsDNA and ssDNA^{60,63,75,81,175–178}, as well as detection of conformational dynamics^72,77,179 (FIG. 7d). More complex DNA geometries can be used to enable investigation of correspondingly more complex processes. For example, proteins mediating the bridging of two DNA molecules are detected whereas the two DNA molecules are manipulated using multiple optical traps^180,181. A DNA ‘Y-structure’ technique, mimicking a DNA replication fork, allows a bound protein to be visualized while the DNA is simultaneously stretched, unzipped and twisted¹⁸².

Optical tweezers have also been employed to determine single-stranded RNA and double-stranded RNA elastic parameters^183,184 (TABLE 1). These RNA elastic properties have enabled the investigation of RNA-interacting proteins such as RNA helicases that unwind double-stranded RNA^164,185 and the ribosome that translocates on single-stranded RNA and invades double-stranded RNA structures^73,186–188.

Protein folding studies

There are several reasons for using controlled force to study molecular folding. First, the application of the force establishes both a well-defined reaction coordinate and a potential energy surface over which the molecule’s folding/unfolding transitions take place. Second, unlike its thermal and chemical counterparts, which act globally, force is a selective denaturant that can be applied to one part of the molecule without acting on another. Finally, force may be the more biologically relevant denaturing agent: proteins targeted for destruction in the cell are processed by specialized molecular machines that use the energy of ATP hydrolysis to generate force and mechanically unfold their client proteins^44,49.

During folding, proteins often populate intermediate states. Although it is difficult to determine whether these intermediates are on-pathway or off-pathway to the native form using bulk studies, optical tweezers folding studies have made it possible to characterize the nature of these intermediates. Cecconi et al. studied RNaseH and found that the molecule unfolded at 19 pN and refolded at ~5 pN, populating an intermediate that was shown to be on-pathway or obligatory to the native state⁴⁵, as attaining the native state occurred invariably from the previously formed, transient intermediate. Further characterization of this intermediate revealed that it was a molten globule state.

Using passive-mode optical tweezers, Stigler et al. characterized the folding pathway of calmodulin, a eukaryotic Ca²⁺-binding protein made up of amino and carboxy-terminal domains, each of which is formed by two EF-hand motifs⁴⁷ (FIG. 8a). Full and truncation fragments of the protein were used to uncover up to six states in the folding pathway using an ultra-stable instrument and applying a hidden Markov model analysis (FIG. 8b). Transitions between different states but involving similar changes in extension were distinguished by the lifetimes of the initial and final states or by their different connectivities to other states. The authors determined the complete native folding and misfolding pathways.

Fig. 8 |. Example applications of optical tweezers to study protein folding.

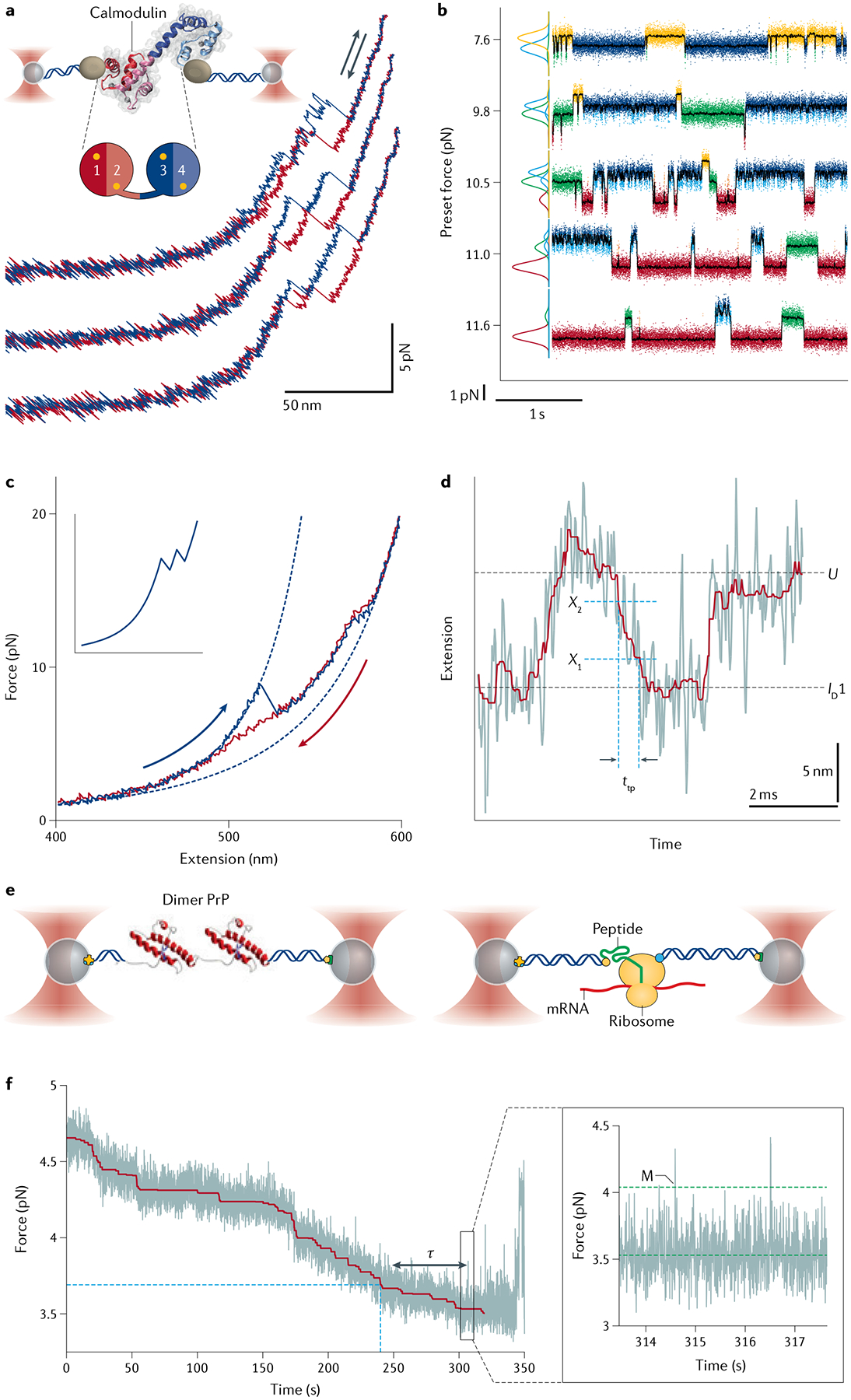
a | Experimental geometry and representative force–extension curves for studying the folding and unfolding of single calmodulin molecules. Stretch and relax cycles are shown in blue and red, respectively. b | Traces of wild-type calmodulin showing folding/unfolding transitions at different preset forces. Data taken in a passive mode. As the preset force increases, the equilibrium is tilted from the native folded state (yellow, all four EF hands folded, F₁₂₃₄) to the unfolded state (red). Four intermediates (blue, F₁₂₃ folded; cyan, F₁₂ or amino-terminal domain folded; green, F₃₄ or carboxy-terminal domain folded; orange, F₂₃ folded) are also populated in a force-dependent manner. Gaussian fits to histograms of each state are shown on the left⁴⁷. c | Force–extension curves for studying the misfolding of prion protein (PrP) dimers. Unfolding (blue) and refolding (red) curves show the formation of stable non-native structures, in contrast to the expected sequential unfolding of independently folded native domains (inset). d | Transition path time (t_tp) for misfolding measured from constant-force trajectories. Barrier region defined by boundaries X₁ and X₂ (REF.¹⁹³). e | Left: experimental geometry for studying the PrP dimers. Right: experimental geometry for studying co-translational folding. DNA handles are attached to the N terminus of the nascent chain and the ribosome itself. f | Example trajectory of real-time translation elongation. The force decreases as the tether gets longer. Blue dashed line corresponds to the codon position where folding would begin under equilibrium conditions. Inset: zoom image showing the folding transitions. I_D1, first dimer intermediate state; M, misfolded state; mRNA, messenger RNA; τ, non-equilibrium delay prior to folding²¹⁰; U, unfolded state. Parts a and b adapted with permission from REF.⁴⁷, AAAS. Parts c, d and e (left panel) adapted with permission from REF.¹⁹³, PNAS. Parts e (right panel) and f adapted from REF.²¹⁰, Springer Nature Limited.

The question of whether individual domains within a protein fold or unfold cooperatively has been investigated using optical tweezers. Shank et al. investigated the folding/unfolding cooperativity of the N-terminal and C-terminal subdomains of T4 lysozyme⁴⁶. This protein is organized in a re-entrant topology in which the first 12 residues of the N terminus fold as a helix with the C-terminal domain in the tertiary structure. When pulled across both domains, the protein showed a single ‘rip’ (~50 pN) corresponding to the concerted unfolding of both domains. When relaxed, the protein displayed a single ‘zip’ (at ~5 pN) reflecting the simultaneous refolding of both domains. When the force was only applied to the N terminus of the full protein, a single shorter unfolding rip was observed at even higher forces, suggesting that the process also involved the unfolding of the C terminus. Because the unfolding and refolding occurred out of equilibrium, the Crooks fluctuation theorem (BOX 4) was used to obtain the free energy of unfolding of the N-terminal domain. The value was 12.3 kcal/mol, very close to the 14.1 kcal/mol determined for the unfolding of the whole protein by bulk methods, indicating that unfolding of the N-terminal domain led to the unfolding of the C-terminal domain, demonstrating strong coupling and cooperativity in the folding/unfolding transitions of both domains. A circular permutant version of the protein that eliminates its re-entrant topology displayed two unfolding/refolding transitions, indicating that its topology was responsible for the folding cooperativity of the wild type. The authors speculate that evolution may have favoured re-entrant topologies to ensure coordinated folding of domains.

Protein misfolding is likely favoured by the ruggedness of their folding energy landscapes, leading to aggregation. Prion proteins (PrPs) are known to misfold and produce self-propagating aggregated states. Yu et al. showed that the PrP transiently populates three different misfolded states not detected by bulk methods¹⁸⁹ (FIG. 8c–e). All three states only formed from the unfolded state. By contrast, folding to the native state occurred as a simple two-state process. Optical tweezers have also been used to resolve some of the complexities arising from intra-domain and inter-domain misfolding in large, multidomain proteins. Jahn et al. dissected the folding of HSP90, a molecular chaperone that functions as a homodimer, with each monomer made of N-terminal, middle and C-terminal domains^48,190. Isolated, the N-terminal and middle domains exhibit very fast misfolding. Interestingly, the folding rates for these isolated N-terminal and middle domains are maximal at approximately 3.5 pN and lower at smaller forces, indicating that the potential energy surface bifurcates into a folding and a misfolding path, and that tension suppresses the latter over the former⁴⁸. Likewise, force also appears to reduce inter-domain interference and misfolding, as the probability of correct folding is higher at 1.8 pN than at 0.6 pN.

Guinn et al. combined a chemical denaturant, mechanical force and site-directed mutagenesis to investigate the two-state folding of the SRC SH3 domain¹⁹¹. These authors showed that the SRC SH3 domain unfolds through a single pathway when pulled in an unzipping geometry, but through two alternative pathways, in a force-dependent manner, when unfolded through a shearing geometry. The existence of these two trajectories was further established using a ϕ–value analysis that describes the effect of a single amino acid mutation on the stability of the transition state. To better characterize the folding intermediates in T4 lysozyme, Motlagh et al. used small molecules that stabilize the folded state in a manner proportional to the change in accessible surface area upon folding (osmolytes)¹⁹². The response of an on-pathway intermediate to two different osmolytes, characterized by optical tweezers, allowed these authors to identify it as the C-terminal domain.

The time spent by a molecule crossing the folding barrier (the transition path time) is intrinsically stochastic, thus precluding direct observation by bulk or ensemble experiments. Single-molecule methods are uniquely suited for transition path time measurements. The time resolution of optical tweezers is determined by the corner or roll-off frequency of the instrument. The corner frequency is equal to the ratio of the trap stiffness to the drag coefficient of the trapped bead, both a function of bead size. Smaller beads lead to weaker traps (lower trap stiffness), whereas the drag coefficient of the beads scales linearly with the bead radius. For reference, for a trap with a stiffness of 1 pN/nm and a bead diameter of 1 μm, the time resolution is ~10 μs. Yu et al. determined a transition path time for PrP from the diffusion constant of the protein over its energy landscape, obtaining a value of 2 μs from the unfolded to the native transition¹⁹³. The transition path time from the unfolded to a misfolded state was 500 μs, which the authors interpreted as reflecting a significantly more rugged landscape (FIG. 8d). They speculate that proteins may have evolved to avoid non-productive interactions, yielding minimally frustrated and smooth energy surfaces. Neupane et al. have determined the transition path time directly using stiff optical tweezers with high temporal resolution¹⁹⁴.

Despite decades of research, a central question remains in protein folding: how the native fold is arrived at in such a way as to avoid Levinthal’s paradox¹⁹⁵. According to the energy landscape model^196–198, proteins attain their native state through many alternative folding pathways over a funnel-shaped energy landscape. In this search, involving bond rotations of each individual residue, the molecule is somehow guided to attain increased native as opposed to non-native interactions by details encoded in the energy landscape. The alternative view, supported by some experimental observations^199–201, is the defined-pathway model, which posits that proteins fold in discrete steps through units of 20–30 residues or foldons. In this view, the complexity of the search for the native fold is greatly reduced by the ‘modular’ character lent by larger multi-residue folding units (foldons), whose sequence encodes the necessary intra-foldon interactions that drives them to fold cooperatively, and possibly sequentially, through inter-foldon interactions, to bring about the native state. Single-molecule folding studies can possibly throw some light onto the discussion. For example, proteins containing multiple domains, which could be seen as larger cooperative folding elements or ‘super foldons’, are seen more often than not to attain their native form in a well-defined order often requiring some degree of inter-domain coupling¹⁶⁶.

The analysis of barrier crossing of a PrP into its first intermediate¹⁷³ reveals diverse molecular trajectories, which have been interpreted as confirming the multiple pathways predicted by the energy landscape model²⁰². However, these same authors found that the distribution of transition path times are exponentially distributed, which is to be expected from the dynamics of a well-defined path²⁰³. These authors point out that the transition through this path is by no means deterministic and small stochastic deviations in the bond rotational configurations at the amino acid residue level may give rise to the heterogeneity of the molecular trajectories observed. Although the controversy at this point has not been resolved, it is likely that the ability to observe the folding trajectories of individual molecules may provide the crucial discrimination between the two models.

The effects of molecular chaperones on protein folding have been investigated using optical tweezers. Bechtluft et al. showed that chaperone SecB prevents the folding of the periplasmic-resident maltose-bonding protein (MBP), thus favouring its insertion into the membrane in the unfolded state²⁰⁴. A similar effect on the folding of MBP was determined by trigger factor, a chaperone known to interact with fully synthesized and nascent chains on the surface of the ribosome²⁰⁵. Unlike SecB, which prevents the folding of the protein, trigger factor seems to locally interact through different sites with the client protein, allowing it only to fold partially. Interestingly, both of these chaperones prevent the misfolded states resulting from the interaction among tandem repeat copies of MBP, suggesting that they may play such a role in preventing undesirable inter-domain misfolding^204,205. During EF-G biosynthesis, the ribosome destabilizes domain II of this GTPase, favouring its interaction with the emerging G domain of the nascent protein and leading to a misfolded state between the two domains. Liu et al.²⁰⁶ showed that trigger factor prevents this interaction. The HSP70 chaperone DnaK binds client proteins transiently in its ATP-bound state, but tightly upon nucleotide hydrolysis. Using optical tweezers, Mashaghi et al.²⁰⁷ found that in addition to its known function of preventing non-native contacts in proteins by binding to their unfolded regions, DnaK stabilizes the core domain of MBP against mechanical unfolding, a conclusion supported by a similar effect of this chaperone observed in bulk on its true client protein RepE.

Optical tweezers were used to characterize the folding of nascent chains on the ribosome surface. Kaiser et al. showed that the refolding of T4 lysozyme tethered by a linker to a ribosome is slowed down >100 times compared with the protein in solution⁵⁰. The slowing down was greater with shorter linker length, and the effect was shown to be electrostatic in nature. In solution, a truncated T4 lysozyme shortened by 15 amino acids from its C terminus misfolded, whereas the same polypeptide on the surface of the ribosome did not fold. Thus, ribosome–nascent chain interactions might delay premature misfolding until sufficient sequence has been synthesized to enable productive folding. A similar effect was observed for the N-terminal G domain of EF-G^206,208. Nascent chain–ribosome interactions also prevent misfolding with other parts of the nascent polypeptide. Misfolding between the two N-terminal domains (G domain and domain II) was markedly reduced on the surface of the ribosome relative to the polypeptide in solution, yielding faster productive folding²⁰⁶.

Finally, optical tweezers have been used to follow the co-translational folding of polypeptides in real time using in vitro reconstituted translation systems. In these experiments, a ribosome is tethered to a bead via a DNA handle and the N terminus of the nascent chain is tethered to another bead via another DNA handle (FIG. 8e). The growth of the polypeptide appears as a lengthening of the end to end distance of the tether, whereas folding transitions are seen as sudden shortening events. Wruck et al. described gradual hydrophobic collapse and partial folding during synthesis²⁰⁹. Using ultra-stable high-resolution optical tweezers, Alexander et al. followed translation of calerythrin in real time²¹⁰, where a misfolding event that occurs readily with polypeptide fragments in vitro, and more slowly but still rapidly in stalled ribosome–nascent chain complexes, was delayed during active translation by an average time of 63 s, presumably to give time for synthesis to complete or for a chaperone to bind (FIG. 8f). Thus, folding on the surface of the ribosome can be a non-equilibrium process. Stalled ribosome–nascent chain complexes do not show delayed misfolding because the nascent chain reaches conformational equilibrium during the preparation of the sample for the optical tweezers, a process that typically takes tens of minutes.

Mechanochemistry of molecular motor operation

Many essential cellular processes take place in a directional manner and are catalysed by nanometre-scale enzymes known as molecular motors^211,212. Ever since the first motor proteins (kinesin and myosin) were discovered^213,214, optical tweezers have been instrumental in characterizing these energy-consuming, force-generating microscopic machines^{18,26,27,105,148}. The high spatio-temporal resolution of optical tweezers (ångstrom-scale movement at sub-second bandwidths³⁴) makes it possible to directly visualize the step size of a motor, one of its fundamental properties. For example, the Escherichia coli RNA polymerase (RNAP) was observed to translocate on the dsDNA template in 1-bp (or 3.4-Å) increments^39,124 (FIG. 9a–c). Base pair stepping was also observed for other motors such as the HCV NS3 (REF.¹⁸⁵) and XPD¹⁵⁶ helicases. A hairpin-unwinding geometry is commonly used for the study of DNA/RNA helicases including the SARS-CoV-2 replicative helicase nsp13 (REF.²¹⁵), in which each base pair of the hairpin substrate opened by the helicase results in an increase in tether extension by two nucleotides. The same geometry was employed to follow the translational dynamics of the ribosome (FIG. 5d), which normally translocates on messenger RNA (mRNA) one codon at a time^186,187. Moreover, the ribosome can also take sub-codon steps in the presence of a strong barrier such as a stable mRNA hairpin⁷³, or larger step sizes at a slippery sequence (a stretch of mRNA where the ribosome tends to change its reading frame)¹⁸⁸. The detection of a motor’s step size provides critical insight into its internal coordination²¹⁶. For example, the finding that the bacteriophage φ29 DNA packaging motor took non-integer 2.5-bp steps — which make up 10-bp translocation cycles — suggested that four, rather than five, subunits of this homopentameric ring ATPase participate in DNA translocation¹⁵⁴ (FIG. 9d–f). This insight led to a ‘division of labour’ model in which the fifth subunit adopts a distinct regulatory role by making specific contacts with DNA to initiate each cycle^155,217,218, which informs the internal coordination among the subunits of the motor.

Fig. 9 |. Example applications of optical tweezers to study molecular motors.

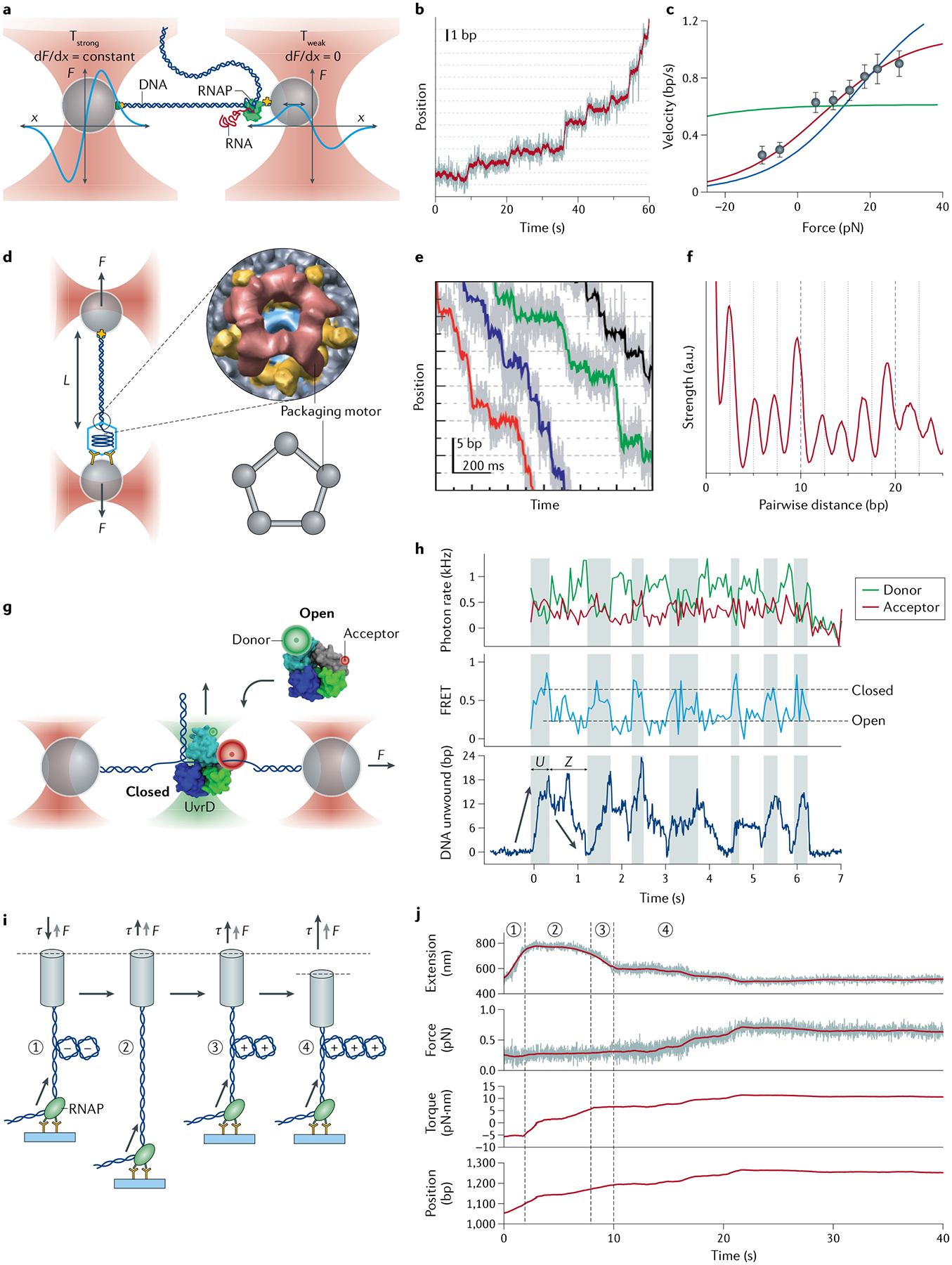
a | Dual-trap optical tweezers set-up for observing the stepping behaviour of Escherichia coli RNA polymerase (RNAP). Schematic force (F) versus position (x) profiles for both traps are shown in cyan. A passive force clamp is maintained in the weak trap (T_weak) on the right. b | Representative trajectory showing a single RNAP translocating on its DNA template in discrete steps. Dotted lines are spaced at 3.4-Å (1-bp) intervals. c | Force–velocity relationship for RNAP at [NTP]_eq = 10 μM GTP, 10 μM UTP, 5 μM ATP and 2.5 μM CTP. Fits to a power stroke model (green), a linear Brownian ratchet model (blue) and a branched Brownian ratchet model (red) are shown³⁹. d | Dual-trap optical tweezers set-up for studying DNA packaging by the bacteriophage φ29 packaging motor, a pentameric ring ATPase. The DNA tether length (L) is monitored as a function of time. e | Representative single-molecule packaging trajectories collected with 250 μM ATP and an external force of ~40 pN. Dotted lines are spaced at 2.5-bp intervals. f | Pairwise distance distribution (PWD) averaged from many packaging trajectories indicates the motor’s step size¹⁵⁴. g | Fleezers set-up for studying the conformational dynamics and DNA unwinding behaviour of the E. coli UvrD helicase. h | Simultaneous measurements of donor/acceptor fluorescence, Förster resonance energy transfer (FRET) efficiency and number of DNA base pairs unwound enable direct correlation of the conformational states of UvrD (‘Open’ and ‘Closed’) with the motor’s helicase activity (rezipping ‘Z’ and unwinding ‘U’)⁷². i | Angular optical tweezers (AOT) set-up for studying the transcriptional dynamics of the E. coli RNAP under torsion. j | Representative data of simultaneous force (F), torque (τ) and extension measurements. Under a low-force clamp, RNAP translocation first neutralizes the preformed (−) plectoneme and then induces the formation of (+) plectoneme. After the force clamp is turned off, RNAP continues to translocate along the DNA template, resulting in an increase in force and the corresponding torque until reaching a stall¹⁷². Parts a–c adapted from REF.³⁹, Springer Nature Limited. Parts d–f adapted with permission from REF.⁷³, Elsevier. Parts g and h adapted with permission from REF.⁷², AAAS. Parts i and j adapted with permission from REF.¹⁷², AAAS.

The term mechanochemistry refers to the mechanism by which a molecular motor couples chemical energy (for example, from ATP hydrolysis) to mechanical motion and force²¹⁹. Similar to its effects on folding, external force — which can be precisely applied by optical tweezers — tilts the free energy landscape along the pulling coordinate that, if designed appropriately, overlaps with the mechanical reaction coordinate of the motor under force. By measuring the dependence of motor velocity on force (F–v relationship), one can distinguish between different classes of mechanisms for force generation and mechanochemical coupling. For example, F–v studies on both bacterial^29,39,148 and eukaryotic^152,220,221 RNAPs, combined with theoretical modelling^222–224, converge on a model in which RNAP operates as a Brownian ratchet (FIG. 9c). In this mechanism, the enzyme oscillates between multiple adjacent positions on the DNA lattice driven by thermal energy; these reversible motions are rectified by the binding of an incoming nucleotide to the active site of RNAP such that net forward translocation is achieved. Similarly, measuring the translation velocity against an applied force by directly tethering the ribosome to a bead, in contrast to the aforementioned hairpin-unwinding geometry, reveals that the ribosome is also a Brownian ratchet motor, generating a maximum force of ~13 pN, just enough to unwind most mRNA secondary structures²²⁵. This mechanism contrasts with the power stroke mechanism adopted by motors such as kinesin²²⁶ and the φ29 DNA packaging motor¹⁵¹, in which motor movement is directly coupled to a largely irreversible chemical transition²²⁷.

By obtaining F–v curves at different substrate (such as ATP) concentrations, one can deduce the Michaelis–Menten kinetic parameters of the motor across force regimes. This information is useful for identifying the location of the force-generating movement step in the motor’s operating cycle^57,211. For example, the φ29 DNA packaging motor exhibits force-sensitive maximum velocity V_max and Michaelis constant K_M, but its V_max/K_M ratio is force-insensitive¹⁵¹. This phenotype rules out ATP binding or any chemical transition within the same kinetic block as ATP binding — including ATP tight-binding and ADP release — as the power stroke step, which led to the conclusion that DNA translocation by the φ29 ATPase is powered by the release of inorganic phosphate upon ATP hydrolysis¹⁵¹. Similar analysis of the force dependence of the Michaelis–Menten parameters was employed to dissect the force-generating mechanism of the ClpXP protease²²⁸ and the SpoIIIE DNA translocase²²⁹. The former uses a constant pulling rate but different gears to translocate polypeptides, whereas the latter displays a biphasic F–v curve that may represent an adaptive mechanism for ultrafast motors such as SpoIIIE to aptly remove DNA-bound roadblocks.

The combination of single-molecule fluorescence spectroscopy with optical tweezers enables multiple aspects of the motor behaviour to be concomitantly measured. For example, fleezers were utilized to follow simultaneously the unwinding activity and the conformational state of UvrD, a DNA repair helicase⁷² (FIG. 9g,h). It was found that UvrD possesses a conformational switch that controls on which strand of the DNA duplex the helicase translocates. Interconversion between the two conformations leads to intermittent periods of DNA unwinding and rezipping. Such a co-temporal fluorescence detection and force manipulation approach was recently applied to other molecular motors, including the ribosome during protein synthesis⁷³, the polypeptide translocase ClpB⁶¹ and the eukaryotic replicative helicase CMG¹⁷⁸.

The ability to monitor additional degrees of freedom, such as rotation, facilitates the study of biological motors that generate twist and torque in conjunction with force. For instance, AOT was employed to measure the stall torque and the torque–velocity relationship for the E. coli RNAP¹⁷², establishing the polymerase as a potent torsional motor (FIG. 9i,j) that generates DNA supercoiling during transcription. It was subsequently shown that transcription factors regulate the capacity of RNAP to deal with the torsional stress stored in DNA¹⁷³, which can be further modulated by the chromatin fibre topology in eukaryotes¹⁷¹.

Reproducibility and data deposition

Optical tweezers experiments present numerous challenges in terms of data reproducibility. The first challenge has to do with the low-throughput nature of the experiments and the relatively low statistics derived from them. Although each single-molecule recording affords rich information on the dynamics of that molecule, it is critical that enough replicates are obtained (typically tens to hundreds) so that the full spectrum of behaviours across a population is surveyed. This is particularly important when the population exhibits significant molecular heterogeneity, either from variation between distinct subpopulations (static heterogeneity) or due to interconversion of the same molecule among multiple states over time (dynamic heterogeneity)²³⁰. Both types of heterogeneity have been observed in diverse experimental systems^{150,231–233}. They must not be confused with the intrinsic stochastic nature of single-molecule dynamics, which entails that no two molecules — even those with identical kinetic parameters — behave the same. Given these sources of variations, single-molecule researchers should strive to report the full distribution of molecular behaviours observed and disclose the criteria used for excluding any molecules from analysis. Generally, acceptable exclusion includes multiple tethers, functionally inactive molecules and obvious aggregates. It is thus critical to obtain samples as biochemically homogeneous as possible prior to single-molecule experiments.

Although there is no universal standard as to how many molecules constitute a sufficiently large sample size (as this necessarily depends on the extent of heterogeneity and the ease of data collection), one should ensure that the results can be reproduced across multiple days and multiple batches of samples, and, if possible, independently examined by multiple researchers. When presenting results, one should always report errors associated with the measurements and statistical test results when making a comparison between conditions. As the data tend to segregate in classes, it is also important to confirm that the existence of these classes can be corroborated using independent methods and that, when averaged together, the signals recover the behaviour observed in ensemble or bulk experiments. These practices will help minimize implicit biases against undesired results, and to prevent any rare but meaningful behaviour from being overlooked. However, caution must be exercised when extrapolating single-molecule results to bulk measurements, as they often do not measure the same experimental variables.

The other challenge against reproducibility has to do with the various instrumental configurations, experimental settings and data analysis pipelines developed in different laboratories, which make a straightforward comparison between studies difficult. Although not unique to optical tweezers, this problem is exacerbated by the complex and adaptable nature of this technology. Therefore, the methods section of a research article should include detailed technical descriptions such as how the data were filtered, what parameters were chosen for theoretical fitting and which statistical tests were performed.

No standard for data repository and format exists to date. Therefore, the community should converge on a set of practices to standardize the open data format (for example, the HDF5 format) as well as deposit raw data (force, extension, kymograph and so on) and analysis algorithms into open-source repositories, facilitating easy access and re-examination of published results. These practices are already widely adopted with other methodologies in fields such as structural biology and genomics. Moreover, a multi-laboratory endeavour to benchmark different optical tweezers-based protocols (for example, of particular trap stiffnesses and pulling speeds) using a simple and common assay (such as unfolding a particular DNA hairpin or protein), akin to the one recently conducted by the single-molecule FRET community²³⁴, may be desirable.

Limitations and optimizations

In this section, we discuss limits to the temporal and spatial resolution, speed of manipulation and throughput of optical tweezers. The temporal resolution of an instrument can be limited by the type of sensors used for detecting bead displacements. Some silicon-based photodetectors exhibit parasitic low-pass filtering above 10 kHz when illuminated with wavelengths >850 nm, above the absorption maximum of silicon²³⁵. Photodetector low-pass filtering results in inaccurate measurements of signals at frequencies >10 kHz, including those from bead Brownian motion that can lead to calibration errors. This effect can be mitigated by using non-silicon-based detectors or infrared-enhanced silicon detectors^6,83 with which data can be collected at rates exceeding 100 kHz using the appropriate data acquisition card.

Nonetheless, the maximum measurement bandwidth is usually not limited by instrumental factors but, rather, by the trapped beads themselves. Because of the hydrodynamic drag experienced by the beads as they move through a fluid, there is a fundamental limit to how fast they can respond to mechanical signals. A trapped bead has a characteristic frequency f_c, above which signals are damped by the viscous drag⁶. f_c depends on the system stiffness and bead size according to Eq. 4. For example, a 1-μm diameter bead and stiffness of 1 pN/nm corresponds to a characteristic frequency of 17 kHz or a temporal resolution of ~10 μs. Temporal resolution can thus be increased by using stiffer systems. In some cases, it can also be increased by decreasing the bead size, although there are practical limits to trapping polystyrene or silica beads smaller than ~200 nm because the polarizability α (see Eq. 1) decreases as the particle volume decreases⁶. In general, smaller beads require higher laser intensities to attain equivalent forces, increasing the chances of sample damage. Recent work has shown that germanium nanoparticles, whose high refractive index compensates for their small size (as small as ~70 nm), are usable for single-molecule optical trap experiments²³⁶. The characteristic frequency f_c of the bead can also affect the dynamics of the biological system under investigation. One study has shown that the rates of some DNA-processing enzymes depend inversely on bead size, because the rate of bead thermal motion controls the rate at which transition states are visited by these enzymes²³⁷.

The spatial resolution of an optical trap is limited, in part, by instrumental sources of noise. Drift in the sample stage position or objective and fluctuations in trap position or power can all lead to bead displacements that are indistinguishable from signals. Various approaches have been developed to improve instrument stability. In single-trap, surface-based assays, the sample stages can be monitored and stabilized by a feedback loop to better than 1 Å in x, y and z^9,37. Drift in the laser focus (particularly along z) due to heating of the objective by absorption of the trap light can be reduced greatly by temperature control of the objective³⁶. Power stability can also be improved by monitoring the trap laser intensity with a photodetector and adjusting the laser power by feedback loop to compensate for intensity fluctuations^43,83. Fibre coupling⁶, in which the laser light is transmitted through an optical fibre, can help improve pointing stability. In dual-trap designs where both traps are formed from the same laser, minimizing differences in the optical paths taken by the two trap-forming beams reduces fluctuations affecting trap separation^51,124.

However, even if all sources of instrument noise are eliminated, there remains a fundamental limit to the spatial resolution — the Brownian motion of the trapped beads^9,34,51. A useful figure of merit for quantifying spatial resolution is the signal to noise ratio (SNR). The maximum possible SNR is given by the ratio of the bead displacement Δx to the root mean square fluctuation in bead position $\sqrt{\langle x^2\rangle }$ due to Brownian motion, calculated by integrating Eq. 3 over the measurement bandwidth B. Assuming B ≪ f_c, it can be shown that the maximum SNR depends on the tether stiffness κ_tether and the drag coefficient of the beads γ as^34,40:

$$SN{R}_{x,\text{max}}=\frac{\Delta x}{\sqrt{\langle x^2\rangle }}=\frac{{\kappa }_{\text{tether}}\Delta \ell }{\sqrt{4k_{\text{B}}T{\gamma }_{\text{eff}}B}}$$ (9)

where Δℓ is the signal of interest, γ_eff = γ for a bead in a single trap and γ_eff = γ/2 for identical beads in dual traps. Importantly, neither the trap stiffness nor the operation mode (such as active versus passive mode) impacts the resolution^34,40. As a result, it is advantageous to design experiments with small beads, subjected to the limitations mentioned above, and stiff tethers if possible. In applications where the tether is DNA-based, stiff tethers are typically achieved by making them as short as possible and by pulling to high force, although recent work with rigid, self-assembled DNA ‘origami’ beams holds promise for high-resolution measurements²³⁸. Assuming reasonable experimental values — for example, beads 1 μm in diameter and a tether stiffness of 0.3 pN/nm (equivalent to that of a 1-μm dsDNA molecule pulled to a force of ~10 pN⁴⁰ or a single kinesin at its stall force²³⁹) — Eq. 9 predicts that a 1-nm signal collected at a 100-Hz bandwidth would be detected with a maximum SNR from 2.5 (for a single trap) to 3.5 (for identical dual traps). Eq. 9 can be used to derive a similar expression for the force resolution of an optical trap:

$$SN{R}_{F,\text{max}}=\frac{\Delta F}{\sqrt{4k_{\text{B}}T{\gamma }_{\text{eff}}B}},$$ (10)

where ΔF is the force signal. The force resolution is thus also independent of trap stiffness. Finally, the spatial (and force) resolution is intrinsically related to the temporal resolution, as temporal averaging of the data reduces the noise by a factor proportional to the square root of the averaging window (reflected in the dependence on measurement bandwidth B in Eqs 9 and 10). Thus, there is a trade-off between spatial and temporal resolution: under identical conditions, a fourfold increase in temporal resolution leads to a twofold decrease in spatial (and force) resolution.

Manipulation speeds are another important consideration, particularly for constant force measurements, which may require feedback control of the trap position. If the signal of interest changes at a rate faster than the speed at which the sample stage or trap position is controlled, then the instrument cannot maintain a constant force. As a general rule, piezo-actuated linear or mirror stages offer fairly slow scan rates below ~1 kHz (REFS^6,51). Other technologies to control the trap position, such as acousto-optic and electro-optic deflectors, which do not rely on moving parts, can achieve much higher scan rates exceeding ~1 MHz (REFS^6,83). The choice of technique for controlling the trap position must be made when designing the instrument. An alternative passive force clamp²² method that exploits the edge of the trapping potential can be used to exert constant forces without the need for feedback control of the trap position. This approach can exert constant forces at higher frequencies than possible with piezo-actuated stages, but the distance range over which constant force is maintained is limited to ~50 nm (REF.²²). Again, however, the characteristic frequency of the trapped beads sets a fundamental speed limit to any manipulation approach.

In contrast to standard optical tweezers, an AOT instrument is significantly more complex in terms of instrument design and control as well as data acquisition and processing. In particular, the linear polarization of the laser input to the objective needs to be maintained, and deviations from linear polarization need to be carefully monitored and corrected. AOT also require trapping particles with specific anisotropic optical properties (such as quartz cylinders). These particles are not commercially available and must be nanofabricated. Precision torque measurements require smaller cylinders, whereas high force generation requires larger cylinders, so these two considerations must be balanced for a given experiment.

One important limitation of optical tweezers is their low throughput. Although the data produced by optical traps are rich in detail owing to the sensitivity of optical traps, this high information content comes at a cost in throughput. Every bead and tether is individually manipulated, and data are collected one molecule at a time. By contrast, other single-molecule approaches such as magnetic tweezers and TIRF microscopy can interrogate hundreds of molecules in parallel^240–243. Nevertheless, this higher throughput is often obtained at the price of reduced spatial and temporal resolution, with the concomitant decrease in information content. Approaches are being explored to parallelize optical traps to increase their throughput.

Outlook

Numerous challenges lie ahead in the application of optical tweezers to the study of biological systems. Some of these will involve incremental, quantitative improvements of the instrument capabilities along the lines discussed above. These developments will likely include the implementation of ever more elaborate methods of controlled microfluidics and improved control of molecular environmental conditions. Likewise, it is clear that the method will witness the increased use of artificial intelligence and machine learning protocols for the control of the experiments and the extraction of the data.

Other developments are, however, more qualitative in nature. Among these we must consider recent efforts aimed at increasing the throughput of optical tweezers. Throughput in optical tweezers experiments is largely limited by the ability to tether the molecular system. ‘Fishing’, as it is commonly referred to, can be automated and computer-controlled, making the task less tedious but not necessarily improving throughput. Once the tether has been formed, the success of the experiment is determined by the robustness of the biological system being studied. Parallelizing optical traps is being explored as a way to increase throughput. By using multiple traps simultaneously, it should be possible to proportionally increase the amount of data obtained from single-molecule experiments. Although time-shared⁴² or holographic optical traps²⁴⁴ can generate arrays of traps, they suffer from high power requirements that scale linearly with the number of traps. Recent advances in the development of a nanophotonic standing-wave array trap hold promise for precision measurements of biomolecular forces at high throughput on a chip²⁴⁵. In this approach, an array of stable on-chip optical traps is formed at the antinodes of a standing wave in a nanophotonic waveguide. In general, all of these efforts at multiplexing the trapping experiment must solve the challenge of reaching simultaneous and precise control of the experimental molecular geometry in all of the traps. Although throughput is currently a limitation in optical tweezers studies, the amount of mechanistic insight derivable in principle from these single-molecule experiments easily compensates the efforts required to build up statistics.

Another important challenge is the need to fill the gap between in vivo and in vitro studies. This divide is not unique to the optical tweezers field; in fact, it is shared by almost all physical techniques used to study complex biomolecular systems under controlled conditions outside the cell²⁴⁶. In the case of optical tweezers, the use of trapping experiments inside the cell remains limited to date, with the exception of a few applications trapping cytoskeletal cargos after in situ calibration of the traps in the viscoelastic cytoplasm^247,248. Because many organelles and vacuoles possess refractive indices slightly above that of the cytoplasm, they are attracted towards the higher intensities of the beam. As a result, it is not possible at present to selectively trap any particular object, even if these are beads specially introduced into the cell by biolistic means. One possible way to address this issue is to develop robust protocols using cell extracts, but this is not a trivial endeavour. In many cases, other components in the extract may bind non-specifically to any part of the system of interest and interfere with the measurement. However, in some cases it may be possible to perform the experiment and use immunoprecipitation to selectively deplete one or another component from the mix, and derive causal relationships from the modified behaviour of the system.

These developments, together with the recent commercial availability of high-resolution optical tweezers, will likely increase both the impact of this powerful technique and its attractiveness among biophysicists, biochemists and quantitative biologists.

Thermal bath.

(Also known as heat bath, or thermal reservoir in thermodynamics and statistical mechanics). A large body held at constant temperature in which the system of interest is immersed and with which it is in thermal equilibrium. It is assumed to possess a large heat capacity and to be essentially an infinite source of thermal energy so that it can exchange energy with the system (as a thermal source or as a heat sink) without altering its temperature.

Torques.

Cross products of the position vector (pointing from the axis of rotation to the point of application of the force) and the force driving the rotation.

Wavelength.

The distance between two maxima of the light’s electric or magnetic field.

Rayleigh scatterer.

An object whose dimensions are much smaller than the wavelength of the light.

Polarizability.

A dipole moment is generated when a distribution of charges experiences a separation of positive and negative charges under the influence of an electric field. The magnitude of the dipole is proportional to the amplitude of the electric field $\stackrel{\rightharpoonup }{E}$. The constant of proportionality is the polarizability of the charge distribution.

Electric dipole.

A pair of electric charges of equal magnitude but opposite signs separated by a finite distance.

Gaussian laser beam.

A light beam whose intensity can be described with a Gaussian function, maximal at its axis and decreasing towards its periphery.

Permittivity.

A measure of the electric polarizability of the medium.

Absorption.

A process in which the energy carried by light is transferred to the sample.

Refraction.

A change in the direction of the travelling beam by the presence of an object that has a different index of refraction to the surrounding medium, when that beam impinges on it obliquely.

Reflection.

A process by which the light that impinges on a surface of an object bounces back from that surface instead of being absorbed or refracted by the object.

Extinction cross-section.

A measure of the efficiency with which a given object can absorb or scatter the light that impinges on it.

Poynting vector.

A quantity that describes the magnitude and direction of the flow of energy of a propagating electromagnetic wave.

Geometric or ray optics.

A description of light in terms of rays that describe in an approximate manner the paths along which the light travels.

Refractive objects.

Objects that possess a different index of refraction to the medium in which they are immersed and that deflect light that impinges on them obliquely.

High numerical aperture.

The range of angles over which a lens can collect light; the larger the numerical aperture, the larger the angular range.

Condenser lens.

A standard optical microscope component typically used to focus the microscope light into the specimen; in optical traps it is often used to collect scattered trap light.

Back focal plane interferometry.

A technique in which the interference pattern between the light transmitted and the light forward-scattered by the trapped particle is used to determine the position of the particle relative to the trap centre.

Linear range.

The range of input parameters over which the output of the system depends linearly on the input.

Measurement bandwidths.

The rates at which data are collected.

Boltzmann constant.

A fundamental physical constant that relates the kinetic energy of a gas to its absolute temperature. It is closely related to the gas constant R.

Hydrodynamic drag coefficient.

A coefficient characterizing the viscous resistance that a particle moving through a fluid encounters.

Pointing drift.

Unwanted changes in the direction of a beam of light.

Brownian motion.

The random fluctuation of a particle’s position (and orientation) at a given temperature.

Feedback loop.

A self-regulating mechanism in which the output of a system is routed back into an input to the system. In negative feedback, the output is fed back in a fashion that tends to reduce fluctuations in the output.

Fluorophores.

Fluorescent chemical compounds or molecules.

Oxygen scavengers.

Enzymatic systems that remove molecular oxygen detrimental to fluorescence.

Extraordinary axis.

(Also known as the ‘optic axis’). For a uniaxial crystal that has a refractive index of one crystal axis that is different from the other two crystal axes, light propagating parallel to this optic axis experiences the same index of refraction regardless of its polarization.

Laser polarization.

The polarization of the light refers to the direction of the electric field.

Laguerre–Gaussian beam.

A mode of laser that can carry both orbital and spin angular momentum.

Michaelis–Menten kinetic parameters.

Parameters that relate the rate of an enzymatic reaction v to the substrate concentration [s] by the formula v = V_max[s] / (K_M + [s]), where V_max and K_M represent the maximum rate and the substrate concentration at which the reaction rate is half of V_max, respectively.

Temporal resolution.

The measure of the fastest signal that can be detected accurately.

Biolistic.

A method of introducing beads inside cells by shooting them ballistically inside the cells at supersonic speeds.