Skip to main content
PMC home page
Elsevier Sponsored Documents logoLink to Elsevier Sponsored Documents
. 2021 Dec;37:100526. doi: 10.1016/j.epidem.2021.100526

Precautionary breaks: Planned, limited duration circuit breaks to control the prevalence of SARS-CoV2 and the burden of COVID-19 disease

Matt J Keeling a,⁎,1, Glen Guyver-Fletcher a,b, Louise Dyson a,1,2, Michael J Tildesley a,1,2, Edward M Hill a,1,2, Graham F Medley c
PMCID: PMC8636324  PMID: 34875583

Abstract

COVID-19 in the UK has been characterised by periods of exponential growth and decline, as different non-pharmaceutical interventions (NPIs) are brought into play. During the early uncontrolled phase of the outbreak (March 2020) there was a period of prolonged exponential growth with epidemiological observations such as hospitalisation doubling every 3–4 days. The enforcement of strict lockdown measures led to a noticeable decline in all epidemic quantities that slowed during the summer as control measures were relaxed. From August 2020, infections, hospitalisations and deaths began rising once more and various NPIs were applied locally throughout the UK in response.

Controlling any rise in infection is a compromise between public health and societal costs, with more stringent NPIs reducing cases but damaging the economy and restricting freedoms. Typically, NPI imposition is made in response to the epidemiological state, are of indefinite length and are often imposed at short notice, greatly increasing the negative impact. An alternative approach is to consider planned, limited duration periods of strict NPIs aiming to purposefully reduce prevalence before such emergency NPIs are required. These “precautionary breaks” may offer a means of keeping control of the epidemic, while their fixed duration and the forewarning may limit their societal impact. Here, using simple analysis and age-structured models matched to the UK SARS-CoV-2 epidemic, we investigate the action of precautionary breaks. In particular we consider their impact on the prevalence of SARS-CoV-2 infection, as well as the total number of predicted hospitalisations and deaths caused by COVID-19 disease. We find that precautionary breaks provide the biggest gains when the growth rate is low, but offer a much needed brake on increasing infection when the growth rate is higher, potentially allowing other measures to regain control.

Keywords: SARS-CoV-2, Covid, Control, Circuit-Break, Non-pharmaceutical interventions

Highlights

  • •

    Simple models show that short-duration precautionary breaks are effective in reducing the burden of COVID-19 disease.

  • •

    More complex age-structured models, matched to available data, support this conclusion.

  • •

    Precautionary breaks provide the greatest short-term reduction in cases when the growth rate would otherwise be large.

  • •

    These breaks are not a long-term solution but allow other measures to regain control of the epidemic.

1. Introduction

The novel coronavirus virus strain that arose in Wuhan city in China in late 2019 has had a dramatic effect on the lives of people worldwide. By 1st October 2020, we had passed the grim milestone of 1 million deaths worldwide and over 30 million cases (World Health Organization, 2020). In the absence of disease specific treatments or prophylactic measures, most countries have adopted social distancing measures (reducing the number of potentially risky contacts) and a range of other interventions (such as mask use and promoting good hand hygiene) as a means of control (Hale et al., 2020). The optimal level of such non-pharmaceutical interventions (NPIs) requires a careful balance between public health and economic needs, from which it could be argued that the optimal strategy is one that minimises economic disruption while still preventing exponential growth of infection (Rowthorn and Maciejowski, 2020).

In the UK, the first cases of COVID-19 were reported on 31st January 2020 in the city of York. Cases continued to be reported sporadically throughout February and by the end of the month guidance was issued stating that travellers from the high-risk epidemic hotspots of Hubei province in China, Iran and South Korea should self-isolate upon arrival in the UK. By mid-March 2020, as the number of cases clearly began to rise, there was advice against all non-essential travel and, over the coming days, several social-distancing measures were introduced including the closing of schools, non-essential shops, pubs and restaurants. This culminated in the introduction of a UK “lockdown”, announced on the evening of 23rd March 2020, whereby the public were asked to remain at home with four exceptions: shopping for essentials; any medical emergency; for one form of exercise per day; and to travel to work if absolutely necessary. By mid-April 2020, these stringent mitigation strategies began to have a noticeable effect, as the number of confirmed cases, hospitalisations and deaths as a result of the disease began to decline (Flaxman et al., 2020, Davies et al., 2020). As the number of daily confirmed cases continued to decline during April, May and into June 2020 (Riley et al., 2020b), measures to ease lockdown restrictions began, with the re-opening of some non-essential businesses and allowing small groups of individuals from different households to meet up outdoors, whilst maintaining some measure of social distancing and compliance with NPIs. This was followed by gradually re-opening primary schools in England from 1st June 2020 and all non-essential retail outlets from 15th June 2020.

The dynamics throughout the summer of 2020 were characterised by the emergence of hot-spots of persistent infection and higher than average growth rates, with such areas facing additional local controls. Notably, Leicester and the Greater Manchester conurbation were identified as regions where the number of identified cases per hundred thousand had increased to high levels, while the infection in many other areas was still in decline. By mid to late August 2020, there was some evidence that the national underlying growth rate had become positive (Riley et al., 2020b), and by the end of September exponential growth had returned in almost all regions (Anderson et al., 2020, Riley et al., 2020a). Like many countries, the UK attempted to curtail growth by introducing stricter controls in the form of localised measures, as a national “lockdown” can be very disruptive to multiple elements of society (Pierce et al., 2020, Office for National Statistics, 2020), especially given that the duration of lockdown restrictions is largely unpredictable to the local populous and businesses.

One potential mechanism of regaining control is to introduce a short period of intense measures to substantially reduce cases — this has been dubbed a ‘circuit breaker’ although “precautionary break” is a more apposite name. It is hoped that by driving infections to a sufficiently low level, other measures such as test-trace-and-isolate will have greater capacity to prevent the spread of infection (Davis et al., 2021). In common with other resource limited controls (Cooper et al., 2004), we expect test-trace-and-isolate to be most effective when the level of infection is relatively low (Kretzschmar et al., 2020). Alternatively, driving infections to low levels would give time for a concerted vaccination programme to build sufficient population-level immunity (Moore et al., 2021a). Additionally, a short lockdown period would limit the economic costs of such a measure (Karin et al., 2020, Tildesley et al., 2021).

In this paper, we consider the application of precautionary breaks to the UK, aligning a two-week period of intense control to school half-term holidays in order to minimise educational disruption. We retain the context of the initial analysis, focusing on control of the second wave of infection in late 2020, but also consider the implications for contemporary control. We utilise both a simple illustrative analysis and an age-structured SARS-CoV-2 transmission model fitted to the UK data, to investigate the likely impact of a break on the trajectory of infection and the subsequent numbers of hospitalised cases and deaths.

2. Simple analysis

Under the simplifying assumption that without additional control measures cases will increase exponentially at rate r (>0), but during the period of the precautionary break cases will decrease at a rate −s (<0), we can develop a simple model for the dynamics:

I(t)=I0exp(rt)t≤TstartI0exp(rTstart)exp(−s(t−Tstart))Tstart≤t≤TendI0exp(rt)exp(−(r+s)(Tend−Tstart))t≥Tend

where Tstart and Tend define the start and end dates of the breaks. From this analysis, we observed two key effects of a short-term lockdown. Firstly, it causes a relative reduction in the level of infection by a factor B=1−exp(−(r+s)(Tend−Tstart)), compared to not having the precautionary break. In principle, this should translate into a similar reduction in the daily number of hospitalisations and deaths — the two epidemiological measures of most concern. We can also conceptualise this reduction as taking the epidemic back in time to when there were fewer cases; this temporal reset, TR, is given by:

TR=(Tend−Tstart)1+sr.

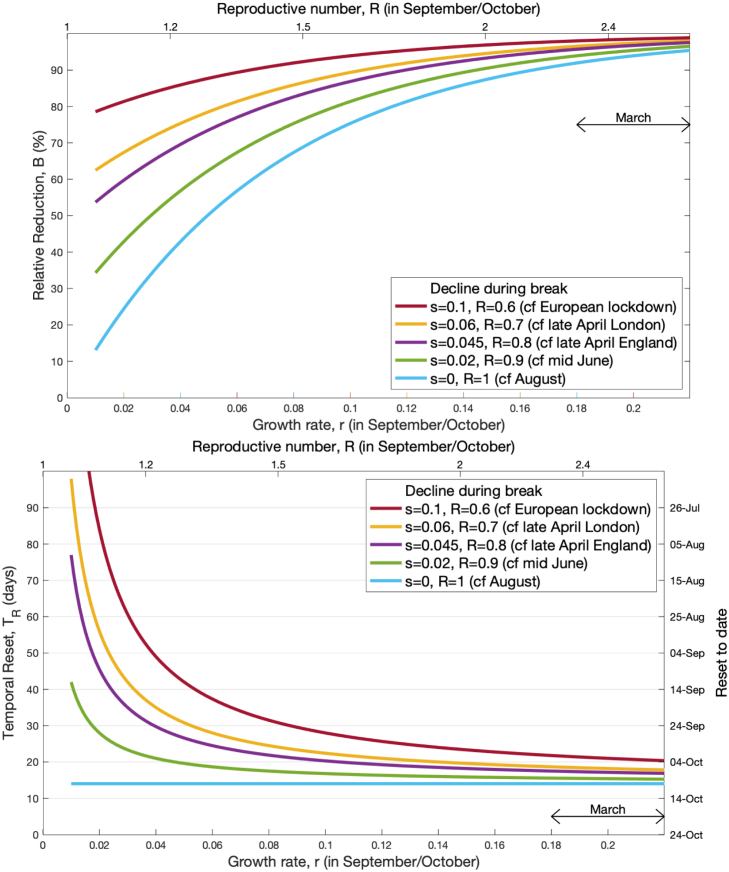
Taken together these two metrics B and TR imply that such breaks, unsurprisingly, have the greatest impact when they are long in duration and lead to a rapid decline in cases (s large). The impact of the uncontrolled growth rate, r, is more ambiguous. When r is large the impact of the precautionary break on the level of infection is more pronounced as it prevents a period of high exponential growth. In contrast, large r reduces the size of the temporal reset as it does not take many days of exponential growth to cancel the decline expected during the break.

3. Age-structured model description

We now wish to increase the realism of the modelling framework to more accurately capture the impact of such precautionary breaks on the number of hospitalisations and deaths as a result of infection, which requires an age-structured model matched to the wealth of epidemiological data (Keeling et al., 2021, Keeling et al., 2020). Even though we have dramatically increased the complexity of the model, the two simple metrics (B and TR) remain of key interest.

The age-structured SARS-CoV-2 transmission model and its matching to the UK data has been described in detail elsewhere (Keeling et al., 2021, Keeling et al., 2020) from which a simplified version of the code is now available (Moore et al., 2021b). Here, for completeness, we provide a basic review of the main salient points with more detail given in the Supplementary Material. The model is an ODE formulation based around SEIR-type dynamics and incorporating five-year age classes. The infectious class is subdivided into symptomatic and asymptomatic infections, with symptomatic infections having greater transmission and being more common in older individuals. In addition, we base transmission between age-groups on POLYMOD-style age-mixing matrices (Prem et al., 2020), together with age-dependent susceptibility to generate the observed age distribution of cases. The model also includes additional structure to account for quarantining of identified cases and isolation of their household (Keeling et al., 2021).

The model is calibrated against different sources of epidemiological data including hospital admissions and occupancy, ICU occupancy, deaths within 28-days of a positive COVID test, age-structured serology from blood donors and the proportion of pillar 2 (community) tests that are positive (Keeling et al., 2020). This matching is done separately for the seven NHS regions in England (East of England, London, Midlands, North East & Yorkshire, North West, South East and South West) and for the three devolved nations (Northern Ireland, Scotland and Wales); although some parameters which we believe are properties of the pathogen and not host behaviour (such as the relative transmission rate from asymptomatic infections) are the same across all regions. We performed the parameter inference within a Bayesian MCMC framework, with the likelihood (our objective function) determined by assuming the daily epidemiological observations are Poisson distributed (for hospital admissions, hospital occupancy, ICU occupancy and deaths) or binomially distributed (for serology and pillar 2 test) with a mean given by the ODEs (Keeling et al., 2020). Of particular note, to achieve a match to the historical and changing pattern of regulations, restrictions and behaviour in each region we employ a single parameter that changes on a weekly basis and rescales the transmission matrix to generate different growth rates.

The model has been used for a variety of purposes and has been shown to be in close agreement with the available epidemiological data (Keeling et al., 2021, Keeling et al., 2020, Moore et al., 2021a). However, the purpose here is to show that a more complex high-dimensional model generates results that are in broad agreement with the simpler results rather than generate detailed policy predictions, which would require a precise set of time-lines, policy objectives and future scenarios.

As such, we consider two distinct forms of simulation. In the first, we tightly constrain the dynamics (by rescaling the transmission matrix) to have a given growth rate r from 1st September 2020, with the growth rate being estimated by an eigenvector approach. During the two-week break (24th October–7th November 2020) we again rescale the transmission matrix to achieved the desired rate of decay −s, before returning to the pre-break matrix. We performed all simulations using the median of the posterior parameter estimates from model fitting performed in September 2020.

In the second set of simulations, we allow more regional heterogeneity by fully exploring the posterior parameter estimates. We chose 1000 samples from the posterior distribution (Keeling et al., 2020), for each region of the UK, and vary the level of NPIs (outside of the precautionary break) to achieve a range of growth rates (r). A two-week break is enacted on 24th October 2020, with the rate of decline (−s) determined by the maximal level of NPIs over the full epidemic from March to September 2020 (as estimated in the posterior parameter distribution); hence introducing far more variability into the process. We again looked at the temporal reset (TR), defined as the time difference between the end of the precautionary break and the previous time when a similar level of infection occurred.

4. Numerical results

To illustrate the simple analytical behaviour in more detail, we pick a definitive case (Fig. 1): a two-week break from 24th October–7th November 2020 to coincide with school half-terms (thereby minimising educational disruption). We consider the relative reduction B and the temporal reset TR across a range of positive growth rates r, from 0.01 to 0.22, with the upper bound corresponding to the highest growth in March 2020 before controls were enacted. We consider five different intensities of break (s=0,0.02,0.045,0.06 and 0.1) with the first four approximating the observed exponential decline over different periods of control (August 2020 UK average, June 2020 UK average, late April 2020 UK average, late April 2020 London estimate), and the latter corresponding to the observed decline in continental Europe where the lockdown restrictions were more intense. We find that, as shown earlier analytically, the greatest effects are found for stricter controls during the precautionary break; lower intrinsic growth (r) outside of the break leads to a longer temporal reset, whereas a higher growth rate is associated with a bigger relative decline in infection.

Fig. 1.

Fig. 1

Open in a new tab

Impact of a two-week precautionary break during half-term on the infection dynamics. For a range of assumed growth rates in September and October 2020 (and associated R values, assuming a generation time of around 4.3 days), we illustrate both the reduction in infection (B) and the temporal reset (TR) of a break starting on 24th October 2020. Each line corresponds to a different strength of control during the two week precautionary break, which is linked to observed epidemic declines.

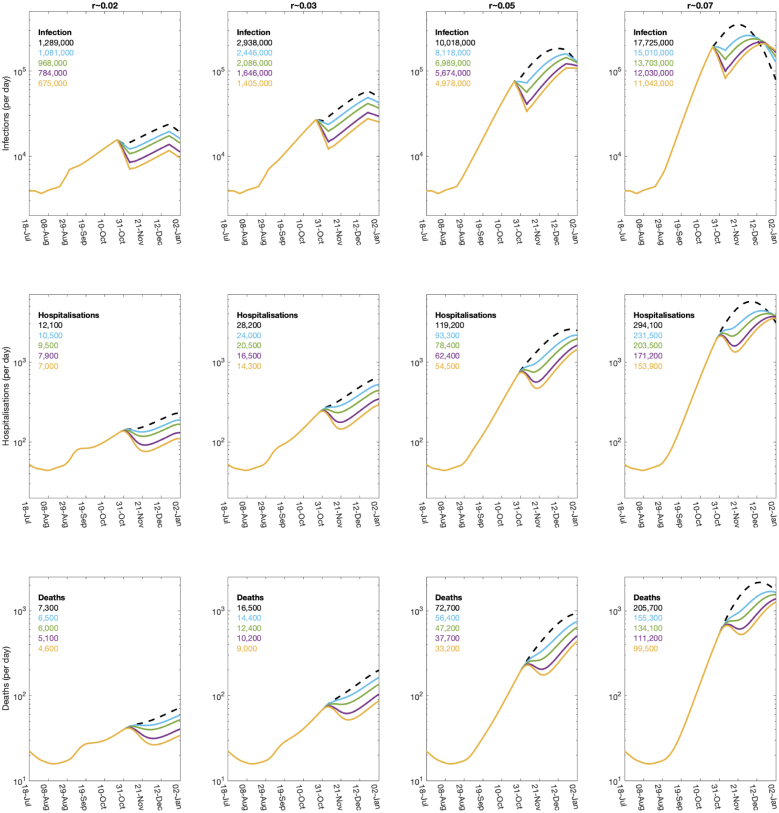
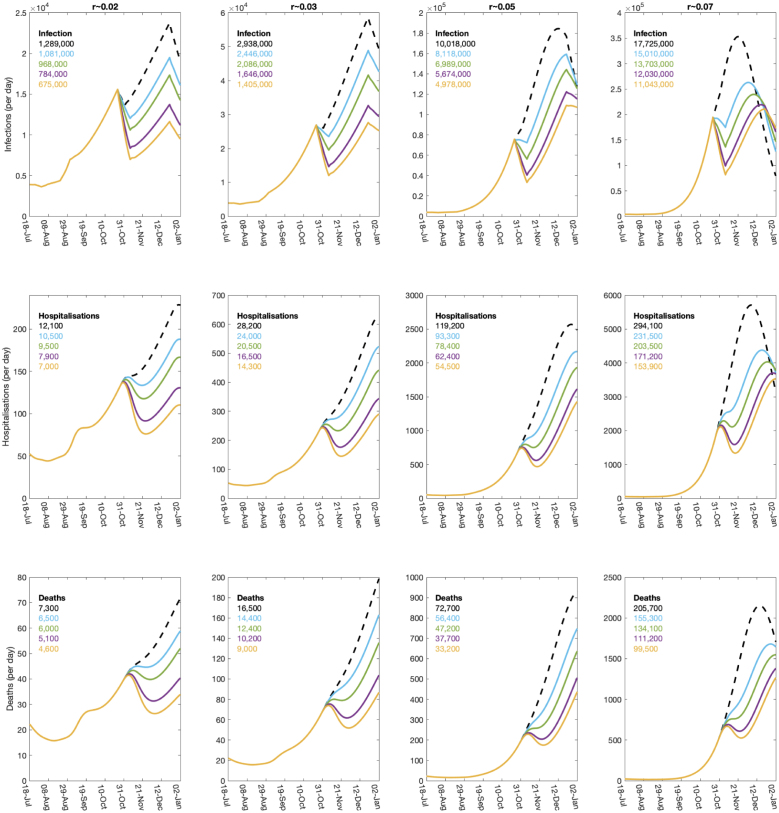
For the age-structured model, we initially focus on the temporal dynamics over the period from August to the end of 2020 (Fig. 2, Fig. 3). The log-scaled version (Fig. 2) makes it clearer to see the exponential dynamics (which are revealed as straight lines), whereas the linear-scaled version (Fig. 3) provides a more intuitive picture of the scale of the outbreak.

Fig. 2.

Fig. 2

Open in a new tab

Impact of a two-week precautionary break during half-term on the dynamics of the full age-structured model. Results are from a single simulation using the median of the posterior parameter estimates from model fitting performed in September 2020. The columns are for four different underlying epidemiological growth rates r≈0.02,0.03,0.05 and 0.07, while within each panel the colours correspond to different rates of decline during the half-term break (from top to bottom in each graph the lines are: dashed black, no-control s=−r; blue s=0; green s=0.02; purple s=0.045; gold s=0.06). The top row shows the number of new infections in the UK, which experiences the most immediate impact of the break; the middle row shows the number of daily hospitalised infections; while the lower row shows the daily mortality. Inset into each figure are the number of infections, hospitalisations and deaths over the period 24th October 2020 to 1st January 2021. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 3.

Fig. 3

Open in a new tab

Impact of a two-week precautionary break during half-term on the dynamics of the full age-structured model. Showing the same results as Fig. 2 but on a linear scale to highlight the magnitude of the projected epidemics.

For four rates of decline during the break (s=0,0.02,0.045 and 0.06), which correspond to rates used in Fig. 1 (using the same colour scheme), we approximate exponential declines in reported cases observed in the first lockdown (late April, s≈0.045 in the UK, s≈0.06 in London), during June (s≈0.02 in the UK) and in August (s≈0 in UK). These rates of exponential decline are generated by imposing a sufficiently high level of NPIs during the two week break.

For comparison we also show the dynamics without a two-week break, but including the standard 1-week half term break for school children (black dashed line). Although the historic dynamics of the full age-structured model are matched to the reported pattern of hospitalisations, cases and deaths, we initially investigate the situation where the intrinsic growth rate from 1st September to 24th October 2020 is set to one of four different growth rates (r≈0.02, r≈0.03, r≈0.05 and r≈0.07, columns of Fig. 2, Fig. 3). To calibrate the model to the specified growth rate, we scaled the level of NPIs during this time period to achieve the desired exponential growth; this level of NPIs is continued after the precautionary break.

Given the extra realism of the age-structured model, we project not just the number of infections (top row), but the number of daily hospitalisations and deaths (middle and bottom row respectively). We also give the total number of infections, hospitalisations and deaths between 1st October 2020 and 1st January 2021 as numerical values.

These results from the age-structured model mirror the findings from the simple analytical framework, but provide greater clarity on the impact of these breaks on the key epidemiological quantities of hospitalisations and deaths. Both of these measures lag behind the changes in infection, and the drop in both quantities after the half-term break is far smoother than is observed for infection. For all three measures, it is clear that the temporal reset increases with the strength of controls during the precautionary break, but decreases with the growth rate; the reset is also longer and more clearly defined for infection than for the lagged measures of hospitalisations and deaths. Looking at the medium term impact of the break (as measured by the total number of deaths between 24th October 2020 and 1st January 2021), we observe that for low growth rates the strongest levels of NPIs during the break reduces deaths by approximately 37%. In contrast, when the growth is high the reduction is approximately 52%.

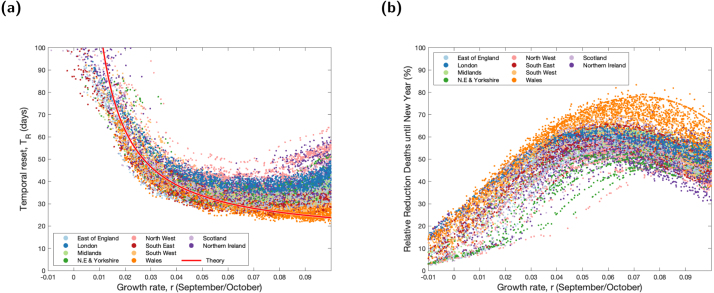
The results of Fig. 3 artificially constrain the dynamics to achieve fixed rates of growth and decline. In Fig. 4 we explore the posterior parameter set (showing 1000 random samples) and constrain the 2-week break (from 24th October to 7th November 2020) to have the maximal level of NPIs estimated for each parameter set — which generally occurs during the main UK lockdown (March and April 2020).

Fig. 4.

Fig. 4

Open in a new tab

Impact of a two-week precautionary break during half-term on the dynamics of the full age-structured model. Each point is from the posterior parameter distribution, with the level of NPIs from 1st September 2020 onwards varied to generate different underlying growth rates. The decline during the precautionary break is the maximum level of NPI at any time for the associated posterior parameter set. (a) The temporal reset that captured the time gained by the precautionary break; the red line is the theoretical result from the simple theoretical model based on the average rate of decline during the precautionary break across all replicates. (b) Relative reduction in deaths between 1st October 2020 and 1st January 2021.

We again looked at the temporal reset (TR) defined as the time difference between the end of the precautionary break and the previous time when a similar level of infection occurred. The results of these replicates that include natural parameter and intervention uncertainty show remarkable agreement with the simple analysis (depicted by the red line, Fig. 4a). The exception is for the very highest levels of considered growth rates (r>0.07); allowing this level of increase since early September 2020 leads to depletion of the susceptible population, which brings a greater temporal reset than expected. However, allowing a growth rate of r>0.07 (a doubling time of less than 10 days) for a long period is not a viable public health option. We find a similar pattern when examining the relative reduction in deaths; in keeping with simple theory there is a rise in the reduction that can be obtained as the growth rate increases, but this again suffers from the non-linear effects of susceptible depletion for growth rates above r=0.07.

5. Discussion

The pandemic of SARS-CoV-2, and the number of severe cases of COVID-19 worldwide, has necessitated the adoption of a range of control measures in different countries. In the absence of a vaccine or other medical approaches during the early stages of the pandemic, control had to rely on often very disruptive non-pharmaceutical interventions to break the chains of transmission. In the UK, the implementation of such NPIs during the lockdown period (23rd March–13th May 2020) reversed the early national increase in hospitalisations and deaths (r≈0.2) and led to a steady decline (r≈−0.05) (Flaxman et al., 2020, Davies et al., 2020). The gradual relaxing of NPIs generated a slowly increasing growth rate, which we estimate became positive again (leading to exponential growth) in mid-August 2020 (Anderson et al., 2020). Against this backdrop of rising cases, we investigated the benefits of a planned two-week precautionary break (or ‘circuit-break’), where strict rules are reapplied in an attempt to drive down cases before their imposition becomes necessary to prevent health system overload. Such breaks are not in themselves long-term solutions, but may allow other methods that work best with low numbers of cases (such as test-trace-and-isolate) to reassert control. In addition, obtaining low levels of infection before the start of a vaccination campaign would allow population-level immunity to be developed through immunisation and thus suppress further rises in cases.

Both simple analytical approaches and an age-structured model fit to a range of UK data show that planned precautionary break could be highly effective short-term control measures. Compared to an absence of such controls, precautionary breaks generate a reduction in infection, hospitalisations and deaths, which is most pronounced when the growth rate is moderately high. This reduction in infection can also be interpreted as a temporal reset, taking the level of infection back (in time) to a lower value, allowing greater opportunity for additional public health measures to be enacted or take effect.

One clear practical question is whether these results are specific to SARS-CoV-2 infections and how generalisable the findings are to other epidemiological setting and hence parameters. If we are dealing with a single homogeneously mixing population (for example simple SIR-type models) then the instantaneous reduction in mixing during the precautionary break will translate into an instantaneous reduction in transmission and hence a reduction in incidence. Although, as shown in Fig. 3, the implications for other important health measures (such as hospital admissions, or deaths) is influenced by the distribution of delays between infection and severe health consequences. For more complex models (including the SEIR-type models or age-structured models) then there can be an additional time delay, even for the incidence of infection, while the system converges to the new dominant eigenvector; for most epidemiological systems this should be relatively quick, occurring within one or two generations. However, none of these issues are specific to the SARS-CoV-2 pandemic and we expect that planned precautionary breaks could be of benefit in many epidemic scenarios, allowing more time for other measures to come into effect.

Short periods of intense control of SARS-CoV-2 have been examined by other researchers. These include: the regular periodic use of planned breaks to minimise SEIR-type infection dynamics (Hindes et al., 2021) and economic disruption (Karin et al., 2020); the optimal timing of a single short-duration break to minimise an epidemic (Di Lauro et al., 2021) which is shown to correspond to the epidemic peak; and the interaction between vaccination and precautionary breaks (Bonsall et al., 2021). Taken together with our findings these results point to some important policy implications:

  • 1.

    Precautionary breaks that generate the most stringent application of NPIs are associated with the greatest immediate rates of declines and, as a consequence, the greatest public health benefits. Therefore, the success of any action is highly contingent on the adherence of the populous to the recommendations and rules; a precautionary break is only effective if there is an average increase in the level of non-pharmaceutical interventions across the country.

  • 2.

    If only a single break can be used to mitigate against an otherwise uncontrolled epidemic, then the break should be carefully timed to occur close to the peak (Di Lauro et al., 2021), effectively splitting the outbreak into two and reducing the peak pressure on health services.

  • 3.

    On shorter time scales (such that the growth of the epidemic remains exponential), we consistently find that the optimal time for a break is always now; there are no good epidemiological reasons to delay the break as this will simply push back any benefits until later, leaving more time for additional cases to accumulate.

  • 4.

    The number and timing of any precautionary breaks is always going to be a compromise between their epidemiological benefits and the societal and economic disruption they cause. This is one reason we focused on combining the precautionary break with the half-term school holidays. However, to define the optimal balance between reducing infection and disruption requires a unified objective function (Tildesley et al., 2021), which is likely to be disease specific.

Some practical implementation of these breaks has already been trialled. Israel began a short-term precautionary break on 18th September 2020, to coincide with their Rosh Hashanah holiday period, with stricter measures introduced on 25th September 2020. This came to an end on 18th October 2020, and led to low numbers of cases throughout October and November with an associated lower number of deaths after the appropriate lag.

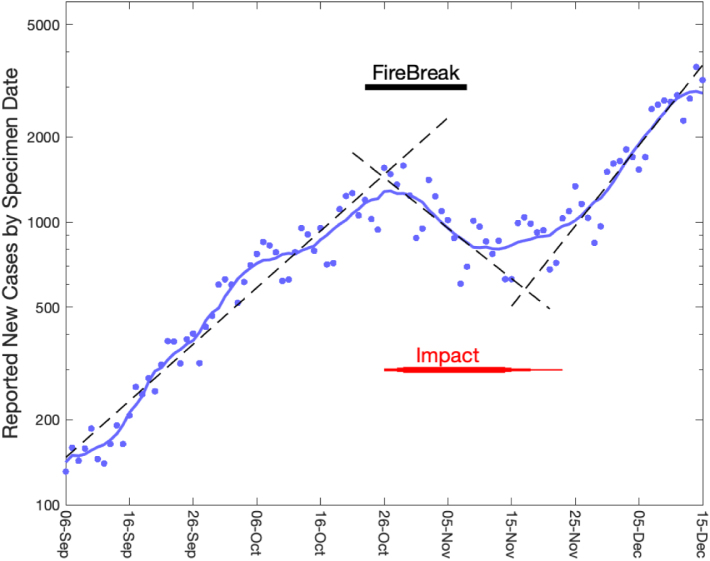
Within the UK, Wales started its 16-day fire-break controls on 23rd October 2020, while Northern Ireland began a series of tighter restrictions on 16th October 2020. Examination of the Welsh fire-break (Fig. 5) shows that cases follow a similar pattern to that illustrated in Fig. 2, Fig. 3, with the precautionary break leading to a period of exponential decay (s≈0.04) separating two periods of exponential growth (r≈0.04 and r≈0.06). While the signal is not as clean as theoretical model results, the impact of the break is clear, although there is a lag due to the delay between infection, symptoms and being swabbed. Of more concern is the evidence of a slightly steeper rise in cases following the break compared to before the break; whether this is attributable to the break (individuals ‘compensating’ for two weeks of limited interactions) or would have occurred regardless (for example due to climatic or other factors) remains unclear.

Fig. 5.

Fig. 5

Open in a new tab

Impact of the Welsh fire-break on reported COVID-19 cases. The blue dots show the reported new COVID-19 cases by date that the specimen was taken (the majority of these are Pillar 2 swabs of suspected cases in the community); while the blue curve gives the 7-day moving average and the dashed lines provide the best exponential fit to the three distinct intervals. The black bar shows the timing of the fire-break, while the red bar shows the likely timing of the impact of the break on reported cases due to the lag between infection and symptoms.

Data from the UK government COVID dashboard (Public Health England, 2021).

Ultimately, such short-term precautionary breaks will only be effective if (i) their planned nature helps to minimise the associated societal harms and economic losses, (ii) there is good compliance with the measures across all regions and sections of society, and (iii) the reduction in cases is used to regain control and bring the growth rate back below zero.

CRediT authorship contribution statement

Matt J. Keeling: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualisation, Writing – original draft, Writing – review & editing. Glen Guyver-Fletcher: Data curation, Writing – review & editing. Louise Dyson: Software, Validation, Writing – original draft, Writing – review & editing. Michael J. Tildesley: Software, Validation, Writing – original draft, Writing – review & editing. Edward M. Hill: Software, Validation, Writing – original draft, Writing – review & editing. Graham F. Medley: Conceptualization, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

Financial disclosure

This work has been supported by the UKRI through the COVID-19 Rapid Response Rolling Call funding the JUNIPER modelling consortium, UK [grant number MR/V038613/1], the UKRI, UK through the COVID-19 Rapid Response Rolling Call [grant number MR/V009761/1], and the Biotechnology and Biological sciences Research Council, UK through the Midlands Integrative Biosciences Training Partnership (MIBTP) [grant number BB/M01116X/1]. MJK is affiliated to the National Institute for Health Research Health Protection Research Unit (NIHR HPRU) in Gastrointestinal Infections at University of Liverpool in partnership with UK Health Security Agency (UKHSA), in collaboration with University of Warwick. MJK is also affiliated to the National Institute for Health Research Health Protection Research Unit (NIHR HPRU) in Genomics and Enabling Data at University of Warwick in partnership with UK Health Security Agency (UKHSA). The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR, the Department of Health and Social Care or UK Health Security Agency. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Ethical considerations

Data from the CHESS database were supplied after anonymisation under strict data protection protocols agreed between the University of Warwick and Public Health England. The ethics of the use of these data for these purposes was agreed by Public Health England with the Government’s SPI-M(O)/SAGE committees.

Patient and public involvement

This was an urgent public health research study in response to a Public Health Emergency of International Concern. Patients or the public were not involved in the design, conduct, or reporting of this rapid response research.

Footnotes

Appendix A

Supplementary material related to this article can be found online at https://doi.org/10.1016/j.epidem.2021.100526.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

Basic model formulation of the age-structured model and parameter inference.

mmc1.pdf (232.4KB, pdf)

Data availability

Data on cases were obtained from the COVID-19 Hospitalisation in England Surveillance System (CHESS) data set that collects detailed data on patients infected with COVID-19. Data on COVID-19 deaths were obtained from Public Health England. These data contain confidential information, with public data deposition non-permissible for socioeconomic reasons. The CHESS data resides with the National Health Service (https://www.nhs.gov.uk) whilst the death data are available from Public Health England (https://www.phe.gov.uk).

References

  1. Anderson Roy M., Hollingsworth T. Déirdre, Baggaley Rebecca F., Maddren Rosie, Vegvari Carolin. Covid-19 spread in the uk: the end of the beginning? Lancet. 2020;396(10251):587–590. doi: 10.1016/S0140-6736(20)31689-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bonsall Michael B., Huntingford Chris, Rawson Thomas. Optimal time to return to normality: parallel use of covid-19 vaccines and circuit breakers. medRxiv. 2021 doi: 10.1101/2021.02.01.21250877. 2021.02.01.21250877. [DOI] [Google Scholar]
  3. Cooper B.S., Medley G.F., Stone S.P., Kibbler C.C., Cookson B.D., Roberts J.A., Duckworth G., Lai R., Ebrahim S. Methicillin-resistant staphylococcus aureus in hospitals and the community: stealth dynamics and control catastrophes. Proc. Natl. Acad. Sci. 2004;101(27):10223–10228. doi: 10.1073/pnas.0401324101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Davies Nicholas G., Kucharski Adam J., Eggo Rosalind M., Gimma Amy, Edmunds W. John, Jombart Thibaut, O’Reilly Kathleen, Endo Akira, Hellewell Joel, Nightingale Emily S., et al. Effects of non-pharmaceutical interventions on covid-19 cases, deaths, and demand for hospital services in the uk: a modelling study. Lancet Public Health. 2020;5(7):e375–e385. doi: 10.1016/S2468-2667(20)30133-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Davis Emma L., Lucas Tim C.D., Borlase Anna, Pollington Timothy M., Abbott Sam, Ayabina Diepreye, Crellen Thomas, Hellewell Joel, Pi Li, Medley Graham F., et al. An imperfect tool: contact tracing could provide valuable reductions in covid-19 transmission if good adherence can be achieved and maintained. medRxiv. 2021 doi: 10.1101/2020.06.09.20124008. 2020.06.09.20124008. [DOI] [Google Scholar]
  6. Di Lauro Francesco, Kiss István Z., Miller Joel C. Optimal timing of one-shot interventions for epidemic control. PLoS Comput. Biol. 2021;17(3) doi: 10.1371/journal.pcbi.1008763. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Flaxman Seth, Mishra Swapnil, Gandy Axel, Unwin H. Juliette T., Mellan Thomas A., Coupland Helen, Whittaker Charles, Zhu Harrison, Berah Tresnia, Eaton Jeffrey W., et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020;584(7820):257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
  8. Hale Thomas, Petherick Anna, Phillips Toby, Webster Samuel. Blavatnik School of Government Working Paper, 31. 2020. Variation in government responses to covid-19. [Google Scholar]
  9. Hindes Jason, Bianco Simone, Schwartz Ira B. Optimal periodic closure for minimizing risk in emerging disease outbreaks. PloS ONE. 2021;16(1) doi: 10.1371/journal.pone.0244706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Karin O., Bar-On Y.M., Milo T., Katzir I., Mayo A., Korem Y., Dudovich B., Yashiv E., Zehavi A.J., Davidovitch N., Milo R., Alon U. Cyclic exit strategies to suppress covid-19 and allow economic activity. medRxiv. 2020 doi: 10.1101/2020.04.04.20053579. [DOI] [Google Scholar]
  11. Keeling Matt J., Dyson Louise, Guyver-Fletcher Glen, Holmes Alex, Semple Malcolm G., Tildesley Michael J., Hill Edward M. Fitting to the UK COVID-19 outbreak, short-term forecasts and estimating the reproductive number. medRxiv. 2020 doi: 10.1101/2020.08.04.20163782. 2020.08.04.20163782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Keeling Matt J., Hill Edward, Gorsich Erin, Penman Bridget, Guyver-Fletcher Glen, Holmes Alex, Leng Trystan, McKimm Hector, Tamborrino Massimiliano, Dyson Louise, Tildesley Michael. Predictions of COVID-19 dynamics in the UK: short-term forecasting and analysis of potential exit strategies. PLoS Comput. Biol. 2021;17(1) doi: 10.1371/journal.pcbi.1008619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kretzschmar Mirjam E., Rozhnova Ganna, Bootsma Martin C.J., Boven Michiel van, Wijgert Janneke H.H.M. van de, Bonten Marc J.M. Impact of delays on effectiveness of contact tracing strategies for covid-19: a modelling study. Lancet Public Health. 2020;5(8):e452–e459. doi: 10.1016/S2468-2667(20)30157-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Moore Sam, Hill Edward M., Tildesley Michael J., Dyson Louise, Keeling Matt J. Vaccination and non-pharmaceutical interventions for covid-19: a mathematical modelling study. Lancet Infect. Dis. 2021;21(6):793–802. doi: 10.1016/S1473-3099(21)00143-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Moore Sam, Hill Edward M., Tildesley Michael J., Dyson Louise, Keeling Matt J. 2021. Vaccination and non-pharmaceutical interventions for covid-19: a mathematical modelling study. URL: https://github.com/sammoore25/Vaccination-and-Non-Pharmaceutical-Interventions-a-mathematical-modelling-study. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Office for National Statistics . 2020. Coronavirus and the Impact on Output in the UK Economy: 2020. URL: https://www.ons.gov.uk/economy/grossdomesticproductgdp/articles/coronavirusandtheimpactonoutputintheukeconomy/august2020. [Google Scholar]
  17. Pierce Matthias, Hope Holly, Ford Tamsin, Hatch Stephani, Hotopf Matthew, John Ann, Kontopantelis Evangelos, Webb Roger, Wessely Simon, McManus Sally, et al. Mental health before and during the covid-19 pandemic: a longitudinal probability sample survey of the uk population. Lancet Psychiatry. 2020;7(10):883–892. doi: 10.1016/S2215-0366(20)30308-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Prem Kiesha, Liu Yang, Russell Timothy W., Kucharski Adam J., Eggo Rosalind M., Davies Nicholas, Flasche Stefan, Clifford Samuel, Pearson Carl A.B., Munday James D., Abbott Sam, Gibbs Hamish, Rosello Alicia, Quilty Billy J., Jombart Thibaut, Sun Fiona, Diamond Charlie, Gimma Amy, Zandvoort Kevin van, Funk Sebastian, Jarvis Christopher I., Edmunds W. John, Bosse Nikos I., Hellewell Joel, Jit Mark, Klepac Petra. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health. 2020;5(5):E261–E270. doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Public Health England . 2021. Coronavirus in the UK. URL: https://coronavirus.data.gov.uk/ [Google Scholar]
  20. Riley Steven, Ainslie Kylie E.C., Eales Oliver, Walters Caroline E., Wang Haowei, Atchison Christina J., Fronterre Claudio, Diggle Peter J., Ashby Deborah, Donnelly Christl A., et al. High prevalence of SARS-CoV-2 swab positivity in England during 2020: interim report of round 5 of REACT-1 study. medRxiv. 2020 doi: 10.1101/2020.09.30.20204727. 2020.09.30.20204727. [DOI] [Google Scholar]
  21. Riley Steven, Ainslie Kylie E.C., Eales Oliver, Walters Caroline E., Wang Haowei, Atchison Christina J., Fronterre Claudio, Diggle Peter J., Ashby Deborah, Donnelly Christl A., et al. Resurgence of SARS-CoV-2 in England: detection by community antigen surveillance. medRxiv. 2020 doi: 10.1101/2020.09.11.20192492. 2020.09.11.20192492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Rowthorn Robert, Maciejowski Jan. A cost–benefit analysis of the covid-19 disease. Oxf. Rev. Econ. Policy. 2020;36(Supplement_1):S38–S55. [Google Scholar]
  23. Tildesley Michael J., Vassall Anna, Riley Steven, Jit Mark, Sandmann Frank, Hill Edward M., Thompson Robin N., Atkins Benjamin D., Edmunds John, Dyson Louise, Keeling Matt J. Optimal health and economic impact of non-pharmaceutical intervention measures prior and post vaccination in england: a mathematical modelling study. medRxiv. 2021 doi: 10.1101/2021.04.22.21255949. 2021.04.22.21255949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. World Health Organization . 2020. Novel Coronavirus (2019-nCoV) Weekly Epidemiological Update. URL: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20201005-weekly-epi-update-8.pdf. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

MMC S1

Basic model formulation of the age-structured model and parameter inference.

mmc1.pdf (232.4KB, pdf)

Data Availability Statement

Data on cases were obtained from the COVID-19 Hospitalisation in England Surveillance System (CHESS) data set that collects detailed data on patients infected with COVID-19. Data on COVID-19 deaths were obtained from Public Health England. These data contain confidential information, with public data deposition non-permissible for socioeconomic reasons. The CHESS data resides with the National Health Service (https://www.nhs.gov.uk) whilst the death data are available from Public Health England (https://www.phe.gov.uk).

RESOURCES