Toward Generalizability in the Deployment of Artificial Intelligence in Radiology: Role of Computation Stress Testing to Overcome Underspecification

Abstract

The clinical deployment of artificial intelligence (AI) applications in medical imaging is perhaps the greatest challenge facing radiology in the next decade. One of the main obstacles to the incorporation of automated AI-based decision-making tools in medicine is the failure of models to generalize when deployed across institutions with heterogeneous populations and imaging protocols. The most well-understood pitfall in developing these AI models is overfitting, which has, in part, been overcome by optimizing training protocols. However, overfitting is not the only obstacle to the success and generalizability of AI. Underspecification is also a serious impediment that requires conceptual understanding and correction. It is well known that a single AI pipeline, with prescribed training and testing sets, can produce several models with various levels of generalizability. Underspecification defines the inability of the pipeline to identify whether these models have embedded the structure of the underlying system by using a test set independent of, but distributed identically, to the training set. An underspecified pipeline is unable to assess the degree to which the models will be generalizable. Stress testing is a known tool in AI that can limit underspecification and, importantly, assure broad generalizability of AI models. However, the application of stress tests is new in radiologic applications. This report describes the concept of underspecification from a radiologist perspective, discusses stress testing as a specific strategy to overcome underspecification, and explains how stress tests could be designed in radiology—by modifying medical images or stratifying testing datasets. In the upcoming years, stress tests should become in radiology the standard that crash tests have become in the automotive industry.

Keywords: Computer Applications-General, Informatics, Computer-aided Diagnosis

© RSNA, 2021

Summary

Underspecification is a major obstacle to the generalizability of machine learning models and defines the inability of the pipeline to ensure that the model has encoded the inner logic of the system; this phenomenon is different and less well known than overfitting in artificial intelligence but can be analyzed and resolved with the use of stress testing.

Key Points

• ■ Overfitting and underspecification are the two major obstacles to the generalizability of artificial intelligence (AI) applications in radiology.

• ■ Overcoming overfitting allows for the deployment of narrowly generalizable AI models when analyzing data from a similarly or identically distributed dataset.

• ■ Overcoming underspecification, which is the inability of the pipeline to ensure that the model has encoded the inner logic of the system, allows for the deployment of broadly generalizable AI models.

Introduction

The use of artificial intelligence (AI) techniques is transforming both the clinical and research fields of medical imaging. As highlighted by the literature in Radiology issues from this year, the use of AI in imaging is an active research field. In 2020, 25% of the articles published in Radiology discussed AI and machine learning (1), including several overviews based on research activity and methods (1–4). The frequency of publications related to AI is even more impressive if we consider the recently launched journal, Radiology: Artificial Intelligence, specifically dedicated to this emerging technology.

Radiologists recognize that AI-driven tools will be critically important to their practice, as there are increasingly complex demands in precision medicine (5). The use of AI tools improves the performance of radiologists in their daily tasks, such as basic diagnostics (6–19). Moreover, these tools allow radiologists to push imaging boundaries by enabling treatment response prediction (20–22) and even provide patient prognostic instruments (23,24). The use of AI involves all disciplines in medical imaging, including, but not limited to, chest (7–11,24–26), COVID-19 (18,19,27,28), cardiac (29–32), breast (20,33–36), neuroradiologic (12–17), and abdominal (21–23,37,38) imaging. To support this trend, the U.S. Food and Drug Administration has proposed a regulatory framework for using AI-based technologies as medical devices (39). The imaging community has also developed scoring systems to design high-quality pipelines, such as the radiomics quality score (40).

As AI becomes better integrated and more common in clinical practice, it is critical for radiologists to understand both the potential of AI and its limitations. Although there is extensive literature about AI uses and applications in medical imaging that would suggest this technology has become mainstream, the actual deployment and daily use of such tools is much more limited. We believe that this gap arises, in part, from the challenges of designing AI models that can maintain the same performance when applied to different datasets, which is the concept known as generalizability. This report focuses on a recent publication by D'Amour et al (41), which highlights a concept hindering generalizability called underspecification that is unaddressed by the current AI medical imaging literature, including that published in Radiology (ie, underspecification was mentioned in zero of 57 Radiology articles about AI in 2020) (1,5–38,42–63). Underspecification can be generally defined as not knowing whether the model has encoded the inner logic of the underlying system. Specific examples of underspecification will be described within this report.

The Basics of AI Model Building

Machine Learning Pipeline: A Series of Steps to Build a Model

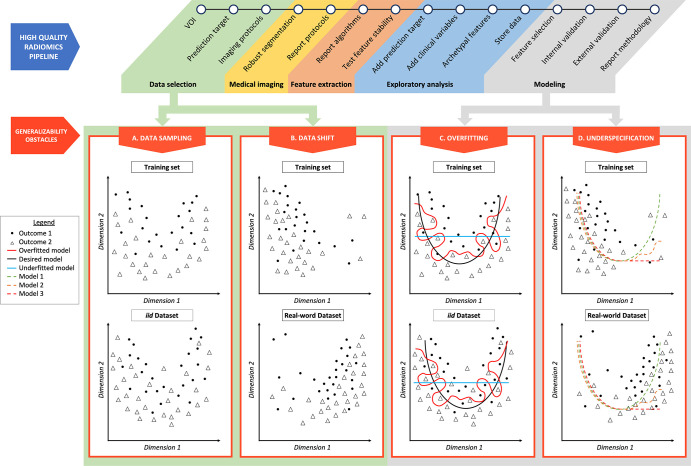
Machine learning is a subset of AI that defines algorithms for which predictions are created without being explicitly programmed. The inner logic of the model remains mostly hidden from the operator or user. The current paradigm in model building relies on a string of multiple steps (Fig 1), called a pipeline, that can ultimately vary among different AI approaches. Data are usually divided into three parts: training, validation, and test sets (3,4,40).

Figure 1:

Radiomics pipeline examples of overfitting and underspecification. A high-quality radiomics pipeline is shown. Data selection can be affected by data sampling and data shift. Modeling can be biased as a result of overfitting and underspecification. (A) Data sampling. The training set and an independent and identically distributed (iid) dataset are represented, respectively, in the top and bottom figures. Even if following the same distribution, resampling data induces small variations in outcome positions. (B) Data shift. The training dataset and a dataset drawn from the real world are represented, respectively, in the top and bottom figures. Outcomes of low values of dimension 1 are overrepresented in the training set, and outcomes of high values of dimension 1 are overrepresented in the real-world dataset. (C) Overfitting. The red line represents an overfitted model, which is able to isolate every outcome 1 from outcome 2 in the training set. When applied to an iid dataset, its performance deteriorates. The black line represents the desired model, performing identically in a training dataset and in an iid dataset. The blue line represents an underfitted model. (D) Underspecification. Three models (green, orange, and red dotted lines) are trained in a training set in which outcomes of low values of dimension 1 are overrepresented (top figure). These three models fit data well for low values of dimension 1. For high values of dimension 1, models 1 (green dotted line), 2 (orange dotted line), and 3 (red dotted line) behave differently. These three models will perform equally in an iid testing set. However, if the real-world dataset (bottom figure) presents a data shift, characterized by an overrepresentation of dimension 1 high values, model 1 segregates outcomes better than models 2 and 3 and represents the best model regarding generalizability. VOI = volume of interest.

Training: the model trying to learn the inner logic of the system.— The first step consists of training a model. Algorithms build predictive models on sample data, typically referred to as training data, that are used to do model fitting. The larger the training dataset, the more the algorithm can improve by identifying patterns able to predict desired outcomes and differentiating them from random associations. The relevance of the patterns used by the model are unknown at this point.

Validation: tuning the model on held-out data.— The second step in the pipeline is to use the validation dataset to perform model selection by confirming modeling choices that avoid overfitting. This step typically uses data that were withheld from analysis during the training step but that were sourced by the same database as the training set, making it independent and identically distributed (iid).

Testing: evaluation of model performance.— The third step is to use an additional dataset, known as the test dataset, to evaluate the performance of the model. Ideally, the test set should be designed to predict real-world performance. Frequently, the predictive performance of models is tested on a dataset that is withheld from the training and validation sets but is sourced from the same data collection as in the training set, resulting in an identically distributed dataset. This report explores why this test-phase step should ideally be enriched with stress tests so that if the model performs well enough, it would then be considered usable in clinical scenarios.

Narrow and Broad Generalizability of Models

Data Can Be “New” in Two Main Ways

One of most substantial drawbacks of machine learning is that the performance of predictive models developed in the aforementioned experimental training framework is often degraded when deployed in real-world clinical scenarios. The major challenge is, therefore, to build a model whose predictions can be generalized to new datasets. However, to address this generalizability issue, it is essential to understand that data can be “new” in different ways. There are two fundamental ways in which data may be considered new: resampling and data shifting.

Resampling Results in Narrow Generalization Issues Such as Overfitting

Resampling relates to the fact that two subsets taken from identically distributed databases will slightly differ because of statistical noise (Fig 1A). Being able to perform well on datasets that are identically distributed as compared with the training set could be labeled as “narrow” generalizability. To generalize in this way, a model must be able to distinguish between a stable signal and noise in a training set. Narrow generalization can be assessed easily, for example, by randomly splitting a single dataset and testing on these subsets. The failure to narrowly generalize is often related to overfitting (Fig 1C).

Data Shift Results in Broad Generalization Issues Such as Underspecification

Data shift represents a change in distribution between two datasets (Fig 1B). Deploying a model to clinical applications involves applying it to new datasets that are often not distributed identically to the training data. This change in distribution between training and deployment domains often leads to generalization failures. For instance, in radiologic applications, a change of distribution can occur when the databases contain different distributions in patients’ ages or ethnicities. Being able to perform well on datasets whose distribution differs from that of the training domain could be labeled as “broad” generalizability. Therefore, to broadly generalize, the model has to find a stable signal for making predictions that filters out noise and must also identify such a signal that will persist in the deployment domain, even in the presence of a data shift. There are many ways to fail at this latter task, and D’Amour et al (41) highlight underspecification as being one of them (Fig 1D).

Continuous Learning Bypasses Generalizability Issues but Does Not Solve Them

Continuous learning AI has been proposed as a potentially effective way to counteract the performance loss of an AI model over time (52). The performance loss becomes a generalizability issue when the model cannot generalize well to data obtained months or years after a model was trained. Continuous learning is a powerful way to bypass potential generalizability issues, but it does not solve the underlying issue.

Overfitting

Overfitting Is a Training Phase Issue

Overfitting is the most critical issue that contemporary AI strategies have been designed to prevent. Overfitting defines a structural failure mode that occurs during the training phase and prevents the model from distinguishing between signal and noise (Fig 1). A model is overfitted when it has learned every aspect of the training set, including irrelevant patterns originating from noise in the dataset. It has “memorized” that a specific combination of parameters is linked to an individual patient with a particular outcome. Although it performs well in the training set, an overfitted model will fail to predict future observations from new datasets, even if those new datasets are identically distributed. The model therefore fails to narrowly generalize. In nonoverfitted models, the AI model has learned to separate signal from noise and to rely on stable patterns that persist even when data are resampled from the same source.

Overfitting Is Common in Medical Imaging

Overfitting is frequent in medical imaging literature because the same scenario has been iterated multiple times. Overly complex models with a high number of features have been designed by single institutions with a small retrospective dataset. First, medical datasets tend to be unbalanced because some conditions are more frequent than others. The incremental value of AI algorithms for the diagnosis of uncommon diseases is obvious, as they can be underdiagnosed by radiologists who are not familiar with such diseases. Nonetheless, the rarer the condition, the smaller its frequency in the training set will be. Second, during the model-building process, the medical community uses an excessively high number of candidate features, because of the fear of missing valuable information, to improve the treatment of patients. Thus, strategies are needed to overcome overfitting issues within medical AI applications.

Strategies to Overcome Overfitting

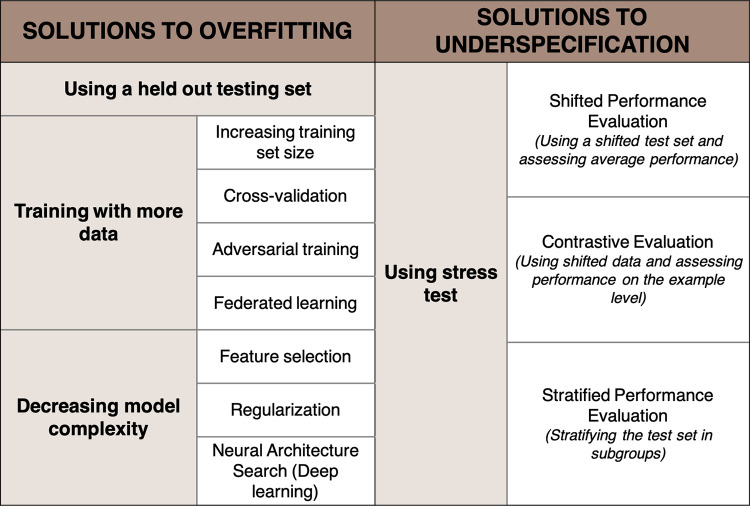
Most modern AI pipelines are designed to address overfitting by mainly using three strategies: using a held-out validation dataset, training with more data, and decreasing model complexity (Fig 2).

Figure 2:

Strategies to overcome overfitting and underspecification.

The first strategy consists of testing the developed model on held-out data that are iid. While the performance of a nonoverfitted model will remain stable, the performance of an overfitted model will drop when applied to this unseen data.

The second strategy consists of training with more data to better detect the signal of interest. Because increasing the training set volume is not always possible, several strategies have been described. One approach is cross-validation, which consists of splitting the training set into multiple folds to calibrate and fine-tune the model. Another strategy is adversarial training, or synthetic training, in which the training set is augmented by purposely adding small perturbations to the data (eg, adding blur) to build and introduce variability in the training data and therefore reduce the probability of overfitting (64). However, the amount of data needed to significantly improve performance is large in practice. Finally, building data networks among organizations could allow for the establishment of large databases. This is the goal of federated learning, which has been well studied and has undergone many recent innovations that can protect patient security (65).

The third strategy is to reduce the complexity of the model, which can be achieved by reducing the number of used features to prevent learning noisy patterns. This is called dimensionality reduction. However, oversimplifying can lead to underfitting when the model fails to spot relevant patterns, which causes a loss of accuracy (Fig 1C). Finding the right spot between an underfitted and an overfitted model is also known as the bias or variance trade-off (66). Bias error defines an error from an erroneous assumption, leading to missing the association between a relevant variable and the predicted outcome. Variance error determines the sensitivity to small fluctuations in the training data, leading the model to consider the random noise. An oversimplified, underfitted model has low variance and high bias and is therefore not accurate. Conversely, an overly complex, overfitted model has low bias and high variance, which hinders its generalizability.

An additional technique to reduce model complexity is regularization, in which a penalty coefficient is added during training to refrain the model from increasing its complexity. In deep learning, neural architecture search is a strategy in which the complexity of the model is tuned by the algorithm itself (67). Neural architecture searches can be used as powerful tools to reduce overfitting.

Example of Overfitting in a Radiologic Application

There are different scenarios in which a model can become overfitted. For example, a model is trained to predict overall survival in patients with metastatic colorectal cancer. The training dataset was sourced from two different hospitals: a tertiary cancer center and a general hospital. In this dataset, the overall survival is higher at the tertiary cancer center because the medical management at this center is more advanced than that at the general hospital. An overfitted model with too many features used could, for example, classify the specific reconstruction setting of the CT scanner at the tertiary cancer center as a predictor of higher disease-free survival rather than actual imaging features of the cancer.

In conclusion, overfitting corresponds to a model perfectly fitted to a specific dataset, which will fail to narrowly generalize when data are resampled, even in an identically distributed dataset.

Underspecification

A Model Must Encode the Problem Structure to Broadly Generalize

A model will be broadly generalizable to datasets that are not identically distributed if the logic it has encoded in the training set is based on the underlying system. Encoding would be considered successful if the model has identified in the training set the causal relations between candidate predictors and the output to be predicted. Particularly in medical applications, the encoded structure should ideally remain invariable to potential confounding factors, such as ethnicity, other unrelated diseases, and the quality of imaging techniques. For instance, a model that predicts the nature of a lesion should use imaging features related to the lesion (such as attenuation or enhancement) or its environment (presence of emphysema for a lung tumor or cirrhosis for a liver tumor). If the training domain is significantly different from the application domain, the encoded logic will probably not capture the system structure. Interestingly, the absence of a noticeable data shift between the training set and the application domains is not sufficient to guarantee that the model will broadly generalize.

A Single Pipeline Can Produce Different Models

A single pipeline, given the same training and iid testing sets, can produce various models. However, each one of these models will likely have a different success level of generalization, despite performing equally during iid testing. D'Amour et al (41) have demonstrated this phenomenon by using retinal fundus image and skin lesion analysis models. They developed multiple versions of deep learning models for both retinal and skin lesions, with differences arising solely from randomized starting weights for the neural network. The first observation was that the models performed equally well on iid tests. However, they did not perform equally when they were run through specific tests designed to check accuracy with different conditions. For example, retinal fundus analysis models were applied to images taken with a different type of camera, and the accuracy of the skin lesion analysis models were evaluated on the skin-type subgroups. They demonstrated that even with an ideal database presenting no data shift (eg, including all skin types for a skin analysis model), some of the models will not perform well when run through these tests (on each skin type). The poorly performing models would not have been ruled out by a simple iid test; crucially, iid test sets often do not contain enough information to distinguish between suitable and spurious models. These findings highlight the need for new strategies to mitigate the risk of underspecification.

Definition of Underspecification

Underspecification describes the inability of the pipeline to identify whether the model has embedded the structure of the underlying system and will remain invariable in response to confounding factors. Models that are either successful or unsuccessful at properly encoding the system structure often perform identically on the iid testing set and thus cannot be distinguished. If the iid-tested chosen model does not encode any part of the structure of the problem of interest, then it will undoubtedly exhibit poor performance in real-life conditions. A critical distinction is that underspecification occurs during the testing phase, whereas overfitting occurs in the training phase.

In more general terms, a system is said to be underspecified when it has “more than one solution.” This can be compared with mathematics, such as in a system of equations with more unknowns than linear equations (eg, x + y = 3). In this algebra problem, several sets of values can solve the system (eg, x = 1 and y = 2, or x = 2 and y = 1, etc). When the system has as many linear equations as unknowns (eg, x + y = 3 and x = 2y), then only one set of values solves the system (eg, x = 2 and y = 1): the system is specified.

In the example shown in Figure 1D, one of the models fitted the training dataset by using an exponential decay (red dotted line, model 3). However, real-world data do not follow this distribution, and model 3 did not encode the inner logic of the system. When applied to a real-world dataset, model 3 failed. Another model trained with the same training dataset successfully encoded the inner logic of the system (green dotted line, model 1), which is a parabolic distribution, and will generalize in the real world. Testing models with data that are distributed identically to the training data did not allow for model 1 to be differentiated from model 3.

In an underspecified pipeline, multiple models can yield good performance in a single iid test set. The testing phase has to be strengthened to be able to select the most generalizable model.

Overcoming Underspecification with Stress Tests

To overcome underspecification, the testing phase must be used to aid in the selection of only broadly generalizable models. Such models should perform equally between training and real-world domains, even in the presence of data shift. To this end, D'Amour et al (41) suggest enriching pipelines by adding customized stress tests specifically designed to reproduce the challenges that the model will face when deployed in the real world. If the performance of the model is high in every stress test, the model has likely encoded the system structure. By using multiple, well-designed stress tests, modelers can ensure that the produced model is broadly generalizable. Stress testing has already been shown to rule out spurious models in other domains such as dermatology and natural language processing (68,69). D'Amour et al (41) considered three types of stress tests: shifted performance evaluation, contrastive evaluation, and stratified performance evaluation (Fig 2).

Stress Tests with Shifted Performance Evaluation

The concept of a stress test with a shifted performance evaluation consists of purposely identifying and using a shifted test set to assess whether the average performance of a model is stable in the presence of a data shift. Different strategies can be used to obtain such shifted datasets. One easy method involves deliberately modifying images of the test set (eg, the changing resolution or simulating a softer reconstruction kernel) (Fig 3). An alternative method is to use an additional testing set that is genuinely shifted (eg, CT scans modified to mimic different acquisition protocols, such as section thickness).

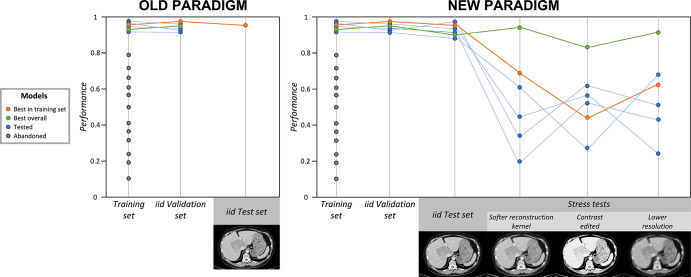
Figure 3:

Old and new paradigms: application of stress tests to counteract underspecification. The gray dots indicate models that were abandoned because of their low performance in the training set. The blue dots indicate models that performed well in the training set and were selected to continue to the validation and testing phases. The orange dots indicate the best-performing model in training, in independent and identically distributed (iid) validation, and in iid testing; however, this model performed poorly during stress tests. The green dots indicate the best overall model, which performed well in training, in iid validation, in iid testing, and during stress tests, and is more likely to be the most broadly generalizable model. In the old paradigm (left), after training, the best-performing model in the training set is validated and then tested with iid data. If the performance is satisfying, the model is deployed. In the new paradigm (right), six models (blue, orange, and green dots and lines) trained on the same training set are selected for validation and testing. After iid validation and iid testing, their performances are assessed by using three stress tests, designed with artificially modified CT scans, with the application of blurring and pixelating filters, and with contrast modification. All six models show great accuracy in the iid validation and iid test sets, but the green model is the only one that performs well throughout all stress tests. Therefore, the green model is the one that is the most likely to broadly generalize well (ie, to maintain high performance even when applied to shifted datasets). Adding stress tests to the pipeline allowed the green model to be distinguished from others.

Stress Tests with Contrastive Evaluation

Contrastive evaluation stress tests also use shifted data. However, contrastive evaluations do not assess the average performance of the model but evaluate performance on the example level: each observation is paired to its transformation (eg, lower resolution or softer reconstruction kernel simulation), and the prediction before and after transformation are compared. If the prediction is often modified by the transformation, the model is likely not generalizable.

Stress Tests with Stratified Performance Evaluation

Stratified performance evaluation involves stratifying the test set into subgroups and testing the model on each subgroup to check whether the performances are consistent across the groups. For example, the performance of a radiomic model can be assessed on a testing set stratified into subgroups according to the acquisition parameters of the CT scan. This type of evaluation can isolate potential confounding variations within the dataset.

Stress Testing in Radiologic Applications

In radiologic applications, specific stress tests could be designed to simulate different acquisition parameters (such as dose-reduction protocols, section thickness, or intravascular contrast attenuation), introduce artificial noise, or introduce artifacts (such as motion, beam hardening, partial volume, aliasing, etc) that will alter the image quality. The testing set could also be divided into subgroups according to the center of origin of the data, or according to acquisition parameters, to assess whether the performance of the model is consistent across centers or acquisition parameters.

Example of Overcoming Underspecification in Radiology

An example of overcoming underspecification in radiology is in a model trained to classify the presence or absence of hepatic steatosis by using a full CT scan section. Steatosis is strongly associated with obesity, and CT scans of patients with obesity are known to present a lower signal-to-noise ratio (70). The best-fitted model is validated and then tested on held-out data originating from the same center. One of the main features used by the selected model to predict the presence of hepatic steatosis is trivial: the signal-to-noise ratio. The model will therefore not generalize well to other imaging datasets, particularly to those with a high number of patients with alcohol use, who often present with steatosis without obesity. The testing phase, which uses data sourced from the same hospital as the training set, would therefore be unable to rule out the model that encoded a trivial feature. Knowing that hepatic steatosis is more frequent in patients with obesity and that CT scans of these patients present a lower signal-to-noise ratio could lead to specific stress tests.

First, the test set could have been artificially modified by randomly changing the signal-to-noise ratio to apply shifted performance evaluation and contrastive evaluation. Both strategies would have used these modified CT scans, but shifted performance evaluation would have compared the average performance of the model between the original test set and the modified test set, whereas contrastive evaluation would have compared the prediction of the model for each CT scan of the test set before and after modification. Another way to detect spurious models would have been by creating subgroups of the testing sets stratified by body mass index (stratified performance evaluation). In this example, the performance of the generalizable model would have been consistent across the subgroups, whereas the performance of the nongeneralizable model would be lower in the low body mass index subgroups.

Stress Testing Drawbacks and Strengths

Stress tests reveal whether the model performance will be stable when applied to a shifted dataset by introducing artificial shifts or by monitoring its predictions in particular subgroups of the testing set. Each stress test assesses the performance of the model under a single shift (such as changes in section thickness or a different signal-to-noise ratio). It is, however, not conceivable to design specific stress tests for each potential shift, particularly in radiology, where numerous image acquisition parameters add up to the wide range of patient characteristics to create a large ensemble of potential distribution shifts. Stress tests should therefore ideally be carefully designed to reproduce specific shifts that can result in model failure. In addition to focusing on how well the model is performing in terms of achieving the task it is designed for, researchers must anticipate under what specific conditions the model will be used and will have to maintain stable performance. There is a need to develop alternative strategies to force the model to identify and use features that remain invariable to most, if not all, confounding factors. This is the aim of causal inference and domain invariance, which are active fields of AI research with emergent applications in medicine and radiology (71,72).

On the other hand, unlike the now mainstream “external dataset” testing procedure, stress tests offer the opportunity to assess the performance of the model under specific conditions that are not represented in the training set but that might not be represented in an external dataset either. Although the use of an external dataset is considered the reference standard testing procedure to acknowledge model generalizability, an externally sourced testing set can still be similar to the training domain regarding certain characteristics. Stress tests introduce a more precise and deliberate method of evaluating model generalizability.

Discussion

This report discussed specific strategies to limit overfitting and underspecification to improve the generalizability of models and the deployment of AI applications in radiology. Overfitting is a structural failure mode that occurs during the learning phase and hinders the model from distinguishing between stable signals and noise, thus narrowly generalizing to identically distributed datasets. Solutions to this challenge include training with more data, decreasing dimensionality, and using external test sets. Underspecification is a testing phase issue representing the difficulty of knowing whether the model has encoded the system structure with an iid test set and thus whether the model will broadly generalize to non–identically distributed datasets. The underspecification concept has previously been discussed in AI literature (73–77), but its extent in practical applications is underestimated and needs to be addressed, particularly in radiologic applications. The use of specifically designed stress tests allows for the identification and selection of broadly generalizable models.

It is worth noting that the absence of a noticeable data shift between the training set and the application domains is not sufficient to guarantee that the model will broadly generalize, and an underspecified pipeline will ultimately produce non–broadly generalizable models. Training sets should be as representative of the target population as possible, but the testing phase should also be enhanced by using specifically designed stress tests.

Yielding high generalizability might nonetheless come at the cost of performance, and researchers must develop new plans to optimize the trade-offs among generalizability, the highest overall performance, and the performance in specific conditions (78). In the current quest toward generalizability, there are two distinct solutions: developing models able to handle heterogeneous data and reducing data heterogeneity by standardizing acquisitions across institutions. The evolution of technology and standardization to address these issues will be fascinating to observe. On the one hand, leading medical imaging manufacturers might be interested in optimizing software specifically designed to achieve the highest performance on their hardware and reconstruction settings. On the other hand, AI start-ups and software companies might favor broadly generalizable models to increase the sale of their product.

The deployment of AI in radiology, however, does not only rely on performance and generalizability issues. Although the most critical issue is to avoid AI errors that could be detrimental to the health of patients, another major challenge is to help radiologists trust AI by opening the black box and creating transparency regarding how it makes decisions. Hence, the development of new software dedicated to this task is required (79).

The advent of AI tools is triggering a profound change in radiology. AI tools will allow radiologists to combine their interpretations with model outputs, which may contain information inconceivable by the human eye. It will therefore be necessary for every radiologist to become aware of AI pitfalls (such as its generalizability issues) to keep a critical mind to prevent making mistakes that could be detrimental to patients and to guarantee a high-quality personalized report that both the patient and their physician are expecting.