Octree Representation Improves Data Fidelity of Cardiac CT Images and Convolutional Neural Network Semantic Segmentation of Left Atrial and Ventricular Chambers

Abstract

Purpose

To assess whether octree representation and octree-based convolutional neural networks (CNNs) improve segmentation accuracy of three-dimensional images.

Materials and Methods

Cardiac CT angiographic examinations from 100 patients (mean age, 67 years ± 17 [standard deviation]; 60 men) performed between June 2012 and June 2018 with semantic segmentations of the left ventricular (LV) and left atrial (LA) blood pools at the end-diastolic and end-systolic cardiac phases were retrospectively evaluated. Image quality (root mean square error [RMSE]) and segmentation fidelity (global Dice and border Dice coefficients) metrics of the octree representation were compared with spatial downsampling for a range of memory footprints. Fivefold cross-validation was used to train an octree-based CNN and CNNs with spatial downsampling at four levels of image compression or spatial downsampling. The semantic segmentation performance of octree-based CNN (OctNet) was compared with the performance of U-Nets with spatial downsampling.

Results

Octrees provided high image and segmentation fidelity (median RMSE, 1.34 HU; LV Dice coefficient, 0.970; LV border Dice coefficient, 0.843) with a reduced memory footprint (87.5% reduction). Spatial downsampling to the same memory footprint had lower data fidelity (median RMSE, 12.96 HU; LV Dice coefficient, 0.852; LV border Dice coefficient, 0.310). OctNet segmentation improved the border segmentation Dice coefficient (LV, 0.612; LA, 0.636) compared with the highest performance among U-Nets with spatial downsampling (Dice coefficients: LV, 0.579; LA, 0.592).

Conclusion

Octree-based representations can reduce the memory footprint and improve segmentation border accuracy.

Keywords CT, Cardiac, Segmentation, Supervised Learning, Convolutional Neural Network (CNN), Deep Learning Algorithms, Machine Learning Algorithms

© RSNA, 2021

Summary

Octrees can reduce the memory footprint of three-dimensional imaging volumes with minimal loss of image quality through a user-controlled intensity tolerance parameter that enables convolutional neural network segmentation at higher spatial resolutions and with deeper feature vectors, leading to improved boundary segmentation performance.

Key Points

• ■ Neural network–based semantic segmentation of three-dimensional (3D) images with a high spatial resolution and a large field of view is constrained by the memory footprint of the input images and the associated computations within the network.

• ■ Octree representation was adapted for use in medical imaging by introducing an intensity tolerance parameter to control image compression; compared with spatial downsampling, octrees improved the representation of 3D imaging volumes.

• ■ Semantic segmentation with an octree-based convolutional neural network increased the accuracy of predicted segmentations, particularly at boundaries between structures.

Introduction

Deep convolutional neural networks (CNNs), such as U-Nets (1), can perform semantic segmentation of medical images, including three-dimensional (3D) CT data (2). However, 3D image volumes are challenging to analyze given their large size and their associated large memory footprint, which limits the implementation of 3D architectures on commercially available graphics processing units (GPUs) to shallow designs (3,4). Although previous approaches have analyzed image volumes as a series of two-dimensional sections (5–7), this process irrevocably disrupts the 3D content and/or information. Further, 3D approaches downsample and/or crop image volumes to keep 3D information intact (3,4). However, cropping reduces the extent of information available to the network and can lead to multiple inferences that may require postprediction combination, whereas downsampling is a lossy operation that decreases image fidelity, thereby limiting the accuracy of the resulting segmentation (8). Although alternative image representations, such as point clouds (9,10) and sparse tensors (11) exist, there is no obvious way to apply CNNs to these data structures.

In this study, we explored an octree-based representation for 3D CT images that provides high data compression without sacrificing 3D content or spatial resolution. The approach maintains a grid structure that enables application of convolution-based neural network architectures. To adapt the framework to medical imaging, we introduced an intensity tolerance parameter in the octree subdivision algorithm to govern image compression. We found that across a range of compression levels, the octree-based representation preserved image and segmentation features better than spatial downsampling. Further, the octree representation enabled semantic segmentation with a 3D U-Net architecture at the native image resolution, which improved segmentation accuracy, especially at the object border. We demonstrated these findings in semantic segmentation of left ventricular (LV) and left atrial (LA) blood pools on clinical cardiac CT angiograms.

Materials and Methods

Dataset

Electrocardiographically gated end-systolic and end-diastolic cardiac CT angiographic studies from 100 patients obtained between June 2012 and June 2018 were anonymously analyzed as part of an institutional review board–approved retrospective study with a waiver of informed consent (study number 191797) in accordance with the Health Insurance Portability and Accountability Act. This cohort of images was previously used to develop a machine learning approach to segment the left ventricle and atria and estimate short- and long-axis imaging planes (12). Studies were included on the basis of the availability of expert segmentations.

Briefly, patients were 67 years ± 16 (standard deviation) old, and there were 60 men. Studies were obtained for preoperative assessment of transcatheter aortic valve replacement (n = 39), suspected coronary artery disease (n = 38), and preoperative assessment of pulmonary vein ablation (n = 23).

Image Acquisition

Images were acquired with three different CT systems: the Toshiba Aquilion One (Canon Medical Systems) (n = 47), GE Revolution (GE Healthcare) (n = 41), and Siemens Somatom Force (Siemens Healthcare) (n = 12). Iohexol (Omnipaque) contrast-enhanced intensity in the LV was 512 HU ± 147 and was greater than 275 HU for all patients.

The median field-of-view diameter in the x–y dimension was 200 mm (interquartile range [IQR], 190–220 mm) with a median in-plane voxel spacing of 0.39 mm (IQR, 0.37–0.43 mm). Along the z dimension, the median field of view was 160 mm (IQR, 120–320 mm) with a median reconstructed section thickness of 0.625 mm (IQR, 0.5–0.625 mm). The typical 3D image volume had a matrix size of 512 × 512 × 256 voxels (left-right, anterior-posterior, and craniocaudal, respectively).

Image Segmentation

ITK-SNAP (http://www.itksnap.org/pmwiki/pmwiki.php) (13) was used by trained undergraduate researchers (A.C. and A.R.) to segment the left side of the heart at the native resolution with two different classes labeled as (a) LV and (b) LA, including the LA appendage. For each patient, end-diastolic and end-systolic frames were segmented, leading to 200 image volumes with corresponding semantic segmentations. Segmentations were visually confirmed or corrected by a radiology resident (D.M.V.), who had 7 years of experience in cardiac image segmentation.

Dataset Preprocessing

After segmentation, all images and segmentations were resampled to a 256 × 256 × 256 volume with a 0.625-mm isotropic resolution spanning 160 mm, which was centered at the center of the LV blood pool to standardize neural network evaluation. Patients were divided into five folds, each with 20 patients (20 end-diastolic and 20 end-systolic images). Fivefold cross-validation (160 training and 40 validation end-diastolic and end-systolic images) was performed, and each fold was used once as the set of validation images. This sample was successfully used to train a CNN to evaluate cardiac function and obtain short- and long-axis imaging views on electrocardiographically gated cine CT images (12).

Implementation of Octree Image Compression

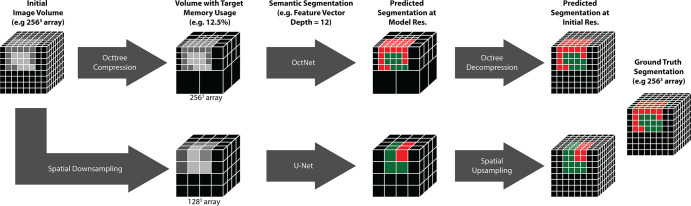
A 3D octree-based architecture, OctNet (14), was modified to compress medical image volumes prior to semantic segmentation by using a user-defined intensity tolerance τ. Octrees exploit similarity among neighboring voxels to generate a memory-efficient, quickly accessible, hierarchic partitioning of the image volume (15). Medical images rarely have identical neighboring intensity values but frequently have regions with nearly homogeneous intensity. Therefore, we introduced a user-defined intensity tolerance parameter τ, which controls the compression (and memory footprint) of the octree representation. An increasing τ value leads to more compression but higher loss of image and segmentation features (Fig 1). The ability of the octree representation to preserve image features in our dataset was compared with conventional spatial downsampling at various levels of image compression (Fig 2).

Figure 1:

Octrees enable compressed image representation while maintaining image and segmentation quality. (A) Octree compression with an intensity threshold τ can decrease the memory (Mem) footprint while avoiding substantial image degradation. In this example, τ = 200 HU leads to 15% memory use with minimal image (root mean square error [RMSE], 0.98 HU) and segmentation (left ventricular [LV] Dice coefficient, 0.979; LV border Dice coefficient [LV bDice], 0.884) errors. (B) To achieve the desired image memory footprint, τ thresholds were identified through a binary search, with increasing τ values leading to more significant memory savings (a lower memory footprint).

Figure 2:

Study schematic. Image volumes were compressed by using either the octree approach or conventional downsampling. Each volume was then used to train a semantic segmentation convolutional neural network. In addition to losing boundary information in the image during downsampling, spatial downsampling leads to postsegmentation upsampling, which can lead to errors in segmentation. The octree representation can avoid these limitations using an intensity tolerance, τ. Res. = resolution.

Octree-based Semantic Segmentation

Octree images were generated at desired memory footprints through a binary search of τ. The ability to specify the memory footprint of an octree representation allowed comparison of OctNet performance with conventional U-Net segmentations of spatially downsampled images.

CNN Architecture

Traditional U-Net architectures have proven successful in performing image segmentation. However, for 256 × 256 × 256 image volumes, a 3D conventional U-Net with a feature vector depth (FVD) of 16 at the input layer (and doubling after each downsampling step) requires approximately 100 GB of GPU memory, which is unrealizable on most GPUs (typical memory range, 8–16 GB).

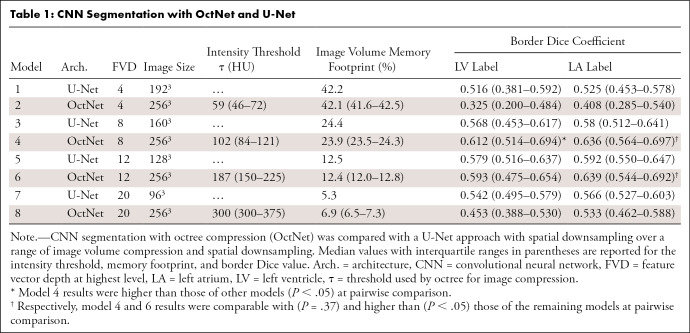
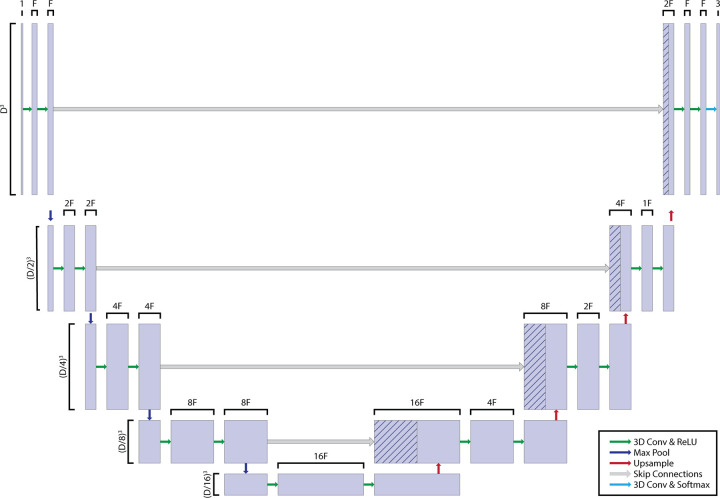
Therefore, we implemented four different 3D networks (eight models in total) that trade off image compression with the FVD, as shown in Table 1 and Figure 3. All the networks required the same memory at runtime (approximately 10 GB), which allowed for training on a single GPU. Model 1 was a 3D U-Net with minor (approximately 1.3 times) spatial downsampling (input 3D array: 192 × 192 × 192 voxels, memory footprint: 42% of the original array) but a very limited FVD (FVD = 4). Model 3 doubled the FVD (FVD = 8) by decreasing the input image size (3D array: 160 × 160 × 160 voxels, memory footprint: 24%). Models 5 and 7 further downsampled the image volume to memory footprints of 12.5% and 5%, respectively, to achieve higher FVDs (FVD = 12 and 20, respectively.) OctNet models (models 2, 4, 6, and 8) operate on images at the native 3D image volume (256 × 256 × 256 array) but achieve the same FVD as the U-Nets by varying τ.

Table 1:

CNN Segmentation with OctNet and U-Net

Figure 3:

Three-dimensional (3D) convolutional neural network (CNN) architecture. As outlined in Table 1, we evaluated different combinations of input 3D volume (variable D) and feature vector depths (variable F). Although this led to differences in the resulting network, other features of architecture, such as convolutions (Conv), max pooling, and upsampling steps, were kept constant. ReLU = rectified linear unit.

CNN Training

For all models, 10 random augmentations were generated for each image before training. Translations ranged from −10% to 10% of the field of view in the x, y, and z directions, and affine scalings between −10% and 10% were applied. An Adam optimizer was used to minimize categorical cross-entropy loss of the predicted segmentation. Each model was trained for 100 epochs, with a learning rate of 0.0001 and a learning rate decay of 0.1 every 15 epochs after the 30th epoch. These values were observed to result in consistent training results across folds. Amazon Web Services instances with NVIDIA (Santa Clara) Tesla V100 GPUs with Python 3.7 were used for all experiments. A GitHub repository with modified octree-based model is available at https://github.com/ucsd-fcrl/med-img-octnet-adaptation.

Assessment of Image Compression and Segmentation Quality

The root mean square error (RMSE) measured in Hounsfield units with respect to the original image was calculated after images underwent octree compression-decompression and spatial downsampling-upsampling. Because the effects of image compression were expected to be observed primarily at label boundaries, the border Dice coefficient of each segmentation label was measured in addition to the global Dice coefficient. The border Dice coefficient was determined by calculating the percentage of correctly labeled boundary pixels (Fig 4), with boundary pixels being defined as the 2-pixel perimeter of the labels (and adjacent background pixels) in the ground truth segmentation. In addition, errors in cardiac chamber volume and function (measured by using the stroke volume and ejection fraction) were analyzed by using the volume in each segmentation label at the two phases (end-diastolic and end-systolic) of the cardiac cycle.

Figure 4:

Example of segmentation error metrics. (A) An axial section of the heart and the corresponding ground truth and predicted segmentation from one of the patients; model combinations are shown. The Dice coefficient was used to assess overall segmentation accuracy and is illustrated by the fused image (right), with agreement shown in white and disagreement in black (in this section, the left ventricular [LV] Dice coefficient = 0.910). (B) Segmentation errors due to the compressed image representations are expected to occur primarily at the boundary. Therefore, we isolated the boundary of each segmentation and calculated a border Dice score (in this section, the LV border Dice coefficient = 0.402).

Statistical Analysis

The Shapiro-Wilk test was used to test for normality. Nonnormal measures are reported as medians with interquartile ranges (first and third quartiles). Friedman test was used to assess statistical significance across trained models for nonparametric measures, given paired patient images. Lin concordance correlation coefficient was used to assess differences in the LV ejection fraction and stroke volume, and these were compared by using Fisher z transformation with multiple-comparison correction. Pairwise assessment was performed by using the Tukey honestly significant difference procedure to account for multiple comparisons. Statistical analysis was performed in MATLAB (MathWorks) by using a significance level of P = .05.

Results

Efficacy of Octree-based Representation

Octree compression enabled image compression while maintaining high image and segmentation fidelity (Fig 1). Specifically, compression-decompression of 85% (ie, 15% memory footprint) resulted in a minimal image RMSE (0.98 HU) and segmentation accuracy (LV Dice coefficient, 0.979; LV border Dice coefficient, 0.884) loss.

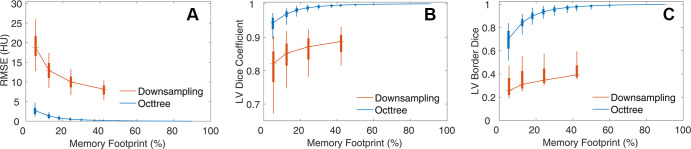
Across our dataset, octrees enabled compression with lower loss of image or segmentation quality, relative to spatial downsampling (Fig 5). For example, 76% compression (24% memory footprint) maintained a low median RMSE (0.5 HU), high LV Dice coefficient (0.988), and high border Dice coefficient (0.935). Further, octree compression had a higher (P < .001) performance than spatial downsampling in terms of the RMSE, LV Dice coefficient, and border Dice coefficient across the entire range of memory values evaluated. For example, octree representation with a 12% memory footprint (median RMSE, 1.3 HU; LV Dice coefficient, 0.970; LV border Dice coefficient, 0.843) had a higher performance than spatial downsampling with the same memory use (128 × 128 × 128 array; median RMSE, 13.0 HU [P < .001]; LV Dice coefficient, 0.852 [P < .001]; LV border Dice coefficient, 0.310 [P < .001]) as well as downsampling with a larger memory footprint (42%; 192 × 192 × 192 array; median RMSE, 8.1 HU [P < .001]; LV Dice coefficient, 0.887 [P < .001]; LV border Dice coefficient, 0.392 [P < .001]).

Figure 5:

Comparison of image and segmentation representation between spatial downsampling-upsampling and octree compression. (A) Use of OctNet leads to lower (P < .001) image distortion as measured by root mean square error (RMSE) than spatial downsampling-upsampling across all levels of compression. (B) Segmentation accuracy of the left ventricular (LV) label is higher (P < .001) with octree compression than with spatial downsampling. (C) Octrees preserve boundary segmentation Dice coefficients better (P < .001) than spatial downsampling. Boxes represent the interquartile range (25th to 75th percentile), and whiskers depict the 5th- and 95th-percentile range.

Improvement in CNN-based Semantic Segmentation Border Dice Coefficient with Octree Representation

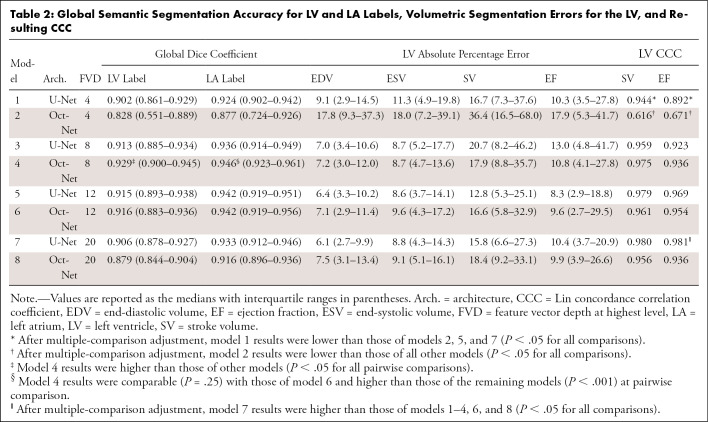
A higher border Dice coefficient was obtained by models that balanced image compression and network complexity (models 3–6 vs models 1, 2, 7, and 8 in Table 1). Model 4 (OctNet with 24% image memory usage) had a higher LV border Dice coefficient (0.612) than other models (P < .001 on Friedman test with P < .05 on pairwise comparisons). The LA border Dice coefficient was not significantly different (P = .37) between model 4 (0.636) and model 6 (0.639), but both models had higher performance than the remaining models (P < .05 for all pairwise comparisons).

Validation of Global Octree-based Semantic Segmentation Performance

In results similar to those found with border Dice coefficients, models 3–7 had higher (Table 2, P < .05) global Dice performance than models with a very limited FVD (models 1 and 2) or very compressed image data (models 7 and 8). The global LV Dice coefficient achieved by model 4 (0.929) was higher than that of the other models (P < .001 for all pairwise comparisons). LA Dice scores were comparable between model 4 and model 6 (0.946 vs 0.942; P = .26) and were higher than those of the remaining models (P > .05).

Table 2:

Global Semantic Segmentation Accuracy for LV and LA Labels, Volumetric Segmentation Errors for the LV, and Resulting CCC

Aside from the lower performance of model 2, global volumetric measures—end-diastolic volume, end-systolic volume, stroke volume, and ejection fraction—were not significantly different (P > .05). After multiple-comparison adjustment, Lin concordance correlation coefficient of the ejection fraction for model 7 was higher than that of models 1–4, 6, and 8 (P < .05 for all comparisons).

Discussion

Semantic segmentation of 3D image volumes is challenging because of the cubic relationship between the spatial resolution and memory footprint. We demonstrate how an octree-based image representation can significantly reduce the memory footprint without significant loss of image and segmentation fidelity. By preserving regions with significant intensity variation (ie, anatomic borders), octrees serve to primarily remove noise in regions of nearly homogeneous intensity.

The boundary of a segmentation is highly sensitive to compression through spatial downsampling. When incorporated into a CNN, octrees improved border and global segmentation accuracy. This suggests that octree compression may provide a useful framework with which to perform 3D segmentation without loss of thin-section features. Certain image analysis applications, such as estimating myocardial strain by using the motion of the segmented endocardial surface (16–20), are highly sensitive to boundary segmentation accuracy. Octree compression and OctNet segmentation would enable automation of this image analysis pipeline.

Although border and global segmentation metrics improved, volumetric measures such as stroke volume or ejection fraction estimates did not significantly change. This is likely due to the limited effect of border pixels on the overall chamber size and confirms that certain metrics (and tasks) can be estimated through segmentation of downsampled images.

The optimal compressibility for a given dataset depends on both the image and the task. For example, images with sharp boundaries are more compressible when using the octree framework than images with smoothly varying intensity. Further, segmentation of small objects (such as coronary arteries) or those with highly textured surfaces are expected to be more sensitive to compression. Task-specific optimization of the threshold parameter τ is likely needed to translate this approach to other applications. We evaluated segmentation of the LV and LA blood pools. These chambers have different sizes, geometry, and textures, and we observed higher border Dice coefficient for the LA (the smaller but smoother of the two chambers). This motivates future work to assess whether octrees can improve segmentation of small features such as coronary arteries and calcified lesions.

Our study had several limitations. First, the time-intensive nature of the 3D segmentation of left-sided cardiac structures limited the size of our dataset. However, differences between the octree- and downsampling-based models were consistent across different folds, and training with this dataset has previously shown clinical utility (12). Further, octree segmentation requires preprocessing (to represent the image as an octree), but U-Net models also required processing (both presegmentation downsampling and postsegmentation upsampling).

In conclusion, we demonstrated the value of octree-based image representation for semantic segmentation of CT images. Specifically, octree compression preserved image and segmentation features better than spatial downsampling, and an octree-based neural network architecture improves Dice coefficients of the border.