Abstract
Amidst a pandemic, operators of emergency medical service (EMS) systems aim at upholding service at sufficiently low response times while reducing the infection probability of their personnel. Designating ambulances to serve only infected patients and suspected cases may reduce the outage probabilities of ambulances and consequently the response times of the EMS. We investigate the benefits that EMS personnel and patients can gain from such a split. As a solution method to quantify these benefits, we apply a two-stage approach. First, we run a first-stage optimization model to pre-select ambulance splits with the highest emergency call coverage. Second, we solve the approximate Hypercube Queuing Model (AHQM) to evaluate the performance of the pre-selected ambulance splits at the second stage. We contribute to the existing literature by including multiple incident categories and outages of ambulances in the AHQM and combining it with the first-stage optimization model. Further, we conduct a case study for the Coronavirus Disease 2019 (Covid-19) pandemic to draw conclusions on the benefits of splitting. We observe that an ambulance split would not reduce the average response time for the examined data set since the Covid-related call volume in Munich and the infection probability are too low. However, a sensitivity analysis shows that long isolation times and high infection probabilities make an ambulance split beneficial for patients and EMS personnel, as an ambulance split reduces the average response time without significantly increasing the mean infection probability for EMS personnel.
Keywords: OR in health services, Ambulance dispatching, Approximate hypercube queuing model, Pandemic
1. Introduction
In January 2020, the Coronavirus Disease 2019 (Covid-19) pandemic was officially declared a Public Health Emergency of International Concern (World Health Organization, 2020c). By the end of 2020, more than 81 million people worldwide were infected with Covid-19 (World Health Organization, 2021). The health of Emergency Medical Service (EMS) personnel is at risk during a disease outbreak such as the Covid-19 pandemic. Paramedics responding to emergency calls are often the first medical personnel in contact with infected individuals. They must operate in uncontrolled environments such as accident scenes while only having limited information about the patient. Thus, especially during a pandemic, personal protective equipment (PPE) is indispensable to protect EMS personnel from infection. However, in many countries, PPE was scarce during the Covid-19 pandemic in 2020 (Dargaville, Spann, Celina, 2020, Ranney, Griffeth, Jha, 2020). This emphasizes the importance of finding supplementary ways to reduce the infection risk for EMS personnel during a pandemic. Further, some paramedics are more likely to get infected and be badly impacted by an infection. For example, Covid-19 may affect people with pre-existing conditions, which increase the risk of a severe disease progression, more seriously. Also, vaccinations may not be available for all groups. Especially early in a pandemic, there is a lack of knowledge about the disease and its transmission routes. In addition, the personnel might not be trained, so insufficient or wrong use of PPE can lead to high infection probabilities despite its availability. Should paramedics need to isolate themselves due to an infection, EMS systems can suffer personnel shortfalls. At the first peak of the Covid-19 pandemic in April 2020, 19.3% of New York City EMS personnel was absent due to self-isolation despite the availability of PPE (Prezant et al., 2020) which significantly reduced the capacity of the EMS system. Thus, it is paramount to improve the dispatching of ambulances in order to uphold service and reduce the infection probability of the medical personnel. Here, EMS operators may face a tradeoff between reducing the time patients have to wait for first aid and protecting the EMS personnel. Thus, ethical considerations are necessary, and decision-makers require data to quantify the effects of possible measures.
According to the World Health Organization (2018 pp. 14-18), the probability for further disease outbreaks with unpredictable nature and origin in the future is high. These prospects justify preparing for future disease outbreaks such as the Covid-19 pandemic. To remain operational, the EMS should adapt to the circumstances of a pandemic. Here, we investigate the benefit of designating ambulances to certain patient categories such as suspected or known cases, further referred to as “ambulance split”. Ko et al. (2004) present an observational study on a practical application of such an ambulance split applied during the severe acute respiratory syndrome (SARS) epidemic in Taipei (Taiwan). In this study, 0.6% of paramedics developed a probable SARS infection. Thus, a possible advantage of an ambulance split could be to restrict the risk of infection when treating suspected or known cases to only a limited share of personnel. Decreasing the risk of infection for paramedics reduces absence times and, therefore, increases available personnel. Since we investigate the categorization of ambulances, we consider an ambulance and its personnel as one unit. A negative effect of an ambulance split could be the reduction of the pooling effect as there are fewer ambulances available from which the ambulance dispatcher can choose from. Thus, some patients may experience longer waiting times if the nearest ambulance is designated to serve only other patient categories. In our context, we divide patients into unsuspicious, suspected and known cases. Thus, to apply this approach in practice, the number and locations of ambulances serving each patient category must be defined in a way that ensures acceptable emergency response times for all patients. Here, we need to decide which ambulance should serve which patient category to obtain the highest system performance evaluated by various performance measures.
Quantified benefits and drawbacks of an ambulance split form the basis for evaluating its ethical justifiability. Depriving patients of the nearest ambulance based on their categorization must have legitimate reasons. When categorizing patients and ambulances, average response times may decrease. However, an ambulance split may lead to an increased health risk for personnel and patients. Patients who cannot be served by the nearest ambulance must accept longer waiting times and a share of personnel must accept a higher mean infection probability. These ethical considerations depend on many factors, such as the EMS infrastructure and disease characteristics. Thus, further research needs to investigate the ethical considerations of an ambulance split.
Evaluating all possible ambulance splits is computationally intractable for large-scale systems. Thus, we apply a two-stage approach. First, to decide on the allocation of ambulances to patient categories, we pre-select ambulance splits based on their emergency call coverage by applying a first-stage optimization model. In this model, the coverage of emergency calls serves as an approximation for the performance of the EMS system. We assume that the better the coverage of emergency calls, the higher the performance of the EMS system in terms of its average response time. In the next step, at the second stage, we calculate performance measures for each pre-selected ambulance split using an adapted approximate Hypercube Queuing Model (AHQM) in which we embed ambulance outages. To evaluate the performance, we consider performance measures perceived by the patients, such as the response time, the share of late arrivals, and the patients’ waiting time in the queue until an ambulance becomes idle and is dispatched. Furthermore, calculating the mean infection probability for paramedics quantifies the benefit experienced by EMS personnel. We evaluate the benefit of an ambulance split by conducting a case study simulating a Covid-19 pandemic based on data of Munich, Germany. Here, we consider disease-specific characteristics such as the infection probability and isolation time of infected paramedics. As unknown future diseases are likely to evolve and pandemic data is subject to many uncertainties such as virus mutations or public health authorities prescribing isolation times, we conduct a sensitivity analysis to quantify the impact of such parameters.
The contribution of this paper is threefold. (i) To calculate the EMS performance measures, we extend Larson’s (1975) AHQM to the pandemic context and adapt Jarvis’ (1985) solution algorithm for faster convergence. (ii) We combine an optimization model with the AHQM to first pre-select ambulance splits and to evaluate their performance thereafter. (iii) We quantify the performance benefit gained by EMS personnel and patients when designating ambulances to serve only suspected and known cases during a pandemic. By doing so, we provide necessary data for evaluating the justifiability of an ambulance split.
Results show that introducing a flexible split can reduce the average response time without significantly increasing the mean infection probability for EMS personnel. This is the case if system workloads are high due to long isolation times or high infection probabilities. Consequently, the general population could benefit from a split which indicates ethical justifiability. Nevertheless, disease specific characteristics, such as isolation times or transmission probabilities, influence the decision whether to split. In the case of short isolation times and a low infection probability, the best average response times are observed when not dividing ambulances into categories. Applying a fixed split can decrease both the average response time and the mean infection risk for personnel serving only unsuspicious cases; in turn, the remaining personnel designated to suspected and known cases must accept higher mean infection probabilities. Here, decision-makers face a tradeoff whether a share of personnel should be protected at the expense of the remaining personnel.
First, we present related literature in Section 2. Section 3 introduces the problem statement and second-stage model. Section 4 explains the solution algorithm based on the AHQM and the calculation of performance measures. We introduce and optimize the ambulance splits in Section 5. In Section 6, we evaluate the tradeoff numerically. Section 7 concludes the paper.
2. Literature and background
The problem of dispatching ambulances is related to allocating service units to customer inquiries such as towing requests for vehicles or repair services for industrial machines causing high costs during downtime. In such fast-response service networks, minimizing response times is paramount. Drent, Keizer, & van Houtum (2020) optimize the dispatching and repositioning process of a service provider responsible for the maintenance of, e.g., industrial machines. Hiller, Krumke, & Rambau (2006) tackle the dispatching problem of a car breakdown service provider in real-time applications by successively solving a re-optimization model using the information available at that time.
In operations and supply chain risk management, there are several streams focusing on the preparation for various unpredictable events such as earthquakes, terrorist attacks, or pandemics. These events can lead to disruptions which one should prepare for. For this reason, measuring and improving supply chain resilience has gained attention. Golan, Jernegan, & Linkov (2020) conduct a systematic literature analysis of trends and applications. Furthermore, Queiroz, Ivanov, Dolgui, & Fosso Wamba (2020) review literature investigating the influence of pandemics on logistics and supply chains. Caunhye, Nie, & Pokharel (2012) provide an overview of optimization models to improve logistics operations before as well as shortly after an emergency event, such as evacuation or transportation of injured people. Dasaklis, Pappis, & Rachaniotis (2012) outline literature dealing with logistics operations preparing and controlling disease outbreaks caused naturally or by bioterrorist attacks. Farahani, Fallah, Ruiz, Hosseini, & Asgari (2019) review the Operations Research (OR) literature including facility location models for large-scale disasters such as earthquakes or terrorist attacks, small-scale emergencies including EMSs, as well as non-emergency healthcare facilities such as hospitals. Similar to Farahani et al. (2019), Altay & Green (2006) review OR literature studying the preparation, response and recovery from disasters, however, excluding daily emergency service operations.
In the OR literature dealing with emergency services (e.g. operations of police forces, fire brigades, or EMS systems), different approaches exist to investigate and optimize their performance. Schmid (2012) applies approximate dynamic programming to investigate dispatching strategies and the relocation of idle ambulances in an EMS system. Another stream of literature investigates the operations of emergency services and their performance applying simulation (Amorim, Ferreira, Couto, 2018, Haghani, Tian, Hu, 2004). Tassone & Choudhury (2020) provide an overview of optimization models and other solution methods applied to solve the routing and location problem of ambulances. Nickel, Reuter-Oppermann, & Saldanha-da Gama (2016) introduce a sampling approach to optimize ambulance depot and vehicle locations. Larson (1974) introduces a descriptive model, the Hypercube Queuing Model (HQM), to determine performance measures of emergency service systems such as the average response time or ambulance workloads. Although the HQM and its extensions can be applied to different emergency services, in our context, ambulances function as servers and patients’ emergency calls reflect the demand. Thus, in the following we refer to these terms interchangeably.
2.1. Hypercube queuing model
Larson’s (1974) HQM is a spatial queuing model based on a continuous-time Markov Process. The examined region consists of a set of geographical areas among which emergency calls and ambulances are spatially distributed. The locations of ambulances can either be fixed or mobile. Mobile locations refer to ambulances that are non-stationary when they are idle. If all ambulances are busy, incoming emergency calls can either be queued or assumed to be lost and served by another system. In the HQM, every state is a binary sequence with each position representing the status of an ambulance. A binary value of 0 indicates an idle ambulance, 1 denotes a busy ambulance. The transition graph forms a hypercube for systems operating more than three ambulances. The times between transitions are exponentially distributed and depend on the arrival and service rates of emergency calls. Under single dispatch, only transitions between states directly connected by an edge in the hypercube are possible (Larson, 1974).
Larson (1975) presents an approximate HQM (AHQM) which does not require an exponential number of constraints compared to the exact HQM when calculating steady-state probabilities. Therefore, it is applicable for large-scale systems. Ghobadi, Arkat, & Tavakkoli-Moghaddam (2019) present key aspects of the exact and approximate HQM and give an overview of possible extensions.
Chelst & Barlach (1981) extend the HQM and AQHM by adding the possibility of multiple-dispatch. In doing so, they can reflect the dispatch of multiple ambulances to incidents requiring increased manpower. In their experiments applied to the context of police forces, the performance measures obtained from the adapted approximate model deviate by less than 2% from the extended exact model, on average. Jarvis (1985) embeds multiple patient types into the AHQM and develops a stable and fast-converging approximation procedure to obtain the steady-state probabilities. In the developed model, service times depend not only on the ambulance but also on the patient type. Souza, Morabito, Chiyoshi, & Iannoni (2015) categorize patients according to their priority and account for these priorities when serving patients from the queue. Comparing the results of the extended HQM with simulated results yields a relative error of 1%, on average. Similarly, Iannoni, Chiyoshi, & Morabito (2015) consider three patient classes based on the patients’ urgency of being served. Looking at small instances, the service quality of the two higher-priority classes increases slightly, at the expense of the lowest-priority class which faces a significantly lower service quality. Goldberg & Paz (1991) develop an optimization model and apply pairwise interchange heuristics to find the best locations for ambulances. Results show that the heuristics perform best if either locations covering the lowest share of emergency calls or locations with the lowest utilization are closed in each iteration of the pairwise interchange heuristics. Iannoni, Morabito, & Saydam (2008), based on Chelst & Barlach (1981), assume that a call can only be answered by specific ambulances, referred to as “partial backup”. Optimizing the size of the geographical areas, each with its own ranked list of preferred ambulances, may improve the performance of the EMS without adapting the ambulances’ locations. Morabito, Chiyoshi, & Galvão (2008) compare the performance measures of the HQM for homogenous and non-homogenous ambulances. They observe that ambulance-specific service times improve the estimation of the actual performance measures. Budge, Ingolfsson, & Erkut (2009) focus on the EMS system’s ambulance depots rather than on the ambulances. They assume that multiple ambulances are located at the same depot and numerically quantify the difference between the iterative approximation approach and a discrete-event simulation to be mainly below 2%. However, there is no proof that the iterative algorithm converges for all problem instances.
In the existing (A)HQM literature, the influence of a pandemic on an EMS system has not yet been adressed. Thus, we close this literature gap by including different patient groups categorized by the infection risk they pose to the EMS personnel. In addition, we include outage times of ambulances if paramedics have been infected. We further investigate different ambulance splits which allocate ambulances to patient categories. Such assignments have not yet been considered in combination with the (A)HQM.
2.2. Analysis of large-scale emergency medical service systems
The presented extensions of the (A)HQM are mostly applied to small problem instances. In the following, we present literature focusing on large-scale systems. Atkinson, Kovalenko, Kuznetsov, & Mikhalevich (2006) present two heuristics for large-scale systems to estimate the systems loss probability and ambulances’ utilization factors in an EMS along a highway. Iannoni, Morabito, & Saydam (2011) build upon Atkinson et al. (2006) to examine performance metrics for large-scale EMSs and to solve the location as well as the districting problem of an EMS. Iannoni et al. (2011) conduct a case study focusing on an EMS system located along a Brazilian highway as well as large-scale systems that are randomly generated. They observe that the increase in their heuristic’s runtime is nearly linear with the number of ambulances. Geroliminis, Kepaptsoglou, & Karlaftis (2011) apply a two-step approach to the repair service of the public bus network in Athens (Greece). They tackle the location problem for large-scale systems by first dividing the examined area into so-called “superdistricts” before they derive the required number of servers and their optimal locations per superdistrict. To find a solution for the location problem of servers, Boyacı & Geroliminis (2015) introduce the so-called 3N HQM in which each server is always in one of the following three states: idle or busy serving an intra-district or inter-district incident. To handle the large number of states, they develop an aggregate HQM in which servers are clustered into sets. Boyacı & Geroliminis (2015) conclude that the time servers substitute a preferred server is significant and cannot be neglected. Furthermore, it is shown that the 3N HQM, as well as the aggregate HQM, can be embedded in a simulated annealing and variable neighborhood search to find near-optimal locations for servers. Similar to Geroliminis et al. (2011), they apply their approach to Athens’ repair service of public transportation vehicles. As the number of states in the HQM grows exponentially with the number of ambulances, the previously presented papers predominantly focus on reducing the state-space of the HQM. Blank (2020) investigates to what extent the computational times can improve when aggregating the demand areas into “super demand areas” without reducing the number of states. Furthermore, a genetic algorithm is applied to improve the location of servers, which leads to near-optimal solutions with a deviation of less than 2% from the optimal solution. Yoon, Albert, & White (2021) show that an ambulance split can improve service times if some ambulances are dedicated to life-threatening conditions. Unlike this work, they do not consider tradeoffs between response times and infection risks, but focus on the tradeoffs between patient groups resulting in different splits.
2.3. Technology choice
The decision of whether to designate a share of ambulances to defined patient categories is related to technology choice problems. Here, decision-makers choose between flexible technology that can handle multiple products and dedicated technologies each applicable for one product only. Flexible machines can better handle demand uncertainties except in the case of perfect demand correlation or when cost savings can be achieved (Fine, Freund, 1990, Van Mieghem, 1998). Cao, He, Huang, & Liu (2020) investigate the benefits and disadvantages of pooling in queuing systems using various performance measures. While it is commonly known that pooling reduces server idle times, dedicated queues may reduce the probability of customers waiting longer than some delay threshold. Late arrivals represent an important performance measure for EMS systems. In the case of an ambulance split, such cost savings may correspond to lower outage probabilities of dedicated technologies which has not yet been addressed in literature.
3. Problem statement and second-stage model
We apply a two-stage approach to design and evaluate the ambulance split. At the first stage, we solve an optimization model to pre-select ambulance splits. At the second stage, we evaluate the pre-selected splits using the AHQM. Before presenting the first-stage model, we introduce the problem statement. Additionally, we describe the second-stage model applied to quantify the EMS system’s performance using performance measures, such as the average response time or the mean infection probability for EMS personnel. Table 6 in Appendix A summarizes the notation.
3.1. Problem statement
During a pandemic, the demand for EMSs putting their personnel at risk increases, as paramedics provide first aid to infected individuals. To improve the performance of the EMS, we designate a share of ambulances and personnel to serve only suspected and known cases. To evaluate the performance of such an ambulance split, we estimate the average response time including the patient’s queuing time, the time for dispatching, and the driving time to the incident. In Bavaria (Germany), the law prescribes that the location of each emergency call must be reachable within 12 min driving time (AVBayRDG §2 (1) Bayerisches Staatsministerium des Innern (2010)). We thus additionally calculate the share of incidents for which the driving time exceeds time threshold and the share of incidents for which the response time exceeds time threshold . The EMS operator aims to find the best possible allocation of ambulances to patient categories, improve the performance measures, and consider uncertain emergency call locations and arrival times. Thus, although capacity planning is a tactical decision, we need to adapt the dispatching processes on an operational basis to improve the system’s performance.
Infrastructure. The EMS operates in a given region, represented by a set of nodes . These nodes serve as possible locations for incoming emergency calls, ambulance depots, and hospitals. Hospitals serve as destinations for patient transfers. ambulances located at ambulance depots which are spatially distributed among the examined region serve the incoming calls. Each depot can hold more than one ambulance. We refer to these ambulances as “co-located”. The assigned depot of each ambulance, , is fixed. This is reasonable since the current allocation of ambulances to depots should be appropriate to fulfill all existing regulations, such as the maximum driving time to incidents. The optimal assignment will not change if the geographic distribution of incidents does not alter significantly.
Incidents. Within the examined region, spatially distributed demand for service occurs, reflecting emergency calls of patients. For the EMS system at the time of a pandemic, we divide the incidents into categories, denoted by . In our case study, these are known cases, suspected cases, and unsuspicious cases. However, the model’s generality allows additional patient groups, such as risk patients requiring higher safety standards or introducing patient priorities. As we assume a risk of infection for personnel when serving a patient, we distinguish between infection types . Here, denotes that the ambulance’s personnel has been infected and the ambulance is taken out of service; otherwise, we set to 0. Incidents arriving at node with a rate of follow a Poisson process.
Ambulances and Personnel. We assume that regular testing procedures detect every staff infection. Thus, the probabilities for infection and outage of personnel coincide. In the case of a transmission, ambulance and personnel are taken out of service for an exponentially distributed outage time. This assumption is based on presuming that the outage time of paramedics is stochastic, as infected individuals may remain in isolation longer than prescribed by public authorities. Furthermore, an earlier release from isolation is often possible after being tested negative. Thus, due to the stochastic nature, we assume exponentially distributed service times. To account for this simplification, we implement a discrete-event simulation in Section 6.3 which studies the impact of applying constant distribution types for the service times including the outage times. In the conducted case study, the expected outage time corresponds to the time an infected person is isolated. When modeling these outages, the ambulance is the smallest unit as we do not consider the personnel separately. We assume that physical distancing between EMS personnel is enhanced, as recommended by the Centers for Disease Control and Prevention (2020b). Thus, we assume that paramedics avoid having contact with their co-workers serving in other ambulances to minimize the infection risk. Further, if a paramedic is infected, there is a high chance that co-workers operating in close contact in the same ambulance are either infected or quarantined, too. However, to reduce the personnel shortfall, the dispatcher can divide ambulances into categories where denotes the category of ambulance . Depending on the assigned category, the ambulance can only serve, or preferentially serves, certain incident types. We assume that an ambulance and incident type can only be assigned to exactly one category. Nevertheless, each ambulance category can serve multiple incident types. Thus, a particular share of emergency calls at node is designated to be served by ambulance category . The model permits an arbitrary number of ambulance categories. The model’s generality is beneficial when analyzing possible ambulance splits, e.g., in regards to emerging Covid-19 variants of concern such as B.1.351 (Beta) or P.1 (Gamma) (Robert Koch Institut, 2021). Furthermore, future research could address additional categories to include patient priorities, distinguish ambulance types according to their equipment, or provide higher safety standards for patients or personnel with pre-existing conditions which increase the risk of a severe disease progression. Considering the infection risk posed by the three patient categories defined for Munich, we limit the numerical analysis to two ambulance categories, one for serving suspected and known cases (S, K), another for unsuspicious cases (U). Thus, . Based on the set of defined ambulance categories , different ambulance splits have the same number of ambulances per category, denoted by . Therefore, we introduce the set which represents the set of all possible combinations of for .
EMS operations. Service times are independent random variables with a common exponential distribution with a mean of which do not depend on the arrival of emergency calls. The service times include the following steps: After dispatching an ambulance which takes a mean dispatching time , it travels to the incident scene. We reflect the driving time from the ambulance location to node as . After treating the patient at the incident scene, the ambulance returns to the depot or transfers the patient to a hospital. Afterward, the personnel cleans the ambulance if the patient is suspected or known to be infected. If the paramedics have been infected, the total service time increases by the personnel’s absence time. For simplicity, we assume that personnel tests themselves in a timely manner to detect infections immediately. When transferring a patient to a medical facility, we always choose the closest hospital. We estimate the mean travel times using the Haversine function and the ambulance’s velocity. We can apply this approximation as we assign all incidents, ambulance depots, and hospitals to the nearest node. In line with Iannoni et al. (2008) and Mendonça & Morabito (2001), we assume that an ambulance always returns to its depot before being dispatched as the return time amounts only to a small share of the total service time. For the dispatching process, we assume single dispatch. This means that we always dispatch exactly one ambulance to an incident. Further, we apply a ranked-ordered list of ambulances for each node and incident type independent of the system’s state. The parameter refers to the ranked ambulance for incident type at node . We dispatch the unit with the lowest rank which is idle. We determine the preference among ambulances located at the same depot at random. Balancing the co-located ambulances’ loads among them counteracts the inaccuracy introduced by this random selection and allows us to model each ambulance individually. We refer to Budge et al. (2009) who introduce a model tackling the problem of co-located ambulances by focusing on the ambulance depots rather than on the individual ambulances.
Queued emergency calls. The higher the system’s workload, the higher is the probability that no ambulance is available to be dispatched. Since all patients must eventually be served, we assume that incoming emergency calls join a First-In-First-Out (FIFO) queue with infinite capacity. This queue becomes more critical in a pandemic context since system unavailability naturally occurs more frequently if the number of emergency calls increases and the EMS personnel may need to self-isolate. Because the service times of ambulances are independent and identically distributed, each ambulance has an equal probability of becoming idle and being dispatched to the next call in the queue if all ambulances are busy. Therefore, in line with Larson, 1974, Larson, 1975 and Batta, Dolan, & Krischnamurthy (1989), we assume that the probability of an ambulance being dispatched to a queued call is equal for all ambulances. In the case the system utilization exceeds 100%, we refer to the system as being “overloaded”. To derive the performance measures of the EMS system, we assume that the system operates in a steady state. Therefore, we calculate the steady-state probabilities by adapting the AHQM.
3.2. Second-stage model
We adapt Larson’s (1975) AHQM by including the incident and infection types and in the performance measures and input parameters. Furthermore, we consider the ambulance split that we decide on, denoted by .
The AHQM with infinite capacity depicts an queuing model. This permits us to derive the probability of the steady state, denoted by , with exactly busy ambulances (Larson, 1975). Unlike the exact HQM, the AHQM does not make use of the detailed state description representing each ambulance independently. For this reason, we approximate the probability of dispatching ambulance as the favored server to an unqueued emergency call of incident type at node by assuming an queuing system in which we randomly draw ambulances without replacement. is the rank of ambulance for incident type at node . Thus, we extend Larson’s (1975) AHQM by having preference lists not only depend on node , but also on incident type . As we consider an queuing system, the system’s utilization is (Larson, 1975, Jarvis, 1985, Tijms, 2003, p. 187-188). We approximate the probability that ambulance is dispatched as the favored ambulance to an unqueued emergency call of type at node by multiplying the availability factor () of ambulance by the workloads of all better ranked ambulances () (Jarvis, 1985, Larson, 1975). As EMS operators consider the status of each ambulance at the time of dispatching, ambulances do not operate independently. For this reason, we amend the result by the correction factor introduced by Larson (1975). We approximate the probability of an ambulance being dispatched to a queued call by , i.e., in the case that all ambulances are busy, each ambulance has an equal probability of becoming idle and dispatched to a queued call. Thus, we obtain the probability that ambulance is dispatched to any incident of type at node .
| (1) |
We present a detailed derivation for in Appendix B. Making use of the dispatching probabilities , the mean service time of the system is
| (2) |
Here, we adapt Jarvis’ (1985) calculation by considering the incident and infection type and in the arrival rates , service times and dispatching probabilities . Contrary to Jarvis (1985), no calls are lost. Thus, to obtain the mean service time, we multiply the probability that ambulance is dispatched to incident type at node by the required service time for this incident. As the share of emergency calls differs among nodes, we account for the share of incidents of type occurring at node by .
We further obtain the rate at which ambulance is assigned to incidents of type at node . Multiplying the assignment rate by the service time , results in the probability that ambulance is busy serving an incident of type , . Taking the sum over all nodes, incident and infection types yields the individual ambulance workload (Jarvis, 1985).
| (3) |
| (4) |
We reformulate in (4) by inserting from (1) and consider all possible ranks that can be assigned to an ambulance in a preference list. To account for the pandemic, we include service times which depend on the ambulance and node , as well as the incident and infection type . To consider queued calls, we add the term which corresponds to the expected time ambulance spends serving patients from the queue, given by the arrival rate multiplied by the expected service time and the probability that any ambulance serves an incident from the queue .
| (5) |
To account for ties in a preference list among ambulances of the same ambulance category located at the same depot, we balance their workloads and dispatching probabilities evenly among them. Thus, we divide the sum of their individual workloads by their number. Similarly, we balance the dispatching probabilities. The binary parameter indicates whether ambulance can serve incident type . Thus, balanced workloads and dispatching probabilities are given by
| (6) |
| (7) |
where is the indicator function and returns 1 iff its input is true.
To obtain the performance measures of the EMS system, we apply an adapted version of the iterative algorithm developed by Jarvis (1985) presented in Section 4. In each iteration, denoted by the iteration counter , we normalize the individual ambulance workloads such that the mean of all workloads corresponds to the average system utilization. Here, we multiply each workload by the normalizing factor . Furthermore, we normalize the dispatching probabilities such that .
| (8) |
| (9) |
| (10) |
4. Solution algorithm and performance measures
In the following, we introduce the iterative solution algorithm applied to estimate the ambulance workloads and dispatching probabilities. We further define performance measures to evaluate the system’s performance.
4.1. Estimating ambulance workloads: An iterative solution algorithm
The developed solution algorithm to obtain the performance measures of the EMS system is based on Jarvis (1985). Algorithm 1 depicts the pseudo-code.
Algorithm 1.

Pseudo-Code of the Iterative Workload Approximation Algorithm.
After initializing the ambulance workloads and the average system service time, we balance the workloads of co-located ambulances of the same category by distributing the sum of their workloads evenly among them. Then, we distribute the workloads of overloaded ambulances to their direct backup ambulances. By doing so, we observe a better runtime in the experimental results. Thus, we first calculate the number of preference lists in which ambulance serves as direct backup of ambulance () as follows:
| (11) |
Then, we derive the workload that is shifted from ambulance to backup ambulance ():
| (12) |
We repeat these steps until no ambulance remains overloaded, if possible. After the initialization and the distribution of work overload, we verify that the system is not overloaded, i.e. . Otherwise, the algorithm terminates without a solution. If this is not the case, we continue and iteratively approximate the ambulances’ workloads by recalculating the average system workload, the dispatching probabilities, and the average system service time in each iteration. As soon as the maximum deviation between the workloads in two consecutive iterations is smaller than threshold , we use the obtained approximations to calculate the performance measures of the EMS. In line with Larson (1975), we assume a convergence threshold of . Applying this threshold, Larson (1975) observes a maximum error of 0.36%.
4.2. Computation of performance measures
Based on the variables obtained by the AHQM, we derive performance measures to evaluate the performance of the EMS system. A widely applied performance measure is the average response time (Schmid, 2012, Souza, Morabito, Chiyoshi, Iannoni, 2015). Before calculating the average, we must derive the response time for ambulance for a given incident of type occurring at node . Here, we take the patients’ average waiting time in the queue , the dispatching time and the travel time into account. According to Tijms (2003, p. 192), the average waiting time in an -queue is:
| (13) |
We can also use the waiting time as an indicator of the system’s congestion. After determining the waiting time, we obtain the average response time by multiplying the fraction of incidents of type occurring at node by the probability that ambulance is dispatched () and the response time required by ambulance .
| (14) |
Similarly, we obtain the average driving time:
| (15) |
We measure the share of incidents for which the driving time exceeds a given time threshold , denoted by . In a pandemic context, the unavailability of ambulances may occur more frequently. Thus, we consider the queuing time by additionally measuring the share of incidents where the response time exceeds time threshold , termed .
| (16) |
| (17) |
Splitting the ambulances into categories may protect EMS personnel from infections. We quantify this benefit by calculating the probability for ambulance to be taken out of service due to infected personnel. We refer to this probability as “infection probability”. For this reason, we multiply the percentage share of incidents for which ambulance is taken out of service () with the probability that ambulance is dispatched to this type of incident ().
| (18) |
where indicates that ambulance is unavailable due to an infection of its personnel.
Making use of the infection probability per ambulance, the mean infection probability over all ambulances is
| (19) |
Here, we divide the sum of all infection probabilities by the number of ambulances. As the mean infection probability may significantly differ among the ambulance categories , we apply the same procedure used for calculating in Eq. (19) for all categories, separately. Thus, we only consider ambulances assigned to the examined category (). denotes the number of ambulances allocated to category .
| (20) |
Based on these performance measures we can evaluate the performance of an EMS and, therefore, quantify the benefit of an ambulance split. In Appendix C, we show that the mean infection probability is not linear in the number of ambulances per category. Furthermore, the mean infection probabilities observed for the flexible split are not convex in the split.
5. First-stage optimization model
In the following, we present the investigated ambulance splits and introduce the first-stage optimization model that pre-selects ambulance splits before evaluating them in the second-stage model.
5.1. Instantiation to multiple vehicle types and ambulance splits
We distinguish three types of ambulance splits: Flexible split, fixed split and no split. When investigating a flexible split, we allocate ambulance categories to certain incident types. However, if all ambulances of a certain category are busy, ambulances designated to other categories can serve as a backup. Thus, if all ambulances are busy, emergency calls join a single queue. When applying a fixed split, ambulances cannot serve as a backup for incident categories to which they have not been assigned. Therefore, an incoming emergency call joins a queue if no designated ambulance is idle. Consequently, we require a separate queue for each ambulance category. Thus, in the case of a fixed split, we assume an independent system for each ambulance category and its assigned incident types, . When applying no split, there is no restriction and each incident type can be served by all ambulances in the system. We additionally combine the flexible split with an ambulance reservation strategy. Further, we combine the reservation strategy with no split. As we include different ambulance categories and do not consider call priorities, we adapt the cutoff policy presented by Iannoni et al. (2015). For both types of splits, we define a cutoff level . For simplification, we assume the same cutoff level for all ambulance categories. In the case that the relation between the busy ambulances per category and the total ambulances per category exceeds this threshold, all remaining idle ambulances of the corresponding category are dedicated to serve only the assigned categories. The ambulance categories for which the cutoff level is not exceeded can continue serving calls according to the flexible or no split policy. Applying the ambulance reservation strategies in the AHQM requires additional adaptations which are beyond the scope of this study. However, to investigate the potential of these strategies, we apply a discrete-event simulation in Section 6.3 and investigate the results obtained by incorporating the ambulance reservation strategies.
Applying a flexible split or no split, without enabling ambulance reservation, requires an adaptation of the preference list for each incident type and node. For the fixed split, the number of ambulances in each system equals the number of ambulances of the analyzed category, , given in (22). As the optimal assignment of ambulances per category is determined in the first-stage, is a first-stage variable which functions as a parameter in the second-stage. The binary parameter indicates whether ambulance category can serve incident type . represents the set of incident types served by ambulance category .
| (21) |
| (22) |
After running the solution algorithm for the fixed split, we obtain separate performance measures for each system, e.g. an average response time for the system serving unsuspicious cases and an average response time for suspected and known cases. The performance measures of the different systems () must be aggregated in order to compare them to the corresponding performance measures of the flexible split and no split. Thus, for each time-related performance measure, i.e. , , and , we separately apply the following weighting method:
| (23) |
For all systems, each served by an ambulance category , we set the variable to the examined performance measure and weight it with the share of emergency calls that occurred in the corresponding system.
Weighting the performance measures according to the share of emergency calls per system is inappropriate for some performance measures. While the time-related performance measures refer to the incidents, the mean infection probability refers to the ambulances. Thus, to obtain the mean infection probability of ambulances over all systems, we multiply the mean infection probability of each system () by the number of ambulances per system divided by the total number of available ambulances .
| (24) |
5.2. Pre-selecting ambulance splits
Calculating all possible ambulance splits is computationally intractable for large-scale systems. For the two examined ambulance categories the iterative solution algorithm must be repeated times. To reduce the number of ambulance splits to be evaluated by the AHQM, we solve a mixed-integer linear program (MILP) for each combination in that determines the “best” split, i.e. the split that covers nodes with a high share of emergency calls with as many ambulances as possible without neglecting the coverage of nodes with a low share of emergency calls. In line with Batta et al. (1989), we assume that ambulance covers node if it can be reached within a time threshold of . We refer to an element in , in our context , as . For example, for we run the optimization model for all combinations in . For our case, if or , the optimal solution of the flexible split equals the objective value of having no split. However, for the fixed split we must exclude these cases from , otherwise, some patient categories are not served by any ambulance leading to a queue of infinite length. Based on preliminary experimental results, we set the weight for both ambulance categories to . is the percentage share of emergency calls occurring for ambulance category at node .
| (25) |
| (26) |
| (27) |
| (28) |
The first objective (25) maximizes the minimum number of ambulances covering a node for all ambulance categories . The minimum coverage of both ambulance categories is weighted by factor 0.5. The indicator function returns 1 iff the driving time from node to the ambulance depot, , is smaller than or equal to the time threshold . Additionally, ambulance must be assigned to category . The second objective (26) maximizes the nodes’ coverages weighted by their share of emergency calls. Again, the value of the indicator function is 1 iff ambulance is assigned to category and covers node . The linearization of the minimization terms in the objective functions is trivial. Constraint (27) ensures that the sum of ambulances assigned to category equals the defined number of ambulances per category (). Constraint (28) defines the domain of variable .
To solve the optimization model, we evaluate the two objectives lexicographically: First, we maximize (25). Second, we maximize (26) without degrading the solution of the first objective. This ensures that the minimal coverage of all nodes is as high as possible. The lexicographical approach obtains feasible splits for all combinations. Depending on the EMS infrastructure, defining a minimum coverage as a hard constraint may prevent the model from finding a feasible solution. For example, nodes covered by only one ambulance can in this case never be covered by all ambulance categories when applying a split, as ambulances can be assigned to one category only. We solve the optimization model for all combinations and obtain the optimal ambulance split for each of them, as the numerical experiments show that there can be multiple local minima. Thus, a local search procedure or gradient descent may result in a suboptimal solution. The existence of multiple local minima has different reasons. First, we heuristically use the emergency call coverage for the EMS system’s performance under a split. Second, as applying the exact HQM is computationally intractable, we approximate the ambulances’ workloads. These approximations can result in local minima if the ambulances’ workloads only slightly differ. Even for large-scale EMS systems, the enumeration of all combinations is computationally feasible.
After obtaining the best ambulance splits for the examined combinations in the first step, in the second step, we compute their performance measures using the developed AHQM.
6. Numerical results
During the Covid-19 pandemic in 2020, Bavaria was one of the most affected states in Germany (Robert Koch Institut, 2020a). From real data for November 2020 provided by Munich’s ambulance dispatching center, we determine the spatial emergency call distribution, interarrival times, and the mean dispatching time. Using the performance measures we calculate in (13)–(20), we evaluate the benefit gained when designating ambulances to serve only known and suspected cases for the Covid-19 pandemic.
We run the numerical experiments on a Linux server with an Intel(R) Xeon(R) Platinum 8160 CPU with 2.10GHz. The model is implemented in Python for computing the steady state of the AHQM, and Gurobi (version 9.1) for obtaining the optimal ambulance split for each combination in applying the MILP (25)–(28).
6.1. Experimental data
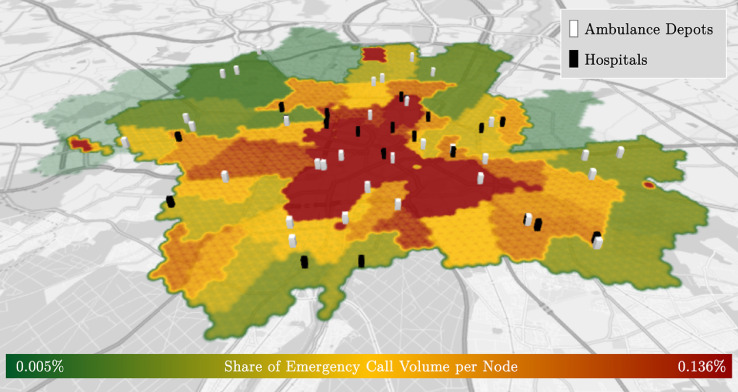
Using the hexagonal hierarchical geospatial indexing system H3 (Brodsky, 2018), we divide Munich into 3045 geographical atoms – each with a size of and an inner circle radius of 174 meters. The center of each atom serves as a node. The arrival rate of emergency calls at each node and the locations of ambulance depots and hospitals are based on real data. 2.6% of the incidents were excluded from the data set as the interarrival time was 0 which indicates multiple dispatch. However, we only consider single dispatches. In total, we consider 22 hospitals and 43 ambulances located at 32 depots. Figure 1 depicts the infrastructure and the spatial emergency call distribution of the EMS system in Munich. In this dataset, interarrival times are exponentially distributed with a mean of 4.42 min. This is statistically significant at a -value of using a Kolmogorov-Smirnov-Test (Massay Jr, 1951). However, the Anderson-Darling test, being more sensitive than the Kolmogorov-Smirnov-Test (Razali & Wah, 2011), indicates otherwise. The reason lies in the variation observed in the mean interarrival times throughout the day. Thus, we take the time dependency into account and divide the day into 12 equally sized time periods. For all periods, except one, we fail to reject the hypothesis that the sample comes from an exponential distribution at a confidence level of 99%. In Section 6.3 we study the impact of applying the real interarrival time distribution.
Fig. 1.
Heatmap of spatial emergency call distribution and Munich’s EMS system’s infrastructure.
In real data of November 2020, on average 3.48% of all emergency calls were suspected cases, and 3.55% were known to be infected. The remaining emergency calls were unsuspicious. The data does not indicate how many patients without any suspicion of Covid-19 carry the virus. Thus, we estimate the number of undetected cases in the general population in order to determine the infection probabilities for EMS personnel.
The total service time is composed of a mean dispatching time of 3.77 min and a mean treatment time of 12 min (Jagtenberg, Bhulai, & van der Mei, 2017). Thus, we set the response time threshold to 15.77. With a probability of 80%, the patient is transferred to a hospital (Jagtenberg et al., 2017), which adds a mean delay of 30 min to the service time (Schwartz et al., 2005). If a suspected or known case was transported, we assume a mean cleaning time of 1 h (Allen et al., 2020). The mean driving times depends on the Haversine distance and the vehicle’s velocity, which we assume to be 30 km/h. Knyazkov, Derevitsky, Mednikov, & Yakovlev (2015) consider a velocity of 40 km/h on road distances, which we reduce to account for traffic and the Haversine distance.
We assume that the probability of an ambulance to be taken out of service can be approximated by the infection risk of EMS personnel serving infected patients. Phucharoen, Sangkaew, & Stosic (2020) observe a transmission probability per exposure of 3.13% for Covid-19. However, we distinguish between the different incident types. For known infections, the probability of 3.13% is reasonable. For suspected cases, we assume that the patient has been exposed to the virus and has been infected with a probability of 3.13%. Thus, we can calculate an infection risk of for paramedics serving the exposed patient. This is most likely a lower bound which we account for by conducting a sensitivity analysis on the infection probability. Considering the infection probability per exposure, the number of undetected cases among the population and the number of infections in Munich in November 2020, we obtain an infection probability of 0.01% when treating unsuspicious cases. The mean outage duration corresponds to the isolation time of 10 days prescribed by health authorities for infected paramedics (Centers for Disease Control and Prevention, 2020a; Robert Koch Institut, 2020b; World Health Organization, 2020a).
6.2. Results
In Table 1 , we present the combination resulting in the best average response time and its performance measures: the average driving time , the average waiting time , the share of late arrivals regarding the response and driving time and , the mean infection probability , the mean infection probability for unsuspicious cases and for suspected and known cases .
Table 1.
Results for Covid-19 applying the AHQM.
| Flexible & No S. | Fixed S. | |
|---|---|---|
| Combination | {32,11} | |
| [min] | 7.27 | 8.72 |
| [min] | 3.50 | 4.85 |
| [min] | 0.00 | 0.10 |
| [%] | 0.39 | 7.03 |
| [%] | 0.39 | 6.34 |
| [%0] | 0.00 | |
| [%0] | 1.48 | |
| [%0] | 0.03 | 0.38 |
Not allocating ambulances to patient categories results in the lowest average response time. Thus, identical values for the performance measures are obtained for the flexible and no split. This split reflects the fraction of the total caseload infected patients account for. For the fixed split, the number of ambulances assigned to the suspected and known cases is disproportionally higher than their relative caseload. This explains why the fixed split results in worse performance regarding all performance measures. The fixed split may become more competitive once the share of Covid-19 patients increases.
Result 1
When applying a fixed split, the loss of pooling advantages and the resulting increase in the average driving time are mainly responsible for higher average response times. Consequently, also the share of late arrivals, does not improve when designating ambulances to serve only known or suspected cases. The patients’ average waiting time in the queue is negligible.
This indicates that for the analyzed cases, the EMS system is capable of handling the increment in workload caused by ambulance outages without becoming congested. Thus, our findings confirm the decision of the Munich EMS operator not to split ambulances into categories during the Covid-19 pandemic in 2020.
6.3. Discrete-event simulation
We implement a discrete-event simulation using SimPy to study the impact of applying the AHQM instead of the exact HQM. In preliminary experiments, we determined the length of the warm-up period and set it to one day. As the real input data for the interarrival times represents a time period of one month (November 2020), we set the simulation length to 30 days. Due to the stochastic nature of the service times and spatial emergency call distribution, we perform 30 replications to increase the accuracy of the simulation results. The results obtained by the discrete-event simulation are depicted in Table 2 .
Table 2.
Comparing results for Covid-19 applying a flexible, fixed and no ambulance split (Simulation [A]: Exponential service times, Simulation [B]: Constant driving, cleaning and isolation times, Simulation [C]: Real interarrival times).
| Simulation [A] |
Simulation [B] |
Simulation [C] |
||||
|---|---|---|---|---|---|---|
| Flexible & No S. | Fixed S. | Flexible & No S. | Fixed S. | Flexible & No S. | Fixed S. | |
| Combination | {32,11} | {32,11} | {32,11} | |||
| [min] | 7.28 | 8.72 | 7.34 | 8.74 | 7.46 | 8.90 |
| [min] | 3.51 | 4.87 | 3.57 | 4.93 | 3.69 | 5.08 |
| [min] | 0.00 | 0.08 | 0.00 | 0.04 | 0.00 | 0.05 |
| [%] | 0.51 | 6.17 | 0.58 | 6.60 | 0.85 | 6.99 |
| [%] | 0.51 | 6.16 | 0.58 | 6.59 | 0.85 | 6.97 |
| [‰] | 0.00 | 0.00 | 0.00 | |||
| [‰] | 0.10 | 0.10 | 0.07 | |||
| [‰] | 0.03 | 0.36 | 0.03 | 0.38 | 0.02 | 0.02 |
The average response and driving times differ by less than 1%. The average waiting time calculated by the AHQM is similar to the average waiting time observed in the simulated results when applying no split. This indicates that in both the simulation and the AHQM the systems are not overloaded. For the fixed split, we observe an absolute difference of less than 2 seconds which we assume negligible. Similar to the mean infection probability, the absolute error of the share of late arrivals amounts to less than 1%. These results indicate that the developed AHQM appropriately estimates the performance measures.
The developed model is based on exponentially distributed service times. However, as we were not provided real data to validate this assumption, we are interested in the impact of having service times which do not follow an exponential distribution. Therefore, we study the impact of having constant isolation, cleaning and driving times by incorporating an additional experiment in the discrete-event simulation (Simulation [B]). Table 2 shows the results.
Applying constant service times only slightly influences the average response and driving times. For both performance measures, the maximum deviation amounts to 2%. The deviations in queuing times are negligible. The observed values for the mean infection probabilities are almost equivalent, the highest absolute difference amounts to comparing the simulations using exponential and constant service times. Thus, the model’s results remain valid if service times were constant.
The results of the statistical tests applied in Section 6.1 to validate the distribution of the interarrival times have not been identical. Therefore, we use the real interarrival times in a simulation experiment (Simulation [C]) to study the error made by assuming exponentially distributed interarrival times.
When applying real interarrival times, the average response and driving times differ by approximately 4%, on average, compared to the AHQM. Small deviations were expected, as the volume of emergency calls varies throughout the day. During peak times, the system must deal with higher workloads resulting in increased response and driving times. However, the average queuing time remains below 7 seconds when applying a fixed split. When applying no split, we observe similar average queuing times. The share of late arrivals only slightly differ. The absolute deviations amount to less than 0.9%. The absolute error made for the mean infection probabilities amounts to a maximum of and is therefore assumed negligible. With such a small error, using exponential distributed interarrival times seems reasonable.
Result 2
Comparing the results obtained by the AHQM with the simulated observations shows that the AHQM appropriately estimates the performance measures and is robust to alternative interarrival and service time distributions.
We further investigate the flexible split and no split combined with the ambulance reservation strategy. Referring to the results of the optimization model, we base our study on the optimal combination of the fixed split. Thus, 32 ambulances are assigned to unsuspicious cases while 11 ambulances serve the remaining incident types. In the case that the threshold is exceeded for a certain ambulance category, the associated ambulances refuse to serve other incident types. We consider three possible cutoff levels . The results are presented in Table 3 .
Result 3
For all cutoff levels, the reservation strategy outperforms the fixed split without ambulance reservation. For a cutoff level of 0.25 and 0.50, applying no split without ambulance reservation performs better than combining no split with the reservation strategy. Looking at the average response and driving time, introducing a cutoff level of 0.75 outperforms no split without reservation by less than 1 second compared to the AHQM.
Table 3.
Application of ambulance reservation strategy based on combination {32,11}.
|
|
|
|
||||
|---|---|---|---|---|---|---|
| No Split | Flex. S. | No Split | Flex. S. | No Split | Flex. S. | |
| [min] | 7.61 | 8.64 | 7.30 | 8.65 | 7.26 | 8.64 |
| [min] | 3.84 | 4.86 | 3.53 | 4.88 | 3.49 | 4.87 |
| [min] | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| [%] | 1.56 | 6.18 | 0.60 | 6.31 | 0.47 | 6.28 |
| [%] | 1.56 | 6.18 | 0.60 | 6.31 | 0.47 | 6.28 |
| [‰] | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 |
The superiority of the ambulance reservation strategy compared to the fixed split results from the increased flexibility gained by applying a flexible split or no split until reaching the cutoff level. However, for low cutoff levels, the reservation strategy limits the flexibility of the corresponding split as soon as the cutoff level is reached. Therefore, incorporating ambulance reservation does not improve the performance of the flexible split or no split for low cutoff levels. However, an improvement in the average response time is visible when introducing a high cutoff level of 0.75. Thus, although the share of late arrivals cannot be improved, slightly shorter response and driving times can be reached.
6.4. Sensitivity analysis
To investigate the effect of varying disease characteristics, we first conduct a sensitivity analysis applying various parameter combinations. Second, we apply data sets parameterized for two specific diseases: Ebola and Influenza A.
6.4.1. Varying disease characteristics
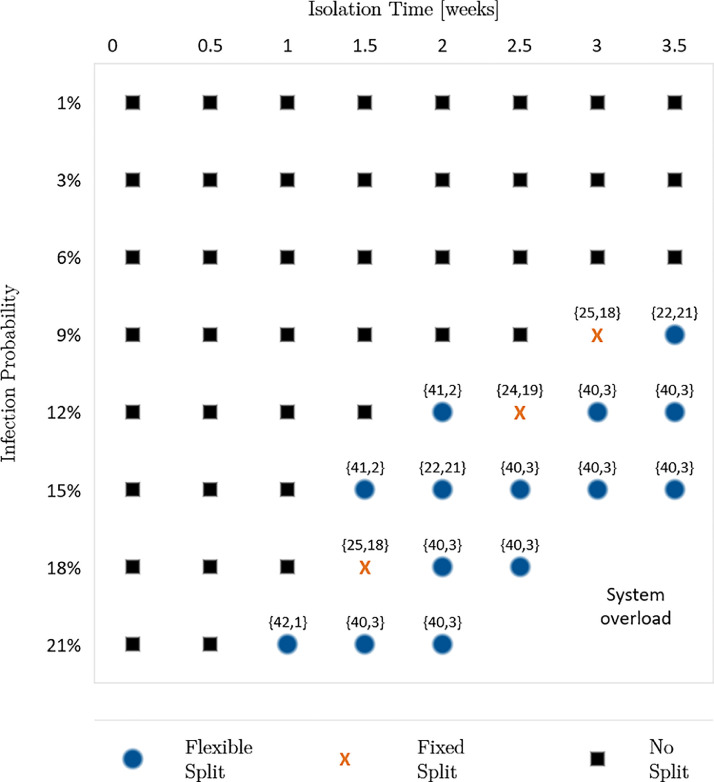
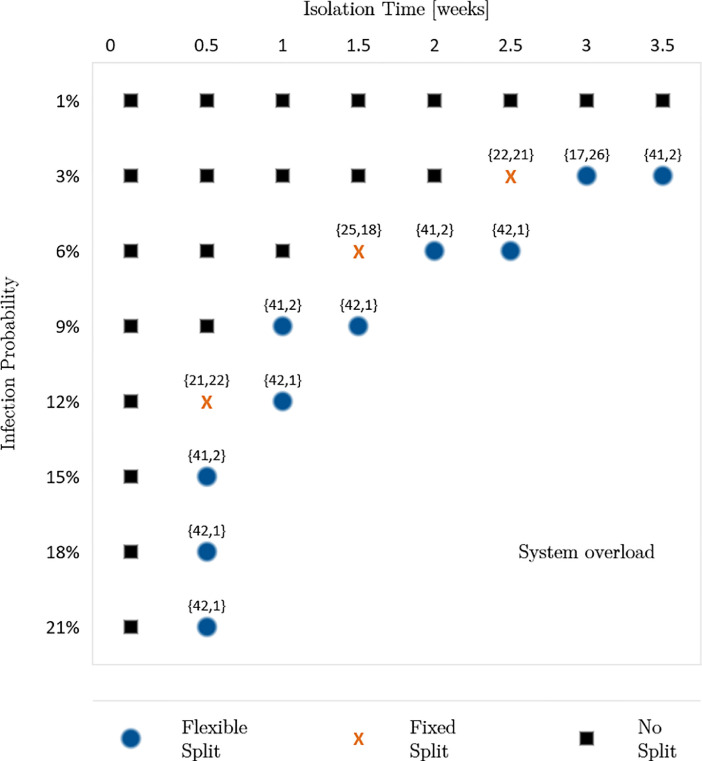
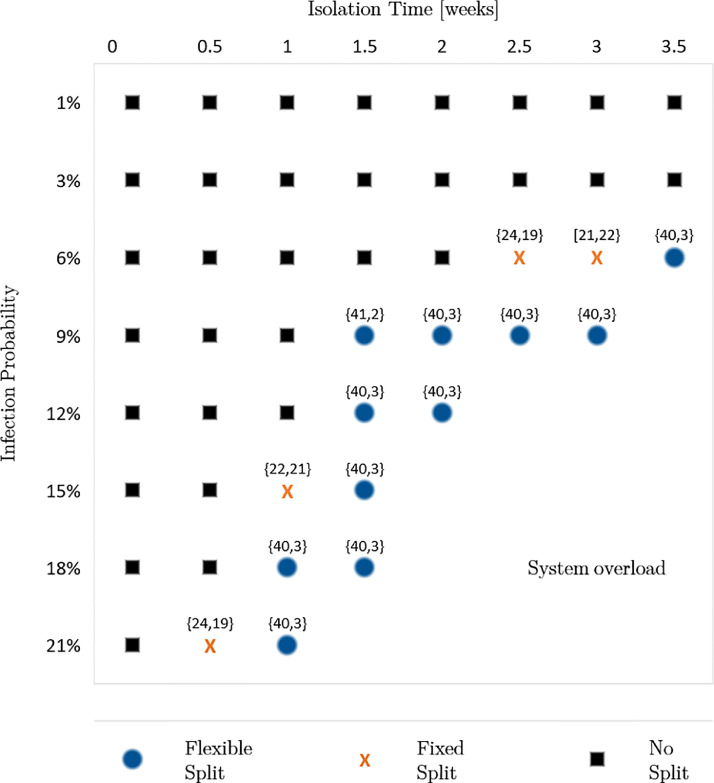
To investigate the benefits of an ambulance split for future pandemics with unknown disease characteristics, we vary the infection probabilities and the isolation times of infected individuals. Moreover, as the number of infected people constantly changes during a pandemic, we consider these dynamics by accounting for different shares of unsuspicious, suspected and known cases, denoted as “incident share”. Here, we investigate three different incident shares: First, the incident share observed in November 2020 for Covid-19: 92.97% unsuspicious cases, 3.48% suspected cases and 3.55% known cases. Second, we increase the share of suspected and known cases by 100%. Third, we decrease the share of suspected and known cases by 50%. For each incident share, we analyze infection probabilities of 1%, 3%, 6%, 9%, 12%, 15%, 18%, and 21%. Furthermore, we increase the isolation times from 1 day to 3.5 weeks in steps of 0.5 weeks. Thus, in the sensitivity analysis, we calculate the performance measures for each combination of the three factors. Fig. 2, Fig. 3, Fig. 4 present the results of the sensitivity analysis for different incident shares. Each figure shows the ambulance split resulting in the lowest average response time.
Result 4
If both isolation time and infection probability exceed certain thresholds, we observe that a flexible or fixed split reduces the average response time and, consequently, the share of late arrivals regarding the response time threshold. Furthermore, reducing the isolation time enables the system to remain operable for higher infection probabilities and vice versa.
Fig. 2.
Optimal split for 96.48% unsuspicious, 1.74% suspected and 1.78% known cases.
Fig. 3.
Optimal split for 85.94% unsuspicious, 6.96% suspected and 7.10% known cases.
Fig. 4.
Optimal split for 92.97% unsuspicious, 3.48% suspected and 3.55% known cases.
This result indicates that the two factors, isolation time and infection probability, can counteract each other. Thus, reducing one factor allows a higher value of the other factor until a certain level is reached. The reason is that both factors influence the mean outage time of personnel either by frequent absences or long absences. Both lead to higher average system service times which increases the system’s workload. Therefore, disease-specific characteristics must be considered as a whole. Looking at the factors separately could result in suboptimal decisions.
We further observe that the thresholds making an ambulance split beneficial depend on the share of suspected and known cases. When decreasing the share of suspected and known cases by 50%, a split is beneficial for an isolation time of 2 weeks or longer, combined with an infection probability of 12% or higher. For shorter isolation times of 1 or 1.5 weeks a split is only beneficial for infection probabilities of at least 21% or 15%, correspondingly. Vice versa, a lower infection probability of 9% requires long isolation times of at least 3 weeks to make a split beneficial (Fig. 2). When doubling the share of suspected and known cases, the thresholds for the isolation time and infection probability making a split favorable are lower (Fig. 3).
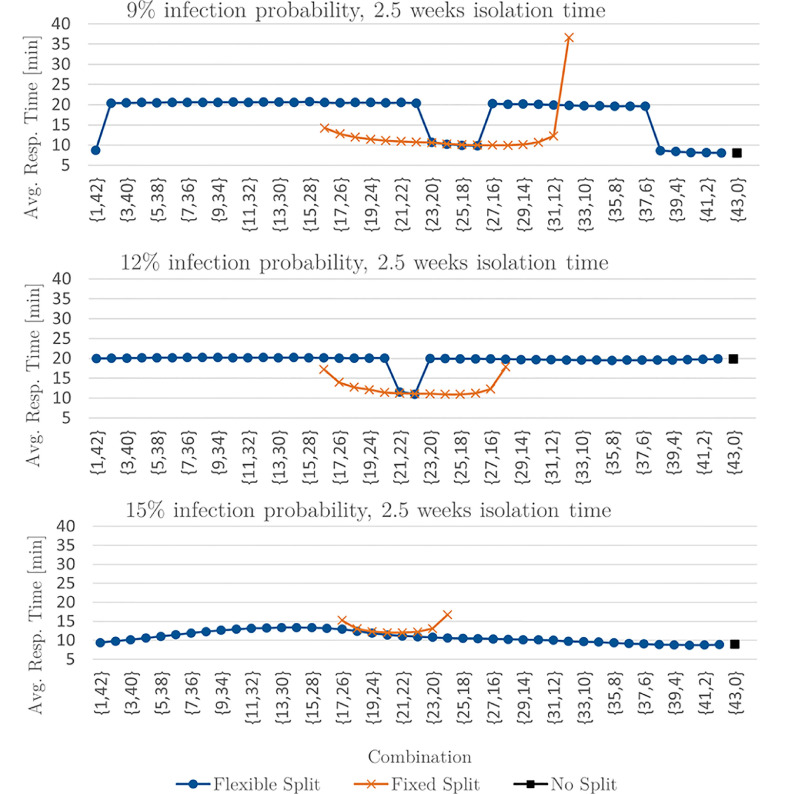
Figure 5 presents the average response times for all possible combinations for an infection probability of 9%, 12% and 15% combined with an isolation time of 2.5 weeks and decreasing the share of suspected and known cases by 50%. For an infection probability of 9%, applying no split is beneficial. For an infection probability of 12%, the flexible split is outperformed by the fixed split for all examined combinations except for the combination {22,21}. Increasing the infection probability to 15% decreases the average response time achieved by the flexible split, making it beneficial.
Result 5
Compared to not splitting, the mean infection probability for ambulances designated to unsuspicious cases can be decreased by 72%, on average, when applying a fixed split. However, the mean infection probability for ambulances assigned to suspected and known cases is, on average, more than a seventy-fold higher. Thus, when weighting the infection probabilities of the two ambulance categories according to their assigned number of ambulances, the fixed split leads to a higher mean infection probability than the flexible split or no split.
Fig. 5.
Extract of avg. response times for 96.48% unsusp., 1.74% susp. and 1.78% known cases.
Thus, if a certain share of personnel must be protected from infection and a higher infection risk for the remaining personnel can be accepted, the fixed split can be beneficial for EMS operators. However, the mean infection probabilities over all splits remain below 0.03%.
6.4.2. Ebola and Influenza A
We conduct a sensitivity analysis for two additional instances parameterized by specific disease characteristics. We focus on diseases which, apart from Covid-19, accounted for the highest number of infections and deaths between 1967 and 2020 worldwide: Ebola, and Influenza A (ScienceAlert, 2021).
Ebola. Since 1976, Ebola outbreaks were reported in the Democratic Republic of the Congo, the Republic of the Congo, South Sudan, Uganda, and Gabon. The biggest outbreak has been documented for West-Africa. However, in 2014–2016, less than 1% of the population has been suspected or confirmed to be infected (The World Bank, 2021; Centers for Disease Control and Prevention, 2019). Ebola is transmitted from animals to humans and from humans to humans. Contaminated objects as well as having direct contact with infected individuals or their body fluids can lead to a transmission of the virus (World Health Organization, 2020b). According to Skrip et al. (2017), a single contact with an infected person poses a transmission risk of 2.70%. A similar approximation procedure as for Covid-19 leads to infection probabilities and of 2.70%, 0.07%, and 0.01% for known, suspected cases and unsuspicious cases, correspondingly. Lacking more precise data for Germany, we assume the isolation period for an Ebola infection to be 16 days which is the average isolation period of infected patients (Fode et al., 2018). The preceding sensitivity analysis indicates that for such a low number of suspected and known cases, and an infection probability of 6% or less, a split will not be beneficial (Fig. 2). Thus, we inspect the case of an Ebola outbreak having the same incident share, similar infection numbers and undetected cases as during the Covid-19 pandemic.
Influenza A. Although the number of infected people (more than 762 million) was higher during the swine flu in 2009 than for the Covid-19 pandemic (252 million until November 2021), fewer people died (ScienceAlert, 2021). Looking at the emergency call volume, we assume that the higher emergency call volume resulting from an increased number of infections is compensated by a reduction in emergency calls due to the fact that less individuals got seriously ill and died. Based on this assumption and lacking emergency call data for Influenza A, we assume having the same incident share, similar infection numbers and undetected cases as during the Covid-19 pandemic. For Influenza A (H1N1), Robert Koch Institut (2010) observed a transmission probability of 10% in households leading to laboratory-confirmed cases despite the availability of hand disinfectants and face coverings. Thus, we consider this probability for the case study. Again, approximating the infection probabilities similarly to Covid-19, we derive values of 10.00%, 1.00%, and 0.04% for known, suspected, and unsuspicious cases. The Centers for Disease Control and Prevention (2010) recommend an isolation period of 7 days or longer in the case that patients show any symptoms after this period. All disease-specific data is summarized in Table 4 .
Table 4.
Disease-specific Data: Ebola, Influenza A.
| Ebola | Influenza A | ||
|---|---|---|---|
| Infection Probability [%] | Unsuspicious case | 0.01 | 0.04 |
| Suspected case | 0.07 | 1.00 | |
| Known case | 2.70 | 10.00 | |
| Isolation time [days] | 16 | 7 | |
The results obtained for the data sets parameterized by Ebola and Influenza A confirm the findings of the preceding sensitivity analysis, Table 5 .
Table 5.
Basic results applying a flexible, fixed and no ambulance split.
| Ebola |
Influenza A |
|||
|---|---|---|---|---|
| Flexible & No Split | Fixed S. | Flexible & No Split | Fixed S. | |
| Combination | {32,11} | {28,15} | ||
| [min] | 7.38 | 9.06 | 7.80 | 9.87 |
| [min] | 3.62 | 4.89 | 4.03 | 5.57 |
| [min] | 0.00 | 0.41 | 0.02 | 0.21 |
| [%] | 0.53 | 9.29 | 1.32 | 13.25 |
| [%] | 0.53 | 6.56 | 1.32 | 9.53 |
| [‰] | 0.00 | 0.01 | ||
| [‰] | 1.27 | 3.70 | ||
| [‰] | 0.03 | 0.33 | 0.10 | 1.30 |
Although Ebola requires a long isolation period of 16 days, the low infection probability of 2.70% does not make a split beneficial. In contrast, for Influenza A, the short isolation time of 1 week is the decisive for not applying a split.
Result 6
For Ebola and Influenza A, either the infection probability or the isolation time is below the threshold observed in the preceding sensitivity analysis, which makes a split favorable.
7. Conclusions
This paper studied the tradeoffs between reducing the average response time for patients and protecting the EMS personnel from infection by designating ambulances to serve only infected patients and suspected cases. We introduced a two-stage approach. At the first stage, we solved an optimization model to pre-select ambulance splits with the highest emergency call coverage. At the second stage, we evaluated how EMS personnel and patients can benefit from these ambulance splits by calculating the performance measures for the pre-selected splits by applying an adapted AHQM. We implemented a discrete-event simulation to investigate the error made by applying the AHQM instead of the exact HQM, as well as assuming exponential service and interarrival times. Comparisons show that the developed AHQM provides an appropriate estimate for the exact solutions and is stable when inserting constant service times and actual interarrival time data. We further conducted a numerical case study for the Covid-19 pandemic in Munich (Germany). Results indicate that the average response time, queuing time, and driving time increase when categorizing patients and allocating ambulances. However, the sensitivity analysis shows that a split can outperform the decision not to split depending on the disease characteristics. A split can reduce the average response time if the system’s workload exceeds a certain threshold due to longer isolation times or higher infection probabilities. Moreover, for the examined factors, the mean infection probability for personnel does not significantly increase when applying a flexible split. When facing long isolation times (2.5 weeks), an infection probability of 6% and the same share of suspected and known cases as observed for the Covid-19 data instance, a flexible ambulance split can reduce the share of late arrivals regarding the response time from 68% to 18%. Short isolation times (1 day) or low infection probabilities (1%) do not make a split worthwhile. Due to the high risk of infection for personnel designated to suspected and known cases, the fixed split is predominantly outperformed regarding the average response time.
Although we provide numerical support that an ambulance split can reduce the average response time, further research is required to evaluate the ethical justifiability of applying an ambulance split. Furthermore, we limit our case study to two ambulance categories. In future work, the numerical analysis could be extended to additional ambulance and patient categories enabling more flexibility when allocating ambulances. Additionally, we introduce two ambulance splits based on an ambulance reservation strategy. However, extending the AHQM to account for these strategies is beyond the scope of this study. Thus, including them in the adapted AHQM and investigating different cutoff levels and strategies could be subject to future research. Moreover, further types of ambulance splits could be defined to investigate whether another split would improve the EMS system’s performance. Here, a possible extension could be to introduce flexible and dedicated ambulances that can serve all or only defined patient groups, respectively.
Acknowledgment
We are grateful for the numerous helpful comments by the three anonymous referees, which led to a much improved version of this paper. The work of the second author was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) 277991500/GRK2201.
Footnotes
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.ejor.2021.11.051.
Appendix A. Supplementary materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
References
- Allen R., Wanersdorfer K., Zebley J., Shapiro G., Coullahan T., Sarani B. Interhospital transfer of critically ill patients because of coronavirus disease 19–related respiratory failure. Air Medical Journal. 2020;39(6):498–501. doi: 10.1016/j.amj.2020.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altay N., Green W.G. OR/MS research in disaster operations management. European Journal of Operational Research. 2006;175(1):475–493. [Google Scholar]
- Amorim M., Ferreira S., Couto A. Emergency medical service response: Analyzing vehicle dispatching rules. Transportation Research Record: Journal of the Transportation Research Board. 2018;2672(32):10–21. [Google Scholar]
- Atkinson J.B., Kovalenko I.N., Kuznetsov N.Y., Mikhalevich K.V. Heuristic methods for the analysis of a queuing system describing emergency medical service deployed along a highway. Cybernetics and Systems Analysis. 2006;42(3):379–391. [Google Scholar]
- Batta R., Dolan J.M., Krishnamurthy N.N. The maximal expected covering location problem: Revisited. Transportation Science. 1989;23(4):277–287. [Google Scholar]
- Blank F. In: Dynamics in logistics. Freitag M., Haasis H.-D., Kotzab H., Pannek J., editors. Springer; Cham: 2020. A hypercube queuing model approach for the location optimization problem of emergency vehicles for large-scale study areas; pp. 321–330. (Lecture Notes in Logistics). [Google Scholar]
- Boyacı B., Geroliminis N. Approximation methods for large-scale spatial queueing systems. Transportation Research Part B: Methodological. 2015;74:151–181. [Google Scholar]
- Brodsky, I. (2018). H3: Uber’s hexagonal hierarchical spatial index. https://eng.uber.com/h3/.
- Budge S., Ingolfsson A., Erkut E. Approximating vehicle dispatch probabilities for emergency service systems with location-specific service times and multiple units per location. Operations Research. 2009;57(1):251–255. [Google Scholar]
- Cao P., He S., Huang J., Liu Y. Operations Research. 2020. To pool or not to pool: Queueing design for large-scale service systems. [Google Scholar]; Forthcoming. Doi:10.1287/opre.2019.1976
- Caunhye A.M., Nie X., Pokharel S. Optimization models in emergency logistics: A literature review. Socio-Economic Planning Sciences. 2012;46(1):4–13. [Google Scholar]
- Chelst K.R., Barlach Z. Multiple unit dispatches in emergency services: Models to estimate system performance. Management Science. 1981;27(12):1390–1409. [Google Scholar]
- Dargaville T., Spann K., Celina M. Opinion to address the personal protective equipment shortage in the global community during the COVID-19 outbreak. Polymer Degradation and Stability. 2020;176:109162. doi: 10.1016/j.polymdegradstab.2020.109162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dasaklis T.K., Pappis C.P., Rachaniotis N.P. Epidemics control and logistics operations: A review. International Journal of Production Economics. 2012;139(2):393–410. [Google Scholar]
- Drent C., Keizer M.O., van Houtum G.-J. Dynamic dispatching and repositioning policies for fast-response service networks. European Journal of Operational Research. 2020;285(2):583–598. [Google Scholar]
- Farahani R.Z., Fallah S., Ruiz R., Hosseini S., Asgari N. OR models in urban service facility location: A critical review of applications and future developments. European Journal of Operational Research. 2019;276(1):1–27. [Google Scholar]
- Fine C.H., Freund R.M. Optimal investment in product-flexible manufacturing capacity. Management Science. 1990;36(4):449–466. [Google Scholar]
- Fode B.S., Mamady M.K., Fode A.T., Aminata O.S., Mavolo T., Moumie B., Mohamed C. People healed of Ebola and their psychosocial life: About 55 cases at the Donka treatment center (conakry) International Journal of Medicine and Medical Sciences. 2018;10(3):42–46. [Google Scholar]
- Geroliminis N., Kepaptsoglou K., Karlaftis M.G. A hybrid hypercube – genetic algorithm approach for deploying many emergency response mobile units in an urban network. European Journal of Operational Research. 2011;210(2):287–300. [Google Scholar]
- Ghobadi M., Arkat J., Tavakkoli-Moghaddam R. Hypercube queuing models in emergency service systems: A state-of-the-art review. Scientia Iranica. 2019;26(2):909–931. [Google Scholar]
- Golan M.S., Jernegan L.H., Linkov I. Trends and applications of resilience analytics in supply chain modeling: Systematic literature review in the context of the covid-19 pandemic. Environment Systems and Decisions. 2020;40:222–243. doi: 10.1007/s10669-020-09777-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg J., Paz L. Locating emergency vehicle bases when service time depends on call location. Transportation Science. 1991;25(4):264–280. [Google Scholar]
- Haghani A., Tian Q., Hu H. Simulation model for real-time emergency vehicle dispatching and routing. Transportation Research Record: Journal of the Transportation Research Board. 2004;1882(1):176–183. [Google Scholar]
- Hiller B., Krumke S.O., Rambau J. Reoptimization gaps versus model errors in online-dispatching of service units for ADAC. Discrete Applied Mathematics. 2006;154(13):1897–1907. [Google Scholar]
- Iannoni A.P., Chiyoshi F., Morabito R. A spatially distributed queuing model considering dispatching policies with server reservation. Transportation Research Part E: Logistics and Transportation Review. 2015;75:49–66. [Google Scholar]
- Iannoni A.P., Morabito R., Saydam C. A hypercube queueing model embedded into a genetic algorithm for ambulance deployment on highways. Annals of Operations Research. 2008;157(1):207–224. [Google Scholar]
- Iannoni A.P., Morabito R., Saydam C. Optimizing large-scale emergency medical system operations on highways using the hypercube queuing model. Socio-Economic Planning Sciences. 2011;45(3):105–117. [Google Scholar]
- Jagtenberg C., Bhulai S., van der Mei R. Markov decision processes in practice. Springer; 2017. Optimal ambulance dispatching; pp. 269–291. [Google Scholar]
- Jarvis J. Approximating the equilibrium behavior of multi-server loss systems. Management Science. 1985;31(2):235–239. [Google Scholar]
- Knyazkov K., Derevitsky I., Mednikov L., Yakovlev A. Evaluation of dynamic ambulance routing for the transportation of patients with acute coronary syndrome in Saint-Petersburg. Procedia Computer Science. 2015;66:419–428. [Google Scholar]
- Ko P.C.-I., Chen W.-J., Ma M.H.-M., Chiang W.-C., Su C.-P., Huang C.-H.…Lin F.-Y. Emergency medical services utilization during an outbreak of severe acute respiratory syndrome (SARS) and the incidence of SARS-associated coronavirus infection among emergency medical technicians. Academic Emergency Medicine. 2004;11(9):903–911. doi: 10.1197/j.aem.2004.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson R.C. A hypercube queuing model for facility location and redistricting in urban emergency services. Computers & Operations Research. 1974;1(1):67–95. [Google Scholar]
- Larson R.C. Approximating the performance of urban emergency service systems. Operations Research. 1975;23(5):845–868. [Google Scholar]
- Massay F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. Journal of the American Statistical Association. 1951;46(253):68–78. [Google Scholar]
- Mendonça F.C., Morabito R. Analysing emergency medical service ambulance deployment on a Brazilian highway using the hypercube model. Journal of the Operational Research Society. 2001;52(3):261–270. [Google Scholar]
- Morabito R., Chiyoshi F., Galvão R.D. Non-homogeneous servers in emergency medical systems: Practical applications using the hypercube queueing model. Socio-Economic Planning Sciences. 2008;42(4):255–270. [Google Scholar]
- Nickel S., Reuter-Oppermann M., Saldanha-da Gama F. Ambulance location under stochastic demand: A sampling approach. Operations Research for Health Care. 2016;8:24–32. [Google Scholar]
- Phucharoen C., Sangkaew N., Stosic K. The characteristics of COVID-19 transmission from case to high-risk contact, a statistical analysis from contact tracing data. EClinicalMedicine. 2020;27:100543. doi: 10.1016/j.eclinm.2020.100543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prezant D.J., Zeig-Owens R., Schwartz T., Liu Y., Hurwitz K., Beecher S., Weiden M.D. Medical leave associated with COVID-19 among emergency medical system responders and firefighters in New York City. JAMA Network Open. 2020;3(7):e2016094. doi: 10.1001/jamanetworkopen.2020.16094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Queiroz M.M., Ivanov D., Dolgui A., Fosso Wamba S. Impacts of epidemic outbreaks on supply chains: Mapping a research agenda amid the COVID-19 pandemic through a structured literature review. Annals of Operations Research. 2020:1–38. doi: 10.1007/s10479-020-03685-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranney M.L., Griffeth V., Jha A.K. Critical supply shortages - the need for ventilators and personal protective equipment during the COVID-19 pandemic. The New England Journal of Medicine. 2020;382(18):e41. doi: 10.1056/NEJMp2006141. [DOI] [PubMed] [Google Scholar]
- Razali N.M., Wah Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. Journal of Statistical Modeling and Analytics. 2011;2(1):21–33. [Google Scholar]
- Schmid V. Solving the dynamic ambulance relocation and dispatching problem using approximate dynamic programming. European Journal of Operational Research. 2012;219(3):611–621. doi: 10.1016/j.ejor.2011.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz B., Cass D., Christian M., Dundas P., Farr B., LeBlanc L.…Smith R. The Report of the Hospital Emergency Department and Ambulance Effectiveness Working Group. Toronto, ON. Minister of Health and Long Term Care. 2005. Improving access to emergency services: A system commitment. [Google Scholar]
- Skrip L.A., Fallah M.P., Gaffney S.G., Yaari R., Yamin D., Huppert A.…Galvani A.P. Characterizing risk of Ebola transmission based on frequency and type of case–contact exposures. Philosophical Transactions of the Royal Society B: Biological Sciences. 2017;372(1721):20160301. doi: 10.1098/rstb.2016.0301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souza R.M., Morabito R., Chiyoshi F.Y., Iannoni A.P. Incorporating priorities for waiting customers in the hypercube queuing model with application to an emergency medical service system in Brazil. European Journal of Operational Research. 2015;242(1):274–285. [Google Scholar]
- Tassone, J., & Choudhury, S. (2020). A comprehensive survey on the ambulance routing and location problems. arXiv preprint arXiv:2001.05288 [cs].
- Tijms H.C. Wiley; Chichester: 2003. A first course in stochastic models. [Google Scholar]
- Van Mieghem J.A. Investment strategies for flexible resources. Management Science. 1998;44(8):1071–1078. [Google Scholar]
- Yoon S., Albert L.A., White V.M. A stochastic programming approach for locating and dispatching two types of ambulances. Transportation Science. 2021;55(2):275–296. [Google Scholar]
References
Regulations and References from Public Health Authorities
Bayerisches Staatsministerium des Innern (2010) Verordnung zur Ausführung des Bayerischen Rettungsdienstgesetzes: AVBayRDG. URL https://www.gesetze-bayern.de/Content/Document/BayAVRDG.
Centers for Disease Control and Prevention (2010) Interim guidance on infection control measures for 2009 H1N1 influenza in healthcare settings, including protection of healthcare personnel. URL https://www.cdc.gov/H1N1flu/guidelines_infection_control.htm.
Centers for Disease Control and Prevention (2019) 2014–2016 Ebola outbreak in West Africa. URL https://www.cdc.gov/vhf/ebola/history/2014-2016-outbreak/index.html.
Centers for Disease Control and Prevention (2020a) Duration of isolation & precautions for adults. URL https://www.cdc.gov/coronavirus/2019-ncov/hcp/duration-isolation.html.
Centers for Disease Control and Prevention (2020b) Interim recommendations for Emergency Medical Services (EMS) systems and 911 Public Safety Answering Points/Emergency Communication Centers (PSAP/ECCs) in the United States during the Coronavirus Disease (COVID-19) pandemic. URL https://www.cdc.gov/coronavirus/2019-ncov/hcp/guidance-for-ems.html.
Robert Koch Institut (2010) Epidemiologisches Bulletin. URL https://www.rki.de/DE/Content/Infekt/EpidBull/Archiv/2010/Ausgaben/45_10.pdf?__blob=publicationFile.
Robert Koch Institut (2019) Rahmenkonzept Ebolafieber: Vorbereitungen auf Maßnahmen in Deutschland. URL https://www.rki.de/DE/Content/InfAZ/E/Ebola/Rahmenkonzept_Ebola.pdf?__blob=publicationFile.
Robert Koch Institut (2020a) Coronavirus Disease 2019 (COVID-19) Daily situation report of the Robert Koch Institute. URL https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Dez_2020/2020-12-31-en.pdf?__blob=publicationFile.
Robert Koch Institut (2020b) Epidemiologisches Bulletin. URL https://www.rki.de/DE/Content/Infekt/EpidBull/Archiv/2020/Ausgaben/39_20.pdf?__blob=publicationFile.
Robert Koch Institut (2021) Übersicht zu besorgniserregenden SARS-CoV-2-Virusvarianten (VOC). URL https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Virusvariante.html.
ScienceAlert (2021) Fallzahl und Todesopfer ausgewählter Virusausbrüche im Zeitraum von 1967 bis 2021. URL https://de.statista.com/statistik/daten/studie/1101352/umfrage/fallzahl-und-todesopfer-ausgewaehlter-virusausbrueche-weltweit/.
The World Bank (2021) Data for Liberia, Guinea, Sierra Leone. URL https://data.worldbank.org/?locations=LR-GN-SL.
World Health Organization (2018) Managing epidemics: Key facts about major deadly diseases. A WHO Handbook (Geneva: World Health Organization), URL https://www.who.int/emergencies/diseases/managing-epidemics-interactive.pdf.
World Health Organization (2020a) Criteria for releasing Covid-19 patients from isolation. URL https://www.who.int/news-room/commentaries/detail/criteria-for-releasing-Covid-19-patients-from-isolation.
World Health Organization (2020b) Ebola virus disease. URL https://www.who.int/news-room/fact-sheets/detail/ebola-virus-disease.
World Health Organization (2020c) Statement on the second meeting of the International Health Regulations (2005) Emergency Committee regarding the outbreak of novel coronavirus (2019-nCoV). URL https://www.who.int/news-room/detail/30-01-2020-statement-on-the-second-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov).
World Health Organization (2021) Daily cases and deaths by date reported to WHO. URL https://covid19.who.int/info.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/