Abstract
On-line data collection is being used more and more, especially in the face of the COVID crisis. To examine the quality of such data, we chose to replicate lexical decision and item recognition paradigms from Ratcliff, Thapar, and McKoon (2010) and numerosity discrimination paradigms from Ratcliff and McKoon (2018) with subjects recruited from Amazon Mechanical Turk (AMT). Along with these tasks, we collected data from either an IQ test or a math computation test. Subjects in the lexical decision and item recognition tasks were relatively well- behaved with only a few giving a significant number of responses with response times (RTs) under 300 ms at chance accuracy, i.e., fast guesses, and a few with unstable RTs across a session. But in the numerosity discrimination tasks, almost half of the subjects gave a significant number of fast guesses with unstable RTs across the session. Diffusion model parameters were largely consistent with the earlier studies as were correlations across tasks and correlations with IQ and age. One surprising result was that eliminating fast outliers from subjects with highly variable RTs (those eliminated from the main analyses) produced diffusion model analyses that showed patterns of correlations similar to the subjects with stable performance. Methods for displaying data to examine stability, eliminating subjects, and implementing RT data collection on AMT including checks on timing are also discussed.
Keywords: Mechanical Turk data, diffusion decision model, response time and accuracy, across-session variability
The use of Amazon Mechanical Turk (AMT, www.mturk.com) in cognitive psychology research goes back nearly 10 years (Mason & Suri, 2012), with detailed reviews of replication attempts (Crump, et al., 2013; Semmelmann & Weigelt, 2017) as well as strengths, weaknesses, ethical concerns, and issues with using the AMT recruitment platform (e.g. Woods et al., 2015; Stewart, et al., 2017). The consensus that has been emerging from this discussion is that on-line reaction time (RT) data appears to be reliable across a range of tasks, including lexical decision (Simcox & Fiez, 2014; Hilbig, 2016), spoken word identification (Slote & Strand, 2015), the flanker task (Crump, et al., 2013; Simcox & Fiez, 2014; Semmelmann & Weigelt, 2017; Anwyl- Irvine, et al., 2020), visual search (de Leeuw & Motz, 2016; Semmelmann & Weigelt, 2017), as well as the Stroop task, attentional blink, and masked priming (Crump, et al., 2013; Semmelmann & Weigelt, 2017).
We began this study before the COVID crisis occurred, but the results here are especially relevant for anyone who now wants to collect and use response time data from on-line platforms. Even before COVID, there has been a move to test subjects with on-line platforms, especially Amazon’s Mechanical Turk. This has the advantages that, for example, many subjects can be tested quickly and a range of abilities and age groups can be tested. But there is still the issue of quality of the data.
The differences in RTs that do occur between web-based and laboratory-based measurement tools are more pronounced in measures of central tendency (median RT) and less so in the variability of RTs (de Leeuw & Motz, 2016; Semmelmann & Weigelt, 2017), although a recent study suggests increased variability may be a problem (Bridges, et al., 2020). Nearly all such analyses have focused on statistical analyses of RT measures leaving accuracy and choice as the targets for model-based analyses of on-line experiments (e.g Hendrickson, et al., 2019; Bramley, et al, 2018; though see Dekel & Sagi, 2020, who modeled a perceptual bias task with the diffusion model, Ratcliff, 1978). The number of measurements per subject that are required for modeling is an issue in some applications. It is not a problem when examining individual differences or group differences between subjects or subject-groups because half an hour of data collection is sufficient to obtain parameter values that are accurate enough for such analyses (Ratcliff & Childers, 2015). However, for use in examining the accuracy of model fit, deviations between theory and data, or model comparison, the larger numbers of observation needed to accurately estimate the parameters of these models is likely one factor that might discourage use of AMT on-line data for such analyses.
In the current study we present a moderately large-scale model-based analysis of response time (RT) and accuracy data collected from AMT subjects. Our aims for the experiments reported here were to provide a comprehensive analysis of the quality of the data collected on-line from AMT subjects, to compare the AMT data to data collected in person from previously published experiments, and to perform model-based analyses of the AMT data using Ratcliff’s diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008) to see if the model-based analyses replicate the results from those studies. We performed two AMT experiments, the first with lexical decision and item recognition, replicating the designs of two experiments in Ratcliff, Thapar, and McKoon (2010), and the second replicating the designs of two numerosity discrimination experiments from Ratcliff and McKoon (2018). By using two tasks in each experiment, we could examine individual differences in model parameters between the two tasks and compare those with prior studies.
However, there are potential problems in such on-line data. Subjects may adopt strategies that might not occur with a dedicated researcher monitoring a test session. This includes distractions during the experiment that might produce a small number of slow trials (for example, a beeping microwave), a decision to respond quickly and randomly at the onset or offset of the presentation of a stimulus, or chance performance due to technical issues or a lack of task understanding. Without dedicated monitoring, subjects are more likely to shift their behavior across trials and blocks, an issue that is potentially more difficult to detect and model appropriately. This could include adjusting speed-accuracy criteria as they explore a task, in some blocks responding quite quickly, while in other blocks delaying responses to produce more accurate performance, or simply losing interest in the task over time. Though we find evidence of these patterns in some, but not all of the experiments reported below, we find relatively consistent best fitting model parameters between on-line and laboratory-based tasks.
In Experiment 1 there were two tasks, lexical decision and item recognition. In the lexical decision task, subjects decided whether strings of letters were or were not words. In the item recognition task, subjects decided whether a test word had appeared in a preceding study list of words or not. Subjects in Experiment 1 were also given the Cattell culture-fair IQ test (Cattell & Cattell, 1960). In Experiment 2 there were also two tasks, one in which subjects decided whether there were more blue dots in an array than yellow dots (we call this the BY task), and one in which they decided whether the number of dots in an array (all of the same color) was or was not larger than 25 (we call this the Y25 task). Some of the subjects in Experiment 2 were given the Cattell culture-fair IQ test and others a simple math-fluency test.
We chose the four tasks used in the experiments in part because they provide a rich set of results as a target for replication and comparison between laboratory-based and on-line-based data collection. Within each task, standard independent variables were manipulated: For lexical decision, word frequency was manipulated, for item recognition, word frequency and number of presentations of study words were manipulated, for the BY task, both the number of blue and yellow dots and the summed area of the dots were manipulated, and for the Y25 task, the number of dots and the summed area were manipulated.
In previous studies (Ratcliff, Thapar, and McKoon, 2010; Ratcliff and McKoon, 2018) these tasks were modeled using the standard diffusion model. The model gives an account of the effects of independent variables on the cognitive processes involved in making simple two-choice decisions in the experiments described here by mapping accuracy and RT data onto underlying components of processing. The main components are evidence from the stimulus (drift rate) that drives the decision process, the amount of evidence needed to make a decision (boundary separation), and the duration of processes other than the decision process (nondecision time). For the lexical decision and item recognition tasks, there is different drift rate for each condition of the experiment. But for the numerosity tasks, there is a model of drift rate (expressions for both the mean and the SD across trials) with many fewer parameters than the number of conditions. The settings of the boundaries are assumed to be under a subject’s control so that when the boundaries are set close to the starting point, responses will be faster and accuracy will be lower. When the criteria are set farther apart, responses will be slower and accuracy will be higher. With the settings of the boundaries and nondecision times abstracted out of RTs and accuracy though application of the model, drift rate gives a direct measure of the quality of the information driving the decision process.
In the current study, we compare the previous laboratory-based results to an analysis of the data collected on-line from AMT subjects. There are four sets of benchmarks on which the experiments and model-based analyses are evaluated. These include: 1. The empirical effects within each task, 2. the ability of the diffusion model to fit the data from each task, 3. the relationships (correlations) between pairs of model parameters across individuals, and 4. The relationships (correlations) between IQ and the math test and model parameters. We now discuss each of these benchmarks in depth.
First, all four tasks have clear, established empirical patterns that should occur. In the lexical decision task, accuracy should be highest and RT lowest for high frequency words, followed by low frequency words, then very low frequency words. In the item recognition task, results should show a standard mirror effect in which accuracy is higher and RT shorter for low frequency words than high frequency words for both studied and new words. Also, for words studied twice, accuracy should be higher and RT lower than for words studied once. For the BY numerosity discrimination task, accuracy should decrease as the difference in numerosity between blue and yellow dots decreases and also as the total numerosity of the two colors increases. RT should decrease as the numerosity difference increases, but counterintuitively, for a fixed small difference, as total numerosity increases RT should decrease (instead of increasing). For the Y25 task, as the numerosity increases from lower counts to the maximum of 25, accuracy should decrease and RT increase.
Second, previous laboratory-based studies have identified stable patterns of best-fitting parameter values across conditions in these tasks. In lexical decision and item recognition tasks, changes in drift rates (but no other parameters) account for differences in accuracy and correct and error RTs across stimulus conditions. In the BY and Y25 tasks, both drift rates and the across-trial SD in drift rate change across stimulus conditions. The diffusion model fit the data from all four tasks in the original studies well and the model parameters provided coherent accounts of the data.
Third, individual difference analyses showed correlations between parameter values.
Specifically, in the recognition memory and lexical decision tasks, drift rates correlated between tasks, boundary separations correlated, and nondecision times correlated. Similarly, for the two numerosity discrimination tasks (BY and Y25), drift rates correlated between tasks, boundary separations correlated, and nondecision times correlated.
Fourth, in the recognition memory and lexical decision tasks drift rates correlated with IQ but did not change with age, and boundary separation and nondecision time both changed with age but were not correlated with IQ. However, IQ and math computation tasks were not studied in the earlier studies of the numerosity tasks.
One important result is that for the numerosity tasks, nearly half the subjects produced over 5% fast guesses. Many of these subjects also had considerable variability with runs of trials that were fast and runs that were slow. This instability is easy to see in plots of each RT from each trial for each subject in time-series plots presented later. In contrast to the numerosity tasks, most AMT subjects for lexical decision and item recognition showed stable performance.
Recruiting Subjects
A total of 308 AMT workers (AMT’s word for subjects) were recruited in batches of between 10 to 50 in parallel, with the intention of recruiting at least 150 subjects in each of the two experiments. To participate in the tasks, subjects were required to have completed at least 50 previous HITs (Amazon’s acronym for an experiment: human intelligence task) and an approval rate of at least 90% on previous HITs. Subjects were also required to be 18 years old or older, with English as their native language, normal or corrected-to-normal vision, and normal color perception (all self-reported). Throughout a session, there was a “STOP TASK” button at the top right-hand corner of the screen so subjects could stop the session at any time. They were paid $10 for the session or if they hit the STOP TASK button before the end of the session, they were paid proportionally according to the amount of the session they had completed. Subjects who did not complete at least 80% of the trials and follow instructions were eliminated from data analyses.
For Experiment 1, 154 subjects began the experiment, 4 subjects finished less than 20% of the item recognition task and one 65% of that task. These subjects were eliminated. One subject did not make many Cattell task responses, and 6 subjects mainly hit one response key or made more than 5% fast guesses in one of the tasks. This left 142 subjects in Experiment 1 that were used for data analysis and modeling.
For Experiment 2, 199 total subjects were recruited, with 136 assigned to the math task and 62 to the Cattell task. Of the subjects who received the math test, 12 subjects completed less than 24% of the second numerosity task, and 3 less than 63%. Of the 121 subjects left, three responded mainly with one response key and 4 had performance at chance leaving 114 used in the analyses. For the Cattell test, 7 subjects completed less than 10% of the last task, one completed 62%, 1 responded with mainly one response key and 1 was at chance, leaving 52 used in the analyses.
General Procedures
At the beginning of each experiment, subjects read a brief description of the tasks for the experiment on the AMT website. If they chose to participate, a consent form, approved by Ohio State University’s Institutional Review Board, was displayed and subjects gave their consent by clicking on a box. After that, a form was displayed on which subjects provided basic demographic data by typing numbers or selecting choices for year of birth, gender, ethnicity, and race. Finally, subjects were asked to close all applications on their computer, to close all other tabs on their browser window, to maximize the size of that window, and to keep the AMT window open until the end of the session. These behaviors were requested but not required in order to run the experiment and they were not checked. After completing the setup, subjects clicked a button and a new browser window opened which contained the experiment tasks. This tab closed at the end of the session.
Stimulus presentation and response collection were performed by a custom-made javascript program (based on Ratcliff’s highly updated laboratory real-time system, Ratcliff, 1994; Ratcliff, Pino, & Burns, 1986) running locally on the subject’s computer. The timing of stimulus presentation and response recording had millisecond accuracy contingent on the refresh rate (scan rate) of the client-computer display. All data were collected on the subject’s computer and then were uploaded automatically to the host computer when either a session finished or a subject hit the “STOP TASK” button. When the session ended or when the STOP button was pressed, a subject was given a “HIT code” to be used to redeem payment.
The Cattell Culture-Fair IQ
This test (Cattell and Cattell, 1960) is a 12.5 min. multiple-choice test intended to measure non-verbal (fluid) intelligence, similar to the Raven’s progressive matrices test. It has three different scales and we used Scale 2, which is aimed at adolescents and adults. A sample test (different from the one we used) that shows questions that are similar to those in the Cattell test that we used can be seen at https://www.psychologytoday.com/us/tests/iq/culture-fair-iq-test.
There were four subtests. Each began with instructions and then the test items were displayed, all on the same page, one line per item. Responses were made by clicking on the buttons next to the choice option using a mouse or touchpad. The first section has three drawings and five options, the aim was to choose the option that completed the sequence. The second section has five drawings and the subject had to choose the one that was different from the others. The third had a 2×2 array with one cell empty and the task was to choose from five options which one completed the array. The fourth had one drawing with a dot in it and five options and the subject was to choose the one that could have a dot drawn in it in the same way as the example drawing. The times for the four sections were 3, 4, 3, and 2.5 min. respectively. The numbers of correct choices for the four subtests were combined (there was a total of 50 items) and then IQ was calculated as a function of age. Ages and scores on the IQ and math fluency test are shown in Table 1 (and distributions are shown in Figures 4 and 11).
Table 1:
Subject ages and scores on IQ and math fluency tests.
| N | Age | Cattell IQ | Math Grade Equivalent | ||||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | ||
| Lex dec/memory w/Cattell | 142 | 35.5 | 10.0 | 96.2 | 13.9 | ||
| Numerosity w/Cattell | 52 | 33.8 | 8.9 | 96.4 | 19.3 | ||
| Numerosity w/Math | 114 | 39.4 | 12.5 | 12.2 | 4.3 | ||
Figure 4.
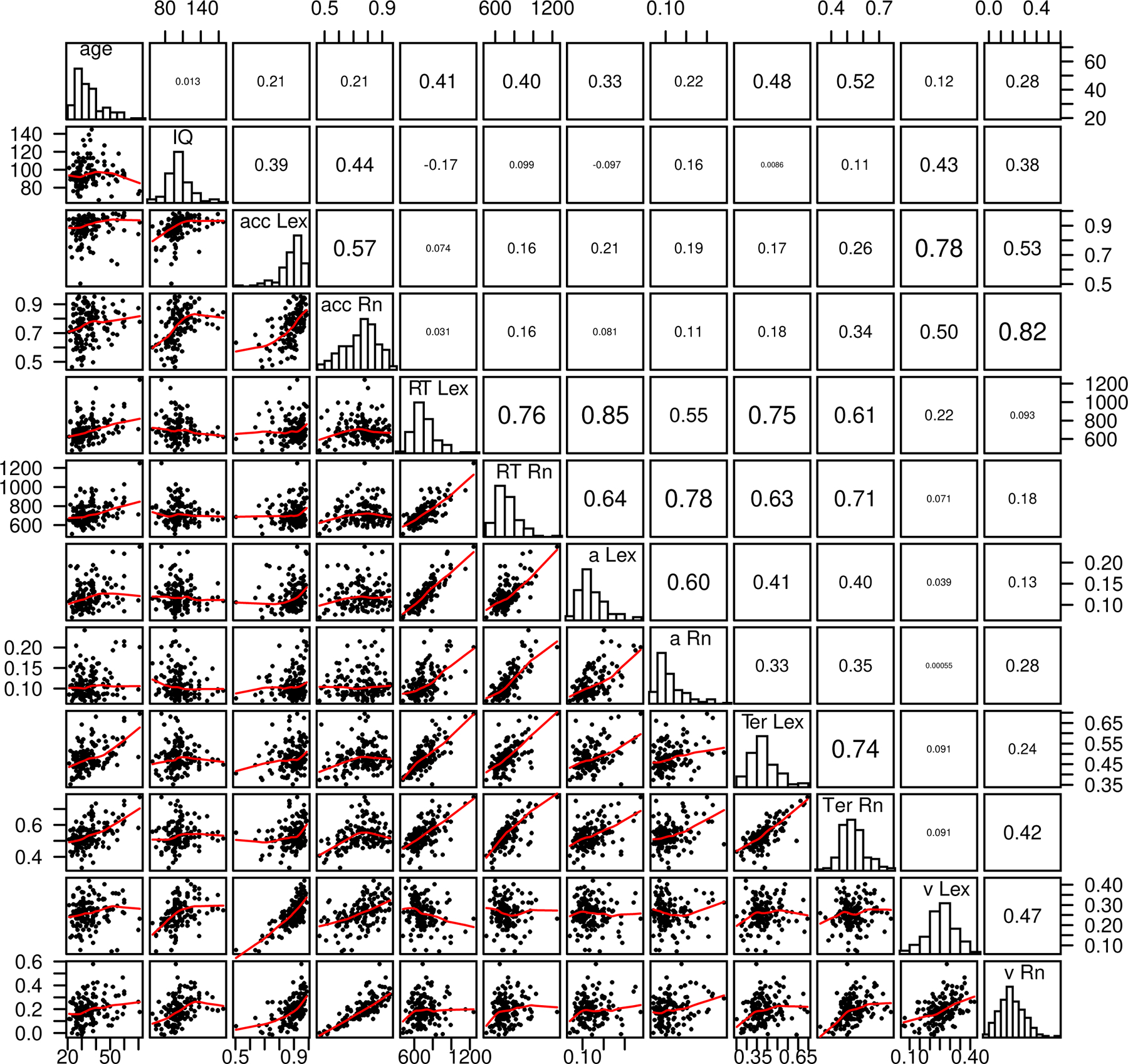
Scatter plots, histograms, and correlations for age, IQ, accuracy and mean RT, and diffusion model parameters, nondecision time, boundary separation, and drift rate averaged over conditions for the lexical decision and item recognition tasks. acc=accuracy, RT=mean RT, a=boundary separation, Ter=nondecision time, v=mean drift rate, Lex is the lexical decision task, and Rn is the item recognition task.
Figure 11.
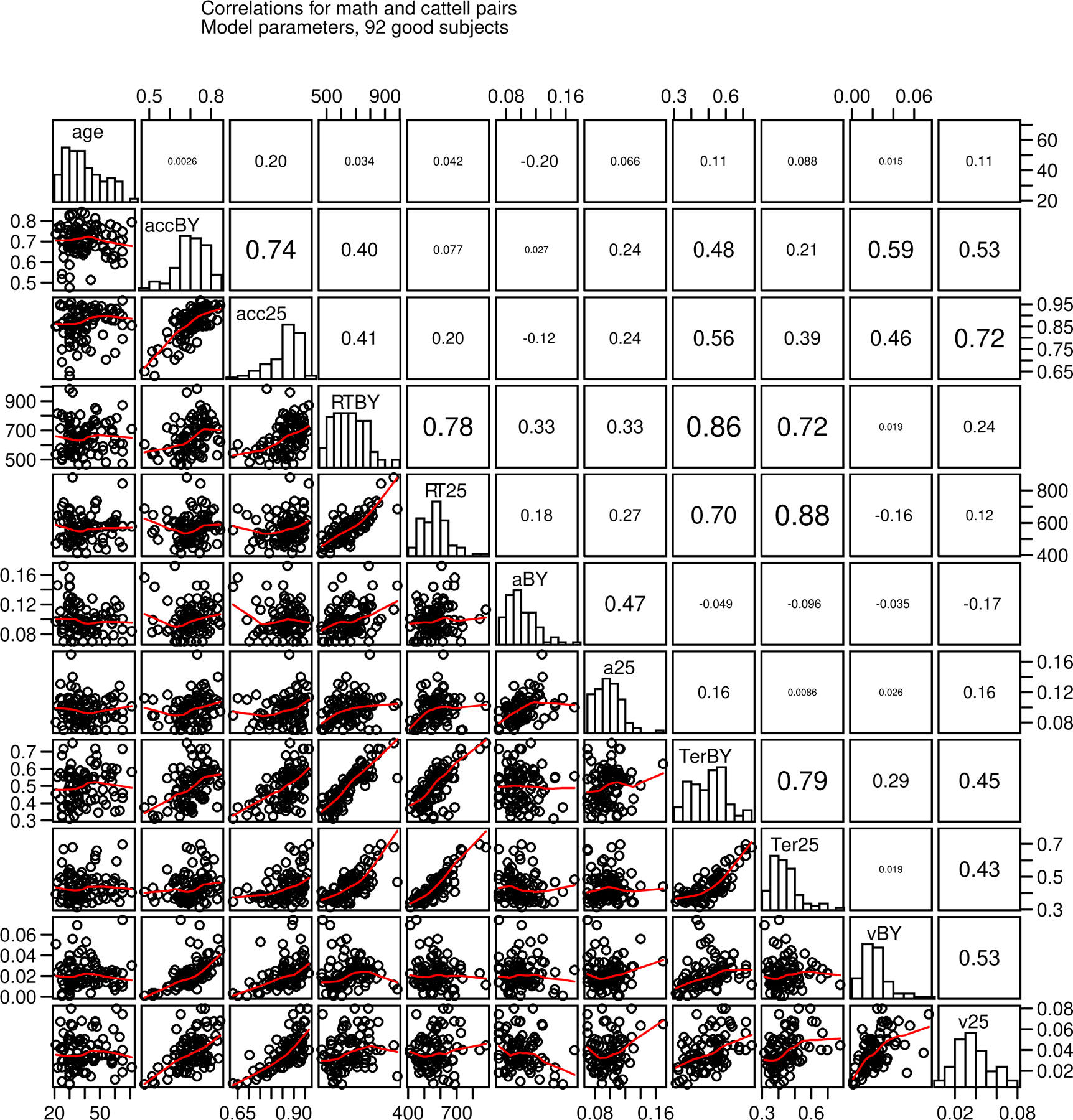
Scatter plots, histograms, and correlations for age, accuracy and mean RT, and diffusion model parameters, nondecision time, boundary separation, and drift rate averaged over conditions for the 92 “good” subjects for the two numerosity discrimination tasks. acc=accuracy, RT=mean RT, a=boundary separation, Ter=nondecision time, v=mean drift rate, BY is the blue/yellow task, and 25 is the Y25 task.
The Math Fluency Test
We constructed a math fluency test that was based on the Math Fluency subtest of the Woodcock-Johnson III Tests of Achievement. The Woodcock-Johnson test is composed of a series of simple addition, subtraction and multiplication problems with integers between zero and 10 and correct responses between 0 and 81 and responses are written on the sheet of paper that contains the problems. We wrote new problems that were similar to those of the subtest. The problems were displayed all at once and remained on the screen during the entire timed test. Subjects typed their answer into a box on the screen that was located below each problem and were instructed to use the tab key to move from one answer box to the next. The test began with 30 typing practice items and for each, a number between 0 and 81 was displayed and subjects were asked to type that number into a response box on the screen. They used the tab key to move from one response box to the next. After the practice, the addition, subtraction, and multiplication problems were displayed, one at a time, and subjects typed their answers into the response box. They were instructed to use the “tab” key to move to the next item, and to respond as quickly and accurately as possible. They were given 3 minutes to complete as many problems as possible out of a total of 160 in 3 min. The time remaining until the 3 min. was up was displayed in a box on the right side of the page. The task was evaluated in post-processing, with the grade-equivalent score derived from how many items could be correctly completed in three minutes from the Woodcock-Johnson subtest scale (corrected for the difference in writing versus typing responses).
Experimental Tasks
The lexical decision and recognition memory experiments were presented as plain text in the top left corner of an 80 column by 24 row HTML textarea window positioned in the center of the screen and surrounded by an 8-pixel wide black border. The font was white, monospace, sans serif with a 50% gray background. The numerosity task experiments were presented as HTML canvas elements (colored dots on a gray square pedestal). Each experiment began with instructions in plain text. Embedded in each experiment were brief reminders and instructions about the correct response keys and the importance of rapid responses. Stimuli were presented with millisecond accuracy (contingent on the refresh rate of the client computer display), and responses were recorded with millisecond accuracy (contingent on the scan rate of the client computer keyboard). In all the tasks, subjects initiated each block by pressing the space bar on the keyboard. A “Stop Task” button was present at all times at the upper right corner of the experiment web page. Full instructions are presented in the supplement.
In both numerosity tasks, the dots were displayed within a 640 by 480 pixel HTML canvas element. The dots had different sizes and dot centers were placed randomly within a 360 by 360 pixel area at the center of the element. The background was a 480 by 480 pixel square, colored gray to control luminance (Halberda et al., 2008). The visual angle of the background and dots was dependent on the screen resolution of the subjects’ display. For a large screen (700 mm wide) with a resolution of 1920 by 1080 pixels (0.365 by 0.365 mm/pixel), the 480×480 gray background was 18.7 × 18.7 degrees of visual angle when viewed from a distance of 53 cm, and the 6, 8, 10, 12, 14, or 16 pixel dot diameters subtended angles of 0.236, 0.315, 0.394, 0.473, 0.552, or 0.631 degrees respectively. For a small screen (256 mm wide) with a resolution of 1366 by 768 pixels, the 480×480 gray background was 9.7 × 9.7 degrees of visual angle when viewed from a distance of 53 cm, and the 6, 8, 10, 12, 14, or 16 pixel dot diameters subtended angles of 0.122, 0.162, 0.203, 0.243, 0.284, or 0.324 degrees respectively. We constrained the positions of the dots so that the maximum horizontal/vertical distance dot centers could be separated by was 360 pixels and the minimum spacing between dot edges was 5 pixels.
One technical aspect of displaying these non-text images has to do with how they are drawn on a screen. An image is drawn on the screen line by line from the top left to the bottom right, usually in 16 ms per frame. If an image took, say, 200 ms, to draw, then the image would appear starting at the top of the screen and gradually strips would appear moving down the screen. In order to allow the image to appear in one sweep, the dots were drawn on a hidden (640 by 480 pixel) HTML canvas element (with colored dots on a gray square pedestal). Then when the whole array was drawn, it was copied to a foreground canvas element and this made it be displayed all in one frame at the onset of the presentation of the image.
For the two numerosity tasks, dot stimuli were presented for 300 ms and then the screen returned to the background color. Responses were collected by key presses on the PC keyboard. For both tasks, there were four example/practice trials and for these, the screen also displayed the correct response so that subjects would be certain to understand the instructions (e.g., it would say “an example of more blue dots” when the decision was about which color had the more dots).
We should also note two issues about timing. As described above, displays are drawn in frames at 16 ms units (though this can be lower with some displays). If the display is not synchronized to the screen refresh, then the image may begin drawing halfway down the screen. If the display is presented in multiples of the refresh rate, then half the last image will be displayed halfway down the screen and the whole image will have been presented for the presentation duration. The visual system integrates these successive screens so the partial displays are averaged over. With 300 ms presentation duration, there is not a problem with the screen refresh. There is another potential issue and that is with the keyboard response detection. Some older keyboards are scanned at quite a slow rate, e.g., 60 ms. This is a uniform distribution with SD: the range divided by the square root of 12, in this example with a 60 ms scan rate, the SD is 17.3 ms. This variability adds variability to the estimate of RTs, but this is small. For example, if the SD in RT is 200 ms, then the combined SD is the square root of the summed variances which is 200.7 ms, i.e., the added variability is minuscule. Thus, screen and keyboard timing issues on the subject’s computer are likely not a problem.
A subject’s progress through the blocks was displayed at the end of each block as the percent of blocks completed, for example, “You are now 17% through the task.” This was done because some pilot subjects were terminating the experiment before the end of this task. In all the tasks, subjects initiated each block by pressing the space bar on the keyboard. A “Stop Task” button was present at all times at the upper right corner of the experiment web page. If subjects chose to stop the experiment prematurely, they clicked on this button, which generated a pop-up dialog box asking for a confirmation, whereupon the data was uploaded to the host computer and the subject was given their HIT code with a suffix attached, indicating an early end to the HIT. Subjects who completed only a portion of the experiment were compensated proportionally to how much of the experiment was completed.
The demographics data and the Cattell or math test data were passed back to the host computer and were incorporated as the first line of the final data file for each subject. This produced a long line with age, ethnicity, race, the cognitive task (lexical decision/item recognition or numerosity), and the scores from the IQ or math test. Once the subject completed the background task, they were immediately taken to the instruction page for the cognitive or numerosity tasks.
The Diffusion Decision Model
A central aim of this research was to determine whether the data collected from AMT subjects produced a replication of model-based analyses in past studies.
As described above, the two-choice diffusion model separates the quality of the evidence entering a decision (drift rate, v) from the decision criteria and nondecision processes. Decisions are made by a noisy process that accumulates evidence over time from a starting point z toward one of the two decision criteria, or boundaries, a and 0. When a boundary is reached, a response is initiated. Drift rate is determined by the quality of the evidence extracted from the stimulus in perceptual tasks and the quality of the match between the test item and memory in memory and lexical decision tasks. The mean of the distribution of times taken up by nondecision processes (the combination of the time for stimulus encoding, the time to extract decision-related information from the stimulus representation, the time for response execution, and so on) is labeled Ter. Within- trial variability (noise) in the accumulation of information from the starting point toward the boundaries results in processes with the same mean drift rate terminating at different times (producing RT distributions) and sometimes at the wrong boundary (producing errors).
The values of the components of processing vary from trial to trial, under the assumption that subjects cannot accurately set the same parameter values from one trial to another (e.g., Laming, 1968; Ratcliff, 1978). Across-trial variability in drift rate is normally distributed with SD η, across-trial variability in starting point is uniformly distributed with range sz, and across-trial variability in the nondecision component is uniformly distributed with range st. The precise form of these distributions is not critical, Ratcliff (2013, also 1978) showed that different distributions produced similar behavior of the model.
Also, there are “contaminant” responses-- slow outlier response times as well as responses that are spurious in that they do not come from the decision process of interest (e.g., distraction, lack of attention). To accommodate these responses, we assume that, on some proportion of trials (po), a uniformly distributed random number between the minimum and maximum RT for the condition is used for the decision RT (see Ratcliff & Tuerlinckx, 2002). The assumption of a uniform distribution is not critical; recovery of diffusion model parameters is robust to the form of the distribution (Ratcliff, 2008). We fit the model with the contaminant assumptions to the item recognition and lexical decision experiments and the estimated proportions of contaminants were 0.7% and 0.2% respectively. These estimates were obtained from data in which fast and slow outliers had been eliminated. The values were too small to perform any further analyses. The two numerosity tasks were fit without this assumption in the original article and so to provide parallel analyses, we left them out of our analyses here.
The values of all the parameters, including the variability parameters, are estimated simultaneously from data by fitting the model to all the data from all the conditions of an experiment. The model can successfully fit data from single subjects with reasonable accuracy if there are around 400–1000 total observations per subject, which typically takes about 20–45 minutes of data collection time for the kinds of tasks considered in this article. Variability in the parameter estimates is much less than differences in the parameters across subjects, resulting in meaningful correlations of individual parameters and measures (e.g. IQ).
The method we use to fit the model to data uses a SIMPLEX minimization routine that adjusts the parameters of the model until it finds the values that give the minimum G-square value (see Ratcliff & Tuerlinckx, 2002, for a full description of the method). The data entered into the minimization routine for each experimental condition were the .1, .3, .5, .7, .9 quantile RTs for correct and error responses and the corresponding accuracy values. The quantile RTs and the diffusion model were used to generate the predicted cumulative probability of a response by that quantile response time. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For the G- square computation, these are the expected values, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .3, .5, .7, .9, and 1.0, which are .1, .2, .2, .2, .2, and .1). The proportions for the observed (O) and expected (E) frequencies and summing over 2N[Olog(O/E)] for all conditions gives a single G2 (a log multinomial likelihood) value to be minimized (where N is the number of observations for the condition).
The diffusion model is tightly constrained. The most powerful constraint comes from the requirement that the model fit the right-skewed shape of RT distributions (Ratcliff, 1978; Ratcliff & McKoon, 2008; Ratcliff et al., 1999). In addition, changes in response probabilities, quantile RTs, and the relative speeds of correct and error responses across experimental conditions that vary in difficulty are all captured by changes in only one parameter of the model, drift rate. The other parameters cannot vary across levels of difficulty. For the decision criteria, subjects could only set them as a function of difficulty if they already knew, before the accumulation process started, what the level of difficulty would be. For the nondecision component, we usually assume that the duration of stimulus encoding, matching against memory, response output, and other such nondecision processes do not vary with difficulty.
Experiment 1
This experiment was composed of the Cattell IQ test, a lexical decision experiment, and an item recognition experiment, presented in that order. For lexical decision and item recognition, the stimuli were words that occurred with high, low, and very low frequency in English. There were 800 high-frequency words with frequencies from 78 to 10,600 per million (mean=325, SD=645, Kucera & Francis, 1967); 800 low-frequency words with frequencies of 4 and 5 per million (mean = 4.41, SD = 0.19); and 741 very-low-frequency words, with frequencies of 1 per million or no occurrence in the Kucera and Francis corpus (mean = 0.37; SD = 0.48). All of the very-low- frequency words occurred in the Merriam-Webster Ninth Collegiate Dictionary (1990) and they were screened by three Northwestern undergraduate students. Any words that they did not know were eliminated. No words were used in both tasks.
For the Cattell test, subjects were given instructions for each of the sections immediately before them and they pressed the space bar to begin each one. The lexical decision and item recognition tasks were each preceded by instructions and subjects pressed the space bar to begin.
In the lexical decision task, there were 17 blocks, each containing 30 letter strings: 5 high- frequency words, 5 low-frequency words, 5 very-low-frequency words, and 15 nonwords. Subjects were asked to press the “/” key if the letter string was a word and the “z” key if it was not, as quickly and accurately as possible. The first block was for practice and for each response the subject made that was incorrect the word “ERROR” was displayed for 750 ms followed by a blank screen for 200 ms and then the next test item. For all the other blocks, there was no error feedback; test items were followed only by a 150 ms blank screen. The words and nonwords were randomly chosen from their pools and they were presented in random order.
In the item recognition task, there were 17 blocks of trials. For each, the list of words to be remembered consisted of 8 high- and 8 low-frequency words, plus a very-low-frequency buffer word at the end of the list. Four of the high- and four of the low-frequency words were displayed once and the other four were displayed twice. Each study word was presented for 1300 ms with a 200 ms blank screen before the next study word was presented. Test words immediately followed the to-be-remembered list, with 17 words from the list and 17 words that had not been on the list. The latter were 8 high- and 8 low-frequency words, plus the buffer word and a very-low-frequency word that had not appeared in the to-be-remembered list.
Words were randomly chosen from their pools and presented in random order. The first two words in a test list were fillers, the buffer word and a very-low-frequency word that had not appeared in the to-be-remembered list. Subjects were asked to press the “/” key if a word had appeared in the to-be-remembered list and the “z” key if it had not, again as quickly and accurately as possible. For the item recognition tasks at the end of each block, feedback on accuracy for that block was displayed on the screen: “excellent, very good, good, below average, or very low” and we defined these as: 31–34, 27–30, 23–26, 20–22, and 0–19 correct, respectively, out of 34.
Results
This section begins with showing that the results from the experimental paradigms used in past research can be replicated with AMT in terms of standard empirical patterns and the effects of independent variables. This is the first critical result for the utility of AMT. We then go on to results from fitting the diffusion model to the data.
Accuracy and RT
RTs less than 300 ms and greater than 4000 ms were eliminated from the analyses (less than 1% of the data, 0.0097). Table 2 shows values of accuracy and mean RTs for correct and error responses for the lexical decision and item recognition tasks as a function of experimental conditions. The data show the same qualitative pattern of results as seen in laboratory-based studies. For lexical decision, accuracy was highest for high-frequency words, lower for low- frequency words, and lowest for very-low-frequency words. Mean RTs were longer for lower accuracy responses. Error mean RTs were longer than correct mean RTs for nonwords but shorter than correct responses for words. For item recognition, accuracy was higher and RTs shorter for low-frequency words than high-frequency words, the standard mirror effect. Responses for studied words were faster and more accurate if the words had been presented twice than once. Even though some of the subjects showed moderate numbers of fast guesses and unstable performance across the session (examined later in the results section), we used data and model fits for all the subjects in this experiment.
Table 2:
Accuracy and correct and error mean RTs for Experiment 1, lexical decision and item recognition
| Lexical decision | Pr “word” | Mean RT “word” | Mean RT “nonword” |
|---|---|---|---|
| HF word | 0.963 | 637 | 577 |
| LF word | 0.863 | 723 | 701 |
| VLF word | 0.727 | 769 | 746 |
| Nonword | 0.074 | 742 | 710 |
| Item recognition | Pr “old” | Mean RT “old” | Mean RT “new” |
| 2P HF | 0.706 | 719 | 748 |
| 2P LF | 0.819 | 706 | 725 |
| 1P HF | 0.580 | 748 | 756 |
| 1P LF | 0.688 | 737 | 746 |
| New HF | 0.228 | 767 | 744 |
| New LF | 0.153 | 774 | 721 |
Fits of the Diffusion Model to Data
We display fits in two reasonably standard ways. The first shows quantile-probability plots in which the 0, .1, .3, .5, .7, and .9 quantile RTs are plotted vertically (Figure 1 for lexical decision). This provides information about how accuracy changes across the conditions of an experiment that differ in difficulty and how shapes of distributions change. The shapes could be seen (approximated) by drawing equal-area rectangles between the quantile RTs, as shown in the bottom right panel of Figure 1. The .1 quantile represents the leading edge of the distribution and the .9 quantile represents the tail of the distribution. The median (.5 quantile) is the middle row. The change in mean RTs across conditions is mainly a spread in the distributions, for both lexical decision and item recognition.
Figure 1.
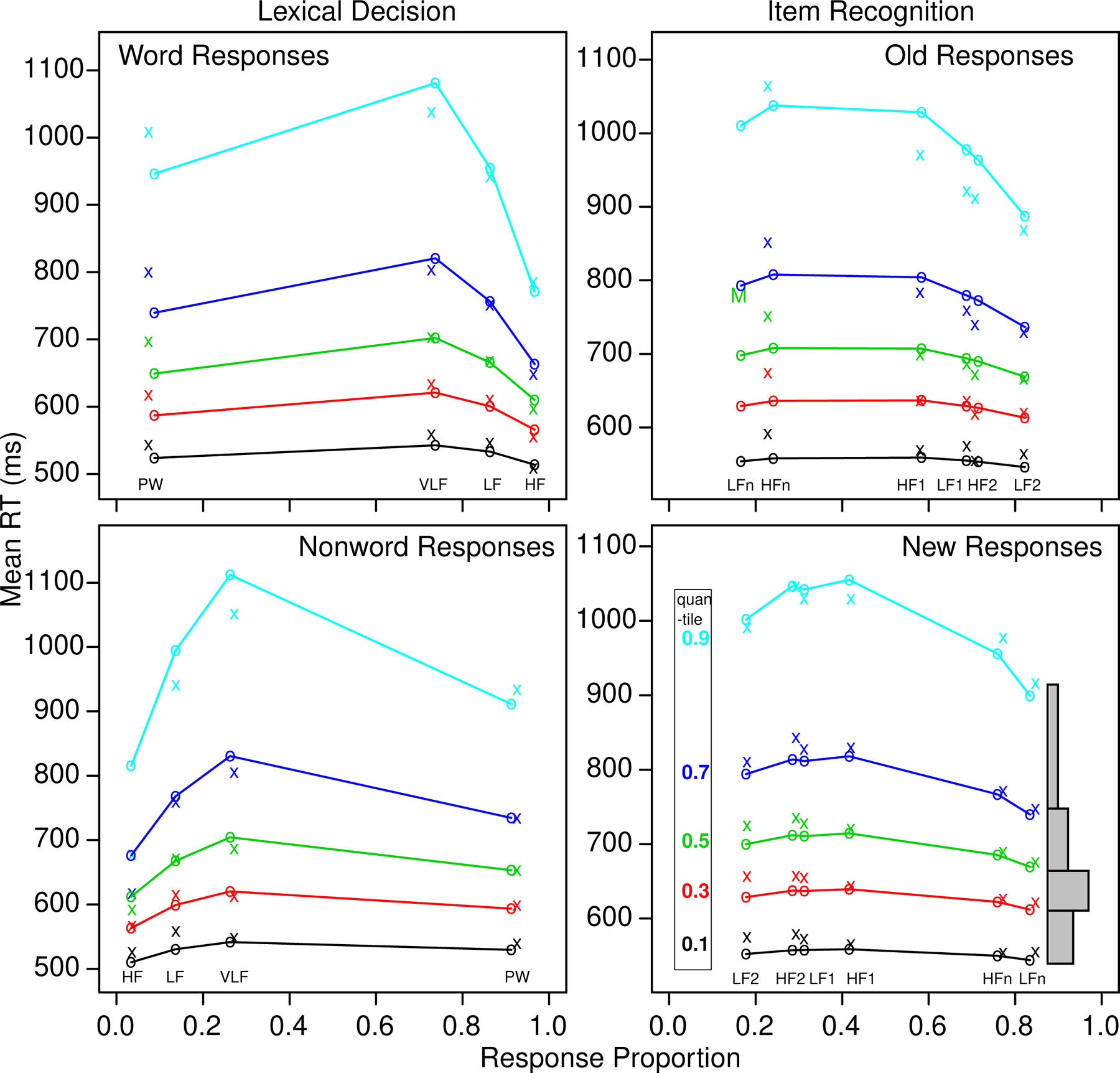
Quantile probability plots for the lexical decision and item recognition tasks for data and model predictions averaged over subjects in the same way. The x’s are the data and the o’s are the predictions joined by the lines. The five lines stacked vertically above each other are the values predicted by the diffusion model for the 0.1, 0.3, 0.5, 0.7, and 0.9 quantile RTs as a function of response proportion for the conditions of the experiments. The quantiles are labeled on the left-hand side of the bottom right plot and equal-area rectangles drawn between the quantiles are shown on the right side of that plot (which represent RT distributions). The M in the top right plot shows the median RT because some subjects did not have enough error responses for low frequency “new” words to compute quantiles.
The diffusion model fit the data from both lexical decision and item recognition well. The G-square multinomial likelihood function is distributed as chi-square and so we can compute the critical chi-square values. For the lexical decision task, the value was 48.6 and for the item recognition task, it was 72.2. The mean values of G-square are close to the critical value, which indicates a good fit of the model to data (see Ratcliff et al., 2010). The average quantiles from the fits to individual subjects (averaged in the same way as the data) are shown in Figure 1 and show little deviation between theory and data.
The second kind of way to display fits of the model to data is that shown in Figures 2 and 3. Accuracy and the .1, .5, and .9 quantile RTs are shown for every subject and every condition, including error RTs for conditions with more than 10 observations. These show no systematic deviations between theory and data.
Figure 2.
Plots of accuracy, the 0.1, 0.5 (median), and 0.9 quantile correct response times (RTs) for every subject and every condition for the lexical decision task. For the quantiles, only values are presented from conditions with over 15 observations. The two SDs in the quantile RTs are computed from a bootstrap method, and for probability (that plots both correct and error probabilities and so has redundancy), they are based on binomial probabilities.
Figure 3.
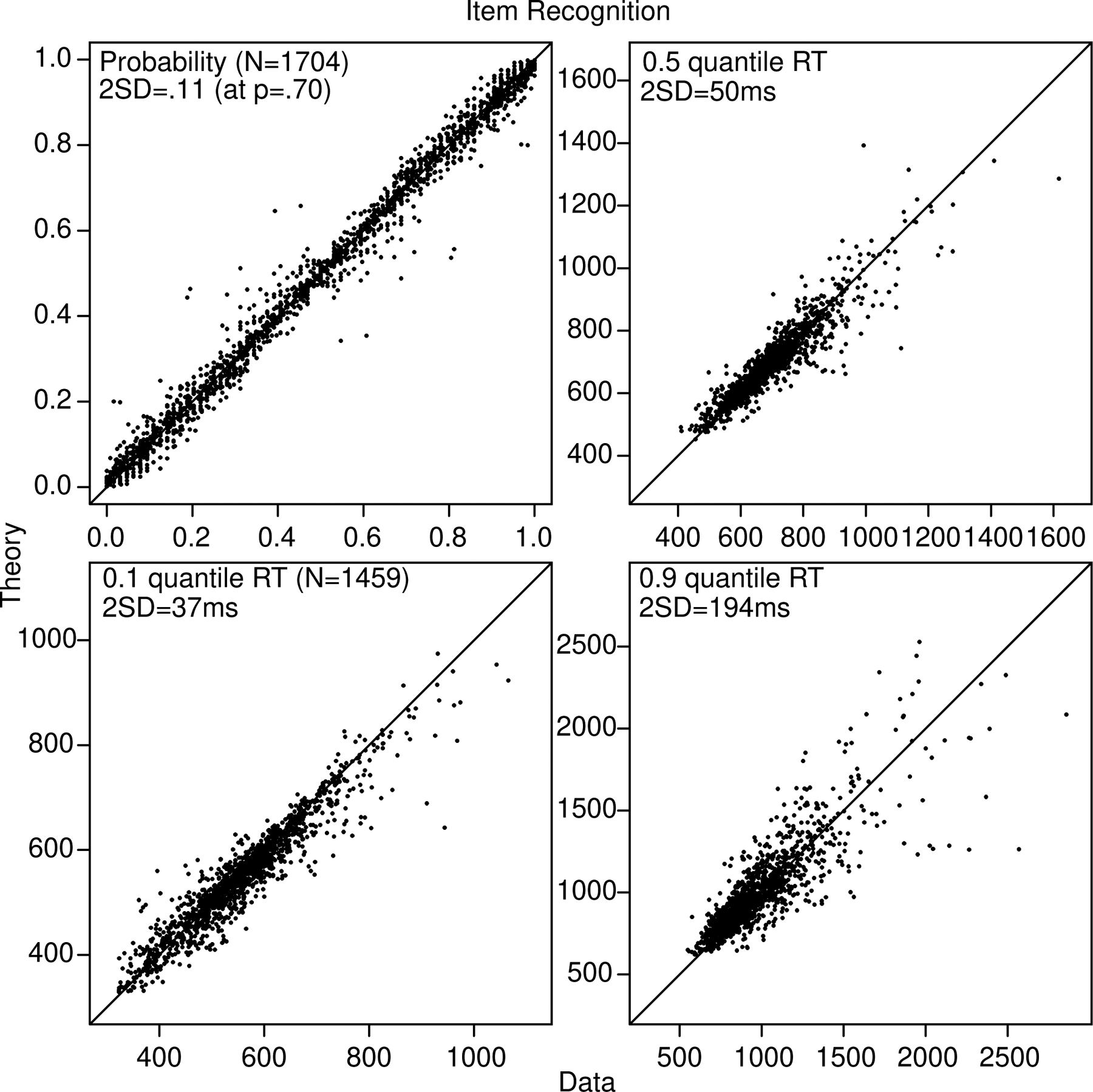
The same plot as in Figure 2 for the item recognition data and model fits.
The 2SDs shown in Figures 2 and 3 are not confidence intervals (i.e., not plus or minus 2 SD). The SD’s for probability were computed from sqrt(p(1-p)/N) with a representative value of p shown in the figure. The SDs in quantiles were computed using a bootstrap method in which the RTs for each condition were sampled with replacement 100 times, the quantiles were computed, and the SDs in the 100 values of each quantile were computed.
The parameters from the best fit of the model to data are shown in Tables 3 and 4. The mean age of the subjects was 35.5 years which is older than the college age subjects in Ratcliff et al. (2010) that we will use as our comparison group (the distribution of ages is shown later). For both tasks, nondecision time was about 40–50 ms longer for our subjects than the young adults in Ratcliff et al. (and about 100 ms shorter than the 60–90 year olds), boundary separation was smaller (by about 0.03), and across-trial variability in drift rate and starting point were both smaller.
Table 3:
Diffusion model parameters for the four tasks from Experiments 1 and 2
| Task (and subject group) | a | T er | η/σ1 | s z | s t | z | G2/χ2 | df |
|---|---|---|---|---|---|---|---|---|
| Lexical decision | 0.122 | 0.482 | 0.051 | 0.037 | 0.128 | 0.061 | 45.2 | 34 |
| Item recognition | 0.111 | 0.535 | 0.126 | 0.043 | 0.191 | 0.055 | 76.4 | 54 |
| Lex dec (RTM 2010, college) | 0.157 | 0.429 | 0.139 | 0.072 | 0.149 | 0.080 | 97 | |
| Lex dec (RTM 2010, 60–74) | 0.204 | 0.539 | 0.113 | 0.028 | 0.154 | 0.095 | 79 | |
| Lex dec (RTM 2010, 75–90) | 0.213 | 0.572 | 0.129 | 0.040 | 0.143 | 0.101 | 77 | |
| Item rec (RTM 2010, college) | 0.141 | 0.489 | 0.230 | 0.063 | 0.189 | 0.069 | 100 | |
| Item rec (RTM 2010, 60–74) | 0.170 | 0.632 | 0.237 | 0.037 | 0.194 | 0.074 | 92 | |
| Item rec (RTM 2010, 75–90) | 0.182 | 0.643 | 0.214 | 0.031 | 0.200 | 0.077 | 88 | |
| BY (“good”) | 0.100 | 0.499 | 0.0607 | 0.049 | 0.252 | 0.050 | 229.4 | 212 |
| Y25 (“good”) | 0.097 | 0.441 | 0.0322 | 0.053 | 0.154 | 0.051 | 121.6 | 122 |
| BY (“bad”) | 0.115 | 0.468 | 0.0750 | 0.068 | 0.258 | 0.057 | 244.8 | |
| Y25 (“bad”) | 0.100 | 0.451 | 0.0339 | 0.058 | 0.209 | 0.053 | 145.0 | |
| BY (R&M 2018) | 0.114 | 0.446 | 0.066 | 0.083 | 0.266 | a/2 | 261 | 212 |
| Y25 (R&M 2018) | 0.102 | 0.386 | 0.027 | 0.076 | 0.203 | 0.054 | 301 | 252 |
good subjects, BY η0=0.064, Y25 η0=0.040, vc=−0.040
bad subjects, BY η0=0.048, Y25 η0=0.076, vc=−0.048
Table 4:
Drift rate parameters for the four tasks from Experiments 1 and 2
| Task (and subject group) | v1 | v2 | v3 | v4 | v5 | v6 |
|---|---|---|---|---|---|---|
| Lexical decision | 0.417 | 0.224 | 0.119 | −0.270 | ||
| Item recognition | 0.175 | 0.296 | 0.064 | 0.149 | −0.186 | −0.281 |
| Lex dec (RTM 2010, college) | 0.457 | 0.227 | 0.127 | −0.240 | ||
| Lex dec (RTM 2010, 60–74) | 0.412 | 0.238 | 0.141 | −0.253 | ||
| Lex dec (RTM 2010, 75–90) | 0.437 | 0.280 | 0.169 | −0.249 | ||
| Item recog (RTM 2010, college) | 0.159 | 0.334 | 0.052 | 0.168 | −0.266 | −0.328 |
| Item recog (RTM 2010, 60–74) | 0.196 | 0.297 | 0.040 | 0.138 | −0.291 | −0.352 |
| Item recog (RTM 2010, 75–90) | 0.192 | 0.271 | 0.044 | 0.113 | −0.249 | −0.317 |
| BY (“good”) | 0.0304 | 0.0141 | ||||
| Y25 (“good”) | 0.0375 | 0.0379 | ||||
| BY (“bad”) | 0.0222 | 0.0100 | ||||
| Y25 (“bad”) | 0.0340 | 0.0337 | ||||
| BY (R&M 2018) | 0.037 | 0.016 | ||||
| Y25 (R&M 2018) | 0.031 | 0.032 |
Boundary separation was smaller in this experiment likely because these AMT subjects prioritized speed and we know that boundary separation is adjustable (Ratcliff, Thapar, & McKoon, 2001, 2003, 2004). Drift rates in Ratcliff et al. (2010) did not differ much over age group and the drift rates for both experiments in this study were quite similar to the those for the three age groups in the Ratcliff et al. study.
In Ratcliff et al. (2010) the boundary separation, nondecision time, and drift rate parameters were found to correlate across subjects in the three tasks used in that study. IQ, but not age, was correlated with drift rates. Boundary separation and nondecision time differed as a function of age but not IQ (ages were distributed over 20–70 in these data, in Ratcliff et al., young and older groups were used with none in the 30–60 year old range). In Figure 4 we present scatter plots and correlation coefficients for the various combinations (for both tasks) of the values of the model parameters, accuracy and mean RT values, as well as age and IQ. The diagonal of Figure 4 shows distributions for each of these values. The results replicate those of Ratcliff et al. (2010). First, boundary separation, nondecision time, and drift rate each correlate between the two tasks as do mean RT and accuracy. The correlations range from 0.47 to 0.76, all highly significant with 131−2=129 degrees of freedom. Boundary separation and nondecision time correlated with each other but neither correlated with drift rates. Age correlated with mean correct RT for the two tasks and more strongly with nondecision time but less strongly with boundary separation. IQ correlated with accuracy for the two tasks and with drift rates for the two tasks. Drift rates correlate with accuracy and mean RT correlated with boundary separation and nondecision time.
These results show a strong replication of the main results from Ratcliff et al. (2010). This means that for these tasks, the AMT subjects provide results that are quite similar to those from subjects that were tested individually by research assistants monitoring the task in Ratcliff et al. This picture changes for the numerosity tasks.
RTs Across the Session
An aspect of data usually not reported in studies in psychology is the stability of RTs across a session for a given task. If regimes change over trials, then aggregating data across trials or blocks of trials can give an incorrect picture of the data and incorrect values for the parameters of any model that is fit to the data. In the lexical decision and item recognition tasks, by and large, RTs were stable, but in the numerosity tasks, as we see later, they were not for many of the subjects.
After some exploration, we found that the simplest way to examine stability across a session was to plot a time series of the RTs for every trial. This mixes all conditions and correct and error responses so there will be a spread of RTs over trials, but for stable performance, the spread of RTs should not change systematically over the session.
Figure 5 shows plots of RTs across the session for a sample of 25 subjects that includes the least stable subjects and a sample of stable subjects. Plots for all the subjects are shown in the supplement.
Figure 5.
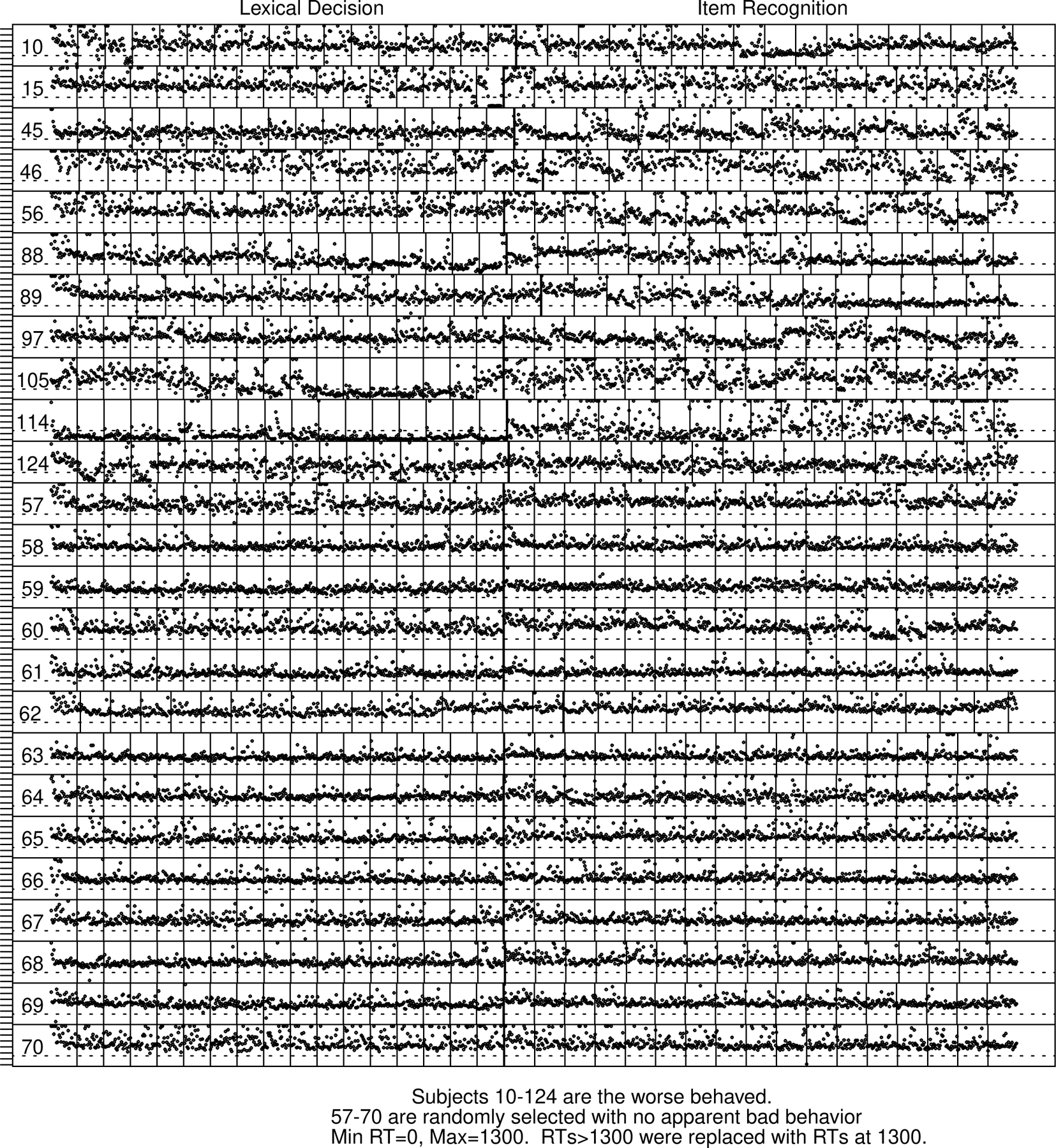
Plots of every RT across the session for the lexical decision and item recognition tasks.
The numbers on the left are the subject numbers in the order analyzed. The vertical thick (double) lines in the middle of the plot represent the point at which the task switched from lexical decision to item recognition. The thin vertical lines represent blocks of trials (when they do not align, the subject did not finish all the trials). The dashed horizontal line is at 300 ms and serves as an approximate way of identifying fast guesses (an RT below this is almost certainly a fast guess, RTs above but close to it may be fast guesses). Long RTs greater than 1300 ms are replaced by 1300 ms (this was done so that the focus could be on the shorter RTs).
Subjects 10, 15, 45, …, 124 are bad subjects for the lexical decision and item recognition tasks with some large vertical excursions for groups of trials. For brevity (and to be evocative), we label subjects as “bad” and “good.” Subjects 57–70 are good subjects, i.e., those without many vertical deviations in the RT distribution across the session. The sample in Figure 5 was hand selected, but plots for all subjects are shown in the supplement. The bad subjects were excluded from the model analyses presented above based on examination and identification of fast guessing. The criteria for identifying the 10 bad subjects were: 5 percent or more of their responses were shorter than 300 ms and their accuracy for these responses was at chance for at least one of the two tasks.
One feature that jumps out from the data from some of the bad subjects is an occasional run of fast guesses with RTs under 300 ms (and accuracy at chance, shown in other analyses). When this occurs, the whole RT distribution shifts down to produce RTs a little higher or lower than 300 ms with very little spread. This is damaging for model-based analyses because it produces a high proportion of fast guesses which stretches the leading edge of the RT distributions thus distorting model fits to the data. Sometimes what appears to be a high proportion of errors from a condition for a subject can be fast guesses. In Figure 5, the vertical lines represent trial blocks and the thick (double) lines in the middle of a session represent the switch from the lexical decision task to the item recognition one. Most of the vertical lines align, but those that do not come from subjects who finished all but a few blocks of trials.
Subjects 105 and 114 show extreme numbers of fast guesses, especially in the lexical decision task. Subject 105 has 10 blocks of lexical decision trials (the 8th through the 16th blocks) with most responses fast guesses. The subject also has large changes in RTs within individual blocks in the item recognition task. Subject 114 has most RTs in lexical decision less than 300 ms and some blocks in item recognition with RTs less than 300 ms. Subjects 10, 45, 46, 56, 88, 89, 97, and 124 show moderate to large shifts in RTs across trials in item recognition with RTs falling to fast guesses in some blocks for most of these subjects.
In the supplement, we show plots for all the subjects in this experiment and the corresponding ones in Ratcliff et al. (2010). There are many more trials per task in Ratcliff et al’s. experiment, and there are only 2 subjects that show instability of the kind for the bad subjects in Figure 5. Subjects 89 and 123 in lexical decision (Ratcliff et al., 2010) show instability, but because there were about 2000 observations in the session for the lexical decision task, eliminating half of the trials left enough data to produce good quality model fits. These subjects showed stable performance in the item recognition task.
One might wonder why subjects in the Ratcliff et al. (2010) experiment had performance that was so stable. There are three possible reasons. First, the subjects had practice for at least half a session on a lexical decision task prior to the three other experiments and this could have allowed them to calibrate. Second (and perhaps more important) they were tested by a research assistant who stayed and observed the individual throughout a session. If they began to change performance in a noticeable way (e.g., fast guessing or slowing down a lot), the research assistant would give verbal feedback between blocks of trials. Third, the subjects were paid well ($18 per session in today’s dollars - which included a travel allowance) and they were tested for four sessions in the experiment and so they were motivated to perform properly because a failure to perform properly would result in loss of pay.
Experiment 2
This experiment also consisted of three tasks, either the Cattell Culture-Fair IQ test or the math fluency test and the two numerosity tasks (the BY and Y25 tasks). The order of the parts of the experiment was first the Cattell test (52 subjects) or the math test (114 subjects), second the BY task, and third the Y25 task. Each of these began with instructions. For the BY and Y25 tasks, there were four examples of stimuli that stayed on the screen until a button was pressed, with text specifying the correct response above the stimulus. Subjects pressed the space bar to see each example and then to begin the blocks of test trials. Each test item was displayed for 300 ms.
Following a response (which could be made during the 300 ms stimulus display), either “correct” or “ERROR” was displayed for 250 ms, then the screen returned to the gray background, and then 250 ms later the next test item was displayed. The test items were displayed for only 300 ms to reduce the possibility that subjects might use slow strategic search processes to perform the task (as discussed in Ratcliff & McKoon, 2018).
In the BY task, blue and yellow dots were intermingled in an array (Figure 4A in Ratcliff & McKoon, 2018) and subjects decided which color had the larger number of dots, pressing the “/” key for yellow and the “z” key for blue. The arrays varied in the numerosities of their dots and the differences between their numerosities. There were 10 combinations of the numbers of blue and yellow dots; 15/10, 20/15, 25/20, 30/25, and 40/35 for differences of 5; 20/10, 30/20, and 40/30 for differences of 10; and 30/10 and 40/20 for differences of 20. The summed areas of the dots of the two colors were either proportional to numerosity or equal to each other; if proportional, they were randomly selected from the 6 dot sizes which produced a larger summed area for the larger numerosity color. If equal, the dots were selected such that the total areas of blue and yellow were the same and so the areas of individual dots were larger for smaller numerosities. Thus, there were 20 conditions in the experiment, 10 pairs of numerosities crossed with 2 area conditions. There were 8 blocks of 100 trials with each condition represented five times in a block. The first 24 trials were eliminated from data analyses, as was the first trial of each block.
In the Y25 task, yellow dots were displayed in a single array (Figure 4F, random arrangement, in Ratcliff & McKoon, 2018). The number of dots in an array was 10, 15, 20, 30, 35, or 40. As for the BY task, there was an area manipulation. Either the dot sizes of an array were selected randomly from the six possibilities so that area was proportional to numerosity, or the dots were selected such that the summed area of the dots in an array was equal to the average area of 25 dots randomly selected. With the six numerosities and the two area conditions, there were 12 conditions in the experiment.
Subjects were instructed to press the “z” key if the number of dots was less than 25 and the “/” key if the number was greater than 25. There were 8 blocks of 96 trials with each condition presented 8 times per block. As for the BY task, we eliminated the first 24 trials in the Y25 task and the first trial in a block as warmup/practice.
Accuracy and RT Results
Before working with the data, we eliminated six subjects who either hit one response key most of the time or who responded at chance through the whole session, leaving 166 subjects. We then eliminated 74 out of the 166 subjects for whom 5 percent or more of their responses were shorter than 300 ms and their accuracy for these responses was at chance for at least one of the two tasks. This left 32 good subjects out of 52 that performed the Cattell test and 60 good subjects out of 114 that performed the math test. We also present analyses and model fits for the data from the bad subjects as reported below.
For the BY task, the data for “blue” and “yellow” responses were symmetric so correct responses for blue and yellow dots were combined and errors for blue and yellow dots were combined. The results replicate those of Ratcliff and McKoon (2018, 2020). Mean RTs and accuracy values collapsed over the area variable are shown in Table 5. Accuracy decreased as the difficulty of the test items increased, that is, as the numerosity of the dots increased and the difference between the numerosities decreased, the standard results with these manipulations. Also as expected, equal-area stimuli were more difficult than proportional-area stimuli, with accuracy higher and RTs shorter with equal-areas.
Table 5:
Accuracy and correct and error mean RTs for the BY and Y25 tasks from Experiment 2 (averaged over the area variable).
| Numerosity | Accuracy | Correct mean RT | Error Mean RT |
|---|---|---|---|
| 15/10 | 0.644 | 709 | 685 |
| 20/15 | 0.635 | 680 | 670 |
| 25/20 | 0.632 | 683 | 660 |
| 30/25 | 0.612 | 675 | 650 |
| 40/35 | 0.598 | 661 | 647 |
| 20/10 | 0.735 | 678 | 646 |
| 30/20 | 0.707 | 663 | 630 |
| 40/30 | 0.675 | 661 | 627 |
| 30/10 | 0.799 | 645 | 603 |
| 40/20 | 0.768 | 642 | 592 |
| Numerosity | Pr “large” | Mean RT “large” | Mean RT “small” |
| 10 | 0.102 | 576 | 564 |
| 15 | 0.157 | 568 | 589 |
| 20 | 0.359 | 589 | 622 |
| 30 | 0.850 | 583 | 580 |
| 35 | 0.904 | 563 | 543 |
| 40 | 0.917 | 557 | 518 |
Most salient, the results replicated a counter-intuitive finding by Ratcliff and McKoon (2018, 2020). For a constant difference of five between the numbers of dots (15/10, 20/15, 25/20, 30/25, and 40/35), as the total number of dots increased, RTs decreased. In other words, as difficulty increased, accuracy decreased, as would be expected, but responses sped up, counter the usual finding that increased difficulty leads to longer RTs. This result is shown in Table 5.
For the Y25 task, the data show the usual (not counter-intuitive) finding that RTs increase and accuracy decreases as difficulty increases. But in this task, unlike the BY task, the area variable had almost no effect on performance, again replicating Ratcliff and McKoon (2018). There was also a bias to call small numerosities “large” with greater probability than to call large numerosities “small” (Table 5). This means that responses were not quite symmetric around 25 but instead biased toward “large” responses. For example, the probability of responding “large” to 30 dots was 0.85 and 0.86 for equal- and proportional-area stimuli, respectively, and the probability of responding “small” to 20 dots was 0.64 and 0.66 for equal- and proportional-area stimuli, respectively.
The area variable had a strong effect on performance in the BY task, but almost no effect in the Y25 task: Averaging over all the numerosity conditions, accuracy and mean RT for the BY task for proportional area were 0.733 and 657 ms and for equal area they were 0.628 and 682 ms. For the Y25 task, the values were 0.841 and 578 ms for proportional area and 0.843 and 578 ms for equal area. These numbers replicate the results from Ratcliff and McKoon (2018).
Diffusion Model Fits
In the lexical decision and item recognition tasks, there were different drift rates for each condition, four for lexical decision and six for item recognition. But for the numerosity tasks, we used a model (Ratcliff & McKoon, 2018) for the cognitive representations of numeracy to determine drift rates directly from the numerosities of the arrays (see also Kang & Ratcliff, 2020, for a more detailed model-based analysis of interaction between numeric and non-numeric variables).
This model is taken from the numerical cognition literature (e.g., Gallistel & Gelman, 1992). The model assumes that numeracy is represented on a linear scale with a normal distribution around each value. As numerosity increases, the means of the values and their standard deviations increase linearly. This makes the model consistent with Weber’s law, which states that as intensity increases, the size of the just-noticeable difference between stimuli increases so that the ratio of the difference in intensity to intensity (ΔS/S) remains constant.
Ratcliff and McKoon used this model to provide drift rates, and the standard deviations (across-trial variabilities) of them, to the diffusion model. In other words, the diffusion model served as a meeting point that translated the predictions of the linear model into accuracy and RT data.
In more detail, for the BY task, Ratcliff and McKoon (2018) assumed that drift rates are a coefficient (v1) multiplied by the difference between the blue and yellow numerosities, i.e., v=v1(N1-N2). In order to deal with different levels of accuracy for equal- and proportional-area stimuli, difference coefficients are used for the equal-area conditions and the proportional-area conditions. Because the SD’s increase linearly, across-trial SD in drift rates is the square root of the sum of the squares of the two SD’s multiplied by a coefficient, σ1 (and we add a constant, η0). Thus, η=σ1sqrt(N12-N22)+η0.
This model explains the counterintuitive result that for a constant difference in numerosity between the blue and yellow dots (e.g., 5), as the SD increases, accuracy decreases but so do RTs. Figure 6 shows two distributions of drift rate with values of accuracy and mean RT as a function of single drift rate values (using parameters from the good subjects in the BY task, Table 3). For the dashed distribution with a small SD, accuracy is an average over drift rates between 0 and 0.2 with accuracy values between 0.5 and 0.86 with RTs between 728 and 680 ms (also weighted by the height of the drift rate distribution). For the solid distribution with a larger SD, accuracy is an average over drift rates between −0.2 and 0.4 with accuracy values between 0.14 and 0.97 with RTs a weighted average over values from 659, to 728, to 616 ms. However, the longer RTs in the left tail are weighted less than the shorter RTs in the right tail because they are weighted by accuracy values of 0.14 and 0.29 while the short RTs of 644 ms and 616 ms are weighted by accuracy values of 0.93 and 0.99 (and by the height of the normal distribution). This produces lower RTs for the wider distribution than the narrow distribution (see also Ratcliff & McKoon, 2018, Figure 8).
Figure 6.
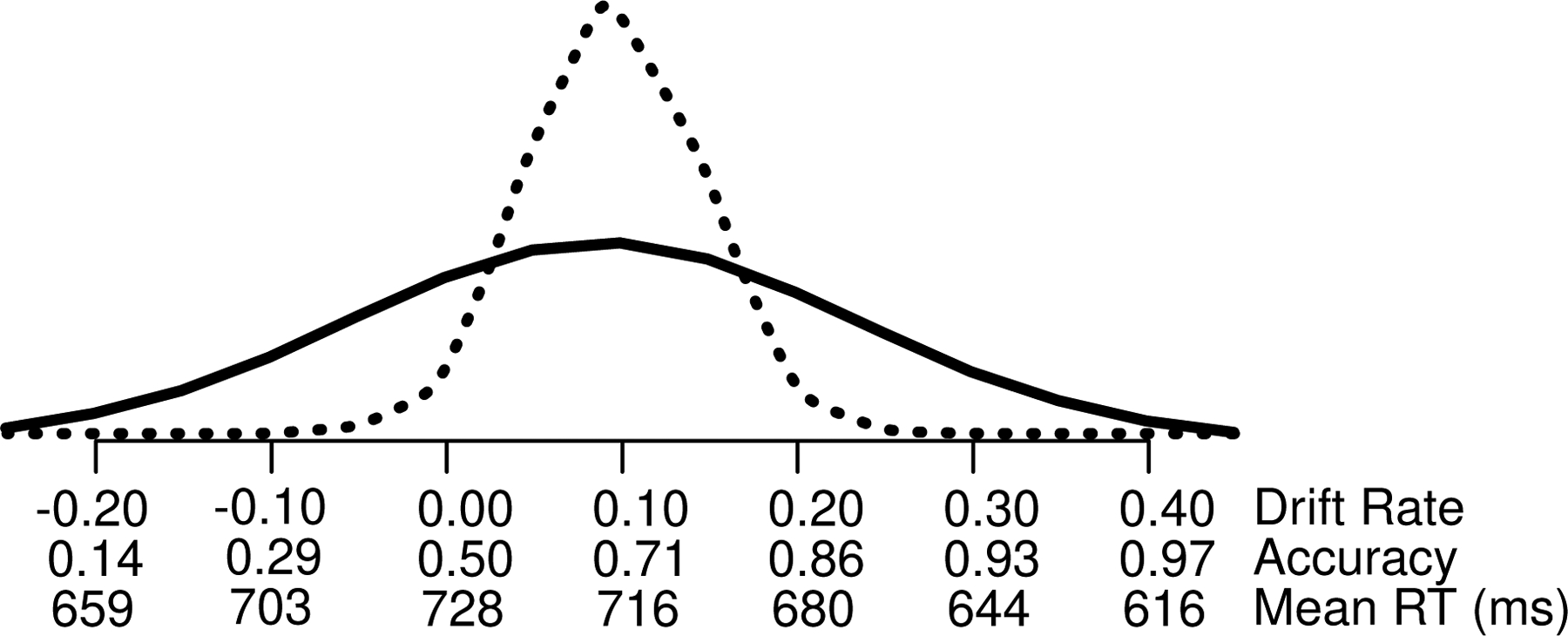
Two distributions of drift rate (with larger and smaller SD’s) and values of accuracy and mean RT corresponding to the values of drift rate on the x-axis.
Figure 8.
Plots of accuracy, the 0.1, 0.5 (median), and 0.9 quantile correct response times (RTs) for every subject and every condition for the BY task as for Figure 2.
The assumptions that drift rate and across trial SD in drift rate are functions of the numbers of dots in the displays reduce the number of parameters considerably. Instead of 20 different drift rates for the BY task (for the 10 different numerosity conditions crossed with the 2 area combinations) and 20 different values of across-trial SD in drift rate, there are two drift rate coefficients (one for each area condition) and one SD coefficient and one constant across-trial SD in drift rate which reduces the number of drift-rate parameters from 40 to 4.
For the Y25 task, one of the numerosities (e.g., N2) is set to 25. For this task, there is also one more parameter, the drift-rate criterion (Ratcliff, 1985). When asked to decide whether the number of dots in an array is more or less than 25, then drift rates should be such that their mean is toward the “large” boundary when there are more than 25 dots and toward the “small” boundary when there are fewer than 25. That is, the drift-rate criterion should be set at 25. However, subjects may set their criterion at 24 or 26 or some other number; if so, there will be a bias in how the numerosity of the dots is interpreted in encoding and transforming the representation to drift rate. It is to accommodate this bias that the drift-rate criterion is a free parameter for the Y25 task.
To fit the model to data for the BY task, we first used a 300 ms lower cutoff for the RTs. This resulted in consistent systematic misfits for many of the good subjects with predicted .1 quantile RTs shorter than those for the data by 30–40 ms on average. This led us to examine the data for each subject and to determine a lower cutoff RT for each individual, below which accuracy was at chance. The accuracy values and RT quantiles were recomputed based only on the data for RTs above these lower cutoffs. This produced good fits with only small deviations between theory and data.
The model misses the leading edge for data with the 300 ms cutoff because there are moderately large excursions up and down (e.g., 30–40 ms) in the 0.1 quantile RTs for some of the 20 experimental conditions, even for the good subjects. This occurs because there are relatively few observations per condition in this experiment (e.g., 40 per condition for the BY task). By random chance, if several very short RTs occur, then this would produce a very short 0.1 quantile RT. If this happens even only once out of the 20 conditions, the fitting method still has to accommodate this short RT quantile and it does this by reducing nondecision time and by increasing the range of nondecision time (across trials). This produces predictions for the other 19 conditions that have predicted leading edges (0.1 quantile RTs) lower than those for the data. Then, averaging over subjects, the result is that the model predicts lower .1 quantile RTs than the data.
This is a warning that for fitting RT models, there needs to be enough data per condition or else model fit and parameter estimates will be compromised. This is the same problem as for maximum likelihood fitting methods discussed in Ratcliff and Tuerlinckx (2002).
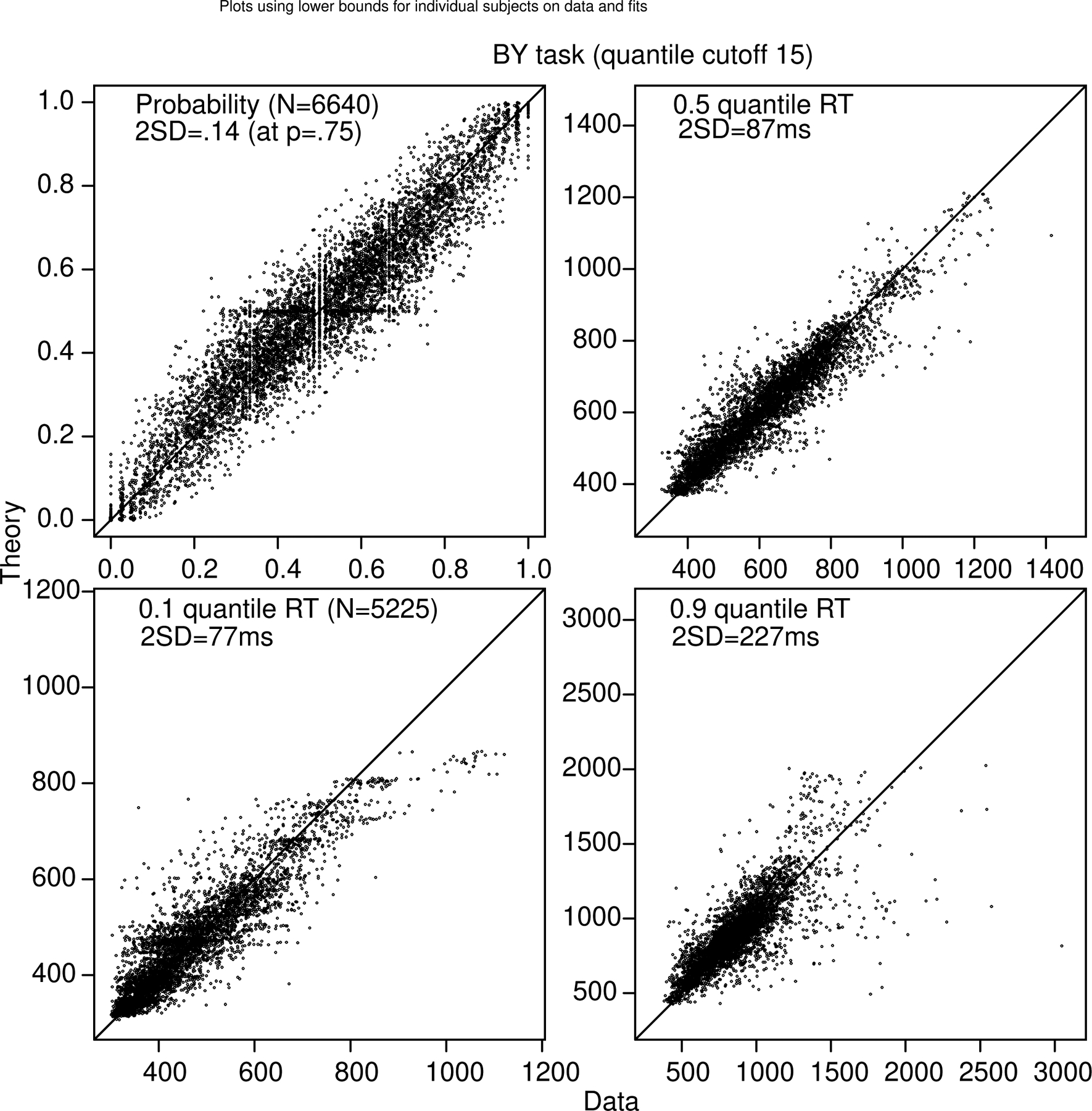
Figure 7 shows quantile probability functions for the BY task from the 92/166 subjects (both those that completed the Cattell test and those that completed that math test) that we labeled as good and the 74/166 subjects that we labeled bad, both using individualized lower bounds for each subject (these were chosen by eye by examining the accuracy of fast responses and determining at what point accuracy rose above chance - this was done blind to whether the model fit missed the data with the fixed bounds across all subjects). Across all subjects, the minimum lower bound was 300 ms, the mean was 478 ms, and the maximum was 700 ms (this excluded 6.7% of the data). The first important result is that the data replicated the counterintuitive pattern of RTs across all the quantiles: for a constant difference of 5, as total numerosity increases, accuracy decreases, but RT also decreases counter to what might be expected. This occurs for the good subjects and the bad subjects and for the equal-area and proportional-area conditions. The good subjects have higher accuracy (by about .1) and longer RTs for the .1 quantile RTs and shorter RTs for the .9 quantiles. We think because this is because of increased variability for the bad subjects (see the next section). It was surprising that other than the accuracy difference, it is hard to see any qualitative difference in the patterns of results between theory and data for the two groups of subjects.
Figure 7.
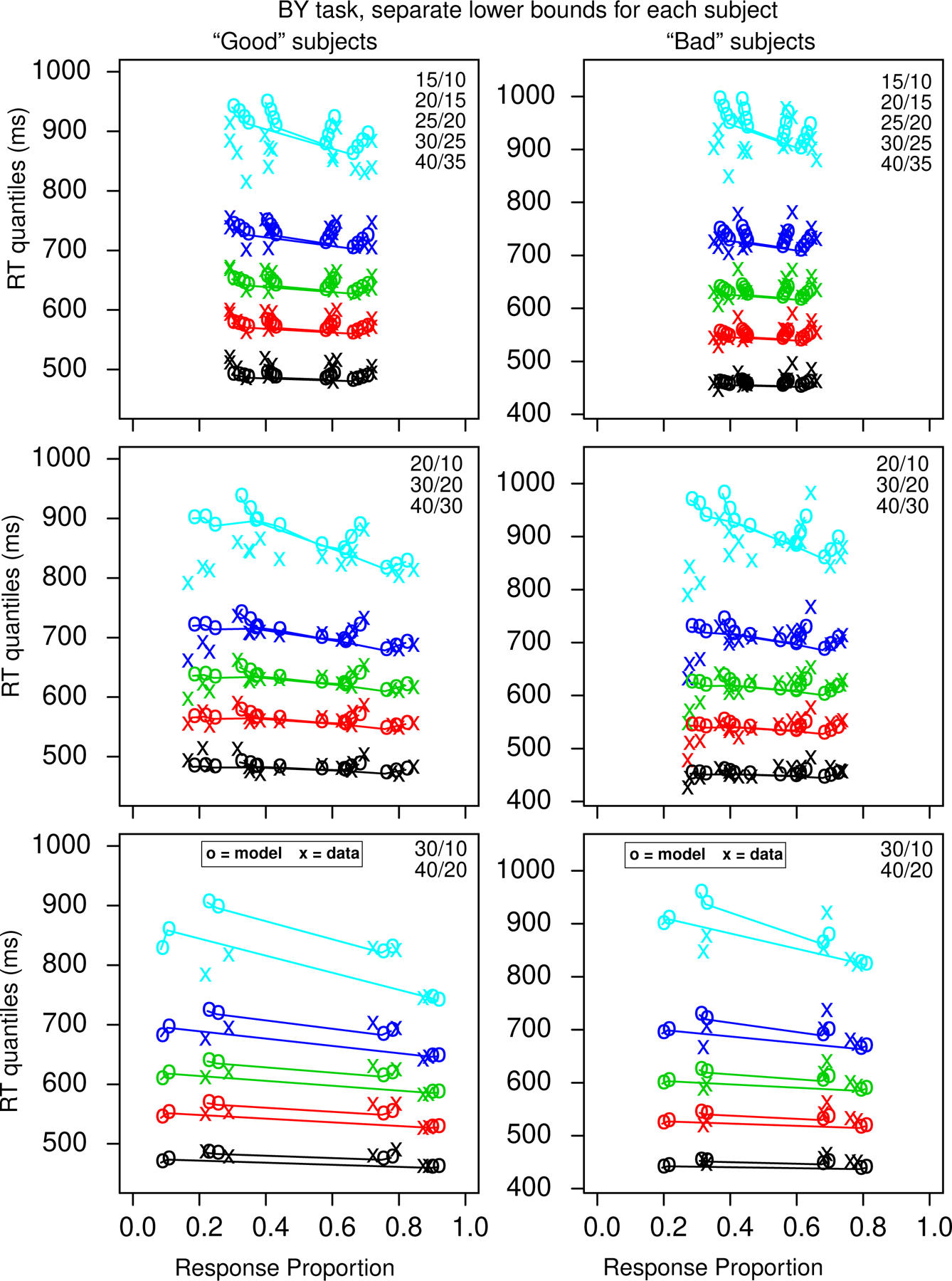
Quantile-probability functions for the BY task for the “good” subjects, left column, and “bad” subjects, right column. These plot RT quantiles against response proportions (correct responses to the right of 0.5 and errors to the left). The green/central lines are the median RTs. The number of dots in the conditions in the plots is shown in the top right corner, with the top one in each condition corresponding to the right-hand point in the plot. The more extreme functions are for proportional-area conditions, and the less extreme for equal-area conditions. In a number of cases for the difference of 20 conditions, some subjects had no errors which means that those error quantile RTs (for data) could not be computed and so are not plotted.
Figure 8 shows plots of data and predictions for accuracy and quantile RTs for all conditions and subjects for the BY task. The variability is higher than in Figures 2 and 3 because of the much lower numbers of observations per condition. The results show little bias between theory and data.
Figure 9 shows quantile probability functions for the good and bad subjects for the Y25 task with quantiles computed from individualized lower RT bounds for each subject. As for the BY task, the two groups of subjects are fit by the model reasonably well. There is one deviation between theory and data, and that is that the model underpredicts accuracy for “large” responses to large stimuli. Figure 10 shows plots of data and predictions for accuracy and quantile RTs for all conditions and subjects for the Y25 task. The spread in the data/predictions is smaller than for the BY task because the number of observations is almost twice as large. Again, there are few systematic deviations between theory and data.
Figure 9.
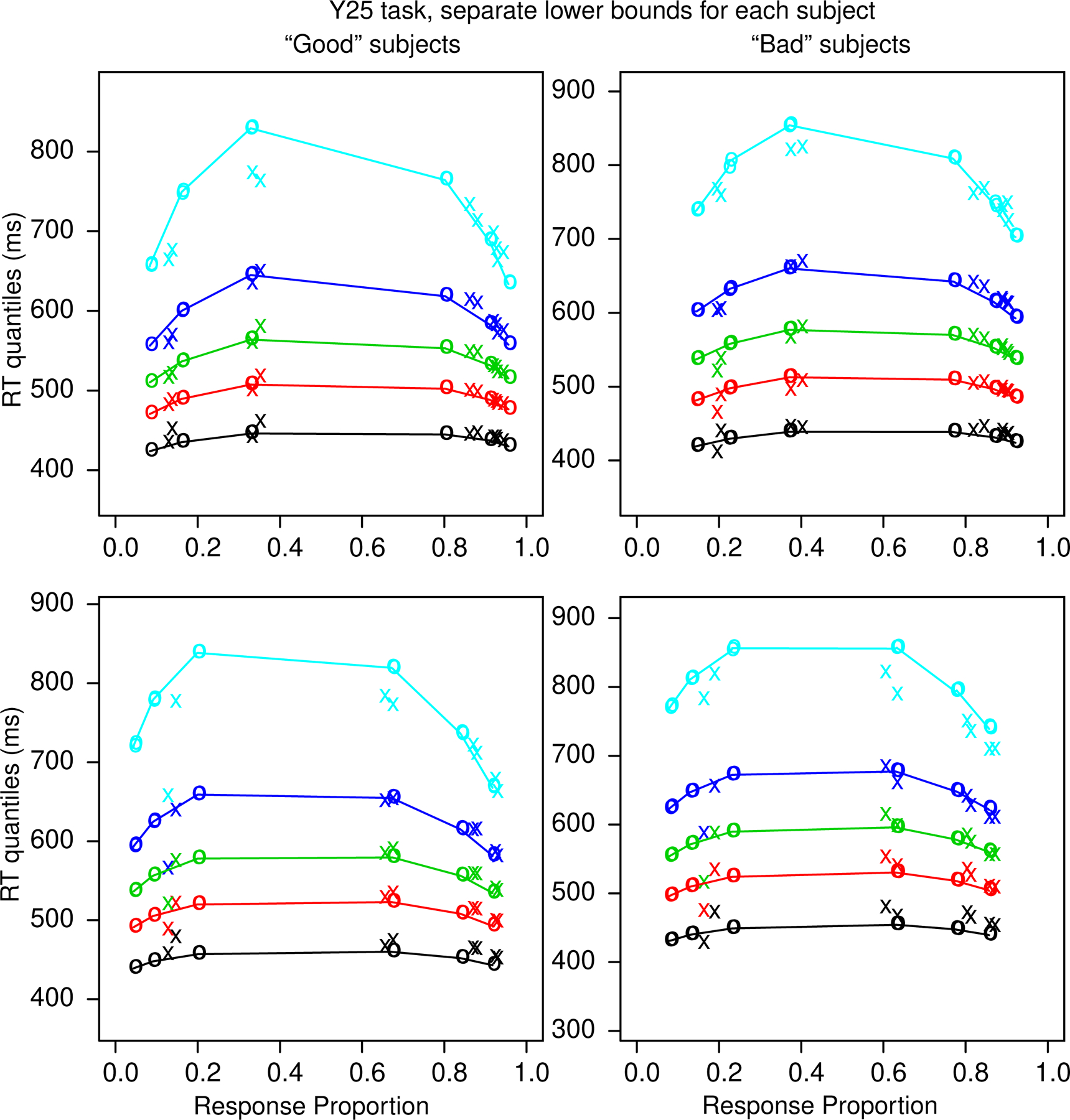
Quantile-probability functions for the Y25 task for the “good” subjects, left column, and “bad” subjects, right column as for Figure 6. Note that for the model predictions there are pairs of circles for the equal-area and proportional-area conditions, but the predictions are so close together that the points almost overlay each other.
Figure 10.
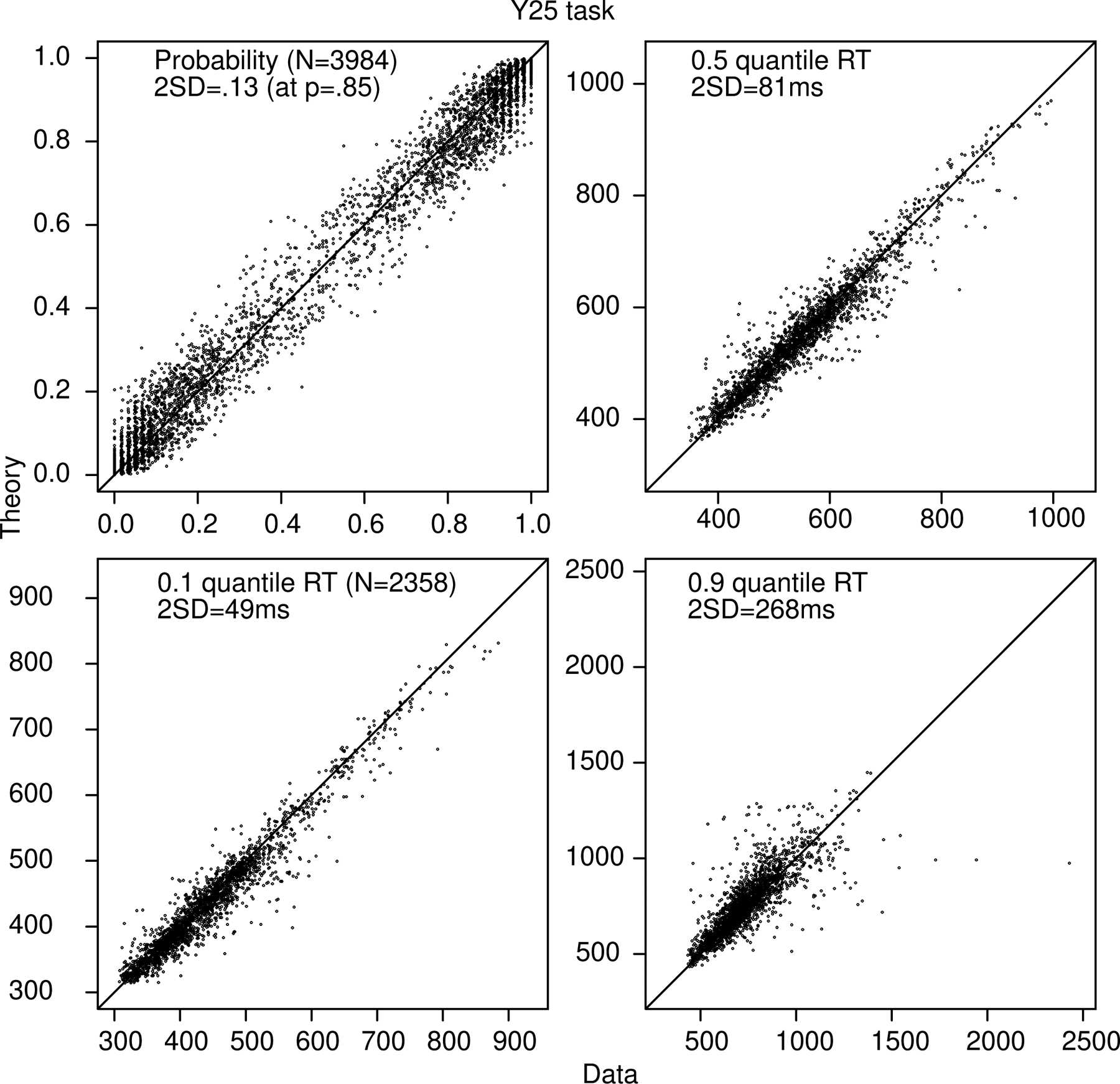
Plots of accuracy, the 0.1, 0.5 (median), and 0.9 quantile correct response times (RTs) for every subject and every condition for the Y25 task as for Figure 2.
The diffusion model parameters for both the BY and Y25 tasks for both the good and bad subjects are shown in Tables 3 and 4. The values are similar to those in Ratcliff and McKoon (2018). The only large difference was that nondecision time in Ratcliff and McKoon was about 50 ms shorter than the values in Table 3. Mean G-square goodness of fit values were a little lower than the chi-square critical values (which were 247.0 for the BY task and 148.8 for the Y25 task). These values were lower than those in Ratcliff and McKoon, partly because of the smaller numbers of observations per subject in this study (if there is a difference between observed and expected frequencies, then this is magnified in G-square as the number of observations increases).
In Ratcliff and McKoon (2018), results from BY tasks produced drift rate coefficients that were twice as large for the proportional-area than the equal-area conditions. Figure 5 shows this with the data x’s for the equal-area conditions with lower accuracy (shifted to the left) than those for the proportional-area conditions. In contrast, there was almost no effect of area in the Y25 task as shown in Figure 9. Table 4 shows the drift rate coefficients for the two tasks and for the good and bad subjects. There was a large effect of area (2:1) in the BY task, and no measurable effect on the Y25 task for both subject groups replicating the results from Ratcliff and McKoon. The drift rate coefficients also show that the difference between the good and bad subjects is much larger for the BY task than the Y25 task.
We performed a similar correlational analysis as for Experiment 1 to examine the relationship between model parameters, accuracy and RT values, and age. Figure 11 shows scatter plots, correlations, and histograms (as in Figure 4) for the 92 subjects we identified as good.
Boundary separation, nondecision time, and drift rate correlate between the two tasks, as do mean RT and accuracy. The values range from 0.47 to 0.78, all highly significant with 90 (92−2) degrees of freedom. Boundary separation and nondecision time did not correlate with each other but nondecision time correlated with drift rate coefficients. Mean RTs correlated strongly with nondecision time and only weakly with boundary separation. Accuracy was strongly correlated with the drift rate coefficients. Age was not correlated with RTs, boundary separation, or nondecision time. This was surprising because this relationship (especially with nondecision time) has been robust and reported many times (as in Experiment 1).
We also performed the correlational analysis on the data and model parameters from the 74 “bad” subjects (a plot is shown in the supplement). The correlations were remarkably similar and Figure 12 shows the values of the correlations (e.g., the numbers above the diagonal on the right of Figure 11) for all combinations of model parameters as in Figure 11 for the good subjects plotted against those for the bad subjects. The result is a strong linear relationship so, for example, if there was a high correlation between, say, Ter for the good subjects (e.g., 0.79) then there was a high correlation for the bad subjects (0.70). The major deviations between the two sets of correlations are in the bottom left corner and these correspond to moderate differences in the correlations for boundary separation with other model parameters for the two tasks. Other than these, the correlations for the two sets of data are mainly within or close to 0.2 of each other (Figure 12). This is surprising because it shows that the diffusion model analysis and data produce similar results for individual differences even when the subjects are not behaving well, i.e., there is enough regularity in the data even when there are large fluctuations in how subjects perform the task.
Figure 12.
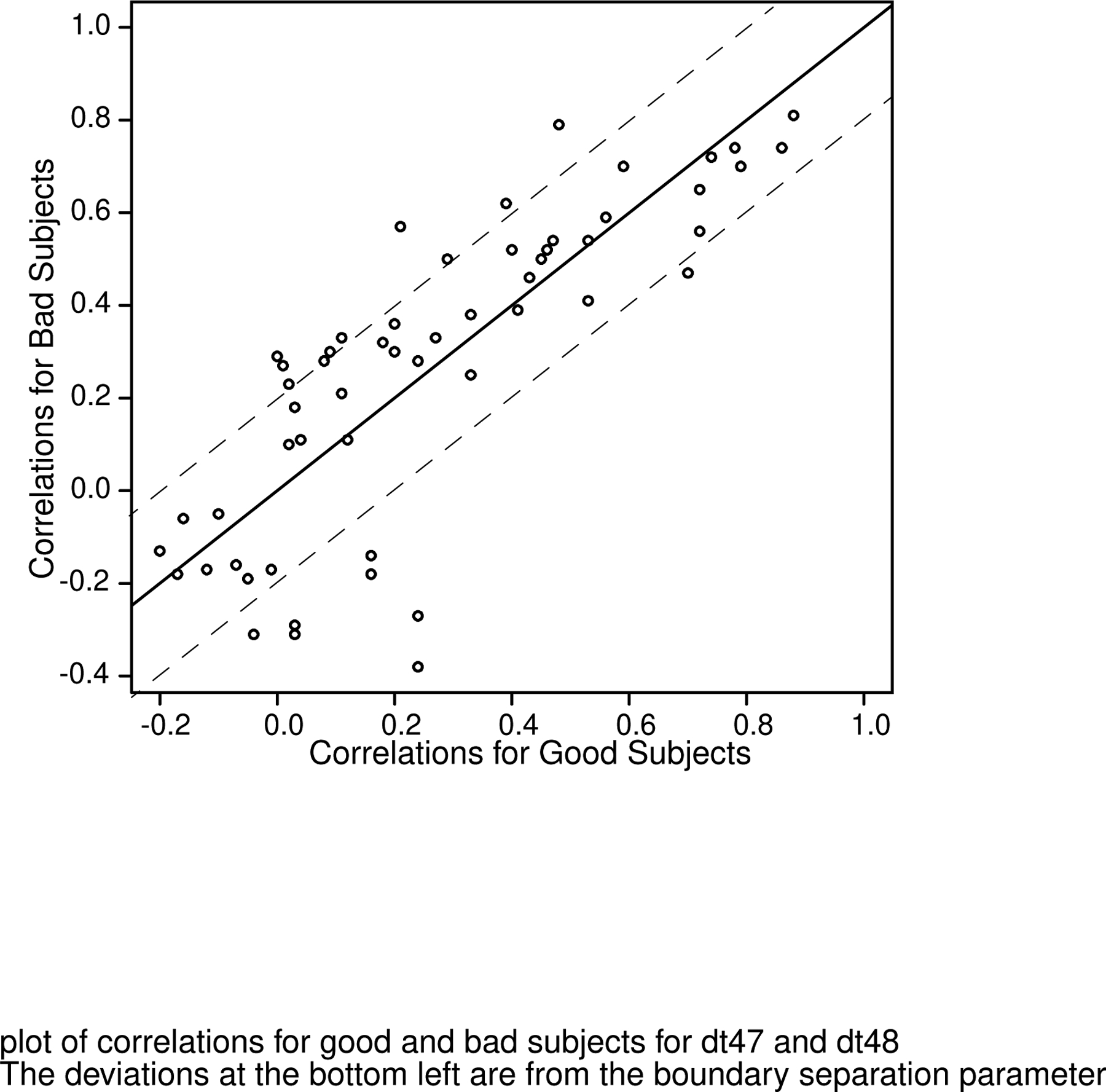
Plots of the correlation coefficients from Figure 10 (above the diagonal) against the same correlations for the “bad” subjects. The dashed lines are parallel to the line with slope 1 and are values of the correlation 0.2 above that line and 0.2 below it.
The IQ and the math test measures and age did not produce the moderate correlations with accuracy, mean RT, and diffusion model parameters that we obtained in Experiment 1. This is not likely a problem with estimation of diffusion model parameters because the parameters and accuracy and mean RT show strong and reliable relationships within and between tasks as in Experiment 1. The largest correlations for IQ (32 good subjects) were with accuracy (for the BY and Y25 tasks, 0.39 and 0.37) and drift rate coefficients (0.25 and 0.22) and all other correlations were below 0.3. For the math test, all correlations for the 60 good subjects were below 0.3.
RTs Across the Session
In Figure 13, we present the same kinds of plots for the two numerosity discrimination tasks as those for Experiment 1 in Figure 5. The vertical lines represent trial blocks and the thick (double) lines in the middle of each session represent the switch from the BY task to the Y25 task. Most of the lines align vertically, but those that do not come from subjects that did not quite finish all the blocks of trials in the session. To help see what responses may be fast guesses, a horizontal dashed line at 300 ms is drawn in each plot. Most responses with RTs below this represent fast guessing and this shows up as chance performance in regular analysis with an upper cutoff of 300 ms.
Figure 13.
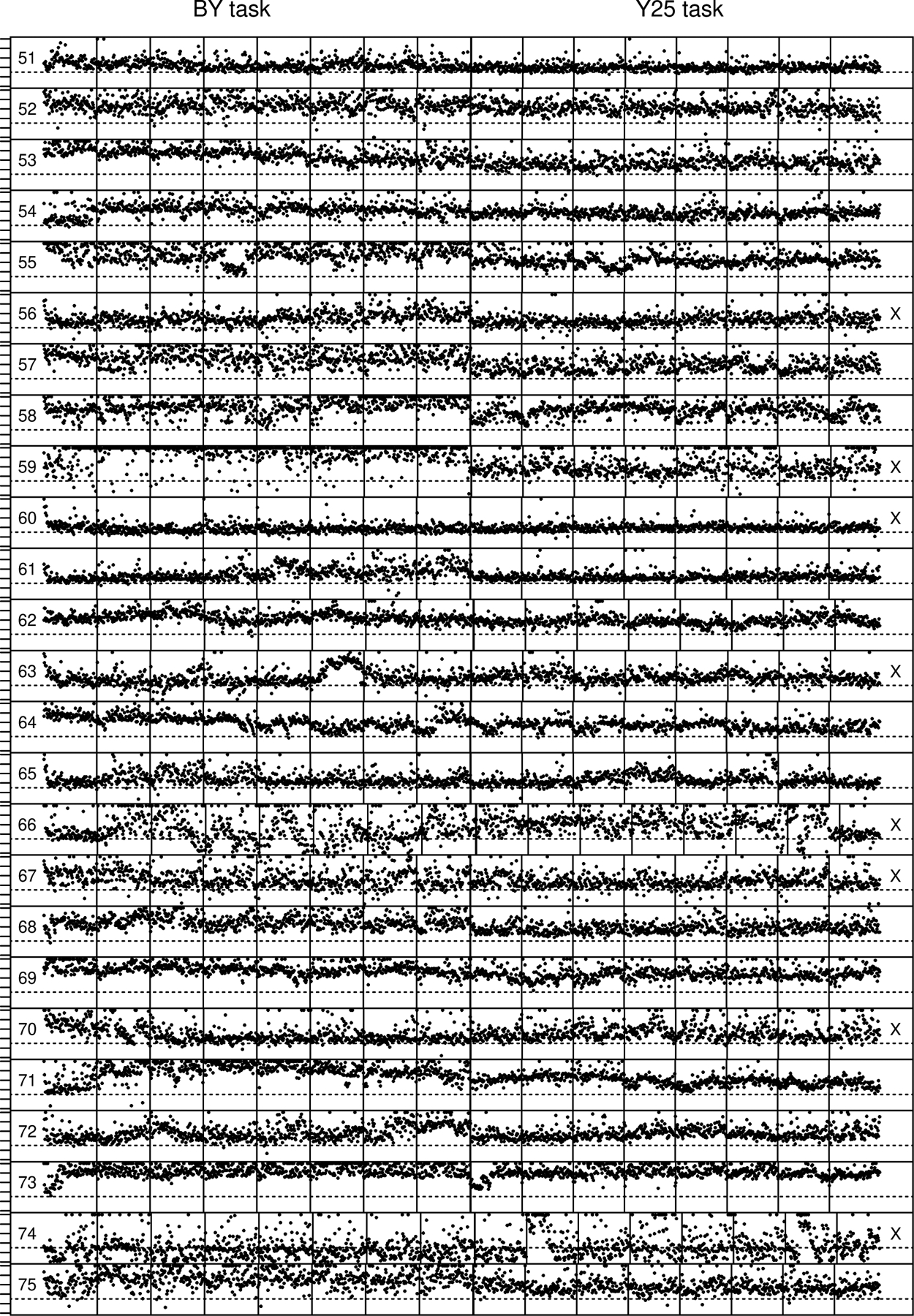
Plots of every RT across the session for the BY and Y25 tasks (see Figure 5). The numbers on the left are the subject number in the order analyzed and the “x” on the right denotes “bad” subjects. The dashed horizontal line is at 300 ms and serves as an approximate way of identifying fast guesses and long RTs greater than 1000 ms are replaced by 1000 ms.
The most important thing to note is that the data are considerably less stable across and within blocks than the data for Experiment 1. Some subjects provide relatively well-behaved data, that is, with stable response times across blocks. But a high proportion (45% by eye) show relatively unstable performance. Some subjects have RTs drifting up and down across blocks of trials and some subjects have this kind of behavior even within blocks of trials. Also, some subjects show sudden large excursions up and down. It is easy to argue that some subjects such as number 66 are trying out different processing strategies with a number of excursions in RTs below 300 ms (fast guesses). Other subjects are simply misbehaving, for example, number 74, with a large proportion of fast guesses.
To quantify the variability, we present the average SDs in correct RTs averaged over conditions and subjects with a lower cutoff of 300 ms and an upper cutoff of 4000 ms. For the BY task, for good subjects SD=179 ms, for bad subjects SD=245 ms and for the Y25 task, for good subjects SD=135 ms, for bad subjects SD=201 ms. This shows an overall increase in the SD in RT of over 60 ms for bad subjects relative to good subjects for both tasks.
We believe that these fluctuations are the result of the subject trying out different ways to perform the task to see what happens if they slow down, go fast, or guess. This may occur for these numerosity tasks for any of several reasons. First, the tasks are difficult and accuracy is relatively low. This may encourage subjects to try out different speed and accuracy regimes to see if they can improve performance. Second, low accuracy might cause some subjects to give up and fast guess. Third, because presentation duration is limited to 300 ms, some subjects may try using this as a cue to respond for a run of trials which would produce fast guessing. Fourth, even if the subject is moderately accurate, he or she might explore the decision space by adjusting speed/accuracy settings thus producing longer or shorter decision times.
These results show problems with the data from these AMT subjects, even taking into account that the subjects have been in many other AMT experiments. But a surprising result was that when fast guesses were trimmed out, data patterns, diffusion model analyses and fits to data, and individual differences were similar to those from the good subjects (but with lowered accuracy).
Discussion
The results from the AMT subjects replicated the four sets of benchmark findings from the original laboratory-based studies (Ratcliff & McKoon, 2018; Ratcliff et al., 2010), across four tasks: lexical decision, item recognition, and two numerosity discrimination tasks. In addition to replicating the empirical patterns in the data, the best-fitting parameters for the diffusion model had similar patterns and ranges (with a few marked differences, for example, nondecision times in Ratcliff et al. were 489, 632, and 643 ms for item recognition and 429, 539, and 572 ms for lexical decision for young adults, 60–74 year olds, and 75–90 year olds, compared with 535 ms for item recognition and 482 ms for lexical decision in the Table 3). Importantly, similar patterns of correlations among model parameters across pairs of tasks were also replicated in the on-line studies. Finally, as in the laboratory-based studies, individual differences in age and IQ were related to accuracy, mean RTs, and diffusion model parameters for lexical decision and item recognition in similar ways to those in Ratcliff et al. (2010). However, IQ, age, and math scores correlated only weakly with model parameters for the numerosity tasks (which were not examined in Ratcliff & McKoon, 2018, 2020).
For lexical decision and item recognition, most of the data were of good quality with only a few subjects producing many fast guesses and/or unstable performance across a session. In contrast, for the numerosity tasks, 45% of the subjects produced many fast guesses (with over 5% of RTs less than 300 ms and at chance accuracy). These subjects also showed instability in responding across a session. There are several possible reasons for this. First, the numerosity tasks are difficult and without an experimenter to guide them, some subjects may try speeding up or slowing down to see if either of these could improve performance. Second, subjects might try fast guessing to see if this helps speed up the experiment. Third, the limited stimulus duration might encourage subjects to try to respond shortly after the offset of the stimulus.
The criteria we suggest for eliminating fast guesses are these: If a large proportion of a subject’s responses have RTs shorter than a low cutoff value and have chance accuracy, then that subject should be eliminated. Several cutoffs should be used to determine the point at which accuracy begins to be above chance (see Ratcliff, 1993). The values of the cutoffs will be a function of a task, for example, longer values for cognitive tasks with longer RTs and shorter values for perceptual tasks with shorter RTs.
Plots of RTs across trials can be used be to examine the stability of responses across a session. If instability across a session is high with the distribution of RTs moving up and down (longer and shorter RTs, or with the distributions compressing and expanding, or with runs of fast guesses (as identified as above), then these subjects might also be eliminated. An example of this kind of instability is subject 105 in Figure 5 who produced about 8 blocks of lexical decision trials with mainly fast guesses and had increasing RTs within blocks in item recognition. This kind of instability produces higher variances in RTs than for subjects who do not show this instability (e.g., Bridges, et al., 2020). There are many more such examples in Figure 13 and in the full set of plots in the supplement. These methods should, of course, be used independent of (without looking at) the hypotheses being tested.
Some researchers may want to link the fluctuations in RTs to long-range correlations in RTs across a session such as might be examined in analyses of 1/f noise (e.g., Gilden, 2001; Wagenmakers, Farrell, & Ratcliff, 2004; Van Orden, Moreno, & Holden, 2003). But it is important to understand whether the fluctuations are automatic and are not the result of conscious strategic changes in the way the task is performed, or whether the subject is experimenting with the task by seeing what happens if they slow down or go fast. If the subject is deliberately trying different strategies, then such fluctuations will be of much less interest than if they were automatic fluctuations in processing.
The model-based analysis for the BY task in Experiment 2 involved exploration of ways to deal with subjects and data after finding systematic deviations between fits to data in the 0.1 quantile RTs because of low numbers of observations per condition. Our best guess for an analysis was one that trims RTs at values that are different for each subject based on the time at which his or her accuracy begins to rise above chance. If a reader does not like the analyses with separate lower bounds for each subject, at least they illustrate potential problems in data and provide a starting point for alternative analyses. In contrast, the fits to data from Experiment 1 used standard methods and did not need separate cutoffs for each subject because of the larger numbers of observations per condition.
Instability over a session produces distortions in data with wider RT distributions than those in local stable regions of responding. What was surprising is that accuracy, RT, and diffusion model analyses produced quite similar patterns of results across conditions for the good and bad subject groups. This is probably because bad data (e.g., 20%) from large fluctuations in RTs can be overwhelmed by good data (e.g., 80%) once fast guesses are eliminated. Before it can be claimed that modeling is robust to bad data in general, this need to be replicated and generalized to tasks other than those used here. Despite this apparent robustness, the diffusion model parameters may be distorted because data would be averaged, for example, over different speed- accuracy settings.
The finding that patterns of results are similar for data from good and bad subjects should not be used to justify the use of bad data in model comparisons. Instability in data could easily produce biases toward one or another model. Thus it is important to eliminate subjects with unstable data for model comparisons (at the very least, such subjects should be identified and examined separately in model comparisons).
Overall, the results from these two experiments and four tasks show that accuracy and RT data from AMT subjects along with diffusion model analyses of those data replicate results from experiments with carefully controlled in-person data collection. However, the results also showed serious problems with data from subjects for whom there were large fluctuations in the location of RT distributions over runs of trials. In many cases, these regions involved runs of fast guesses.
These results show that a lot of care needs to be taken in using RT data from AMT or other data collected on-line (or even laboratory experiments that have little experimenter interaction and guidance). We suggested some simple methods of identifying subjects who are not behaving in a stable manner. The use of these or similar methods should be routine in data analysis and can only help to reduce failures to replicate experimental results or model-based analyses.
Supplementary Material
Funding:
This work was supported by funding from the National Institute on Aging (Grant numbers R01-AG041176 and R01-AG057841).
Footnotes
Conflicts of interest/Competing interests:The authors have no relevant financial or non-financial interests to disclose.
Ethics approval: Approval was obtained from the Institutional Review Board of The Ohio State University. The procedures used in this study adhere to the tenets of the Declaration of Helsinki.
Consent to participate: Informed consent was obtained from all individual participants included in the study.
Code availability: The code used in this study is available at https://osf.io/za9y8/.
Open Practices Statement
Data and materials have been deposited at https://osf.io/za9y8/. The experiments were not preregistered.
Availability of data and materials:
The datasets generated during and analyzed during the current study are available at https://osf.io/za9y8/.
References
- Anwyl-Irvine AL, Massonni J, Flitton A et al. (2020). Gorilla in our midst: An online behavioral experiment builder. Behavioral Research Methods, 52, 388–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bramley NR, Gerstenberg T, Tenenbaum JB, & Gureckis TM (2018). Intuitive experimentation in the physical world. Cognitive Psychology, 105, 9–38. [DOI] [PubMed] [Google Scholar]
- Bridges D, Pitiot A, MacAskill MR, Peirce JW (2020). The timing mega-study: comparing a range of experiment generators, both lab-based and online. PeerJ, 8, e9414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattell RB, & Cattell AKS (1960). The individual or group culture fair intelligence test. Champaign: IPAT. [Google Scholar]
- Crump MJC, McDonnell JV, Gureckis TM (2013) Evaluating Amazon’s Mechanical Turk as a tool for experimental behavioral research. PLoS ONE, 8, e57410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekel R, Sagi D (2020). Perceptual bias is reduced with longer reaction times during visual discrimination. Communications Biology, 3, 59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Leeuw JR, Motz BA (2016). Psychophysics in a Web browser? Comparing response times collected with JavaScript and Psychophysics Toolbox in a visual search task. Behavioral Research Methods, 48, 1–12. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, & Gelman R (1992). Preverbal and verbal counting and computation. Cognition, 44, 43–74. [DOI] [PubMed] [Google Scholar]
- Gilden DL (2001). Cognitive emissions of 1/f noise. Psychological Review, 108, 33–56. [DOI] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MMM, & Feigenson L (2008). Individual differences in nonverbal number acuity predict maths achievement. Nature, 455, 665–668. [DOI] [PubMed] [Google Scholar]
- Hendrickson AT, Perfors A, Navarro DJ, & Ransom K (2019). Sample size, number of categories and sampling assumptions: Exploring some differences between categorization and generalization. Cognitive Psychology, 111, 80–102. [DOI] [PubMed] [Google Scholar]
- Hilbig BE (2016). Reaction time effects in lab- versus Web-based research: Experimental evidence. Behavioral Research Methods, 48, 1718–1724. [DOI] [PubMed] [Google Scholar]
- Kucera H, & Francis W (1967). Computational analysis of present-day American English. Providence, RI: Brown University Press. [Google Scholar]
- Laming DRJ (1968). Information theory of choice reaction time. New York: Wiley. [Google Scholar]
- Mason W, & Suri S (2012). Conducting behavioral research on Amazon’s Mechanical Turk. Behavior Research Methods, 44, 1–23. [DOI] [PubMed] [Google Scholar]
- Merriam-Webster. (1990). Merriam-Webster’s ninth new collegiate dictionary (9th ed.). Springfield, MA: Author. [Google Scholar]
- Ratcliff R (1978). A theory of memory retrieval. Psychological Review, 85, 59–108. [Google Scholar]
- Ratcliff R (1985). Theoretical interpretations of speed and accuracy of positive and negative responses. Psychological Review, 92, 212–225. [PubMed] [Google Scholar]
- Ratcliff R (1993). Methods for dealing with reaction time outliers. Psychological Bulletin, 114, 510–532. [DOI] [PubMed] [Google Scholar]
- Ratcliff R (1994). Using computers in empirical and theoretical work in cognitive psychology. Behavior Research Methods, Instruments and Computers, 26, 94–106. [Google Scholar]
- Ratcliff R (2008). Modeling aging effects on two-choice tasks: response signal and response time data. Psychology and Aging, 23, 900–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R (2013). Parameter variability and distributional assumptions in the diffusion model. Psychological Review, 120, 281–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R & Childers R (2015). Individual differences and fitting methods for the two-choice diffusion model. Decision, 2, 237–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20, 873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (2018). Modeling numeracy representation with an integrated diffusion model. Psychological Review, 125, 183–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (2020). Decision making in numeracy tasks with spatially continuous scales. Cognitive Psychology, 116, Article 101259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Pino C, & Burns WT (1986). An inexpensive real-time microcomputer-based cognitive laboratory system. Behavior Research Methods, Instruments, & Computers, 18, 214–221. [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2001). The effects of aging on reaction time in a signal detection task. Psychology and Aging, 16, 323–341. [PubMed] [Google Scholar]
- Ratcliff R, Thapar A & McKoon G (2003). A diffusion model analysis of the effects of aging on brightness discrimination. Perception and Psychophysics, 65, 523–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2004). A diffusion model analysis of the effects of aging on recognition memory. Journal of Memory and Language, 50, 408–424. [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2010). Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology, 60, 127–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Tuerlinckx F (2002). Estimating the parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review, 9, 438–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, & McKoon G (1999). Connectionist and diffusion models of reaction time. Psychological Review, 106, 261–300. [DOI] [PubMed] [Google Scholar]
- Semmelmann K, Weigelt S (2017) Online psychophysics: reaction time effects in cognitive experiments. Behavioral Research Methods, 49, 1241–1260. [DOI] [PubMed] [Google Scholar]
- Simcox T, & Fiez JA (2014). Collecting response times using Amazon Mechanical Turk and Adobe Flash. Behavior Research Methods, 46, 95–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slote J, Strand JF (2016). Conducting spoken word recognition research online: Validation and a new timing method. Behavior Research Methods, 48, 553–566. [DOI] [PubMed] [Google Scholar]
- Stewart N, Chandler J, & Paolacci G (2017). Crowdsourcing samples in cognitive science. Trends in Cognitive Sciences, 21, 736–748. [DOI] [PubMed] [Google Scholar]
- Van Orden GC, Moreno MA, & Holden JG (2003). A proper metaphysics for cognitive performance. Nonlinear Dynamics, Psychology, and Life Sciences, 7, 49–60. [DOI] [PubMed] [Google Scholar]
- Wagenmakers E-J, Farrell S, & Ratcliff R (2004). Estimation and interpretation of 1/f noise in human cognition. Psychonomic Bulletin and Review, 11, 579–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods AT, Velasco C, Levitan CA, Wan X, Spence C (2015). Conducting perception research over the internet: a tutorial review. PeerJ, 3, e1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and analyzed during the current study are available at https://osf.io/za9y8/.


