Real-space imaging of nanoparticle transport and interaction dynamics by graphene liquid cell TEM

Thermal motion and interactions of sub–4-nm particles are directly observed by graphene liquid cell electron microscopy.

Abstract

Thermal motion of colloidal nanoparticles and their cohesive interactions are of fundamental importance in nanoscience but are difficult to access quantitatively, primarily due to the lack of the appropriate analytical tools to investigate the dynamics of individual particles at nanoscales. Here, we directly monitor the stochastic thermal motion and coalescence dynamics of gold nanoparticles smaller than 5 nm, using graphene liquid cell (GLC) transmission electron microscopy (TEM). We also present a novel model of nanoparticle dynamics, providing a unified, quantitative explanation of our experimental observations. The nanoparticles in a GLC exhibit non-Gaussian, diffusive motion, signifying dynamic fluctuation of the diffusion coefficient due to the dynamically heterogeneous environment surrounding nanoparticles, including organic ligands on the nanoparticle surface. Our study shows that the dynamics of nanoparticle coalescence is controlled by two elementary processes: diffusion-limited encounter complex formation and the subsequent coalescence of the encounter complex through rotational motion, where surface-passivating ligands play a critical role.

INTRODUCTION

Thermal motion of colloidal nanoparticles and their coalescence in liquids have been observed in many systems (1–3). When the dimension of the medium surrounding nanoparticles is comparable to the scale of the particles, the dynamics of colloidal nanoparticle motion and coalescence can be greatly different from the dynamics in unconfined colloidal systems; even at the micrometer scale, the particle dynamics is strongly affected by medium boundaries (4–6). It has been difficult to perform a successful, quantitative investigation into nanoparticle dynamics in a confined medium. This is primarily because of the lack of appropriate methods that can directly observe individual colloidal nanoparticles in highly confined media. Furthermore, the complex, structural characteristics of colloidal nanoparticles make it difficult to explain their transport and interaction dynamics using previously proposed theoretical models developed for particles with simpler structures. Colloidal nanoparticles are passivated by ligands, usually flexible organic molecules with sizes similar to or even greater than the nanoparticle they surround (7). Those ligands can form surface layers with various disordered configurations (8, 9). This nonuniformity in the ligand shells covering a nanoparticle core can diversify interactions of a nanoparticle with the neighboring environment and other nanoparticles, which perturbs the thermal motion and coalescence dynamics of colloidal nanoparticles, causing their dynamics to be different from the dynamics of homogeneous colloidal particles without ligands. However, conventional microscopy does not provide sufficient spatial resolution required for quantitative investigation into the dynamics of ligand-passivated colloidal nanoparticles with sizes far below the optical diffraction limit.

Liquid-phase transmission electron microscopy (TEM) has recently been developed as a direct imaging method for nanoscale dynamics. Although it enables direct tracking of the individual space-time trajectories of nanoscale objects in liquid (10–12), the observed motion is often disturbed by electrostatic interactions with substrates, or the medium boundaries, which are caused by electron beam–induced substrate charging during TEM imaging (13–16). In addition, the number of observed trajectories is typically too few to capture the diverse behavior of nanoparticles. Thus, for quantitative understanding of nanoparticles dynamics, the imaging method must have subnanoscale spatial resolution, minimizing disruption of the thermal motion of nanoparticles from charged substrates, and must provide a sufficient number of trajectories for reliable statistical analysis.

To address this issue, here, we use graphene liquid cell (GLC) TEM (17, 18) to track the individual trajectories of ligand-passivated gold nanoparticles, as small as a few nanometers, undergoing thermal motion and coalescence. Thermal motion of nanoparticles exhibits a non-Gaussian displacement distribution, which is not explainable by the conventional theory of Brownian motion. In addition, the nanoparticle coalescence dynamics cannot be explained by the classical chemical kinetics or Smoluchowski’s diffusion-limited reaction kinetics. We therefore propose a new theoretical model capable of quantitatively explaining the transport and coalescence dynamics of colloidal nanoparticles. Our analysis shows that the non-Gaussian displacement distribution of nanoparticles results from dynamic fluctuations in their diffusivity. Nanoparticle coalescence can be successfully explained by a two-step model composed of the diffusion-limited formation of the nanoparticle encounter complex, mediated by surface ligands, and the subsequent coalescence of the nanoparticles.

RESULTS AND DISCUSSION

GLC TEM of nanoparticles

Thermal motion of gold nanoparticles in aqueous buffer solution encapsulated within a GLC was monitored using in situ TEM (Fig. 1A, Materials and Methods, and fig. S1). Nanoparticles are passivated by tris(4-N-methylcarbamoylphenyl)phosphine ligand molecules (19), and their diameters range from 0.8 to 4 nm (fig. S2). The nanoparticle solution is confined between two sheets of a few-layer graphene with few defects and little contamination (fig. S3). The graphene serves as an electron-transparent window, which generates little charge on its surface under electron beam illumination and acts as a scavenger capturing radicals generated from radiolysis (20).

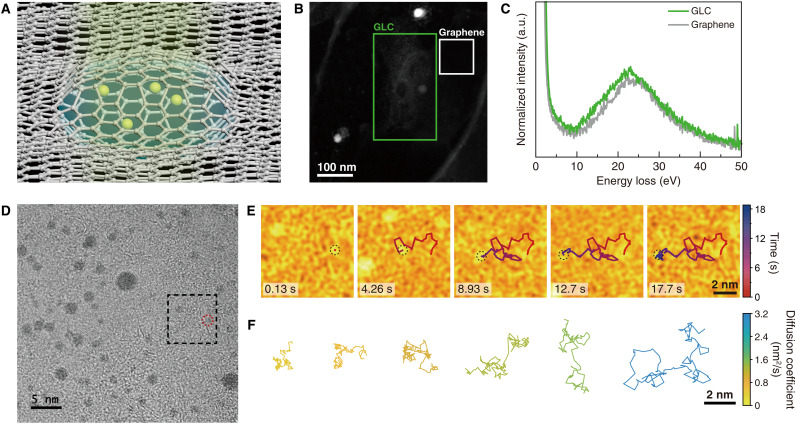
Fig. 1. Thermal motion of ligand-passivated gold nanoparticles in GLC.

(A) Schematic illustration of nanoparticles moving in a GLC. (B) Annular dark-field scanning TEM image of a GLC, where electron energy loss (EEL) spectroscopy was performed. (C) Low-loss EEL spectra of the GLC (green line) and the graphene-only region (gray line). The regions where EEL spectroscopy was performed are marked in (B). The peak at ~23 eV in the EEL spectrum of the GLC originates from the plasmon of water (23). The peak at ~25 eV in the EEL spectrum of the graphene-only region originates from the plasmon of multilayer graphene (22). a.u., arbitrary units. (D) A snapshot of the in situ TEM movie of the gold nanoparticles in a GLC. (E) False-color TEM images of the boxed region in (D), showing the random movement of the nanoparticle. (F) Representative trajectories of gold nanoparticles tracked longer than 8 s, color-coded by their diffusion coefficient (see also Fig. 2A).

The presence of water within the GLC is confirmed by transient formation of nanobubbles (fig. S4) (21) and spectroscopic measurements of the GLC (Fig. 1, B and C, and figs. S5 and S6) (22, 23). The thickness of the graphene-encapsulated liquid is estimated to be ~10 nm based on the electron energy loss spectroscopy (section S1) (24–27) and the geometrical relationship between the lateral and vertical dimensions of liquid pockets (fig. S6 and section S1) (28). The estimated liquid thickness of ~10 nm is further verified by the event where the images of three nanoparticles overlap with each other (fig. S7). We identified the hexagonal patterns of the two graphene sheets from the TEM images of the GLC (fig. S8). The hexagonal patterns would disappear for a thicker liquid pocket (fig. S9) (29–31).

In movie S1, we observed the space-time trajectories of 69 nanoparticles at an estimated dose rate of 1.0 × 10⁴ to 1.4 × 10⁴ e⁻/Ų·s (Fig. 1D, Materials and Methods, and figs. S10 to S12). The typical trajectory of a nanoparticle undergoing thermal motion is presented in Fig. 1E. Our experimental data show that the mobilities of individual nanoparticles vary substantially (Fig. 1F). The nanoparticle displacements during the experimental time resolution do not show large-step events, typically characterized by multimodal features (12) or power-law tails of the displacement distributions (fig. S12) (10, 15).

Fickian diffusion of nanoparticles in a GLC

Gold nanoparticles exhibit Fickian diffusion in our GLC. The thermal motion of the gold nanoparticles can be characterized by the time-dependent variance of the individual nanoparticle’s displacements, $\overline{\mathrm{\delta }\mathrm{\Delta }{\mathbf{r}}_{\mathit{i}}{(\mathit{t})}^2}$. Here, $\mathrm{\delta }\mathrm{\Delta }{\mathbf{r}}_{\mathit{i}}(\mathit{t})[=\mathrm{\Delta }{\mathbf{r}}_{\mathit{i}}(\mathit{t})-\langle \overline{\mathrm{\Delta }\mathbf{r}(\mathit{t})}\rangle ]$ denotes the deviation of the ith nanoparticle’s displacement from the mean displacement, $\langle \overline{\mathrm{\Delta }\mathbf{r}(\mathit{t})}\rangle$, at a given time lag, t, where the upper bar and the bracket respectively represent the time average and the average over the ensemble of nanoparticle trajectories (figs. S13 to S15; see section S2 for details). The time ensemble–averaged variance, $\langle \overline{\mathrm{\delta }\mathrm{\Delta }\mathbf{r}{(\mathit{t})}^2}\rangle$, of the nanoparticle displacement linearly increases with time, indicating that the nanoparticles in the GLC undergo Fickian diffusion during our observation (Fig. 2A, black symbols). The mean diffusion coefficient of the nanoparticles, 〈D〉, is estimated to be 0.12 nm²/s by using the relation $\langle \overline{\mathrm{\delta }\mathrm{\Delta }\mathbf{r}{(\mathit{t})}^2}\rangle =4\langle \mathit{D}\rangle \mathit{t}$ in two dimensions (Fig. 2A, black line). This value is far smaller than the diffusion coefficient value, ~10⁸ nm²/s, calculated by the Stokes-Einstein relation and the viscosity of bulk water. In addition, we observed that nanoparticle mobility does not show any noticeable dependence on the electron flux (fig. S16), indicating that charges and radicals produced by electron beam–induced reactions within the GLC do not perturb nanoparticle mobility. We also investigated thermal motion of oleylamine-passivated Pt nanoparticles suspended in an o-dichlorobenzene solvent and found that this system also exhibits Fickian diffusion with a small diffusivity, i.e., 〈D〉 ≅ 0.073 nm²/s (fig. S17 and movie S2). These consistent results observed across different nanoparticle colloidal systems suggest that the retarded Fickian diffusion of nanoparticles with a diffusion coefficient far smaller than the prediction of the Stoke-Einstein relation occurs in a spatially confined environment, regardless of solvents and ligands surrounding nanoparticles (32, 33).

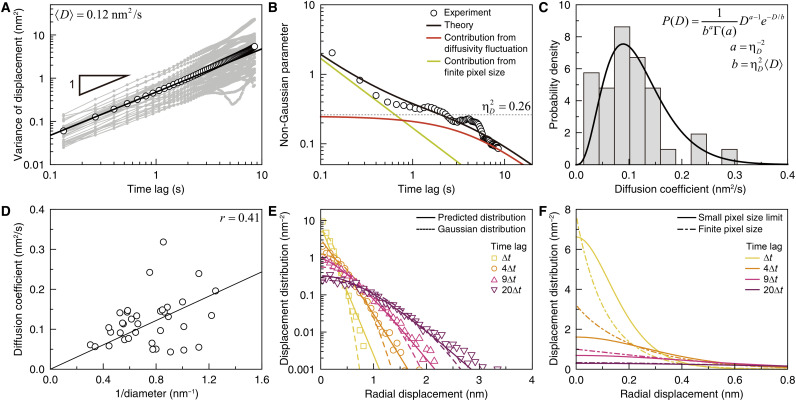
Fig. 2. Transport dynamics of gold nanoparticles in GLC.

(A) Single-particle variance (gray symbols) and time ensemble–averaged variance (black symbols) of nanoparticle displacements. (Black line) Best fit by 4〈D〉t. (B) Non-Gaussian parameter (NGP) of the nanoparticle displacement. (Symbols) Experimental data. (Black line) Optimized theoretical estimation of the experimental data according to Eq. 1A. (Red and green lines) Theoretical estimations of the contribution from diffusion coefficient fluctuation and the contribution from the finite pixel size of the TEM detector. (Dotted line) Relative variance, ${\mathrm{\eta }}_{\mathit{D}}^2=0.26$, of nanoparticle diffusion coefficients. The relaxation time of diffusion coefficient fluctuation is found to be 3.58 s. (C) Distribution of the diffusion coefficients of nanoparticles, measured from the single-particle variances at times shorter than 1 s. The single-particle variances are presented in (A). (D) Inverse size dependence of nanoparticle diffusion coefficient. (Line) Stokes-Einstein relation. (E) Distributions of nanoparticle displacements at various times. (Symbols) Experimental data. (Dashed lines) Gaussian distributions calculated with the time ensemble–averaged variance of nanoparticle displacements in (A). (Solid lines) Theoretical prediction made by Eq. 1B. (F) Theoretical prediction of the nanoparticle displacement distribution in the small pixel limit (solid lines) compared to Eq. 1B (dot-dashed lines).

One may suspect that surface diffusion of nanoparticles, caused by strong interactions of the nanoparticles with the graphene, may be responsible for the retarded motion of nanoparticles. However, interactions between the nanoparticles and the graphene surface are strong enough only on nanoparticles that happen to be located in the close vicinity of the graphene surface; in another GLC TEM experiment, nanoparticles adsorbed onto the graphene surface appear immobile, while nanoparticles distant from the graphene surface move vigorously (fig. S18 and movie S3). This observation suggests that nanoparticles moving in a GLC are sufficiently distant from the graphene surface to be absorbed onto the surface. In addition, we observed that nanoparticles located at various distance from the graphene surface have the similar degree of nanoparticle mobility, which indicates that the nanoparticle-graphene interaction is not the main cause of the small diffusion coefficient of our nanoparticle systems (fig. S7). The Fickian nanoparticle diffusion observed in our system is qualitatively different from non-Fickian nanoparticle diffusion in the presence of strong electrostatic interactions between nanoparticles and charged substrates of the liquid cells (12, 15, 16).

We believe that the slow thermal motion of the nanoparticles observed in our system originates from an increased shear viscosity of the small medium highly confined within the GLC. There are previous studies reporting that water molecules in a nanoscale confinement exhibit structure and dynamics largely different from those of bulk water (34–37). While liquid structure in a confined space is still a debatable topic needing further experimental and theoretical investigations, our observations also indicate that nanoscale confined liquids have a far greater viscosity than their bulk counterpart.

Fluctuation in diffusion coefficients of nanoparticles in a GLC

The nanoparticle displacement distribution deviates from a Gaussian distribution throughout our experiment. This result reflects the fluctuation of the nanoparticle diffusion coefficient (38). Deviation of the displacement distribution from Gaussian can be quantified using the non-Gaussian parameter (NGP), defined as ${\mathrm{\alpha }}_2(t)=\mathrm{\langle }\overline{\mathrm{\delta }\mathrm{\Delta }\mathbf{r}{(\mathit{t})}^4}\mathrm{\rangle }/(2{\mathrm{\langle }\overline{\mathrm{\delta }\mathrm{\Delta }\mathbf{r}{(\mathit{t})}^2}\mathrm{\rangle }}^2)-1$ for two-dimensional trajectories (39, 40). The NGP vanishes for normal Brownian motion, for which the displacement distribution is Gaussian. For our nanoparticle system, the NGP assumes positive values, indicating that the nanoparticle displacement is distributed according to a super-Gaussian distribution characterized by a sharper peak and heavier tails than a standard normal distribution (41). In addition, the NGP decreases with time; its value rapidly decreases from 2 to 0.3 in less than 1 s but undergoes a slower relaxation at times longer than 1 s (Fig. 2B, symbols). It is known that, for thermal motion in a continuous space, the time profile of the NGP is related to the time autocorrelation function, 〈δD(t)δD(0)〉, of the diffusion coefficient fluctuation, δD(t) = D(t) − 〈D〉, by $\langle \mathrm{\delta }\mathit{D}(\mathit{t})\mathrm{\delta }\mathit{D}(0)\rangle /{\langle \mathit{D}\rangle }^2\cong 2^{-1}{\mathrm{\partial }}_{\mathit{t}}^2[{\mathit{t}}^2{\mathrm{\alpha }}_2(\mathit{t})]$, at times where Fickian diffusion emerges (38). This result allows us to extract the time correlation function of the diffusion coefficient fluctuation from the NGP time profile. However, care must be taken in applying this formula to experimental data at short times where the nanoparticle trajectory length is comparable to the pixel size of the TEM image.

The NGP time profile can be explained by our environment-coupled random walk model (see section S3 and fig. S19 for more details) (38, 42–46). In this model, the jump rate or the diffusion coefficient is treated as a dynamic, stochastic variable to account for environmental fluctuation. We further introduce the jump-length distribution into this model because the nanoparticle displacements during the temporal resolution, 0.13 s, of our measurement are distributed. For our model, the diffusion coefficient follows a gamma distribution, P(D) ~ D^{a − 1}e^−D/b, where ab and ab² are the mean, 〈D〉, and variance, 〈δD²〉, respectively. Using the values of 〈D〉 and 〈δD²〉 estimated from the variance of nanoparticle displacement shown in Fig. 2A, P(D) is consistent with the experimentally measured diffusion coefficient distribution of our nanoparticle system (Fig. 2C). For simplicity, we assume that the time correlation function of the diffusion coefficient fluctuation is an exponential function, that is, 〈δD(t)δD(0)〉/〈δD²〉 = e^−t/τ, where τ is the characteristic relaxation time. This model yields the following analytic expressions for the NGP time profile and the displacement distribution in the Fourier domain

$${\mathrm{\alpha }}_2(\mathit{t})=\frac{\langle {\mathit{l}}^4\rangle /\langle {\mathit{l}}^2\rangle }{8\langle \mathit{D}\rangle \mathit{t}}+{\mathrm{\eta }}_{\mathit{D}}^2\frac{2(\mathit{t}/\mathrm{\tau })-1+{\mathit{e}}^{-2\mathit{t}/\mathrm{\tau }}}{2{(\mathit{t}/\mathrm{\tau })}^2}$$ (1A)

$$\tilde{p}(\mathbf{k},t)={\left[\frac{4{\mathrm{\mu }}_k{e}^{-({\mathrm{\mu }}_k-1)t/\mathrm{\tau }}}{{({\mathrm{\mu }}_k+1)}^2-{({\mathrm{\mu }}_k-1)}^2{e}^{-2{\mathrm{\mu }}_{k}t/\mathrm{\tau }}}\right]}^a;{\mathrm{\mu }}_k={(1+\frac{8b\mathrm{\tau }}{\mathrm{\langle }{l}^2\mathrm{\rangle }}[1-\tilde{f}(\mathbf{k})\left]\right)}^{1/2}$$ (1B)

where ${\mathrm{\eta }}_{\mathit{D}}^2$ denotes the relative variance, 〈δD²〉/〈D〉², of the diffusion coefficient. In Eq. 1B, $\tilde{\mathit{f}}(\mathbf{k})$ denotes the Fourier transform of the jump length distribution, f(l), of our random walk model. We model f(l) as an exponential distribution, f(l)~$e^{-\mathit{l}/{\mathit{l}}_{\mathrm{c}}}$, with l_c = 0.09 nm, which is in good agreement with the experimentally measured distribution of the nanoparticle displacement during our experimental time resolution, ∆t ≅ 0.13 s (fig. S20). Using the values of 〈l²〉, 〈l⁴〉, 〈D〉, and ${\mathrm{\eta }}_{\mathit{D}}^2$, extracted from the experimental data in Fig. 2A and fig. S20, Eq. 1A provides a quantitative explanation of the NGP time profile (Fig. 2B, black line). The only adjustable parameter is the relaxation time scale, τ, of the diffusion coefficient fluctuation; the extracted value of τ is 3.58 s.

The relaxation of the NGP at times shorter than 0.4 s is dominantly contributed to from the first term on the right-hand side of Eq. 1A (Fig. 2B, green line), arising from the finite spatial resolution of our TEM observation. The distance a nanoparticle travels, (〈D〉∆t)^1/2 = 0.126 nm, during the temporal resolution is comparable to the pixel size, 0.07 nm, of our measurement. This causes nanoparticle motion to appear as a random walk at short times but has a negligible effect on the NGP time profile at long times.

The fluctuation of the diffusion coefficient is the dominant contributor to the relaxation of the NGP at times longer than 1 s, which is accounted for by the second term on the right-hand side of Eq. 1A (Fig. 2B, red line). This second term represents the NGP time profile of our model in the continuum limit, which satisfies $\langle \mathrm{\delta }\mathit{D}(\mathit{t})\mathrm{\delta }\mathit{D}(0)\rangle /{\langle \mathit{D}\rangle }^2\cong 2^{-1}{\mathrm{\partial }}_{\mathit{t}}^2[{\mathit{t}}^2{\mathrm{\alpha }}_2(\mathit{t})]$ at long times. According to this result, the short-time limit value of the second term approaches the relative variance of the nanoparticle diffusion coefficient (Fig. 2B, dotted line).

Origin of diffusion coefficient fluctuations

The diffusion coefficient fluctuation of the nanoparticles has multiple origins. The different sizes of nanoparticles can contribute to the diffusion coefficient fluctuation because the measured diffusion coefficient shows a positive correlation with the inverse nanoparticle diameter (Fig. 2D). However, we find that the nanoparticle size distribution alone cannot explain the diffusion coefficient fluctuation observed in our nanoparticle system. If the nanoparticle size fluctuation were the only dominant source of the diffusion coefficient fluctuation of nanoparticles, then the relative variance of the diffusion coefficient should be similar to 0.16, the relative variance of the inverse of the nanoparticle radius (fig. S21). However, this value is substantially smaller than the relative variance, 0.26, of experimentally measured diffusion coefficient fluctuation. This fact indicates that there is another source of the nanoparticle diffusion coefficient fluctuation. The long-time tail of the NGP time profile tells us that the diffusion coefficient fluctuation of our nanoparticle system results from dynamic motility fluctuation; if the diffusion coefficient fluctuation originated solely from a quenched disorder or a static distribution of nanoparticle properties, then the NGP time profile would saturate to a constant value and would not have changed over time at long times (38).

We believe that the diffusion coefficient fluctuation is contributed from the dynamically heterogeneous environment surrounding the nanoparticles, which includes both solvent molecules and nanoparticle-passivating ligands. It is well known that self-diffusion coefficients in condensed phases follow the Arrhenius-type temperature dependence, i.e., D = D₀ exp [−E_a/k_BT], where E_a and k_BT denote the activation energy associated with the translational motion and thermal energy, respectively. The temperature-insensitive factor, D₀, is related to structural fluctuation of surrounding medium via excess entropy (47). When the structural fluctuation is sufficiently fast, D₀ can be regarded as constant. On the other hand, when the structural fluctuation is slow, nanoparticles experience heterogeneous environments so that we need to consider the environment-coupled fluctuation of D₀. Note that the value, 3.58 s, of the diffusivity fluctuation time scale, τ, extracted from our analysis is comparable to the time taken for water molecules in the nanoconfinement to undergo rearrangement in response to external force (48). In addition, the soft ligand molecules with dynamically heterogeneous configurational states can contribute to the fluctuation in nanoparticle diffusivities (49), especially when the dimension of the soft shell is comparable to the size of the hard core, as in our system. The chemical environment around the nanoparticles can be another source of the diffusivity fluctuation but is presumably static during our observation, as the concentrations of radiolysis-induced species reach equilibrium values within a millisecond time scale, far shorter than the temporal resolution of our measurement (50).

The non-Gaussian nanoparticle motion observed in our nanoconfined system is in direct contrast with the Gaussian nanoparticle motion in the absence of substrates near nanoparticles (51). This fact implies that nanoparticles in nanoconfined liquids suffer a motility fluctuation, absent in bulk liquids. For our nanoparticle system in highly confined GLCs, the Fickian-yet-non-Gaussian diffusion of nanoparticles is persistently observed regardless of intensity of the electron fluxes in the TEM (fig. S16). This suggests that the motility fluctuation of nanoparticles in our system does not originate from electrostatic interactions between nanoparticles and graphene substrates.

Precise prediction of displacement distribution of nanoparticles in a finite pixel size

We can predict the time-dependent shape of nanoparticle displacement distribution using Eq. 1B with the optimized parameter values extracted from our analysis of the MSD (mean square displacement) and NGP time profiles at hand. At all times investigated, the prediction of Eq. 1B is in good agreement with the experimentally measured displacement distribution of nanoparticles (Fig. 2E). Note that both the theoretical prediction and the experimental results of the nanoparticle displacement have exponential-like tails, which results from the diffusion coefficient fluctuation (52–54). At short times, the peak shape of the displacement distribution is affected by the finite pixel resolution of our TEM experiment.

From the analysis based on our model, we can extract the nanoparticle displacement distribution without the deformation of the peak shape at short times caused by the finite pixel size of the TEM detector (Fig. 2F). Note that this nanoparticle displacement distribution, obtainable from Eq. 1B in the small pixel size limit, has a smooth peak, while the experimentally measured displacement distribution has a sharp peak, an artifact arising from the finite pixel resolution. The peak shape distortion of the displacement distribution at short times occurs for any microscopic technique using a detector with a finite pixel size. However, as demonstrated here, our analysis method enables one to circumvent this problem and extract the true displacement distribution without this distortion due to the finite pixel size.

Encounter complex formation and coalescence of nanoparticles

We observed coalescence events between nanoparticles undergoing thermal motion in a GLC (Fig. 3, A and B, and movie S1). To coalesce, nanoparticles first form an encounter complex at the surface-to-surface distance, r_surf, between the two nanoparticles around 1.4 nm. Given that the length of the ligand is about 0.7 nm (19), the value, 1.4 nm, of r_surf implies the formation of the double ligand layers between two nanoparticles in the complex. A few seconds after the complex formation, the nanoparticles undergo coalescence through rapid movement over one- or two-time frames (Fig. 3C).

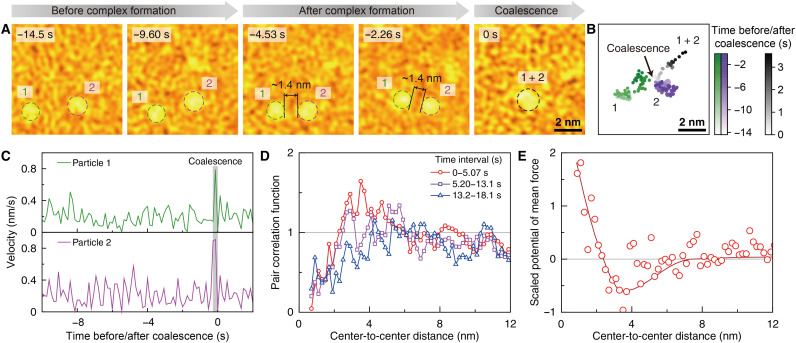
Fig. 3. Coalescence and interaction between nanoparticles.

(A and B) Time-series false-color TEM images (A) and trajectories (B) of two nanoparticles showing a coalescence event. Coalescence of the two nanoparticles happens at 0 s, and the nanoparticles maintain their surface-to-surface distance of around 1.4 nm for 4.53 s before the coalescence. The surface-to-surface distance of 1.4 nm amounts to the thickness of double ligand layers (see Fig. 4A). (C) Velocity profiles of the two nanoparticles shown in (A), which show abrupt changes at the moment of coalescence. (D) Pair correlation function measured over three consecutive time ranges during the observation. The pair correlation at short distances gradually diminishes due to the coalescence events. (E) Potential of mean force, u(r), scaled by thermal energy k_BT, corresponding to the pair correlation function obtained from the initial period over which nanoparticles do not undergo any coalescence events. The resulting u(r) shows a shallow potential well at the distance of ~3 nm (see also fig. S22). (Solid line) Guide for the eyes.

Nanoparticle coalescence alters the spatial profile of the nanoparticle pair correlation over time. This is reflected in the time-dependent pair correlation function of nanoparticles, ρ(r,t). In the earliest stage, ρ(r,t) reaches its maximum at the center-to-center distance of ~3 nm (Fig. 3D, red symbols). As coalescence proceeds, the nanoparticle pairs initially close to each other vanish so that the maximum position of ρ(r,t) increases and its peak height decreases (Fig. 3D, purple and blue symbols). We extract the potential of mean force, u(r), between our nanoparticles from ρ(r,t) at short times where coalescence between nanoparticles has not yet occurred. The resulting u(r) shows a shallow potential well at a distance of ~3 nm (Fig. 3E and fig. S22), which amounts to the sum of the average diameter of the nanoparticles, 1.5 nm, and the thickness of the double ligand layer between nanoparticles, 1.4 nm.

The attractive potential well in the potential of mean force u(r) facilitates the formation of a nanoparticle complex and hence nanoparticle coalescence (Fig. 4A). The complex formation can be monitored through r_surf between a coalescing pair of nanoparticles, in which the most probable value of r_surf is close to twice the ligand length, 1.4 nm (Fig. 4B and fig. S23). Upon contact between two ligand shells, r_surf typically assumes values around 1.4 nm, which results because a nanoparticle pair forms an encounter complex in which their ligands partially overlap (Fig. 4C). The small fluctuations in r_surf around 1.4 nm are attributable to the soft bodies of the ligand molecules.

Fig. 4. Formation of encounter nanoparticle complex.

(A) Schematic illustrations for the entire coalescence process. When pairs of nanoparticles initially distant from each other undergo diffusive contact at the surface-to-surface distance, r_surf, of ~1.4 nm, roughly twice the ligand length, they form an encounter complex, exhibit correlated motion, and finally coalesce. (B) Changes in r_surf of 20 coalescing nanoparticle pairs over time (left panel), and a histogram (right panel) of r_surf measured for times within 10 frames before the coalescence event (shaded area in the left panel; see also fig. S23). Dashed horizontal line indicates 1.4 nm. (C) Profile of r_surf shown in Fig. 3A, which is marked with a black bold line in (B). The moment of an encounter complex formation is determined by the time at which r_surf crosses 1.4 nm in the inward direction and stays near or less than a value of 1.4 nm until coalesence. (D and E) Variance of nanoparticle displacements (D) and variance of relative displacements (E) between nanoparticles, calculated by using trajectories before and after the complex formation. (Symbols) Experimental data. (Solid lines) Best linear fits. Mean relative diffusion coefficients of nanoparticles, before and after the complex formation, are nearly the same as twice the mean diffusion coefficients calculated in both cases.

The existence of the encounter complex is supported by monitoring changes in the displacement statistics both before and after r_surf reaches twice the ligand length. We calculated the variances of nanoparticle displacements using nanoparticle trajectories before and after the complex formation. While the nanoparticles show diffusive motion in both regimes, we observed a decrease in the mean diffusion coefficient, from 0.204 to 0.154 nm²/s, upon the formation of the encounter complex. This indicates an increase of the effective hydrodynamic size, caused by the formation of encounter complexes.

The formation of the encounter complex also restricts the relative motion of nanoparticles forming the encounter complex. This feature can be characterized by the variance of relative displacements between nanoparticles that form an encounter complex (Fig. 4E). After complex formation, the variance of the relative displacements linearly increases at times shorter than 1 s but reaches a plateau at longer times. However, before complex formation, the variance of the relative displacements keeps increasing with time. Note that the mean relative diffusion coefficients, 〈D_r〉, identified from the linear time dependence of the variance of relative displacements are essentially twice the mean diffusion coefficients estimated from the variance of the nanoparticle displacement (Fig. 4E, solid lines).

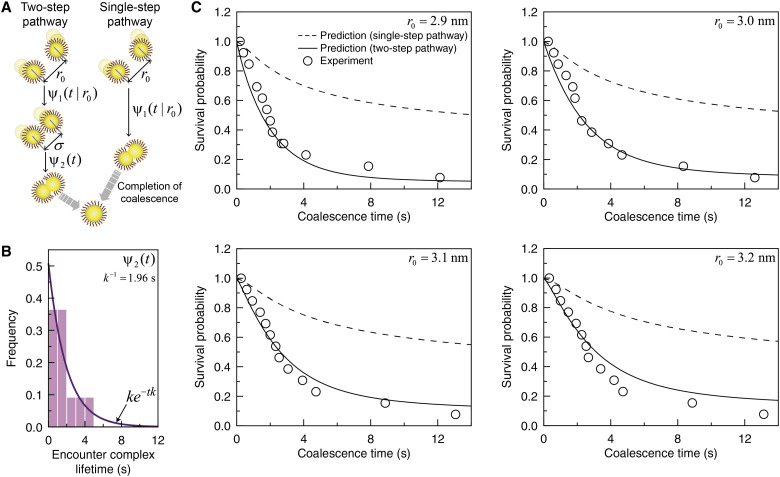
Our theoretical investigation into the coalescence kinetics supports a two-step coalescence scheme: (i) the formation of the encounter complex through the diffusive contact between nanoparticles and (ii) the ensuing coalescence (Fig. 5A, left panel). Each step in our coalescence scheme is characterized by the corresponding waiting time distribution; ψ₁(t∣r₀) denotes the distribution of time taken for a pair of nanoparticles initially distant by r₀ to form the complex at contact separation, σ, and ψ₂(t) denotes the lifetime distribution of the encounter complex (Fig. 5B, fig. S20, and section S4). ψ₁(t∣r₀) accounts for the first encounter between a pair of nanoparticles in the presence of fluctuating diffusivity, consistent with the coalescence-free nanoparticle transport discussed in Fig. 2. ψ₂(t) is given by an exponential distribution, ψ₂(t) = ke^−tk, with the mean lifetime, k⁻¹ = 1.96 s, obtained from the best fit of our experimental data (Fig. 5B, solid line).

Fig. 5. Theoretical predictions and experimental results for coalescence dynamics for coalescence kinetics.

(A) Schematic illustrations for the two-step coalescence pathway involving an encounter complex formation (left panel) and the single-step coalescence pathway without assuming the formation of the encounter complex (right panel). At the first step of the two-step pathway, the distribution of time taken for a pair of nanoparticles initially distant by r₀ to form the complex at the contact separation, σ, is denoted by ψ₁(t|r₀). At the second step, the lifetime distribution of the encounter complex is denoted by ψ₂(t), which is given by an exponential distribution, ψ₂(t) = ke^−tk. For the single-step pathway, nanoparticles coalesce at the sum of the nanoparticle radii (section S4). (B) Lifetime distribution of the encounter complex. (Histogram) Experimental data. (Solid line) Best fit of exponential distribution, ke^−tk, to the experimental lifetime distribution, with the value of k given by 0.51 s⁻¹. (C) Survival probability of nanoparticles at various values of initial separations. (Symbols) Experimental data. (Solid lines) Theoretical predictions based on the two-step coalescence pathway shown in the left panel of (A). (Dashed lines) Theoretical predictions based on the single-step pathway shown in the right panel of (B).

Lifetimes of the encounter complex are closely related to the rotational motion of nanoparticles forming the complex. Because the alignment between crystallographic planes of two nanoparticles through rotation is essential for the nanoparticle pair to coalescence (55–57), the mean lifetime of the encounter complex can be considered as the rotational relaxation time, τ_R = 1/2D_R, with D_R denoting the rotational diffusion coefficient (58). Using the relation D_R/D_T = 3/d², where the values of the particle diameter, d, and the translational diffusion coefficient, D_T, are respectively given by the mean diameter, 1.32 nm, and the mean diffusion coefficient of nanoparticles forming encounter complexes, 0.154 nm²/s, the rotational diffusion coefficient, D_R, can be calculated as 0.265 rad²·s⁻¹. This value is in good agreement with the coefficient estimated from tracking the lattice fringes of rotating nanoparticles for a short time period (fig. S24, section S5, and movie S4) (59). Here, the in-plane rotation is captured in the middle of the three-dimensional rotational motion. In addition, the value, 1.89 s, of the rotational relaxation time, τ_R, is close to the mean lifetime, 1.96 s, of the encounter complex, indicating that the oriented attachment of two nanoparticles is crucial for coalescence and related to their rotation; nanoparticle coalescence cannot occur when their rotational motion is hindered (figs. S25 and S26, section S6, and movie S5).

On the basis of the time distributions, ψ₁(t/r₀) and ψ₂(t), introduced in our theoretical model for the two-step coalescence scheme, the coalescence kinetics for ligand-passivated nanoparticles is explained at a quantitative level. Using the size distribution of nanoparticles undergoing coalescence and their relative displacement statistics before the complex formation, we can calculate the survival probability, S(t|r₀), that pairs of nanoparticles do not coalesce as of time t (section S4 and figs. S27 to S29) (42, 60–62). This theoretical prediction reproduces the experimentally measured survival probability time profiles at various r₀ values (Fig. 5C, solid lines). We note here that the survival probability calculated assuming the single-step diffusion-reaction mechanism, which ignores involvement of the encounter complex (Fig. 5A, right panel), fails to reproduce the experimental results for the survival probability (Fig. 5C, dashed lines).

In summary, we observe colloidal nanoparticles, as small as a few nanometers, undergoing thermal motion and coalescence in GLC using liquid TEM. Colloidal nanoparticles suspended in GLC exhibit a Fickian-yet-non-Gaussian diffusion signifying dynamic heterogeneity in the diffusivities of ligand-passivated colloidal particles. We analyzed our experimental results using our new model of a random walk in a dynamically heterogeneous environment. This model provides a unified, quantitative explanation of our experimental results for the MSD and NGP and a quantitative prediction of the time-dependent nanoparticle displacement distribution, which is in good agreement with experimental results. Our model and analysis method enable one to extract the true displacement distribution free of the peak-shape distortion due to finite spatial resolution of modern imaging methods. We propose a two-step diffusion-reaction mechanism for nanoparticle coalescence, which quantitatively explains experimentally measured nanoparticle coalescence dynamics. This mechanism is characterized by the formation of an encounter nanoparticle complex and the ensuing oriented attachment. There is no question that there is a high degree of complexity in confined systems in biology, colloid physics, and materials science. Nonetheless, this work extends our fundamental understanding of transport and reaction dynamics in a confined medium to a single-particle level at the nanometer scale. Imaging platform based on GLCs can be further modified to represent the complexity in diverse confined media, and the theoretical models we introduce here can be used to understand transport and reaction dynamics in those nanoconfined systems.

MATERIALS AND METHODS

GLC preparation

We synthesized few-layer graphene by the low-pressure chemical vapor deposition method on a copper foil with a thickness of 25 μm (Alfa Aesar). The copper foil was inserted into a quartz tube and heated to 1000°C for 20 min under an 8 standard cubic centimeter per minute (SCCM) H₂ flow at 0.082 torr, followed by annealing for 30 min. Then, a gas mixture of 8 SCCM H₂ and 24 SCCM CH₄ was introduced for 20 min at 0.46 torr to synthesize graphene sheets. After the synthesis completed, fast cooling to room temperature with 8 SCCM H₂ flow was performed at 0.082 torr.

Procedures for preparing graphene-coated TEM grids were the same as previously described (63); briefly, one side of a Cu foil was gently milled with sandpaper to remove the graphene from one side of the Cu foil. Gold TEM grids with a perforated carbon film of hole diameter of 1.2 μm (Quantifoil) were placed on the graphene-deposited side of the Cu foil. The holey carbon TEM grid was fully adhered to the graphene by placing a drop of isopropyl alcohol and allowing for drying. The Cu substrate was removed by floating on ammonium persulfate solution for about an hour (10 g/100 ml). After the Cu substrate was completely etched away, the remaining TEM grids on the freestanding graphene were carefully transferred to distilled water using a Pt loop twice. The graphene-coated TEM grids floating on the distilled water were picked up using reverse-action tweezers and oven-dried at 70°C overnight.

GLCs were fabricated by sandwiching 0.4 μl of gold nanoparticle solution between the two graphene-coated TEM grids. The gold nanoparticle solution contains 3 μM gold nanoparticles with a diameter of approximately 1.4 nm, 2 mM sodium phosphate buffer, and 15 mM sodium chloride (Nanoprobes). The GLC was left in an ambient condition for about 30 min before imaging to ensure complete adherence between the two graphene sheets.

Liquid-phase TEM

Liquid-phase TEM was conducted with JEOL JEM-2100F TEM that operates at 200 kV and equipped with Gatan US1000XP detector with a frame rate of 10 frames per second. In our experiment of the bubble-free GLC (Figs. 1 to 5 and movie S1), the electron flux is estimated to range from 1.0 × 10⁴ e⁻/Ų·s to 1.4 × 10⁴ e⁻/Ų·s. In other experiments using different electron fluxes, the values of electron fluxes were estimated to be 2.0 × 10³ e⁻/Ų·s, 6.0 × 10³ to 8.0 × 10³ e⁻/Ų·s (movie S5), and 4.0 × 10⁴ e⁻/Ų·s (see also fig. S16). Under these electron beam conditions, a rise in temperature during the imaging was estimated to be less than a few kelvins (section S7) (26, 64–66). The movies were recorded at a frame rate of 7.5 frames per second. We typically imaged the region where two holes of the carbon TEM grids overlapped (fig. S1), as the resolution of the other regions was degraded by the scattering of electrons from the carbon film. To reduce possible effects of electron beam on the GLCs, we began recording in situ TEM movies at the moment of observation. Subfraction analysis of the acquired TEM movies was also conducted to compare nanoparticle motion in different time periods and remove the later part of the in situ data where nanoparticle motion is influenced. Prolonged observation causes nanoparticle dynamics to appear different from the dynamics described above (fig. S30 and movie S6). In the absence of nanobubbles, 69 nanoparticle trajectories were recorded from the quiescent liquid pocket for 18 s (movie S1). In the experiments conducted at dose rates of 2.0 × 10³ e⁻/Ų·s, 6.0 × 10³ to 8.0 × 10³ e⁻/Ų·s, and 4.0 × 10⁴ e⁻/Ų·s, we recorded 2, 14, and 2 nanoparticle trajectories, respectively (see also fig. S16). In experiments with dose rates of 2.0 × 10³ e⁻/Ų·s and 6.0 × 10³ to 8.0 × 10³ e⁻/Ų·s, nanobubbles were observed throughout imaging, and the effect of moving nanobubble-liquid interfaces is deconvoluted for tracking the nanoparticle motion (section S6) (21). Various sizes of liquid pockets were produced from the GLC preparation. Among them, we selected thin liquid pockets whose thickness is estimated to be as thin as 10 nm. The concentration of salts in the graphene-encapsulated liquid was below the solubility limits (fig. S5), and accordingly, we did not observe precipitated salt crystals throughout TEM imaging.

Single-particle tracking and drift correction

We first divided the in situ TEM movies into a series of snapshots using scripts provided by MATLAB (MathWorks). Before tracking the nanoparticle movement from the time-series TEM images, we applied a Gaussian filter to reduce background noise and enhance the signal. We additionally used a local contrast enhancement (CLAHE) algorithm implemented in Fiji software (67, 68). The trajectories of individual nanoparticles throughout the time-series TEM images were obtained by the combined use of the two-dimensional particle tracking algorithm provided by the Mosaic plugin (69) in the Fiji software and manual tracking of nanoparticle centers in the time-series images. As a result, 69 trajectories were tracked. Nanoparticle trajectories before and after a coalescence event are considered to be different trajectories. To correct the movement of the TEM specimen stage, the mean displacements of nanoparticles between adjacent frames were smoothed using fast Fourier transform filter and subtracted from the tracked nanoparticle coordinates (fig. S10; see section S2 for details). The validity of this drift correction procedure was confirmed on the basis of the in situ TEM of immobile nanoparticles dried on a graphene substrate (fig. S11). Nanoparticle movement shows no preferential direction after this procedure (fig. S12).

Survival probability calculation

The survival probability of the nanoparticles, S(t|r₀), that pairs of nanoparticles initially distant by r₀ do not coalesce by time t is calculated using the relation $\mathit{S}(\mathit{t}\mid {\mathit{r}}_0)={\mathit{N}}^{-1{\sum }_{\mathit{i}=1}^{\mathit{N}}\mathrm{\Theta }(\mathit{t}-{\mathit{t}}_{\mathit{i}})}$, with Θ(z) denoting the unit-step function defined by Θ(z ≥ 0) = 1 and Θ(z < 0) = 0. Here, t_i and N respectively denote the time taken for the ith nanoparticle pair initially distant by r₀ to complete coalescence and the number of the coalescing pairs.

Supplementary Materials

This PDF file includes:

Sections S1 to S7

Figs. S1 to S30

Legends for movies S1 to S6

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S6