Atomistic level characterisation of ssDNA translocation through the E. coli proteins CsgG and CsgF for nanopore sequencing

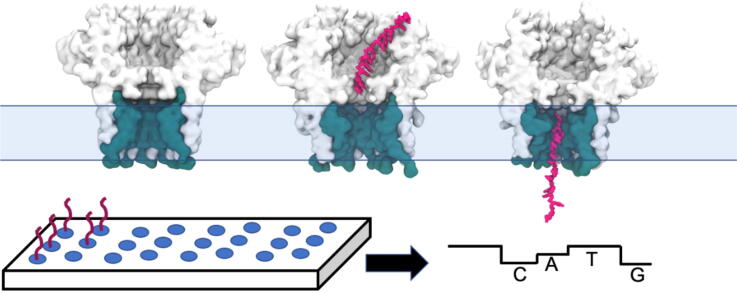
Graphical abstract

Abstract

Two proteins of the Escherichia coli membrane protein complex, CsgG and CsgF, are studied as proteinaceous nanopores for DNA sequencing. It is highly desirable to control the DNA as it moves through the pores, this requires characterisation of DNA translocation and subsequent optimization of the pores. In order to inform protein engineering to improve the pores, we have conducted a series of molecular dynamics simulations to characterise the mechanical strength and conformational dynamics of CsgG and the CsgG-CsgF complex and how these impact ssDNA, water and ion movement. We find that the barrel of CsgG is more susceptible to damage from external electric fields compared to the protein vestibule. Furthermore, the presence of CsgF within the CsgG-CsgF complex enables the complex to withstand higher electric fields. We find that the eyelet loops of CsgG play a key role in both slowing the translocation rate of DNA and modulating the conductance of the pore. CsgF also impacts the DNA translocation rate, but to a lesser degree than CsgG.

1. Introduction

Nanopore sequencing is a fourth-generation DNA sequencing technique that exploits the propensity for charged molecules to move across a membrane, through a nanoscale pore, under an applied electric field. Nanopores used for sequencing can be formed by proteins or synthetic materials, providing they accommodate single stranded (ss) DNA and allow an ionic current to pass through them. As the DNA translocates through the smallest constriction of the pore, each base will produce a characteristic reduction in the measured ionic current, thereby allowing them to be distinguished [1], [2], [3], [4]. Several proteinaceous nanopores have previously been studied experimentally and by MD simulations for DNA sequencing, most notably ɑ-hemolysin [5], [6], [7], [8], MspA [9], [10], CsgG as well as hybrid protein-synthetic pores [7], with efforts to optimise them via mutagenesis often focussed on the pore constriction, referred to as the ‘sensing region’ [11], [12]. The principles of DNA sequencing using nanopores have also been applied for protein sequencing and analysis [13], [14], [15]. Since 2016 a mutant pore of CsgG, derived from the curli secretion system in Escherichia coli has been employed in DNA sequencing devices [16]. An independent study has shown that the dual constriction of the CsgG-CsgF complex, formed by incorporating the CsgF peptide into the CsgG pore improved the accuracy of homopolymer regions of DNA strands compared to uncomplexed CsgG [17].

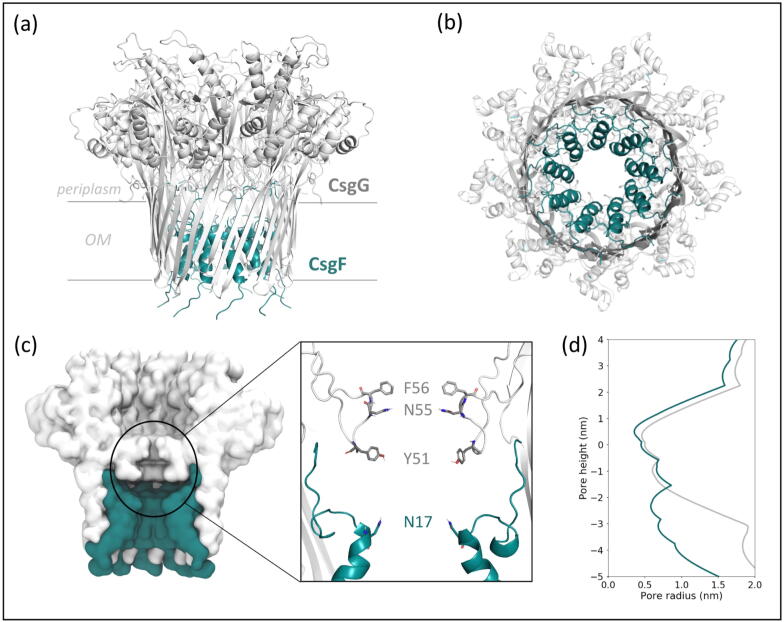
In E. coli, the native CsgG-CsgF complex is an essential component of the curli biogenesis system, which is a multi-protein machinery that facilitates the secretion of amyloidogenic curli subunits and their assembly into highly aggregative amyloid fibres associated with biofilm formation. CsgA and CsgB are the major and minor curli subunits, respectively, that form the extracellular fibres, whilst CsgE, CsgF and CsgG coordinate their secretion and assembly [18]. CsgG is a nonameric outer membrane lipoprotein that comprises a 36-stranded transmembrane β-barrel, connected to a large solvent-accessible periplasmic vestibular region. The β-barrel and the vestibule domains are separated by a central constriction of ∼ 1 nm diameter, which is wide enough for passage of unfolded or partially folded curli subunits [19], [20]. CsgG forms an ungated peptide diffusion channel that becomes substrate-specific during curli biogenesis by binding two soluble nonameric accessory proteins, CsgE and CsgF [21], [22], [23]. CsgE binds to the CsgG vestibule, acting as a ‘cap’ that effectively gates the channel at the periplasmic side [19]. CsgF is secreted into through the CsgG pore, and its N-terminus folds into an α-helix that remains bound in the CsgG β-barrel, narrowing the channel and forming a second constriction in the pore lined by CsgF Asn-17 residues (Fig. 1). The C-terminus sits outside the CsgG pore for attachment of the growing amyloid fibre [20], [24], [25].

Fig. 1.

The CsgG-CsgF complex is shown from side (a) and extracellular (b) views in ribbon representation. A cross-sectional side view is also shown in surface representation, with a close-up view of CsgG and CsgF constrictions and residues shown in stick representation (c). The pore radius of the CsgG and the CsgG-CsgF complex is plotted against pore height (d), coloured as labelled in (a).

Here, we have characterised the conformational dynamics of CsgG and the CsgG-CsgF complex using advanced molecular dynamics simulations. The stability of CsgG in the absence or presence of CsgF is probed by simulating the systems under applied electric fields of varying strengths. Translocation of ssDNA through CsgG and the CsgG-CsgF complex is investigated, to explore the impact of single- or dual-constrictions on the DNA translocation behaviour. Our results show that CsgG within the CsgG-CsgF complex is able to withstand electric fields of greater magnitude, largely due to a network of hydrogen bonds and electrostatic interactions between CsgF and the CsgG β-barrel. The translocation of ssDNA is retarded to a greater extent by the CsgG eyelet loop constriction compared to the CsgF constriction region. Several key indirect effects are observed in the presence of bound CsgF which would positively impact the performance of nanopore sequencing. Notably, the CsgG-CsgF complex exhibits significantly improved pore stability within an electric field, restricts the mobility of CsgG eyelet loop constriction and maintains translocating DNA in a more extended conformation.

2. Results and discussion

In order to facilitate presentation and interpretation of the results, the simulations performed in this study are summarised in Table 1.

Table 1.

Summary of simulations performed in this study.

System	DNA	Simulations
		0 V	0.05 V nm−1	0.075 V nm−1	Steered MD
CsgG	no	4 × 100 ns 2 × 200 ns	6 × 100 ns	6 × 50 ns	–
	yes	–	6 × 50 ns	–	8 × 70 ns
CsgG-CsgF complex	no	4 × 100 ns 2 × 200 ns	6 × 100 ns	6 × 100 ns	–
	yes	–	9 × 50 ns	–	8 × 75 ns

2.1. Conformational dynamics of CsgG and the CsgG-CsgF complex

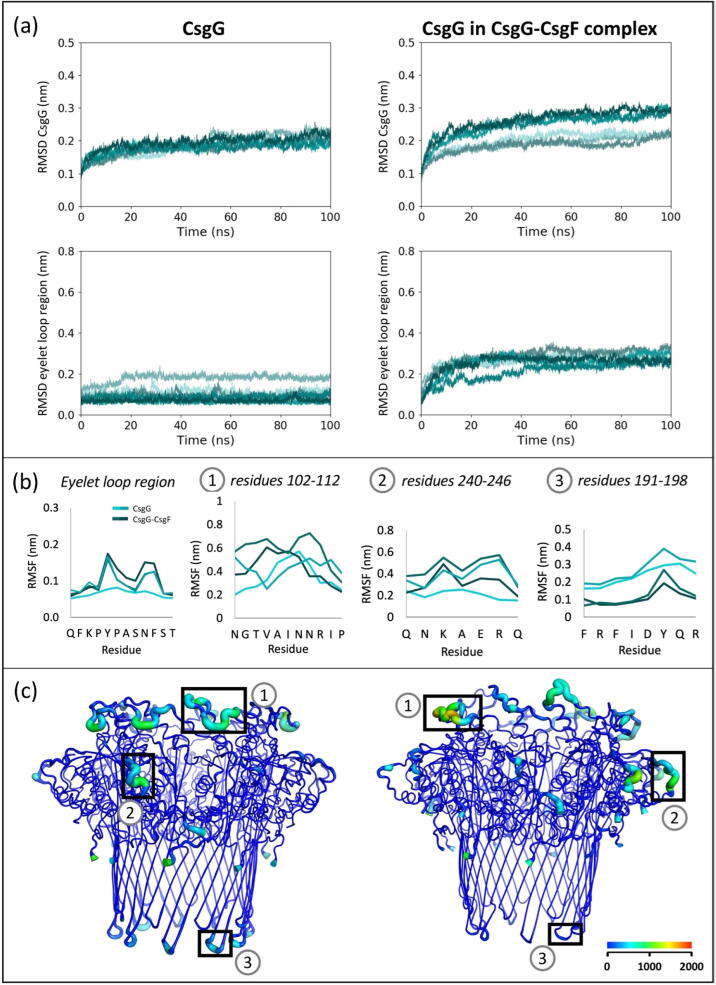
To explore the conformational behaviour of uncomplexed CsgG and in the CsgG-CsgF complex, we performed six independent simulations in total (2 × 200 ns and 4 × 100 ns). The simulation systems consisted of the protein embedded in a phosphatidylcholine (POPC) lipid bilayer and solvated in 1 M KCl. The conformational drift of CsgG from the initial structure was evaluated by monitoring the root mean square deviation (RMSD) of the protein backbone (Cα atoms) from its initial conformation at 0 ns (Table 2, Fig. 2 and Fig. A.1). The uncomplexed CsgG reached a plateau RMSD of ∼ 0.18–0.22 nm, compared to ∼ 0.22–0.30 nm when in complex with CsgF. The eyelet loops forming the constriction region (residues 47–58) exhibited reduced conformational drift in uncomplexed CsgG, with RMSD at a plateau value of < 0.10 nm in five simulations, compared to in the CsgG-CsgF complex for which the RMSD converged to ∼ 0.25–0.35 nm. Plateau RMSD values for CsgF in the CsgG-CsgF complex were in the range ∼ 0.32–0.42 nm across all simulations (Fig. A.2).

Table 2.

Summary of RMSD of the protein backbone Cα atoms at 100 ns in 0 V, from six independent simulations.

System	RMSD CsgG (nm)	RMSD CsgG eyelet loops (nm)	RMSD CsgF (nm)
CsgG	∼ 0.18–0.22	∼ 0.05–0.18	–
CsgG-CsgF complex	∼ 0.22–0.30	∼ 0.25–0.35	∼ 0.32–0.42

Fig. 2.

Comparison of conformational drift and flexibility of CsgG, uncomplexed and in the CsgG-CsgF complex, in 0 V. (a) RMSD of backbone Cα atoms in CsgG and eyelet loop region, compared to initial conformation, in six independent simulations. (b) RMSF of residues of interest (labelled in panel (c)), calculated for 100–200 ns of two simulations of CsgG and the CsgG-CsgF complex. RMSF of residues of the eyelet loop region are an average of values for the nine CsgG monomers. (c) B-factor representation of CsgG; the blue to red colouring and widening of the tube indicate regions with higher B-factors. The B-factors shown are calculated for 100–200 ns of one simulation each of CsgG and the CsgG-CsgF complex.

Next, the conformational flexibility of the protein domains was examined by calculating the root mean square fluctuation (RMSF) and B-factors of individual residues during the last 100 ns of the 200 ns simulations, which correspond to the time-frame of the plateau regions in the RMSD data (Fig. 2). The loop regions were the most flexible in all simulations; the RMSF of residues forming the extended loops linking the α2 helix to β1-sheet in the vestibule mouth (residues 102–112), and the short loops linking the α3 and αC helices near the C-termini (residues 240–246), ranged from ∼ 0.20–0.60 nm. The eyelet loops forming the CsgG constriction were comparatively less flexible, with RMSF of residues ranging from ∼ 0.05–0.17 nm.

The CsgG transmembrane β-barrel was the least flexible region of the protein. The short turns linking the transmembrane β-sheets (residues 191–198) were more rigid in the CsgG-CsgF complex (RMSF ∼ 0.07–0.20 nm) compared to in uncomplexed CsgG (RMSF ∼ 0.20–0.35 nm). In CsgF, the C-termini were the most flexible, with RMSF of residues 30–35 progressively increasing from ∼ 0.30–0.90 nm (Fig. A.2). This is unsurprising as the CsgF C-termini are unfolded in the absence of the curli fibre and protrude from the CsgG β-barrel and therefore are unrestricted.

2.2. Stability of CsgG and the CsgG-CsgF complex under an applied electric field

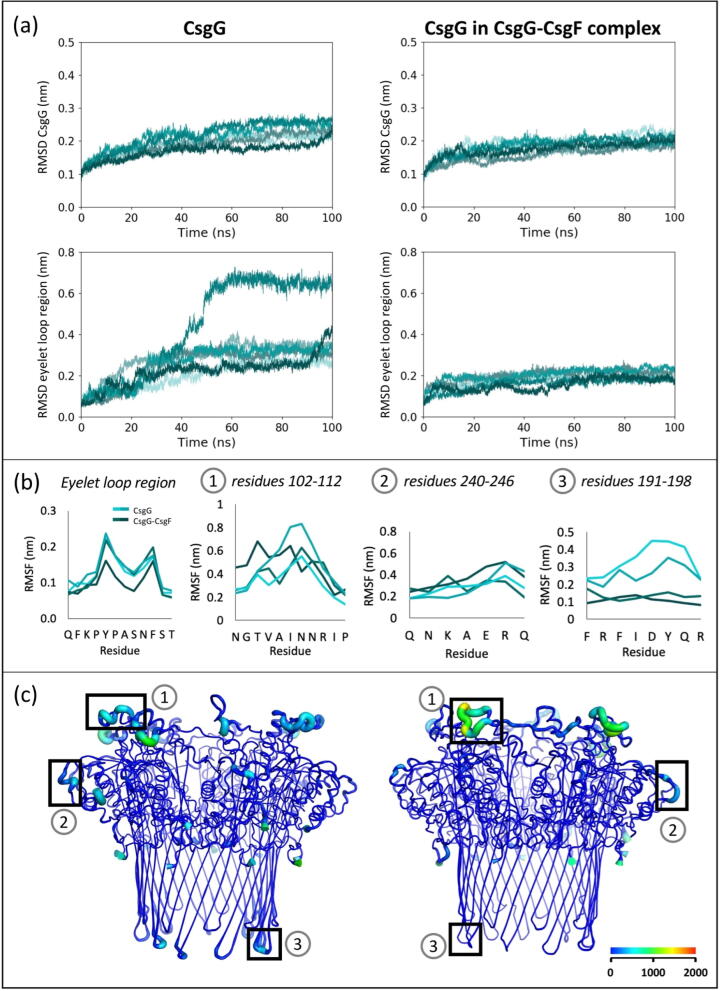
DNA sequencing using nanopores requires the pores to be stable under the applied electric field that is employed to drive the movement of DNA through the pore. We next assessed the properties of uncomplexed CsgG and the CsgG-CsgF complex under applied electric fields of two strengths: 0.05 V nm⁻¹ and 0.075 V nm⁻¹, equivalent to 0.9 V and 1.6 V across the membrane respectively. To magnify any differences, applied electric fields that are approximately five and nine times higher respectively than 0.18 V typically used for DNA sequencing. Under an applied electric field of 0.05 V nm⁻¹, the uncomplexed CsgG showed a slightly higher deviation from its initial conformation compared to in absence of electric field, with plateau RMSD values of ∼ 0.20–0.27 nm in six independent simulations (Table 3 and Fig. 3). This was largely due to the eyelet loops becoming more flexible; up to two eyelet loops were observed to move upwards into the vestibule of CsgG to varying degrees, which resulted in the RMSD of the eyelet loop region increasing to ∼ 0.25–0.40 nm by 100 ns in five simulations (compared to ∼ < 0.10 nm in 0 V). In one simulation, an eyelet loop flipped upwards during ∼ 48–60 ns, and the RMSD of the eyelet loop region during this period increased from ∼ 0.48 nm to ∼ 0.65 nm. The loop conformation remained unchanged following this, hence the RMSD plateaued to ∼ 0.65 nm by 100 ns. The flipping of the eyelet loop did not affect the protein conformation nor its stability in any significant way (Fig. A.3).

Table 3.

Summary of RMSD of the protein backbone Cα atoms at 100 ns in 0.05 V nm⁻¹, from six independent simulations.

System	RMSD CsgG (nm)	RMSD CsgG eyelet loops (nm)	RMSD CsgF (nm)
CsgG	∼ 0.20–0.27	∼ 0.25–0.40	–
CsgG-CsgF complex	∼ 0.17–0.23	∼ 0.16–0.24	∼ 0.26–0.34

Fig. 3.

Comparison of conformational drift and flexibility of CsgG, uncomplexed and in the CsgG-CsgF complex, in 0.05 V nm⁻¹. (a) RMSD of backbone Cα atoms in CsgG and eyelet loop region, compared to initial conformation, in six independent simulations. (b) RMSF of residues of interest (labelled in panel (c)), calculated for 50–100 ns of two simulations of CsgG and the CsgG-CsgF complex. RMSF of residues of the eyelet loop region are an average of values for the nine CsgG monomers. (c) B-factor representation of CsgG; the blue to red colouring and widening of the tube indicate regions with higher B-factors. The B-factors shown are calculated for 50–100 ns of one simulation each of CsgG and the CsgG-CsgF complex.

Interestingly, the CsgG-CsgF complex exhibited less conformational drift from its initial structure under 0.05 V nm⁻¹ compared to in the absence of an electric field, as indicated by lower plateau RMSD of ∼ 0.17–0.23 nm for CsgG (Fig. 3) and ∼ 0.26–0.34 nm for CsgF (Fig. A.4). The RMSD of the eyelet loop region at 100 ns is ∼ 0.16–0.24 nm, which is also significantly lower than in uncomplexed CsgG. This behaviour is counter to what was observed for uncomplexed CsgG; for which the converged RMSD was higher under 0.05 V nm⁻¹ compared to the absence of an applied field. We note here that this effect is observed in over five independent simulations. Furthermore, the CsgG eyelet loops did not move upwards into the vestibule for the CsgG-CsgF complex but did in six simulations of uncomplexed CsgG.

The flexibility of loops in the CsgG vestibule was similar in both uncomplexed CsgG and the CsgG-CsgF complex and was not greatly affected by the electric field. The RMSF of residues forming the loops at the vestibule mouth ranged from ∼ 0.20–0.80 nm, and loops near the C-termini ranged from ∼ 0.20–0.60 nm, similar to in 0 V. However, the short turns linking the β-sheets (residues 191–198) were more flexible in the electric field in uncomplexed CsgG (RMSF ∼ 0.20–0.50 nm) but remained comparatively inflexible in the CsgG-CsgF complex (RMSF ∼ 0.10–0.20 nm).

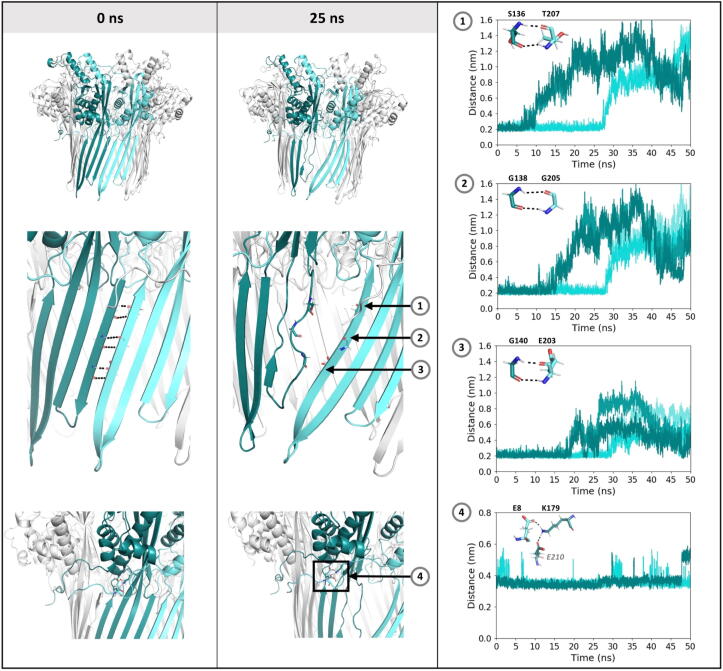
CsgG was unstable under a higher electric field strength of 0.075 V nm⁻¹ (Fig. 4). Inspection of the protein structure revealed that the hydrogen bonds between the backbone atoms at the interface of β-sheets of two of the nine monomers break, leading to separation of these monomers in the CsgG transmembrane β-barrel. This occurred within 20–30 ns in six independent simulations. However, following the destabilisation of the β-barrel, interactions between monomers persisted in the vestibule region. Specifically, electrostatic interactions between Glu-8 in the N-terminus of monomer 1 and Lys-179 of monomer 2 persisted for as long as 50 ns in all simulations. The sidechain of Lys-179 also forms a salt bridge with Glu-210 in the same monomer, which would likely contribute to the stability of the interaction between the two monomers. The N-terminus of monomer 1 remained wrapped around the adjacent monomer 2, in a similar conformation to that adopted in stable CsgG.

Fig. 4.

CsgG is unstable in 0.075 V nm⁻¹. CsgG at 0 ns and 25 ns from one simulation is shown, with the two monomers that separate coloured teal and cyan (left and centre panels). The distance over time is plotted between backbone atoms that form inter-monomer hydrogen bonds (plots 1–3), and between carboxylate and ammonium groups of glutamate and lysine residues respectively. Data is from two independent simulations, shown in teal and cyan. Inset shows residues, with hydrogen bonds marked by dashed lines.

In contrast, CsgG within the CsgG-CsgF complex remained stable in 0.075 V nm⁻¹, as indicated by the RMSD of ∼ 0.19–0.28 nm in six independent simulations (Fig. A.5). The RMSD of CsgF was ∼ 0.28–0.32 nm, similar to when under the electric field of 0.05 V nm⁻¹ (Fig. A.6). To establish the origins of CsgG stability in the CsgG-CsgF complex, the interactions between CsgG and CsgF were characterised.

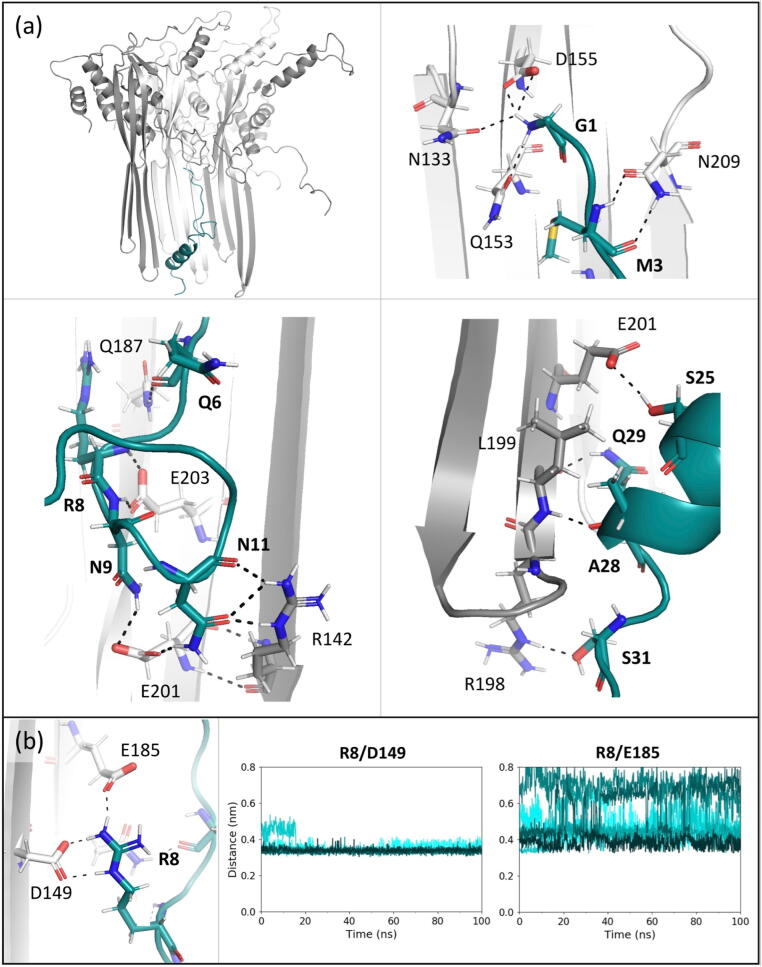
In the starting structure, CsgF monomers are inserted inside the CsgG β-barrel with the N-terminus lying close to the β-barrel surface, which kinks into the lumen forming the CsgF constriction. This is followed by a 13-residue helix that angles outwards towards the CsgG β-barrel exit (Fig. 1). The CsgF N-terminus was observed to form a network of hydrogen bonds with the β-barrel residues of CsgG monomers, which remained stable in 0.075 V nm⁻¹ (Fig. 5). CsgF was observed to interact with two CsgG monomers simultaneously; the kinking of the CsgF N-terminus allowed Asn-11 to form hydrogen bonds with Arg-142 in β-sheet of an adjacent CsgG monomer, which provides additional stabilisation to the inter-monomer interactions in CsgG (between Arg-142 and Glu-201 residues) and the β-barrel.

Fig. 5.

Interactions between CsgG and CsgF monomers in the CsgG-CsgF complex. (a) Residues in a CsgF monomer form hydrogen bonds with residues in three CsgG monomers. Hydrogen bonds are marked by dashed lines between interacting atoms (distance of < 0.32 nm). (b) Electrostatic interactions between CsgF Arg-8 and CsgG Asp-149 and Glu-185 residues. The bond distance is plotted for nine monomers over 100 ns simulation in 0.075 V nm⁻¹.

Some of the interactions reported in starting structures of the CsgG-CsgF complex, including hydrogen bonds between CsgF Gly-1 and CsgG Asn-133 or Gln-153 residues, and CsgF Gln-6 and CsgG Gln-187 residues, were not present in all monomer pairs in 0.075 V nm⁻¹ (Fig. A.7). Moreover, hydrogen bonds formed by threonine residues of CsgF (Thr-2 and Thr-4) and CsgG (Thr-207) in the starting structures were not present in the simulations. Additional interactions that were not observed in the starting structure include hydrogen bonds between residues in the CsgF C-terminus and near the CsgG β-barrel exit. As a consequence, the short turns of the β-barrel (residues 191–198) remained ordered, with RMSF similar to when in 0 V and 0.05 V nm⁻¹ (∼ 0.05–0.20 nm).

In addition to hydrogen bonding, Arg-8 in the CsgF N-terminus also forms stabilizing electrostatic interactions with Asp-149 and Glu-185 residues in CsgG. The interactions between Arg-8 and Asp-149 residues were observed in all monomer pairs, however the interactions between Arg-8 and Glu-185 residues were observed for some monomer pairs only (Fig. 5).

2.3. DNA translocation

The movement of ssDNA through uncomplexed CsgG and the CsgG-CsgF complex was investigated. A 12-nucleotide polyA ssDNA strand, with the DNA 5′ terminal nucleotide initially positioned inside the eyelet loop region, was pulled through the protein pore at a rate of 0.15 nm ns⁻¹ by applying a force on the 5′ terminal nucleotide. Eight independent simulations were performed for uncomplexed CsgG and the CsgG-CsgF complex. The position of the center of mass of the DNA nucleotides as a function of time was calculated to characterize the DNA translocation through the pore (Fig. A.8 and Fig. A.9). Overall, DNA exited the CsgG-CsgF complex by ∼ 70–75 ns, and uncomplexed CsgG by ∼ 70 ns, in five simulations. DNA remained in the pore exit by 75 ns in three simulations of uncomplexed CsgG and the CsgG-CsgF complex due to the DNA 3′ terminal nucleotides interacting with residues at the pore exit. DNA moved through the CsgG eyelet loop constriction in a stepwise manner, as a result of hindered movement past the side chains of Phe-56, Asn-55, and Tyr-51 residues. Some nucleotides were halted for as long as 5 ns in these regions. The movement of DNA was unhindered once past the eyelet loop constriction in uncomplexed CsgG. In the CsgG-CsgF complex, the translocation of nucleotides was also slower past the Asn-17 residues which forms the CsgF constriction.

The translocation rates through regions of uncomplexed CsgG and the CsgG-CsgF complex were calculated as the distance traversed by a nucleotide per nanosecond, for two regimes of DNA translocation: (1) when the DNA strand is threaded through the CsgG eyelet loop region, and; (2) after the 3′ terminus is no longer present within the eyelet loop region (Table 4). Regime (1) mimics behaviour of long DNA strands that remain threaded through the CsgG eyelet loop region during DNA sequencing.

Table 4.

DNA nucleotide translocation rates through regions of uncomplexed CsgG and the CsgG-CsgF complex.

Region	Average DNA nucleotide translocation rate (nm ns−1) ± SD
	Regime (1)		Regime (2)
	CsgG	CsgG-CsgF complex	CsgG	CsgG-CsgF complex
CsgG eyelet loop region	0.18 ± 0.03	0.17 ± 0.04	N/A	N/A
CsgF region (β-barrel region in uncomplexed CsgG)	0.17 ± 0.02	0.14 ± 0.02	0.23 ± 0.06	0.18 ± 0.03

In regime (1), the translocation rate through the eyelet loop region is essentially the same in uncomplexed CsgG (0.18 ± 0.03 nm ns⁻¹) and the CsgG-CsgF complex (0.17 ± 0.04 nm ns⁻¹). DNA translocation is faster through the CsgG β-barrel region (0.17 ± 0.02 nm ns⁻¹) than through CsgF in the CsgG-CsgF complex (0.14 ± 0.02 nm ns⁻¹), but not significantly (p = 0.08), which suggests that the translocation rate is not dramatically altered by CsgF.

In regime (2), DNA translocation is substantially faster than in regime (1) in both uncomplexed CsgG and the CsgG-CsgF complex; as a reminder, the eyelet loops are not involved in interactions with DNA in this regime. The translocation rate is significantly faster (p = 0.0002) through the CsgG β-barrel region (0.23 ± 0.06 nm ns⁻¹) than through the CsgF region (0.18 ± 0.03 nm ns⁻¹). Thus, while CsgF presents an additional barrier to DNA translocation, the eyelet loop region has a greatest impact on the translocation rate of DNA.

We next examined the conformational behaviour of the DNA strand and the DNA-protein interactions during translocation, to elucidate the origins of the differences in translocation rates through uncomplexed CsgG and the CsgG-CsgF complex. Cluster analysis was performed to characterise the conformations adopted by the DNA strand as it is pulled through the protein pores. We consider uncomplexed CsgG first. The DNA populations can be placed into three groups, according to the position of the DNA inside the pore: group 1 in which the DNA is halted in the CsgG vestibule and the eyelet loop region, with the 5′ terminus below the eyelet loop region; group 2 in which the DNA is threaded through the eyelet loop region, with the 5′ terminus in the β-barrel; and group 3 in which the DNA has exited the eyelet loop region. Groups 1 and 3 are not directly relevant to DNA sequencing and are also likely to be most impacted by the choice of the DNA length and so here we focus only on the DNA conformations of group 2 (as we have done in our previous work on DNA translocation through model pores) [26].

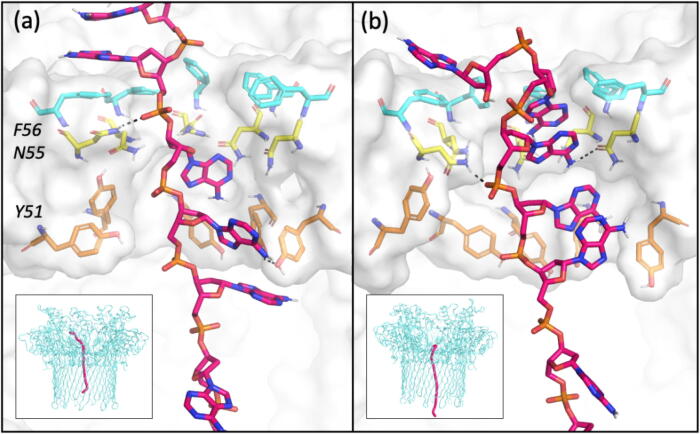
Group 2 is formed by four cluster populations comprising 12% of simulation time (∼ 58 ns) (Fig. 6). The end-to-end distances of DNA conformations in these clusters ranged from ∼ 5.7–6.2 nm, with the DNA becoming more extended as it translocated further downwards through the pore. This is in contrast to previously reported observations from simulations of a model of the ɑ-hemolysin barrel, in which the 12-nt ssDNA was more coiled with end-to-end distances ranging from ∼ 3.8–4.5 nm [27]. In the eyelet loop region, residues Asn-55 and Tyr-51 formed hydrogen bonds with the DNA bases and backbone phosphate groups, and Phe-56 and Tyr-51 residues interacted with nucleotides via pi-stacking. The interactions with Phe-56 residues led to nucleotides being halted at the entrance of the eyelet loop region, whilst nucleotides below formed interactions with Asn-55 and Tyr-51 residues. The nucleotides once moving past Phe-56 residues were subsequently halted again by Asn-55 and then by Tyr-51 residues during translocation. The combined effect of these interactions resulted in the DNA segment becoming extended in the eyelet loop region. This is especially evident during the translocation of the DNA 3′ terminus region, which uncoiled as it moved through the eyelet loop region (Fig. A.10).

Fig. 6.

Representative DNA conformations from two clusters of uncomplexed CsgG. A cross-sectional view of the DNA segment and residues in the CsgG eyelet loop region is shown. Hydrogen bonds are shown as dashed lines. Inset shows the position of the DNA strand in uncomplexed CsgG.

In the CsgG-CsgF complex, the DNA populations can be placed into three groups, according to the position of the DNA inside the pore; group 1 in which the DNA is halted in the CsgG vestibule and the eyelet loop region, with the 5′ terminus below the eyelet loop region; group 2 in which the DNA is threaded through both CsgG and CsgF constriction regions, with the 5′ terminus in CsgF; and group 3 in which the DNA has exited the CsgG eyelet loop region, with the 3′ terminus in CsgF. Group 1 is not directly relevant to DNA sequencing, and the DNA conformations are also likely to be most impacted by the choice of DNA length and so here we focus only on the DNA conformations of groups 2 and 3.

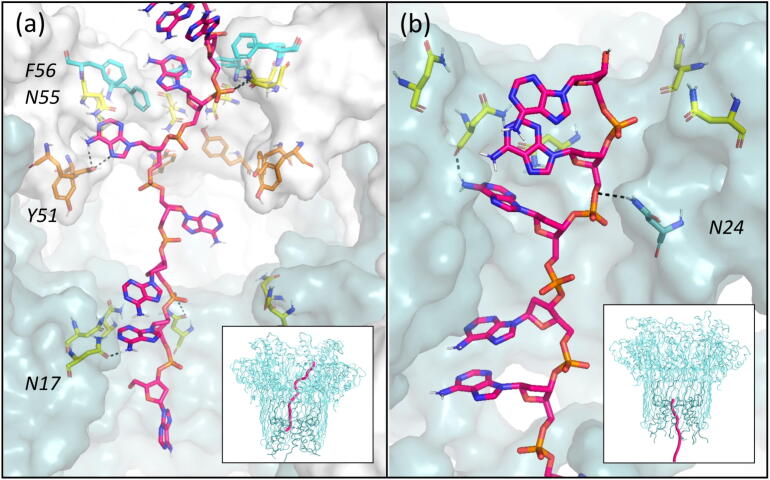
Group 2 is formed by four cluster populations comprising 29% of simulation time (∼ 162 ns) (Fig. 7a). The end-to-end distances of DNA conformations in these clusters ranged from ∼ 6.3–7.2 nm, with the DNA becoming more extended as it translocated further downwards through the pore. The DNA strand is retained in an extended conformation due to nucleotides forming interactions with residues in the CsgG and CsgF constrictions. Phe-56, Asn-55, and Tyr-51 residues in the eyelet loop region form pi-stacking and hydrogen bonding interactions, and Asn-17 residues in the CsgF constriction form hydrogen bonding interactions with the DNA.

Fig. 7.

Representative DNA conformations in four clusters of the CsgG-CsgF complex. A cross-sectional view of the DNA segment and residues in CsgG eyelet loop region and CsgF constriction is shown. Hydrogen bonds are marked by dashed lines. Inset shows the position of the DNA strand in the CsgG-CsgF complex.

Group 3 consists of a cluster population comprising 8% simulation time (∼ 45 ns), in which the DNA 3′ terminus region is translocating through CsgF after exiting the CsgG eyelet loop region (Fig. 7b). An Asn-24 residue is also observed to interact with the DNA backbone phosphate group along with an Asn-17 residue in the CsgF constriction. DNA adopted group 3 conformations for a shorter duration than group 2, in which DNA is threaded through both CsgG and CsgF constrictions. This is consistent with the significant increase in translocation rate observed following DNA exit from the CsgG eyelet loop region into the CsgF constriction.

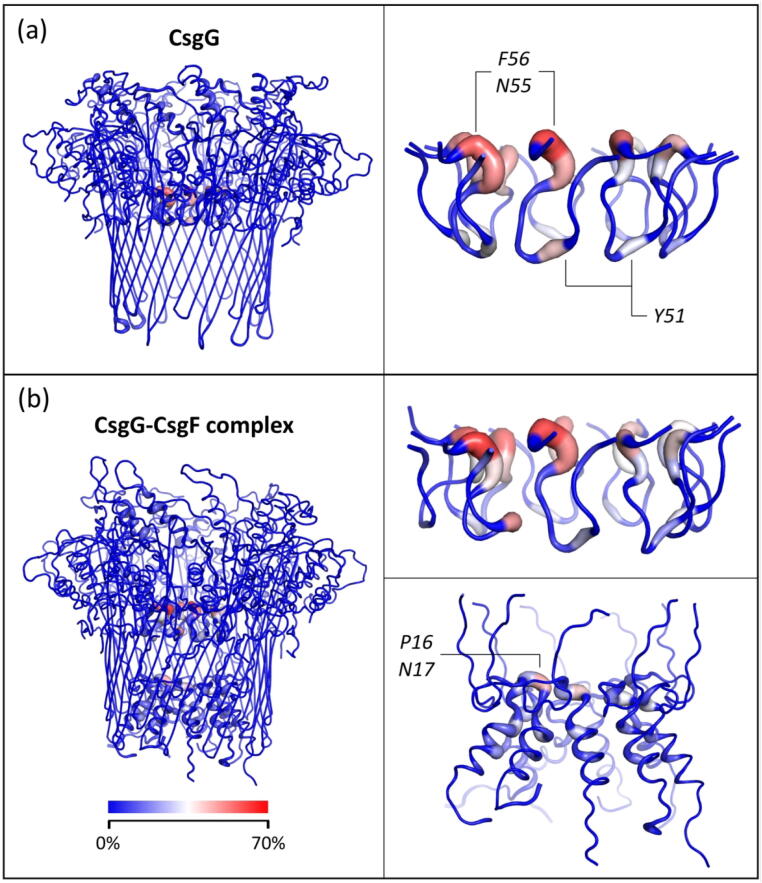
The interactions of the translocating DNA with uncomplexed CsgG and the CsgG-CsgF complex were quantified by calculating the percentage simulation time that the residues were within 0.4 nm of the DNA strand (Fig. 8). Overall, DNA largely formed interactions with Phe-56, Asn-55, and Tyr-51 residues in the CsgG eyelet loop region in both uncomplexed CsgG and the CsgG-CsgF complex. Asn-17 residues in the CsgF constriction also interacted with the DNA in the CsgG-CsgF complex, but to a lesser extent than the residues in the eyelet loop region. The higher frequency of DNA interactions with residues in the CsgG eyelet loop region compared to in CsgF suggests that the eyelet loop region has a greater impact on the DNA translocation rate.

Fig. 8.

DNA-protein interactions. CsgG (a) and the CsgG-CsgF complex (b) are coloured by the percentage of simulation time for which the residues interact with DNA, in 8 independent simulations. Side-views of the CsgG eyelet loop region (residues 47–58) and CsgF are also shown. Interactions are defined as an inter-atomic distance of < 0.4 nm.

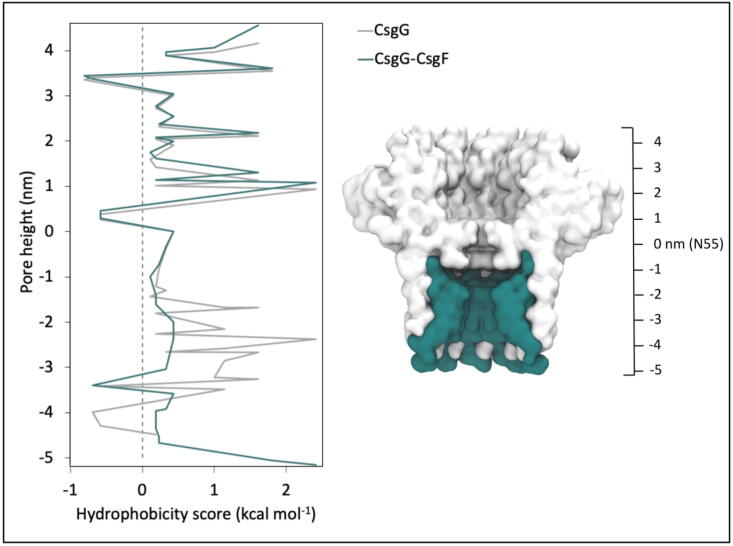
Although the translocating DNA remained linear in both uncomplexed CsgG and the CsgG-CsgF complex, it was retained in a more extended conformation in the CsgG-CsgF complex. It has been previously shown that DNA is retained in a largely linear conformation in hydrophobic model pores based on 14-stranded β-barrel architecture [28], and more so in pores containing two hydrophobic constriction regions compared to one [26]. Comparison of the pore-lining residues of uncomplexed CsgG and the CsgG-CsgF complex revealed that the CsgG-CsgF complex forms a more hydrophobic pore compared to CsgG, due to residues with acidic and basic side chains in the CsgG β-barrel region being replaced by hydrophobic residues in the CsgF monomers (Fig. 9). Together, this suggests that the extended conformation of the DNA in the CsgG-CsgF complex is a consequence of the presence of two constriction regions and the hydrophobic nature of the pore.

Fig. 9.

Hydrophobicity of pore-lining residues in CsgG and the CsgG-CsgF complex, according to the scale proposed by Wimley and White [29]. The scale ranges from −0.81 kcal mol⁻¹ to 2.41 kcal mol⁻¹, for very hydrophobic to very hydrophilic residues respectively. The dashed line marks the score of 0. A cross-sectional view of the CsgG-CsgF complex is also shown for reference.

2.4. Conductance of CsgG and the CsgG-CsgF complex in the presence of immobilised DNA

During DNA sequencing, the characteristic reduction in the ionic current through the nanopore is caused by the translocating nucleotides and is analysed to read the sequence. To evaluate the impact of the additional CsgF constriction on the pore ionic conductance during DNA translocation, the uncomplexed CsgG and the CsgG-CsgF complex were simulated with immobilised DNA threaded through the pore and with an applied electric field equivalent to 0.9 V (five times higher than 0.18 V used for DNA sequencing). The ionic currents through uncomplexed CsgG and the CsgG-CsgF complex in presence of immobilised polyA ssDNA are reported in Table 5 and Table A.1. The mean bidirectional flux of water and ions through the pores are given in Table A.2.

Table 5.

Ionic currents through uncomplexed CsgG and the CsgG-CsgF complex with immobilised polyA ssDNA in 0.9 V, calculated for 50 ns. Data is average calculated from three independent simulations for each system.

System	Itotal (pA)	IK (pA)	ICl (pA)
CsgG	333 ± 77.5	311 ± 80.2	22 ± 15.4
CsgG-CsgF complex	181 ± 122.1	172 ± 115.4	8 ± 7.0

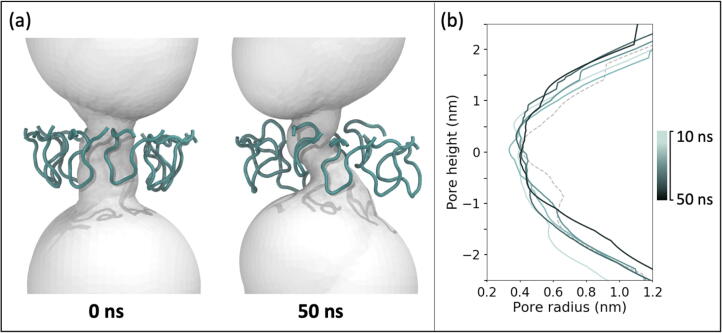
Overall, the mean water flux and the ionic current were higher through uncomplexed CsgG compared to the CsgG-CsgF complex, the latter contains an additional constriction region formed by CsgF. In CsgG systems, there is a large variability in water flux in three independent simulations (average: 993 ± 58.7 ns⁻¹). This is due to the variability in motion of the eyelet loops. In one simulation, three eyelet loops flipped upwards by 50 ns, which caused the constriction to become narrower; consequently, the water flux through the pore was significantly lower in this simulation (926 ns⁻¹) compared to the other two simulations (1034 ns⁻¹ and 1020 ns⁻¹) (Fig. 10). In the two simulations with higher water flux, the eyelet loops were observed to move closer to the β-barrel wall which widened the CsgG constriction. In contrast, the eyelet loops did not flip upwards in any of the simulations of the CsgG-CsgF complex (consistent with aforementioned simulations of this complex with an applied electric field, but no DNA). Overall, the presence of CsgF resulted in reduced water flux and ionic current compared to uncomplexed CsgG (Table 5).

Fig. 10.

Panel (a) shows the change in pore shape in response to change in the conformations of the eyelet loops in a simulation of uncomplexed CsgG with immobilised DNA, in which the lowest water flux was observed. Panel (b) shows the change in the radius of the eyelet loop region over 50 ns. The pore radius at the start of the simulation is plotted as a dashed line.

We next simulated the systems with positional restraints applied to CsgG eyelet loops (backbone atoms of residues 47–58) to prevent large loop motion. The ionic currents through uncomplexed CsgG and the CsgG-CsgF complex for these simulations are reported in Table 6 and Table A.3. The mean bidirectional flux of water and ions through the pores are reported in Table A.4. In the absence of large eyelet loop motion, as expected the CsgG simulations resulted in a more consistent water flux amongst three independent simulations (average: 859 ± 31.1 ns⁻¹), indicating that reducing the motion of these loops may lead to less noisy sequencing data. The flux of water and the total ionic currents in simulations of the CsgG-CsgF complex are similar to the simulations without positional restraints applied to the CsgG eyelet loops (Table A.5). This is consistent with the observation that the eyelet loops did not flip in the presence of CsgF. The presence of CsgF resulted in ∼ 80% reduction in water flux through the CsgG-CsgF complex compared to uncomplexed CsgG.

Table 6.

Ionic currents through uncomplexed CsgG and the CsgG-CsgF complex with immobilised DNA and CsgG eyelet loops in 0.9 V, calculated for 50 ns. Data is average calculated from three independent simulations for each system.

System	DNA	Itotal (pA)	IK (pA)	ICl (pA)
CsgG	polyA	271 ± 102.4	269 ± 101.5	2 ± 1.1
CsgG-CsgFcomplex	polyA	151 ± 76.4	149 ± 76.3	2 ± 1.8
	polyT	349 ± 28.1	346 ± 30.4	2 ± 2.8

To evaluate the ability of the CsgG-CsgF complex to discriminate between distinct nucleotides, we next simulated the pore with immobilised polyT ssDNA. The ionic currents through the CsgG-CsgF complex for these simulations are reported in Table 6 and Table A.3. The mean bidirectional flux of water and ions through the pores are reported in Table A.4. The total ionic current through the CsgG-CsgF complex was ∼ 2 × higher in the presence of polyT compared to polyA. This can be explained by the larger steric bulk of the purine adenine physically occluding the pore to a greater extent compared to thymine.

Experimentally, direct comparisons between studies are hindered by differences in experimental conditions such as temperature, ion concentration, and the voltage applied. To circumvent this, blockage current ratios are calculated by dividing the ionic current in presence of DNA by the open pore current. A lower blockage current ratio therefore corresponds to a greater degree of open pore current blocked by DNA. The blockage current ratios for the CsgG and the CsgG-CsgF complex are shown in Table 7, and the open pore currents are reported in Table A.7. The total blockage current ratio in presence of polyA is lower for the CsgG-CsgF complex (0.29) than uncomplexed CsgG (0.44). Thus, the presence of CsgF resulted in a more distinct change in channel conductance in presence of DNA.

Table 7.

Blockage current ratios for uncomplexed CsgG and the CsgG-CsgF complex with immobilised DNA, in 0.9 V. Ratios calculated for average ionic currents, calculated from three independent simulations.

System	DNA	Itotal	IK	ICl
CsgG	polyA	0.44	0.62	0.01
CsgG-CsgFcomplex	polyA	0.29	0.42	0.01
	polyT	0.68	0.98	0.01

In the CsgG-CsgF complex, the blockage current ratio is nucleobase size-dependent; the larger purines in polyA impede the open pore current to a greater degree than smaller pyrimidines in polyT (total blockage current ratio is 0.29 and 0.68 respectively).

Interestingly, in wild-type ɑ-hemolysin the current blockage is not solely nucleobase size-dependent; the larger purines in polyA blocked current to a lesser degree than smaller pyrimidines in polyT when immobilised inside the pore (blockage current ratio polyA = 0.18, polyT = 0.15, in 0.12 V) [30]. However, ɑ-hemolysin mutants modified to increase the hydrophobicity of the constriction region (E111N/K147N/M113X, X  = V, L, or I) resulted in improved and size-dependent base discrimination i.e., A caused a greater current blockage than T [31]. Furthermore, a hydrophobic solid-state nanopore was also shown to be able to discriminate between polyA and polyC [32]. Similarly in our simulations, the hydrophobic pore formed by the CsgG-CsgF complex (Fig. 9) is able to discriminate between polyA and polyT on a nucleobase size-basis.

Despite the differences in the current blockages by the two DNA bases, we were unable to detect significant differences in their respective interaction energies with the CsgG-CsgF complex based on enthalpic calculations both from postprocessing our MD simulations (Table A.8) and also treating representative frames by Density Functional Theory (DFT) (Table A.9). The major stabilisation interaction comes from water-DNA and ion-DNA interactions as has been observed from similar calculations on solid state hydrophobic pores [32].

3. Conclusions

In conclusion, we find that the conformational behaviour of CsgG when uncomplexed and in the CsgG-CsgF complex differs under an applied electric field. The eyelet loops forming the CsgG constriction region are observed to be more flexible in uncomplexed CsgG compared to in CsgG-CsgF complex under an applied electric field. Eyelet loops ‘flip’ upwards into the vestibule of uncomplexed CsgG to varying degrees, while not impacting the protein conformation and stability. The presence of CsgF stabilises the conformation of the eyelet loops and prevents large loop motion in the presence of an electric field in the CsgG-CsgF complex. Uncomplexed CsgG is unstable in high electric strengths, due to the disruption of hydrogen bonds between β-sheets of two monomers which leads to separation of the monomers in the CsgG transmembrane β-barrel. However, the CsgG-CsgF complex remains stable due to the residues of the CsgG transmembrane β-barrel forming a network of hydrogen bonds and electrostatic interactions with CsgF monomers.

DNA translocation through uncomplexed CsgG and the CsgG-CsgF complex is slowed down by the CsgG eyelet loop region and the CsgF constriction. The translocating DNA is slowed down in the eyelet loop region by Asn-55 residues forming hydrogen bonds, and Phe-56 and Tyr-51 residues interacting with nucleotides via pi-stacking. In the CsgG-CsgF complex, DNA is also slowed by transient interactions with Asn-17 residues within CsgF constriction; however, the frequency of these interactions is lower than in the eyelet loop region, hence DNA translocation is faster through the CsgF region after the strand exits the CsgG constriction. Therefore, DNA translocation rate is influenced principally by the CsgG eyelet loop region, with the CsgF constriction playing a minor role. Our simulations of systems with the immobilised DNA threaded through uncomplexed CsgG and the CsgG-CsgF complex revealed that: (1) the change in the channel conductance in presence of DNA is more distinct through the CsgG-CsgF complex compared to uncomplexed CsgG, and (2) the CsgG-CsgF complex channel conductance is sensitive to the size of the nucleobases A and T.

In summary, our simulations reveal that CsgG-CsgF complex provides a more hydrophobic, but less conformationally labile nanopore compared to CsgG. Although CsgF introduces a second constriction within the CsgG pore, it has a minor effect on the DNA translocation speed. Specific transient interactions with key residues in the CsgG eyelet loops provide the major contribution to the retarding and facilitating progressive movement of DNA through the pore. This feature is a key requirement for electrophoretic nanopore sequencing.

The presence of the second constriction formed by CsgF has several important indirect effects. Notably, the CsgG-CsgF complex has significantly improved stability in high electric fields over uncomplexed CsgG and also a profound reduction in eyelet loop mobility, which has concomitant reduction in ion flux. Furthermore, the shape and the hydrophobicity of the dual constriction region in the CsgG-CsgF complex maintains the translocating DNA in a more extended conformation during its passage. Lastly, the presence of CsgF results in a more distinct change in the channel conductance when polyA is added to the pore. We postulate that these features combined provide an improved electric current density signature for different nucleotide sequences and allow for better single base discrimination. Our work provides new structural and dynamics insights that will inform the future design of novel biology nanopores with improved performance.

4. Materials and methods

In this study, 2 different structures were used for both the uncomplexed CsgG and the CsgG-CsgF complex. These will be labelled as follows in this section: CsgG-1 - crystal structure obtained from the Protein Data Bank (PDB 4UV3, 3.59 Å) and CsgG-2 - electron cryo-EM structure taken from the structure of the CsgG-CsgF complex with CsgAN6 peptide (PDB 6L7C, 3.34 Å); CsgG-CsgF-1 complex - electron cryo-EM structure (PDB 6SI7, 3.4 Å); and CsgG-CsgF-2 complex - electron cryo-EM structure taken from the structure of the CsgG-CsgF complex with CsgAN6 peptide (PDB 6L7C, 3.34 Å).

The missing protein loops in CsgG-1 (residues 144, 193–199) were built by fitting the structure into the map density (PDB 4Q79, 3.1 Å) using Coot [33]). The missing residues in CsgG-CsgF-1 (residues 1–9, 103–110) were added using Modeller 9.02 based on sequence alignment and fitting with CsgG-1 [34]. CsgG N-termini cysteine residues in all 4 structures were lipidated, and the protein was embedded in POPC bilayer (CsgG: 1026 lipids; CsgG-CsgF: 1106) using CHARMM-GUI membrane builder [35], [36], [37], [38]. The systems were solvated using the TIP3P water model, with ions added to a concentration of 1.0 M [39]. Additional ions were added to neutralise the systems prior to simulation. The systems were energy minimised and equilibrated using a stepwise equilibration protocol, which involved running multiple simulations with stepwise reduction of positional restraints applied to the protein and membrane lipids. Initial equilibration steps were run for 385 ps in total, with the temperature of the systems maintained at 303.15 K to pack the membrane around the lipid anchors of the protein. The temperature was increased to 310 K in subsequent equilibration steps run for 225 ps in total, before running longer simulations without positional restraints applied. An electric field was applied after simulating the systems without positional restraints applied for 100 ns.

4.1. Steered Molecular dynamics simulations with DNA

The ssDNA models used were 12-nucleotide polyA and polyT ssDNA generated using the 3DNA package [40]. The systems with DNA were solvated, with ions added to concentration of 0.15 M and additional ions added to neutralise the systems prior to simulation. The systems were energy minimised and equilibrated using the step-wise equilibration protocol as described earlier, with the temperature of the systems maintained at 310 K. Positional restraints with force constant of 1000 kJ mol⁻¹ nm² were applied to DNA 5′ terminal nucleotide during equilibration.

In steered MD simulations, DNA 5′ terminal nucleotide was selected as the pull group and proline residues (P52) in CsgG were selected as the reference group. The reaction coordinate was defined as a vector in -z direction, parallel to the protein axis, along which the DNA 5′ terminal nucleotide was pulled at a rate of 0.15 nm ns⁻¹ and using a spring constant of 1000 kJ mol⁻¹ nm².

4.2. Conductance of CsgG and the CsgG-CsgF complex in presence of immobilised DNA

The starting structures of CsgG and the CsgG-CsgF complex with DNA were extracted from steered MD simulations. Positional restraints of 1000 kJ mol⁻¹ nm² were applied to DNA backbone phosphorus atoms. In simulations where the CsgG eyelet loops were restrained, positional restraints of 500 kJ mol⁻¹ nm² were applied to backbone atoms of residues 47–58.

All simulations were performed using GROMACS version 2018.3 [41] and the CHARMM36m force field [42]. All simulations were performed in the NPT ensemble, with the temperature maintained using the v-rescale thermostat and coupling constant of 0.1 ps, and the pressure maintained semi-isotropically using the Parrinello-Rahman barostat at 1 bar and a time constant of 5 ps [43]. Constraints were used for bond lengths using the LINCS algorithm enabling a timestep of 2 fs. The long-range electrostatics were treated using the Particle Mesh Ewald method with a short-range cutoff of 1.4 nm [44]. The van der Waals interactions were truncated at 1.4 nm with long-range dispersion corrections applied to the energy and pressure. In simulations with an applied electric field, the electric field was imposed by a constant voltage drop across the simulation box.

Analyses were conducted using the functions available in the GROMACS package and locally written code. Clustering analysis was performed using the GROMOS method [45] implemented in GROMACS (gmx cluster). The trajectories from independent simulations for a given system were concatenated prior to clustering DNA conformations with a root mean-square deviation cutoff of 0.28 nm, using the initial conformation of DNA as a reference. Pore radius profiles for the proteins were calculated using HOLE [46]. Molecular graphic images were produced using the Visual Molecular Dynamics VMD package [47] and PyMOL [48]. Mean water and ion flux rates were calculated as described by Haynes et al [28]. The ionic currents were calculated as described by Aksimentiev et al [5].

4.3. Energetics

MD simulation trajectories were post-processed and the average interaction energies of interest were extracted using the GROMACS energy module. Interaction energies from DFT were obtained using the ONETEP code [49], [50], full details are provided in the supporting information.

4.4. Statistical analysis

The differences in nucleotide translocation rates, mean water flux rates, and ionic currents were assessed using unpaired t-tests. Values of p < 0.05 were regarded as significant.

CRediT authorship contribution statement

Punam Rattu: Investigation, Writing – original draft. Flo Glencross: Investigation, Writing – original draft. Sophie Mader: Investigation. Chris-Kriton Skylaris: Supervision. Stephen J. Matthews: Supervision, Conceptualization, Writing – review & editing. Sarah L. Rouse: Supervision, Conceptualization, Writing – review & editing. Syma Khalid: Supervision, Conceptualization, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: