Summary.
Causal mediation analysis aims to characterize an exposure’s effect on an outcome and quantify the indirect effect that acts through a given mediator or a group of mediators of interest. With the increasing availability of measurements on a large number of potential mediators, like the epigenome or the microbiome, new statistical methods are needed to simultaneously accommodate high-dimensional mediators while directly target penalization of the natural indirect effect (NIE) for active mediator identification. Here, we develop two novel prior models for identification of active mediators in high-dimensional mediation analysis through penalizing NIEs in a Bayesian paradigm. Both methods specify a joint prior distribution on the exposure-mediator effect and mediator-outcome effect with either (a) a four-component Gaussian mixture prior or (b) a product threshold Gaussian prior. By jointly modeling the two parameters that contribute to the NIE, the proposed methods enable penalization on their product in a targeted way. Resultant inference can take into account the four-component composite structure underlying the NIE. We show through simulations that the proposed methods improve both selection and estimation accuracy compared to other competing methods. We applied our methods for an in-depth analysis of two ongoing epidemiologic studies: the Multi-Ethnic Study of Atherosclerosis (MESA) and the LIFECODES birth cohort. The identified active mediators in both studies reveal important biological pathways for understanding disease mechanisms.
Keywords: Composite null hypothesis, Environmental exposure to phthalates, Epigenetics, Gaussian mixture models, High-dimensional mediators, Pathway Lasso, Posterior inclusion probability, Product threshold Gaussian prior
1. Introduction
Mediation analysis is of increasing importance across a wide range of disciplines (MacKinnon et al., 2007). It investigates how an intermediate variable, called a mediator, explains the mechanism underlying a known relationship between the exposure and the outcome. The main goal of such an analysis is to disentangle the exposure’s effect and identify effect that acts through the mediator of interest, which is often referred to as the indirect/mediation effect. Built on the counterfactual framework, a causal approach to mediation analysis (VanderWeele, 2016) specifies assumptions for a potentially causal interpretation of estimated indirect effects using the classical formulas from Baron and Kenny (1986). Univariate mediation analysis, which analyzes one mediator at a time, has been studied extensively in areas of social, economic, epidemiological and genetic studies (MacKinnon, 2008). With the rapid development of high-throughput technologies and the increasing availability of large-scale omics data, however, there is an expanding interest in performing mediation analysis in the presence of a large number of mediators. As one of our motivating examples, the Multi-Ethnic Study of Atherosclerosis (MESA) measured gene expression and DNA methylation (DNAm) levels at the genome-wide scale. These molecular-level omics traits are proposed as part of the mediating mechanism through which neighborhood disadvantages affect physical health (Smith et al., 2017). As another motivating example, the LIFECODES prospective birth cohort collected data on a large group of endogenous biomarkers of lipid metabolism, inflammation, and oxidative stress. These biomarkers are hypothesized to mediate the effects of prenatal exposure to environmental contamination on adverse pregnancy outcomes. Mediation analysis in the above high-dimensional mediator settings can facilitate our understanding of disease etiology but is particularly challenging because the causal ordering among mediators is often unknown a priori due to a lack of in-depth biological knowledge acquired on the relationship among the mediators. On the other hand, it is not preferable to apply univariate mediation analysis to the high-dimensional setting due to potential confounding of other mediators in the association with the outcome and mis-specification of the true model.
To enable high-dimensional mediation analysis, several statistical methods have been recently developed. For example, Huang and Pan (2016) and Chén et al. (2017) transform the high-dimensional unordered set of mediators into lower-dimensional orthogonal components using dimension reduction techniques. The extracted low-dimensional components are then analyzed through single mediation analysis. However, it is often not straightforward to interpret the low-dimensional components in these approaches. Shrinkage methods via regularization have also been explored to tackle this high-dimensional regression problem involving two models, the exposure-mediator model and the outcome-exposure model. The Lasso (Tibshirani, 1996) penalty can be naturally applied to the two models in mediation analysis. Zhang et al. (2016) also proposed a regularized regression with minimax concave penalty for the outcome model after a sure independence screening on mediators. The above methods penalize the mediator-outcome and exposure-mediator coefficients separately without taking into account the structure of the indirect effect. To directly target the mediators with strong indirect effects, Zhao and Luo (2016) recently developed a new convex, Lasso-type penalty on the indirect effect, which is the product of the two path coefficients. This direct penalization on the pathway effects is shown to improve power for mediator selection and reduce the estimation bias of indirect effects. In addition to frequentist approaches, Bayesian non-parametric models (Kim et al., 2019) have been applied in the analysis with a moderate number of mediators. Song et al. (2019) handles high-dimensional mediators through a Bayesian variable selection method and specifies separate shrinkage priors on both the exposure-mediator effects and mediator-outcome effects. However, not modeling the indirect effects in a targeted way may lead to loss of power for selection of active mediators. Therefore, a more effective mediation analysis will require the development of statistical methods that can both handle high-dimensional mediators and select active mediators via direct targeting of their indirect contribution to the joint NIE. There is also interesting connection between mediation analysis and directed acyclic graph (DAG), where the ordering of the nodes (exposure, mediators, and outcome) is known. Our goal of identifying active mediators then corresponds to graph structural learning of the edges, and any mediator with inferred links both from the exposure and to the outcome completes a mediation pathway.
The indirect effect of a mediator is known to be proportional to the product of the exposure-mediator and mediator-outcome effects under certain assumptions (MacKinnon, 2008). Testing for this product term is not easy due to the complexity in its null distribution. Recent literature began to recognize and leverage the composite structure in the null hypothesis of no indirect effect in the genome-wide mediation analysis setting, where a one-at-a-time single mediator analysis is performed across the entire set of mediators (Huang, 2019). Given a large number of mediators, we can characterize the composite space and learn about the structure of mediation through the four components arising from the product of the two effects, i.e. one component of mediators with non-zero indirect contributions (active mediators), and three components with zero indirect contributions.
Motivated by the goal of directly targeting the non-null indirect contributions to identify active mediators in a high-dimensional mediator setting, we are interested in seeking the Bayesian parallel with a joint prior on the exposure-mediator and mediator-outcome coefficients, which is so far lacking in the literature. One common choice of the bivariate prior would be a Gaussian prior, and it is natural to assume a four-component Gaussian mixture structure on the two effects, corresponding to the composite structure underlying their product. On the other hand, a direct thresholding prior on the indirect contributions would also achieve the same goal, and we can extend the hard-thresholding priors (Ni et al., 2019; Cai et al., 2020) to product thresholding for mediation analysis. Therefore, in this paper, building on the potential outcome framework for causal inference, we develop two novel prior models for high-dimensional mediation analysis: (a) four-component Gaussian mixture prior, and (b) product threshold Gaussian prior. Both models can simultaneously analyze a large number of mediators without making any path-specific or causal ordering assumptions on mediators. The mediator categorization into four groups provides useful interpretations on the way in which a mediator links or does not link exposure to outcome. More importantly, by jointly modeling the exposure-mediator and mediator-outcome coefficients via either bivariate Gaussian distributions or thresholding functions, we place direct shrinkage on the product of the two coefficients in a targeted way. Hence, our methods are expected to outperform other penalization methods that apply separate shrinkage in the two regression models independently, for identifying active mediators with non-zero indirect contributions.
The proposed methods are generally applicable to many settings, and we examine their performance for both large-scale genomic and environmental data. Specifically, in the MESA cohort, our methods are implemented for high-dimensional mediation analysis with DNAm as mediators (Bild et al., 2002), focusing on the relationship between neighborhood disadvantage (exposure) and body mass index (BMI) as outcome. BMI is a critical risk factor for various diseases like type 2 diabetes (T2D) and cardiovascular disease (CVD) (Hjellvik et al., 2012). The important scientific discoveries made in the present study will advance biological understanding of how adverse social circumstances influence our internal molecular environment and in turn lead to cardiometabolic diseases. In the LIFECODES birth cohort, the proposed methods are applied to study the collective impact of endogenous biomarkers in biological pathways in mediating exposure to phthalates (a group of chemicals used to make plastic more flexible) during pregnancy on the gestational age of the newborn at delivery. The integration of molecular/biological data with epidemiologic data in the mediation framework provides interesting and important insights into underlying disease mechanisms. Besides the data analysis, we also perform extensive simulation studies under different structures of effects. We show through both simulations and data analysis that our proposed methods can increase power of a joint analysis and enable efficient identification of individual mediators.
The rest of the paper is organized as follows. In Section 2, we first define the causal effects of interest for the multivariate mediator setting with the counterfactual framework. Then we review the mediation estimands under the regression models with high-dimensional mediators and one continuous outcome. In Section 3, we propose two novel methods for direct shrinkage on natural indirect effects. Simulation studies are conducted and discussed in Section 4. We apply our methods to MESA and LIFECODES data in Section 5, and conclude the paper with discussions in Section 6.
2. Notations, Definitions and Models
Consider a study of n subjects and for subject i, i = 1, . . . , n, we collect data on one exposure Ai, p candidate mediators , one outcome Yi, and q covariates . In particular, we focus on the case where Yi and Mi are all continuous variables. With the same counterfactual framework as in Song et al. (2019), let the vector denote the ith subject’s counterfactual value of the p mediators if he/she received exposure a. Let Yi(a, m) denote the ith subject’s counterfactual outcome if the subject’s exposure were set to a and mediators were set to m. The effect of an exposure can be decomposed into its direct effect and effect mediated through mediators. The natural direct effect (NDE) of the given subject is defined as , where the exposure changes from a⋆ (the reference level) to a and mediators are hypothetically controlled at the level that would have naturally been with exposure a⋆. The natural indirect effect (NIE) of the given subject is defined by . The total effect (TE) can then be expressed as the summation of the NDE and the NIE: .
The counterfactual variables, which are useful concepts to formally define causal effects, are not necessarily observed. To connect the counterfactuals to observed data and estimate the average NDE and NIE from observed data, further assumptions are required, including the consistency assumption and four non-unmeasured confounding assumptions (VanderWeele, 2016). We elaborate those assumptions in Section 1 of the Supplementary Materials (SM). It has been shown that under the required assumptions, the average NDE and NIE can be identified by modeling and Mi|Ai, Ci using observed data (Song et al., 2019). Therefore we can work with the two conditional models for Yi|Ai, Mi, Ci and Mi|Ai, Ci. We propose two linear models for the two conditional relationships Yi|Ai, Mi, Ci and Mi|Ai, Ci. For the outcome model, we assume
| (1) |
where ; ; and . For the mediator model, we consider a multivariate regression model that jointly analyzes all p potential mediators together as dependent variables:
| (2) |
where ; ; are q-by-1 vectors; , with Σ capturing potential residual error covariance. and are assumed to be independent of each other and independent of Ai and Ci. With the identifiability assumptions and the modeling assumptions (linearity, no interaction in the outcome and mediator model) in (1)–(2), we can compute the average NDE, NIE and TE as below (Song et al., 2019). In the rest of the paper, we refer to NDE as direct effect and NIE as indirect/mediation effect.
| (3) |
| (4) |
| (5) |
As seen from (4), the global NIE equals to the sum over mediators, M(1),M(2), . . . , M(p), of the product of αaj and βmj. Each of the individual terms in the sum have no causal interpretation of NIE corresponding to a specific mediator j, but rather its marginal contribution to this global NIE. The TE here can also be identified by modeling Yi|Ai, and by definition should not be affected by the model for mediators. Both βa and are conditional on mediators, and their summation estimates the same TE. Alternatively, one may define the common total effect first, and then define the direct effect by the difference . We jointly model βmj and αaj and perform targeted shrinkage on the NIE using two prior models described in the next section.
3. Methods
3.1. Gaussian Mixture Model (GMM)
The first model we develop to characterize the composite structure of the exposure-mediator and mediator-outcome effects in mediation analysis and induce targeted shrinkage on NIE is the four-component Gaussian mixture model. Mixture models have been studied vastly for classifying subjects into different categories and inferring their association patterns or category-specific properties (Zeng et al., 2018). In the context of mediation analysis, previous mixture model approaches have primarily been proposed in the form of a principal stratification model (Gallop et al., 2009). Here, we introduce a Gaussian mixture model for the joint modeling of βmj and αaj and the subsequent inference of the composite association patterns. Specifically, we consider four components in the Gaussian mixture model: a component representing βmjαaj ≠ 0, that both βmj and αaj are non-zero; a component representing βmj ≠ 0 and αaj = 0; a component representing βmj = 0 and αaj ≠ 0; and a component representing βmj = 0 and αaj = 0. To characterize the composite structure underlying the product βmjαaj, we assume that the effects for each mediator follow a four-component Gaussian mixture distribution:
with prior probabilities πk (k = 1, 2, 3, 4) summing to one and MVN2 denoting a bivariate normal distribution. Here, π1 represents the prior probability of being an active mediator, with non-zero marginal mediation effect βmjαaj; and V1 models the covariance of in model (1) and (2) when both effects are non-zero. Any inactive mediator will fall into one of the remaining three components. π2 is the prior probability of having non-zero mediator-outcome effect but zero exposure-mediator effect; and is a low-rank covariance matrix restricting that only the effect of mediator on outcome βmj is non-zero. π3 is the prior probability of having non-zero exposure-mediator effect but zero mediator-outcome effect; and is a low-rank covariance matrix restricting that only the effect of exposure on mediator αaj is non-zero. Lastly, π4 denotes the prior probability of zero mediator-outcome effect and zero exposure-mediator effect; and δ0 is a point mass at zero. Our method automatically classifies all the mediators into four groups based on their relationship with exposure and outcome. We note that the recently developed Bayesian mediation analysis method (BAMA, Song et al., 2019) can be viewed as a two-component version of GMM: in BAMA, the mediator-outcome effect is non-zero and follows a normal distribution with probability π1 + π2; while the exposure-mediator effect is non-zero and follows another normal distribution with probability π1 + π3. Consequently, the active mediator in BAMA has a priori probability (π1 + π2)(π1 + π3).
In GMM, we specify a conjugate inverse-Wishart prior on V1, V1 ~ Inv-Wishart(Ψ0, υ), where Ψ0 = diag {Ψ01, Ψ02} is a diagonal matrix, and ν is the degree of freedom, and inverse-gamma priors on , , , . We also assume {π1, π2, π3, π4} ∼ Dirichlet(a1 ,a2, a3, a4) with a1, a2 and a3 set to be smaller than a4 to encourage sparsity of the first three components. For the coefficients of the other covariates, we assume and . Since we often have adequate information from the data to infer βc and αc, we simply use a limiting prior by setting . For the convenience of modeling, we also set the correlation structure among mediators Σ as . We use weakly informative inverse-gamma priors on the variance hyper-parameters (, and ) in the models.
To facilitate computation, for the jth mediator, we create a four-vector membership indicator variable γj, where γjk = 1 if is from normal component k and γjk = 0 otherwise. Since the priors used here are all conjugate, we implement a standard Gibbs sampling algorithm and iterate each mediator one at a time to obtain posterior samples. The full details of the algorithm appear in Section 2 of the SM available online. With posterior samples, we can estimate the direct effect as the posterior mean of βa, and for the j-th mediator, estimate its indirect contribution as the product of the posterior mean of βmj and αaj. We also calculate the posterior probability of both βmj and αaj being non-zero as the posterior inclusion probability (PIP), which is P(γj1 = 1| Data). The PIP provides evidence for a non-zero indirect contribution, and therefore we identify mediators with the highest PIP as potentially active mediators.
3.2. Product Threshold Gaussian (PTG) Prior
Although the GMM model is flexible for a range of applications, the method does not directly impose sparsity on βmjαaj for mediator selection. To address this issue, we develop a product threshold Gaussian (PTG) prior for the indirect contribution of the j-th mediator. Threshold priors have been recently proposed for Bayesian variable selection. For example, Ni et al. (2019) introduced a hard-thresholding mechanism in edge selection for sparse graphical structure; Cai et al. (2020) performed a feature selection over networks using the threshold graph Laplacian prior; and Kang et al. (2018) developed a soft-thresholding Gaussian process for scalar-on-image regression. As compelling alternatives to shrinkage priors, the threshold priors are equivalent to the non-local priors (Rossell and Telesca, 2017) which enjoy appealing theoretical properties and excellent performance in variable selection for high-dimensional regression, especially when the predictors are strongly correlated (Kang et al., 2018; Cai et al., 2020). In this work, we extend the threshold priors to the product threshold priors for mediation analysis. In particular, for the bivariate vector (βmj, αaj), j = 1, . . . , p,
where the underlying un-thresholded effects and is the indicator function with if occurs and otherwise. We denote (βmj, αaj) ∼ PTG(Σu, λ) with λ = (λ0, λ1, λ2) being thresholding parameters.
As one may note, a mediator would escape thresholding and have non-zero indirect contribution βmjαaj only when (i) both the absolute values of the marginal effects and are larger than the threshold values, or (ii) the absolute value of the un-thresholded product is larger than the threshold value. In practice, condition (ii) does not necessarily indicate condition (i). The product threshold prior will facilitate the selection of active mediators by thresholding on the indirect contribution of the j-th mediator in addition to its marginal effects, and shrinking insignificant effects to zero. Similar to GMM, one group of active mediators and three groups of inactive ones are naturally formed. The thresholding on the product term also adds dependency between βmj and αaj, and we impose no more dependency on the un-thresholded values, namely setting in the rest of the paper.
The threshold parameters λ = (λ0, λ1, λ2) control a priori the sparsity of the non-zero effects, and larger values tend to produce a smaller subset of active mediators. Previous literature (Ni et al., 2019; Cai et al., 2020) have considered uniform priors on those threshold parameters, e.g. λ0 ∼ U[0, λ0h], λ1 ∼ U[0, λ1h], λ2 ∼ U[0, λ2h], with the upper bounds λ0h, λ1h, λ2h being some pre-defined large values. This approach is straightforward and requires little prior knowledge. However, the control of false positives is a concern due to the common under-estimation of λ. In this paper, we instead determine the threshold parameters from the un-thresholded distributions and the desired number of declared positives, and fix them a priori. For example, if we set λ0 = 0.36, λ1 = λ2 = 0.6 under , , then the Monte Carlo estimate of the prior proportion of active mediators is approximately 0.01, which could also be tuned to match with π1 in the Gaussian mixture model. In practice, we can grid search the three hyper-parameters together with priors on and , and find the values that achieve desired prior proportions. The thresholds λ can also be interpreted as the minimal detectable signal, and determined based on their practical meaning. Although the resulting selection may be conservative and heavily informed by the pre-defined thresholds, our specification is helpful in guarding against false positive findings. As in the GMM model described in 3.1, conjugate inverse-gamma priors are used for the variance terms (, , and ) in the model. The full conditional distributions for βmj and αaj are mixtures of truncated normals and can be sampled from Gibbs sampling (Section 3 of the SM). Similar to GMM, we can calculate the posterior mean of βmj and αaj, and the posterior probability of both βmj and αaj being non-zero as PIP, and use the PIP to rank and select active mediators.
The proposed GMM relies on small values of π1, π2, π3 to reflect sparsity on the effects. The Gaussian priors shrink the effects continuously toward zero, and help the model achieve better estimation and prediction performance, but not necessarily mediator selection by the product of βmjαaj. On the other hand, the PTG utilizes a hard threshold function to directly select on βmjαaj and map near zero effects to zero. Instead of centering around zero, the effects produced from PTG will be similar to truncated normals away from zero. As a practical procedure, we suggest median inclusion probabilities (PIP = 0.5) as the significance threshold for mediator selection.
3.3. Other Approaches for High-dimensional Mediation Analysis
Besides GMM and PTG, we also explore a few other approaches. Many of them place simple penalty functions or shrinkage priors on the natural indirect effects.
Univariate Mediation Analysis is perhaps the simplest approach to perform mediation analysis. In univariate mediation analysis, we examine one mediator at a time and test whether the mediator has non-zero indirect effect. We extract P-values for testing the indirect effects using the R package mediation.
Bi-Lasso
The least absolute shrinkage and selection operator (Lasso) introduced by Tibshirani (1996) is a widely used penalty function to perform both variable regularization and selection. Here, we consider placing Lasso regularization on the mediator-outcome effects and the exposure-mediator effects separately. For the mediator-outcome effects, we attempt to minimize the following loss function based on the outcome model (1): . For the exposure-mediator effects, we attempt to minimize the following loss function based on the mediator model (2): . We perform optimization in the first function using the R package glmnet and perform optimization in the second function using soft-thresholding. We choose the two tuning parameters λ1 > 0 and λ2 > 0 through 10-fold cross validation in the two functions separately. We refer this approach of applying Lasso separately to the outcome and mediator models as Bi-Lasso.
Bi-Bayesian Lasso is effectively the Bayesian version of Bi-Lasso. It is equivalent to placing a Bayesian Lasso prior (Park and Casella, 2008) on the mediator-outcome effects βm and a separate Bayesian Lasso prior on the exposure-mediator effects αa. Here, we specify the Bayesian Lasso prior for the j-th element of βm or αa as a scale mixture of normal distributions , where the scale parameter zj follows an exponential distribution exp(s2/2) and 1/s2 is given a diffuse inverse-gamma prior. We implement the Bi-Bayesian Lasso using a Gibbs sampler following Park and Casella (2008) and obtain posterior samples for βm and αa.
Pathway Lasso is a method developed by Zhao and Luo (2016) for high-dimensional mediation analysis under the linear structural equation modeling (LSEM) framework. The squared-error loss in the joint model is defined from equations (1) and (2) as . The Pathway Lasso then aims to minimize the penalized function, .
The first penalty term P1 stabilizes and shrinks the estimates for the product βmjαaj. The second penalty term P2 provides additional shrinkage on βm and αa through a common Lasso penalty placed on both of them. We use the algorithm from Zhao and Luo (2016) to fit Pathway Lasso. We choose the three tuning parameters (φ, ω, and λ): φ = 2, ω = 0.1λ, and choose λ through 10-fold cross-validation as in the original paper. HIMA is another frequentist method developed for high-dimensional mediation analysis (Zhang et al., 2016). HIMA first applies a sure independence screening to the outcome model to select a small set of potential mediators. With the selected mediators, HIMA then places a minimax concave penalty on the mediator-outcome effects in the outcome model (1) to obtain effect estimates. The method finally performs a joint significance test and rejects the null hypothesis of no indirect effect with the j-th mediator if both βmj and αaj are significant. Using the HIMA software, we obtain the Bonferroni corrected P-values for testing the indirect effects.
In addition to the aforementioned methods, we note that several other approaches exist. For example, the methods developed by Huang and Pan (2016) and Chén et al. (2017) first perform dimension reduction on the mediators to extract low dimensional factors on the reduced dimensional space, and then carry out mediation analysis by treating the low dimensional factors as new mediators. Because these approaches analyze the latent factors instead of the original mediators, we do not compare our methods with them in the present study.
4. Simulation
Simulation Overview and Evaluation Metrics
We evaluate the performance of the two proposed methods (GMM and PTG) and compare them with existing methods in different simulation scenarios. As described in Section 3, we consider a total of eight methods: one univariate method and seven multivariate methods that include four Bayesian methods (GMM, PTG, BAMA and Bi-Bayesian Lasso) and three frequentist methods (Bi-Lasso, Pathway Lasso, and HIMA). We examine the power of different methods to detect true mediators in the simulations. To do so, we rely on PIP to prioritize mediators in PTG, GMM and BAMA; rely on P-value to rank mediators in the univariate method and HIMA; and rely on the estimated indirect contributions as an measure of evidence for mediation for the remaining methods. To evaluate selection accuracy, we calculate the true positive rate (TPR) based on a fixed false discovery rate (FDR) of 10% and area under the ROC curve (AUC). To evaluate estimation accuracy, we compute the mean square error (MSE) for the indirect contributions (βmjαaj) of the truly active mediators (MSEnon-null), and MSE for the indirect contributions of the truly inactive mediators (MSEnull). We also include the bias metric on joint NIE, NDE and TE in the SM. We perform 200 simulation replicates for each scenario to report the average of the above metrics.
Simulation Design –
Fixed Effect Simulations
We consider one small sample scenario with n = 100, p = 200, and one large sample scenario with n = 1000, p = 2000. In both scenarios, we set the proportions of the four different mediator groups to be π1 = 0.05, π2 = 0.05, π3 = 0.10, π4 = 0.80. In each scenario, we further explore two different settings. In Setting (I), we fix the non-zero effects of both βmj and αaj to be 0.5, with their signs randomly assigned as positive or negative. In Setting (II), we fix 40% of the non-zero βmj (or αaj) to be 0.3, 30% of them to be 0.5, and 30% of them to be 0.7, with their signs randomly assigned as positive or negative. In both settings, we simulate the continuous exposure {Ai, i = 1, . . . , n} independently from a standard normal distribution N(0, 1). We also included three confounders in the fixed effect simulations: the first two continuous covariates C1 and C2 are simulated from N(2,1) and N(0,1) respectively, and the third binary covariate C3 is simuated from Binom(1, 0.6). We simulate the residual error ϵYi in the outcome model independently from N(0, 1), and simulate the residual errors ϵMi in the mediator model from MVN(0, Σ). Here, we use the sample covariance estimated from MESA data to serve as Σ in the simulations. Afterwards, we generate a p-vector of mediators for the ith individual from , where . We also generate the outcome Yi for the ith individual from , with βa = 0.5.
Random Effect Simulations
In the above settings, we have fixed the effect sizes to specific values across replicates. To further examine the performance of our methods over a wide range of effect sizes, we perform additional simulations where we simulate randomly in each simulation replicate. Specifically, we generate these two effects from three different joint distributions detailed below (Figure S1): the first two correspond to the prior distributions assumed in PTG and GMM, respectively, while the last one is a horseshoe distribution, i.e.
Simulate effects under the PTG model: , where λ = (λ0, λ1, λ2) are set to satisfy the desired proportions of the four groups (π1, π2, π3, π4). We set for p = 200, and for p = 2000.
Simulate effects under the GMM model: . We set σ2 = 0.3 for p = 200, and σ2 = 0.1 for p = 2000.
Simulate effects from a mixture of bivariate horseshoe distributions, which can be generated from a scale mixture of normals: . Here, Zj ∼ halfCauchy(0, 1), but truncated at a value of b to avoid impractically large values. We set σ2 = 0.5 for p = 200, and σ2 = 0.3 for p = 2000, and b = 3. Note that the effect size distribution assumed here is different from either of our proposed models, thus allowing us to study the robustness of our methods. With the effect size distributions, we follow the same procedure described as in the fixed effects settings.
We apply different methods to analyze the simulated data. In GMM, we set the Dirichlet parameters a1 = 0.01p, a2 = a3 = 0.05p, a4 = 0.89p. We adopt an empirical Bayesian approach to set the diagonal entries of Ψ0 as the sample variances of the non-zero βm and αa fitted through Lasso. We set the degree of freedom ν in the inverse-Wishart distribution to be two, which makes the distribution reasonably noninformative while still well-defined. In PTG, we set the pre-defined minimal detectable effect sizes (λ0, λ1, λ2) to be the 90% quantiles of the estimated |βm| and |αa| fitted through Lasso. To be consistent with the GMM, we choose the parameter in the priors , to ensure that the prior inclusion probability is around 0.01. For the Bayesian methods, we perform 150,000 iterations and discard the first 100,000 iterations as burn-in. The MCMC convergence has been checked using the potential scale reduction factor (PSRF) for the PIPs.
Results for Fixed Effect Simulations: Setting (I)-(II)
Table 1 shows the results under the fixed effects for the small sample scenario n = 100, p = 200 and the large sample scenario n = 1000, p = 2000. Overall, our proposed methods, GMM and PTG, outperform the other methods. These two methods achieve the highest AUC and are up to ∼ 30% more powerful than the other methods in identifying active mediators, with performance gain more apparent in the large sample scenario. Under Setting (I) where the mediation effects are large, the PTG method has the highest average TPR for both small and large sample settings. The performance of PTG is followed by GMM and BAMA. In contrast, under Setting (II) where the mediation effects are uneven, PTG may fail to identify some of the active mediators with small effects due to the thresholding set by the pre-defined parameter λ. Instead, GMM performs the best and its performance is followed by PTG and BAMA. Importantly, median inclusion probabilities (PIP = 0.5) in both GMM and PTG can be used as a criterion to declare active mediators (details in SM), producing decent empirical estimates for FDR in simulations (Table S1, S2). Among the frequentist methods, the Bi-Lasso performs best over the others and is also competitive in the small sample setting. HIMA and the univariate method are among the worst methods for mediator selection, presumably because neither models the entire set of mediators jointly in the outcome model.
Table 1.
Simulation results for fixed effects under n = 100, p = 200 and n = 1000, p = 2000, p11 is the number of truly active mediators. TPR: true positive rate at false discovery rate (FDR) = 0.10. MSEnon-null: mean squared error for the indirect contributions of truly active mediators. MSEnull: mean squared error for the indirect contributions of truly inactive mediators. The results are based on 200 replicates for each setting, and the standard errors are shown within parentheses. For PTG, we include the pre-defined thresholds (λ0, λ1, λ2) under each setting. Bolded TPRs indicate the top two performers.
|
n = 100, p = 200, p11 = 10, fixed effects (I) | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10−4 |
|
| ||||
| PTG (0.15,0.4,0.4) | 0.99(0.001) | 0.52(0.026) | 0.043 | 0.395 |
| GMM | 0.98(0.001) | 0.44(0.022) | 0.047 | 1.409 |
| BAMA | 0.97(0.002) | 0.38(0.021) | 0.063 | 2.471 |
| Bi-BLasso | 0.90(0.005) | 0.27(0.015) | 0.092 | 21.879 |
| PathLasso | 0.81(0.004) | 0.35(0.019) | 0.045 | 1.418 |
| Bi-Lasso | 0.80(0.008) | 0.36(0.018) | 0.043 | 0.661 |
| HIMA | 0.61(0.005) | 0.23(0.010) | 0.056 | 2.895 |
| Univariate | 0.80(0.007) | 0.25(0.014) | 0.060 | 49.764 |
|
n = 100, p = 200, p11 = 10, fixed effects (II) | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10−4 |
|
| ||||
| PTG (0.15,0.4,0.4) | 0.96(0.003) | 0.35(0.016) | 0.073 | 0.309 |
| GMM | 0.96(0.003) | 0.37(0.017) | 0.062 | 0.940 |
| BAMA | 0.95(0.003) | 0.31(0.015) | 0.075 | 2.389 |
| Bi-BLasso | 0.90(0.005) | 0.25(0.013) | 0.044 | 11.040 |
| PathLasso | 0.70(0.009) | 0.28(0.015) | 0.092 | 0.576 |
| Bi-Lasso | 0.72(0.006) | 0.29(0.013) | 0.079 | 0.422 |
| HIMA | 0.60(0.005) | 0.21(0.010) | 0.083 | 1.923 |
| Univariate | 0.82(0.007) | 0.23(0.013) | 0.081 | 26.540 |
|
n = 1000, p = 2000, p11 = 100, fixed effects (I) | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10−4 |
|
| ||||
| PTG (0.15,0.4,0.4) | 0.98(0.001) | 0.64(0.008) | 0.028 | 0.070 |
| GMM | 0.99(0.001) | 0.61(0.009) | 0.023 | 0.134 |
| BAMA | 0.98(0.001) | 0.54(0.007) | 0.040 | 0.150 |
| Bi-BLasso | 0.90(0.002) | 0.23(0.004) | 0.063 | 5.711 |
| PathLasso | 0.70(0.002) | 0.20(0.005) | 0.057 | 3.982 |
| Bi-Lasso | 0.72(0.001) | 0.23(0.003) | 0.051 | 0.293 |
| HIMA | 0.54(0.001) | 0.15(0.003) | 0.077 | 1.780 |
| Univariate | 0.89(0.002) | 0.10(0.005) | 0.092 | 225.056 |
|
n = 1000, p = 2000, p11 = 100, fixed effects (II) | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10−6 |
|
| ||||
| PTG (0.15,0.4,0.4) | 0.96(0.002) | 0.40(0.008) | 0.008 | 0.164 |
| GMM | 0.97(0.001) | 0.48(0.006) | 0.003 | 3.437 |
| BAMA | 0.95(0.001) | 0.35(0.005) | 0.005 | 7.485 |
| Bi-BLasso | 0.85(0.001) | 0.18(0.004) | 0.011 | 184.761 |
| PathLasso | 0.67(0.002) | 0.19(0.003) | 0.017 | 19.540 |
| Bi-Lasso | 0.70(0.001) | 0.23(0.005) | 0.007 | 5.059 |
| HIMA | 0.56(0.002) | 0.08(0.003) | 0.013 | 25.432 |
| Univariate | 0.85(0.001) | 0.12(0.003) | 0.075 | 208.660 |
In terms of the effects estimation, GMM has the lowest MSEnon-null across most simulation scenarios. Due to hard thresholding, PTG tends to provide a conservative list of the active mediators. Consequently, the non-zero indirect contributions of some active mediators are shrunk to zero in PTG, leading to relatively high MSEnon-null but small MSEnull by PTG. Both methods provide lower bias on joint NIE and NDE, especially in the large sample scenario. Meanwhile, we find that the Pathway Lasso does not appear to exhibit much advantage over the simple alternative Bi-Lasso. Indeed, Pathway Lasso requires multiple tuning parameters for inducing the penalty term on the indirect effects, and those parameters may benefit from more careful specifications than the default setting. The univariate method in particular has a quite high MSEnull (also large bias for NIE and NDE) as it does not apply any shrinkage on the effect estimates. We also performed a sensitivity analysis to examine how robust the posterior inference of PTG is regarding mild changes in terms of the prior choices. The results are summarized in Table S8. In general, the lambda parameters, especially the lower bounds for βmj and αaj, play an important role in PTG’s performance. As the lambda parameters vary, the TPR and MSE vary in a reasonable range, and is mostly better than the other methods.
Results for Random Effect Simulations: Setting (A)-(C)
Table 2 shows the results in the small sample scenario and Table 3 shows the results in the large sample scenario. In all the settings, our proposed methods, PTG and GMM, outperform the other methods with an approximately 10% power gain in identifying active mediators. Between PTG and GMM, we find that both methods work preferably well in the setting where their corresponding effect size distribution is used. Specifically, in Setting (A) with p = 2000, the PTG method has the highest AUC (0.98) and TPR (0.40) at FDR = 10%. The performance of PTG is followed by GMM (AUC = 0.98, TPR = 0.37). In Setting (B) with p = 2000, the GMM method has the highest AUC (0.95) and TPR (0.51). The performance of GMM is followed by PTG (AUC = 0.92, TPR = 0.42). In Setting (C) where the effects are simulated with a horseshoe distribution, we find that GMM performs the best and its performance is followed by PTG and BAMA. The horseshoe distribution has a tall spike near zero and heavy tails, and therefore leads to a particularly challenging setting for most methods. The good performance of GMM in Setting (C) thus supports the robustness of the method. In addition, as before, both PTG and GMM provide reasonable empirical estimates of FDR and TPR (Table S1, S2 of SM) based on a PIP = 0.5 cutoff. The accuracy gain in effects estimation basically follows the same pattern as the power gain in mediator selection. The computing time of the proposed methods is reported in Table S3 of SM, with both methods being relatively efficient for p = 200 and p = 2000 cases.
Table 2.
Simulation results for random effects under n = 100, p = 200, p11 is the number of truly active mediators. TPR: true positive rate at false discovery rate (FDR) = 0.10. MSEnon-null: mean squared error for the indirect contributions of truly active mediators. MSEnull: mean squared error for the indirect contributions of truly inactive mediators. The results are based on 200 replicates for each setting, and the standard errors are shown within parentheses. For PTG, we include the pre-defined thresholds (λ0, λ1, λ2) under each setting. Bolded TPRs indicate the top two performers.
|
n = 100, p = 200, p11 = 10, PTG, = 0.3 | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10 −4 |
|
| ||||
| PTG (0.15, 0.4, 0.4) | 0.98(0.002) | 0.45(0.020) | 0.05 | 1.59 |
| GMM | 0.98(0.001) | 0.43(0.015) | 0.03 | 4.25 |
| BAMA | 0.98(0.001) | 0.41(0.019) | 0.04 | 2.64 |
| Bi-BLasso | 0.89(0.006) | 0.35(0.017) | 0.05 | 6.83 |
| PathLasso | 0.65(0.013) | 0.31(0.015) | 0.06 | 2.43 |
| Bi-Lasso | 0.78(0.009) | 0.40(0.020) | 0.05 | 1.12 |
| HIMA | 0.60(0.007) | 0.29(0.012) | 0.07 | 5.46 |
| Univariate | 0.85(0.008) | 0.29(0.023) | 0.15 | 76.25 |
|
n = 100, p = 200, p11 = 10, Gaussian, σ2 = 0.3 | ||||
| Method | AUC | TPR | MSEnon-null × 10−3 | MSEnull × 10 −5 |
|
| ||||
| PTG (0.04, 0.2, 0.2) | 0.92(0.002) | 0.38(0.008) | 6.24 | 4.05 |
| GMM | 0.94(0.003) | 0.41(0.006) | 3.92 | 3.56 |
| BAMA | 0.95(0.003) | 0.38(0.011) | 5.06 | 3.39 |
| Bi-BLasso | 0.83(0.006) | 0.28(0.014) | 23.31 | 14.38 |
| PathLasso | 0.75(0.008) | 0.30(0.011) | 11.57 | 3.09 |
| Bi-Lasso | 0.75(0.003) | 0.36(0.011) | 7.50 | 1.52 |
| HIMA | 0.65(0.005) | 0.21(0.009) | 14.98 | 7.93 |
| Univariate | 0.75(0.006) | 0.26(0.025) | 62.46 | 234.30 |
|
n = 100, p = 200, p11 = 10, Horseshoe, σ2 = 0.5, b = 3 | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10−4 |
|
| ||||
| PTG (0.15, 0.5, 0.3) | 0.80(0.009) | 0.30(0.015) | 0.42 | 7.16 |
| GMM | 0.83(0.006) | 0.33(0.011) | 0.03 | 5.21 |
| BAMA | 0.80(0.008) | 0.28(0.017) | 0.11 | 6.28 |
| Bi-BLasso | 0.76(0.011) | 0.23(0.010) | 0.45 | 42.36 |
| PathLasso | 0.65(0.019) | 0.25(0.026) | 0.51 | 6.04 |
| Bi-Lasso | 0.68(0.009) | 0.27(0.017) | 0.46 | 5.41 |
| HIMA | 0.60(0.006) | 0.20(0.010) | 0.41 | 26.51 |
| Univariate | 0.72(0.009) | 0.20(0.020) | 0.44 | 512.33 |
Table 3.
Simulation results for random effects under n = 1000, p = 2000, p11 is the number of truly active mediators. TPR: true positive rate at false discovery rate (FDR) = 0.10, MSEnon-null: mean squared error for the indirect contributions of truly active mediators. MSEnull: mean squared error for the indirect contributions of truly inactive mediators. The results are based on 200 replicates for each setting, and the standard errors are shown within parentheses. For PTG, we include the pre-defined thresholds (λ0, λ1, λ2) under each setting. Bolded TPRs indicate the top two performers.
|
n = 1000, p = 2000, p11 = 100, PTG, = 0.1 | ||||
| Method | AUC | TPR | MSEnon-null × 10−4 | MSEnull × 10−6 |
|
| ||||
| PTG (0.05,0.15,0.15) | 0.98(0.001) | 0.40(0.008) | 5.28 | 2.46 |
| GMM | 0.98(0.001) | 0.37(0.010) | 3.86 | 4.26 |
| BAMA | 0.98(0.001) | 0.30(0.012) | 4.84 | 3.62 |
| Bi-BLasso | 0.92(0.003) | 0.29(0.018) | 7.92 | 11.38 |
| PathLasso | 0.77(0.009) | 0.22(0.007) | 7.02 | 1.74 |
| Bi-Lasso | 0.83(0.003) | 0.28(0.014) | 5.60 | 1.81 |
| HIMA | 0.53(0.002) | 0.14(0.004) | 9.96 | 4.96 |
| Univariate | 0.85(0.003) | 0.11(0.023) | 60.24 | 214.57 |
|
n = 1000, p = 2000, p11 = 100, Gaussian, σ2 = 0.1 | ||||
| Method | AUC | TPR | MSEnon-null × 10−3 | MSEnull × 10−5 |
|
| ||||
| PTG (0.02,0.2,0.1) | 0.92(0.002) | 0.42(0.006) | 4.76 | 0.874 |
| GMM | 0.95(0.001) | 0.51(0.007) | 2.09 | 0.712 |
| BAMA | 0.90(0.003) | 0.41(0.018) | 2.85 | 0.722 |
| Bi-BLasso | 0.88(0.002) | 0.32(0.007) | 4.85 | 1.632 |
| PathLasso | 0.78(0.011) | 0.25(0.003) | 4.88 | 1.256 |
| Bi-Lasso | 0.81(0.002) | 0.38(0.010) | 2.53 | 0.368 |
| HIMA | 0.55(0.002) | 0.19(0.004) | 8.41 | 1.544 |
| Univariate | 0.82(0.003) | 0.19(0.017) | 34.08 | 20.05 |
|
n = 1000, p = 2000, p11 = 100, Horseshoe, σ2 = 0.3, b = 3 | ||||
| Method | AUC | TPR | MSE non-null | MSEnull × 10−4 |
|
| ||||
| PTG (0.03,0.3,0.1) | 0.74(0.002) | 0.29(0.008) | 0.18 | 10.04 |
| GMM | 0.80(0.001) | 0.38(0.007) | 0.14 | 2.94 |
| BAMA | 0.75(0.002) | 0.27(0.006) | 0.25 | 3.88 |
| Bi-BLasso | 0.71(0.002) | 0.09(0.003) | 0.26 | 127.55 |
| PathLasso | 0.66(0.008) | 0.05(0.002) | 0.41 | 2.03 |
| Bi-Lasso | 0.72(0.003) | 0.24(0.007) | 0.24 | 1.57 |
| HIMA | 0.55(0.002) | 0.09(0.004) | 0.39 | 1.56 |
| Univariate | 0.77(0.003) | 0.09(0.015) | 0.59 | 644.07 |
Finally, among the three frequentist methods, the bi-Lasso yields higher power as compared to the other two in all the scenarios and has smaller MSE in almost all the settings except for the horseshoe setting. Between bi-Lasso and bi-Bayesian Lasso, we find that the former outperforms the latter with higher TPR and smaller MSEnull. This comparison suggests that under this sparse setup, the estimated non-sparse indirect estimates in bi-Bayesian Lasso may not be ideal for classifying mediators as compared to the sparse solutions produced by bi-Lasso.
Alternative to fixing the threshold parameter λ, we also consider a data-adaptive uniform prior that favors large positive value of λ’s. That is, we first fit the Lasso method and then use the posterior quantiles (e.g. 95% to 99%) of the estimated |βm|, |αa| to determine the range of corresponding λ’s. To be specific, a priori, , , and we always set the value of λ0 as λ1λ2. The results (Table S6 in SM) indicate that uniform priors with adequately large lower bounds (e.g. 95% quantiles) of λ1 (and λ2) can boost the selection power and estimation accuracy. The thresholds specified this way also cover a reasonably wide range, e.g. 0.2 ∼ 0.6 when the non-zero true effect is 0.5 in our simulation. This relatively objective approach can be used to guide the selection of λ’s in grid search.
In summary, the simulations demonstrate that GMM enjoys superior and robust performance for mediator selection and effect estimation, while PTG is preferable under potentially large non-zero effects in mediator selection.
5. Data Application
5.1. Analysis of DNA Methylation in the MESA Cohort
We applied the proposed GMM and PTG to investigate the mediation mechanism of DNAm in the pathway from neighborhood socioeconomic disadvantage to BMI in the MESA data. Neighborhood SES is the exposure variable and is created based on a principal components analysis of 16 census-tract level variables reflecting dimensions of education, occupation, income, poverty, housing, etc. BMI is the outcome variable and also a critical risk factor for various diseases including T2D and CVD (Hjellvik et al., 2012). Understanding how methylation at different CpG sites mediates the effects of neighborhood SES on BMI can shed light on the molecular mechanisms of complex diseases, thus leading to potential therapeutic strategies. The detailed processing steps for MESA data are provided in the SM. Briefly, we selected 1,225 individuals with non-missing data. Due to computational reasons, we focused on a final set of 2,000 CpG sites that have the strongest marginal associations with neighborhood SES. We applied various methods for the mediation analysis. In the outcome model, we adjust for age, gender, race/ethnicity, childhood socioeconomic status (SES) and adult SES (more details on the SES variables can be found at Smith et al. (2017)). In the mediator model, we control for age, gender, race/ethnicity, childhood SES, adult SES, and enrichment scores for 4 major blood cell types (neutrophils, B cells, T cells and natural killer cells) to account for potential contamination by non-monocyte cell types. All the continuous variables are standardized to have zero mean and unit variance.
We display the PIP values for each of the 2,000 CpG sites from PTG and GMM in Figure 1. GMM identified nine CpG sites with significant evidence for mediating the neighborhood SES effects on BMI based on 0.5 cutoff of PIPs. In contrast, PTG identified twelve significant CpG sites at the same threshold, which include all the nine sites selected by GMM method. The top five CpG sites identified by the two methods are identical. The rank correlation for the mediator rank lists obtained from both methods is 0.87, supporting the high consistency between the two methods. We carefully examine the nearby genes of the detected methylation sites by GMM and PTG. Among them, genetic variation in PTK2, a gene encoding structural protein in muscle, may be associated with BMI (Zeller et al., 2018); genetic variations in PCID2 and NFE2L1 have been shown to be associated with cardiovascular disease, glucose and insulin resistance in human and animal systems (Zheng et al., 2015; Erdmann et al., 2018); Differences in COX6A1P2 methylation was robustly recognized to link with obesity development in multiple epigenome-wide studies (Kvaløy et al., 2018) and EVI2B was reported as one of the regulatory genes related to obesity in a porcine model (Kogelman et al., 2014). Therefore, the genes nearby the detected CpG sites may play an important role in transmitting the effects of neighborhood SES to BMI. For the other competing methods, BAMA and the univariate methods do not have sufficient power to identify any significant CpG sites at 0.10 FDR. HIMA identifies one CpG site in the gene region of PCID2 as active mediator through its joint significance test (adjusted P-value = 6.3×10−5), and this single site has also been detected by PTG and GMM methods. Bi-Lasso and Pathway Lasso tend to produce a large number of false positives in simulations, and thus it is hard to verify their findings in the real data application.
Fig. 1.
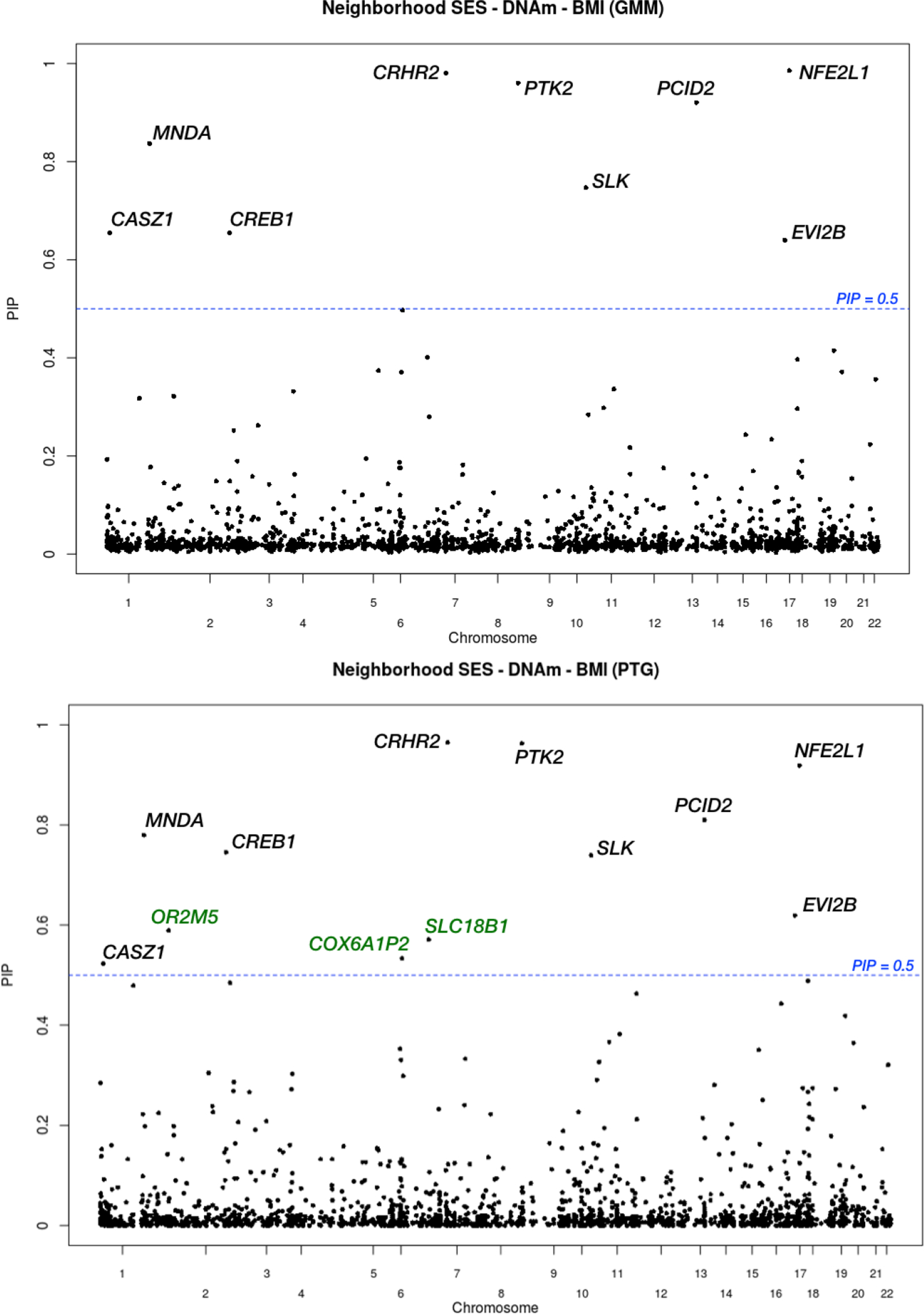
Data analysis results for the trio Neighborhood SES → DNAm → BMI in MESA data. The upper panel shows the PIPs obtained from the GMM method, and the lower panels shows the PIPs obtained from the PTG method. The blue lines mark the PIP = 0.5 threshold, and we include the nearby genes of the selected CpG sites. Most of the sites are identified by both methods, and the three genes in green are additional findings from PTG.
5.2. Analysis of Endogenous Biomarkers and Environmental Data in the LIFECODES Birth Cohort
As another data example, we study the collective impact of endogenous signaling molecules derived from lipids, peptides, and DNA in mediating prenatal exposure to environmental contaminants on the risk of preterm birth in the LIFECODES birth cohort. Detailed description of the study is provided in the SM. Briefly, we consider n = 161 pregnant women registered at the Brigham and Women’s Hospital in Boston, MA between 2006 and 2008. Subjects’ urine and plasma specimens were collected at one study visit occurring between 23.1 and 28.9 weeks gestation. Four classes of environmental contaminants, including phthalates, phenols, polycyclic aromatic hydrocarbons, and trace metals, were measured in each urine sample. Among them, phthalates are the high-production volume chemicals commonly used as plasticizers in numerous consumer products. Previous studies have shown that everyday exposure to phthalates during pregnancy would increase risk of delivering preterm (Ferguson et al., 2014). Recent studies have also uncovered associations between multiple lipid biomarkers and preterm birth (Aung et al., 2019). Based on those evidence, we aim to understand the molecular mechanism underlying the effects of phthalates on preterm. We first follow Aung et al. (2020) to create an environmental risk score for the phthalate class and treat such risk score as the exposure variable. The gestational age at delivery was recorded as the continuous birth outcome. For mediators, we obtained 61 endogenous biomarkers from urine and plasma that included 51 eicosanoids, five oxidative stress biomarkers and five immunological biomarkers. In the analysis, we perform log-transformation on all measurements of the exposure metabolites and endogenous biomarkers. We adjust for age and maternal BMI from the initial visit, race, and urinary specific gravity levels inside both models of the mediation analysis. Since the cohort is oversampled for preterm cases (< 37 weeks gestation), we multiply the data by the case-control sampling weights to adjust for that.
We summarize the application results in Table 4. Both PTG and GMM identified significant mediators that mediate the effects of the phthalate exposure on gestational age at delivery based on PIP = 0.5 cutoff (Figure 2), with rank lists of mediators positively correlated with each other (rank correlation = 0.48). Specifically, GMM identified two significant biomarkers (9-oxooctadeca-dienoic acid [9-oxoODE], 12, 13-epoxy-octadecenoic acid [12(13)-EpoME]). PTG identified three significant biomarkers (8-hydroxydeoxyguanosine [8-OHdG], 12(13)-EpoME, leukotriene D4 [LTD4]), one of which (12(13)-EpoME) overlaps with those identified by GMM. Among the identified biomarkers, 8-OHdG is commonly utilized as a marker of oxidative stress generated upon repair of oxidative DNA damage and has been found to be strongly associated with decreased gestational length and increased risk of preterm (Ferguson et al., 2015); while LTD4 has been shown to exhibit significant associations with preterm birth, and 9-oxoODE and 12(13)-EpoME had an important protective effect on preterm birth (Aung et al., 2019). As a comparison, BAMA, HIMA and the univariate methods fail to identify any significant active mediators at 0.10 FDR in this application. Our results help improve the understanding of the molecular mechanisms underlying the effects of environmental exposure on preterm, and could further lead to improvement of treatment and prevention strategies.
Table 4.
Summary of the identified active mediators from the data application on MESA and LIFECODES study. For PTG, we include the pre-defined thresholds (λ0, λ1, λ2) for the two real datasets.
| Method | Selected Mediators |
|---|---|
|
| |
|
MESA : Neighborhood SES → DNAm → BMI | |
| GMM | CRHR2, NFE2L1, PTK2, PCID2, MNDA, SLK, CREB1, CASZ1, EVI2B |
| PTG (0.01,0.05,0.1) | CRHR2, NFE2L1, PTK2, PCID2, MNDA, CREB1, SLK, EVI2B, OR2M5, SLC18B1, COX6A1P2, CASZ1 |
|
LIFECODES: Phthalates → Biomarkers → Gestational age | |
| GMM | 12(13)-EpoME, 9-oxoODE |
| PTG (3.0,2.0,1.5) | 12(13)-EpoME, 8-OHdG, LTD4 |
Fig. 2.

Data analysis results for the LIFECODES cohort. The panel shows the PIPs obtained from GMM (blue) and PTG (yellow) methods for the trio Exposure to phthalates → Biomarkers → Gestational age of the newborn at delivery.
6. Discussion
In this paper, we present two novel joint modeling approaches, PTG and GMM, for high-dimensional mediation analysis. Our methods can jointly model a large number of mediators and enable penalization on the indirect effects in a targeted way. Our methods effectively characterize the high-dimensional set of potential mediators into four groups based on the exposure-mediator and mediator-outcome effects: the active mediating group and three non-mediating groups. These group categorizations are in consonance with the composite structure for testing the indirect effect recently proposed in genome-wide mediation analyses (Huang, 2019). With extensive simulations, we show that our methods achieve up to 30% power gain in identifying true non-null mediators as compared with other existing alternatives, including several recently developed penalized and Bayesian methods for mediation analysis. We have demonstrated the benefits of our methods with both genetic and environmental data in the MESA and LIFECODES cohorts. For example, in the MESA cohort, we identify several DNAm and their nearby genes, e.g. NFE2L1 and PTK2, with strong evidence for mediating neighborhood SES effects on BMI. This is an important finding in biosocial research where we try to characterize how the insults from our external environment influence the internal cellular environment and finally manifest into development of a chronic disease.
On the methodological front, we still have challenges remaining that are unsolved in this modeling exercise. Bayesian FDR control is of great importance to safeguard false positives in the scientific discovery. For PTG and GMM, we rely on the median inclusion probabilities (PIP = 0.5) to identify active mediators, which provides effective FDR control as validated through simulations. For bi-Bayesian Lasso and other continuous shrinkage methods, such as the scale mixture of normals prior, we have attempted to define PIP using shrinkage factors following Carvalho et al. (2010). However, we find it challenging to adapt the shrinkage factors to devise an optimal strategy for computing PIP analogs and ranking correlated mediators. Consequently, we have to rely on the estimated indirect contributions from these methods to rank mediators, which may account for at least partially the relatively poor performance of these methods. Therefore, coming up with an analog of PIP as the selection criterion in mediation analysis for various other methods remains a topic of future investigation.
One limitation of our current work is that the proposed methods do not explicitly incorporate the correlation structure among mediators in the modeling process. Treating mediators independent a priori, the models may fail to distinguish among highly correlated mediators and lose power in mediator selection when two truly active mediators tend to be correlated with each other. Correlations among mediators are commonly seen in modern data analysis; such examples include genomic data that measure hundreds of thousands of gene expressions/single nucleotide polymorphisms (SNPs), and brain image data that contain a large number of voxels/regions. Incorporating mediator correlation information explicitly into our Bayesian paradigm could be a promising direction for future work.
7. Software
Software in the form of C++ codes is available on github https://github.com/yanys7/GMM_PTG_Mediation.
Supplementary Material
Acknowledgments
This work was supported by NSF DMS1712933 (B.M., X.Z.), NIH R01HG009124 (X.Z.), NIH R01HL141292 (J.S.), NIH R01MD011724 (B.N.), NIH R01DA048993 (J.K.), NIH R01MH105561 (J.K.), and NIH R01GM124061(J.K.). MESA and the MESA SHARe project are conducted and supported by the National Heart, Lung, and Blood Institute (NHLBI) in collaboration with MESA investigators. Support for MESA is provided by contracts HHSN268201500003I, N01-HC-95159, N01-HC-95160, N01-HC-95161, N01-HC-95162, N01-HC-95163, N01-HC-95164, N01-HC-95165, N01-HC-95166, N01-HC-95167, N01-HC-95168, N01-HC-95169, UL1-TR-000040, UL1-TR-001079, UL1-TR-001420, UL1-TR-001881, and DK063491. The MESA Epigenomics & Transcriptomics Study was funded by NHLBI, NIA, and NIDDK grants: 1R01HL101250, R01 AG054474, and R01 DK101921. The authors thank the other investigators, the staff, and the participants of the MESA study for their valuable contributions. A full list of participating MESA investigators and institutions can be found at http://www.mesa-nhlbi.org.
Contributor Information
Yanyi Song, University of Michigan, Ann Arbor, MI, USA.
Xiang Zhou, University of Michigan, Ann Arbor, MI, USA.
Jian Kang, University of Michigan, Ann Arbor, MI, USA.
Max T. Aung, University of Michigan, Ann Arbor, MI, USA
Min Zhang, University of Michigan, Ann Arbor, MI, USA.
Wei Zhao, University of Michigan, Ann Arbor, MI, USA.
Belinda L. Needham, University of Michigan, Ann Arbor, MI, USA
Sharon L. R. Kardia, University of Michigan, Ann Arbor, MI, USA
Yongmei Liu, Duke University, Durham, NC, USA.
John D. Meeker, University of Michigan, Ann Arbor, MI, USA
Jennifer A. Smith, University of Michigan, Ann Arbor, MI, USA
Bhramar Mukherjee, University of Michigan, Ann Arbor, MI, USA.
References
- Aung MT, Song Y, Ferguson KK, Cantonwine DE, Zeng L, McElrath TF, Pennathur S, Meeker JD and Mukherjee B (2020) Application of an analytical framework for multivariate mediation analysis of environmental data. Nature communications, 11, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aung MT, Yu Y, Ferguson KK, Cantonwine DE, Zeng L, McElrath TF, Pennathur S, Mukherjee B and Meeker JD (2019) Prediction and associations of preterm birth and its subtypes with eicosanoid enzymatic pathways and inflammatory markers. Scientific reports, 9, 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baron RM and Kenny DA (1986) The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of personality and social psychology, 51, 1173. [DOI] [PubMed] [Google Scholar]
- Bild DE, Bluemke DA, Burke GL, Detrano R, Diez Roux AV, Folsom AR et al. (2002) Multi-ethnic study of atherosclerosis: objectives and design. American journal of epidemiology, 156, 871–881. [DOI] [PubMed] [Google Scholar]
- Cai Q, Kang J and Yu T (2020) Bayesian network marker selection via the thresholded graph laplacian gaussian prior. Bayesian Analysis, 15, 79–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho CM, Polson NG and Scott JG (2010) The horseshoe estimator for sparse signals. Biometrika, 97, 465–480. [Google Scholar]
- Chén OY, Crainiceanu C, Ogburn EL, Caffo BS, Wager TD and Lindquist MA (2017) High-dimensional multivariate mediation with application to neuroimaging data. Biostatistics, 19, 121–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdmann J, Kessler T, Munoz Venegas L and Schunkert H (2018) A decade of genome-wide association studies for coronary artery disease: the challenges ahead. Cardiovascular research, 114, 1241–1257. [DOI] [PubMed] [Google Scholar]
- Ferguson KK, McElrath TF, Chen Y-H, Loch-Caruso R, Mukherjee B and Meeker JD (2015) Repeated measures of urinary oxidative stress biomarkers during pregnancy and preterm birth. American journal of obstetrics and gynecology, 212, 208–e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson KK, McElrath TF, Ko Y-A, Mukherjee B and Meeker JD (2014) Variability in urinary phthalate metabolite levels across pregnancy and sensitive windows of exposure for the risk of preterm birth. Environment international, 70, 118–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallop R, Small DS, Lin JY, Elliott MR, Joffe M and Ten Have TR (2009) Mediation analysis with principal stratification. Statistics in medicine, 28, 1108–1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hjellvik V, Sakshaug S and Strøm H (2012) Body mass index, triglycerides, glucose, and blood pressure as predictors of type 2 diabetes in a middle-aged norwegian cohort of men and women. Clinical epidemiology, 4, 213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y-T (2019) Genome-wide analyses of sparse mediation effects under composite null hypotheses. The Annals of Applied Statistics, 13, 60–84. [Google Scholar]
- Huang Y-T and Pan W-C (2016) Hypothesis test of mediation effect in causal mediation model with high-dimensional continuous mediators. Biometrics, 72, 402–413. [DOI] [PubMed] [Google Scholar]
- Kang J, Reich BJ and Staicu A-M (2018) Scalar-on-image regression via the soft-thresholded gaussian process. Biometrika, 105, 165–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim C, Daniels M, Hogan J, Choirat C and Zigler C (2019) Bayesian methods for multiple mediators: Relating principal stratification and causal mediation in the analysis of power plant emission controls. arXiv preprint arXiv:1902.06194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kogelman LJ, Cirera S, Zhernakova DV, Fredholm M, Franke L and Kadarmideen HN (2014) Identification of co-expression gene networks, regulatory genes and pathways for obesity based on adipose tissue rna sequencing in a porcine model. BMC medical genomics, 7, 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kvaløy K, Page CM and Holmen TL (2018) Epigenome-wide methylation differences in a group of lean and obese women–a hunt study. Scientific reports, 8, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP (2008) Introduction to statistical mediation analysis. Routledge. [Google Scholar]
- MacKinnon DP, Fairchild AJ and Fritz MS (2007) Mediation analysis. Annu. Rev. Psychol, 58, 593–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni Y, Stingo FC and Baladandayuthapani V (2019) Bayesian graphical regression. Journal of the American Statistical Association, 114, 184–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park T and Casella G (2008) The bayesian lasso. Journal of the American Statistical Association, 103, 681–686. [Google Scholar]
- Rossell D and Telesca D (2017) Nonlocal priors for high-dimensional estimation. Journal of the American Statistical Association, 112, 254–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JA, Zhao W, Wang X, Ratliff SM, Mukherjee B, Kardia SL, Liu Y, Roux AVD and Needham BL (2017) Neighborhood characteristics influence dna methylation of genes involved in stress response and inflammation: the multi-ethnic study of atherosclerosis. Epigenetics, 12, 662–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y, Zhou X, Zhang M, Zhao W, Liu Y, Kardia SL, Roux AVD, Needham BL, Smith JA and Mukherjee B (2019) Bayesian shrinkage estimation of high dimensional causal mediation effects in omics studies. Biometrics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58, 267–288. [Google Scholar]
- VanderWeele TJ (2016) Mediation analysis: a practitioner’s guide. Annual review of public health, 37, 17–32. [DOI] [PubMed] [Google Scholar]
- Zeller Z, Al-Amoodi M, Jones W, Lee D, Mckenzie S, Miller H, Stubblefied S, Knoblach S, Gordish-Dressman H, Hittel D and Tosi L (2018) Impact of polymorphisms in ptk2 on intrinsic muscle strength.
- Zeng P, Hao X and Zhou X (2018) Pleiotropic mapping and annotation selection in genome-wide association studies with penalized gaussian mixture models. Bioinformatics, 34, 2797–2807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Zheng Y, Zhang Z, Gao T, Joyce B, Yoon G, Zhang W, Schwartz J, Just A, Colicino E et al. (2016) Estimating and testing high-dimensional mediation effects in epigenetic studies. Bioinformatics, 32, 3150–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y and Luo X (2016) Pathway lasso: estimate and select sparse mediation pathways with high dimensional mediators. arXiv preprint arXiv:1603.07749. [Google Scholar]
- Zheng H, Fu J, Xue P, Zhao R, Dong J, Liu D, Yamamoto M, Tong Q, Teng W, Qu W et al. (2015) Cnc-bzip protein nrf1-dependent regulation of glucose-stimulated insulin secretion. Antioxidants & redox signaling, 22, 819–831. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


