Place-Based Drivers of Mortality: Evidence from Migration

Abstract

We estimate the effect of current location on elderly mortality by analyzing outcomes of movers in the Medicare population. We control for movers’ origin locations as well as a rich vector of pre-move health measures. We also develop a novel strategy to adjust for remaining unobservables, using the correlation of residual mortality with movers’ origins to gauge the importance of omitted variables. We estimate substantial effects of current location. Moving from a 10th to a 90th percentile location would increase life expectancy at age 65 by 1.1 years, and equalizing location effects would reduce cross-sectional variation in life expectancy by 15 percent. Places with favorable life expectancy effects tend to have higher quality and quantity of health care, less extreme climates, lower crime rates, and higher socioeconomic status.

Mortality rates vary substantially across the US. Focusing on the 100 most populous commuting zones, Chetty et al. (2016) estimate that life expectancy at age 40 ranges from a high of 85 in San Jose, California to a low of 81 in Las Vegas, Nevada, with a standard deviation across commuting zones of 1.2 years.¹ Murray et al. (2006) estimate that county-level life expectancy at birth in 1999 ranged from 66.6 years in Bennett County, South Dakota to 81.3 years in Summit County, Colorado. Currie and Schwandt (2016) likewise document substantial disparities across county groups in life expectancy at birth as well as in mortality at older ages.

Why do people in some parts of the US live longer than others? The long list of possible causes can be divided into two broad categories: differences in residents’ stocks of health capital (Grossman 1972), and differences in the environment associated with their current location. Health capital includes genetic endowments, as well as the persistent effects of prior health behaviors (e.g., smoking, diet, exercise), prior medical care, and other past experiences that impact current mortality. Potentially mortality-relevant aspects of residents’ current locations include the quality and quantity of available medical care, local climate and pollution, and risk factors such as crime and traffic accidents. Chetty et al. (2016) find that the main correlates of area mortality in the cross section are health capital factors such as smoking, obesity, and exercise, and that correlations with place factors such as health care spending or local environmental conditions are weak. Neither they nor other past work, however, isolate the causal impact of place effects.

In this paper, we use mortality outcomes of migrants in the elderly Medicare population to separately identify the effects of health capital and current location on mortality in the U.S. We will refer to the impact of current location by the shorthand place effects. Our strategy proceeds in two steps. First, we analyze mortality differences among movers to different destinations, controlling for both their origin locations and a rich vector of pre-move observable health measures in Medicare claims data. The idea behind our approach is to take two patients from the same origin (say, Boston), one of whom moves to a low-mortality area (say, Minneapolis), and the other of whom moves to a high-mortality area (say, Houston), and to compare their mortality outcomes after they move. If origin location plus pre-move health measures capture all differences in health capital potentially correlated with choice of destination, this would provide a valid estimate of the place effects.

Second, we apply a novel strategy to try to correct for any remaining selection on unobserved health capital. Our strategy builds on prior work (Murphy and Topel 1990; Altonji et al. 2005; Oster 2016) in using variation in observable characteristics to adjust for variation in unobservables. In our context, this amounts to using the correlation between movers’ choice of destination and their observed health capital to adjust for potential correlation between choice of destination and unobserved health capital. We weaken the assumptions of the standard approach by using the correlation between origin locations and residual post-move mortality as an additional moment to pin down the overall importance of the unobservables.

We use data on all Medicare beneficiaries aged 65 and older from 1999 through 2014 (CMS 1998–2014b). The enrollee-level panel data contain information on zip code of residence and date of death (if any), along with demographic variables such as age, race, sex, and enrollment in Medicaid (a proxy for low income). The claims data provide us with detailed annual measures of health conditions based on recorded diagnoses, as well as measures of health care utilization. Our geographic unit of analysis is a Commuting Zone (CZ), a standard aggregation of counties that partitions the US and is designed to approximate labor markets. The main outcome we focus on is life expectancy at age 65. We model log mortality as an additive function of age, place effects, and health capital, following the standard Gompertz specification for age-mortality gradients (Olshansky and Carnes 1997; Chetty et al. 2016b).

Our analysis depends on two strong simplifying assumptions; we present supporting evidence for both and also assess robustness to possible violations. The first key assumption is that health capital and place effects are additively separable in the equation for log mortality. This is analogous to additive separability assumptions in prior work using movers. It implies that health capital and place effects enter the level of the mortality rate multiplicatively, so that moving to a place with more favorable health care or other environmental factors matters more for those in worse health to begin with. We see this an appealing implication broadly, but note that it rules out factors that induce a constant level shift in mortality and also precludes more complex interactions.

The second key assumption is that health capital is constant over the post-move time horizon of our analysis. Of course, in general health capital will evolve endogenously as a function of environment and health behaviors, and late-life mortality can depend on health behaviors like smoking and exercise over an individual’s entire lifetime. However, we see it as a reasonable approximation to treat health capital as constant in the post-65 population over the 1 to 12 years we observe them post-move. Conditional on behavior prior to age 65, it seems reasonable to assume that the impact of any late-life behavior changes on health capital is relatively modest. Moreover, to the extent that health capital does evolve endogenously following a move, this should produce gradual changes in mortality, rather than the on-impact changes in mortality we document.

We find that current location has a large impact on mortality. In our analysis sample, mean life expectancy at age 65 is 83.3 years, with an across-area standard deviation of 0.79 years. Our results imply that moving from an area at the 10th percentile of estimated place effects to an area at the 90th percentile would increase life expectancy at age 65 by 1.1 years, or about half of the 90–10 cross-sectional difference. These findings suggest that policies which affect short-run determinants of mortality such as medical care or environmental factors can potentially produce large and immediate changes in outcomes, as can policies such as the Moving to Opportunity Project (Ludwig et al. 2012; Chetty et al. 2016a) that relocate small numbers of vulnerable individuals to areas with more favorable conditions.

At the same time, our findings suggest that health capital also plays an important role. We estimate that equalizing place effects across areas would reduce the cross-sectional variation in life expectancy at age 65 by 15 percent. By comparison, equalizing health capital across areas would reduce the cross-sectional variation by about 70 percent. This in part reflects the fact that while our estimated place effects are positively correlated with average area life expectancy, this correlation is far from perfect. Our place-by-place estimates of these components identify areas such as Santa Fe, New Mexico and El Paso, Texas as having negative effects despite relatively high average life expectancy, and other areas such as Charlotte, North Carolina as having positive effects despite relatively low average life expectancy.

Finally, we present evidence on the observable area-level correlates of our estimated place effects. The results are intuitive. Areas with positive place effects tend to have higher-quality hospitals, more primary care physicians and specialists per capita, and higher health care utilization. The positive correlation between an area’s healthcare utilization and its impact on life expectancy contrasts with the lack of correlation between utilization and average health outcomes which has been emphasized in the Dartmouth Atlas literature (Fisher et al. 2003a, b; Skinner 2011) and which we replicate here. Areas with favorable place effects also tend to have less extreme climates, less pollution, fewer homicides, fewer automobile fatalities, and higher urban shares. They also tend to have higher socioeconomic status (SES) as measured by income and education, as well as better health behaviors, which may reflect higher willingness to pay for healthcare quality and other favorable place characteristics among such individuals. We emphasize that these are simply bivariate correlations which need not reflect causal relationships.

We emphasize a number of important caveats for interpreting our findings. A crucial one is that our place effects capture the impact of place in an elderly population for whom we treat health capital as approximately constant. These estimates are appropriate for evaluating relatively short-run impacts of policies that change key place characteristics (e.g., improving a local health care system or reducing pollution) or move small numbers of people across space. Long-run effects of such policies could differ, however, as resulting changes in the evolution of health capital could play a larger role. The effect of moving larger numbers of people across space may also differ, as the place effects themselves may evolve endogenously due to supply side responses or peer effects. Finally, effects could be different in younger populations.

A second important caveat is that mortality is an absorbing state, and so we are unable to look at changes in mortality over time for a single individual. This means that our identification strategy is similar to that of cross-sectional movers designs such as Chetty and Hendren (2018b) and Bronnenberg et al. (2012), and requires stronger assumptions than panel mover analyses such as Finkelstein et al. (2016). Although we adjust for selection on unobservables, our identifying assumptions are also likely to be stronger than those in papers such as Doyle (2011) and Deryugina and Molitor (2018) that study the impact of location on mortality using explicit natural experiments to create variation in place factors.²

Our work contributes to the large literature on the determinants of mortality. McGovern et al.’s (2014) recent review of studies on health determinants concludes that this literature tends to attribute the largest importance for mortality to health capital — specifically to behaviors (35–50%) and to genetics (20–30%). Among potential place effects, it attributes between 5–20% of the determinants of mortality to environment and around 10% to medical care. While the methodologies of the studies underlying these estimates vary, they generally all rely on correlational analyses to quantify the relative importance of these different factors.³ Our analysis advances this body of descriptive work with a research design that more convincingly isolates causal effects.

Our work is particularly related to prior work on the drivers of geographic variation in mortality. This work has also tended to highlight the importance of health capital, particularly health behaviors. Fuchs (1974) famously attributed the lower mortality rates of clean-living, predominantly Mormon residents of Utah to better health behaviors than their neighbors in the more dissolute state of Nevada.⁴ Chetty et al. (2016b) show that geographic variation in life expectancy for low-income individuals is significantly correlated with health behaviors such as smoking, obesity and exercise, but not significantly correlated with measures of health care quality or quantity. This is consistent with the large Dartmouth Atlas literature which has found health care utilization to be uncorrelated with mortality (Fisher et al. 2003a, b; Skinner 2011).⁵

Summarizing the state of knowledge on both the determinants of mortality and the determinants of geographic variation in mortality, Cutler (2018) concludes, “Behavior is the key. When we compare geographic regions, the dominant factor driving health differences is how Americans behave. Unhealthy areas smoke more, drink more and eat to excess; healthier areas avoid these behaviors.” The large role we estimate for health capital is consistent with this conventional wisdom. However, our results also show that there is a substantial impact of place-based factors that this conventional wisdom may understate.

Our empirical strategy for correcting for selection on unobservables may have applications in other contexts. Oster (2016) emphasizes the sensitivity of the standard approach to assumptions about the overall explanatory power of the observables, and notes that direct information to guide such assumptions is often limited. We propose weaker assumptions under which this decision can be guided by the data. Our approach is most obviously relevant to other contexts in which individuals move across geographies, firms, or other units of analysis, and in which selection on unobserved individual characteristics is a potential confound; this could arise due to data limitations (e.g. Bronnenberg et al. 2012) or because an outcome cannot be measured repeatedly in individual panel-level data (such as mortality in our case or inter-generational mobility in Chetty and Hendren 2018b). It may also be applied to other settings where there are auxiliary variables whose relative correlation with observables and unobservables is plausibly similar to that of the treatment of interest.

The rest of the paper proceeds as follow. Sections I and II describe our model and empirical strategy, and Section III presents our data and summary statistics. Section IV presents evidence on the selection of movers across origins and destinations and describes how our empirical strategy addresses this selection. Section V presents our main results on the impact of current environment on life expectancy, and explores some observable correlates of the place effects. Section VI provides additional support for some of our key assumptions and shows robustness of our main results to alternative specifications. The last section concludes.

I. Model

We consider a set of individuals indexed by i and a set $\mathcal{J}$ of locations indexed by j. We analyze a continuous-time survival model in which an individual’s mortality rate at a given age depends on her accumulated stock of health capital θ_i and the place effect γ_i associated with her current location.⁶ The individuals are either (i) movers who live in an origin location $o\in \mathcal{J}$ in years $t<t_i^{\ast }$, move in year $t_i^{\ast }$ from o to $j\in \mathcal{J}$, and then live in destination location j thereafter; or (ii) non-movers who live in the same location $j\in \mathcal{J}$ throughout the sample, and to whom we assign a reference year $t_i^{\ast }$ as discussed below.

We follow Chetty et al. (2016b) in adopting a Gompertz specification in which the log of the mortality hazard rate m_ij (a) that individual i would experience at age a if she lived in location j is linear in age:

$$\text{log}\left(m_{ij}(a)\right)=\beta a+{\gamma }_j+{\theta }_i.$$ (1)

This specification embeds two key simplifying assumptions. The first is that age, place effects, and health capital are additively separable. Analogous assumptions are standard in the literature using changes in residence or employment to separate effects of individual characteristics from geographic or institutional factors (e.g. Card et al. 2013; Chetty and Hendren 2018a, b; Finkelstein et al. 2016).

This is a strong assumption, but we see it as a reasonable one in our setting. It has the intuitive implication that health capital and current location affect the level of mortality multiplicatively, and, thus, that the level of mortality of individuals with poor health capital (high θ_i) will vary more across areas than that of individuals who have better health capital (low θ_i); this has indeed been documented by Chetty et al. (2016b). More concretely, suppose that there are two possible levels of health capital, such that in an average location, individuals have either a 0.1% annual mortality hazard or a 10% annual mortality hazard. The additive separability assumption implies that anything about the current environment that reduces mortality — such as the quality of health care or the air quality — will reduce mortality by a constant proportion for all individuals, with a larger percentage point effect on individuals with worse health capital. Our specification rules out place effects that cause the same level shift in mortality for all patients regardless of their health capital. For example, if some places have a higher risk of death from auto accidents and this probability is independent of health capital, our assumption would be violated. We present empirical support for additive separability in Section VI below.

The second key assumption is that both γ_j and θ_i are time constant, with the only systematic changes in mortality risk over time coming from aging and changes in location. In general, θ_i will evolve endogenously as a function of an individual’s genetic endowment, health behaviors such as exercise and smoking, and the health care and other environmental factors she experiences. Importantly, this evolution may be affected by the locations where she lives. Different locations will affect the environmental factors she experiences, and may also change her health behaviors through channels including prices, information, and peer effects. Thus, in general, current location may impact mortality both through the contemporaneous causal effect γ_j and through changes in the future values of θ_i. We abstract from this endogenous response of health capital to current location, and instead assume that health capital is approximately constant in the elderly population we study over the relatively short time horizon of our sample post-move (1 to 12 years). This strikes us as a reasonable approximation: it seems likely that any changes in health behavior in an elderly population upon moving will be modest and gradual, and any impacts on mortality from such behavioral changes in turn should cumulate over longer time horizons.⁷ We present evidence in support of this approximation in Section VI below.

To define the main quantities we will seek to measure, we let ${\overline{\theta }}_j$ denote the average health capital of non-movers in j. In order to mirror the literature, which focuses on race and sex adjusted mortality rates as the object of interest, in computing ${\overline{\theta }}_j$ we assign each area j the national average racial and gender composition. We define the mortality rate of an average non-mover in j at age a to be ${\overline{m}}_j(a)=\text{exp}\left[\beta a+{\gamma }_j+{\overline{\theta }}_j\right]$. We refer to the sum (γ_j + θ_i) as the mortality index of individual i, and to $\left({\gamma }_j+{\overline{\theta }}_j\right)$ as the average mortality index in area j.

Our main outcome of interest is life expectancy at age 65, hereafter, life expectancy. Given a generic continuous mortality hazard rate m (a), the probability the individual survives to age a conditional to surviving to age 65 is given by the survival function $S(a)=e^{-{\int }_{65}^{a}m(v)dv}$. The life expectancy of an individual who survives until age 65 is $65+{\int }_{65}^{\infty }S(a)da$.⁸ We define the life expectancy at 65 of an average non-mover in j by substituting ${\overline{m}}_j(a)$ into these expressions. We will denote this L_j, and refer to it simply as average life expectancy in area j.

Our ultimate goal is to estimate the causal effect on life expectancy of living in area j. We define this by considering a thought experiment in which an individual with average health capital is assigned to live counterfactually in each location j beginning at age 65. Letting $\overline{\theta }$ denote the average health capital over the full population of non-movers, this defines a set of counterfactual mortality rates ${\overline{m}}_j^{\ast }(a)=\text{exp}\left[\beta a+{\gamma }_j+\overline{\theta }\right]$ that differ across j only because of the place effects γ_j. Substituting ${\overline{m}}_j^{\ast }(a)$ into the expression for life expectancy yields the counterfactual life expectancy $L_j^{\ast }$. Letting $\overline{\gamma }$ denote the population-weighted average of the γ_j, and letting $\overline{L}$ denote the life expectancy associated with mortality hazard $\text{exp}[\beta a+\overline{\gamma }+\overline{\theta }]$, we define the treatment effect of area j to be $L_j^{\ast }-\overline{L}$.

II. Empirical Strategy

A. Observables and Unobservables

We assume that health capital θ_i can be decomposed into a component that depends on demographics X_i, a component that depends on observed health H_i, a series of terms capturing unobserved health capital orthogonal to X_i and H_i but correlated with locations, and an orthogonal residual:

$${\theta }_i=X_i\psi +H_i\lambda +{\eta }_{j(i)}^{nm}+{\eta }_{o(i)}^{\mathit{\text{orig}}}+{\eta }_{j(i)}^{\mathit{\text{dest}}}+{\tilde{\eta }}_i.$$ (2)

Here, both X_i and H_i are measured as of year $t_i^{\ast }-1$, i.e. the year prior to move. We let j (i) denote the observed location of individual i (permanent location if i is a non-mover, and destination if i is a mover), and o(i) denote the observed origin of mover i.⁹ We define ${\eta }_{j(i)}^{nm}$, ${\eta }_{o(i)}^{\mathit{\text{orig}}}$, and ${\eta }_{j(i)}^{\mathit{\text{dest}}}$ to be the fixed effects from a hypothetical regression of θ_i on X_i, H_i, and fixed effects for non-movers’ locations, movers’ origins, and movers’ destinations respectively. (We fix ${\eta }_{j(i)}^{nm}=0$ for movers and ${\eta }_{o(i)}^{\mathit{\text{orig}}}={\eta }_{j(i)}^{\mathit{\text{dest}}}=0$ for non-movers.) We define ${\tilde{\eta }}_i$ to be the residual from this regression. We thus have $E\left({\tilde{\eta }}_i\mid X_i,H_i,o(i),j(i)\right)=0$ for movers and $E\left({\tilde{\eta }}_i\mid X_i,H_i,j(i)\right)=0$ for non-movers by construction.

Our definition of ${\tilde{\eta }}_i$ as a residual that is orthogonal by construction mirrors Altonji et al. (2005) and Oster (2016). It means that the coefficients ψ and λ capture both the causal effects of X_i and H_i and the effects of any unobservables that may be correlated with X_i and H_i. It is natural to assume that such correlations will exist, as unobserved determinants of health capital such as smoking will generally be correlated with observed measures of health capital such as diagnoses of hypertension. This means that equation (2) does not define a structural relationship, and the η terms include only the components of the unobservables orthogonal to X_i and H_i.

B. Estimation and Identification

Our main goal in estimation is to identify the place effects γ_j. This will in turn allow us to recover the average health capital θ_i of movers and non-movers in each location. Combining equations (1) and (2) yields the following estimating equation for the realized mortality rate m_i (a):

$$\text{log}\left(m_i(a)\right)=\beta a+X_i\psi +H_i\lambda +{\tau }_{o(i)}^{\mathit{\text{orig}}}+{\tau }_{j(i)}^{\mathit{\text{dest}}}+{\tau }_{j(i)}^{nm}+{\tilde{\eta }}_i.$$ (3)

where ${\tau }_{o(i)}^{\mathit{\text{orig}}}$, ${\tau }_{j(i)}^{\mathit{\text{dest}}}$, and ${\tau }_{j(i)}^{\mathit{\text{dest}}}$ are fixed effects for movers’ origins, movers’ destinations, and non-movers’ locations respectively, and we have ${\tau }_{o(i)}^{\mathit{\text{orig}}}={\eta }_{o(i)}^{\mathit{\text{orig}}}$, ${\tau }_{j(i)}^{nm}={\gamma }_{j(i)}+{\eta }_{j(i)}^{nm}$, and ${\tau }_{j(i)}^{\mathit{\text{dest}}}={\gamma }_{j(i)}+{\eta }_{j(i)}^{\mathit{\text{dest}}}$.

We estimate this model by maximum likelihood. Given the estimated parameters, we can consistently estimate the area j mortality rate ${\overline{m}}_j(a)$ by ${\widehat{m}}_j(a)=\text{exp}\left[\widehat{\beta }a+{\overline{X}}_j\widehat{\psi }+{\overline{H}}_j\widehat{\lambda }+{\widehat{\tau }}_j^{nm}\right]$, where ${\overline{X}}_j$ and ${\overline{H}}_j$ are the averages of X_i and H_i over non-movers in j.¹⁰ Consistent with the definition of ${\overline{\theta }}_j$ above, when we compute ${\overline{X}}_j$ we set the elements of the vector associated with race and sex to their national rather than their area averages. We compute estimates ${\widehat{L}}_j$ of average life expectancy L_j in area j by substituting ${\widehat{m}}_j(a)$ for ${\overline{m}}_j(a)$ in the derivation of L_j in Section I. All of our reported estimates of average life expectancy in area j are therefore race- and sex-adjusted.

The central challenge is identification of γ_j. Simply comparing average mortality rates across areas in the cross-section does not recover γ_j, because locations may differ in their average health capital E(θ_i|j (i) = j). An optimistic assumption would be that X_i and H_i absorb all such differences. In this case, ${\eta }_j^{nm}$, ${\eta }_o^{\mathit{\text{orig}}}$, and ${\eta }_j^{\mathit{\text{dest}}}$ would be equal to zero for all j, $o\in \mathcal{J}$, and we would not need to use movers at all; we could simply estimate equation (3) using non-movers and the ${\widehat{\tau }}_j^{nm}$ would be consistent estimators of γ_j.

A more plausible assumption would be that X_i and H_i do not absorb all area differences in health capital, but that the remaining differences for movers are absorbed by the origin fixed effects ${\eta }_o^{\mathit{\text{orig}}}$, so that ${\eta }_j^{\mathit{\text{dest}}}=0$ for all j. In this case, the estimated destination fixed effects ${\widehat{\tau }}_j^{\mathit{\text{dest}}}$ from equation (3) would be consistent estimators of γ_j. This assumption would follow from a model in which the locations where people are born and live up to age 65 or older may be related to their genetic endowments, health behaviors, and other determinants of health capital, but in which late-life moving decisions are driven by idiosyncratic factors.

Our findings below are qualitatively consistent with this intuition, in the sense that conditioning on movers’ origins eliminates a significant amount of non-random selection on observables. However, our results also suggest that some non-random selection may remain, implying that ${\eta }_j^{\mathit{\text{dest}}}\ne 0$ and thus that ${\widehat{\tau }}_j^{\mathit{\text{dest}}}$ may not exactly recover γ_j. The selection correction strategy we develop in the next sub-section is designed to deal with any such remaining selection.

Given consistent estimates ${\widehat{\gamma }}_j$ of γ_j, we can estimate the treatment effects $L_j^{\ast }-\overline{L}$ of each area j. To do so, we estimate $\overline{\theta }$ as the mean across all non-movers of $X_i\widehat{\psi }+H_i\widehat{\lambda }+{\widehat{\tau }}_j^{nm}-{\widehat{\gamma }}_j$, a consistent estimator of ${\widehat{\theta }}_i$. We estimate $\overline{\gamma }$ by the non-mover population-weighted mean of the ${\widehat{\gamma }}_j$. We then substitute these estimates in place of their population counterparts in the definitions of $L_j^{\ast }$ and $\overline{L}$ in Section I.

We will at various points form estimates of variances of CZ-level terms such as γ_j. Unless otherwise noted, all such estimates $\widehat{\text{Var}}(z)$ for CZ-level variables z are based on a split-sample approach in which we randomly partition our sample into two parts, form separate estimates ${\widehat{z}}^1$ and ${\widehat{z}}^2$ using the two samples, and then define $\widehat{\text{Var}}(z)=\text{Cov}\left({\widehat{z}}^1,{\widehat{z}}^2\right)$. We compute confidence intervals via 100 iterations of the Bayesian bootstrap procedure (Rubin 1981).¹¹

When we report individual values of the place effects ${\widehat{\gamma }}_j$ or the life expectancy treatment effects that depend on them, we adjust the ${\widehat{\gamma }}_j$ estimates for sampling error using a standard Empirical Bayes’ procedure, producing adjusted estimates we denote ${\widehat{\gamma }}_j^{EB}$. This closely follows the approach of Chetty and Hendren (2018b) and Finkelstein et al. (2017). Appendix A provides more detail on this procedure.

C. Adjusting for Selection on Unobservables

In this section, we introduce our strategy to allow for the possibility that movers’ destinations are correlated with their unobserved health—i.e., that ${\eta }_j^{\mathit{\text{dest}}}\ne 0$. Our approach builds on the now-standard methodology developed by Murphy and Topel (1990) and Altonji et al. (2005), and expanded on by Oster (2016), which uses variation in observables to make inferences about the likely bias due to unobservables.

The standard approach relies on two key assumptions. The first is that the relationship between the treatment of interest and the index of observables is similar to the relationship between the treatment of interest and an index of unobservables. Altonji et al. (2005) and Oster (2016) refer to this as the equal selection assumption. Intuitively, it allows us to learn about the direction of bias induced by the unobservables from the bias induced when we omit the observables. In a standard labor economics context where we would attempt to measure returns to education, equal selection would imply that if education is increasing in observed proxies for worker skill, it will be increasing in unobserved skill as well. In our context, equal selection implies that if movers to a particular destination tend to have unusually good observed health capital they will probably have unusually good unobserved health capital as well.

The second assumption pins down the overall importance of the unobservables relative to the observables. Oster (2016) operationalizes this as an assumed value for the R² of a hypothetical regression of the outcome on the treatment, the observables, and all the relevant unobservables.¹² We will refer to this as the R² assumption. Intuitively, specifying this value allows us to determine the magnitude of the bias induced by the unobservables. In the labor economics example, the bias would be small if there is very little variation in unobserved skill conditional on the observed proxies, or large if this variation is large. In our context, the bias would be small if observed proxies captured most of the variation in health capital, and so the variance of the unobserved components was small. Oster (2016) emphasizes that the choice of the R² value is by necessity arbitrary in typical applications, and suggests some benchmark values researchers could use to obtain conservative bounds.

What distinguishes our strategy from prior work is that we use an additional moment of the data to weaken the R² assumption. That moment is the variance of the origin component of unobserved health—${\eta }_o^{\mathit{\text{orig}}}$ in equation (2), which we recall is consistently estimated by the origin fixed effect ${\widehat{\tau }}_o^{\mathit{\text{orig}}}$ from equation (3). If our observable measures H_i captured all relevant dimensions of health capital, movers’ origins would have no further predictive power, and we would have ${\eta }_o^{\mathit{\text{orig}}}=0$ for all o. The extent to which origins remain predictive of mortality after we control for H_i is a gauge of the extent to which important unobserved components remain.

To apply this logic formally, we first introduce some new constructs and notation. First, define a “treatment” indicator T_ij = 1 (j (i) = j) for movers equal to one if i’s destination is j. Second, as an input to our selection correction strategy, we will need to estimate the components of observed health capital related to movers’ origins and destinations respectively. Let h_i = H_iλ (where λ is defined in equation (3)) be the index of observed health capital for individual i; we refer to it throughout as “observed health” for short. Define the following regression in the sample of movers:

$$h_i={\beta }^{h}a+X_i{\psi }^h+h_{o(i)}^{\mathit{\text{orig}}}+h_{j(i)}^{\mathit{\text{dest}}}+{\tilde{h}}_i,$$ (4)

where $h_{o(i)}^{\mathit{\text{orig}}}$ and $h_{j(i)}^{\mathit{\text{dest}}}$ are origin and destination fixed effects respectively and ${\tilde{h}}_i$ is a residual. We refer to $h_{o(i)}^{\mathit{\text{orig}}}$ and $h_{j(i)}^{\mathit{\text{dest}}}$ as the origin and destination components of observed health respectively. These are by construction the residual components of observed health after partialing out age and demographics. We normalize $h_{o(i)}^{\mathit{\text{orig}}}$ so the population mean of $h_{j(i)}^{\mathit{\text{dest}}}$ is zero. To estimate these terms, we first form ${\widehat{h}}_i=H_i\widehat{\lambda }$ using the estimates $\widehat{\lambda }$ from equation (3). We then estimate equation (4) replacing h_i with ${\widehat{h}}_i$.

Our two key assumptions can now be stated as follows.

• Assumption 1. (Proportional Selection) $\text{Corr}\left(T_{ij},h_{j(i)}^{\mathit{\text{dest}}}\right)={\phi }_1\text{Corr}\left(T_{ij},{\eta }_{j(i)}^{\mathit{\text{dest}}}\right)$ in the sample of movers for all $j\in \mathcal{J}$, where φ₁ is a constant.

• Assumption 2. (Relative Importance) $\frac{\text{StDev}\left({\eta }_{j(i)}^{\mathit{\text{orig}}}\right)}{\text{StDev}\left(h_{j(i)}^{\mathit{\text{orig}}}\right)}={\phi }_2\frac{\text{StDev}\left({\eta }_{j(i)}^{\mathit{\text{dest}}}\right)}{\text{StDev}\left(h_{j(i)}^{\mathit{\text{dest}}}\right)}$ in the sample of movers, where φ₂ is a constant.

Assumption 1 is a version of the equal selection assumption of Altonji et al. (2005) and Oster (2016) applied to our setting. There are two key differences. First, we weaken their assumption to allow selection on unobservables to be proportional to selection on observables, with a coefficient of proportionality of φ₁; this nests the special case of equal selection (i.e. φ₁ = 1). Second, our setting differs from the one they consider in that our “treatment” is multidimensional—a vector of indicators for moving to the various destinations in $\mathcal{J}$. To map this back to the standard case, we imagine a setting where the treatment of interest was the effect of moving to one particular destination j, and so the treatment variable is just the binary indicator T_ij. We then assume the assumption applies separately for each possible destination $j\in \mathcal{J}$.¹³

Assumption 2 allows us to use information from origin unobservables in place of the R² assumption. Rather than assuming an arbitrary value for the variance of the destination unobservables $\text{Var}\left({\eta }_{j(i)}^{\mathit{\text{dest}}}\right)$ as the standard approach would dictate, we assume that the variance of these unobservables relative to the variance of the destination observables $\text{Var}\left(h_{j(i)}^{\mathit{\text{dest}}}\right)$ is proportional to the corresponding ratio for movers’ origins, with a coefficient of proportionality of φ₂. Again, this nests as a special case the assumption that the ratios are not just proportional, but are in fact equal (i.e. φ₂ = 1). Combining these two assumptions allows us to consistently estimate the key unobservables ${\eta }_j^{\mathit{\text{dest}}}$ for each j from observed moments of the data, given assumed values of φ₁ and φ₂. We impose φ₁ = φ₂ = 1 in our baseline results and assess robustness to alternative values of φ₁ and φ₂.

Assumption 1 and 2 are strong, but they follow naturally from economic primitives. They will hold in a broad class of models of selective migration so long as selection of locations is related to overall health capital but not differentially to the observed and unobserved components. We show this formally in Appendix B. Specifically, we show that under some additional structure on the distributions of observables and unobservables, Assumptions 1 and 2 with φ₁ = φ₂ = 1 are both implied by the assumption that selection of origins and destinations may depend on the single index ${\tilde{\theta }}_i=h_i+{\eta }_i$, where ${\eta }_i={\eta }_{o(i)}^{\mathit{\text{orig}}}+{\eta }_{j(i)}^{\mathit{\text{dest}}}+{\tilde{\eta }}_i$, but that origins and destinations are independent of h_i and η_i conditional on ${\tilde{\theta }}_i$.

If the dimensions of health capital relevant to selection are not captured by a single index, our baseline assumption of φ₁ = φ₂ = 1 requires that the relative importance of unobservable to observable health in determining origin must be the same as the relative importance of unobservable to observable health in determining destination. This could be violated if, for example, observed dimensions of health capital such as diabetes are more strongly related to people’s choice of where to live when young, while unobserved dimensions such as physical mobility are more strongly related to their migration decisions when they are elderly. It could be violated if late-life events such as widowhood affect both the likelihood of moving to different destinations and mortality but are uncorrelated with observed health capital. We provide empirical support for the assumptions behind our selection correction approach in Section VI.C below.

Proposition 1.

Assumption 1 is equivalent to

$${\eta }_j^{\mathit{\text{dest}}}={\phi }_1\frac{\text{StDev}\left({\eta }_{j(i)}^{\mathit{\text{dest}}}\right)}{\text{StDev}\left(h_{j(i)}^{\mathit{\text{dest}}}\right)}{h}_j^{\mathit{\text{dest}}}.$$ (5)

Proof.

Recalling that $h_{j(i)}^{\mathit{\text{dest}}}$ and ${\eta }_{j(i)}^{\mathit{\text{dest}}}$ are normalized to have mean zero, it is straightforward to show that $\text{Cov}\left(T_{ij},h_{j(i)}^{\mathit{\text{dest}}}\right)=\frac{N}{N^{\prime }}{h}_j^{\mathit{\text{dest}}}p(1-p)$ and $\text{Cov}\left(T_{ij},{\eta }_{j(i)}^{\mathit{\text{dest}}}\right)=\frac{N}{N^{\prime }}{\eta }_j^{\mathit{\text{dest}}}p(1-p)$, where N is the total number of movers, N′ is the number with T_ij = 0, and p = Pr(T_ij = 1).¹⁴ Assumption 1 is then equivalent to

$$\frac{\frac{N}{N^{\prime }}{h}_j^{\mathit{\text{dest}}}p(1-p)}{\text{StDev}\left(T_{ij}\right)\text{StDev}\left(h_{j(i)}^{\mathit{\text{dest}}}\right)}={\phi }_1\frac{\frac{N}{N^{\prime }}{\eta }_j^{\mathit{\text{dest}}}p(1-p)}{\text{StDev}\left(T_{ij}\right)\text{StDev}\left({\eta }_{j(i)}^{\mathit{\text{dest}}}\right)}.$$

Canceling terms yields the desired result.

This proposition is intuitive. It says that under our proportional selection assumption, the destination component ${\eta }_j^{\mathit{\text{dest}}}$ — i.e., the average unobserved, residual health in destination j — is equal to the observed term $h_j^{\mathit{\text{dest}}}$ scaled by a constant. Under our baseline assumption (φ₁ = 1) the value of that constant is the ratio of the standard deviations of ${\eta }_{j(i)}^{\mathit{\text{dest}}}$ and $h_{j(i)}^{\mathit{\text{dest}}}$, and it can be interpreted as the relative importance of the unobserved and observed components of health capital correlated with destinations. Assumption 2 then allows us to estimate this ratio using the analogous ratio for movers’ origins.

Corollary 1.

Let $\text{St}\widehat{\text{D}}\text{ev}\left({\tau }_{j(i)}^{\mathit{\text{orig}}}\right)$ and $\text{St}\widehat{\text{D}}\text{ev}\left({\tau }_{j(i)}^{\mathit{\text{orig}}}\right)$ be consistent estimators of the standard deviations of ${\tau }_{j(i)}^{\mathit{\text{orig}}}$ and $h_{j(i)}^{\mathit{\text{orig}}}$ and define φ ≡ φ₁φ₂. Under Assumptions 1 and 2,

$${\widehat{\eta }}_j^{\mathit{\text{dest}}}=\phi \frac{\text{St}\widehat{\text{D}}\text{ev}\left({\tau }_{j(i)}^{\mathit{\text{orig}}}\right)}{\text{St}\widehat{\text{D}}\text{ev}\left(h_{j(i)}^{\mathit{\text{orig}}}\right)}{\widehat{h}}_j^{\mathit{\text{dest}}}$$ (6)

is a consistent estimator of ${\eta }_j^{\mathit{\text{dest}}}$, and ${\widehat{\gamma }}_j={\widehat{\tau }}_j^{\mathit{\text{dest}}}-{\widehat{\eta }}_j^{\mathit{\text{dest}}}$ is a consistent estimator of γ_j.

III. Data and Summary Statistics

A. Data and Variable Definitions

We use administrative data on Medicare enrollees for a 100% panel of Medicare beneficiaries — both Traditional Medicare and Medicare Advantage — from 1999 to 2014 (CMS 1998–2014b).¹⁵

We observe each enrollee’s zip code of residence each year. We define a year t for the purposes of our analysis to run from April 1 of calendar year t to March 31 of calendar year t + 1 since, for most years, we observe residence as of March 31st of that year.

For each enrollee, we observe time-invariant indicators for race and gender. We observe time-varying indicators for age, as well as enrollment in Medicaid (the supplemental public health insurance program for low income elderly), Medicare Parts A and B, and Medicare Advantage. We observe all claims for inpatient and outpatient care for enrollee-years in Traditional Medicare. For individuals who die during our sample, we observe the date of death.

Our primary analysis focuses on a sample of movers and non-movers defined below. We restrict attention to movers whose CZ of residence changes exactly once. For each mover, we define year $t_i^{\ast }$ (an individual’s “move year”) to be the year in which their location changes and $t_i^{\ast }+1$ to be their first full year in the new location. For non-movers, we define $t_i^{\ast }$ to be the second year we observe them in the data without any missing covariates, so that we can measure their characteristics in the prior year. As discussed below, we restrict our analysis to beneficiaries enrolled in Traditional Medicare during year $t_i^{\ast }-1$.

We use the Chronic Conditions segment of the Master Beneficiary Summary File from 1999 to 2014 to define 27 health status indicators for each person-year, with each indicator capturing the presence of a specific chronic condition (CMS 1998–2014b). Examples include lung cancer, diabetes, and depression; the share of patients with each of these conditions and the estimated coefficients for each from the Gompertz mortality hazard model (equation (3)) can be seen in Appendix Table A.1. The algorithms defining these measures are publicly available¹⁶ and are based on definitions used in the medical literature.¹⁷ Importantly, because we measure observed health H_i pre-move, and equation (3) controls for origin fixed effects, we are not concerned about bias arising in our estimation from the type of place-specific measurement error of health in claims data that prior work has highlighted (Song et al. 2010; Finkelstein et al. 2016, 2017).

We measure total health care utilization for each person-year in Traditional Medicare, defined to be total inpatient and outpatient spending, adjusted for price differences following the procedure of Gottlieb et al. (2010).¹⁸ Because we restrict our analysis sample to those enrolled in Traditional Medicare in year $t_i^{\ast }-1$, total health care utilization is observed in that year for all individuals in our analysis sample, even if those individuals may be enrolled in Medicare Advantage (and hence have unobserved health care utilization) during years other than $t_i^{\ast }-1$.

We define areas j to be Commuting Zones (CZs). Specifically, we use the 709 CZs defined by the Census Bureau in 2000. These are aggregations of counties designed to approximate local labor markets. CZs have been used previously to analyze geographic variation in life expectancy (e.g. Chetty et al. 2016b).¹⁹

All of the enrollee-level covariates in our analysis (i.e. H_i and X_i) are measured as of year $t_i^{\ast }-1$. In our baseline specification, observable health (H_i) is a series of indicator variables for each of the 27 chronic conditions in the Chronic Conditions segment of the Master Beneficiary Summary file and log(utilization + 1). X_i is a set of indicators for race (white or non-white), gender, and their interaction; we also include an indicator variable for Medicaid status (as a proxy for low income), a series of indicator variables for the calendar year corresponding to $t_i^{\ast }$, and a constant.

Sample Restrictions and Summary Statistics

Our data contain approximately 81 million people and over 665 million person-years. We drop from this sample person-years in which the enrollee is younger than 65 or older than 99.²⁰ This leaves us with a core sample of about 69 million beneficiaries; we exclude a few hundred thousand beneficiaries with incomplete data.

To define our non-mover sample, we begin with the 62 million enrollees whose CZ of residence does not change over the years we observe them. We need to assign each non-mover a valid reference year $t_i^{\ast }$ such that we are able to see observable health characteristics in year $t_i^{\ast }-1$. We therefore eliminate all non-movers who do not have a pre-2012 year $t_i^{\ast }$ such that they are 99 or younger and alive until the end of that year, and also on Traditional Medicare during year $t_i^{\ast }-1$. We take a random 10% sample of the remaining 43 million non-movers and define their $t_i^{\ast }$ to be the second year they are in the sample. When we estimate equation (3) using the pooled sample of movers and non-movers, we upweight the non-movers by ten.

To define our mover sample, we begin with the 7 million enrollees whose CZ of residence changes at least once during our sample period. To ensure changes in address reflect real changes in location, we define a mover’s “claim share” in a particular year to be the ratio of the number of claims located in their destination to the number located in either their origin or their destination. We then follow Finkelstein et al. (2016) in excluding those for whom the claim share does not increase by at least 0.75 in their post-move years relative to their pre-move years. Appendix C provides more detail.

A natural question is of course why individuals in this sample are choosing to move. In Finkelstein et al. (2016), we use the Health and Retirement Study (HRS) data to tabulate survey responses about why individuals in this age group move; Choi (1996) provides a similar tabulation in the Longitudinal Survey of Aging (LSOA), and both datasets lead to similar conclusions. The most frequently reported reason for moves in this age group is to be near/with children or other kin, followed by health reasons, financial reasons, or other amenities.²¹

We further restrict the sample to movers who are not on Medicare Advantage in the year immediately prior to or immediately after the move (since we need to measure claim shares in those years) and who moved in years 2000–2012 (so that we can observe pre-move characteristics and post-move mortality).²² We also exclude those who move at age 99 or later or do not survive through the end of their move year $\left(t_i^{\ast }\right)$. Our final sample contains 6.3 million individuals, of whom 2 million are movers. Appendix C provides more detail on the sample restrictions. By construction, we are able to observe mortality for all beneficiaries for at least one year following $t_i^{\ast }$. We are able to observe mortality at least 7 years after $t_i^{\ast }$ for 63 percent of movers and at least 10 years after $t_i^{\ast }$ for 35 percent of movers.

Because our strategy for estimating place effects requires that we observe a significant number of movers to each area, we aggregate CZs that receive small numbers of movers to form larger areas within states. Specifically, we first collect the bottom quartile of CZs by the number of incoming movers. Then, in any case where a state contains two or more such CZs, we consolidate those CZs into a single area. Appendix Figure A.1 shows the locations of the bottom quartile of CZs; they are predominantly in the Great Plains. The number of movers to these CZs ranges from 2 to 359, with a median of 155. Our final sample has 528 CZs and 35 aggregated CZs; these are the areas corresponding to the j index in our model and we refer to these simply as “CZs” in what follows.²³ Appendix Table A.2 shows summary statistics on the number of movers to each CZ; the minimum number of movers to a CZ is 48, and the median is about 1,500.

Table 1 reports summary statistics for comparable samples of movers and non-movers. The first row shows our full sample, which consists of roughly 2 million movers and 4.3 million non-movers. The remainder of the table shows characteristics of a sub-sample of movers and non-movers with reference year $t_i^{\ast }=2006$. We focus on this subset to facilitate comparison of movers’ and non-movers’ characteristics.²⁴ Movers tend to be older than non-movers, are slightly more likely to be female and white, and slightly less likely to be on Medicaid. Not surprisingly given the age differences, movers are also less healthy as measured by their count of chronic conditions and their one and four year mortality.

Table 1:

Summary Statistics

	(1) Movers	(2) Non-movers
Estimation sample (# of individuals)	2,032,872	4,312,726
2006 comparison sample (# of individuals)	168,853	168,853
Age:
65–74	0.48	0.54
75–84	0.35	0.35
85+	0.17	0.11
Female	0.60	0.57
White	0.89	0.86
Region:
Northeast	0.19	0.20
South	0.43	0.37
Midwest	0.19	0.27
West	0.19	0.16
On Medicaid	0.10	0.12
Avg. # of chronic conditions	3.08	2.82
1-year mortality	0.09	0.05
4-year mortality	0.29	0.20

Notes: The first row shows the sample size for the full estimation sample. The summary statistics on movers in the comparison sample are restricted to those who moved in the year 2006 (8.30% of movers in the whole sample). A random subset of non-movers that meet sample restrictions in 2006 are included, with their reference years set to 2006, such that the number of movers is equal to the number of non-movers. Rows for female, white, age, and region report the share of individuals with the given characteristics. Time-varying characteristics are measured in the year prior to each enrollee’s reference year.

IV. Preliminary Evidence

A. Patterns of Mortality and Migration

Figure 1 shows our estimates ${\widehat{L}}_j$ of average non-mover life expectancy by area, constructed from the estimated model of equation (3) as described in Section II.B. The average life expectancy across areas is 83.3 years, with a standard deviation of 0.79 years. Our life expectancy estimates for the 100 largest CZs are highly correlated (nearly 0.9) with the life expectancy estimates at age 40 of Chetty et al. (2016b), as shown in Appendix Figure A.2.

Figure 1:

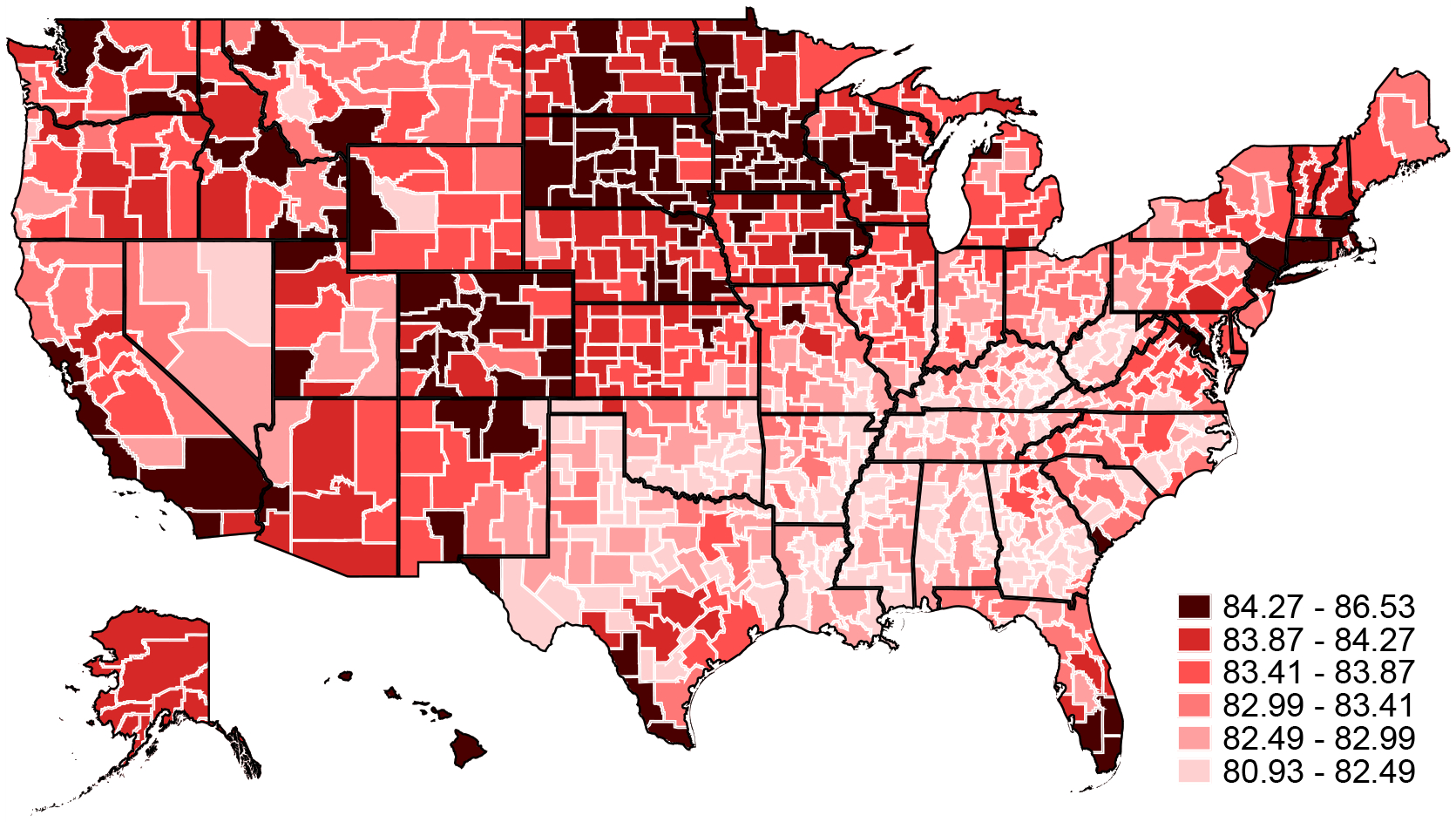
Age 65 Life Expectancy

Notes: Figure reports estimated life expectancy at age 65 for non-movers in each CZ (L_j). Average life expectancy at 65 in each CZ is computed assuming a non-mover with the average characteristics in that CZ, except for race and sex for which national averages are used. Note that small CZs have been aggregated within each state (see Appendix Figure A.1) and a single life expectancy estimate is reported for each aggregate CZ.

Since moves will be key to identifying place effects, we briefly discuss the characteristics of moves in our sample. There is substantial variation across moves in the destination-origin difference in non-mover life expectancy (L_j). The standard deviation of this gap is roughly one year, and the share of movers to higher life expectancy destinations (48 percent) is similar to the share of moves to lower life expectancy destinations (52 percent); Appendix Figure A.3 shows more detail on the destination-origin differences in average life expectancy. Conditional on origin, the average standard deviation of destination life expectancy across CZs is 0.67.

We next examine the extent to which the observed health of movers differs systematically according to their destinations. In panel (a) of Figure 2, we compare the average observed health of movers to different destinations adjusted for age and demographics (X_i). For each area j, we compute the mean across movers to j of the residuals from a regression of our observed health index ${\widehat{h}}_i=H_i\widehat{\lambda }$ on age in year $t_i^{\ast }-1$ and demographics X_i. The left-hand figure shows the distribution of these average values across destinations. If movers were randomly assigned to destinations, these averages should vary little; this is not the case. The right-hand figure is a binned scatterplot showing how these average observed health values for movers to different destinations are correlated with the average estimated mortality index γ_j +θ_i of non-movers in each destination. The relationship is significant and positive, suggesting that low-mortality destinations tend to attract healthier movers.

Figure 2:

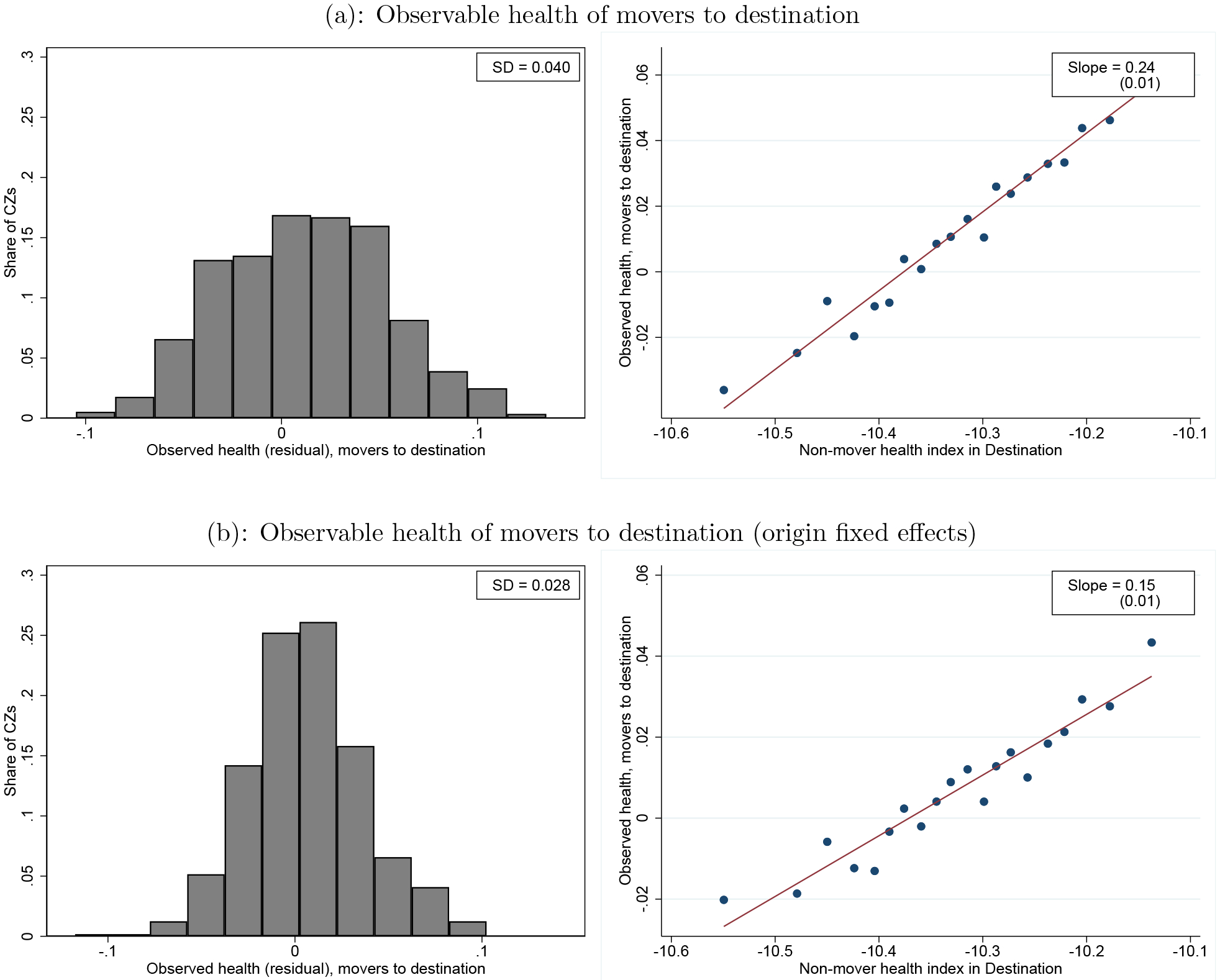
Observable Health and Non-Mover Mortality

Notes: The left panels plot the distribution across CZs of the average observable, residualized health of movers to CZ j. Specifically, the top left panel plots average residual observed health $\left({\widehat{h}}_i\right)$, conditional on X_i and age. The bottom left panel plots $h_j^{\widehat{\mathit{\text{dest}}}}$ as defined in the text, and also conditions on origin fixed effects in addition to X_i and age. All estimates are normalized such that the mean (across movers) of each is zero; both panels also report the cross-CZ standard deviation. The right panels show binned scatterplots of these two measures of average, residualized observable health of movers to CZ j against the average mortality index in CZ j $\left({\overline{m}}_j\right)$. The average mortality index estimates come from the sample and model estimates of only non-movers (i.e. the same estimates as are used in Figure 1). The regression line and standard errors are both estimated using the CZ level data.

In panel (b) of Figure 2, we partial out fixed effects for movers’ origins (in addition to the age and demographics that were already partialed out in panel (a). These values capture the extent to which healthier movers from a given origin select systematically different destinations. The results indicate that conditional on origin, mover observed health is still correlated with destination mortality, but conditioning on origin lowers the slope from 0.24 to 0.15. While the selection on observed health shown here will be accounted for by the explicit H_i controls in our model, it suggests that there may be remaining selection on unobserved health which we will need to address with our selection correction strategy.

B. Inputs to Selection Correction

Table 2 shows the standard deviations of the components of health capital that enter our selection correction. For each component, we report the standard deviation across CZs, estimated using our split-sample strategy, as well as 95-percent confidence intervals based on our Bayesian bootstrap. The magnitudes are not easily interpretable, as they are in units of the log mortality rate log (m_i), but to get a sense, note that a 65-year old with average health capital $\overline{\theta }$ and sample-wide average place effect $\overline{\gamma }$ (which is 0 by construction) has an annual mortality rate of m = 0.013, and increasing her health capital by one standard deviation (among 65-year-olds) would increase her mortality rate by 0.005.

Table 2:

Inputs to Selection Correction

	Standard Deviation
Origin Components:
Observed health $\left(h_{j(i)}^{\mathit{\text{orig}}}\right)$	0.037 [0.036, 0.037]
Unobserved health $\left({\eta }_{j(i)}^{\mathit{\text{orig}}}\right)$	0.061 [0.058, 0.064]
Destination Components:
Observed health $\left(h_{j(i)}^{\mathit{\text{dest}}}\right)$	0.024 [0.024, 0.025]
Unobserved health $\left({\eta }_{j(i)}^{\mathit{\text{dest}}}\right)$, inferred based on Corollary 1	0.040 [0.037, 0.043]

Notes: Standard deviations are computed using the split-sample approach, and are weighted by the number of movers with each CZ as their destination. Confidence intervals are computed using 100 replications of the Bayesian bootstrap.

The first two rows report the estimated standard deviations of the components $h_{j(i)}^{\mathit{\text{orig}}}$ and ${\eta }_{j(i)}^{\mathit{\text{orig}}}$ correlated with movers’ origins. Recall that our estimators of these terms are the origin fixed effects from equations (3) and (4) respectively. We find that the standard deviation of the unobservable component ${\eta }_{j(i)}^{\mathit{\text{orig}}}$ is 0.061, and the standard deviation of the observable component $h_{j(i)}^{\mathit{\text{orig}}}$ is 0.037. This suggests that, despite the richness of our observable health measures, the remaining systematic variation in health capital correlated with locations is substantial. The ratio of these terms $\frac{0.061}{0.037}=1.65$ is the key conversion factor that is used in Corollary 1 to pin down the relative importance of unobservables and observables.

The last two rows report the estimated standard deviations of the components $h_{j(i)}^{\mathit{\text{dest}}}$ and ${\eta }_{j(i)}^{\mathit{\text{dest}}}$ correlated with movers’ destinations. The $h_{j(i)}^{\mathit{\text{dest}}}$ components are estimated by the destination fixed effects in equation (4); we find that their standard deviation is 0.024. The ${\eta }_{j(i)}^{\mathit{\text{dest}}}$ components cannot be directly estimated, and are the key objects our selection correction is designed to infer. Applying Corollary 1 with our baseline constants φ₁ = φ₂ = 1, we estimate that the standard deviation of ${\eta }_{j(i)}^{\mathit{\text{dest}}}$ is $0.024\times \frac{0.061}{0.037}=0.040$.

V. Main Results

A. Place Effects

Table 3 reports our decomposition of the area average mortality index ${\gamma }_j+{\overline{\theta }}_j$. As shown in the first row, the standard deviation across CZs of this index is 0.099.

Table 3:

Mortality Components

	Standard Deviation
Mortality Index $\left({\gamma }_j+{\overline{\theta }}_j\right)$	0.099 [0.095, 0.103]
Unadjusted:
Place Effects (γj)	0.077 [0.067, 0.087]
Health Capital $\left({\overline{\theta }}_j\right)$	0.073 [0.057, 0.085]
Correlation of γj and ${\overline{\theta }}_j$	−0.139 [−0.322, 0.281]
Selection Corrected:
Place Effects (γj)	0.054 [0.040, 0.069]
Health Capital $\left({\overline{\theta }}_j\right)$	0.088 [0.071, 0.099]
Correlation of γj and ${\overline{\theta }}_j$	−0.093 [−0.322, 0.413]

Notes: These standard deviations across CZ give equal weight to each CZ and standard deviations for the mortality index, place effects, and health capital use the split-sample approach. 95% confidence intervals are computed using 100 replications of the Bayesian bootstrap. For the “unadjusted” results in the top panel, γ_j is defined as the destination fixed effects ${\widehat{\tau }}_j^{\mathit{\text{dest}}}$ from equation (3), and average health capital ${\overline{\theta }}_j$ is given by the average value of the remaining terms in that equation (excluding the age term a_iβ) within each bootstrap and split-sample. For the “selection corrected” results in the bottom panel, γ_j is defined as the difference ${\widehat{\tau }}_j^{\mathit{\text{dest}}}-{\widehat{\eta }}_j^{\mathit{\text{dest}}}$, where ${\widehat{\tau }}_j^{\mathit{\text{dest}}}$ is the destination fixed effect from equation (3) and the unobservable component ${\widehat{\eta }}_j^{\mathit{\text{dest}}}$ is inferred following the steps broken out in Table 2; average health capital ${\overline{\theta }}_j$ is then calculated using the same approach as in the unadjusted results. Within each bootstrap, the correlation of γ_j and ${\overline{\theta }}_j$ are calculated as $\left[\mathit{\text{Var}}\left({\gamma }_j+{\overline{\theta }}_j\right)-\mathit{\text{Var}}\left({\gamma }_j\right)-\mathit{\text{Var}}\left({\overline{\theta }}_j\right)\right]/\left[2\mathit{\text{StDev}}\left({\gamma }_j\right)\mathit{\text{StDev}}\left({\overline{\theta }}_j\right)\right]$, with each variance and standard deviation calculated using the split-sample approach.

The following three rows report the decomposition of this index when we do not apply our selection correction — i.e., when we assume ${\eta }_j^{\mathit{\text{dest}}}=0$ for all j. In this case, our estimate of the place effects γ_j is simply the destination fixed effects ${\widehat{\tau }}_j^{\mathit{\text{dest}}}$ from equation (3), and average health capital ${\overline{\theta }}_j$ is given by the average value of the remaining terms in that equation (excluding the age term a_iβ, and taking the national average of race and sex as discussed in Section II.B. In this case, we estimate that the standard deviation of the place effects is 0.077, or three-quarters of the standard deviation of the overall index. The standard deviation of average health capital is 0.073, and the correlation between the two components is slightly negative.

The bottom three rows report our preferred estimates applying the selection correction. Here, our estimate of the place effects γ_j is the difference ${\widehat{\tau }}_j^{\mathit{\text{dest}}}-{\widehat{\eta }}_j^{\mathit{\text{dest}}}$, where the unobservable component ${\widehat{\eta }}_j^{\mathit{\text{dest}}}$ is inferred following the steps broken out in Table 2. Average health capital ${\overline{\theta }}_j$ is again given by the average value of the remaining terms in equation (3) (excluding the age term a_iβ, and taking the national average of race and sex as discussed in Section II.B). The standard deviation of the selection-corrected place effects is 0.054, about one-third smaller than the uncorrected version, and roughly half the standard deviation of the overall index. The standard deviation of average health capital is 0.088, and the correlation between the two components remains negative.

Figure 3 shows a map of our estimated treatment effects $\left(L_j^{\ast }-\overline{L}\right)$. These are defined in Section I and capture the impact of moving to an area on life expectancy for a mover with average health capital. Places with the most favorable effects are found along the east and west coasts as well as in major cities such as Chicago. Many of the places with the most adverse effects are in the deep south (Alabama, Arkansas, Georgia, Louisiana, and parts of Florida) and in the Southwest (Texas, Oklahoma, New Mexico, and Arizona).

Figure 3:

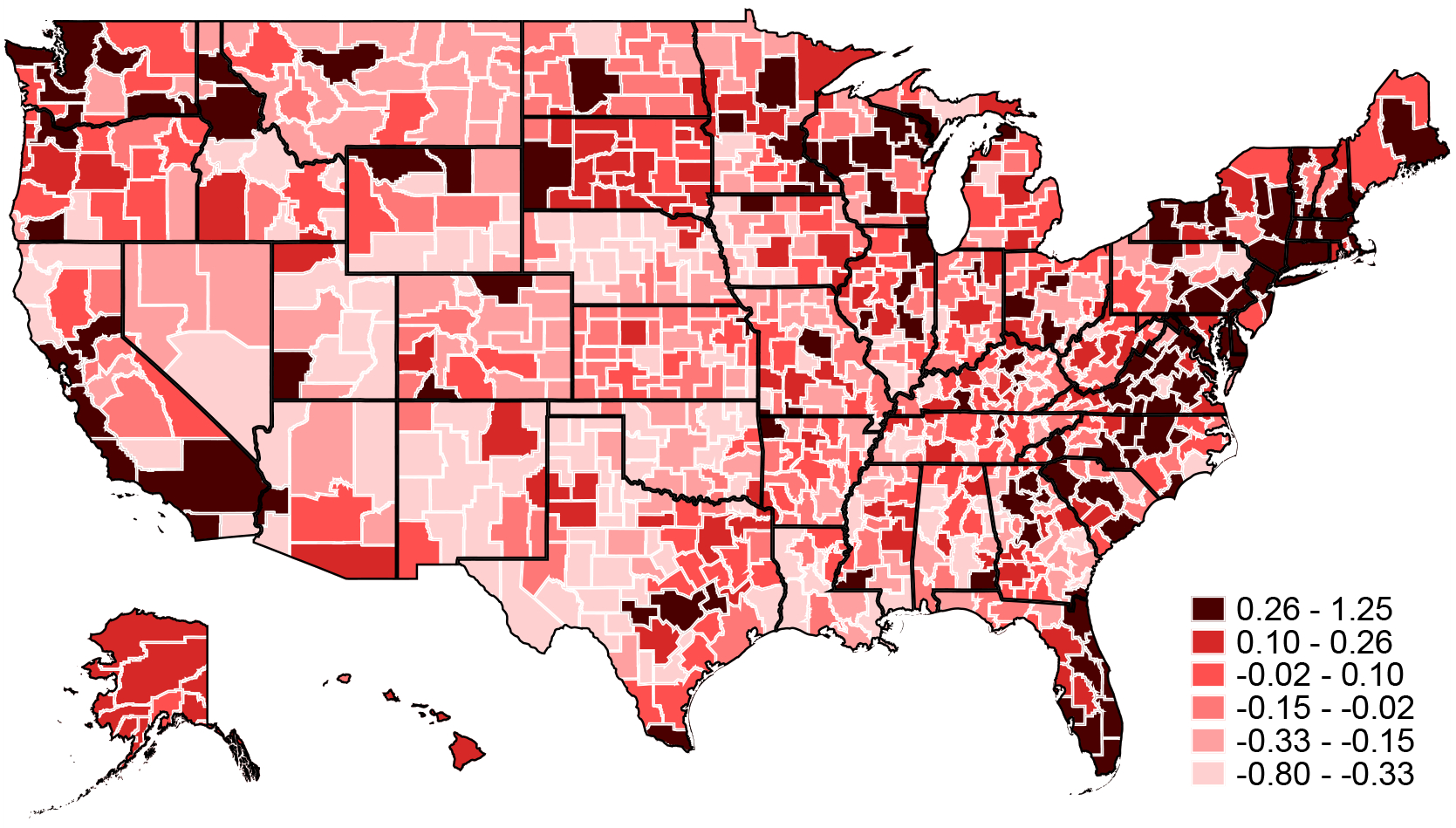
Life Expectancy Treatment Effects

Notes: The map shows the Empirical Bayes-adjusted estimates of life-expectancy treatment effects $\left(L_j^{\ast }-\overline{L}\right)$. Note that small CZs have been aggregated within state (see Appendix Figure A.1) and a single life expectancy estimate is reported for each aggregate CZ.

Figure 4 shows a scatterplot of these treatment effects against estimated average life expectancy ${\widehat{L}}_j$ in each place. The two are positively correlated: a one unit increase in average life expectancy is associated with a 0.23 year increase in the treatment effect. Interestingly, for Medicare survivors of Hurricane Katrina, Deryugina and Molitor (2018) estimate larger effects. They find that moving to a place with a one percentage point higher mortality rate is associated with an increase in migrant mortality of approximately one percentage point. The fact that they find larger effects could reflect the fact that our estimates are adjusted for selection, the specific sub-sample of destinations that their migrants move to, and the specific circumstances of the hurricane.

Figure 4:

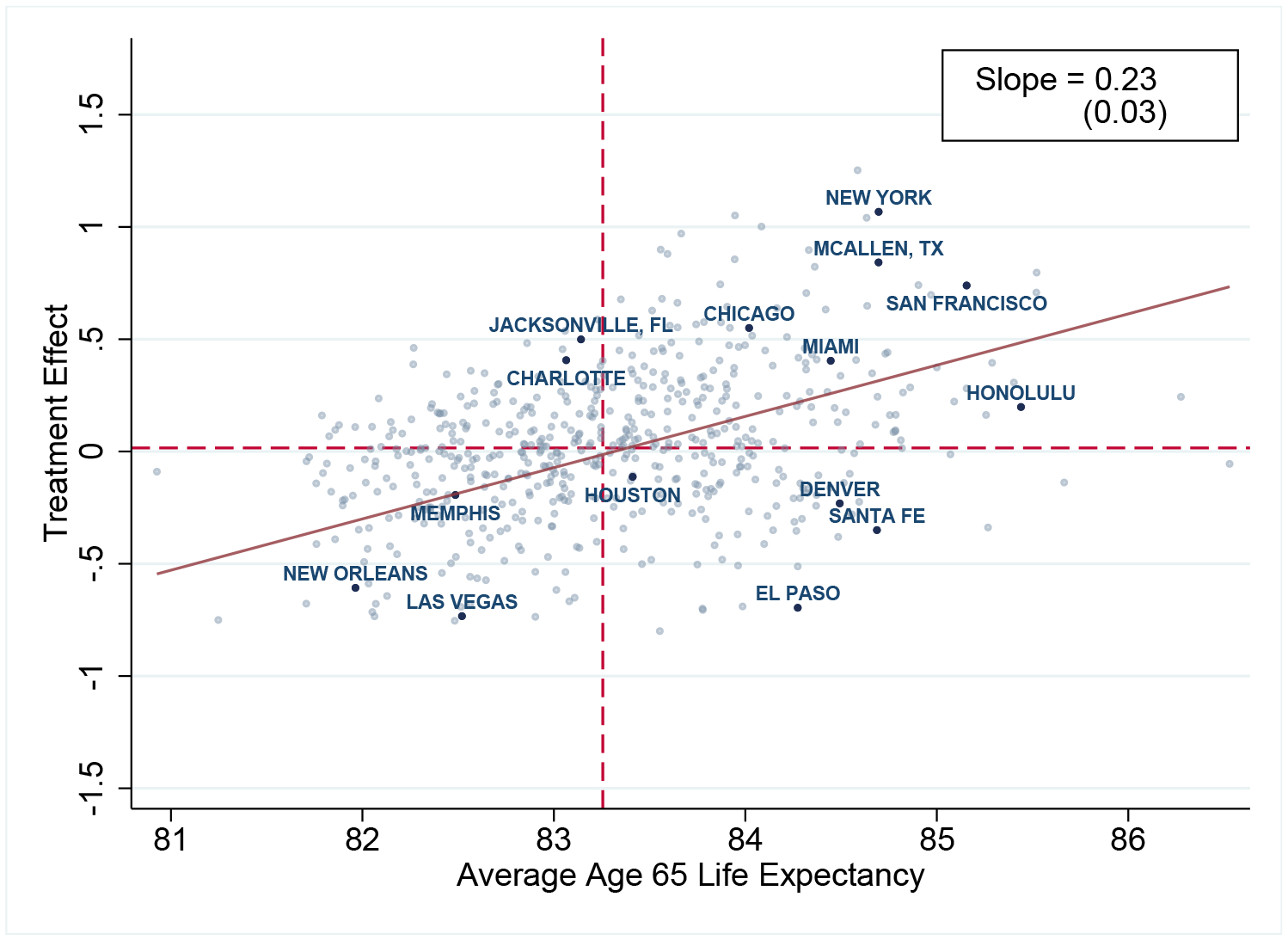
Life Expectancy Treatment Effects vs. Life Expectancy

Notes: The plot shows a scatterplot of the Empirical Bayes (EB)-adjusted age 65 life-expectancy treatment effects for CZ j $\left(L_j^{\ast }-\overline{L}\right)$ on the average age 65 non-mover life expectancy (L_j). The line of best fit comes from a regression of non-EB-adjusted treatment effects on average non-mover life expectancy. The horizontal and vertical dashed lines show the medians of treatment effects and life expectancy, respectively, over all CZs. Confidence intervals for the treatment effects and life expectancies of all CZs are provided online.

Figure 4 also shows a number of examples that highlight how average life expectancy and treatment effects can diverge. For example, Charlotte, North Carolina is a place that in the cross-section has low average life expectancy, despite a relatively favorable treatment effect. The gap reflects Charlotte unusually poor average health capital. At the other extreme, Santa Fe, New Mexico is an example of a place with relatively high average life expectancy despite a negative treatment effect. The gap reflects the unusually good health capital of Santa Fe residents.

Figure 5 shows the treatment effects - and their 95 percent confidence intervals - for the 20 most populous CZs. For comparison, we also show average life expectancy in each location. The treatment effects of these locations range from −0.23 in Denver, CO to 1.07 years in New York, NY. Estimates for each CZ’s treatment effect and confidence interval are available online.

Figure 5:

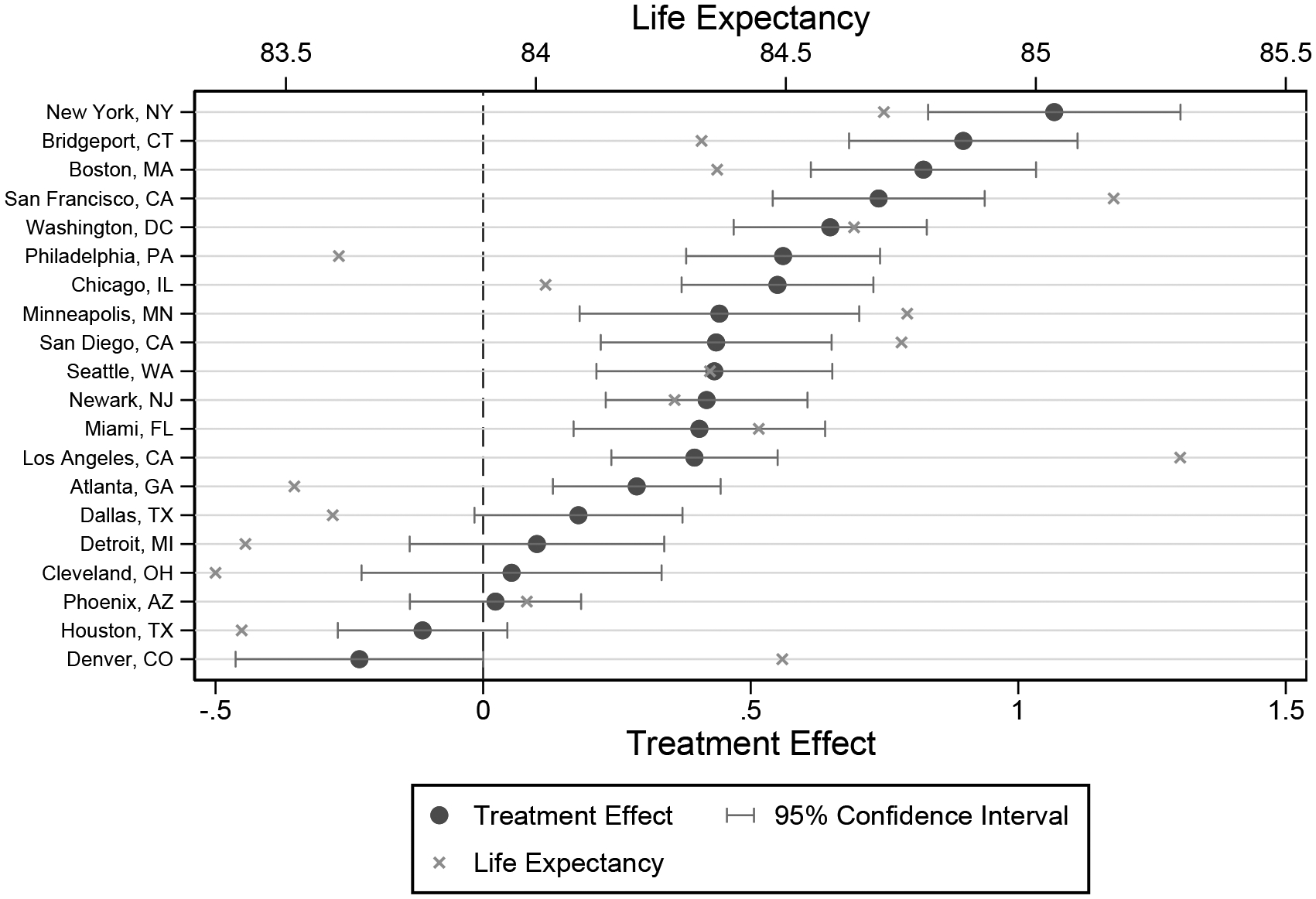
Life Expectancy Treatment Effects for 20 Largest CZs

Notes: This figure plots the Empirical Bayes-adjusted life expectancy treatment effect for the 20 most populous CZs (calculated using the 2000 and 2010 census), sorted by their Empirical Bayes-adjusted life-expectancy treatment effects. 95% confidence intervals are calculated as described in Appendix A using the mean-squared error of each optimal prediction of the Empirical Bayes-adjusted life expectancy treatment effect. The x marks indicate the point estimates for the age-65 life-expectancy within each CZ.

Table 4 summarizes our estimated treatment effects across commuting zones. The top row reports the standard deviation across CZs of average life expectancy, which is 0.79 years. The second row shows the standard deviation of our estimated treatment effects, which is 0.44, or roughly half of the cross-sectional variation in life expectancy.

Table 4:

Life Expectancy Decompositions

Cross-CZ standard deviation of:
(1) Age 65 Life Expectancy (Lj)	0.79 [0.76, 0.83]
(2) Treatment Effects $\left(L_j^{\ast }-\overline{L}\right)$	0.44 [0.32, 0.55]
(3) Health Capital Effects	0.73 [0.60, 0.83]
(4) Correlation of Treatment and Health Capital Effects	−0.04 [−0.15, 0.09]
Share variance would be reduced if:
(5) Place Effects were Made Equal	0.15 [−0.10, 0.46]
(6) Health Capital was Made Equal	0.69 [0.53, 0.83]

Notes: All objects are computed at the CZ level using the split-sample approach described in Section II.B and give equal weight to each CZ; 95% confidence intervals are computed via 100 replications of the Bayesian bootstrap. In row (2), we compute the standard deviation of life expectancy if health capital were held constant; specifically, for each CZ j, we compute the counterfactual age 65 life expectancy if each CZ had its own γ_j but the nationally representative health capital $\overline{\theta }$ as defined in the text. In row (3), we compute the standard deviation in life expectancy if the place effects were held constant; specifically, we define the nationally representative place effect as the median of γ_j among non-movers, and for each CZ j, compute the counterfactual age 65 life expectancy where the CZ has its own ${\overline{\theta }}_j$, but a nationally representative place effect. Row (4) reports the correlation between the health capital component of life expectancy (whose standard deviation is shown in row 3) and the place component of life expectancy (whose standard deviation is shown in row 2). This is computed by calculating the correlation between the treatment effects in one split-sample and the health capital effects in the other split-sample, and then averaging the resulting correlations from each pair. In row (5) we show the share of the variance that would be reduced if place effects were made equal; this is computed by calculating the variance of life expectancy with place effects held constant (i.e. the square of row 3) and the variance in life expectancy (i.e. the square of row 1), and taking 1 minus the ratio of these numbers. Row (6) is computed in an analogous fashion. Confidence intervals for rows (5) and (6) are computed by using this procedure within each bootstrap.

To translate these estimates into the impact on life expectancy from moving from a place at one part of the distribution of treatment effects to another, we assume the treatment effects are normally distributed with a standard deviation equal to our estimate in row (2) of the table. This provides a simple summary measure that incorporates our split-sample correction for sampling error. This exercise suggests that moving from a 25th percentile area to a 75th percentile area would increase life expectancy by 0.60 years; moving from a 10th to a 90th percentile area would increase life expectancy by 1.1 years, or roughly half the cross sectional 90–10 gap in life expectancy.

The final rows of the table show how much of the cross-sectional variation in life expectancy can be explained by our treatment effects. We find that about 15 percent of the cross-CZ variance in life expectancy would be eliminated if place effects were made equal across areas (with the observed variation in health capital remaining the same). Conversely, we find that about 70 percent of the variation would be eliminated if health capital were equalized (with the observed variation in the causal effects of place remaining the same).²⁵

B. Heterogeneity

Previous work has found that geographic variation in life expectancy is higher for lower-income individuals (Chetty et al. 2016b). We replicate this result here, and examine to what extent it results from different variances of place effects and health capital respectively. We restrict attention to the 100 largest CZs (which constitute about half of the non-mover population) to ensure sufficient sample sizes to estimate treatment effects for each subgroup.

Table 5 summarizes the results. The first column shows that our main results are similar in this restricted sample. The remaining columns re-estimate the model separately by race and by Medicaid enrollment (an indicator of low socio-economic status), partitioning both movers and non-movers. Row (2) is consistent with the prior Chetty et al. (2016b) finding: the standard deviation of life expectancy is larger for individuals on Medicaid compared to those not on Medicaid, and larger for non-white individuals compared to white individuals. We estimate that the standard deviation of health capital effects is larger for Medicaid enrollees compared to non-Medicaid (row 4), while the standard deviation of treatment effects is more similar (row 3). Similar patterns also are apparent for non-whites compared to whites, although the results are less precise.

Table 5:

Heterogeneity by Medicaid Status and Race

		Medicaid Status		Race
	Baseline (Large CZs)	Non-Medicaid	Medicaid	White	Non-White
(1) Number of movers	710,990	650,246	60,744	629,126	81,864
Cross-CZ standard deviation of:
(2) Life expectancy (Lj)	0.66 [0.64, 0.68]	0.63 [0.61, 0.65]	1.54 [1.49, 1.59]	0.56 [0.53, 0.58]	1.35 [1.23, 1.46]
(3) Treatment effects $\left(L_j^{\ast }-\overline{L}\right)$	0.47 [0.40, 0.53]	0.46 [0.38, 0.54]	0.72 [0.37, 1.01]	0.48 [0.41, 0.54]	0.74 [0.00, 1.17]
(4) Health capital effects	0.53 [0.44, 0.59]	0.52 [0.44, 0.63]	1.50 [1.30, 1.81]	0.52 [0.45, 0.62]	1.04 [0.72, 1.57]

Notes: This table summarizes the decompositions for the largest 100 CZs by population in 2000, estimated separately by race and Medicaid status during the year prior to the reference year. Both non-mover and mover samples are partitioned by race or Medicaid status. Sample sizes in row (1) exclude movers to or from any CZ outside of the 100 largest CZs; this leaves us with about one-third of the baseline mover sample. Row (2) shows the cross-CZ standard deviation of life expectancy at 65 among non-movers in the indicated sample. All standard deviations in rows (2), (3), and (4). are computed using the split-sample approach, giving equal weight to each CZ. Brackets show the 95% confidence intervals computed via 100 iterations of the Bayesian bootstrap. Since standard deviations cannot be negative, any split-sample approach that produces a negative result we set to 0.00.

These estimates suggest that the greater geographic variation in life expectancy for low-income populations may be particularly driven by variation in their health capital, rather than by variation in treatment effects of place. This is consistent with evidence in Chetty et al. (2016b) suggesting that variation in area life expectancy for low-income individuals is strongly correlated with health behaviors such as smoking and exercise.

C. Correlates of Treatment Effects

To provide some suggestive evidence on what may drive the treatment effects we estimate, we explore their correlation with various observable place characteristics. In keeping with the existing literature, we focus primarily on observables that proxy for the environment and for medical care. We present detailed definitions, data sources, and summary statistics for these measures in Appendix D.

Figure 6 reports bivariate correlations of both average life expectancy and our estimated treatment effects with various area level characteristics. Each place characteristic has been normalized to have mean zero and standard deviation one. We emphasize that these are simply correlations and need not reflect causal effects. Still, most of the results follow intuitive patterns.

Figure 6:

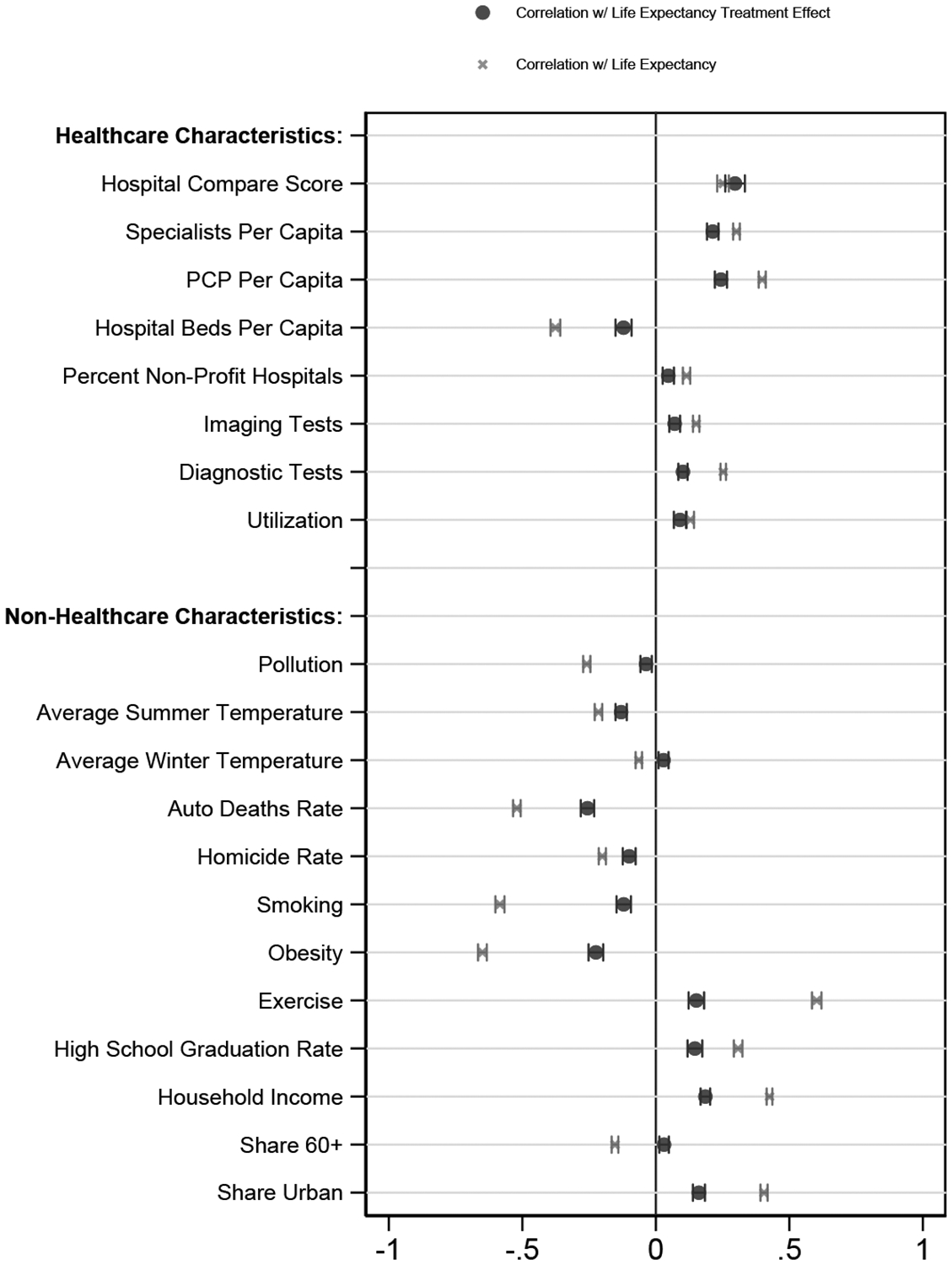
Correlations with Place Characteristics

Notes: The dots in this panel report bivariate variance-weighted least squares regression results of our life expectancy treatment effects $\left(L_j^{\ast }-\overline{L}\right)$ on z-scores of the indicated place characteristic; Appendix D provides more detail on their definitions. The x marks report bivariate variance-weighted least squares regression results of our age 65 life-expectancy estimates (L_j) on z-scores of the indicated place characteristic. All regressions are at the CZ level, and the regressions are weighted by the inverse variance of each measure. 95% confidence intervals are based on standard errors from the regressions. In this figure, the sample for each bivariate regression is all CZs for which that place characteristic is defined (see Appendix Table A.11 column 3), although the results are nearly identical if we instead use the 554 CZs for which every place characteristic (except homicide rates) is defined.

The top panel shows that places with favorable treatment effects tend to have higher quality and quantity of health care. Treatment effects are significantly positively correlated with hospital quality (as measured by the Hospital Compare score), primary care physicians per capita, and specialists per capita. Areas with favorable treatment effects have fewer hospital beds per capita.

Measures of utilization – including utilization itself, along with imaging tests and diagnostic tests – are also positively correlated with our treatment effects, though the magnitudes are smaller than they are for hospital quality or physician quantity. Our finding of a positive correlation between an area’s health care utilization and its estimated impact on life expectancy is intriguing in light of the large literature debating the impact of health care utilization on health outcomes (Chandra and Staiger (2007); Doyle (2011); Skinner (2011); Doyle et al. (2015)).

The bottom panel examines correlates with various non-healthcare area characteristics. Areas with favorable place effects on life expectancy tend to have less pollution, less extreme summer and winter temperatures, fewer homicides, and fewer automobile fatalities. They also tend to have higher income and education, which could reflect either greater demand for quality health care and amenities that reduce mortality or sorting of people with higher incomes and more education to high-treatment-effect areas. These areas also tend to exhibit better health behaviors (more exercise, less smoking, and lower obesity), which may similarly reflect either demand or sorting. Places with higher shares of urban populations tend to have more favorable treatment effects. The share of people over the age of 60 is uncorrelated with our treatment effects.

In general, the correlation of the characteristic with the estimated place component of life expectancy is smaller (in absolute value) than the correlation with the cross-sectional life expectancy. This difference is particularly pronounced for health behaviors and demographics, consistent with the raw correlations reflecting not only the causal effects but also the direct impacts of these variables on health capital.

VI. Validation and Robustness

A. Addictive Separability

Equation (1) assumes that health capital and current place have additively separable effects on log mortality. As discussed above, we consider this a strong assumption but one that is attractive economically since it has the intuitive implication that health capital and current location affect the level of mortality multiplicatively. Thus, the level of mortality of individuals with poor health capital (high θ_i) will vary more across areas than that of individuals who have better health capital.

One way to assess the validity of the assumption that place effects are separable from health capital is to test whether these place effects differ across subsets of enrollees. We construct four partitions of our mover sample based on move year, gender, age at move, and individual health at move. Each partition results in two groups with approximately the same number of movers; we estimate the model separately for movers in each group. For each partition, we use two summary statistics to evaluate the stability of place effects across the two groups. Appendix Table A.5 shows the results.

First, we analyze the standard deviation of place effects for each group. For five of the eight groups the estimated standard deviations fall within the confidence interval [0.038, 0.067] of our baseline estimates. The three exceptions are “young movers” (standard deviation = 0.075), movers in “good health” (standard deviation = 0.101), and male movers (standard deviation = 0.068).²⁶

Second, we examine the correlation of place effects between the two groups. The correlation of the place effects between the two subsamples ranges from 0.16 (when we partition by individual health) to about 0.24 (when we partition by gender or move year). To assess these correlations, we need to adjust for the role of sampling error, as it reduces the correlation between any two independent subsamples even if the true place effects are the same. Appendix Figure A.4 compares the estimated correlations to the distribution of correlation coefficients produced by randomly partitioning the mover sample into two equally sized groups and re-estimating the model 200 times. The median correlation of place effects between two random partitions is 0.29. For partitions based on age, move year, and gender, the correlation coefficients are within the 95% confidence interval formed from the distribution of correlation coefficients from the random partitions. Only the correlation coefficient for the partition based on individual health is outside of this interval.

Overall, the evidence for the additive separability assumption is somewhat mixed. It is comforting that the estimates are relatively stable across sub-samples, and that in most cases we cannot reject equality. However, there are some statistically significant deviations from additivity, particularly along the dimension of baseline health.

While this is an important point of caution, note that when we split the sample by health in the final panel of Table A.5 (and thus relax additivity along this dimension), the estimated standard deviation of place effects actually increases in both sub-samples.²⁷ This suggests that any bias due to imposing additivity may render our main results conservative.

B. Health Capital Fixed Post-Move

Equation (1) also assumes that health capital (θ_i) is time constant. This means that the only systematic changes in health over time allowed by our model are due to age and calendar year. While this is a strong assumption, we believe that it is a reasonable approximation for our elderly population over the relatively short time horizon of our sample (1–12 years post-move).

The key threat to this assumption would be an immediate causal effect of destination on health capital. Movers to some locations might tend to adopt healthier eating habits, start exercising, or stop smoking, perhaps due to peer effects and/or the supply of complementary amenities. Movers to other locations might see their health affected by environmental factors such as pollution. If such changes in behavior or environment translate into large and immediate changes in health capital, some of our estimated place effects would partly capture the effect of these health capital adjustments. However, our read of the existing literature as well additional analyses we conduct of the time path of the treatment effects on mortality suggest that any threats to our identifying assumption may be quantitatively modest.

C. Evidence of behavioral responses and their impact

Three key facts lead us to expect that the magnitude of any such confounds is likely to be modest. First, available evidence suggests health behaviors are often relatively inelastic to environmental changes, particularly for the elderly. Substantial dietary changes are rare among adults of any age, even in the presence of significant events such as a diabetes diagnosis or retirement (Hut and Oster 2018). Consistent with this, a recent study of the impact of moving on nutrition finds no relationship between the diets of movers and the average nutrition of residents in their destinations (Hut 2018).²⁸ Evidence of systematic changes in smoking behavior around moves for the general adult population is mixed,²⁹ and rates of starting and stopping smoking decline sharply with age.³⁰

Second, the impact of any behavioral change on mortality is also likely to be smaller for the elderly, as they have accumulated a large stock of existing health capital from experiences earlier in life. For example, Doll et al. (2004) find that the gain in life years from smoking cessation is decreasing in age of cessation, with someone who stops smoking at age 60 achieving only 30 percent of the gain of someone who stops smoking at age 30.

Third, even if health behaviors did change immediately on move, we would still expect the resulting changes in health capital, and thus the observable impact on mortality, to cumulate gradually over time rather than changing discretely on impact. For example, studies of the impact of smoking cessation on mortality find effects that grow gradually over the subsequent 10–15 years; estimated effects in the first few years are a small share of the total effect of cessation (Kawachi et al. 1993; Mons et al. 2015; U.S. Department of Health and Human Services 2020). The evidence in the next section suggests that the place effects we measure affect mortality on impact and do not grow over time, making it less likely they are driven by the effect of behavioral change.

Time path of the treatment effects of place

Results from two types of analyses suggest that the treatment effects of place following moves appear immediately upon move and do not grow over time. First, we consider an alternative binary Logit model of mortality, in which the outcome is mortality within a fixed window of n years. This allows us to estimate effects separately for different window lengths n, providing insight into the time path of mortality effects. It also provides a check on the robustness of our results to the Gompertz functional form assumed in our main model. We replace estimating equation (3) with a binary Logit model of n-year mortality. All covariates are the same as in equation (3) except that we include in the X_i a fully interacted set of five year age bins, race, and sex, rather than including age linearly and interacting race and gender. We estimate the Logit model for 1-year, 2-year, 3-year, and 4-year mortality.

Table 6 reports the results. The first row reports our baseline estimates of the standard deviation of the mortality index $\left({\gamma }_j+{\overline{\theta }}_j\right)$ and the standard deviation of the selection-corrected place effects γ_j from Table 3. In our baseline, the standard deviation of γ_j is about half the standard deviation of ${\gamma }_j+{\overline{\theta }}_j$. The last four rows show the results of the Logit model for different horizons. The impact of place shows up immediately in the first year after move. Place effects on mortality are similar, and statistically indistinguishable, over the first four years post-move. This pattern is consistent with our place effects picking up contemporaneous place effects γ_j rather than endogenous health capital changes which we would expect to adjust more slowly.

Table 6:

Logistic Model

	(1)	(2)
	Standard Deviation of Mortality Index $\left({\gamma }_j+{\overline{\theta }}_j\right)$	Standard Deviation of Place Effects (γj)
Baseline	0.099 [0.095, 0.103]	0.054 [0.040, 0.069]
Logistic Model:
1-year mortality	0.062 [0.061, 0.063]	0.081 [0.071, 0.090]
2-year mortality	0.068 [0.068, 0.069]	0.073 [0.062, 0.079]
3-year mortality	0.077 [0.076, 0.077]	0.083 [0.076, 0.088]
4-year mortality	0.086 [0.086, 0.086]	0.082 [0.075, 0.089]

Notes: Column (1) reports the cross-CZ standard deviation of our mortality index. Row (1) reports results for the baseline Gompertz specification (See Table 3). For the baseline specification, the mortality index is age, race, and sex adjusted; for the logit specifications it is not. Furthermore, in the logit specifications, rather than a β · t term, five-year age bins are fully interacted with race and sex. Column (2) reports the cross-CZ standard deviation of our place effects. 95% confidence intervals are reported underneath the point estimates, and are computed with 100 replications of the Bayesian bootstrap. All standard deviations are computed using the split-sample approach, and all standard deviations in both columns give equal weight to each CZ.

Second, we limit the observation window for movers in our baseline model to 2, 4, or 6 years post-move. As with the subsample analyses in Table 5, we restrict this analysis to the 100 largest CZs to ensure sufficient sample sizes for these subsamples. Appendix Table A.6 shows that the cross-CZ standard deviation of treatment effects and health capital effects are similar when we use either the full sample or these more limited observation windows. Appendix Figure A.5 shows the scatterplot of treatment effects and health capital effects for the sub-sample including only moves 4 years after the move against the baseline estimates; the estimates are highly positively correlated, and clustered around a line with a slope of 1. As further evidence, the robustness analysis in Section VI.D below shows similar results when we limit the sample to movers 70 or older (who we expect are even less likely to change their health behaviors upon move).

Taken together, this evidence is consistent with our estimated place effects capturing causal effects that affect movers on-impact, and argues against bias due to endogenous adjustment of health capital. To explain the large effects we see in the first years post-move, any such bias would need to be associated with large changes in behavior that translate into immediate rather than cumulative mortality impacts.

C. Selection Correction Assumptions

The key novel assumption in our selection correction strategy is Assumption 2: that the relative importance of the unobserved and observed components of health capital correlated with movers’ destinations is proportional to the relative importance of the components correlated with movers’ origins. In our baseline approach we make a stronger assumption and assume that these ratios are not just proportional, but in fact are equal (i.e., that φ = 1). Here, we provide some support for this assumption, and also document the robustness of our findings to relaxing it.

Empirical support

One way to provide support for this baseline assumption is to ask whether the analogous condition would hold if some of our observed health measures had in fact been unobserved. That is, suppose we divide H_i into K subsets $H_i^k$. For each subset, we imagine a hypothetical world where the elements of $H_i^k$ are the unobservables and the elements of $H_i^{-k}=H_i\setminus H_i^k$ are the observables, so the analogues of h_i and η_i would be $h_i=H_i^{-k}{\lambda }^{-k}$ and ${\eta }_i=H_i^k{\lambda }^k$ (where λ^−k and λ^k are the appropriate sub-vectors of λ). Denote the associated origin and destination components by $h_{j,k}^{\mathit{\text{dest}}}$, $h_{j,k}^{\mathit{\text{orig}}}$, ${\eta }_{j,k}^{\mathit{\text{dest}}}$, ${\eta }_{j,k}^{\mathit{\text{orig}}}$. We would like to confirm that

$$\frac{\text{StDev}\left({\eta }_{j(i),k}^{\mathit{\text{orig}}}\right)}{\text{StDev}\left(h_{j(i),k}^{\mathit{\text{orig}}}\right)}\approx \frac{\text{StDev}\left({\eta }_{j(i),k}^{\mathit{\text{dest}}}\right)}{\text{StDev}\left(h_{j(i),k}^{\mathit{\text{dest}}}\right)}\forall k.$$

To implement this test, we define 100 different subsets $H_i^k$, each of which is a random draw of 13 of the 27 total conditions. In each case we include log utilization in $H_i^{-k}$. For each subset, we estimate equation (3) and compute ${\widehat{\eta }}_{j,k}^{\mathit{\text{orig}}}={\widehat{\tau }}_{j,k}^{\mathit{\text{orig}}}$, ${\widehat{h}}_i=H_i^{-k}{\widehat{\lambda }}^{-k}$, and ${\widehat{\eta }}_i=H_i^k{\widehat{\lambda }}^{-k}$. We then compute the implied ${\widehat{h}}_{j,k}^{\mathit{\text{dest}}}$ and ${\widehat{h}}_{j,k}^{\mathit{\text{orig}}}$ by re-estimating equation (4), and compute ${\widehat{\eta }}_j^{\mathit{\text{dest}}}$ from equation (6) maintaining our baseline assumption that φ = 1.

Panel (a) of Figure 7 shows the results. This figure plots $\frac{\text{StDev}\left({\eta }_{j(i),k}^{\mathit{\text{orig}}}\right)}{\text{StDev}\left(h_{j(i),k}^{\mathit{\text{orig}}}\right)}$ on the x-axis and $\frac{\text{StDev}\left({\eta }_{j(i),k}^{\mathit{\text{dest}}}\right)}{\text{StDev}\left(h_{j(i),k}^{\mathit{\text{dest}}}\right)}$ on the y-axis. If these ratios vary proportionately for any subset of health measures k, they should lie on a line that goes through the origin. The results support this; the points have a clear monotonic relationship and we estimate an intercept of −0.26.³¹

Figure 7:

Support for Selection-Correction Assumptions

Notes: Panel (a) plots $\frac{\text{StDev}\left({\eta }_{j(i),k}^{\mathit{\text{dest}}}\right)}{\text{StDev}\left(h_{j(i),k}^{\mathit{\text{dest}}}\right)}$ against $\frac{\text{StDev}\left({\eta }_{j(i)}^{\mathit{\text{orig}}},k\right)}{\text{StDev}\left(h_{j(i),k}^{\mathit{\text{orig}}}\right)}$ for 100 different subsets $H_i^k$; each point in the scatter plot represents a different definition of k. For each k, H_i includes log(overall utilization) and a random subset of 13 of the 27 chronic conditions. Panel (b) reports various summary statistics about the treatment effects $\left(L_j^{\ast }-\overline{L}\right)$ produced by each of the 100 different definitions of k in panel (a). The left figure in panel (b) plots the standard deviation across CZs of the treatment effects from each of these alternate specifications; the dotted line shows the standard deviation across CZs of the treatment effects in the baseline specification (Table 4). All standard deviations are computed using the split-sample approach. The right figure in panel (b) plots the correlation of the treatment effects in each of the alternate specifications with the baseline treatment effects.

Panel (b) of Figure 7 directly examines how our key estimates vary if we re-estimate the entire model using the different subsets of observables H_i in panel (a). It plots the distribution of these 100 estimates for the standard deviation of treatment effects (left-hand panel) and the correlation of the estimated treatment effects with our baseline estimates (right-hand panel). The results indicate that the standard deviation of treatment effects is lowest in our baseline model, suggesting it is conservative, and that the correlation of treatment effects with the baseline is high.

Another way to assess the validity of our baseline approach is to apply it to outcomes which, unlike mortality, are observed repeatedly for the same individual. For such outcomes, we can follow Finkelstein et al. (2016) and adjust for selection directly by including individual fixed effects. We can then compare the fixed effects estimates for these outcomes to those we obtain using our selection-correction approach.

The panel regression of Finkelstein et al. (2016) is:

$$y_{ijt}={\alpha }_i+{\gamma }_j+{\omega }_t+x_{it}\beta +{ϵ}_{ijt}$$ (7)

where y_ijt is an outcome observed in a panel, such as a particular measure of health care utilization; α_i, γ_j, and ω_t are individual, CZ, and calendar year fixed effects; and x_it consists of dummies for five-year age bins as well as fixed effects for relative year for movers.

We consider three panel outcomes y_ijt that we can construct using the inpatient and outpatient claims data: an indicator for any hospital admission, an indicator for any emergency room visit, and an indicator for any outpatient visit. For each of these outcomes, we first assume that we only observe the outcome once post-move (as we do for mortality), and estimate equation (3) for the binary outcome measured one year post-move. We report results both with and without the selection correction. We then estimate equation (7) and compare.

The results are shown in Appendix Table A.7. In all cases, the selection correction moves the estimates closer to the panel estimates. For both any hospital admission and any emergency room visit, this is a substantial change, closing more than half the gap between the naive uncorrected estimates and the panel estimates. For any outpatient visit, the effect of the selection correction is smaller, though in the right direction. These results provide independent validation that our selection correction succeeds in reducing bias due to unobservables.

Relaxing the assumptions

We assess robustness to relaxing our baseline assumptions of equal selection and equal ratios, which together imply φ = 1. We focus on the implied variability of the place effects γ_j and of the treatment effects $L_j^{\ast }-\overline{L}$ as summary outcomes in this exercise. The results are summarized in Appendix Table A.8.

The first row reports results from our baseline approach (φ = 1); our baseline estimate of the standard deviation of treatment effects is 0.44. Row (2) considers the value of φ that minimizes the implied StDev (γ_j). StDev (γ_j) is not monotonic in φ, but is minimized when $\phi =\frac{\text{Cov}\left({\tau }_j^{\mathit{\text{dest}}},{\eta }_j^{\mathit{\text{baseline}}}\right)}{\text{Var}\left({\eta }_j^{\mathit{\text{baseline}}}\right)}$, where ${\eta }_j^{\mathit{\text{baseline}}}=\frac{\text{StDev}\left({\tau }_{j(i)}^{\mathit{\text{orig}}}\right)}{\text{StDev}\left(h_{j(i)}^{\mathit{\text{orig}}}\right)}{h}_j^{\mathit{\text{dest}}}$ is the population value of our baseline estimator ${\widehat{\eta }}_j^{\mathit{\text{dest}}}$ in equation (6).³² In our data $\frac{\text{Cov}\left({\tau }_j^{\mathit{\text{dest}}},{\eta }_j^{\mathit{\text{baseline}}}\right)}{\text{Var}\left({\eta }_j^{\mathit{\text{baseline}}}\right)}=1.26$, suggesting that assuming our baseline assumption of φ = 1 implies a conservative estimate of the importance of place effects relative to alternatives φ < 1 or φ > 1.26. In practice, the results in row (2) indicate that if we choose the variance minimizing value φ = 1.26, the implied standard deviation of treatment effects falls to 0.43. In the row (3), we show that if we set φ equal to the median value 1.97 from Figure A.6, the implied standard deviation of treatment effects is 0.45.³³

In the bottom rows of the table, we show results for the values of φ that minimize the absolute difference between the standard deviation of the place effects estimated via the panel approach and via the adjusted cross-sectional approach, separately for the different outcome variables from Table A.7. Specifically, in rows (4) through (6) we choose the value of φ that minimize this difference for the outcomes of any ER visit, any hospital admission, and any outpatient visit respectively, while in row (7) we use the value of φ that minimizes the average absolute difference across all three outcomes. The values of φ range from 1.75 to 7.10, and the resultant standard deviation of the treatment effects is increasing in φ, from 0.48 (for φ = 1.75) to 2.27 (for φ = 7.10). We conclude that our results are not sensitive to modest deviations from our baseline assumption φ = 1, and that this assumption is, if anything, conservative in the sense that the alternatives imply even larger effects of place.

D. Robustness

Appendix Table A.9 reports a suite of additional robustness checks. For each, we report a number of key results: the standard deviation of average life expectancy (L_j), the standard deviation of area treatment effects $\left(L_j^{\ast }-\overline{L}\right)$, the correlation between the treatment effects estimated in that row and the baseline treatment effects, and the correlation between average life expectancy and the treatment effects $\left(\text{Corr}\left(L_j,L_j^{\ast }\right)\right)$. The first row repeats our baseline estimates for reference; once again, we focus on the 100 largest CZs since many of the robustness analyses are conducted on sub-samples of the data.

In row (2), we estimate a variant of our baseline model that allows the coefficients on age, demographics, and health (β, ψ, and λ, respectively in equation (3)) to differ for movers and non-movers.

In row (3), we interact the components of observed health H_i with an enrollee’s age in the year prior to their reference year $t_i^{\ast }$. Since we define H_i as of $t_i^{\ast }-1$ for all enrollees, our baseline specification assumes that the coefficients that relate specific chronic conditions to log mortality are independent of age. This robustness check relaxes that assumption in a limited way.

In row (4), we add an interaction between gender and age to the Gompertz model.

In row (5), we add average race- and sex-adjusted mortality rates in a mover’s origin county as a control variable. This adjusts for selection of movers across different areas within origin CZs.

In row (6), we restrict the sample of moves to those of more than 100 miles, as measured between the centroids of the mover’s origin and destination zip codes.

In row (7), we restrict the sample of movers to those who are 70 or older at the time of move and moved after 2003. Given the range of years that we observe in our data, this ensures that movers who joined Medicare at age 65 were observed in their origin for at least five years.

In rows (8) and (9), we focus on moves in which the gap between life expectancy in the mover’s origin and in her destination is either above or below the median gap among all movers.

In row (10), we exclude any moves in which the origin CZ is geographically adjacent to the destination CZ.

In row (11), we exclude moves to Florida, Arizona, and California. This provides a check that patterns of selection specific to these popular retirement destinations are not biasing our results.

Rows (12) and (13) restrict the sample to moves occurring in 1999–2003 or to moves occurring in 2004–2012 respectively. In the latter case we define the reference year $t_i^{\ast }$ for non-movers to be the second year they appear in the data in the 2004–2012 period.

In all of these cases, the results are qualitatively unchanged. The correlation between the estimated treatment effects and our baseline treatment effects is above 0.9 in all but three cases, and above 0.8 in all cases.

VII. Conclusion

This paper documents a substantial impact of current locations on mortality. We estimate that moving from the 10th percentile area in terms of impact on life expectancy to the 90th percentile area would increase life expectancy at 65 by 1.1 years, or about 5 percent of average remaining life expectancy at 65. Equalizing place effects would reduce the cross-sectional variation in life expectancy at 65 by 15 percent.

We emphasize that these findings capture short-run, partial equilibrium impacts of place on life expectancy for an elderly population. Effects could well be different in younger populations. They could also be different over longer time horizons during which health capital itself could be substantially affected by location. We consider this a promising area for further work, especially since our results suggest an important role for heath capital in affecting life expectancy. More work is needed to understand what aspects of health capital are important causal determinants of life expectancy, and the extent to which current environment in childhood or adulthood affects health capital.

Our findings also suggest that it is important to better understand what aspects of current environments are important for life expectancy. We present suggestive, cross-sectional evidence on the characteristics of places that are more favorable for life expectancy. More work is needed to understand the causal mechanisms. In addition, while our partial equilibrium analysis takes place characteristics as fixed, it would be interesting to understand the extent to which they are endogenously determined by the composition of an area’s population in equilibrium.