A machine learning approach for classifying and quantifying acoustic diversity

Abstract

1. Assessing diversity of discretely varying behavior is a classical ethological problem. In particular, the challenge of calculating an individuals’ or species’ vocal repertoire size is often an important step in ecological and behavioral studies, but a reproducible and broadly applicable method for accomplishing this task is not currently available.

2. We offer a generalizable method to automate the calculation and quantification of acoustic diversity using an unsupervised random forest framework. We tested our method using natural and synthetic datasets of known repertoire sizes that exhibit standardized variation in common acoustic features as well as in recording quality. We tested two approaches to estimate acoustic diversity using the output from unsupervised random forest analyses: (i) cluster analysis to estimate the number of discrete acoustic signals (e.g., repertoire size) and (ii) an estimation of acoustic area in acoustic feature space, as a proxy for repertoire size.

3. We find that our unsupervised analyses classify acoustic structure with high accuracy. Specifically, both approaches accurately estimate element diversity when repertoire size is small to intermediate (5–20 unique elements). However, for larger datasets (20–100 unique elements), we find that calculating the size of the area occupied in acoustic space is a more reliable proxy for estimating repertoire size.

4. We conclude that our implementation of unsupervised random forest analysis offers a generalizable tool that researchers can apply to classify acoustic structure of diverse datasets. Additionally, output from these analyses can be used to compare the distribution and diversity of signals in acoustic space, creating opportunities to quantify and compare the amount of acoustic variation among individuals, populations, or species in a standardized way. We provide R code and examples to aid researchers interested in using these techniques.

Introduction

Many animals use vocal signals to transmit information and mediate a wide range of social behaviors, from resource competition to attracting mates (Payne et al. 1986, Kroodsma and Miller 1996, Gerhardt and Huber 2002, Catchpole and Slater 2003, Janik 2009). Owing to the ubiquity and ecological importance of acoustic signaling, quantifying and comparing animal vocalizations is a major part of animal behavior and communication systems research. Data from several studies suggest that signals often fall into distinct categories based on their acoustic structure (e.g. birds, Kroodsma 1982; cetaceans, Janik 2009; primates, Owren et al. 1992). Such categories are often observed at the species level when conspecifics use a shared repertoire of distinct acoustic signals that are associated with different contexts (Marler 1982, Seyfarth and Cheney 2003). Distinct categories can also arise within a signal type, as when an individual uses several signal variants that have the same functional role (e.g., the song repertoires of many songbirds comprise multiple song types, Catchpole and Slater 2003).

Classifying or quantifying variation in animal signals is fundamental to many questions in animal communication. For example, metrics derived from measuring the number of unique elements or vocalizations produced by an individual, such as repertoire size or acoustic diversity, have been shown to correlate with quality indicators, including territory size, cognitive ability, brain morphology, and levels of stress during early stages of development (Sewall et al. 2013, Devoogd et al. 1993, Podos et al. 2009). At the population level, differences in acoustic signals can facilitate species recognition (e.g., amphibians, Ryan 1985) and can play an important role in speciation by promoting isolation between sympatric groups (e.g., crickets, Mullen et al. 2007; birds, Mason et al. 2017). When assessing entire ecosystems, acoustic diversity, or the amount of variation within and among populations’ vocal repertoires, can provide a metric to assess ecosystem health or demographic aspects of communities (Sueur et al. 2008a, Laiolo et al. 2008, Pijanowski et al. 2011). For these reasons, quantifying acoustic diversity is often an important step in addressing questions and testing hypotheses regarding the social and ecological factors influencing signal function and evolution.

Classifying signals can be difficult or time consuming because acoustic variation across environments, individuals, or even different renditions of a signal by the same individual can be considerable. Furthermore, not all variation in acoustic structure is discrete. Often, acoustic signals do not fall into distinct categories, but rather exhibit continuous variation on multiple axes, and therefore can be difficult to classify (Wadewitz et al. 2015). Within behavioral ecology, a common approach for quantifying variation among signals is to estimate repertoire size or element diversity. In this study, we consider a repertoire to be the complete set of discrete vocalization types, hereafter elements, used by an individual or species. Accordingly, as elements are subunits of which repertoires are composed, we define element diversity as the number of unique elements a repertoire contains (this differs from ecological definition of diversity, which describes both the number and evenness of entities in the environment). While it is theoretically possible to count every discrete acoustic element in a dataset of vocal elements, for animals with large repertoire sizes it is common to subsample a species repertoire and use either accumulation curves or a capture-recapture analysis to estimate repertoire size (Wildenthal 1965, Garamzegi et al. 2002, Catchpole and Slater 2003, Garamzegi et al. 2005, Kershenbaum et al. 2015, but see Botero et al. 2008). However, this approach requires first manually classifying elements or vocalizations, a process that can be subjective and may become unwieldy for species with large repertoires or multispecies studies. In recent years, several techniques have been developed which improve upon these methods (e.g., Peshek and Blumstein 2011; Kershenbaum et al. 2015), including approaches that use information theory-based approaches to quantify individuality of vocal signals (Beecher 1989, Freeberg and Lucas 2012, Linhart et al. 2019). Additionally, methods have been developed to help distinguish among more graded element types (e.g., Wadewitz et al. 2015). Nevertheless, the general challenge of quantifying repertoire size still exists with many of these methods: human-based classification is both time intensive and unavoidably subjective, and researchers would benefit from an automated and generalizable method that would enable rapid, objective estimation of repertoire size.

In passive acoustic monitoring and quantification of soundscapes, there is an emphasis on creating fully automated approaches for classification and measurement of acoustic signals. One such approach, acoustic indices, has been used to quantify ecosystem–level to individual behavioral variation (Sueur et al. 2014). Such metrics have become increasingly important to ecological assessment and monitoring (Gibb et al. 2019), however, they are often calculated at scales that are more appropriate to ecosystem or community ecology.

Unlike soundscape analysis, measuring acoustic diversity on the species- or individual-level requires quantifying differences between discrete elements. Machine learning offers an automated and objective approach for such classification tasks, and is a powerful tool for detecting and distinguishing vocal signals (e.g., Acevedo et al. 2009, Briggs et al. 2013, Hershey et al. 2017, Stowell et al. 2019). In particular, unsupervised machine learning approaches offer several advantages that enhance their value for assessing behavioral diversity, namely in that they do not require a labeled training dataset or a priori assumptions about the structure of data (Valletta et al. 2017). Unsupervised techniques can also determine which acoustic parameters contribute most to classification or splitting data into classes, therefore relieving researchers from the need to make potentially subjective choices about feature selection (Breiman 2001). Unsupervised analyses have shown high performance in the classification of vocal signals to species as compared to other approaches (Keen et al. 2014), including in the case of large datasets (Stowell and Plumbley 2014), and there appears to be much promise in applying these techniques to evaluate acoustic diversity (Ulloa et al. 2018). However, a widely applicable tool for assessing acoustic diversity at the individual, species, or community-level is not readily available.

In this paper, we present and evaluate the use of unsupervised machine learning for classifying and quantifying acoustic diversity in animal signals. Specifically, we examine two approaches for estimating repertoire size: (1) a clustering method to identify discrete numbers of acoustic units and (2) an acoustic area calculation as a proxy for repertoire size. Here, acoustic area refers to the amount of space inside the boundary encompassing all signals in a dataset within the acoustic feature space We evaluate the accuracy of these approaches on multiple datasets with known acoustic structure. Three unique aspects of our approach help ensure this method will be highly generalizable to diverse acoustic signals. First, we test algorithm performance using both field-recorded and synthesized acoustic datasets with known sample sizes and variation, allowing us to evaluate our method under a variety of conditions. Second, we incorporate several of the most commonly used acoustic parameters for characterizing signal structure. Third, we used test datasets with realistic distributions of variation and background noise, making it possible to evaluate the robustness of this approach to variable acoustic structures and across a range of recording scenarios. We also provide R code for implementing this approach. Our results suggest that this technique offers a powerful tool for researchers to quantify a diversity across taxa and communities.

Methods

We estimated acoustic diversity for a collection of natural and synthetic acoustic signals using a machine learning approach (random forest) and evaluated the performance of this method following the workflow in Fig. 1. This process involved creating sets of synthetic acoustic signals with known repertoire sizes and known amounts of structural variation, extracting acoustic features from these signals, running unsupervised random forest analyses to calculate pairwise distances between signals, and estimating repertoire size using both cluster analysis as well as the size of the acoustic feature space (i.e., the range encompassing all possible spectrotemporal variation in signals, hereafter referred to as acoustic space). We also evaluated the effects of variation in repertoire size and acoustic structure on the accuracy of our analyses.

Figure 1.

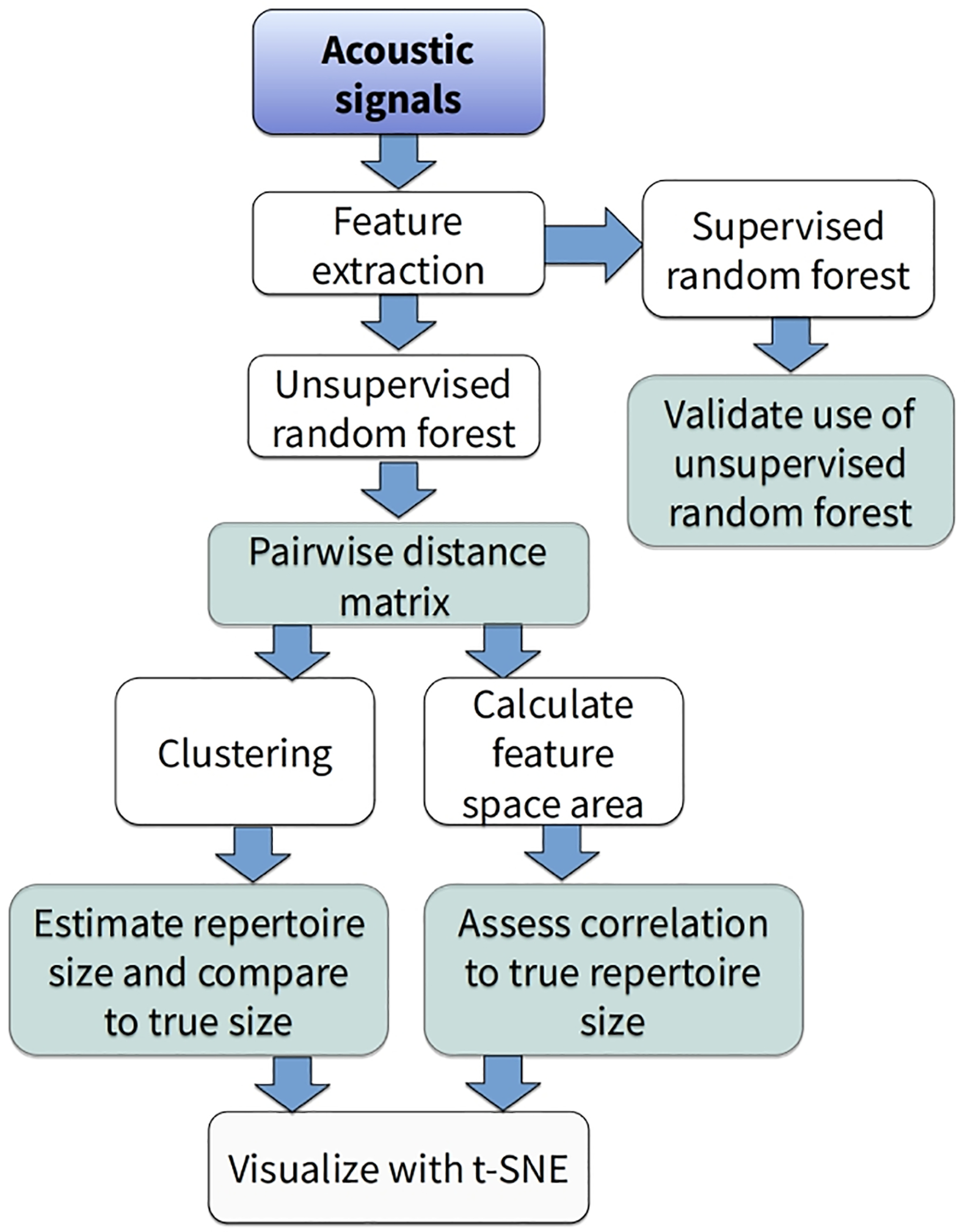
Flowchart of study design. White boxes represent data analysis steps and shaded boxes represent evaluation and validation steps.

Using a random forest approach was integral to our workflow for several reasons. A key advantage of random forest is its ability to determine which feature measurements best divide data into distinct categories; therefore, it is possible to use a large number of features and allow the algorithm to determine which are most useful for a given dataset. Random forest also offers several additional advantages over other machine learning techniques: it is robust to collinearity, outliers and unbalanced datasets, is efficient even with large and highly multi-dimensional datasets, can be used in both a supervised and unsupervised manner, can handle non-monotonic relationships, ignores non-informative variables, produces low bias estimates, computes proximity of observations which can be used for representing trait spaces, and can be used to identify variables that contribute most to finding structure within a dataset (Valletta et al. 2017). For these reasons, combining random forest with a large suite of automated acoustic feature measurements holds much promise as a generalizable tool for acoustic classification tasks.

Test datasets

We evaluated the performance of our proposed method using four datasets: annotated field recordings of long-billed hermits (Phaethornis longirostris), annotated lab recordings of budgerigars (Melopsittacus undulatus), and two collections of synthetic datasets that were modeled on natural vocalizations of these two species (see Table 1 for a summary of datasets and Fig. 2 for sample spectrograms). This enabled us to assess performance using vocal signals collected from live birds that reflect the naturally occurring variation between individuals, as well as datasets comprising signals with distinct spectrotemporal properties, as the vocalizations used by these species are considerably different from one another (see ESM). Another advantage of using vocalizations from long-billed hermits and budgerigars was the availability of large datasets of live recordings from numerous individuals of each species that were previously labeled by human experts, which provided ground truth with which to test our proposed method. The use of 96 synthetic datasets as test cases also allowed us to conduct repeated tests of algorithm performance under different conditions and to test whether repertoire size can be approximated using acoustic area. Such thorough assessment would not be feasible with field or lab recordings, as the process of collecting, annotating, and measuring vocal repertoires is prohibitively time consuming. Additionally, a primary aim of using a large number of labeled test datasets was to demonstrate that our approach can accurately approximate human analysis on diverse datasets, and to allow others to minimize time spent on manual analysis in future acoustic studies.

Table 1.

Summary of test datasets used to evaluate performance.

Description	Recording type	Number of datasets	Unique elements in repertoire	Examples of each element
Long billed hermit songs	Field	1	50	10
Budgerigar calls	Laboratory	1	15	35
Synthetic long- billed hermit songs	Synthetic	48	8 × 5	10
			8 × 10
			8 × 15
			8 × 20
			8 × 50
			8 × 100
Synthetic budgerigar calls	Synthetic	48	8 × 5	10
			8 × 10
			8 × 15
			8 × 20
			8 × 50
			8 × 100

Figure 2. Spectrograms with examples from each dataset.

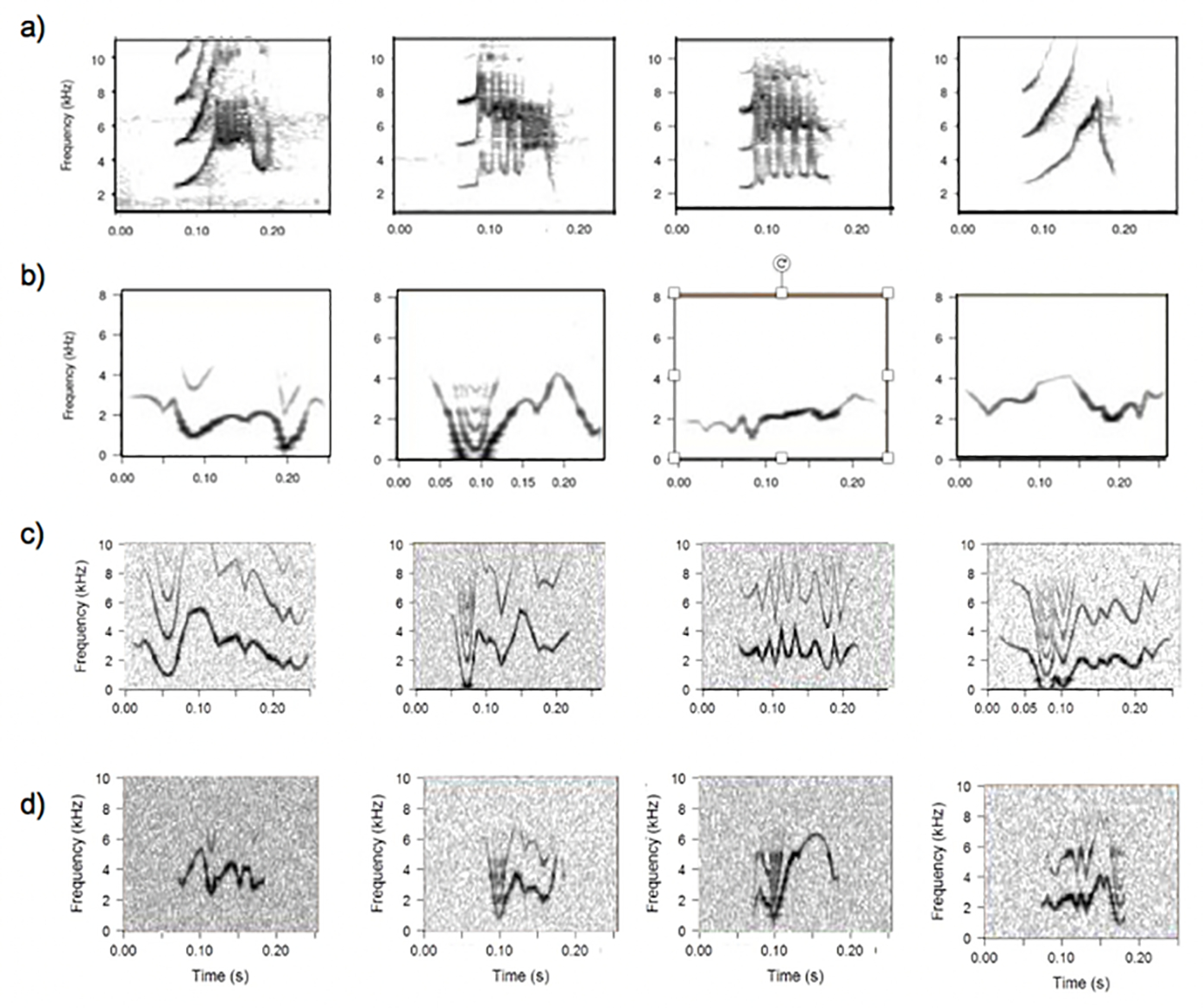
Example spectrograms showing signals in the four datasets used to test algorithm performance, including a) field recordings of long billed hermit songs, b) laboratory recordings of budgerigar songs, c) synthetic long billed hermit songs with added noise, and d) synthetic budgerigar songs with added noise.

Field recordings of long-billed hermits were collected from 43 known individuals in wild populations at La Selva Biological Station, Costa Rica (10°, 25’ N; 84°, 00’ W), between 2008 and 2017. Males in this species live in territorial leks that exhibit local songs that are shared by sub groups of individuals (i.e., singing neighborhoods) within a lek (Araya-Salas and Wright 2013; see ESM for further details). For this study, we used songs recorded from 16 leks (mean ± SE songs per group = 3.1 ± 0.51). Because the song types used by long-billed hermits change over time, it was possible to use songs recorded from the same lek in different years to compile a sample of 50 unique song types. We visually assessed spectrograms of all signals to verify that song types exhibited distinct spectro-temporal structures. To create the test dataset for this study, we identified the 50 song types had the most samples, and selected the 10 recordings with the highest signal-to-noise ratio for each type, yielding a dataset of 500 signals.

Laboratory recordings of budgerigar contact calls were collected between July and November 2010 from a laboratory population originally acquired from a captive breeder. Individual budgerigars typically have repertoires of 2–5 acoustically distinct contact call types that are shared with some other individuals within their flock. Contact calls were recorded from 38 different individuals that were temporarily isolated from their flock mates in a homemade acoustic chamber constructed of an Igloo cooler lined with acoustic foam with a clear plexiglass door as described in Dahlin et al. (2014). Trained research assistants visually assessed spectrograms made from wav files and assigned calls to classes using Raven 1.3 (Cornell Lab of Ornithology). Call classification was subsequently verified using a discriminant function analysis as described in Dahlin et al. (2014). We then randomly selected 35 contact calls from each of 15 unique call types, resulting in a dataset of 525 signals.

Synthetic data creation

To create the synthesized song datasets used for testing, we first extracted the dominant frequency contours, defined as the curves that track changes in the dominant frequency of signal over time, of the natural bird vocalizations (long-billed hermit songs and budgerigar calls). We then synthesized frequency contours similar to those of the exemplar species and saved these signals as audio clips using the R soundgen package (Anikin 2019). We allowed the synthetic sounds to vary in three features: duration (short: 150 ms; long: 300 ms; defined as the length of the continuous tonal signal within the spectrogram), harmonic content (low and high; defined as the amount of power in harmonic bands above the fundamental frequency) and background noise (low: 20 dB signal-to-noise ratio; high: 2 dB signal-to-noise ratio). To test the ability of our method to estimate repertoire size and to determine whether this can be approximated by calculating the area occupied in acoustic space, we synthesized datasets with repertoire sizes of 5, 10, 15, 20, 50, or 100 unique elements. Each element type was represented by 10 examples. For each repertoire size, we used all possible combinations of duration, harmonic content, and background noise, resulting in 48 synthetic datasets for both long-billed hermit songs and budgerigar calls (Table 1). Sample spectrograms of signals from each dataset are shown in Fig. 2. See ESM for further details of data collection and synthesis.

Acoustic feature measurements

We collected a suite of common acoustic feature measurements from each audio clip. We first applied a 500 Hz high pass filter to all audio clips to remove low frequency noise, and then created spectrograms for each sample clip using 300-point FFT with a Hann window and 90% overlap. From these spectrograms, we extracted 179 descriptive statistics of mel frequency cepstral coefficients (MFCCs; Lyon and Ordubadi 1982, sensu Salamon et al. 2014) and 28 acoustic parameters using the R packages warbler and seewave (Araya-Salas and Smith-Vidaurre 2017, Sueur et al. 2008b). All features we used are commonly used metrics in bioacoustics analyses and are described in further detail in the ESM. We also calculated two pairwise distance matrices for every dataset: one using spectrogram cross-correlation (Clark et al. 1987) and one using dynamic time warping (Wolberg 1990). We used classical multi-dimensional scaling (MDS) to translate the SPCC and DTW distance matrices into five-dimensional space, and used the axis coordinates for each sample as additional feature measurements (i.e., five SPCC MDS coordinates and five DTW MDS coordinates per sample). Together, this resulted in a vector of 217 feature measurements for each signal. We collated the feature vectors for each audio clip into a single matrix for each dataset, then removed any collinear measurements, applied a Box-Cox transformation to improve normality, and scaled and centered all feature values. The resulting matrix was used as the input into the supervised and unsupervised random forest models.

Supervised random forest analyses

To evaluate the ability of random forest to classify signals into the correct categories, we used a supervised random forest created with the randomForest R package (Liaw and Weiner 2002), to classify the signals in each data. Here, “supervised” denotes that the random forest model was created using a labeled dataset; in our study, field and lab recordings were labeled by human experts and synthetic data were labeled by software. We assessed how well the supervised random forest models were able to classify signals from the same category together using the out-of-bag error estimate (Breiman 2001), which is an unbiased means of assessing prediction performance (Ljumovic and Klar 2015). These analyses served as a proof of concept, as they confirmed that models constructed from the selected acoustic features could accurately assess similarity amongst signals and allowed us to evaluate the distribution of error rates for the test datasets described in Table 1. We expect that researchers using this method will have unlabeled data and therefore will only apply unsupervised random forest models.

Unsupervised random forest analyses

To determine whether our method can be used to estimate repertoire size or acoustic diversity for unlabeled data, we created an unsupervised random forest model for each dataset listed in Table 1 using the randomForest R package (Liaw and Weiner 2002). Unlike the supervised random forest approach, an unsupervised random forest can be used to find underlying structure within unlabeled data (Breiman 2001). This approach also produces dissimilarity measure between all samples, which can be used to identify groupings within data. Although all test datasets were labeled and repertoire sizes were known, in this step we ignored this information in order to simulate the workflow that other researchers might use for their data. For each dataset, we constructed an unsupervised random forest model using 10,000 decision trees that were built using the unlabeled feature measurements. We then used the output of each unsupervised model to obtain pairwise distances between all samples within each dataset.

Performance evaluation

We used several metrics to evaluate how well our method could assign samples into different classes. First, we assessed performance of each supervised random forest model by calculating out-of-bag error rates, which provided a misclassification rate for each dataset. Using these values, we examined whether duration of audio clips (long vs. short), harmonic content (high vs. low), level of background noise (high vs. low), or number of discrete elements influenced the ability of models to assign signals to the correct class.

We evaluated how well the unsupervised random forest could measure acoustic diversity using two approaches: by estimating number of unique elements (i.e., repertoire size) in each dataset and by calculating the area of the acoustic space occupied by all signals in a dataset. To estimate repertoire size, we applied partitioning around medoids (a variation of k-means clustering; Kaufman and Rousseeuw 2009) to the pairwise distance matrix returned by the unsupervised random forests for each dataset. For each dataset, we calculated silhouette width to determine the optimal number of clusters (see Fig. S4). Using the labels that were omitted during the design of the unsupervised models, we then calculated the difference between the optimal number of clusters (i.e., the estimated repertoire size) and the true repertoire size. We also calculated the classification accuracy by assigning each cluster in a dataset a label corresponding to the signal type that was most frequently placed in that cluster, and then dividing the total number of correctly assigned samples by the number of samples in the dataset. Additionally, we calculated the adjusted Rand index, which is a metric of how often samples of the same type are assigned to the same cluster and different types assigned to different clusters (Rand 1971). This value represents the similarity of datapoints within each cluster and can range between 0, indicating completely random classification, to 1, indicating that assigned classes perfectly match labels.

To create the acoustic space for each dataset, we used multidimensional scaling to transform the pairwise distance matrix produced by the unsupervised random forest. We then calculated acoustic area as the 95% minimum convex polygon (i.e., excluding the proportion of outliers above 95%) of these points. We used Spearman’s rank correlation to test whether acoustic area increased with true repertoire size.

Lastly, in order to visualize how well the unsupervised analyses clustered distinct signal types, we used t-distributed stochastic neighbor embedding (t-SNE) dimensionality reduction to display all samples in two dimensions (Maaten and Hinton 2008). All statistical analyses were conducted using the R packages cluster, tsne, MASS, and adehabitatHR (Maechler et al. 2019, Donaldson 2016, Venables and Ripley 2002, Calenge 2006). See ESM for further details of analyses.

Results

Supervised random forest performance

Out-of-bag error was below what would be expected by chance (see ESM) for all supervised random forest models: field recordings of long-billed hermits: 0.04, lab recordings of budgerigars: 0.093; synthetic long-billed hermit datasets (mean ± SE): 0.02 ± 0.043; synthetic budgerigar datasets: 0.049 ± 0.017. However, we observed that certain signal characteristics in our synthetic calls sets influenced error rates. Namely, synthetic long billed hermit songs that have low harmonic content or high background noise have higher out-of-bag error rates, and typically error rates were higher in long billed hermits than in budgerigars. Synthetic datasets with higher numbers of discrete element types also had higher out-out bag error rates (Fig. 3). Variable importance rankings indicating which feature measurements were most useful in splitting data into distinct classes were different for each of the four dataset types used for testing (Table S1).

Figure 3.

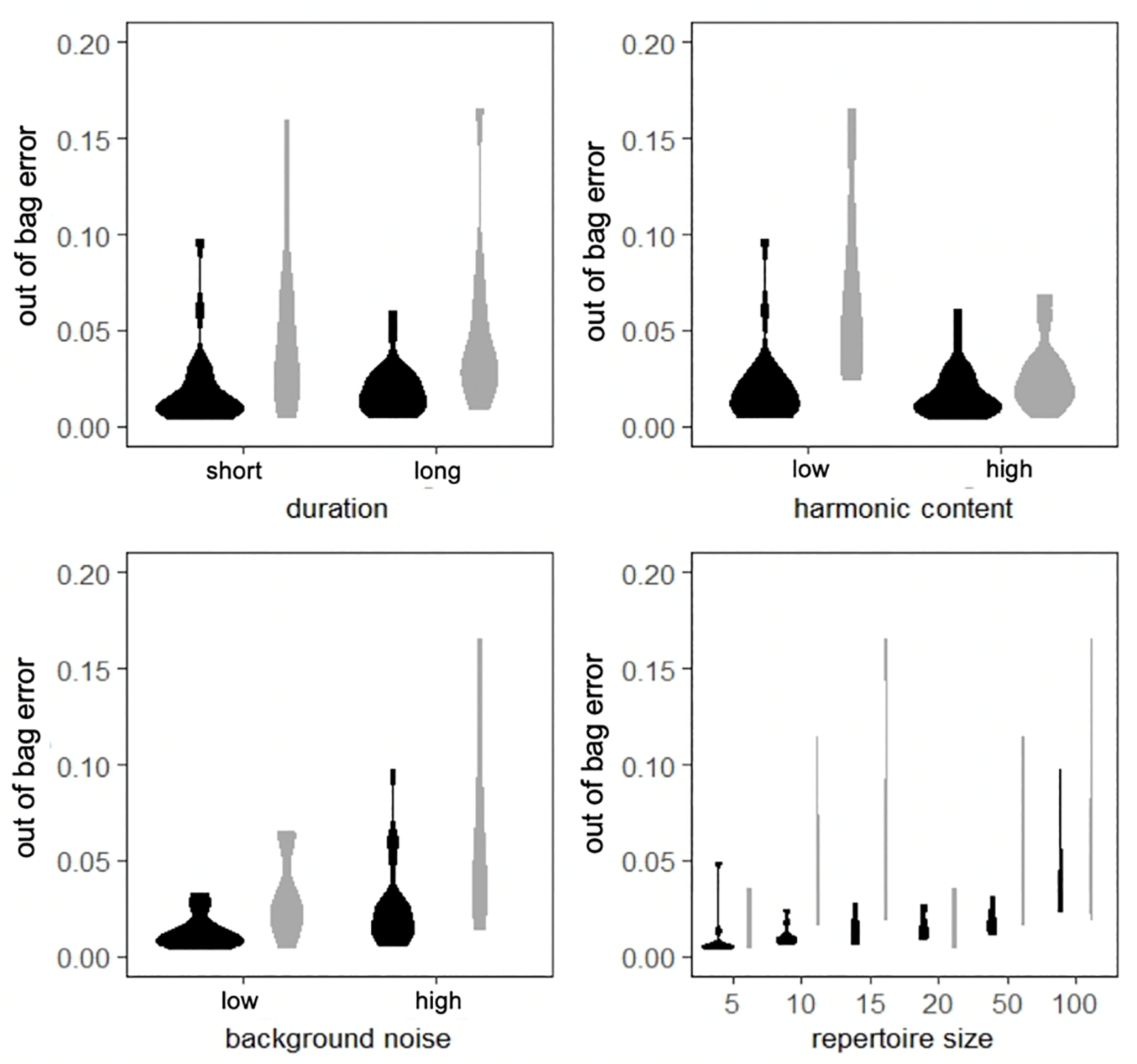
Out-of-bag error rates for supervised random forest models created for synthetic datasets with varying a) duration, b) harmonic content, c) levels of background noise. Black violin plots show results for synthetic budgerigar and gray plots results for synthetic long billed hermit datasets.

Unsupervised random forest performance and calculating acoustic diversity

We observed that our estimates of repertoire size were most accurate for synthetic datasets that contained 20 or fewer unique elements (Fig. 4a). Classification accuracy was often above 90% for datasets with five unique elements, and decreased as the true number of discrete elements in a dataset increased, reaching around 60% for datasets with 100 unique elements (Fig. 4b). Similarly, adjusted Rand indices were relatively high for synthetic datasets with small numbers of unique elements, and decreased among datasets as the number of unique elements increased (Fig. 4c). An exception to this pattern was the synthetic budgerigar datasets with five unique elements, which had lower adjusted Rand indices because data were often clustered into fewer than five classes. The scatter plots in Fig. 5a–d illustrate the ability of the unsupervised analysis to cluster synthetic signals of the same class together.

Figure 4. Unsupervised performance varies with number of unique elements in synthetic datasets.

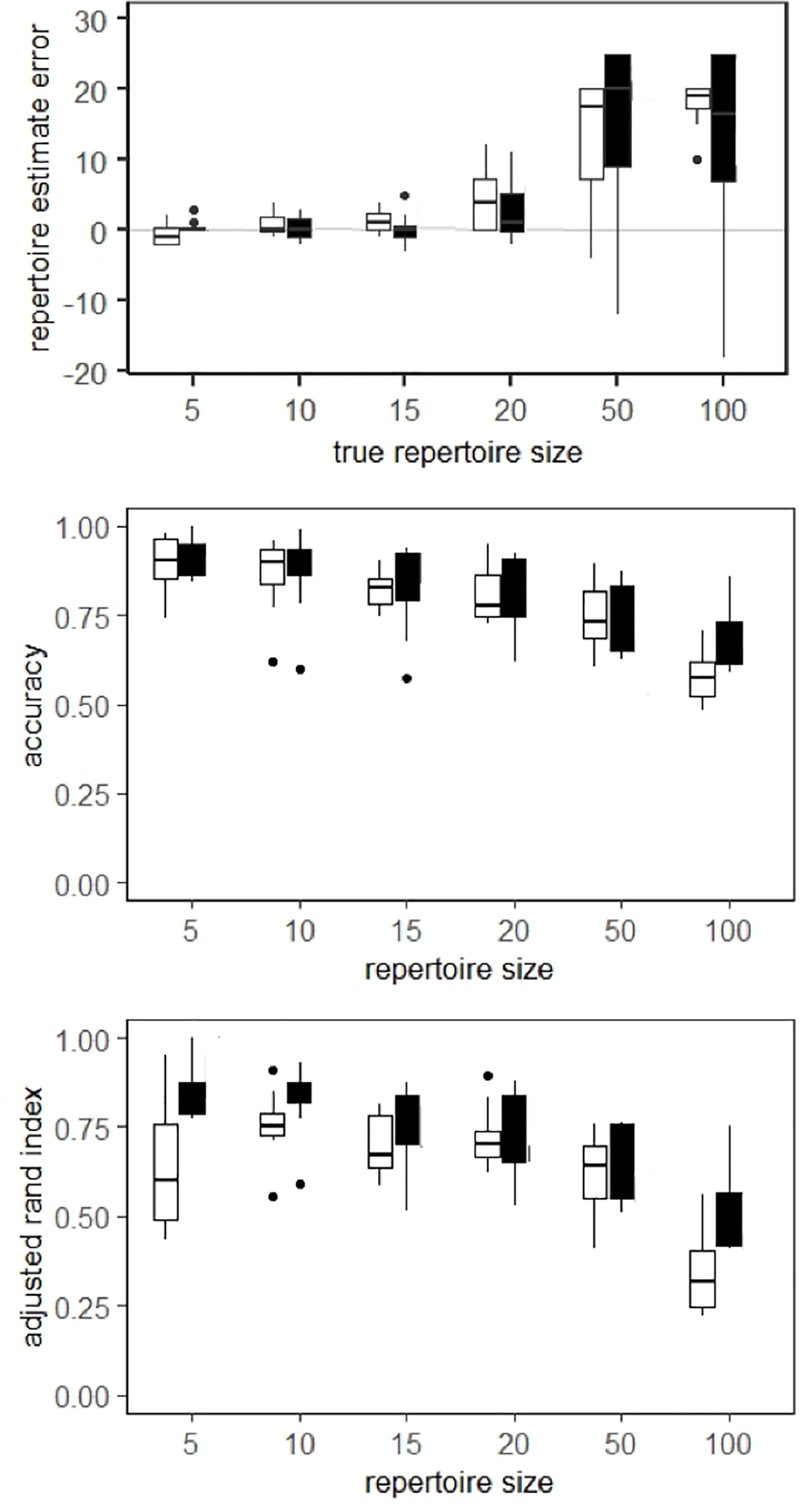
Plots of results from cluster analysis of unsupervised random forest output showing a) estimated repertoire size, b) classification accuracy, c) adjusted Rand index versus true repertoire size. White and black boxes represent results from synthetic budgerigar calls and synthetic long billed hermit songs, respectively.

Figure 5. Examples of unsupervised clustering of elements within datasets.

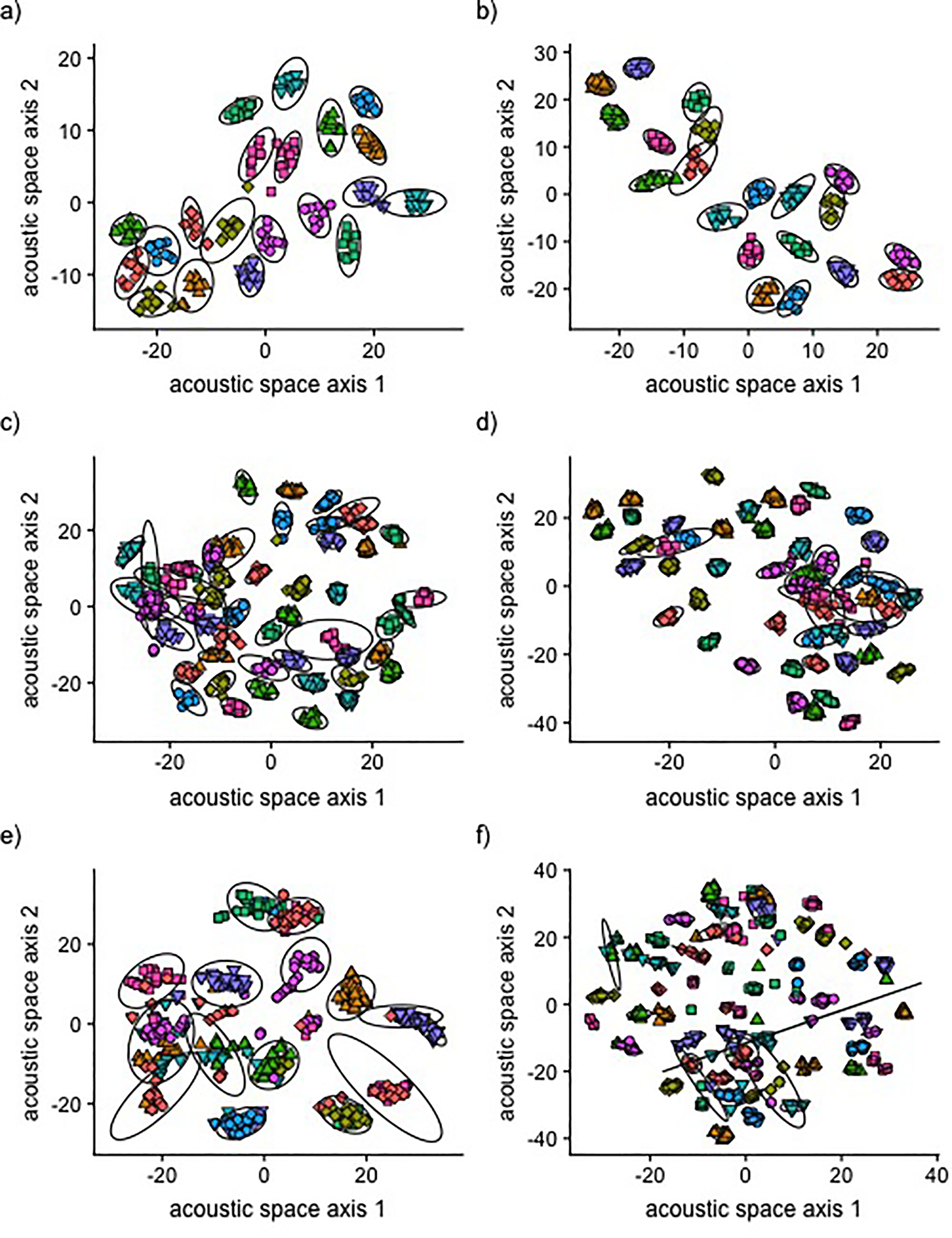
To illustrate the ability of our method to cluster similar element types together within datasets of different sizes and with different signal properties, we show plots of six datasets used in this study: a) synthetic budgerigar calls with 20 unique elements, short duration, low harmonic content, and low background noise (clustered into 20 groups), b) synthetic long-billed hermit dataset with 20 unique elements, short duration, high harmonic content, and low background noise (clustered into 20 groups), c) synthetic budgerigar dataset with 50 unique elements, long duration, low harmonic content, and low background noise (clustered into 46 groups), d) synthetic long billed hermit dataset with 50 unique elements, short duration, high harmonic content, and low background noise (clustered into 47 groups), e) live budgerigar dataset with 15 unique elements (clustered into 15 groups), f) live long billed hermit dataset with 50 unique elements (clustered into 75 groups). We used t-SNE to display all data points in two dimensions, thus creating a two-dimensional acoustic space. Each point represents a single signal within a dataset, and the unique colors and shapes of points indicate the distinct element types within a dataset. Ellipses represent clusters assigned by the algorithm as it aimed to group identical element types together. In some cases, ellipses are too small to be visible within plots.

When analyzing the live budgerigar calls, our approach correctly estimated that there were 15 unique signal types in the dataset. However, all calls of the same element type were not always assigned to the same cluster (Fig. 4c), which is reflected by the classification accuracy of 79.6 % and adjusted Rand index of 0.615. The unsupervised analysis of field-recorded long-billed hermit songs incorrectly estimated 75 unique signal types in the dataset, which was the maximum allowed number of clusters during our testing, rather than the true number of 50 unique signal types. However, the classification accuracy for this dataset was 76.4 %, and the adjusted Rand index was 0.73, indicating that signals of the same class were often clustered together. Scatter plots showing the unsupervised clustering of live bird datasets are shown in Fig. 5e, f.

When acoustic area as used to estimate repertoire size, we observed a significant, positive correlation between acoustic area and the number of discrete elements. In addition, the acoustic area metric estimated repertoire size with similar accuracy across all values of true repertoire size (Fig. 6). We observed this same pattern for synthetic datasets of long-billed hermit songs and budgerigar calls (Spearman correlation: budgerigars: r = 0.91, N = 99, p < 0.0001, long-billed hermits: r = 0.95, N = 99, p < 0.0001; Fig. 6).

Figure 6. Datasets with more discrete elements have larger distributions in acoustic space.

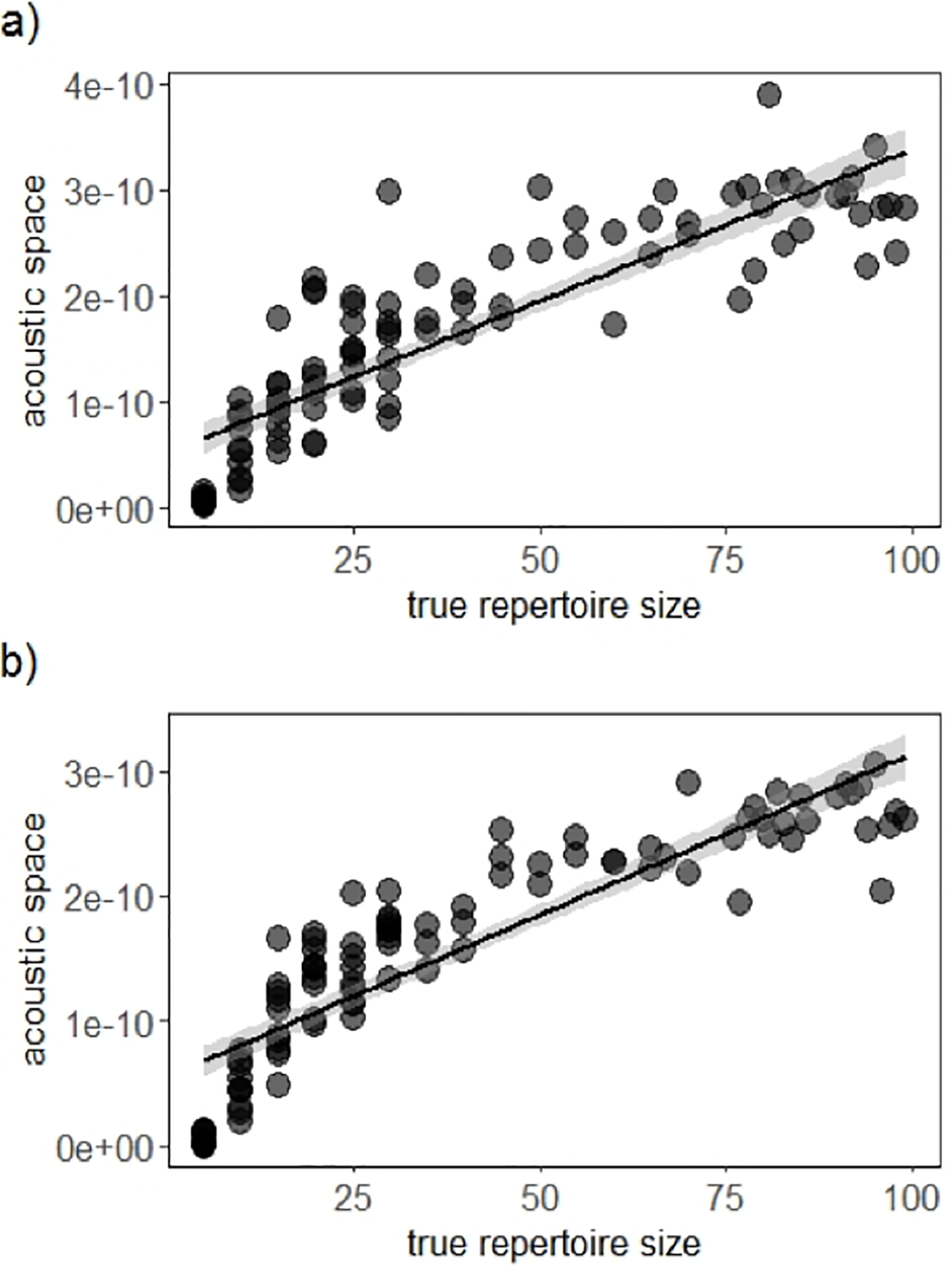
As repertoire size increases, the distribution of samples in acoustic space occupies a larger area for a) synthetic budgerigar calls, b) synthetic long-billed hermit songs. Acoustic space values have been squared to better illustrate differences between values on a small scale.

Discussion

Our goal was to provide researchers with a flexible, unsupervised method for quantifying diversity in acoustic signals, a general problem encountered when evaluating the vocal repertoires of individuals, populations, or species. We aimed to replicate the process researchers might use when assessing variation in unlabeled data and tested our method on 98 datasets containing between five and 100 unique elements. We find that unsupervised learning paired with either cluster analyses or acoustic area calculations can approximate small and intermediate sample sizes well. In datasets with many discrete elements, however, quantifying the size of the area occupied in acoustic space may offer a more accurate alternative to estimating repertoire size than cluster analyses. Below, we make specific recommendations about which signal characteristics might influence the accuracy of estimating acoustic diversity under different conditions, repertoire sizes, and acoustic features.

Supervised analyses

Supervised analyses allowed us to verify that random forests can accurately identify underlying patterns in acoustic data and to confirm that our test data had the expected structure. Our results suggest that signal duration (short vs. long) and harmonic content (low vs. high) largely do not affect classification accuracy in most cases (Fig. 3). Interestingly, synthetic long-billed hermit songs that have low harmonic content or high background noise suffered from higher out-of-bag error. Additionally, in almost all cases, synthetic long-billed hermit songs exhibited higher out-of-bag error rates than synthetic budgerigar songs. A likely explanation is that the harmonic content of natural long-billed hermit songs provides acoustic structure that aids in classification among element types, and low power content in harmonic bands of our synthetic songs or high background noise may mask this helpful feature. Harmonic structure is known to help conspecifics discern fine differences in signals and has been shown to encode individual identity in some species (e.g., penguins, Aubin et al. 2000; humans, Imperl et al. 1997). As for the higher classification error for hermit elements in general, it is possible that the feature measurements we used might not be as effective at identifying the spectrotemporal variation for this species compared to budgerigars. Hence, it is likely that our simulation underestimated the overall discriminatory power of the methods. For synthetic data, we observed that error rates increased with true repertoire size, suggesting that the method is less effective at finding structure in data when there are large numbers of discrete elements. This decrease in discriminatory power with increasing repertoire size might be due to a saturation of the acoustic space.

Unsupervised estimation of repertoire size

Cluster analysis using output from unsupervised random forest models showed that it was possible to estimate the true number of discrete elements in synthetic datasets with little error when the number of discrete elements was equal to or less than 20 (Fig. 4a). For datasets with 50 or 100 discrete elements, unsupervised clustering often estimated repertoire size as being much higher than its true value. One possible reason for this may be overfitting during clustering, i.e., when subsets of samples of the same signal type are assigned to separate clusters, which can occur when there is high similarity among a subset of samples in a class. Additionally, higher inaccuracy is expected as more unique elements are introduced when the acoustic space becomes saturated. Classification accuracy and adjusted Rand indices were also higher for datasets with few discrete elements, and both metrics were consistently slightly higher for synthetic long-billed hermit datasets relative to synthetic budgerigar datasets (Fig. 4b, d). This might be explained by the fact that the synthetic long-billed hermit exhibit more pronounced differences between classes than the synthetic budgerigar calls, which might allow for classes to be more easily distinguished. One possible explanation for this is that the long-billed hermit recordings from which synthetic signals were created contained diverse songs from many different leks, producing more distinct signals than the lab population of budgerigars.

For the field and lab recorded datasets, we also observed limitations of the clustering method. Although cluster analysis accurately estimated small repertoire sizes for the synthetic data, for the lab-recorded budgerigar dataset, which included only 15 unique element types, signals of the same class were sometimes placed in separate clusters. This could be one shortcoming of using clustering, as the algorithm may not assign the correct labels to every signal in a dataset, although we observed that classification accuracy was rather high overall (80%). For the field-recorded long-billed hermit dataset with 50 unique elements, the unsupervised analysis overestimated the repertoire size to be 75, likely due to overfitting as described above. However, we note that this analysis aimed to distinguish among signals from the same functional category, as opposed to signals from different functional categories across an entire repertoire (e.g. songs, alarm calls, etc.). Clustering similar song types is expected to be the more difficult task given the high acoustic similarity within a functional category.

Unsupervised calculation of acoustic space occupancy

Our second approach of quantifying acoustic diversity by calculating the size of the acoustic area occupied in acoustic space avoids the issue of needing to assign signals to discrete classes. For both synthetic budgerigar and long-billed hermit datasets, acoustic area was positively correlated with the number of discrete elements in a dataset (Fig. 6). Additionally, unlike the clustering approach, acoustic area estimates were robust to large repertoire sizes. We suggest that this may be a useful technique for quantifying diversity in species anticipated to have large repertoires, high element diversity, or those in which vocalizations may change over time (e.g. budgerigars, Dahlin et al. 2014), as it precludes the need for defining discrete categories which may be difficult to define statistically in a crowded acoustic space. We note, however, that making relative comparisons between different datasets requires that all data points are analyzed concurrently; acoustic area is defined by its composite data points and has no inherent comparability between different data sets.

Potential Uses

Both methods we tested allowed for accurate estimates of repertoire size, however, we see promising attributes and limitations of both approaches. We observed that cluster analysis was particularly useful for assessing small or intermediate repertoire sizes. Interestingly, previous work has shown that parrot repertoires often contain 10–15 elements (Bradbury 2003) and that most songbird repertoires typically include below 20 elements or song types (MacDougall-Shackelton 1997, Byers and Kroodsma 2009, Snyder and Creanza 2018). Repertoires can refer both to total signal repertoire in a species (signal ethogram) and total number of signals of a certain type within an individual (song repertoire or call repertoire). We foresee clustering of signals as being especially useful in this case.

We envision that acoustic space is an especially promising method to estimate and compare acoustic diversity across individuals, populations, or species. Previous work has shown that acoustic diversity may correspond to a number of ecological characteristics, including viability of populations (Lailo et al. 2008), local habitat structure (Morton 1975, Boncoraglio and Saino 2007), social system structure and complexity (Dunbar 1998, Freeburg 2006, elephants, Leighton 2017), and is also linked to social and sexual signaling (Tobias and Seddon 2009, Wilkins et al. 2013). Our acoustic space approach is well suited for large comparative analyses, particularly in cases in which repertoire sizes are unknown or anticipated to be large, and therefore cluster analysis may not be appropriate. In addition, all species or individuals can be compared in the same acoustic space, allowing for comparable estimates of acoustic area for all species. Although the analyses presented here were conducted in a two-dimensional acoustic space, future analyses could calculate multi-dimensional acoustic volumes (as opposed to 2-D acoustic areas).

New algorithms such as UMAP and other data visualization procedures may improve classification for grouping elements into distinct clusters in a two-dimensional feature space (Sainburg et al. 2019, Goffinet et al. 2019). Therefore, such approaches may enable researchers to more accurately determine the numbers of unique elements within an animal’s repertoire based on spatial separation. However, similar to our cluster analysis findings, these methods could still be limited by the number of groupings that can be delineated in a two-dimensional space and thus may be more appropriate for small sample sizes. In general, the challenge of assigning signals to categories is expected to scale in difficulty as the number of classes increase and the acoustic space becomes saturated. This inherent challenge cannot be entirely avoided, but certain aspects of our acoustic area technique help to mitigate this issue, namely by comparing how entire repertoires occupy acoustic space as an estimate of repertoire size rather than counting or comparing numbers of discrete groupings to calculate the actual repertoire size. Acoustic space may not linearly correlate with the number of discrete elements in a dataset, but we can use this approach to capture differences between large versus small repertoires across species, populations, or individuals. Researchers should be careful if the intent is to compare the size, location, distance, or overlap of element groupings derived from UMAP and other data visualization procedures as these techniques focus on maximizing local separation. Therefore, global structure can be lost and broad spatial comparisons might not be accurate.

The feature measurements that were most useful in the unsupervised random forest approach varied among test datasets, presumably because different signal types were best distinguished by different features (Table S1). For most datasets, the MFCC descriptive statistics were consistently among the most important features for creating supervised random forest models. Interestingly, for the lab-recorded budgerigar calls, the SPCC MDS coordinates were among the highest-ranking features. We expect that because these recordings were collected in a controlled environment with little background noise that the SPCC analysis could detect small differences among call types that were not visible in the synthetic or field recorded data. The ability for the analysis to detect this latent variation without requiring us to specify a priori which features we expected to vary exemplifies one of the primary strengths of random forest analysis. For this reason alone, we expect this approach may permit a high degree of adaptability to diverse acoustic datasets. The ability of this method to accurately evaluate acoustic diversity among disparate signal types also suggests that this method can be readily applied to vocalizations from other species or taxa. Overall, given the relatively low out-of-bag error rates, we were confident that constructing random forest models in an unsupervised manner would be a useful tool for assessing acoustic diversity.

Conclusions

We build upon previous work that has demonstrated the utility of unsupervised analyses for classifying acoustic signals and propose a novel combination of techniques for quantifying vocal diversity and/or measuring differences among individuals, species, and ecosystems. This method can be used to characterize vocalizations, either by estimating repertoire size or calculating acoustic space occupancy. By testing this method under diverse conditions, we hope to offer researchers a robust and generalizable method for acoustic analyses. Most importantly, we include R code to make these tools accessible to biologists.

Data Availability

Dataset and R code used for analysis were archived with Figshare at https://figshare.com/articles/dataset/Acoustic_diversity_dataset/13661315 (doi:10.6084/m9.figshare.13661315).