A downscaling approach to compare COVID‐19 count data from databases aggregated at different spatial scales

Abstract

As the COVID‐19 pandemic continues to threaten various regions around the world, obtaining accurate and reliable COVID‐19 data is crucial for governments and local communities aiming at rigorously assessing the extent and magnitude of the virus spread and deploying efficient interventions. Using data reported between January and February 2020 in China, we compared counts of COVID‐19 from near‐real‐time spatially disaggregated data (city level) with fine‐spatial scale predictions from a Bayesian downscaling regression model applied to a reference province‐level data set. The results highlight discrepancies in the counts of coronavirus‐infected cases at the district level and identify districts that may require further investigation.

1. INTRODUCTION

By the end of December 2019, a pneumonia of unknown cause was identified in Wuhan, Hubei province. The World Health Organization (WHO) temporarily named the cause of the pneumonia as severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2). The disease associated with the syndrome took the name coronavirus disease 2019 or COVID‐19 (Chen et al., 2020; Wang et al., 2020; Zheng et al., 2020). On the 30 January 2020, the WHO declared the outbreak of COVID‐19 a Public Health Emergency of International Concern, the highest level of international emergency response given to infectious diseases (Fang et al., 2020). By August 25th 2021, COVID‐19 had spread worldwide, infected more than 213 million individuals, and had led to about 4.4 million deaths (confirmed cases that died) worldwide (World Health Organization, 2020a).

Efforts have been made by various institutions to collect near‐real‐time data at the city level (disaggregated data) on COVID‐19 worldwide and to make it publicly available (Johns Hopkins University Center for Systems Science and Engineering, 2020; Pengpai News Agency, 2020a; Xu et al., 2020a, 2020b). While there is a race against time to contain the outbreak, reliability and accuracy of COVID‐19 data should remain a top priority for the research community. Policymakers require evidence‐based analysis to design and implement efficient interventions to mitigate and prevent the spread of the virus. A key condition for efficient evidence‐based interventions is to ensure that policy recommendations are based on reliable data measured with sufficient accuracy (Vespignani et al., 2020).

COVID‐19 is part of a large family of coronaviruses, which seems to have transferred from animals to humans between November and December 2019, according to the phylogeny of genomic sequences obtained from early cases (GISAID, 2020). Recent work showed that COVID‐19 can transfer quickly and easily among individuals (Andersen et al., 2020). While the symptoms are often mild, the virus seems to be more lethal for old people and individuals with pre‐existing medical conditions (Fang et al., 2020). A large number of countries are highly vulnerable to a COVID‐19 epidemic. In the early stages of the pandemic, only 50% of countries had a national infection prevention and control programme and about 30% of countries had no COVID‐19 national preparedness and response plans (Usher, 2020).

The establishment of containment areas, production and distribution of respiratory masks, and the delivery of urgent medical care tend to be very costly (Fang et al., 2020; World Health Organization, 2020b). To improve the efficiency of interventions, and hence, reduce the number of infected individuals and associated fatalities, epidemiological models based on geolocalised data can be employed to: (a) make inference on the true number of cases in spatial locations; (b) investigate the mechanisms behind the spread of the virus; (c) identify locations at risk; and (d) quantify and forecast the spread of the virus at fine spatial scales to help decision makers target interventions.

Epidemiological models using geolocalised data require sufficient accuracy with regard to both the number counts and the spatial locations of the reported cases. In order to assess data accuracy, we compare two major providers of spatially disaggregated COVID‐19 data with province‐level data from Johns Hopkins University Center for Systems Science and Engineering (JHU) (Dong et al., 2020). An exploratory analysis based on reported data in China from January to February 2020 indicates that both the number of corona‐infected cases from disaggregated data sets and the spatial locations of the reported cases exhibit important divergences between the investigated data sets. We further investigate differences in the counts at a fine spatial scale (district level) between reported values from spatially disaggregated data sets and values estimated from a Bayesian downscaling modelling approach.

The downscaling approach presented in this paper estimates the counts of COVID‐19 and its uncertainty at fine scale (5 km grid‐cells) using spatially aggregated (province‐level) data and covariates (5 km grid‐cells) as input. Predictions from the downscaling model are compared at the district level with COVID‐19 from spatially disaggregated data sets. The results of this analysis suggest that COVID‐19 counts reported by the disaggregated data sets are often consistent with the range of plausible estimated counts from the downscaling model, however data coverage and discrepancies in the counts remain important in various districts. The resulting maps can be visualised in an ESRI dashboard (https://arcg.is/0O8GDX).

2. METHOD

2.1. Data

As an initial exploratory analysis, we examine two fundamental metrics on COVID‐19: the number of confirmed COVID‐19‐infected cases and the locations of the reported cases. We investigate two major providers of COVID‐19 spatially disaggregated data which provide the location (longitude, latitude) of cities and the date of reported coronavirus‐infected cases. We compare two disaggregated data sets: (1) Xu et al. data (Xu et al., 2020) and (2) The Paper data. Xu et al. data has been published in Scientific Data (Xu et al., 2020) and is publicly available through GitHub repository (Xu et al., 2020a, 2020b). The Paper data is provided by the Pengpai News Agency (2020a), also refers to as The Paper. The disaggregated data from the two providers are regularly updated online. In this case study, we compare them with province‐level data provided by JHU (Dong et al., 2020).

First, we compared the count of confirmed COVID‐19 infected cases reported from January to February 2020 in China at province level. For consistency, we used data that has been updated by the investigated databases on the same day (April 9, 2020). In Hubei province—the Chinese province most affected by coronavirus—the reported number of COVID‐19‐infected cases shows large differences among the databases: JHU (65,914 cases), The Paper (58,292 cases), and Xu et al. (20,336 cases).

For the sake of readability, we split the results into two groups: high‐impacted provinces counting a maximum number of COVID‐19 cases (all providers combined) larger than the median (Figure 1, left panel) and low‐impacted provinces counting a maximum number of COVID‐19 cases (all providers combined) smaller or equal to the median (Figure 1, right panel). We observe important discrepancies in other provinces (Figure 1) between the reported cases provided by The Paper and Xu et al. with JHU data. This may suggest that the providers use different collection methodologies and control processes to gather and select the cases.

FIGURE 1.

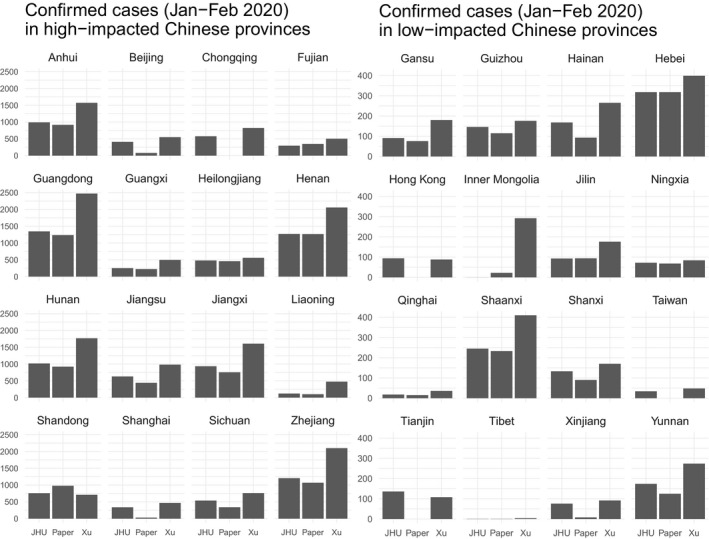
Cases of coronavirus in high‐impacted (left panel) and low‐impacted (right panel) provinces in China. The plot indicates the number of coronavirus‐infected individuals in China in high‐impacted (left panel) and low‐impacted (right panel) provinces from January to February 2020. Note that data from Macau are included in Guangdong province. Sources (updated April 9, 2020): (left bar) Johns Hopkins University CSSE (Johns Hopkins University Center for Systems Science & Engineering, 2020), (center bar) The Paper (Pengpai News Agency, 2020a), and (right bar) (Xu et al., 2020)

Second, we examine spatial variability of the data measured as the number of unique spatial coordinates associated with the reported COVID‐19 cases. JHU is excluded from this comparison since it does not provide spatial coordinates along with the reported cases. Therefore, we compared the number of unique locations and associated observed cases provided by Xu et al. and The Paper only. We illustrate the results for cases reported in Hubei province. In this province, The Paper (Figure 2, left panel) provides nine locations with reported cases. Figure 2 (right panel) shows that the number of locations that reported cases is systematically higher in Xu et al. compared to the Paper data (except in Hebei province).

FIGURE 2.

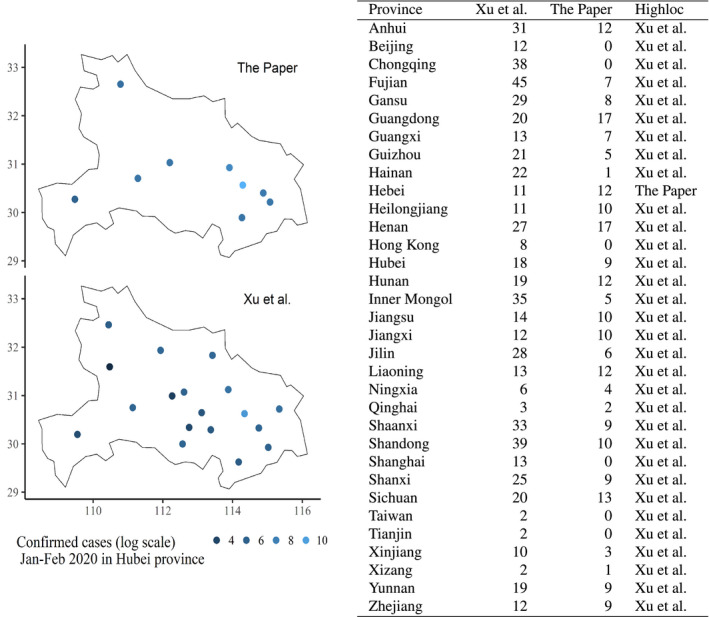
Spatial accuracy of disaggregated data sets. Left panel: geolocalisation and associated counts (in natural logarithm scale) of coronavirus‐infected individuals in Hubei from January to February 2020. Right panel: number of locations corresponding to COVID‐19 cases (January and February 2020) reported by Xu et al. and The Paper in Chinese provinces. The column Highloc indicates the data source that has the largest number of locations with data. Sources (updated April 9, 2020): The Paper (Pengpai News Agency, 2020a) (left panel), and Xu et al. (right panel) (Xu et al., 2020) [Colour figure can be viewed at wileyonlinelibrary.com]

2.2. Downscaling COVID‐19 province‐level data

To further investigate the observed discrepancies among COVID‐19 data, we use a downscaling approach to predict at a fine spatial scale the expected cases from data provided by JHU (Dong et al., 2020), a major reference for national and subnational data on COVID‐19, which provides data consistent with daily data from the Chinese centre for disease control and prevention and WHO situation reports (Dong et al., 2020). We use the R package disaggregation which implements a Bayesian approach to carry out spatial disaggregation modelling, also called downscaling (Nandi et al., 2020). Similar approaches have been recently used to estimate fine‐scale (grid‐cell) risk of disease based on spatially aggregated (polygon‐level) data (Arambepola et al., 2022; Diggle et al., 2013; Li et al., 2012; Sturrock et al., 2014; Weiss et al., 2019; Wilson & Wakefield, 2020). We apply a downscaling method to estimate cases of COVID‐19 and their uncertainty within fine grid cells (about 5 km spatial resolution) in China using JHU data aggregated at the province level (Dong et al., 2020). The model predictions are compared with observed values from two investigated disaggregated COVID‐19 data: Xu et al. (2020) and the Paper (Pengpai News agency, 2020a).

The model is implemented in template model builder (TMB) (Kristensen et al., 2015), an R package that provides a framework based on C++ to build and efficiently fit hierarchical Bayesian models, including downscaling models. TMB implements an automatic Laplace approximation with exact derivatives to approximate Bayesian posterior distribution functions. The method uses the Laplace approximation, which reduces time needed for the fitting process, by calculating the marginal likelihood of the model with a method that approximates integrals using automatic differentiation to compute the first and second order derivatives of the objective function (Griewank & Walther, 2008; Skaug & Fournier, 2006). Common R optimization routines are used to find the maximum a posteriori estimate, and then evaluate the Laplace approximation of the posterior (i.e., the multivariate normal that best approximates the posterior) having integrated out random effects (Kristensen et al., 2015).

Making predictions at a spatial scale finer than the input data is subject to potential validity threats that result from a mismatch between the scale from which the data and the prediction are considered (Wakefield & Shaddick, 2006). One issue, known as the ‘ecological fallacy’, has been well documented in geography and spatial epidemiology since the early 1950s (Robinson, 2009). A classical example is the study of Durkheim (Le Suicide, 1897), whose analysis showed that suicide rates in Prussia were highest in provinces that were heavily Protestants and wrongly concluded that stronger social control among Catholics would result in lower suicide rates. The author did not envision that it may have been non‐Protestants (primarily Catholics) who were committing suicide in predominantly Protestant provinces (Piantadosi et al., 1988). Analogously, an observed relationship between average population density and the risk of COVID‐19 at the province level may not hold at the city level.

A second issue is associated with the effects of the choice of spatial units on the results. This potential validity threat refers to the ‘modifiable areal unit problem’ (MAUP), well known by geographers and epidemiologists (Holt et al., 1996). Within a lattice framework which uses polygons defined as the spatial unit, one needs to choose the shape (regular or irregular polygons) and size of the polygons used to make predictions at a desired spatial scale (Python & Brandsch, 2019). To avoid the risk of ecological fallacy and mitigate the effect of the MAUP, the downscaling approach used here takes benefit of the spatial information gathered from fine‐scale covariates to model the underlying processes behind the observed data that explain the spatial variations of COVID‐19 counts within provinces.

We model the count of coronavirus‐infected cases y _j for each 5 km grid cell j that covers China. A continuous‐space data‐generating process is discretised into 5 km grid cells from which data is aggregated and estimates are generated. The incidence rate, a relevant risk metric of COVID‐19, is defined as the number of new coronavirus‐infected during our investigated period (January–February 2020), divided by the population at the beginning of the period. The incidence rate λ _j in pixel j is associated via a log link function to a linear predictor η _j composed of an intercept ${\beta }_0$, covariates x _qj , with coefficients ${\beta }_q$ (q = 1, …, Q), a spatial random field ζ _j , and an i.i.d random effect u _i(j) associated with each Chinese province (polygon i = 1, …, 33) (Nandi et al., 2020):

$$\log ({\lambda }_j)={\eta }_j={\beta }_0+\sum _{q=1}^Q{\beta }_q{x}_{\mathit{qj}}+{\zeta }_j+u_{i(j)}$$ (1)

Since the predicted response in a grid cell is a rate, we obtain the predicted COVID‐19 counts in each predicted grid cell by multiplying the predicted incidence rate by the corresponding population size (weight). The weights correspond to population size estimates provided by Worldpop (Tatem, 2017) for each grid‐cell (Figure 3, top‐right).

FIGURE 3.

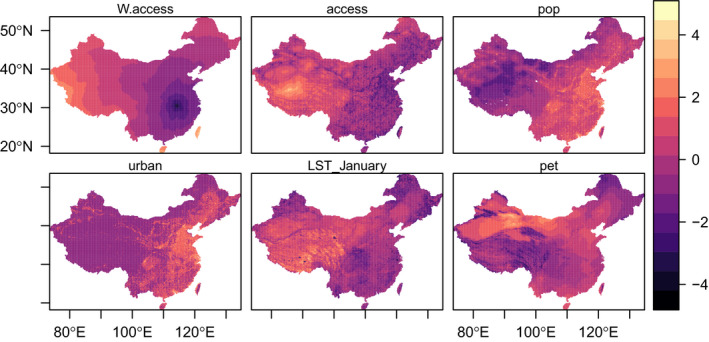
Covariates investigated in the downscaling model. The maps show the standardised values of six potential covariates used in the downscaling model. We investigate travel time to Wuhan, China (W.access), travel time to to the nearest city with more than 50,000 inhabitants (access), population size (pop), urbanity (urban), January land surface temperatures (LST), potential evapotranspiration (pet) [Colour figure can be viewed at wileyonlinelibrary.com]

At the province level (polygon), the conditional distribution of the number of coronavirus‐infected individuals approximately follows a Poisson distribution y _i  ∼ Pois(μ _i ), with expected cases ${\mu }_i={\sum }_{k=1}^{N_i}{a}_{i,k}{\lambda }_{i,k}$ with weight a _i,k (population size) in grid cell $k=1,\dots ,N_i$, with $N_i$ the total number of cells in polygon i. The estimated incidence rate λ _i corresponds to the expected total number of cases μ _i divided by the sum of the weights in province i, with ${\lambda }_i={\mu }_i/{\sum }_{k=1}^{N_i}{a}_{i,k}$.

The linear predictor includes a polygon random effect $u_i\stackrel{\mathrm{iid}}{\sim }\mathcal{N}(0,{\sigma }_u^2)$, which accounts for variation among provinces, with variance ${\sigma }_u^2$. The spatial structure ζ _j is represented by a zero‐mean Gaussian Markov random field (GMRF) with a Matérn covariance function. The Matérn covariance between two points s and t separated by Euclidean distance d is specified as follows (Equation 2):

$$Cov(s,t)={\sigma }_{\zeta }^2\frac{1}{\mathrm{\Gamma }(\psi )2^{\psi ‐1}}{(\kappa \times d)}^{\psi }{K}_{\psi }(\kappa \times d),$$ (2)

where K _ψ is the modified Bessel function of the second kind. We set the Matérn smoothness parameter ψ = 1 using the RINLA default value. The Matérn covariance function is defined by two parameters: (1) the range ρ, which corresponds to the distance from which spatial correlation becomes negligible (about 0.1 for ψ > 0.5). For ψ = 1, the range can be empirically derived from the scale parameter κ with $\rho =\sqrt{8}/\kappa$; and (2) the marginal variance ${\sigma }_{\zeta }^2$ (Lindgren & Rue, 2015; Lindgren et al., 2011; Rue et al., 2009).

Covariates associated with COVID‐19 infections are numerous and operate at various spatial levels, from the host genetics to large‐scale transnational factors that affect travel between countries for example. To make predictions at the pixel level (about 5 km resolution), we gather covariate data from raster data (covariates aggregated into regular grids) which cover China. Climate and meteorological factors can affect the life cycle of respiratory diseases and their propensity to spread (Roussel et al., 2018). However, the extent of the role of climate drivers on the spread of COVID‐19 compared to those associated with human behaviour is not well understood (Baker et al., 2020). The transmission of COVID‐19 can potentially occur in any ecological context by human contact. Therefore, the main drivers of the transmission of COVID‐19 are likely to be associated with human behaviour rather than environmental factors (Carlson et al., 2020). We consider mainly covariate data that are associated with human activity and behaviour and include only a few relevant environmental variables. We also note that we are not making predictions outside of the area or time of study but restrict our analysis to the downscaling of cases in China which avoids many of the main issues associated with using fine‐scale covariates.

COVID‐19 appears to transfer rapidly and easily among humans, with a basic reproductive number R ₀ (also called transmission rate) seemingly between 2 and 3. R ₀ represents the expected number of direct infections from one case in a completely susceptible population (The Royal Statistical Society 2020). This means that one person infected by COVID‐19, in a completely susceptible population, transfers on average the virus to 2 or 3 people (World Health Organization, 2020b). The basic reproductive rate depends on various factors associated with the virus itself and the risk of individuals transferring the virus, directly or indirectly, to other individuals as well.

We consider six covariates (1–6) with full coverage in China at 5 km resolution (Figure 3). The selected set of covariates include proxies for human activity, population density, and transportation: (1) travel time to the nearest city of with more than 50,000 inhabitants (access) (Weiss et al., 2018), (2) population size (pop) from WorldPop (Tatem, 2017), and (3) urbanity (urban) from Global Urban Footprint data (Esch et al., 2017). Along with population size and urbanity, travel time to the nearest large city is likely to be an important contributor of the spread of coronavirus at the pixel level, since it measures proximity to large urban centres. Locations close to city centres affected by COVID‐19 are more likely to be affected by a spread of the disease. Since COVID‐19 was first identified in Wuhan, we include (4) travel time to Wuhan, China (W.access) (computed from Weiss et al., 2018) to account for a potential diffusion from Wuhan, as suggested by Zhang et al (2020).

We consider two environmental covariates that are likely to have a role in the spread of COVID‐19. We include (5): January land surface temperatures (LST_January) from the US National Oceanic and Atmospheric Administration for meteorological (NOAA) Geostationary Operational Environmental Satellites (GOES) (United States National Oceanic and Atmospheric Administration, 2020). Temperatures in January can affect the life cycle of COVID‐19 and their propensity to spread (Roussel et al., 2018), but can also affect human behaviour. The effects of cold temperatures on human transmission of COVID‐19 are not clear. On the one hand, cold weather can increase the risk of transmission as people spend more time indoors, but could also reduce the risk of transmission due to a decrease of contact resulting from a reduction human activity.

There is evidence that humidity affects influenza‐type virus transmission in both experimental and observational studies (Lowen & Steel, 2014; Shaman & Kohn, 2009), and in population‐level studies (Shaman et al., 2010). High levels of humidity may provide a suitable framework for an outbreak of COVID‐19 and modulate the magnitude of the pandemic (Baker et al., 2020). To account for the role of humidity, we include: (6) potential evapotranspiration (pet), which provides a measure of the potential amount of evaporation (if a water body is present), which is associated with the quantity and lifetime of droplets in the air that can directly affect the spread of the disease in the air, or indirectly (e.g., reduce the protective ability of masks) (Bourouiba, 2020).

To mitigate a potential risk of multicollinearity, we compute a variance–inflation factor (VIF) function to identify and remove covariates that show high levels of correlation using a step‐wise procedure from the R package usdm (Naimi et al., 2014). We use the function vifcor which is a step‐wise procedure used to identify and remove collinear covariates. First, it runs an ordinary least square regression with a covariate X _q as a function of all other covariates. For each iteration, it computes ${\text{VIF}}_q={(1‐R_q^2)}^{‐1}$, where $R_q^2$ is the proportion of the variance in X _q explained by the other covariates. Then, it identifies pairs of covariates with a correlation coefficient (Pearson's ρ) greater than a threshold, which are associated with a large value of VIF.

In our context, dropping covariates only because they show some degree of correlation would lead to a model that is not theoretically well motivated (see, e.g., O’brien, 2007). We consider high multicollinearity when VIF is above 5, which is large enough to remove highly correlated variables while keeping theoretically important variables in the model. VIF values are computed based on a random sample of 5000 observations and is repeated until no pair of covariates exhibits a VIF greater than the defined threshold. To increase reliability in the results, we replicate the procedure 2000 times and derived the corresponding average value of the estimated ρ values for each pair of covariates.

The results show that population size (pop) (Tatem, 2017) and urbanity (urban) (Esch et al., 2017) are systematically highly correlated (|ρ| > 0.8) with travel time to the nearest city of more than 50,000 inhabitants (access) (Weiss et al., 2018). We removed population size and urbanity to avoid multicollinearity issues in the models. We kept access, since there is evidence that connectivity to large cities via coaches and high‐speed trains has played a major role in the diffusion of COVID‐19 in China (Zhang et al., 2020).

Due to the Bayesian setting of the downscaling model, priors need to be defined for all parameters (and hyperparameters) in the model. We used default priors (normally distributed with mean and standard deviation) for the intercept ${\beta }_0\sim \mathfrak{N}(0,2)$ and covariate coefficients ${\beta }_q\sim \mathfrak{N}(0,0.4)$. We used penalised complexity (PC) priors (Fuglstad et al., 2019) for the polygon i.i.d effects $u_i\sim \mathfrak{N}(0,{\tau }_u)$, with standard deviation σ _u (precision ${\tau }_u=1/{\sigma }_u^2$). Here, we used the default configuration that favours a base model without polygon‐specific effect, with P(σ _u  > σ _u,max) = σ _u,prob , with σ _u,max and σ _u,prob that can be defined by the user (Simpson et al., 2017).

For the parameters of the random field (range and scale), we used PC priors (Fuglstad et al., 2019) so that P(ρ < 3) = 0.01 and P(σ _ζ  > 5) = 0.01. Without specific a priori knowledge on the true range of the parameters of the spatial field, we constrained the model to favour a random field with a small magnitude and a large range. We compare the predictive out‐of‐sample and in‐sample performance of different model specifications, which include variations on the priors set for the spatial parameters (see details in SI).

3. RESULTS

We carried out a leave‐one‐out out‐of‐sample procedure to compare the predictive performance (MAE, RMSE) of different model specificities by varying several components (see details in SI). The investigated models include: (1) all covariates; (2) only anthropogenic covariates; and (3) only environmental covariates. In addition, we built four alternative models (4–7) that include all covariates but use alternative PC priors on the spatial parameters. The results show that the model including only anthropogenic covariates has in general the highest predictive performance. This is expected, since the spread of COVID‐19 is likely to be mainly driven by anthropogenic factors (Carlson et al., 2020).

3.1. Parameter estimation

The estimated mean and 95% credible intervals of the fixed effects (Figure S1) and posterior distribution (Figure S2) are provided for: the log precision of the i.i.d effects (polygon level), intercept, spatial hyperparameters log ρ and log σ _ζ , and the β coefficients associated with the covariates (access and W. access).

As expected, travel time to Wuhan (W. access) is negatively associated with COVID‐19 incidence rate (95% CI: −0.76; −0.34). The expected COVID‐19 incidence rate increases with proximity to Wuhan, where the virus was first identified. We also observe a negative effect of accessibility to large cities (access) on COVID‐19 incidence rate (95% CI: −0.70; −0.07), which suggests that areas close to large cities are more prone to COVID‐19 infections.

There is evidence of an effect from the i.i.d. province‐specific random effects (log(τ) 95% CI: −0.85; −0.23), which is expected especially in the early stages of the epidemic, where Hubei province had a much higher number of reported cases compared to the other provinces. Furthermore, the strength of the connection with Hubei province, and hence vulnerability to a spread of COVID‐19, are expected to vary considerably among Chinese provinces.

3.2. Downscaling model predictions of COVID‐19 cases at fine spatial scales

A sampling process (n = 2000) from the posterior distribution allows us to estimate the expected incidence rate of COVID‐19 for January‐February 2020 at 5 km grid‐cell across China. In addition, we compute the higher and lower bound of the 95% credible intervals estimates of the incidence rate, which provides a measure of uncertainty of the predictions. To compare the results of the downscaling model with the spatially disaggregated data sets (Xu et al. and the Paper), we convert the predicted rates (mean) and their uncertainty (lower bound, and higher bound estimations) into predicted cases by multiplying them with population size for each grid‐cell in China.

Figure 4 shows the (natural log) COVID‐19 infected cases for January and February 2020 from the original JHU data set at the province level in China (top‐left). In addition, it shows an estimation of the (natural log) infected cases based on the downscaling approach with lower bound of the 95% CI (top‐right), mean (bottom‐left), and higher bound of the 95% CI (bottom‐right) predictions at 5 km grid‐cell.

FIGURE 4.

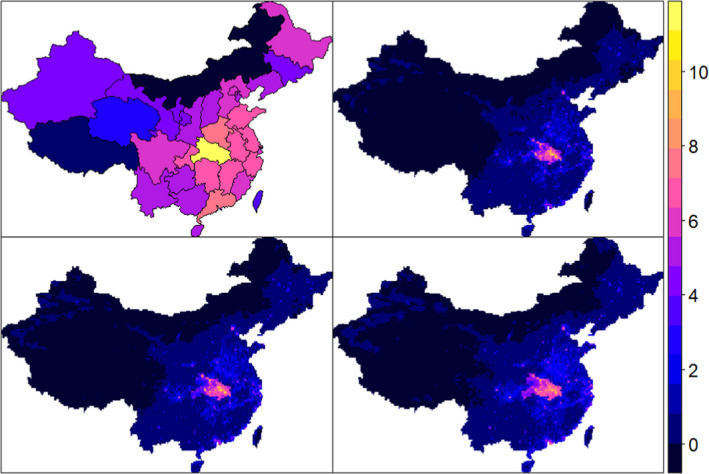
JHU original COVID‐19 data and estimated cases (January–February 2020) with downscaling (natural logarithm scale). The maps show the original data set of JHU of (natural log) COVID‐19 infected cases for January and February 2020 at province level in China (top‐left), along with an estimation of the (natural log) infected cases based on the downscaling approach with lower bound of the 95% CI (top‐right), mean (bottom‐left) and higher bound of the 95% CI (bottom‐right) predictions at 5 km grid‐cell [Colour figure can be viewed at wileyonlinelibrary.com]

3.3. Comparing model predictions with disaggregated data sets at the district level

Since the reported cases from the disaggregated data sets are reported at the city level, they are likely to include cases that occur in the neighbourhood of the reported locations. To ease their comparison with the predicted cases from the downscaling approach, we compare the data at district level, which include 340 districts corresponding to one administrative level below province in China (Taiwan districts are merged into one single entity).

Figure 5 shows the number of (natural log) COVID‐19‐infected cases for January and February 2020 at the district level (340 districts) in China from the Paper (left), Xu et al. (center), along with an estimation of the (natural log) mean infected cases based on the downscaling approach (right). Figures S3 and S4 show the number of (natural log) COVID‐19 infected cases for January and February 2020 at the district level (340 districts) in China from the Paper (blue triangles), Xu et al. (red points), along with an estimation of the (natural log) mean (white squares), 95% credible intervals (grey segments) of the infected cases based on the downscaling approach. For each district, the colour of the symbol is faded for the corresponding data set (Xu et al. or The Paper) that exhibits the most distant values (in absolute terms) to the predicted (natural log) mean cases from the downscaling approach.

FIGURE 5.

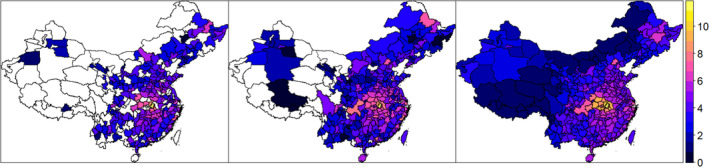
The Paper, Xu et al., and estimated cases (January–February 2020) with downscaling (natural logarithm scale) in Chinese districts. The maps show the number of (natural log) COVID‐19 infected cases for January and February 2020 at district‐level (340 districts) in China from the Paper (left), Xu et al. (center), with blank areas corresponding to locations without observations provided by the corresponding disaggregated dataset. Right: estimated (natural log) mean infected cases based on the downscaling approach [Colour figure can be viewed at wileyonlinelibrary.com]

Figures S3 and S4 show that in most districts, the values of the (natural log) reported cases from Xu et al. and the Paper lie within the 95% credible intervals of the predicted (natural log) cases based on the downscaling approach. This suggests that there is relative consistency between the investigated spatially disaggregated data sets (when data is provided) and the predictions from the downscaling model at the district level. We observe that the counts from Xu et al. tend to be closer to the predictive values from the downscaling approach. To further analyse potential discrepancies, we compute the absolute error (MAE) and the root mean squared error (RMSE) between the observed counts and the predictions based on several downscaling model specifications at the district level.

Tables S1 and S2 show the MAE and RMSE computed at the district level between each disaggregated data set (Xu et al. and the Paper) and mean predicted values from downscaling models with eight specifications (Model spec). The models differ by the use of: anthropogenic covariates (Socio. cov.), environmental covariates (Env. cov.), and i.i.d random polygon‐specific effects (i.i.d random), and parameter tuning on the spatial parameters. We used default PC priors the spatial parameters with thresholds ${\rho }_{\mathtt{min}}=1$ and ${\sigma }_{{\zeta }_{\mathtt{max}}}=5$ and used alternative thresholds in model specifications (5–8).

Note that the data coverage varies among the disaggregated data sets. Xu et al. provides data in more districts (301) compared to The Paper (234). Missing data can be visualised in Figure 5 as blank areas. Data coverage is usually better in the East of China. The results of the analysis at the district level show that Xu et al. data have a larger data coverage and exhibit a number of reported cases closer to the model predictions compared to The Paper data. The predictive performance metrics MAE and RMSE are systematically lower with Xu et al. data (lower in 7/8 model specifications).

4. DISCUSSION

The Bayesian downscaling model suggested in this paper made possible an assessment of discrepancies in the COVID‐19 counts between databases aggregated at different spatial scales. By investigating reported cases from January to February 2020, the suggested approach allowed us to quantify differences in COVID‐19 counts between two near real‐time spatially disaggregated data sets and a reference province‐level data set at the district level in China. Furthermore, our analysis benefited from the Bayesian structure of the model, which provided a coherent framework to estimate and visualise uncertainty in the predictions across a fine spatial grid that covers our study area.

The method proposed in this paper exhibits several shortcomings. Our initial exploratory analysis remains descriptive and does not capture the processes behind the generated data. As such, it has only allowed us to identify potential data mismatches. However, the exploratory phase led us to investigate the observed data discrepancies in further detail. The second step of our analysis consisted of a comparison between reported coronavirus‐infected cases and their locations gathered from two spatially disaggregated data sets (Xu et al., 2020 and The Paper Pengpai News Agency, 2020b) and predictions from a downscaling approach using JHU data as reference province‐level database (Dong et al., 2020). Without reference data at a finer scale (city level), we were not able to rigorously validate the results of the grid‐cell predictions, and hence, identify data discrepancies with high confidence. Furthermore, our model did not distinguish age and gender classes of the population at risk. A potential refinement of the model informed by population structure could be used to better estimate the population at risk.

We reported a relatively good robustness to changes in the priors overall. However, predictions in the province of Xingjiang are less accurate and the investigated models are more sensitive to changes in prior specifications to predict COVID‐19 counts in this region. We hope that in the future, additional covariates relevant to COVID‐19 will become available, which should contribute to improve the model performance and decrease sensibility to changes in prior for predictions in this region.

Assuming a well‐specified model, the downscaling model is likely to have provided an accurate representation of the uncertainty (Arambepola et al., 2022), which has allowed us to quantify deviations of the counts from the disaggregated databases with regard to the estimated mean and 95% credible intervals of the predicted counts from the downscaling model. To prevent the risk of overfitting, we built a relatively parsimonious model by selecting a few theoretically‐relevant covariates and constraining them to be linearly associated with COVID‐19 counts to keep the model as simple as possible.

Since in‐sample predictions may not provide accurate predictive metrics in the presence of overfitting (Hawkins, 2004), we selected the model based on the results of an out‐of‐sample iterative procedure that made predictions at grid‐cell within each hold‐out province from different model specifications. This procedure ensures that the resulting predictive metrics are based exclusively on data that has not been used in the fitting procedure. The model with the best predictive performance includes exclusively anthropogenic covariates, which brings evidence of the dominant role of human factors in the spread of COVID‐19 (Carlson et al., 2020).

A recent study that investigates the predictive performance of downscaling models exploring different contexts (various point data, aggregated areas sizes, and types of model misspecifications) suggests that predictive performance is likely to improve with a high number of data points and small polygon areas. If these conditions are not satisfied, predictions should remain accurate enough if the model is well‐specified (Arambepola et al., 2022). With a total of 33 polygons used to fit a relatively parsimonious model, we are confident that the predicted mean and uncertainty (95% credible intervals) should be accurate enough to provide reliable estimates of COVID‐19 counts at the district level.

Despite the measures implemented to mitigate the effects of several major validity threats, our results remain dependent on the accuracy and reliability of the data. Comparing the disaggregated data sets remains challenging since they rely on different sources of information and data collection methods. Discrepancies in the reporting delays are likely to affect their number of reported cases of COVID‐19 in the study period. Furthermore, at the national and province levels, estimating the true number of positive cases of COVID‐19 remains challenging. The number of individuals with a positive test result for the virus is inevitably smaller than the actual number of cases since a large proportion of infected people will not experience symptoms and may not get tested for the virus. Furthermore, the quality and efficiency of tests are subject to errors, which may lead to important discrepancies between reported and true counts (The Royal Statistical Society, 2020).

5. CONCLUSION

The analysis of spatially disaggregated COVID‐19 data in January and February 2020 in China highlights important discrepancies in the counts of COVID‐19 cases at a fine spatial scale. The results of an initial exploratory analysis led us to compare the observed differences in COVID‐19 cases in China gathered from two spatially disaggregated data sets, Xu et al. (2020) and The Paper (Pengpai News Agency, 2020b), with fine‐scale predictions using a Bayesian downscaling approach applied to a province‐level data provided by JHU (Dong et al., 2020). At the district level, COVID‐19 counts from the spatially disaggregated data sets tend to be consistent with the range of plausible values of the predictions obtained by the downscaling model. We showed that, in comparison with The Paper (Pengpai News Agency, 2020b), Xu et al. data (Xu et al., 2020) has a larger data coverage and the number of reported COVID‐19 cases tend to exhibit a higher degree of consistency with the expected values of the predictions obtained from the downscaling model.

The discrepancies in the counts of COVID‐19 observed at province and district levels in China could also occur in other spatial and temporal frameworks. We believe that the data discrepancies highlighted in this case study are substantial enough to be considered by the providers of disaggregated data and the research community. As the COVID‐19 pandemic continues to threaten various regions around the world, accuracy and reliability of the disaggregated COVID‐19 data are crucial for governments and local communities to ensure rigorous assessment of the extent and magnitude of the threat posed by the virus and draw relevant conclusions. We hope that our analysis can help the data providers to identify at fine spatial scales potential data collection issues and remedy to them.

Governmental measures to mitigate the spread of the virus, such as quarantine, social distancing, and community containment are costly (Wilder‐Smith et al., 2020). The efficiency of measures can be improved through evidence‐based analysis grounded on reliable and accurate data (May, 2020). Given the observed data discrepancies at various spatial scales, we recommend that the providers of disaggregated COVID‐19 data join efforts with the WHO, as well as national and regional governments to build and maintain a comprehensive and reliable disaggregated database on COVID‐19, which would help the research community and policy makers in their combat against the global threat posed by the virus.

ACKNOWLEDGEMENTS

We declare no competing interests. AP has been funded by Zhejiang University (Educational Funding Grant No. 2020XGZX054, Global Partnership Fund Grant No. 188170‐11103, and Fundamental Research Funds for the Central Universities Grant No. 2021QN81029). JY has been funded by the National Natural Science Foundation of China (Grant No. 61825205 and Grant No. 61772459). BL has been funded by the National Natural Science Foundation of China (Grant No. 41601001) and The Royal Society, United Kingdom (Grant No. NF171120). AB has been funded by the German Federal Ministry of Education and Research (BMBF) (Grant No. 01IS18036A). The authors of this work take full responsibilities for its content.

Supporting information