Establishing design principles for emissive organic SWIR chromophores from energy gap laws

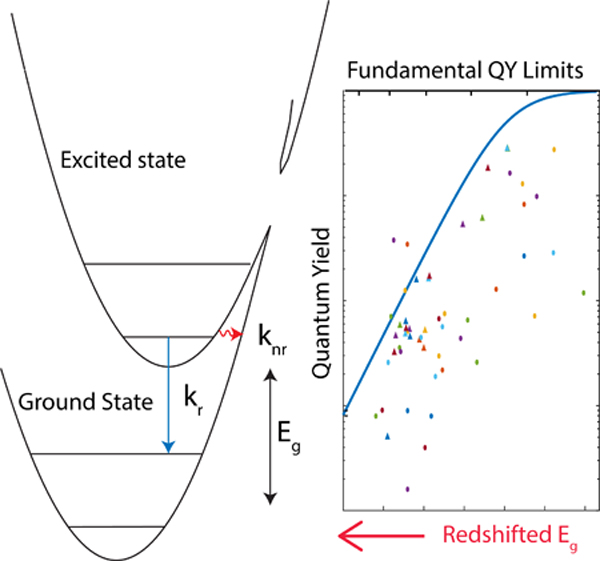
Summary:

Rational design of bright near and shortwave infrared (NIR: 700–1000 SWIR: 1000– 2000 nm) emitters remains an open question with applications spanning imaging and photonics. Combining experiment and theory, we derive an energy gap quantum yield master equation (EQME), describing the fundamental limits in SWIR quantum yields (ϕ_F) for organic chromophores. Evaluating the photophysics of 21 polymethine NIR/SWIR chromophores to parameterize the EQME, we explain the precipitous decline of ϕ_F past 900 nm through decreasing radiative rates and increasing nonradiative losses via high frequency vibrations relating to the energy gap. Using the EQME we develop an energy gap independent ϕ_F NIR/SWIR chromophore comparison metric. We show electron donating character on polymethine heterocycles results in relative increases in radiative efficiency obscured by a simultaneous redshift. Finally, the EQME yields rational chromophore design insights shown by how deuteration (backed by our experimental results) or molecular aggregation increases SWIR ϕ_F.

Graphical Abstract

eTOC:

Near and shortwave infrared emitters are vital to a wide range of applications from deep tissue imaging to photonic materials. However, the low quantum yield of organic NIR/SWIR emitters represents a defining struggle in the field. Combining experiment and theory, we model the impact of energy gap on quantum yield. Through analysis of this model and designing an energy gap independent comparison, we created a roadmap to more emissive near and shortwave infrared dyes.

Introduction:

Shortwave infrared (SWIR, or NIR-II/III, ~1000–2000 nm) radiation offers imaging capabilities with superlative contrast and feature resolution. Reflective and fluorescent imaging in the SWIR has been shown to enable penetrative imaging—through fog, foliage, skin and bone,^1–3 enabling broad applications ranging from image-guided surgery to self-driving cars.^4–7 The SWIR spectral region has lower background due to few natural sources of radiation (e.g. blackbody radiation, tissue autofluorescence), compared to the visible (VIS, 350–700 nm) and near-infrared (NIR, 700–1000) regions. Expanding and improving the library of bright SWIR chromophores that can sense biological, chemical or physical changes in complex and opaque environments represents a fundamental technological aim.

While nanoscale emitters like quantum dots and lanthanide nanoparticles can achieve high quantum yields (ϕ_F > 0.1) in the SWIR, organic chromophores have thus far displayed very low emission past 1000 nm (ϕ_F ≤ 0.03).^8–12 Nevertheless, organic emitters are biocompatible and provide a breadth of chemical functionalities that make them highly desirable for biological applications.¹³ There is a clear trade-off between smaller HOMO-LUMO gaps and ϕ_F. Even among NIR/SWIR emitters, the higher ϕ_F dyes tend to be those with maximum absorption wavelength ( λ_max ) on the blue edge of the SWIR spectral window. In this manuscript, we apply experiment and theory to answer the questions: What dictates fundamental limits on ϕ_F for narrow HOMO-LUMO gaps? Can we compare enhancement of ϕ_F due to a structural change between chromophores, independent of energy gap changes? What additional structural parameters provide a handle to overcome the current limits on ϕ_F?

To address these questions, we must consider how the energy gap modulates the fluorescence quantum yield, or the ratio of the radiative rate (k_r) to the sum of radiative rate and nonradiative rate (k_nr),

$${\varphi }_F=\frac{k_r}{k_r+k_{nr}}.$$ (1)

Known energy gap laws modulate the radiative/non-radiative rate, which, when combined with Equation 1, allow us to derive an estimate of the maximum ϕ_F as a function of singlet energy gap (E_g) for any chromophore. This Energy gap law Quantum yield Master Equation (EQME) will allow us to frame changes in ϕ_F in terms of E_g independent parameters, such as the transition dipole moment (μ₂₁), Stokes shift (E_ST), and the strength of nonadiabatic coupling between excited and ground states (C).

To parametrize and assess EQME, we utilize absorption cross sections, fluorescent spectra, excited state decay rates and quantum yields for 21 related symmetric polymethine fluorophores with absorption maxima ranging from 800–1100 nm (Figure 1).^14,15 This unique data set was acquired using sensitive superconducting nanowire single photon detectors (SNSPDs) which are capable of probing the often short excited state lifetimes of these chromophores in the SWIR, beyond the bandgap of silicon avalanche photodiodes (details in supporting information).^15–17 Comparing our results to the quantum yield of an additional 33 reported NIR and SWIR polymethine dyes demonstrates the general applicability of EQME for determining maximum quantum yield for organic chromophores in the SWIR.

Figure 1: Chromophores studied in this manuscript.

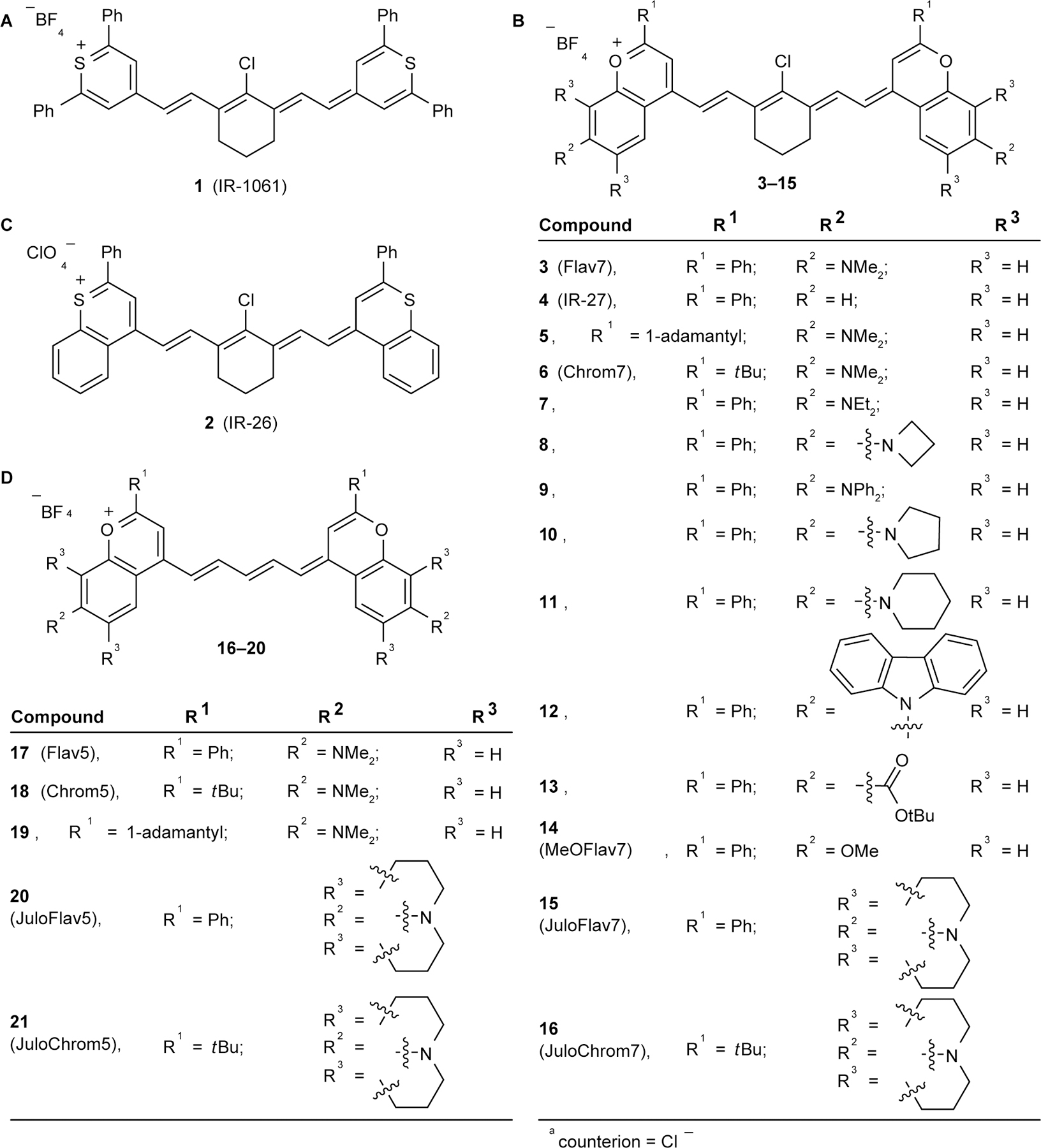
(a/b) Laser dyes IR-1061 (a) and IR-26 (b). (c/d) Flavylium and chromenylium heptamethine (c) and pentamethine (d) fluorophores.

The EQME equation also allows us to develop an energy gap independent comparison methodology for SWIR chromophores, enabling practical quantitative exploration how changes within a dye scaffold can lead to improved Φ_F independent of shifts in energy. Using this method, we show electron donating groups increase relative quantum yield while red-shifting the λ_max for the flavylium polymethine scaffold, a relationship previously obscured due to redshifting energy gaps. Furthermore, EQME quantifies other avenues for increasing quantum yield, such as deuteration, increasing the transition dipole moment through J-aggregation, or increasing the radiative rate through plasmonic coupling. We experimentally demonstrate such improvement through partial deuteration of the Flav7 (chromophore 3) scaffold. Our results define a metric and roadmap for overcoming limitations in SWIR quantum yields.

Results:

In Figure 2, we show an example of the collected data used to define measured values and errors for quantum yield (ϕ_F), λ_max, energy gap (E_g), total rate (k_tot), and Stokes shift (E_ST). All values are reported, which were taken in DCM, in Table 1 and their measurement and fitting is detailed in Section I of the supporting information. For all derived values, we will use SI units, however the tables will report values in more conventional wavenumber units (cm⁻¹). For convenience, the values in Table 1 can be used in each equation by converting to joules e.g. multiplying by ${\alpha }_E={10}^{2}hc\frac{J}{c{m}^{-1}}$ or $1.986\times 10^{-23}\frac{\text{J}}{{\text{cm}}^{-1}}$). E_g is defined as $\frac{hc}{{\lambda }_{max}}-\frac{1}{2}{E}_{ST}$ (Figure 2a). From the values in Table 1, we calculate the radiative and nonradiative rates (k_r and k_nr respectively), oscillator strengths of absorption and emission (f₁₂ and f₂₁), and the excited to ground transition dipole moment (μ₂₁, ${\mu }_{21}^{\prime }$)—calculated from the emission lifetime and absorption cross section, respectively (Table 2). The procedure for calculating these parameters is described in Section II of the supporting information and a script which goes through these calculations is provided as Data S1.

Figure 2: Representative plots of photophysical measurements used to determine energy law constants.

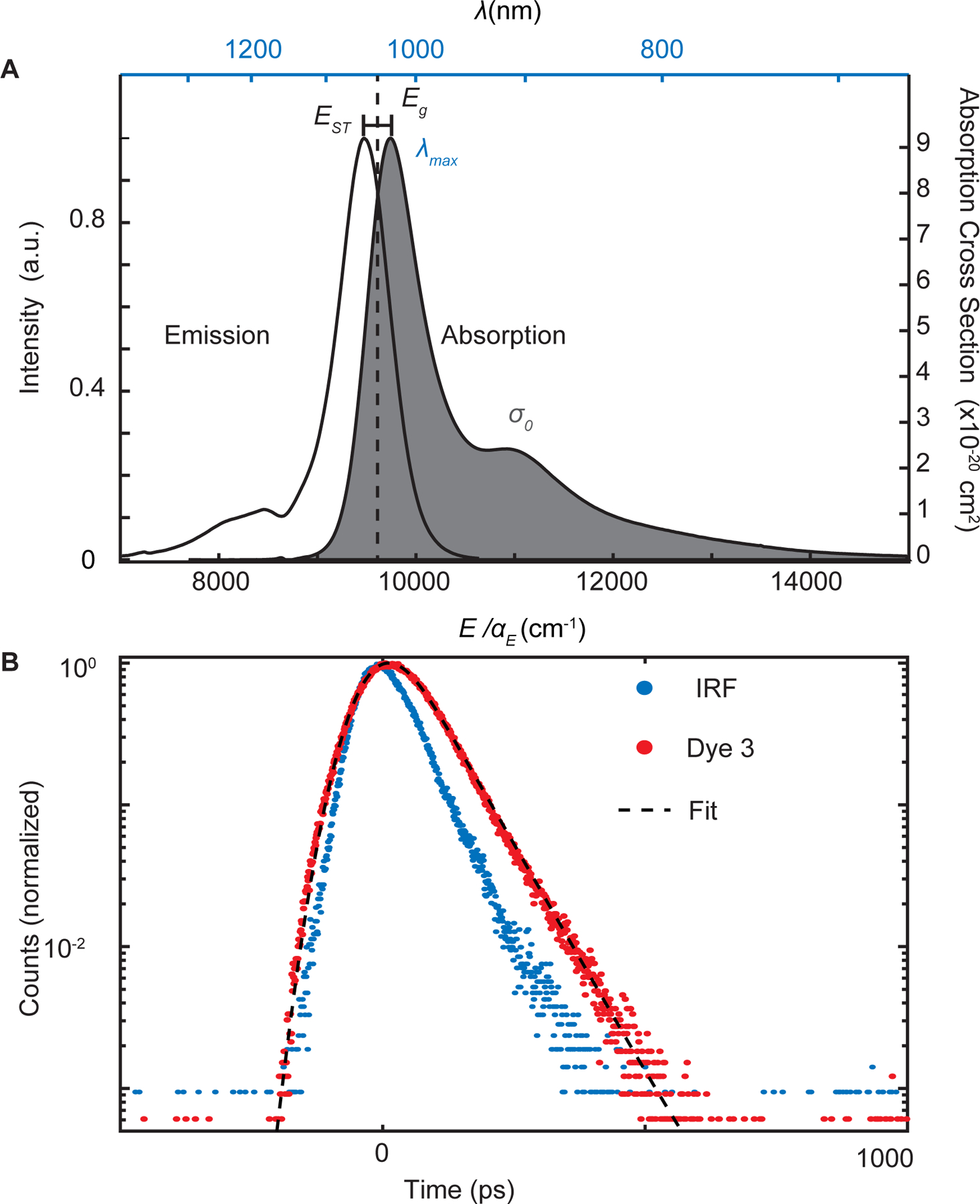
a) Absorption and emission spectra for dye 3 (Flav7) in dichloromethane is plotted. λ_max is defined as the maximum absorption point, the E_ST is defined as the difference between absorption and emission maxima and σ₀ is the integrated absorption cross section. E_g is the midpoint between maximum absorption and emission values. b) Fluorescent lifetime measurement for 3, instrument response function (IRF), and the data fit curve.

Table 1:

Experimentally Derived Values for the Energy Gap Las

Dye	ΦF(× 10−2)	$\frac{E_g}{{\alpha }_E}\left({\text{cm}}^{-1}\right)$	λmax (nm)	ktot (× 108 s−1)	σ0 (× 10−39 m2J)	$\frac{E_{ST}}{{\alpha }_E}\left({\text{cm}}^{-1}\right)$
1	0.32 ± 0.01	9276	1063	147 ± 2	3.25 ± 0.03	258.2
2	0.05 ± .03	9107	1080	490 ± 20	2.35 ± 0.04	298.7
3	0.61 ± 0.02	9603	1027	147 ± 2	2.68 ± 0.01	267.7
4	0.35 ± 0.01	10011	987	192 ± 4	2.37 ± 0.04	240.5
5	1.61 ± 0.02	10148	975	66.2 ± 0.4	2.63 ± 0.05	216.3
6	1.70 ± 0.04	10128	977	68.6 ± 0.5	2.58 ± 0.03	215.4
7	0.62 ± 0.02	9560	1033	144 ± 2	2.07 ± 0.07	237.7
8	0.51 ± 0.02	9585	1029	160 ± 3	2.86 ± 0.05	266.37
9	0.58 ± 0.02	9414	1047	147 ± 2	2.76 ± 0.01	274.7
10	0.48 ± 0.02	9548	1034	151 ± 2	2.91 ± 0.01	246.1
11	0.54 ± 0.01	9571	1030	151 ± 2	2.48 ± 0.09	274.8
12	0.45 ± 0.01	9668	1021	161 ± 3	1.46 ± 0.08	252.3
13	0.42 ± 0.02	9902	998	169 ± 3	1.16 ± 0.02	235.3
14	0.52 ± 0.01	10042	984	155 ± 2	2.03 ± 0.03	242.0
15	0.46 ± 0.01	9308	1061	180 ± 3	2.59 ± 0.02	233.9
16	1.58 ± 0.02	9814	1007	84.7 ± 0.7	2.51 ± 0.05	240.1
17	6.1 ± 0.1	11468	862	32.2 ± 0.1	3.20 ± 0.04	276.9
18	28 ± 2	12086	819	9.79 ± 0.01	3.46 ± 0.05	248.3
19	28.3 ± 0.5	12077	819	9.49 ± 0.01	2.83 ± 0.05	262.6
20	5.3 ± 0.02	10980	897	33.8 ± 0.1	2.66 ± 0.03	337.5
21	18.3 ± 0.4	11602	852	13 ± 0.1	3.67 ± 0.03	269.2
3’	0.63 ± 0.03	9626	1027	141 ± 2	4.35 ± 0.07	240.5
3”	0.66 ± 0.05	9626	1027	139 ± 2	4.40 ± 0.12	240.5

Table 2:

Calculated Values for Dyes Studied

Dye	kr (eq 1) (× 107s−1)	knr (eq 1) (× 10 8s−1)	f 12	f 21	${\mu }_{21}^{\prime }$ (eq 4) (D)a	μ21 (eq 3) (D)
1	4.7 + 0.2	147 ± 5	2.09 ± 0.02	−0.58 ± 0.02	17 ± 1	11.5 ± 0.2
2	2.4 ± 1.4	476 ± 286	1.51 ± 0.03	−0.30 ± 0.18	15 ± 1	8.4 ± 3.0
3	9.0 ± .03	146 ± 5	1.72 ± 0.01	−1.02 ± 0.04	15 ± 1	15.0 ± 0.3
4	6.7 ± 0.2	192 ± 7	1.50 ± 0.02	−0.71 ± 0.02	14 ± 1	12.3 ± 0.3
5	10.6 ± 0.3	67 ± 2	1.69 ± 0.03	−1.14 ± 0.01	15 ± 1	15.4 ± 0.1
6	11.6 ± 0.3	65 ± 1	1.66 ± 0.02	−1.16 ± 0.03	15 ± 1	15.6 ± 0.2
7	9.0 ± 0.3	144 ± 5	1.33 ± 0.05	−1.04 ± 0.04	14 ± 1	15.2 ± 0.1
8	8.2 ± 0.2	160 ± 7	1.66 ± 0.01	−0.95 ± 0.04	15 ± 1	14.5 ± 0.4
9	8.5 ± 0.3	146 ± 5	1.59 ± 0.06	−1.02 ± 0.04	15 ± 1	15.2 ± 0.3
10	7.3 ± 0.3	151 ± 7	1.77 ± 0.01	−0.84 ± 0.04	16 ± 1	13.7 ± 0.4
11	8.2 ± 0.2	151 ± 4	1.88 ± 0.01	−0.94 ± 0.02	16 ± 1	14.5 ± 0.2
12	7.3 ± 0.2	161 ± 4	0.94 ± 0.05	−0.82 ± 0.02	11 ± 1	13.4 ± 0.2
13	7.2 ± 0.4	172 ± 9	0.74 ± 0.02	−0.78 ± 0.04	10 ± 1	12.9 ± 0.4
14	8.1 ± 0.2	155 ± 4	1.31 ± 0.01	−0.85 ± 0.02	13 ± 1	13.4 ± 0.2
15	8.2 ± 0.3	178 ± 5	1.84 ± 0.03	−1.00 ± 0.03	16 ± 1	15.2 ± 0.4
16	13.4 ± 0.6	83.4 ± 4	1.61 ± 0.03	−1.47 ± 0.08	15 ± 1	17.8 ± 0.5
17	19.7 ± 0.8	30 ± 1	2.05 ± 0.03	−1.66 ± 0.03	19 ± 1	17.5 ± 0.2
18	27.4 ± 0.5	7.0 ± 0.3	2.23 ± 0.03	−2.03 ± 0.14	19 ± 1	18.9 ± 0.8
19	26.8 ± 0.4	6.8 ± 0.1	1.82 ± 0.03	−1.95 ± 0.02	17 ± 1	18.5 ± 0.2
20	18.0 ± 0.8	32 ± 1	1.71 ± 0.01	−1.49 ± 0.01	17 ± 1	17.0 ± 0.1
21	24.3 ± 0.5	10.8 ± 0.02	2.35 ± 0.03	−1.91 ± 0.04	20 ± 1	18.7 ± 0.2
3’	8.9 ± 0.5	140 ± 2	1.76 ± 0.02	−1.02 ± 0.06	15 ± 1	15.0 ± 0.4
3’’	9.2 ± 0.7	138 ± 2	1.78 ± 0.05	−1.06 ± 0.08	15 ± 1	15.3 ± 0.6

^aFor 1–16 (17–21), g₂/g₁ = 1. 6± 0. 2(1. 1± 0. 1)

The First Energy Gap Law – Radiative Rates:

The first law relates k_r to the density of photonic modes in vacuum and the transition dipole moment (details in Section II of supporting information). Briefly, time dependent perturbation theory results in a spontaneous emission rate:

$$k_r=\frac{2\pi }{\hslash }{\left|M_{21}\right|}^{2}g\left(E_g\right),$$ (2)

where M₂₁ is the transition integral and g(E_g) is the density of photon states that bridge the transition energy between ground and excited states (e.g. Fermi’s golden rule). In general, as one increases the energy gap, the density of photonic modes increases with $g\left(E_g\right)\propto E_g^2$ while the matrix element that couples a dipole allowed transition between excited and ground state increases with ${\left|M_{21}\right|}^2\propto E_g$, leading to a k_r which is proportional to E_g³. For dipole allowed transitions in a solvent, the precise relationship in SI units is:

$$k_r=\frac{n{\mu }_{21}^2}{3\pi {ϵ}_0{\hslash }^4{c}^3}{E}_g^3,$$ (3)

where ϵ₀ is the vacuum permittivity, and n is the refractive index of the solvent (n = 1.42 for dichloromethane).

To assess the validity of the radiative rate energy gap law across different chromophores, we must normalize each rate by the molecule’s squared transition dipole moment $\left({\mu }_{21}^2\right)$ as assessed by a separate measurement, in this case the integrated absorption cross section:¹⁸

$${\left|{\mu }_{21}^{\prime }\right|}^2=3\frac{g_1{ϵ}_{0}nc}{g_2\pi E_g}{\sigma }_0.$$ (4)

where, g₂/g₁is the ratio of oscillator strength of polymethines of absorption and emission, respectively, or − f₁₂/f₂₁. We note that in polymethine chromophores, the absorption oscillator strength depends on the length of the methine bridge. For cyanine dyes with 7 methine units, prior reports show values between 2–3 and with shorter methine bridges values between 1.7–1.9 are reported.^19–21 We therefore use the average values g₂/g₁ = 1.6 ± 0.2 for 7-methines (1–16) and 1.1 ± 0.1 for 5-methines (17–21), which though lower show a similar trend.^* In Figure 3, we plot the radiative rate divided by the transition dipole moment, and compare to the following universal gap law:

$$\frac{k_r}{{\mu }_{21}^2}=K_{\mu }\frac{n}{3\pi {ϵ}_0{\hslash }^4{c}^3}{E}_g^3.$$ (5)

Figure 3: Polymethines follow the radiative rate energy gap law.

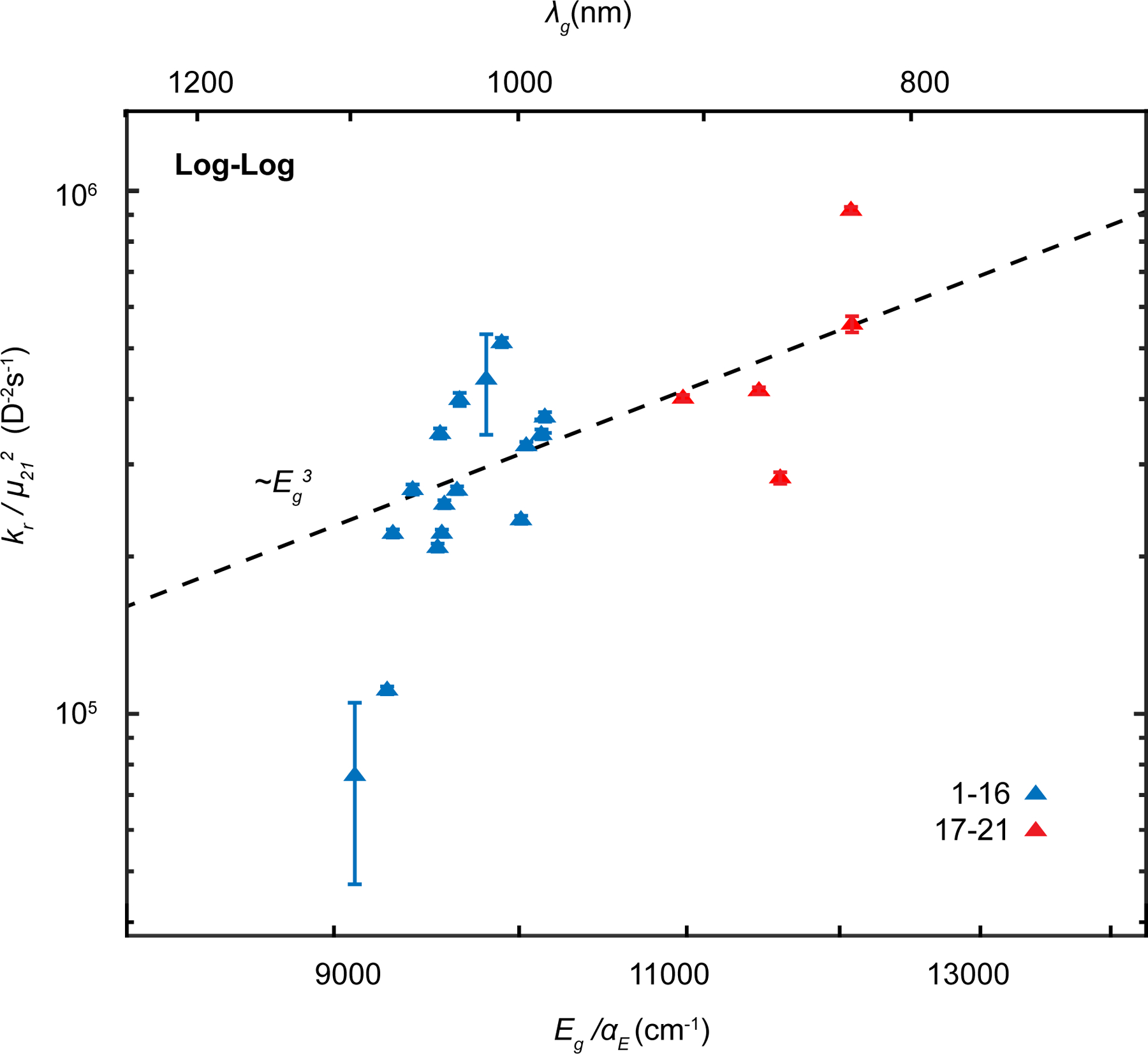
Radiative rates from Table 2 divided by transition dipole moment from Equation 4 for heptamethines (blue) and pentamethines (red). Line represents Equation 5, the radiative rate gap law normalized to transition dipole moment, allowing us to compare the dyes independent of the specific molecular parameters. Data are represented as value±SEM.

Here, K_μ = 1.11 × 10⁻⁵⁹C²m²D⁻² (a conversion factor which allows us to express μ₂₁ in more convenient Debye units). We observe that the transition dipole moment normalized radiative rate follows an approximate $E_g^3$ power law. This is consistent with the change in the density of states as a function of gap.

The Second Energy Gap Law – Nonradiative Rates:

Nonradiative rates are governed by multiple excited state loss channels including internal conversion (decay through vibrational modes), intersystem crossing (decay through an intermediate triplet state), and nuclear reorganization (decay to a lower energy molecular configuration, for example through isomerization or proton transfer).^22–24 The second energy gap law states that nonradiative relaxation rates for intersystem crossing and internal conversion (k_nr) exponentially decrease at higher E_g. Here, we focus on singlet states and thus nonradiative decay through internal conversion, allowing us to establish a lower bound on k_nr for infrared chromophores.

The experimental values for nonradiative rates are compared to the expression derived by Englman and Jortner,²⁴ which provides the nonradiative gap law in systems that have small Stokes shifts (E_ST) relative to their energy gap, E_g. We present a modified expression below (derived in the supporting information Section III) which relates this equation to values found in Table 1:

$$k_{nr}=\frac{C^2\sqrt{2\pi }}{\hslash \sqrt{E_M{E}_g}}\exp \left[-\frac{E_g}{E_M}\left(\ln \left(\frac{2E_g}{{\gamma }_M{E}_{ST}}\right)-1\right)\right].$$ (6)

Here, C is the non-adiabatic coupling term between singlet ground and excited states and E_M is the energy of the deactivating vibrational mode. γ_M is a parameter representing the degree to which the deactivating mode contributes to the Stokes shift given by:

$${\gamma }_M=\frac{S{E}_M}{E_{ST}},$$ (7)

where S is the Huang-Rhys parameter for the collection of near degenerate vibrational modes at or near E_M. Over the range of energies considered, the nonradiative rate will exponentially decrease with increasing energy gap, as observed in many systems, including gold nanoclusters,²⁵ metal to ligand charge transfer complexes,^26,27 aromatic thiones,²⁸ and platinum containing conjugated polymers.²⁹

To predict the energy gap dependence of nonradiative rates for polymethine chromophores studied here, we require semi-empirical estimates of E_M, γ_M, and C. For all estimates, we will use the largest Stokes shift for 7-methine dyes in Table 1 (dye 2, E_ST = 298.7 cm⁻¹). E_M is the energy of the vibration which contributes most strongly to the tunneling from excited to ground state. While a more detailed derivation is provided in reference 24, conceptually the gap law arises from the overlap between ground and excited state potentials, which varies nonlinearly with the vibrational energy. If the energy gap and Stokes shift are fixed, the tunneling distance between potentials decreases with the vibrational curvature (energy) of the mode. In the limit of large E_g relative to E_ST, higher energy vibrations dominate contributions to the overlap integral between ground and excited states. As in reference 21, we will use E_M = 3000 cm⁻¹ for Equation 7, the approximate energy of the collection of C-H vibrational modes. In order to reinforce the assumption that the highest frequency vibrational mode would dominate the nonradiative rate, we note the linear change in log(k_nr) as a function of energy gap in Figure 4. Despite a large variance in quantum yield among these dyes, this linear trend strongly implies that energy gap law considerations dominate the nonradiative relaxation rates in the SWIR. We plot the nonradiative rate estimate from Equation 6 using the parameters described in the preceding section (E_ST = 298.7 cm⁻¹, C = 1623 cm⁻¹), which shows good agreement with the nonradiative rate data. We also perform a linear fit of the data from which we extract the slope, which corresponds to

$$\frac{d\log \left(k_{nr}\right)}{d{E}_g}=-\log \left(e\right)\left(\frac{1}{2E_g^{\prime }}-\frac{\ln \left(\frac{2E_g^{\prime }}{{\gamma }_M{E}_{ST}}\right)}{E_M}\right)$$ (8)

Figure 4: k_nr are governed by high frequency vibrational modes E_M > 3000 cm⁻¹.

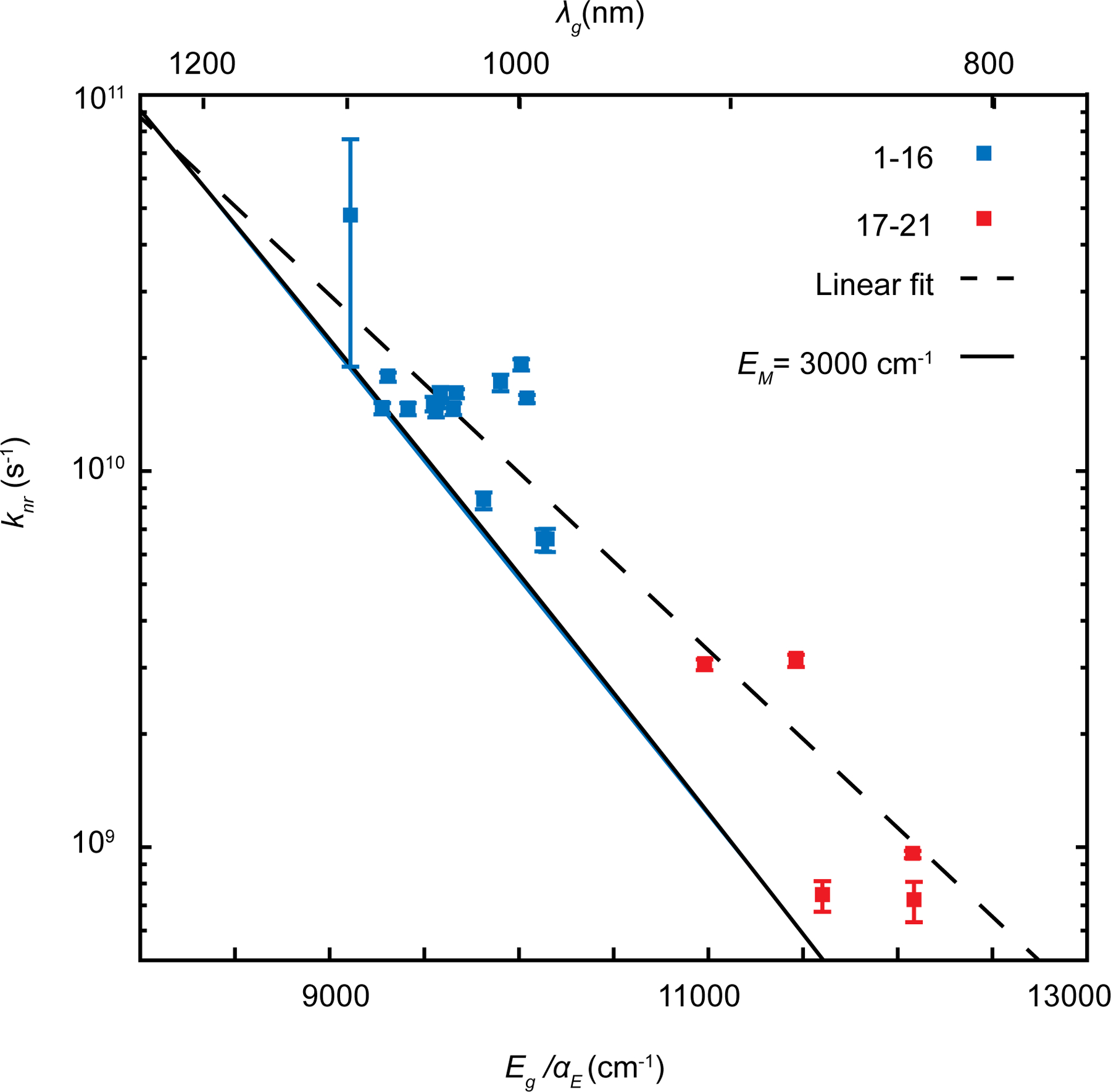
Nonradiative rates from Table 2 plotted against linear fit of log(k_nr), and Equation 6, evaluated using the parameters described in the text. . Data are represented as value±SEM.

For simplicity, we will use the midpoint $E_g^{\prime }=10,000{\text{cm}}^{-1}$, which leads to a fit for the deactivating vibrational mode of $E_M^{fit}=4086{\text{cm}}^{-1}$. Taken together, both the agreement of the model and the slope from the linear fit agree with the apparent dominance of high-frequency vibrational modes (≥ 3000 cm⁻¹, i.e. C-H stretches) in setting the non-radiative rate limit in SWIR-emitting polymethines.

Energy Gap Quantum Yield Master Equation:

We can combine Equations 1, 3 and 6 to derive EQME, which sets the maximum quantum yield of as function of energy gap, dielectric and molecular parameters:

$${\varphi }_F\left(E_g\right)={\left(1+K\frac{C^2}{n{\mu }_{21}^2{\left(E_M{E}_g^7\right)}^{\frac{1}{2}}}\exp \left[-\frac{E_g}{E_M}\left(\ln \frac{2E_g}{{\gamma }_M{E}_{ST}}-1\right)\right]\right)}^{-1},$$ (9)

where $K=\left(\frac{3{ϵ}_0{c}^2}{{\left(2^5{\pi }^3\right)}^{1/2}}\right)$. In Figure 5, we plot the functional form of the predicted “highest” quantum yield using γ_M = 1, C₁ = 1623 cm⁻¹, μ₂₁ = 18 D and E_ST = 298.7 cm⁻¹. We also include a more optimistic limit, using C₂ = 798 cm⁻¹ (which approximates a median value for the derivative coupling from literature on polyacenes and polyenes)^30,31 and a smaller coupling to the high frequency stretches (γ_M = 0.5) (Figure S4 shows effects of changes C and γ_M independently). We plot both our measured quantum yields from this work and 33 additional dyes from literature reports (see Figure S5 for labeled points).^{4,13,38,14,15,32–37} Our results demonstrate that even under pessimistic assumptions, quantum yields of almost all observed polymethine dyes do not exceed our predicted maximum line, with an exception of the LZ series of dyes recently reported by Li et al.^12,39 Given that our pessimistic estimation likely over-estimates the impact of nonadiabatic coupling, a few outliers can be expected. What is clear is that the model demonstrates that the precipitous falloff in quantum yields around 900 nm is an unavoidable consequence of energy gap laws applied to organic chromophores.

Figure 5: EQME provides consistent upper bounds for SWIR quantum yields.

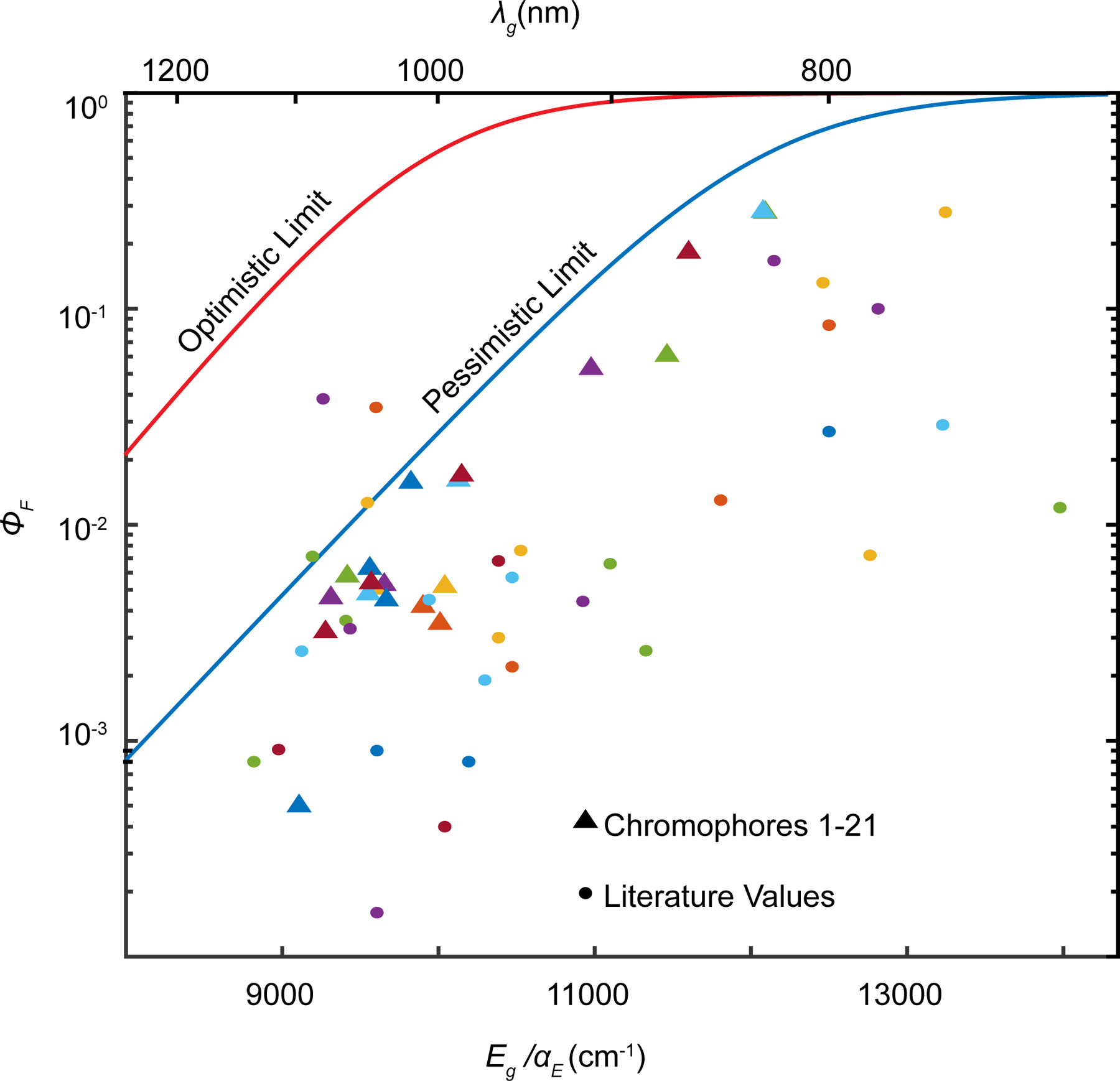
Comparison of quantum yields of 54 NIR and SWIR polymethine chromophores to the prediction of EQME (Equation 9). See Figure S5 and Table S2 for the labels points for chromophores 1–21 and chromophores from the literature.

Comparing Chromophore Quantum Yield while Accounting for Energy Gap Changes:

It is challenging to predict how structural modifications of a chromophore will alter the quantum yield. We hypothesize that the dearth of predictive metrics (particularly in the SWIR) arises from the contribution of energy gap QY changes which disguise the underlying effects of molecular change. Using EQME, we can establish an energy-gap independent parameter (ξ or ‘xi’) to study the effect of structural changes on quantum yields within a chromophore family. As supporting information, we provide a brief video tutorial on how to calculate ξ (Video S1).

We first define a conventional improvement factor (χ or ‘chi’) as the fractional change in quantum yield, e.g. χ = ϕ_b/ϕ_a − 1 (χ > 0 indicates a direct improvement in ϕ_F). To create an energy gap independent metric, we first note that when k_nr ≫ k_r (e.g., when ϕ_F < 0.1), log(ϕ_F) is approximately linear with respect to E_g changes. We therefore can extrapolate ϕ_F of a chromophore at one E_g to its equivalent value at another point in the SWIR. Comparing the extrapolated quantum yield of the standard fluorophore (a) to a second fluorophore (b) at the E_g

$$\xi =\frac{{\varphi }_b}{{\varphi }_a}{e}^{-\kappa \left(E_b-E_a\right)}-1$$ (10)

of b gives us an energy-gap independent improvement factor, ξ. Where κ is

$$\kappa =\frac{\ln \left(2E_{g,a}/{\gamma }_M{E}_{ST,a}\right)}{E_M}+\frac{7}{2E_{g,a}}$$ (11)

ξ > 0 indicates an improvement in the quantum yield factoring in the effect of changing the energy gap. The differences between χ and ξ are illustrated in Figure 6a; Equation 11 is derived in section V of the supporting information, with Figure S6 showing the validity of our constant κ, and section Va and Figure S7 shows a worked example using ξ.

Figure 6: Energy gap free QY comparator, ξ uncovers a linear free energy relationship.

a) Example of the difference between ξ and χ b) ξ shows correlation with Hammett parameter while χ shows negligible correlation. X through points denotes dye 9 which is excluded from all fits as done in ref. 14. c) There is a negative correlation between Hammett parameter σ_m and transition dipole moment. Data are represented as value±SEM.

Having established a comparative metric for SWIR fluorophore quantum yield that is independent of energy gap, we compare across heptamethine fluorophores with systematic changes at the 7-position of the flavylium ring (dyes 3, 4, 7–11, 13–15). Using Equation 10, we computed ξ values using the unsubstituted IR-27 (4) as the comparative fluorophore (i.e. fluorophore a). These values are in Table 3 (see Figure S8 for all values plotted). The ξ parameter reveals large energy gap independent changes in quantum yield hidden in the direct improvement factor.

Table 3:

Enhancement of Dyes Compared to Dye 4 (IR-27)

Dye	ξ	χ
1	1.73	−0.09
2	−0.45	−0.86
3 a	1.97	0.74
5	2.75	3.60
6	3.08	3.86
7 a	2.47	0.77
8 a	1.75	0.46
9 a	3.03	0.66
10 a	1.73	0.37
11 a	1.97	0.54
12	1.14	0.29
13 a	0.41	0.20
14 a	0.42	0.49
15 a	2.75	0.31
16	5.05	3.51

^aincluded in figure 6

Using ξ we sought to correlate the energy gap independent improvement factor with the Hammett σ_m parameter.⁴⁰ Prior work demonstrated that the absorption and emission maximum correlated well to σ_m (R² = 0.96); however, the quantum yield showed no direct correlation.¹⁴ In Figure 6b, we show no correlation between σ_m and χ (blue line, R² = 0.015). However, when ξ is plotted against σ_m values, a linear correlation emerges (Figure 6b, red line, R² = 0.757). Our results suggest that electron donation enhances the quantum yield. In Figure 6c, we show that transition dipole moment, μ₂₁, also increases with decreasing σ_m (R² = 0.452). We therefore hypothesize that electron donating groups appended to the heterocycle functionally increase the delocalization length of the excitation, leading to redshifting chromophores and larger transition dipole moments. The redshift induced by adding electron donating groups would lead to lower quantum yields, but the effect is partially compensated by increasing transition dipole moment, and thus increased quantum yields.

Overcoming energy gap laws:

The EQME suggests pathways to directly improve the quantum yield of organic chromophores through changes in radiative and nonradiative rates (Figure 7a). To alter the radiative rate of the chromophore, one can either A) alter the transition dipole moment, μ₁₂, or B) control the local photon density of states (g(E_g)). For (A), a potential approach is molecular J-aggregation in which coupled chromophores collectively interact with an electric field, resulting in superradiant emission.⁴¹ Furthermore, J-aggregation has the advantage of both modulating the radiative rate and redshifting the absorption and emission. Indeed, several groups have had success in using this strategy to access highly redshifted organic chromophores though superradiance has not been shown.^42,43 Sun et al. demonstrated that FD-1080 J-aggregates when encapsulated in a phospholipid nanoparticle and has a λ_max of 1370 nm and a quantum yield of 5.45 × 10⁻⁴ compared to the monomer values of 1046 nm and ϕ_F = 3.1 × 10⁻³ in ethanol.^34,43 The aggregate thus has a χ value of −0.8, but a ξ value of 7.3, demonstrating that energy gap laws can obscure improvements in molecular photophysics. For (B), the most common path discussed is through incorporation of photonic cavities or coupling to plasmonic nanoparticles.^44–46 Historically, microdroplets have been shown to modulate the radiative rate; for example, Rhodamine-6G showed an improvement of 2 in smaller droplet compared to larger droplets, including a change in fluorescence rate.^44,45 Srinivasan and Ramamurthy showed that Rhodamine-6G in cermet nanocavities had greater than 50-fold fluorescence enhancement.⁴⁷ Though these pathways are promising, the impact of plasmonic/photonic modifications may also simultaneously increase nonradiative rates.^48–50

Figure 7: Deuteration and increased transition dipole moment enhances PLQY in SWIR.

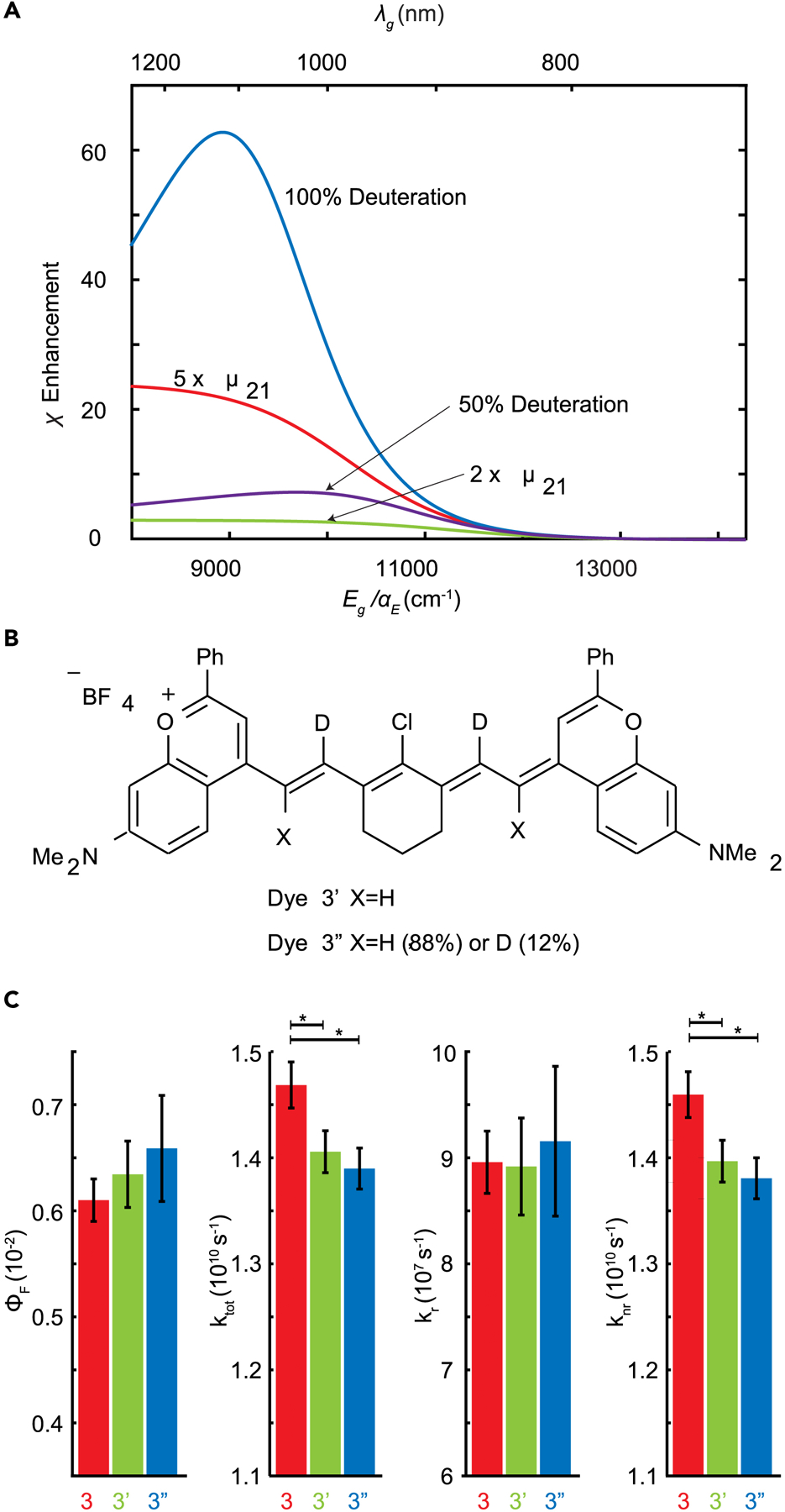
a) Ratiometric enhancement in quantum yield as a function of energy gap for different strategies for circumventing the energy gap laws including complete deuteration of the alkenyl CH stretches (blue), 50 percent deuteration (purple), increasing the transition dipole moment by 5 and 2 (red and yellow). b) Structures of dye 3’ and 3”. c) Deuteration on the polymethine scaffold increases but not significantly quantum yield, decreases total rate, has negligible effect on radiative rate, and decreases nonradiative rate. Data are represented as value±SEM based on confidence interval from lifetime fit (See SVId for more details). The asterisk indicates that the difference between dyes is significant p < 0.05.

For nonradiative rates, the highest vibrational frequency plays a large role in setting k_nr, typically the alkenyl C-H stretch at 3000 cm⁻¹. Complete substitution of H for D would change the highest vibrational energy to 2200 cm⁻¹. Assuming no change in the Huang-Rhys parameter (S = 0.1) we predict a maximum ~60 fold enhancement in quantum yield, using the pessimistic assumptions (Figure 7a, ~40 under optimistic assumptions (Figure S9)). Prior work on iridium complexes,⁵¹ benzene,⁵² oxazine,⁵³ and small molecule for blue LEDs⁵⁴ also demonstrated increased quantum yields with deuteration suggesting deactivation through these modes is a common feature in chromophores.

To test the effect of deuteration on polymethine chromophores, we synthesized two partially deuterated Flav7 (3), derivatives, 3’ and 3” (structures in Figure 7b, synthetic details in supporting information section VI). We hypothesized that partial deuteration will only have a modest effect on the nonradiative rate by decreasing the collective Huang-Rhys parameter of the highest energy mode. Measuring absorption, quantum yield, and time resolved photoluminescence lifetime we observe that dyes 3’ and 3” have nearly identical absorption and emission spectra (Figure S10) but may display a slight quantum yield enhancement. While the changes of quantum yield and radiative rate changes are within the error of the measurement, the change in k_tot and k_nr are significant (p < 0.05 for both compared to dye 3, Figure 7c, and details in section S5). The trend suggests that further deuteration may significantly enhance ϕ_F.

Discussion:

Every chromophore system is subject to the same energy gap laws described above, however, our data suggests that polymethine dyes have some of the best intrinsic properties for SWIR absorption and emission, including high transition dipole moments and small Stokes shifts.⁵⁵ To show this in comparison to other chromophores, we plot the energy where k_r = k_nr (or ϕ_F = 0.5) for fixed C, but variable μ₁₂ and E_ST in Figure 8. For simplicity, we assume the Stokes shift largely arises due to coupling to the 3000 cm⁻¹ C-H stretches (details in SI section VII). We then overlay the transition dipole moments and Stokes shifts of other common dye classes.^56–59 Within this model our results suggest that common chromophore scaffolds (e.g. BODIPY and xanthene derivatives such as fluorescein) may be challenging to shift into the SWIR while retaining high quantum yields, though squaraines provide a potential avenue for further exploration. Donor acceptor dyes with D-A-D structures or A-D-A fused ring structures have SWIR ϕ_F emission at 0.03 and are intriguing given their large Stokes shift (1000 − 3000 cm⁻¹), which would seem to be deleterious to the quantum yield.^8,60,61 However, the E_g of these SWIR emitting chromophores are bluer than other scaffolds. For example, COTIC-4F in toluene absorbs at 832 nm and emits at 915 nm with ϕ_F = 0.055, and an E_gof 11474 cm⁻¹. Its E_g is thus comparable to Dye 17, (11468 cm⁻¹) which has a similar quantum yield of 0.061, however, Dye 17 absorbs at 863 nm and emits at 883 nm.⁶¹ Therefore, one might trade stokes shifts in order to have larger energy gaps, and thus higher quantum yields.

Figure 8: 50% Quantum Yield Energy Map.

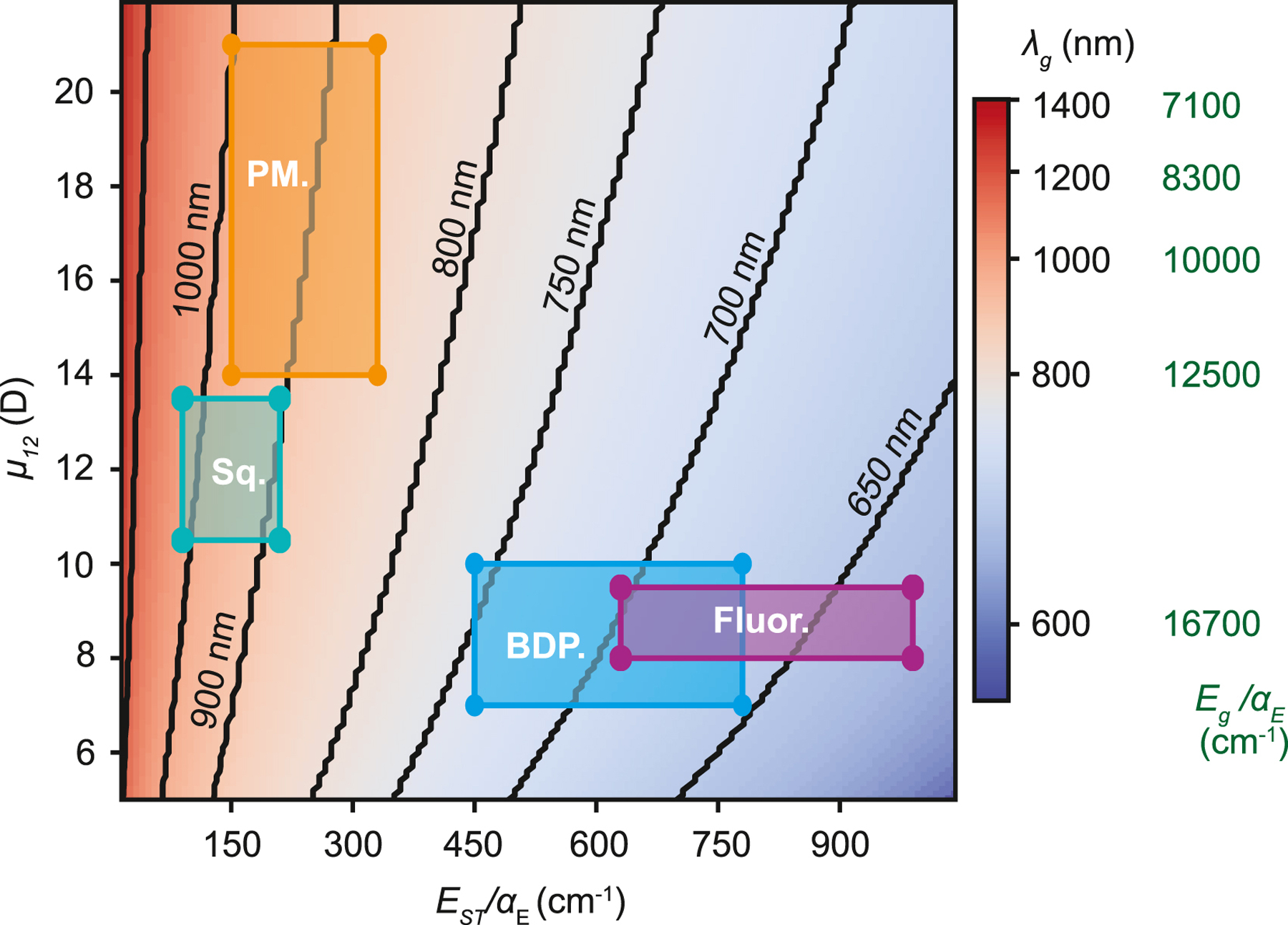
Solving for EQME=0.5 using two varying μ₂₁ and E_ST, demonstrates that high transition dipole moments and low Stokes shifts are necessary for scaffolds to have SWIR fluorescence. The predicted range for different dye scaffolds are in boxes as follows: polymethine (PM., orange), squaraine (Sq., teal), BODIPY (BDP., blue), and fluorescein (xanthene) (Fluor., purple).

Even with these favorable properties, the energy gap laws imply emission quantum yields of NIR/SWIR organic fluorophores will remain around 3% or less unless fundamental changes to the radiative and non-radiative pathways are realized. Stated succinctly, a chromophore is only as good as its worst non-radiative decay pathway. For visible chromophores, chemists have developed powerful tools to systematically improve quantum yields (e.g. rigidification), but these decay channels are no longer the limiting pathways for NIR/SWIR chromophores, with the vibrational relaxation as the limiting pathway. For example, conformationally restricted cyanine dyes (the CyB class) has shown dramatic increases to ϕ_F in the visible (e.g 0.09 to 0.85 for Cy3 and Cy3B^62–64, 0.15 to 0.69 for Cy5 and Cy5B)⁶⁵ but very small changes in the NIR (0.24 to 0.29 for Cy7 and Cy7B)²⁰ Though all have a decrease in Stokes shift with rigidification, they also notice less impact of viscosity of solvent in Cy7 versus Cy5 indicative less impact of torsional rotation.^20,65 The decreased stokes shift does suggest that the contribution of the highest frequency mode to the stokes shift is not 1, and adds credence to the optimistic limit in EQME. Nevertheless, high frequency deactivation does appear to be the limiting factor. In the NIR/SWIR, decreased energy gaps lead to short tunneling barriers and concomitant high k_nr. Eliminating these pathways requires fundamentally altering the high-frequency vibronic manifold (through deuteration or fluorination), or short circuiting the radiative pathways for the chromophore. On the other hand, deuteration may not significantly improve quantum yields in the visible, as other nonradiative pathways govern excited state dissipation. Energy gap law analysis may help determine the theoretical maximum quantum yield, and help researchers decide the appropriate path toward systematic quantum yield improvement.

We find that SWIR chromophores are deactivated via omnipresent vibronic coupling which directly connects ground and excited states through tunneling, mediated by C-H stretches. However, identifying precisely which C-H stretches should be modified remains an open question. Recent work by Hirata et al. on deuteration of N,N′-diphenyl-N,N′-(3-methyl phenyl)-1,1′-biphenyl-4,4′-diamine suggests that the location of the deuteration will have differential effects on the vibronic manifold, suggesting that some stretches are privileged in dissipative dynamics.⁵⁴ Further supporting this view, systems with high quantum yields in the SWIR (Pb and Hg chalcogenide nanocrystals, lanthanide f-orbital centers), have transitions which couple mostly to low-frequency phonon modes, i.e. E_M/a_E ≤ 300 cm⁻¹,⁹ consistent with higher QYs and considerably weaker direct nonradiative decay pathways. Mode-specific chemical transformations should be further explored as a pathway to improve quantum yields.

Many studies have made note of the deleterious effect of water as a solvent for quantum yields.^66,67 EQME only considers solvent refractive index and its effect on radiative rates (water has a lower refractive index of 1.33 vs 1.41 for DCM, resulting in a small decrease in radiative rates and quantum yields). However, this is insufficient to explain both the magnitude of quenching in water compared to other solvents, and the effect of deuterated water which increases quantum yields. Recent work has suggested that FRET into overtone vibrational bands of O-H stretches can impact quantum yields.^66,68 This is supported by prior work on SWIR emissive quantum dots⁶⁷ and preliminary data in section SVIII. This latter solvent effect is an additional deactivation pathway so for most cases the trend from EQME that we see in organics will transfer into water and other biologically relevant solvents. Still, further research exploring the effect of solvent environment in the SWIR will be fruitful.

Conclusion

To make systematic improvements to SWIR chromophores, we first explore the validity of energy gap laws for radiative and nonradiative rates and apply it to analyze a large data set of NIR/SWIR polymethine dyes. We derive an energy gap quantum yield master equation which demonstrates that the precipitous drop in quantum yields in the SWIR is consistent with the exponentially increasing nonradiative decay rates and decreasing radiative rates, with the former mediated by the presence of high frequency vibrational modes. Energy gap laws must be considered when comparing NIR/SWIR chromophores as improvements to quantum yield are directly correlated to the energy gap. By creating energy gap neutral comparators, we elucidate the impact of simple structural derivatives on quantum yield. We thus assess the natural limits of quantum yield in chromophores and provide a path forward in the inverse design problem. The presence of organic alkenyl C-H stretches likely limits the maximum possible quantum yield for SWIR emitters, but our preliminary results suggest that deuteration and judicious chromophore design may provide a path forward. We believe that a general and unified framework will enable the design of novel SWIR chromophore systems beyond the polymethine chromophore class and enable rational optimization of fluorescence in these systems.

Supplementary Material

1. Data S1: Python tutorial for using the Energy Gap Laws:

Annotated python code explaining how to convert values in Table 1 to values in Table 2, as well as the estimation of a C parameter for nonradiative rate. It is also available as a Google Colaboratory file at the link: https://colab.research.google.com/drive/1RBXHqPAVUrHd3_gxGoxl2VcNwEHywZ2m?usp=sharing

3. Video S1: Derivation of the ξ parameter.

This method video contains the derivation for the energy gap independent parameter, ξ, and how to use it.

Highlights:

• Combined energy gap law predicts declining quantum yields in redshifted chromophores

• Ability to compare quantum yields while considering redshifts among related dyes

• Molecular design principles toward increasing quantum yields in shortwave infrared.

Bigger Picture:

Bright near and shortwave infrared (NIR: 700–1000 SWIR: 1000–2000 nm) molecular and nanoscale emitters are vital toward applications ranging from deep tissue imaging to new photonic materials. However, all reported organic chromophores with energy gaps in the SWIR have very low quantum yields. Is there a fundamental limit for the quantum yield of organic chromophores in the SWIR? We formulate an energy gap master equation using experiment and theory to explain the precipitous fall in quantum yields as one redshifts into the infrared. We create an energy gap independent improvement factor, so we can uncover what synthetic modifications impact parameters important to the quantum yield. We additionally show that rational design changes based off EQME improved quantum yields. These insights will enable optimal chromophore designs for SWIR fluorescence.