Kinematic self-replication in reconfigurable organisms

Significance

Almost all organisms replicate by growing and then shedding offspring. Some molecules also replicate, but by moving rather than growing: They find and combine building blocks into self-copies. Here we show that clusters of cells, if freed from a developing organism, can similarly find and combine loose cells into clusters that look and move like they do, and that this ability does not have to be specifically evolved or introduced by genetic manipulation. Finally, we show that artificial intelligence can design clusters that replicate better, and perform useful work as they do so. This suggests that future technologies may, with little outside guidance, become more useful as they spread, and that life harbors surprising behaviors just below the surface, waiting to be uncovered.

Abstract

All living systems perpetuate themselves via growth in or on the body, followed by splitting, budding, or birth. We find that synthetic multicellular assemblies can also replicate kinematically by moving and compressing dissociated cells in their environment into functional self-copies. This form of perpetuation, previously unseen in any organism, arises spontaneously over days rather than evolving over millennia. We also show how artificial intelligence methods can design assemblies that postpone loss of replicative ability and perform useful work as a side effect of replication. This suggests other unique and useful phenotypes can be rapidly reached from wild-type organisms without selection or genetic engineering, thereby broadening our understanding of the conditions under which replication arises, phenotypic plasticity, and how useful replicative machines may be realized.

Like the other necessary abilities life must possess to survive, replication has evolved into many diverse forms: fission, budding, fragmentation, spore formation, vegetative propagation, parthenogenesis, sexual reproduction, hermaphroditism, and viral propagation. These diverse processes however share a common property: all involve growth within or on the body of the organism. In contrast, a non–growth-based form of self-replication dominates at the subcellular level: molecular machines assemble material in their external environment into functional self-copies directly, or in concert with other machines. Such kinematic replication has never been observed at higher levels of biological organization, nor was it known whether multicellular systems were even capable of it.

Despite this lack, organisms do possess deep reservoirs of adaptive potential at all levels of organization, allowing for manual or automated interventions that deflect development toward biological forms and functions different from wild type (1), including the growth and maintenance of organs independent of their host organism (2–4), or unlocking regenerative capacity (5–7). Design, if framed as morphological reconfiguration, can reposition biological tissues or redirect self-organizing processes to new stable forms without recourse to genomic editing or transgenes (8). Recent work has shown that individual, genetically unmodified prospective skin (9) and heart muscle (10) cells, when removed from their native embryonic microenvironments and reassembled, can organize into stable forms and behaviors not exhibited by the organism from which the cells were taken, at any point in its natural life cycle. We show here that if cells are similarly liberated, compressed, and placed among more dissociated cells that serve as feedstock, they can exhibit kinematic self-replication, a behavior not only absent from the donating organism but from every other known plant or animal. Furthermore, replication does not evolve in response to selection pressures, but arises spontaneously over 5 d given appropriate initial and environmental conditions.

Results

Pluripotent stem cells were collected from the animal pole of Xenopus laevis embryos (SI Appendix, Fig. S1A), raised for 24 h in 14 °C mild saline solution. These excised cells, if left together as an animal cap (11) (SI Appendix, Fig. S1 A and B) or brought back in contact after dissociation (12) (SI Appendix, Fig. S1 C and D), naturally adhere and differentiate into a spheroid of epidermis covered by ciliated epithelium (13, 14) over 5 d (9) (SI Appendix, section S1 and Fig. 1A). The resulting wild-type reconfigurable organisms move using multiciliated cells present along their surface (which generate flow through the coordinated beating of hair-like projections) and typically follow helical trajectories through an aqueous solution for a period of 10 to 14 d before shedding cells and deteriorating as their maternally provided energy stores are depleted.

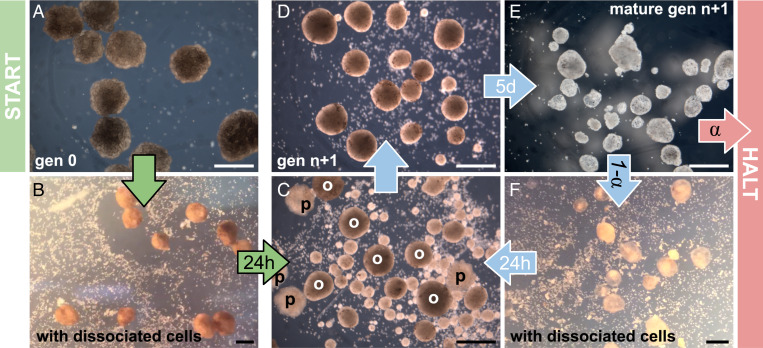
Fig. 1.

Spontaneous kinematic self-replication. (A) Stem cells are removed from early-stage frog blastula, dissociated, and placed in a saline solution, where they cohere into spheres containing ∼3,000 cells. The spheres develop cilia on their outer surfaces after 3 d. When the resulting mature swarm is placed amid ∼60,000 dissociated stem cells in a 60-mm-diameter circular dish (B), their collective motion pushes some cells together into piles (C and D), which, if sufficiently large (at least 50 cells), develop into ciliated offspring (E) themselves capable of swimming, and, if provided additional dissociated stem cells (F), build additional offspring. In short, progenitors (p) build offspring (o), which then become progenitors. This process can be disrupted by withholding additional dissociated cells. Under these, the currently best known environmental conditions, the system naturally self-replicates for a maximum of two rounds before halting. The probability of halting (α) or replicating( 1 − α) depends on a temperature range suitable for frog embryos, the concentration of dissociated cells, the number and stochastic behavior of the mature organisms, the viscosity of the solution, the geometry of the dish’s surface, and the possibility of contamination. (Scale bars, 500 μm.)

Previous studies reported spontaneous aggregation of artificial particles by groups of wild-type self-organizing (9) and artificial intelligence (AI)–designed (10) reconfigurable organisms: the particles were gathered and compressed as a side effect of their movement. Here, kinematic self-replication was achieved by replacing the synthetic particles in the arena with dissociated X. laevis stem cells as follows.

When 12 wild-type reconfigurable organisms are placed in a Petri dish amid dissociated stem cells (Fig. 1B), their combined movement reaggregates some of the dissociated cells into piles (Fig. 1 C and D). Piled cells adhere, compact, and over 5 d, develop into more ciliated spheroids (Fig. 1E) also capable of self-propelled movement. These offspring are then separated from their progenitor spheroids and placed in a new Petri dish containing additional dissociated stem cells (Fig. 1F). There, offspring spheroids build further piles, which mature into a new generation of motile spheroids (Movie S1).

In four of five independent trials using densities of 25 to 150 cells/mm², wild-type reconfigurable organisms kinematically self-replicated only one generation. In the fifth trial, two generations were achieved. Each successive generation, the size and number of offspring decreased until offspring were too small to develop into self-motile organisms, and replication halted.

To determine if offspring were indeed built by the kinematics of progenitor organisms rather than just fluid dynamics and self-assembly, the dissociated stem cells were observed alone without the progenitors. With no progenitor organisms present, no offspring self-assembled at any of the stem cell concentrations tested (SI Appendix, Fig. S2E).

Kinematic Self-Replication.

Given their rapid loss of replicative ability, reconfigurable organisms can be viewed as autonomous but partially functioning machines potentially amenable to improvement. Autonomous machines that replicate kinematically by combining raw materials into independent functional self-copies have long been known to be theoretically possible (15). Since then, kinematic replicators have been of use for reasoning about abiogenesis, but they have also been of engineering interest: If physical replicators could be designed to perform useful work as a side effect of replication, and sufficient building material were discoverable or provided, the replicators would be collectively capable of exponential utility over time, with only a small initial investment in progenitor machine design, manufacture, and deployment. To that end, computational (16–18), mechanical (19), and robotic (20–23) self-replicators have been built, but to date, all are made from artificial materials and are manually designed. Kinematic self-replication may also, in contrast to growth-based biological forms of reproduction, offer many options for automated improvement due to its unique reliance on self-movement. If progenitor machines could be automatically designed, it may become possible to automatically improve machine replication fidelity (24), increase or alter the utility performed as a side effect of replication, allow replication to feed on more atomic materials (25), control replication speed and spread, and extend the number of replication cycles before the system suffers a loss of replicative ability. We introduce an AI method here that can indeed extend replication cycles by designing the shape of the progenitor reconfigurable organisms.

Amplifying Kinematic Self-Replication.

Determining sufficient conditions for self-replication requires substantial effort and resources. Each round of replication takes 1 wk, and regular media changes are required to minimize contamination. Thus, an evolutionary algorithm was developed and combined with a physics simulator to seek conditions likely to yield increased self-replication, measured as the number of rounds of replication achieved before halting, in the simulator. Progenitor shape was chosen as the condition to be varied, as previous work demonstrated that shapes of simulated organisms can be evolved in silico to produce locomotion in cardiac tissue–driven reconfigurable organisms (10), or enhanced synthetic particle aggregation by cilia-driven reconfigurable organisms (9).

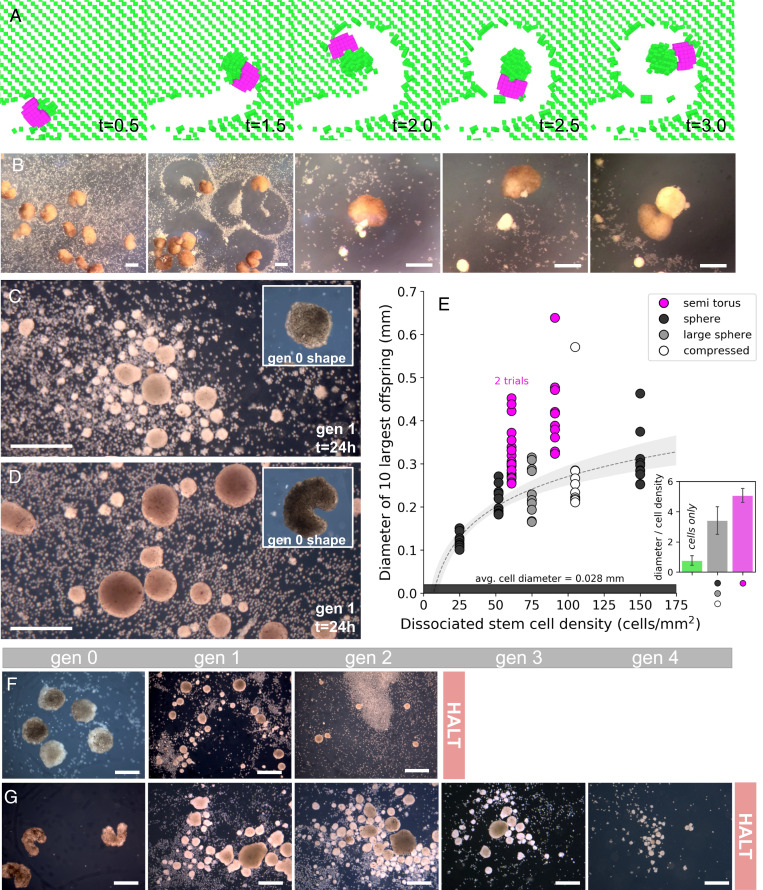
Simulations indicated that some body shapes amplified pile size and replication rounds, while others damped or halted self-replication. Some but not all geometries were better than the spheroids. The most performant geometry discovered by the evolutionary algorithm in silico and manufacturable in vivo was a semitorus (Fig. 2A). When 12 semitoroidal progenitor organisms were constructed and placed in an arena filled with densities of 61 to 91 dissociated stem cells/mm², they exhibited the same enhanced piling behavior in vivo observed in silico (Fig. 2B). The offspring produced by the progenitor spheroids (Fig. 2C) were significantly smaller than those produced by the progenitor semitoroids (Fig. 2D), although both progenitor groups produced spheroid offspring. Controlling for dissociated cell density, the diameter of offspring produced by progenitor spheroids was increased 149% by the progenitor semitoroids (P < 0.05) (Fig. 2E). The replication rounds achieved by progenitor spheroids (mean = 1.2 ± 0.4 SD, max of 2 shown in Fig. 2F) was increased 250% by the progenitor semitoroids (mean = 3 ± 0.8 SD, max of four shown in Fig. 2G) (P < 0.05). The only trial using semitoroids that reproduced less than three rounds was terminated early due to fungal contamination. Across the five trials with wild-type progenitor spheroids and the three trials with AI-designed progenitor semitoroids, the size of the first generation of offspring correlated with the total number of generations achieved (ρ = 0.93; P < 0.001).

Fig. 2.

Amplifying kinematic self-replication. Due to surface tension, reconfigurable organisms naturally develop into ciliated spheroids, but they can be sculpted into nonspheroidal morphologies manually during development to realize more complex body shapes. Progenitor shapes were evolved in silico to maximize the number of self-replication rounds before halting. (A) Shapes often converge to an asymmetrical semitoroid (C-shape; pink) with a single narrow mouth in which dissociated cells (green) can be captured, transported, and aggregated. This evolved shape was fabricated and released in vivo (B), recapitulating the behavior observed in silico (A). Offspring built by wild-type spheroids (C) were smaller than those built by the semitoroids (D), regardless of the size and aspect ratios of the spheroids, and across different concentrations of dissociated cells (E). The maximum of two rounds of self-replication achieved by the spheroids (F) was extended by the semitoroids to a maximum of four rounds (G). (Scale bars, 500 μm.)

Given the observation that larger spheroids yielded more replication rounds, another, simpler route to increasing self-replication seemed possible: increasing the density of dissociated cells. However, Fig. 2E shows that spheroid offspring size does not appreciably increase even when tripling density from 50 to 150 cells/mm² in the presence of sphere progenitors.

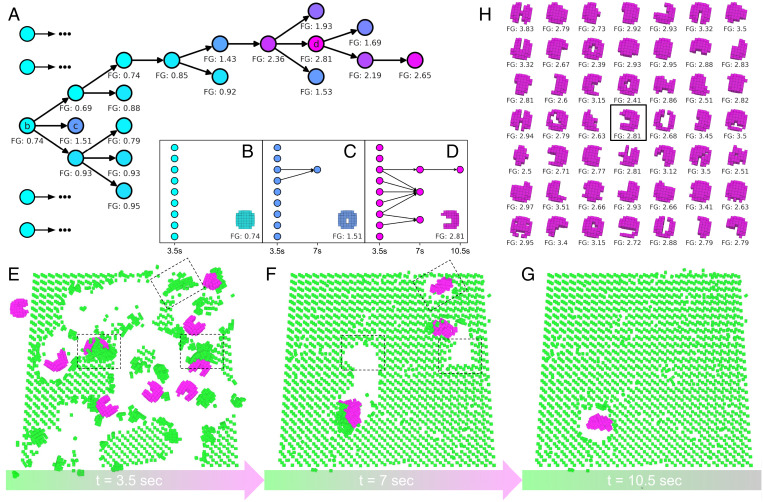
The semitoroidal design was found in silico using an evolutionary algorithm (Fig. 3A). First, 16 progenitor shapes are randomly generated. For each shape, nine simulated organisms with that shape are evaluated within a simulated Petri dish (Fig. 3E). If the swarm creates piles large enough to mature into offspring, the simulated offspring are transferred to a fresh dish (Fig. 3F), and the process continues (Fig. 3G). When self-replication halts, the shape is assigned a performance score computed as the number of filial generations achieved. Higher-performing progenitor shapes are copied, mutated, and replace shapes in the population with poorer performance. Each of the newly created progenitor shapes is expanded into a swarm, simulated, and scored (Fig. 3C). The algorithm terminates after a fixed amount of computational effort has been expended, and the shape that produced the most replication rounds is extracted (Fig. 3D). A total of 49 independent optimization trials were conducted, yielding 49 high-performing progenitor shapes (Fig. 3H) that, in silico, produce larger offspring (P < 0.0001) and more replication rounds (P < 0.0001) than simulated wild-type spheroids (SI Appendix, Fig. S6).

Fig. 3.

Evolving self-replication. (A) An evolutionary algorithm, starting with random swarms, evolves swarms with increasing self-replicative ability. (FG = number of filial generations achieved by a given swarm. The fractional part denotes how close the swarm got to achieving another replication round.) The most successful lineage in this evolutionary trial originated from a spheroid that built piles no larger than 74% of the size threshold required to self-replicate (B). A descendent swarm composed of nine flexible tori (C) contained two members that built one pile large enough to self-replicate (two arrows), which, alone, built piles no larger than 51% of the threshold. A descendent of the toroid swarm, a swarm of semitori (D), contained six members (E) that collectively built three piles large enough to mature into offspring (F). One of those offspring built a pile large enough to mature into a second generation offspring (G). An additional 48 independent evolutionary trials (H) evolved self-replicative swarms with diverse progenitor shapes.

Conditions other than progenitor shape can be optimized to improve self-replication. To that end, the algorithm was modified to evolve terrain shape rather than progenitor shape to amplify self-replication in silico for wild-type spheroid progenitors. Terrain was shaped by the inclusion of reconfigurable walls that, once positioned along the bottom surface of the simulated dish, constrain the stochastic movement of organisms along more predictable trajectories within predefined limits. Starting with randomly generated terrains, the algorithm evolved terrains that, in silico, increased the number of replication rounds achieved by the wild-type spheroid progenitors compared to their performance on a flat surface (P < 0.0001) (SI Appendix, Figs. S7 and S8).

The algorithm not only can amplify kinematic self-replication in a given environment but can also bestow this capability on swarms otherwise incapable of achieving it in adverse environments. In a cluttered environment, the wild-type progenitors cannot move enough to self-replicate. However, the algorithm discovered progenitor shapes with ventral surfaces that elevated the simulated organisms above the clutter while maintaining frontal plane curvatures that facilitated pile making and the achieving of self-replication (SI Appendix, Fig. S9).

In contrast to other known forms of biological reproduction, kinematic self-replication allows for the opportunity to significantly enlarge and miniaturize offspring each generation. This was observed in vivo (Fig. 1C) and in silico (SI Appendix, Fig. S10). This suggests that swarms may be automatically designed in future to produce offspring of diverse size, shape, and useful behaviors beyond simply more self-replication.

Exponential Utility.

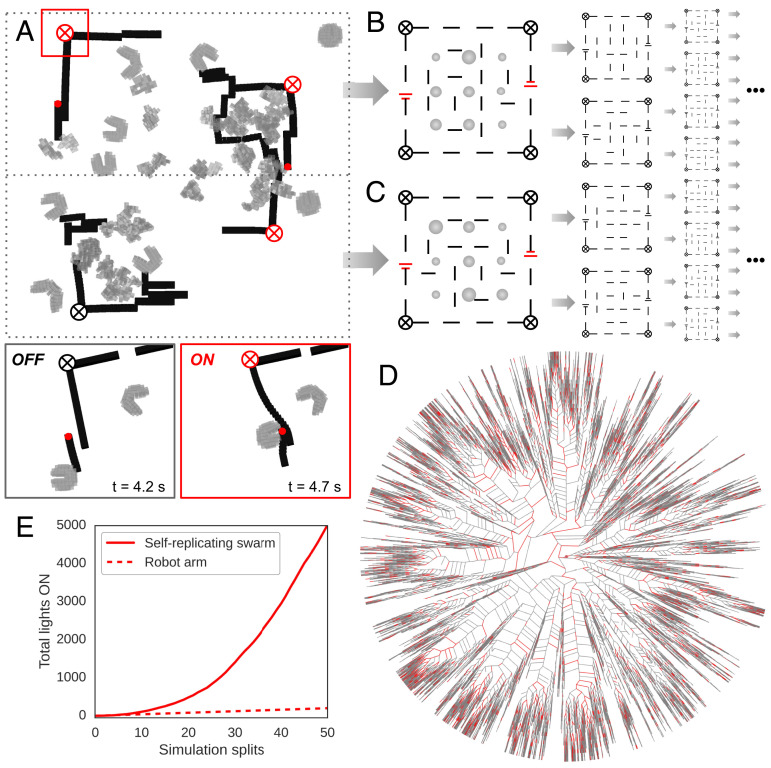
von Neumann’s original self-replicating machine (15) was capable in theory of not just building a functional self-copy but also other machines as a side effect of the replicative process. If these tangential machines performed useful work, the entire system was capable of exponential utility. As long as sufficient feedstock was available, only a small expenditure of energy and manufacture was required to build the first replicative machine. To estimate whether the self-replicating reconfigurable organisms introduced here may be capable of exponential utility, we created a computational model using known features of the physical semitoroids to forecast their potential rate of increase in utility. It is assumed that progenitor machines will be placed in semistructured environments, sufficient feedstock will be within reach, and random action of the swarm will be sufficient to result in useful work. Given these requirements, the task of microcircuit assembly was chosen (Fig. 4A). Although current circuit assembly systems are fast, efficient, and reliable, in situ repair or assembly of simple electronics in hostile or remote environments is currently impossible using traditional robots, rendering this a use case worthy of investigation. The simulated environment contains microscale power supplies (26), light emitters (27), and disconnected flexible adhesive wires (28) (SI Appendix, Fig. S11). Random action by swarm members can inadvertently move wires and close a circuit between a power supply and a light emitter (Fig. 4A), considered here as useful work. The environment is also assumed to contain dissociated stem cells, such that offspring organisms may be built in parallel with circuit assembly. If any offspring are built, they are divided into two groups and moved into two new dishes with more electronic components and stem cells (Fig. 4 B and C). If no offspring are built, the process terminates (Fig. 4D). In this model, utility increases quadratically over time (Fig. 4E).

Fig. 4.

Forecasting utility. (A) A swarm of self-replicating semitoroidal organisms (gray) was placed inside a partially completed circuit (black) containing two power sources (red dots), four light emitters (circled X; black when OFF, red when ON), and disconnected flexible adhesive wires (black lines). Dissociated stem cells (not pictured), if pushed into piles, develop into offspring (irregularly shaped gray masses). Dissociated cells are replaced every 3.5 s. After 17.5 s of self-replication and circuit building within a single dish, the progenitors are discarded, and all first through fourth filial generation offspring are divided into two equal-sized groups and placed into two new dishes, each containing a partially completed circuit (B and C). If only one offspring is built, one dish is seeded with it. If no offspring are built, bifurcation halts. This process results in an unbalanced binary tree (D). The red edges denote circuits in which at least one light emitter was switched on by closing a circuit from power source to light emitter (OFF/ON inset). The gray edges denote circuits in which no light emitters were switched on. The number of lights switched on increased quadratically with time (E). This differs from k nonreplicative robots that can switch lights on in k Petri dishes per unit of time, resulting in a line with slope k (e.g., a single robot arm could switch on all four lights in its dish at every unit of time [dotted line in E]). With sufficient time, the self-replicative swarm can achieve higher utility than the nonreplicative swarm for any arbitrarily large value of k.

Superlinear utility here depends on a superlinearly increasing supply of dissociated stem cells. This may be more achievable than mining artificial materials for nonbiological robot replicators given that a single female X. laevis can produce thousands of eggs daily, with each embryo containing ∼3,000 cells for dissociation, and X. laevis itself is capable of reproduction and thereby superlinearly increasing egg production. Reconfigurable organisms are thus constructed from a renewable material source which requires less invasive component sourcing than other existing self-motile biological machines (29, 30). The quadratic increase in utility predicted by the model in Fig. 4 may not be achievable when in situ circuit assembly and repair matures and the model can be tested empirically. But, as long as the components are small enough in weight and size to be moved, an acceptable temperature range is maintained, sufficient components have already been created and deployed and are nontoxic, and self-replication is maintained, the system will produce superlinear increases in utility. This can be contrasted with nonreplicative robot technology for the same task, which would require superlinear investments in robot construction, deployment, and maintenance to realize superlinear utility.

Discussion

The ability of genetically unmodified cells to be reconfigured into kinematic self-replicators, a behavior previously unobserved in plants or animals, and the fact that this unique replicative strategy arises spontaneously rather than evolving by specific selection, further exemplifies the developmental plasticity available in biological design (1–8). Although kinematic self-replication has not been observed in extant cellular life forms, it may have been essential in the origin of life. The amyloid world hypothesis (31), for instance, posits that self-assembling peptides were the first molecular entity capable of self-replication, and would thus represent the earliest stage in the evolution of life, predating even the RNA world. Unlike self-replicating RNAs which template themselves during replicative events, amyloid monomers can form seeds which produce a variety of amyloid polymorphs, yielding either larger or smaller “offspring” depending on peptide availability, kinematics, and thermodynamic conditions. This variation is similar to modern-day prions, where self-propagating misfolded proteins are capable of forming aggregates of multiple sizes and polymorphisms (32). Although reconfigurable organisms are not a model for origin of life research, which strives to describe the first information unit capable of self-replication, they may shed light on its necessary and sufficient initial conditions.

Traditional machine self-replication is assumed to require a constructor, a copier, a controller, and a blueprint to describe all three (15). However, there are no clear morphological or genetic components in the organisms described here that map onto these distinct structures. The concept of control in reconfigurable organisms is further muddied by their lack of nervous systems and genetically modified behavior. This suggests that reconfigurable organisms may in future contribute to understanding how self-amplifying processes can emerge spontaneously, in new ways and in new forms, in abiotic, cellular, or biohybrid machines, and how macroevolution may proceed if based on kinematic rather than growth-based replication.

Today, several global challenges are increasing superlinearly in spatial extent (33), intensity (34), and frequency (35), demanding technological solutions with corresponding rates of spread, adaptability, and efficacy. Kinematic self-replication may provide a means to deploy a small amount of biotechnology that rapidly grows in utility, but which is designed to be maximally controllable (36) via AI-designed replicators. Even if the behaviors exhibited by reconfigurable organisms are currently rudimentary, such as those shown in past (10) and this current work, AI design methods have been shown to be capable of exploiting this flexibility to exaggerate these behaviors and, in future, possibly guide them toward more useful forms.

Materials and Methods

Manual Construction of Reconfigurable Organisms.

Wild-type reconfigurable organisms were constructed manually from amphibian X. laevis epidermal progenitor cells using methods described previously (9). Briefly, fertilized Xenopus eggs were cultured for 24 h at 14 °C [Nieuwkoop and Faber stage 10 (37)] in 0.1× Marc’s Modified Rings (MMR), pH 7.8, after which the animal cap of the embryo was removed with surgical forceps (Dumont, 11241-30 #4) and transferred to 1% agarose–coated Petri dish containing 0.75× MMR. Under these conditions, the tissue heals over the course of 1 h and differentiates into a ciliated spheroid capable of locomotion after 4 d of incubation at 14 °C. Water exchanges were done three times weekly, and the organisms were moved to fresh 1% agarose–coated Petri dishes containing 0.75× MMR and 5 ng/µL gentamicin (ThermoFisher Scientific, 15710072) until ready for experimental use.

For nonspheroid designs, morphology was shaped via microcautery and microsurgery (SI Appendix, Fig. S1 E–H). The initial production of these organisms began using the methods described above; however, after 24 h at 14 °C, the spheroids were subjected to 3 h of compression with a force of 2.62 mg/mm². This compression results in a mild flattening of the developing tissue, producing a disk that is more amenable to shaping because it is less likely to rotate out of plane. Following compression, the organisms were cultured for an additional 24 h at 14 °C, after which final shaping was performed. Shaping was accomplished using a MC-2010 micro cautery instrument with 13-μm wire electrodes (Protech International Inc., MC-2010, 13-Y1 wire tip cautery electrode) in combination with a hand sharpened pair of surgical forceps. Each organism was shaped by first subtracting tissue to make a coarse morphology, then by fine sculpting to remove any cellular debris. After 1 h of healing, the morphology became stable for the remainder of the organism's lifespan. Following shaping, individuals were moved to fresh 1% agarose–coated Petri dishes containing 0.75× MMR and 5 ng/µL gentamicin and cultured until ready for experimental use.

All animal use was approved by the Institutional Animal Care and Use Committee and Tufts University Department of Laboratory Animal Medicine under protocol No. M2020-35.

Dissociated Stem Cells.

Dissociated cell layers for all self-replication experiments were obtained from the same starting material as the manually constructed reconfigurable organisms: X. laevis embryos 24 h of age (raised 14 °C). Similar to the manual construction of reconfigurable organisms, the animal cap of each embryo was explanted, and the rest of the tissue was discarded. Excised tissue was then moved via transfer pipette to a fresh 1% agarose–coated Petri dish containing a calcium- and magnesium-free dissociation medium (50.3 mM NaCl, 0.7 mM KCl, 9.2 mM Na₂HPO₄, 0.9 mM KH₂PO₄, 2.4 mM NaHCO3, 1.0 mM edetic acid, pH 7.3) and allowed to sit for 5 min. The pigmented outer ectoderm layer does not break down in this solution and was gently separated from the underlying stem cells with surgical forceps and discarded. The remaining tissues were agitated with manual flow from a pipetman until fully dissociated.

Material from 30 embryos were combined into a pool of cells (progenitor organisms are made from the same material, taken from a single embryo, and are composed of ∼3,000 cells), which was then collected and transferred to a sterile Eppendorf tube containing 1 mL 0.75× MMR. This solution was further mixed via manual pipetting up and down an additional five times, creating a final stem cell suspension. Using a clean transfer pipette, this solution was moved to a new 1% agarose–coated Petri dish containing 0.75× MMR. The speed and angle of the suspension deposition determined the concentration of the cells in the dish, and this concentration was quantified by imaging five random areas in the arena, then counting and averaging the number of cells per sq. mm. Cells were allowed to settle for 2 min before beginning kinematic self-replication experiments.

Conditions for Kinematic Self-Replication.

All experiments were initiated by distributing a stem cell suspension into a 1% agarose–coated 60- × 15-mm Petri dish filled with 15 mL 0.75× MMR, as described above in the preceding paragraph. Dishes were placed on the stage of a stereo microscope equipped with an eyepiece-mounted camera allowing for still photographs and timelapse imaging across the duration of the experiment. Cell suspensions were allowed to settle for 2 min, after which an image was captured of the center of the arena for cell density quantification. Following the initial setup, 12 adult organisms were placed in the center of the area among the dissociated cells via transfer pipette. All experiments were performed with adult reconfigured organisms aged 5 to 6 d at 14 °C, as this time point was previously found to represent the middle of their lifespan, and provides a standard movement rate (9).

Combinations of progenitors and dissociated stem cells were allowed to interact overnight (20-h total trial length) at 20 °C, and once the progenitors were placed in the arena, the Petri dishes were not moved or manipulated in any way to avoid disturbing the dissociated cell distribution. Imaging lights were also turned off for the duration of each generation of self-replication, as the heat generated by the light source was found to induce mild convection currents in the solution. Following completion of a generation, dishes were immediately imaged under the stereo microscope and then moved to a Nikon SMZ-1500 microscope with substage illumination for offspring size quantification. All aggregated stem cell tissue, now compacted as individual spheroids, were then pipetted to the center of the dish, and offspring size was calculated by measuring the diameter of each spheroid in the dish.

Upon completion of self-replication, adult organisms were returned to their original dishes, and their spheroid offspring were moved to a fresh 1% agarose–coated Petri dish containing 0.75× MMR and 5 ng/µL gentamicin. Each dish is washed as often as necessary to remove any remaining loose stem cells. The offspring were then cultured 14 °C for 5 to 6 d to verify the mobility and viability of the following generation. Where applicable, further rounds of replication proceed exactly as the first: 12 individuals (the largest individuals are chosen in successive generations) are placed among feeder cells, allowed to self-replicate for 20 h, and then offspring are quantified and separated for culture.

Evolving Swarms In Silico.

An evolutionary algorithm (38) was used to evolve simulated swarms with better self-replication, and for exhibiting diverse ways of doing so. Each independent trial starts with its own unique set of 16 initially random, genetically encoded replicator shapes. Each encoding is evaluated by prompting it to generate its shape, that shape is copied eight times, the resulting nine-progenitor swarm is simulated, and the amount (if any) of self-replication is recorded. The process is repeated 15 times with each of the remaining encodings. Each of the 16 encodings is then copied, randomly modified, and the swarm it generates is simulated. A 33rd random encoding is added to the expanded population to inject genetic novelty into the population, and its swarm is also simulated and scored. Encodings are then evaluated in pairs: if one encodes a swarm more self-replicative and evolutionarily younger than that encoded by the other, the latter encoding is deleted. Giving a selective advantage to younger swarms in this way maintains diversity in the population. Pairwise competitions continue until the population is reduced back to 16 encodings. This process of random variation, simulation, and selection is repeated for 48 h of wall-clock time on eight NVIDIA Tesla V100s.

Generating Initial Swarms In Silico.

Each replicator shape was encoded as a generative neural network (39) that places voxels at some positions within an empty volume of fixed size. The largest contiguous collection of voxels output by the network was taken to be the shape of the replicator. Randomly modifying the edges or nodes in the network modifies the shape it generates.

Simulating Replication.

Reconfigurable organisms and dissociated stem cells were simulated as elastic voxels using a version of a voxel-based soft-body simulator (40) modified to run on highly parallelized (GPU-based) computing platforms (SI Appendix, Fig. S5). Interactions between two voxels are modeled as deformations of an Euler–Bernoulli beam (translational and rotational stiffness). Collisions between voxels and the bottom of the Petri dish are resolved by Hookean springs (translational stiffness). The height of the aqueous solution, and the walls of the Petri dish, were modeled as soft boundaries that repel voxels penetrating predefined bounds with an opposite force proportional to the squared penetration (SI Appendix, section S2.1). The aggregate metachronal wave force produced by patches of cilia was modeled as an impulse force against each surface voxel, pointing in any direction in the horizontal (x,y) plane. The vertical (z) moments and forces of a simulated organism’s voxels were locked in plane to better approximate the behavior of the physical organisms which maintained constant dorsoventral orientation. The dissociated stem cells were simulated by adhesive voxel singletons with neutral buoyancy, and were free to be moved and rotated in three-dimensional space. When two adhesive voxels collided with each other, they bonded. Compaction and spherification, observed in vivo, is modeled in simulated piles of stem cells by stochastically detaching voxels around the surface of a pile, applying forces pulling them inward toward the center of the pile. Voxels were simulated with material properties manually tuned to allow for the largest stable time step of numerical integration. All other parameters of the model were estimated from biology according to SI Appendix, Table S1. At the start of each simulation, the simulated dish is seeded with the nine progenitors and 1,262 dissociated stem cells. After 3 s of simulation time, the progenitors and any piles with 108 or fewer voxels are deleted. Any piles with more than 108 voxels (incipient offspring; Fig. 3E) are then given an additional 0.5 s to compact and spherify. Empty space in the dish is then replenished with dissociated stem cells. The offspring are matured by adding random cilia forces on their surface voxels (Fig. 3F), after which they are simulated for another 3 s. This process continues until no piles greater than 108 voxels are achieved (Fig. 3G).

Measuring Self-Replication In Silico.

The self-replicative ability of a swarm was taken to be the following:

$$f=s/p+g,$$ [1]

where g is the total number of filial generations achieved, s is the size of the largest pile, in voxels, at the end of an evaluation period of 3.5 s (16,366 time steps with step size 2.14 × 10⁻⁴ s), and p is the pile size threshold required for a pile to develop into an organism. If s is greater than p, a new filial generation begins; otherwise, the simulation terminates. A conservative threshold of p = 108, two-thirds the size of the simulated wild-type spheroids, was selected such that relatively few randomly generated shapes achieved g > 0 (SI Appendix, section S2.2). Such overly conservative estimates can compensate for inaccuracies in other simulated parameters.

Statistical Hypothesis Testing.

The diameters of the 10 largest physical offspring (generation 1) built by wild-type organisms across five independent trial, and across different cell concentrations (gray points, Fig. 2E) were compared to the diameters of those built by the semitoroidal organisms in three independent trials (pink points, Fig. 2E). The diameters of all offspring were normalized by dividing by the cell concentration at which they were built. Comparing offspring size in this way is a conservative test since the volumetric difference between two spheres is eight times as large as their diametric difference. A Mann–Whitney U test was performed with a sample of eight independent measurements: the average offspring diameter within the eight independent trials (three trials with progenitor semitoroids, five trials with progenitor spheroids). The null hypothesis is that the average size of the semitoroid’s offspring (normalized by cell concentration) was no different from the average size of wild-type spheroids’ offspring (P = 0.037). Controlling for false discovery rate (41), this null hypothesis can be rejected at the 0.05 level of significance (SI Appendix, section S4.1).

Wild-type organisms produced just a single filial generation in four of the five independent trials. The only trial to produce two generations of offspring was the one with the highest cell concentration tested (150 cells/mm²). The first of three independent trials using the semitoroidal organisms resulted in two filial generations at 61 cells/mm² but was then halted because the organisms all contracted a motility-compromising fungal infection. In the second and third trials using semitoroids, additional precautions were taken to avoid fungal infections. Three successive generations of offspring were produced at 61 cells/mm²; four successive generations of offspring were produced at 91 cells/mm². A Mann–Whitney U test was performed. The null hypothesis is that the number of generations of self-replication achieved by the semitoroids (2, 3, and 4 g) was no greater than the number of generations produced by the wild-type spheroids (1, 1, 1, 1, and 2 g) (P = 0.019). Controlling for false discovery rate, the null hypothesis is rejected at the 0.05 level of significance (SI Appendix, section S4.2).

A Spearman rank-order correlation coefficient of 0.9322 (P = 0.00074) holds between the number of generations achieved and the aggregate size of the 10 largest first generation offspring.

Forecasting Utility.

Three kinds of microelectronic components that adhere permanently upon collision were added to the simulation: light emitters, batteries, and wire (Fig. 4A). Each component contains vertically stacked and insulated conductors which maintain connectability under translational and rotational movement in plane (SI Appendix, Fig. S11 C–E). As a side effect of movement, reconfigurable organisms will randomly push together microelectronics modules present in the dish (SI Appendix, section S5.1). If a light emitter connects by an unbroken circuit of wire to a battery, the light emitter switches on permanently (as indicated by a red circled X in Fig. 4 and SI Appendix, Fig. S11).

The swarm builds piles, which, if large enough, develop into offspring, and the dissociated cells are replenished every 3.5 s. Piles under the size threshold are removed to make way for fresh dissociated cells. Because we are interested in estimating utility rather than self-replication, progenitors are left in the dish and continue building additional offspring alongside their former offspring for another four, 3.5-s periods. After 17.5 s of simulation time, the number of light emitters connected to a power supply was recorded, the progenitors were removed, and all offspring were extracted. The offspring were then split equally into two new simulated Petri dishes, each with a new partially completed circuit (SI Appendix, section S5.2). Self-replication and circuit building begin afresh in these two dishes, again for 17.5 s. This is the start of a binary simulation tree (Fig. 4D) in which each simulation begets at most two simulation branches, each containing one-half of the produced offspring of their root simulation. If only a single offspring is created by a swarm after 17.5 s, then only one new simulation branch is started. If no offspring were built, then that branch of the binary simulation tree terminates.

After 50 simulation bifurcations, 5,024 light emitters were switched on. Symbolic regression (42) was used to find the degree of a polynomial function that best explains the cumulative number of lights switched on. Regression found that utility increases quadratically with time, as estimates found by symbolic regression all converged toward the quadratic curve derived by ordinary least squares: 2.7x² − 43x + 182.4, where x is the number of simulation bifurcations (R² = 0.9988).

Data Availability

Source code is available in the GitHub repository (https://github.com/skriegman/kinematically_replicating_organisms). All other data are included in the manuscript and/or supporting information.