Predicting patient response with models trained on cell lines and patient-derived xenografts by nonlinear transfer learning

Significance

Cell lines have been extensively used to study anticancer agents, thereby establishing vast molecular and drug response datasets. Unfortunately, the translation of cell line–derived biomarkers often fails. To bridge this gap between model systems and clinical practice, we developed a mathematical framework to capture gene expression patterns shared between model systems and human tumors in a consensus space. In this space, we trained drug response predictors on a panel of 1,000 cell lines and successfully predicted drug response on approximately 1,300 human tumors. Finally, we derived an approach to interpret the predictors, and we propose potential mechanisms mediating the cytotoxic effects of two drugs. Experimental validation is required to confirm these results.

Abstract

Preclinical models have been the workhorse of cancer research, producing massive amounts of drug response data. Unfortunately, translating response biomarkers derived from these datasets to human tumors has proven to be particularly challenging. To address this challenge, we developed TRANSACT, a computational framework that builds a consensus space to capture biological processes common to preclinical models and human tumors and exploits this space to construct drug response predictors that robustly transfer from preclinical models to human tumors. TRANSACT performs favorably compared to four competing approaches, including two deep learning approaches, on a set of 23 drug prediction challenges on The Cancer Genome Atlas and 226 metastatic tumors from the Hartwig Medical Foundation. We demonstrate that response predictions deliver a robust performance for a number of therapies of high clinical importance: platinum-based chemotherapies, gemcitabine, and paclitaxel. In contrast to other approaches, we demonstrate the interpretability of the TRANSACT predictors by correctly identifying known biomarkers of targeted therapies, and we propose potential mechanisms that mediate the resistance to two chemotherapeutic agents.

The accumulation of somatic alterations on the genome and epigenome transforms healthy cells into malignant tumor cells. Although these alterations are required for tumor growth, they also confer vulnerabilities on tumor cells. Some well-known examples of such genetic vulnerabilities are the amplification of ERBB2 in breast cancer (1), the BRAF^V600E mutation in skin melanoma (2), or the BCR/ABL fusion in leukemia (3). These vulnerabilities have been successfully exploited clinically by directing drugs against them. However, for the vast majority of cancer patients, no clear biomarkers exist. Hence, expanding our arsenal of accurate biomarkers would pave the way for personalized medicine by identifying the most effective drug for each patient (4).

In order to discover such biomarkers, preclinical models have been used extensively in the past decades, either in the form of cell lines, patient-derived xenografts (PDX), or organoids. This was partially fueled by the relative ease with which these model systems can be subjected to drug screening. This has led to breakthrough discoveries with broad clinical impact (5). However, Paul Valery’s statement, “what is simple is always wrong; what is not, is unusable” (6), also applies to these model systems. Specifically, their simplicity also confers weaknesses: the lack of a microenvironment in cell lines and the absence of an immune system in cell lines, PDXs, and organoids. These shortcomings are further amplified by culture artifacts (7, 8) that lead to a reduced clinical significance of these models (9, 10) and a high attrition rate in drug development (11).

Computational approaches that correct for these differences are therefore needed to improve the identification of truly predictive biomarkers (12). In the particular case of cancer, approaches that identify biomarkers are divided into two distinct categories. In the first category, mechanistic models are developed on preclinical models and subsequently “humanized” to focus on the similarities between preclinical models and human tumors (13). The second category approaches the problem in a statistical fashion. Using molecular profiles and drug screens from large-scale panels of preclinical models (14, 15), cell line drug response predictors are inferred (16–18). The resulting models are then applied to predict the sensitivity of patients to certain drugs (19–21). Although already promising, these approaches either do not take into account the fundamental differences between preclinical models and human tumors (22) or only model these differences as a technical batch effect (19–21). Recently, transfer learning and multitask learning approaches have been developed to explicitly take these differences into account, either partially using tumor responses during training (23, 24) or solely based on preclinical labels (25) while employing linear approaches to correct for differences between preclinical models and human tumors.

We present TRANSACT (Tumor Response Assessment by Nonlinear Subspace Alignment of Cell lines and Tumors), a versatile framework for subspace-based transfer learning (26–30) that enables the transfer of drug response predictors trained on a source domain (e.g., cell lines and PDXs) to a target domain (e.g., human tumors). TRANSACT employs the powerful and robust mathematical framework of kernel methods (31–36) to capture both linear and nonlinear molecular processes expressed in both the source and target domains. In doing so, we obviate the need for cell line preselection (37–39) and limit the loss of statistical power. While TRANSACT cannot compensate for inherent deficiencies in model systems, it identifies and exploits the space where model systems do represent human tumors accurately. First, we demonstrate that, compared to existing methods (20, 21, 25), modeling nonlinearities using TRANSACT improves drug response prediction in PDXs after training on cell line responses only. We fix the hyperparameter controlling the degree of nonlinearity on the PDX data and then employ TRANSACT to transfer predictors of drug response trained on cell lines to two human tumor datasets: primary tumors from The Cancer Genome Atlas (TCGA) and metastatic lesions from the Hartwig Medical Foundation (HMF). Specifically, the median performance of TRANSACT exceeds that of competing approaches in seven of 13 challenges on TCGA and the HMF sets. Importantly, this performance improvement is attained without any training on data from the human tumors. We finally employ the interpretability of our approach to identify genes and pathways associated with drug response. We provide a thorough mathematical derivation of our algorithm in which we propose a principled way to compare kernel principal components based on loadings by extending the framework of principal vectors (PVs) to the nonlinear kernel principal component analysis (PCA) setting. We generated a completely reproducible pipeline and a fully open-source software package.

Results

TRANSACT: Generating Nonlinear Manifold Representations to Transfer Predictors of Response from Preclinical Models to Tumors.

TRANSACT compares genomic signals contained in the source (e.g., preclinical models) and target (e.g., human tumors) datasets and outputs a consensus space—a representation of processes that are present in both datasets. The nature of this representation depends on the similarity function, $K$, that characterizes the relationships between samples (Methods). Depending on the similarity function employed, various types of nonlinear relationships can be represented in the consensus space. For instance, in the case of a Gaussian similarity function, these nonlinearities include constant, linear, second, and higher-order interaction terms (Methods).

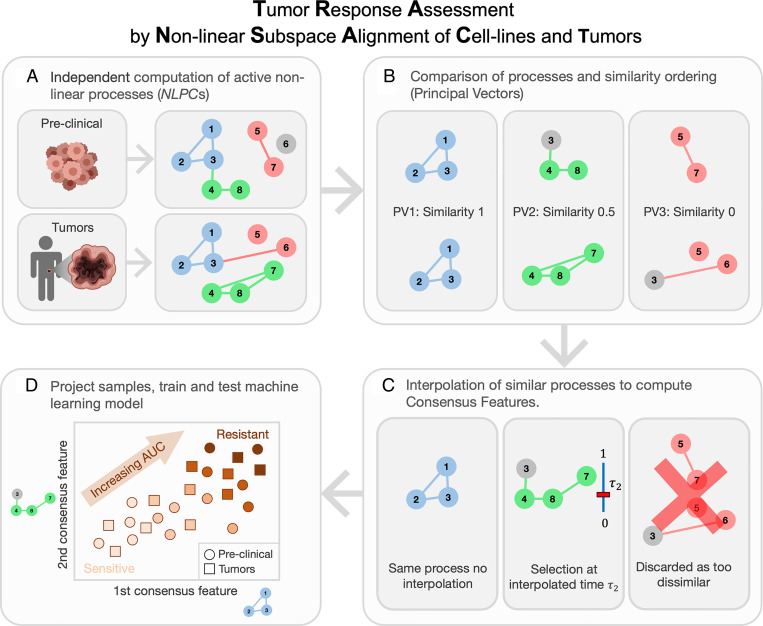
In a first step, TRANSACT computes processes active in preclinical models and human tumors, referred to as nonlinear principal components (NLPCs) (Fig. 1A and SI Appendix, Fig. 1 A and B). These NLPCs correspond to nonlinear combinations of gene activities that capture the variation in source and target sets (SI Appendix, Fig. 2A). However, these two sets of processes typically display limited similarity, simply because preclinical models are not perfect models of human tumors (SI Appendix, Fig. 1C). In order to capture the biological signal common to both preclinical models and tumors, we align the two sets of NLPCs using the notion of PVs (Fig. 1B). These PVs are pairs of nonlinear processes—one preclinical and one tumor process—ranked by decreasing similarity (Fig. 1B). The top PVs correspond to highly similar processes, while bottom PVs are essentially different processes. We first filter out PVs with low similarity (below 0.5) in order to discard information specific to either preclinical models or tumors (Fig. 1C). Since the remaining PVs represent pairs of highly correlated processes, we perform, within each PV pair, an interpolation between the preclinical and the tumor processes (Fig. 1C). We then select one intermediate vector that best balances the contribution of each dataset (Fig. 1C and SI Appendix, Fig. 1E). These intermediate processes are called consensus features and correspond to biological processes that are 1) important in both preclinical and tumor signals and 2) geometrically filtered to ensure that the signal is not specific to either one of the datasets. We then project preclinical and tumor samples on the consensus features (Fig. 1D, SI Appendix, Fig. 1F, and Methods). Finally, we use the projected scores as input in a predictive model of drug response trained using preclinical response data (SI Appendix, Fig. 1G).

Fig. 1.

TRANSACT generates a nonlinear representation to transfer predictors of drug response from preclinical models to tumors. (A) In the first step, we use a nonlinear dimensionality reduction method to find biological processes active in preclinical models and in tumors. This step is performed independently in preclinical models and tumors and gives two sets of nonlinear processes called NLPCs. Here, we consider eight genes and three NLPCs for both preclinical models and tumors. A colored circle means that the corresponding gene contributes to the NLPC, while a gray circle is a gene that does not contribute. A colored connection is the interaction, or product, of two genes that contribute to the NLPC. For instance, the red preclinical NLPC represents the expression of Genes 5 and 7 and the product of the expression of Genes 5 and 7. (B) These two sets of processes are compared and ranked by similarity. For that purpose, we compute PVs, which are pairs of processes, one from preclinical, one from tumor, ordered by decreasing similarity. Here, the first PV is conserved between preclinical models and tumors, the second shows a 50% similarity, while the last PV corresponds to two distinct processes. (C) We first discard the PVs with low similarity, for example, PV 3. We then aggregate each PV pair into one consensus feature (CF) by finding an intermediate feature that balances the effect of the preclinical and tumor dataset. (D) Preclinical and tumor data are finally projected on each consensus feature, yielding a sample-by-CFs matrix. These CF scores represent the activity of biological processes essentially important for both preclinical models and tumors. These scores can then be used in any machine learning model to predict drug response.

We theoretically show that, in the case of a linear similarity function, TRANSACT reduces to PRECISE (25) (SI Appendix, Equivalence with Geodesic Flow Kernel) and is fundamentally different from approaches such as canonical correlation analysis (CCA) (40) (SI Appendix, Difference with CCA on the Genes).

Nonlinearities Improve Response Prediction of Predictors Transferred from Cell Lines to PDXs.

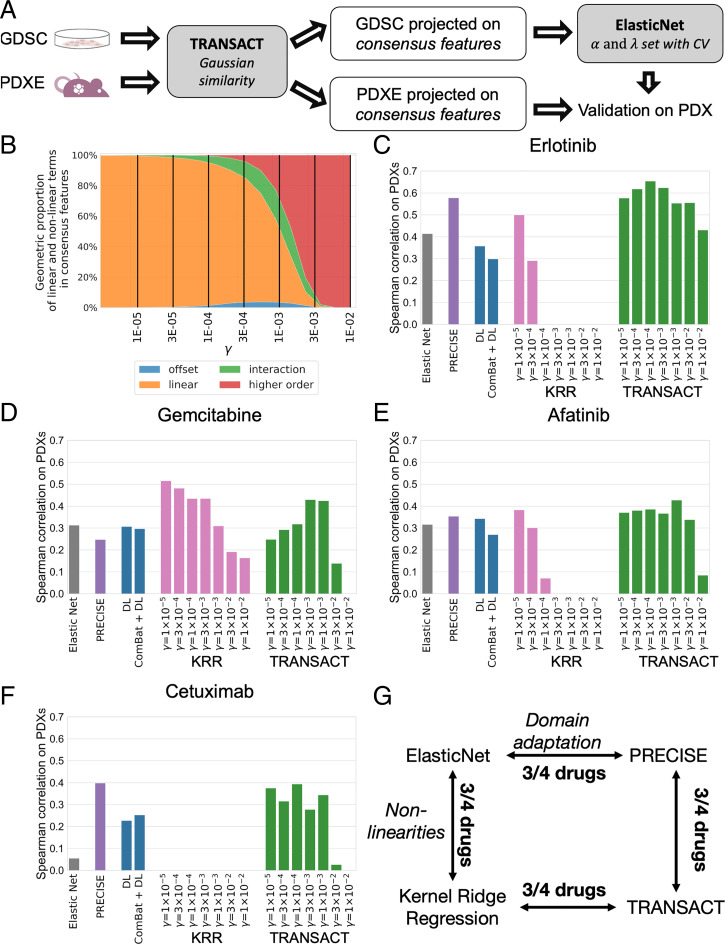
When it comes to predicting drug response in one model system, it is known that inducing nonlinearities can lead to improved performance (36), although linear methods remain competitive (18, 41). We investigated whether the introduction of nonlinearities in the computation of sample similarities resulted in improved response prediction of predictors trained on cell lines (source domain) and transferred to PDXs (target domain). Since gene expression is known to have predictive power comparable to other omics datasets combined (16, 18, 42, 43), we restricted our analysis to the expression of 1,780 genes known to be related to cancer (44). Using TRANSACT, we computed consensus features for cell lines (1,049 cell lines from 26 different tissues) and all PDXs (399 samples from 5+ different tissues) (Methods). We projected the gene expression data of all cell lines and all PDXs onto these consensus features. We employed ElasticNet to train models of drug response. We employed the projected cell line expression data as input and the drug response, quantified as the area under the drug response curve (AUC), as target output (see Methods). We applied this trained predictor on the projected PDX expression data and compared the predicted response to the measured best average response by Spearman correlation (Fig. 2A). We made use of the standard Gaussian similarity function (Methods) to vary the level of nonlinearity introduced. This similarity function is characterized by a single scaling factor $\mathit{\gamma }$, whose size is directly proportional to the proportion of nonlinearity introduced (Fig. 2B). We studied the predictive performance in PDXs for seven different values of $\mathit{\gamma }$, ranging from a set of consensus features with an almost purely linear ($\mathit{\gamma }=1 \times {10}^{-5}$) to an almost purely nonlinear composition ($\mathit{\gamma }=1 \times {10}^{-2}$). We compared the performance of TRANSACT to three approaches that do not perform domain adaptation: ElasticNet (22), a deep learning regression model (Methods) referred to as deep learning (DL), and a kernel ridge regression model (KRR) with the same nonlinear kernel settings as TRANSACT. We further compared it to two state-of-the-art domain adaptation approaches: ComBat batch correction followed by a deep learning regression (ComBat+DL) (21) and PRECISE (25), a linear domain adaptation approach. All models were trained to predict response to four different drugs (Erlotinib, Cetuximab, Gemcitabine, and Afatinib) for which we had response data available for both PDX models and cell lines (Fig. 2 C–F). For ComBat+DL and DL, we report the median performance obtained over 50 independent random initializations (Methods). Three other drugs were also studied: Paclitaxel, Ruxolitinib, and Trametinib (Dataset S1); however, these show no significant association between predicted and actual response in PDXs for any of the tested methods.

Fig. 2.

Impact of modeling nonlinearities for drug response prediction transfer from cell lines to PDXs. (A) Main workflow of the prediction on PDXs. Using cell lines and PDX gene expression, we compute consensus features and project each dataset onto these. We then train a predictor of drug response (ElasticNet regression) on the projected scores of cell lines and the cell line response, measured as the AUC. Finally, we use this regression model to predict drug response on PDXs and correlate the predicted AUC to the known best average response. (B) Proportion of nonlinearities induced by the Gaussian similarity function as a function of the scaling factor $\mathit{\gamma }$. For different values of $\mathit{\gamma }$, we compute the average contribution over all consensus features of offset, linear, interaction, and higher-order features (Methods). Offset is here to be understood as the exponential of the squared depth and does not correspond to a constant term. We finally evaluate the response prediction on PDX models for different values of $\mathit{\gamma }$ and for five competing approaches: ElasticNet, DL, ComBat+DL, PRECISE, and a KRR with same nonlinearities as TRANSACT. We report results for Erlotinib (C), Gemcitabine (D), Afatinib (E), and Cetuximab (F), which show the Spearman correlation between predicted AUC and best average response on the PDX models. (G) Diagram summarizing the effect of nonlinearities and domain adaptation in our predictor.

The studied methods can be divided along two axes: linear versus nonlinear and domain adapted versus nonadapted (Fig. 2G), and we evaluated the performances along these axes for the four drugs. For KRR and TRANSACT, we performed the comparisons for the values of gamma that gave the best performance. We observe that nonlinear methods (KRR and TRANSACT) prevail over linear approaches (ElasticNet and PRECISE) for three of the four drugs in each separate comparison (Fig. 2G). Furthermore, domain-adapted approaches (PRECISE and TRANSACT) prevail over nondomain-adapted approaches (ElasticNet and KRR) for three of the four drugs in each comparison (Fig. 2G).

When considering DL-based approaches, we observe, in general, a clear improvement for approaches that employ domain adaptation (PRECISE and TRANSACT) over those that either do not (DL) or use a naïve correction (ComBat+DL), confirming our earlier observation, namely the necessity to correct the input signal when moving from the source to the target domain. Moreover, this also suggests that the correction required to transfer from cell lines to PDXs is more complicated than correcting for a technical batch effect as performed by ComBat. When comparing TRANSACT to DL, a nonlinear and nonadapted method, we observe better performance for TRANSACT for all four drugs.

We note that for KRR, additional nonlinearity tends to reduce performance. In contrast, the introduction of additional nonlinearity in TRANSACT increases performance. Specifically, we observe for several drugs that the predictive performance increases with the scaling factor until a maximal performance is reached ($\mathit{\gamma }={10}^{-4}$ for Erlotinib, Cetuximab, and Afatinib and $\mathit{\gamma }={10}^{-3}$ for Gemcitabine), after which the predictive performance drops. As we only have three drugs in common between the PDX and human cohorts, we decided to fix the scaling factor to the average of these two values (${\mathit{\gamma }}^{*}=5\times {10}^{-4}$) and employ the associated consensus space to transfer the predictors of response to the tumor samples (Dataset S1). For the drugs in common, we applied the predictors with drug-specific values of $\mathit{\gamma }$ optimized on the PDX models to the TCGA and HMF cohorts (Dataset S2). We only did so for the drugs in which the drug-specific value of $\mathit{\gamma }$ differed from ${\mathit{\gamma }}^{*}$, that is, not for Afatinib. For Gemcitabine, we observe a small increase in performance (0.01 in AUC) for TCGA and no difference for HMF, while for Cetuximab, the prediction result still failed to reach significance. As a further check of the selected value of ${\mathit{\gamma }}^{*}$, we analyzed the properties of the consensus space obtained using ${\mathit{\gamma }}^{*}$. We observe a concentration of the offset contribution in the top consensus features and an increasing proportion of nonlinear terms contribution to lower order features (SI Appendix, Fig. 7C). The UMAP (45) projection of the consensus features shows a clear coclustering of cell lines and PDXs of the same tissue (SI Appendix, Fig. 7D).

Consensus Features between Cell Lines (GDSC) and Human Tumors Conserve Primary Tumor Information.

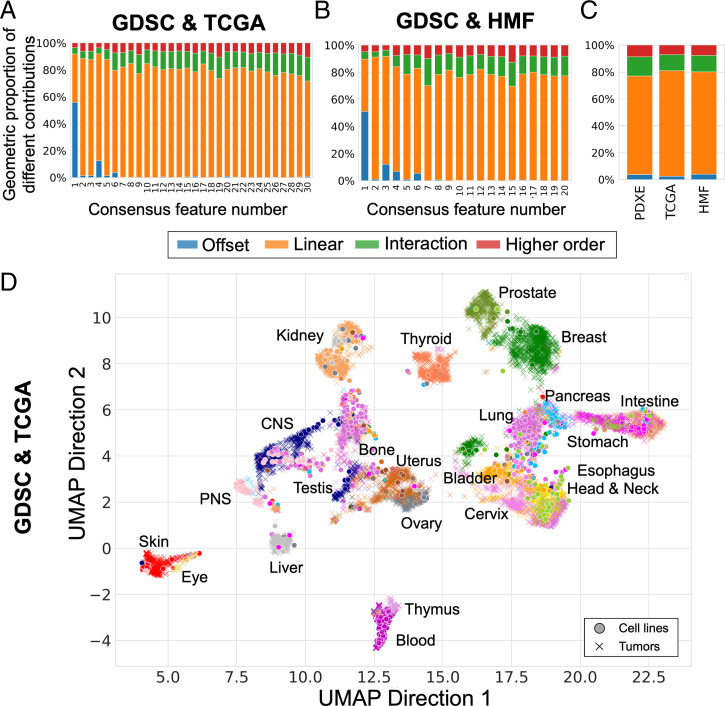
With the scaling factor ($\mathit{\gamma }$) calibrated on PDX models, we moved to the clinical setting to investigate domain adaptation between cell lines and two different human tumor datasets: primary tumors from TCGA and metastatic lesions from the HMF. We selected 30 consensus features in the genomics of drug sensitivity in cancer (GDSC)–TCGA analysis (SI Appendix, Fig. 9) and 20 in the GDSC–HMF analysis (SI Appendix, Fig. 10). We arrived at these numbers by first selecting NLPCs based on the inflection point of the cumulative eigenvalues and subsequently only retaining PVs with a similarity above 0.5. We observe that the consensus features computed between GDSC and TCGA (Fig. 3A) and between GDSC and HMF (Fig. 3B) show a concentration of offset and linearities in the top consensus features and overall the same proportion of nonlinearities as in the GDSC-to-Patient Derived Xenografts Encyclopedia (PDXE) analysis (Fig. 3C).

Fig. 3.

Pan-cancer consensus features between cell lines and tumors conserve tissue type information. We used cell lines (GDSC) as source data and compute two sets of consensus features with two different target datasets: primary tumors (TCGA, A and D) and metastatic lesions (HMF, B and E). (A) Proportion of linear and nonlinear contributions to each of the 30 GDSC-to-TCGA consensus features. (B) Proportion of linear and nonlinear contributions to each of the 20 GDSC-to-HMF consensus features. (C) Comparison of global contributions in the three analyses, that is, GDSC-to-PDXE, GDSC-to-TCGA, and GDSC-to-HMF. (D) UMAP plot of primary tumors (TCGA, 21 tissues) and cell lines (GDSC, 22 tissues) projected on the consensus features using the same parameters as selected in Fig. 2. The full legend for D and E is depicted in SI Appendix, Fig. 11.

In order to visualize the structure retained in the consensus space, we embedded our consensus scores into a two-dimensional space using UMAP (45). We observed that primary tumors cluster together based on their tissue type (Fig. 3D). Most cell lines cluster with the tumors from a similar tissue of origin. However, some groups of cell lines cluster together but away from the tumors with the same tissue of origin as observed in previous studies (37, 38). For example, there is a cell line cluster consisting of peripheral nervous system and bone cell lines that cocluster with central nervous system tumors. To quantify the degree of coclustering of cell lines and tumors, we compared distances between tumors and cell lines from similar and nonsimilar tissues and observed, as expected, a higher similarity between tumors and cell lines from the same tissue (SI Appendix, Fig. 11D). Metastatic lesions show a weaker clustering based on the primary tumor’s tissue of origin (SI Appendix, Fig. 11 A and E). This is not unexpected, as the expression profiles are derived from biopsy sites distant from the primary tissue. Of particular interest, we observe the existence of a hematopoietic cell line cluster that coclusters with metastatic samples from various biopsy sites. Most of these tumor samples (7 out of 12 samples) are lymph node metastases and most likely display a hematopoietic expression profile due to blood infiltration in the samples (SI Appendix, Fig. 11C).

Consensus Features Increase Transfer of Response Predictors from Cell Lines to Primary Tumors and Metastatic Lesions.

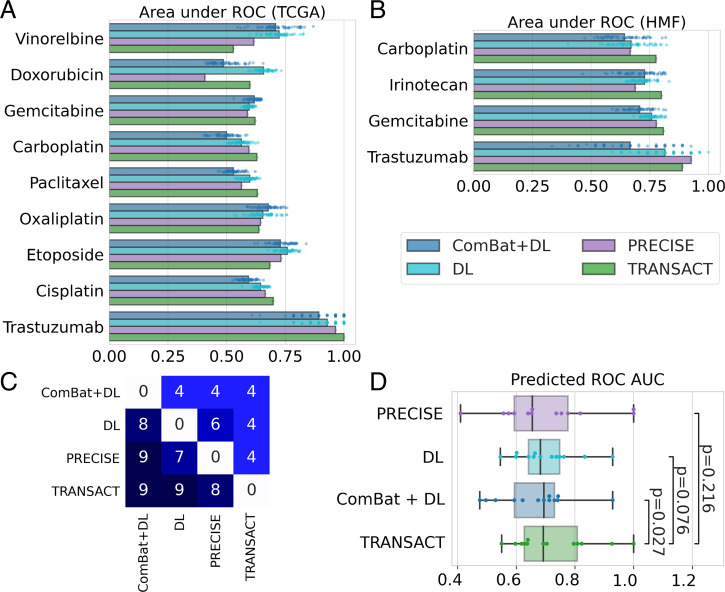
To further validate our approach, we transferred response predictors from cell lines to the TCGA and HMF collections of human tumors. First, we projected the GDSC and TCGA expression data onto the GDSC–TCGA consensus features. Then we trained, for each drug, a regression model using solely the cell line response data (measured as AUC). These drug-specific regression models were then used to predict response on the projected TCGA data for patients that received the target drug as monotherapy or in combination with other standard-of-care therapies (Dataset S2 and Methods). Finally, we compared the predicted patient responses to the known categorical clinical responses using a one-sided Mann–Whitney U test and computed the corresponding effect size. We trained models for 17 different drugs (Table 1). We compared the performance of TRANSACT to the performance obtained by four competing approaches (ElasticNet, DL, ComBat+DL, and PRECISE) (Table 1, Fig. 4A, and Methods). For the DL approaches (DL and ComBat+DL), we selected the architecture and hyper parameters for each drug by fivefold cross-validation on GDSC (Methods). We subsequently trained 50 models with different and independent initializations (Methods) and reported the median performance obtained on TCGA.

Table 1.

Results of TRANSACT compared to four competing approaches—ElasticNet, DL, ComBat ± DL, and PRECISE—for 17 drugs on TCGA

GDSC		TCGA			p-val [effect size] on TCGA
Drug	Samples	Drug	Samples		Elastic Net	DL	DL + ComBat	PRECISE	TRANSACT
			Resp.	NR.
Afatinib	800	Trastuzumab	16		0.089	0.034	0.034	0.026	0.016
			14	2	[0.82]	[0.93]	[0.93]	[0.96]	[1.00]
Bleomycin	856	Bleomycin	53		0.15	0.17	0.47	0.11	0.091
			47	6	[0.63]	[0.62]	[0.51]	[0.66]	[0.67]
Cetuximab	868	Cetuximab	19		0.12	0.52	0.45	0.45	0.077
			9	10	[0.67]	[0.50]	[0.52]	[0.52]	[0.70]
Cisplatin	764	Cisplatin	308		1.1E-6	2.0E-4	1.1E-2	2.2E-5	3.9E-7
			242	66	[0.69]	[0.64]	[0.59]	[0.66]	[0.70]
Cisplatin	764	Carboplatin	166		0.042	0.15	0.69	0.024	0.0035
			111	55	[0.58]	[0.55]	[0.48]	[0.59]	[0.63]
Cyclophosphamide	747	Cyclophosphamide	102		0.57	0.62	0.85	0.11	0.64
			96	6	[0.48]	[0.46]	[0.38]	[0.65]	[0.46]
Docetaxel	665	Docetaxel	102		0.62	0.30	0.73	0.78	0.11
			67	35	[0.48]	[0.53]	[0.46]	[0.46]	[0.58]
Doxorubicin	871	Doxorubicin	101		0.81	0.0048	0.52	0.99	0.054
			68	33	[0.45]	[0.66]	[0.50]	[0.32]	[0.60]
Etoposide	880	Etoposide	84		0.21	0.0030	0.005	0.0071	0.027
			73	11	[0.58]	[0.76]	[0.62]	[0.73]	[0.68]
5-Fluorouracil	801	Fluorouracil	186		0.22	0.70	0.79	0.82	0.35
			129	57	[0.54]	[0.48]	[0.46]	[0.46]	[0.52]
Gemcitabine	752	Gemcitabine	156		0.25	0.015	0.0052	0.029	0.0057
			75	81	[0.53]	[0.60]	[0.62]	[0.59]	[0.62]
Irinotecan	796	Irinotecan	25		0.81	0.39	0.757	0.54	0.46
			7	18	[0.39]	[0.54]	[0.41]	[0.49]	[0.52]
Oxaliplatin	724	Oxaliplatin	66		0.38	0.017	0.0059	0.028	0.035
			43	23	[0.52]	[0.66]	[0.69]	[0.64]	[0.64]
Paclitaxel	753	Paclitaxel	160		0.032	0.026	0.28	0.10	0.0042
			111	49	[0.59]	[0.60]	[0.53]	[0.56]	[0.63]
Pemetrexed	898	Pemetrexed	38		0.16	0.38	0.56	0.16	0.367
			18	20	[0.60]	[0.53]	[0.49]	[0.59]	[0.53]
Temozolomide	746	Temozolomide	96		0.56	0.34	0.51	0.59	0.19
			11	85	[0.49]	[0.54]	[0.50]	[0.48]	[0.58]
Vinorelbine	746	Vinorelbine	30		0.31	0.048	0.053	0.19	0.35
			23	7	[0.57]	[0.71]	[0.71]	[0.61]	[0.55]

For each drug, we train five predictors and compare in each scenario the predicted AUC to the known clinical response using one-sided Mann–Whitney U test. Samples were divided in two categories: Responders and Nonresponders (NR) (Methods). For each predictor, we report the P value and the effect size (area under the ROC, effect size associated with the Mann–Whitney U test) in brackets. Italic cells correspond to significant associations (P < 0.05). Bold cells correspond to significant associations with the largest effect size across the five methods.

Fig. 4.

Consensus features improve response prediction in patients. (A) We used consensus features computed between the GDSC and each tumor dataset to train a predictor for 17 drugs on TCGA and six drugs on HMF using only GDSC drug response. We then predicted the continuous response in patients for each drug and compared this predicted value to the observed clinical response using a one-sided Mann–Whitney U test (Tables 1 and 2). We performed the same prediction tasks using three state-of-the-art approaches (ComBat+DL, DL, and PRECISE), and we summarized the results in a boxplot for TCGA (A) and HMF (B), restricting to the drugs in which at least one method reaches a significant prediction. For ComBat+DL and DL, we display the results obtained using 50 different random initializations. (C) Table of performance comparing each method; to read as “method on y-axis obtained higher AUC than method on x-axis,” for example, “PRECISE obtained higher AUC than ComBat+DL for nine drugs.” (D) Comparison of ROC AUCs obtained with each of the four methods for the 13 drugs with significant prediction. P values computed using a one-sided Wilcoxon paired rank-sum test.

ElasticNet and PRECISE obtain significant associations (bold entries in Tables 1 and 2) for three and six drugs, respectively, but neither approach ever outperforms (i.e., achieves a larger AUC) all other approaches. DL and ComBat+DL achieve significant associations for eight and five drugs, respectively—however, both approaches outperform all others (red, bold entries in Tables 1 and 2) for only three and one drug, respectively. In contrast, TRANSACT achieves significant associations for seven drugs and obtains a larger AUC than all other approaches for five drugs.

For both deep learning approaches, we observe an important dependency on the network initialization (Fig. 4A). More importantly, we observe no correlation between the training error achieved on the source domain (cell lines) and the prediction accuracy on the target domain (human tumors), making it impossible to select a proper initialization solely based on the source domain performance (SI Appendix, Figs. 12A and 13A). The results obtained with TRANSACT, on the contrary, do not depend on a random initialization.

For the HMF data, we repeated the steps above while employing the GDSC–HMF consensus features as well as the HMF and GDSC expression and response data. We trained models for six drugs (Table 2 and Fig. 4B). Across all approaches, we observe a significant association between the predicted AUC and clinical responses for four of the six drugs (Table 2 and SI Appendix, Fig. 14). PRECISE reaches significance for two drugs, whereas ElasticNet, DL, and Combat+DL reach significance for a single drug. TRANSACT outperforms PRECISE on three drugs, and ComBat+DL, DL, and ElasticNet on four drugs. TRANSACT achieves a borderline nonsignificant association for Paclitaxel but achieves an effect size of 0.7. In contrast, all competing approaches fail to achieve any association with effect sizes around 0.5, corresponding to random chance. Also, for the HMF cohort, deep learning approaches show a strong dependency on parameter initialization (Fig. 4B) and a lack of correlation between source and target domain performance (SI Appendix, Figs. 12B and 13B).

Table 2.

Results of TRANSACT compared to four competing approaches—ElasticNet, DL, ComBat ± DL, and PRECISE—for six drugs on HMF

GDSC		HMF				p-val [effect size] on HMF
Drug	Samples	Drug	Samples			Elastic Net	DL	DL + ComBat	PRECISE	TRANSACT
			PR	SD	PD
Afatinib	800	Trastuzumab	25			0.18	0.069	0.13	0.021	0.032
			9	11	3	[0.70]	[0.81]	[0.74]	[0.93]	[0.89]
Irinotecan	796	Irinotecan	67			0.060	0.060	0.082	0.10	0.020
			5	34	25	[0.73]	[0.75]	[0.71]	[0.69]	[0.80]
Cisplatin	764	Carboplatin	64			0.23	0.051	0.054	0.59	0.0045
			22	27	12	[0.58]	[0.68]	[0.67]	[0.67]	[0.78]
5-Fluorouracil	801	5-Fluorouracil	61			0.065	0.14	0.14	0.21	0.24
			10	33	18	[0.68]	[0.63]	[0.63]	[0.59]	[0.58]
Paclitaxel	753	Paclitaxel	45			0.56	0.30	0.34	0.39	0.061
			14	19	9	[0.48]	[0.43]	[0.43]	[0.53]	[0.70]
Gemcitabine	752	Gemcitabine	50			0.039	0.019	0.039	0.0089	0.0042
			22	17	9	[0.71]	[0.74]	[0.71]	[0.78]	[0.81]

For each drug, we train five predictors and compare in each scenario the predicted AUC to the known clinical response using one-sided Mann–Whitney U test between PR and PD (Methods). For each predictor, we report the P value and the effect size (area under the ROC, effect size associated with the Mann–Whitney U test) in brackets. Italic cells correspond to significant associations (P < 0.05). Bold cells correspond to significant associations with the largest effect size across the five methods.

In summary, across the 23 drug prediction challenges on the TCGA and HMF cohorts, 13 lead to a significant prediction for at least one method. Among these, TRANSACT performs best, reaching significance in 11 challenges, followed by DL and ComBat+DL reaching significance in nine and six challenges, respectively. TRANSACT yields larger AUCs than DL, ComBat+DL, and PRECISE for nine, nine, and eight drugs respectively (Fig. 4C). It should be noted that only three of these comparisons are significant based on the bootstrap CIs of the AUC (Dataset S2). Nevertheless, when comparing methods in a paired fashion across the 13 drugs in which at least one method reaches significance, we observe that AUCs obtained by TRANSACT are significantly larger than the AUCs obtained by ComBat+DL (P = 0.021, one-sided paired Wilcoxon rank-sum test) (Fig. 4D). When comparing TRANSACT to DL or PRECISE, we observe larger obtained median AUCs, but these differences are not significant (P = 0.07 and P = 0.21, respectively).

Interpretability of Consensus Features Confirms Known Mechanisms for Targeted Therapies and Unveils Potential Biomarkers of Sensitivity for Cytotoxic Drugs.

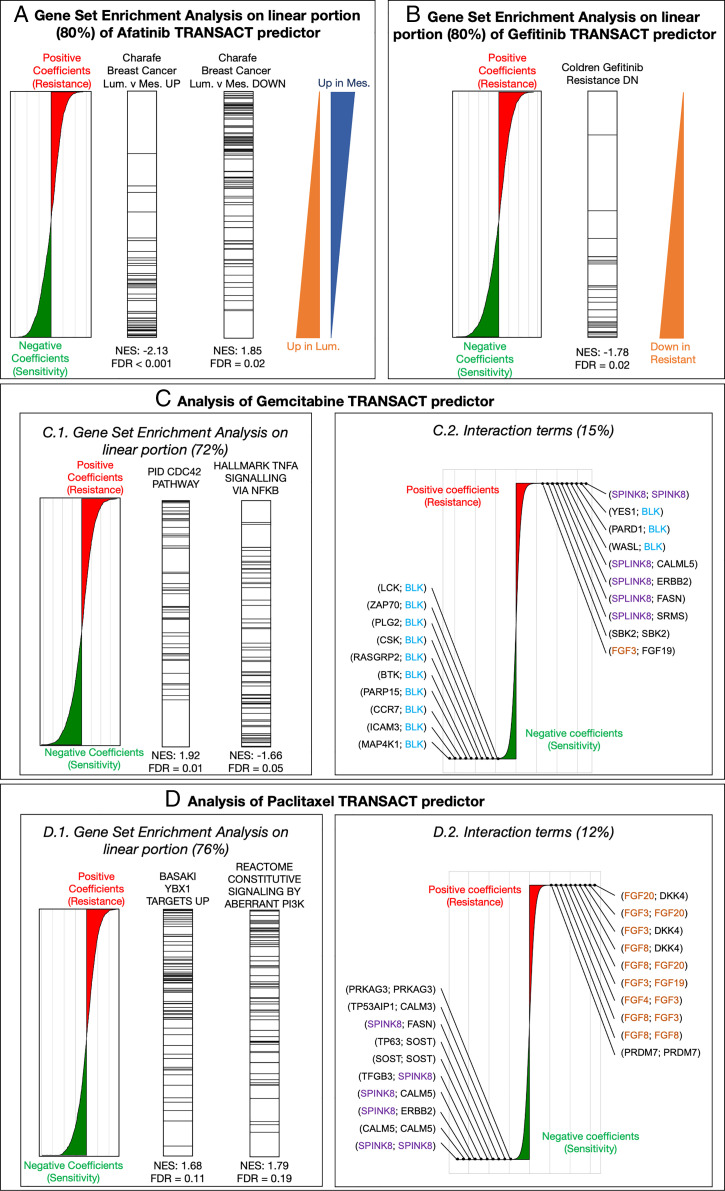
Finally, we made use of the interpretability of our approach to mechanistically validate our predictors (Methods). We first validated targeted therapies with documented modes of action. We started with the TRANSACT predictor of response for Afatinib, a small molecule inhibitor of the EGFR family, which includes HER2 (Fig. 5A). We performed a gene set enrichment analysis of the linear terms that constitute 80% of the predictor (Dataset S3). Most enriched gene sets are related to breast cancer subtypes as defined by Charafe and colleagues (46) in which, contrary to the definition based on the intrinsic breast cancer subtypes, the Luminal subtype contains both ER+ and HER2+ tumors. The top ranked gene set among the genes associated with sensitivity (genes with a negative coefficient in the predictor) are genes associated with the “luminal” subtypes (false discovery rate [FDR] < 0.001). Conversely, genes associated with resistance (genes with a positive coefficient in the predictor) show enrichment for the “mesenchymal” molecular signatures, shared by basal and mesenchymal subtypes. This corresponds with HER2-negative samples, which is in line with our expectation, as an absence of the drug target would indicate lack of response. Similarly, in the TRANSACT response predictor for Gefitinib (EGFR inhibitor), the genes constituting the linear portion and associated with sensitivity (negative predictor coefficients) show an enrichment for genes down-regulated in Gefitinib-resistant tumors (Fig. 5B and Dataset S4). Interestingly, two gene sets related to breast cancer subtypes also show a significant enrichment in the negative coefficients of the predictor, linked to sensitivity: “Luminal versus Basal Down” (normalized enrichment score [NES] = −1.94, FDR < 0.001) and “Luminal versus Mesenchymal Up” (NES = −1.85, FDR = 0.004). The first gene set contains EGFR, the target of Gefitinib, implying that high levels of EGFR are, as one would expect, associated with sensitivity. The association of the second set with Gefitinib response is supported by the fact that mesenchymal tumors have been shown to be resistant to EGFR inhibition (47). Further support is provided by the presence of two genes in the leading edge of the enrichment: ERBB2 and PTPN6 (SHP-1) (Dataset S4). ERBB2 is a member of the EGFR family, which heterodimerizes with EGFR, resulting in the activation of the EGFR pathway. Such cells tend to be sensitive to the inhibition of the pathway, that is, to Gefitinib treatment. PTPN6, on the other hand, inhibits the PI3K pathway (48, 49), the activation of which is a known resistance mechanism to Gefitinib (50). Therefore, high levels of PTPN6 prevents the pathway from being activated to circumvent Gefitinib treatment effects.

Fig. 5.

Interpretability of TRANSACT consensus features recapitulates modes of action for Afatinib and Gefitinib and highlights mechanisms of sensitivity and resistance to Gemcitabine and Paclitaxel. (A) For the Afatinib (HER-2 protein kinase inhibitor) response model trained on GDSC samples projected on GDSC-to-TCGA consensus features, we show the contribution of each gene to the predictor. (Left) Positive (negative) weights in the predictor indicate that high (low) expression of the genes leads to resistance (sensitivity) represented by larger (smaller) AUCs. We performed a PreRanked gene set enrichment analysis on these weights and highlight genes associated to two significantly enriched gene sets: “Charafe […] Luminal versus Mesenchymal UP” (Center Left) and “Charafe […] Luminal versus Mesenchymal DOWN” (Center Right). The two triangles on the right illustrate these two gene set distributions. (B) Interpretation of the linear part of the Gefitinib (EGFR inhibitor) model. We display gene weights ordered by contribution (Left) and the ranks of genes known to be down-regulated in Gefitinib-resistant tumors (Right). (C) Interpretation of Gemcitabine predictor. (Left) We display the positions of genes associated to two significantly enriched gene sets: “CDC42 pathway,” associated to positive weights (resistance), and “TNF-$\alpha$ signaling,” associated to negative weights (sensitivity). (Right) Interaction terms make 15% of Gemcitabine predictor. We show the distribution of their weights annotated with the 10 largest weights (resistance) and 10 smallest weights (sensitivity). (D) Interpretation of Paclitaxel predictor. (Left) We display the positions of genes associated to two significantly enriched gene sets, both to resistance: “Basaki YBX1 target UP” and “constitutive signaling by PI3K-aberrant signaling.” (Right) Interaction terms for Paclitaxel that make 12% of the predictor alongside the top 10 resistant and top 10 sensitive interactions.

Cytotoxic drugs such as Gemcitabine or Paclitaxel have complex modes of actions involving different pathways, the crosstalk between which remains challenging to understand. Since the predictions of these two drugs showed a significant association in both PDXs and patients, we set out to interpret the mechanisms of sensitivity or resistance inferred by our predictor. In Gemcitabine (Dataset S5), we observe that overexpression of the CDC42 pathway is a significant marker of resistance (FDR = 0.012, Fig. 5C, Left) together with pathways linked to microtubule formation and cell migration (SI Appendix, Fig. 15), both known to be promoted by CDC42 (51). Together, these enriched pathways highlight CDC42 overexpression as a potential mechanism of Gemcitabine resistance, which suggests the use of CDC42 inhibitors (52, 53) for Gemcitabine-resistant tumors. Another interesting finding is the significant enrichment of TNF-$\mathit{\alpha }$ signaling in the genes associated with sensitivity (FDR = 0.046) (Fig. 5C, Left). A clinical trial has shown that coadministration of TNF with gemcitabine improves patient survival and further inhibits tumor growth (54), lending additional credence to this finding. Last, we observe a concentration of sensitive interactions involving BLK, a proapoptotic Src-proto-oncogene involved in B cell signaling and differentiation (Fig. 5C, Right). Since hematopoietic cell lines respond better to Gemcitabine, these interactions can either act as a tissue-type marker or could potentially represent a sensitive pathway.

Finally, we looked for enriched pathways in the Paclitaxel predictor (Fig. 5D, Left and Dataset S6) and observed three potential mechanisms of resistance. We first observe that in the linear terms, the genes associated with resistance are significantly enriched in genes linked to the silencing of YBX1 (55) (FDR = 0.106), a gene associated with proliferation in certain tumor types (56). In ovarian cancer, YBX1 has been shown to regulate ABCB1 expression levels, a gene related to Paclitaxel resistance (57–61). Our pan-cancer analysis therefore further supports the role of drug transporters in Paclitaxel resistance. Second, we observe a significant enrichment in genes associated with resistance for PI3K activation (FDR = 0.18), which is corroborated by the observed activation of the PI3K/AKT/mTOR signaling pathway in Paclitaxel-resistant cancer cells (62, 63). Moreover, a recent investigation suggests that PI3K catalytic subunits can regulate ABCB1 expression (64). Finally, when it comes to the nonlinear part, we observe a concentration of fibroblast growth factor interactions in the nonlinearities associated with resistance, in particular FGF3, FGF20, and FGF8 and FGF4 (Fig. 5D, Right and Dataset S6). This behavior, although suggested by previous studies (65, 66), is all the more interesting, as cell lines do not contain any microenvironment that would elicit such resistance.

Discussion

We introduced an approach to integrate preclinical and clinical data in a fully unsupervised way. Our approach geometrically aligns sample-to-sample similarity matrices and extracts directions of important variations for both datasets without requiring any sample-level pairing. By performing a geometrical alignment instead of a direct distribution comparison, our approach limits the effect of a potential sample selection bias. This geometrical alignment is implicitly performed in a space induced by our similarity function, which enables the integration of various assumptions regarding nonlinearities in the system. Although we restricted ourselves to a single Gaussian similarity function for all drugs, designing similarity functions that incorporate a wide range of prior knowledge, specifically tailored for each drug, is a potentially promising avenue. Learning the similarity matrix, for example, using multiple kernel learning (67) or deep learning methods such as variational autoencoders (68), may also help increase performance.

TRANSACT compares directions computed using kernel PCA, but our approach can be extended to other basis expansion methods by modulating the way the coefficients ${\mathit{\alpha }}^s$ and ${\mathit{\alpha }}^t$ are computed. More generally, our method is versatile, generalizable, and can be applied beyond the scope of our study, for example, to integrate single-cell sequencing data.

We showed that the consensus features can be used to build translatable predictors of drug response. Although we do not require a strong covariate shift assumption as in a previous study (69), we do assume the functions modeling the response from these consensus features follow the same monotonicity in preclinical models and human tumors. This assumption, albeit reasonable, may be questioned.

In this study, we limited ourselves to gene expression. Making use of other genomics levels—for example, mutations, copy number, methylation, and chromatin accessibility—may help refine the prediction by providing additional signal. The integration of our approach with multiomics integration strategies (70, 71) may offer a solution to the translation of multiomics signatures.

Finally, we evaluated the predictors on a variety of drug prediction tasks in human data that are quantitatively far greater and mechanistically more diverse than prior work. We were able to predict response in patients that received a particular treatment, either as monotherapy or in combination with other therapies, even though the cell line predictors were trained on monotherapies only. We convincingly demonstrate that response predictions are now substantially better than random guessing for a number of therapies of high clinical importance, such as platinum-based chemotherapies, gemcitabine and paclitaxel. In addition, we include results of a new dataset from HMF, which provides independent validation of performance on TCGA data. Intriguingly, none of the methods were able to predict the human responses to cyclophosphamide. However, no effect in vitro has been observed for this prodrug, which might be considered as a negative control for the approaches.

Although our results are encouraging, we recognize that the drug response prediction models we present here are still far from clinical applicability. For example, one would never withhold a standard-of-care therapy based on the accuracy with which the presented predictors can identify nonresponsive patients. However, a more likely scenario in which such predictors could become useful sooner is in providing guidance in drug repurposing for patients that have become refractory to all standard-of-care treatments. To reach accuracies that are acceptable for clinical application, we anticipate that large-scale model system drug (combination) screens could provide the required training samples sizes.

The recent advent of immunotherapies calls for methods with the ability to predict the clinical response from model systems. This requires model systems capable of mimicking the action of the immune system and screening technologies able to measure the response for large panels. We believe that our approach can be extended to such problems once data are made available.

Methods

Public Data Download and Preprocessing.

GDSC dataset, download, and processing.

We made use of the GDSC1000 cell line panel (14), which contains complete molecular profiles for 1,049 cell lines (SI Appendix, Fig. 3). Gene expression is provided in the form of both read counts and fragments per kilobase per million (FPKM). For both settings, we normalized the dataset for library size and potential sampling artifacts using trimmed mean of M values (TMM) (72) and log transformed the adjusted read counts (73, 74). Finally, we performed a gene-level mean centering and standardization. When comparing GDSC to PDXE, we employed the FPKM data; in the two other analyses (GDSC to TCGA and GDSC to HMF), we made use of the read count data. In this way, FPKM and read count were never used at the same time.

Novartis PDXE dataset, download, and processing.

We made use of the NIBR PDXE dataset for patient-derived xenografts (15), which contains the gene expression profiles of 399 PDXs (SI Appendix, Fig. 4). Gene expression is provided in the form of FPKM. We normalized the dataset using TMM (72) and log transformed the adjusted read counts (73, 74). Finally, we performed a gene-level mean centering and standardization.

TCGA dataset, download, and processing.

We made use of the TCGA dataset for analyzing human biopsies (75), which comprises 10,347 human tumors (SI Appendix, Fig. 5). Gene expression is provided in the forms of both read counts and FPKM, and we used the same preprocessing pipeline as for GDSC. Response data have been obtained from Ding et al. (76). Following Ding et al., for each drug, we consider the response to patients who were administered a particular drug either as monotherapy or in combination with other drugs.

HMF dataset download and processing.

We validated our approach on a cohort of 1,049 patients provided by the HMF (SI Appendix, Fig. 6A) (77, 78). Gene expression was measured for each metastatic sample prior to the indicated drug regimen. We used MultiQC for quality control (79), salmon v1.0.0 for alignment to reference transcriptome (80), and finally edgeR for gene-level quantification (81). A comparison with results obtained using STAR (82) and featureCounts (83) shows high degree of concordance (SI Appendix, Fig. 6D), and we used this comparison to refine our filtering. Read counts were then processed using the same pipeline as in GDSC and TCGA.

The drug response was measured in 802 unique metastatic samples using the response evaluation criteria in solid tumors (RECIST) criteria. The response was measured differently for each patient (SI Appendix, Fig. 6B), with most patients having one single measure of response around 10 to 15 wk after treatment started (SI Appendix, Fig. 6C). Since we are interested in the response of the drug given the molecular characterization measured, we considered for each patient the first response after treatment. Since most drugs are administered in combination, we considered for each drug all the patients that received it, whether in combination with other drugs or as monotherapy. For instance, in the case of Gemcitabine, we predicted the drug response for all patients that received Gemcitabine as part of their treatment strategies.

Measure of Drug Response.

In our different analysis, we rely on drug response measurements, either to train a predictor (GDSC) or to validate it (PDXE, TCGA, and HMF). For cell lines (GDSC), drug response is measured as AUC. For PDX, drug response is measured as best average response, which corresponds to the relative variation of tumor volume induced by a certain treatment. For both AUC and best average response, large values are associated with resistance. For TCGA and HMF, clinical responses have been measured using the RECIST criteria (84). Based on various metrics, patients get assigned to one of the following four groups: Complete Response (CR), Partial Response (PR), Stable Disease (SD), and Progressive Disease (PD). Following the division used in previous works (21, 23), we divide TCGA patients into two categories: Responders (CR and PR) and Nonresponders (SD and PD). For HMF, we discriminate between each possible couple: PR versus PD, PR versus SD, and SD versus PD. Since only a couple of patients showed a complete response, we did not consider these patients.

Mathematical Notation.

We denote by $p$ the number of genes. We consider one source dataset ${\mathrm{X}}_s=\left\{x_1^s,\dots , x_{n_s}^s\right\}\subset {\mathrm{ℝ}}^p$ and one target dataset ${\mathrm{X}}_t=\left\{x_1^t,\dots , x_{n_t}^t\right\}\subset {\mathrm{ℝ}}^p$ with corresponding source and target data matrices $X_s\in {\mathrm{ℝ}}^{n_s\times p}$ and $X_t\in {\mathrm{ℝ}}^{n_t\times p}$.

We consider a similarity function $K$—also called kernel function—that assigns to two samples a scalar value that is large for similar samples and small for dissimilar samples. In this work, we assume the kernel to be positive definite (SI Appendix, Reproducing Hilbert Space), and specifically use the following two kernels:

• ▪Linear kernel: $K^{\mathit{linear}}\left(x,y\right)=x^{T}y$.
• ▪Gaussian kernel or radial basis function: $K_{\gamma }^{\mathit{rbf}}(x,y)=\exp (-\gamma {||x-y||}^2),$ with $\mathit{\gamma }>0$.

We denote by $K_s$ the matrix of similarity between source samples, $K_t$ between target samples, and $K_{st}$ the matrix of similarity between source and target (SI Appendix, Centered Kernel Matrices). These similarity matrices are then mean centered (SI Appendix, Centered Kernel Matrices), yielding matrices ${\tilde{K}}_s$, ${\tilde{K}}_t$ and ${\tilde{K}}_{st}$.

Kernel PCA by Eigendecomposition of Centered Kernel Matrix for Capturing Directions of Principal Variance.

Using the so-called kernel trick (83) (SI Appendix, Reproducing Hilbert Space), the similarity matrices from K_s, K_t and K_st can be seen as sample covariance matrices and therefore decomposed to compute principal components inside the embedded space, a procedure known as kernel PCA (86). We perform kernel PCA on source and target data independently to compute $d_s$ and $d_t$ principal components, respectively. Kernel PCA on the source dataset consists of an eigendecomposition of the matrix ${\tilde{K}}_s$, yielding ${\mathit{\alpha }}^s\in {\mathrm{ℝ}}^{d_s\times n_s}$, while kernel PCA on the target dataset decomposes $\widetilde{K_t}$, yielding ${\mathit{\alpha }}^t\in {\mathrm{ℝ}}^{d_t\times n_t}$ (SI Appendix, Nonlinear Source and Target Principal Components).

Comparing and Aligning Preclinical and Tumor Nonlinear Principal Components.

Similarly to the “cosine similarity matrix” in other related works (25, 29), we define the nonlinear cosine similarity matrix ${\mathit{M}}^K$ as the matrix that geometrically compares the source NLPCs to the target NLPCs (SI Appendix, Cosine Similarity Matrix). This matrix can be computed as follows (SI Appendix, Computation of Cosine Similarity Matrix):

$$\begin{array}{c}{\mathit{M}}^K={\alpha }^s{\tilde{K}}_{st}{\alpha }^{t^T}= {\alpha }^s{C}_{n_s}{K}_{st}{C}_{n_t}{\alpha }^{t^T}.\end{array}$$ [1]

In a first step of our domain adaptation approach, we use the matrix ${\mathit{M}}^K$ to align NLPCs, yielding nonlinear PVs $s_1,., s_d$ for the source and $t_1,., t_d$ for the target domains, with $d=\min \left(d_s, d_t\right)$ (SI Appendix, Kernel Principal Vectors). These PVs are pairs of vectors: one linear combination of source NLPCs and one linear combination of target NLPCs ordered by decreasing similarity with the first pair being the most similar. The computation of these PVs relies on the singular value decomposition (87) of ${\mathit{M}}^K$, ${\mathit{M}}^K= {\mathit{\beta }}^s\text{Σ}{\mathit{\beta }}^t{}^T,$ that helps us define the source and target sample importance loadings ${\mathit{\rho }}^s$ and ${\mathit{\rho }}^t$ as follows (SI Appendix, Principal Vector Sample Importance Loadings):

$$\begin{array}{c}{\rho }^s={\beta }^s{}^T{\alpha }^s \mathit{and} {\rho }^t= {\beta }^{t^T}{\alpha }^t.\end{array}$$ [2]

Interpolation between Kernel PVs for Balancing Effect of Source and Target.

Each pair of PVs contains two vectors that are geometrically similar. The projection on them will create two highly correlated covariates that would not be optimal for subsequent statistical treatment. In order to compute one vector out of each pair, we interpolate between the source and the target PV within each pair (SI Appendix, Geodesic Flow between Principal Vectors). For the $k^{th}$ PV, the interpolation is modulated by a coefficient ${\mathit{\tau }}_k$ that ranges between 0, when the interpolation returns the source PV, and 1, when the interpolation returns the target PV. To compute this interpolation, we need two functions, $\text{Γ}\left(\text{τ}\right)={\left[{\text{Γ}}_1\left({\mathit{\tau }}_1\right), .,{\text{Γ}}_d\left({\mathit{\tau }}_d\right)\right]}^T$ and $\text{ξ}\left(\text{τ}\right)={\left[{\text{ξ}}_1\left({\mathit{\tau }}_1\right), .,{\text{ξ}}_d\left({\mathit{\tau }}_d\right)\right]}^T$ defined as (ref. of SI Appendix, Angular Interpolation Function).

For a set of $d$ interpolation coefficients $[{\tau }_1,., {\tau }_d]$, we compute the projection of source and target datasets $F\left(\mathit{\tau }\right)\in R^{\left(n_s+n_t\right)\times d}$ as follows (SI Appendix, Theorem Supp. 6.6):

$$\begin{array}{c}F\left(\tau \right)=\left[\begin{array}{cc}{K}^s& K^{st}\\ K^{ts}& K^t\end{array}\right]\left[\begin{array}{cc}{C}_{n_s}& 0\\ 0& C_{n_t}\end{array}\right]\left[\begin{array}{cc}{\rho }^s{}^T& 0\\ 0& {\rho }^t{}^T\end{array}\right]\left[\begin{array}{c}\mathrm{\Gamma }\left(\tau \right)\\ \xi \left(\tau \right)\end{array}\right].\end{array}$$ [3]

Such an interpolation between PVs balances the effect of source and target datasets. We prove that, in the case of a linear kernel, our interpolation scheme is equivalent to the one from previous approaches (27, 88) (SI Appendix, Equivalence with Geodesic Flow Kernel).

Within each pair of PVs, we select one intermediate representation in which the source and target projections match the most. For the $k^{th}$ PV pair, we compare the source and target projected data using a Kolmogorov–Smirnov statistic and select the interpolation coefficient ${\tau }_k^{*}$ in which the statistic is minimal. We obtain a set of optimal interpolation coefficients ${\mathit{\tau }}^{*}\in {\left[0,1\right]}^d$ when, for each PV, source and target influence are balanced. We call the corresponding vector consensus features. These consensus features show the minimal difference between source and target domain, a theoretical necessary condition for domain adaptation (89).

Prediction Using ElasticNet.

In order to predict drug response, we use ElasticNet regression (90). ElasticNet is a linear model that imposes two penalties on the coefficients to predict an ${\ell }_1$ penalty that leads to a sparse model and an ${\ell }_2$ penalty that jointly shrinks correlated features.

We chose ElasticNet first because it has repeatedly been shown in the drug response prediction literature to give equivalent, if not better, predictive performance compared to complex models (16, 18, 41). Using a linear classifier limits the complexity and therefore makes the transfer more robust in practice.

Taylor Expansion of the Similarity Function for Interpretability of the Model.

In the case of radial basis function, we perform a PCA in an infinite-dimensional feature space. Although this space cannot be analytically computed, it can be approximated using a Taylor expansion (91) (SI Appendix, Gene Set Enrichment Analysis of Consensus Features). For the q-th consensus feature, we differentiate three kinds of contributions (SI Appendix, Offset, Linear and Interaction Terms for Consensus Features):

• -Offset ${\mathcal{O}}_q$: a Gaussian term that models the squared depth.
• -Linear contributions ${\left({\mathcal{L}}_{q,j}\right)}_{1\le j\le p}:$ a linear term resembling the expression of one gene.
• -Interaction terms ${\left({\mathcal{I}}_{q,j,k}\right)}_{1\le j,k\le p}$: an interaction term that expresses the product of two genes.

These contributions can be computed from sample importance loadings of consensus features (SI Appendix, Prop. Supp. 7.7). We consider the contributions’ sum of squares as a geometrical proportion since these sum up to one (SI Appendix, Def. Supp. 7.8).

In order to look for enrichment in a particular consensus feature, we look for the enrichment of particular gene sets (92). Specifically, for the linear contribution, we compute the loading of all linear terms (SI Appendix, Equation Supp. 48) corresponding each to one gene. We then use these gene scores to perform a preranked gene set enrichment analysis with 1,000 permutations and use a threshold of 20% for FDR. Since these loadings correspond to an Euclidean geometric proportion, we used a squared statistic to compare them.

Comparison to Competing Approaches.

We compare TRANSACT to four different approaches. The two first approaches consist in applying a regression model trained on a source dataset to a target dataset without any correction; we use one linear ElasticNet model (referred to as ElasticNet) and a nonlinear neural network model (referred to as DL). In both cases, we perform a grid search fivefold cross-validation on cell lines to select the model with the best performance: on ElasticNet, we vary the ${\ell }_1$ ratio and the total regularization; on DL, following the protocol from Sakellaropoulos et al. (21), we use a hyperbolic tangent activation function while varying the global network structure, the ${\ell }_2$ penalty, and the input and output dropout levels (Dataset S7).

The other two approaches first correct the signal and then train a regression model. The third approach (referred to as ComBat+DL) reproduces the approach from Sakellaropoulos et al. (21) by first performing a ComBat technical batch effect correction between source and target and then applying a neural network on the corrected signal, similar to DL (Dataset S8). The last competing approach, referred to as PRECISE, consists of using a linear similarity function followed by an ElasticNet model, which is equivalent to PRECISE (SI Appendix).

For the two deep learning approaches, we first performed cross-validation on the source dataset (with or without correction) to select the hyper parameters and the network structures with the largest predictive performance. We then reinitialize the network and train it on the complete GDSC dataset.

In all comparisons, receiver operating characteristic (ROC) curves and areas were computed using the pROC package (93). The 95% CIs were computed using the “bootstrap” submethod with 1,000 samplings with stratification.

Data Availability

TRANSACT is available as a Python 3.6 module (https://github.com/NKI-CCB/TRANSACT). All our experiments are reproducible and use state-of-the-art libraries (94–99) (https://github.com/NKI-CCB/TRANSACT_manuscript). The dataset(s) supporting the conclusions of this article are available in the “download_data” repository of the aforementioned GitHub page, except for the HMF data, which is freely available for academic research through an access-controlled mechanism (see https://www.hartwigmedicalfoundation.nl/applying-for-data/ for details and request procedures). The gene and interaction weights obtained for the four studied predictors (Fig. 5) are available in SI Appendix and Datasets S3–S6.