Twenty-three–millisecond electron spin coherence of erbium ions in a natural-abundance crystal

A scheelite crystal with residual concentration of erbium is cooled down to 10 mK, yielding a record spin coherence time of 23 ms.

Abstract

Erbium ions embedded in crystals have unique properties for quantum information processing, because of their optical transition at 1.5 μm and of the large magnetic moment of their effective spin-1/2 electronic ground state. Most applications of erbium require, however, long electron spin coherence times, and this has so far been missing. Here, by selecting a host matrix with a low nuclear-spin density (CaWO₄) and by quenching the spectral diffusion due to residual paramagnetic impurities at millikelvin temperatures, we obtain a 23-ms coherence time on the Er³⁺ electron spin transition. This is the longest Hahn echo electron spin coherence time measured in a material with a natural abundance of nuclear spins and on a magnetically sensitive transition. Our results establish Er³⁺:CaWO₄ as a potential platform for quantum networks.

INTRODUCTION

Future quantum networks will require coherent interfaces between optical photons and other long-lived degrees of freedom or processing units. Trivalent erbium ions (Er³⁺) embedded in a crystal are uniquely suited for this task. They have an optical transition at 1.5 μm that is well suited for fiber-based telecommunication (1). Their electronic ground state also forms an effective spin-1/2 with a large magnetic moment, which can couple to other quantum systems such as superconducting circuits or nuclear spins (2). Thanks to these properties, they may be used for optical and microwave quantum memories (2, 3), as well as optical-to-microwave coherent conversion (4, 5) making it possible, for instance, to interface distant superconducting quantum processors. These potential applications require a long electron spin coherence time (for the memory) and a narrow electron spin linewidth (for the optical-microwave conversion), none of which have been so far reported for erbium.

Dilute paramagnetic impurities in a crystal lose phase coherence by interacting with the surrounding fluctuating magnetic moments of other paramagnetic species and nuclear spins of the host matrix. To obtain long coherence times, it is thus beneficial to use crystals that have minimal concentrations of paramagnetic impurities and a low nuclear-spin density. For instance, Hahn echo coherence times close to 1 s were obtained with low-doped phosphorus donor spins in a chemically pure silicon crystal that was isotopically enriched in the nuclear spin–free ²⁸Si isotope (6).

However, host matrices for rare-earth ions (REIs) are often based on yttrium, such as Y₂SiO₅ (YSO) and YVO₄, and tend to have high residual REI paramagnetic impurities due to the chemical similarity among rare-earth elements. Moreover, Y has only one natural isotope with nuclear spin I = 1/2 in 100% abundance, so it cannot be isotopically enriched to suppress nuclear magnetic noise. Therefore, it has been difficult to achieve long coherence times with magnetically sensitive electron-spin transitions in these materials. Whereas Hahn echo coherence times up to 4 ms have been measured on the optical transition of Er³⁺:YSO (7, 8), Hahn echo electron spin coherence times no greater than 10 μs were reported for Er³⁺ ions in Y-based materials (3) because of their high first-order magnetic sensitivity reaching up to 200 GHz/T. For this reason, most demonstrations of long spin coherence in yttrium-based matrices have relied on magnetically insensitive electron-spin transitions such as zero-first-order Zeeman (ZEFOZ) or clock transitions (9–11). Although such approaches have demonstrated coherence times up to 5 ms in Yb³⁺:YSO and 2 s in Bi:Si (12, 13), the required transition frequencies are often highly constrained, leading to potential incompatibility with quantum technologies that require tuneable or broadband microwave transitions. In all these systems, dynamical decoupling can be used to further extend the coherence time, at the expense of more complex pulse sequences (14–16).

Here, we use a non–yttrium-based crystal, namely, calcium tungstate (CaWO₄), as the host matrix for Er³⁺, and demonstrate long electron spin coherence times without having to resort to ZEFOZ transitions or isotopic purification. Most nuclei in CaWO₄ have no spin. Only the ¹⁸³W isotope of tungsten (14% natural abundance) contributes substantially to magnetic noise, with nuclear spin I = 1/2 and a relatively low gyromagnetic ratio of 1.8 MHz/T. This results in one of the lowest nuclear magnetic moment densities among natural-abundance crystals, leading to recent predictions that a Hahn echo electron spin coherence time of 20 ms should be achievable in this matrix (17). To characterize spin coherence, we rely throughout this article on the Hahn echo pulse sequence, because its widespread use enables direct comparison with other spin systems and materials.

Calcium tungstate has a tetragonal body-centered structure with lattice constants a = b = 0.524 nm and c = 1.137 nm (as shown in Fig. 1A), in which Er³⁺ ions substitute Ca²⁺ with compensation of the additional positive charge occurring in the crystal. At low temperatures, only the two lowest energy levels are occupied. Known as a Kramers doublet, they form an effective electron spin S = 1/2 system whose g tensor is diagonal in the crystal frame with values g_aa = g_bb = 8.38 ≡ g_⊥ and g_cc = 1.247 ≡ g_∥ (18, 19). Here, we will consider only the zero-nuclear-spin isotopes of erbium, thus excluding ¹⁶⁷Er. The large magnetic moment in the ab plane, up to four times larger than a free electron, makes it particularly interesting for coupling to superconducting circuits (20).

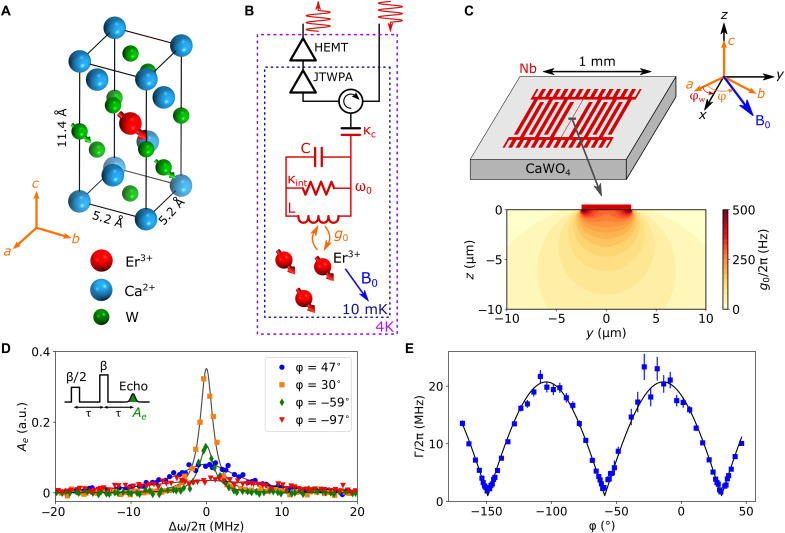
Fig. 1. Schematics of the experiment and erbium spins spectroscopy.

(A) Unit cell of CaWO₄ with a central Er³⁺ dopant. Oxygen atoms are removed for clarity. A fraction 0.14 of tungsten atoms has a nuclear spin. (B) Experimental EPR setup. The erbium spins, subjected to a magnetic field B₀, are coupled with strength g₀ to an LC resonator. The latter has an internal loss rate κ_int and is coupled to a measurement line with rate κ_c. Microwave pulses are sent to the device, and the reflected signal containing the spin echo is routed toward a JTWPA (Josephson traveling-wave parametric amplifier), followed by a HEMT (high–electron-mobility transistor) at 4 K and by further amplification and demodulation at room temperature. (C) Sketch of one of the three 50-nm-thick niobium LC resonators fabricated on top of the CaWO₄ sample, in the ab plane. The dc magnetic field B₀ is applied in the ab plane at an angle φ with respect to the a axis, the resonator inductor making an angle φ_w with this axis. The cross section shows the coupling g₀ between the resonator and erbium spins around the 5-μm-wide inductance wire when B₀ is applied along its direction (x axis). (D) Spin echo integral A_e as a function of B₀, around 67.2 mT, converted into a frequency detuning Δω. Full symbols are measurements for various values of φ, whereas solid lines are Lorentzian fits to the data which are plotted in arbitrary units (a.u.). (E) Full width at half maximum linewidth Γ/2π as a function of φ. The solid line is a fit following the model of (26, 27), yielding a typical magnitude of inhomogeneous electric fields along the c axis of 32 kV/cm.

RESULTS AND DISCUSSION

Experimental setup

The sample used in this study is a CaWO₄ crystal grown from high-purity natural-abundance materials and the boule from which the sample has been extracted is described in an independent article (21). Electron paramagnetic resonance (EPR) spectroscopy reveals that all trivalent paramagnetic REIs are present at a level of ∼1 to 100 parts per billion (ppb); in particular, [Er³⁺] = 0.7 ± 0.1 ppb (see sections S1.1 and S1.5). Such concentrations are barely detectable with standard EPR spectroscopy; therefore, we use quantum-limited EPR spectroscopy with superconducting resonators and amplifiers that offer higher detection sensitivity (22, 23). We measure the spin coherence at millikelvin temperatures, where decoherence due to residual paramagnetic impurities is quenched owing to their polarization in the ground state.

Schematic descriptions of the sample and setup are shown in Fig. 1 (B and C). The sample is cut from a larger CaWO₄ crystal into a 3 mm by 6 mm rectangular slab with 0.5 mm thickness in the c-axis direction. A dc magnetic field B₀ is applied parallel to the sample surface in the ab crystallographic plane, with a controllable amplitude and angle φ with respect to the a axis, determined using x-ray diffraction with a precision of ±2°. Three superconducting microresonators with frequency ω₀ are patterned in a 50-nm niobium thin film deposited on top of the crystal. They allow us to independently probe the spins at frequencies between 7 and 8 GHz. They consist of an interdigitated capacitor in parallel with a few-micrometer-wide wire inductor (2 μm for one resonator and 5 μm for the two others) (22). At the single-photon level, all three resonators have an internal loss rate κ_int lower than 10⁶ s⁻¹ (corresponding to an internal quality factor larger than 4 × 10⁴), which is sufficient for high-sensitivity spin detection. The resonators allow for detection of Er³⁺ electron spins located in the vicinity of the inductor, the latter generating an oscillating magnetic field B₁ that couples to each spin with strength g₀ = (μ_B/ℏ)〈0∣S∣1〉 · g · δB₁. Here, δB₁ is the rms vacuum fluctuations of the field at the spin location. Because of the spatial variation of δB₁, g₀ varies with the spin location in the plane perpendicular to the wire as shown in Fig. 1C when the dc field B₀ is applied along the wire (φ = φ_w). The angle made by the resonator inductor with the crystalline a axis is determined from the maximum of the integrated echo line shape as a function of φ and corresponds to φ_w = 51^∘ ± 3^∘.

Each resonator is capacitively coupled with a rate κ_c to a measurement line through which microwave pulses are applied at the resonance frequency ω₀. These pulses induce Rabi nutations of the spins at a frequency $4{\mathit{g}}_0\mathrm{\beta }\sqrt{{\mathrm{\kappa }}_{\mathrm{c}}}/\mathrm{\kappa }$, where $\mathrm{\beta }=\sqrt{{\mathit{P}}_{\text{in}}/\mathrm{\hslash }{\mathrm{\omega }}_0}$ is the pulse amplitude in (number of photons per second)^1/2, P_in is the input power, and κ = κ_c + κ_int is the total energy damping rate (24). The Rabi frequency is proportional to g₀ and thus also varies spatially so that a given pulse amplitude applies different Rabi rotations to spins at different locations. Here, we measure spin coherence using the Hahn echo pulse sequence (Figs. 1D and 2A); it is composed of two pulses of same duration Δt and amplitudes β/2 and β, respectively, separated by a delay τ, leading to the emission of a spin echo at a delay τ after the second pulse. Because the spins contributing the most to the Hahn echo are those undergoing rotations of first π/2 then π, an echo with pulse amplitude β probes mainly spins with a coupling constant close to ${\mathit{g}}_0=\mathrm{\pi }\mathrm{\kappa }/(4\mathrm{\Delta }\mathit{t}\mathrm{\beta }\sqrt{{\mathrm{\kappa }}_{\mathrm{c}}})$ (24). The reflected pulses, together with the spin signals, are amplified through a low-noise detection chain consisting of a Josephson traveling-wave parametric amplifier (JTWPA) (25), followed by a high–electron-mobility transistor (HEMT) (Fig. 1B), and demodulated at room temperature.

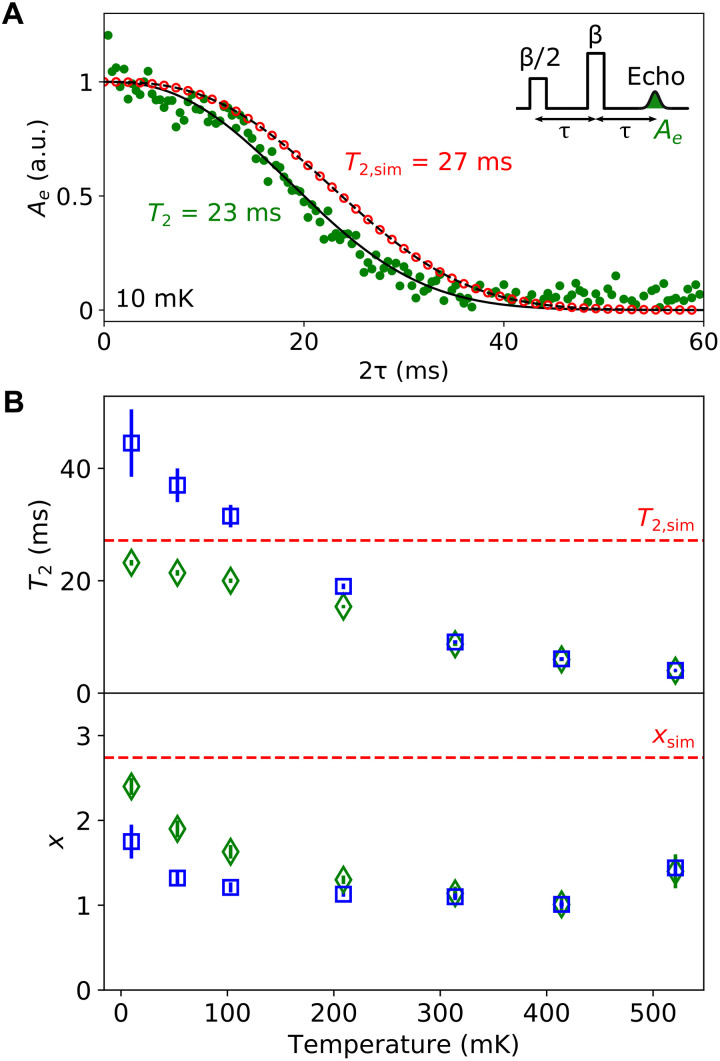
Fig. 2. Er³⁺ electron spin coherence time T₂.

(A) Measured normalized Hahn echo integral A_e (green full circles) as a function of the delay 2τ between the first pulse and the echo, at 10 mK cryostat temperature, φ = 47^∘ and high pulse power (β = 700 ns^−1/2). Each data point is magnitude averaged over 60 measurements with a repetition time of 4 s. The solid black line is a fit to $A_e^2=exp\{-2{(2\mathrm{\tau }/T_2)}^x\}+C$ (with the offset C subtracted from the data and the fit), yielding T₂ = 23.2 ± 0.5 ms and x = 2.4 ± 0.1. Open red circles are the result of a cluster-correlation expansion (CCE) simulation of the nuclear spin bath for the same field orientation. The dashed black line is a fit to the simulation, yielding T_{2, sim} = 27.2 ms and x_sim = 2.74. (B) Measured coherence time T₂ and exponent x (green diamonds) as a function of the cryostat temperature. The red dashed line is the result of the CCE simulation. The blue squares result from a second fit of the data as $A_e^2=exp\{-2[{(2\mathrm{\tau }/T_{2,\text{sim}})}^{x_{\text{sim}}}+{(2\mathrm{\tau }/T_2)}^x]\}+C$ to extract the net decoherence effect of spectral diffusion due to paramagnetic impurities.

Spectroscopy

An echo-detected field sweep of the erbium line shape (see section S1.3) is shown in Fig. 1D, around B₀ = 67.2 mT, for several magnetic field angles φ in the ab plane. We used a pulse power such that bulk-like spins (several micrometers from the surface) are probed. An approximately Lorentzian line shape is observed, with a full width at half maximum strongly dependent on φ, reaching a minimum value of Γ/2π = 1 MHz for φ = φ₀ = 31^∘ (Fig. 1E). A similar orientation-dependent linewidth was previously observed by Mims and Gillen (26). Mims explained this phenomenon by inhomogeneous internal electric fields, likely caused by the presence of charged defects around the erbium ions and possibly related to charge compensation. He showed that in CaWO₄, when the magnetic field B₀ is applied in the ab plane, applying an external electric field has an impact on the perpendicular g factor g_⊥ of the erbium ions through its component along the c axis, E_c. Therefore, ∂ω/∂E_c takes a finite value except when B₀ is applied along φ₀, where ∂ω/∂E_c = 0 (27). In our sample, a typical electric field value of 32 kV/cm yields quantitative agreement with the data following the analysis of Mims and Gillen (26) (see section S1.4). The 1-MHz linewidth at φ = φ₀ is likely due to a combination of dipolar coupling to nuclear spins and to other paramagnetic species in the sample and to a slight misalignment of B₀ from the ab plane; we note that erbium-erbium dipolar interactions are however negligible owing to the low concentration. We estimate that the erbium concentration may be increased up to a few parts per million without significantly broadening the linewidth. To our knowledge, this is the narrowest inhomogeneous linewidth reported for erbium electron spins, supporting the application of erbium to microwave-optical conversion (4).

Hahn echo coherence time

To measure the longest possible spin coherence in this system, we first cool the sample to 10 mK, the base temperature of the cryostat. A Hahn echo pulse sequence is applied with sufficient microwave power to probe bulk-like spins. The spin-echo integral A_e is recorded as a function of the delay 2τ (Fig. 2A). Here, the angle is φ = 47^∘, close to the wire direction φ_w = 51^∘ so that B₀ is orthogonal to B₁ for all spins. A modulation of the spin-echo envelope around the overall Gaussian decay is visible and is due to the coupling to the proximal ¹⁸³W nuclear spins (see section S1.7). A fit to the square of the magnitude ${\mathit{A}}_{\mathit{e}}^2=\text{exp}\{-2{(2\mathrm{\tau }/{\mathit{T}}_2)}^{\mathit{x}}\}+\mathit{C}$ (28), with C being a spurious vertical shift due to noise rectification (see section S1.6), yields a coherence time T₂ = 23.2 ± 0.5 ms and x = 2.4 ± 0.1. This value of T₂ is nearly three orders of magnitude longer than previous measurements of Er³⁺ electron spin coherence in CaWO₄ at 2 K (29). We attribute this drastic improvement to both the low residual paramagnetic impurity concentration and enhanced thermal spin polarization at 10 mK, both of which greatly reduce electronic spin-spin interactions in the crystal. Also, this is more than an order of magnitude longer than previous state-of-the-art measurements of electron spin coherence in a natural-abundance material (30), away from a ZEFOZ transition.

In Fig. 2A, we plot simulations of the echo signal decay calculated using the cluster-correlation expansion method (31, 32) (see section S2), which describes the effect of the magnetic dipole interactions between the measured Er³⁺ and the ¹⁸³W nuclear spin bath. The similarity between simulation and experiment indicates that the measured coherence time is mostly limited by the nuclear spin bath dynamics. This suggests in particular that instantaneous diffusion (ID) (6) caused by the other erbium ions is negligible, due to the low erbium concentration and to the inhomogeneous broadening (signatures of ID were observed at φ ≃ φ₀ where the linewidth is narrower; see section S1.8). We also note that the simple formula derived in (17) predicts a coherence time of 8 ms, a factor of 3 shorter than both our simulation and experiment. This discrepancy is attributed to the random nuclear spin positions assumed in (17), whereas in CaWO₄, the nuclear spins occupy random sites on a regular lattice, which has been taken into account in the simulations of the present work (see section S2.3).

As explained above, the data are averaged in magnitude to mitigate global magnetic field noise, which causes the echo to be emitted with a random phase for values of τ larger than ∼2 ms (see section S1.6). Such magnitude averaging is frequently used in EPR (6, 33) and optical (7–11, 14–16) echo measurements. Future applications to quantum memories will therefore require active stabilization of B₀ or, alternatively, to encode the quantum states in a way that is insensitive to the global echo phase, for instance, using time-bin qubits (34).

We then measure T₂ as a function of cryostat temperature (Fig. 2B) and observe a decrease in coherence time with increasing temperature. Since the nuclear-spin contribution is temperature independent in the experimental range, we attribute this decrease to spectral diffusion caused by all the other paramagnetic impurities present in similar or larger concentrations than erbium (see section S1.1). This spectral diffusion is quenched at low temperatures when most paramagnetic impurities are highly polarized into their ground state (30, 35, 36). We use the theoretical nuclear spin decoherence curve of Fig. 2A to quantitatively extract the paramagnetic contribution; Fig. 2B shows that the latter is suppressed by a factor of ∼20 by cooling the sample from 500 to 10 mK.

Relaxation time and Purcell effect

We now turn to measurements of the longitudinal spin relaxation time T₁, using an inversion-recovery pulse sequence. A Hahn echo measures the longitudinal polarization at delay T after application of a first pulse of the same amplitude and duration as the refocusing pulse. We use CPMG (Carr-Purcell-Meiboom-Gill sequences) to increase the signal-to-noise ratio (SNR; see Materials and Methods). The echo integral is shown in Fig. 3A as a function of T, for various pulse amplitudes β. The data are well fitted by an exponential, yielding a spin relaxation time T₁ that is strongly dependent on β. Figure 3B shows T₁(β) for two resonators. An approximately quadratic increase of T₁ with β is observed for small β, followed by a saturation at a maximum value for larger β.

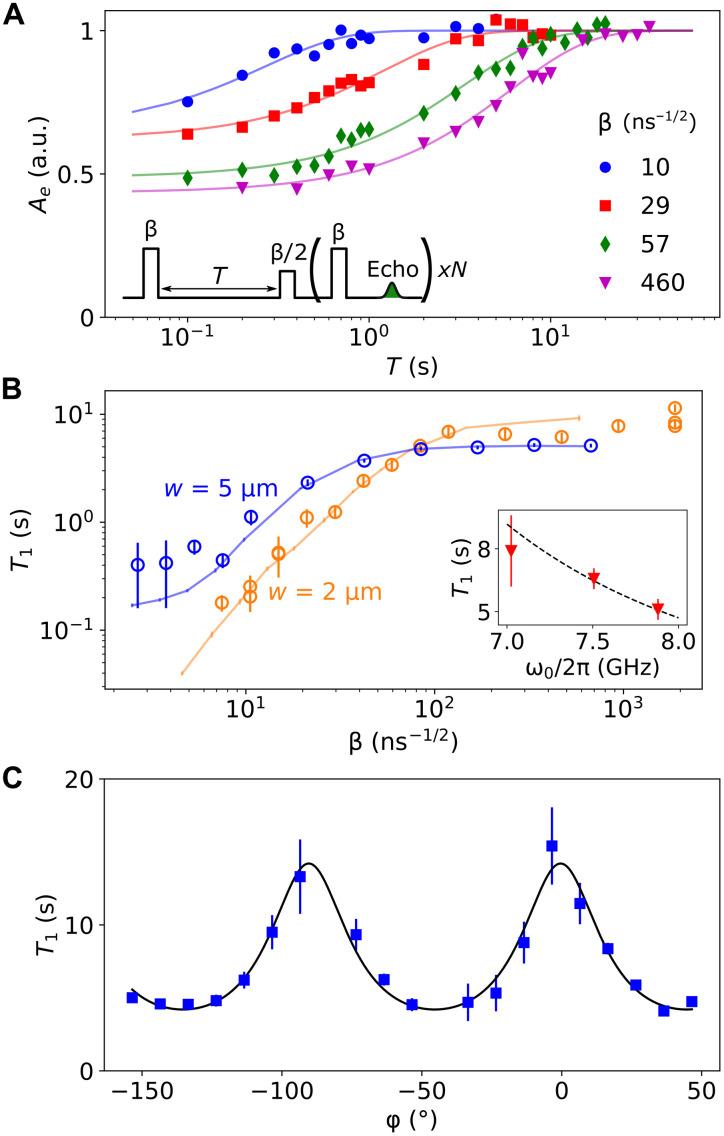
Fig. 3. Spin relaxation time T₁.

(A) The inversion recovery sequence includes a first pulse of amplitude β, followed after a delay T by a Hahn echo detection sequence also of amplitude β. The last pulse and the echo are repeated N times for enhanced signal averaging (see Materials and Methods). Solid symbols are the measured echo integral A_e as a function of T, for various values of β shown in the figure. Solid lines are exponential fits, yielding the spin relaxation time T₁. The data are measured with the 2-μm-wide inductor resonator. In (A) and (B), φ was set to 30^∘ to maximize the signal. (B) Measured values of T₁ as a function of β for a 2- and 5-μm-wide inductor resonator (open circles). The solid lines result from simulations where the only adjustable parameters are the input line attenuation and the spin-lattice relaxation time (see section S1.10). Inset shows the measured phonon-limited T₁ for all three resonators (red triangles). The black dashed line indicates that the data are compatible with a dependence of Γ_sl as ${\mathrm{\omega }}_0^5$ (38). (C) Measured T₁ (squares) at high input pulse amplitude (β = 700 ns^−1/2) as a function of φ for the 5-μm-wide inductor resonator. The solid black line is a fit with (T₁)⁻¹ = A + B sin (4φ + φ₁), as described in (39), where φ₁ is found to be 92^∘ ± 3^∘.

This dependence of T₁ on β can be understood qualitatively by the competition between two relaxation channels: the Purcell relaxation rate ${\mathrm{\Gamma }}_{\mathit{P}}=4{\mathit{g}}_0^2/\mathrm{\kappa }$ (37) and the spin-lattice relaxation rate Γ_sl. Low-β measurements probe spins with a large g₀, close to the inductive wire, where Purcell relaxation dominates, whereas spin-lattice relaxation becomes the limiting rate for weakly coupled spins, far from the resonator, measured with large β. This is validated by simulations that take into account the distribution of theoretical coupling constants as well as Purcell and spin-lattice relaxation (24). We obtain quantitative agreement with the data for all three resonator geometries, where the attenuation of the input line and Γ_sl are the only adjustable parameters (data for two resonators are shown on Fig. 3B). The spin-lattice relaxation times measured for the three resonators (at high power) show a frequency dependence compatible with the expected ω⁻⁵ dependence for the direct-phonon process in a Kramers ion (Fig. 3B) (38). Because of the anisotropy of the spin-lattice coupling, the relaxation rate in Kramers ions is itself often anisotropic (38, 39); here, we also observe such anisotropy in the high-power relaxation time, whose dependence on φ shown in Fig. 3C is well accounted for by the model described in (39).

Conclusion

Our observation of a near–nuclear spin–limited coherence time of 23 ms in Er³⁺:CaWO₄ at millikelvin temperature is meaningful for several reasons. It proves that decoherence due to paramagnetic impurities in a REI-doped crystal can be almost entirely suppressed by spin-polarizing the impurities through cooling, which places Er³⁺:CaWO₄ among some of the most coherent spin systems currently known, such as donors in isotopically purified silicon. It also confirms the predictions that CaWO₄ is among the best natural-abundance host crystals for long coherence time paramagnetic defects (17). We note that the growth of a calcium tungstate crystal enriched in the nuclear spin–free tungsten isotopes is also feasible and should lead to even longer coherence times. Combined with the observation of Purcell spin relaxation, our work establishes Er³⁺:CaWO₄ as a potential platform for implementing a microwave quantum memory as well as microwave-to-optical conversion.

MATERIALS AND METHODS

Microwave resonator properties

The measurements are performed using three microwave resonators with different frequencies.

• Resonator 1 has frequency ω₀/2π = 7.025 GHz, coupling rate κ_c = 2 × 10⁵ s⁻¹, internal loss rate κ_int = 1.0 × 10⁶ s⁻¹, and total energy damping rate κ = κ_c + κ_int. It was used for the data of Fig. 3 (A and B, orange curve) and inset of Fig. 3B.

• Resonator 2 has frequency ω₀/2π = 7.508 GHz, coupling rate κ_c = 3.1 × 10⁶ s⁻¹, internal loss rate κ_int = 7 × 10⁵ s⁻¹, and total energy damping rate κ = κ_c + κ_tint. It was used for the data of the inset of Fig. 3B.

• Resonator 3 has frequency ω₀/2π = 7.881 GHz, coupling rate κ_c = 1.7 × 10⁶ s⁻¹, internal loss rate κ_int = 5 × 10⁵ s⁻¹, and total energy damping rate κ = κ_c + κ_tint. It was used for all other data of the main text.

Pulse sequence

In all the data shown in the main text, 4-μs-long pulses were used. This pulse length of Δt = 4 μs corresponds to a pulse bandwidth Δω_pulse/2π ≈ 250 kHz, which roughly matches the cavity bandwidth of resonator 3, κ/2π = 350 kHz.

CPMG enhanced T₁ measurements

Except for the relaxation measurements presented in Fig. 3 (A and B), all data presented in the manuscript are taken with high pulse powers. For the relaxation measurements in Fig. 3 (A and B), however, the SNR is insufficient for Hahn echo measurements at low pulse powers. It is therefore necessary to use CPMG sequences to enhance the SNR in this low power regime. Thus, the usual Hahn echo sequence (π/2 − τ − π − τ − echo) is followed by a CPMG sequence consisting in a chosen number N-1 of refocusing pulses (τ − π − τ − echo) × (N-1) (40).

In the measurement presented in Fig. 3 (A and B), τ is chosen to be 30 μs, the spacing between the CPMG pulses is 2τ = 60 μs, and N is set to 333. The spin-echo amplitude is then computed as the weighted average of the N. Here, the weights are measured from the integral of each refocused echo when no initial inversion pulse is applied. The data presented in Fig. 3C are recorded without CPMG pulses, as the high pulse powers give sufficient SNR with just single-shot Hahn echoes.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S12

Tables S1 and S2

References