RETRACTED ARTICLE: A brief comparative examination of tangent hyperbolic hybrid nanofluid through a extending surface: numerical Keller–Box scheme

Abstract

A novel hybrid nanofluid was explored in order to find an efficient heat-transmitting fluid to replace standard fluids and revolutionary nanofluids. By using tangent hyperbolic hybrid combination nanoliquid with non-Newtonian ethylene glycol (EG) as a basis fluid and a copper (Cu) and titanium dioxide (TiO₂) mixture, this work aims to investigate the viscoelastic elements of the thermal transferring process. Flow and thermal facts, such as a slippery extended surface with magnetohydrodynamic (MHD), suction/injection, form factor, Joule heating, and thermal radiation effects, including changing thermal conductivity, were also integrated. The Keller–Box method was used to perform collective numerical computations of parametric analysis using governing equivalences. In the form of graphs and tables, the results of TiO₂–Cu/EG hybrid nanofluid were compared to those of standard Cu/EG nanofluid in important critical physical circumstances. The entropy generation study was used to examine energy balance and usefulness for important physically impacting parameters. Detailed scrutiny on entropy development get assisted with Weissenberg number, magnetic parameter, fractional volumes, injection parameter, thermal radiation, variable thermal conductivity, Biot number, shape variation parameter, Reynolds and Brinkman number. Whereas the entropy gets resisted for slip and suction parameter. In this case, spotted entropy buildup with important parametric ranges could aid future optimization.

Introduction

Nanoliquids are of outstanding importance to researchers, because, due to their raised heat transfer rates, they have significant manufacturing and engineering uses. Hybrid nanofluid a trending class of fluid with double or more kind of metal particles suspended in the base fluid. This progressive kind of nanoliquids presented encouraging improvement in thermal transferring features and thermo-physical and hydrodynamic possessions related to traditional single suspended fluids. HNF can be employed in numerous branches of heat transfer, for example, transports, engineering, and health sciences. HNF can be formulated by deferment of different nanoparticles in a composite/mixture of base fluids. In nature, most of all actions are highly related to nonlinearity, which is very difficult to solve. To introduce an acceptable solution to the problem, it usually requests irregular solutions using different techniques such as numerical, approximate, or methodical techniques. They can be employed to solve nonlinear ordinary differential equations without using linearization or discretization^1–5.

A non-Newtonian fluid (NNF) is a special class of fluid such as ketchup, tooth paste and paints etc. in which the quantity of shear and the stress created by such particular measure were nonlinearly connected. It requires some added efforts to trace such kind of viscous behavior when compared to the traditional Newton fluids like water, gasoline and motor oils. Such fluids can be considered at some extent with viscosity in the form of time variant. Hence those stress changes may not be tracked with any stable procedure which requires specifically modeled functions.

The distinct feature of exerting both aspects of shear stiffing and retarding can be incorporated from the tangential hyperbolic nanoliquids. This class of fluid trend sets for more innovative works on the studies on boundary layer flows¹. Lorentz force influence on tangential hyperbolic nanoliquid were pulls notable attention among the researchers and they have published frequent article under this topic^2–5 while passing over the stretching sheet. The works^6–9 are some examples to the works which tends to explore the altering heat transference in tangential hyperbolic nanoliquid when passing over the nonlinear stretching sheets. Updated magnetohydrodynamic versions of above mentioned works can be found in^10–15.

Being such kind of nonlinear in fluid dynamical aspects, the representing equations also requires some special form of approaches for to be solved. Literature concludes the fact that, semi-analytic techniques and numerical way so solving procedures were preferred by the authors. Homotopy based analysis looks to be widely employed for solving such class of fluid problems. Improved accuracy level and reduced and faster coherence in solution made the researchers to move towards these kind of hybrid methodology^16–20.

It is recognized that the result of every thermal process, the entropy assesses the quantity of irretrievable energy loss. Cooling and warming are essential cases in numerous manufacturing areas of engineering studies that are used mostly in energy and electronic devices. Consequently, it is natural to enhanced entropy formation²¹. Shahsavar et al.²² studied through numerical perspective to explore the entropy generation of HNF flow. Huge developments in nanoliquid thermo-physical possessions on the straight fluids have controlled the fast progress of using HNFs of thermal transference deliberated by Hussien et al.²³. Ellahi et al.²⁴ analyzed the effect of hydromagnetic thermal transference flow with maximized entropy. Lu et al.²⁵ studied the entropy analysis and nonlinear thermal in the flow of HNF over a sheet. The technique of finite-difference is utilized to resolve it numerically. Newly, the employability of maximized energy loss and other physical phenomena is located in the works of Khan et al.²⁶, Sheikholeslami et al.²⁷, Zeeshan et al.²⁸, Ahmad et al.²⁹, Moghadasi et al.³⁰, Shorbagy et al.³¹, Ibrahim et al.^32–35, Majid et al.³⁶, Gul et al.^37,38, Wajdi et al.³⁹, Arshad Khan et al.⁴⁰, Jawad et al.⁴¹ and Saeed et al.⁴².

Based on the above literature, this research purposes to plug in the spot by intending to explore the flow and thermal aspects of the radiative tangent hyperbolic hybrid combo nanoliquid with variant heat conducting ability with passing an extending permeable surface. The model of Tiwari and Das for nanofluid⁴³ are to be used for the modeling the flow mathematically. The hybrid nanoparticle involved in this study are copper (Cu) and titanium dioxide (TiO₂) and the based fluid used is ethylene glycol (EG).

The main objective of this work is to trace the irreversible energy loss, the study of entropy forming will be undertaken with the flow effects of the hybrid nanoparticle. The prevailing equations of tangent hyperbolic nanofluid are converted into possible ODEs by employing the apt similarities variables. Subsequently, the ODEs will be numerically solved for the parametrical influences using the Keller–Box method. The outcomes of the studies were displayed in the graphical form for technical discussions. The influence of parameters reflecting hydromagnetic, viscous based dissipation, joule heating, shapes of the suspended particles under thermal radiation subjected to the Newtonian boundary conditions were deliberated thoroughly.

Flow analysis

The flow movement investigation describes the fluidity across the non-regular flat surface with the extending velocity⁴⁴:

$$U_w\left(x,0\right)=bx,$$ 2.1

where $b$ is a initial extending rate. Isolated surface temperature is ${\yen }_w\left(x,0\right)={\yen }_{\infty }+b^{\ast }x$ and for aptness it is supposedly considered to be constant at $x=0$, $b^{\ast }$ and ${\yen }_{\infty }$ give the rate of heat variant and ambient temperature, respectively.

Guesses and limitations of model

In the following Guesses and limita requirements, the mathematical model is considered as 2D, stable, laminar, hydromagnetic, steady boundary-layer guesstimate of non-Newtonian Tangent Hyperbolic hybrid nanoliquids with variant thermal conductivity, Ohmic heating, viscous dissipation and radiative flow with convective and slip effects on stretching plate.

Geometric flow system

Figure 1 geometrically depicts the inflow structure as below.

Figure 1.

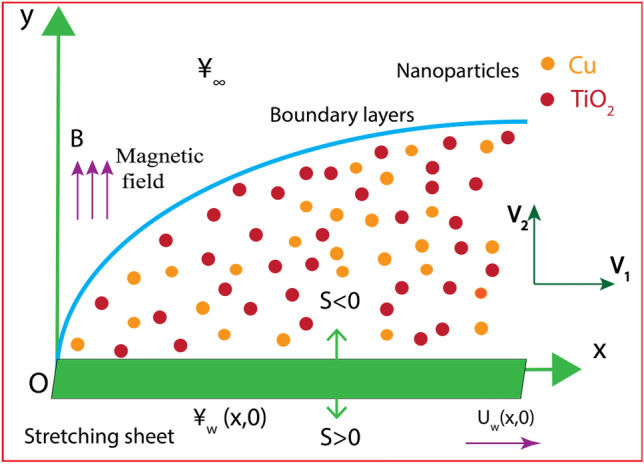
Diagram of the flow model.

Model equations

The key modelling equations⁴⁵ of tangent Hyperbolic hybrid nanoliquid under steady form subjected to Joule heating, viscous, MHD, varying thermal conductivity, dissipation, and thermal based radiation are:

$$\frac{\partial v_1}{\partial x}+\frac{\partial v_2}{\partial y}=0,$$ 2.2

$$v_1\frac{\partial v_1}{\partial x}+v_2\frac{\partial v_1}{\partial y}=\frac{{\mu }_{\mathit{hnf}}}{{\rho }_{\mathit{hnf}}}\left[\left(1-n\right)+n\sqrt{2}\zeta \left(\frac{\partial v_1}{\partial y}\right)\right]\frac{{\partial }^2{v}_1}{\partial y^2}-\frac{{\sigma }_{\mathit{hnf}}{B}^2}{{\rho }_{\mathit{hnf}}}u,$$ 2.3

$$v_1\frac{\partial \yen }{\partial x}+v_2\frac{\partial \yen }{\partial y}=\frac{1}{{(\rho C_p)}_{\mathit{hnf}}}\left[\frac{\partial }{\partial y}\left({\kappa }_{\mathit{hnf}}^{\ast }\left(\yen \right)\frac{\partial \yen }{\partial y}\right)-\left(\frac{\partial q_r}{\partial y}\right)+{\mu }_{\mathit{hnf}}{\left(\frac{\partial v_1}{\partial y}\right)}^2+{\sigma }_{\mathit{hnf}}{B}^2{u}^2\right].$$ 2.4

the pertinent boundary constraints are (see Aziz et al.⁴⁶):

$$v_1\left(x,0\right)=U_w+N_w\left(\frac{\partial v_1}{\partial y}\right),v_2\left(x,0\right)=V_w,-k_g\left(\frac{\partial \yen }{\partial y}\right)=h_g\left({\yen }_w-\yen \right),$$ 2.5

$$v_1\to 0,\yen \to {\yen }_{\infty }asy\to \infty .$$ 2.6

The components of the fluidity is denoted as $\overleftarrow{v}=\left[v_1\left(x,y,0\right),v_2\left(x,y,0\right),0\right]$. $\yen$ as the temperature state of the fluid. surface permeability as $V_w$, slip length as $N_w,$ thermal transference coefficient as $h_g$ and thermal conductivity of solid as $k_g$. Slippery shear stressed and Newtonianly heated surface are considered.

Thermo-physical aspects of the tangential hyperbolic nanoliquid

The formulas in Table 1 depict topographies of nanoliquid^46,47:

Table 1.

Thermo-physical aspects of nanofluid.

Features	Nanoliquid
Viscidness $\left(\mu \right)$	${\mu }_{\mathit{nf}}={\mu }_f{(1-\varphi )}^{-2.5}$
Density $\left(\rho \right)$	${\rho }_{\mathit{nf}}=\left(1-\varphi \right){\rho }_f-\varphi {\rho }_s$
Heat capacity $\left(\rho C_p\right)$	${(\rho C_p)}_{\mathit{nf}}=\left(1-\varphi \right){(\rho C_p)}_f-\varphi {(\rho C_p)}_s$
Electrical conductivity $\left(\sigma \right)$	$\frac{{\sigma }_{\mathit{nf}}}{{\sigma }_f}$ = $\left[1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_s}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }\right]$
Thermal conductivity $\left(\kappa \right)$	$\frac{{\kappa }_{\mathit{nf}}}{{\kappa }_f}=\left[\frac{\left({\kappa }_s+\left(m-1\right){\kappa }_f\right)-\left(m-1\right)\varphi \left({\kappa }_f-{\kappa }_s\right)}{\left({\kappa }_s+\left(m-1\right){\kappa }_f\right)+\varphi \left({\kappa }_f-{\kappa }_s\right)}\right]$

$\varphi$ indicates the nanoparticle concentration factor. ${\mu }_f$, ${\rho }_f$, ${(C_p)}_f$, ${\sigma }_f$ and ${\kappa }_f$ are fluid viscous, density, operative heat capacitance, electrical and thermal ability of the basefluid, respectively. The additional aspects like ${\rho }_s$, ${(C_p)}_s$, ${\sigma }_f$ and ${\kappa }_s$ symbolize the particle density, operative heat capacitance, electrical and thermally conductivity of the solid-particle, respectively.

Thermo properties

In Table 2^48–50, ${\mu }_{\mathit{hnf}}$, ${\rho }_{\mathit{hnf}}$, $\rho {(C_p)}_{\mathit{hnf}}$, ${\sigma }_{\mathit{hnf}}$ and ${\kappa }_{\mathit{hnf}}$ are the representations of dynamical viscosity, intensity, specific heat capacitance electrical, and thermal conductance of hybrid class of nanofluids respectively. $\varphi$ is the volume of solid based nanomolecules coefficient for mono nanofluid and ${\varphi }_{\mathit{hnf}}={\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}$ is the nano magnitude of solid-particles coefficient for the combination of nanofluid. ${\rho }_{p_1}$, ${\rho }_{p_2}$, ${(C_p)}_{p_1}$, ${(C_p)}_{p_2}$, ${\sigma }_{p_1}$, ${\sigma }_{p_2}$, ${\kappa }_{p_1}$ and ${\kappa }_{p_2}$ are the intensity, specific heat capacitance electrical, and thermal conductivity of the nano-molecules. The temperature-dependent conductance for mixture nano level fluid is presumed as^50,51:

$${\kappa }_{\mathit{hnf}}^{\ast }\left(\yen \right)=k_{\mathit{hnf}}\left[1+\lambda \frac{\yen -{\yen }_{\infty }}{{\yen }_w-{\yen }_{\infty }}\right],$$ 2.7

Table 2.

Thermo-physical aspects of hybrid class of nanofluid.

Features	Hybrid class of nanofluid
Viscosity $\left(\mu \right)$	${\mu }_{\mathit{hnf}}$ = ${\mu }_f{(1-{\varphi }_{\mathit{Cu}})}^{-2.5}{(1-{\varphi }_{Ti{O}_2})}^{-2.5}$
Density $\left(\rho \right)$	${\rho }_{\mathit{hnf}}$ = [$\left(1-{\varphi }_{Ti{O}_2}\right)\left\{\left(1-{\varphi }_{\mathit{Cu}}\right){\rho }_f+{\varphi }_{\mathit{Cu}}{\rho }_{p_1}\right\}]$ + ${\varphi }_{Ti{O}_2}{\rho }_{p_2}$
Heat capacity $\left(\rho C_p\right)$ Electrical conductivity $\left(\sigma \right)$	${(\rho C_p)}_{\mathit{hnf}}$ = $[\left(1-{\varphi }_{Ti{O}_2}\right)\{\left(1-{\varphi }_{\mathit{Cu}}\right){(\rho C_p)}_f+{\varphi }_{\mathit{Cu}}{(\rho C_p)}_{p_1}\}]$$+{\varphi }_{Ti{O}_2}{(\rho C_p)}_{p_2}$ $\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}$ = $\left[1+\frac{3\left(\frac{{\varphi }_{\mathit{Cu}}{\sigma }_{p_1}+{\varphi }_{Ti{O}_2}{\sigma }_{p_2}}{{\sigma }_f}-\left({\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}\right)\right)}{\left(\frac{{\varphi }_{\mathit{Cu}}{\sigma }_{p_1+{\varphi }_2{\sigma }_{p_2}}}{\left({\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}\right){\sigma }_f}+2\right)-\left(\frac{{\varphi }_{\mathit{Cu}}{\sigma }_{p_1}+{\varphi }_{Ti{O}_2}{\sigma }_{p_2}}{{\sigma }_f}-\left({\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}\right)\right)}\right]$
Thermal conductivity $\left(\kappa \right)$	$\frac{{\kappa }_{\mathit{hnf}}}{{\kappa }_{\mathit{gf}}}=\left[\frac{\left({\kappa }_{p_2}+\left(m-1\right){\kappa }_{\mathit{gf}}\right)-\left(m-1\right){\varphi }_{Ti{O}_2}\left({\kappa }_{\mathit{gf}}-{\kappa }_{p_2}\right)}{\left({\kappa }_{p_2}+\left(m-1\right){\kappa }_{\mathit{gf}}\right)+{\varphi }_{Ti{O}_2}\left({\kappa }_{\mathit{gf}}-{\kappa }_{p_2}\right)}\right],$ $\frac{{\kappa }_{\mathit{gf}}}{{\kappa }_f}=\left[\frac{\left({\kappa }_{p_1}+\left(m-1\right){\kappa }_f\right)-\left(m-1\right){\varphi }_{\mathit{Cu}}\left({\kappa }_f-{\kappa }_{p_1}\right)}{\left({\kappa }_{p_1}+\left(m-1\right){\kappa }_f\right)+{\varphi }_{\mathit{Cu}}\left({\kappa }_f-{\kappa }_{p_1}\right)}\right]$

The hybrid combo nanoliquid is blended by the copper (Cu) nano-sized particles suspended in the ethylene glycol (EG). The effectual fractional volume (${\varphi }_{\mathit{Cu}}$) and it is made secure at $0.09$ through out the study. Titanium dioxide (TiO₂) nano sized level particles were unified with the mixture to alter it a crossbred nano level fluid at the concentration size (${\varphi }_{Ti{O}_2}$).

Nano sized particles and base fluid

Table 3^47,52 represents the values of the above mentioned property.

Table 3.

Considerable properties of base fluid and nano sized particles at 293 K.

Thermophysical	$\rho \left({\text{kg/m}}^3\right)$	$c_p\left(\text{J/kg}\text{K}\right)$	$k\left(\text{W/m}\text{K}\right)$	$\sigma \left(\text{S/m}\right)$
Copper (Cu)	8933	385.0	401.00	5.96 × 107
Ethylene glycol (EG)	1110	22,000	0.253	5.5 × 10–6
Titanium dioxide (TiO2)	4250	686.2	8.953	2.38 × 106

Topographies of nanoparticles and base fluid

Table 4 exemplifies the various shape values of particle from⁵³:

Table 4.

Shape factor value for diverse particle shapes.

Particle shapes	Sphere	Hexahedron	Tetrahedron	Column	Lamina
$m$	3	3.7221	4.0613	6.3698	16.1576

Estimated Rosseland procedure

The Rosseland-guesstimation is suitable for minor disparities in the thermal states amid the plate and the nearby fluid. The energy formulation is nonlinear nature in $\yen$ and challenging to expound, so a immense interpretation in ${\yen }_{\infty }$ is replacing ${\yen }^3$ with ${({\yen }_{\infty })}^3$. The estimated Rosseland form⁵⁴ is exploited in formulation (10) and given by:

$$q_r=-\frac{4{\sigma }^{\ast }}{3k^{\ast }}\frac{\partial {\yen }^4}{\partial y},$$ 2.8

where ${\sigma }^{\ast }$ is the Stefan–Boltzmann secure value and $k^{\ast }$ is the speed.

Solution for the problem

The BVP designs (2.2)–(2.4) are transformed in the non-dimensional systems by similar translations which modifies the partial to ordinary differential equations. Offering the $\psi$ as:

$$v_1=\frac{\partial \psi }{\partial y},v_2=-\frac{\partial \psi }{\partial x}.$$ 3.1

and expressed as

$$\mathrm{\Gamma }\left(x,y\right)=\sqrt{\frac{b}{{\nu }_f}}y,\psi \left(x,y\right)=\sqrt{{\nu }_{f}b}xf\left(\mathrm{\Gamma }\right),\theta \left(\mathrm{\Gamma }\right)=\frac{\yen -{\yen }_{\infty }}{{\yen }_w-{\yen }_{\infty }}.$$ 3.2

into Eqs. (2.2)–(2.4). We obtain

$$f^{″\prime }\left(\left(1-n\right)+n{W}_e{f}^{″}\right)+{\varphi }_a{\varphi }_b\left[f{f}^{″}-f^{\prime 2}\right]-{\varphi }_a{\varphi }_{e}M{f}^{\prime }=0,$$ 3.3

$${\theta }^{″}\left(1+\lambda \theta +\frac{1}{{\varphi }_d}{P}_r{N}_r\right)+\lambda {\theta }^{\prime 2}+P_r\frac{{\varphi }_c}{{\varphi }_d}\left[f{\theta }^{\prime }-f^{\prime }\theta +\frac{E_c}{{\varphi }_a{\varphi }_c}{f}^{″2}+\frac{{\varphi }_{\text{e}}}{{\varphi }_{\text{c}}}M{E}_c{f}^{\prime 2}\right]=0.$$ 3.4

with

$$\left(\begin{array}{c}f\left(0\right)=S,f^{\prime }\left(0\right)=1+\mathrm{{\rm Y}}{f}^{″}\left(0\right),{\theta }^{\prime }\left(0\right)=-B_i\left(1-\theta \left(0\right)\right)\hfill \\ f^{\prime }\left(\mathrm{\Gamma }\right)\to 0,\theta \left(\mathrm{\Gamma }\right)\to 0,as\mathrm{\Gamma }\to \infty \hfill \end{array}\right\}$$ 3.5

where ${\varphi }_i^{\prime }s$ is $a\le i\le d$ inequalities (3.3)–(3.4) indicate the successive thermo-physical aspects for tangential hyperbolic hybrid class nanofluid

$${\varphi }_a={(1-{\varphi }_{\mathit{Cu}})}^{2.5}{(1-{\varphi }_{Ti{O}_2})}^{2.5},{\varphi }_b=\left(1-{\varphi }_{Ti{O}_2}\right)\left\{\left(1-{\varphi }_{\mathit{Cu}}\right)+{\varphi }_1\frac{{\rho }_{p_1}}{{\rho }_f}\right\}+{\varphi }_{Ti{O}_2}\frac{{\rho }_{p_2}}{{\rho }_f},$$ 3.6

$${\varphi }_c=\left(1-{\varphi }_{Ti{O}_2}\right)\left\{\left(1-{\varphi }_{\mathit{Cu}}\right)+{\varphi }_{\mathit{Cu}}\frac{{(\rho C_p)}_{p_1}}{{(\rho C_p)}_f}\right\}+{\varphi }_{Ti{O}_2}\frac{{(\rho C_p)}_{p_2}}{{(\rho C_p)}_f},$$ 3.7

$${\varphi }_d=\left[\frac{\left({\kappa }_{p_2}+\left(m-1\right){\kappa }_{\mathit{gf}}\right)-\left(m-1\right){\varphi }_{Ti{O}_2}\left({\kappa }_{\mathit{gf}}-{\kappa }_{p_2}\right)}{\left({\kappa }_{p_2}+\left(m-1\right){\kappa }_{\mathit{gf}}\right)+{\varphi }_{Ti{O}_2}\left({\kappa }_{\mathit{gf}}-{\kappa }_{p_2}\right)}\right]\left[\frac{\left({\kappa }_{p_1}+\left(m-1\right){\kappa }_f\right)+{\varphi }_{\mathit{Cu}}\left({\kappa }_f-{\kappa }_{p_1}\right)}{\left({\kappa }_{p_1}+\left(m-1\right){\kappa }_f\right)-\left(m-1\right){\varphi }_{\mathit{Cu}}\left({\kappa }_f-{\kappa }_{p_1}\right)}\right].$$ 3.8

$${\varphi }_e=\frac{{\sigma }_{\mathit{hnf}}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\varphi }_{\mathit{Cu}}{\sigma }_{p_1}+{\varphi }_2{\sigma }_{p_2}}{{\sigma }_f}-\left({\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}\right)\right)}{\left(\frac{{\varphi }_{\mathit{Cu}}{\sigma }_{p_1+{\varphi }_{Ti{O}_2}{\sigma }_{p_2}}}{\left({\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}\right){\sigma }_f}+2\right)-\left(\frac{{\varphi }_{\mathit{Cu}}{\sigma }_{p_1}+{\varphi }_{Ti{O}_2}{\sigma }_{p_2}}{{\sigma }_f}-\left({\varphi }_{\mathit{Cu}}+{\varphi }_{Ti{O}_2}\right)\right)}\right].$$ 3.9

Depiction of the entrenched regulating physical constraints

Equation (2.2) is accurately confirmed. In earlier equations, the symbolization ${}^{\prime }$ used for signifying the derivatives regarding $\mathrm{\Gamma }$. Here $W_e=\zeta x\sqrt{\frac{2c^3}{{\nu }_f}}$ (Weissenberg number), $n$ (power law index) and $M=\frac{{\sigma }_f{B}^2}{c{\rho }_f}$ (magnetic) constraints defined respectively along with the $P_r$ = $\frac{{\nu }_f}{{\alpha }_f}$ (Prandtl number), ${\alpha }_f=\frac{{\kappa }_f}{{(\rho C_p)}_f}$ (Thermal diffusivity), $S=-V_w\sqrt{\frac{1}{{\nu }_{f}b}}$ (mass transfer),$N_r=\frac{16}{3}\frac{{\sigma }^{\ast }{\yen }_{\infty }^3}{{\kappa }^{\ast }{\nu }_f{(\rho C_p)}_f}$ (thermal radiation), $\mathrm{{\rm Y}}=\sqrt{\frac{b}{{\nu }_f}}{N}_w$(velocity slip), $E_c=\frac{U_w^2}{{(C_p)}_f\left({\yen }_w-{\yen }_{\infty }\right)}$ (Eckert number)and $B_i=\frac{h_g}{k_g}\sqrt{\frac{{\nu }_f}{b}}$ (Biot number) parameters respectively.

Drag energy and Nusselt number

The drag strength $\left(C_f\right)$ together with the local number of Nusselt $\left(N{u}_x\right)$ designate the possible quantities of cognizance which measured the inflow and detailed in the next⁴⁵

$$C_f=\frac{{\tau }_w}{{\rho }_{\mathit{hnf}}{U}_w^2},N{u}_x=\frac{x{q}_w}{k_f\left({\yen }_w-{\yen }_{\infty }\right)},$$ 3.9

wherein ${\tau }_w$ and $q_w$ signify the thermal flux specified by

$${\tau }_w={\mu }_{\mathit{hnf}}\left(1-n\right){\left(\frac{\partial v_1}{\partial y}\right)}_{y=0}+n\sqrt{2}\zeta {\left(\frac{\partial v_1}{\partial y}\right)}_{y=0}^2,q_w=-k_{\mathit{hnf}}\left(1+\frac{16}{3}\frac{{\sigma }^{\ast }{T}_{\infty }^3}{{\kappa }^{\ast }{\nu }_f{(\rho C_p)}_f}\right){\left(\frac{\partial \yen }{\partial y}\right)}_{y=0}.$$ 3.10

Executing the dimensionless conversions (3.2), we acquire

$$C_{f}R{e}_x^{\frac{1}{2}}=\frac{1}{{\varphi }_a{\varphi }_b}\left[\left(1-n\right)f^{″}\left(0\right)+\frac{n{W}_e}{2}{(f^{″}\left(0\right))}^2\right],N{u}_{x}R{e}_x^{-\frac{1}{2}}=-\frac{k_{\mathit{hnf}}}{k_f}\left(1+N_r\right){\theta }^{\prime }\left(0\right).$$ 3.11

where $N{u}_x$ signifies Nusselt number and $C_f$ specifies reduced skin friction. $R{e}_x=\frac{u_{w}x}{{\nu }_f}$ is local Reynolds quantity based on the stratching surface quickness $\left(u_w\left(x\right)\right)$.

Keller–Box method: an efficient numerical strategy

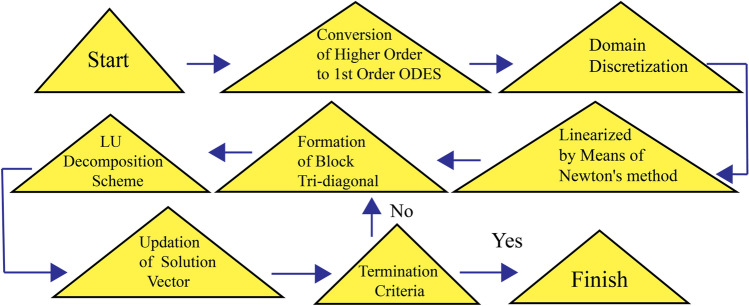
Analytical method of solving the mathematical model in terms of system of nonlinear ODEs for problem of such kind are technically intricate to solve. Researcher are in search of optimal numerical techniques with better convergence and accuracy. Keller–Box method (KBM)⁵⁵ is one of the healthier choice for those kind of complex set of ODEs like (3.3)–(3.4). Figure 2 displays the flow of working procedure of the Keller–Box scheme.

Figure 2.

Methodology of Keller–Box method.

Stage 1: Conversion of ODEs

The initial phase includes changing all the ODEs (3.3)–(3.5) into first order ODEs, that is

$$z_1=f^{\prime },$$ 4.1

$$z_2=z_1^{{}^{\prime }},$$ 4.2

$$z_3={\theta }^{\prime },$$ 4.3

$$z_2^{{}^{\prime }}\left(\left(1-n\right)+n{W}_e{z}_2\right)+{\varphi }_a{\varphi }_b\left[f{z}_2-z_1^2\right]-{\varphi }_a{\varphi }_{e}M{z}_1=0,$$ 4.4

$$\left(z_3^{{}^{\prime }}\left(1+\lambda \theta +\frac{1}{{\varphi }_d}{P}_r{N}_r\right)+\lambda z_3^2+P_r\frac{{\varphi }_c}{{\varphi }_d}\left[f{z}_3-z_1\theta +\frac{E_c}{{\varphi }_a{\varphi }_c}{z}_2^2+\frac{{\varphi }_{\text{e}}}{{\varphi }_{\text{c}}}M{E}_c{z}_1^2\right]\right)=0.$$ 4.5

$$f\left(0\right)=S,z_1\left(0\right)=1+\mathrm{{\rm Y}}{z}_2\left(0\right),z_3\left(0\right)=-B_i\left(1-\theta \left(0\right)\right),z_1\left(\infty \right)\to 0,\theta \left(\infty \right)\to 0.$$ 4.6

Stage 2: Separation of domains

Interested Domain has to separated with equal grid size. Accuracy of the outcome depends of the fact of fine grids. Hence lesser grid size are the choice of researchers to obtain highly exactitude results.

${\mathrm{\Gamma }}_0=0,{\mathrm{\Gamma }}_j={\mathrm{\Gamma }}_{j-1}+h,j=1,2,3,\dots ,J-1,{\mathrm{\Gamma }}_J={\mathrm{\Gamma }}_{\infty }$.

To represents the lateral separation of the domain, $j$ is applied to represent h-space for positioned coordinates. Prompt initial guess values between $=0$ and $\mathrm{\Gamma }=\infty$ for the process to attain the flow, thermal, entropy loss and thermal transference rate with good convergence. Most importantly the boundary constraints should be satisfied at the first place. Choice of initial guess is based on the limitations to attain minimal time process to convergence of solution without replication (see Fig. 3):

Figure 3.

Net rectangle for difference approximations.

ODEs from (4.1)–(4.5) were abridged in to customized nonlinear algebraic forms through central difference technique which provides the favour of mean average benefits.

$$\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}=\frac{f_j-f_{j-1}}{h},$$ 4.7

$$\frac{(z_2{)}_j+(z_2{)}_{j-1}}{2}=\frac{(z_1{)}_j-(z_1{)}_{j-1}}{h},$$ 4.8

$$\frac{(z_3{)}_j+(z_3{)}_{j-1}}{2}=\frac{{\theta }_j-{\theta }_{j-1}}{h},$$ 4.9

$$\begin{array}{c}\left(\frac{(z_2{)}_j-(z_2{)}_{j-1}}{h}\right)\left((1-n),+,n,W_e,\left(\frac{(z_2{)}_j+(z_2{)}_{j-1}}{2}\right)\right)\hfill \\ +{\varphi }_a{\varphi }_b\left(\left(\frac{f_j+f_{j-1}}{2}\right),\left(\frac{(z_2{)}_j+(z_2{)}_{j-1}}{2}\right),-,{\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right)}^2\right)\hfill \\ -{\varphi }_a{\varphi }_{e}M\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right)=0,\hfill \end{array}$$ 4.10

$$\begin{array}{c}\left(\frac{(z_3{)}_j-(z_3{)}_{j-1}}{h}\right)\left(1,+,\lambda ,\left(\frac{{\theta }_j+{\theta }_{j-1}}{2}\right),+,\frac{1}{{\varphi }_d},P_r,N_r\right)\hfill \\ +\lambda {\left(\frac{(z_3{)}_j+(z_3{)}_{j-1}}{2}\right)}^2+P_r\frac{{\varphi }_c}{{\varphi }_d}\left[\left(\frac{f_j+f_{j-1}}{2}\right),\left(\frac{(z_3{)}_j+(z_3{)}_{j-1}}{2}\right)\right]\hfill \\ -P_r\frac{{\varphi }_c}{{\varphi }_d}\left[\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right),\left(\frac{{\theta }_j+{\theta }_{j-1}}{2}\right)\right]\hfill \\ +P_r\frac{{\varphi }_c}{{\varphi }_d}\left[+,\frac{{\varphi }_4}{{\varphi }_3},E_c,{\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right)}^2,+,\frac{E_c}{{\varphi }_a{\varphi }_c},{\left(\frac{{z_2}_j+{z_2}_{j-1}}{2}\right)}^2\right]=0.\hfill \end{array}$$ 4.11

Stage 3: Linearization based on Newtons method

Through the renowned Newton process, the updated formulae were made linearized. Among those the $\left(i+1\right)\text{th}$ iteration can be contracted from the prior procedures as

$$({)}_j^{(i+1)}=({)}_j^{(i)}+{\epsilon }^{\ast }({)}_j^{(i)}.$$ 4.12

After neglecting higher order terms of ${{\epsilon }_j^{\ast }}^i$ and the applicability of Eq. (4.12) in the set of equations from (4.7) to (4.11) the following outcome are obtained and written as

$${\epsilon }^{\ast }{f}_j-{\epsilon }^{\ast }{f}_{j-1}-\frac{1}{2}h({\epsilon }^{\ast }(z_1{)}_j+{\epsilon }^{\ast }(z_1{)}_{j-1})=(r_1{)}_{j-\frac{1}{2}},$$ 4.13

$${\epsilon }^{\ast }(z_1{)}_j-{\epsilon }^{\ast }(z_1{)}_{j-1}-\frac{1}{2}h({\epsilon }^{\ast }(z_2{)}_j+{\epsilon }^{\ast }(z_2{)}_{j-1})=(r_2{)}_{j-\frac{1}{2}},$$ 4.14

$${\epsilon }^{\ast }{\theta }_j-{\epsilon }^{\ast }{\theta }_{j-1}-\frac{1}{2}h({\epsilon }^{\ast }(z_3{)}_j+{\epsilon }^{\ast }(z_3{)}_{j-1})=(r_3{)}_{j-\frac{1}{2}},$$ 4.15

$$\begin{array}{c}(a_1{)}_j{\epsilon }^{\ast }{f}_j+(a_2{)}_j{\epsilon }^{\ast }{f}_{j-1}+(a_3{)}_j{\epsilon }^{\ast }{z_1}_j+(a_4{)}_j{\epsilon }^{\ast }{z_1}_{j-1}+(a_5{)}_j{\epsilon }^{\ast }{z_2}_j+(a_6{)}_j{\epsilon }^{\ast }{z_2}_{j-1}\hfill \\ +(a_7{)}_j{\epsilon }^{\ast }{\theta }_j+(a_8{)}_j{\epsilon }^{\ast }{\theta }_{j-1}+(a_9{)}_j{\epsilon }^{\ast }(z_3{)}_j+(a_{10}{)}_j{\epsilon }^{\ast }(z_3{)}_{j-1}=(r_4{)}_{j-\frac{1}{2}},\hfill \end{array}$$ 4.16

$$\begin{array}{c}(b_1{)}_j{\epsilon }^{\ast }{f}_j+(b_2{)}_j{\epsilon }^{\ast }{f}_{j-1}+(b_3{)}_j{\epsilon }^{\ast }{z_1}_j+(b_4{)}_j{\epsilon }^{\ast }{z_1}_{j-1}+(b_5{)}_j{\epsilon }^{\ast }{z_2}_j+(b_6{)}_j{\epsilon }^{\ast }{z_2}_{j-1}\hfill \\ +(b_7{)}_j{\epsilon }^{\ast }{\theta }_j+(b_8{)}_j{\epsilon }^{\ast }{\theta }_{j-1}+(b_9{)}_j{\epsilon }^{\ast }(z_3{)}_j+(b_{10}{)}_j{\epsilon }^{\ast }(z_3{)}_{j-1}=(r_5{)}_{j-\frac{1}{2}}.\hfill \end{array}$$ 4.17

where

$$(r_1{)}_{j-\frac{1}{2}}=-f_j+f_{j-1}+\frac{h}{2}(z_1{)}_j+((z_1{)}_{j-1}),$$ 4.18

$$(r_2{)}_{j-\frac{1}{2}}=-(z_1{)}_j+(z_1{)}_{j-1}+\frac{h}{2}((z_2{)}_j+(z_2{)}_{j-1}),$$ 4.19

$$(r_3{)}_{j-\frac{1}{2}}=-{\theta }_j+{\theta }_{j-1}+\frac{h}{2}((z_3{)}_j+(z_3{)}_{j-1}),$$ 4.20

$$\begin{array}{cc}\hfill (r_4{)}_{j-\frac{1}{2}}& =h\left[\left(\frac{(z_2{)}_j-(z_2{)}_{j-1}}{h}\right),\left((1-n),+,n,W_e,\left(\frac{(z_2{)}_j+(z_2{)}_{j-1}}{2}\right)\right)\right]\hfill \\ \hfill & -h\left[\left(\left(\frac{f_j+f_{j-1}}{2}\right),\left(\frac{(z_2{)}_j+(z_2{)}_{j-1}}{2}\right),+,{\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right)}^2\right),{\varphi }_a,{\varphi }_b\right]+h\left[M,\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right)\right]=0,\hfill \end{array}$$ 4.21

$$\begin{array}{cc}\hfill (r_5{)}_{j-\frac{1}{2}}& =-h\left[\frac{\left((,z_3,{)}_j,-(,z_3,{)}_{j-1}\right)\left(1,+,\lambda ,\left(\frac{{\theta }_j+{\theta }_{j-1}}{2}\right),+,\frac{1}{{\varphi }_d},P_r,N_r\right)}{h},+,\left[\lambda ,{\left(\frac{(z_3{)}_j+(z_3{)}_{j-1}}{2}\right)}^2\right]\right]\hfill \\ \hfill & -h\frac{{\varphi }_c{P}_r}{{\varphi }_d}\left[\left(\frac{((z_3{)}_j+(z_3{)}_{j-1})(f_j+f_{j-1})}{4}\right),-,\left(\frac{{z_1}_j+{z_1}_{j-1}}{2}\right),\left(\frac{{\theta }_j+{\theta }_{j-1}}{2}\right)\right]\hfill \\ \hfill & -h\frac{{\varphi }_c{P}_r}{{\varphi }_d}\left[\frac{E_c}{{\varphi }_a{\varphi }_c},{\left(\frac{{z_2}_j+{z_2}_{j-1}}{2}\right)+\frac{{\varphi }_{\mathrm{e}}}{{\varphi }_{\mathrm{c}}}{E}_{c}M{\left(\frac{(z_1{)}_j+(z_1{)}_{j-1}}{2}\right)}^2}^2\right].\hfill \end{array}$$ 4.22

Converted boundary conditions are

$${\epsilon }^{\ast }{f}_0=0,{\epsilon }^{\ast }(z_1{)}_0=0,{\epsilon }^{\ast }(z_3{)}_0=0,{\epsilon }^{\ast }(z_1{)}_J=0,{\epsilon }^{\ast }{\theta }_J=0.$$ 4.23

Stage 4: The block tridiagonal matrix

Inorder to linearize the Eqs. (4.13)–(4.17), the bulk tridiagonal-form is engaged and writtened the matrix form of structured matrix vector,

For $j=1;$

$${\epsilon }^{\ast }{f}_1-{\epsilon }^{\ast }{f}_0-\frac{1}{2}h({\epsilon }^{\ast }(z_1{)}_1+{\epsilon }^{\ast }(z_1{)}_0)=(r_1{)}_{1-\frac{1}{2}},$$ 4.24

$${\epsilon }^{\ast }(z_1{)}_1-{\epsilon }^{\ast }(z_1{)}_0-\frac{1}{2}h({\epsilon }^{\ast }(z_2{)}_1+{\epsilon }^{\ast }(z_2{)}_0)=(r_2{)}_{1-\frac{1}{2}},$$ 4.25

$${\epsilon }^{\ast }{\theta }_1-{\epsilon }^{\ast }{\theta }_0-\frac{1}{2}h({\epsilon }^{\ast }(z_3{)}_1+{\epsilon }^{\ast }(z_3{)}_0)=(r_3{)}_{1-\frac{1}{2}},$$ 4.26

$$\begin{array}{c}(a_1{)}_1{\epsilon }^{\ast }{f}_1+(a_2{)}_1{\epsilon }^{\ast }{f}_0+(a_3{)}_1{\epsilon }^{\ast }{z_1}_1+(a_4{)}_1{\epsilon }^{\ast }{z_1}_0+(a_5{)}_1{\epsilon }^{\ast }{z_2}_1+(a_6{)}_1{\epsilon }^{\ast }{z_2}_0\hfill \\ +(a_7{)}_1{\epsilon }^{\ast }{\theta }_j+(a_8{)}_1{\epsilon }^{\ast }{\theta }_0+(a_9{)}_1{\epsilon }^{\ast }(z_3{)}_1+(a_{10}{)}_1{\epsilon }^{\ast }(z_3{)}_0=(r_4{)}_{1-\frac{1}{2}},\hfill \end{array}$$ 4.27

$$\begin{array}{c}(b_1{)}_1{\epsilon }^{\ast }{f}_1+(b_2{)}_1{\epsilon }^{\ast }{f}_0+(b_3{)}_1{\epsilon }^{\ast }{z_1}_1+(b_4{)}_1{\epsilon }^{\ast }{z_1}_0+(b_5{)}_1{\epsilon }^{\ast }{z_2}_1+(b_6{)}_1{\epsilon }^{\ast }{z_2}_0\hfill \\ +(b_7{)}_1{\epsilon }^{\ast }{\theta }_1+(b_8{)}_1{\epsilon }^{\ast }{\theta }_0+(b_9{)}_1{\epsilon }^{\ast }(z_3{)}_1+(b_{10}{)}_1{\epsilon }^{\ast }(z_3{)}_0=(r_5{)}_{1-\frac{1}{2}}.\hfill \end{array}$$ 4.28

In matrix form,

$$\left[\begin{array}{ccccc}0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ -h/2\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & -h/2\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ (a_2{)}_1\hfill & (a_{10}{)}_1\hfill & (a_3{)}_1\hfill & (a_1{)}_1\hfill & (a_9{)}_1\hfill \\ (b_2{)}_1\hfill & (b_{10}{)}_1\hfill & (b_3{)}_1\hfill & (b_1{)}_1\hfill & (b_9{)}_1\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_2{)}_0\hfill \\ {\epsilon }^{\ast }(\theta {)}_0\hfill \\ {\epsilon }^{\ast }(f{)}_1\hfill \\ {\epsilon }^{\ast }(z_2{)}_1\hfill \\ {\epsilon }^{\ast }(z_3{)}_1\hfill \end{array}\right]+\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ (a_5{)}_1\hfill & (a_7{)}_1\hfill & 0\hfill & 0\hfill & 0\hfill \\ (b_5{)}_1\hfill & (b_7{)}_1\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_1{)}_1\hfill \\ {\epsilon }^{\ast }(\theta {)}_1\hfill \\ {\epsilon }^{\ast }(f{)}_2\hfill \\ {\epsilon }^{\ast }(z_2{)}_2\hfill \\ {\epsilon }^{\ast }(z_3{)}_2\hfill \end{array}\right]=\left[\begin{array}{c}(r_1{)}_{\frac{1}{2}}\hfill \\ (r_2{)}_{\frac{1}{2}}\hfill \\ (r_3{)}_{\frac{1}{2}}\hfill \\ (r_4{)}_{\frac{1}{2}}\hfill \\ (r_5{)}_{\frac{1}{2}}\hfill \end{array}\right].$$ 4.28

That is

$$[A_1][{\epsilon }_1^{\ast }]+[C_1][{\epsilon }_2^{\ast }]=[r_1].$$ 4.29

For $j=2;$

$${\epsilon }^{\ast }{f}_2-{\epsilon }^{\ast }{f}_1-\frac{1}{2}h({\epsilon }^{\ast }(z_1{)}_2+{\epsilon }^{\ast }(z_1{)}_1)=(r_1{)}_{1-\frac{1}{2}},$$ 4.30

$${\epsilon }^{\ast }(z_1{)}_2-{\epsilon }^{\ast }(z_1{)}_1-\frac{1}{2}h({\epsilon }^{\ast }(z_2{)}_2+{\epsilon }^{\ast }(z_2{)}_1)=(r_2{)}_{1-\frac{1}{2}},$$ 4.31

$${\epsilon }^{\ast }{\theta }_1-{\epsilon }^{\ast }{\theta }_0-\frac{1}{2}h({\epsilon }^{\ast }(z_3{)}_2+{\epsilon }^{\ast }(z_3{)}_1)=(r_3{)}_{1-\frac{1}{2}},$$ 4.32

$$\begin{array}{c}(a_1{)}_2{\epsilon }^{\ast }{f}_2+(a_2{)}_2{\epsilon }^{\ast }{f}_1+(a_3{)}_2{\epsilon }^{\ast }{z_1}_2+(a_4{)}_2{\epsilon }^{\ast }{z_1}_1+(a_5{)}_2{\epsilon }^{\ast }{z_2}_2+(a_6{)}_2{\epsilon }^{\ast }{z_2}_1\hfill \\ +(a_7{)}_2{\epsilon }^{\ast }{\epsilon }_2+(a_8{)}_2{\epsilon }^{\ast }{\theta }_1+(a_9{)}_2{\epsilon }^{\ast }(z_3{)}_2+(a_{10}{)}_2{\epsilon }^{\ast }(z_3{)}_1=(r_4{)}_{2-\frac{1}{2}},\hfill \end{array}$$ 4.33

$$\begin{array}{c}(b_1{)}_2{\epsilon }^{\ast }{f}_2+(b_2{)}_2{\epsilon }^{\ast }{f}_1+(b_3{)}_2{\epsilon }^{\ast }{z_1}_2+(b_4{)}_2{\epsilon }^{\ast }{z_1}_1+(b_5{)}_2{\epsilon }^{\ast }{z_2}_2+(b_6{)}_2{\epsilon }^{\ast }{z_2}_1\hfill \\ +(b_7{)}_2{\epsilon }^{\ast }{\theta }_2+(b_8{)}_2{\epsilon }^{\ast }{\theta }_1+(b_9{)}_2{\epsilon }^{\ast }(z_3{)}_2+(b_{10}{)}_2{\epsilon }^{\ast }(z_3{)}_1=(r_5{)}_{2-\frac{1}{2}}.\hfill \end{array}$$ 4.34

In matrix form,

$$\begin{array}{cc}& \left[\begin{array}{ccccc}0\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ 0\hfill & 0\hfill & (a_4{)}_2\hfill & (a_2{)}_2\hfill & (a_{10}{)}_2\hfill \\ 0\hfill & 0\hfill & (b_4{)}_2\hfill & (b_2{)}_2\hfill & (b_{10}{)}_2\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_2{)}_0\hfill \\ {\epsilon }^{\ast }(\theta {)}_0\hfill \\ {\epsilon }^{\ast }(f{)}_1\hfill \\ {\epsilon }^{\ast }(z_2{)}_1\hfill \\ {\epsilon }^{\ast }(z_3{)}_1\hfill \end{array}\right]+\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ -1\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & -1\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ (a_6{)}_2\hfill & (a_8{)}_2\hfill & (a_3{)}_2\hfill & (a_1{)}_2\hfill & (a_9{)}_2\hfill \\ (b_6{)}_2\hfill & (b_8{)}_2\hfill & (b_3{)}_2\hfill & (b_1{)}_2\hfill & (b_9{)}_2\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_1{)}_1\hfill \\ {\epsilon }^{\ast }(\theta {)}_1\hfill \\ {\epsilon }^{\ast }(f{)}_2\hfill \\ {\epsilon }^{\ast }(z_2{)}_2\hfill \\ {\epsilon }^{\ast }(z_3{)}_2\hfill \end{array}\right]\hfill \\ \hfill & +\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 1\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ (a_5{)}_2\hfill & (a_7{)}_2\hfill & 0\hfill & 0\hfill & 0\hfill \\ (b_5{)}_2\hfill & (b_7{)}_2\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_1{)}_1\hfill \\ {\epsilon }^{\ast }(\theta {)}_1\hfill \\ {\epsilon }^{\ast }(f{)}_2\hfill \\ {\epsilon }^{\ast }(z_2{)}_2\hfill \\ {\epsilon }^{\ast }(z_3{)}_2\hfill \end{array}\right]=\left[\begin{array}{c}(r_1{)}_{\frac{3}{2}}\hfill \\ (r_2{)}_{\frac{3}{2}}\hfill \\ (r_3{)}_{\frac{3}{2}}\hfill \\ (r_4{)}_{\frac{3}{2}}\hfill \\ (r_5{)}_{\frac{3}{2}}\hfill \end{array}\right].\hfill \end{array}$$ 4.35

That is

$$[B_2][{\epsilon }_1^{\ast }]+[A_2][{\epsilon }_2^{\ast }]+[C_2][{\epsilon }_3^{\ast }]=[r_2].$$ 4.36

For $j=J-1;$

$${\epsilon }^{\ast }{f}_{J-1}-{\epsilon }^{\ast }{f}_{J-2}-\frac{1}{2}h({\epsilon }^{\ast }(z_1{)}_{J-1}+{\epsilon }^{\ast }{z_1}_{J-2})=(r_1{)}_{J-1-\frac{1}{2}},$$ 4.37

$${\epsilon }^{\ast }(z_1{)}_{J-1}-{\epsilon }^{\ast }(z_1{)}_{J-2}-\frac{1}{2}h({\epsilon }^{\ast }(z_2{)}_{J-1}+{\epsilon }^{\ast }(z_2{)}_{J-2})=(r_2{)}_{J-1-\frac{1}{2}},$$ 4.38

$${\epsilon }^{\ast }{\theta }_{J-1}-{\epsilon }^{\ast }{\theta }_{J-2}-\frac{1}{2}h({\epsilon }^{\ast }(z_3{)}_{J-1}+{\epsilon }^{\ast }(z_3{)}_{J-2})=(r_3{)}_{J-1-\frac{1}{2}},$$ 4.39

$$\begin{array}{c}(a_1{)}_{J-1}{\epsilon }^{\ast }{f}_{J-1}+(a_2{)}_{J-1}{\epsilon }^{\ast }{f}_{J-2}+(a_3{)}_{J-1}{\epsilon }^{\ast }{z_1}_{J-1}+(a_4{)}_{J-1}{\epsilon }^{\ast }{z_1}_{J-2}\hfill \\ +(a_5{)}_{J-1}{\epsilon }^{\ast }{z_2}_j+(a_6{)}_{J-1}{\epsilon }^{\ast }{z_2}_{J-2}+(a_7{)}_{J-1}{\epsilon }^{\ast }{\theta }_{J-1}+(a_8{)}_{J-1}{\epsilon }^{\ast }{\theta }_{J-2}\hfill \\ +(a_9{)}_{J-1}{\epsilon }^{\ast }(z_3{)}_{J-1}+(a_{10}{)}_{J-1}{\epsilon }^{\ast }(z_3{)}_{J-2}=(r_4{)}_{J-1-\frac{1}{2}},\hfill \end{array}$$ 4.40

$$\begin{array}{c}(b_1{)}_{J-1}{\epsilon }^{\ast }{f}_{J-1}+(b_2{)}_{J-1}{\epsilon }^{\ast }{f}_{J-2}+(b_3{)}_{J-1}{\epsilon }^{\ast }{z_1}_{J-1}+(b_4{)}_{J-1}{\epsilon }^{\ast }{z_1}_{J-2}\hfill \\ +(b_5{)}_{J-1}{\epsilon }^{\ast }{z_2}_{J-1}+(b_6{)}_{J-1}{\epsilon }^{\ast }{z_2}_{J-2}+(b_7{)}_{J-1}{\epsilon }^{\ast }{\theta }_{J-1}+(b_8{)}_{J-1}{\epsilon }^{\ast }{\theta }_{J-2}\hfill \\ +(b_9{)}_{J-1}{\epsilon }^{\ast }(z_3{)}_{J-1}+(b_{10}{)}_{J-1}{\epsilon }^{\ast }(z_3{)}_{J-2}=(r_5{)}_{J-1-\frac{1}{2}}.\hfill \end{array}$$ 4.41

In matrix form,

$$\left[\begin{array}{ccccc}0\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ 0\hfill & 0\hfill & (a_4{)}_{J-2}\hfill & (a_2{)}_{J-2}\hfill & (a_{10}{)}_{J/2}\hfill \\ 0\hfill & 0\hfill & (b_4{)}_{J-2}\hfill & (b_2{)}_{J-2}\hfill & (b_{10}{)}_{J-2}\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_2{)}_{J-3}\hfill \\ {\epsilon }^{\ast }(\theta {)}_{J-3}\hfill \\ {\epsilon }^{\ast }(f{)}_{J-2}\hfill \\ {\epsilon }^{\ast }(z_2{)}_{J-2}\hfill \\ {\epsilon }^{\ast }(z_3{)}_{J-2}\hfill \end{array}\right]+\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ -1\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & -1\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ (a_6{)}_{J-2}\hfill & (a_8{)}_{J-2}\hfill & (a_3{)}_{J-2}\hfill & (a_1{)}_{J-2}\hfill & (a_9{)}_{J-2}\hfill \\ (b_6{)}_{J-2}\hfill & (b_8{)}_{J-2}\hfill & (b_3{)}_{J-2}\hfill & (b_1{)}_{J-2}\hfill & (b_9{)}_{J-2}\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_2{)}_{J-2}\hfill \\ {\epsilon }^{\ast }(\theta {)}_{J-2}\hfill \\ {\epsilon }^{\ast }(f{)}_{J-1}\hfill \\ {\epsilon }^{\ast }(z_2{)}_{J-1}\hfill \\ {\epsilon }^{\ast }(z_3{)}_{J-1}\hfill \end{array}\right]+\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ (a_5{)}_{J-2}\hfill & (a_9{)}_{J-2}\hfill & 0\hfill & 0\hfill & 0\hfill \\ (b_5{)}_{J-2}\hfill & (b_9{)}_{J-2}\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_1{)}_{J-1}\hfill \\ {\epsilon }^{\ast }(\theta {)}_{J-1}\hfill \\ {\epsilon }^{\ast }(f{)}_J\hfill \\ {\epsilon }^{\ast }(z_2{)}_J\hfill \\ {\epsilon }^{\ast }(z_3{)}_J\hfill \end{array}\right]=\left[\begin{array}{c}(r_1{)}_{(J-1)-\frac{1}{2}}\hfill \\ (r_2{)}_{(J-1)-\frac{1}{2}}\hfill \\ (r_3{)}_{(J-1)-\frac{1}{2}}\hfill \\ (r_4{)}_{(J-1)-\frac{1}{2}}\hfill \\ (r_5{)}_{(J-1)-\frac{1}{2}}\hfill \end{array}\right].$$ 4.42

That is

$$[B_{J-1}][{\epsilon }_{J-2}^{\ast }]+[A_{J-1}][{\epsilon }_{J-1}^{\ast }]+[C_{J-1}][{\epsilon }_J^{\ast }]=[r_{J-1}].$$ 4.43

For $j=J;$

$${\epsilon }^{\ast }{f}_J-{\epsilon }^{\ast }{f}_{J-1}-\frac{1}{2}h({\epsilon }^{\ast }(z_1{)}_J+{\epsilon }^{\ast }(z_1{)}_{J-1})=(r_1{)}_{J-\frac{1}{2}},$$ 4.44

$${\epsilon }^{\ast }(z_1{)}_J-{\epsilon }^{\ast }(z_1{)}_{J-1}-\frac{1}{2}h({\epsilon }^{\ast }(z_2{)}_J+{\epsilon }^{\ast }(z_2{)}_{J-1})=(r_2{)}_{J-\frac{1}{2}},$$ 4.45

$${\epsilon }^{\ast }{\theta }_J-{\epsilon }^{\ast }{\theta }_{J-1}-\frac{1}{2}h({\epsilon }^{\ast }(z_3{)}_J+{\epsilon }^{\ast }(z_3{)}_{J-1})=(r_3{)}_{J-\frac{1}{2}},$$ 4.46

$$\begin{array}{c}(a_1{)}_J{\epsilon }^{\ast }{f}_J+(a_2{)}_J{\epsilon }^{\ast }{f}_{J-1}+(a_3{)}_J{\epsilon }^{\ast }{z_1}_J+(a_4{)}_J{\epsilon }^{\ast }{z_1}_{J-1}+(a_5{)}_J{\epsilon }^{\ast }{z_2}_J+(a_6{)}_J{\epsilon }^{\ast }{z_2}_{J-1}\hfill \\ +(a_7{)}_J{\epsilon }^{\ast }{\theta }_J+(a_8{)}_J{\epsilon }^{\ast }{\theta }_{J-1}+(a_9{)}_J{\epsilon }^{\ast }(z_3{)}_J+(a_{10}{)}_J{\epsilon }^{\ast }(z_3{)}_{J-1}=(r_4{)}_{J-\frac{1}{2}},\hfill \end{array}$$ 4.47

$$\begin{array}{c}(b_1{)}_J{\epsilon }^{\ast }{f}_J+(b_2{)}_J{\epsilon }^{\ast }{f}_{J-1}+(b_3{)}_J{\epsilon }^{\ast }{z_1}_J+(b_4{)}_J{\epsilon }^{\ast }{z_1}_{J-1}+(b_5{)}_J{\epsilon }^{\ast }{z_2}_J+(b_6{)}_J{\epsilon }^{\ast }{z_2}_{J-1}\hfill \\ +(b_7{)}_J{\epsilon }^{\ast }{\theta }_J+(b_8{)}_J{\epsilon }^{\ast }{\theta }_{J-1}+(b_9{)}_J{\epsilon }^{\ast }(z_3{)}_J+(b_{10}{)}_J{\epsilon }^{\ast }(z_3{)}_{J-1}=(r_5{)}_{J-\frac{1}{2}}.\hfill \end{array}$$ 4.48

In matrix form,

$$\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ -1\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & -1\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ (a_6{)}_1\hfill & (a_8{)}_1\hfill & (a_3{)}_1\hfill & (a_1{)}_1\hfill & (a_9{)}_1\hfill \\ (b_6{)}_1\hfill & (b_8{)}_1\hfill & (b_3{)}_1\hfill & (b_1{)}_1\hfill & (b_9{)}_1\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_2{)}_0\hfill \\ {\epsilon }^{\ast }(\theta {)}_0\hfill \\ {\epsilon }^{\ast }(f{)}_1\hfill \\ {\epsilon }^{\ast }(z_2{)}_1\hfill \\ {\epsilon }^{\ast }(z_3{)}_1\hfill \end{array}\right]+\left[\begin{array}{ccccc}-h/2\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ -1\hfill & 0\hfill & 0\hfill & -h/2\hfill & 0\hfill \\ 0\hfill & -1\hfill & 0\hfill & 0\hfill & -h/2\hfill \\ (a_6{)}_{J-2}\hfill & (a_8{)}_{J-2}\hfill & (a_3{)}_{J-2}\hfill & (a_1{)}_{J-2}\hfill & (a_9{)}_{J-2}\hfill \\ (b_6{)}_{J-2}\hfill & (b_8{)}_{J-2}\hfill & (b_3{)}_{J-2}\hfill & (b_1{)}_{J-2}\hfill & (b_9{)}_{J-2}\hfill \end{array}\right]\left[\begin{array}{c}{\epsilon }^{\ast }(z_2{)}_{J-2}\hfill \\ {\epsilon }^{\ast }(\theta {)}_{J-2}\hfill \\ {\epsilon }^{\ast }(f{)}_{J-1}\hfill \\ {\epsilon }^{\ast }(z_2{)}_{J-1}\hfill \\ {\epsilon }^{\ast }(z_3{)}_{J-1}\hfill \end{array}\right]=\left[\begin{array}{c}(r_1{)}_{\frac{1}{2}}\hfill \\ (r_2{)}_{\frac{1}{2}}\hfill \\ (r_3{)}_{\frac{1}{2}}\hfill \\ (r_4{)}_{\frac{1}{2}}\hfill \\ (r_5{)}_{\frac{1}{2}}\hfill \end{array}\right].$$ 4.49

That is

$$[B_J][{\epsilon }_{J-1}^{\ast }]+[A_J][{\epsilon }_J^{\ast }]=[r_J].$$ 4.50

Phase 5: Block network with exclusion

In the termination, a tri-diagonal form is accomplished from formulations (4.24)–(4.48) as follows,

$$R{\epsilon }^{\ast }=p,$$ 4.51

where

$$R=\left[\begin{array}{cccccc}{A}_1\hfill & C_1\hfill & & & & \\ B_2\hfill & A_2\hfill & C_2\hfill & & & \\ \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & & \\ \hfill & & \ddots \hfill & \ddots \hfill & \ddots \hfill & \\ \hfill & & & B_{J-1}\hfill & A_{J-1}\hfill & C_{J-1}\hfill \\ \hfill & & & & B_J\hfill & A_J\hfill \end{array}\right],{\epsilon }^{\ast }=\left[\begin{array}{c}{\epsilon }_1^{\ast }\hfill \\ {\epsilon }_2^{\ast }\hfill \\ ⋮\hfill \\ {\epsilon }_{j-1}^{\ast }\hfill \\ {\epsilon }_j^{\ast }\hfill \end{array}\right],p=\left[\begin{array}{c}(r_1{)}_{j-\frac{1}{2}}\hfill \\ (r_2{)}_{j-\frac{1}{2}}\hfill \\ ⋮\hfill \\ (r_{J-1}{)}_{j-\frac{1}{2}}\hfill \\ (r_J{)}_{j-\frac{1}{2}}\hfill \end{array}\right].$$ 4.52

form the comprehensive sized $J\times J$, that $5\times 5$ blocks were represented with the label of ‘R’. In the intervening time both then ${\epsilon }^{\ast }$ and $p$ characterize $J\times 1$ column vector. Then an renowned LU technique of factorization has been employed to obtain the solutions of ${\epsilon }^{\ast }$. The matrix form of representation can be framed for the equation $R{\epsilon }^{\ast }=p$ to get the solution for ${\epsilon }^{\ast }$. The equality $R{\epsilon }^{\ast }=p$ represents the fact of outputs as p with the combination of the matrix $R$ and $\mathrm{\Delta }$ to produce a vector based fabricating solutions. Later by the splitting of matrices as in the tiagonal of kinds mentioned as apper and lower representations. Following that, for $LU{\epsilon }^{\ast }=p$ which plays vital role in solution from $Ly=p$ methodology. At last computed and fine tuned into $U{\epsilon }^{\ast }=y$ to sovle for more ${\epsilon }^{\ast }.$ By opting the renowned tridiognal outcomes combined with back substitution and it could used the familiar way of solving for optimal solutions.

Encryption authentication

The legality in the solution of the system was assessed with the identical way on the raw of thermal conversion were compared with prevailing outcomes from the preceding works^56–59. Conclusive evidence could be viewed from the Table 5 which provides the confidence to proceed with this working setup.

Table 5.

Evaluation of $-{\theta }^{\prime }\left(0\right)$ with varied Prandtl number, $\varphi =0$, ${\varphi }_{\mathit{hnf}}=0$, $\lambda =0$, $\mathrm{{\rm Y}}=0$, $M=0$, $N_r=0$, $E_c=0$,$S=0$ and $B_i=0$.

$\mathit{Pr}$	Ref.56	Ref.57	Ref.58	Ref.59	Present
72 × 10–2	08,086 × 10–4	08,086 × 10–4	080,863,135 × 10–8	080,876,122 × 10–8	080,876,181 × 10–8
1 × 100	1 × 100	1 × 100	1 × 100	1 × 100	1 × 100
3 × 100	19,237 × 10–4	19,236 × 10–4	192,368,259 × 10–8	192,357,431 × 10–8	192,357,420 × 10–8
7 × 100	30,723 × 10–4	30,722 × 10–4	307,225,021 × 10–8	307,314,679 × 10–8	307,314,651 × 10–8
10 × 100	37,207 × 10–4	37,006 × 10–4	372,067,390 × 10–8	372,055,436 × 10–8	372,055,429 × 10–8

Analysis of entropy formation

Irreversible energy drains in the system were modelled as entropy formation. Factor like permeability looks in favour prices of such kind. Das et al.⁵⁹ quantified the prevailing nanofluid entropy formation as:

$$E_G=\frac{k_{\mathit{hnf}}}{{\yen }_{\infty }^2}\left\{{\left(\frac{\partial \yen }{\partial y}\right)}^2+\frac{16}{3}\frac{{\sigma }^{\ast }{\yen }_{\infty }^3}{{\kappa }^{\ast }{\nu }_f{(\rho C_p)}_f}{\left(\frac{\partial \yen }{\partial y}\right)}^2\right\}+\frac{{\mu }_{\mathit{hnf}}}{{\yen }_{\infty }}{\left(\frac{\partial v_1}{\partial y}\right)}^2+\frac{{\sigma }_{\mathit{hnf}}{B}^2{u}^2}{{\yen }_{\infty }}.$$ 6.1

The dimensionless form of entropy form was represented as^59–64,

$$N_G=\frac{{\yen }_{\infty }^2{b}^2{E}_G}{k_f{\left({\yen }_w-{\yen }_{\infty }\right)}^2}.$$ 6.2

Entropy is expressed as:

$$N_G=R_e\left[{\varphi }_d\left(1+N_r\right){\theta }^{\prime 2}+\frac{1}{{\varphi }_a}\frac{B_r}{\mathrm{\Omega }}\left(f^{″2}+{\varphi }_{\text{a}}{\varphi }_{\text{e}}M{f}^{\prime 2}\right)\right],$$ 6.3

Here $R_e=\frac{U_w{b}^2}{{\nu }_{f}x}$ is the Reynolds number, $B_r=\frac{{\mu }_f{U}_w^2}{k_f\left({\yen }_w-{\yen }_{\infty }\right)}$ shows the Brinkmann amount and $\mathrm{\Omega }=\frac{{\yen }_w-{\yen }_{\infty }}{{\yen }_{\infty }}$ is the variance in thermal states.

Upshots and analysis

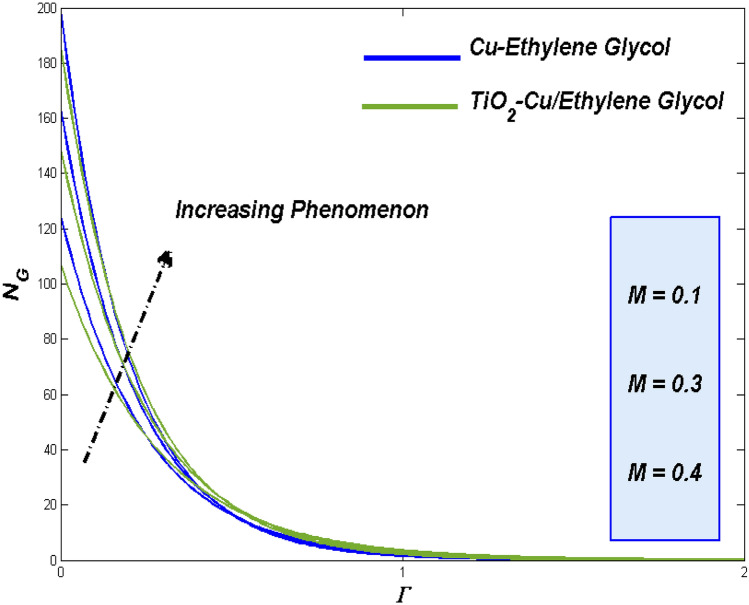
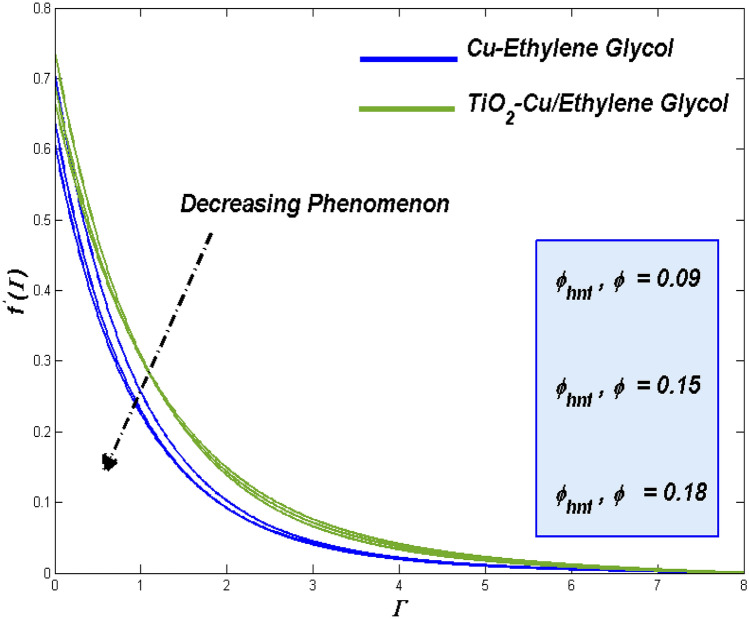
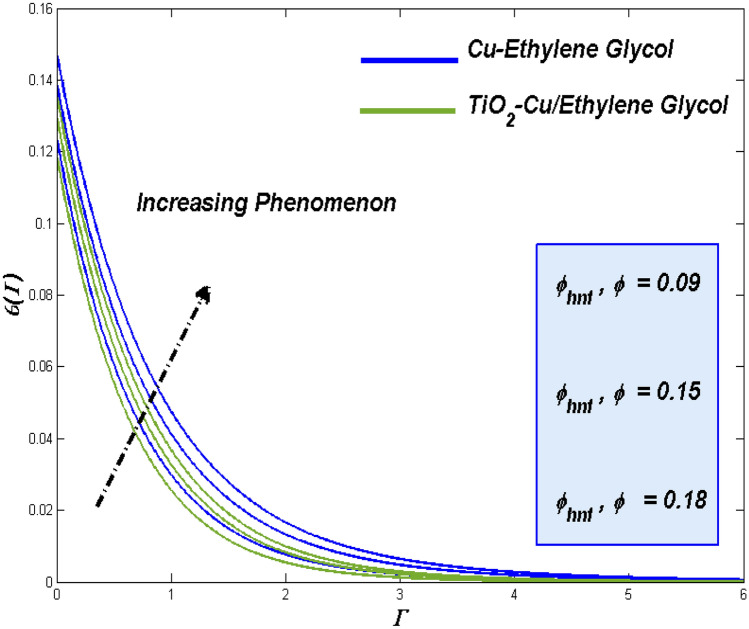
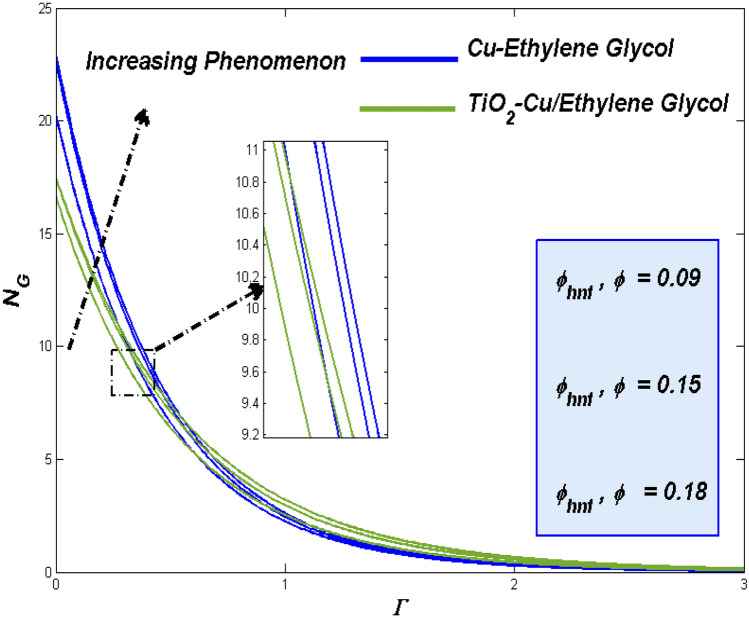
In view of the upshots from the combined effort of the model with the optimal numerical scheme, the parametric specific analysis has to be done under this section. The impending constrains like $W_e,$ $M$, $\varphi$, $\mathrm{{\rm Y}}$, $N_r$ $B_i$, $\lambda$, $E_c,$ $S$, $n,$ $R_e$ and $B_r$ are to be spotted in this segment. Sequence of graphical presentation of Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 and 33 were portrayed in view of exploring the physical aspects like fluidity, thermal and irreversible energy loss related to this problem.

Figure 4.

Velocity discrepancy against $W_e$.

Figure 5.

Temperature discrepancy against $W_e$.

Figure 6.

Entropy discrepancy against $W_e$.

Figure 7.

Temperature discrepancy against $m$.

Figure 8.

Entropy discrepancy against $m$.

Figure 9.

Velocity discrepancy against $M$.

Figure 10.

Temperature discrepancy against $M$.

Figure 11.

Entropy discrepancy against $M$.

Figure 12.

Velocity discrepancy against $\varphi$ and ${\varphi }_{\mathit{hnf}}$.

Figure 13.

Temperature discrepancy against $\varphi$ and ${\varphi }_{\mathit{hnf}}$.

Figure 14.

Entropy discrepancy against $\varphi$ and ${\varphi }_{\mathit{hnf}}$.

Figure 15.

Velocity discrepancy against $\mathrm{{\rm Y}}$.

Figure 16.

Temperature discrepancy against $\mathrm{{\rm Y}}$.

Figure 17.

Entropy discrepancy against $\mathrm{{\rm Y}}$.

Figure 18.

Velocity discrepancy against $S>0$.

Figure 19.

Temperature discrepancy against $S>0$.

Figure 20.

Entropy discrepancy against $S>0$.

Figure 21.

Velocity discrepancy against $S<0$.

Figure 22.

Temperature discrepancy against $S<0$.

Figure 23.

Entropy discrepancy against $S<0$.

Figure 24.

Temperature discrepancy against $N_r$.

Figure 25.

Entropy discrepancy against $N_r$.

Figure 26.

Temperature discrepancy against $E_c.$

Figure 27.

Entropy discrepancy against $E_c.$

Figure 28.

Temperature discrepancy against $\lambda$.

Figure 29.

Entropy variations versus $\lambda$.

Figure 30.

Temperature discrepancy against $B_i$.

Figure 31.

Entropy discrepancy against $B_i$.

Figure 32.

Entropy discrepancy against $R_e$.

Figure 33.

Entropy discrepancy against $B_r$.

For the Tangent hyperbolic nanofluids with Cu-EG nano variant and TiO₂-Cu/EG hybrid variant, the fallouts are attained. Table 6 designates the drag force coefficients and disparities of thermal state.

Table 6.

Values of skin friction $=C_{f}R{e}_x^{\frac{1}{2}}$ and Nusselt number $=N{u}_{x}R{e}_x^{\frac{-1}{2}}$ for $P_r=7.38$, and $n=0.2$

$W_e$	$M$	$\varphi$	${\varphi }_{Ti{O}_2}$	$\mathrm{{\rm Y}}$	$N_r$	$B_i$	$E_c$	$\lambda$	$S$	$C_{f}R{e}_x^{\frac{1}{2}}$ Cu–EG	$C_{f}R{e}_x^{\frac{1}{2}}$ TiO2–Cu/EG	$N_{u}R{e}_x^{\frac{-1}{2}}$ Cu–EG	$N_{u}R{e}_x^{\frac{-1}{2}}$ TiO2–Cu/EG
0.1	0.1	0.18	0.09	0.3	0.3	0.3	0.3	0.2	0.1	2.3839	2.7558	1.2114	1.2589
0.2										2.3654	2.7355	1.1972	1.2368
0.3										2.3343	2.7124	1.1716	1.1942
	0.1									2.3839	2.7558	1.2114	1.2589
	0.3									2.4065	2.7704	1.1946	1.2333
	0.4									2.4202	2.7928	1.1717	1.2147
		0.09								2.3839	-	1.2114	-
		0.15								2.4025	-	1.2273	-
		0.18								2.4242	–	1.2392	–
			0.0							–	2.3839	–	1.2114
			0.06							–	2.7339	–	1.2439
			0.09							–	2.7558	–	1.2589
				0.1						2.4245	2.7953	1.2523	1.2992
				0.2						2.4024	2.7721	1.2325	1.2778
				0.3						2.3839	2.7558	1.2114	1.2589
					0.1					2.3839	2.7558	1.1969	1.2336
					0.3					2.3839	2.7558	1.2114	1.2589
					0.5					2.3839	2.7558	1.2388	1.2793
						0.1				2.3839	2.7558	1.1745	1.2129
						0.3				2.3839	2.7558	1.2114	1.2589
						0.4				2.3839	2.7558	1.2368	1.2945
							0.1			2.3839	2.7558	1.2358	1.2718
							0.3			2.3839	2.7558	1.2114	1.2589
							0.4			2.3839	2.7558	1.1989	1.2346
								0.1		2.3839	2.7558	1.2114	1.2589
								0.2		2.3839	2.7558	1.1946	1.2365
								0.3		2.3839	2.7558	1.1729	1.2146
									0.1	2.3839	2.7558	1.2114	1.2589
									0.2	2.4034	2.7746	1.2337	1.2754
									0.3	2.4226	2.7952	1.2582	1.2972

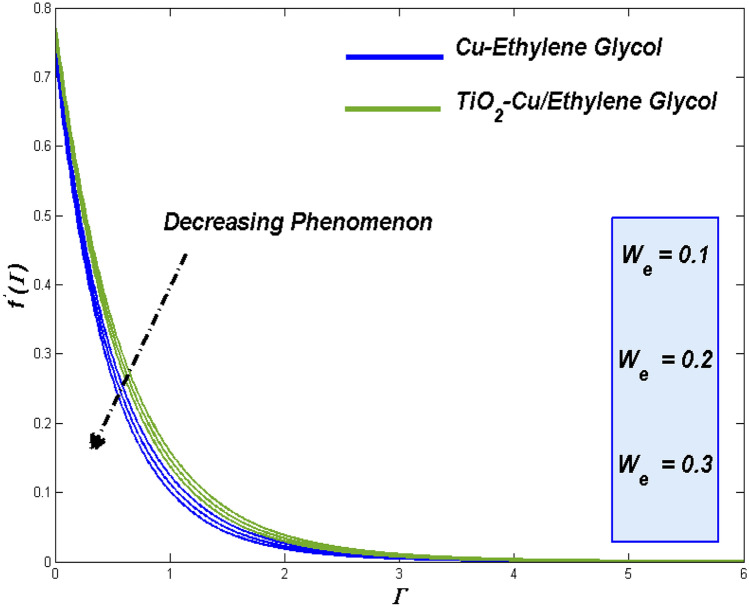
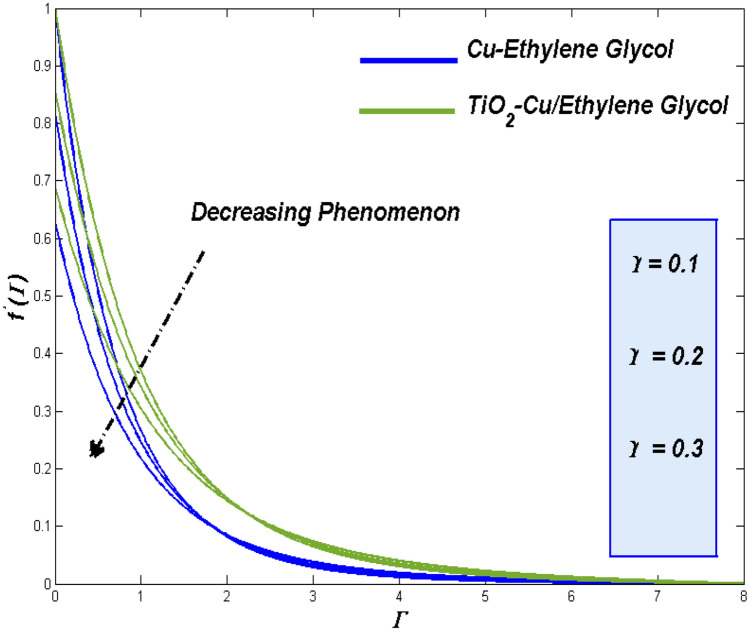
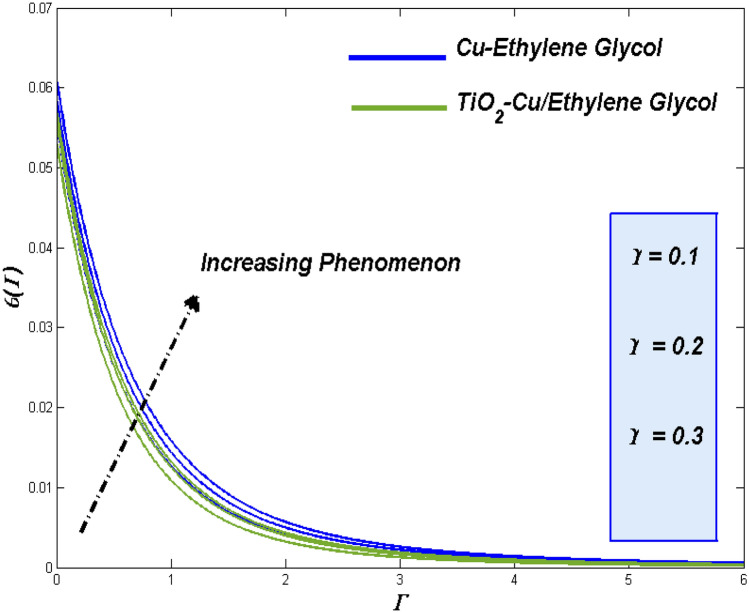
Impression of Weissenberg number (${\mathit{W}}_{\mathit{e}}$)

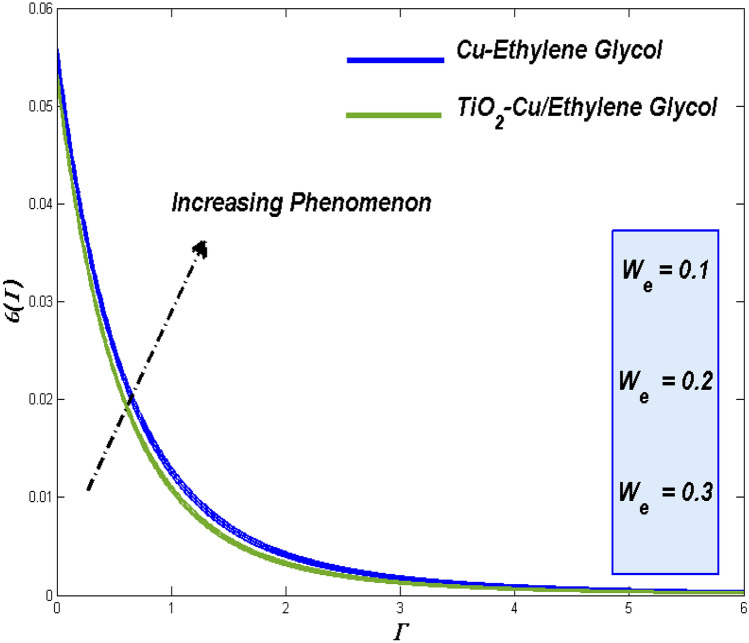
The raise in Weissenberg number ($W_e$) reflects in improved viscous and frictional aspects of the flow fluid and makes it tougher to move. Figure 4 evident the lagging in the fluidity for such enhancement in Weissenberg number ($W_e$). It reflects in improve thermal transference (Fig. 5) through the fact of more in contact time with the surface to clutch more heat from it. More the thermal transference more the entropy.

In Fig. 4, the flow is reduced for thermal absorption and the elevation of thermal distribution (Fig. 5) due to the slow movement of the hybrid nanofluid for higher values of Weissenberg number ($W_e$). At the same time, the reduced viscosity allows the nanofluid to retain its contact with the surface. At plate, the entropy level of hybrid combo stays ahead of nanofluid, and moving on it inverted as it move beyond the plate (Fig. 6).

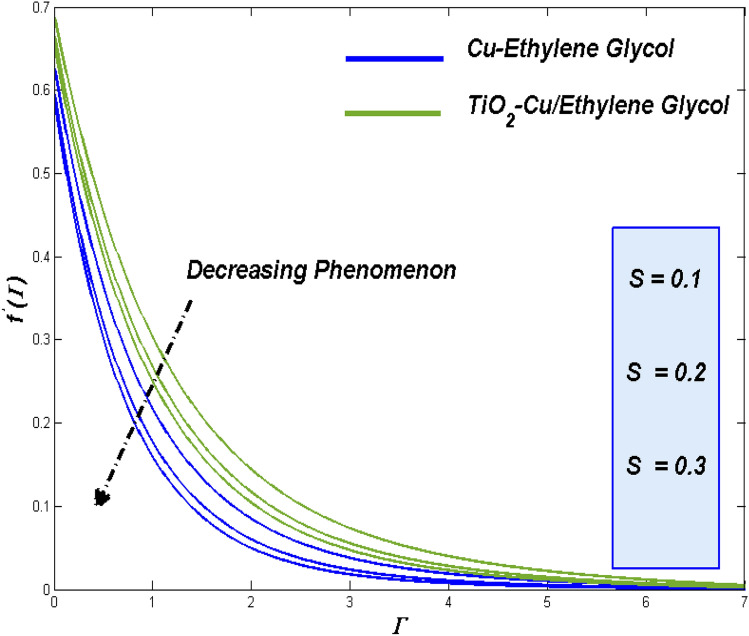
Impact of shape factor ($m$)

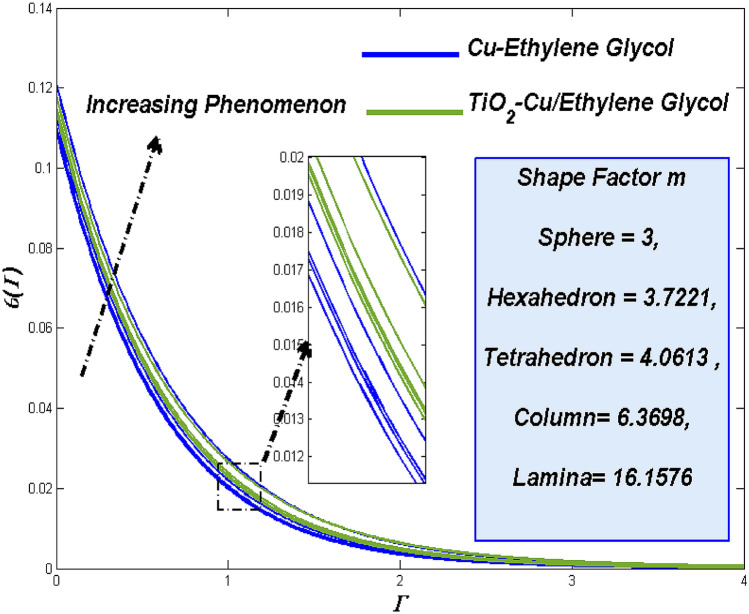
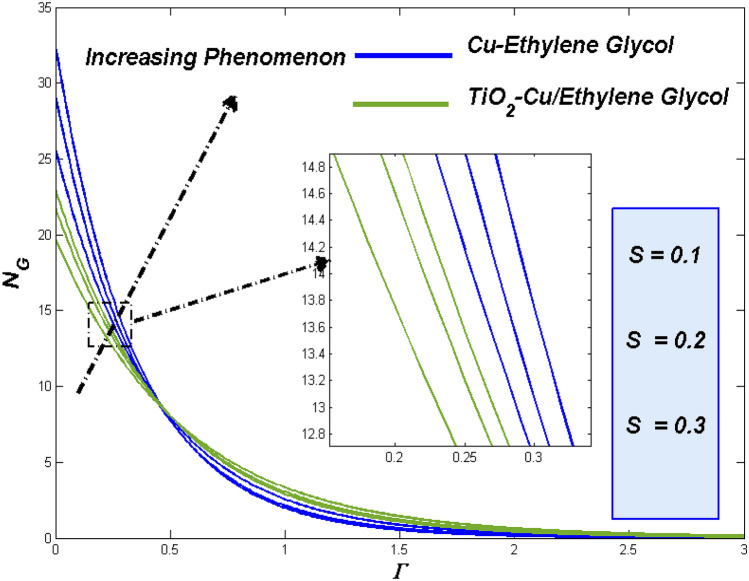
The variable $\left(m\right)$ has been employed to manipulate the shape factor of nanoparticle engaged in this study. The shape variation was made to start from spherical, hexahedron, tetrahedron column, and finally into laminar. Physically, this order of changes was introduced based on their thermal transmitting ability. Figure 7 exhibits the elevated thermal diffusion for varied shapes with enhanced thermal transmitting capacity.

Figure 8 presents the improved entropy production for the shape variants. As the shapes tended to improvise the transmitting process, which exerts more irreversible energies this may lead to raise in entropy state for vital shape alterations in both hybrid TiO₂–Cu/EG fluid and Cu–EG nanofluid.

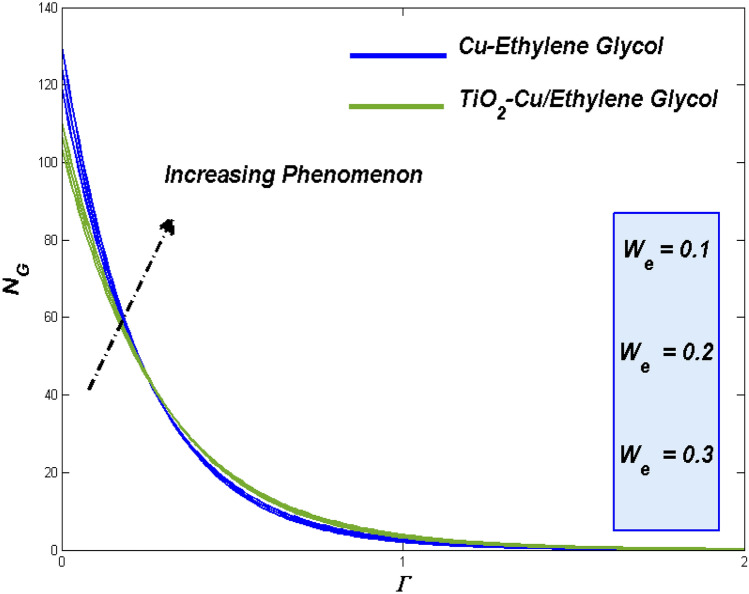
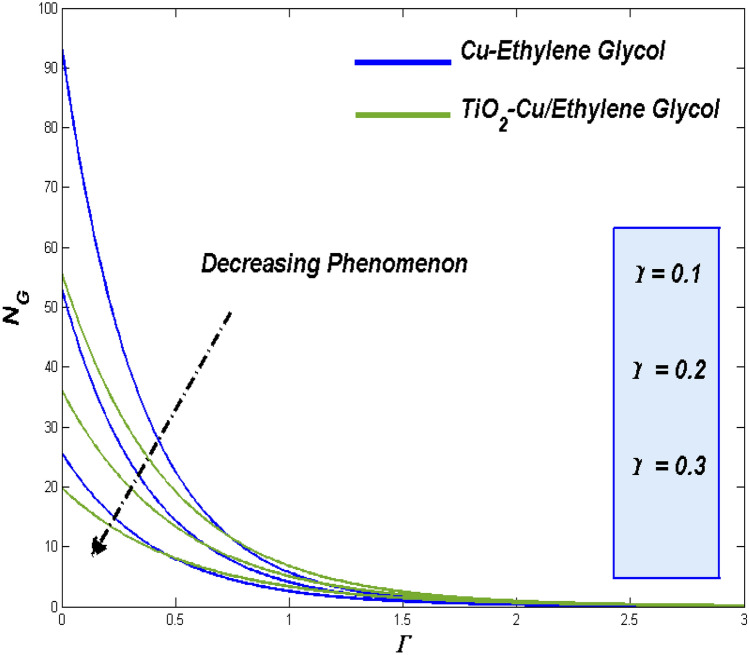
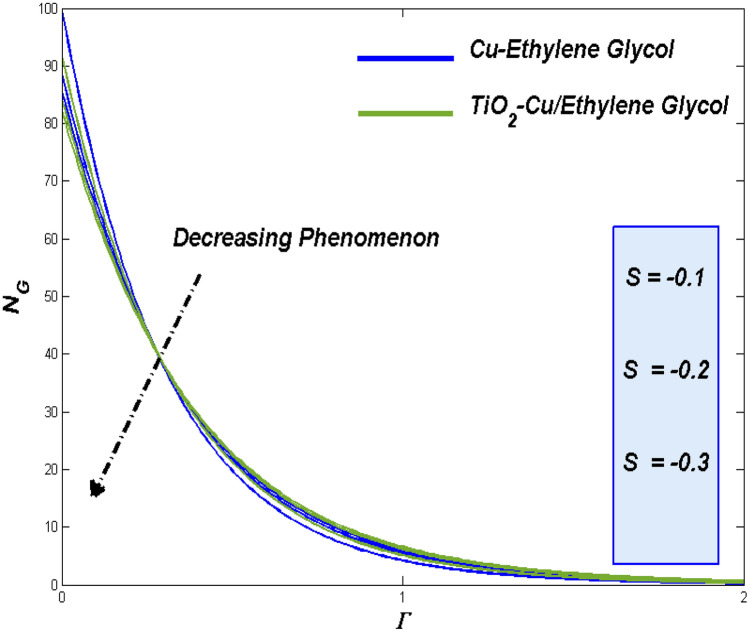
Impact of magnetic variable ($M$)

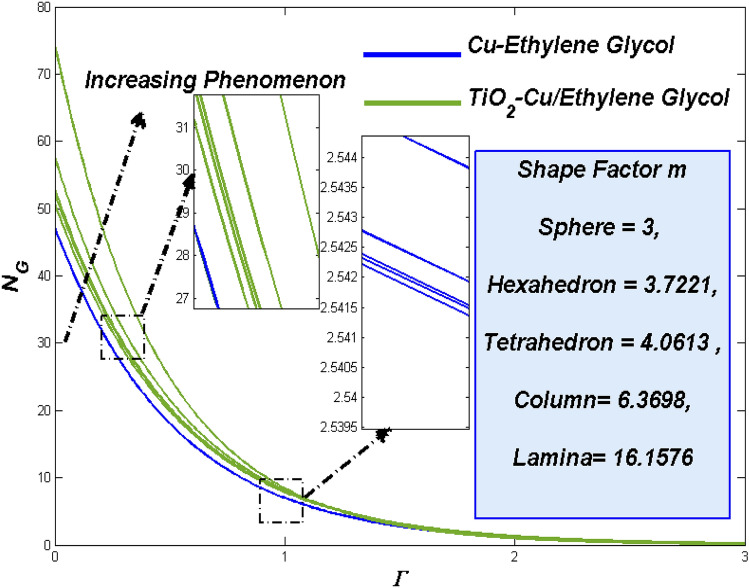
Despite of Lorentz force, a major factor holds influencing behavior on both the fluidity and thermal transference process. Performance of Nano class of fluids in those works were decided through the quantity of nano particle in the flow. Suction/injection may have greater impact in such particle strength while it can also manipulate the other key factors of the fluid too. More the particle more drag from Lorenz force this reflects in Fig. 9 where the TiO₂–Cu/EG hybrid class fluid passes forward than the Cu–EG nano class fluid.

Figure 10 exhibits the renowned thermal dispersal for the TiO₂–Cu/EG hybrid class fluid and of Cu–EG nano class fluid. In additional top the enhanced thermal transferring abilities, the hybrid class fluid holds yet another reason for it better performance in thermal transference. More the particle slower the flow, slower flow holds more time around the surface to fetching more heat. This also one of the reason for improved thermal transfer rate for the TiO₂–Cu/EG hybrid class fluid.

Entropy formation is the process of assessing the irreversible energy loss from the system. It happens during the thermal transference process. If that is the case, hybrid class fluid with TiO₂–Cu/EG combo induced more thermal transfer and by means it causes more entropy while compared to the Cu–EG nano class fluid. Fact looks clear in Fig. 11 under magnetic interaction parameter influence.

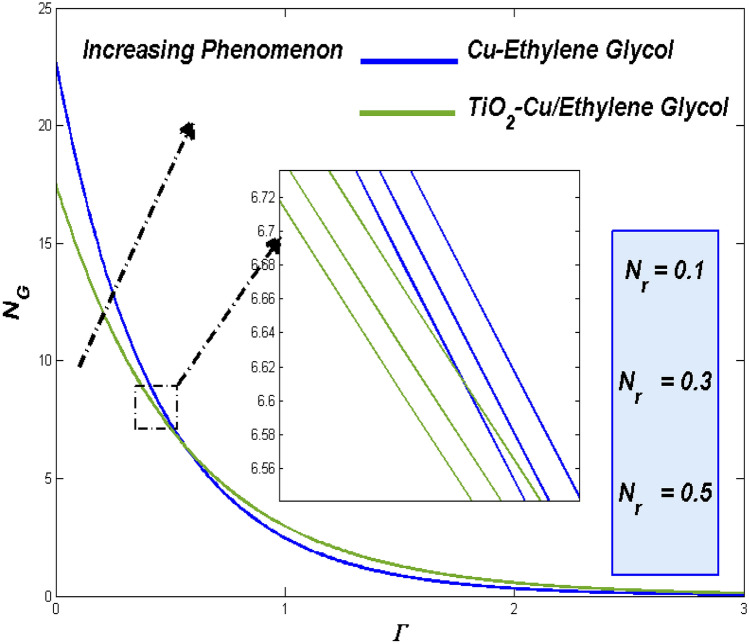
Influence of nanoparticle fractional volume ($\varphi$) and (${\varphi }_{\mathit{hnf}}$)

Acknowledging the fact that, fluidity plays the noticeable role in heat transference and energy loss tracing similar kind of influence may exerts for fractional volume too. Fluid with better flow ability can exhibit minimal contact time with the surface, resulting nominal heat transfer. Figure 12 signifies the altering way of added particle fraction can make the fluidity leisurelier. This sets the favorable circumstance for grater thermal transference and it reflect in the plots too.

Fluid with restricted velocity possess the grater thermal attraction time. This could be the reason behind the enhanced thermal dispersion for increasing fractional volume in addition to that technical advantage of nano particle grasping more heat which reflects in Fig. 13. Respective entropy loss as the resulting process of heat transference can be traced for the fractional volume impacts in Fig. 14 which shows the fact that the hybrid combo utilize the entropy more than the other combo.

Impact of velocity slip variable ($\mathrm{{\rm Y}}$)

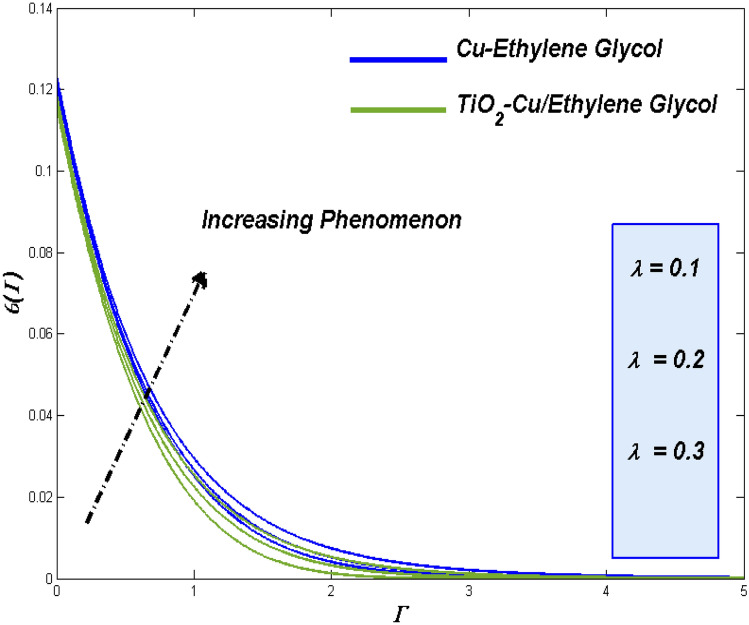
Figure 15 represent the fact of slippery effect which manipulates the flow rates of both fluids. Particles in the fluid plays the vital role in dominating the slippery assistance provided for the fluid. This makes the overall fluidity slower than usual. As like to the above results Fig. 16 shows that, the thermal dispersal seems to be in the higher side for elevated values of slip constraints because of the slowness provides enough time to grasp more form it. Strength of the particle to assist more thermal transference process leads to elevate more entropy process and the more energy drains occurs which can be evident in Fig. 17.

Impact of suction ($S>0$)/injection ($S<0$) constraints

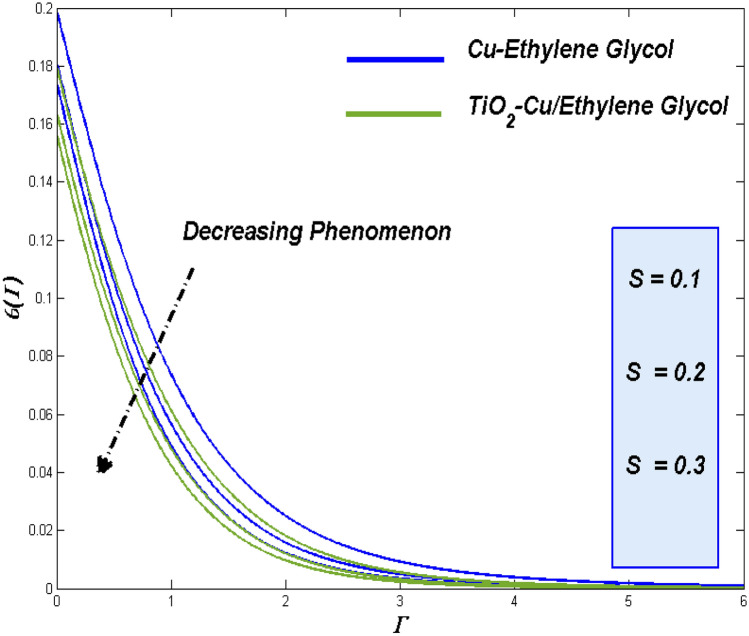
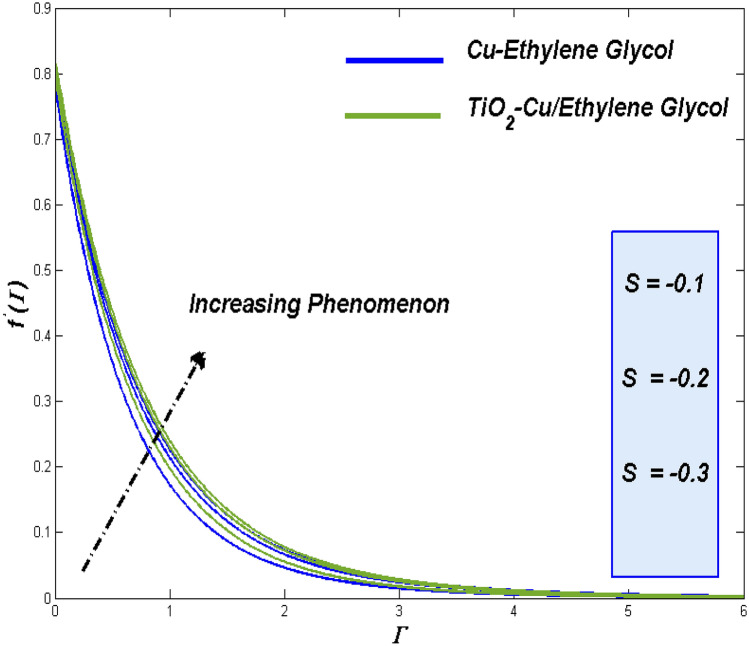
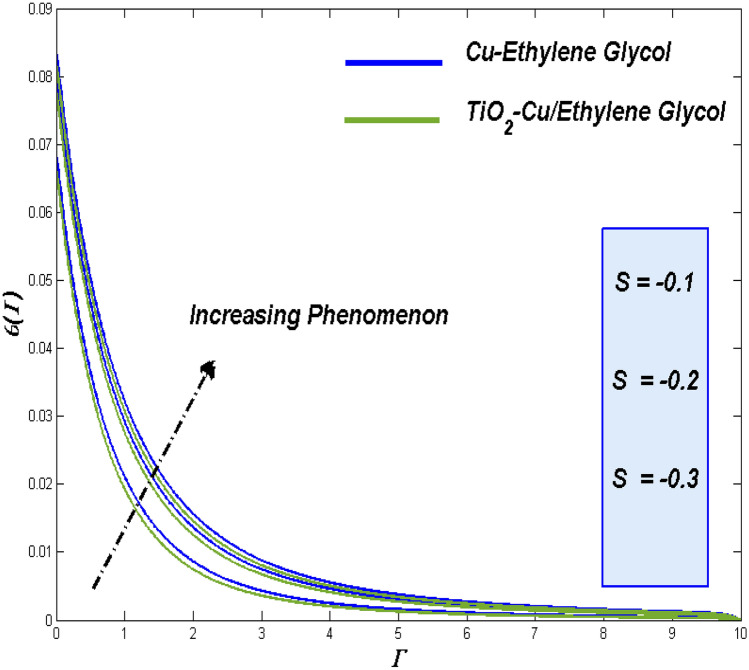
Suction/Injection constrain provides us to control the fluidity of the flow fluids at the first place. Flow problems over the permeable surface has such privileges to manipulate the fluidity either by suction out or injecting in the flow in the system. Through this fluidity, the control over the thermal and entropy aspects are possible as for the previous discussion are concerned. Figures 18, 19 and 20 portray the suction $(S>0)$ impact on fluidity, energy and entropy state, while the Figs. 21, 22 and 23 reveal the impact of inoculation $(S<0)$.

The raise in suction constrain reflecting the fact of taking out some fluid form the system through the surface. This reduces the system fluid flow which can be viewed in Fig. 18. On other hand injecting more fluid in to the system will tends to raise the over all fluid velocity which can be depicted in Fig. 21.

Figures 19 and 20 correspondingly showcased the enriched thermal dispersion and energy loss with the assistance of slower flow by suction. For injection, improved fluidity works more and interestingly even it raise in thermal dispersion rather than the entropy loss gets elevate and these trends can be found in Figs. 22 and 23.

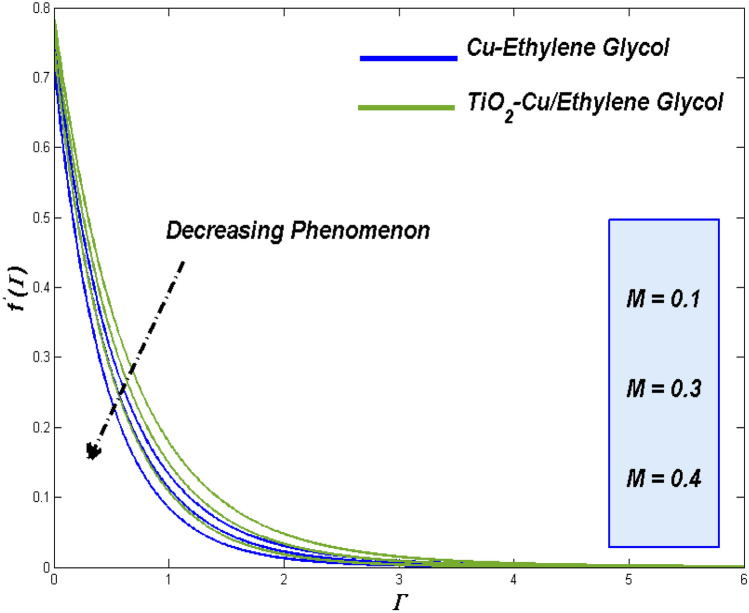
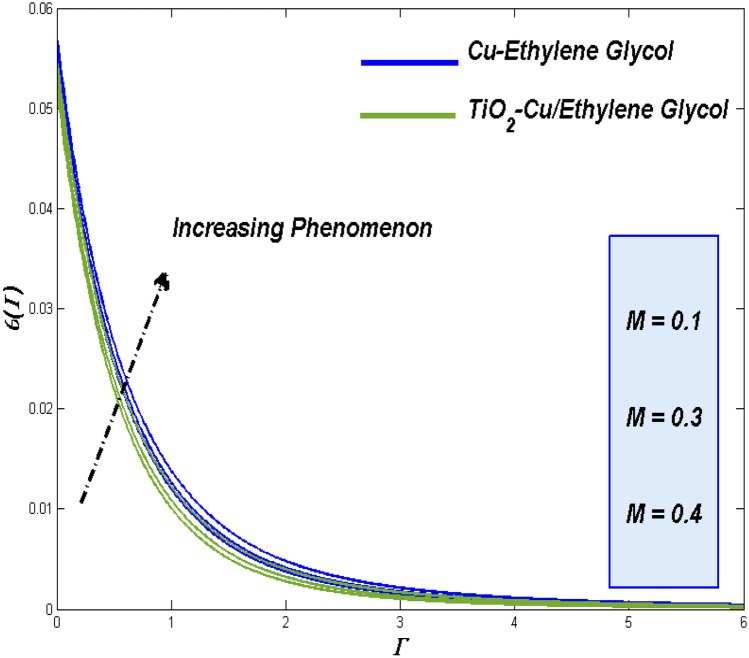
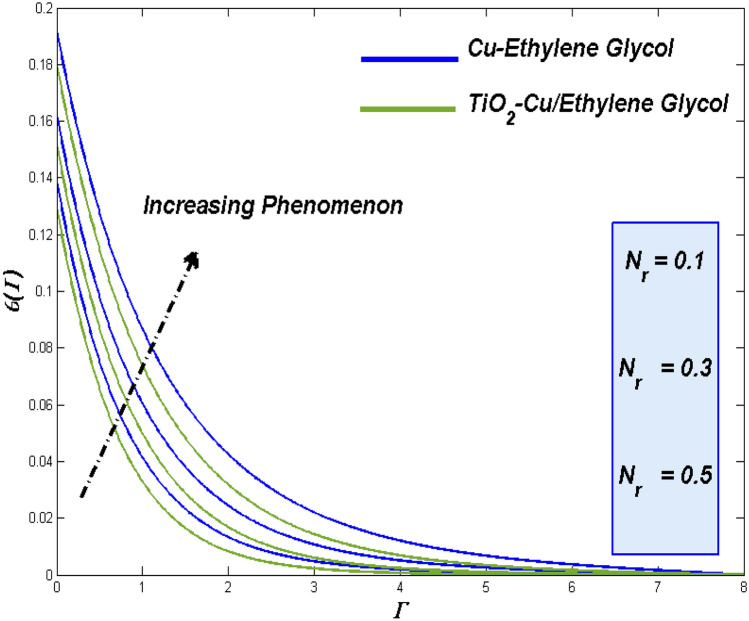
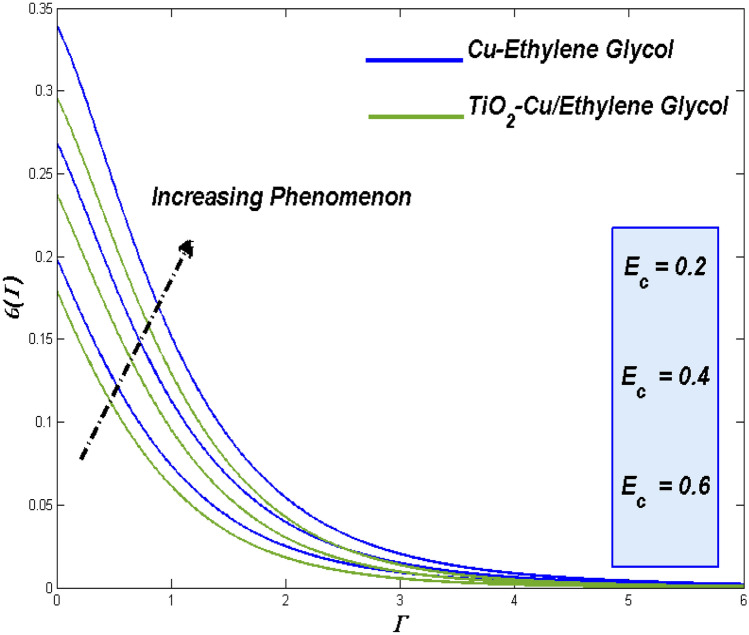
Upshot of the thermal radiation variable ($N_r$) and Eckert number ($E_c$)

Figures 24 and 25 reveal a state of the thermal diffusion and entropy formation respectively for the enhancing values of thermal based radiation $\left(N_r\right).$

More thermal impact can be influenced towards the flow field thermal states. This makes the thermal transference to work more to remove those added thermal inflows which reflects in Fig. 24. Among the two class of flow fluids Fig. 25 reflects the fact that of TiO₂–Cu/EG hybrid class of nanofluid holds the upper hand while compared to Cu–EG nanofluid. Portrays the minimal impact of thermal radiation constrain $\left(N_r\right)$ over the entropy formation.

Figures 26 and 27 respectively assist to explore the mass transportation aspects towards the Thermal and entropy traces of the system for fluids together. Enhancement in thermal and entropy aspects can be evident for the both class of flow fluids. Additional thermal transference provides favorable circumstances for the better energy loss in the irreversible mode. The entropy gets triggered by such a heated environment can be viewed in Fig. 27.

Impact of variable thermal conductivity ($\lambda$)

Compared with the thermal ability of nano and hybrid combinations, the individual variation in the thermal conductivity $\left(\lambda \right)$ seems to be dominated in both thermal and entropy aspects. This reflects in both Figs. 28 and 29 represent the influence of variable thermal conductivity parameter $\left(\lambda \right)$ over the thermal status and entropy formation. Even though the varying parameter tends to elevate both the thermal and entropy ranges, the thinner thermal layers and closer entropy variation tend to prove the nominal impact of $\left(\lambda \right)$. In both these parametrical behaviours, TiO₂–Cu/EG hybrid class fluid underplays the Cu–EG nano class fluid.

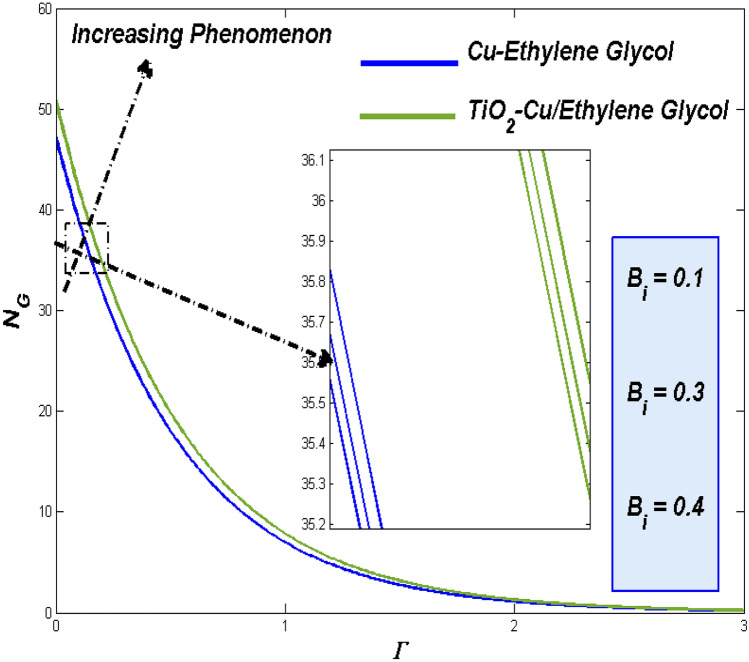
Impact of the Biot number ($B_i$)

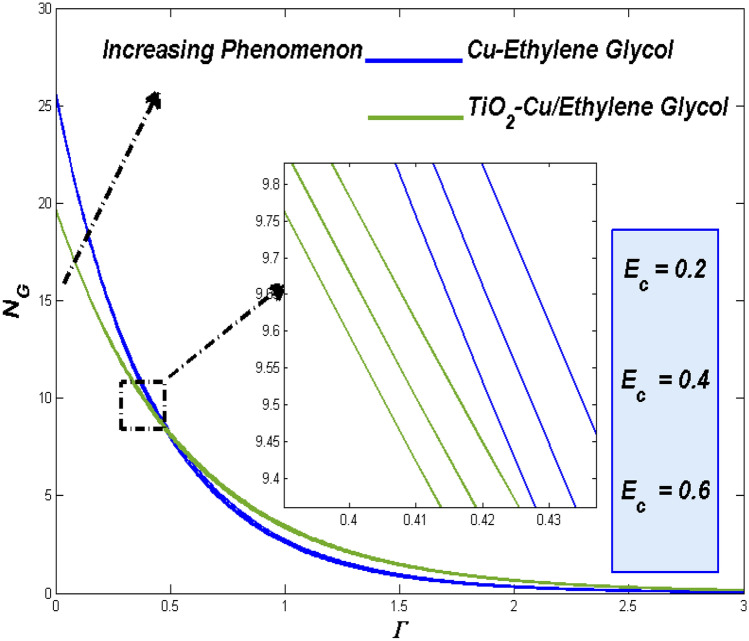
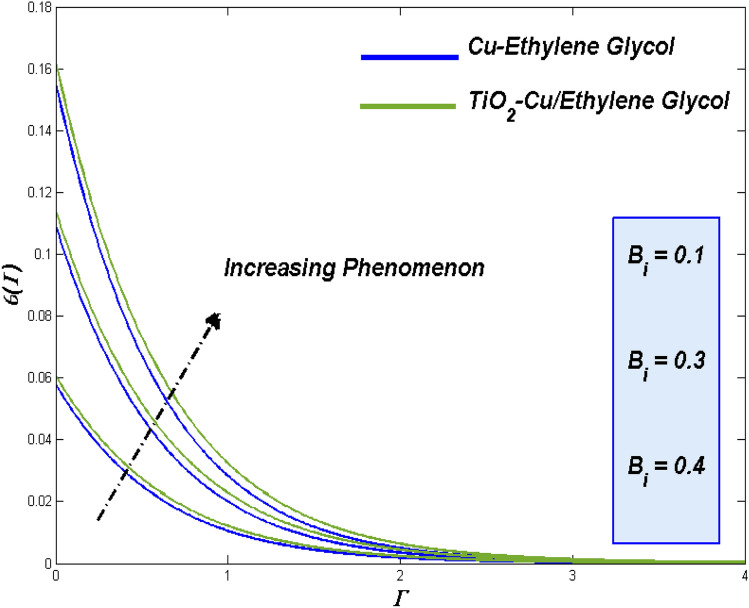
Augmented heat in the convectively heated progress, the Biot number $(B_i$) representation looks inevitable while the region of interest were underwent the Newtonian heating. The thermal state of the flow environment gets boosted with those extra heat which was exerted for the higher values of Biot numbers. Figures 30 and 31 shows the parametrical impact with the both combos. In both the cases, the significant improvement in thermal transference progress simultaneously escalates the energy loss too. This reflects in enriched entropy formation for higher convective flows.

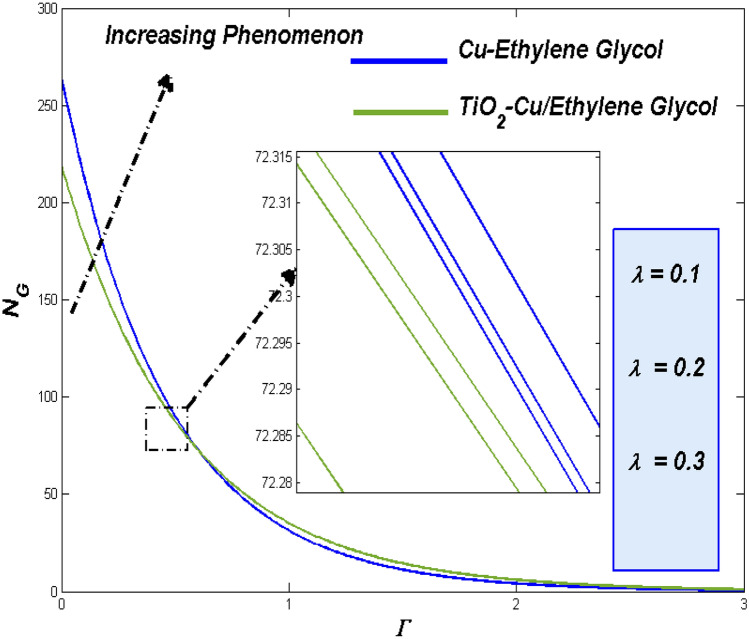
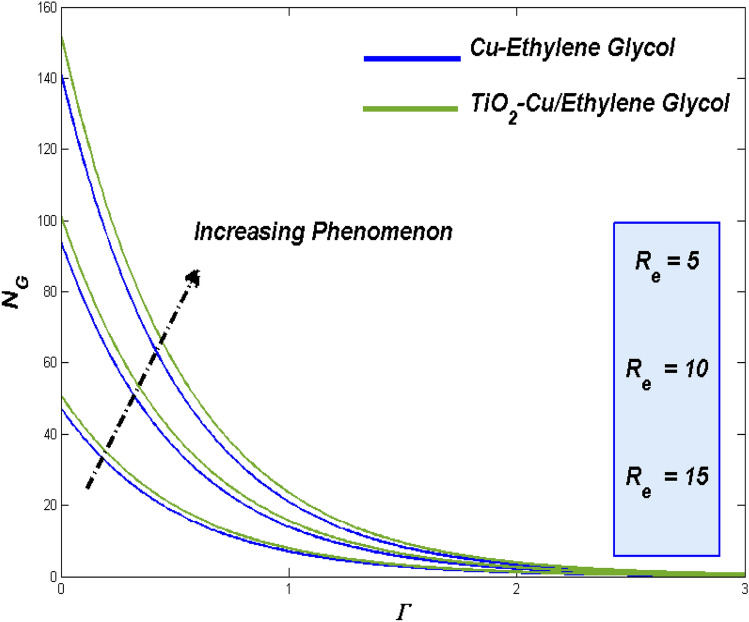
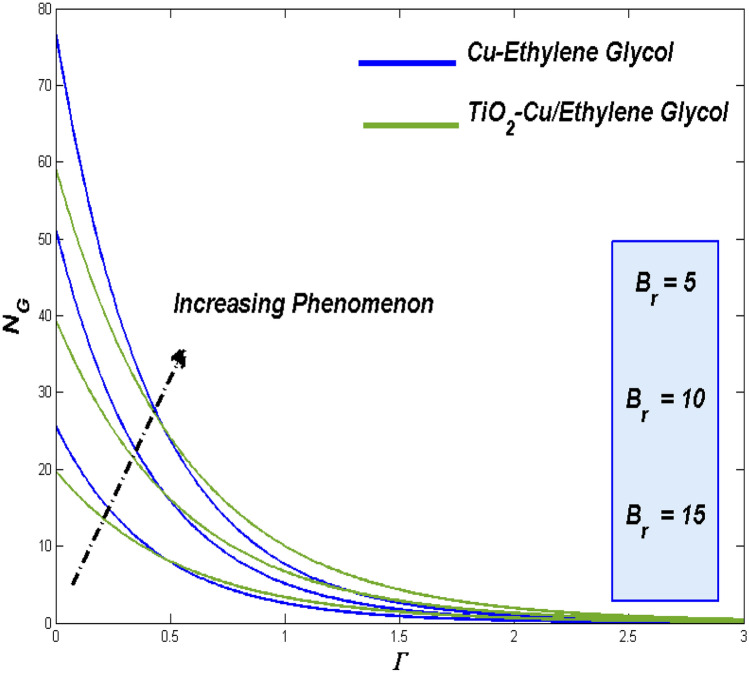
Entropy disparities for Reynolds number ($R_e$) and Brinkman number ($B_r$)

Raise in thermal state due to the physical aspects of improved fluidity which drives more heat from the surface reflects through the situation of improved Reynolds number (Re). On other hand, these kind of enriched irreversible energy losses could be traced with the impact of enhanced Brinkman number $\left(B_r\right)$ through elevated dissipative effect. Figures 32 and 33 respectively discloses such behavioral aspects Reynolds number $\left(R_e\right)$ and Brinkman number $\left(B_r\right)$ on the two class of flow fluids. Results of those two plots tends to assist the claims proposed previously above.

Parametrical study on skin friction $\left(C_f\right)$ and Nusselt number $\left(N_u\right)$

The parametrical perspectives were presented in Table 6. Basically, the both kind of flow fluids are rich in viscous aspect, more such kind of factors holds the noticeable improved frictional control over the fluidity. As the reaction to such viscous flow behaviour, the thermal transference also gets improved and it could be visible through the improved Nusselt number in both class of flow fluids.

Additional parametrical influences over the frictional resistance $\left(C_f\right)$ and thermal transmitting rate (Nu) were disclosed beneath the above mentioned places.

For increased values of the Weissenberg number ($W_e$) and the slip parameter $\mathrm{{\rm Y}}$ both tends improve while it swifts while to resist the skin friction just like greases the surface to swifts over it. Based on the other physical aspects of hydromagnetic effect (M), quality enhancement in nano class fluid through the fractional volume $\left(\varphi ,{\varphi }_{\mathit{hnf}}\right)$ and in/out flow motion across the surface with suction phenomena $(S>0)$ and injection happening for $\left(S<0\right).$ In the frictional aspects most parameters hold the upper hand o raise it in both the class of fluids. Comparatively, TiO₂–Cu/EG undergoes to the larger frictional rates rather than the further mono suspended Cu–EG nanofluid.

Predominant objective of working with the improved class of flow fluids are towards the expectations of enhanced thermal transference rates. Nusselt number are the hotspots to get such clear insights about the thermal performance of the flow fluids under various parametrical circumstances. Because of it improve nature TiO₂–Cu/EG hybrid class of combinations holds better performance rather than the Cu–EG nanofluid in most aspects. Parameter like suction, fractional volume, radiation and Newtonian heating are shows the favourable phases towards the heat transmitting process. Meanwhile, Weissenberg number ($W_e$), magnetic parameter $\left(M\right),$ slip parameter $\left(\mathrm{{\rm Y}}\right)$, Eckert number $\left(\mathit{Ec}\right)$ and the variable thermal conductivity parameter $\left(\lambda \right)$ are shows the retarding phase over the Nusselt number.

Concluding outputs and impending direction

In this article, we shows a computational analysis of tangent hyperbolic hybrid nanofluid boundary-layer flowing with thermal transport and entropy production. The study subjected to the MHD, flexible heat conductiveness, shape feature, Joule heating, viscous dissipation, entropy formation and thermally influenced radiative possessions. Similarity conversions are used for non-linear partial-differential formulas, relating fluidity and thermal transference models, to convert them into non-linear ordinary-differential formulas (ODEs). The transformed ODEs are hence resolved by utilizing the Keller–Box method numerical method for numerous evolving constraints. The computational outcomes presented in this work are new and may help to control the entropy generation in heat transfer procedures. Following are the important findings of our analysis:

1. Fluidity features of hybrid and nano fluids across the field were hurdled by a majority of the physical parameters except for the injection parameter $(S<0)$. Other parameters like the Weissenberg number ($W_e$), fractional volumes $\left(\varphi ,{\varphi }_{\mathit{hnf}}\right)$ and the suction parameter $(S>0)$ tends to lay obstacles to the flowing fluid.

2. Thermal behavior investigation has key thermal influencing constraints of the work. Among those, excluding the suction parameter $(S>0)$ parameter all other vital parameters were on the favoring side of gathering the possible amount of heat from the surface which makes the elevated thermal state in the distributive region.

3. Detailed scrutiny on entropy development connected to this effort delivers the list of supporting constraints for entropy as Weissenberg number ($W_e$), magnetic parameter $\left(M\right)$, fractional volumes $\left(\varphi ,{\varphi }_{\mathit{hnf}}\right)$, injection parameter $(S<0)$, thermal radiation parameter $\left(N_r\right)$, variable thermal conductivity parameter $\left(\lambda \right)$, Biot number $\left(B_i\right)$, shape variation parameter $\left(m\right)$, Reynolds number $\left(R_e\right)$ and Brinkman number $\left(B_r\right)$. Whereas the entropy gets resisted for slip $\left(\mathrm{{\rm Y}}\right)$ and suction parameter $(S>0)$.

4. Beyond the fluid type classification, the constrains like nanofluid quality, fluid suction through surface are in the assisting phase towards the fractional impact and also towards the thermal transference rate. On other hand elastic–viscous ratio and frictional slip reacts against it.

5. Special case of distinct impact can be observed from the parametrical studies towards the two class of flow fluids engaged in this work. In which the hydromagnetic constrain favours the frictional aspects but stays against the heat transference rate. Other parameters like Flow slip and Eckert number are stands against the thermal transference process while the radiation and Newtonian heating constraint works on opposing way.

6. Dominance of TiO₂–Cu/EG hybrid class fluid can be evident in thermal transferring aspect while compared to nano class of fluid. Rather in entropy point of view, still hybrid produces more energy drains than the Cu–EG nano class fluid.

This Work is still open to explore the various mixtures of particle in preferred ratio under various flow conditions which is suitable of the industrial problems.

Author contributions

W.J. formulated the problem. W.J., S.U.D.S, P.M., and M.R.E solved the problem. W.J., P.M., S.U.D.S., R.W.I., F.S., K.S.N., M.R.E., A.H.A.A., M.M.K and I.S.Y, computed and scrutinized the results. All the authors equally contributed in writing and proof reading of the paper. All authors reviewed the manuscript.

Data availability

The results of this study are available only within the paper to support the data.

Competing interests

The authors declare no competing interests.