Abstract
Centroiding is one of the major approaches used for size reduction of the data generated by high-resolution mass spectrometry. During centroiding, performed either during acquisition or as a pre-processing step, the mass profiles are represented by a single value (i.e., the centroid). While being effective in reducing the data size, centroiding also reduces the level of information density present in the mass peak profile. Moreover, each step of the centroiding process and their consequences on the final results may not be completely clear. Here, we present Cent2Prof, a package containing two algorithms that enables the conversion of the centroided data to mass peak profile data and vice versa. The centroiding algorithm uses the resolution-based mass peak width parameter as the first guess and self-adjusts to fit the data. In addition to the m/z values, the centroiding algorithm also generates the measured mass peak widths at half-height, which can be used during the feature detection and identification. The mass peak profile prediction algorithm employs a random-forest model for the prediction of mass peak widths, which is consequently used for mass profile reconstruction. The centroiding results were compared to the outputs of the MZmine-implemented centroiding algorithm. Our algorithm resulted in rates of false detection ≤5% while the MZmine algorithm resulted in 30% rate of false positive and 3% rate of false negative. The error in profile prediction was ≤56% independent of the mass, ionization mode, and intensity, which was 6 times more accurate than the resolution-based estimated values.
Introduction
High-resolution mass spectrometry (HRMS) coupled with either liquid or gas chromatography (LC/GC-HRMS) is one of the main analytical tools for the comprehensive chemical characterization of complex samples, from environmental to biological (as reviewed elsewhere1,2). The generated datasets are extremely information rich and are typically used for structural elucidation of unknown chemicals as well as fingerprinting or trend analysis.3−9 These techniques, while being comprehensive with wide applications, generate large amounts of complex data (up to 5 GB per sample). Therefore, their processing becomes a challenging task, particularly when dealing with unknown chemicals in highly complex sample matrices.1,2,10,11
Centroiding is one of the main strategies employed prior to feature detection for reduction of data size and information density.12−14 During centroiding, the distribution of the mass profile peak is represented with one point that is commonly associated with the mass peak apex.12−14 This approach is performed either on the fly (i.e., by the instrument during acquisition) or as one of the steps in the data processing workflow using vendor and/or open-source software.1,2,13,15 Centroiding could potentially reduce the size and information density of the data by more than 10 folds. However, this comes with a cost associated with the loss of information related to the mass peak distribution, which provides valuable insight into the mass accuracy and precision. Additionally, depending on the centroiding strategy employed (i.e., on the fly or post acquisition), access to the profile data may be limited. This implies that the information related to the mass peak widths may be lost during centroiding, independently from the algorithm used. It is widely accepted that vendor software packages are more accurate in performing centroiding due to their access to instrument-specific information that is not reported in the open format (e.g., mzXML) data files. To our knowledge, there has not been a systematic evaluation of the performance of different centroiding approaches and their impact on data integrity.1 Moreover, none of the currently existing open-access/source centroiding algorithms generate the mass peak widths for the generated centroids.
There are different open-source/access algorithms for processing (e.g., feature detection) of both profile and centroided data during non-targeted workflows.1,2,15 Some of these data processing tools are specifically designed to handle the profile data16,17 while others can only process the centroided data.18,19 Most of these algorithms employ a set of user defined (i.e., applied to all peaks) parameters such as mass tolerance. These mass tolerances are used as a means to group the signals that belong to the same chemical constituents, for example, all the measured points of a chromatographic feature in both time and mass domains.16,18 This implies that such parameters are dependent on the distribution of the measured m/z values in the mass domain and thus the mass peak width. However, previous studies have shown that such parameter setting strategies may cause a high level of uncertainty in the final outcome, particularly for complex samples with a wide variety of chemicals and concentration levels.20−22 This is typically translated into reproducibility issues both for hypothesis testing and identification of unknown chemicals of interest.11,23,24
Recent studies on feature detection of profile data have shown higher levels of reproducibility and reliability as compared to the centroid data.16,25,26 The observed higher levels of reliability have been associated with the algorithm access to the information related to the peaks in both the time and mass domains. Additionally, the same information can be utilized during spectral deconvolution and feature identification to set feature specific mass and time tolerances.1,27 Most of the currently existing centroiding algorithms do not produce such information (i.e., mass peak width), and there is no algorithm that can estimate the peak mass widths from the centroided data.
Here, we report the development and validation of the Cent2Prof package developed in julia language28 for seamless conversion of centroided data to profile data and vice versa. The algorithms in Cent2Prof were tested and validated using seven previously analyzed datasets produced by three different vendors in both positive and negative modes. The algorithms consist of a self-adjusting centroiding algorithm, a random forest model for prediction of mass peak width, and a mass profile prediction algorithm. Cent2Prof enables the conversion of profile and centroided data in both directions. The centroiding algorithm was compared to an existing algorithm implemented via MZmine, whereas for profile prediction, the difference between the measured and predicted profiles was used as a means for performance evaluation.
Methods
Overall Workflow
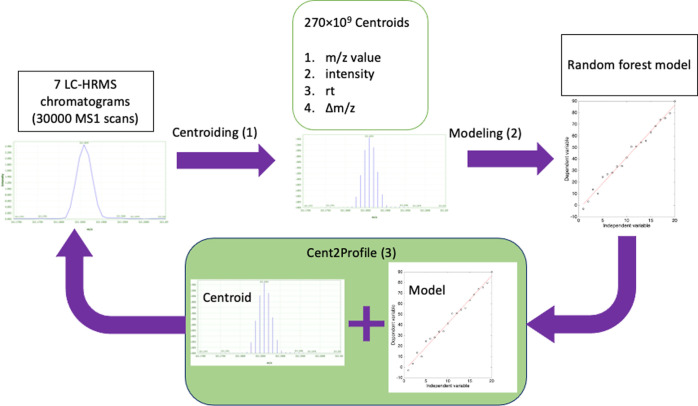
To develop, validate, and test these algorithms, we followed three steps consisting of (1) centroid calculations, (2) developing a model for the prediction of mass peak widths, and finally (3) predicting the mass profiles using the model and centroids, Figure 1. All the steps are explained in detail below.
Figure 1.
All the steps taken from the raw data to profile prediction.
Chromatograms
Previously acquired data of complex samples were used for the algorithm development, validation, and testing. The data consisted of 30,000 MS1 scans between the m/z values of 50 and 1200 Da generated with quadrupole time of flight (QToF) instruments using electrospray ionization (ESI) sources. These scans belonged to seven LC-HRMS runs, four in positive mode and three in negative mode. Additionally, the data were generated by three different instruments/vendors (i.e., two Sciex, three Waters, and two Agilent) using different experimental conditions (Section S1 of the Supporting Information). Finally, all samples consisted of complex sample matrices ranging from surface water extracts to biosolid extracts. More details regarding the type of samples and experimental conditions are provided elsewhere3,16,29−31 and in the Supporting Information S1.
Data
Prior to data processing, all chromatograms were converted to the mzXML format32 using ProteoWizard software package version 3, 64 bit.33 The mzXML files were then imported into julia programing language using MS_Import.jl package (see Code Availability). Peaks in the mass domain were extracted from these scans to generate the dataset used consisting of 2.7 × 1011m/z values, intensities, retention factors,34,35 and mass peak width at half-height. The first three parameters were used as independent variables (i.e., predictors) while the fourth was used as a dependent variable (i.e., to be predicted). For the extraction of this information, we developed a self-adjusting centroiding algorithm (details are provided below). The centroiding algorithm uses input parameters of the raw data, nominal resolution, signal to background ratio, minimum intensity threshold, and R2 threshold to assess the goodness of fit for a Gaussian distribution (details are provided in Section S2 of the Supporting Information).
For the data pre-processing, the intensity of each peak was divided by the maximum signal of that scan, which resulted into unit scaling of the intensities. This pre-processing step minimized instrument and sample-dependent variance observed in the data. After pre-processing, the data was divided into training, validation, and test sets. The training and validation sets consisted of the data coming from 28,000 scans, which was divided in ratios of 70 and 30%, respectively (selected at random). On the other hand, the test set was used for the assessment of the generated model as well as for the profile14 prediction.
Self-Adjusting Centroiding Algorithm
The centroiding process includes five steps consisting of signal selection, smoothing, Gaussian fit, calculating the centroid, and signal removal (Figure S3). A detailed explanation of each step follows below.
Signal Selection
The centroiding algorithm starts with the most intense signal in each scan. After locating the maximum signal (i.e., apex of a mass peak), the algorithm employs the user-provided nominal resolution to estimate the mass peak width. The algorithm isolates a mass window two times the estimated window based on the first guess. In the next step, the algorithm follows the measured signal from the apex until either reaching the half-height intensity or the minimum intensity threshold set by the user.
Smoothing
The selected signal is then smoothed using a simple moving-average filter with a window size of 3 points, which guarantees the removal of the instrument associated signal fluctuations without altering the analytical signal.36
Gaussian Fit
The smoothed signal is used to calculate the mass window (“c”), m/z value (“b”), and the intensity (“a”) that are used for the Gaussian fit, eq 1, which previously has been shown to be adequate in predicting the mass peak profiles.16,37 The algorithm fits a three parameter Gaussian to the smoothed signal and compares the generated adjusted R2 to the threshold set by the user, eq 1. In the case where the calculated R2 is ≥ the set threshold, the fit is considered successful and the signal is assumed to be a real peak.
| 1 |
Calculating the Centroid
To calculate the mass of the centroid, the algorithm uses the average of the estimated centroid mass using the fitted Gaussian and the apex of the measured signal. Before accepting the average value as the centroid, the algorithm calculates the difference between the m/z value of the measured and Gaussian predicted apex. If the difference is smaller than half of the measured mass peak width at half height, then the algorithm accepts the average value as the true centroid. This approach was employed as a filtering strategy for distinction of the true signal from the noise while providing a more accurate estimate of the centroid. Consequently, the signals that generate a successful Gaussian fit and meet this requirement were considered as true positives while signals that did not produce an acceptable fit or did not meet the above-mentioned criterion were considered true negative (i.e., noise). At this point, the calculated centroid and the maximum intensity are recorded.
Signal Removal
The algorithm follows the measured intensity until it reaches the minimum intensity threshold set by the user. All the measured signals within this interval is set to half of the user defined intensity threshold, which enables the algorithm to move to the next most intense mass peak in the scan.
The algorithm repeats the above mentioned steps in an iterative approach until no signal above the user defined threshold is present in the data. For the performance assessment of the centroiding algorithm, we used MZmine due to the fact that the algorithms deployed within this software represent a suite of the most commonly used data processing tools. Moreover, our dataset included data acquired by three different vendors which hinder the possibility of direct comparison. Finally, the lack of knowledge regarding the used algorithms in the vendor products makes the direct comparison impossible. The detailed list of parameters and their selected values are reported in Table S2 of the Supporting Information. It should be noted that these parameters were employed for all chromatograms independently from their matrix and/or vendor.
Modeling
For modeling, a random forest regression38 (RFR) strategy implemented in julia language v 1.5.328 (package DecisionTree.jl v. 0.10.10) was employed. The model utilized the m/z values, relative intensities, and the retention factors to predict the mass peak widths at half height. The model was initialized with 100 trees and minimum number of data in a leaf of 30. This model then went through an optimization procedure where a new model was built by varying each of the parameters at a time. The number of trees varied between 50 and 350 with steps of 50, whereas the minimum number of data points in the leaves varied between 1 and 30 with steps of 5. This resulted in a two-dimensional grid which was used to find the optimized model setting. The quality of each model was evaluated by monitoring the root mean square error of prediction as well as the correlation coefficient between the measured and predicted values, when applying the model to the validation set (i.e., the portion of data unseen by the model).38 This strategy resulted in a final/optimized model with 250 trees and minimum leaf population of 10, which enabled the prediction of mass peak width via relative retention time, m/z value, and the relative intensity. It should be noted that this model used all three variables and only had access to the training set.
The optimized model was further validated, using an out-of-bag strategy including 500 bootstrapping samples as well as five-fold cross validation.38,39 These two approaches enabled the mitigation of overfitting while resulting in a robust and reliable model.
Profile Prediction
During profile prediction, a mass window of twice the size of the predicted peak width, consisting of 8 points, was used for profile generation. The number of points for the full mass profile prediction were selected based on the median number of points detected in the experimental mass profiles. On the other hand, the size of the mass window was selected to compensate for the fact that the predicted peak widths were associated to the half height of the peak and not the full profile. The combination of the predicted mass window (“c”), measured m/z value (“b”), and measured intensity (“a”) provided the necessary information to estimate the profile of mass peaks, thus moving from the centroided data to profile data.
Calculations
All calculations were performed using a personal computer (PC) with Intel Core i7 CPU and 16 GB of RAM operating Ubuntu 20.04.2 LTS. All the data processing and statistical analysis were performed using julia language 1.5.3.
Results and Discussion
Seven chromatograms consisting of 30,000 scans were employed for the model development, validation, and final testing. The signals within these scans were centroided resulting in 2.7 × 1011 measurements of the mass peak widths at half-height, relative intensity (%), the mass (Da), and the retention factor (%). The latter three parameters were used for prediction of the first parameter via a random forest regression model. Additionally, an algorithm for prediction of mass peak profiles based on the developed model was developed.
Performance of the Centroiding Algorithm
The centroiding algorithm is self-adjusting and iterative, where for each iteration, one mass profile peak was converted to a centroid. During this process, the algorithm used the nominal resolution of the instrument as a first guess to estimate the mass peak width. This mass window was adjusted to the true values using the measured data. Prior to the application of the centroiding algorithm, all its parameters were optimized using 50 randomly selected mass peaks in two chromatograms. Moreover, these parameters, when optimized, were in close agreement with the parameters optimized for the self-adjusting feature detection algorithm.16
The visual inspection of the output of the centroiding algorithm for one chromatogram resulted in around 8000 correctly detected centroid masses (Figure S2), zero false positive identifications (i.e., noise being detected as signal), and 167 false negative identifications (i.e., true signal being identified as noise) (Figure S3). This process was performed by plotting every single mass peak processed via the algorithm, which resulted in a total of around 11,000 figures (please see Code Availability), including true positives (Figure S2), false negatives (Figure S3), and true negatives (Figure S4). The same chromatogram was processed via the centroiding algorithm implemented in the MZmine213 utilizing the same minimum intensity threshold (i.e., 1000 c/s). The direct comparison between the outputs of the two algorithms enabled us to assess the false detection rates of the MZmine2 method. The MZmine2 algorithm resulted in larger rates of false positive 35% while having false negative rates as low as 3% (Figure S5). Overall, our algorithm resulted in both false positive and false negative rates ≤5%, which is smaller than the MZmine213 centroiding algorithm for false positives and is comparable for the rate of false negatives (i.e., a false positive rate of 35% and a false negative rate of 3%).
We also evaluated the impact of the R2 threshold and the signal to background ratio parameters on the rates of false detection. A list of 100 randomly selected mass peaks generated under optimized conditions was used as our reference. The same 100 peaks were reevaluated using a grid with a resolution of ten (i.e., ten steps) generated for each parameter. The R2 threshold ranged between 0 and 1 while the signal to background ratio ranged between 0 and 5. The detected peaks were compared to the reference list to assess the number of false detection cases (i.e., sum of false positive and negative cases). For R2 values of ≥0.9, the algorithm resulted in false detection cases ranging between 60 and 98 cases out of total evaluated 100 peaks, which was attributed to the extreme case scenario (i.e., perfect Gaussian fit) (Figure S6). On the other hand, for signal to background ratios >2.5, the algorithm generated up to 100 cases of false detection out of the 100 evaluated peaks (Figure S6), which was attributed to the fact that the mass peaks rarely meet this criterion. Expect for extreme cases, the algorithm appeared to be robust toward changes in these parameters. In fact, for R2 threshold set between 0.5 and 0.85 and signal to background ratio range of 1–2.5, the observed changes in the number of false detections were not statistically significant (Kruskal–Wallis test40p ≤ 0.01) (Figure S6).
The self-adjusting centroiding algorithm fared comparably in terms of the false negative rate to MZmine2 with the same parameter setting, while performing better in terms of the false positive rate. Moreover, the algorithm appeared to be robust in terms of the changes in the parameter settings. Finally, the algorithm generates a mass peak width for each centroided m/z value, which can be used during feature detection, componentization, and identification.
Exploration of the Model Parameter Space
The centroiding algorithm employing optimized settings was used to generate the necessary parameters for the model building. Three parameters consisting of relative intensity (%), mass (Da), and the retention factor (%) were employed for the prediction of mass peak widths at half-heights via a random forest regression model. These parameters were selected based on the fact that they could be extracted automatically from the raw data, given their importance in prediction of mass peak widths.1,14,41
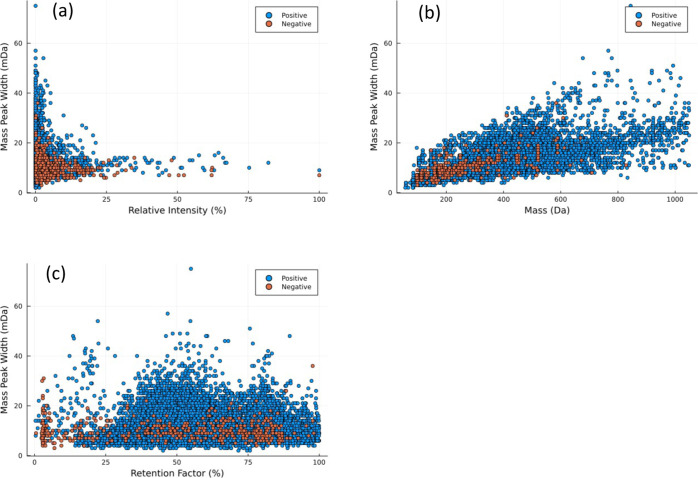
The measured mass peak widths of the 2.7 × 1011 profiles ranged from 3 to 80 mDa. More than 95% of the data used for our model had a mass peak width ranging between 3 and 20 mDa, regardless of the relative intensity or the ionization mode (i.e., ESI– or ESI+) (Figure 2). This was in agreement with previously reported mass accuracies related to QToF instruments with a nominal mass resolution of 35,000.4,16,27,41,42 We did not observe a statistically significant (i.e., p ≤ 0.05) linear correlation between the relative intensity and the measured peak widths (r = 0.06),43 which indicates that there is no direct relationship between these two parameters.
Figure 2.
Distribution of 100,000 randomly selected measured mass peak widths (mDa) as a function of (a) relative intensity (%), (b) the m/z value (Da), and (c) the retention factor (%). The red points were measured in the negative mode(i.e., ESI−) while the blue points were measured in the positive mode(i.e., ESI+).
An increase in the measured masses showed a slight increase in the measured peak widths with an r value of 0.46 (p ≤ 0.05) (Figure 2). In this case also, the observed correlation was independent from the analysis mode (i.e., ESI– or ESI+). The observed correlation between these two parameters is in agreement with the nominal mass resolution and the set sampling rate of QToF instruments.1,14 The observed correlation, even though significant, indicates that the m/z value alone is not able to describe the variance in the measured peak widths.
As with the relative intensity, the retention factor did not show a statistically significant correlation with the measured peak widths (r = 0.1) (Figure 2). The observed trend indicated that the location of the peak in the chromatogram did not impact the mass peak width, suggesting the negligible impact of ion suppression on the mass accuracy.1,14
Overall, for all three parameters, the ionization mode did not affect the measured mass peak widths (Figure 2). Moreover, the observed weak relationship between the independent and dependent variables suggested that the conventional approaches such as principal component regression and/or partial least square regression may not be able to capture the observed variance in the measured mass peak widths, given their needs for the presence of correlation between the dependent and independent variables. Therefore, the use of a more sophisticated modeling strategy is warranted.
Modeling
A regression model was developed and validated for the prediction of m/z peak widths at half-height, based on relative intensity (%), the mass (Da), and the retention factor (%) via a random forest modeling strategy. To assess the importance of each parameter, a model was generated including only one independent variable of the training set. Each model was then used for the prediction of the mass peak widths of the test set. The percentage variance explained in the predictions compared to the experimental data was used as a measure of variable importance.38
The model with all three variables described ≈85% of variance in the test sets, whereas the individual variables descriptive power ranged from ≈46% for the m/z value to ≈6% for the retention factor (Figures S7–S9). Given that none of the variables generated an explained variance ≤5%, we opted for the inclusion of all three variables in the model to be able to predict the mass peak widths with a higher level of accuracy. Moreover, we used the standard error of prediction, defined as the error divided by the measured values, as a means of assessing the quality and accuracy of the model outputs. The inclusion of all three parameters resulted in a statistically significant decrease in the average prediction error from 139 (Figures S10 and S11) to 56%, which further indicated the importance of all three parameters (Figures S7–S9).
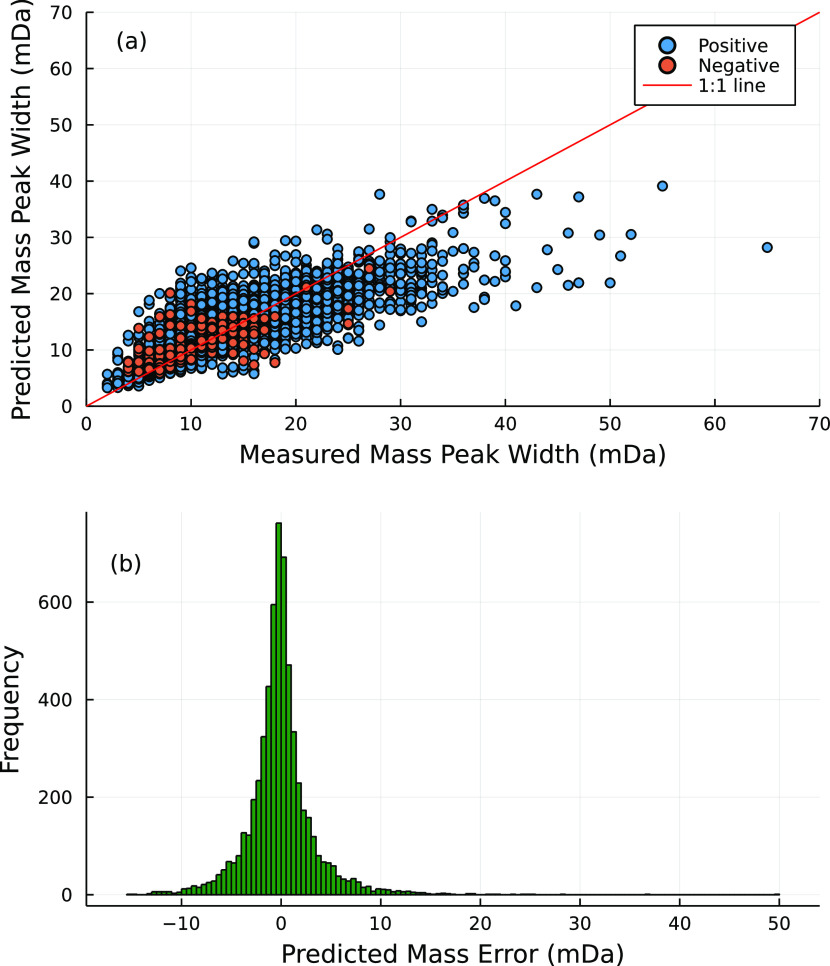
The final model resulted in an average prediction error of ±6 mDa (56%), for ≈90% of the test set (Figure 3). The largest prediction errors of up to 200% were observed for the peak widths between 8 and 15 mDa. On the other hand, for peak widths ≤8 and ≥15 mDa, the average observed prediction error was around 47%. Moreover, for peak widths ≥35 mDa, the model appeared to consistently underestimate the measured peak widths. However, even in this case, the average prediction error did not exceed 50%. We also compared the model average prediction error to the estimates of mass peak widths using the constant resolution and the accurate mass. The average prediction error of 56% via model was 6 times smaller than the average error of the resolution-based estimates.
Figure 3.
(a) Distribution of 10,000 randomly selected measured mass peak widths (mDa) from the test set vs the predicted mass peak widths and (b) the distribution of the prediction errors in mDa. The red points were measured in the negative mode(i.e. ESI−) while the blue points were measured in the positive mode(i.e. ESI+).
Overall, the developed and validated model was able to predict the mass peak width using parameters directly extracted from the raw data with an average prediction error of 56%. The random distribution of error across all mass peak widths further suggested that a lack of systematic error as well as overfitting in the final model. To our knowledge, this is the first study predicting the mass peak width for HRMS data.
Profile Prediction
The mass, absolute intensity, and predicted mass peak width were used for predicting the profile of a centroid. We evaluated the profile prediction algorithm using the output of the centroiding algorithm, which consisted of two arrays of centroided m/z values and intensities.
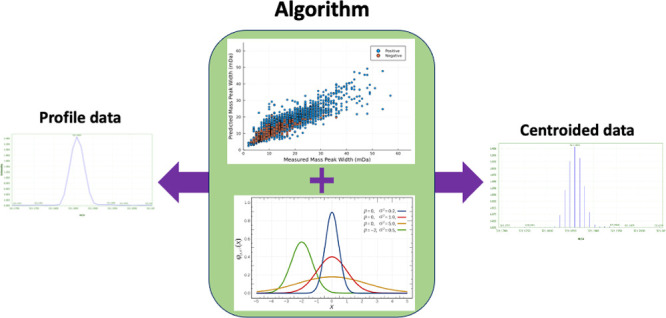
Based on 25,000 randomly selected centroided m/z values from all seven samples, the standard error of profile prediction ranged between 7.5 and 29.5%, independent of the ionization mode, mass, intensity, and sample matrix (Figure 4). To assess the error of the profile prediction, we calculated the difference between the predicted profiles and the measured profiles for a chromatogram from an untreated wastewater influent sample. Additionally, we visually inspected all 7 TICs and 100 randomly selected predicted profiles to further assess the observed standard errors of prediction. Except for six cases where the absolute intensities (i.e., 1200 c/s) were close to the minimum intensity threshold of 1000 c/s (i.e., average 0.01% relative intensity), all remaining 94 cases resulted in a successful profile prediction. A successful profile prediction was defined as cases where the predicted profiles have a prediction error ≤ the model prediction error (i.e., 56%). The profile prediction appeared to be more effective (i.e., smaller prediction errors) closer to the apex while deviating from the measured profile between the half height and the baseline (Figure 4). This was in agreement with the fact that the m/z profiles are generally better explained by the Gaussian function above the half height and that there is lower levels of signal fluctuations (e.g., noise and/or shadow peaks14) close to the apex (Figure 4a).
Figure 4.
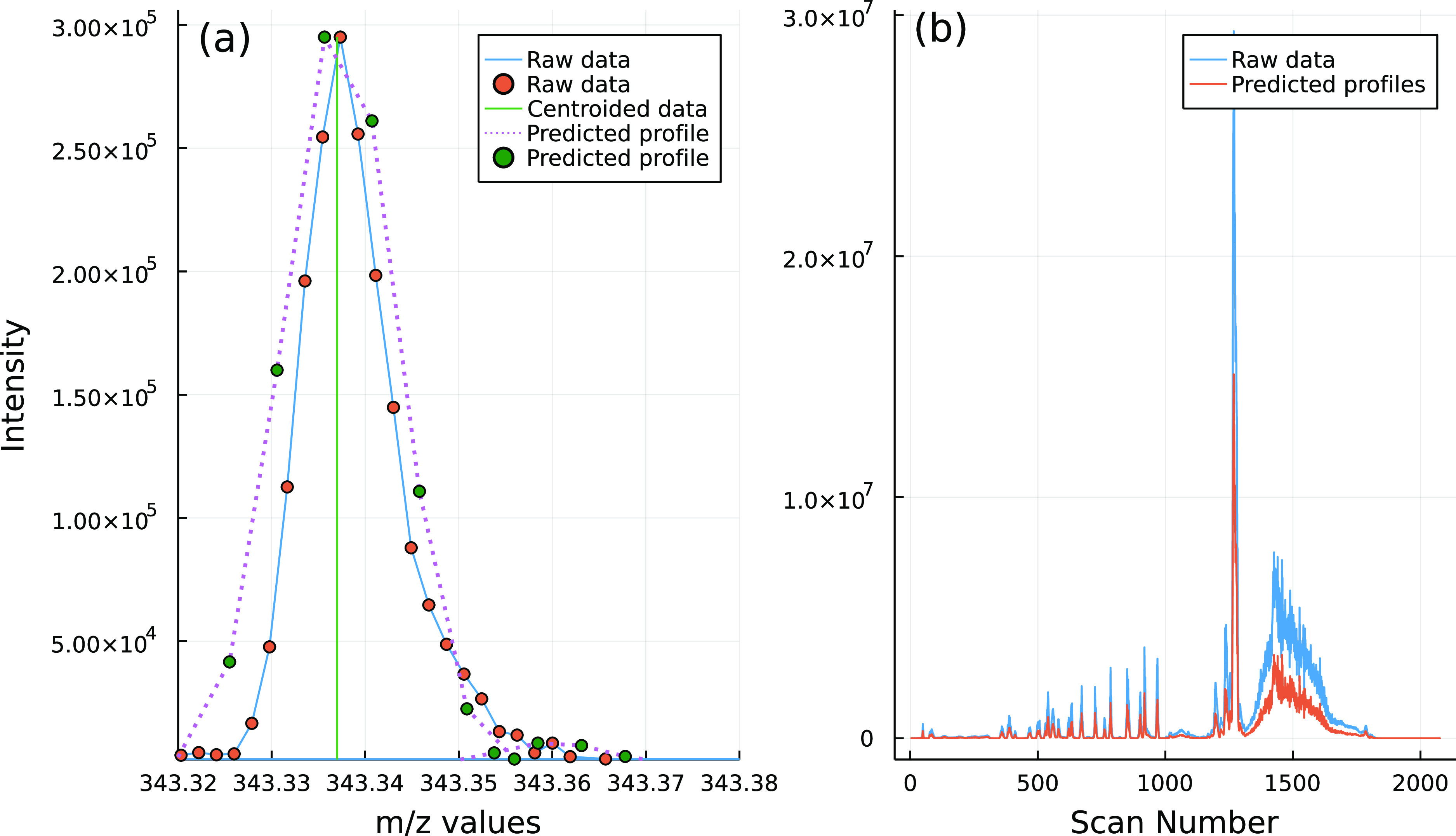
Examples of the (a) the predicted profile of an m/z value profile at scan 1400 based on the centroided data and (b) the measured and predicted TICs of a wastewater influent sample. These plots show case the ability of the developed algorithms to predict the mass profiles of the centroided data using relative intensity, m/z value, and the retention factor.
When generating the total ion currents (TICs), based on the predicted profiles, we observed a 32% increase (i.e., total observed error of 62%) in the deviation observed between the signals (i.e., measured vs predicted TICs) (Figures 4, S12 and S13). We identified two main sources for the observed discrepancies, namely, the signals below the set intensity threshold (Figure S12) and the number of points present in the measured mass peaks versus the limited number of points in the predicted profiles (Figure 4a). The deviation caused by the number of the points appeared to be 5 times larger than the fraction caused by the signals below the threshold, based on the 100 randomly selected profiles. This was assessed by calculating the difference between the sum of the points (i.e., intensities) in measured versus predicted profiles. When looking at the number of points in the measured profiles, they vary between 4, for low intensity signals, and 35 points, for higher intensity ones with an average of 8 points over the seven chromatograms. For the signals below the threshold, regions of high noise (e.g., around scan 1500, Figure 4b) were impacted more than lower noise areas of the chromatogram due to the higher density of signals below the threshold in those regions.
Overall, the profile prediction algorithm was successful in generating profile data based on the centroided data and the previously developed and validated model. This algorithm enables seamless conversion between the centroided and profile data for LC-HRMS data acquired with a QToF mass analyzers.
Conclusions
The presented algorithms, for the first time, enable the processing of the centroided and profile data by algorithms which only accept one or another (e.g., SAFD16 for profile and XCMS18,19 for centroided). Current version of the algorithm is implemented in SAFD16 as well enabling the processing of both centroid and profile data. Additionally, one of the outputs of the centroiding algorithm is the mass peak width at half-height, which can be used during data processing workflows (e.g., region of interest detection,18 XIC-based feature detection algorithms,44 and setting of mass accuracies for feature identification27,45). However, a recent study has highlighted the potential of the XIC-based feature detection approaches for these techniques.46 Thus, the presented algorithms, additionally, enable detailed (i.e., XIC based) feature detection in the dataset generated by higher dimension instruments such as comprehensive two-dimensional chromatography coupled with HRMS, which as of today rely on TIC level feature detection due to data complexity.37,47 All the algorithms are developed in an open source and open access manner and consequently are vendor-independent.
The current model, available for use with the Cent2Profile and SAFD.jl packages, is based on QToF data, which limits the application of the algorithm for orbitrap data. For the orbitrap data, an additional model is needed and will be the topic of our future work. Additionally, the impact of the profile prediction on the feature integration has not been evaluated and will be the subject of future studies. However, it should be noted that the algorithm maintains the measured peak intensity. Finally, the current version of the algorithm requires around 16 min for a chromatogram consisting of around 2000 scans, which could be improved by further optimization of the algorithms..
Acknowledgments
The authors are grateful to the members of CAST for their editorial input and fruitful discussions. S.S. and B.P. are thankful to the Agilent UR grant number 4523. The Queensland Alliance for Environmental Health Sciences (QAEHS), The University of Queensland, gratefully acknowledges the financial support of the Queensland Health and Australian Research Council ARC Discovery Project (DP190102476).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.1c03755.
Two tables with details related to the samples and parameter settings and 13 figures associated with the centroiding algorithm workflow, example cases (i.e., TP, TN, FP, FN), performance of MZmine 2, sensitivity analysis, model optimization, and model performance (PDF)
The authors declare no competing financial interest.
Notes
Code Availability: The julia package MS_Import.jl for reading mzXML and CDF files into julia environment is freely available for use via https://bitbucket.org/SSamanipour/ms_import.jl/src/master/. The algorithms for centroiding and profile prediction, including the trained model for QToF are available via julia package Cent2Profile.jl at https://bitbucket.org/SSamanipour/cent2profile.jl/src/master/. The SAFD package is available for use via https://bitbucket.org/SSamanipour/safd.jl/src/master/. The generated figures for quality control are available at https://doi.org/10.21942/uva.14618085.
Supplementary Material
References
- Schulze B.; Jeon Y.; Kaserzon S.; Heffernan A. L.; Dewapriya P.; O’Brien J.; Gomez Ramos M. J.; Ghorbani Gorji S.; Mueller J. F.; Thomas K. V.; Samanipour S. An assessment of quality assurance/quality control efforts in high resolution mass spectrometry non-target workflows for analysis of environmental samples. Trends Anal. Chem. 2020, 133, 116063. 10.1016/j.trac.2020.116063. [DOI] [Google Scholar]
- Gorrochategui E.; Jaumot J.; Lacorte S.; Tauler R. Data analysis strategies for targeted and untargeted LC-MS metabolomic studies: Overview and workflow. Trends Anal. Chem. 2016, 82, 425–442. 10.1016/j.trac.2016.07.004. [DOI] [Google Scholar]
- Samanipour S.; Reid M. J.; Thomas K. V. Statistical variable selection: an alternative prioritization strategy during the nontarget analysis of LC-HR-MS data. Anal. Chem. 2017, 89, 5585–5591. 10.1021/acs.analchem.7b00743. [DOI] [PubMed] [Google Scholar]
- Samanipour S.; Kaserzon S.; Vijayasarathy S.; Jiang H.; Choi P.; Reid M. J.; Mueller J. F.; Thomas K. V. Machine learning combined with non-targeted LC-HRMS analysis for a risk warning system of chemical hazards in drinking water: A proof of concept. Talanta 2019, 195, 426–432. 10.1016/j.talanta.2018.11.039. [DOI] [PubMed] [Google Scholar]
- Purschke K.; Vosough M.; Leonhardt J.; Weber M.; Schmidt T. C. Evaluation of Nontarget Long-Term LC-HRMS Time Series Data Using Multivariate Statistical Approaches. Anal. Chem. 2020, 92, 12273–12281. 10.1021/acs.analchem.0c01897. [DOI] [PubMed] [Google Scholar]
- Albergamo V.; Schollée J. E.; Schymanski E. L.; Helmus R.; Timmer H.; Hollender J.; De Voogt P. Nontarget screening reveals time trends of polar micropollutants in a riverbank filtration system. Environ. Sci. Technol. 2019, 53, 7584–7594. 10.1021/acs.est.9b01750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menger F.; Gago-Ferrero P.; Wiberg K.; Ahrens L. Wide-scope screening of polar contaminants of concern in water: A critical review of liquid chromatography-high resolution mass spectrometry-based strategies. Trends Environ. Anal. Chem. 2020, 28, e00102 10.1016/j.teac.2020.e00102. [DOI] [Google Scholar]
- Christensen J. H.; Tomasi G. Practical aspects of chemometrics for oil spill fingerprinting. J. Chromatogr. A 2007, 1169, 1–22. 10.1016/j.chroma.2007.08.077. [DOI] [PubMed] [Google Scholar]
- Yang J. Y.; Sanchez L. M.; Rath C. M.; Liu X.; Boudreau P. D.; Bruns N.; Glukhov E.; Wodtke A.; De Felicio R.; Fenner A.; et al. Molecular networking as a dereplication strategy. J. Nat. Prod. 2013, 76, 1686–1699. 10.1021/np400413s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollender J.; Schymanski E. L.; Singer H. P.; Ferguson P. L. Nontarget screening with high resolution mass spectrometry in the environment: ready to go?. Environ. Sci. Technol. 2017, 51, 11505–11512. 10.1021/acs.est.7b02184. [DOI] [PubMed] [Google Scholar]
- Samanipour S.; Martin J. W.; Lamoree M. H.; Reid M. J.; Thomas K. V. Letter to the Editor: Optimism for nontarget analysis in environmental chemistry. Environmen. Sci. Technol. 2019, 53, 5529–5530. 10.1021/acs.est.9b01476. [DOI] [PubMed] [Google Scholar]
- Vergeynst L.; Van Langenhove H.; Joos P.; Demeestere K. Accurate mass determination, quantification and determination of detection limits in liquid chromatography-high-resolution time-of-flight mass spectrometry: Challenges and practical solutions. Anal. Chim. Acta 2013, 789, 74–82. 10.1016/j.aca.2013.06.024. [DOI] [PubMed] [Google Scholar]
- Pluskal T.; Castillo S.; Villar-Briones A.; Orešič M. MZmine 2: modular framework for processing, visualizing, and analyzing mass spectrometry-based molecular profile data. BMC Bioinf. 2010, 11, 395. 10.1186/1471-2105-11-395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Hoffmann E.; Charette J.; Stroobant V.. Mass Spectrometry: Principles and Applications, 1997. [Google Scholar]
- Neumann S.; Böcker S. Computational mass spectrometry for metabolomics: identification of metabolites and small molecules. Anal. Bioanl. Chem. 2010, 398, 2779–2788. 10.1007/s00216-010-4142-5. [DOI] [PubMed] [Google Scholar]
- Samanipour S.; O’Brien J. W.; Reid M. J.; Thomas K. V. Self adjusting algorithm for the nontargeted feature detection of high resolution mass spectrometry coupled with liquid chromatography profile data. Anal. Chem. 2019, 91, 10800–10807. 10.1021/acs.analchem.9b02422. [DOI] [PubMed] [Google Scholar]
- Treviño V.; Yañez-Garza I.-L.; Rodriguez-López C. E.; Urrea-López R.; Garza-Rodriguez M.-L.; Barrera-Saldaña H.-A.; Tamez-Peña J. G.; Winkler R.; Díaz de-la-Garza R.-I. GridMass: a fast two-dimensional feature detection method for LC/MS. J. Mass Spec. 2015, 50, 165–174. 10.1002/jms.3512. [DOI] [PubMed] [Google Scholar]
- Tautenhahn R.; Böttcher C.; Neumann S. Highly sensitive feature detection for high resolution LC/MS. BMC Bioinf. 2008, 9, 1–16. 10.1186/1471-2105-9-504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith C. A.; Want E. J.; O’Maille G.; Abagyan R.; Siuzdak G. XCMS: processing mass spectrometry data for metabolite profiling using nonlinear peak alignment, matching, and identification. Anal. Chem. 2006, 78, 779–787. 10.1021/ac051437y. [DOI] [PubMed] [Google Scholar]
- Hohrenk L. L.; Itzel F.; Baetz N.; Tuerk J.; Vosough M.; Schmidt T. C. Comparison of Software Tools for Liquid Chromatography-High-Resolution Mass Spectrometry Data Processing in Nontarget Screening of Environmental Samples. Anal. Chem. 2019, 92, 1898–1907. 10.1021/acs.analchem.9b04095. [DOI] [PubMed] [Google Scholar]
- Myers O. D.; Sumner S. J.; Li S.; Barnes S.; Du X. Detailed investigation and comparison of the XCMS and MZmine 2 chromatogram construction and chromatographic peak detection methods for preprocessing mass spectrometry metabolomics data. Anal. Chem. 2017, 89, 8689–8695. 10.1021/acs.analchem.7b01069. [DOI] [PubMed] [Google Scholar]
- Li Z.; Lu Y.; Guo Y.; Cao H.; Wang Q.; Shui W. Comprehensive evaluation of untargeted metabolomics data processing software in feature detection, quantification and discriminating marker selection. Anal. Chim. Acta 2018, 1029, 50–57. 10.1016/j.aca.2018.05.001. [DOI] [PubMed] [Google Scholar]
- Hites R. A.; Jobst K. J. Is nontargeted screening reproducible?. Environ. Sci. Technol. 2018, 52, 11975–11976. 10.1021/acs.est.8b05671. [DOI] [PubMed] [Google Scholar]
- Hites R. A.; Jobst K. J. Response to “Letter to the Editor: Optimism for nontarget analysis in environmental chemistry”. Environmen. Sci. Technol. 2019, 53, 5531–5533. 10.1021/acs.est.9b02473. [DOI] [PubMed] [Google Scholar]
- Vivó-Truyols G. Bayesian approach for peak detection in two-dimensional chromatography. Anal. Chem. 2012, 84, 2622–2630. 10.1021/ac202124t. [DOI] [PubMed] [Google Scholar]
- Woldegebriel M.; Derks E. Artificial neural network for probabilistic feature recognition in liquid chromatography coupled to high-resolution mass spectrometry. Anal. Chem. 2017, 89, 1212–1221. 10.1021/acs.analchem.6b03678. [DOI] [PubMed] [Google Scholar]
- Samanipour S.; Reid M. J.; Bæk K.; Thomas K. V. Combining a Deconvolution and a Universal Library Search Algorithm for the Nontarget Analysis of Data-Independent Acquisition Mode Liquid Chromatography–High-Resolution Mass Spectrometry Results. Environmen. Sci. Technol. 2018, 52, 4694–4701. 10.1021/acs.est.8b00259. [DOI] [PubMed] [Google Scholar]
- Bezanson J.; Karpinski S.; Shah V. B.; Edelman A. J.. A Fast Dynamic Language for Technical Computing. 2012, arXiv preprint arXiv:1209.5145. [Google Scholar]
- Choi P. M.; O’Brien J. W.; Tscharke B. J.; Mueller J. F.; Thomas K. V.; Samanipour S. Population socioeconomics predicted using wastewater. Environ. Sci. Technol. Lett. 2020, 7, 567–572. 10.1021/acs.estlett.0c00392. [DOI] [Google Scholar]
- Choi P. M.; Tscharke B.; Samanipour S.; Hall W. D.; Gartner C. E.; Mueller J. F.; Thomas K. V.; O’Brien J. W. Social, demographic, and economic correlates of food and chemical consumption measured by wastewater-based epidemiology. Proc. Natl. Acad. Sci. 2019, 116, 21864–21873. 10.1073/pnas.1910242116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samanipour S.; Hooshyari M.; Baz-Lomba J. A.; Reid M. J.; Casale M.; Thomas K. V. The effect of extraction methodology on the recovery and distribution of naphthenic acids of oilfield produced water. Sci. Total Environ. 2019, 652, 1416–1423. 10.1016/j.scitotenv.2018.10.264. [DOI] [PubMed] [Google Scholar]
- Keller A.; Eng J.; Zhang N.; Li X. J.; Aebersold R. A uniform proteomics MS/MS analysis platform utilizing open XML file formats. Mol. Syst. Biol. 2005, 1, 2005. 10.1038/msb4100024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessner D.; Chambers M.; Burke R.; Agus D.; Mallick P. ProteoWizard: open source software for rapid proteomics tools development. Bioinformatics 2008, 24, 2534–2536. 10.1093/bioinformatics/btn323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poole C. F.; Poole S. K. Foundations of retention in partition chromatography. J. Chromatogr. A. 2009, 1216, 1530–1550. 10.1016/j.chroma.2008.10.092. [DOI] [PubMed] [Google Scholar]
- den Uijl M. J.; Schoenmakers P. J.; Pirok B. W. J.; Bommel M. R. Recent applications of retention modelling in liquid chromatography. J. Sep. Sci. 2021, 44, 88–114. 10.1002/jssc.202000905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J.; Miller J. C.. Statistics and Chemometrics for Analytical Chemistry; Pearson Education, 2018. [Google Scholar]
- Samanipour S.; Dimitriou-Christidis P.; Gros J.; Grange A.; Samuel Arey J. Analyte quantification with comprehensive two-dimensional gas chromatography: Assessment of methods for baseline correction, peak delineation, and matrix effect elimination for real samples. J. Chromatogr. A 2015, 1375, 123–139. 10.1016/j.chroma.2014.11.049. [DOI] [PubMed] [Google Scholar]
- Segal M. R.Machine Learning Benchmarks and Random Forest Regression, 2004. [Google Scholar]
- Janitza S.; Hornung R. On the overestimation of random forest’s out-of-bag error. PloS One 2018, 13, e0201904 10.1371/journal.pone.0201904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKight P. E.; Najab J.. Kruskal-wallis Test; Wiley Online Library, 2010; pp 1. [Google Scholar]
- Alygizakis N. A.; Samanipour S.; Hollender J.; Ibáñez M.; Kaserzon S.; Kokkali V.; Van Leerdam J. A.; Mueller J. F.; Pijnappels M.; Reid M. J.; et al. Exploring the potential of a global emerging contaminant early warning network through the use of retrospective suspect screening with high-resolution mass spectrometry. Environmen. Sci. Technol. 2018, 52, 5135–5144. 10.1021/acs.est.8b00365. [DOI] [PubMed] [Google Scholar]
- Samanipour S.; Baz-Lomba J. A.; Reid M. J.; Ciceri E.; Rowland S.; Nilsson P.; Thomas K. V. Assessing sample extraction efficiencies for the analysis of complex unresolved mixtures of organic pollutants: A comprehensive non-target approach. Anal. Chim. Acta 2018, 1025, 92–98. 10.1016/j.aca.2018.04.020. [DOI] [PubMed] [Google Scholar]
- Benesty J.; Chen J.; Huang Y.; Cohen I.. Noise Reduction in Speech Processing; Springer, 2009; pp 1–9. [Google Scholar]
- Loos M.enviMass, version 3.5 LC-HRMS Trend Detection Workflow–R Package, 2018.
- Samanipour S.; Baz-Lomba J. A.; Alygizakis N. A.; Reid M. J.; Thomaidis N. S.; Thomas K. V. Two stage algorithm vs commonly used approaches for the suspect screening of complex environmental samples analyzed via liquid chromatography high resolution time of flight mass spectroscopy: A test study. J. Chromatogr. A. 2017, 1501, 68–78. 10.1016/j.chroma.2017.04.040. [DOI] [PubMed] [Google Scholar]
- Cain C. N.; Schöneich S.; Synovec R. E. Development of an enhanced total ion current chromatogram algorithm to improve untargeted peak detection. Anal. Chem. 2020, 92, 11365–11373. 10.1021/acs.analchem.0c02136. [DOI] [PubMed] [Google Scholar]
- Samanipour S.; Dimitriou-Christidis P.; Nabi D.; Arey J. S. Elevated Concentrations of 4-Bromobiphenyl and 1,3,5-Tribromobenzene Found in Deep Water of Lake Geneva Based on GC×GC-ENCI-TOFMS and GC×GC-μECD. ACS Omega 2017, 2, 641–652. 10.1021/acsomega.6b00440. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.