Automatic Liver Tumor Localization Using Deep Learning-based Liver Boundary Motion Estimation and Biomechanical Modeling (DL-Bio)

Abstract

Purpose:

Recently, two-dimensional-to-three-dimensional (2D-3D) deformable registration has been applied to deform liver tumor contours from prior reference images onto estimated cone-beam computed tomography (CBCT) target images to automate on-board tumor localizations. Biomechanical modeling has also been introduced to fine-tune the intra-liver deformation-vector-fields (DVFs) solved by 2D-3D deformable registration, especially at low-contrast regions, using tissue elasticity information and liver boundary DVFs. However, the caudal liver boundary shows low contrast from surrounding tissues in the cone-beam projections, which degrades the accuracy of the intensity-based 2D-3D deformable registration there, and results in less accurate boundary conditions for biomechanical modeling. We developed a deep-learning (DL) based method to optimize the liver boundary DVFs after 2D-3D deformable registration, to further improve the accuracy of subsequent biomechanical modeling and liver tumor localization.

Methods:

The DL-based network was built based on the U-Net architecture. The network was trained in a supervised fashion to learn motion correlation between cranial and caudal liver boundaries to optimize the liver boundary DVFs. Inputs of the network had three channels, and each channel featured the 3D DVFs estimated by the 2D-3D deformable registration along one Cartesian direction (x, y, z). To incorporate patient-specific liver boundary information into the DVFs, the DVFs were masked by a liver boundary ring structure generated from the liver contour of the prior reference image. The network outputs were the optimized DVFs along the liver boundary with higher accuracy. From these optimized DVFs, boundary conditions were extracted for biomechanical modeling to further optimize the solution of intra-liver tumor motion.

We evaluated the method using 34 liver cancer patient cases, with 24 for training and 10 for testing. We evaluated and compared the performance of three methods: 2D-3D deformable registration, 2D-3D-Bio (2D-3D deformable registration with biomechanical modeling), and DL-Bio (DL model prediction with biomechanical modeling). The tumor localization errors were quantified through calculating the center-of-mass-errors (COMEs), DICE coefficients, and Hausdorff distance between deformed liver tumor contours and manually-segmented ‘gold-standard’ contours.

Results:

The predicted DVFs by the DL model showed improved accuracy at the liver boundary, which translated into more accurate liver tumor localizations through biomechanical modeling. On a total of 90 evaluated images and tumor contours, the average (± s.d.) liver tumor COMEs of the 2D-3D, 2D-3D-Bio, and DL-Bio techniques were 4.7±1.9 mm, 2.9±1.0 mm, and 1.7±0.4 mm. The corresponding average (± s.d.) DICE coefficients were 0.60±0.12, 0.71±0.07, and 0.78±0.03; and the average (± s.d.) Hausdorff distances were 7.0±2.6 mm, 5.4±1.5 mm, and 4.5±1.3 mm, respectively.

Conclusion:

DL-Bio solves a general correlation model to improve the accuracy of the DVFs at the liver boundary. With improved boundary conditions, the accuracy of biomechanical modeling can be further increased for accurate intra-liver low-contrast tumor localization.

1. Introduction:

Radiotherapy, especially stereotactic body radiotherapy, has become increasingly popular a treatment option for liver cancer patients due to its advantage of non-invasiveness and improved tumor control, especially for un-resectable cases [1–4]. However, tumor localization remains a challenge for liver radiotherapy, due to the low contrast of liver tumors against surrounding normal liver parenchyma in on-board x-ray imaging [5]. In addition, respiration-associated liver motion adds further uncertainties to liver tumor localizations when using conventional two-dimensional (2D) or 3D imaging techniques [6, 7]. These uncertainties mandated large treatment margins to be added to the liver tumor contours [8], which can extend 1 – 1.5 cm beyond actual tumor boundaries. Accurate liver tumor localization is key to substantial margin reduction, and is critical to improve the tumor control, reduce the radiation toxicity to normal liver tissues, and enable dose-escalation trials to further improve the radiotherapy therapeutic ratio. The neighboring critical organs to liver, such as stomach and small bowel, similarly demand accurate liver tumor localization for better normal organ sparing [9].

Many techniques have been developed or investigated to track liver tumors on-board during radiotherapy [10, 11]. Intravenous contrast is frequently administered during planning computed tomography (CT) acquisition to improve liver tumor contrast [5]. However, its use for on-board localization is rare due to complicated timing control logistics as well as potential contrast agent toxicity [12]. Fiducial markers have been used as surrogates for tumor position [7, 13–15], but implementing the markers requires invasive procedures which can cause inflammation [16]. Moreover, marker migration is possible and leads to tumor localization errors. Noninvasive surrogates such as breathing signals from surface imaging can also be used for real-time tumor tracking [17–20], but the motion correlation between the external markers and internal target motions may not be perfect [21] and are usually patient-specific. Markerless tracking using online magnetic resonance imaging has been used to track tumors [22–25]. While magnetic resonance imaging provides superior soft-tissue contrast, it requires dedicated machine and lacks electron density information for dose calculation.

In addition to the above techniques, linear accelerator (LINAC)-integrated cone-beam CT (CBCT) can provide on-board 3D anatomy of patients immediately before treatment delivery [26], and has become a clinical routine for image-guided radiation therapy to assist patient setup and tumor localization. In contrast to the conventional 3D-CBCT, which presents motion-averaged anatomy blurred by respiration, 4D-CBCT presents motion-resolved volumetric images of moving targets throughout a nominal respiratory cycle [27]. On-board 4D-CBCT images enable 4D tumor localization, and can reduce the margins added to tumors to spare more normal tissues, to potentially contribute to dose escalation while maintaining a low toxicity rate. However, for liver tumors, the lingering low-contrast issue in x-ray imaging substantially limits the applicability of 4D-CBCT towards accurate 4D liver tumor localization.

Rather than directly visualizing and delineating tumors on each phase of 4D-CBCT for localization, which is rather challenging, we may alternatively estimate a motion model to correlate the tumor shape and location between 4D-CBCT phases, or between prior images (for instance, the planning CT) and the 4D-CBCT phases. The motion model, which often takes the form of deformation-vector-fields (DVFs), allows automatic tumor propagation and localization even if such tasks may be visually challenging. Out of the many deformable registration methods, 2D-3D deformable registration has proved effective to estimate on-board CBCTs from prior CT/CBCT images, especially for scenarios where the number of available cone-beam projections are insufficient to reconstruct a high-quality CBCT for direct 3D-3D registration [28–32]. The 2D-3D deformable registration method estimates DVFs between a prior reference image and new on-board target images, by matching the pixel-wise intensities between 2D digitally-reconstructed-radiographs (DRRs) of the deformed 3D prior image and acquired 2D on-board projections. It can be especially effective towards scenarios of limited-angle or sparse-view projections, including 4D-CBCT imaging since the respiratory phase-sorting of 4D imaging leads to angular under-sampling at each phase.

In general, the intensity-matching-based 2D-3D deformable registration method can perform well in projection regions of high imaging contrast such as the lung boundary. However, its performance is degraded in regions where projection pixel intensity remains almost invariant [33]. To address the limitations of intensity-based deformable registration methods, biomechanical modeling has recently been investigated to solve DVFs [34–40]. By applying tissue material models with appropriate boundary conditions, biomechanical modeling can derive intra-organ DVFs using finite element analysis. The performance of biomechanical modeling for intra-lung motion estimation has been evaluated and validated in the Bio-CBCT-est [41] and SMEIR-Bio [42] studies, where DVFs generated by the 2D-3D deformable registration method at the lung surface serves as the boundary condition. A recent preliminary study has also demonstrated the benefit of combining biomechanical modeling with 2D-3D deformable registration for 4D liver tumor localization [40]. However, as shown for liver (Fig. 1), it is relatively straightforward to detect the cranial (upper) liver boundary and its motion in 2D projections, whereas the caudal (lower) liver boundary is more difficult to be differentiated and tracked from surrounding tissues of similar intensities [33, 43]. Therefore, less accurate 2D-3D DVFs at the caudal liver boundary may propagate the errors into biomechanical modeling and reduce the accuracy of intra-liver tumor localization [43].

Figure 1.

A CBCT projection for the liver site. The solid and dashed boxes highlight, respectively, the cranial and caudal regions of the liver. A large portion of the cranial liver boundary can be detected easily in the projection, while the caudal liver boundary is challenging to be differentiated due to lack of sufficient contrast.

To address this issue, recently we developed a principal component analysis (PCA) based liver boundary optimization method, named MM-Bio-CBCT [43]. PCA is an orthogonal linear-transformation method that transforms a high-dimensional vector into a low dimensional PCA projection to reduce redundancy information and find the correlation of features through a motion model. Correlations between the DVFs of upper and lower boundaries were learned implicitly from the PCA model, and the fine-tuned caudal boundary DVFs were combined with high accuracy cranial boundary DVFs to serve as the boundary condition in biomechanical modeling. The results proved the feasibility of using PCA to optimize the boundary DVFs to further improve the intra-liver motion estimation accuracy. However, MM-Bio-CBCT requires a patient-specific PCA model to be built from a 4D-CT/4D-CBCT scan of each patient, which adds additional logistic burdens to clinical deployment. Moreover, a 4D-CT/4D-CBCT set may not be available for each patient, especially for cases using breath-hold treatments [44].

In this study, we developed a convolutional neural network (CNN) based method to improve the liver motion model for on-board liver tumor localization. Specifically, we used a U-Net-structured model [45], which features multiple encoding and decoding layers at different resolutions to promote information extraction, sharing, and inference. Through a U-Net, we can extract both local and global features from input data and make predictions based on learned high-dimensional non-linear relations. Recently, U-Net has found many potential applications in medical imaging processing and analysis tasks such as de-noising [46] and segmentation [45, 47, 48]. In this study, liver DVFs obtained from the 2D-3D deformable registration were fed into a U-Net-based DVF optimization model to enhance the liver boundary DVF accuracy, especially along the caudal side. We then used the optimized DVFs as the boundary conditions for biomechanical modeling to derive the intra-liver motion and localize the tumors. The unified deep learning (DL) and biomechanical modeling method (DL-Bio) were evaluated and compared with methods including conventional 2D-3D deformable registration [33] and 2D-3D deformable registration with biomechanical modeling (2D-3D-Bio) [40]. Furthermore, in order to compare the DL-Bio scheme with other published algorithms [6, 49–53], the open-source software package Elastix [54] was combined with biomechanical modeling to perform a 3D-3D deformable registration for liver tumor localization, and its performance was compared with the DL-Bio and the other techniques.

2. Materials and Methods:

The DL-Bio scheme comprises three steps, and Fig. 2 summarizes the workflow of the proposed scheme. The first step was based on a 2D-3D deformable registration method to generate initial DVFs from CBCT projections by deforming a reference CT/CBCT image. In the second step which is highlighted by the shaded box in Fig. 2, a U-Net-based DL model was trained to learn liver boundary motion correlations, and deployed to optimize the 2D-3D DVFs around the liver boundary. Finally, biomechanical modeling was employed to derive intra-liver DVFs using the optimized liver surface DVFs as the boundary condition. Since the first and last steps have been detailed in Refs. [40, 43], we summarized both steps in Sec. 2.A and discussed details of the network architecture and input/output channels in Sec. 2.B. Section 2.C presents the schemes of evaluating the DL-Bio performance.

Figure 2.

Workflow of the proposed scheme to optimize and solve intra-liver motion. First, a 2D-3D deformable registration method is used to generate initial deformation-vector-fields (DVFs) that describe the liver motion with respect to the prior reference image. Then a convolutional neural network (CNN) is trained to optimize the DVFs to reduce their uncertainties, especially around the liver caudal boundary region. Finally, a biomechanical model uses the optimized DVFs at the liver boundary to solve intra-liver motions. The square boxes represent data operations in the workflow, and the rounded boxes represent input/output data which are connected by the arrows.

2.A. Methodology Background

2.A.1. 2D-3D deformable registration method

We applied a 2D-3D deformable registration method to estimate motion between a 3D reference image and on-board target projections. The motion is characterized by a DVF ${\mathit{D}}^{0\to t}$ that maps the voxel coordinates of the on-board image (t) from those of the reference image (0):

$$I_t\left(\mathit{x}\right)=I_0\left(\mathit{x}+{\mathit{D}}^{0\to t}\right),$$ (1)

where I_t(⋅) is the estimated new image at the coordinates x, and I₀(⋅) is the reference CT/CBCT image. Note that the DVF ${\mathit{D}}^{0\to t}\left(\mathit{x}\right)$ in Eq. (1) is defined on the spatial coordinates of the deformed image I_t(⋅). The deformation is subject to the data fidelity constraint that DRRs of the deformed volumetric image I_t(⋅) should match the measured 2D projections from the CBCT acquisition. Thus, the DVF can be solved by an iterative scheme which successively estimates the DVF and deforms the 3D reference image to attain intensity or feature matching in the 2D projections.

Specifically, the intensity matching can be accomplished by minimizing the objective function:

$$f\left({\mathit{D}}^{0\to t}\right)={‖P^t-A{I}_0\left(\mathit{x}+{\mathit{D}}^{0\to t}\right)‖}_{l_2}^2,$$ (2)

where P^t denotes the acquired CBCT projections, A is the projection matrix generating the corresponding DRRs, and ${‖\cdot ‖}_{l_2}$ is the Euclidian norm. Trilinear interpolation was used to deform the prior reference image [29], and then the deformed image was projected to generate the DRRs through a ray-tracing technique [55]. This iterative scheme, however, can be unstable if only limited 2D projections (i.e., constraints) are available. In order to stabilize the optimization, a term ϕ was added to the objective function to regularize the DVF. The regularization ϕ was chosen as the deformation energy in a quadratic form, which smoothes the DVF in a minimization process [21]. Thus, ϕ provides a trade-off between the data fidelity and DVF smoothness.

As shown in Eq. (1), ${\mathit{D}}^{0\to t}$ is defined on the voxel grid of the deformed image and points to the reference image. However, in biomechanical modeling, it is the inverse DVF ${\mathit{D}}^{t\to 0}\left(\mathit{X}\right)$, defined on the reference coordinates X, being used to deform the reference image to solve intra-liver motions. While in theory one can solve the inverse DVF directly from ${\mathit{D}}^{0\to t}$, in practice it may suffer from the inverse consistency errors (i.e., inconsistencies between registrations from the forward and inverse directions) [23]. In order to address this issue, we adopted a symmetric 2D-3D deformable registration approach that simultaneously solves ${\mathit{D}}^{0\to t}$ and ${\mathit{D}}^{t\to 0}$ by incorporating the data fidelity constraints of the inverse deformation into the objective function. Thus, the final objective function is

$$\begin{gathered} f\left({\mathit{D}}^{0\to t}\right)={{‖P^t-A{I}_0\left(\mathit{x}+{\mathit{D}}^{0\to t}\right)‖}_{l_2}^2+‖P^0-A\left\{\left[I_0\left(\mathit{x}+{\mathit{D}}^{0\to t}\right)\right]\left(\mathit{X}+{\mathit{D}}^{t\to 0}\right)\right\}‖}_{l_2}^2 \\ +\beta \left[\varphi \left({\mathit{D}}^{0\to t}\right)+\varphi \left({\mathit{D}}^{t\to 0}\right)\right], \end{gathered}$$ (3)

where P⁰ denotes the simulated symmetric projections at the reference phase using the same system matrix A, and β is the weighting factor for the regularization term ϕ. In this study, β was set as 0.025 from trial-and-error experiments. We also made the approximation of ${\mathit{D}}^{0\to t}={-\mathit{D}}^{t\to 0}$ in Eq. (3). The detailed implementation can be found in Refs. [40, 43]. As described, the 2D-3D deformable registration is an intensity-driven method, which shows higher accuracy at high-contrast regions including organ boundaries, but lower accuracy at homogeneous regions such as intra-liver regions [33].

2.A.2. Biomechanical modeling

In comparison to the 2D-3D deformable registration method, biomechanical modeling does not rely on the intensity variations to solve DVFs, which can improve the intra-liver DVF accuracy. Biomechanical modeling builds a mathematical representation of a biological system using the principle of mechanics to study the mechanical properties such as structure, functions, and motions. Since biomechanical models of living organs can incorporate material-specific properties such as morphology, material composition, and tissue elasticity, the simulated organ deformations are more physiologically and physically meaningful. Finite element method is frequently employed to simulate and analyze the biomechanical models. To solve intra-liver motions by biomechanical modeling, the livers are first partitioned into small elements (i.e., finite element mesh). Then the DVFs at the liver boundaries are used as the boundary conditions, and the intra-liver DVFs are solved by the finite element method.

We modeled the liver using the Mooney-Rivlin material model, which has been applied to model soft tissues of liver [56, 57] and lung [41, 58]. The Mooney-Rivlin material model describes the strain energy function W in terms of the first I₁ and second invariants I₂ of the left Cauchy-Green deformation tensor and the Jacobian J of the deformation gradient tensor:

$$W=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)+\frac{1}{2}{k(J-1)}^2,$$ (4)

where C₁₀ and C₀₁ are the material constants describing the elastic material behaviors, and k denotes the bulk modulus. The first and second terms in Eq. (4) represent the strain energy of a shape deformation, and the last term represents the strain energy of a volume change. The material is incompressible if the last term is zero. In this study, we simplified the strain energy function by setting C₁₀ = C₀₁ = C. According to the previous studies [40, 43], we used C = 0.135 kPa and k = 27 kPa.

For biomechanical modeling, we generated liver surface meshes, composed of triangles, based on the liver segmentations on the reference images using the Iso2Mesh package [59]. The liver segmentations were contoured manually. Tetrahedral meshes inside the livers were generated to fill the volume covered by the surface meshes. Depending on the liver volume, the number of nodes varied among patients and ranged from about 4100 to 7300. We extracted the DVFs on the liver surface meshes from the inverse DVF ${\mathit{D}}^{t\to 0}$ (Eq. (3)), and applied them as displacement-based boundary conditions in the biomechanical modeling to derive the intra-liver motions. The workflow of generating the tetrahedral meshes is illustrated in Fig. 3. In this study, we used the open-source FEBio package to perform the finite element analysis [60]. The detailed implementation can be found in Refs. [40, 43].

Figure 3.

Workflow of generating a tetrahedral mesh of a liver for biomechanical modeling. The liver was manually contoured from the reference image. Then, a surface mesh was generated using the contoured liver segmentation, and a tetrahedral mesh was created to fill the liver volume defined by the surface mesh.

2.B. U-Net-based DVF optimization

Since the biomechanical modeling derives intra-organ deformations from boundary conditions, the quality of the boundary DVFs will directly affect the accuracy of the resulting intra-organ DVFs. As aforementioned, it can be difficult to differentiate the caudal liver boundary from its surrounding tissues in a CBCT projection (Fig. 1). As a result, the DVFs from the intensity-based 2D-3D deformable registration method contain uncertainties at the caudal liver boundary region [33, 43]. Therefore, we used a CNN-based network to build a general correlation model to learn the motion correlation between the caudal and cranial liver boundary and thus enhance the accuracy of lower liver boundary DVFs before feeding them into finite element analysis to drive biomechanical modeling.

2.B.1. Network architecture

The correlation model is built using the U-Net architecture [45], which is illustrated in the second panel of Fig. 4. It comprises a contraction (left side) path and an expansion (right side) path. The contraction path gradually reduces the size of an input image, and meanwhile it captures and extracts features from the image. The expansion path restores the original image size to recover the information at specific positions by up-sampling procedures in a symmetric manner. In this study, the contraction path comprises four blocks, each of which contains two convolution layers followed by one max pooling layer to down-sample the image. The initial feature number is 16, and the number is doubled after each max pooling layer. All convolution layers use the same kernel size of 3×3×3, and the kernel size of max pooling layers is 2×2×2 with a stride of two for each dimension. The expansion path also consists of four blocks, and each block contains one 2×2×2 transposed convolution layer and two convolution layers. The feature maps after the transposed convolution layers are concatenated with the corresponding feature maps from the contraction path (horizontal connections in the second panel of Fig. 4), and the feature number is halved after each transposed convolution. The contraction and expansion paths are connected by two convolution layers. Two more convolution layers are added after the last block of the network to further reduce the feature dimension from 16 to 3. A dropout layer is inserted between the last two convolution layers with a dropout rate 0.5 to avoid over-fitting and improve the robustness of the network. The activation functions in the convolution and transposed convolution layers are tanh functions. The structure of the U-Net was optimized via a parameterized study (see supplementary material). We implemented the model in Python with the Keras [61] and Tensorflow [62] libraries, and applied the Adam algorithm [63] for optimization.

Figure 4.

The architecture of the convolutional neural network (CNN) to optimize initial 2D-3D DVFs. The architecture is based on the U-Net structure. The inputs of the network are the DVFs from the 2D-3D deformable registration method, masked by a boundary ring structure (see Sec. 2.B.2). The gold-standard DVFs for the supervised learning are generated from the Demons algorithm with the same boundary ring mask. The outputs are the optimized DVFs.

2.B.2. Input and gold-standard DVFs

As shown in Fig. 4, the input of the network is the DVFs from the 2D-3D deformable registration method, masked by a boundary ring structure. The three-channel input represents DVFs along three Cartesian directions: left-right (x), anterior-posterior (y), and superior-inferior (z). The network output contains similarly three channels, representing the three optimized DVFs.

In order to train the model, a ‘gold-standard’ DVF with accurate boundary motion is needed to drive the supervised training. The gold-standard DVFs were generated using 3D-3D deformable registration by the Demons algorithm [64], which considers non-rigid image-to-image matching as a diffusion process. In this study, we used a graphic processing unit (GPU)-based Demons registration algorithm that has been validated for its accuracy [65]. Specifically, we density-overrode the manually-segmented liver contour on each phase image (Fig. 5), and performed the Demons registration between phase 0% (the phase used as the prior reference) and all other phases to derive the DVFs. As the intensity-based deformable registration was performed directly between high-quality 3D volumes, and the tumor boundary contrast was substantially enhanced after density-override, the Demons DVFs are highly accurate at the liver boundary, and can represent the ‘gold-standard’ of liver boundary motion.

Figure 5.

Density-override livers to obtain ‘gold-standard’ liver boundary DVFs from the Demons algorithm. Subfigures A₁, A₂ and A₃ are the original CT images in the axial, sagittal and coronal planes, respectively. Subfigures B₁, B₂ and B₃ are the correspondingly density-overridden CT images in the same three planes, respectively.

Although the Demons DVFs are accurate at the liver boundaries, the accuracy of the intra-liver DVFs is mostly unchanged as intra-liver local contrast remains the same. Therefore, applying a boundary mask to the Demons DVFs can help the supervised model training to focus on learning the motion correlations at liver boundaries, and avoid making inaccurate inferences of intra-liver DVFs. Figure 6 illustrates the procedures to generate the boundary mask and select boundary DVFs. The boundary mask was generated through subtracting the dilated (with 10 voxels) liver contour of the prior reference image by the eroded (with 10 voxels) liver contour of the same image, rendering a ring-shaped structure in an axial view. In addition to the ‘gold-standard’ DVFs, the patient-specific ring mask was also applied to the input DVFs during training, validation and testing.

Figure 6.

Workflow of generating masked ‘gold-standard’ DVFs in network training. The liver contour of the prior reference image (phase 0%) are eroded and dilated to generate a boundary mask that selects a region near the liver boundaries. Then the mask is applied to Demons DVFs (as shown in this figure) or 2D-3D DVFs to obtain the DVFs near the liver boundaries.

2.C. Implementation and Evaluation of the DL-Bio scheme

2.C.1. Data preparation and U-Net model training/testing

To evaluate DL-Bio, we retrospectively used 34 liver patient cases from our institute, with the study approved under an umbrella institutional review boards (IRB) protocol. During the CT simulation, each patient received a contrast-enhanced 4D-CT scan. Twenty-six of the 34 patient cases have a 4D-CT of 10 saved respiratory phases (from 0% to 90%), and seven other cases have a 4D-CT of three saved phases (0%, 50% and 90%), and the remaining one case has two saved phases (0% and 50%). Because of inconsistent image resolutions across these cases, all 4D-CT images were resampled to the same volume size of 256×256×128, at a voxel resolution of 2.00×2.00×2.00 mm³. For each 4D-CT, the end-inhale phase (0%) was extracted to simulate the prior reference image, and all other phases were used as new on-board images to simulate cone-beam projections. For each volume, 20 projections were simulated to distribute across a 360° scan angle [55]. The CBCT imaging geometry was characterized by a source-to-isocenter distance of 1000 mm and a source-to-detector distance of 1500 mm. Each projection had 512×384 pixels, with the pixel resolution of 0.776×0.776 mm². As the reference-phase liver contours were used in the U-Net-based DVF optimization and biomechanical modeling to generate boundary masks and liver meshes, we manually segmented liver contours.

For each case, the prior reference image, along with the phase-specific cone-beam projections, were fed into the 2D-3D deformable registration method (Sec. 2.A.1) to generate initial 2D-3D DVFs. We separated the patient-specific 2D-3D DVFs into training, validation, and testing groups, which contained the DVFs from 17, 7, and 10 patients, respectively, to train the U-Net-based CNN model (Sec. 2.B).

To reduce the memory footprint of the network to fit the memory limit of the GPU, we further cropped all masked DVFs from 256×256×128 to 192×192×128 by removing peripheral backgrounds, and down-sampled the resulting DVFs by a factor of two along all the dimensions, before feeding them into the network for training. Since we had limited samples to train the model, data augmentation was employed to mitigate overfitting. For each DVF fed into the network, we randomly displaced the DVF in three directions under a uniform probability distribution. A NVIDIA Tesla v100-sxm2 GPU card was used to train the model, using a batch size of 4. For testing, the output DVFs of the network were rescaled back to the original 256×256×128 size using cubic interpolation [66] and zero-padding.

2.C.2. Evaluation Schemes

Evaluation of the liver boundary deformation accuracy

Since the Demons DVFs were used as the ‘gold-standard’ DVFs to train the U-Net-based CNN model, we first evaluated the accuracy of the Demons registration. The accuracy was evaluated using the DICE coefficient [67] and Hausdorff distance between the deformed and the ‘gold-standard’ manually-segmented liver contours. Furthermore, the registrations with and without the density-override of the liver were evaluated to demonstrate the improvement of the deformation accuracy after density-override.

Given two liver contours V₁ and V₂ represented as binary volumes, the DICE coefficient evaluates the similarity between the two contours by calculating

$$DICE=\frac{2\times \left|V_1\cap V_2\right|}{\left|V_1\right|+\left|V_2\right|},$$ (5)

where |V| represents the cardinality of V. The value of a DICE coefficient ranges from zero to one with one representing identical V₁ and V₂. The Hausdorff distance measures the overall distance between two sets X and Y, and is defined as

$$d_H=\max \{{\max }_{x\in X}d\left(x,Y\right),\underset{y\in Y}{\max }d\left(y,X\right)\},$$ (6)

where

$$d\left(x,Y\right)={\min }_{y\in Y}{\Vert x-y\Vert }_{l_2}.$$ (7)

X and Y denote the deformed and manually-segmented liver contours, respectively. A smaller Hausdorff distance indicates better match between two volumes.

Evaluation of the liver tumor localization accuracy

Depending on the combinations of different sub-techniques (Secs. 2.A – 2.B), we compared three methods in solving the intra-liver DVFs for liver tumor localization: 2D-3D, 2D-3D-Bio and DL-Bio. We calculated the DICE coefficient, tumor center-of-mass error (COME), and Hausdorff distance to quantitatively evaluate the accuracy of the liver tumor localization. The COME is defined as the center-of-mass distance between deformed and ‘gold-standard’ manual contours.

In addition to the methods discussed above, currently, 3D-3D deformable registration using biomechanical modeling is often treated as the state-of-the-art to register or localize low-contrast liver tumors in CT/CBCT [6, 49–53]. These methods mostly rely on extracting liver boundary conditions from direct 3D-3D image registration, as compared to the 2D-3D deformable registration used in our method. To mimic the approach applied in these methods [49, 51–53], we first reconstructed the 3D images from the cone-beam projections used in our study via the Feldkamp-Davis-Kress (FDK) algorithm [68], and then used a popular, state-of-the-art open-source software package Elastix [54] to perform registrations between the prior reference images and on-board CBCT images reconstructed by FDK. The registrations were performed using a B-spline transformation with a multi-resolution strategy. The number of resolution levels was 4, and the resolution was doubled every level. Mutual information was used as the similarity metric. Since the reconstructed CBCT images have an axial field-of-view around 265×265 mm², which is less than the field-of-view of the prior reference images, a registration mask was applied to match the field-of-view of the reconstructed CBCT during the registrations. The Elastix DVFs were subsequently applied in the biomechanical modeling to derive the intra-liver DVFs. The performance was measured using the liver tumor DICE coefficient, center-of-mass error, and Hausdorff distance as well, and compared against the other methods.

Evaluation of correlations between the liver tumor COME and the relative intra-liver tumor position

In addition to directly evaluating liver boundary deformation with Hausdorff distance, the capability of the DL model to optimize the 2D-3D DVFs, especially in the caudal liver regions, can be analyzed by examining the correlation between the liver tumor COME and the intra-liver tumor position. It has been shown that boundary conditions are the major factor influencing the accuracy of a biomechanical model [69], thus the tumor COME can be mainly attributed to the inaccuracy of the boundary conditions. Since the 2D-3D DVFs are less accurate at the caudal liver boundary, tumors positioned closer to the caudal boundaries are expected to have larger COME than those closer to the cranial boundaries. Therefore, the liver tumor COME can be correlated with the tumor’s relative location within the liver, and the reduction of this correlation implies the improvement of the caudal liver boundary DVFs, relative to the cranial ones.

Thus, we analyzed such correlation for the 2D-3D-Bio and DL-Bio techniques. To account for the fact that the tumor motion range varies significantly within our studied patient cohort, we scaled the COME results of each patient by the tumor motion range measured on the patient-specific 4D-CT. In addition, we defined the tumor position in a liver based on its relations to the liver boundary along the superior-inferior direction. Specifically, considering various sizes and shapes of livers and liver tumors, the relative tumor position is defined through voxel-wise averaging. We calculated the voxel-wise, superior-inferior distances between the tumor and the cranial liver boundary, averaged them over the entire tumor volume, and then scaled the resulting distance by the average distance between the caudal and cranial liver boundaries. This scaled tumor-boundary distance was named ‘percentile distance’, with higher value indicating the tumor locating closer to the caudal liver boundary.

3. Results

3.A. Evaluation of the liver boundary deformation accuracy

Figure 7 presents the quantitative evaluation of the Demons algorithm with and without the density-override of the liver contours. For comparison, we also calculated the DICE coefficients and Hausdorff distances between the liver contours of the prior reference phase (phase 0%) and other phases, which indicates the extent of the liver deformation due to respiratory motion. It can be observed that the accuracy of the registration is improved by the density-override in terms of both metrics.

Figure 7.

(a) Average DICE coefficients and (b) Hausdorff distances between the deformed and manually-segmented liver contours, as a function of respiratory phase. The deformation is based on the Demons DVFs with or without the density-override of the livers (Sec. 2.B.2). For comparison, the DICE coefficients and Hausdorff distances between the prior reference phase (Phase 0%) and other phases are also presented. The error bar indicates the standard deviation.

The deformed contours were also overlaid with the ‘gold-standard’ contours to assess their mismatch, for the 50% (end-exhale) phase (Fig. 8). The end-exhale phase was chosen because it typically corresponded to the phase with the largest extent of motion/deformation from the prior reference image (phase 0%, end-inhale). As shown, the DL model helped to further improve the match between the deformed liver contour and the ‘gold-standard’ manual contour, especially at the caudal liver boundary (pointed to by the dashed arrows). It can also be observed that the improvement of deformation also occurred at a portion of the upper liver boundary (pointed to by the solid arrow) adjacent to the heart and thus also with limited contrast (Fig. 1, Fig. 5).

Figure 8.

(First column) Overlay of the ‘gold-standard’ liver contours at the end-exhale phase (50%, shown in red mesh) and the liver contours of the prior reference volumes (end-inhale 0% phase, shown in yellow mesh). Each row represents one patient case. (Second and third columns) Overlay of the deformed contours (yellow) and the ‘gold-standard’ contours (red). The second column uses the deformed contours based on the DVFs from the 2D-3D deformable registration method. The third column uses the deformed contours based on the DVFs corrected by the DL model. The arrows highlight the regions of the liver contours showing clear improvement after the DL model-based correction.

3.B. Evaluation of the liver tumor localization accuracy

Figure 9 presents the average DICE coefficients, COMEs, and Hausdorff distances of all 10 patients in the testing group. The DL-Bio provided the best tumor localization accuracy, with more improvements observed for respiratory phases with larger motion. Wilcoxon signed-rank tests were carried out for the DICE coefficient, COMEs, and Hausdorff distances on the 2D-3D, 2D-3D-Bio, and DL-Bio techniques. The tests are between the 2D-3D and 2D-3D-Bio, between the 2D-3D and DL-Bio, and between the 2D-3D-Bio and DL-Bio techniques. In all cases the p-values are smaller than 10⁻⁴, showing that the 2D-3D-Bio method provided better tumor localization accuracy than the 2D-3D method after additional biomechanical modeling, and the DL-Bio method provided statistically significant improvement in liver tumor localization than the other two methods.

Figure 9.

(a) Average tumor DICE coefficient, (b) COME, and (c) Hausdorff distance as a function of respiratory phases. The DICE coefficients, COMEs, and Hausdorff distance were averaged over the 10 patients in the testing group. The error bar indicates the standard deviation.

Table 1 summarizes the average DICE coefficients, COME, and Hausdorff distance of the 90 evaluated images. For comparison, we performed the registration using the Elastix package with biomechanical modeling (Elastix-Bio) and calculated these similarity metrics as well. The Elastix deformable registration was performed between the prior reference images and reconstructed images from the CBCT projections. It can observed that Elastix-Bio performs much worse than the other techniques due to the degraded CBCT images reconstructed from sparse projections with limited field-of-view.

Table 1.

Average (± s.d.) liver tumor DICE, COME, and Hausdorff distance of the 2D-3D, 2D-3D-Bio, DL-Bio, and Elastix-Bio techniques.

Technique	DICE	COME (mm)	Hausdorff distance (mm)
2D-3D	0.60±0.12	4.7±1.9	7.0±2.6
2D-3D-Bio	0.71±0.07	2.9±1.0	5.4±1.5
DL-Bio	0.78±0.03	1.7±0.4	4.5±1.3
Elastix-Bio	0.42±0.27	8.9±6.5	15.0±12.0

3.C. Evaluation of correlations between the liver tumor COME and the relative intra-liver tumor position

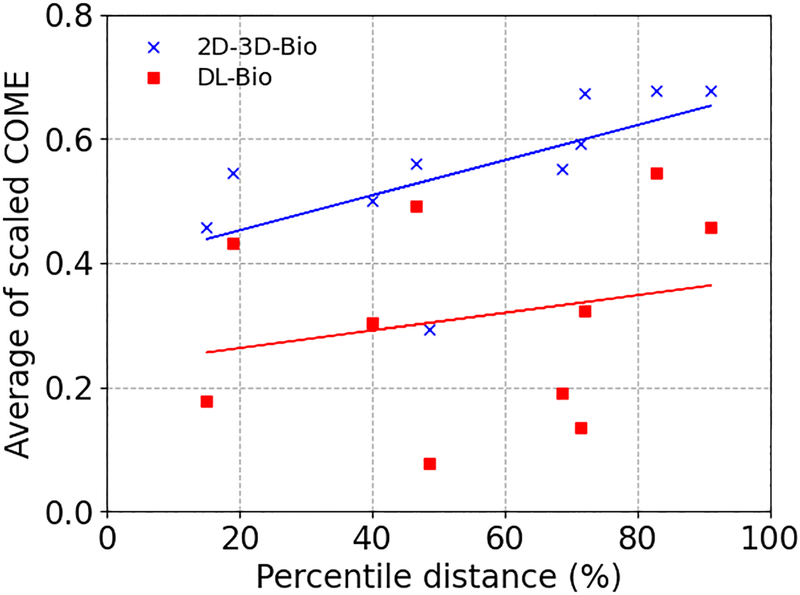
Figure 10 compares the scaled tumor COME (averaged over phases 40%−70%) as a function of the tumor percentile distance to the cranial liver boundary for each testing patient, between the 2D-3D-Bio and DL-Bio. Phases 40%−70% were selected because they corresponded to the largest deformations from the prior reference image (phase 0%), and thus more representative on inaccurate liver boundary DVFs. Zero and 100% percentile distance corresponded to tumors positioned at the cranial and caudal liver boundaries, respectively. Compared with the 2D-3D-Bio, the DL-Bio shows not only a smaller scaled COME for each patient but also a weaker correlation with the tumor percentile distance. The two-sided p-value for the Wald test with t-distribution were 0.056 and 0.53 for the 2D-3D-Bio and DL-Bio dataset, respectively, showing the tumor localization accuracy of 2D-3D-Bio was more correlated with the relative intra-liver tumor position. As the DL-Bio corrected the lower liver boundary motion using the DL model, its tumor localization accuracy not only improved, but also was less dependent on the relative intra-liver tumor position. This implies the DL-optimized DVFs improves the overall liver boundary deformation and, in particular, the caudal liver boundary.

Figure 10.

Scaled tumor COME as a function of percentile distance of the tumor to the liver cranial boundary for the 10 patients in the testing group. The scaled COME was averaged over phases 40%−70%. The lines show linear regression trend lines for the 2D-3D-Bio and DL-Bio dataset, respectively.

4. Discussion

In this study, we developed a DL-based method to build a motion correlation model between the liver cranial and caudal boundaries, using a U-Net-based structure. The DVFs solved by the intensity-based 2D-3D deformable registration method have large uncertainties at the caudal liver boundary, due to the low tissue contrast there. Using the DL-based method, high-accuracy DVFs can be obtained by applying the learnt, implicit boundary motion correlations to optimize the caudal liver boundary DVFs using information from the more accurate DVFs at the cranial side. The optimized boundary DVFs can then serve as boundary conditions in biomechanical modeling to derive the intra-liver motion. Our results support our hypothesis that the optimized DVFs have higher accuracy around the liver boundary region (Fig. 8), and can increase the accuracy of the intra-liver DVFs for tumor localization (Figs. 9, 10). The improvement of the liver boundary deformation, however, is not restricted to the caudal liver side only. As shown in Fig. 8, the deformation at the cranial side but close to the heart, where the liver boundary contrast was also low (Figs. 1, 5), similarly saw clear improvements. The DL-based model improved the overall liver boundary DVFs, which translated into more accurate liver tumor localization after biomechanical modeling.

In Fig. 10, there shows a positive correlation between the scaled COMEs and the percentile distances (between the liver tumor and the liver cranial boundary) for the 2D-3D-Bio DVFs. It is expected, since increasing percentile distances indicates closer-to-caudal-boundary liver tumors, where the intra-liver DVFs were more impacted by less-accurate caudal boundary DVFs from biomechanical modeling. On the other hand, for the case of the DL-Bio DVFs, the correlation between the scaled COME and the tumor percentile distance is less established, indicating the tumor localization accuracy becomes less intra-liver position dependent after the caudal-boundary DVF accuracy increases. Statistical tests showed that the significance of correlation for the 2D-3D-Bio dataset was at borderline (based on a 0.05 significance level), which is potentially due to the fluctuations from a limited sample size and remains to be investigated in future when more patient data become available.

To run the DL-based model, the liver segmentation at the prior reference images is needed to generate a boundary ring mask. It is also needed for mesh generation to drive biomechanical modeling. Since liver is almost always segmented in planning CTs as a critical organ-at-risk in liver cancer treatments, the clinical contour can be directly applied to our use. In addition, automatic liver segmentation techniques have also been developed, which can also be used to generate the liver contours [70–73].

Whereas the DL-Bio scheme is not restricted to solving respiratory motion only, in this study we simulated prior reference image and new on-board images from 4D-CT sets, and estimated inter-phase liver motions within a nominal respiratory cycle. Since these 4D-CTs were contrast-enhanced, the tumors can be contoured by radiation oncologists with high confidence to provide ‘gold-standard’ references to quantitatively evaluate tumor localization results by different methods. Note that although the tumor contrast has been enhanced in the 4D-CT, it was still low, especially on limited-view 2D cone-beam projections, and was insufficient to guide accurate 2D-3D deformable registration (Fig. 9). In addition to the respiratory motion, future studies are warranted to include training and testing data of other liver deformation scenarios including the compression-device induced liver deformation, and deformation at different breath-holds (which are similar to respiratory motion, though). The challenges remain on how to extract ‘gold-standard’ liver tumor shape and location from these data for quantitative evaluation, while implanted liver fiducial markers may help to localize the liver tumors.

In this study, the cone-beam projections were simulated from the 4D-CT phase images using ray-tracing techniques. Real cone-beam projections will contain degrading signals including scatter and noise, which may affect the 2D-3D deformable registration results, and thus the overall DL-Bio accuracy. However, previous studies using real cone-beam projections, or simulated cone-beam projections by Monte-Carlo techniques showed that the 2D-3D deformable registration can perform well by adjusting the objective function. For instance, we can use normalized cross-correlation instead of the sum-of-squared-error metric [31], or add scaling and shift factors to re-normalize the projection intensities [40]. Other techniques, including applying deep-learning techniques to correct the degradation signals, or using hardware/software-based scatter correction methods, can also be used [74, 75].

The DL-Bio method only used a DL-based model to enhance the DVF accuracy at the liver boundary, with the 2D-3D deformable registration and the biomechanical modeling steps based on previously-developed iterative methods. Recent developments also found DL-based 2D-3D deformable registration and biomechanical modeling methods to be accurate and highly efficient [76, 77]. The combination of these methods into one network, however, may require substantial memory footprint and special network design and training to improve its robustness, which remains to be investigated.

A different approach to track on-board liver tumors is to directly segment liver tumors from reconstructed CBCT images [78]. However, it is very challenging in our scenario, due to the low contrast of the tumors against their surrounding tissues, as well as the degraded CBCT image quality from reconstructions using sparse and limited-size projections. Alternatively, new techniques were developed to combine deformable registration and biomechanical modeling to indirectly localize the liver tumors via solved DVFs, circumventing the difficulties of directly segmenting the low-contrast liver tumors embedded in normal tissues [6, 49–53]. The DVF-driven method also enjoys additional benefits for applications including DVF-driven dose accumulation and adaptive radiotherapy [6, 50, 51, 53]. However, direct 3D-3D deformable registration between the prior reference and reconstructed CBCT images, as used by these state-of-the-art biomechanical modeling methods, still suffered from the low CBCT quality due to under-sampling. As shown in Table 1, the Elastix-Bio method failed to localize the liver tumors accurately. On the other hand, the 2D-3D deformable registration technique avoids direct 3D-3D registration on quality-compromised CBCT images. It instead measures similarity in the 2D projection domain to allow more accurate DVF solution for further DL-based boundary DVF enhancement and biomechanical modeling.

One disadvantage of the proposed DL-Bio scheme is that the network is trained in a supervised fashion, thus ground-truth DVFs are required to train the network. Since deformable image registration is an ill-posed problem, true DVFs may not exist. Nevertheless, we used the Demons algorithm with density-overridden liver images to enhance its accuracy at liver boundaries, and achieved results of high accuracy (Fig. 7). In addition, liver boundary masks were applied to focus the training/inference on liver boundary DVFs, avoiding inaccurate inference from less accurate intra-liver DVFs of Demons registration. The results on liver boundary deformation accuracy enhancement (Fig. 8) and liver tumor localization (Fig. 9) further corroborate the accuracy of the Demons DVFs around liver boundaries. In this study, the liver boundary DVF solved by the Demons registration after the additional density-override step is used as the ‘gold-standard’ for model training. Similarly, previous studies also used supervised learning with assumed ‘gold-standard’ DVFs to train their model and generated good results (e.g., [79]). However, we acknowledge that no deformable registration algorithm is optimal, and there will be residual errors after registration. Nonetheless, our framework of generating ‘gold-standard’ DVFs can be readily adapted to future new deformable registration algorithms if they offer better accuracy at liver boundary deformation, which could help our technique to further improve the tumor localization accuracy.

The pilot investigation performed in this study helped to confirm a general motion correlation model can be learned by a DL network and its ability to optimize the 2D-3D DVFs at the liver boundary to further improve biomechanical modeling. This pilot study is based on patient-specific 4D-CT images of a cohort of 34 patients, which translate into hundreds of images for training/validation/testing. In addition, we used data augmentation including shift during the deep learning model training to help mitigate the small dataset issue. Moreover, a dropout layer was also included in the network architecture to further improve the robustness of the network to mitigate overfitting. However, we acknowledge that 34 patients make a small sample, and a larger patient cohort will help to better support and evaluate the proposed DL-Bio scheme, and to improve the generalizability of the method. Future studies are warranted when more data become available.

In conclusion, we developed a DL-Bio scheme to combine deep learning and biomechanical modeling to substantially improve the liver tumor localization accuracy in low-contrast x-ray imaging. The intra-liver DVFs solved by this method can also be readily applied towards adaptive radiotherapy for other applications including dose accumulation [80]. In future studies more patient data are warranted to be included to further train and test the model towards more motion scenarios and evaluate its robustness.

Data availability statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.