Abstract
Although the need for addressing matching in the analysis of matched case-control studies is well established, debate remains as to the most appropriate analytical method when matching on at least 1 continuous factor. We compared the bias and efficiency of unadjusted and adjusted conditional logistic regression (CLR) and unconditional logistic regression (ULR) in the setting of both exact and nonexact matching. To demonstrate that case-control matching distorts the association between the matching variables and the outcome in the matched sample relative to the target population, we derived the logit model for the matched case-control sample under exact matching. We conducted simulations to validate our theoretical conclusions and to explore different ways of adjusting for the matching variables in CLR and ULR to reduce biases. When matching is exact, CLR is unbiased in all settings. When matching is not exact, unadjusted CLR tends to be biased, and this bias increases with increasing matching caliper size. Spline smoothing of the matching variables in CLR can alleviate biases. Regardless of exact or nonexact matching, adjusted ULR is generally biased unless the functional form of the matched factors is modeled correctly. The validity of adjusted ULR is vulnerable to model specification error. CLR should remain the primary analytical approach.
Keywords: biased estimate, logistic regression, matched case-control study, restricted cubic spline, selection bias
Abbreviations
- CLR
conditional logistic regression
- L
linear term of the matching factor(s)
- SP
restricted cubic spline transformation of the matching factor(s)
- ULR
unconditional logistic regression
The case-control design is one of the most commonly used designs in epidemiology and clinical research to assess risk factors for rare diseases, particularly those with long latency periods. In the presence of strong confounders, the matched case-control design is generally more efficient than the unmatched design (1, 2). In individually matched studies, controls are randomly selected and matched to individual cases using exact or caliper matching. Matching can be performed on many different types of variables, including binary factors, such as sex; nominal factors with many categories, such as neighborhood, sibship, or referring physician; continuous factors, such as age; or mixed types of factors, such as age and sex.
Depending on the number and type of matching variables, matched data can be analyzed in at least 2 different ways: 1) by conditional logistic regression (CLR) or 2) by unconditional logistic regression (ULR). When the number of participants per stratum of the matched factors is low, such as when cases and controls are matched on nominal factors with many categories (e.g., neighborhood or sibship) or on many different factors (e.g., sex, race, and age categories), CLR is the well-accepted choice for analysis (3). ULR adjusting for many matched sets as covariates is not appropriate in this setting because maximum likelihood estimation can yield highly biased point estimates in the presence of many nuisance parameters (3). In contrast, when the number of participants per stratum is high, such as when cases and controls are matched on one binary factor (e.g., sex), both CLR and ULR adjusting for the matching factor are appropriate, with ULR providing greater efficiency of estimation. This advantage was recently illustrated in a widely cited study by Pearce (4). In this study, Pearce used a hypothetical example to illustrate that covariate-adjusted ULR can outperform CLR in a matched case-control design with a binary matching factor. However, some researchers have taken this conclusion even further and applied it to matched studies in which cases and controls are matched on a continuous factor (5–7), a design in which the most practical analytical method is still debated.
Breslow and Day (3) noticed several decades ago that ULR controlling for linear terms of continuous matching variables produced very similar results to CLR in some cases (8, 9), despite breaking the matched sets. However, other investigators have demonstrated that case-control matching can alter the functional form of continuous matching variables in such a way that even though the matching variables may have a linear logistic form in the source population, they have a highly nonlinear form in the matched sample (10, 11). In this case, fitting a naive ULR including a linear term of the matching variable(s) will likely yield biased results because the model is misspecified (12). On the other hand, when matching is not exact, unadjusted CLR estimates could be biased from a mixture of residual confounding from nonexact matching and the noncollapsibility of the odds ratio in a logit model (13–15). This bias often goes unnoticed in practice (12).
Given remaining uncertainties over the most appropriate method for analyzing case-control studies matched on at least 1 continuous factor, we compared the performance of unadjusted ULR, ULR including a linear term of the matching factor(s) (ULR + L), and ULR including a restricted cubic spline transformation of the matching factor(s) (ULR + SP) to CLR. In the exact matching setting, all comparisons were made to unadjusted CLR, whereas in the nonexact setting, comparisons were made to CLR including a linear term of the matching factor(s) (CLR + L) and CLR including a restricted cubic spline transformation of the matching factor(s) (CLR + SP). We performed this additional analysis in the nonexact setting to investigate the bias introduced by nonexact matching (12) and to determine the best approach to address this bias.
METHODS
CLR versus adjusted ULR when matching is exact
For simplicity, we first assume the disease outcome in a hypothetical source population is rare (e.g., proportion of cases in each level of matching factors of <10%) and discuss the common outcome later. We let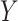 
denote a binary disease outcome variable, where Y = 1 for a case and Y = 0 for a control. We similarly denote the exposure variable by 
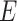, where 
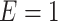if exposed and 
if not exposed. Next, we denote a vector of p discrete and continuous confounders by 
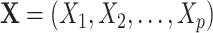. We assume there are no unmeasured confounders and that the size of 
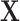is feasible for matching. In practice, we commonly match on 1 or 2 variables such as sex and age. We further assume the relationship between 
, 
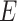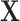, and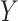 
in the source population is described by the following logit model:
 |
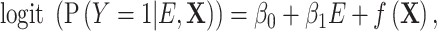(1) |
where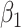 
measures the conditional effect of the exposure and 
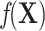represents an arbitrary function of 
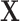. For example, when 
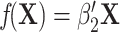, where 
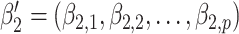, only the linear terms of confounders are included and the confounders are linearly associated with the logit probability of having the disease. 
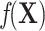can take more complex forms by including nonlinearity and interaction terms. Because the disease outcome is rare, the logit model 1 can be approximated by a log-linear model and thus 
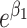can be interpreted as both an odds ratio and relative risk.
The relationship between the exposure and confounder in the source population is specified by:
 |
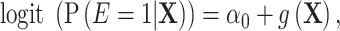(2) |
where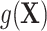 
is an arbitrary function of 
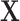. For example, when 
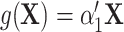, where 
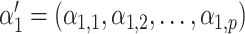, the confounders are linearly associated with the logit probability of being exposed. 
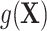can also take more complex forms by including nonlinearity and interaction terms.
In matched strata formed by matching cases and controls on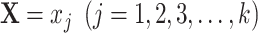 
, we can reasonably assume there are more potential controls available than cases because the disease outcome is rare, and we select all cases and an equal number of controls in each matched stratum to create a matched case-control sample. Because cases are oversampled and controls are undersampled, the population that the matched sample represents might be very different from the source population. Therefore, we should not expect the matched sample to have the same outcome model 1 describing the relationship among the outcome, exposure, and confounders as the source population.
To fit an ULR to the matched sample, it is necessary to derive the underlying “correct” logit model for the matched sample first. The logit model describing the association between the exposure, confounders, and outcome in the matched data can be derived as:
 |
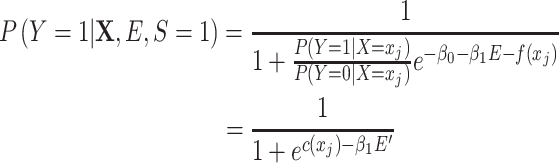(3) |
where the nuisance term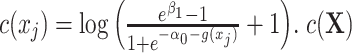 
can be considered as a nuisance term because it does not include the exposure variable and can be seen as the stratum-specific intercept for each matched set. We are usually not interested in estimating these intercepts. 
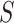is the selection indictor that takes the value of 
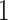if a participant is randomly selected into the matched set and 0 if this participant is not selected. Of note, 
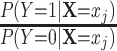can be interpreted as the chance that a control is selected into the matched set from all controls with 
, whereas for cases, this probability is 1 because every case will be selected. Details are provided in Web Appendix 1 and Web Table 1 (available at https://doi.org/10.1093/aje/kwab056).
By comparing models 1 and 3, we can make the following observations. First, model 3 for the matched sample does not retain the confounding term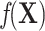 
from model 1. Intuitively, the reason this term cancels out can be explained using a causal diagram (16). The selection indicator 
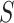in the matched design is a collider between the confounders 
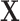and outcome Y because the selection decision is determined by the confounders and outcome, so 
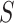is a common effect of both 
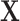and Y. Conditioning on 
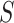by matching introduces a selection bias and induces a new association between 
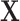and Y. This new association has to cancel out the confounding association between 
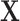and Y in the source population, represented by 
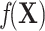, to ensure that 
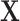and Y are “marginally” (unconditionally) unassociated in the matched sample because the distributions of X are the same in cases and controls through individual matching (15). The conditional odds ratio in model 3 is still 
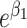, which is the same as in model 1. As expected, the matched case-control design delivers the same effect measure as in the source population.
Second, a new nuisance term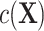 
appears in model 3 because of the selection bias introduced by matched case-control sampling. In fact, 
in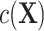 
comes from the exposure model 2. As shown in model 3, 
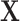can still be “conditionally” associated with Y in the matched sample via 
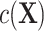conditioning on 
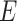. Even in settings in which 
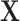is not a confounder in the source population (e.g., 
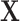is associated with the exposure but not the outcome), matching on 
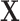can still induce a conditional association between 
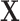and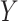 
given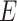 
. By definition, this 
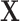is a confounder in the matched data and thus contributes to confounding in the matched sample (17). This finding supports previous conclusions that matching in case-control studies can introduce confounding (4, 16).
As a result, matched designs routinely require controlling for the matching factors in the analysis (4), unless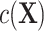 
is negligible. Failing to control for 
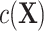, such as through use of unadjusted ULR, results in an omitted-variable bias in the logistic regression model. This bias is attributable to a mixture of confounding and the noncollapsibility of the odds ratio in a logit model. Noncollapsibility of the odds ratio is a phenomenon in which the marginal or crude odds ratio is not equal to the average of conditional or adjusted odds ratios (averaged over the distributions of covariates), even when confounding is absent. In the framework of a logit regression model, noncollapsibility occurs when omitting an independent variable alters the coefficients of the remaining variables in the logit regression model (13–15). This bias tends to bias estimates toward the null hypothesis (17) and to underestimate the true association between the exposure and the outcome (see details in Web Appendix 2). The degree of this bias is determined by the variability of 
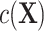. Thus, we might estimate a different quantity than 
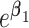when we fail to adjust for 
.
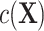CLR controls for the matched factors by conditioning out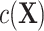 
in model 3. Therefore, CLR avoids the model misspecification by not modeling the nuisance term and serves as a robust solution. By contrast, the validity of adjusted ULR requires modeling 
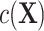correctly. If 
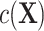is approximately linear in the domain of 
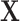, then ULR + L, a common analytical approach, will estimate 
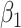with minimal bias because ULR + L approximates model 3. However, if the functional form of 
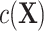deviates from linearity, then ULR + L will be misspecified and might cause biased estimates of 
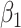. The complexity of exposure model 2 determines the level of deviation of 
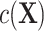from linearity and thus the magnitude of bias. ULR + SP can alleviate this bias if the spline transformation approximates the functional form of 
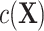well, but this method is not used often in practice.
When the outcome is not rare, the nuisance term can become even more complicated because it includes regression terms from both the outcome (i.e.,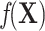 
) and exposure models (i.e., 
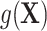). Details are provided in Web Appendix 1. These terms further increase the complexity of modeling 
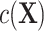and the risk of fitting an incorrect ULR model, particularly if they include nonlinearity forms and interaction terms. Thus, the main findings discussed previously under the rare outcome assumption still hold for the common outcome scenario.
CLR versus adjusted ULR when matching is not exact
In practice, we often select controls within a certain range of the value of the matching factor of cases (e.g., controls matched to cases within 5 years of age). In this setting, unadjusted CLR could also be biased. The conditional likelihood constructed for each matched pair routinely assumes exact matching and that the matched pairs have the same risk of developing the outcome, allowing the matching factors to be conveniently canceled out from the conditional likelihood function. However, CLR fails to account for the fact that cases and controls in the same match sets have different matching values from nonexact matching and thus different risks of developing the outcome. The resulting bias can be interpreted as the omitted variable bias problem in the noncollapsible logit model (14, 15). Details are provided in Web Appendix 3. One way to address this bias is to include matching factors in the CLR logit model (18), but incorrect specification of the functional form of the matching factors in CLR could also produce biased results.
SIMULATION
We designed simulation studies to compare the potential biases of ULR and CLR in 2 separate situations: 1) when matching is exact and 2) when matching is not exact. To evaluate their performance under model misspecification, we fine-tuned the level of nonlinearity and complexity of the matching variables in the population outcome model 1 and exposure model 2 to generate different levels of complexity in the functional form of c(X) in model 3 for the matched data. We also considered scenarios in both rare and common settings.
CLR versus adjusted ULR when matching is exact
The simulation algorithm for comparing ULR and CLR under exact matching is outlined as follows:
Step 1: We generated the disease outcome variable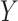 
, the exposure variable 
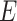, and confounders X1 and X2 from a source population. Specifically, we generated confounders and exposures for 6 scenarios. We selected 
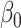to ensure that the proportion of participants with the disease outcome was under 10% in scenarios 1–5 and ~40% in scenario 6.
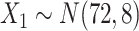. c(X) is approximately linear (Figure1A). The model coefficients are from a published case study on endometrial cancer (11). 
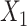is linear in both outcome and exposure models. In this scenario, we expect that ULR + L is unbiased because c(X) is linear.We modified scenario 1 by adding a quadratic term for
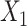in the population outcome model (Figure 1B) to show that, when the outcome is rare, ULR + L will still be adequate for the matched data as long as c(X) is approximately linear. Nonlinearity in 
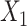in the population outcome model does not contribute to bias.
. 
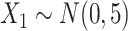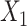is linear in both population outcome and exposure models. c(X) has a nonlinear S shape (Figure 1C). We expect ULR + L to be biased because of the nonlinearity of c(X) even though 
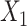is linear in the outcome model.We modified scenario 3 by adding a quadratic term for
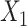in both the population outcome and exposure models to increase the complexity of c(X) (Figure 1D).
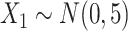and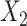 
follow a discrete uniform distribution taking values of 1–4 with equal probability of 0.25. We let 
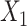interact with 
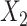in the exposure model 2. Thus, the curves of c(X) also interact with each other (Figure 1E).To generate a common outcome scenario, we modified scenario 4 by changing
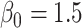. The common outcome setting might further increase the complexity of c(X) (Figure 1F).
Figure 1.
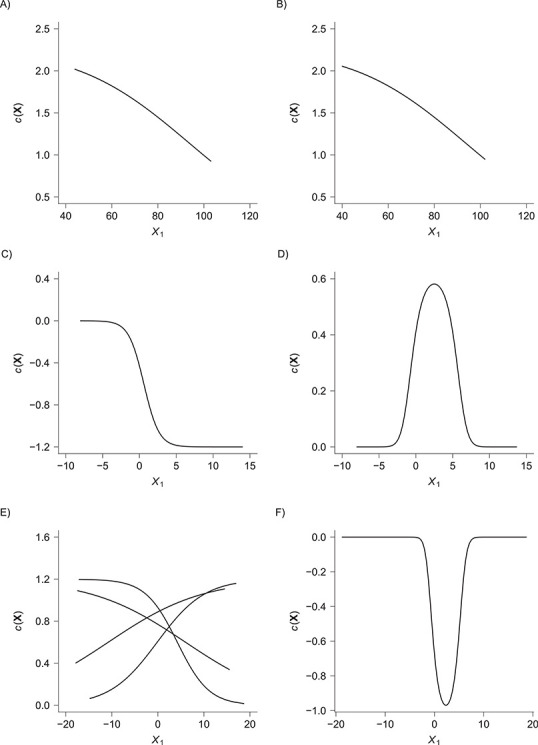
The functional form of c(X) in 6 scenarios: A) Exposure: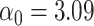 
, 
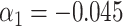for intercept and 
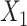; outcome: 
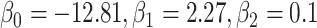for intercept, exposure, and 
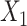. B) Exposure: 
, 
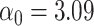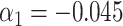for intercept and 
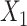; outcome: 
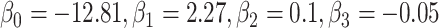for intercept, exposure, 
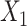, and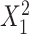 
. C) Exposure: 
, 
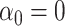for intercept and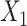 
; outcome: 
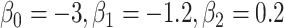for intercept, exposure and 
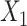. D) Exposure: 
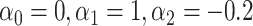for intercept, 
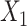and 
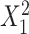; outcome: 
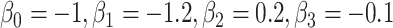for intercept, exposure, 
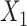and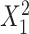 
. E) Exposure: 
, and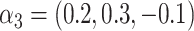 
for intercept, 
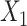, and 3 dummy variables of 
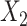, and 3 interaction terms of 
× 
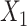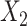; outcome: 
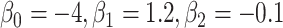, and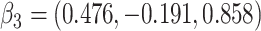 
for intercept, exposure, 
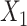, and 3 dummy variables of 
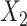. F) Exposure: 
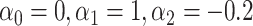for intercept, 
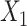and 
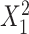; outcome: 
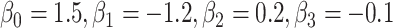for intercept, exposure, 
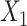and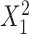 
.
Of note, we rounded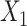 
to the nearest integer in scenarios 1 and 2 or to 1 decimal place in the remaining scenarios to allow exact matching to be performed for continuous variables.
Step 2: After generating the source population (sample size n = 10,000), we used a greedy matching algorithm to randomly select 1 control for each case from all candidate controls sharing the same values of the matching variables. In scenarios 1–4 and 6, we performed unadjusted ULR, ULR + L, ULR + SP, and unadjusted CLR in each matched sample and reported estimates of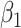 
and their model-based standard errors. For the restricted cubic spline transformation of 
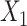, we selected 5 knots, located at the 5th, 20th, 33rd, 67th, and 95th percentiles. In scenario 5, which included 2 matching variables, we performed unadjusted ULR, ULR + L1 (without the 
× 
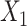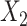interaction), ULR + L2 (with the interaction), ULR + SP1 (without the interaction between the spline function of 
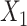and 
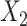), ULR + SP2 (with the interaction) and unadjusted CLR. We repeated this process 10,000 times and then averaged the point estimates and model-based standard errors. We also computed empirical standard errors by calculating the standard deviations of 10,000 estimates of 
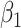. When averaged model-based standard errors differ substantially from averaged empirical standard errors, model-based standard errors are likely biased and model-based inference is not reliable (e.g., P value is not correct) because the empirical standard error approximates the true variability of estimates. Finally, we reported the coverage probability of 95% confidence intervals for each method.
CLR versus adjusted ULR when matching is not exact
We used 4 of the previous scenarios (1, 3, 5, 6) to generate the data, but we reduced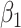 
from 2.27 to 1 in scenario 1 to make the confounding effect of 
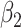stronger relative to the exposure effect. We defined 6 different matching calipers for the continuous matching variable 
(d = 1, 2, 3, 4, 5, 6). In scenarios 1, 3, and 6, we performed unadjusted CLR, CLR + L, and CLR + SP, and unadjusted ULR, ULR + L, and ULR + SP. In scenario 5, we performed unadjusted CLR, CLR + L, CLR + SP and unadjusted ULR, ULR + L, ULR + L2, ULR + SP1, and ULR + SP2. In this scenario, adjusted CLR only included linear or spline functions of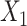 
. The interaction term was not included.
RESULTS
CLR versus adjusted ULR when matching is exact
As shown in Table 1, unadjusted ULR underestimated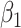 
in all 6 settings. In scenarios 1 and 2, in which c(X) was approximately linear, both ULR + L and CLR were unbiased. ULR + L was more efficient than CLR with smaller standard errors, even though, in scenario 2, the matching variable had a quadratic term in the population outcome model. The coverage probability for both ULR + L and CLR was at the nominal level.
Table 1.
Simulation Results Comparing Unconditional Logistic Regression and Conditional Logistic Regression When Matching Is Exact
| Unadjusted ULR | ULR + L | ULR + SP | Unadjusted CLR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario |
|
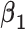
Estimate | Estimate | Empirical SE | Model SE | 95% CI Coverage | Estimate | Empirical SE | Model SE | 95% CI Coverage | Estimate | Empirical SE | Model SE | 95% CI Coverage |
| 1 | 2.270 | 2.203 | 2.277 | 0.207 | 0.205 | 0.949 | 2.292 | 0.209 | 0.206 | 0.947 | 2.277 | 0.269 | 0.264 | 0.950 |
| 2 | 2.270 | 2.204 | 2.277 | 0.207 | 0.205 | 0.949 | 2.293 | 0.209 | 0.206 | 0.947 | 2.279 | 0.271 | 0.264 | 0.950 |
| 3 | −1.200 | −0.349 | −0.793 | 0.163 | 0.202 | 0.479 | −1.207 | 0.264 | 0.262 | 0.951 | −1.209 | 0.289 | 0.282 | 0.953 |
| 4 | −1.200 | −0.871 | −1.028 | 0.086 | 0.092 | 0.541 | −1.202 | 0.100 | 0.101 | 0.951 | −1.204 | 0.109 | 0.109 | 0.950 |
| 5 | 1.200 | 1.044 | 1.115a | 0.106 | 0.110 | 0.883 | 1.117b | 0.107 | 0.111 | 0.887 | 1.202 | 0.125 | 0.124 | 0.953 |
| 5 | 1.200 | 1.044 | 1.202c | 0.116 | 0.115 | 0.951 | 1.213d | 0.117 | 0.116 | 0.950 | 1.202 | 0.125 | 0.124 | 0.953 |
| 6 | −1.200 | −0.687 | −0.831 | 0.053 | 0.063 | 0 | −1.195 | 0.077 | 0.077 | 0.951 | −1.202 | 0.083 | 0.083 | 0.951 |
Abbreviations: CI, confidence interval; CLR, conditional logistic regression; L, linear term of the matching factor(s); SE, standard error; SP, restricted cubic spline transformation of the matching factor(s); ULR, unconditional logistic regression.
a ULR + L1: ULR that includes a linear term for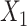 
and dummy variables for 
.
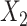b ULR + SP1: ULR that includes a spline function for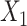 
and dummy variables for 
.
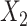c ULR + L2: ULR that includes a linear term for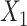 
and dummy variables for 
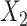, and their interaction terms.
d ULR + SP2: ULR that includes a spline function for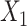 
and dummy variables for 
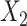, and their interaction terms.
In scenarios 3, 4, and 6 in which c(X) was nonlinear, ULR + L underestimated the true parameter despite the fact that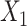 
was linear in the population outcome model. CLR produced unbiased estimates. The model-based standard errors of ULR + L were generally larger than the empirical standard errors, whereas the model-based and empirical standard errors for CLR were close to each other, indicating that ULR + L can produce biased estimates and invalid inferences in matched case-control studies when c(X) is modeled incorrectly. ULR + SP reduced this bias. The coverage probability for ULR + L in the 3 scenarios was below 0.95, whereas the coverage probability for ULR + SP and CLR was nominal.
Finally, in scenario 5 in which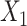 
and 
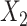interact in the exposure model, ULR + L1 and ULR + SP1 gave biased estimates as expected. However, ULR + L2 and ULR + SP2 reduced this bias and performed similarly to unadjusted CLR. The coverage probability for ULR + L1 and ULR + SP1 was below 95%, whereas the coverage probability for ULR + L2, ULR + SP2, and CLR were at the nominal level. These results demonstrate that CLR depends less on modeling and is less susceptible to model misspecification than ULR.
CLR versus adjusted ULR when matching is not exact
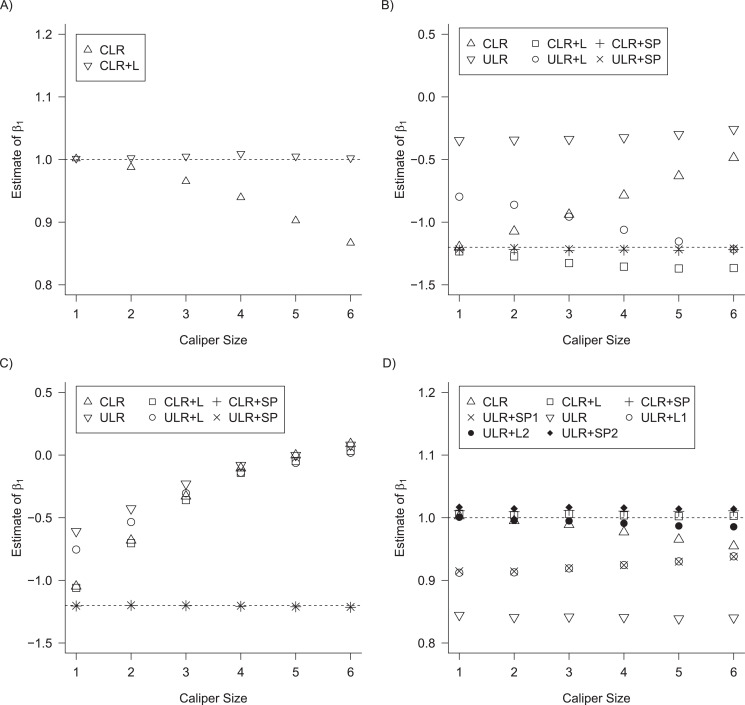
In all 4 scenarios (Figure 2), the bias of unadjusted CLR estimates increased as caliper size increased. However, it is worth noting that when the caliper size was small (d = 1), unadjusted CLR had minor biases in each setting. This might be explained by the fact that the residual from the nonexact matched confounder is negligible when the caliper size is small, and not adjusting for this residual effect does not affect CLR estimates appreciably. Unadjusted ULR was always biased. In scenario 1 in which c(X) was approximately linear (Figure 2A), the adjusted CLR (CLR + L) estimates were close to the true parameter at all levels of caliper size. In scenario 3 (Figure 2B), the biases of CLR + L increased first and then stabilized. The biases of ULR + L were largest at the smallest caliper size (d = 1), but steadily decreased as the matching caliper size increased. This might be attributable to the observation that matched case-control sampling begins to resemble case-control sampling as caliper size increases and the matching factor is linear in the population outcome model 1 (Web Figures 1 and 2). The estimates for CLR + SP and ULR + SP were close to the true parameters at all levels of caliper size, mainly because spline transformation well approximated the complex form of the matching factor. However, in scenario 6 (Figure 2C), in which the matching factor was nonlinear in the population outcome model and the outcome is common, the biases of both ULR + L and CLR + L increased as caliper size increased. The estimates for CLR + SP and ULR + SP were close to the true parameters at all caliper sizes. In scenario 5 in which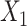 
× 
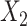interact in the exposure model (Figure 2D), the estimates from CLR + L and CLR + SP were close to the true parameter. In contrast, ULR + L1 or ULR + SP1 still gave biased estimates because ULR did not capture the interaction between 
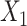and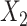 
. After including the interaction term, ULR + L2 and ULR + SP2 alleviated these biases. Overall, these findings suggest that CLR depends less on modeling than ULR in the nonexact setting.
Figure 2.
Bias of conditional logistic regression (CLR) and unconditional logistic regression (ULR) when caliper size increases. A) Scenario 1 with rare outcome but we set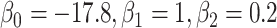 
, and we defined 6 different matching calipers (d = 1, 2, 3, 4, 5, 6). B) Scenario 3 with rare outcome, c(X) has a nonlinear shape. C) Scenario 6 with common outcome, 
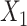has quadratic terms in both the population and exposure models. D) Scenario 5 with rare outcome, 
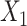and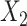 
have interaction. L, linear term of the matching factor(s); SP, restricted cubic spline transformation of the matching factor(s).
DISCUSSION
Whether we can break the match and use ULR instead of CLR to analyze individually matched case-control data has long been debated. There appears to be some consensus in certain scenarios, but uncertainty remains among applied researchers as to the most appropriate analytical approach when one of the matched factors is continuous. We revealed the trade-off between CLR and ULR. On the one hand, CLR with exact matching or tight caliper size depends less on modeling but its estimates can be less efficient with larger standard errors. On the other hand, adjusted ULR can produce more efficient estimates, but this advantage requires correct model specification. A misspecified ULR can give both biased estimates and invalid inferences.
Building upon findings from previous studies (10, 11, 19), we analytically and by simulation arrived at the following conclusions: First, our results confirm previous conclusions that matching does not remove confounding (4, 16). Thus, we need to control for the matching variables in matched case-control studies. Unadjusted ULR in general underestimates the true association between the exposure and the outcome. Second, we showed that the correct logit model for the matched data includes a nuisance function of matched factors, which is derived from the exposure model when the outcome is rare or from the exposure and outcome models when the outcome is common. As a result, ULR is vulnerable to model specification error because ULR needs to model this term correctly. CLR circumvents this model misspecification problem by conditioning out the nuisance term, making it a more robust approach in the exact setting.
The advantage of CLR over ULR with respect to dependence on modeling is also evident in the setting of nonexact matching. In this situation, unadjusted CLR can produce biased results because of a mixture of residual confounding and the noncollapsibility of the logit model. This bias increases with larger matching caliper size. In our analysis, we showed that controlling for the matching variable using a proper form in CLR can reduce this bias when the caliper size is relatively large. Although ULR with smoothing of the matching variable can yield similar results, CLR depends less on modeling, particularly when the caliper size is small.
In summary, the logit model for the matched sample can be different from the logit model for the target population, and might take a more complex form, making it challenging to fit adjusted ULR correctly in practice. By contrast, CLR is less vulnerable to model misspecification. Although more complex regression modeling techniques such as smoothing splines can alleviate this bias for ULR (11) and model diagnosis methods exist for specification error (e.g., graphic analysis using residuals) (20), it is worth emphasizing that, in practice, we rarely know the true form of the unconditional logit model for matched data. Thus, it is always appealing to applied researchers to design their study rigorously first and then to follow up with simple-to-implement analytical approaches. Bringing in the additional complexity of modeling the correct functional form of the matched variables, testing for the existence of interaction effects after designing the study, and performing model diagnosis might not always be the best approach in practice. Even in situations in which researchers think it might be appealing to break the matched sets and use adjusted ULR (e.g., more efficient estimate, missing data), it is still advisable to compare the results with those from CLR.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Division of Public Health Sciences, Department of Surgery, Washington University School of Medicine, Saint Louis, Missouri, United States (Fei Wan, Graham A. Colditz, Siobhan Sutcliffe); and Siteman Cancer Center Biostatistics Shared Resources, Washington University School of Medicine, Saint Louis, Missouri, United States (Fei Wan, Graham A. Colditz, Siobhan Sutcliffe).
This work was supported by the Foundation for Barnes-Jewish Hospital and the Alvin J. Siteman Cancer Center (grant P30 CA091842).
We thank Dr. Sander Greenland of the University of California at Los Angeles for his constructive comments. We also thank the associate editor and 3 anonymous reviewers who gave valuable suggestions that improved the quality of the manuscript.
Data sharing not applicable to this article as no data sets were analyzed during the present study.
Conflict of interest: none declared.
REFERENCES
- 1.Thomas DC, Greenland S. The relative efficiencies of matched and independent sample designs for case-control studies. J Chronic Dis. 1983;36(10):685–697. [DOI] [PubMed] [Google Scholar]
- 2.Hansson L, Khamis HJ. Matched samples logistic regression in case-control studies with missing values: when to break the matches. Stat Methods Med Res. 2008;17(6):595–607. [DOI] [PubMed] [Google Scholar]
- 3.Breslow E, Day NE. Statistical Methods in Cancer Research: Volume 1—The Analysis of Case-Control Studies. Lyon, France: International Agency for Research on Cancer; 1980. [PubMed] [Google Scholar]
- 4.Pearce N. Analysis of matched case-control studies. BMJ. 2016;352:i969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cheung YB, Ma X, Lam KF, et al. . Bias control in the analysis of case-control studies with incidence density sampling. Int J Epidemiol. 2019;48(6):1981–1991. [DOI] [PubMed] [Google Scholar]
- 6.Kridin K, Zelber-Sagi S, Comaneshter D, et al. . Association between pemphigus and neurologic diseases. JAMA Dermatol. 2018;154(3):281–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jacobs R, Lesaffre E, Teunis PF, et al. . Identifying the source of food-borne disease outbreaks: an application of Bayesian variable selection. Stat Methods Med Res. 2019;28(4):1126–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Marshall LM, Hunter D, Connolly JL, et al. . Risk of breast cancer associated with atypical hyperplasia of lobular and ductal types. Cancer Epidemiol Biomarkers Prev. 1997;6(5):297–301. [PubMed] [Google Scholar]
- 9.London SJ, Connolly JL, Schnitt SJ, et al. . A prospective study of benign breast disease and the risk of breast cancer. JAMA. 1992;267(7):941–944. [PubMed] [Google Scholar]
- 10.Greenland S. Partial and marginal matching in case-control studies. In: Moolgavkar SH, Prentice RL, eds. Modern Statistical Methods in Chronic Disease Epidemiology. New York, NY: Wiley; 1986:35–49. [Google Scholar]
- 11.Levin B, Paik MC. The unreasonable effectiveness of a biased logistic regression procedure in the analysis of pair-matched case-control studies. J Stat Plann Infer. 2001;96(2):371–385. [Google Scholar]
- 12.Mansournia MA, Jewell NP, Greenland S. Case-control matching: effects, misconceptions, and recommendations. Eur J Epidemiol. 2018;33(1):5–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wan F, Mitra N. An evaluation of bias in propensity score-adjusted nonlinear regression models. Stat Methods Med Res. 2018;27(3):846–862. [DOI] [PubMed] [Google Scholar]
- 14.Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Stat Sci. 1999;14(1):29–46. [Google Scholar]
- 15.Neuhaus JM, Jewell NPA. Geometric approach to assess bias due to omitted covariates in generalized linear models. Biometrika. 1993;80(4):807–815. [Google Scholar]
- 16.Mansournia MA, Hernán MA, Greenland S. Matched designs and causal diagrams. Int J Epidemiol. 2013;42(3):860–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.VanderWeele TJ, Shpitser I. On the definition of a confounder. Ann Stat. 2013;41(1):196–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rothman KJ, Greenland S, Lash TL. Case-control studies. In: Rothman KJ, Greenland S, Lash TL, eds. Modern Epidemiology. 3rd ed. Philadelphia, PA: Lippincott Williams and Wilkins; 2008:111–127. [Google Scholar]
- 19.Qian J, Payabvash S, Kemmling A, et al. . Variable selection and prediction using a nested, matched case-control study: application to hospital acquired pneumonia in stroke patients. Biometrics. 2014;70(1):153–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Landwehr J, Pregibon D, Shoemaker A. Graphical methods for assessing logistic regression models. J Am Stat Assoc. 1984;79(385):61–71. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.