Impact of intraoperative data on risk prediction for mortality after intraabdominal surgery

Abstract

Background:

Risk prediction models for postoperative mortality after intraabdominal surgery have typically been developed using preoperative variables. It is unclear if intraoperative data add significant value to these risk prediction models.

Methods:

With IRB approval, an institutional retrospective cohort of intraabdominal surgery patients in the 2005–2015 American College of Surgeons National Surgical Quality Improvement Program was identified. Intraoperative data were obtained from the electronic health record. The primary outcome was 30-day mortality. We evaluated the performance of machine learning algorithms to predict 30-day mortality using (A) baseline variables and (B) baseline + intraoperative variables. Algorithms evaluated were: 1) logistic regression with elastic net selection, 2) random forest (RF), 3) gradient boosting machine (GBM), 4) support vector machine (SVM), and 5) convolutional neural networks (CNN). Model performance was evaluated using the area under the receiver operator characteristic curve (AUC). The sample was randomly divided into a training/testing split with 80%/20% probabilities. Repeated 10-fold cross-validation identified the optimal model hyperparameters in the training dataset for each model, which were then applied to the entire training dataset to train the model. Trained models were applied to the test cohort to evaluate model performance. Statistical significance was evaluated using P<0.05.

Results:

The training and testing cohorts contained 4322 and 1079 patients, respectively, with 62 (1.4%) and 15 (1.4%) experiencing 30-day mortality, respectively. When using only baseline variables to predict mortality, all algorithms except SVM (AUC 0.83 [95% CI 0.69–0.97]) had AUC >0.9: GBM (AUC 0.96 [0.94–1.0]), RF (AUC 0.96 [0.92–1.0]), CNN (AUC 0.96 [0.92–0.99]), and logistic regression (AUC 0.95 [0.91–0.99]). AUC significantly increased with intraoperative variables with CNN (AUC 0.97 [0.96–0.99]; P=0.047 vs. baseline), but there was no improvement with GBM (AUC 0.97 [0.95–0.99]; P=0.3 vs. baseline), RF (AUC 0.96 [0.93–1.0]; P=0.5 vs. baseline), and logistic regression (AUC 0.94 [0.90–0.99]; P=0.6 vs. baseline).

Conclusions:

Postoperative mortality is predicted with excellent discrimination in intraabdominal surgery patients using only preoperative variables in various machine learning algorithms. The addition of intraoperative data to preoperative data also resulted in models with excellent discrimination, but model performance did not improve.

Introduction

Perioperative risk stratification is a critically important aspect of surgical patient management. Many clinical tools have been developed to assess the risk of mortality and other complications following surgery, and risk stratification has typically been performed using preoperative data.^1–3 However, perioperative risk stratification should not be thought of as a singular event, but as a dynamic process where risk information is continuously updated as new data become available. The electronic capture of intraoperative management data has facilitated the development of risk prediction tools using the intraoperative period as an additional source of data,^4,5 but the specific utility of intraoperative data for mortality risk stratification has not been clearly delineated.

Patient factors are extremely important in assessing postoperative mortality risk, perhaps more so than surgical factors,⁶ and preoperative models for mortality have excellent performance characteristics.^1,2 Although we recently demonstrated that intraoperative data meaningfully contributed to risk prediction models for postoperative acute kidney injury,⁷ it is not readily apparent if intraoperative data can also improve risk stratification models for mortality as the performance of risk prediction models have varying performance based on the specific complication being assessed.⁸ Intraoperative data improved prediction models for combined morbidity and mortality in cardiac surgery patients,⁹ but it is not clear if improvement would be seen for all outcomes if assessed individually. Thus, we questioned whether intraoperative data were necessary to optimize the performance of risk stratification models for postoperative mortality, or if preoperative data were sufficient for this purpose.

We used a cohort of patients at a large academic institution undergoing intraabdominal general surgery to determine whether the addition of intraoperative data to a preoperative prediction model for postoperative mortality improved its performance. Intraabdominal surgery represents a major class of surgical patients with significant risk of morbidity and mortality. We evaluated several machine learning algorithms [1) logistic regression with elastic net selection, 2) random forest, 3) gradient boosting machine, 4) support vector machine, and 5) convolutional neural network] for the prediction of 30-day mortality, comparing the performance of a preoperative model containing only baseline patient data and surgical procedure information to an intraoperative model containing both preoperative and intraoperative data. Our aim is to provide perioperative physicians with important insights on the ways in which intraoperative data can be utilized to stratify surgical patients based on their risk for subsequent mortality.

Methods

Patient selection

This study was approved by the Columbia University Medical Center (CUMC; New York, NY) IRB, including waiver of consent. This is a retrospective study of intraabdominal surgery patients at CUMC participating in the American College of Surgeons National Surgical Quality Improvement Program (ACS NSQIP) from 2005–2015. A different subset of the initial cohort was evaluated for the outcome of acute kidney injury.⁷ The study was guided by the TRIPOD¹⁰ framework. There were 14,606 patients in the ACS NSQIP at CUMC from 2005–15 (Figure 1). Patients with missing or incomplete Anesthesia Information Management Systems (AIMS; CompuRecord, Philips Medical Systems, Eindhoven, The Netherlands) data were excluded. Intraabdominal procedures were identified using the Clinical Classifications Software for Services and Procedures (Agency for Healthcare Research and Quality, Rockville, MD) (Supplemental Table 1). Outpatient procedures were excluded as they have a low risk for mortality. The final cohort included 5401 patients.

Figure 1.

Selection of inpatient intraabdominal surgery procedures, 2005–15. ACS NSQIP, American College of Surgeons National Surgical Quality Improvement Program; AIMS, anesthesia information management system.

Preoperative and intraoperative variables

Variables included in the analyses are listed in Supplemental Tables 2 and 3. Preoperative patient characteristics and demographic data – including comorbidities and laboratory data – were collected from the ACS NSQIP. Missing data were present in preoperative laboratory values and body mass index (BMI; kg/m2) (Supplemental Table 4). No missing data were present in intraoperative variables. Missing laboratory data were imputed using medians within patient groups defined by American Society of Anesthesiologists Physical Status (ASA PS) and emergency status. Missing BMI values were imputed with whole sample average BMI. Intraoperative variables were obtained from the AIMS and reflect routine clinical care. AIMS data were stored in a relational database (Microsoft SQL Server Enterprise 12.0, Redmond, WA) and extracted using structured query language queries.

Intraoperative data were collected as previously described.⁷ Continuously streamed variables (e.g., blood pressure, anesthetic agent concentration) were captured by the AIMS. Other variables were manually entered by the anesthesia provider (e.g., medications, fluids, etc.). For most medications, the total dose administered to the patient was determined. Exceptions include mannitol (Yes/No), furosemide (Yes/No), ketorolac (Yes/No), and individual antibiotics (Yes/No). We created a variable indicating the number of distinct antibiotics administered, as well as a separate variable indicating the number of distinct antibiotics not including cefazolin, as this was the most commonly used antibiotic. For fluids (both inputs and outputs), total volumes were determined. Blood pressure data (both invasive and non-invasive) were captured in 15-second intervals. If an interval had both invasive and non-invasive measurements, the invasive measurement took precedence. Linear interpolation was used to assign values to intervals without a recorded blood pressure. For this analysis, we measured the duration of time (min) with mean arterial pressure below 55 mm Hg, 60 mm Hg, and 65 mm Hg, and the time-weighted average below the same 3 thresholds (mm Hg × min). For each inhaled anesthetic (sevoflurane, desflurane, isoflurane, and nitrous oxide), two variables were created: 1) a binary variable indicating its use (Yes/No) and 2) the cumulative exposure (%-hours), calculated as the average end-tidal concentration (%) multiplied by the duration of exposure (hours).

Clinical end point

The primary outcome was 30-day mortality, as recorded in the ACS NSQIP dataset.

Statistical Analysis

The analysis plan was approved prior to data analysis. Models were developed in two phases: A) preoperative model incorporating patient characteristics, demographics, and surgical procedure category; and B) intraoperative model incorporating both preoperative and intraoperative variables. The following machine learning algorithms to predict 30-day mortality were evaluated: 1) logistic regression with elastic net selection, 2) random forest (RF), 3) gradient boosting machine (GBM), 4) support vector machine (SVM), and 5) convolutional neural network (CNN). For RF, the Gini index was used as the splitting rule. For GBM, decision trees were used as the weak learners and AdaBoost¹¹ as the loss function. Training data were centered and scaled before fitting the logistic regression, SVM and CNN models. That is, each predictor was subtracted by its mean and divided by its standard deviation.

We used a machine learning framework to tune, train, and test the models to maximize performance while guarding against overfitting.¹² The dataset was randomly split by the outcome into training (80%) and testing (20%) datasets. Sampling was done within the levels of the outcome in order to balance the distribution of patients with mortality within the splits. Of the 5401 patients in the sample, 4322 (80.0%) were allocated to the training dataset. Model hyperparameters, which are model parameters not directly learned from the data, were optimized (“tuned”) with repeated 10-fold cross-validation in the training dataset. The optimal hyperparameters, maximizing the cross-validation mean area under the receiver operator characteristic curve (AUCROC), were applied to the entire training dataset to identify model parameters (“training”). The trained models were applied to the testing dataset to evaluate model performance (“testing”), assessed using the AUCROC, area under the precision-recall curve (AUCPR), and calibration plots. The PR curve plots recall (sensitivity) on the x-axis and precision (positive predictive value) on the y-axis to summarize the tradeoff between positive predictive value and sensitivity at different probability thresholds. Point estimates and 95% confidence intervals (CI) for AUCROC and AUCPR were computed with 2000 bootstrap replicates.¹³ Statistical significance was evaluated using P<0.05.

For interpretable algorithms, variable importance measures (RF and GBM) and odds ratios (logistic regression) evaluated the relative importance of individual variables. For GBM, relative importance measures¹⁴ were used, and for RF, Gini impurity¹⁵ was used.

Statistical analyses were performed using R Studio (version 1.2.5019; R Studio, Inc., Boston, MA) and R (version 3.6.1; The R Foundation for Statistical Computing, Vienna, Austria). The R package pROC¹³ calculated AUCROC and compared the AUCROCs of the preoperative and intraoperative models. The R package precrec¹⁶ calculated AUCPR. The R package caret¹⁷ identified optimal tuning parameters and then fit the final model with the optimal parameters. Logistic regression used the R packages glmnet¹⁸ and Matrix.¹⁹ Random forest used the R packages ranger²⁰ and e1071.²¹ GBM used the R package gbm.²² SVM used the R package e1071. Finally, CNN used the R package nnet.²³

Results

Preoperative and intraoperative variables among patients with and without 30-day mortality

Of the 4322 patients in the training dataset, 62 (1.4%) died within 30 days of surgery. Many preoperative patient characteristics and comorbidities were significantly different between patients with and without mortality (Table 1). Patients who died were older, more likely to undergo emergent procedures, and had higher rates of risk factors such as diabetes, hypertension, and preoperative sepsis/septic shock. The procedure categories with the highest mortality risk were ‘exploratory laparotomy’ (12%; 16/129), ‘colorectal resection’ (4.3%; 20/469), and ‘excision, lysis peritoneal adhesions’ (3.5%; 2/57). There were no statistically significant differences in preoperative characteristics between the training and testing datasets (data not shown).

Table 1.

Preoperative characteristics and surgical procedure category for intraabdominal surgery patients, by 30-day mortality status.

	Total	Died	Alive
Variable	4322	62 (1.4%)	4260 (99%)	P-Value
Age (years)	53 (18)	72 (14)	53 (18)	<0.0001
Female	2517 (58%)	39 (63%)	2478 (58%)	0.5
Race				0.3
White	1882 (44%)	23 (37%)	1859 (44%)
Hispanic	1358 (31%)	20 (32%)	1338 (31%)
Black	495 (11%)	11 (18%)	484 (11%)
Other	481 (11%)	8 (13%)	473 (11%)
Asian	106 (2%)	0 (0.0%)	106 (2.5%)
Emergency	1130 (26%)	36 (58%)	1094 (26%)	<0.0001
Body Mass Index (kg/m2)	31 (9.9)	28 (8.1)	31 (9.9)	0.03
Diabetes	759 (18%)	21 (34%)	738 (17%)	0.001
Hypertension	1872 (43%)	51 (82%)	1821 (43%)	<0.0001
Chronic Obstructive Pulmonary Disease	70 (1.6%)	7 (11%)	63 (1.5%)	<0.0001
Current Smoker	565 (13%)	12 (19%)	553 (13%)	0.2
Dyspnea	374 (8.7%)	16 (26%)	358 (8.4%)	<0.0001
Mechanical Ventilation	36 (0.8%)	17 (27%)	19 (0.4%)	<0.0001
Functionally Dependent	188 (4.3%)	31 (50%)	157 (3.7%)	<0.0001
Ascites	31 (0.7%)	6 (10%)	25 (0.6%)	<0.0001
Estimated Glomerular Filtration Rate (mL/min/1.73 m2)	87 (30)	63 (47)	87 (29)	<0.0001
Preoperative Transfusion	28 (0.6%)	7 (11%)	21 (0.5%)	<0.0001
Bleeding Disorder	28 (0.6%)	7 (11%)	21 (0.5%)	<0.0001
Preoperative Steroid	28 (0.6%)	7 (11%)	21 (0.5%)	<0.0001
Disseminated Cancer	122 (2.8%)	9 (15%)	113 (2.7%)	<0.0001
Wound Infection	28 (0.6%)	7 (11%)	21 (0.5%)	<0.0001
Preoperative Renal Insufficiency/Dialysis	28 (0.6%)	7 (11%)	21 (0.5%)	<0.0001
Preoperative Sepsis/Septic Shock	252 (5.8%)	23 (37%)	229 (5.4%)	<0.0001
Albumin (g/dL)	4.1 (0.6)	3.1 (0.8)	4.1 (0.6)	<0.0001
Alkaline Phosphatase (U/L)	99 (92)	126 (126)	98 (92)	0.01
Bilirubin (mg/dL)	0.9 (1.5)	1.2 (1.0)	0.9 (1.5)	0.07
Blood Urea Nitrogen (mg/dL)	16 (9.3)	29 (21)	16 (8.9)	<0.0001
Hematocrit (%)	39 (5.2)	33 (7.0)	39 (5.1)	<0.0001
International Normalized Ratio (Unitless)	1.1 (0.2)	1.4 (0.5)	1.1 (0.2)	<0.0001
Platelets (103/μL)	266 (94)	248 (135)	266 (94)	0.12
Partial Thromboplastin Time (sec)	31 (6.5)	36 (13)	31 (6.3)	<0.0001
Aspartate Aminotransferase (U/L)	35 (108)	169 (747)	33 (56)	<0.0001
Sodium (mmol/L)	138 (2.9)	137 (4.5)	138 (2.9)	0.004
White Blood Cells (103/μL)	9.0 (4.3)	13 (8.4)	9.0 (4.2)	<0.0001
Procedure Category				<0.0001
Colorectal resection	469 (11%)	20 (32%)	449 (11%)
Exploratory laparotomy	129 (3.0%)	16 (26%)	113 (3%)
Ileostomy and other enterostomy	450 (10%)	8 (13%)	442 (10%)
Other operating room gastrointestinal therapeutic procedures	449 (10%)	7 (11%)	442 (10%)
Small bowel resection	129 (3.0%)	3 (4.8%)	126 (3.0%)
Excision, lysis peritoneal adhesions	57 (1.3%)	2 (3.2%)	55 (1.3%)
Other operating room lower gastrointestinal therapeutic procedures	166 (3.8%)	2 (3.2%)	164 (3.8%)
Cholecystectomy and common duct exploration	572 (13%)	2 (3.2%)	570 (13%)
Appendectomy	615 (14%)	1 (1.6%)	614 (14%)
Gastric bypass and volume reduction	813 (19%)	1 (1.6%)	812 (19%)
Procedures on spleen	26 (0.6%)	0 (0.0%)	26 (0.6%)
Colostomy, temporary and permanent	18 (0.4%)	0 (0.0%)	18 (0.4%)
Gastrectomy, partial and total	77 (1.8%)	0 (0.0%)	77 (1.8%)
Other hernia repair	352 (8.1%)	0 (0.0%)	352 (8.3%)

For continuous variables, the mean and (standard deviation) are displayed for each group and compared with the t-test. For categorical variables, counts and (%) are displayed for each group and compared with the chi-square test.

There were also many differences in intraoperative variables between patients with and without mortality (Table 2; Supplemental Table 3). Patients who died had longer duration of hypotension, greater estimated blood loss, and received larger doses of vasopressor medications, while also having received larger volumes of fluids such as albumin 5%, red blood cells, colloids, and fresh frozen plasma. There were no statistically significant differences in most intraoperative variables between the training and testing datasets (data not shown). There were statistical differences in cumulative isoflurane exposure and the proportion of patients receiving nitrous oxide (data not shown), but these differences likely had negligible effects on the models.

Table 2.

Intraoperative variables for intraabdominal surgery patients, by 30-day mortality status.

	Total	Died	Alive
Variable	4322	62 (1.4%)	4260 (99%)	P-Value
Minutes with MAP <55 mm Hg	2.8 (6.4)	6.5 (10)	2.7 (6.3)	<0.0001
Minutes with MAP <60 mm Hg	7.7 (15)	16 (22)	7.6 (14)	<0.0001
Minutes with MAP <65 mm Hg	18 (27)	31 (41)	18 (27)	<0.001
Time Weighted Average with MAP <55 mm Hg (mm Hg*mins)	14 (35)	43 (100)	13 (33)	<0.0001
Time Weighted Average with MAP <60 mm Hg (mm Hg*mins)	40 (82)	100 (162)	39 (80)	<0.0001
Time Weighted Average with MAP <55 mm Hg (mm Hg*mins)	104 (180)	221 (305)	102 (177)	<0.0001
Albumin 5% (mL)	118 (351)	298 (510)	115 (347)	<0.0001
Albumin 25% (mL)	0.3 (7.3)	0.0 (0.0)	0.3 (7.3)	0.8
Lactated Ringer’s (mL)	2604 (1731)	2707 (1992)	2603 (1727)	0.6
Other Crystalloid Fluids (mL)	65 (368)	411 (990)	60 (348)	<0.0001
Red Blood Cells (mL)	52 (276)	495 (1165)	45 (235)	<0.0001
Colloids (mL)	27 (144)	89 (231)	26 (143)	<0.001
Fresh Frozen Plasma (mL)	15 (165)	294 (1023)	11 (107)	<0.0001
Platelets (mL)	2.6 (36)	32 (121)	2.2 (33)	<0.0001
Cryoprecipitate (mL)	0.1 (4.4)	0.0 (0.0)	0.1 (4.4)	0.9
Ascites (mL)	16 (352)	56 (287)	16 (352)	0.4
Estimated Blood Loss (mL)	263 (720)	947 (2958)	253 (627)	<0.0001
Urine Output (mL)	287 (388)	409 (592)	285 (384)	0.01
Phenylephrine (mg)	0.80 (2.4)	2.4 (4.8)	0.78 (2.4)	<0.0001
Ephedrine (mg)	5.9 (12)	12 (31)	5.8 (11)	<0.0001
Norepinephrine (mg)	0.04 (0.4)	0.94 (2.4)	0.03 (0.3)	<0.0001
Vasopressin (units)	0.26 (1.8)	4.7 (8.2)	0.20 (1.4)	<0.0001
Epinephrine (mg)	0.004 (0.1)	0.202 (1.0)	0.001 (0.02)	<0.0001
Dopamine (mg)	0.041 (2)	2.4 (16)	0.007 (0.4)	<0.0001
Labetalol (mg)	2.3 (8.9)	2.2 (7.1)	2.3 (9.0)	0.9
Esmolol (mg)	2.7 (13)	8.2 (29)	2.6 (13)	<0.001
Metoprolol (mg)	0.28 (1.7)	0.29 (1.2)	0.28 (1.7)	1.0
Hydralazine (mg)	0.009 (0.2)	0.081 (0.6)	0.008 (0.2)	0.02
Enalaprilat (mg)	0.001 (0.038)	0.000 (0.000)	0.001 (0.038)	0.9
Clonidine (mg)	0.0001 (0.003)	0.0000 (0.0)	0.0001 (0.003)	0.9
Nicardipine (mg)	0.006 (0.085)	0.005 (0.038)	0.006 (0.085)	0.9
Nitroglycerin (mcg)	0.000 (0.02)	0.000 (0.000)	0.0004 (0.02)	0.9
Mannitol (Yes/No)	2 (0.05%)	0 (0%)	2 (0.05%)	1.0
Furosemide (Yes/No)	79 (1.8%)	8 (13%)	71 (1.7%)	<0.0001
Ketorolac (Yes/No)	1088 (25%)	4 (6.5%)	1084 (25%)	0.001
Sevoflurane (Yes/No)	3632 (84%)	51 (82%)	3581 (84%)	0.8
Sevoflurane (%-Hours)	3.2 (3.1)	3.0 (3.7)	3.2 (3.1)	0.6
Desflurane (Yes/No)	1308 (30%)	10 (16%)	1298 (30%)	0.02
Desflurane (%-Hours)	2.3 (5.6)	1.0 (4.1)	2.4 (5.6)	0.06
Isoflurane (Yes/No)	691 (16%)	21 (34%)	670 (16%)	<0.001
Isoflurane (%-Hours)	0.5 (1.3)	0.4 (0.8)	0.5 (1.3)	0.7
Nitrous Oxide (Yes/No)	2403 (56%)	26 (42%)	2377 (56%)	0.04
Nitrous Oxide (%-Hours)	8.7 (20)	8.6 (23)	8.7 (20)	1.0
Number of distinct antibiotics administered	0.9 (0.5)	0.9 (0.7)	0.9 (0.5)	0.4
Number of distinct antibiotics administered (not including cefazolin)	0.6 (0.6)	0.7 (0.7)	0.5 (0.6)	0.01
Propofol (mg)	218 (231)	89.3 (131)	220 (232)	<0.0001
Midazolam (mg)	1.9 (8.5)	11 (70)	1.8 (1.2)	<0.0001
Fentanyl (mg)	0.3 (0.2)	0.3 (0.3)	0.3 (0.2)	0.6
Morphine (mg)	1.8 (4.3)	1.5 (3.5)	1.8 (4.3)	0.6
Hydromorphone (mg)	0.6 (0.9)	0.4 (0.7)	0.6 (0.9)	0.1
Remifentanil (mg)	0.040 (0.3)	0.035 (0.3)	0.040 (0.3)	0.9
Operative Time (min)	162 (108)	177 (139)	162 (108)	0.3

For continuous variables, the mean and (standard deviation) are displayed for each group and compared with the t-test. For categorical variables, counts and (%) are displayed for each group and compared with the chi-square test.

Comparison of model performance in preoperative and intraoperative machine learning models

When using only preoperative data, the AUCROCs in the test set for GBM, RF, CNN, and logistic elastic net were 0.96 [95% CI 0.94–0.99], 0.96 [95% CI 0.92–1.00], 0.96 [95% CI 0.92–0.99], and 0.95 [95% CI 0.91–0.99], respectively (Table 3; ROC curves in Figure 2). SVM had lower discrimination with an AUCROC of 0.83 [95% CI 0.69–0.97]. When intraoperative data were added to the preoperative model, the AUCROCs in the test set for GBM, RF, CNN, logistic elastic net, and SVM were 0.97 [95% CI 0.95–0.99], 0.97 [95% CI 0.96–0.99], 0.97 [95% CI 0.95–0.99], 0.95 [95% CI 0.91–0.99], and 0.88 [95% CI 0.75–1.00], respectively. The AUCROCs for the preoperative and intraoperative models were significantly different only in the CNN model (P=0.029).

Table 3.

Area under the curve of the receiver operator characteristic curve of preoperative and intraoperative models to predict 30-day mortality in intraabdominal surgery patients.

Algorithm	Preoperative Model		Intraoperative Model
	AUC	95% CI	AUC	95% CI	P-value*
Gradient Boosting Machine	0.96	[0.94, 0.99]	0.97	[0.95, 0.99]	0.4
Random Forest	0.96	[0.92, 1.00]	0.97	[0.96, 0.99]	0.3
Convolutional Neural Network	0.96	[0.92, 0.99]	0.97	[0.95, 0.99]	0.029
Logistic Regression	0.95	[0.91, 0.99]	0.95	[0.91, 0.99]	0.9
Support Vector Machine	0.83	[0.69, 0.97]	0.88	[0.75, 1.00]	0.6

AUC, area under the curve of the receiver operator characteristic curve; CI, confidence interval.

AUCs are reported as applied in the test cohort.

Intraoperative model includes both preoperative and intraoperative variables.

^*P-value compares the preoperative model to the intraoperative model using deLong’s test.

Figure 2.

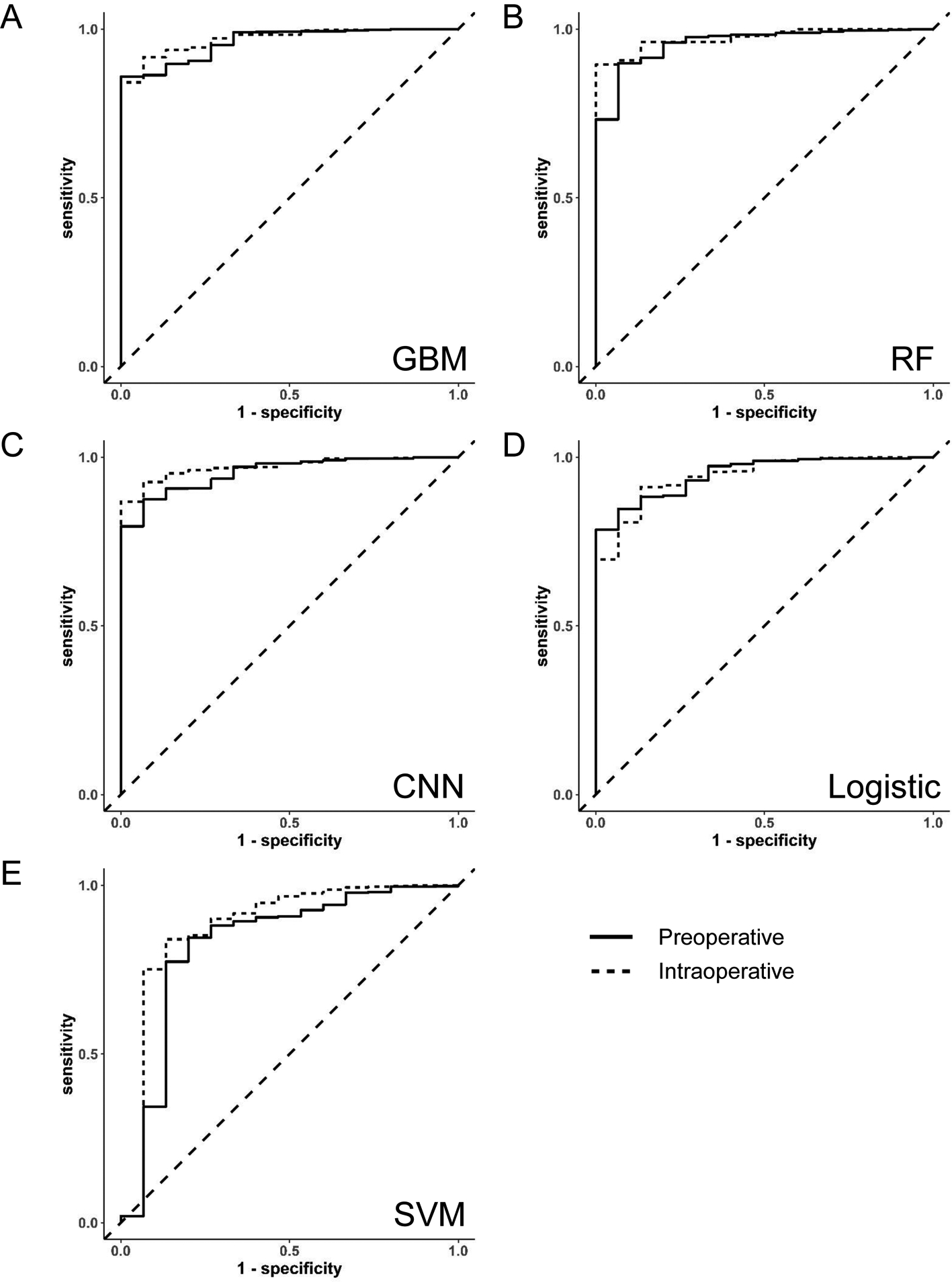
Area under the receiver operator characteristic curve for preoperative and intraoperative machine learning models to predict 30-day mortality in intraabdominal surgery patients. Algorithms evaluated were (A) gradient boosting machine (GBM), (B) random forest (RF), (C) convolutional neural networks (CNN), (D) logistic regression (logistic), and (E) support vector machine (SVM).

Model performance was also assessed with AUCPR. When using only preoperative data, the AUCPRs in the test set for GBM, RF, CNN, logistic elastic net, and SVM were 0.48 [95% CI 0.25–0.70], 0.30 [95% CI 0.16–0.55], 0.30 [95% CI 0.14–0.57], 0.30 [95% CI 0.14–0.55], and 0.12 [95% CI 0.05–0.30], respectively (Supplemental Table 5; PR curves in Supplemental Figure 1). When intraoperative data were added to the preoperative model, the AUCPRs in the test set for GBM, RF, CNN, logistic elastic net, and SVM were 0.50 [95% CI 0.25–0.73], 0.53 [95% CI 0.30–0.75], 0.37 [95% CI 0.18–0.63], 0.43 [95% CI 0.20–0.67], and 0.31 [95% CI 0.10–0.54], respectively. The AUCPRs for the preoperative and intraoperative models were significantly different in the RF (P=0.01) and SVM (P=0.01) models.

Calibration plots are displayed in Figure 3. The logistic regression and SVM models were well-calibrated, while GBM, RF, and CNN had evidence of underestimating or overestimating mortality risk in portions of the calibration plots, particularly in the intraoperative models.

Figure 3.

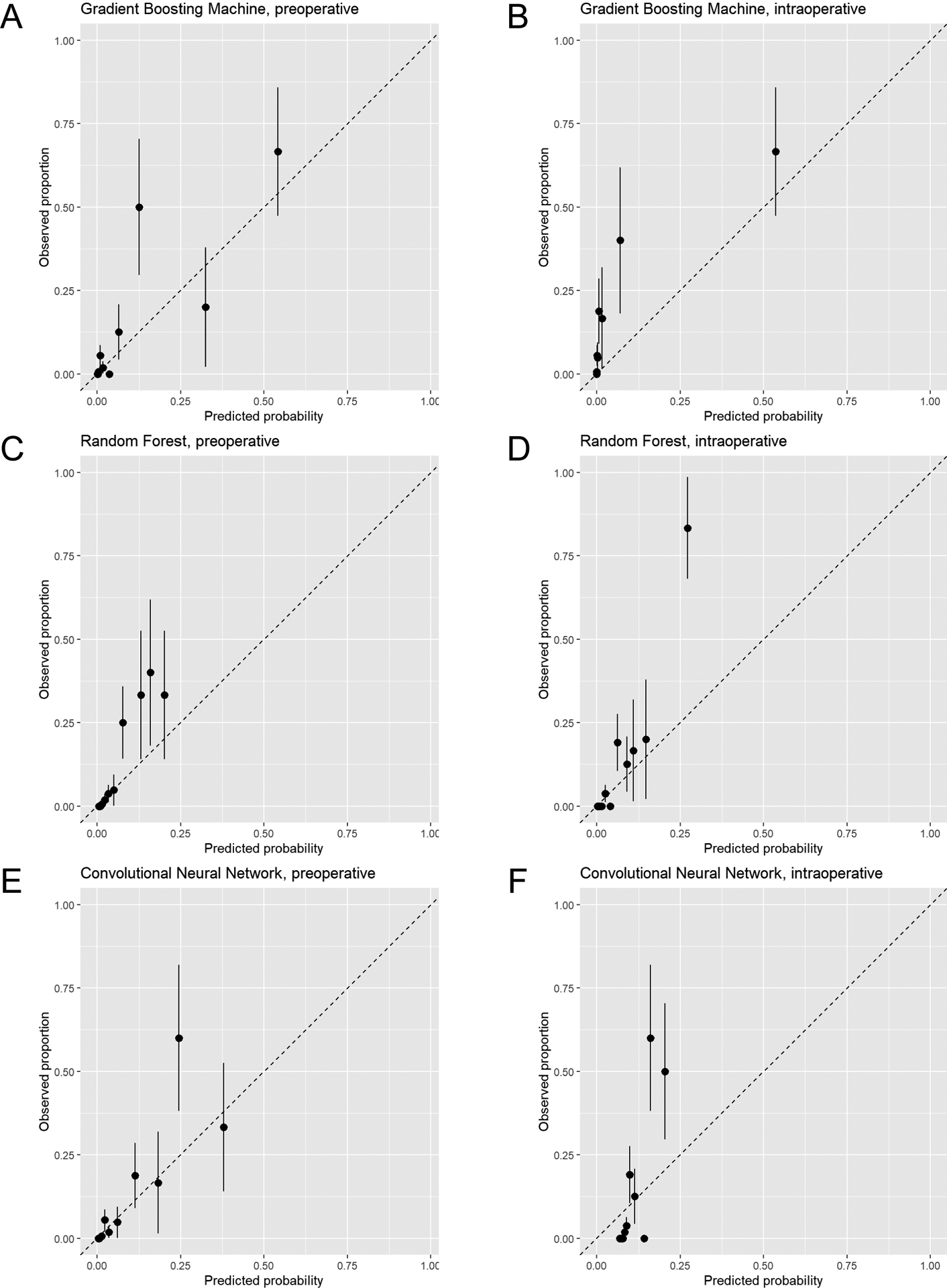
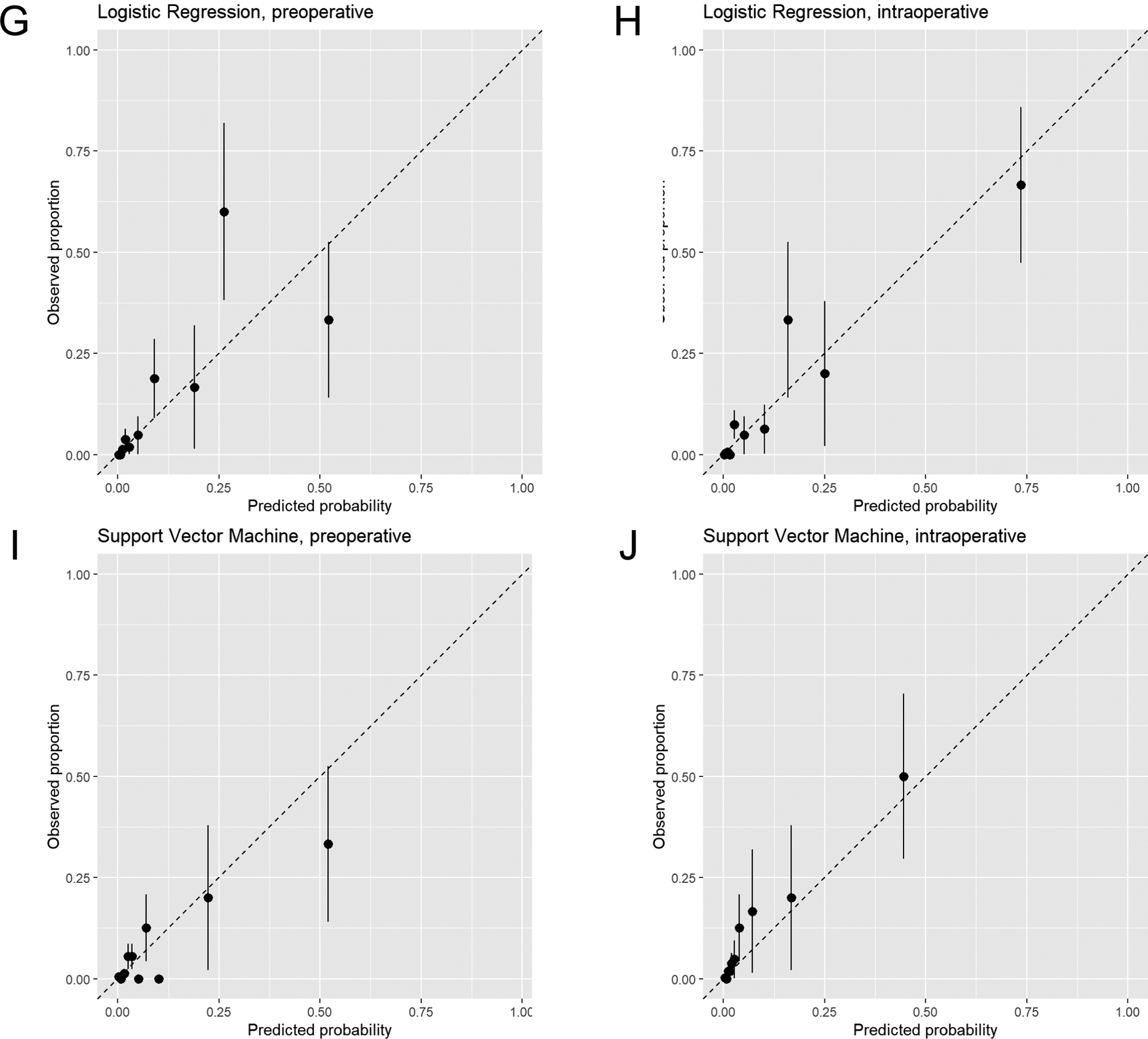
Calibration plots of predicted mortality risk (x-axis) vs. observed mortality (y-axis) in intraabdominal surgery patients. Plots for models using only preoperative data and both preoperative and intraoperative data (intraoperative) are displayed for gradient boosting machine (A and B), random forest (C and D), convolutional neural network (E and F), logistic regression (G and H), and support vector machine (I and J) models. The subjects are divided into 10 groups using the 45th, 70th, 85th, 90th, 95th, 97th, 98.5th, 99th, and 99.5th percentiles of the predicted probability of the fitted model. Groups are divided unequally to account for the right-skewed distribution of predicted probabilities and to focus on patients with high predicted probabilities. Mean predicted probability and 30-day mortality are calculated within each group. All plots reflect calibration in the test dataset.

Variable importance measures in machine learning models

Metrics regarding relative feature importance were available for certain machine learning algorithms (Supplemental Figure 2). Variables with high relative importance included both preoperative characteristics, such as age, functional dependence, and mechanical ventilation, and intraoperative variables such as vasopressor use (e.g., norepinephrine, epinephrine, and vasopressin).

Discussion

We used a machine learning approach to predict 30-day mortality in patients undergoing intraabdominal surgery at a single academic medical center. For 4 out of the 5 machine learning algorithms evaluated, there was excellent performance, as measured by model discrimination, when the models were trained using preoperative patient characteristics and surgical procedure, mimicking the preoperative phase of risk stratification. We then assessed the incremental value of adding intraoperative data to these models and found that while the intraoperative models also had high performance, they did not perform significantly better than models using only preoperative data. Our results suggest that while postoperative mortality after intraabdominal surgery is well-predicted by patients’ underlying medical conditions and intended surgical procedure, the addition of intraoperative data leads to models that have equally high performance.

Anesthesiologists were early proponents of perioperative risk stratification with the development of the ASA PS,²⁴ which has held up over time as a reliable indicator of postoperative morbidity and mortality risk.²⁵ While the ASA PS is somewhat subjective, other risk stratification measures have been developed, such as the Physiological and Operative Severity Score for the enUmeration of Mortality and morbidity (POSSUM)²⁶ that incorporates physiological variables. These measures are evaluated prior to surgery, and preoperative data have been used to develop many well-performing risk stratification models for postoperative mortality.^1–3

The advent of AIMS and electronic health records have made the automated capture of data possible, and combined with machine learning approaches, there has been tremendous interest in using these additional data sources to improve perioperative risk stratification. Indeed, machine learning using automated capture of preoperative data outperformed the ASA PS and other traditional risk stratification metrics such as the Charlson comorbidity score.^27,28 Automated methods also outperformed the highly-regarded but resource-intensive ACS NSQIP calculator.^29,30 It is clear that the availability of electronic patient data has the potential to improve risk stratification in the perioperative period.

The specific benefits of including intraoperative data in mortality prediction models remain unclear. Deep learning using intraoperative features produced well-performing prediction models for postoperative mortality,^4,5 but these models did not outperform traditional methods.^4,31 Few studies have directly compared preoperative and intraoperative models to assess the incremental value of intraoperative data. Datta et al.³² report that the addition of intraoperative data improved the performance of risk prediction models for in-hospital mortality and other complications, such as mechanical ventilation, neurological complications, cardiovascular complications, and acute kidney injury. We also found that intraoperative data improved models to predict acute kidney injury.⁷ The value of intraoperative data in predicting surgical outcomes likely varies by the specific outcome being evaluated.

We incorporated a host of intraoperative variables designed to represent various aspects of intraoperative care, such as blood pressure, vasopressor use, fluid management, and anesthetic drug administration. Many studies of the intraoperative period focus on one specific aspect of management (e.g., hypotension)³³ but may not adequately account for related aspects that also contribute to adverse outcomes (e.g., vasopressor use). Our models incorporated a wide array of intraoperative variables and machine learning algorithms can account for complex relationships between predictor variables. Many intraoperative variables ranked high in terms of variable importance (Supplemental Figure 2), indicating large effects on model performance, but these analyses are not designed to provide detailed inference on these variables. Future studies may provide a better understanding of the specific relationships between individual variables and mortality through “interpretable” machine learning methodologies.³⁴

Risk prediction for mortality may have different implications than risk prediction for other complications. Surgeons may decline to operate on a patient with a high mortality risk (or patients may refuse surgery),³⁵ but it is not clear if a high predicted risk of other complications, especially potentially reversible complications such as acute kidney injury, would preclude a complicated surgical procedure. For certain conditions, surgeons may choose to operate on a high-risk patient, but perform only a minimal, palliative procedure. Perioperative mortality attributable to anesthesia has dramatically decreased over time,³⁶ and this may be an additional reason why intraoperative data did not improve our models. Our models only include patients who had a surgical procedure, so their utility to assist in the decision to proceed with surgery in a high-risk patient will have to be further evaluated.

There are several differences between our study and others in the literature. We focus on a cohort of intraabdominal surgery patients but many studies include broader categories of surgical procedures,^4,5,32 and model performance may be affected by the underlying patient population. Another important aspect of model building using intraoperative data are the specific variables used in the models. For example, intraoperative data include streams of physiological data (e.g., blood pressure every minute), but some degree of data transformation is required (e.g., min, max, mean, standard deviation of blood pressure). The specific variables used vary across studies, and the extent to which these differences account for variation in results is not clear. The type of data may also play a role. For preoperative variables, we used data from the ACS NSQIP which has both advantages and disadvantages compared to automatically captured electronic health record data.³⁷ In addition, machine learning models predominantly use data from a single institution, so institutional differences may account for differences in the results.

While intraoperative data did not improve model performance using our primary metric (AUCROC), there were suggestions of improved performance with AUCPR (Supplemental Table 5). The AUCPR has advantages in evaluating performance in imbalanced datasets.³⁸ However, we are cautious in our interpretation of these results as AUCPR was not our primary metric for assessing model performance. In addition, our models were tuned to optimize AUCROC, and training the models to optimize AUCPR may have produced more optimal results for assessing performance. The AUCROC has consistent interpretations based on its value, but it is difficult to judge model performance based on the AUCPR value alone. The AUCPR of an uninformative model is the baseline event rate, in our case 0.014, and all models had AUCPR values much greater than this baseline rate. As the AUCPR only considers precision (positive predictive value) and recall (sensitivity), true negative results are ignored and a larger sample may be required as a large proportion of patients would be considered true negatives in our analyses.

Our study is subject to certain limitations. The models were developed using data from completed cases, and as such, it is not clear whether there are modifiable factors that can be altered to change the final outcome. However, this study is an initial step towards this goal and future work will delineate the role of modifiable factors, both preoperative and intraoperative, that can improve clinical outcomes after surgery. Machine learning models benefit from larger sample sizes, and it is possible that a larger sample would have altered our results. Imbalanced datasets may affect model performance,³⁹ but we did not specifically perform any data preprocessing, such as oversampling, as our models performed well without this additional step. As an alternative assessment of model performance, we evaluated the precision-recall curve, which may better assess performance in imbalanced datasets.⁴⁰ In addition, some well-performing models had evidence of miscalibration, particularly in the intraoperative models, and may benefit from recalibration.⁴¹

In conclusion, our analyses demonstrate that both preoperative data and intraoperative data can be used to develop well-performing models to predict postoperative mortality in intraabdominal surgery patients. However, in terms of model building, we did not find evidence that intraoperative models outperformed models using only preoperative data. Intraoperative data, nonetheless, has tremendous clinical value but we must determine the specific ways in which this data can be used to improve the care of surgical patients.

Key Points Summary.

Question:

Does the addition of intraoperative data to a preoperative model for 30-day mortality after intraabdominal surgery improve the model’s performance?

Findings:

Using several machine learning algorithms, 30-day mortality was predicted with excellent discrimination using only preoperative data, with negligible improvement after adding intraoperative data.

Meaning:

Surgical mortality is well predicted using preoperative patient characteristics, including comorbidities, risk factors, and surgical procedure.

Glossary of Terms

ACS NSQIP

American College of Surgeons National Surgical Quality Improvement Program

AIMS

Anesthesia Information Management System

ASA PS

American Society of Anesthesiologists Physical Status

AUC

area under the curve

AUCPR

area under the precision-recall curve

AUCROC

area under the receiver operator characteristic curve

BMI

body mass index

CI

confidence interval

CNN

convolutional neural network

CUMC

Columbia University Medical Center

GBM

gradient boosting machine

RF

random forest

SVM

support vector machine