Endocytic proteins with prion-like domains form viscoelastic condensates that enable membrane remodeling

Significance

The uptake of molecules into cells, known as endocytosis, requires membrane invagination and the formation of vesicles. A version of endocytosis that is independent of actin polymerization is aided by the assembly of membraneless biomolecular condensates at the site of membrane invagination. Here, we show that endocytic condensates are viscoelastic bodies that concentrate key proteins with prion-like domains to enable membrane remodeling. A distinct molecular grammar, namely the preference for glutamine versus asparagine residues, underlies the cohesive interactions that give rise to endocytic condensates. We incorporate material properties inferred using active rheology into a mechanical model to explain how cohesive interactions within condensates and interfacial tensions among condensates, membranes, and the cytosol can drive membrane invagination to initiate endocyosis.

Abstract

Membrane invagination and vesicle formation are key steps in endocytosis and cellular trafficking. Here, we show that endocytic coat proteins with prion-like domains (PLDs) form hemispherical puncta in the budding yeast, Saccharomyces cerevisiae. These puncta have the hallmarks of biomolecular condensates and organize proteins at the membrane for actin-dependent endocytosis. They also enable membrane remodeling to drive actin-independent endocytosis. The puncta, which we refer to as endocytic condensates, form and dissolve reversibly in response to changes in temperature and solution conditions. We find that endocytic condensates are organized around dynamic protein–protein interaction networks, which involve interactions among PLDs with high glutamine contents. The endocytic coat protein Sla1 is at the hub of the protein–protein interaction network. Using active rheology, we inferred the material properties of endocytic condensates. These experiments show that endocytic condensates are akin to viscoelastic materials. We use these characterizations to estimate the interfacial tension between endocytic condensates and their surroundings. We then adapt the physics of contact mechanics, specifically modifications of Hertz theory, to develop a quantitative framework for describing how interfacial tensions among condensates, the membrane, and the cytosol can deform the plasma membrane to enable actin-independent endocytosis.

Endocytosis in eukaryotic cells can occur via two separate mechanisms: actin-dependent and actin-independent pathways. In this study, we used the budding yeast Saccharomyces cerevisiae as a tractable model system to uncover the mechanistic basis for actin-independent endocytosis. This is directly relevant to the early stages of endocytic membrane invagination that occurs in mammalian cells through homologs of the proteins that we identify and study here in yeast (1, 2). In S. cerevisiae, membrane invagination that enables endocytosis is normally driven by growth of membrane-bound branched actin (3). A second actin-independent route to endocytosis is realized when intracellular turgor pressure is reduced. This reduction of turgor pressure alleviates the tension on plasma membranes that would normally oppose membrane invagination (1, 4). Although this actin-independent mechanism is not evident under laboratory conditions, it does occur at the hyperosmotic, high-sucrose concentrations that can be found in the wild when yeast grow on rotting fruit and under industrial fermentation conditions, particularly in the context of bioethanol production (1).

In both mechanisms, endocytosis is initiated by the coordinated recruitment of a number of proteins associated with distinct stages of endocytic maturation (5). Clathrin heavy and light chains first interact with initiator proteins (Ede1 and Syp1) to form a lattice on the membrane. Subsequently, early coat proteins such as Sla1, Sla2, Ent1, Ent2, and Yap1801 (6) bind directly to the adaptor–clathrin lattice and form the cortical body (5). Electron microscopy data highlight the existence of hemispherical membraneless bodies around endocytic sites. These bodies are identifiable by following the localization of labeled endocytic coat proteins such as Sla1. The observed Sla1-labeled bodies are known to exclude ribosomes from regions that are near the cortical sites in the cytosol. Importantly, these endocytic bodies form even when actin is not polymerized, and the membrane is flat (7).

Many of the coat proteins in bodies that form around endocytic sites include prion-like domains (PLDs). These are low-complexity intrinsically disordered domains that are enriched in polar amino acids such as glutamine, asparagine, glycine, and serine and are interspersed by aromatic residues (6, 8). Proteins with PLDs have the ability to drive the formation of membraneless biomolecular condensates through phase separation in cells (9) and in vitro (10). Condensates are mesoscale, nonstoichiometric macromolecular assemblies that concentrate biomolecules (11–13). Here, we show that endocytosis in S. cerevisiae involves the concentration of PLD-containing proteins, including the essential protein Sla1, within biomolecular condensates that form at cortical sites (14). Inferences from indirect measurements suggest that these condensates have viscoelastic properties and that they are scaffolded by a dense network of PLD-containing proteins. We show that condensate formation requires an intact PLD and the coat protein Sla1 is at the hub of the condensate-driving protein–protein interaction network. The distinctive compositional biases within PLDs of coat proteins contribute to condensate formation and function. We present a model, motivated by Hertz contact theory (15–17), to provide a plausible explanation for how interfacial tensions among condensates, the membrane, and the cytosol can enable membrane invagination and drive actin-independent endocytosis. This model shows that the formation of condensates and cohesiveness of molecular interactions within them are likely to be essential for mechanoactive processes associated with actin-independent endocytosis.

Results

Sla1-Labeled Puncta Form and Dissolve Reversibly as a Function of Temperature.

We sought to determine the role of PLD-containing early coat proteins in endocytosis. In the budding yeast S. cerevisiae, we investigated actin-independent endocytosis by deleting the gene that codes for glycerol-3-phosphate dehydrogenase, a key enzyme of glycerol synthesis (GPD1Δ) (4). Glycerol is the major osmolyte in yeast cells, and glycerol deficiency alleviates turgor pressure and tension on the membrane in GPD1Δ cells (SI Appendix, Fig. S1A). We could then interrogate actin-independent endocytosis in GPD1Δ cells by treating them with latrunculin A (Lat A), an inhibitor of actin polymerization. The concentrations of Lat A that we use in our experiments cause a loss in localization of the filamentous actin marker Abp1 (SI Appendix, Fig. S1 B and C) (18). We then tracked the formation and internalization of Sla1-labeled endocytic puncta at cortical sites (SI Appendix, Fig. S1D).

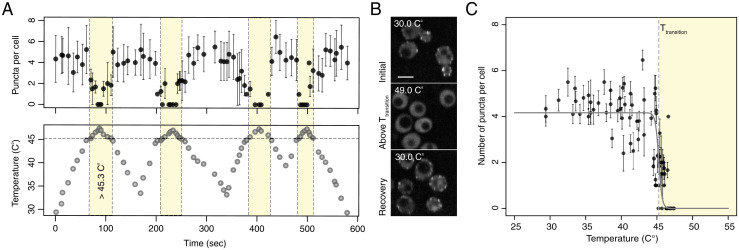
Proteins with PLDs and many PLDs themselves undergo reversible thermoresponsive phase transitions with upper critical solution temperatures (UCST) in cells (9) and in vitro (10). Systems characterized by UCST phase behavior will undergo phase separation below a critical temperature T_c and transition to homogeneous single phases above T_c (19). The ability to undergo a reversible switch between two phases at a distinct temperature, and do so over multiple heating and cooling cycles, is a defining feature of reversible thermoresponsive phase transitions (20). Motivated by published results for PLDs and proteins with PLDs, we assessed whether the Sla1-labeled endocytic puncta also form and dissolve reversibly in response to increases/decreases in temperature. To investigate such behavior for endocytic puncta, we quantified their sensitivity to multiple cycles of heating and cooling. Sla1-labeled puncta in GPD1Δ cells dissolved and reassembled within seconds as the temperature of the growth medium was cycled between 30 °C and 49 °C (Fig. 1 A–C). Quantification of the number of puncta per cell showed a bistable response to increases/decreases in temperature with an apparent transition temperature (T_t) of 45.3 °C. Specifically, cells did not contain puncta above T_t, whereas puncta were observed in cells below T_t (Fig. 1 A and B). Importantly, cells remained viable above T_t, and endocytic function was restored when the temperature dropped below T_t (SI Appendix, Fig. S2 A and B).

Fig. 1.

Endocytic proteins with PLDs form thermosensitive puncta. (A) Reversible, temperature-dependent dissolution and formation of Sla1-labeled endocytic puncta when cells are cycled above and below an apparent T_t of 45.3 °C (yellow region) over multiple heating and cooling cycles (Left; mean ± SD; n > 8 cells). (B) Representative images of temperature-dependent dissolution and reformation of Sla1-labeled endocytic puncta in GPD1Δ cells treated with Lat A when cells are cycled above and below a T_t over a heating and cooling cycle. (Scale bar, 4 μm.) (C) Average number of puncta per cell is bistable as a function of temperature.

Proteins Are Labile within Endocytic Condensates.

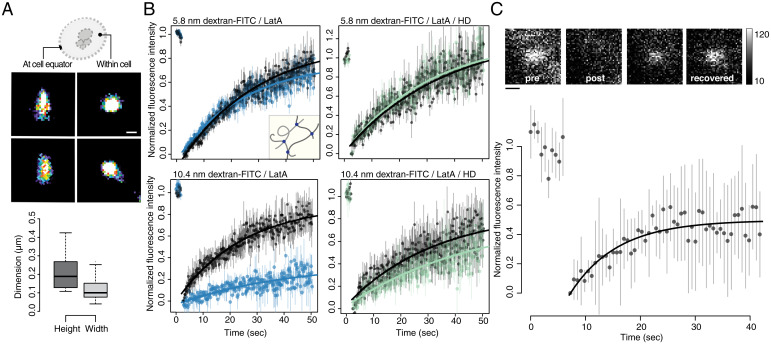
Using superresolution fluorescence imaging, we quantified the dimensions of Sla1-labeled bodies to be 209 ± 10 nm long and 118 ± 6 nm wide. These inferences were based on the orientation of puncta in the imaging plane (Fig. 2A). Our observations for top projections are similar to previous reports of Sla-labeled spherical structures (21). They are also consistent with electron microscopy data highlighting hemispherical bodies that exclude ribosomes from the cytosol near cortical sites that form in a manner that is independent of actin polymerization (7).

Fig. 2.

Endocytic puncta form dense condensates of labile molecules. (A) Dimensions of Sla1-GFP–labeled puncta measured using superresolution microscopy (dSTORM). Lateral x, y resolution was ∼10 nm. Pseudocolor reconstructed images show circular structures when viewed from the top or within cells (Top Right) and narrow ellipses when imaged at the equator of cells (Top Left). Automatic segmentation (Center) was performed on these images to determine the lengths (209 ± 10 nm) and widths (118 ± 6 nm) of the endocytic puncta (n = 250). (B) These puncta are dense lattices that exclude molecules having dimensions >10 nm. FRAP of dextran-FITC molecules within endocytic puncta or neighboring cytosol. FRAP of the bleached 5.8 nm dextran-FITC within either a Sla1-mCherry (Top Left; Lat A–treated cells; blue) or a Syp1-mCherry (Top Right; Lat A and 5% HD-treated cells; green) puncta and neighboring cytosol regions (black) without Sla1 or Syp1 signals, respectively. Inset illustrates porous latticework composed of amorphous protein chains (gray filaments) with binding sites (dots) through which they are noncovalently associated. Same experiment with 10.4 nm dextran-FITC that scarcely permeates the Sla1 puncta (Bottom Left; Lat A–treated cells; blue) but are mobile when puncta are dissolved by HD (Bottom Right; Lat A and 5% HD-treated cells; green). Data points (mean ± SEM; n = 10 cells) were fitted to a single term recovery function (Materials and Methods). (C) Coat proteins exchange with endocytic puncta at rates typical of those observed for biomolecular condensate proteins. FRAP of Sla2-GFP: Signal recovery was measured within a segmented Sla1-mCherry region of interest to ensure that FRAP was acquired within the endocytic puncta (mean ± SD; n = 10 cells). Data were fit to a single term exponential; see Materials and Methods. Incomplete fluorescence recovery suggests that endocytic puncta are viscoelastic. Representative foci images (insert) before and upon bleaching and after recovery. Eight-bit grayscale values, 10 to 120. (Scale bar, 250 nm.)

To determine whether endocytic condensates have a characteristic mesh size, we measured the diffusivity and permeability of probe molecules within and between condensates and the cytosol and at endocytic sites in cells where condensates were dissolved using 1,6-hexanediol (HD). HD has been shown to dissolve a number of cellular structures, including different types of protein condensates in vivo (22) and in vitro (23). Sla1-labeled puncta as well as those labeled with all of the PLD-containing proteins that are associated with endocytic puncta, including Sla2, Ent1, Ent2, Yap1801, and Yap1802, dissolve in the presence of HD (SI Appendix, Fig. S3A) (24, 25). However, Syp1-mCherry, a membrane-bound endocytic initiator containing a scaffold-forming Fes/CIP4 homology-Bin/Amphiphysin/Rvs (F-BAR) domain, was insensitive to HD (SI Appendix, Fig. S3B). This suggests that membrane targeting of endocytic sites through F-BAR domain oligomerization was unperturbed by HD. We also noted that HD does not disrupt membrane integrity, as monitored by membrane leakage of carboxy-fluorescein (SI Appendix, Fig. S3 C–E). These results imply that HD disrupts endocytic condensates, and therefore, in cells treated with HD, the diffusivity and permeability of endocytic sites should be identical to those of the surrounding cytosol.

We quantified the apparent mesh sizes within the endocytic puncta using fluorescence recovery after photobleaching (FRAP) and colocalization of fluorescein-5-isothiocyanate (FITC)–conjugated dextran molecules of 2.4-, 5.8-, and 10.4-nm dimensions. The dextran probes were osmoporated into cells and FRAP was measured within either Sla1-labeled or Syp1-labeled puncta. Maintenance of cell mechanical properties following osmoporation was evaluated by monitoring passive diffusion of expressed viral microNS protein nanoparticles (SI Appendix, Fig. S7 A–F) (26). Syp1 was used as a reference marker for cortical patches because it was not sensitive to HD at concentrations that dissolved endocytic puncta (SI Appendix, Fig. S3B). Although the density of the FITC-labeled 5.8 nm dextran was lower in Sla1-labeled puncta than in the surrounding cytosol, the mobility of the 5.8-nm probe was equivalent in both regions (Fig. 2B and SI Appendix, Fig. S4 C–F). Similarly, the fluorescence intensities of 2.4 nm and 5.8 nm FITC-labeled dextran recovered equally well in the Sla1-labeled puncta and cytosolic zones (Fig. 2B and SI Appendix, Fig. S4F). It is known that weakly charged molecules such as proteins do not encounter hindered diffusion across phase boundaries of biomolecular condensates (27). Instead, the key determinants of diffusion of proteins across phase boundaries are the differential affinities to the coexisting phases and the concentration gradients (27). Our data are consistent with these expectations.

In contrast to the transport of 2.4 and 5.8 nm FITC-labeled dextran particles, only a few 10.4 nm dextran molecules were taken up by the endocytic puncta, although these were mobile in the cytosol (Fig. 2B). Furthermore, when Sla1-labeled puncta were disrupted by HD, we observed equivalent mobility of 10.4 nm FITC-labeled dextran molecules within cortical membrane sites, labeled with HD-resistant protein Syp1-mCherry, and the neighboring cytosol (Fig. 2B). Our results suggest that endocytic condensates are porous bodies with apparent mesh sizes that are between 5 and 10 nm. These results are consistent with mesh sizes of networks of proteins that engage in noncovalent physical cross-links in biomolecular condensates, and with published electron microscopy data showing that endocytic puncta exclude ribosomes (7, 23, 28).

To measure the exchange of endocytic proteins between condensates and the cytosol, we used FRAP to measure the dynamics of the coat protein Sla2. To control for dynamic Sla2 recruitment that occurs early in formation of the endocytic puncta, we evaluated fluorescence recovery during periods in which the apparent number of Sla2 molecules in the fluorescent foci of individual puncta was constant. FRAP measurements of entirely bleached whole puncta showed signal recovery within seconds and equivalent mobile and immobile fractions (0.50 ± 0.02; mean ± SEM) for the protein Sla2, indicating that mobile fractions of Sla2 proteins are able to exchange with their surroundings on time scales of tens of seconds (Fig. 2C).

PLDs Are Necessary for the Formation of Functional Endocytic Condensates.

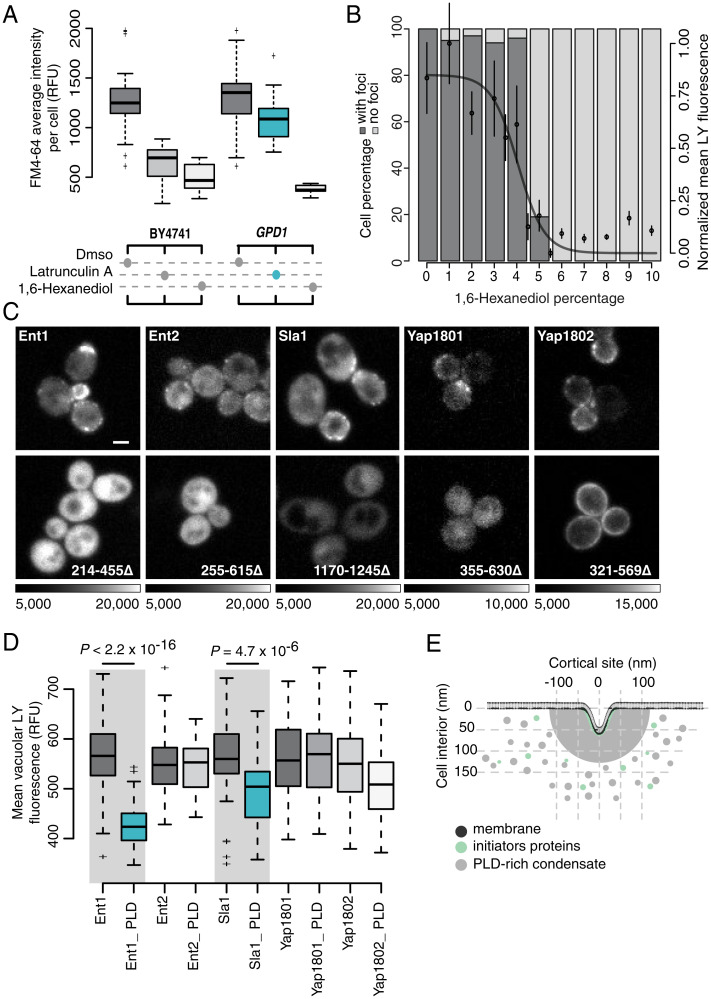
Next, we explored whether endocytic condensates formed by PLD-containing proteins require their PLDs to associate with the condensates and enable actin-independent endocytosis. Since HD generally disrupts interactions among PLD-containing proteins in biomolecular condensates, we tested whether dissolution of Sla1-labeled puncta with HD inhibited both actin-dependent and independent endocytosis in GPD1Δ cells as quantified by the uptake of the external fluid-phase (measured by Lucifer Yellow [LY] uptake) and membrane components (measured by fn4-64 uptake), respectively (Fig. 3 A and B). Dissolution by HD (concentration of 5% weight/volume) led to inhibition of the uptake of membrane components. The HD concentration we used is considerably lower than the concentration necessary to disrupt membrane or Syp1-labeled cortical patch structures (Fig. 3B and SI Appendix, Fig. S3 B–E). Importantly, the inhibitory effect of HD on endocytosis was independent of turgor pressure or actin polymerization (Fig. 3A and SI Appendix, Fig. S5).

Fig. 3.

Puncta formed by PLD-containing proteins are necessary for actin-independent endocytosis. (A) Quantification of the membrane uptake of a lipophilic membrane-bound fluorescent dye (FM4-64) in wild-type BY4741 (Left) and GPD1Δ cells (eliminates turgor pressure; Right) treated with either DMSO, Lat A (prevents F-actin polymerization), or HD (nonspecifically alters solvent quality). Each boxplot shows the relative fluorescence units of n = 50 cells. GPD1Δ cells can undergo endocytosis in the absence of F-actin polymerization (blue) because there is no turgor pressure in these cells. (B) At fixed temperature, HD dissolves endocytic puncta, and this in turn inhibits endocytosis. The bar plot quantifies the percentage of cells that contain Sla1-GFP foci (dark gray), or not (light gray), as a function of HD concentration monitored as counts of endocytic puncta labeled with Sla1-GFP (n = 150 cells). Plot overlay: fluid uptake of water-soluble fluorescent dye LY into vacuoles (mean ± SD; n = 25 foci; logistic fit). (C) PLDs of endocytic coat proteins are essential for their localization to endocytic puncta. Fluorescence images of cortical localization of Ent1, Ent2, Sla1, Yap1801, and Yap1802 fused to Venus YFP. Full-length (Upper) versus C-terminal PLD truncation mutants of the proteins (Lower). Sequence ranges of deleted PLDs indicated (Lower) and grayscale dynamic ranges for image pairs. (Scale bar, 2 μm.) (D) LY dye uptake for strains that express either full-length or PLD deletion mutants of Ent1, Ent2, Yap1801, Yap1802, and Sla1 (as detailed in C). Reductions in Ent1 and Sla1 mutants are significant (n = 100 cells; two-sided t test; see Materials and Methods). (E) Illustration of the membrane topology (dark gray) and remodeling into the cell during endocytosis in the absence of actin. Electron microscopy data suggest that clathrin-coated plasma membrane patches are surrounded by a cortical body of ∼200 nm diameter (light gray) before appearance of actin structures (7). Clathrin heavy and light chains (Chc1 and Clc1) interact with initiator proteins (Ede1 and Syp1) to form a lattice on the membrane (in green). Subsequently, PLD-containing coat proteins (light gray), such as Sla1/2, Ent1/2, and Yap1801/2, directly bind to the initiator–clathrin lattice and form the endocytic puncta (in gray).

Next, we assessed the specific importance of PLDs in endocytosis. For this, we tested whether specific PLDs are required for the assembly of endocytic condensates and actin-independent endocytosis. Deletion of the PLDs caused mislocalization of the Sla1, Ent1, Ent2, Yap1801, or Yap1802 proteins and also impaired endocytosis for Sla1 or Ent1 with their PLDs deleted (Fig. 3 C and D). These observations are consistent with previous reports regarding the effects of deletion mutants of Sla1 and Ent1 on actin-dependent endocytosis, suggesting that formation of the endocytic condensate is essential to organizing the proteins required for both driving actin-independent endocytosis and for nucleating the machinery essential for actin polymerization in actin-dependent endocytosis (29, 30). Partitioning of Ent2, Yap1801, and Yap1802 to endocytic condensates required their PLDs but were not essential to endocytosis, though they may serve other roles in regulating endocytosis.

The Interaction Network within Endocytic Puncta Is Governed by Distinct Sequence Features of PLDs.

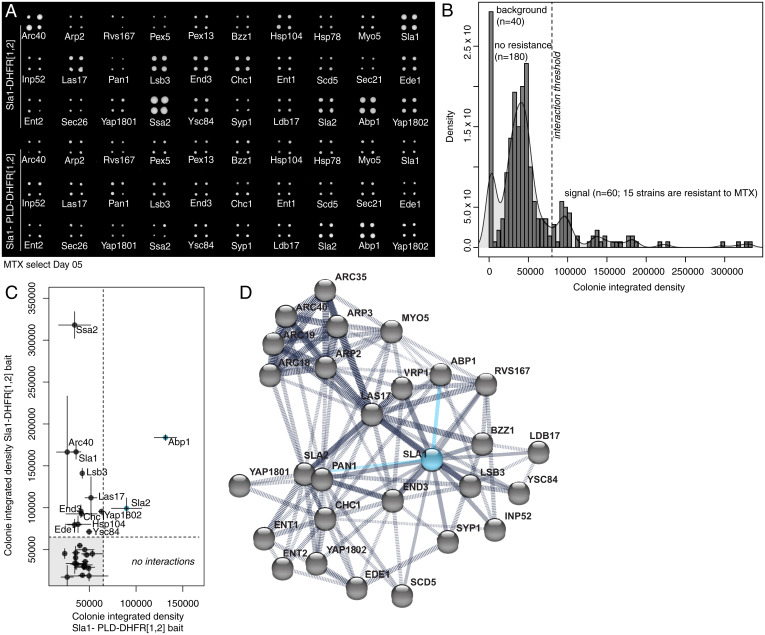
Recent studies have shown that multicomponent biomolecular condensates, such as stress granules, are governed by a core macromolecular network with an uneven distribution of interactions across nodes of the network (31, 32). Such networks are wired by specific types of network motifs or features. The functional importance of Sla1 and Ent1 and their PLDs suggests that they play the roles of scaffolds in organizing endocytic condensates (7, 23, 28). To probe the organization of the protein–protein interaction network that underlies endocytic condensates, we performed an in vivo screen for protein–protein interactions. Specifically, we used a protein–fragment complementation assay with the reporter protein DiHydroFolate reductase (DHFR PCA) to quantify the effects of PLD deletion on in vivo interactions involving or mediated by Sla1 (Fig. 4A). Selection for DHFR reconstitution with Sla1 in which its PLD was deleted (Sla1 ΔPLD) revealed the preservation of only 2 out of the 13 interactions that were detected with the full-length Sla1. The interactions that were preserved are relevant only to actin-dependent endocytosis (Fig. 4 B–D). These results highlight the importance of sequence features of the Sla1 PLD that coordinate the network of interactions and organization of endocytic condensates.

Fig. 4.

Proteins can partition into endocytic puncta through a network for interactions coordinated by PLDs. (A) DHFR PCA and methotrexate (MTX) selection plate after 5 d of growth shows that the PLD deletion mutant of Sla1 loses all but two interactions of wild-type Sla1. (B) Density (number of colonies with given total pixel intensity) versus colony-integrated growth (total pixel intensity) after 5 d of MTX selection for DHFR reconstitution. Peaks are labeled with their corresponding measurements for plate background (n = 40 empty spots), colonies with no resistance to MTX (n = 180 colonies; 45 strains), and colonies that grow on MTX (n = 60 colonies; 15 strains) above a selected integrated density threshold. We detected 13 interactions for full-length Sla1 protein. (C) Colony-integrated growth (total pixel intensity) after 5 d of MTX selection for DHFR reconstitution with wild-type Sla1 versus colony integrated growth (total pixel intensity) after 5 d of MTX selection for DHFR reconstitution with PLD deletion mutant of Sla1. Compared to wild-type Sla1 interactions, we detect two interactions (blue points) for the mutant Sla1 protein that do not contain the PLD. (D) Protein interaction network from STRING (version 11.0) for the selected subarray of 30 potential interactors (gray dots) of Sla1 (blue dot). We represent the 13 direct Sla1 interactions (solid black lines) and DHFR PCA interactions with Apb1 and Sla2 that are preserved with the PLD deletion mutant of Sla1 (solid blue lines) among all the protein–protein interactions (dashed black lines) determined experimentally.

Glutamine-Rich PLDs Are Required for Proteins to Partition into Endocytic Puncta.

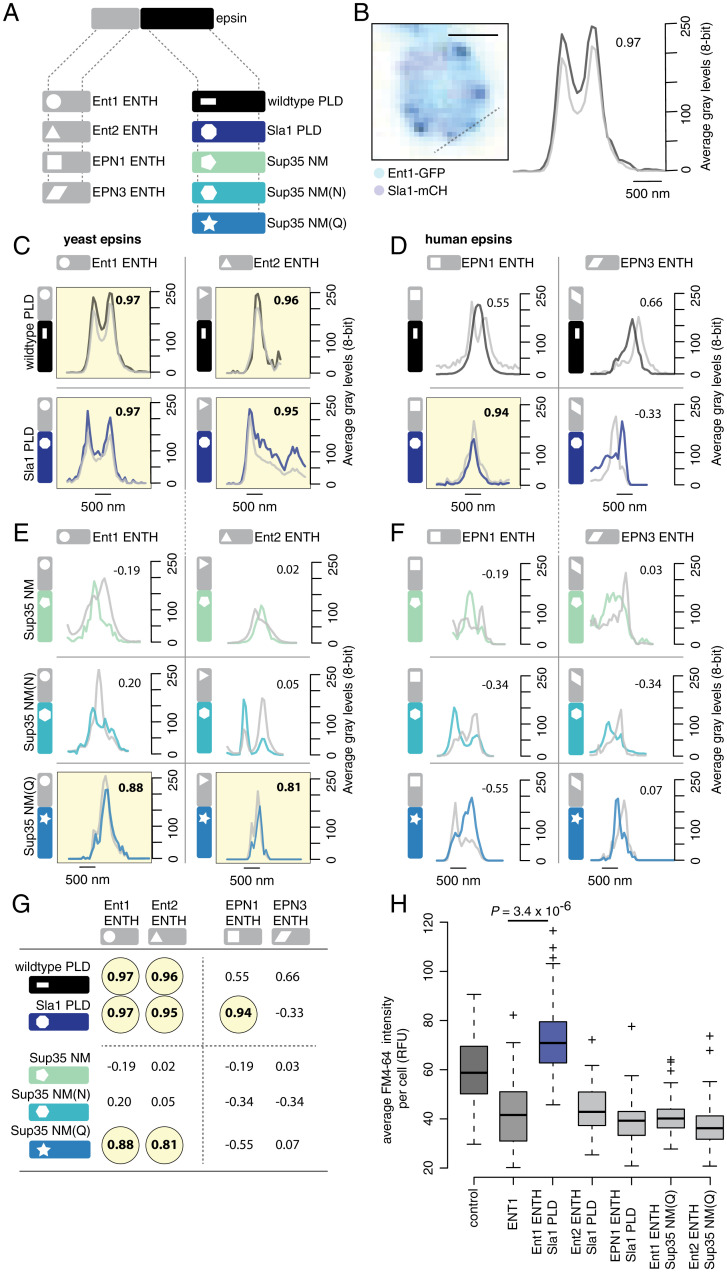
Given that the PLD of Sla1 is central to coordinating the network of essential protein–protein interactions, we reasoned that protein partitioning into endocytic condensates and the interactions among them should depend on the amino acid compositions of their PLDs (23, 33–36). PLDs in yeasts have distinctive compositional biases that include ratios of Asn versus Gln and the uniform sequence distribution of aromatic amino acids (10). Alberti et al. showed that PLDs that drive the formation of amorphous deposits and insoluble amyloid fibrous bodies have a clear preference for Asn over Gln. Conversely, PLDs with higher Gln:Asn ratios form soluble puncta (8). Sla1, Sla2, and the endocytic epsin proteins Ent1 and Ent2 have high-Gln and -Asn contents with a clear preference for Gln. The Gln:Asn ratios in these PLDs are 2:1 in Sla1, ∼5:1 in Sla2, ∼3:1 in Ent1, and ∼4:1 in Ent2, respectively.

To test if higher-Gln content is essential for partitioning into endocytic condensates and impact their material properties, we used artificial PLDs to substitute for the native endocytic PLDs. Specifically, we leveraged the work of Halfmann et al., who compared the prion-forming potential of the NM domain of wild-type Sup35 (Sup35 NM) to those of Sup35 in which all NM domain Gln residues are substituted for Asn [Sup35 NM(N)] or all Asn substituted with Gln [Sup35 NM(Q)] (37). The Gln:Asn ratios in these PLDs are ∼1.5:1 (Sup35 NM), 1:33 [Sup35 NM(N)], and 9:1 [Sup35 NM(Q)]. We designed different chimeras of the endocytic epsin proteins Ent1 and Ent2, in which the cognate PLDs within these proteins were replaced with either that of Sla1 or variants of the nonendocytic protein Sup35 NM domain (Fig. 5A). Although the Sla1 PLD shares little sequence identity with either Ent1 or Ent2 PLDs (SI Appendix, Fig. S6 A and B), Sla1 PLD chimeras of Ent1 and Ent2 partitioned into endocytic condensates (Fig. 5 B and C and SI Appendix, Fig. S6 C–G). Lowering the Gln:Asn ratio or inverting this in favor of Asn increases the amyloid forming potential of PLDs (37). We tested additional Ent1 or Ent2 chimeras wherein the cognate PLDs were replaced with Sup35 NM, NM(N), or NM(Q). We assessed the effects of these substitutions on the partitioning of chimeras into endocytic condensates (Fig. 5A). Consistent with the need for a clear asymmetry between the numbers of Gln versus Asn, we observed that only the Sup35 NM(Q) chimeras of Ent1 and Ent2 partitioned into Sla1-labeled endocytic condensates (Fig. 5E and SI Appendix, Fig. S6 F and G). Conversely, the Sup35 NM and Sup35 NM(N) chimeras did not partition into endocytic condensates; instead, they formed distinct puncta, indicative of structural features and interaction preferences that are distinct from those of endocytic condensates (Fig. 5 E and G). We further surmised that the fibrillar content of Sla1 labeled puncta must be low; to test this hypothesis, we measured the staining of Sla1-labeled endocytic condensates using thioflavin T (ThT), which is a marker for amyloid-like aggregates (SI Appendix, Fig. S6 H and I) (9, 33). These data showed an absence of ThT staining in Sla1-labeled endocytic condensates or in puncta formed by Sup35 NM(Q) (37).

Fig. 5.

PLDs with shared sequence features can be interoperable and drive assembly of functional endocytic condensates. (A) Illustration of the general structure of epsin proteins (Top) with the four ENTH modules (Bottom Left; shape coded) and five PLD modules (Bottom Right; color and shape coded) we used to construct 16 different protein chimeras. (B) Colocalization of Ent1-GFP signal (black) with signal of Sla1-mCherry–labeled endocytic puncta (gray) in yeast cells (Left), line scan on confocal fluorescence images (Right) was performed as indicated on the cell image (Left; dashed line). Pearson correlation values between the fluorescence signals are given (Top Right of plot) to confirm whether the signals colocalize (values above 0.8 are considered significant and highlighted in yellow in C–F; corresponds to a P value < 0.005). (Scale bar 1 µM.) (C) Wild-type yeast epsin proteins Ent1 and Ent2 (Top) and chimeras of Ent1 ENTH and Ent2 ENTH respectively fused to Sla1 PLD (Bottom). (D) Wild-type human epsin proteins EPN1 and EPN3 (Top) and chimeras of EPN1 ENTH and EPN3 ENTH respectively fused to Sla1 PLD (Bottom). (E) Chimeras of Ent1 ENTH and Ent2 ENTH respectively fused to either Sup35 NM (Top), Sup35 NM(N) (Middle), or Sup35 NM(Q) (Bottom). (F) Chimeras of human EPN1 ENTH and EPN3 ENTH respectively fused to either Sup35 NM (Top), Sup35 NM(N) (Middle), or Sup35 NM(Q) (Bottom). (G) Summary of the Pearson correlation values for colocalization of all wild-type and chimera proteins with endocytic puncta described in C–F. Values above 0.8 are considered significant and highlighted in yellow, corresponding to a P value < 0.005. (H) fn4-64 dye uptake in cells for strains that overexpress fusions of the yeast Ent1 ENTH, yeast Ent2 ENTH, or human EPN1 ENTH respectively fused to either Sla1 PLD or Sup35 NM(Q) that are shown to colocalize with endocytic puncta in C–F (n = 100 cells; two-sided t test; SI Appendix, Extended Materials and Methods).

Our data show that the compositional features of PLDs, particularly the asymmetry between numbers of Gln versus Asn, define the selective partitioning of proteins into endocytic condensates. In addition, the human orthologs of epsins, EPN1 and EPN3, expressed in yeast did not partition into Sla1-labeled endocytic puncta (Fig. 5D and SI Appendix, Fig. S6 C–E). Among the human chimeric proteins that we generated, only the Sla1 PLD chimera of EPN1 partitioned to endocytic puncta, whereas all other chimeras formed independent puncta (Fig. 5 D, F, and G). These data point to a clear preference for Gln-rich, nonamyloid-forming PLDs derived from yeast, which have different compositional biases than proteins with PLDs from other organisms. It is also worth noting that even if several PLDs share generic physical properties that result in their partitioning into the same biomolecular condensates, each resulting condensate does not have the same material properties (33). This is important because material properties of endocytic condensates likely contribute to the tuning of their mechanoactive potentials. Consistent with this view, among all of the PLD chimeras of Ent1, including those that did partition to endocytic condensates, only the Sla1 chimera supported endocytosis as measured by fn4-64 dye uptake in ENT1Δ cells (Fig. 5H).

Endocytic Condensates are Viscoelastic Mechanoactive Objects That Can Drive Endocytosis.

We have presented data to show that endocytic condensates form at cortical sites, and these hemispherical bodies require cohesive interactions provided by PLDs within endocytic coat proteins. Endocytic condensates form reversibly, and they are required to drive clathrin- and actin-independent endocytosis. HD-sensitive condensates composed of the initiator protein Ede1 have also been shown to be involved in an autophagosomal degradation pathway (38). Different models have been proposed for actin-dependent and actin-independent mechanisms of membrane bending [reviewed in Lacy et al. (39) and Kaksonen and Roux (40)]. How might condensates contribute to endocytosis in the absence of actin? Several mechanisms could act in synergy with the formation of the endocytic condensates to drive mechanical invagination of the plasma membrane. These include 1) contributions from membrane curvature-inducing proteins and protein complexes, including convex-shaped BAR (for Bin, Amphiphysin, and Rvs) domain-containing proteins (41, 42); 2) insertion of an amphipathic helix into the outer leaflet of the membrane bilayer, which pushes the head groups apart (43, 44); 3) modulation of lipid composition (45, 46); 4) local relief of turgor pressure (47); and 5) “steric pressure” exerted at cortical sites because of the excluded volumes of proteins that encompass certain categories of disordered domains (48, 49). Finally, analogous to condensates formed by synthetic polymers that are known to drive membrane vesicle formation from artificial phospholipid bilayers (50), we postulate that cohesive interactions that contribute to the formation of endocytic condensates also make these condensates mechanoactive by providing the free energy to drive membrane remodeling (51).

Of the mechanisms enumerated above, two stand out for the distinctive roles that are ascribed to intrinsically disordered regions (IDRs) of proteins, the steric pressure model, and our mechanoactive model (51, 52). Busch et al. have proposed that IDRs can drive membrane remodeling and endocytosis via excluded volume effects—a phenomenon referred to as “steric pressure” (48). Their recent studies suggest that phase separation of IDRs involved in generating steric pressure also undergo phase separation via depletion-mediated forces (52). Of course, not all IDRs adopt expanded conformations with high excluded volumes (53). Instead, IDRs come in different flavors; for instance, IDRs, such as the PLDs of Sla1, Sla2, Ent1, and Ent2, are deficient in charged or proline residues and are characterized by cohesive interactions with one another that are likely to engender compact conformations with average radii similar to those of folded proteins (54), albeit with larger fluctuations. Therefore, there appear to be two distinct categories of IDRs that drive membrane invagination, namely those that do so via “hard” repulsive interactions afforded by expanded IDRs and a different category of IDRs that drive condensate formation via cohesive interactions, as occurs in our mechanoactive model (51). This raises the interesting prospect of synergies between the two curvature generation mechanisms by two distinct classes of IDRs.

We hypothesize that the energy stored within endocytic condensates can be converted into mechanical work to deform the membrane and the cytosol. The mechanics of this process can be described by analogy to a soft viscoelastic and sticky balloon bound to a soft elastic sheet (Movie S1). A balance between binding and the elastic/surface deformation energies is achieved upon membrane invagination. This idea can be captured in a simple phenomenological model where we express the mean-field energy U stored in a condensate as the sum of mechanical strain energy (ϕ term) and the useful work derivable from a condensates (ψ term), respectively (SI Appendix):

$$\begin{array}{c}U = \varphi \cdot {\delta }^{1+\epsilon }-\psi \cdot \delta \end{array}.$$ [1]

Here, U is a mean-field energy, δ is the invagination depth of both the membrane and cytosol (which are coupled by virtue of conservation of volume of the condensate), and the exponent ε > 0 is determined by the deformation geometry (SI Appendix). At equilibrium, (∂U/∂δ) = 0, and we expect invagination to balance the two contributions such that the value of δ* that minimizes the mean-field energy Eq. 1 is computed as the following:

$$\begin{array}{c}{\delta }^{*}={\left( \frac{\psi }{\varphi (1+\epsilon )}\right)}^{\frac{1}{\epsilon }}.\end{array}$$ [2]

Eq. 2 shows that the invagination depth δ is determined by the ratio ψ/ϕ and the deformation geometry that is captured in the exponent ε. The numerical values of ϕ and ψ can be estimated from the dimensions of the condensates as well as the viscoelastic properties of the cytosol, condensate, and membrane, respectively (SI Appendix).

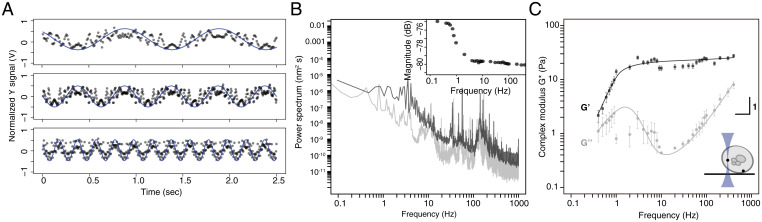
To test whether the endocytic condensates have viscoelastic properties that are required to drive membrane invagination, we used active rheology to measure the material properties of the cytosol in which endocytic condensates are embedded. The endocytic condensates are too small to be probed using active rheology that is useful for measuring material properties, viz., viscosity and moduli, directly. Therefore, we inferred their material properties using Hertz contact theory (17). This theory relates the moduli of elastic materials in contact with one another through the resulting geometries of their contacting surfaces. We probed the material properties of the yeast cytoplasm with optical tweezers (OT) to measure the frequency-dependent amplitude and phase responses of 200-nm-diameter polystyrene beads that are embedded in cells (Fig. 6 and SI Appendix, Fig. S7 G and H). We used an acousto-optic device to oscillate the position of the OT in the specimen plane at frequencies that spanned over four orders of magnitude and measured the displacement of trapped beads from the OT center using back focal plane interferometry (Fig. 6 A–C). We quantified the viscoelastic properties of the cytosol surrounding the beads by measuring the phase and amplitude of displacements of beads in response to oscillations of the OT and calculated the power spectrum of unforced fluctuations of the bead to obtain storage (G′) and loss (G″) moduli as a function of frequency (Fig. 6 B and C and SI Appendix) (55). We used both the dimensions and time-lapse fluorescence imaging of Sla1-labeled puncta to determine that endocytic condensates expand at a rate of 2,360 ± 120 nm ⋅ s⁻¹ (SI Appendix, Fig. S7 I and J), corresponding to a stress at ∼30 ± 2 Hz. At this timescale, the cytosol is principally elastic with a shear modulus of ∼20 Pa (Fig. 6C). We also measured the linear displacement of Sla1-labeled puncta within the confocal volume as a function of time. Membrane invagination occurs at a velocity of 7.4 ± 2.5 nm ⋅ s⁻¹, and this corresponds to a frequency of 0.4 ± 0.04 Hz (SI Appendix, Fig. S7 I and J). In this regime, the cytoplasm is viscoelastic and mechanically compliant (Fig. 6C). We use the term “mechanically compliant” to mean that the cytoplasm responds to mechanical perturbations and achieves force and motion transmission by deforming like an elastic material. The G′ and G″ values we measured here are similar to those of the cytoplasm of adherent mammalian cells (56–59).

Fig. 6.

Sla1-labeled condensates are embedded in a viscoelastic cytosol. (A) Position-sensitive detector (PSD) output signal in volts versus time for acquisitions made at 1 Hz (Top), 2 Hz (Middle), and 5 Hz (Bottom). A bead located in the cytoplasm was oscillated with the acousto-optic deflector in the y-axis of the specimen plane with fixed tweezer movement amplitude (normalized blue curve) at different frequencies. The recorded PSD raw traces (black points) were normalized to a corresponding magnitude range (coherence cutoff of 0.9). (B, Inset) Power spectrum of the oscillated bead (black) with magnitude of response as a function of frequency. (C) Decomposition of G* as a function of frequency into G′ (storage modulus; darker squares) and G″ (loss modulus; light shade circles) for beads distributed at both the cell periphery and interior (see schematic Inset; mean ± SD; n = 17 cells) with an average trap stiffness k_trap (mean ± SE; 8.0 × 10⁻⁵ ± 2.7 × 10⁻⁵ N⋅m⁻¹) and photodiode sensitivity factor β (mean ± SE; 10.7 × 10³ ± 2.3 × 10³ nm⋅V⁻¹).

Based on the parameters obtained from active rheology, including the dynamic modulus of the cytoplasm, we were able to determine the material properties of endocytic condensates embedded in the cytoplasm using Hertz theory and measurements of the dimensions of condensates that we determined by superresolution microscopy (Fig. 2A) . Specifically, we estimated the apparent Young’s modulus of endocytic condensates to be 59 ± 24 Pa at 1 Hz. This is on the same order of magnitude as that of the cytosol at 43.5 ± 18 Pa at 1 Hz (Fig. 6C and SI Appendix, Extended Materials and Methods and Eqs. 3.7–3.10). These results are consistent with those obtained for other protein-based elastic materials (60). The Young–Laplace equation yields an estimate of γ_dc = 7 × 10⁻⁵ Nm⁻¹ for the interfacial tension at the condensate-cytosol interface. This estimate is based on the pressure difference across the cytosolic interface and the mean curvature of the condensate (SI Appendix, Extended Materials and Methods and Eq. 4.6). It falls within the range of values that have been reported for other protein condensates, including nucleoli and P granules (SI Appendix, Extended Materials and Methods and Eq. 4.9) (61, 62).

Using the inferred apparent elastic modulus for the endocytic condensate, we computed the mechanical strain (ϕ) and mechanical work (ψ), respectively, as functions of membrane and cytosol invagination δ (Fig. 7A, SI Appendix, Fig. S8 and Extended Materials and Methods and Eqs. 4.25 and 4.26). Our physical framework suggests that the formation of endocytic condensates generates 4.9 × 10⁻¹⁸ J (Fig. 7A and SI Appendix, Table S4), and this is within the range of the energies required to provide the necessary membrane invagination. Rheology experiments also yield estimates for the energy of deformation that are strikingly similar. This points to a clear route for force generation by condensates that enables membrane invagination, thereby activating membrane constriction and vesicle scission to drive actin-independent endocytosis (63).

Fig. 7.

Endocytic condensates do mechanical work to deform the membrane and cytosol. (A, Inset) Energy U_total versus membrane invagination d determined from Eq. 1, determined by opposing (ϕ) and favoring (ψ) energy terms. U_total (dark blue), ϕ (black), and ψ (light blue) versus δ. The energy is favorable for δ between about 15 to 80 nm (solid blue line) and unfavorable above 80 nm (dashed blue line). Quantities used to calculate energies are detailed in SI Appendix, Fig. S8A and Tables S2, S3, and S4. (B) Mechanical description of endocytic, condensate-driven membrane invagination. Endocytic condensate (yellow) binds to (wets) the bilayer membrane (black) and drives membrane invagination as the condensate expands to maximize contact with the cytosol (Top to Bottom). Forces balance under a Young-Dupré adhesion gradient (blue lines and arrows) and resistance of the cytosol (gray curved lines).

Our use of Hertz contact mechanics and linear viscoelastic models follows from their use in describing the mechanical properties of other biological materials. In our model, we propose that the cytoplasm is being pushed aside as the condensate forms, implying that the cytoplasm can be approximated as an elastic material. The endocytic condensates are formed by interactions among PLDs of proteins. Recent work has shown that the volume fraction of PLDs in condensates is in the range of 0.5 to 0.6 (10, 64). This implies that the condensates have roughly equivalent or even higher fractions of protein versus solvent. It is worth noting that water content is high throughout the whole cell, and hydration is not expected to be the main determinant of elastic behavior of different cell structures under normal physiological conditions. For example, water-swelled hydrogels such as chromatin can also have high elastic moduli. Furthermore, Shin et al. showed, using light-activated condensate formation, that chromatin can be pushed or pulled by condensate formation (65). Here, we transpose these phenomena to the cytoplasm. As noted by Rubiano et al. (66), interpretations of mesoscale indentations of soft tissues to infer mechanical properties can be made using Hertzian contact mechanics, providing care is taken to work in a regime of appropriate hydration levels, and the size scales for probe sizes versus sample thickness. Our use of Hertzian contact mechanics is also supported by its adoption for analyzing data from atomic force microscopy for systems with high water content including biological soft matter (67, 68). Variants of the contact theory of Hertz have also been applied to nonbiological microgel particles (69). In fact, it is worth noting that most theories are anchored, in some way or another, to the tenets of Hertz contact theory because this formalism provides a framework for describing the elastic responses of solids as well as viscoelastic materials (70, 71). Finally, our use of Hertz contact theory is intended to yield order of magnitude estimates for moduli and ask if they are in the range where condensates can deform membranes.

Discussion

A mechanical analogy can aid in understanding our model (Fig. 7B and Movie S1). Adhesion of the endocytic condensate to the cytosol tends to drive the condensate to maximize the contact surface area between the condensate and the cytosol. Because the condensate is a viscoelastic material, its volume must remain constant on timescales corresponding to that of membrane invagination. The area of the condensate–cytosol interface is proportional to the square of the radius. Any increase in interfacial area must be compensated by a decrease in volume of the condensate, which varies as the cube of the radius of the condensate. Since the drive to increase the condensate–cytosol contact is symmetrical, the only way that the condensate volume can be reduced is by invagination of the membrane. This, however, increases the favorable condensate–membrane surface contact, thus acting as a positive feedback to further drive membrane invagination. The system comes to equilibrium when the viscoelastic properties of the condensate and cytosol prevent further expansion and invagination. This is the point at which scission of a mature endocytic vesicle must occur.

There remains the question of how the geometry of the observed membrane invagination comes about. Evidence from electron and superresolution fluorescence microscopy indicates that the favored geometry of the membrane is flat with invagination centered in the middle of the endocytic condensate. Such geometries can be explained by a local radial stress gradient generated by adhesion of the viscoelastic condensate to the membrane on one side and the cytosol to the other (72). Local radial stress gradients can also be generated by asymmetries in local binding of adaptor proteins, or by distinct lipid compositions. Overall, our model and the questions they raise provide the motivation for continued investigation of the details of regulation of endocytosis in eukaryotic cells. Our model also provides motivation for investigating the mechanoactive roles of viscoelastic condensates that contribute to vesicle trafficking processes and involve proteins with PLDs (73).

Materials and Methods

Strains and Model System.

We performed in vivo experiments in the S. BY4741 MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0 background. To decouple the effects of turgor pressure on endocytosis we performed experiments in a yeast strain with the gene for glycerol-3-phosphate dehydrogenase deleted, GPD1Δ. We acquired the GPD1Δ and other deletion strains from the yeast knockout (YKO) deletion collection and GFP fluorescent strains from the Yeast GFP Clone Collection (74), which were generous gifts from J. Vogel at McGill University. A complete list of strains used in this study are in SI Appendix, Table S1.

Cell Culture, Gene Manipulations, and Fluorescent Reporters.

Cells were normally grown to exponential phase (optical density at a wavelength of 600 nm [OD₆₀₀] 0.1 to 0.6) in either rich yeast extract–peptone–dextrose medium (YPD) or low fluorescence medium (LFM) (75). Liquid media or solid–agar cultures were incubated at 30 °C. For two-color imaging and other specific needs, oligonucleotides corresponding to the coding sequences for different fluorescent proteins were integrated into the genome, 3′ to reporter protein open reading frames (ORFs) by homologous recombination (76). In short, mCherry and Venus YFP tags were integrated via homologous recombination by amplifying the HPH or NAT resistance cassettes from the respective pAG32 or pAG25 vectors with primer tails homologous to flanking sequences to the respective loci. BY4741, GPD1Δ, or other YKO strains were then transformed with the respective PCR cassettes, selected for HPH or NAT resistance in YPD medium, and confirmed by diagnostic PCR.

Truncation and Site-Directed Mutagenesis within ORFs.

Integration of oligonucleotides corresponding to the coding sequence for fluorescent protein Venus YFP by homologous recombination into the genome was also used to truncate the PLD sequences in the ORFs of Sla1, Ent1, Ent2, Yap1801, and Yap1802. In order to truncate the required gene fragments, the Venus YFP coding sequence was integrated at precise locations prior to the STOP codon. The amino acid sequences that are deleted in each PLD truncation mutant are Sla1 (1170-1245Δ), Ent1 (214-455Δ), Ent2 (255-615Δ), Yap1801 (355-630Δ), and Yap1802 (321-569Δ).

Cell Temperature Cycling.

Cells were grown to mid-log phase (OD₆₀₀ ∼0.6) in YPD media and washed in LFM twice. Prior to temperature cycles cells were treated for about 15 min in LFM containing Lat A and then for 5 to 7 min in LFM containing Lat A and HD or HT from 0 to 2% weight/volume. Signal for Sla1-YFP at different temperatures during heating and cooling cycles was assessed on Quorum Diaskovery platform (see Diffraction-Limited Fluorescence Microscopy) in LFM containing Lat A and HD or HT from 0 to 2% weight/volume. We used a concentration of 20 µM Lat A in all the temperature cycle measurements. Temperature was controlled by air from a heat gun and monitored by the temperature sensors of FCS2 and FCS3 closed chamber system controllers (Bioptechs) using the FCS2 chamber in such a way that heater contacts did not heat the slide. The perfusion tubes were filled with medium to prevent liquid loss due to evaporation. The temperature was cycled in the vicinity of the T_t at which endocytic puncta dissolved and reappeared below T_t, over three heating and cooling cycles. We replicated this experiment three times. To confirm the uncertainty in the critical temperature of temperature cycles, we also measured T_t for control experiments using a digital thermometer in an eight-chamber Lab-TekII cover-glass system and observed the same temperatures as measured by the FCS2 and FCS3 temperature sensor. Viability of cells was confirmed before and after the temperature cycles and this experiment was replicated four times.

Diffraction-Limited Fluorescence Microscopy.

For most experiments, cells were grown in LFM to an OD₆₀₀ of ∼0.1 to 0.6 and plated on either Nunc glass bottom 96-well plates (Thermo Scientific; 164588), glass bottom 8-well plates (Ibidi), or glass bottom 35-mm round dishes (MatTek). We used concanavalin A (Sigma-Aldrich ConA # C-7275) as a cell surface binding agent. Each well was loaded with 1 mg/mL final concentration of ConA solution at room temperature for 15 min. ConA was then removed and wells were completely air dried before cells were added. Fluorescence images were acquired with distinct imaging platforms.

For the assessment of PLD truncations, we imaged cells on a Nikon TE2000 inverted microscope equipped with a 100×/1.45 plan APO lambda oil objective (Nikon), X-Cite lamp source (Excelitas), respective FITC (Chroma 41001HQ), EYFP (Chroma 49003ET), and mCH/TR (Chroma 49008ET) dichroic cubes and a Cool SNAP HQ camera. Z-stacks were acquired through a 1-μm-deep region with five planes and presented by maximal Z-projection.

For the measurements of LY fluorescent probe uptake and cell sizes under different osmotic pressures, fluorescence images were collected on an InCell 6000 automated confocal microscope configured with a 100×/0.9 Plan FLUOR objective (Nikon) and 488 nm laser diode and FITC 525/20 emission filter for GFP fluorescence or 561 nm DPSS laser and dsRed 605/52 emission filter (GE Healthcare Life Sciences). Single or two-color images were collected sequentially on a single focal plane with an exposure time of 100 ms and a confocal slit of 2 AU. Image analysis and signal automated segmentation was performed with the InCell Developer software (GE Healthcare Life Sciences), and the data were further analyzed and plotted in the R environment.

For other imaging data, the Quorum Diskovery platform was used in widefield, confocal, and superresolution imaging modes. Our Quorum Diskovery platform consists of a Leica DMi6000 inverted microscope equipped with a Diskovery multimodal imaging system (Spectral) attached to either a Hamamatsu EM ×2 camera or ORCA FLASH 4.0 V2 digital complementary metal-oxide-semiconductor camera. Wide field or confocal excitation are achieved with a spectral laser merge module with mounted 405, 440, 488, 561, and 640 nm diode pumped solid state laser sources linked to a Borealis beam conditioning unit. Images were acquired with an HCX PL APO 63×/1.47 NA oil-corrected total internal reflection fluorescence (TIRF) objective (Leica). This platform was remote controlled by Metamorph software (Molecular Devices), and images were acquired and analyzed through distinct pipelines. For particle tracking and mean squared displacement analyses, we used the Wave Tracer plugin to localize fluorescent foci centroid positions through a wavelet algorithm and tracks particles in time stacks to calculate particle movement.

Fluorescent Probes to Quantify Endocytosis or Detect Amyloid Structures.

To quantify endocytosis, LY (Life Technologies) assays were performed at a final concentration of 1 mg/mL in YPD medium. Cells were incubated with the LY for 20 min or more. We then centrifuged at 3,000 × g and washed cells three times in phosphate-buffered saline (PBS; 137 mM sodium chloride, 10 mM phosphate, and 2.7 mM potassium chloride) before imaging in PBS with excitation wavelength (λ_ex) of 428 nm and emission wavelength (λ_em) of 536 nm. Measurements were taken from multiple cells in a single sample, and this experiment was replicated 6 times.

The lipophilic stryryl dye fn4-64 [N-(3-triethylammoniumpropyl)-4-(6-[4-(diethylamino) phenyl] hexatrienyl) pyridinium dibromide] (Life Technologies) was used to monitor plasma membrane uptake and staining of vacuolar membranes. Plasma membrane was labeled with 10 to 20 µM fn4-64 in YPD medium, and cells were incubated for 5 to 120 min. Cells were washed once in PBS and resuspended in LFM for imaging. fn4-64–stained cells were quantified by fluorescence microscopy (λ_ex of 510 nm, λ_em of 750 nm) on our Quorum platform (see Diffraction-Limited Fluorescence Microscopy).

We determined whether Sla1-mCherry puncta were labeled with the amyloid binding dye ThT in both live and fixed cells. Live cell ThT staining was performed as described by Kroschwald and collaborators (25). Cells grown to OD₆₀₀ ∼0.6 were harvested and resuspended in 30 µM ThT, 10 mM Tris/EDTA buffer (pH 7) for 20 min. Cells were then washed three times in PBS and resuspended in LFM medium for imaging. Fluorescence microscopy (λ_ex of 405 nm, λ_em of 450/50 nm) or (λ_ex of 488 nm, λ_em of 525/50 nm) were performed on the Quorum Diskovery platform (see Diffraction-Limited Fluorescence Microscopy). BY4741 cells transformed with the plasmid pRS416-GAL-Sup35NM-RFP and induced for 2 h in 2% galactose LFM were used as positive ThT stain controls. Alternatively, we confirmed ThT in vivo results with ThT staining of fixed cells. Cells were fixed with 4% paraformaldehyde and 2% sucrose PBS for 20 min and washed once in PBS. Cells were then permeabilized with 0.1% Triton X phosphate buffered (pH 7.5) detergent solution and treated with 0.001% ThT for 10 min at room temperature. ThT-stained cells were washed 3 to 4 times with PBS and imaged on the Quorum Diskovery platform (λ_ex of 488 nm, λ_em of 525/50 nm) (see Diffraction-Limited Fluorescence Microscopy). This experiment was replicated three times.

Direct Stochastic Optical Reconstruction Microscopy.

Direct stochastic optical reconstruction microscopy (dSTORM) data were acquired with the Quorum Diskovery platform (see Diffraction-Limited Fluorescence Microscopy). Sample preparation for dSTORM was performed according to Ries et al. with minor modifications (77). Cells were grown to an OD₆₀₀ = 0.1 and plated on ConA coated glass bottom 35-mm round dishes for 10 min. Cells were then fixed with 4% paraformaldehyde and 2% sucrose PBS for 15 min. Fixation was stopped with two sequential incubations of 10 min in 50 mM NH₄Cl PBS, and cells were further permeabilized and blocked in 0.25% Triton X-100, 5% bovine serum albumin (BSA), 0.004% NaN₃ PBS for another 30 min. We used GFP-Booster-Atto647N nanobodies (Chromotek; code gba647n) to label Sla1-GFP at a concentration of 10 μM in 0.25% Triton X-100, 1% BSA, and 0.004% NaN₃ PBS for 60 min. Cells were washed extensively in PBS before imaging in blinking buffer 150 mM Tris⋅HCl pH 8.0, 30 mM β-mercaptoethylamine, 0.5% glucose, 0.25 mg/mL glucose oxidase, and 20 μg/mL catalase. We acquired streams of 10,000 to 20,000 frames at 30-ms exposures, and we used the Wave Tracer plugin (Molecular Devices) to detect and gate events with a 16-bit intensity threshold of 10³. Measurements were taken from distinct samples to reach a count of 250 bodies, and this experiment was replicated five times. When possible, we did not use gain on the EMCCD camera to better calculate resolution; the camera has a conversion factor of 6e⁻/count when no gain is used. Based on photon counts, we estimate an x, y resolution of ∼10 nm with the 647 nm wavelength Atto647N fluorophore and a z resolution of ∼50 nm with the astigmatic lens in three-dimensional configuration calibrated on TetraSpeck beads (Thermo Fisher Scientific). Center of mass for each event was calculated and we reconstructed images in Wave Tracer before further analysis in Metamorph (Molecular Devices). Sla1-labeled structures were separated in circular and narrow elliptical shapes that correspond respectively to structure within or at the equator of cells.

DHFR PCA.

We performed the DHFR PCA procedure as previously described (76) with minor modifications for a selected subarray of 30 potential Sla1 interactors from Biogrid. MATa strains harboring either Sla1-DHFR-F[1,2]-nat1 or Sla1-ΔPLD-DHFR-F[1,2]-nat1 fusions were grown in liquid YPD supplemented with 100 µg/mL nourseothricin in a square v-bottom 96-well array block (3960; Corning). Each MATa strain was distributed in 3 rows by 10 columns arrangement to obtain a 6 rows by 10 columns array on a single 96-well block. Another block array (6 rows by 10 columns arrangement) of 30 different MATα strains with ORF.X-DHFR-F[3]-hph fusions was cultured in liquid YPD with 250 µg/mL hygromycin B. The strains were grown in liquid array for 24 h at 30 °C. The mating procedure was performed in a 96-well liquid array (6 rows by 10 columns arrangement) for 24 h at 30 °C. MATa and MATα strains were combined one-to-one in fresh liquid YDP without selection for mating so that each resulting diploid strain had respective genes tagged with either of the DHFR fragments. The array was then transferred in quadruplicate in a 1,536-format using a robotically manipulated 384-pin tool (0.787 mm flat round-shaped pins, custom AFIX384FP3 BMP Multimek FP3N, V&P Scientific Inc.) to synthetic complete agar plates (omnitrays, Nunc) without lysine and without methionine and with 100 µg/mL nourseothricin and 250 µg/mL hygromycin B and were incubated for 48 h at 30 °C to select for diploid cells. This step was repeated to further select for diploid cells using a robotically manipulated 1,536-pin tool (0.457 mm flat round-shaped pins, custom AFIX1536FP1 BMP Multimek FP1N (V&P Scientific Inc.) to transfer the array on to fresh plates. For selective growth, the strains were printed in 1,536 format on SC agar medium without adenine (pH 4.8) containing 4% weight/volume Noble agar, 2% glucose, 1.74 g/L YNB without ammonium sulfate, and methotrexate (200 µg/mL) to select for DHFR reconstitution with either Sla1-DHFR-F[1,2]-nat1 or Sla1-ΔPLD-DHFR-F[1,2]-nat1 baits. We repeated the methotrexate selection on three distinct replicate plates. Printed methotrexate plates were incubated at 30°C throughout the imaging process and individual plates were photographed each day for 7 d with a 4 megapixel Canon digital camera (Powershot A520). Quantification of colony growth was performed as described in Stynen et al. (78) with a custom-made macro on imaging software Fiji (v1.45b) to extract the integrated density of each colony. Briefly, for each colony, a 17-by-17 pixel area was screened around an initial central position to find the central intensity gravity point. From this central point, we scanned for the first pixels with intensity values that equal background intensity in the left, right, bottom, and upper directions and used these cardinal coordinates to determine a new central pixel. We iterated this process to get the borders of the colony in all four directions and a final central pixel. An oval was created and analyzed for integrated density, which is the mean density times the area. Further analyses were performed using a custom-made script in R (version 3.2.3). The integrated densities calculated in the previous section were log₂ transformed.

Statistical Analysis and Software for Microscopy.

Software used in microscopy measurements and microscopy data analysis are also outlined in Diffraction-Limited Fluorescence Microscopy, Direct Stochastic Optical Reconstruction Microscopy, and SI Appendix, Fluorescence Recovery After Photobleaching. For dSTORM images, center of mass for each event was calculated, and we reconstructed images in Wave Tracer before further analysis in Metamorph (Molecular Devices). For the measurements of fluorescent probe uptake and cell sizes under different osmotic pressures, image analysis and signal automated segmentation was performed with the InCell Developer software (GE Healthcare Life Sciences), and the data were further analyzed and plotted in the R environment. Quantification of LY or fn4-64 membrane probe was performed with Metamorph image analysis software (Molecular Devices). When cell populations were compared for quantified fluorescence, we applied a Welch’s two-sided t test with sample sizes (n = 100) to achieve a power greater than 0.9 with a 95% confidence. Pearson correlation values for colocalization were considered significant for values above 0.8 that correspond to a P value < 0.005. Statistical analysis was done with the R software package. Kymographs were also generated with the Metamorph image analysis software (Molecular Devices). Analysis of the images intensity (I) fluctuations and segmentation of regions of interest for FRAP experiments were performed on the LASX imaging software (Leica). FRAP data were plotted using subroutines of the R package.

Optical Tweezers Measurements and Calibration.

Dynamic mechanical analysis of yeast cytoplasm was performed with a custom OT platform. Our OT system is an inverted microscope (Nikon Ti-E) equipped with a CFI APO SR TIRF 100×/1.49 NA oil immersion objective (Nikon), a 1,064 nm Nd:YVO₄ 10 W infrared laser (IPG Photonics), an X-Cite lamp source (Excelitas), and a nano-positioning stage (Mad City Labs). Oscillation of the tweezers on the specimen plane from 0.1 Hz to 2,000 Hz was achieved with an acousto-optic deflector (AA Optoelectronics) coupled to a digital frequency synthesizer that we controlled with in-house LabVIEW (National Instruments) routines. Light transmitted through the specimen was collected with a condenser lens and reflected onto a position-sensitive detector (Thorlabs, PDP90A) to perform back focal plane interferometry. Before acquisitions, we adjusted the microscope for Köhler illumination and ensured that all the optics were conjugate to the respective specimen plane or back focal plane. At each frequency of excitation, we recorded the signals (120,000 samples at 1,000 Hz to 2,000,000 samples at 0.1 Hz at 20 kHz) and performed Fourier analysis. Measurement time for each frequency sweep was about 15 min on distinct samples, and this experiment was replicated two times. For each sample, we covered the frequency domain from high-to-low frequencies, and then we repeated the procedure from low to high to ensure consistent frequency response with prolonged laser exposure.

Calibration of the OT measures was performed as previously described with minor modifications (17, 56, 79). Data were analyzed using in-house MATLAB code. Data quality was first confirmed by assessment of the sinusoidal shape of the response to the applied stress. Traces with a coherence of 0.95 or greater were included in the analysis. We averaged 17 traces in distinct cellular locations and determined their trap stiffness k_trap (mean ± SE; 8.0 × 10⁻⁵ ± 2.7 × 10⁻⁵ N⋅m⁻¹), photodiode sensitivity factor β (mean ± SE; 10.7 × 10³ ± 2.3 × 10³ nm⋅V⁻¹), and frequency-dependent viscoelastic moduli G’ (elastic storage modulus) and G’’ (viscous loss modulus) (Fig. 6C).

Data Availability

All study data are included in the article and/or supporting information.