Transcriptome marker diagnostics using big data

Abstract

The big omics data are challenging translational bioinformatics in an unprecedented way for its complexities and volumes. How to employ big omics data to achieve a rivalling‐clinical, reproducible disease diagnosis from a systems approach is an urgent problem to be solved in translational bioinformatics and machine learning. In this study, the authors propose a novel transcriptome marker diagnosis to tackle this problem using big RNA‐seq data by viewing whole transcriptome as a profile marker systematically. The systems diagnosis not only avoids the reproducibility issue of the existing gene‐/network‐marker‐based diagnostic methods, but also achieves rivalling‐clinical diagnostic results by extracting true signals from big RNA‐seq data. Their method demonstrates a better fit for personalised diagnostics by attaining exceptional diagnostic performance via using systems information than its competitive methods and prepares itself as a good candidate for clinical usage. To the best of their knowledge, it is the first study on this topic and will inspire the more investigations in big omics data diagnostics.

1 Introduction

With the surge in translational bioinformatics and medical informatics, the sheer enormity of omics data, i.e. big omics data, are available to make complex disease diagnosis in a more data drive way by providing comprehensive information from transcriptomics, proteomics, genomics data, metabolomics, and others [1–3]. Unlike electric health record data, the big omics data are generated from high‐throughput profiling technologies (e.g. RNA‐seq) and usually distributed in different publicly available databases [e.g. The Cancer Genome Atlas (TCGA) data portal] [1, 4]. However, how to diagnose complex disease phenotypes using big omics data to achieve reproducible disease diagnosis remains an urgent problem to be solved in translational bioinformatics and computational systems biology.

It is noted that existing diagnostic methods are usually built on finding a set of differentially expressed gene markers or network markers to discriminate different pathological states [5]. The methods have achieved a good success in finding statistically significant genes or network modules. However, they have been known for the lack of reproducibility in diagnosis, i.e. a specific set of gene markers or network markers may work for one data set, but usually cannot generalise its good performance to another one, due to the complexities of diseases, artefacts of computing models, or even less reproducible source data. For example, TMPRESS2‐ERG fusion transcripts are recognised as a good biomarker candidate for prostate cancer detection, but it usually cannot be found in as many as 50% prostate tumours [5, 6]. In fact, different gene/network discovery methods may produce totally different gene/network markers even for a same omics data set [5, 6]. Furthermore, some omics data (e.g. serum proteomics data) are even not reproducible themselves, not to mention the reproducibility of those biomarkers discovered from the data [7].

However, the coming era of big omics data provides exciting opportunities to leverage intensive data information to conduct complex disease diagnosis, treatment, and prevention in a more accurate and reproducible way. Big omics data usually has very special characteristics compared with other large‐volume data. First, they are less‐structured data that may even have millions of variables. It could be overwhelming to understand the relationships among variables and their possible associations. In fact, a large amount of missing data can be found often in a big omics data set because not all variable values can be collected or observed in data acquisition. As such, a uniform preprocessing routine to extract all informative entries seems to be too expensive or even unrealistic from a data analytic viewpoint. Second, they are typical heterogeneous data with multiple data types that are produced from different high‐throughput technologies, platforms, quantification, analytes, and participants [4]. Third, they are not noise‐free data for analysis. Instead, they contain different types of noise from different sources. For example, the noise may include system noise from high‐throughput technologies, artefacts in experiment design, or even biological complexities of diseases [4, 6]. The general normalisation procedures may not be able to remove these noises [8]. Moreover, some redundant variables may somewhat present themselves as ‘noise’ to overshadow the expressions of true signals in big omics data. Thus, a de‐noising or its similar process will be needed to separate true signals from red herrings the sake of robust disease diagnosis. It is noted that de‐noising in our context not only means removing noise, but also refers to retrieve essential data characteristics, especially latent data characteristics from input big RNA‐seq data.

Though there are different types of omics data available in TCGA data for some complex disease (e.g. breast cancer), there is almost no data integration model available to integrate these heterogeneous data for disease diagnosis. As such, using a whole TCGA data set to seek reproducible disease diagnosis is not only theoretically challenging, but also practically immature. Thus, we investigate complex disease diagnosis in this paper by focusing on big RNA‐seq data, which is an important component in TCGA data [1, 9]. We have the following two reasons for using big RNA‐seq data. First, it is a typical big omics data and any results obtained from such data can be extended to others. Second, deciphering transcriptome is essential for understanding complex disease mechanism and RNA‐seq technologies model transcription in a more accurate and reproducible approach than traditional technologies (e.g. microarray) [10]. In other words, big RNA‐seq data prepares itself as a good candidate for diagnosing complex diseases by monitoring gene expression differentiation in the whole transcriptome. In the following descriptions, big omics data refers to big RNA‐seq data unless there is a special notation.

It is noted that big RNA‐seq data in our context means RNA‐seq quantification data rather than their original sequence data before alignment and normalisation. Big RNA‐seq data is still high‐dimensional data, where the number of variables is much larger than the number of observations, i.e. n ≫ p. However, the ratio between the number of variables and the number of samples: n/p may decrease remarkably compared with those of traditional omics data. For example, the ratio for a big RNA‐seq data set is in the order of Θ (10), but the ratio for the traditional omics data usually reaches Θ(10²) or higher. Obviously, the availability of the large number of samples in big RNA‐seq data will enable more prior knowledge in training for disease diagnosis than the other omics data, which is believed to contribute to enhancing diagnostic robustness.

However, how to achieve a reproducible rivalling‐clinical disease diagnostic in a systems approach by using big RNA‐seq data? To our knowledge, no previous work addressed this significant topic yet. In this paper, we propose a transcriptome marker diagnosis by viewing the whole transcription data as a profile marker to achieve reproducible diagnosis. As a more personalised diagnostic approach, it allows the diagnostic results to repeat themselves instead of finding gene or network markers. As we pointed out before, as a big omics data, big RNA‐seq data needs a serious de‐noising or similar procedure to retrieve true signals from the whole transcriptome for the sake of robust diagnosis. Traditional feature selection methods, however, usually fail to separate true signals from red herrings due to the limitations of their single‐resolution data analysis [11, 12].

To tackle this problem, we employ a novel derivative component analysis (DCA) that evolves from our previous work in proteomics data analysis to retrieve true signals from transcriptome in this paper [11]. Furthermore, a state‐of‐the‐art learning machine [e.g. support vector machine (SVM)] is employed to discriminate phenotypes from true signals, which can be viewed as true ‘disease signatures’, to seek reproducible disease diagnosis.

The transcriptome marker diagnosis demonstrates a novel way to investigate and solve the diagnostic reproducibility issue in a systems approach. It has a built‐in advantage to avoid the reproducibility issue, because diagnosis of an unknown sample is totally based on comparing its transcriptome expression with a set of known transcriptome expressions (training data). In other words, the whole transcription information is involved in the diagnostic decision making. That is, reproducible diagnosis is no longer sought from a set of gene markers or network markers, which usually express themselves in one experiment, but not in another, due to the complexity of diseases and tumour micro‐environments, and limitation of existing high‐throughput technologies [5, 6, 13]. Instead, the reproducible diagnosis will totally rely on whether such a transcriptome marker, i.e. a profile marker can achieve rivalling‐clinical diagnostic results computationally each time. For the convenience of description, we interchangeably use terminologies profile marker and transcriptome marker in our context.

2 Methods

It is noted that big RNA‐seq data used in our experiment is publicly available level‐3 data in the National Institute of Health (NIH) TCGA database [1]. The level‐3 data are the aggregation of processed omics data from single samples that usually include RNA‐seq, array‐based expression, protein expression, DNA methylation, and single‐nucleotide polymorphism (SNP) data. A big RNA‐seq data set usually includes three transcript quantification data obtained after the alignment for each sample: exon, gene, and splice junction quantification, in addition to other associated information. Each quantification data further have raw count, coverage, and Read per Kilobase per Million mapped reads (RPKM) normalisation data, where the coverage data are actually another normalisation data that normalise the raw data by the gene median length [8].

2.1 Big data preprocessing

Each big RNA‐seq data set usually counts about several to hundred gigabytes storage. In this paper, we include three benchmark data sets: Breast, Prostate, and Kidney data that count 20.7, 10.9, and 12.5 GB, respectively, all of which are from two major platforms: IlluminaGA_RNASeq and IlluminaHiSeq_RNASeqV2.

We filter out all exon and splice junction quantification data in our preprocessing and only keep gene quantification for its importance in complex disease diagnosis. The Breast data consist of 20,352 genes across 775 solid invasive breast cancer tumour and 100 normal samples, which count about 280 MB and include the raw data and its coverage and RPKM normalisation data [10]. Similarly, the Kidney data consist of 20,352 genes across 475 solid kidney renal cell carcinormal tumour and 68 normal samples that count about 115 MB. Unlike the Breast and Kidney data, the Prostate data, which count 78 MB, uses a different algorithm RNA‐Seq. by expectation maximisation (RSEM) to determine the gene expression levels [14]. It consists of 20,351 genes across 374 solid prostate adenocarcinoma tumour and 52 normal samples. The raw data are normalised by dividing a scale factor s = Q ₃/1000, where Q ₃ is the 75‐percentile of each sample. Table 1 illustrates the detailed information about the three data sets.

Table 1.

Big RNA‐seq data

Data	Number of genes	Number of samples	Raw data, Gb	Platform
Breast	20,532	775 solid invasive breast cancer tumours 100 normal samples	20.7	IlluminaGA_RNASeq
Prostate	20,531	374 solid prostate adenocarcinoma tumour 52 normal samples	10.9	IlluminaHiSeq_RNASeqV2
Kidney	20,532	475 kidney renal cell carcinormal tumours 68 normal samples	12.5	IlluminaGA_RNASeq

2.1.1 True signals

As we have pointed out before, the essential component for the transcriptome marker diagnosis relies on the successful separation between true signals and red herrings for input big RNA‐seq data. True signals are not only clean data with a system noise removal, but also those that capture both holistic and subtle (local) data behaviours of the original data. It is noted that subtle data behaviours reflect subtle or latent data characteristics that interpret transient data changes in a short‐time interval or a small set of genes. In contrast, holistic data behaviours reflect global data characteristics and interpret long‐time interval data changes or data changes over a large set of genes, which happen more often than those subtle data behaviours.

However, traditional feature selection methods have their built‐in weaknesses in capturing subtle data behaviour and removing system noise. We categorise them into input‐space and subspace ones. The former seeks a feature subset $X^{\mathrm{\prime }}\in {\mathrm{\Re }}^{m\times p}$, m ≪ n in the input data space ${\mathrm{\Re }}^{n\times p}$ by conducting a hypothesis test, wrapping a classifier to features recursively, or simply filtering features according to some metrics [12]. The latter conducts a dimension reduction by transforming data X into a subspace induced by a linear or non‐linear transformation before seeking meaningful linear combinations of the features. In fact, principal component analysis (PCA), independent component analysis (ICA), non‐negative matrix factorisation (NMF), and their extensions such as non‐negative PCA, and other related matrix decomposition methods fall into this category [15–17].

The input‐space methods usually lack serious de‐noising schemes because they assume input data are clean or nearly clean. However, such an assumption is obviously inappropriate for big omics data. Alternatively, the subspace methods face difficulties in capturing subtle data characteristics because they transform data into a subspace to seek meaningful feature combinations. Since the original spatial coordinates are lost in the transformation, it is almost impossible to track mapping relationships between features and subtle data characteristics they interpret or contribute to. In contrast, global data characteristics are more likely to be extracted than subtle data characteristics, because there are more features contributing to holistic data behaviours [16, 18]. As such, global data characteristics are usually overexpressed, and subtle data characteristics are shadowed or even missed. However, subtle data characteristics are essential to achieve high‐accuracy diagnosis, because different samples not only share similar holistic data behaviour, but have their own subtle behaviours.

The major reasons for these methods’ weaknesses in true signal extraction can be summarised as follows. First, they are single‐resolution data analysis methods that view each feature as an indivisible information unit, which makes system noise removal almost impossible; second, they treat all features uniformly despite their frequencies in the input space, where much more features contribute to holistic data behaviour than those to subtle data behaviour, which makes subtle data behaviour detection quite difficult. On the other hand, retrieving subtle data behaviours that occur in a short‐time interval means to seek the derivatives of the original data theoretically. However, it is quite difficult to accomplish it in a single‐resolution data analysis mode for discrete data such as big RNA‐seq data.

2.2 Derivative component analysis

We propose a modified DCA to separate true signals from red herrings for big RNA‐seq data by capturing data derivatives and removing system noise via multi‐resolution analysis according to our previous work [11, 12, 18]. Unlike traditional methods, it no longer treats each feature as an indivisible information element. Instead, all features are hierarchically decomposed into different components, to capture subtle data characteristics, retrieve holistic data characteristics, and remove system noise. The wavelet‐based hierarchical decomposition not only separates subtle and holistic data behaviours, but also makes subtle data characteristics extraction and system noise removal possible in disease signature retrieval from transcriptome. Our modified DCA mainly consists of the following three steps.

First, a discrete wavelet transform (DWT) is applied to each feature to decompose it hierarchically as a set of detail coefficients and an approximation coefficient by employing high‐pass and low‐pass filters under a transformation level J by assuming each sample is collected at a corresponding time point [19]. The low (high)‐pass filters only pass low (high)‐frequency signals and attenuates the signals higher (lower) than a cutoff. Since the low (high)‐frequency signals contribute to holistic (subtle) data behaviours that sketch data tendency in a long (short) time interval, holistic, and subtle data characteristics are separated under such a DWT, where approximation coefficients and coarse level detail coefficients represent holistic data characteristics, and fine‐level detail coefficients represent subtle data characteristics. Collecting the detail coefficient and approximation coefficients for all features, we have a set of detail coefficient matrices cD ₁, cD ₂, …, cD _J and an approximation matrix cA _J , where the approximation matrix and coarse level detail coefficient matrices (e.g. cD _J ) capture global data characteristics, and the fine‐level detail coefficient matrices (e.g. cD ₁, cD ₂) capture subtle data characteristics. In fact, the fine‐level detail matrices are the components to reflect data derivatives in different short‐time windows and can be called derivative components for its functionality in describing data behaviour. Furthermore, most system noises are transformed to the derivative components for its heterogeneity with respect to those features contributing to holistic data behaviour. Clearly, the DWT separates global characteristics, subtle data characteristics, and system noise in different resolutions.

Second, DCA retrieves the most important subtle data characteristics and remove system noise by reconstructing the fine‐level detail coefficient matrices before or at a presetting cutoff level τ (e.g. τ = 2). The reconstruction can be summarised as the two steps: (i) conduct PCA for the detail matrices before or at the cutoff. (ii) Reconstruct each detail coefficient matrix by using the first m principal components (PCs) to reconstruct each detail coefficient matrix to retrieve the most important subtle data characteristics in the detail coefficient matrix reconstruction. Usually, we set m = 1, i.e. we employ the first PC to reconstruct each detail coefficient matrix to retrieve the most important subtle data characteristics in the detail coefficient matrix reconstruction. The first PC‐based reconstruction also conducts de‐noising because the system noises are usually least likely to appear on the first PC. Moreover, we have found that most big RNA‐seq data sets usually have >60% variability explanation ratio on its first PC (see definition in the next paragraph) in our studies.

On the other hand, those coarse level detail coefficient matrices: cD _{τ + 1}, cD _{τ + 2}, …, cD _J , which are after the cutoff τ, and approximation coefficient matrix cA _J are reconstructed using at least variability explanation ratios 95% to retrieve global data characteristics. The variability explanation ratio ρ _m is the ratio between the variance explained by the first m PCs and the total data variances

$${\rho }_m=\sum _{i=1}^m{\sigma }_i/\sum _{i=1}^p{\sigma }_i$$

where σ _i is the variance explained by the ith PC.

Third, DCA conducts corresponding inverse DWT by using the updated detail and approximation coefficient matrices to obtain true signals X*, the corresponding meta‐data (true signals) with subtle data characteristics extraction, system noise removal, and global data characteristics retrieval. The meta‐data X* are sharing the same dimensionality with the original data, but with less memory storage because less important PCs are dropped in the reconstruction. Algorithm 1 gives DCA's details as follows, where we use X ^t instead of X to represent input RNA‐seq data for the convenience of description, i.e. each row is a sample and each column is a feature in the current context.

DCA

1. Input: X ^t = [x ₁, x ₂, …, x _n ], $x_i\in {\mathrm{\Re }}^p$, DWT level J; cutoff τ; wavelet ψ; and threshold ρ

2. Output: true signals: X*

3. Step 1: Conduct J‐level DWT with a wavelet ψ for X ^t to obtain [ cD ₁, cD ₂, …, cD _J ; cA _J ], where $\mathit{c}{\mathit{D}}_j\in {\mathrm{\Re }}^{p_j\times n}$, $\mathit{c}{\mathit{A}}_J\in {\mathrm{\Re }}^{p_J\times n}$, $p_j=⌈p/2^j⌉$

4. Step 2: Extract subtle data characteristics, remove systems noise, and retrieve global data characteristics

   • (a) Conduct PCA for cD _j , 1 ≤ j ≤ τ to obtain its PC matrix U and score matrix $\mathit{S}:\mathit{U}=[u_1,u_2,\dots ,u_{p_j}]$, $u_i\in {\mathrm{\Re }}^n$ and score matrix $\mathit{S}=[s_1,s_2,\dots ,s_{p_j}]$, $s_i\in {\mathrm{\Re }}^{p_j}$, i = 1, 2, …, p _j .
   • (b) Identify PCs u _i , u ₂, …, u _m , such that its variability explanation ratio ρ _m ≥ ρ
   • (c) Reconstruct $\mathit{c}{\mathit{D}}_j\leftarrow (1/p_j)\mathit{c}{\mathit{D}}_j(\mathbf{1})(\mathbf{1}){}^{\mathrm{T}}+{\sum }_{i=1}^m{u}_i\times s_i^{\mathrm{T}}$, $(\mathbf{1})\in {\mathrm{\Re }}^{p_j}$ with all entries being ‘1's
   • (d) Reconstruct cD _j , τ ≤ j ≤ J and c A _J under the variability explanation ratio at least 95%

5. Step 3: Approximate the original data by the corresponding inverse DWT with the wavelet X* ← inverseDWT([ cD ₁, cD ₂, …, cD _J ; cA _J ]).

2.2.1 Parameter tuning

Though an optimal DWT level can be obtained theoretically by following the maximum entropy principle [20], it is reasonable to adaptively select the DWT level J according to the nature of input big RNA‐seq data, where large sample number corresponds to a relatively large J value, for the convenience of computation. In fact, we have found that a large transform level does not show advantages compared with a small transform level in true signal extraction. However, a too small transform level (e.g. J = 2) may bring some hard time in separating subtle and global data characteristics because of the limited choice for the cutoff value. As such, we select the DWT level as $3\le J\le ⌈{\log }_{2}p⌉$, where p is the number of samples of input big RNA‐seq data, $p\sim O({10}^2)$. Correspondingly, we empirically set the cutoff 1 < τ ≤ J/2 as to separate the fine and coarse level detail coefficient matrices for its robust performance.

Furthermore, we require the wavelet ψ to be orthogonal and have compact supports such as Daubechies wavelets (e.g. ‘db8’), for the sake of subtle data behaviour retrieval. A non‐orthogonal wavelet choice may lead to the failure of subtle data behaviour capturing in data reconstruction. Since the first PC of each fine‐level detail coefficient matrix usually count quite a high variability explanation ratio (e.g. >60%) for each fine‐level detail coefficient matrix cD _j (1 ≤ j ≤ τ) in RNA‐seq data, we relax the variability explanation ratio threshold ρ by only using the first PC to reconstruct each cD _j matrix to catch the subtle data characteristics along the maximum variance direction for the sake of efficient implementation.

The first four plots in Fig. 1 show the true signals of the ten cancer and control samples between the 1500th and 1600th genes, which are randomly selected from the Breast data with total 775 control and 100 cancer samples, extracted by DCA under the cutoff τ = 2, transform‐level J = 7, and wavelet ‘db8’. The x and y axes represent the genes and the gene expression after DCA, respectively.

Fig. 1.

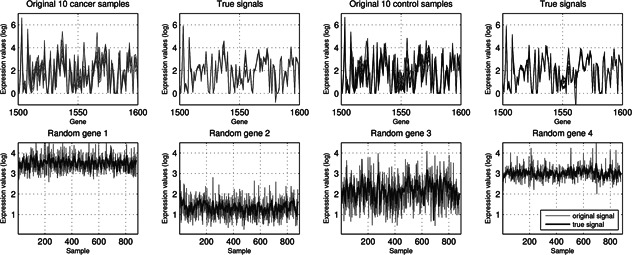
Original and true signals of ten cancer and control samples of the Breast data between 1500th and 1600th genes, and four randomly selected genes across 875 samples. The true signals of the samples appear to be smoother and more proximal to each other besides demonstrating less variations. The true signals of the genes obviously capture the global and subtle data characteristics better than the original ones

It is obvious that the true signals of two types of samples appear to be smoother and more proximal to each other besides demonstrating less variations, because of major subtle data characteristics extraction and system noise removal. Similarly, the second row plots in Fig. 1 illustrate four randomly selected genes from the Breast data and their corresponding true signals extracted by DCA. It is clear that they capture global and subtle data characteristics better than the original ones, and make it easy to distinguish different expression patterns of genes.

2.3 Transcriptome marker diagnosis

Our transcriptome marker views input RNA‐seq data as a transcriptome marker to discriminate disease phenotypes in a systems approach with the wish to achieve reproducible rivalling‐clinical diagnosis. However, which learning machine will be suitable for such a transcriptome marker that invites the whole transcriptome in diagnosis? We believe an ideal learning machine should satisfy the following criteria. First, it should have a good scalability that can handle massive data input well because the true signals extracted from the big RNA‐seq data can be large or even huge. Second, it should demonstrate a good generalisation capability for the sake of achieving reproducible rivalling‐clinical diagnostics. Third, it should have a transparent machine learning structure for optimisation and rigorous learning analysis, in addition to a good library support.

According to the criteria, we choose SVMs for its efficiency and advantages in handling large‐scale data, popularity in omics data diagnosis, transparent learning structures, and sufficient library support resources [21, 22]. As such, we propose novel DCA‐based SVMs (DCA‐SVM) to conduct transcriptome marker diagnosis, which is actually equivalent to a binary classification problem.

Given training RNA‐seq samples X = [x ₁, x ₂, …, x _p ]^T and their labels $\{x_i,c_i\}{}_{i=1,}^p{c}_i\in \{-1,1\}$, its corresponding true signals Y = [y ₁, y ₂, …, y _p ]^T are computed by using DCA. Then, a maximum‐margin hyperplane: O _h:w ^T y + b = 0 in ${\mathrm{\Re }}^n$ is constructed to separate the ‘−1’ (‘cancer’) and ‘+1’ (‘control’) types of the samples in true signals Y, which is equivalent to solving the following quadratic programming problem (classification support vector machine type 1 (C‐SVM) with a soft margin implemented by an L ₁ norm):

$$\begin{array}{cc}\underset{w,b,\xi }{\min }& \frac{1}{2}{∥w∥}_2^2+C\sum _{i=1}^p{\xi }_i\\ \mathrm{s}.\mathrm{t}.& c_i(w^{\mathrm{T}}{y}_i+b)\ge 1-{\xi }_i,i=1,2,\dots ,p\\ & {\xi }_i\ge 0.\end{array}$$ (1)

The C‐SVM can be solved by seeking the solutions to the variables α _i of the following Lagrangian dual problem:

$$\begin{array}{cc}\underset{\alpha }{\max }& \sum {\alpha }_i-\frac{1}{2}\sum _{i=1}^p\sum _{j=1}^p{\alpha }_i{\alpha }_j{c}_i{c}_j{y}_i^{\mathrm{T}}{y}_j\\ \mathrm{s}.\mathrm{t}.& \sum _{i=1}^p{\alpha }_i{c}_i=0,0\le {\alpha }_i\le C_i,i=1,2,\dots ,p\\ & {\xi }_i\ge 0.\end{array}$$ (2)

The normal of the maximum‐margin hyperplane can be calculated as $w={\sum }_{i=1}^p{\alpha }_i{c}_i{y}_i$, where the sparsity of variables α _i makes classification only dependent on few training points. The decision rule

$$f(x^{\mathrm{\prime }})=\text{sign}\left(\sum _{i=1}^p{\alpha }_{i}k(y_i\cdot {\mathit{y}}^{\mathbf{\prime }})+b\right)$$

is used to determine the class type of a testing sample x′, where y′ is its corresponding vector computed from DCA. The function k(y _i · y′ ) is a kernel function mapping y _i and y′ into a same‐dimensional or high‐dimensional feature space. In this paper, we employ the ‘linear’ kernel because we believe complex disease diagnosis is a linearly separable problem for extracted true signals and non‐linear kernels (e.g. ‘rbf’ kernel) will cause overfitting for omics data [23].

3 Results

We demonstrate our transcriptome marker diagnosis can achieve rivalling‐clinical diagnosis by using the three big RNA‐seq data sets and compare it with state‐of‐the‐art peers in this section. The state‐of‐the‐art comparison algorithms include three groups of classification algorithms from different analytic viewpoints. The first group only consists of the standard C‐SVM with a soft margin specified by L ₁ norms. The second group consists of three algorithms that integrate the standard C‐SVM with input‐space and subspace feature selection methods, i.e. PCA‐SVM, ICA‐SVM, and nfs‐SVM. The PCA‐SVM and ICA‐SVM project the training data to the subspace spanned by principal/independent component analysis to detect disease phenotypes [12]. The nfs‐SVM filters input data by using a naive feature selection (NFS) to glean genes with relatively high average gene counts before employing SVM to diagnose disease phenotypes. As a widely used input‐space feature selection method, NFS is usually used to remove low‐count genes for normalised data with the assumption that the genes with high‐counts after normalisation are more likely to be informative genes [5, 10]. The third group consists of a partial least‐square (PLS)‐based linear logistic regression (PLS‐LLR) that employs PLS to conduct dimension reduction for LLR analysis. Though there are other more complicate PLS‐based with logistic regression methods, they cannot apply to our data directly due to their requirements for relatively low data dimensionality [24, 25].

3.1 Cross‐validation, parameter setting, and input data choice

To avoid potential biases from a specific cross‐validation method, we employ the k‐fold (k = 5) cross‐validation and an independent training and test set approach in our experiments for the sake of more comprehensive performance analysis for the proposed transcriptome marker. In the independent training and test set approach, we randomly select 50% of the data for training and another 50% for test to fully leverage the large number of samples from big RNA‐seq data. In addition to choosing the first ten PLS‐components in the PLS‐LLR classifier, we uniformly set the transform level J = 7; cutoff τ = 2; and apply the first PC‐based detail coefficient matrix reconstruction in DCA for all data for the convenience of comparison, though these parameter setting may not be optimal theoretically.

To avoid the possibly negative impacts from sequencing‐depth and gene‐length biases on classification and regression, we employ RNA‐seq normalisation data instead of RNA‐seq raw count data in diagnosis. Moreover, we have found that the RPKM normalisation data generally show a slight advantage in diagnosis than the coverage data for RNA‐seq data (data not shown) [10]. Thus, we choose the RPKM normalisation or the default normalisation data of each big RNA‐seq data in diagnosis for the sake of algorithm performance.

Fig. 2 demonstrates that the proposed transcriptome marker diagnosis achieves almost perfect performance and demonstrates obviously leading advantages over its peers for all data sets in terms of diagnostic accuracy, sensitivity, specificity, and positive predication ratios. The big RNA‐seq data is actually linearly separable data in our transcriptome marker diagnosis due to DCA‐based true signal extraction. Alternatively, all the comparison algorithms demonstrate high oscillations with respect to the diagnostic measures, which indicate they lack good generalisation and stability across different data sets and exclude them as candidates for clinical diagnosis.

Fig. 2.

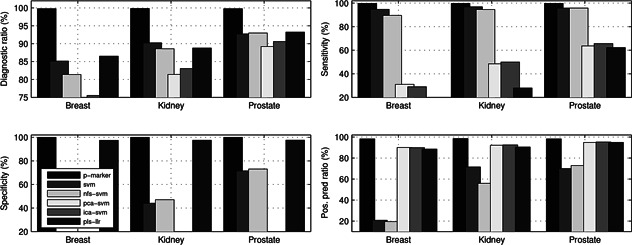
Comparisons of transcriptome marker's average diagnostic accuracies sensitivity, specificity, and positive predication ratio with those of other peers across three big RNA‐seq data under the five‐fold cross‐validation

Furthermore, it seems that both SVM and PLS‐LLR diagnoses achieve almost a same level performance, both of which demonstrate slightly better diagnoses than the other comparison methods. However, they both demonstrate serious diagnostic biases that mean they are only good at diagnosing one type of sample and ignoring the other. Such a diagnostic bias usually reflects as quite a large average positive predictive ratio (PPR) and a small negative predictive ratio (NPR) or vice versa. Correspondingly, they will have imbalanced sensitivity and specificity values. For example, the SVM diagnosis attains an average PPR 89.19% and NPR 20.78% for the Breast data, which lead to an imbalanced sensitivity (94.71%) and specificity (11.00%) correspondingly. That is, it demonstrates a bias by diagnosing the positive targets well, but the negative targets poorly. On the other hand, the PLS‐LLR diagnosis attains an average PPR 24.00% and NPR 88.51% for the Breast data, which lead to an imbalanced sensitivity (2.00%) and specificity (97.42%) also, i.e. it diagnoses the negative targets well, but the positive target poorly.

Fig. 3 illustrates the receiver operating characteristic (ROC) plots of the proposed transcriptome diagnosis (p‐marker) and four SVM‐based comparison peers under the five‐fold cross‐validation for all three data sets [26]. It is interesting to see that the proposed profile‐marker diagnosis has achieved perfect performance for all data sets and it seems that there is no statistically significant difference between the other comparison diagnostic methods. In particular, though average count‐based NFS is widely used in RNA‐seq differential analysis, such a coverage‐related measure does not seem to contribute to enhancing the following SVM diagnosis. It further suggests that using a subset of genes may not achieve a desirable diagnostic result because of the unpredictability of feature selection and complexity of disease.

Fig. 3.

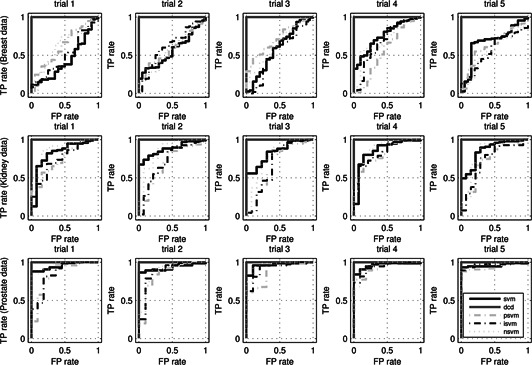
ROC plots of transcriptome marker diagnosis (p‐marker), SVM, PCA‐SVM, ICA‐SVM, and NFS‐SVM under the five‐fold cross‐validation

In contrast to the comparison methods, the proposed systems diagnostic method achieves a 99.77% diagnostic accuracy (sensitivity 99.74% and specificity 100%) for the Breast data, a 99.81% diagnostic accuracy (sensitivity 99.79% and specificity 100%) for the Kidney data, a 99.76% diagnostic accuracy (sensitivity 99.73% and specificity 100%) for the Prostate data. We have to point out that such a clinical‐level performance is that because the true signals extraction in DCA that forces the SVM hyperplane construction to rely on both subtle and global data characteristics of the whole profile in a de‐noised feature space, which seems to contribute to a robust and consistent high‐accuracy diagnosis greatly. In fact, since such a consistent performance applies all three data sets rather than work only on an individual data set, it almost prevents from any overfitting possibility and provides a solution for reproducible diagnostic by viewing the extracted true signals as a uniform profile marker systematically.

In the independent training and test set approach, we include an ensemble learning method: random undersampling boost (RUBoost) as well as the original SVM diagnosis in the comparison algorithms [27, 28]. The reason we choose the ensemble learning method is because it is believed to perform well for imbalanced data [29, 30]. We employ an ensemble of 1000 deep trees that have minimal leaf size of 5 with a learning rate 0.1 in RUBoost learning to attain high ensemble accuracy.

Table 2 compares the performance of the transcriptome marker diagnosis (p‐diagnosis) with those of RUBoost and SVM diagnoses. Not surprisingly, the proposed transcriptome marker diagnosis still outperforms the other methods by its rivalling‐clinical diagnosis for almost all data sets. In particular, it achieves 100% specificity for the Breast and Kidney data, which means the corresponding transcriptome marker diagnosis has a zero false positive rate. On the other hand, both SVM and RUBoost diagnoses have quite a high false positive rate due to their low specifies: 31.43 and 65.71% for the Kidney data. Though our transcriptome marker diagnosis only achieves 96.26% accuracy with 100% sensitivity and 70.37% specificity for the Prostate data, it is easy to detect there is a zero false negative in the diagnosis, which indicates that all negative targets (‘normal’) are correctly reported.

Table 2.

Comparisons of three diagnoses with independent training and test sets

Algorithm	Accuracy, %	Sensitivity, %	Specificity, %	NPR, %	PPR, %
		Breast data
p‐marker	99.54	99.49	100.00	96.00	100.00
SVM	98.86	98.97	97.92	92.16	99.74
RUBoost	99.77	100.00	97.92	100.00	99.74
		Kidney data
p‐marker	99.63	99.58	100.00	97.22	100.00
SVM	90.41	99.15	31.43	84.62	90.70
RUBoost	87.82	91.10	65.71	52.27	94.71
		Prostate data
p‐marker	96.26	100.00	70.37	100.00	95.88
SVM	92.49	94.62	77.78	67.74	96.70
RUBoost	94.84	97.85	74.07	83.33	96.30

Table 3 compares the performance of the transcriptome marker diagnosis (p‐marker) with those of SVM diagnoses by generating 100 trials of independent training and test data sets by following the same setting as before. It is interesting to see that the proposed method (p‐marker) still keeps its leading performance than its peer method. We drop RUBoost for its statistically almost same level performance with SVM in diagnosis. On the other hand, we can see that a smaller training data for the Breast data can even lead to better performance in SVM diagnosis, which may indicate the instability of SVM diagnosis.

Table 3.

Comparisons of the proposed method with SVM

Algorithm	Accuracy ± standard, %	Sensitivity ± standard, %	Specificity ± standard, %	NPR ± standard, %	PPR ± standard, %
		Breast data
p‐marker	99.77 ± 0.282	99.80 ± 0.264	99.41 ± 1.360	98.52 ± 2.062	99.92 ± 0.195
SVM	98.61 ± 0.524	98.71 ± 0.629	97.82 ± 1.759	91.04 ± 4.065	99.70 ± 0.235
		Prostate data
p‐marker	99.46 ± 0.553	99.57 ± 0.530	98.70 ± 3.718	97.13 ± 3.385	99.83 ± 0.507
SVM	92.60 ± 1.547	95.97 ± 1.484	68.46 ± 9.535	70.41 ± 7.904	95.65 ± 1.546
		Kidney data
p‐marker	99.55 ± 0.617	99.75 ± 0.404	98.25 ± 4.331	98.33 ± 2.609	99.74 ± 0.660
SVM	88.52 ± 1.712	96.61 ± 1.558	31.93 ± 8.586	58.39 ± 13.44	90.89 ± 1.682

Considering the randomness in training and test data selection, it is obvious that such an exceptional diagnostic demonstrates its consistency, and such performance is an impossible result from classification overfitting by considering the results from the previous five‐fold cross‐validation. Instead, the transcriptome marker's clinical‐level diagnostic performance is from our effective true signal retrieval mechanism from DCA.

3.2 Big RNA‐seq phenotype separation: verify the correctness of our method from a visualisation viewpoint

Our transcriptome marker diagnosis indicates that big RNA‐seq data diagnosis is a linearly separable problem after true signal extraction. In other words, big RNA‐seq data is linearly separable data. It means we can always find a hyperplane to separate two types of data completely [21]. That is, we should be able to identify support vectors, which are normal or tumour samples closest to the optimal hyperplane, to separate the two groups of data geometrically. However, what does it mean to find support vectors from a translational bioinformatics viewpoint?

It means that we should be able to find gene markers to conduct phenotype separation for big RNA‐seq data and identify the corresponding support vectors from a visualisation viewpoint. That is, the phenotype separation with few gene markers will provide an alternatively strong support for the correctness of our profile‐marker diagnosis, in addition to shedding light on a systems gene‐marker identification. In other words, we should be able to identify gene markers that can separate big RNA‐seq data spatially if our diagnostic results are correct or at least not subject to overfitting.

To tackle this problem, we present a novel gene‐marker finding approach to demonstrate the linear separability of big RNA‐seq data. The gene‐marker finding algorithm consists of the following steps. We first approximate a corresponding normally distributed data by conducting the transform $Y=\mathit{E}(\log (X+1))/\mathrm{var}(\log (X+1))$. Then, we apply DCA to retrieve true signals of the original big RNA‐seq data for the following differential expression analysis; finally, we employ classic t‐test to look for the differentially expressed genes with the smallest p‐values [31].

Fig. 4 illustrates that the phenotype separations of three data sets by employing their corresponding top three genes with the smallest p‐values. The reason for choosing the top three genes is for the sake of three‐dimensional visualisation, where the expressions of the first, second, and third gene markers are represented by the x, y, and z axes, respectively. Each light/dark grey dot represents a tumour/normal sample in Fig. 4 and it is quite easy to identify the corresponding support vectors to separate the two groups of samples. In other words, we separate two types of data in the subspace generated by the three top‐ranked gene markers. That is, RNA‐seq data is linear separable data under our technology, which strongly indicates the correctness of our proposed profile‐marker method from a visualisation standing point. As such, big RNA‐seq disease diagnosis is actually a linearly separable problem under our technology.

Fig. 4.

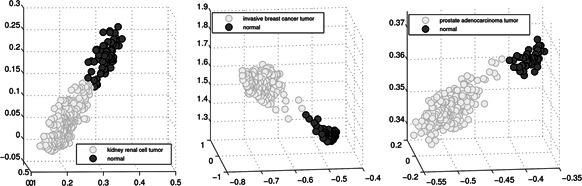
Phenotype separation for big RNA‐seq data sets with identified top three gene markers. Each light/dark grey dot represents a tumour/normal sample. The expressions of the first, second, and third gene markers are represented by the x, y, and z axes, respectively

3.2.1 Represent transcriptome markers by using exon expression data

Moreover, we have used exon expression data to represent a transcriptome marker to further test the effectiveness of our method. The exon expression data of the three data sets have the same number of samples, but a huge number of features compared with their gene expression data sets. For example, the Breast and Kidney data sets have 239,886 exons and the Prostate data has 239,322 exons, which count 1.2 GB, 788 and 566 MB storage, respectively. However, our transcriptome marker attains the identically rivalling‐clinical performance for all three data sets. This is probably because the feature spaces of two different data sets are identical in classification. On the other hand, it suggests that our proposed method can also work quite well for the big data such as exon expression data with at least half gigabytes storage. It further suggests our method demonstrates a favourable sub‐linear property in handling big omics data [32].

4 Discussion and conclusion

It is worthwhile to point out that our transcriptome marker diagnosis relies on the true signals extraction by DCA from big RNA‐seq data. Since we drop splice quantification information in the big data preprocess in this paper for the convenience of computing, we are interested in investigating its role in disease diagnosis in our future work to unveil its genomic root. Moreover, it will be an urgent task for us to collect related clinical‐level information from TCGA database to further enrich our profile‐marker diagnostic results for the sake of deciphering complex disease diagnostic mechanism in a more comprehensive approach. Our experimental results demonstrated that the DCA's parametric tuning works efficiently though they may not be the optimal ones theoretically. It is possible to seek optimally parametric settings in DCA for each proteomic data from an information entropy analysis or Monte Carlo simulation standing point [20, 33]. However, we are not sure such a computing‐demand way is partially worthwhile because some rivalling‐clinical‐level diagnostics have already attained under our current experimental parametric tuning.

In this paper, we present a transcriptome marker approach for disease diagnosis using big RNA‐seq data and demonstrate its advantages by comparing it with its competitive methods. Such a systems approach seems to fit the personalised diagnostics better for its reproducible diagnosis by viewing input data as a profile marker. This is because it can be difficult both biologically and computationally to achieve a reproducible clinical‐level diagnostics for the complex diseases that have usually involved thousands of genes. Our transcriptome marker diagnosis not only avoids the overhead in tedious gene‐marker or network‐marker validation, but also makes the corresponding clinical implementation efficient, which is an essential component in personalised diagnostics.

As we pointed out before, the proposed method demonstrates linear separable performance for all data sets in this paper. Such a result not only demonstrates the correctness of the proposed method from a visualisation viewpoint, but also provides a novel gene‐marker discovery approach for big RNA‐seq data. This is because the gene markers that can separate the whole big RNA‐seq data spatially can be further investigated to find its potential usage in disease diagnosis. The following work can even go through the gene markers to identify its corresponding network markers. As such, our work is both biologically and computationally important. On the other hand, it suggests complicate non‐linear predictive models could not be a desirable choice for big RNA‐seq data. For example, we have applied the feed‐forward deep‐learning model to the Breast data and found almost all the test samples are diagnosed as the majority‐count sample (tumour type) [34].

Though we are quite optimistic to see that our transcriptome marker diagnosis will be a potential candidate to achieve a clinical disease diagnosis from big RNA‐seq data to overcome the reproducibility problem in the traditional methods, rigorous clinical tests are needed urgently to explore such a potential and validate its clinical effectiveness. In our ongoing work, we are working with pathologists to investigate the transcriptome biomarker diagnosis in clinical tests to validate its profile‐marker discovery mechanism [35, 36].