Comparison of adaptation motifs: temporal, stochastic and spatial responses

Abstract

The cells’ ability to adapt to changes in the external environment is crucial for the survival of many organisms. There are two broad classes of signalling networks that achieve perfect adaptation. Both rely on complementary regulation of the response by an external signal and an inhibitory process. In one class of systems, inhibition comes about from the response itself, closing a negative feedback (NFB) loop. In the other, the inhibition comes directly from the external signal in what is referred to as an incoherent feedforward (IFF) loop. Although both systems show adaptive behaviour to constant changes in the level of the stimulus, their response to other forms of stimuli can differ. Here the authors consider the respective response to various such disturbances, including ramp increases, removal of the stimulus and pulses. The authors also consider the effect of stochastic fluctuations in signalling that come about from the interaction of the signalling elements. Finally, the authors consider the possible effect of spatially varying signals. The authors show that both the NFB and the IFF motifs can be used to sense static spatial gradients, under a local excitation, global inhibition assumption. The results may help experimentalists develop protocols that can discriminate between the two adaptation motifs.

1 Introduction

The ability to adjust behaviour in response to changes in the environment is one of the hallmarks of living organisms. In many cases, this requires the capacity to filter out the mean level of signal, thereby allowing the response to focus on the change from these set points. This property, known as adaptation, has long been an area of great interest to biologists.

Adaptation can be partial – for example, in our eye's ability to adjust its sensitivity to changes in ambient light [1] – or perfect. The latter is observed in the chemotactic response of a number of cells, including Escherichia coli bacteria [2, 3] and D ictyostelium discoideum amoebae [4, 5]. Adaptation to chemoattractant stimuli is also perfect in some, though not all, cells of the mammalian immune system. For example, neutrophils exhibit perfect adaptation to step changes in concentration of chemoattractant Formyl‐Methionyl‐Leucyl‐Phenylalanine [6] but the response of fibroblasts to stimulation by PDGF (platelet‐derived growth factor) displays only partial adaptation [7]. Interestingly, chemotaxis in these cells shows much lower efficiency than that of cell types that do show perfect adaptation, and this reduced efficiency is recreated in chemotaxis models that do not include adaptation [8].

Adaptation is related to homeostasis, the ability for systems to remain at constant operating points in response to external perturbations, which is usually associated with negative feedback (NFB) regulation. In fact, it is a well‐known fact in control engineering that if the strength of a NFB loop is increased then the precision of adaptation increases. In particular, if the disturbance is in the form of a step change in magnitude, perfect adaptation is achieved if the gain is infinite. Although this is clearly not possible in general, it can be achieved at steady‐state by implementing an integrator in the feedback loop [9]. Such as a system is the basis of a now widely accepted model, originally proposed by Barkai and Leibler, used to describe the chemosensory system of E. coli [10].

Not all adaptive schemes require NFB. In 1977, Koshland proposed a scheme that achieved perfect adaptation based on complementary feedforward regulation of a response regulator [11]. This scheme, which is usually referred now to as an incoherent feedforward (IFF) loop [12], has been used to describe the regulation of a number of biological systems [13–16].

Since the ubiquitous nature of the adaptive response, recent years has seen a particular focus on the mechanisms by which adaptation can be achieved by simple signalling motifs. By carrying out extensive simulation of all possible three node enzymatic networks, Ma et al. showed that the two schemes described above are essentially the only two that achieve perfect adaptation to step changes in the simulus [17]. However, though the two schemes show adaptive behaviour to step changes in stimulus, their response to other signals can vary. Only now are these differences being appreciated with a particular eye using them to distinguish between these systems experimentally [18, 19]. The goal of this paper is to contrast the relative properties of these two signalling motifs with particular emphasis on the ways that the two systems differ. Our hope is that these differences may be used by experimentalists to design protocols that would help to elucidate the particular nature of the underlying adaptive system.

The rest of the paper is arranged as follows. We first introduce generic forms of the two signalling motifs and study their respective responses to a number of temporal stimuli, including step and ramp changes and their response to the removal of stimuli. We then consider stochastic effects. Finally, we assume that the motifs form part of a spatial signalling scheme. We show that both motifs can be used to detect spatial gradients in the external stimulus under assumptions that that the excitation and inhibition process are local and global, respectively.

2 Results

2.1 Preliminaries: Adaptation to step changes in stimulus levels

We begin by introducing specific forms of the two motifs that we will consider in the analysis. As illustrated in Fig. 1, both schemes take an external signal, whose level (e.g. concentration of a signalling molecule) is denoted by U (t), as the input. Both involve excitation and inhibition signalling processes that are in both inactive (E and I, respectively) and active (E ^★ and I ^★, respectively) forms. We consider the level of E ^★ (t) as the output of the system. In both systems, the external signal activates the excitation process

$$E(t)\stackrel{U(t)}{-⟶}{E}^{\star }(t)$$ (1)

Fig. 1.

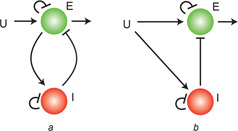
Motifs considered in the analysis

a NFB loop

b IFF loop. Both systems involve complementary regulation of an excitation (E) signal by an external signal (U) and an inhibitory signal (I). The only difference is the way that the inhibition is activated. In the NFB topology, this comes from the excitation. In the IFF loop, this is direct from the external stimulus

In the NFB system, excitation activates the inhibitory signal

$$I(t)\stackrel{E^{\star }(t)}{-⟶}{I}^{\star }(t)$$ (2)

which in turn provides NFB on the excitation

$$E^{\star }(t)\stackrel{I^{\star }(t)}{-⟶}E(t)$$

In the case of the IFF loop, the starting point is the same: we assume a system consisting of excitation (as in (1)) and inhibition signals, driven by an external signal. The main difference is that the external signal activates the inhibitor directly: $I\stackrel{U}{-⟶}{I}^{\star }$.

2.2 Mathematical description

To describe these two motifs mathematically requires that we make assumptions regarding the various processes and their interactions. In practice, the motifs may represent the action of various regulatory processes, which may even be mechanical or electrical rather than biochemical [20]. For simplicity, we will assume that the various signals refer to concentrations of interacting enzymes and that the action of these enzymes follow Michaelis–Menten kinetics. In this case, the concentrations of the active forms of the excitation and inhibition processes are dictated by the differential equations

$${\mathrm{\Sigma }}_{\text{NFB}}=\left\{\begin{array}{c}\frac{\mathrm{d}{E}^{\star }}{\mathrm{d}t}=\frac{K_{1}UE}{K_{M_1}+E}-\frac{K_2{I}^{\star }{E}^{\star }}{K_{M_2}+E^{\star }}\\ \frac{\mathrm{d}{I}^{\star }}{\mathrm{d}t}=\frac{K_3{E}^{\star }I}{K_{M_3}+I}-\frac{K_4{I}^{\star }}{K_{M_4}+I^{\star }}\end{array}\right.$$

where the different terms (e.g. S, E, I, E ^★ and I ^★) all denote the concentrations of the various species. These equations can be simplified considerably.

First, rather than using absolute concentrations, we can write equations describing normalised concentrations. That is, we replace the absolute concentrations (E, E ^★, I and I ^★) with terms describing the fractions of the enzymes in the respective states (e.g. e = E ^★ /(E + E ^★) etc.) with a similar normalisation for the external signal (from U to u).

Second, we make some assumptions regarding the enzyme concentrations relative to the various Michaelis–Menten terms. In particular, we assume that the two reactions regulating the inhibitor are near saturation and the two reactions regulating the excitation process are both in the linear regime. As shown in Appendix 1, these assumptions lead to the following differential equations

$$\frac{\mathrm{d}e}{\mathrm{d}t}=u-ie$$ (3)

$$\frac{\mathrm{d}i}{\mathrm{d}t}=e-k\frac{i}{ϵ+i}$$ (4)

We will usually assume that ε ≪ i so that the fraction in the right‐hand side of (4) is one.

We emphasise that there is a difference in the two steps undertaken here. The first, normalisation, is one purely of mathematical convenience that allows us to reduce the number of variables in the differential equations. It has no effect on the results that follow. The second step makes specific assumptions that guarantee perfect adaptation. If we relax these assumptions, then perfect adaptation will be lost in general.

Proceeding in a similar manner with the IFF motif, we obtain differential equations for the excitation and inhibition processes

$${\mathrm{\Sigma }}_{\text{IFF}}=\left\{\begin{array}{c}\frac{\mathrm{d}{E}^{\star }}{\mathrm{d}t}=\frac{K_{1}UE}{K_{M_1}+E}-\frac{K_2{I}^{\star }{E}^{\star }}{K_{M_2}+E^{\star }}\\ \frac{\mathrm{d}{I}^{\star }}{\mathrm{d}t}=\frac{K_{3}UI}{K_{M_3}+I}-\frac{K_4{I}^{\star }}{K_{M_4}+I^{\star }}\end{array}\right.$$

As shown in Appendix 1, after normalisation, and assuming that the forward reactions (E → E ^★ and I → I ^★) are both at saturation and the reverse reactions (E ← E ^★ and I ← I ^★) are both linear, these equations can be can be replaced with the system described by

$$\frac{\mathrm{d}e}{\mathrm{d}t}=u-ie$$ (5)

$$\frac{\mathrm{d}i}{\mathrm{d}t}=k(u-i)$$ (6)

In this case, the variable k should be smaller than one. If it were not, then the inhibitor concentration would reach steady‐state faster than the excitation. Hence, the equation for the excitation process would lead to i (t) ≃ u (t), which would mean that e (t) would never move far from its equilibrium value. However, if k is small, then e (t) ≃ u (t)/i (t). In this case, an increase in u (t) leads to a large transient [21], allowing the system to detect any change in the concentration of the external signal.

Our simulations will assume that k = 1 in both (4) and (6) and that the stimulus is u = 1. This makes the steady‐state of the excitation processes the same for both systems and also makes sure that the two time scales are comparable.

2.3 Demonstrating perfect adaptation

The property of perfect adaption is usually defined in terms of the response to a step change in the concentration of the external signal. To show that both systems adapt perfectly to constant changes in the concentration of the stimulus, we assume that u (t) ≡ u ₀ ≠ 0, a constant. In this case, if the NFB system reaches steady state, then

$$e_{\text{ss}}=\frac{2k}{1+\sqrt{1+4kϵ/u_0}}\simeq \frac{k}{1+kϵ/u_0}\simeq k$$

and i _ss = u ₀ /k. Thus, the steady‐state level of activity is constant and, following a change to a different constant value of u, the system eventually settles to the same level of e; see Fig. 2 a. Note that we require that kε ≪ u ₀ hold for our assumption that ε ≪ i be valid. In particular, if u ₀ = 0, then the system has a unique equilibrium (with e _ss = i _ss = 0) that differs from that which arises from non‐zero values of the external signal.

Fig. 2.

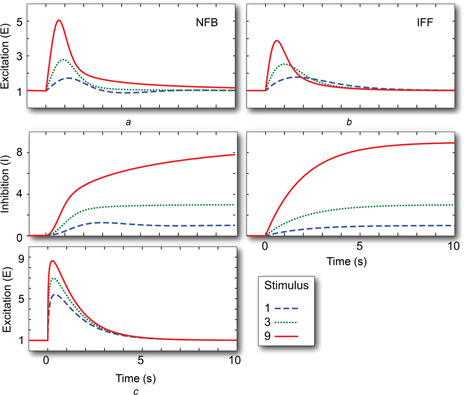
Adaptation to step changes

Shown are the excitation and inhibition signals following an increase from u = 0.1 to 1 (dashed), 3 (dotted) and 9 (solid) lines for the NFB (a) and IFF (b) motifs. (c) The excitation response for the IFF in which the inhibitor acts as an enzyme inhibitor; see (7)

In the case of the IFF, the analysis is similar. If u ₀ ≠ 0 is constant, then at steady‐state, i _ss = u ₀ and e _ss = u ₀ /i _ss = u ₀ /u ₀ = 1. Thus, the steady‐state level is also constant; see Fig. 2 b. In this motif, if the input signal is zero, then the inhibitor drops to zero and (5) does not have a unique equilibrium.

2.4 Uniqueness

Although the two sets of equations given above satisfy the requirements of the two schemes of Fig. 1, they are by no means the only way of implementing these systems guaranteeing perfect adaptation. For example, the IFF considered here ((5) and (6)) makes no distinction between response regulator and excitation processes though these are usually assumed to be distinct elements [11, 17, 21–23].

In fact, the process of information from external signal to E and I could take a number of different paths. For example, in the IFF, instead of a direct connection from U to E and I, a number of intermediate steps can exist, which could lead to the following differential equations

$$\begin{array}{rl}\frac{\mathrm{d}{e}_1}{\mathrm{d}t}& =u-e_1\\ \frac{\mathrm{d}{e}_j}{\mathrm{d}t}& =e_{j-1}-e_j,j=2,\dots ,n-1\\ \frac{\mathrm{d}{e}_n}{\mathrm{d}t}& =e_{n-1}-i_m{e}_n\\ \frac{\mathrm{d}{i}_1}{\mathrm{d}t}& =k_1(u-i_1)\\ \frac{\mathrm{d}{i}_j}{\mathrm{d}t}& =k_j(i_{j-1}-i_j),j=2,\dots ,m\end{array}$$

These changes do not affect the property of perfect adaptation, but do affect the nature of any transients and other features of the response, such as noise propagation. Similar modifications can be made to the NFB motif.

We also note that, in both motifs, the inhibitor is implemented as an enzyme that accelerates the down‐regulation of the excitation process. An alternative formulation is to assume that the inhibition process acts as an enzyme inhibitor (either competitive or allosteric). In this case, the effect of inhibition appears as

$$\frac{\mathrm{d}e}{\mathrm{d}t}=\frac{u}{ϵ+i}-e$$ (7)

instead of (3) or (5). This change also has no effect on the steady‐state response of the system but does affect the transient behaviour. In particular, in the original formulations, the speed at which the transient response decays depends on the magnitude of the change in the level of the stimulus, with larger stimuli leading to greater peaks but faster decays (Figs. 2 a and b). This follows from the fact that in both (3) and (5), the variable i acts as the rate constant that dictates the response of the system. Since the steady‐state level of i depends on the concentration of the external signal, greater signals lead to faster decays of the transient. However, if we implement the inhibition as in (7), then the rate constant does not depend on the level of the stimulus; see Fig. 2 c.

Other changes are possible. For example, in the NFB or IFF, the sign of the interconnections could be switched by having U inhibit I and I positively regulate E. Once again, these modifications do not change the steady‐state behaviour, but do affect transient behaviour. Faced with this large number of possibilities, we will keep the analysis tractable and restrict ourselves to the simplest formulations ((3)–(6)).

2.5 Adaptation to ramps and other signals

Having established that both systems achieve perfect adaptation to steady (non‐zero) signals, we now consider other stimuli. An alternative way of viewing the adaptation properties of the system is to consider the transfer function between the stimulus and response after linearisation [24].

This approach assumes that changes in the stimulus and the ensuing signals are sufficiently small that they do not deviate much from the steady‐state [24]. Thus, in the non‐linear differential equation, any second order or higher deviations are ignored, resulting in a linear differential equation. In particular, assume that the different signals are given by changes away from their equilibria: u (t) = u ₀ + δ_u (t), e (t) = e _ss + δ_e (t) and i (t) = i _ss + δ_i (t). In both motifs, the linearised equation for the excitation process is

$$\frac{\mathrm{d}{\delta }_e}{\mathrm{d}t}={\delta }_u-e_{\text{ss}}{\delta }_i-i_{\text{ss}}{\delta }_e$$

Whereas the linearised inhibitor equation (assuming ε = 0) for the NFB is

$$\frac{\mathrm{d}{\delta }_i}{\mathrm{d}t}={\delta }_e$$

for the IFF, the equation is already linear. In terms of the deviation variables, it is

$$\frac{\mathrm{d}{\delta }_i}{\mathrm{d}t}=k({\delta }_u-{\delta }_i)$$

These equations describe the temporal evolution of the variables. A common technique for studying such linear differential equations is by taking Laplace transforms of the linearised variables [24]. In this case, the ratio between the Laplace transforms of the response and stimulus is termed the transfer function and is a measure of how the system transforms dynamic stimuli. In this case, we obtain the following two transfer functions

$$G_{\text{NFB}}(s)=\frac{s}{s^2+(u_0/k)s+k},$$

and

$$G_{\text{IFF}}(s)=\frac{s}{(s+u_0)(s+k)}$$

where the variable ‘s’ is the Laplace‐transform variable. It is clear that both systems exhibit a ‘zero’ at zero – that is, the variable s appears alone in the numerator of both transfer functions and G _NFB (0) = G _IFF (0) = 0. This is a hallmark of integral control mechanisms [9, 22, 25] and shows that the system is performing temporal differentiation. Thus, perfect adaptation can be viewed as differentiation of constant perturbations or disturbances in the input which leads to zero perturbations away from the steady‐state output. Moreover, the presence of a quadratic polynomial in the denominator of both transfer functions shows that this differentiation is accompanied by low‐pass filtering. This low‐pass filtering is an important signal processing element in a number of adaptive signalling systems [26–28].

Continuing with the linear view of the system, it is well known that if a ramp signal is applied to transfer functions with a zero at zero (such as G _NFB and G _IFF), the output will eventually settle to a constant non‐zero value that reflects the rate of increase in the stimulus. This follows because the derivative of a ramp is a step. To examine whether this is the case for these two systems, we considered the response of the two systems of non‐linear differential equations to linearly increasing concentration of: u (t) = αt, where the variable α denotes the rate of increase. As shown in Fig. 3, the two schemes led to considerably different responses. In both cases, the systems settled to a constant level of activity (concentration of e). However, in the NFB, the level differed depending on the rate of growth of the stimulus. In the IFF, this was the same for all rates considered.

Fig. 3.

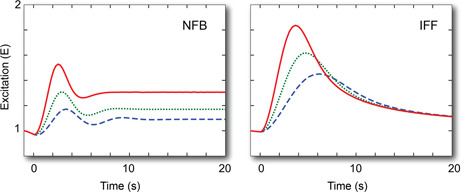
Response of linearly growing stimuli for the NFB (a) and IFF (b) motifs

Initial concentration has u = 0.1 and, after t = 0, grows as αt where α = 1 (dashed), 3 (dotted) and 9 (solid) lines

To explain the origin of this discrepancy, we analyse the different equations. We first consider the response of the NFB motif. Suppose that the system settles onto a constant level of excitation, that is, e (t) = e ₀. From the equation for the inhibitor

$$\frac{\mathrm{d}i}{\mathrm{d}t}=e_0-k$$

which, after integration, results in i (t) = (e ₀ − k) t. Replacing this into the equation for the excitation yields

$$\frac{\mathrm{d}e}{\mathrm{d}t}=\alpha t-(e_0-k)e_{0}t$$

and this is zero, since e (t) is constant. Thus, solving for e ₀ yields

$$e_0=\frac{1}{2}(k+\sqrt{k^2+4\alpha })$$

It follows that as the system settles to a constant, the level of activity must depend on the input signal, implying that the system does not adapt perfectly to ramp inputs, as seen in Fig. 3 a. If we consider input signals of higher order, for example, u (t) = αt ², we can quickly see that e (t) cannot settle into a constant value, but rather must grow unboundedly. These results are consistent with the transfer‐function (linear) view of the system.

In contrast, the IFF system does adapt to ramps and higher order signals [29]. To see this, note that the equation for the inhibitor is linear, so that it can be easily solved. In the case of the ramp

$$i(t)=\alpha \left(t-\frac{1}{k}(1-{\mathrm{e}}^{-kt})\right)=u(t)-\frac{\alpha }{k}(1-{\mathrm{e}}^{-kt})$$

This can be replaced into the equation for e (t) to obtain a general solution. However, as this equation is also linear (with time‐varying coefficients) and we are only interested in the long‐term behaviour, the equation for e (t) simplifies to

$$\frac{\mathrm{d}e}{\mathrm{d}t}\simeq s(1-e)$$ (8)

for large t and this has steady‐state solution with e = 1 – the same level of activity obtained in response to constant stimuli! The analysis can be carried out for more complex signals. In particular, if the input is given by u (t) = αtⁿ , then, on long time‐scales, i (t)≃u (t) and (8) still holds.

There is another way of understanding why the IFF but not the NFB adapts to non‐constant signals without explicitly solving the equations. In the IFF, excitation approaches the ratio of the external stimulus over the inhibition, which itself approaches the stimulus; that is, e (t) ≃ u (t) i (t) and i (t) ≃ u (t). The linear nature of the inhibition equation guarantees that the latter will hold for signals that grow. Hence e (t) ≃ ‘constant’. The NFB inhibitor equation does not have this flexibility.

The fact that the transfer function G _IFF does not accurately predict the response of this motif to ramp inputs should not be surprising as the linearlisation is carried out about a constant operating point – an assumption that is clearly violated with these stimuli.

2.6 Response to the removal of signal

We next seek to determine what happens to the systems if the stimulus is removed – does the system de‐adapt? That is, does the system return to the same steady‐state value irrespective of the starting point?

We assume that, at time t = 0, the systems are at an adapted state assuming a constant level u ₀. Thus, the NFB has e (0) = k and i (0) = u ₀ /k and the IFFL has e (0) = 1 and i (0) = u ₀. At this point in time, the stimulus is removed, so that u (t) = 0 for t > 0. Simulations of the two motifs show quite similar responses. In both schemes, the inhibitor decreases from its steady‐state value; Fig. 4. In the NFB, this decrease is approximately linear, at least while i ≫ ε. In the IFF, the decay is exponential. In both systems the excitation appears to reach zero steady state when the initial condition had large inhibitor concentration (u ₀ = 3 or 9), but appears to plateau when the original stimulus was small (u ₀ = 1).

Fig. 4.

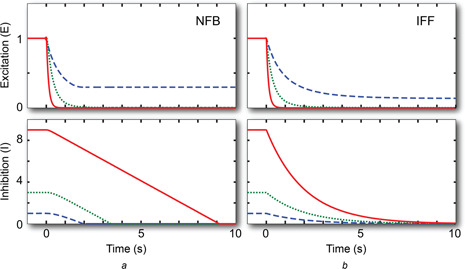
De‐adaptation following complete removal of the stimulus

Initial condition assumes that the system was at steady state for an external concentration u = 1 (dashed), 3 (dotted) and 9 (solid) lines for both the NFB (a) and IFF (b) motifs

To explain this behaviour, we consider the equation for the excitation in the absence of stimulus

$$\frac{\mathrm{d}e}{\mathrm{d}t}=-ei,e(0)=k$$

Clearly, the only possible equilibria have e (t) = 0 and/or i (t) = 0. Consider first the IFF motif. In this case, the inhibitor concentration obeys the differential equation

$$\frac{\mathrm{d}i}{\mathrm{d}t}=-ki,i(0)=u_0$$

which has the solution i (t) = u ₀ exp(−kt). Thus, the excitation concentration follows

$$\frac{\mathrm{d}e}{\mathrm{d}t}=-u_0\text{exp}(-kt)e,e(0)=u_0$$

whose solution is

$$e(t)=u_0\text{exp}\left(\frac{u_0}{k}(\text{exp}(-kt)-1)\right)$$

Note that, as t increases, the response approaches e _ss = u ₀ exp(−u ₀ /k), thus, the system does not de‐adapt perfectly after complete removal of the signal. Rather, its steady‐state value is a biphasic function of u ₀ peaking when u ₀ = k.

For the NFB, as i (t) the assumption i (t) ≫ ε will eventually be violated. For this reason, we no longer assume that e ≪ i and work with a non‐zero ε in (4). The presence of ε ≠ 0 ensures that, if i (t) approaches zero, then the right‐hand term goes to zero. Moreover, if e (t) approaches zero, then i (t) cannot cross zero. In fact, it can be shown analytically that e (t) does go to zero; see Appendix 2. In particular, this analysis shows that the system settles to a unique equilibrium with e _ss = i _ss = 0 which does not depend on the starting point. However, because the inhibitor concentration acts as the rate constant for decay of e (t), this decay can be quite slow. In our simulations, the concentrations of e (t) and i (t) were approximately 0.15 and 10⁻⁴, respectively, after 10,000 s. Thus, though the system decays to zero, the vanishingly slow rate at which this decay takes place makes it impractical for distinguishing between the two motifs.

We now consider the situation in which, following initial stimulation, the system is not allowed to reach steady state before the stimulus is removed. In this case, the stimulus can be seen as a pulse [30]. Here we consider two possibilities. In the first, the system starts and ends at a small concentration u ₀ = 0.1 and a pulse of size u ₁ = 1 is applied for varying length before returning the stimulus to u ₀; see Figs. 5 a and c. The second case assumes that u ₀ = 0; see Figs. 5 b and d. In both systems, the u ₀ = 0.1 stimulus ensures that the systems return to steady state. Interesting, the NFB shows oscillatory behaviour in its return to the prestimulus level of activity. In contrast, the recovery of the IFF is monotonic. In both systems, but particularly for the IFF, the recovery of the system to longer pulses is slower. This can be explained by the higher level of inhibition reached in both systems following longer stimulation.

Fig. 5.

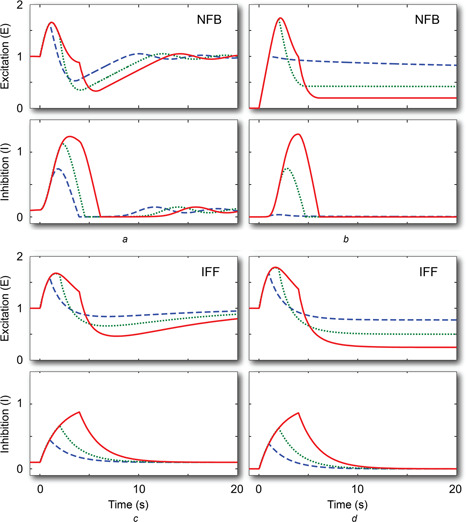
Pulse responses

In the left column, the stimulus goes from u = 0.1, changes to u = 1 at time 0 and returns to 0.1 after T = 1 (dashed, blue), 2 (dotted, green) and 4 (solid, red) seconds. The right column assumes that the ‘low’ signals are at u = 0. Panels a and b use the NFB motif; panels c and d use the IFF motif

The appearance of oscillatory behaviour in the pulse response of the NFB motif, but not in IFF, can be explained by the form of the denominators of the two transfer functions given above. In G _NFB, the denominator will have roots that are complex when u ₀ is small, which is the case when the stimulus is removed. The complex roots lead to oscillatory behaviour [25]. In G _IFF, both roots are real regardless of the value of u ₀, and this prevents oscillatory behaviour.

When considering the complete removal of the stimulus (u ₀ = 0) following the pulse, we see that neither system appears to return to the starting point (although, as mentioned above, we would expect that the NFB would eventually do so). In both cases, longer stimuli lead to greater recovery towards the initial point. This can be explained by the lower level of accumulation of the inhibitor: short pulses lead to low accumulation of i, which means that the rate constant for e is smaller and hence recovery is slower.

2.7 Effects of stochastic signalling

In practice, deterministic models such as those considered here are adequate for describing chemical reactions in which the number of interacting molecules and the reaction volume is large. In other situation, stochastic models are needed [31]. There are a number of ways of describing such systems. Here we use the Langevin approach [32, 33]. In this case, the deterministic equations above can be replaced by

$$\begin{array}{rl}\frac{\mathrm{d}e}{\mathrm{d}t}& =u-ei+\sqrt{(u+ei)}{n}_e(t)\\ \frac{\mathrm{d}i}{\mathrm{d}t}& =e-k+\sqrt{(e+k)}{n}_i(t)\end{array}$$

for the NFB and, for the IFF

$$\begin{array}{rl}\frac{\mathrm{d}e}{\mathrm{d}t}& =u-ei+\sqrt{(u+ei)}{n}_e(t)\\ \frac{\mathrm{d}i}{\mathrm{d}t}& =k(u-i)+\sqrt{k(u+i)}{n}_i(t)\end{array}$$

We see that the first terms in the right‐hand side of these equations are the same as in the deterministic equations. The functions n_e (t) and n_i (t) represent independent, zero‐mean Gaussian white noise processes. Thus, then square root terms in front of these signals dictate the variance in the fluctuations around the mean (which are given by the solutions of the deterministic equations.)

We carried out a series of stochastic simulations of the step responses for both systems; Fig. 6. For simulations in which the size of the signal change was small, the mean level of the response matched that of the deterministic equations, showing perfect adaptation. The standard deviation was in the order of 15–20%. In these cases the two systems behaved quite similarly. However, as the size of the step increased, the size of the fluctuations increased. This was also true of the mean level of signal for sufficiently large stimuli (u ₀ > 20, not shown). These increases were more accute in simulations of the IFF motif than those of the NFB. Moreover, in the IFF, the excitation process appeared to undergo a series of fast oscillations. These may represent stochastic resonances, a frequently observed behaviour of non‐linear stochastic systems [34].

Fig. 6.

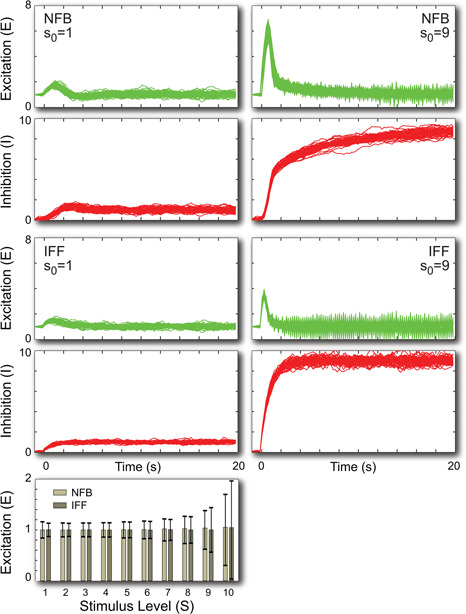
Stochastic response to step changes

In the left column, the stimulus goes from u = 0.1, changes to u ₀ = 1 or u ₀ = 9 at time 0. The time traces show individual responses from 20 simulations for each case. The bar graph shows the mean level and standard deviations at steady state (t = 20 s) for 10,000 simulations at various signalling levels. The equations were solved assuming a noise variance of σ ² = 0.01 with a step size of 0.2 s using the Euler‐Maruyama algorithm [33]

Analysis of the equations suggests a possible reason for the different behaviours. In the NFB, the variance in the inhibitor equation depends on e + k = k + k = 2k which is independent of the level of the external signal. In the IFF, however, the variance depends on k (u + i) = k (u + u) = 2ku which does depend on the level of the external signal. When u = 1, the difference is not observed. However, as u is increased, the difference between the two motifs becomes more significant.

2.8 Response to spatially graded signals

Finally, we assume that two motifs are part of a spatial sensing mechanism. This is motivated by models used to describe the chemotactic signalling mechanism of eukaryotic cells [21, 35, 36]. Stimulation by spatially uniform signal triggers a transient response before the systems setttle to their homogeneous steady‐state behaviour. This adaptation behaviour is identical to that described above. However, application of a spatially graded signal eventually leads to a persistent signal with higher activity facing the side of the gradient [35, 37].

To achieve this behaviour, a number of local‐excitation, global‐inhibition (LEGI) models have been proposed based on the IFF framework [21, 36, 38]. The idea is that the excitation process is local, and obeys the same equation as above, but indexed by the spatial dimension, which we assume to be θ ∈ [−pi, π) in a periodic, one‐dimensional model of the environment

$$\frac{\partial e}{\partial t}=u-ei$$

The term ‘local’ refers to the fact that the excitation does not diffuse and hence its steady‐state value reflects the local level of the external signal. In contrast, the inhibitor is global, by which we mean that it is free to diffuse in the enviroment with diffusion coefficient D

$$\frac{\partial i}{\partial t}=u-i+D\frac{{\partial }^{2}i}{\partial {\theta }^2}$$

The ‘global’ designation assume that diffusion is sufficiently large that, at steady‐state, the inhibitor concentration does not depend on the angle θ. In practice, both molecules can diffuse. All that is needed is that the dispersion of the inhibitor is greater than that of the excitation. It is also worth pointing out the mechanism does not depend on the spatial dimension or particular boundary assumptions [39]. For simplicity, we assume periodic boundary conditions.

Suppose that the external gradient satisfies a simple sinusoidal relationship

$$u(\theta )=u_0+u_1\cos \theta ,-\pi \le \theta \le \pi$$

where u ₀ > u ₁ > 0 to ensure that the concentration is positive everywhere. As shown previously [21, 39], the steady‐state behaviour can be obtained by solving the steady‐state diffusion equation using a Fourier series decomposition of the inhibitor. In particular, it has only zeroth and first cosine modes

$$i_{\text{ss}}(\theta )=u_0+\frac{u_1}{1+D}\cos \theta$$

At steady‐state

$$e_{\text{ss}}(\theta )=\frac{u(\theta )}{i_{\text{ss}}(\theta )}=\frac{u_0+u_1\cos \theta }{u_0+(u_1/(1+D))\cos \theta }$$

A truly global inhibitor (D → ∞) leads to a spatially invariant inhibition signal i _ss = u ₀ and response

$$e_{\text{ss}}(\theta )=1+\frac{u_1}{u_0}\cos \theta$$

Note how the response depends on the ‘ratio’ of local signalling over mean level of signal. This fact can be used to test for the presence of a LEGI mechanism. In particular, if the two components of the gradient (u ₀ and u ₁) are altered independently, the model predicts that the response should depend on the ratio between these two variables. This experiment was carried out by measuring the chemoattractant‐induced response of D. discoideum cells and the results agreed with the LEGI prediction [37].

We next considered the possible use of the NFB motif as a basis for a LEGI mechanism. In particular, we assume that the NFB scheme has a spatial profile mimicking that above

$$\frac{\partial e}{\partial t}=u-ei$$ (9)

$$\frac{\partial i}{\partial t}=e-k+D\frac{{\partial }^{2}I}{\partial {\theta }^2}$$ (10)

We would expect that, if i is truly global, the divergence will be zero in which case e would track k. This would make the steady‐state values of both e and i spatially homogeneous, which would make it impossible to satisfy the first equation. However, as shown in Appendix 3, we can show that both e _ss (θ) and i _ss (θ) follow the external gradient, but that the dependence of e _ss is greater than that of i_ss (θ) leading to a persistent signal facing the gradient.

To contrast the spatial behaviour of the two motifs, we simulated the systems, as shown in Fig. 7. In both systems the concentration of the excitation and inhibition processes formed gradients that point in the direction of the external gradient. Moreover, the gradient sensing mechanism improved as the diffusion coefficient increased and the concentration of the inhibitor became spatially homogeneous.

Fig. 7.

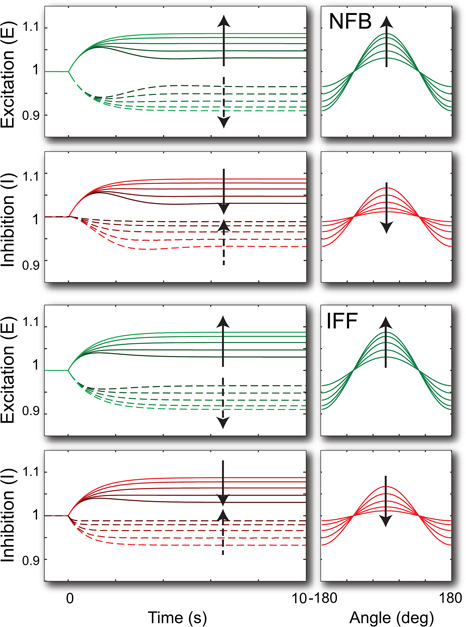
Response to graded signals

Stimulus, initially at u = 1, changed to u = 1 + 0.1cos(θ) at time t = 0. Shown are the responses at θ = 0 (solid line) and θ = π (dotted line). The different curves represent the responses for varying diffusion coefficients, from D = 100, 200, 400, 800 to 1600. The arrow points towards the simulations with increasing diffusion coefficient. The panels on the right show the steady‐state concentration across θ = [−π, π). To simulate the spatial component, the system was spatially discretised using 90 grid points

3 Discussion

A common refrain heard by theoretical biologists from their experimental brethren is: ‘how do I test your model?’ In the case of systems achieving adaptation, where two different classes of systems appear to achieve the same goal, this presents a particularly challenging problem. However, as shown here, the systems’ responses to other stimuli can help to differentiate between the two classes of systems and also among different manifestations of the two networks.

The response of the two classes of systems to step changes of different magnitude led to similar results, in which the height of the transient was largely determined by the size of the stimulus. As such, experiments by which the magnitude of the stimulus is changed would not help to discriminate between the two systems. However, these experiments can help to differentiate between implementations of the networks that differ as to how the inhibitor acts; compare Eq. 2 b,c. Experimenally, this fact was used to elucidate the nature of the chemotactic signalling network of D. discoideum cells. Takeda et al. stimulated D. discoideum cells using varying chemoattractant concentrations and observed that the rate of decay increased with the concentration of chemoattractant [40]. In doing so, they concluded that the form of (3) rather than (7) more closely matched their experimental results.

The contrasting behaviours of the two motifs when responding to ramp inputs could be used to differentiate between the two motifs [18]. Such experiments have been carried out for the chemotactic responses of bacteria and amoebae. In particular, whereas E. coli was found not to adapt to ramps [41, 42], D. discoideum cells do [43]. These experiments suggest that E. coli uses a signalling mechanism based on the NFB motif to adapt (as previously postulated [10]), but D. discoideum relies on an IFF mechanism (as suggested previously [21, 35, 40]). It should be noted that, in the case of E. coli, the ramps are not linearly increasing as considered here, but exponentially increasing so as to compensate for the non‐linear effect of receptor signalling [28].

Biologically, the ability to distinguish between ramps of different rates would be advantageous to E. coli cells, which rely on a temporal sensing mechanism to guide their movement. These cells require the ability to discern whether the concentration of chemoattractant that they are encountering is increasing or decreasing and, if so, by how much. Thus, temporal differentiation affords them a measure of the temporal gradient and the adaptation observed in the non‐physiological conditions of step changes is but a consequence of this differentiation. Were they to rely on an IFF mechanism to sense chemoattractants, the cells would not be able to distinguish between chemoattractant gradients of varying strength, reducing the effectiveness of their chemotactic ability. In contrast, D. discoideum cells do not rely on a temporal sensing, but rather use adaptation to adjust the sensitivity of their spatial sensing mechanism so that the response depends on the relative, not absolute gradient [37]. Thus, the ability to discern among ramps of varying steepness is not particularly advantageous to these cells.

The stochastic behaviour of both systems points to a potential problem in studying adaptive systems: in practice, the adaptive behaviour is seen only in the mean signalling level. This is especially important if the number of signalling molecules is small so that large relative variances away from the mean are to be expected. Moreover, if the adaptive mechanism feeds into a non‐linear system that may include thresholds [8, 21, 43–45], the greater variance could lead to higher probability of crossing the threshold, causing the overall response to depend on the level of stimulus. As an example, the adaptation mechanism in D. discoideum and neutrophils is believed to signal to an excitable network which eventually triggers actin polymerisation [8, 44, 46, 47]. Our analysis suggests that, as the concentration of the external signal increases, the mean level of response will adapt, but fluctuations will rise. This increase would lead to more frequent firings of the excitable network resulting in more actin polymerisation and hence greater motility. This klinokinesis, or increase in random migration in response to increases in stimulus intensity has been reported in neutrophils and D. discoideum cells [48, 49].

As noted above, within the two motif classes, there is no unique system representation and that certain aspects of the response depend on the particular choice made. It is worth asking whether our conclusions would hold if we consider other forms of the IFF and NFB motifs. We expect that steady‐state responses would not show much difference. Thus, other NFB models would still not adapt to ramp inputs, but IFF models would. However, properties related to the transient behaviour – including the noise response – would be greatly influenced by the particular implementation of the motif. One such property is fold‐change detection (FCD), in which the complete response (transient and steady‐state) depends only on the relative rather than absolute change in the stimulus concentration. There are examples of NFB and IFF circuits that achieve FCD, and others that do not [50–52]. Moreover, the difference can be as subtle as changing the nature of the inhibition. For example, the IFF described by (5) does not achieve FCD, but when modified to (7), does [51].

In this paper, we have focused on changes that can be effected through the external stimulus. However, powerful new experimental techniques are being developed that can alter the systems components directly can also shed some light [19]. For example, changing the feedback component directly would affect the NFB, but not the IFF system. We also not that, in interpreting these results, it is important to understand that the particular biosensor used may not properly represent the system whose properties we wish to investigate. For example, in D. discoideum, chemoattractant receptor signalling is mediated through a G‐protein coupled receptor, which shows no sign of adaptation [53]. The first element downstream of the G‐proteins that shows an adaptive behaviour appears to be Ras [40]. However, it is also known that Ras takes part in the excitable system, with non‐linear dynamics including all‐or‐nothing responses and a refractory period [44, 46, 47]. Thus, equating the response of Ras with that of the adaptive network may lead to incorrect interpretations about this system.

5.1 Appendix 1: Deriving the equations describing both motifs

5.1.1 NFB motif

We begin by performing simple normalizations. Our starting point is the enzymatic equations that assume Michaelis–Menten kinetics. We first define the total amount of enzymes, and variables $\hat{e}$ and $\hat{ı}$ that describe the fraction of total enzymes that are in the active state

$$\begin{array}{rl}{E}_T& =E(t)+E^{\star }(t),I_T=I(t)+I^{\star }(t)\\ & \hat{e}=E^{\star }/E_T,\hat{\iota }=I^{\star }/I_T\end{array}$$

Second, we normalise each of the Michaelis–Menten constants relative to their respective enzyme concentrations

$$\begin{array}{rl}{k}_{m_1}& =K_{M_1}/E_T,k_{m_2}=K_{M_2}/E_T\\ k_{m_3}& =K_{M_3}/I_T,k_{m_4}=K_{M_4}/I_T\end{array}$$

Note that since the constants have dimensions of concentration, these new variables are all non‐dimensional. Third, we normalise the various enzymatic rates (K ₂, K ₃ and K ₄)

$$k_2=K_2{I}_T/E_T,k_3=K_3{E}_T/I_T,k_4=K_4/I_T$$

Finally, we normalise the stimulus concentration: $\hat{u}=K_{1}U/E_T$.

Making these substitutions in the differential equations for ∑_NFB, leads to the following non‐dimensional equations

$$\begin{array}{rl}\frac{\mathrm{d}\hat{e}}{\mathrm{d}t}& =\frac{\hat{u}(1-\hat{e})}{k_{m_1}+1-\hat{e}}-\frac{k_2\hat{ı}\hat{e}}{k_{m_2}+\hat{e}}\\ \frac{\mathrm{d}\hat{ı}}{\mathrm{d}t}& =\frac{k_3\hat{e}(1-\hat{ı})}{k_{m_3}+1-\hat{ı}}-\frac{k_4\hat{ı}}{k_{m_4}+\hat{ı}}\end{array}$$

We now look for conditions in which perfect adaptation is achieved – that is, when the steady‐state of $\hat{e}$ is independent of the level of the external signal. This can be accomplished when the two reactions regulating the inhibitor are near saturation. That is, $k_{m_3}\ll 1-\hat{ı}$ and $k_{m_4}\ll \hat{ı}$. In this case

$$\frac{\mathrm{d}\hat{ı}}{\mathrm{d}t}\simeq k_3\hat{e}-k_4$$

which guarantees that, at steady‐state, ${\hat{e}}_{\text{ss}}=k_4/k_3$, a constant. Note that in this case

$${\hat{ı}}_{\text{ss}}=\hat{u}\times \frac{(1-{\hat{e}}_{\text{ss}})}{k_{m_1}+1-{\hat{e}}_{\text{ss}}}\times \frac{k_{m_2}+{\hat{e}}_{\text{ss}}}{k_2{\hat{e}}_{\text{ss}}}\propto \hat{u}$$

That is, the steady‐state level of the inhibitor is proportional to the external signal. It is important to note that if the saturation assumptions are violated, then perfect adaptation does not hold. In particular, if the external signal is zero, then $\hat{ı}=0$ in which case the assumption is violated. In what follows, we also assume that the reactions regulating the excitation are both linear

$$k_{m_1}\gg 1-e_{\text{ss}},\text{and}{k}_{m_2}\gg e_{\text{ss}}$$

These assumptions are not necessary for achieving perfect adapation, but they simplify the analysis below.

We carry out one last simplification. If we define

$$e=\frac{k_2{k}_3}{k_{m_2}}\hat{e},i=\frac{k_2}{k_{m_2}}\hat{ı},u=\frac{k_2{k}_3}{k_{m_1}{k}_{m_2}}\hat{u}$$

and $k=k_2{k}_4/k_{m_2}$, then

$$\begin{array}{rl}\frac{\mathrm{d}e}{\mathrm{d}t}& =u-ie\\ \frac{\mathrm{d}i}{\mathrm{d}t}& =e-k\end{array}$$

We use this formulation in the main text.

5.1.2 IFF motif

Proceeding as above, we write

$$\begin{array}{rl}\frac{\mathrm{d}\hat{e}}{\mathrm{d}t}& =\frac{\hat{u}(1-\hat{e})}{k_{m_1}+1-\hat{e}}-\frac{k_2\hat{ı}\hat{e}}{k_{m_2}+\hat{e}}\\ \frac{\mathrm{d}\hat{ı}}{\mathrm{d}t}& =\frac{k_3^{\prime }\hat{u}(1-\hat{ı})}{k_{m_3}+1-\hat{ı}}-\frac{k_4\hat{ı}}{k_{m_4}+\hat{ı}}\end{array}$$

where $k_3^{\prime }=k_3/K_1$. As above, we make some assumptions that guarantee perfect adapation. Assume that the forward reactions are both at saturation: $k_{m_1}\ll 1-\hat{e}$ and $k_{m_3}\ll 1-\hat{ı}$. In contrast, the reverse reactions are both linear: $k_{m_2}\gg \hat{e}$ and $k_{m_4}\gg \hat{ı}$ leading to

$$\begin{array}{rl}\frac{\mathrm{d}\hat{e}}{\mathrm{d}t}\simeq & \hat{u}-\frac{k_2}{k_{m_2}}\hat{ı}\hat{e}\\ \frac{\mathrm{d}i}{\mathrm{d}t}\simeq & k_3^{\prime }\hat{u}-\frac{k_4}{k_{m_4}}\hat{ı}\end{array}$$

At steady state

$${\hat{e}}_{\text{ss}}=\frac{k_{m_2}}{k_2}\times \frac{\hat{u}}{{\hat{ı}}_{\text{ss}}},\text{and}{\hat{ı}}_{\text{ss}}=\frac{k_3^{\prime }{k}_{m_4}}{k_4}\hat{u}$$

which leads to

$${\hat{e}}_{\text{ss}}=\frac{k_4{k}_{m_2}}{k_2{k}_3^{\prime }{k}_{m_4}}$$

once again showing that the steady‐state value is independent of the level of the external signal. As above, note that if the external signal is zero, the assumptions will not be satisfied. In particular, ${\hat{ı}}_{\text{ss}}=0$, but there is no unique equilibrium for ${\hat{e}}_{\text{ss}}$.

We can simplify the system by defining

$$e=\frac{k_2{k}_3^{\prime }{k}_{m_1}{k}_{m_4}}{k_{m_2}{k}_{m_3}}\hat{e},i=\frac{k_2}{k_{m_2}}\hat{ı},u=\frac{k_2{k}_3^{\prime }{k}_{m_4}}{k_{m_2}{k}_{m_3}}\hat{u}$$

and $k=k_4/k_{m_4}$; then

$$\begin{array}{rl}\frac{\mathrm{d}e}{\mathrm{d}t}& =u-ie\\ \frac{\mathrm{d}i}{\mathrm{d}t}& =k(u-i)\end{array}$$

We use this formulation of the IFF in the analysis.

5.2 Appendix 2: Stability analysis of the NFB system in the absence of stimuli

To show that that NFB system reaches steady‐state in the absence of an external stimulus we use LaSalle's invariance principle [54]. We define the function V = (1/2)e ². Its derivative along the differential equations is given by

$$\frac{\mathrm{d}V}{\mathrm{d}t}=e\frac{\mathrm{d}e}{\mathrm{d}t}=-e^{2}i\le 0$$

since e (t) ≥ 0 and i (t) ≥ 0. If $\dot{V}\equiv 0$, then either e ≡ 0 or i ≡ 0. If the latter, then di /dt ≡ 0 in which case e (t) ≡ 0 as required.

5.3 Appendix 3: Derivation of the LEGI response of the NFB motif

To carry out the analysis, we let the steady‐state concentrations of the excitation and inhibition processes be given by

$$e_{\text{ss}}(\theta )=e_0+\sum _{n\ge 1}{e}_n\cos (n\theta )+{\hat{e}}_n\sin (n\theta )$$

and

$$i_{\text{ss}}(\theta )=i_0+\sum _{n\ge 1}{i}_n\cos (n\theta )+{\hat{ı}}_n\sin (n\theta )$$

respectively. At steady‐state, (10) simplifies to

$$\begin{array}{rl}& k=\left(e_0+\sum _{n\ge 1}{e}_n\cos (n\theta )+{\hat{e}}_n\sin (n\theta )\right)\\ & -D\left(\sum _{n\ge 1}{n}^2{i}_n\cos (n\theta )+n^2{\hat{ı}}_n\sin (n\theta )\right)\end{array}$$

Because the cosine and sine terms are orthogonal, if follows that e ₀ = k, e_n = Dn ² i_n and ${\hat{e}}_n=D{n}^2{\hat{ı}}_n$, for n ≥ 1. Note that this means that the coefficients of the inhibitor must decay at least n ² times faster than those of the excitation. We can now solve for these coefficients using (9), evaluated at steady state. In particular

$$\begin{array}{rl}{u}_0+u_1\cos \theta & =e_{\text{ss}}(\theta )i_{\text{ss}}(\theta )\\ & =\left(e_0+\sum _{n\ge 1}{e}_n\cos (n\theta )+{\hat{e}}_n\sin (n\theta )\right)\\ & \times \left(i_0+\sum _{n\ge 1}{i}_n\cos (n\theta )+{\hat{ı}}_n\sin (n\theta )\right)\end{array}$$

In general, an analytic solution of this equation is impractical. However, we take advantage of the fact that the terms are decreasing rapidly. Using the identities

$$\begin{array}{rl}{\cos }^2\theta & =\frac{1}{2}(1+\cos 2\theta )\\ {\sin }^2\theta & =\frac{1}{2}(1-\cos 2\theta )\\ \sin \theta \cos \theta & =\frac{1}{2}\sin 2\theta \end{array}$$

and dropping higher order terms leads to the following

$$\begin{array}{rl}& u_0+u_1\cos \theta \simeq e_0{i}_0+\frac{1}{2}[e_1{i}_1+{\hat{e}}_1{\hat{ı}}_1]\\ & +[e_0{i}_1+e_1{i}_0]\cos \theta +[e_0{\hat{ı}}_1+{\hat{e}}_1{i}_0]\sin \theta \\ & =k{i}_0+\frac{D}{2}[i_1^2+{\hat{ı}}_1^2]+[k{i}_1+D{i}_0{i}_1]\cos \theta +[k{\hat{ı}}_1+D{i}_0{\hat{ı}}_1]\sin \theta \end{array}$$

From orthogonality of the sinusoidal terms, we have three (non‐linear) equations in three unknowns

$$u_0=k{i}_0+\frac{D}{2}\left[i_1^2+{\hat{ı}}_1^2\right]$$ (11)

$$u_1=k{i}_1+D{i}_0{i}_1$$ (12)

$$0=k{\hat{ı}}_1+D{i}_0{\hat{ı}}_1$$ (13)

Note that the last equation can be rewritten as

$$(k+D{i}_0){\hat{ı}}_1=0$$

from which it follows that either k + Di ₀ = 0 or ${\hat{ı}}_1=0$. If the former is true then, by (12)

$$u_1=(k+D{i}_0)i_1$$

is impossible. Thus, ${\hat{ı}}_1=0$ and we are left with two equations, which we write in terms of e ₁ and i ₀

$$\begin{array}{rl}{u}_0& =k{i}_0+\frac{1}{2D}{e}_1^2\\ u_1& =\frac{k}{D}{e}_1+i_0{e}_1\end{array}$$

Isolating i ₀ in the equations and equating the two expressions leads to the following equation for e ₁

$$e_1^3-2(k^2+D{u}_0)e_1+2Dk{u}_1=0$$ (14)

Equation (14) is a cubic equation. In general, the number of real solutions is dictated by the discriminant

$$\mathrm{\Delta }=32(k^2+D{u}_0){}^3-27(2Dk{u}_1){}^2$$

If Δ is less than zero, then there is only one real solution for (14) but this is negative by the law of Descartes. When Δ > 0, there are three real roots, of which one is negative and two positive. Note that this imposes limits on the size of u ₁ relative to u ₀ or on the size of D relative to k. In particular, if u ₁ = 0, we obtain three solutions. The first, e ₁ = 0 matches our spatially homogeneous case. Of the other two, one is negative, and hence not physical. The other is positive and equals $e_1=\sqrt{2(k^2+D{u}_0)}$. However, for i ₀ > 0 to hold we require that

$$e_1^2<2D{u}_0$$

which is violated by this second positive equation. Thus, only one solution is physically valid. Similarly, in the limit D → ∞, the cubic equation simplifies to the linear case, and

$$e_1=k\frac{u_1}{u_0}$$

implying that the system reflects the local/global ratio of the spatially graded stimulus.